P.S.
Конечно, навряд ли можно научиться дифференцировать функции, используя исключительно Wolfram|Alpha. Однако, система Wolfram|Alpha вполне подходит, чтобы проверить свои знания, освежить их, например, перед экзаменом, и убедиться, что вы к нему вполне готовы.
Преподавателям Wolfram|Alpha поможет оценить сложность и время на выполнение заданий на производные, которые предлагаются студентам.
Новое в Wolfram Language | Аналитическое решение уравнений в частных производных / Блог компании Wolfram Research / Хабр
Перевод поста Devendra Kapadia «New in the Wolfram Language: Symbolic PDEs».
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации.
Уравнения в частных производных (УрЧП) играют очень важную роль в математике и ее приложениях. Их можно использовать для моделирования реальных явлений, таких как колебания натянутой струны, распространения потока тепла в стержне, в финансовых областях.
История УрЧП восходит к работам известных математиков восемнадцатого века — Эйлера, Даламбера, Лапласа, однако развитие этой области в последние три столетия так и не остановилось. И потому в статье я приведу как классические, так и современные примеры УрЧП, что позволит рассмотреть эту область знаний под разными углами.
Давайте начнем с рассмотрения колебаний натянутой струны с длиной π, закрепленной на обоих концах. Колебания струны можно смоделировать с помощью одномерного волнового уравнения, приведённого ниже. Здесь u(x,t) — вертикальное смещение точки струны с координатой х в момент времени t
:
Затем мы задаём граничные условия, указав тем самым, что концы струны при колебаниях сохраняют свои положения.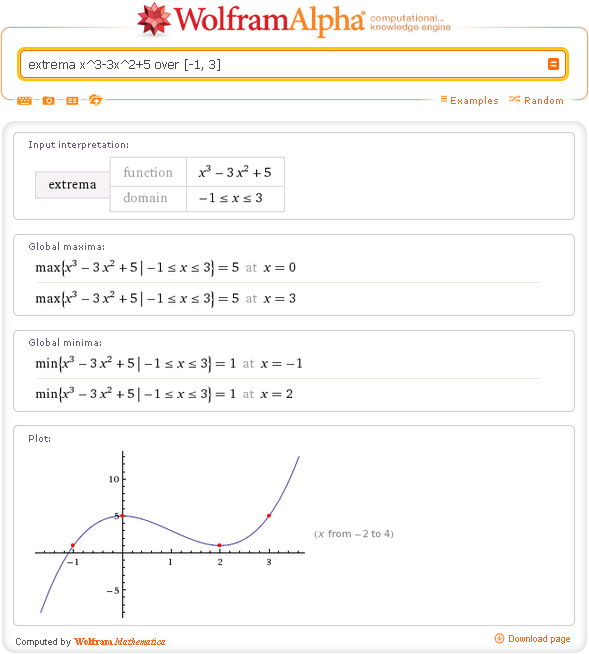
Зададим теперь начальные условия для движения струны, указав смещения и скорости различных точек струны в момент времени t=0:
Теперь мы можем использовать DSolve для решения волнового уравнения с начальными и краевыми условиями:
Как указано выше, решение есть бесконечная сумма тригонометрических функций. Сумма возвращается в невычисленной форме (Inactive), поскольку каждый отдельный член разложения имеет физическую интерпретацию, и зачастую даже небольшое количество членов может являться хорошим приближением. К примеру, мы можем взять первые четыре члена для получения приближенного решения asol(x,t)
Каждый член в сумме представляет собой стоячую волну, которые могут быть представлены следующим образом:
И все эти стоячие волны складываются воедино, образуя гладкую кривую, как показано на анимации ниже:
Волновое уравнение относится к классу линейных гиперболических уравнений в частных производных, описывающих распространение сигналов с конечными скоростями.
Это УрЧП представляет собой удобный способ для моделирования колебаний в струне или в каком-то другом деформирумом теле, однако ещё более важную роль оно играет в современной физике и инженерных приложениях, т.к. оно описывает распространение света и электромагнитных волн.
Давайте теперь смоделируем поток тепла в стержне единичной длины, изолированном с обоих концов, с помощью представленного ниже уравнения теплопроводности:
Поскольку стержень изолирован с обоих концов, то через них проходит нулевой поток тепла, что можно выразить как граничные условия вида х = 0 и х = 1:
Теперь нужно указать начальное температурное распределение в стержне. В этом примере мы будем использовать приведённую ниже линейную функцию. В левом конце (х = 0) начальная температура — 20 градусов, в правом (х = 1) — 100:
И теперь мы можем решить уравнение теплопроводности с заданными условиями:
Как и в приведённом выше примере с волновым уравнением, мы можем извлечь несколько членов суммы и получить приближенное решение:
Первый член приближенного решения — 60 — среднее от температур на границах стержня, и она является стационарной температурой для этого стержня.
Как показано на графике функции температуры от длины, представленном ниже, температура стержня быстро достигает стационарного значения в 60 градусов:
Уравнение теплопроводности относится к классу линейных параболических уравнений в частных производных, которые описывают процессы диффузии. Это простое на вид уравнение часто можно встретить в самых различных, а иногда и весьма неожиданных областях. Далее в статье мы рассмотрим два примера этого явления.
Рассмотрим теперь уравнение Лапласа, которое используется для моделирования стационарного состояния систем, т. е. поведения после некоторых зависящих от времени уже законченных переходных процессов. В двумерном случае это уравнение можно представить следующим образом:
Ограничим координаты х и у прямоугольной областью Ω, как показано ниже:
Классическая задача Дирихле — найти функцию u(x,y), удовлетворяющую уравнению Лапласа внутри области Ω с заданным условием Дирихле (DirichletCondition), которое определяет значения на границах области Ω, как показано ниже:
Задачу Дирихле можно решить с помощью функции DSolve, весьма изящно задав при этом область:
Как и в примерах ранее, мы можем извлечь некоторое количество членов (скажем, 100) из суммы и визуализировать решение:
Следует заметить, что решение u(x,y) задачи Дирихле представляется гладким в Ω, несмотря на то, что граничные условия имеют резкие черты.
Помимо этого, u(x,y) достигает экстремальных значений на границах, в то время как в центре прямоугольника находится седловая точка. Эти черты характерны для линейных эллиптических уравнений — класса уравнений в частных производных, к которым и принадлежит уравнение Лапласа.
Волновое уравнение, уравнение теплопроводности, уравнение Лапласа — самые известные примеры классических УрЧП. Теперь мы рассмотрим три примера типичных современных УрЧП, первым среди которых будет уравнение Бюргерса для вязкой жидкости, которое может быть представлено следующим образом:
Это нелинейное УрЧП было введено Иоханнесом Бюргерсом в сороковых годах в качестве простой модели для турбулентных потоков (параметр ϵ в уравнении представляет собой вязкость жидкости). Однако, десять лет спустя, Э. Хопф и Д. Коул показали, что уравнение Бюргерса сводится к уравнению теплопроводности, а это значит, что данное уравнение не может проявлять хаотического поведения. Преобразование Коула-Хопфа позволяет решать уравнения Бюргерса в замкнутой форме для начального условия, заданного, к примеру, так:
В этом примере мы будем использовать функцию DSolveValue, которая возвращает только выражение для решения.
Члены с функцией ошибок (Erf) в формуле ниже возникают из решения соответствующей граничной задачи теплового уравнения:
Представленный ниже график демонстрирует изменение во времени гипотетического одномерного поля скоростей потока. Решение представляется гладким для положительного ϵ, при том что начальное условие есть кусочно заданная функция:
Как можно заметить на нижепреведённых графиках, решение стремится к разрывному при сремлении вязкости ϵ к нулю. Подобные решения с резким переходом (shock solutions) — известная особенность уравнений Бюргерса для невязкой (ϵ = 0) среды.
В качестве второго примера современных УрЧП рассмотрим уравнение Блэка-Шоулза, используемое в финансовых расчётах. Это уравнение впервые представили Фишер Блэк и Майрон Шоулз в 1973 году в качестве модели для определения теоретической цены на европейские опционы, и формулируется оно следующим образом:
где:
c — цена опциона как функция от стоимости акций s и времени t,
r — процентная ставка без риска,
σ — волатильность акций.
В их эпохальной статье (которая была процитирована более 28000 раз), Блэк и Шоулз отметили, что их уравнения с помощью преобразования переменных могут быть сведены к уравнению теплопроводности. Это резкое упрощение приводит к знаменитой формуле Блэка-Шоулза для европейских опционов с конечными условиями, основанными на цене исполнения (strike price) k актива в момент времени t=Т:
Вооружившись этой формулой, мы можем вычислить значения финансовых опционов для типичных значений параметров:
Ответ согласуется со значением, полученным с помощью встроенной функции FinancialDerivative:
В качестве третьего примера современных УрЧП рассмотрим уравнение Шредингера для электрона в одномерной потенциальной яме с глубиной d и соответствующим начальным условием. Уравнение и условия можно сформулировать следующим образом:
Этот пример имеет элементарное решение, которое принимает мнимые значения из-за наличия I в уравнении Шредингера:
Функция плотности вероятности для электрона ρ = Ψ⊹ Ψ, с использованием подходящих значений параметров в задаче, может быть вычислена следующим образом:
Мы можем создать анимацию изменения плотности вероятности во времени, которая показывает, что «центр» электрона в яме движется из стороны в сторону:
youtube.com/embed/WuiCjqWkxiA?feature=oembed» frameborder=»0″ allowfullscreen=»»/>
Собственные значения и собственные функции играют важную роль как в решении уравнения Шрёдингера, так и в других УрЧП. В частности, они предоставляют «строительные блоки» для решений волновых уравнений и уравнений теплопроводности в виде бесконечных сумм, которые приводились ранее в статье. Поэтому, в качестве нашего последнего примера рассмотрим задачу о нахождении девяти наименьших собственных значений и собственных функций для
Новая функция DEigensystem в версии 10.3 позволяет вычислить требуемые собственные значения и функции следующим образом:
Собственные значения в этой задаче выражаются через BesselJZero. Вот пример:
Собственные значения можно визуализировать с помощью функции DensityPlot3D, которая возвращает красивые графики, как показано ниже:
УрЧП являются важным инструментом во многих отраслях науки и техники, в статистике и финансах.
На более фундаментальном уровне они предоставляют точные математические формулировки некоторых самых глубоких и тонких вопросов о нашей Вселенной, скажем, о возможности существования голых сингулярностей. По моему опыту, изучение УрЧП награждает редким сочетанием из практических идей и интеллектуального удовлетворения.
Рекомендую изучить документацию по DSolve, NDSolve, DEigensystem, NDEigensystem и методу конечных элементов, чтобы узнать больше о различных подходах к решению УрЧП в Wolfram Language.
УрЧП в символьной форме поддерживаются в Wolfram Mathematica и Wolfram Language с версии 10.3, а в ближайшее время будут представлены и во всех остальных программных продуктах Wolfram.
Новые производные функций Бесселя выведены с помощью языка Wolfram Language
Почти через двести лет после того, как Бессель ввёл свои одноименные функции, были найдены выражения для их производных по параметрам, справедливые во всей комплексной плоскости
В этом блоге мы приведём и прокомментируем некоторые ранее неизвестные производные специальных функций (в первую очередь функций Бесселя и связанных с ними функций), а также коснёмся истории и текущего состояния дифференцирования по параметрам гипергеометрических и других функций.
Одной из основных новых формул (более подробно ниже) является замкнутое выражение для первой производной одной из самых популярных специальных функций — функции Бесселя J:
Многие функции математической физики (то есть функции, которые часто используются и поэтому имеют специальные названия) зависят от нескольких переменных. Один из них, как правило, называется аргументом, в то время как другие, как правило, называются параметрами или иногда индексами (значками). Эти специальные функции могут иметь любое количество параметров. Например (см. Wolfram Functions Site), функции Бесселя (z) и (z), Неймана (z), Макдональда (z), и Струве (z) и (z) имеют только один параметр (так называемый индекс), в то время как функции Уиттекера (z) и (z), а также вырожденные гипергеометрические функции (a;b;z) и U(a,b,z) имеют два параметра. Функции Aнгера (z) и (z), а также функции Вебера (z) и (z) могут иметь один или два параметра (в случае двух параметров они называются обобщенными функциями Ангера и Вебера).
Функции Аппеля и Гумберта имеют от трех до пяти параметров, в то время как более сложные специальные функции, такие как обобщенная гипергеометрическая функция , могут иметь любое конечное количество параметров.
Среди других свойств, дифференцирование специальных функций играет существенную роль, так как производные характеризуют поведение функций при изменении этих переменных, и они также важны для изучения дифференциальных уравнений этих функций. Как правило, дифференцирование специальной функции по ее аргументу не представляет существенных трудностей. Самая большая коллекция таких производных, включающая первую, вторую, символьную и даже дробного порядка для более чем 200 функций доступна в разделе “Differentiation” (Дифференцирование) на сайте Wolfram Functions (скажем, эта секция включает в себя выражения для 21 производной функции Бесселя (z)), или в книге Ю. А. Брычкова Handbook of Special Functions). Большинство этих формул также доступны непосредственно в языке Wolfram Language.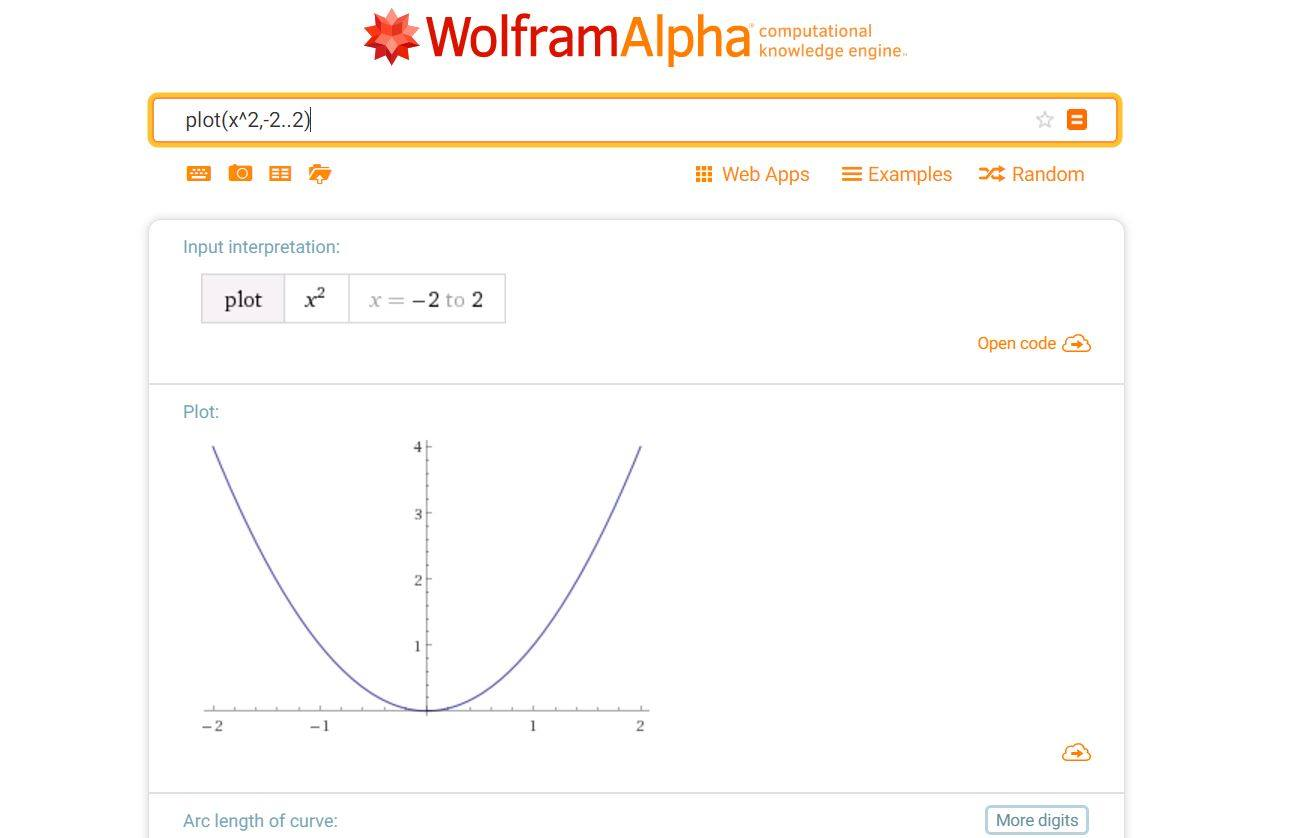
Их можно получить с помощью новых функций MathematicalFunctionData и EntityValue.
Однако производные по параметрам (в отличие от аргумента) в общем случае вычислить гораздо сложнее. Примечательно, что приведённая выше формула, включающая производную первого порядка (относительно параметра ν) одной из наиболее часто встречающихся специальных функций математической физики, лишь недавно была найдена в замкнутом виде, и этот, может быть, удивительный факт говорит о сложности общей задачи. Таким образом, с помощью функции Бесселя J в качестве характерного примера, мы предпримем краткую экскурсию по истории дифференцирования этой специальной функции.
Вычисление производных не всегда просто
Часто люди, даже хорошо знакомые с математическим анализом, склонны думать, что интегрировать трудно, а дифференцировать легко. Известна “народная” мудрость, гласящая, что “дифференцирование — дело техники, а интегрирование — это искусство”. Но это высказывание полностью справедливо только для элементарных функций, для которых дифференцирование приводит снова к элементарным функциям (или их комбинациям).
Если же дифференцирование проводится по параметрам, оно, как правило, приводит к сложным функциям более общего класса.Различие между дифференцированием по параметрам и дифференцированием по аргументу может быть проиллюстрировано на функции Бесселя J. Производная Бесселя J по ее аргументу z была известна в течение достаточно долгого времени и имеет относительно простой замкнутый вид:
Однако аналитическое вычисление её производной по параметру ν является более сложным. Часто производные по параметрам могут быть записаны в виде интеграла или бесконечного ряда, но эти объекты не могут быть представлены в замкнутой форме через другие простые или известные функций. Исторически сложилось, что некоторые специальные функции были введены с единственной целью — дать простое обозначение для производных известных функций. Например, полигамма-функция возникла как средство для представления производных гамма-функции.
Обобщенная гипергеометрическая функция и её производные играют существенную роль в решении различных задач теоретической и прикладной математики (см.
, например, статью L. U. Ancarani и G. Gasaneo относительно применения производных по параметрам в квантовой механике). Обобщенная гипергеометрическая функция порождает в качестве частных случаев многие из наиболее часто используемых элементарных функций (например, тригонометрические, гиперболические, логарифмические, и обратные тригонометрические функции), а также многие специальные функции, в том числе функции Бесселя, Струве, Кельвина, Ангера-Вебера, неполную гамма-функцию и интегральные функции (показательную, синус и косинус). В случае, если p=0, q=1, обобщенная гипергеометрическая функция содержит семейство функций Бесселя (z), (z), (z), и (z). Функция Бесселя J, например, имеет следующее гипергеометрическое представление:
Интересно, что история функции (z) начинается почти ровно 200 лет назад. В докладах Берлинской академии за 1816-17 годы (опубликовано в 1819 г.), в работе Analytische Auflösung der Keplerschen Aufgabe, Фридрих Вильгельм Бессель рассматривает так называемое уравнение Кеплера M=E-e sin(E), где M — средняя аномалия, E — эксцентрическая аномалия, а e — эксцентриситет кеплеровской орбиты. Решение этого уравнения может быть представлено (в современной записи) через функции Бесселя целого порядка:
В этой первой работе Бессель ещё не использует современные обозначения, но его функция появляется уже в неявном виде. Например, он использует следующую сумму (обратите внимание, что Бессель использует обозначение Гаусса для i!):
В наше время мы можем записать это выражение в виде суммы двух функций Бесселя на языке Wolfram Language следующим образом:
Эта сумма как раз и является первой производной функции Бесселя -2 a e (e i):
В своей следующей работе в 1824 г. Бессель использует почти современные обозначения (замена J I) для обозначения своей функции:
Он также выводит фундаментальные соотношения для этой функции, такие как:
Различные специальные случаи общей функции Бесселя встречаются уже в трудах Бернулли, Эйлера, Даламбера и других (подробнее см. статью). Основным справочником по функциям Бесселя по сей день остается классическая монография Г. Н. Ватсона “Теория бесселевых функций”, которая была многократно переиздана и существенно дополнена по сравнению с первым изданием 1922 г.
Таким образом, в то время как производные функции Бесселя J относительно аргумента z были известны с начала девятнадцатого века, только к середине двадцатого века были найдены частные случаи для производных по индексу. Производные некоторых функций Бесселя по ν в точках ν=0,1,2,… и ν=1/2 были даны Дж. Р. Эйри в 1935 году, а выражения для других функций семейства Бесселя в этих точках — в книге В. Магнуса, Ф. Бейтмена и Р. П. Сони “Формулы и теоремы для специальных функций математической физики“ (1966):
Обобщение на любые полуцелые значения ν было представлено на Международной конференции по абстрактному и прикладному анализу (Ханой, 2002) в следующем виде:
Эти результаты, наряду с выражениями для производных по параметру функций Струве в целых и полуцелых точках, были опубликованы в 2004-2005 гг. Различные новые формулы для дифференцирования по параметрам функций Ангера и Вебера, функций Кельвина, неполных гамма-функций, функции параболического цилиндра, функций Лежандра и Гаусса, обобщенных и вырожденных гипергеометрических функций можно найти в “Справочнике по специальным функциям: Производные, интегралы, ряды и другие формулы”. Краткий обзор и ссылы см. H. Cohl.
Вероятно, покажется удивительным, что при наличии всех этих результатов, первые производные функций Бесселя в замкнутом виде при произвольных значениях параметра были получены только в 2015 г. (Ю. А. Брычков, ”Высшие производные функций Бесселя относительно индекса“, 2016 г.). Они выражаются в виде комбинаций произведений функций Бесселя и обобщенных гипергеометрических функций. Например:
Графики ниже дают некоторое представление о поведении функции Бесселя (z) и ее производной в областях, представляющих интерес. Во-первых, мы приводим (в действительной ν—z-плоскости) выражение для первой производной от (z) по ν (см. уравнение в начале статьи):
Для фиксированного индекса, а именно ν=π, мы приводим графики функции Бесселя вместе со своими первыми двумя производными (по аргументу и индексу):
Интересно отметить, что производные (по z и по ν) имеют почти совпадающие нули.
Как мы получили это?
Примечательно, что даже почти через 300 лет после введения классической функции (функция Бесселя (z) была введена Даниилом Бернулли в 1732 г.), по-прежнему можно найти новые и относительно простые формулы, относящиеся к таким функциям. Фактически формулы для введенной выше производной (вместе с соответствующими результатами для производной , и функций Неймана, Макдональда и Кельвина) были получены с помощью языка Wolfram Language. Подробная информация о том, как искались эти производные опубликована здесь. В этом посте мы приведём лишь набросок одного из вариантов подхода, который может быть использован и для других специальных функций.
Во-первых, напомним, что функции Бесселя и другие, которыми мы сейчас интересуемся, являются функциями гипергеометрического типа; но дифференцирование по параметрам общей гипергеометрической функции одной переменной требует более сложных функций гипергеометрического типа более чем одной переменной (см. статью L. U. Ancarani и G. Gasaneo). Первая производная по отношению к “верхним” параметрам , и все производные символьного целого порядка m по отношению к “нижним” параметрам обобщенной гипергеометрической функции, могут быть выражены в терминах гипергеометрической функции Кампе де Ферье двух переменных по следующим формулам:
Вышеуказанная гипергеометрическая функция Кампе де Ферье определяется двойным рядом (см. здесь и здесь):
Функцию Кампе де Ферье можно рассматривать как обобщение гипергеометрической функции на две переменные:
Соответствующая регуляризованная версия функции также может быть определена путем замены произведения символов Похгаммера в знаменателе на .
Функция Кампе де Ферье может быть использована для представления производных функции Бесселя J по параметру:
Это выражение совпадает с простой формулой выше, которая включает в себя гипергеометрические функции одной переменной, хотя это сразу не очевидно (мы пока ещё не имеем полного набора формул для упрощения многомерных гипергеометрических функций до выражений, содержащих только одномерные гипергеометрические функции).
Двойные ряды, аналогичные приведенному выше определению обобщенной гипергеометрической функции двух переменных, также возникают при вычислении преобразования Меллина от произведений трех G-функций Мейера:
Правая часть этой формулы включает в себя G-функцию Мейера двух переменных, которая в общем (нелогарифмическом) случае может быть представлена в виде конечной суммы гипергеометрических функций Кампе де Ферье с некоторыми коэффициентами, по аналогии с двумя формулами (первая, вторая) для G-функции Мейера одной переменной. Наконец, функция Кампе де Ферье также возникает при разделении действительной и мнимой частей гипергеометрических функций от одной переменной, z = x+iy, с действительными параметрами:
(вышеприведенная формула была выведена Э. Д. Крупниковым, но не опубликована).
Следует отметить, что в последние годы гипергеометрические функции многих переменных находят все большее число приложений в таких областях, как квантовая теории поля, химия, машиностроение, теория связи и радиолокации. Многие практические результаты могут быть представлены с использованием таких функций, и поэтому большинство основных результатов в этой области получены в прикладной научной литературе. Теория таких функций в теоретической математике до сих пор разработана относительно слабо.
Символьные производные в языке Wolfram Language
Автор этих новых и интересных формул с символьными производными, Юрий Брычков, является членом нашей команды, что позволяет нам довести эту постоянно развивающуюся область математики до внимания наших пользователей. Нам также повезло, что в нашем распоряжении имеется новая функция системы Mathematica (языка Wolfram Language) — Entity, которая позволяет, помимо прочего, быстро (в течение нескольких недель или дней) представлять новые результаты в вычисляемом формате и на всех платформах, где используется язык Wolfram Language, нашим пользователям. Например, в системе Mathematica, можно вычислитьследующее выражение:
Тем самым мы получаем основную формулу этой статьи. Мы можем проверить формулу численно, подставив сначала символьные значения ν и z, и получив выражение:
Далее, мы отделяем левую и правую части и подставляем случайные значения для аргумента и параметра:
Численная производная от левой части вычисляется в языке Wolfram Language с помощью предельной процедуры. Равенство левой и правой частей, и, следовательно, правильность исходной формулы для производной очевидны.
Помимо множества новых результатов относительно символьных и параметрических производных, которые упоминались в этой статье и доступны только через EntityValue (хотя более глубокая интегрирация этого функционала в будущих версиях языка Wolfram Language требует постоянных усилий), большое количество результатов в этой области уже было имплементировано в ядро системы Mathematica и ядро языка Wolfram Language. Такие производные по параметрам не вычисляются автоматически по причине их сложности, но их можно увидеть, используя команду FunctionExpand. Например:
Производные по индексу второго и более высокого порядка функций Бесселя и связанных с ними функций могут быть выражены в терминах гипергеометрической функции Кампе де Ферье двух переменных , но полученные формулы могут быть довольно сложными, и могут включать в себя полиномы Белла Y:
Последнее выражение возникает из представления функции Бесселя (z) через композицию функции (;ν+1;w) и :
Мы используем формулу Фаа-ди-Бруно, которая позволяет получить выражение n-й производную композиции m функций . В случае m = 2 (см. здесь и здесь), мы получаем, например, выражение:
Соответствующая формула для общих m и n может быть получена и проверена в языке Wolfram Language:
В то время как многочлены Белла Y, для которых не существует общего замкнутого вида, как правило, необходимы для представления производных высшего порядка, один из авторов этого поста, Юрий Брычков, нашел способ устранить многочлены Y из n-х производных по параметру функций Бесселя, оставляя нас с замечательным результатом:
Для удобства заинтересованных пользователей, которые хотели бы видеть в одном месте все известные формулы для производных специальных функций по параметрам (в том числе те, которые перечислены выше), мы собрали и представили эти форм
Новое в Wolfram Language | Аналитическое решение уравнений в частных производных / Wolfram Research corporate blog / Habr
Перевод поста Devendra Kapadia «New in the Wolfram Language: Symbolic PDEs».
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации.
Уравнения в частных производных (УрЧП) играют очень важную роль в математике и ее приложениях. Их можно использовать для моделирования реальных явлений, таких как колебания натянутой струны, распространения потока тепла в стержне, в финансовых областях. Цель этой статьи — приоткрыть завесу в мир УрЧП (тем кто еще с ним не знаком) и ознакомить читателя с тем, как можно эффективно решать УрЧП в Wolfram Language, используя новый функционал для решения краевых задач в DSolve, а так же новую функцию DEigensystem, которая появилась в версии 10.3.
История УрЧП восходит к работам известных математиков восемнадцатого века — Эйлера, Даламбера, Лапласа, однако развитие этой области в последние три столетия так и не остановилось. И потому в статье я приведу как классические, так и современные примеры УрЧП, что позволит рассмотреть эту область знаний под разными углами.
Давайте начнем с рассмотрения колебаний натянутой струны с длиной π, закрепленной на обоих концах. Колебания струны можно смоделировать с помощью одномерного волнового уравнения, приведённого ниже. Здесь u(x,t) — вертикальное смещение точки струны с координатой х в момент времени t:
Затем мы задаём граничные условия, указав тем самым, что концы струны при колебаниях сохраняют свои положения.
Зададим теперь начальные условия для движения струны, указав смещения и скорости различных точек струны в момент времени t=0:
Теперь мы можем использовать DSolve для решения волнового уравнения с начальными и краевыми условиями:
Как указано выше, решение есть бесконечная сумма тригонометрических функций. Сумма возвращается в невычисленной форме (Inactive), поскольку каждый отдельный член разложения имеет физическую интерпретацию, и зачастую даже небольшое количество членов может являться хорошим приближением. К примеру, мы можем взять первые четыре члена для получения приближенного решения asol(x,t)
Каждый член в сумме представляет собой стоячую волну, которые могут быть представлены следующим образом:
И все эти стоячие волны складываются воедино, образуя гладкую кривую, как показано на анимации ниже:
Волновое уравнение относится к классу линейных гиперболических уравнений в частных производных, описывающих распространение сигналов с конечными скоростями. Это УрЧП представляет собой удобный способ для моделирования колебаний в струне или в каком-то другом деформирумом теле, однако ещё более важную роль оно играет в современной физике и инженерных приложениях, т.к. оно описывает распространение света и электромагнитных волн.
Давайте теперь смоделируем поток тепла в стержне единичной длины, изолированном с обоих концов, с помощью представленного ниже уравнения теплопроводности:
Поскольку стержень изолирован с обоих концов, то через них проходит нулевой поток тепла, что можно выразить как граничные условия вида х = 0 и х = 1:
Теперь нужно указать начальное температурное распределение в стержне. В этом примере мы будем использовать приведённую ниже линейную функцию. В левом конце (х = 0) начальная температура — 20 градусов, в правом (х = 1) — 100:
И теперь мы можем решить уравнение теплопроводности с заданными условиями:
Как и в приведённом выше примере с волновым уравнением, мы можем извлечь несколько членов суммы и получить приближенное решение:
Первый член приближенного решения — 60 — среднее от температур на границах стержня, и она является стационарной температурой для этого стержня. Как показано на графике функции температуры от длины, представленном ниже, температура стержня быстро достигает стационарного значения в 60 градусов:
Уравнение теплопроводности относится к классу линейных параболических уравнений в частных производных, которые описывают процессы диффузии. Это простое на вид уравнение часто можно встретить в самых различных, а иногда и весьма неожиданных областях. Далее в статье мы рассмотрим два примера этого явления.
Рассмотрим теперь уравнение Лапласа, которое используется для моделирования стационарного состояния систем, т. е. поведения после некоторых зависящих от времени уже законченных переходных процессов. В двумерном случае это уравнение можно представить следующим образом:
Ограничим координаты х и у прямоугольной областью Ω, как показано ниже:
Классическая задача Дирихле — найти функцию u(x,y), удовлетворяющую уравнению Лапласа внутри области Ω с заданным условием Дирихле (DirichletCondition), которое определяет значения на границах области Ω, как показано ниже:
Задачу Дирихле можно решить с помощью функции DSolve, весьма изящно задав при этом область:
Как и в примерах ранее, мы можем извлечь некоторое количество членов (скажем, 100) из суммы и визуализировать решение:
Следует заметить, что решение u(x,y) задачи Дирихле представляется гладким в Ω, несмотря на то, что граничные условия имеют резкие черты. Помимо этого, u(x,y) достигает экстремальных значений на границах, в то время как в центре прямоугольника находится седловая точка. Эти черты характерны для линейных эллиптических уравнений — класса уравнений в частных производных, к которым и принадлежит уравнение Лапласа.
Волновое уравнение, уравнение теплопроводности, уравнение Лапласа — самые известные примеры классических УрЧП. Теперь мы рассмотрим три примера типичных современных УрЧП, первым среди которых будет уравнение Бюргерса для вязкой жидкости, которое может быть представлено следующим образом:
Это нелинейное УрЧП было введено Иоханнесом Бюргерсом в сороковых годах в качестве простой модели для турбулентных потоков (параметр ϵ в уравнении представляет собой вязкость жидкости). Однако, десять лет спустя, Э. Хопф и Д. Коул показали, что уравнение Бюргерса сводится к уравнению теплопроводности, а это значит, что данное уравнение не может проявлять хаотического поведения. Преобразование Коула-Хопфа позволяет решать уравнения Бюргерса в замкнутой форме для начального условия, заданного, к примеру, так:
В этом примере мы будем использовать функцию DSolveValue, которая возвращает только выражение для решения. Члены с функцией ошибок (Erf) в формуле ниже возникают из решения соответствующей граничной задачи теплового уравнения:
Представленный ниже график демонстрирует изменение во времени гипотетического одномерного поля скоростей потока. Решение представляется гладким для положительного ϵ, при том что начальное условие есть кусочно заданная функция:
Как можно заметить на нижепреведённых графиках, решение стремится к разрывному при сремлении вязкости ϵ к нулю. Подобные решения с резким переходом (shock solutions) — известная особенность уравнений Бюргерса для невязкой (ϵ = 0) среды.
В качестве второго примера современных УрЧП рассмотрим уравнение Блэка-Шоулза, используемое в финансовых расчётах. Это уравнение впервые представили Фишер Блэк и Майрон Шоулз в 1973 году в качестве модели для определения теоретической цены на европейские опционы, и формулируется оно следующим образом:
где:
c — цена опциона как функция от стоимости акций s и времени t,
r — процентная ставка без риска,
σ — волатильность акций.
В их эпохальной статье (которая была процитирована более 28000 раз), Блэк и Шоулз отметили, что их уравнения с помощью преобразования переменных могут быть сведены к уравнению теплопроводности. Это резкое упрощение приводит к знаменитой формуле Блэка-Шоулза для европейских опционов с конечными условиями, основанными на цене исполнения (strike price) k актива в момент времени t=Т:
Вооружившись этой формулой, мы можем вычислить значения финансовых опционов для типичных значений параметров:
Ответ согласуется со значением, полученным с помощью встроенной функции FinancialDerivative:
В качестве третьего примера современных УрЧП рассмотрим уравнение Шредингера для электрона в одномерной потенциальной яме с глубиной d и соответствующим начальным условием. Уравнение и условия можно сформулировать следующим образом:
Этот пример имеет элементарное решение, которое принимает мнимые значения из-за наличия I в уравнении Шредингера:
Функция плотности вероятности для электрона ρ = Ψ⊹ Ψ, с использованием подходящих значений параметров в задаче, может быть вычислена следующим образом:
Мы можем создать анимацию изменения плотности вероятности во времени, которая показывает, что «центр» электрона в яме движется из стороны в сторону:
Собственные значения и собственные функции играют важную роль как в решении уравнения Шрёдингера, так и в других УрЧП. В частности, они предоставляют «строительные блоки» для решений волновых уравнений и уравнений теплопроводности в виде бесконечных сумм, которые приводились ранее в статье. Поэтому, в качестве нашего последнего примера рассмотрим задачу о нахождении девяти наименьших собственных значений и собственных функций для оператора Лапласа с однородным (нулевым) условием Дирихле для трехмерной сферической области. Найдем девять наименьших значений λ и соответствующих им функций ϕ, удовлетворяющих Λϕ = λ ϕ, которые определяются следующим образом:
Новая функция DEigensystem в версии 10.3 позволяет вычислить требуемые собственные значения и функции следующим образом:
Собственные значения в этой задаче выражаются через BesselJZero. Вот пример:
Собственные значения можно визуализировать с помощью функции DensityPlot3D, которая возвращает красивые графики, как показано ниже:
УрЧП являются важным инструментом во многих отраслях науки и техники, в статистике и финансах. На более фундаментальном уровне они предоставляют точные математические формулировки некоторых самых глубоких и тонких вопросов о нашей Вселенной, скажем, о возможности существования голых сингулярностей. По моему опыту, изучение УрЧП награждает редким сочетанием из практических идей и интеллектуального удовлетворения.
Рекомендую изучить документацию по DSolve, NDSolve, DEigensystem, NDEigensystem и методу конечных элементов, чтобы узнать больше о различных подходах к решению УрЧП в Wolfram Language.
УрЧП в символьной форме поддерживаются в Wolfram Mathematica и Wolfram Language с версии 10.3, а в ближайшее время будут представлены и во всех остальных программных продуктах Wolfram.
Хочу учиться — Wolfram Alpha
Краткий список обозначений и операторов WolframAlpha
для решения задач онлайн
| + | сложение | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | вычитание | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | умножение | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| / | деление | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ^ | возведение в степень | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| solve | решение уравнений, неравенств, систем уравнений и неравенств | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| expand | раскрытие скобок | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| factor | разложение на множители | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sum | вычисление суммы членов последовательности | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| derivative | дифференцирование (производная) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| integrate | интеграл | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| lim | предел | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| inf | бесконечность | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| plot | построить график функции | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| log (a, b) | логарифм по основанию a числа b | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin, cos, tg, ctg | синус, косинус, тангенс, котангенс | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sqrt | корень квадратный | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| pi | число «пи» (3,1415926535.2), {x, 0.5, 2}История вольфрамовых и вольфрамовых проволок от компании Midwest TungstenИстория вольфрамовой и вольфрамовой проволокиШеелитСлово «вольфрам», вероятно, впервые было использовано А. Ф. Кронштедтом в 1755 году, который применил его к минералу, впоследствии известному как «шеелит», который является естественной формой вольфрамата кальция. Леонхард назвал этот минерал шеелитом в 1821 году в знак признания открытия, сделанного К.В. Шееле в 1781 году, о том, что минерал представляет собой соединение извести с ранее неизвестной кислотой, которую он назвал «вольфрамовой кислотой». известный.До того, как Шееле сделал свое открытие, обычно считалось, что этот минерал содержит олово. Слово вольфрам означает вещество с высокой плотностью и происходит от шведского языка: «tung», что означает «тяжелый», и «sten», что означает «камень». ВольфрамВ 1783 году испанские братья Дж. Дж. И Ф. д’Эльхуджар опубликовали результаты своих исследований вольфрамита, проведенных со шведом Т. Бергманном, когда они работали в его лаборатории. Они показали, что этот минерал содержит ту же вольфрамовую кислоту, ранее обнаруженную в шеелите, но в сочетании с железом и марганцем вместо кальция.Они также были первыми, кто зарегистрировал получение элементарного вольфрама, который они получили путем восстановления оксида вольфрама древесным углем и которому дали название «Вольфрам». Происхождение слова вольфрам неясно. Меннике приписывает это алхимикам, которые назвали этот металл «spuma lupi», что означает волчья пена или пена. Другое предположение состоит в том, что это слово имеет немецкое происхождение от слова «волк», что означает хищный зверь, и «рабин» или «баран», что имеет несколько значений, включая грязь и сажу. Это слово также может быть образовано от шведского слова «Wolf rig», что означает еда.Предполагается, что все эти значения связаны с ранними трудностями извлечения олова из касситерита, когда оно было загрязнено вольфрамитом; два минерала часто встречаются вместе, и считалось, что вольфрам ест олово, как волк ест овец. Обычное окончание, используемое в минералогии, чтобы дать минералу название «вольфрамит», было использовано в 1820 году А. Брейтауптом в его книге Kurze Charalderistik des Mineral Systems . Химический знакЭтот металл известен как вольфрам в некоторых странах и как вольфрам в других, включая Швецию, страну происхождения названия вольфрам.Химический символ W , который повсеместно используется для обозначения вольфрама, предполагает, что раньше вольфрам был более общепринятым названием элемента. В Великобритании минерал вольфрамит также известен как вольфрам. Первоначальное использованиеВ течение многих лет вольфрам оставался одним из редких элементов , и только в 1847 году, когда Оксланд получил патент на производство вольфрамата натрия, вольфрамовой кислоты и вольфрама из касситерита (оловянного камня), этот элемент стал любое промышленное значение.Второй патент Оксланда, полученный в 1857 году, описывает производство сплавов железо-вольфрам, которые составляют основу современных быстрорежущих сталей. Однако сам металл не нашел применения почти пятьдесят лет спустя, когда он был впервые использован в производстве нити для электрических ламп накаливания . С 1878 года, когда Свон продемонстрировал в Ньюкасле свои угольные лампы мощностью восемь и шестнадцать свечей, начались поиски более подходящего материала для нити накала, чем углерод. Ранняя углеродная лампа имела КПД около 1.0 люмен на ватт, который был улучшен в течение следующих 20 лет за счет изменений в методах подготовки углерода, примерно до 2,5 люмен на ватт. Дальнейшее улучшение было сделано в 1898 году до примерно 3,0 люмен на ватт за счет электрического нагрева нитей в атмосфере паров нефти, что вызвало отложение углерода в порах нити и придало ей яркий металлический вид. В то же время A. Von Welsbach произвел первую успешную металлическую нить с использованием осмия. Ранее предпринимались попытки использовать платину, но с ее относительно низкой температурой плавления 1774 ° C.помешал его успешному развитию. Лампы с использованием осмиевых нитей имели эффективность около 6,0 люмен на ватт. Поскольку осмий является самым редким из платиновых металлов, его никогда нельзя было использовать в больших масштабах. Тантал с температурой плавления 2996 ° C по сравнению с осмием 2700 ° C широко использовался в качестве тянутой проволоки с 1903 по 1911 год после работы Фон Болтона из Siemens and Halske. Лампы с танталовой нитью имели эффективность около 7,0 люмен на ватт. Разработки в области использования вольфрама начались примерно в 1904 году, и он используется исключительно примерно с 1911 года. Современная лампа накаливания с вольфрамовой нитью , используемая для общего освещения, в которой используется тянутый провод, имеет эффективность около 12 люмен на ватт, тогда как лампы высокой мощности имеют эффективность до 22 люмен на ватт. Современная люминесцентная лампа, хотя и использует вольфрамовые катоды, не зависит от вольфрама из-за ее гораздо более высокой эффективности, которая составляет порядка 50 люмен на ватт. ПроводВ 1904 году компания Siemens-Halske Co. попыталась применить процесс вытяжки, разработанный для тантала, для производства нитей из более тугоплавких металлов, вольфрама, тория и т. Д.Хрупкость и недостаточная пластичность вольфрама помешали им добиться успеха этим методом, хотя позже, в 1913-1914 годах, было продемонстрировано, что плавленый вольфрам можно прокатывать и вытягивать при очень высоких температурах, используя очень небольшие шаги восстановления. Путем зажигания дуги между вольфрамовым стержнем и частично спеченной вольфрамовой таблеткой в графитовом тигле, покрытом изнутри порошком металлического вольфрама и содержащим атмосферу водорода, небольшие кусочки плавленого вольфрама, размером около 10 мм.диаметром и длиной 20-30 мм, с трудностями в обработке. Было обнаружено, что рабочие свойства могут быть в некоторой степени улучшены добавлением оксида тория, который снижает тенденцию к образованию столбчатой структуры во время охлаждения расплавленной массы. Этот процесс никогда не использовался в коммерческих целях. В том же году Just and Hannaman запатентовали процесс производства вольфрамовых нитей путем смешивания тонкоизмельченного металлического порошка с органическим связующим, экструзии через фильеры и нагревания в подходящих газах для удаления связующего, оставляя чистую вольфрамовую нить.В течение 1906–1907 годов был разработан хорошо известный процесс экструзии, с помощью которого в течение следующих четырех или пяти лет производилось большинство вольфрамовых нитей. НитиПроцесс заключался в смешивании очень тонкого черного порошка вольфрама с декстрином или крахмалом с целью образования пластичной массы, которую продавили под гидравлическим давлением через тонкую алмазную головку. Полученная таким образом нить была достаточно прочной, чтобы ее можно было наматывать на карты и сушить. Затем нить нарезали на «шпильки», которые нагревали в инертном газе до красного тепла, чтобы удалить влагу и более легкие углеводороды.Затем каждую «шпильку» закрепляли в зажимах и нагревали до яркого накала при прохождении электрического тока, при этом они были окружены газом, например водородом, выбранным для реакции со связующим материалом, так что оставался только чистый вольфрам. При самой высокой температуре мелкие частицы вольфрама спекались вместе и образовывали твердую однородную металлическую нить. Эти нити, хотя и эластичные, были довольно хрупкими, но им можно было придать форму при красном нагреве. Джаст и Ханнаман одновременно разработали и другой процесс.Этот процесс был известен как «нанесение покрытия» и показал удивительную изобретательность. Углеродная нить размером 0,02 мм. в диаметре использовалась в качестве основы, и она была покрыта вольфрамом, нагревая его до накала в атмосфере водорода и гексахлорида вольфрама. Затем покрытая нить накаливания доводили до яркого накала в водороде при давлении около 20 мм. ртути. Углеродное ядро растворялось в вольфраме, образуя карбид вольфрама, причем изменение было настолько полным, что получившаяся нить была трубчатой в поперечном сечении, без углерода в ядре.Полученная таким образом нить имела блестящий белый вид и была очень хрупкой. Следующий шаг заключался в нагревании нити в водороде, содержащем пар, который окислял углерод и оставлял плотную нить из чистого вольфрама. Полученные таким образом волокна были аналогичны волокнам, полученным способом экструзии, за исключением того, что они были трубчатыми в поперечном сечении. Многие другие процессы производства вольфрамовых нитей появились в последующие годы, но полученный продукт во всех случаях был однотипным, а именно эластичной, но хрупкой вольфрамовой нитью.Среди наиболее важных можно упомянуть коллоидный метод Кузеля, впервые разработанный в 1904 году. По этому методу гелеобразная пастообразная масса металлического вольфрама была приготовлена путем зажигания дуги между вольфрамовыми электродами под водой. Материал не содержал связующей среды, но сам был достаточно пластичным, чтобы его можно было экструдировать в тонкие нити. При нагревании их до высокой температуры в водороде с помощью электрического тока коллоидная масса превращалась в кристаллический металл, и нити во всех отношениях были подобны нитям, полученным с помощью обычного процесса экструзии.Этот метод широко использовался на Европейском континенте и в некоторой степени в Соединенных Штатах. Амальгамный процессЕще один метод, успешно разработанный в Америке в 1906 году, — это процесс амальгамы . Тонкоизмельченный порошок вольфрама механически смешивали с удвоенной массой кадмиево-ртутной амальгамы, из которой путем экструзии были сформированы нитей . Нити были прочными и чрезвычайно пластичными. Затем амальгаму удалили испарением при высокой температуре и получили чистую вольфрамовую нить.Метод, который добился значительного успеха и использовался между 1908 и 1910 годами Siemens and Halske Co., заключался в смешивании порошка металлического вольфрама с 6-10% никеля в виде оксида никеля, прессовании порошка в слитки и спекании в водород при 1575 ° C. Слитки сначала прокатывали до прутка 1 мм. диаметром при 350 ° C, а затем, с частыми отжигами при 1500 — 1600 ° C, вытягивают в холодном состоянии до проволоки толщиной до 0,03 мм. Тянутая проволока была довольно пластичной. Никель удаляли нагреванием готовых нитей в вакууме при 1500 ° C.Полный отчет об этом процессе был дан М. Пирани. Были разработаны и другие процессы, такие как волочение проволоки из танталовых трубок, заполненных вольфрамовым порошком. Однако только в 1909 году Кулиджу в Америке удалось получить пластичный вольфрам из металлического порошка с помощью подходящей термической обработки и механической обработки. Во всех предыдущих процессах использовалось некоторое связующее, органическое или металлическое, для придания необходимой пластичности, которое впоследствии было удалено с помощью химической или термической обработки.Полученные в результате нити были чистым вольфрамом, насколько показал анализ, и все же металл во всех случаях был полностью хрупким. Однако даже эти хрупкие волокна можно сгибать и обрабатывать до некоторой степени при относительно низкой температуре и даже при температурах ниже температуры, при которой происходит окисление. Таким образом, проблема изготовления пластичного вольфрама не заключалась в очистке материала, хотя было понятно, что чистый металл, вероятно, был необходим для получения пластичного продукта.Скорее, проблема была вызвана зеренной структурой самого вольфрама. При первоначальном использовании достаточно высокой температуры было обнаружено, что по мере того, как металл подвергался механической работе, его пластичность увеличивалась, пока, наконец, он не стал настолько пластичным, что его можно было катать или вытягивать в проволоку при комнатной температуре. Хотя только небольшой процент руды, которая поступает на рынок, используется для производства ламп накаливания и аналогичных продуктов, большое значение, которое вольфрам приобрел с научной и технической точки зрения, является результатом работы, направленной на его производство для этой цели.Полученные знания также имеют неоценимое значение для специалистов в новых областях порошковой металлургии, особенно в производстве твердых карбидов. Рассмотрение пройденных этапов развития современных процессов дает некоторое представление о преодоленных трудностях. Дополнительные ресурсы: Свойства вольфрама и Дополнительная информация о вольфраме Что такое вольфрам? (с иллюстрациями)Вольфрам — это металлический химический элемент, относящийся к переходным металлам периодической таблицы элементов.Он хорошо известен своей прочностью и долговечностью, что делает его чрезвычайно полезным в широком спектре промышленных применений. Некоторые потребители также владеют продуктами, содержащими вольфрам или произведенными из металла. Основными мировыми источниками этого элемента являются Россия, Австрия, Китай и Португалия, где он добывается из таких минералов, как шеелит и вольфрамит. Вольфрам используется в качестве нити накаливания в лампах накаливания.Этот элемент в чистом виде не встречается в природе. Когда он изолирован, вольфрам представляет собой очень твердый, хрупкий металл от серого до белого цвета, который чрезвычайно устойчив к коррозии. У него самая высокая точка плавления и предел прочности на разрыв среди всех металлов, а также самая низкая точка давления пара. Металл обозначается символом W в периодической таблице элементов, что является ссылкой на его альтернативное название, вольфрам. Атомный номер вольфрама 74. Из-за его высокой прочности на разрыв и температуры плавления вольфрам используется для изготовления многих тяжелых инструментов.Люди знали о существовании вольфрама по крайней мере с начала 1700-х годов, когда наблюдатели заметили, что металл взаимодействует с оловом. В 1784 году братьям де Эльхуяр удалось выделить его в Испании, используя вольфрамовую кислоту, извлеченную из вольфрамита.Вольфрам традиционно считался очень ценным металлом, поскольку его долговечность и прочность делают его чрезвычайно полезным для использования в военных и промышленных целях. Название элемента происходит от шведского tung , что означает «тяжелый», и sten , что означает «камень». Вольфрам обозначается символом W в периодической таблице элементов, а его атомный номер 74.Одно из самых известных применений вольфрама — это нить накала в лампах. Металл также используется в ряде сплавов для повышения их твердости и прочности на разрыв. Его используют во многих конструкционных металлических сплавах, поскольку металл имеет чрезвычайно высокую температуру плавления, а также этот элемент используется для изготовления износостойких инструментов.Хотя эти инструменты могут быть дорогими, они нравятся многим рабочим из-за их долговечности и долговечности. Tungsten требует некоторых мер безопасности. Пыль от металла может быть легковоспламеняющейся или взрывоопасной, а также раздражать слизистые оболочки, например, внутри носа и рта.В некоторых регионах вольфрам был связан с серьезными инфекциями легких у людей, которые регулярно работают с этим элементом без надлежащей защиты. Воздействие металла также коррелировало с увеличением заболеваемости раком, хотя убедительных доказательств того, что эта корреляция превратилась в причинно-следственную связь, обнаружено не было. Россия — один из основных мировых источников вольфрама.Вольфрам (Вольфрам) Недир? (Озелликлери, Куллаными)Вольфрам, ее ortamda bulunan ampullerin tellerinin üretiminde kullanılan metaldir. Fiziksel özellikleri sebebiyle binlerce ürünün hammaddesidir. Вольфрам, diğer adı volfram olan bir metaldir. Fiziksel yapısı ve özellikleri çok sağlam ve dayanıklıdır. Tungstenden üretilmiş filamanlar (ampul teli), 1900’lü yılların başından bu yana dünyada kullanılmaktadır.Ампул telinden füzelere, torna bıçağından takılara kadar çok farklı alan ve ürünlerde rastladığımız tungsten, adını pek duymasak da her evin en yüksek yerinde odalarımınılakızı. Tungstenin özelliklerinin çelik ve uranyumla kıyaslanması, ne kadar ilginç bir metal olduğunu da ortaya koyuyor. Makalemizde tungstenin tarihinden Türkiye’deki rezervlerine kadar birçok bilgiyi bulabilirsiniz. TarihçesiВольфрам, 1781 yılında yeni bir element olarak tanımlandı ve ilk olarak 1783 yılına izole edildi.1779 yılında İsveç’te bulunan bir Minerali inceleyen Peter Woulfe, yeni bir metal türünü fark etti; ancak bu metali tanımlayamadı. 1781 год yılında İsveçli kimyager Карл Вильгельм Шееле, bu Mineraldeki araştırmaları sırasında bir oksit ürünü elde etti. 1783 yılında ise Jose ve Fausto Elhuyar adlı kardeşler вольфрамитовый минералinden tungsteni izole etti. Bazı kaynaklarda tungstenin kâşifi olarak Scheele, bazılarında ise Elhuyar kardeşler gösteriliyor. Tungstenin keşfinden sonra bazı tarihi gelişmeler ise şöyle;
Fiziksel ve Kimyasal ÖzellikleriВольфрам kimyasal sembolü , bulunduğu Mineralin ismi sebebiyle “W” реж. Номер атома 74, атом ağırlığı 183,85, yoğunluğu 19,25’tir. Erime noktası 3422 derece, kaynama noktası 5555 derecedir. Алашим олмаян металлист, арасында эриме ноктасы ан юксек металдир. Kaynama noktası en yüksek ikinci elementtir. Periyodik cetvelin 6-B grubunda yer alır.Elik grisi veya beyaz rengindedir. ok sert ve ağır bir metaldir . Kristal yapısı kübik olan bir geçiş metalidir. Yoğunluğu sudan yaklaşık 20 kat daha fazladır. Fiziksel özellikleri bakımından molibden ile benzerlik gösterir. Dünyadaki en sert ve sıcaklığa dayanıklı metallerden biridir. Saf tungstenin sertliği birçok çelikten daha yüksektir; ancak kolayca işlenebilir. Sünektir, tel haline getirilebilir, dövülebilir. Колай окситленмез. Aşınmaya karşı direnci yüksektir.Isı ve elektriği iyi düzeyde iletebilir. Genleşme katsayısı düşüktür. 1650 derecenin üzerindeki sıcaklıklarda mukavemeti en yüksek metaldir. Geri dönüştürülebilir. Oksijen, asitler ve alkalilere karşı uzun süre direnç gösterebilir. Hidrojenle 1000 derecede indirgenerek tungsten tozu elde edilir. Doğadaki izotopik özellik gösteren tek metaldir. Яни ее yönde aynı özellikleri gösterir. Tungsten, yerkabuğunda yaklaşık yüzde 0,00011 oranında bulunur. Doğada en yaygın wolframite ve scheelite (şelit) Minerallerinde bulunur.Ekonomik olarak kullanılabilen Mineraller de Bunlardır. Bunun dışında yaklaşık 20 adet tungsten içeren Mineral Bulunur. Doal tungsten, yarılanma ömürleri çok uzun olan 5 kararlı izotoptan oluşur. Yaklaşık 30 adet de yapay radyoizotopu bulunur. Hangi Alan ve Ürünlerde Kullanılır?Tungstenin en yaygın kullanımı ampul filamanları ve kesme aşındırma aletlerinin uçlarıdır. Genellikle alaşım ве bileşik halinde kullanımı yaygındır. En yaygın ве zorlu bileşiği tungsten karbürdür.Вольфрам telinin direnci çok yüksektir. Fiziksel ufalanmaya karşı dayanıklıdır. Bu sebeple hemen hemen bütün ampullerin lamba telleri olan filamanlar tungstenden üretilir. Bu özelliği sebebiyle yüksek direnç ve dayanıklılık gerektiren elektrikli fırınların rezistanslarının telleri de tungsten ürünüdür. Saf tungsten, bazı elektronik uygulamalarda kullanılır. Demir alaşımları ve çeliklerin hazırlanmasında da tungstenin rolü vardır. Otomotiv, uçak, gemi ve iş makinelerinin üretildiği sanayilerde de tungstenin fiziksel özellikleri sebebiyle tercih edildiği birçok ürün ve parça bulunmaktadır.Uzay teknolojisinde yüksek alaşım ürünlerinde kullanılmaktadır. Toz haline getirilen formuna tungsten bronzları adı verilir ve bu tozlar süsleme uygulamalarında kullanılır. Yüzde 80 oranında tungsten içeren demir alaşımı ferrotungsten, takım çeliklerinin üretiminde kullanılır. Вольфрам bileşikleri aynı zamanda endüstriyel uygulamalarda katalizör görevi görür. Вольфрам disülfür bileşiği, yüksek sıcaklıklarda kuru yağlayıcı olarak kullanılır. Silah ве савунма sanayisinde де вольфрам ве alaşımları önemli бир хаммаддедир.Altına yakın younluğu sebebiyle takı ve mücevherlerde platin ве altına alternatif olarak kullanılabilmektedir. Vanadyum dioksitle tungsten bileşiği, camlarda kullanılan güneş filmlerinin hammaddesidir. Tungsten, alaşımları ve bileşiklerinin kullanıldığı bazı ürünler şunlardır ; х ışını Cihazları, Elektrik kontakların parçaları, radyasyon önleyici ekranlar, egzoz subapları Kaplamaları, matkap uçları, ısıtıcı direnç telleri, Askeri zırhlılar, Торна Калого в Фреза Gibi kesim Aletleri в uçları, Терма iyonik lambalar, Рентген lambaları, öğütücü Aletler, Таки ве mücevherler, enstrüman telleri, roket motorları, elektron tabancası, boyalar, televizyon tüpleri, otomobil distribütörleri, testere bıçakları, diş delme ve kesme aletleri… Bunları Biliyor Musunuz?
Hangi Ülkelerde Rezervi Bulunur?Dünyadaki toplam tungsten rezervinin 5 milyon ton civarında olduğu tahmin edilmektedir. İşletilebilir rezerv ise yaklaşık 2 milyon tondur. Dünyadaki mevcut rezerv yaklaşık 50 yıl tungsten ihtiyacını karşılayabilecek kapasitededir. Dünyadaki tungsten üretimi yıllık toplam 50 bin ton civarındadır. Tungsten rezervi bakımından en zengin ülkeler Çin ve Rusya’dır .Dünya tungsten rezervinin neredeyse yarısı bu iki ülkede bulunur. In, dünya tungsten ihtiyacının yüzde 30’unu karşılamaktadır. Diğer tungsten rezervi bulunan ülkeler; Канада, Кузей Коре, АБР, Боливия, Вьетнам, Портекиз, Авустурья, Руанда, Испания, Брезилья, Авустраля, Перу, Брунди ве Мьянмар’дыр. En fazla tungsten tüketen ülkeler ise ABD, İngiltere, Fransa, Almanya ve İsveç’tir. Türkiye’de ilk tungsten cevheri 1945 yılında Söğüt-Dudaş antimuan yatağında bulunmuştur. Ancak bazı kaynaklarda 1910’lu yıllarda Türkiye’den Almanya’ya tungsten konsantresi ihraç edildiği bilgisi yer almaktadır.Türkiye’deki en önemli tungsten yatakları Bursa Uludağ ve Keban bölgelerinde bulunmaktadır. Uludağ’daki tungsten oluşumları, dünyadaki tungsten rezervinin yüzde 4’üne tekabül eder. Bunun dışında Türkiye’de; Чанаккале (akıroba, Hamdibey), Nide (Gümüşler), Yozgat (Akdağmadeni) ile birlikte yaklaşık 30 farklı tungsten yatağı bulunmaktadır. Tungsten cevherleri bulunduğu halde Türkiye’de tungsten madenciliği ve üretimi yapılmamaktadır. Bu sebeple tungsten ürünleri ithal edilmektedir.En fazla ferrotungsten alaşımı ithal edilmektedir. Производные правилаПроизводная сообщает нам наклон функции в любой точке. Есть правила , которым мы можем следовать, чтобы найти множество производных. Например:
Вот полезные правила, которые помогут вам вычислить производные многих функций (с примерами ниже). Примечание: маленькая метка ’означает« производную от », а f и g — функции.
Также пишется «Производная от» г dx Так г dx sin (x) и sin (x) ’оба означают« производную sin (x) » ПримерыПример: какова производная sin (x)?Из приведенной выше таблицы это указано как cos (x) Это можно записать как: грех (х) = соз (х) или: sin (x) ’= cos (x) Правило мощностиПример: Что такое. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||