Сопряжение окружности и прямой линии дугой заданного радиуса
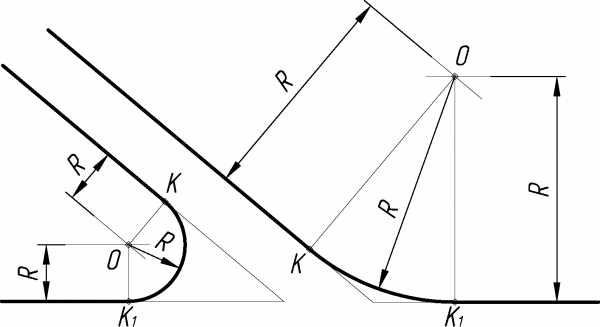
Здесь может быть рассмотрено два случая: внешнее сопряжение (рисунок 37, а) и внутреннее (рисунок 37, б). В том и в другом случае при построении сопрягающей дуги радиуса R центр сопряжения О лежит на пересечении геометрических мест точек, равно удаленных от прямой и дуги радиуса R на величину R1.
При построении внешнего сопряжения параллельно заданной прямой на расстоянии R1в сторону окружности проводят вспомогательную прямую, а из центра О радиусом,равным R + R1,— вспомогательную окружность, и на их пересечении получают точку О1— центр сопрягающей окружности. Из этого центра радиусом R проводят сопрягающую дугу между точками А и А1, построение которых видно из чертежа.
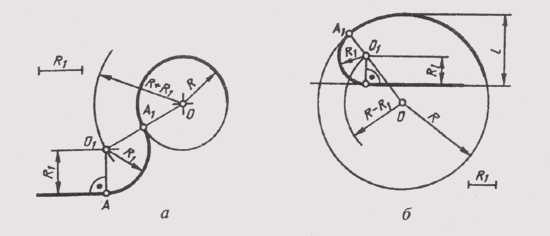
Рисунок 37 — Сопряжение окружности и прямой линии второй дугой
Построение внутреннего сопряжения отличается тем, что из центра О проводят вспомогательную дугу радиусом, равным R — R1.
Овалы
Плавные выпуклые кривые, очерченные дугами окружностей разных радиусов, называют овалами. Овалы состоят из двух опорных окружностей с внутренними сопряжениями между ними.
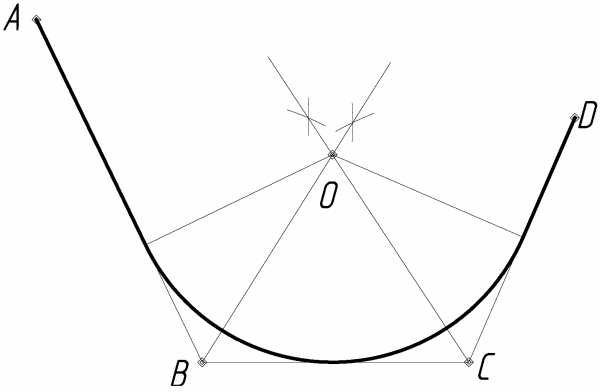
Различают овалы трехцентровые и многоцентровые. При вычерчивании многих деталей, например кулачков, фланцев, крышек и других, контуры их очерчивают овалами. Рассмотрим пример построения овала по заданным осям. Пусть для четырехцентрового овала, очерченного двумя опорными дугами радиуса R и двумя сопрягающими дугами радиуса r , заданы большая ось АВ и малая ось CD. Величину радиусов R u r надо определить путем построений (рисунок 38). Соединим концы большой и малой оси отрезком AС,
на котором отложим разность СЕ большой и малой полуосей овала. Проведем перпендикуляр к середине отрезка AF, который пересечет большую и малую оси овала в точках О1и О2. Эти точки будут центрами сопрягающихся дуг овала, а точка сопряжения будет лежать на самом перпендикуляре.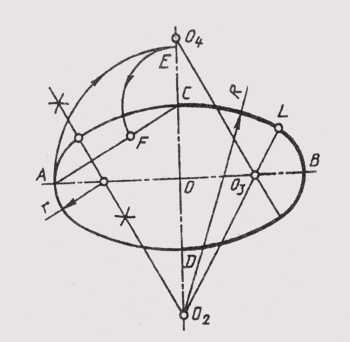
Рисунок 38 – Построение овала
Лекальные кривые
Лекальныминазывают плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс параболу, гиперболу, циклоиду, синусоиду эвольвенту и др.
Эллипспредставляет собой замкнутую плоскую кривую второго порядка. Она характеризуется тем, что сумма расстояний от любой ее точки до двух точек фокусов есть величина постоянная, равная большей оси эллипса. Построить эллипс можно несколькими способами. Например, можно построить эллипс по его большой
Можно привести пример построения эллипса по двум сопряженным диаметрам (рисунок 39,б) MN и KL. Сопряженными два диаметра называют, если каждый из них делит пополам хорды, параллельные другому диаметру. На сопряженных диаметрах строят параллелограмм. Один из диаметров MN делят на равные части; на такие же части делят и стороны параллелограмма, параллельные другому диаметру, нумеруя их, как показано на чертеже. Из концов второго сопряженного диаметра KL через точки деления проводят лучи. В пересечении одноименных лучей получают точки эллипса.
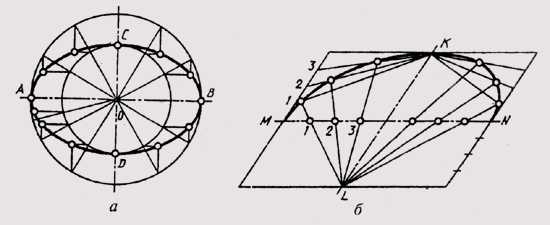
Рисунок 39 – Построение эллипса
Параболойназывают незамкнутую кривую второго порядка, все точки которой равно удалены от одной точки — фокуса и от данной прямой — директрисы.
Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В (рисунок 40, а). С этой целью строят прямоугольник ОABC и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.
Можно привести пример построения параболы в виде кривой, касательной прямой с заданными на них точками А и В (рисунок 40, б). Стороны угла, образованного этими прямыми, делят на равные части и нумеруют точки деления. Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую этих прямых.

Рисунок 40 – Построение параболы
Гиперболой называют плоскую незамкнутую кривую второго порядка, состоящую из двух веток, концы которых удаляются в бесконечность, стремясь к своим асимптотам. Гипербола отличается тем, что каждая точка ее обладает особым свойством: разность ее расстояний от двух данных точек-фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Если асимптоты гиперболы взаимно перпендикулярны, она называется равнобокой. Равнобокая гипербола широко применяется для построения различных диаграмм, когда задана своими координатами одна точка М (риссунок 40, в). В этом случае через заданную точку проводят линии АВ и KL параллельно координатным осям. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.
Циклоидойназывают кривую линию, представляющую собой траекторию точки А при перекатывании окружности (рисунок 41). Для построения циклоиды от исходного положения точки А откладывают отрезок АА], отмечают промежуточное положение точки А. Так, в пересечении прямой, проходящей через точку 1, с окружностью, описанной из центра О1, получают первую точку циклоиды. Соединяя плавной прямой построенные точки, получают циклоиду.
Рисунок 41 – Построение циклоиды
Синусоидойназывают плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рисунок 42) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2лR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.
Рисунок 42 – Построение синусоиды
Эвольвентойназывают плоскую кривую, являющуюся траекторией любой точки прямой линии, перекатываемой по окружности без скольжения. Построение эвольвенты выполняют в следующем порядке (рисунок 43): окружность делят на равные части; проводят касательные к окружности, направленные в одну сторону и проходящие через каждую точку деления; на касательной, проведенной через последнюю точку деления окружности, откладывают отрезок, равный длине окружности 2лR, который делят на столько же равных частей. На первой касательной откладывают одно деление 2лR/n , на второй — два и т. д.
Полученные точки соединяют плавной кривой и получают эвольвенту окружности.
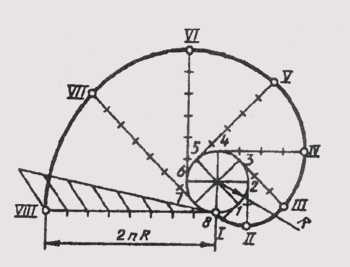
Рисунок 43 – Построение эвольвенты
Вопросы для самопроверки
1 Как разделить отрезок на любое равное число частей?
2 Как поделить угол пополам?
3 Как разделить окружность на пять равных частей?
4 Как построить касательную из заданной точки к данной окружности?
5 Что называется сопряжением?
6 Как сопрячь две окружности дугой заданного радиуса с внешней стороны?
7 Что называется овалом?
8 Как строится эллипс?
Дата добавления: 2017-12-05; просмотров: 809;
znatock.org
2.1.4 Сопряжение пересекающихся прямых дугой окружности данного радиуса
Построение сводится к проведению окружности, касающейся обеих данных прямых (рис. 2.5). Для нахождения центра этой окружности проводят вспомогательные прямые, параллельные данным, на расстоянии, равном радиусу R
| |
Рисунок 2.5
Этими точками и ограничивается дуга сопряжения. Если одна из точек касания, например К, является заданной, а радиус закругления не указан, то искомый центр О находится на пересечении перпендикуляра, проведенного из точки К, и биссектрисы угла, образуемого данными прямыми.
Если требуется провести окружность так, чтобы она касалась трех данных пересекающихся прямых АВ, ВС и СD, то в этом случае радиус не может быть задан наперед. Центр О искомой окружности находится в точке пересечения биссектрис углов В и С. Радиусом ее является перпендикуляр, опущенный на любую из трех данных прямых (рис. 2.5, б).
2.1.5 Сопряжение данной окружности и данной прямой дугой заданного радиуса r
При внешнем касании (рис. 2.6) из центра О данной окружности радиусом R проводится дуга вспомогательной окружности радиусом R + R1, а на расстоянии R – прямая, параллельная заданной. Точка пересечения проведенной прямой и дуги вспомогательной окружности определяет положение центра дуги сопряжения О1. Соединяя найденный центр О1 с центром О данной окружности и опуская из О1 перпендикуляр на прямую, находят точки касания К и К1
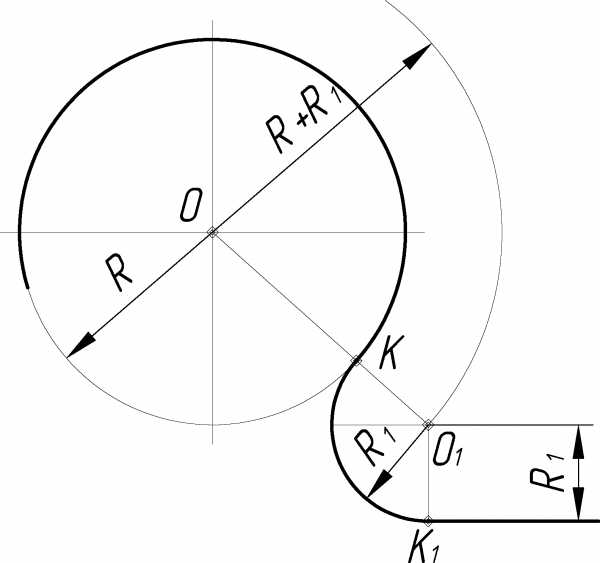
Рисунок 2.6
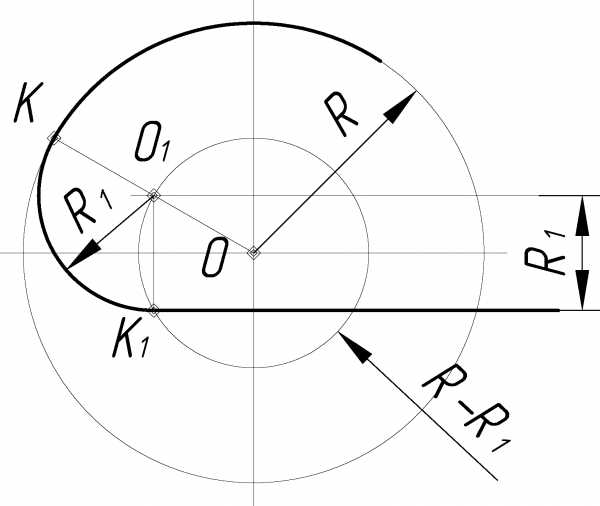
Рисунок 2.7
2.1.6 Сопряжение двух данных окружностей дугой заданного радиуса r3
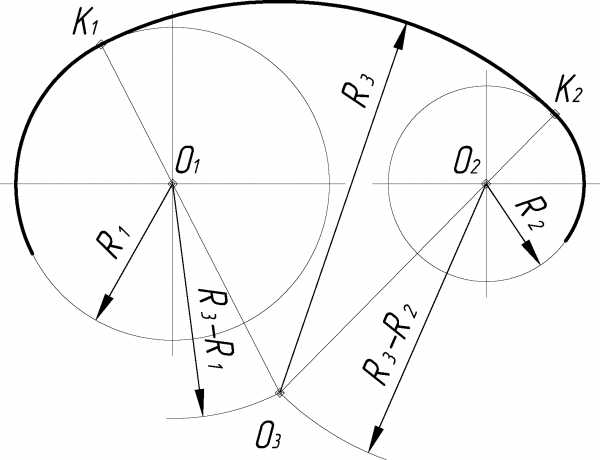
При внешнем касании (рис. 2.8) из центра О1 окружности радиусом R1 описывается дуга вспомогательной окружности радиусом R1+ R3 и из центра О2 окружности радиусом R2 – дуга радиусом R2 + R3. Точка О3 пересечения этих дуг является центром искомой дуги окружности радиусом R3. Соединяя центры О3 и О1, а также О3 и О2, определяют точки касания К1 и К2.
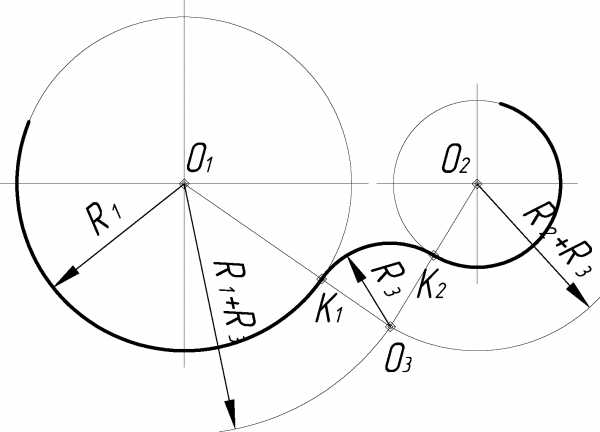
Рисунок 2.8
При внутреннем касании (рис. 2.9, а) вспомогательные дуги проводятся радиусами R3–R1, и R3–R2.
| |
Рисунок 2.9
2.1.7 Случаи внешнего и внутреннего касания
Даны окружности радиусами r1 и r2 с центрами О1 и О2 (рис. 2.9, б). Требуется провести окружность данного радиуса R так, чтобы она имела с одной из данных окружностей внутреннее касание, а с другой – внешнее. Центр искомой дуги находится в точке пересечения двух дуг, описанных из центра О1 радиусом R – r1 и из центра О2 –радиусом R + r2; К и К1 – точки касания.
2.1.8 Проведение касательной к окружности через заданную точку, лежащую вне окружности
Данную точку А соединяют с центром окружности О и из точки А через центр О очерчивают вспомогательную окружность. В точках пересечения вспомогательной и данной окружностей получают точки касания К и К1; остаётся точку А соединить с этими точками (рис. 2.10).
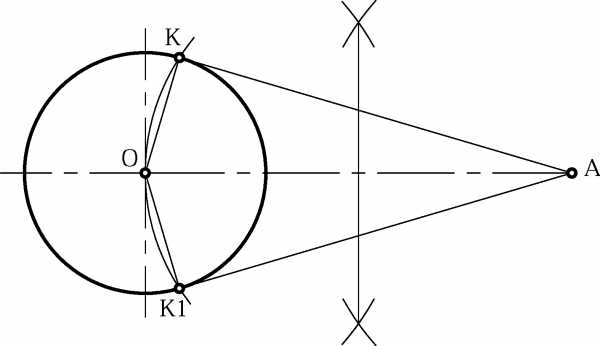
Рисунок 2.10
studfiles.net
Сопряжения прямой с окружностью — МегаЛекции
Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.
Пример 1. Пусть задана окружность радиусом R1с центром в точке O1и прямая m. Требуется построить сопряжение окружности с прямой дугой окружности заданного радиуса R (рис. 18).
Рис. 18
Для решения задачи выполним следующие построения.
1. Построим прямую m’, параллельную m и отстоящую от неё на расстоянии R.
2. Построим окружность n’ с центром в точке О1, проведенную радиусом R1 + R.
3. Центр сопряжения О находим как точку пересечения линий n’ и m’.
4. Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо провести линию центров OO1, т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
5. Проведем дугу сопряжения АВ.
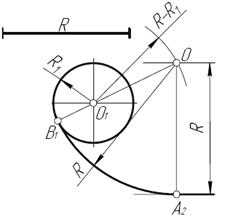
Рис. 19
Пример 2. При построении внутреннего сопряжения (рис. 19) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра О1 , радиусом R – R1.
Сопряжение двух окружностей
Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.
Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами R1и R2дугой заданного радиуса R (рис. 20).
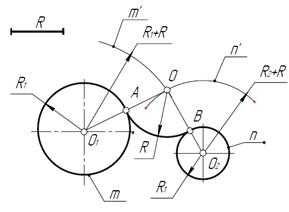
Рис. 20
1. Для нахождения центра сопряжения О проведем окружность m’, удаленную от данной окружности m на расстоянии R .Так как сопряжение с внешним касанием, то радиус окружности m’ равен R1 + R.
2. Радиусом R2 + R проведем окружность n’, удаленную от данной окружности n на расстоянии R.
3. Найдем центр сопряжения О как точку пересечения окружностей m’ и n’ .
4. Найдем точку сопряжения А как пересечение линии центров O1O с дугой m.
5. Аналогично найдем точку В как пересечение линии центров О2О с дугой n .
6. Проведем дугу сопряжения АВ.
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами R1и R2дугой радиусом R (рис. 21).
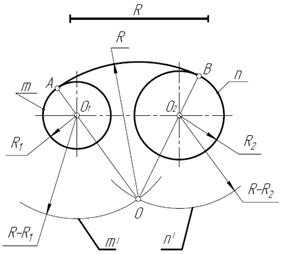
Рис. 21
1. Для нахождения центра сопряжения О проведем окружность m’ на расстоянии R – R1от данной окружности m.
2. Проведем окружность n’ на расстоянии R – R2от данной окружности n.
3. Центр сопряжения О найдем как точку пересечения окружностей m’ и n’.
4. Точку сопряжения А найдем как точку пересечения линии центров ОО1с заданной окружностью m.
5. Точку сопряжения В найдем как точку пересечения линии центров OO2c заданной окружностью n.
6. Проведем дугу сопряжения AВ с центром в точке O.
Пример 3. На рис. 22 приведен пример построения сопряжения со смешанным касанием.
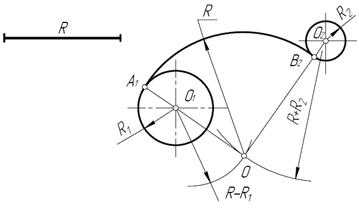
Рис. 22
Рассмотрев наиболее характерные случаи сопряжений при заданном радиусе, можно выявить общее правило построения сопряжений для подобных случаев. Центр сопряжения определяется пересечением двух вспомогательных линий, параллельных заданным прямым или концентричных заданным дугам и отстоящих от заданных линий на расстоянии радиуса сопряжения.
Точки сопряжений определяются: на прямых – перпендикуляром, опущенным из центра сопряжений на прямую; на дугах – прямой, соединяющей центр сопряжений с центром заданной дуги.
Построение касательных
Пример 1. Дана окружность с центром в точке О2и точка О1вне её. Через данную точку О1провести касательную к данной окружности (рис. 23).
Рис. 23
Для решения задачи выполним следующие построения.
1. Соединим точку O1с центром окружности O2.
2. Находим середину С отрезка O1О2.
3. Из точки С, как из центра, проведем вспомогательную окружность радиусом CO1 = CО2.
4. В точке пересечения вспомогательной окружности с заданной получим точку касания А. Соединим точку О1 с точкой А.
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов R1и R2(рис. 24).
Рис. 24
1. Находим середину С отрезка O1О2.
2. Из точки С, как из центра, радиусом CO1 = CO2проведем вспомогательную окружность.
3. Из центра большей окружности O2проведем вторую вспомогательную окружность радиусом R2 – R1.
4. Пересечение двух вспомогательных окружностей определяет точку К, через которую проходит радиус О2К, идущий в точку касания В.
5. Для построения второй точки касания А проведем О1А || О2В.
6. Соединим точки А и В отрезком прямой линии.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
3.3.2 Сопряжение дуги и прямой дугой окружности заданного радиуса
Могут встретиться два случая такого сопряжения: внешнее касание сопрягающей дуги с заданной и внутреннее касание. В обоих случаях задача сводится к определению центра сопрягающей дуги и точек касания.
При внешнем касании (рисунок 52, а) из центра заданной дуги – точки O1 проводят вспомогательную дугу радиусомR +Rс. На расстоянии, равном радиусуRcсопрягающей дуги, параллельно заданной прямой проводят прямую. ТочкаОпересечения вспомогательной дуги и прямой есть центр сопрягающей дуги. На пересечении прямой, соединяющей точкиОиO1с заданной дугой, отмечают точку касанияA. Вторую точку касанияВопределяют как точку пересечения заданной прямой с перпендикуляром, опущенным на нее из точкиО.
При внутреннем касании (рисунок 52, б) определение центра сопрягающей дуги и точек касания аналогичны предыдущему случаю с той лишь разницей, что радиус вспомогательной дуги равен Rc – R.
а б
Рисунок 52
3.3.3 Сопряжение двух дуг дугой окружности заданного радиуса
Различают три вида такого сопряжения:
1) внешнее сопряжение при внешнем касании сопрягающей дуги с двумя заданными;
2) внутреннее сопряжение при внутреннем касании сопрягающей дуги с двумя заданными;
3) смешанное сопряжение при внешнем касании сопрягающей дуги с одной заданной и внутреннем касании с другой.
При внешнем сопряжении(рисунок 53, а) центр сопрягающей дуги точкаO располагается в точке пересечения вспомогательных дуг радиусамиr +Rc иR +Rc, проведенных соответственно из центров сопрягаемых дуг – точекO2 иO1. Точки касанияA иB определяются как точки пересечения заданных дуг с прямымиOO1 иOO2.
Внутреннее сопряжениедуг радиусамиr иR дугой радиусомRcпоказано на рисунке 53, б. Для определения центра сопрягающей дуги – точкиОпроводят вспомогательные дуги радиусамиRc–r иRc–Rсоответственно из центров заданных дуг – точекO2иO1. ТочкаОпересечения этих дуг и явится центром сопрягающей дуги. Из точкиОчерез точкиO1 иO2проводят прямые до пересечения с заданными дугами и получают соответственно две точки касания –A иB.

Рисунок 53
При смешанном сопряжении центр сопрягающей дуги – точкаОопределяется как точка пересечения двух вспомогательных дуг радиусамиRc+R иRс–r (рисунок 53, в) илиRс–R иRс+r, проведенных соответственно из центров заданных дуг – точекO1 иO2. Для определения точек касания сопрягающей дуги с заданными проводят две прямые: одну через точкиО и O1, другую через точки О и O2. Точки пересечения каждой из них с заданными дугами дают искомые точки касания A и B.
3.3.4 Вычерчивание контуров деталей
Последовательность вычерчивания контуров деталей в основном зависит от их формы. Поэтому можно указать только на некоторые общие положения, справедливые для всех случаев.
Перед вычерчиванием любого контура необходимо установить, из каких линий и их сочетаний он состоит, а также решить, какие геометрические построения следует выполнить при вычерчивании контура. Только после подобного анализа можно приступать к построению контура.
Последовательность вычерчивания контура проследим на примере контура скобы (рисунок 54, а). Вычерчивание начинают с проведения осей симметрии (вертикальная ось на рисунке 54, б), осевой (горизонтальная ось на рисунке 54, б) и центровых линий контура. Затем проводят линии, связанные с горизонтальной осью (рисунок 54, в), и строят остальные основные линии контура (рисунок 54, г). Далее выполняют скругления углов (рисунок54, д) и вычерчивают внутренние очертания, не связанные с другими линиями (прорезь, рисунок 54, е). Последними вычерчивают контуры, не содержащие элементов сопряжения. Заканчивают построение проведением выносных и размерных линий с простановкой размеров (рисунок 54, а).
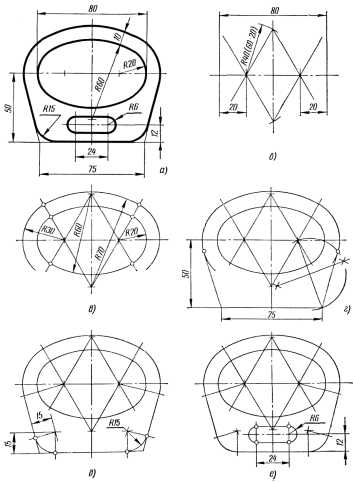
Рисунок 54
studfiles.net