Уравнение спирали в декартовых координатах: Спираль Архимеда — это что и как построить спираль Архимеда

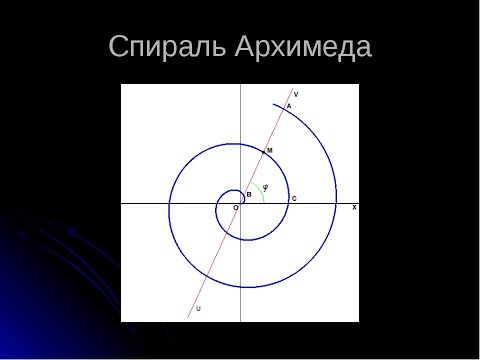
Спираль Архимеда

Одна из ветвей спирали Архимеда, задаваемая уравнением для .

Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:

r(φ) = a + bφ.

Изменения параметра a приводят к повороту спирали, а параметра b — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для φ > 0 а другую для φ < 0. Две ветви плавно соединяются в полюсе. Зеркальное отображение одной ветви относительно прямой, проходящей через угол 90°/270°, даст другую ветвь. Эта кривая интересна тем, что была описана в математической литературе одной из первых, после конического сечения, и лучше других определяется именно полярным уравнением.

[править] Конические сечения

Эллипс.

Коническое сечение, один из полюсов которого находится в полюсе, а другой где-то на полярной оси (так, что малая полуось лежит вдоль полярной оси) задаётся уравнением:

где e — эксцентриситет, а — фокальный параметр. Если e > 1, это уравнение определяет гиперболу; если e = 1, то параболу; если e < 1, то эллипс. Отдельным случаем является e = 0, определяющее окружность с радиусом .

Комплексные числа

Пример комплексного числа , нанесённого на комплексную плоскость.

Пример комплексного числа, нанесённого на график, с использованием формулы Эйлера.

Каждое комплексное число может быть представлено точкой на комплексной плоскости, и, соответственно, эта точка может определяться в декартовых координатах (прямоугольная или декартова форма), либо в полярных координатах (полярная форма). Комплексное число z может быть записано в прямоугольной форме так:

z = x + iy,

где i — мнимая единица, или в полярной (см. формулы преобразования между системами координат выше):

и отсюда:

z = re^iφ,

где e — число Эйлера. Благодаря формуле Эйлера, оба представления эквивалентны^[16] (Следует отметить, что в этой формуле, подобно остальным формулам, содержащим возведения в степень углов, угол задан в радианах)

Для перехода между прямоугольным и полярным представлением комплексных чисел, могут использоваться указанные выше формулы преобразования между системами координат.

Операции умножения, деления и возведения в степень с комплексными числами, как правило, проще проводить в полярной форме. Согласно правилам возведения в степень:

• Умножение:

• Деление:

(re^iφ)ⁿ = rⁿe^inφ.

Для полярных координат можно применить элементы векторного анализа. Любое векторное поле можно записать в полярной системе координат, используя единичные векторы:

в направлении , и

Связь между декартовыми компонентами поля F_x и F_y и его компонентами в полярной системе координат задаётся уравнениями:

F_x = F_rcos φ − F_φsin φ;

F_y = F_rsin φ + F_φcos φ.

Спирали

Архимедова спираль

Спирали (франц., единственное число spirale, от лат. spira, греч. speira — виток), плоские кривые линии, бесчисленное множество раз обходящие некоторую точку, с каждым обходом приближаясь к ней или с каждым обходом удаляясь от неё. Если выбрать эту точку за полюс полярной системы координат, то полярное уравнение Спирали r = f(j) таково, что f(j + 2p) > f(j) или f(j + 2p) < f(j) при всех j. В частности, Спирали получаются, если f(j) — монотонно возрастающая или убывающая положительная функция. Наиболее простой вид имеет уравнение архимедовой Спирали (см. рис.): r = аj, изученной древнегреческим математиком Архимедом (3 в. до н. э.) в связи с задачами трисекции угла и квадратуры круга в сочинении «О спиралях». Архимед нашёл площадь сектора этой Спирали, что было одним из первых примеров квадратуры криволинейной области. Архимедова Спирали является подерой (см. Подера и антиподера) эвольвенты круга (см. Эволюта и эвольвента), что используется в некоторых конструкциях разводных мостов для уравновешивания переменного натяжения цепи. Если эксцентрик ограничен дугами архимедовой Спирали (сердцевидный эксцентрик), то он преобразует равномерное вращательное движение в равномерное поступательное, причём расстояние между диаметрально противоположными точками эксцентрика постоянно. Французский математик П. Ферма исследовал обобщённые архимедовы Спирали (r/a)ⁿ = (j/2p)^m и нашёл площадь их сектора.

Уравнение r = ае^кj задаёт логарифмическую Спирали (см. рис.). Логарифмическая Спирали пересекает под одним и тем же углом а все радиус-векторы, проведённые из полюса, причём ctga =

k. Это свойство логарифмической Спирали используется при проектировании вращающихся ножей, фрез и т. д. для достижения постоянства угла резания. Логарифмическая Спирали встречается также в теории спиральных приводов к гидравлическим турбинам и т. д. В теории зубчатых колёс используется возможность качения без скольжения одной логарифмической Спирали по другой, равной с ней, когда обе Спирали вращаются вокруг своих полюсов. При этом получаются зубчатые передачи с переменным передаточным числом. При стереографической проекции плоскости на сферу логарифмической Спирали переходит в локсодромию (кривую, пересекающую все меридианы под одним и тем же углом). Определение длин дуг логарифмической Спирали дано итал. учёным Э. Торричелли. Длина дуги логарифмической

Спирали пропорциональна разности длин радиус-векторов, проведённых в концы дуги, точнее равна . Швейц. учёный Я. Бернулли показал, что эволюта и каустика (см. Каустическая поверхность) логарифмической Спирали являются логарифмическими Спирали При вращении вокруг полюса логарифмической Спирали получается кривая, гомотетичная (см. Гомотетия) исходной. При инверсии логарифмическая Спирали переходит в логарифмическую Спирали

Из других Спирали практическое значение имеет Корню Спирали (или клотоида), применяемая при графическом решении некоторых задач дифракции (см. рис.). Параметрическое уравнение этой

Спирали имеет вид:
, .

Корню Спирали является идеальной переходной кривой для закругления железнодорожного пути, так как её радиус кривизны возрастает пропорционально длине дуги. Спирали являются также эвольвенты замкнутых кривых, например эвольвента окружности.

Названия некоторым Спирали даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например параболическая Спирали (см. рис. ): (а — r)² = bj, гиперболическая Спирали(см. рис.): r = а/j. К Спирали относятся также жезл (см. рис.): r² = a/j и si-ci-cпираль, параметрические уравнения которой имеют вид:
,

[si (t) и ci (t) — интегральный синус и интегральный косинус]. Кривизна si-ci-cпирали изменяется с длиной дуги по закону показательной функции. Такие Спирали применяют в качестве профиля для лекал.

Напоминает Спирали кривая , называемая кохлеоидой (см. рис.). Она бесконечное множество раз проходит через полюс, причём каждый следующий завиток лежит в предыдущем.
Спирали встречаются также при рассмотрении особых точек в теории дифференциальных уравнений (см. Особые точки).
Спирали иногда называют также пространственные кривые, делающие бесконечно много оборотов вокруг некоторой оси, например винтовая линия.
Лит. см. при ст. Линия.

>> >> >>

Статья про «Спирали» в Большой Советской Энциклопедии была прочитана 315 разГеометрия

— допустимо ли это параметрическое уравнение для создания контрольных точек спирали в трехмерном пространстве?

Ваши уравнения не создают спираль. Спираль обладает тем свойством, что она имеет постоянную кривизну и постоянное кручение при описании системой Френе-Серре. Если мы напишем вашу кривую как \begin{уравнение} p(u) = \begin{bmatrix} x(u) \\ y(u) \\ z(u) \end{bmatrix} \end{уравнение} тогда касательный вектор определяется как \begin{уравнение} T(u) = \dfrac{p'(u)}{\left\lVert p'(u) \right\rVert} \end{уравнение} 9{-1} \право| \end{equation}

В вашем уравнении $\left \lVert \dfrac{dT}{du} \right \rVert$ имеет постоянную величину, но $\left| \dfrac{ds}{du} \right| = \lVert p'(u) \rVert$ нет, поэтому кривая не имеет постоянной кривизны. 2 \end{уравнение} Здесь я выбрал $R$ как матрицу вращения, которая выполняет минимальное вращение, необходимое для выравнивания оси спирали с нормалью треугольника. 92 } \Delta t$ и на угол просто $\Delta t$ радиан.

дифференциальная геометрия — Как выразить параметризованную кривую в сферических координатах

Задай вопрос

спросил 3 года, 4 месяца назад

Изменено 3 года, 4 месяца назад

Просмотрено 2к раз 92т = 1$. А вот с хеликсом такого соответствия вроде не нашел. И я думаю, что, возможно, его не существует, потому что для одного и того же значения $x$ существуют бесконечные значения для $z$. Так что я даже не знаю, имеет ли смысл этот вопрос. Спасибо за внимание.

• дифференциальная геометрия
• системы координат
• параметрические
• сферические координаты
• параметризация

$\endgroup$

$\begingroup$ 92\theta=1\\\phi=r\cos\theta$$

$\endgroup$

$\begingroup$

Ваш вопрос сбивает с толку, потому что, с одной стороны, вы просите выразить (3D) параметрическую кривую в сферических координатах, а с другой стороны, вы приводите пример (2D) параметрической кривой, обращенной к неявному уравнению и не использующей полярные координаты .