Упакованные bcd-числа
Как уже отмечалось ранее, упакованные BCD-числа можно только складывать и вычитать. Для выполнения других действий над ними их нужно дополнительно преобразовывать либо в неупакованный формат, либо в двоичное представление. Таким образом, сами по себе упакованные BCD-числа представляют не слишком большой интерес для программиста, поэтому мы их рассмотрим кратко.
Сложение
Вначале разберемся с сутью проблемы и попытаемся сложить два двузначных упакованных BCD-числа:
67 =01100111
+
75 =01110101
=
142=11011100 = 220
Как видим, в двоичном виде результат
равен 1 101 1 100 (или 220 в десятичном
представлении), что неверно. Это происходит
по той причине, что процессор не
подозревает о существовании BCD-чисел и
складывает их по правилам сложения
двоичных чисел. На самом деле результат
в двоично-десятичном виде должен быть
равен 0001 0100 0010 (или 142 в десятичном
представлении).
Команда DAA преобразует содержимое регистра AL в две упакованные десятичные цифры (по алгоритму, приведенному в приложении А, где данная команда описана более подробно). Получившаяся в результате сложения единица (если результат сложения больше 99) запоминается во флаге CF, тем самым учитывается перенос в старший разряд.
Проиллюстрируем сказанное на примере сложения двух двузначных BCD-чисел в упакованном формате (листинг 8.12).
Листинг 8.12. Сложение упакованных BCD-чисел
<1> ;prg_8_12.asm<2> …
<3> . data ;сегмент данных
data ;сегмент данных
<4> b db 17h ;упакованное число 17
<5> с db 45h ;упакованное число 45
<6> sum db 2 dup (0)
<7> .code ;сегмент кода
<8> main: ;точка входа в программу
<9> …
<10> mov al ,b
<11> add al,c
<12> daa
<13> jnc $+6 ;переход через команду, если результат <= 99
<14> mov sum+l,ah ;учет переноса при сложении (результат > 99)
<15> mov sum.al ;младшие упакованные цифры результата
<16> exit:
Вычитание
Аналогично сложению, при вычитании процессор рассматривает упакованные BCD-числа как двоичные. Выполним вычитание 67 — 75. Так как процессор выполняет вычитание способом сложения, то и мы последуем этому:
67 =01100111
+
-75 =10110101
=
-8 =00011100 = 28.
Как видим, результат равен 28 в десятичной
системе счисления, что является абсурдом.
В двоично-десятичном коде результат
должен быть равен 0000 1000 (или 8 в десятичной
системе счисления). При программировании
вычитания упакованных BCD-чисел программист,
как и при вычитании неупакованных
BCD-чисел, должен сам осуществлять контроль
за знаком. Это делается с помощью флага
CF, который фиксирует заем из старших
разрядов. Само вычитание BCD-чисел
осуществляется обычной командой
вычитания SUB или SBB. Коррекция результата
вычитания для его представления в
десятичном виде осуществляется командой
DAS(DecimalAdjustforSubstraction).
В приложении описан алгоритм, по которому команда DAS преобразует содержимое регистра AL в две упакованные десятичные цифры.
Итоги
Процессор имеет довольно мощные средства для реализации вычислительных операций. Для этого у него есть блок целочисленных операций и блок операций с плавающей точкой. Для большинства задач, использующих язык ассемблера, достаточно целочисленной арифметики.
Команды целочисленных операций работают с данными двух типов: двоичными и двоично-десятичными числами (BCD-числами).
Двоичные данные могут либо иметь знак, либо не иметь такового. Процессор, на самом деле, не различает числа со знаком и без. Он лишь помогает отслеживать изменение состояния некоторых битов операндов и состояние отдельных флагов. Операции сложения и вычитания чисел со знаком и без знака проводятся одним устройством и по единым правилам.
Контроль за правильностью результатов
и их надлежащей интерпретацией полностью
лежит на программисте. Он должен
контролировать состояние флагов CF и OF
регистра EFLAGS во время вычислительного
процесса.
Он должен
контролировать состояние флагов CF и OF
регистра EFLAGS во время вычислительного
процесса.
Для операций с числами без знака нужно контролировать флаг CF. Установка его в 1 сигнализирует о том, что число вышло за разрядную сетку операндов.
Для чисел со знаком установка флага OF в 1 говорит о том, что в результате сложения чисел одного знака результат выходит за границу допустимых значений чисел со знаком в данном формате, и сам результат меняет знак (пропадает порядок).
По результатам выполнения арифметических операций устанавливаются так-же флаги PF, ZF и SF.
В отличие от команд сложения и вычитания, команды умножения и деления позволяют учитывать знаки операндов.
Арифметические команды очень «капризны» к размерности операндов, поэтому в систему команд процессора включены специальные команды, позволяющие отслеживать эту характеристику.
Хотя диапазон значений двоичных данных
довольно велик, для коммерческих
приложений его явно недостаточно,
поэтому в архитектуру процессора введены
средства для работы с так называемыми
двоично-десятичными (BCD) данными.
Двоично-десятичные данные представляются в двух форматах, упакованном и неупакованном. Наиболее универсальным является неупакованный формат.
|
⇐ ПредыдущаяСтр 4 из 6Следующая ⇒ Упакованные BCD-числа хранятся по две цифры в байте в виде четырехбитовых групп, называемых тетрадами, причем каждая тетрада представляет собой двоичную комбинацию, соответствующую одной десятичной цифре, т.е. двоичное число в диапазоне 0000b – 1001b. Неупакованное BCD-число содержит одну десятичную цифру в младшей тетраде байта, старшая тетрада должна быть нулевой, однако для команд сложения и вычитания содержимое старшей тетрады несущественно. Команды десятичной коррекции упакованных чисел Для упакованных десятичных чисел допустимы только операции сложения и вычитания. Каждая операция выполняется в два этапа. На первом выполняется операция – сложение или вычитание (add, adc, sub, sbb) двух упакованных десятичных чисел, первое из которых должно находиться в регистре AL, на втором – десятичная коррекция результата в регистре AL (daa, das). Рассмотрим подробнее одну из команд коррекции – daa, коррекция после сложения BCD-чисел. После первого этапа – двоичного сложения правильных BCD-чисел возможно появление неправильного BCD-результата в двух ситуациях: · получена недопустимая тетрада, т.е. тетрада, двоичный эквивалент которой больше 9; · получена допустимая тетрада, но при сложении из нее возник двоичный перенос с весом 16, в то время как правильный вес единицы переноса должен быть равен 10. Отметим, что перенос из младшей тетрады фиксируется флагом AF , а из старшей – CF. Алгоритм выполнения команды daa состоит из двух шагов: · если AF=1 или младшая тетрада регистра AL содержит запрещенную комбинацию, к содержимому AL прибавляется 06 и флаг AF устанавливается в 1; · если CF=1 или старшая тетрада регистра AL содержит запрещенную комбинацию, к содержимому AL прибавляется 60h и флаг CF устанавливается в 1. Например. Содержимое регистров AL=65h и BL=28h , что соответствует десятичным числам 65 и 28.
и вычитание
das ; AL=37h, AF=1, CF=0, ZF=0 в комментариях показаны значения регистра AL и флагов после выполнения соответствующей команды. Команды десятичной коррекции неупакованных чисел Для неупакованных чисел или, как их еще называют ASCII-чисел, существуют аналогичные команды коррекции после сложения – aaa и вычитания – aas. Сложение и вычитание ASCII-чисел также выполняется в два этапа. Кроме того, над ASCII-числами допустимо выполнение операций умножения и деления. Умножение ASCII-чисел выполняется в два этапа: · умножение одноразрядных сомножителей, представленных байтами, в которых младшие тетрады содержат десятичные цифры, а старшие тетрады – нулевые. Умножение выполняется командой mul, которая формирует в регистре AL двоичное произведение; · коррекция результата с помощью команды aam, которая преобразует полученный результат в двухбайтовое произведение, находящееся в регистрах AH (старший десятичный разряд) и AL (младший разряд). Деление также выполняется в два этапа, но в отличие от остальных команд коррекция выполняется не после, а перед выполнением операции: · коррекция делимого с помощью команды aad, которая предполагает, что в регистрах AH и AL находится двухразрядное делимое, причем AH содержит цифру десятков, а AL – цифру единиц и обе старшие тетрады нулевые. Она формирует в AX соответствующее двоичное число; · деление полученного в AX делимого на одноразрядный делитель, с получением частного в AL и остатка в AH. ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ Написать программу сложения двух десятиразрядных неупакованных десятичных чисел. Текст программы:
model SMALL stack 100h
dataseg Ask1 db 0Ah,0Dh,’Введите первое слагаемое (не более 10 цифр):$’ Ask2 db 0Ah,0Dh,’Введите второе слагаемое (не более 10 цифр):$’ Buf1 db 11 Len1 db ? Opnd1 db 12 dup( ? ) Buf2 db 11 Len2 db ? Opnd2 db 12 dup( ? ) ResT db 0Ah,0Dh,’Сумма ‘ Res db 12 dup(‘ ‘),’$’ AskCont db 0Ah,0Dh db ‘Завершить работу — Esc, продолжить — ЛЮБАЯ ÊËÀÂÈØÀ’ db ‘$’
codeseg startupcode push DS pop ES ; ES <- DS
BEGIN: ;Ввод первого слагаемого B1: lea DX, Ask1 mov AH, 09h int 21h lea DX, Buf1 mov AH, 0Ah int 21h cmp Len1, 0 je B1 ;проверка 0-9 и очистка старш. lea BX, Opnd1 xor CX, CX mov CL, Len1 xor SI, SI T1: mov AL, [BX][SI] cmp AL, ‘0’ jb B1 ; ошибка cmp AL, ‘9’ ja B1 ; ошибка and AL, 0Fh mov [BX][SI], AL inc SI loop T1 ;прижать к правому краю mov CL, Len1 cmp CL, 10 je E1 mov DI, 9 mov SI, CX dec SI P1: mov AL, [BX][SI] mov [BX][DI], AL dec DI dec SI loop P1 ;обнулить лишнее xor DI, DI mov CL, 10 sub CL, Len1 N1: mov byte ptr [BX][DI], 0 inc DI loop N1 E1: ;Ввод второго слагаемого B2: lea DX, Ask2 mov AH, 09h int 21h lea DX, Buf2 mov AH, 0Ah int 21h cmp Len2, 0 je B2 ;проверка 0-9 и очистка старш.тетрады lea BX, Opnd2 xor CX, CX mov CL, Len2 xor SI, SI T2: mov AL, [BX][SI] cmp AL, ‘0’ jb B2 ; ошибка cmp AL, ‘9’ ja B2 ; ошибка and AL, 0Fh mov [BX][SI], AL inc SI loop T2 ;прижать к правому краю mov CL, Len2 cmp CL, 10 je E2 mov DI, 9 mov SI, CX dec SI P2: mov AL, [BX][SI] mov [BX][DI], AL dec DI dec SI loop P2 ;обнулить лишнее xor DI, DI mov CL, 10 sub CL, Len2 N2: mov byte ptr [BX][DI], 0 inc DI loop N2 E2: ;Сложение mov CX, 10 clc lea SI, Opnd1+9 lea DI, Opnd2+9 lea BX, Res+10 A1: mov AL, [SI] adc AL, [DI] aaa mov [BX], AL dec SI dec DI dec BX loop A1 mov AL, 0 adc AL, 0 mov [BX], AL ;Преобразование результата в ASCII mov CX, 11 A2: or byte ptr [BX], 30h inc BX loop A2 ;Вывод результата lea DX, ResT mov AH, 09h int 21h ;Запрос на продолжение работы lea DX, AskCont mov AH, 09h int 21h mov AH, 08h int 21h cmp AL, 27 ;ESC je QUIT jmp BEGIN
;Конец работы QUIT: exitcode 0 end ВАРИАНТЫ ЗАДАНИЙ 1. 2. Введите два десятичных числа разрядностью не более 10 цифр, выполните преобразование в упакованный BCD-формат, сложите их и выведите результат. 3. Введите два десятичных числа разрядностью не более 10 цифр, выполните преобразование в упакованный BCD-формат, вычтете второе из первого и выведите результат. 4. Введите два десятичных числа, первое разрядностью не более 10 цифр, второе – из одной цифры выполните преобразование в неупакованный BCD-формат, перемножьте их и выведите результат. 5. Введите два десятичных числа разрядностью не более 10 цифр, выполните преобразование в неупакованный BCD-формат, вычтете второе из первого и выведите результат. 6. Введите два десятичных числа, первое разрядностью не более 10 цифр, второе – из одной цифры выполните преобразование в неупакованный BCD-формат, поделите первое на второе и выведите результат. 7. Напишите программу – калькулятор выполняющую действия + –, внутреннее представление чисел – упакованный BCD-формат. 8. Напишите программу – калькулятор выполняющую действия + – *, внутреннее представление чисел – неупакованный BCD-формат. 9. Напишите программу – калькулятор выполняющую действия + – /, внутреннее представление чисел – неупакованный BCD-формат. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Чем отличаются упакованный и неупакованный BCD-форматы представления десятичных чисел ? 2. Что такое десятичная коррекция результата арифметической операции? 3. Почему используются различные команды десятичной коррекции для различных арифметических операций ? 4. Как организовать выполнение операций сложения и вычитания над многоразрядными операндами ? 5. Зачем нужны команды десятичной арифметики ? 6. Почему коррекция для деления выполняется перед операцией, а для остальных операций – после ?
ЦЕЛЬ РАБОТЫ Цель настоящей работы – изучение приемов программирования с использованием подпрограмм. ОСНОВНЫЕ СВЕДЕНИЯ Описание подпрограмм Описание подпрограммы в языке ассемблера имеет следующую структуру:
Здесь «тип» — одно из слов NEAR (ближняя) или FAR (дальняя). Если тип не задан, по умолчанию принимается NEAR. Процедура NEAR должна вызываться из того же сегмента кода, в котором она описана. Процедура FAR может вызываться из других сегментов, с другим значением регистра CS. Такие процедуры обычно используются как отдельные объектные модули или в составе библиотек. Команда ret выполняет возврат из процедуры в вызывающую программу. Она не обязана быть последней по тексту процедуры, но является последней по порядку выполнения. Команда ret также имеет ближний и дальний варианты в зависимости от типа подпрограммы, внутри описания которой встретилась команда. Допускается вложение описания подпрограммы внутрь описания другой подпрограммы. В заголовке подпрограммы рекомендуется комментировать ее. Как правило, следует отразить следующие моменты: действие, выполняемое подпрограммой; входные и выходные параметры; ограничения и особенности подпрограммы. Вызов подпрограмм Вызов подпрограммы выполняется командой call. Вызов также бывает ближний или дальний. При ближнем вызове в стеке запоминается текущее значение регистра IP, используемое затем командой ret (ближней) для возврата в точку вызова. При дальнем вызове в стек заносится также значение сегментного регистра CS, что позволяет команде ret (дальней) выполнить возврат в другой сегмент. Тип вызова определяется типом операнда команды. Если в качестве операнда указано имя подпрограммы, то тип FAR или NEAR выбирается в зависимости от описания подпрограммы. Если в качестве операнда используется слово или двойное слово памяти, то выполняется косвенный, соответственно ближний или дальний вызов подпрограммы по адресу, хранящемуся в памяти. Например. Пусть в сегменте данных описаны переменные: FADDR dd ? а в сегменте кода описаны подпрограммы: FPROC proc FAR Рассмотрим следующие примеры команд вызова: call FPROC ;Дальний прямой вызов п/п FPROC Передача параметров Программист имеет полную свободу в выборе способа передачи входных параметров в подпрограмму и выходных – из подпрограммы, важно лишь, чтобы обработка параметров в подпрограмме была согласована с заданием параметров в вызывающей программе. Чаще всего применяется передача параметров через регистры или через стек. При передаче через регистры программа перед вызовом заносит входные параметры в некоторые регистры процессора, а после возврата выбирает из регистров значения результатов. При передаче через стек программа перед вызовом заносит параметры в стек с помощью команды push. Обычно при этом считается, что подпрограмма имеет только входные параметры (как функция в языке Си). Чтобы подпрограмма могла изменять значения параметров, следует передавать ей не сами значения, а адреса параметров. Для доступа к параметрам, переданным в стеке, в начале подпрограммы обычно выполняются команды: push BP После этого можно адресовать величины в стеке, указывая их смещения относительно верхушки стека, адрес которой – в регистре BP. При подсчете смещения нужно учитывать, что команда call, как отмечалось выше, помещает в стек адрес возврата (одно или два слова). Можно применять смешанные способы передачи параметров. В частности, для подпрограмм-функций удобно возвращать результат в регистре, даже если входные параметры получены в стеке. Рассмотрим пример. Пусть подпрограмма типа near имеет два словных параметра, передаваемых через стек. В этом случае после вызова подпрограммы, сохранения и загрузки регистра BP (см. выше), стек будет выглядеть, как показано ниже:
Если описать следующую структуру: __arg struc __saveBP dw ? __retAddr dw ? __Param2 dw ? __Param1 dw ? __arg ends, то доступ к параметрам можно осуществить с помощью команд: mov AX, __Param1[BP]; загрузить в AX значение первого параметра Для облегчения чистки стека от переданных параметров используется разновидность команды ret с операндом – числом байтов, которые нужно убрать из стека сразу после возврата. ret 4 Сохранение регистров Каждая подпрограмма должна либо сохранять значения всех регистров процессора (кроме тех, которые используются для возврата результатов), либо, в крайнем случае, в описании подпрограммы должно быть четко указано, какие регистры она портит. Для сохранения регистров используется стек. Команды push служат для помещения регистров в стек, а pop – для их восстановления перед возвратом из подпрограммы. Сохранение регистров должно выполняться после загрузки BP (см. предыдущий параграф). Локальные переменные Переменные, размещенные в сегменте данных, являются статическими (аналогично переменным с классом static в Си). Конечно, их можно рассматривать как локальные переменные подпрограмм, обеспечив локализацию области действия с помощью директивы locals (см. Предположим, что в подпрограмме должно быть две локальные переменные длиной в слово. Чтобы обеспечить выделение памяти, для них перед командами сохранения регистров следует добавить команду: sub SP, 4 которая резервирует в стеке два слова. После выполнения этой команды стек будет выглядеть следующим образом:
И, если определить структуру: __locvars struc __var1 dw ? __var2 dw ? __locvars ends, то доступ к локальным переменным можно осуществить с помощью команд: mov AX, __var1[BP-4];загрузить в AX значение 1-й локальной переменной Чистка стека от локальных переменных должна выполняться после восстановления сохраненных регистров, это можно сделать с помощью команды: add SP, 4 или mov SP, BP ⇐ Предыдущая123456Следующая ⇒ Читайте также: |
Арифметические операции с BCD числами (стр. 1 из 2)
По курсу: “Системное программирование и вычислительные системы”
На тему: “Арифметические операции с BCD числами”
Содержание:
1. ДВОИЧНО-ДЕСЯТИЧНЫЙ ФОРМАТ (BCD)……………………….3
ДВОИЧНО-ДЕСЯТИЧНЫЙ ФОРМАТ (BCD)……………………….3
2. Арифметические инструкции…………………………………………..4
2.1. Форматы арифметических данных…………………………………..4
2.2. Арифметические операции и флаги…………………………………5
2.3. Сложение………………………………………………………………6
2.4. Вычитание……………………………………………………………..7
2.5. Умножение…………………………………………………………….8
2.6. Деление…………………………………………………………………9
3. ЛИТЕРАТУРА………………………………………………………….12
1. ДВОИЧНО-ДЕСЯТИЧНЫЙ ФОРМАТ (BCD)
Пусть в некотором примере деления в ASCII-формате было получено частное 00090204. Если сжать это значение, сохраняя только правые цифры каждого байта, то получим 0924. Такой формат называется двоично-десятичным (BCD — Binary Coded Decimal) (или упакованным). Он содержит только десятичные цифры от 0 до 9. Длина двоично-десятичного представления в два раза меньше ASCII-представления.
Заметим, однако, что десятичное число 0924 имеет основание 10 и, будучи преобразованным в основание 16 (т.е. в шест. представление), даст шест.039C.
представление), даст шест.039C.
ПРЕОБРАЗОВАНИЕ ASCII-ФОРМАТА В ДВОИЧНЫЙ ФОРМАТ
Выполнение арифметических операций над числами в ASCII или BCD форматах удобно лишь для коротких полей. В большинстве случаев для арифметических операций используется преобразование в двоичный формат. Практически проще преобразование из ASCII-формата непосредственно в двоичный формат, чем преобразование из ASCII- в BCD-формат и, затем, в двоичный формат:
Метод преобразования базируется на том, что ASCII-формат имеет основание 10, а компьютер выполняет арифметические операции только над числами с основанием 2. Процедура преобразования заключается в следующем:
1. Начинают с самого правого байта числа в ASCII-формате и обрабатывают справа налево.
2. Удаляют тройки из левых шест. цифр каждого ASCII-байта.
3. Умножают ASCII-цифры на 1, 10, 100 (шест.1, A, 64) и т.д. и складывают результаты.
Для примера рассмотрим преобразование числа 1234 из ASCII-формата в двоичный формат:
Десятичное Шестнадцатеричное
H
4 х 1 = 4 4
3 х 10 = 30 1E
2 х 100 = 200 C8
1 х 1000 = 1000 — 3E8 –
Результат: 04D2
Из этого примера видно, что шестнадцатеричное число .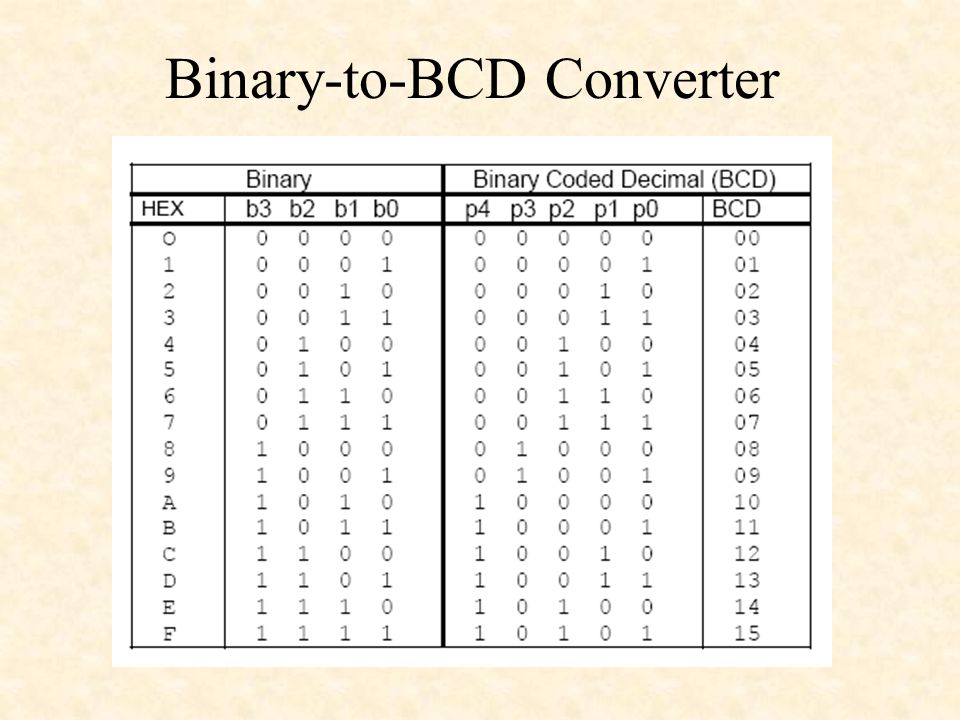 04D2 действительно соответствует десятичному 1234.
04D2 действительно соответствует десятичному 1234.
2.1. Форматы арифметических данных.
Арифметические операции процессоров 8086/8088 могут выполняться над операндами 4-х типов (таблица 2.1):
1. Двоичные без знака.
2. Двоичные со знаком (целые).
3. Упакованные десятичные без знака.
4. Распакованные десятичные без знака.
Таблица 2.1. Арифметическая интерпретация 8-битовых чисел.
| 16-ричное | битовое | дв. беззнака | дв. сознаком | распак.десятич. | упак.десят. |
| 0789C5 | 000001111000100111000101 | 7137197 | +7-119-59 | 7некорр.некорр. | 789некор. |
Двоичные числа могут занимать 1 или 2 байта. Десятичные числа хранятся побайтно по 2 десятичной цифре на байт для упакованного формата или по 1 десятичной цифре на байт для распакованного формата. Процессор предполагает, что определенные в арифметических инструкциях операнды содержат данные, представляющие корректные для данной инструкции числа. Некорректные данные могут привести к непредсказуемым результатам.
Некорректные данные могут привести к непредсказуемым результатам.
Двоичные числа без знака могут занимать 8 или 16 бит; все биты значимы. Диапазон значений 8-битового числа — от 0 до 255, 16-битового — от 0 до 65535. Над двоичными числами без знака можно выполнять операции сложения, вычитания, умножения и деления.
Двоичные числа со знаком (целые) могут занимать также 8 или 16 бит. Значение старшего бита (самого левого) задает знак числа : 0 — положительное, 1 — отрицательное. Отрицательные числа представляются стандартным дополнением до 2. Поскольку один разряд отведен под знак, диапазон изменения 8-битового числа — от -127 до +127, 16-битового -от -32768 до +32767. Число 0 имеет положительный знак. Над двоичными числами со знаком могут быть выполнены операции умножения и деления. Сложение и вычитание выполняются без учета знака. Для обнаружения переноса в знаковый разряд в результате беззнаковой операции можно использовать инструкции условного перехода.
Упакованные десятичные числа хранятся как беззнаковые байтовые величины. Каждый байт содержит 2 десятичные цифры, занимающие по 4 бита каждая. Цифра в старшем полубайте более значима. В каждом полубайте допустимы только 16-ричные значения от 0 до 9; соответственно пределы изменения десятичного числа — от 0 до 99. Сложение и вычитание таких чисел выполняются в 2 стадии. Сначала применяется обычная беззнаковая двоичная инструкция, которая формирует в регистре AL промежуточный результат. Затем выполняется операция настройки (инструкция DAA или DAS), преобразующая содержимое AL в корректный упакованный десятичный результат. Умножение и деление упакованных десятичных чисел невозможно.
Каждый байт содержит 2 десятичные цифры, занимающие по 4 бита каждая. Цифра в старшем полубайте более значима. В каждом полубайте допустимы только 16-ричные значения от 0 до 9; соответственно пределы изменения десятичного числа — от 0 до 99. Сложение и вычитание таких чисел выполняются в 2 стадии. Сначала применяется обычная беззнаковая двоичная инструкция, которая формирует в регистре AL промежуточный результат. Затем выполняется операция настройки (инструкция DAA или DAS), преобразующая содержимое AL в корректный упакованный десятичный результат. Умножение и деление упакованных десятичных чисел невозможно.
Распакованные десятичные числа хранятся как беззнаковые байтовые величины. Десятичная цифра располагается в младшем полубайте. Допустимы и интерпретируются как десятичные числа 16-ричные значения от 0 до 9. Для выполнения операций умножения и деления старший полубайт должен быть заполнен нулями; для сложения и вычитания он может содержать любое значение. Арифметические операции над распакованными десятичными числами выполняются в 2 стадии.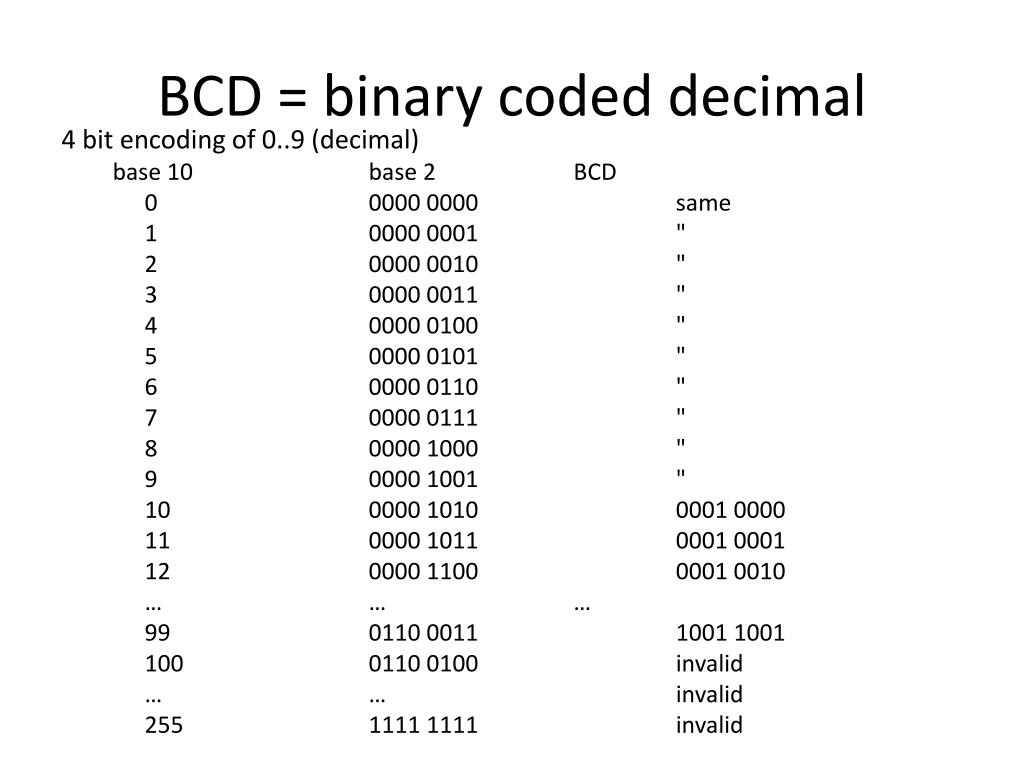 Сначала используются обычные беззнаковые инструкции сложения, вычитания или умножения, которые формируют в регистре AL промежуточный результат. Затем выполняется операция настройки (инструкция AAA,AAS или AAM), преобразующая содержимое AL в результирующее корректное распакованное десятичное число. Деление выполняется аналогично, за исключением того, что сначала следует настроить числитель в AL (инструкция AAD), а затем выполнить инструкцию беззнакового двоичного деления, результатом которого будет корректное распакованное десятичное число.
Сначала используются обычные беззнаковые инструкции сложения, вычитания или умножения, которые формируют в регистре AL промежуточный результат. Затем выполняется операция настройки (инструкция AAA,AAS или AAM), преобразующая содержимое AL в результирующее корректное распакованное десятичное число. Деление выполняется аналогично, за исключением того, что сначала следует настроить числитель в AL (инструкция AAD), а затем выполнить инструкцию беззнакового двоичного деления, результатом которого будет корректное распакованное десятичное число.
Формат десятичных распакованных чисел подобен представлению десятичных цифр в коде ASCII. При этом для числа в коде ASCII старший полубайт содержит 16-ричное значение 3. Возможное содержимое старшего полубайта для распакованного формата приведено выше. Преобразование из одного вида в другой сложности не представляет.
Арифметические инструкции процессоров 8086/8088 оставляют после своего выполнения некоторые характеристики результатов операций в виде значений 6 флагов. Большинство из них могут анализироваться последующими инструкциями условного перехода; может также использоваться инструкция прерывания по переполнению INTO. Влияние каждой инструкции на флаги указано при описании инструкции.
Большинство из них могут анализироваться последующими инструкциями условного перехода; может также использоваться инструкция прерывания по переполнению INTO. Влияние каждой инструкции на флаги указано при описании инструкции.
Однако имеются следующие общие правила:
1. Флаг переноса CF устанавливается в 1, если в результате операции сложения был перенос из старшего бита или в результате операции вычитания был заем в старший бит результата. Если же переноса или заема не было, CF устанавливается в 0. Заметим, что знаковый перенос характеризуется различными значениями флагов CF и OF. Флаг CF может использоваться для обнаружения беззнакового переполнения. Следует помнить, что 2 инструкции, ADC (сложение с переносом) и SBB (вычитание с заемом) вовлекают CF в свои операции и могут быть поэтому использованы для мультибайтного (32-, 64-разрядного) сложения и вычитания.
2. Флаг промежуточного переноса AF устанавливается в 1 при переносе из младшего полубайта результата во время сложения или при заеме в младший полубайт результата во время вычитания. Если же переноса или заема не было, AF устанавливается в 0. Флаг AF введен для выполнения десятичной настройки и обычно в других целях не используется.
Если же переноса или заема не было, AF устанавливается в 0. Флаг AF введен для выполнения десятичной настройки и обычно в других целях не используется.
3. Флаг знака SF устанавливается арифметическими и логическими инструкциями равным старшему (7-му или 15-му) биту результата. Для двоичных чисел со знаком SF будет равен 0 в случае положительного результата и 1 — в случае отрицательного (если нет переполнения). Значение флага SF может анализироваться после сложения или вычитания инструкциями условного перехода. Программы, выполняющие беззнаковые операции, обычно игнорируют SF, т.к. старший бит результата в этом случае интерпретируется как двоичная цифра, а не как знак.
4. Флаг нуля ZF устанавливается в 1, если результат арифметической или логической операции равен 0, и устанавливается в 0, если результат отличен от 0. Значение флага может анализироваться инструкциями условного перехода.
5. Флаг паритета PF устанавливается в 1, если младшие 8 бит результата арифметической или логической операции содержат четное число единиц, и устанавливается в 0, если число единиц нечетно. Флаг PF введен для совместимости с процессорами 8080/8085; он может также использоваться для контроля символов в коде ASCII на корректность паритета.
Флаг PF введен для совместимости с процессорами 8080/8085; он может также использоваться для контроля символов в коде ASCII на корректность паритета.
6. Флаг переполнения OF устанавливается в 1, если результат слишком велик для положительного числа или слишком мал для отрицательного и не помещается в операнд-приемник (не считая знаковый разряд). В противном случае значение OF -0. Состояние этого флага отражает наличие арифметического переполнения со знаком. Он может анализироваться инструкциями условного перехода или инструкцией INTO. В беззнаковых операциях OF обычно игнорируется.
ADD приемник,источник СЛОЖЕНИЕ БАЙТОВ ИЛИ СЛОВ
Арифметическая сумма 2-х операндов, которыми могут быть байты или слова, замещает операнд-приемник. Оба операнда могут содержать двоичные числа со знаком или без него (см. AAA и DAA). ADD модифицирует флаги AF, CF, OF, PF, SF и ZF.
ADC приемник,источник СЛОЖЕНИЕ С ПЕРЕНОСОМ
Эта инструкция выполняет арифметическую сумму своих операндов, добавляет 1, если установлен в 1 флаг CF, и помещает результат на место операнда-приемника. Оба операнда могут содержать двоичные числа со знаком или без него (см. AAA и DAA). ADC модифицирует флаги AF, CF, OF, PF, SF и ZF. Поскольку ADC использует перенос от предыдущей операции, она может применяться для сложения чисел длиннее 2 байтов.
Оба операнда могут содержать двоичные числа со знаком или без него (см. AAA и DAA). ADC модифицирует флаги AF, CF, OF, PF, SF и ZF. Поскольку ADC использует перенос от предыдущей операции, она может применяться для сложения чисел длиннее 2 байтов.
1. ДВОИЧНО-ДЕСЯТИЧНЫЙ ФОРМАТ (BCD). Арифметические операции с BCD числами
Арифметические операции с BCD числами
доклад
Пусть в некотором примере деления в ASCII-формате было получено частное 00090204. Если сжать это значение, сохраняя только правые цифры каждого байта, то получим 0924. Такой формат называется двоично-десятичным (BCD — Binary Coded Decimal) (или упакованным). Он содержит только десятичные цифры от 0 до 9. Длина двоично-десятичного представления в два раза меньше ASCII-представления.
Заметим, однако, что десятичное число 0924 имеет основание 10 и, будучи преобразованным в основание 16 (т.е. в шест. представление), даст шест.039C.
ПРЕОБРАЗОВАНИЕ ASCII-ФОРМАТА В ДВОИЧНЫЙ ФОРМАТ
Выполнение арифметических операций над числами в ASCII или BCD форматах удобно лишь для коротких полей. В большинстве случаев для арифметических операций используется преобразование в двоичный формат. Практически проще преобразование из ASCII-формата непосредственно в двоичный формат, чем преобразование из ASCII- в BCD-формат и, затем, в двоичный формат:
В большинстве случаев для арифметических операций используется преобразование в двоичный формат. Практически проще преобразование из ASCII-формата непосредственно в двоичный формат, чем преобразование из ASCII- в BCD-формат и, затем, в двоичный формат:
Метод преобразования базируется на том, что ASCII-формат имеет основание 10, а компьютер выполняет арифметические операции только над числами с основанием 2. Процедура преобразования заключается в следующем:
1. Начинают с самого правого байта числа в ASCII-формате и обрабатывают справа налево.
2. Удаляют тройки из левых шест. цифр каждого ASCII-байта.
3. Умножают ASCII-цифры на 1, 10, 100 (шест.1, A, 64) и т.д. и складывают результаты.
Для примера рассмотрим преобразование числа 1234 из ASCII-формата в двоичный формат:
Десятичное Шестнадцатеричное
H
4 х 1 = 4 4
3 х 10 = 30 1E
2 х 100 = 200 C8
1 х 1000 = 1000 — 3E8 —
Результат: 04D2
Из этого примера видно, что шестнадцатеричное число . 04D2 действительно соответствует десятичному 1234.
04D2 действительно соответствует десятичному 1234.
Делись добром 😉
Зчитування сектора з диска
1.2.4 Формат FAT
Перший байт FAT називається «Описувач середовища» (Media Descriptor) або байт ID ідентифікації FAT. Він має таке ж значення, як і байт-описувач середовища, що знаходиться в BOOT-секторі логічного диска…
Интерфейс и основные принципы работы в информационной системе «MS Publisher»
1.5 Формат
В пункте меню содержаться команды для форматирования публикации или ее отдельных частей…
Микропрограммное устройство деления двоично-десятичных чисел с плавающей точкой
1. Деление двоично-десятичных чисел с плавающей точкой
…
Наладчик АО и ПО на ПК. Дисковые приводы. Установка периферийных устройств
5. ФОРМАТ DVD
Формат DVD (Digital Versatile Disk), разработанный корпорацией Sony совместно с рядом фирм, позволяет записывать на компакт-диск полнометражный фильм студийного качества. В дальнейшем стандарт дорабатывался. ..
..
Основы распараллеливания программ, их динамический анализ
4.2 Формат результатов
В качестве результата анализатор предоставляет дерево контекстов с дополнительной информацией, размещенной в вершинах: список зависимостей между витками каждого с векторами расстояний, группированные по переменным…
Представление графических данных. Преобразование форматов. Использование специальных эффектов
1.1 Формат TGA
…
Представление графических данных. Преобразование форматов. Использование специальных эффектов
1.2 Формат BMP
Формат файла BMP (сокращенно от BitMaP) — это «родной» формат растровой графики для Windows, поскольку он наиболее близко соответствует внутреннему формату Windows, в котором эта система хранит свои растровые массивы. Для имени файла…
Разработка автономного аппаратно-программного комплекса средств для подсистемы управления «Роботом-дозиметристом»
4.1.1 Формат пакетов
Передача данных по радиоканалу довольно сложный процесс, поскольку среда передачи может быть довольно сильно зашумлена, поэтому данные могут не дойти до получателя или дойти, но не целыми. По этому, чем меньше длинна пакета при передаче…
По этому, чем меньше длинна пакета при передаче…
Разработка программы по воспроизведению и обрезке mp3 и wav файлов
1.2.1 Формат WAV
WAVE или WAV является короткой формой Wave Audio File Format (реже именуемой как Аудио для Windows). Этот формат является стандартом для хранения аудио потока на ПК. Он является сферой приложения формата RIFF для хранения аудио в «цепочках»…
Создание документации в среде Enterprise Architect
RTF формат
документация программный генерация пользовательский Rich Text Format, RTF — проприетарный межплатформенный формат хранения размеченных текстовых документов, предложенный группами программистов, основавшими компании Microsoft и Adobe…
Создание и обработка изображений с помощью графического редактора растровой графики Adobe Photoshop
1.3.2 Формат GIF
Другим широко распространенным в Internet форматом является GIF
(Graphics Interchange Format). Более того, он был создан компанией CompuServe специально для передачи изображений в глобальных сетях. К моменту появления формат обладал самым эффективным методом сжатия…
К моменту появления формат обладал самым эффективным методом сжатия…
Создание и обработка изображений с помощью графического редактора растровой графики Adobe Photoshop
1.3.3 Формат BMP
Формат BMP (Bitmap) предназначен для Windows и поэтому поддерживается всеми приложениями, работающими в этой среде. Позволяет хранить полноцветные изображения в цветовой модели RGB и индексированные изображения…
Создание и обработка изображений с помощью графического редактора растровой графики Adobe Photoshop
1.3.4 Формат PNG
Само название формата, Portable Network Graphics, говорит о его предназначении — для передачи изображений в сетях. Поддерживает полноцветные изображения RGB и индексированные изображения…
Создание и обработка изображений с помощью графического редактора растровой графики Adobe Photoshop
1.3.5 Формат PSD
Формат PSD (Adobe PhotoShop Document) является внутренним для программы Adobe Photoshop. Поддерживает все типы изображений, от черно-белых штриховых до полноцветных CMYK. В нем сохраняются все сведения о документе, включая слои, каналы, контуры…
В нем сохраняются все сведения о документе, включая слои, каналы, контуры…
Табличный процессор Excel. Формат ячеек
3.5 Десятичный разряд
Количество десятичных разрядов, заданное в формате Денежный, С разделителем группы разрядов и Процентный, можно увеличить или уменьшить…
Преобразование в bcd
В вычислительных и электронных систем, двоично-десятичном BCD представляет собой класс бинарных кодирований десятичных чисел , где каждая десятичная цифра представлена фиксированным количеством битов , обычно четыре или восемь. Специальные модели битовых иногда используются для знака или по другим показаниям например, ошибка или переполнение. В байт-ориентированных систем то есть самые современные компьютеры , термин распакованы BCD обычно подразумевает полный байт для каждой цифры часто включая знак , в то время как упакованном BCD обычно кодирует два десятичных цифр в пределах одного байта, воспользовавшись тем фактом , что четыре бита достаточно , чтобы представить диапазон от 0 до 9. Основное достоинство BCD является его более точным представлением и округлением десятичных величин, а также легкость превращения в человека считываемых представлений, по сравнению с бинарными позиционными системами. Основными недостатками BCD являются небольшое увеличение сложности схем , необходимых для реализации основных арифметику и немного менее плотное хранение.
Основное достоинство BCD является его более точным представлением и округлением десятичных величин, а также легкость превращения в человека считываемых представлений, по сравнению с бинарными позиционными системами. Основными недостатками BCD являются небольшое увеличение сложности схем , необходимых для реализации основных арифметику и немного менее плотное хранение.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Операции с числами в формате BCD
- Easyelectronics.ru
- PLCforum.uz.ua
- Двоично-десятичный код
- Двоично-десятичный код
- BCD формат на Assembler в AVR Atmega
- ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА
- ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА
- Операции с числами в формате BCD
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Основы ООП C++. Урок 5. Преобразование типов
Урок 5. Преобразование типов
Операции с числами в формате BCD
Автор-составитель: Ерещенко Александр. Двоично-десятичная система счисления. Такая запись очень часто используется как промежуточный этап перевода числа из десятичной системы в двоичную или обратно. Так как 10 не является точной степенью 2, то используются не все 16 тетрад, а алгоритмы арифметических операций над многозначными числами здесь более сложны, чем в основных системах счисления.
Поскольку человеку наиболее привычны представление и арифметика в десятичной системе счисления, а для компьютера — двоичное представление и двоичная арифметика, была введена компромиссная система двоично-десятичной записи чисел.
Такая система чаще всего применяется там, где существует необходимость частого использования процедуры десятичного ввода-вывода. В таких устройсвах не всегда целесообразно предусматривать универсальный микрокод перевода двоичных чисел в десятичные и обратно по причине небольшого объема программной памяти. Преобразуем двоично-десятичное число в его десятичный эквивалент.
Преобразуем двоично-десятичное число в его десятичный эквивалент.
Каждая группа из 4 бит преобразуется в её десятичный эквивалент. Микропроцессоры используют чистые двоичные числа, однако понимают и команды преобразования в двоично-десятичную запись. Полученные двоично-десятичные числа легко представимы в десятичной записи, более понятной людям.
Арифметико-логическое устройство AVR-микроконтроллеров как и других микропроцессоров выполняет элементарные арифметические и логические операции над числами, представленными в двоичном коде. В двоичном коде считываются результаты преобразования АЦП, в двоичном коде в формате целых чисел или чисел с плавающей точкой удобно выполнять обработку результатов измерения.
Однако, когда окончательный результат отображается на индикаторе, он должен быть преобразован в десятичный формат, удобный для восприятия человеком. В настоящее время распространены два формата представления десятичных чисел в микропроцессорах — упакованный двоично-десятичный код BCD-Binary-Coded Decimal и неупакованный десятичный код [1].
Упакованный BCD-код — это такое представление десятичного числа, когда каждая десятичная цифра представляется 4-х битным двоичным позиционным кодом При этом байт содержит две десятичные цифры.
Многоразрядные BCD-числа занимают несколько смежных байт. Если число является знаковым, то для представления знака в BCD-формате отводится старшая тетрада старшего байта. Для кодирования знака можно использовать шесть двоичных кодовых комбинаций, которые не используются для представления десятичных цифр.
Это коды A-F в шестнадцатеричном представлении. Обычно для кодирования знака плюс применяют код С , а для знака минус — D. Видно, что для хранения неупакованных десятичных чисел требуется в два раза больше памяти, так как каждая цифра представляется 8-битным кодом.
На сайте www. В данной статье рассматривается программа «bin16bcd5» см. Приложение, Программа 1 , написанная Терешкиным А. Последняя программа по быстродействию, длине кода и количеству используемых регистров оказалась более эффективной, чем первая. Алгоритм программы «bin16bcd5» заключается в следующем.
Алгоритм программы «bin16bcd5» заключается в следующем.
Предположим, что имеется целое беззнаковое битное число диапазон от 0 до Очевидно, что необходимо найти 5 десятичных цифр. Способ преобразования заключается в том, чтобы, вычитая из исходного числа число , сначала определить десятичную цифру десятков тысяч.
Затем находится цифра тысяч последовательным вычитанием числа и т. Вычитание каждый раз производится до получения отрицательной разности с подсчетом числа вычитаний. При переходе к определению каждого следующего десятичного разряда в регистрах исходного числа восстанавливается последняя положительная разность. После того, как будет найдена десятичная цифра десятков, в регистрах исходного числа останется десятичная цифра единиц.
Приложение, Программа 2 преобразует целое двоичное битное число в десятичное неупакованное число. При этом используется тот же алгоритм. Из этого представления следует алгоритм преобразования Рис. На каждом шаге к двоично-десятичному результату прибавляется очередная двоичная цифра и весь результат делится на 2. На изображены двоичный регистр, который содержит исходную двоичную дробь и регистр двоично-десятичного упакованного результата.
На изображены двоичный регистр, который содержит исходную двоичную дробь и регистр двоично-десятичного упакованного результата.
Для наглядности у обоих регистров также показаны разряд единиц и положение точки, которые в памяти микропроцессора никак не представлены, но положение которых всегда строго оговорено.
Количество циклов рассматриваемого алгоритма равно количеству бит двоичной дроби. Разрядность двоично-десятичного регистра определяется требуемой точностью вычислений. Сложить эту цифру с двоично-десятичным числом означает, что ее нужно поместить в разряд единиц двоично-десятичного числа, откуда при последующем делении на два цифра A-i сдвинется в старший разряд старшей тетрады десятичной дроби. При программировании мы можем представлять, что разрядом единиц десятичной дроби является бит переноса С.
При делении на два двоично-десятичного упакованного числа, так же как и при делении двоичного числа, его сдвигают вправо на один разряд. При этом на два делится каждая тетрада, то есть каждая десятичная цифра. При делении четной десятичной цифры в соответствующем разряде снова получается десятичная цифра, и никакой коррекции не требуется.
При делении четной десятичной цифры в соответствующем разряде снова получается десятичная цифра, и никакой коррекции не требуется.
При делении на 2 нечетной десятичной цифры остаток, равный 5, должен быть добавлен к более младшему десятичному разряду, но на самом деле при двоичном сдвиге в более младшую тетраду добавляется число 8 вес старшего разряда тетрады.
Поэтому требуется коррекция результата, которая заключается в вычитании числа 3 из содержимого тех тетрад, которые после сдвига вправо имеют установленные старшие разряды. Такое представление часто используется и в десятичной системе счисления для представления очень больших или очень малых чисел.
Мантисса и порядок представляют собой целые знаковые числа. Знак мантиссы является знаком всего числа. Порядок показывает истинное положение точки вместо того, которое она занимает в изображении мантиссы. Двоичное число с плавающей точкой отличается от привычного нам десятичного тем, что точка является двоичной, то есть порядок показывает на количество двоичных а не десятичных разрядов, на которое необходимо переместить эту точку влево или вправо. Нормализованным представлением числа с плавающей точкой называют такое представление, когда мантисса является правильной дробью, и старшая ее цифра отличается от нуля.
Нормализованным представлением числа с плавающей точкой называют такое представление, когда мантисса является правильной дробью, и старшая ее цифра отличается от нуля.
Но для двоичного числа требование того, что старшая цифра отличается от нуля означает, что эта цифра равна 1. Если старшая цифра точно известна, то ее можно не хранить в памяти. Преобразование двоичных чисел в двоично-десятичные.
Перейти к: навигация , поиск. Преобразование двоичных чисел в двоично-десятичные Арифметико-логическое устройство AVR-микроконтроллеров как и других микропроцессоров выполняет элементарные арифметические и логические операции над числами, представленными в двоичном коде.
В данном разделе рассматриваются программы преобразования двоичных чисел в двоично-десятичные. Форматы представления десятичных чисел В настоящее время распространены два формата представления десятичных чисел в микропроцессорах — упакованный двоично-десятичный код BCD-Binary-Coded Decimal и неупакованный десятичный код [1]. Преобразование целых битных чисел в двоично-десятичные числа На сайте www. Преобразование двоичной дроби в двоично-десятичную дробь Двоичная дробь, по определению, представляется следующим выражением: 0.
Преобразование целых битных чисел в двоично-десятичные числа На сайте www. Преобразование двоичной дроби в двоично-десятичную дробь Двоичная дробь, по определению, представляется следующим выражением: 0.
Тест 1. Категория : ТГУ. Просмотры Статья Обсуждение Просмотр история. Личные инструменты Представиться системе.
Easyelectronics.ru
Двоично-десятичный код англ. При помощи 4 бит можно закодировать 16 цифр. Из них используются Остальные 6 комбинаций в двоично-десятичном коде являются запрещёнными. Таблица соответствия двоично-десятичного кода и десятичных цифр:. Двоично-десятичный код также применяется в телефонной связи. Для записи этих символов в двоично-десятичном коде используются запрещенные комбинации:.
1) преобразовать значение BCD в десятичное значение (D) byte bcd = ( byte)0x98;//BCD value: int decimal = (bcd & 0xF) + (((int)bcd & 0xF0).
PLCforum.uz.ua
Автор-составитель: Ерещенко Александр. Двоично-десятичная система счисления. Такая запись очень часто используется как промежуточный этап перевода числа из десятичной системы в двоичную или обратно. Так как 10 не является точной степенью 2, то используются не все 16 тетрад, а алгоритмы арифметических операций над многозначными числами здесь более сложны, чем в основных системах счисления. Поскольку человеку наиболее привычны представление и арифметика в десятичной системе счисления, а для компьютера — двоичное представление и двоичная арифметика, была введена компромиссная система двоично-десятичной записи чисел. Такая система чаще всего применяется там, где существует необходимость частого использования процедуры десятичного ввода-вывода. В таких устройсвах не всегда целесообразно предусматривать универсальный микрокод перевода двоичных чисел в десятичные и обратно по причине небольшого объема программной памяти. Преобразуем двоично-десятичное число в его десятичный эквивалент. Каждая группа из 4 бит преобразуется в её десятичный эквивалент. Микропроцессоры используют чистые двоичные числа, однако понимают и команды преобразования в двоично-десятичную запись.
Такая запись очень часто используется как промежуточный этап перевода числа из десятичной системы в двоичную или обратно. Так как 10 не является точной степенью 2, то используются не все 16 тетрад, а алгоритмы арифметических операций над многозначными числами здесь более сложны, чем в основных системах счисления. Поскольку человеку наиболее привычны представление и арифметика в десятичной системе счисления, а для компьютера — двоичное представление и двоичная арифметика, была введена компромиссная система двоично-десятичной записи чисел. Такая система чаще всего применяется там, где существует необходимость частого использования процедуры десятичного ввода-вывода. В таких устройсвах не всегда целесообразно предусматривать универсальный микрокод перевода двоичных чисел в десятичные и обратно по причине небольшого объема программной памяти. Преобразуем двоично-десятичное число в его десятичный эквивалент. Каждая группа из 4 бит преобразуется в её десятичный эквивалент. Микропроцессоры используют чистые двоичные числа, однако понимают и команды преобразования в двоично-десятичную запись.
Двоично-десятичный код
Арифметические инструкции………………………………………….. Форматы арифметических данных………………………………….. Арифметические операции и флаги………………………………… 5. Сложение……………………………………………………………… 6. Деление………………………………………………………………… 9.
В следующей итерации хотелось бы заменить метод ввода на что-то более удобоваримое. Выбор пал на ручные переключатели, которые thumbwheel switches, например Omron A7D
Двоично-десятичный код
С помощью команды Передать значение можно присваивать конкретные значения переменным. ENO имеет то же состояние сигнала, что и EN. С помощью блока MOVE команда Передать значение может копировать все типы данных длиной 8, 16 или 32 бита. Пример и биты слова состояния команды передать значение. Выходной параметр OUT содержит результат. ENO всегда имеет то же состояние сигнала, что и EN.
BCD формат на Assembler в AVR Atmega
В повседневной жизни мы имеем дело с обычными числами от 0 до 9, из которых складываем более значимые числа — двухзначные, трехзначные, четырех-, пяти-, шести-, восьми-, двадцати- и т. Эти числа представлены в так называемом, десятичном представлении. Почему так? Потому, что для представления любого числа используется 10 цифр — от 0 до 9. Мы с детства знаем этот формат, но не задумываемся о том, что он именно десятичный.
Эти числа представлены в так называемом, десятичном представлении. Почему так? Потому, что для представления любого числа используется 10 цифр — от 0 до 9. Мы с детства знаем этот формат, но не задумываемся о том, что он именно десятичный.
Форум Компании ДЭП — BCD преобразование из аналога.
ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА
Я использовал двойной алгоритм dabble для преобразования битного двоичного числа в BCD, а затем извлек 4 цифры. Я уверен, что проблема вызвана чем-то из первого процесса, где генерируются цифры BCD, но я не мог понять, в чем проблема. Вот код компонента:.
ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА
ВИДЕО ПО ТЕМЕ: Восстановление Windows 7 из резервного архива Windows (VHD) (+звук)
При этом существует два вида форматов представления десятичных чисел. Это упакованный формат BCD и распакованный. В данном формате один разряд десятичного числа помещается в один байт. А именно в младшую тетраду байта, тогда как старшая тетрада именуемая зоной заполняется единицами.
А именно в младшую тетраду байта, тогда как старшая тетрада именуемая зоной заполняется единицами.
Форум Список пользователей Все разделы прочитаны Справка Расширенный поиск.
Операции с числами в формате BCD
Имя Запомнить? Как реализовать BCD-преобразование на языке Си? Здравствуйте, уважаемые Специалисты! У меня такой вопрос. Чтобы МК выводил на ЖК дисплей цифры, их сначала нужно преобразовать из двоичного в двоично-десятичный код. На ассемблере это получается без проблем. На данный момент начал изучать язык Си.
Иногда при программировании микроконтроллеров требуется выводить на дисплей или терминал какие-то числовые данные. Это могут быть показания АЦП, значение внутренних часов, коды ошибок, состояния автомата и т. Процедура вывода числа состоит из следующих шагов, нужно преобразовать двоичное число в двоично-десятичное, перевести двоично-десятичное число в символьное представление и после этого передать полученный результат какой-то функции вывода.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит. Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному… Динамика и детерминанты показателей газоанализа юных спортсменов в восстановительном периоде после лабораторных нагрузок до отказа… Интересное: Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным… Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов… Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 9 из 43Следующая ⇒ Для получения высокой производительности компьютер выполняет aрифметические операции над числами в двоичном формате. При программировании на языках высокого уровня для обозначения порядка числа или положения десятичной запятой (точки) можно положиться на компилятор. Однако, компьютер не распознает десятичную запятую (точку) в арифметических полях. Так как двоичные числа не имеют возможности установки десятичной (или двоичной) запятой (точки), то именно программист должен подразумевать и определить порядок обрабатываемых чисел. ASCII-формат Данные, вводимые с клавиатуры, имеют ASCII-формат, например, буквы SAM имеют в памяти шестнадцатеричное представление 53414D, цифры 1234 — шест. С помощью следующих ассемблерных команд можно выполнять арифметические операции непосредственно над числами в ASCII-формате: AAA (ASCII Adjust for Addition — коррекция для сложения AAD (ASCII Adjust for Division — коррекция для деления AAM (ASCII Adjust for Multiplication — коррекция для умножения ASCII-кода) AAS (ASCII Adjust for Subtraction — коррекция для вычитания Эти команды кодируются без операндов и выполняют автоматическую коррекцию в регистре AX. Коррекция необходима, так как ASCII-код представляет так называемый распакованный десятичный формат, в то время, как компьютер выполняет арифметические операции в двоичном формате. Сложение многобайтовых ASCII-чисел требует организации цикла, который выполняет обработку справа налево с учетом переноса. Вычитание в ASCII-формате Команда AAS (ASCII Adjust for Subtraction — коррекция для вычитания ASCII-кодов) выполняется aналогично команде AAA. Команда AAS проверяет правую шест. цифру (четыре бита) в регистре AL. В случае, если эта цифра лежит между A и F или флаг AF равен 1, то из регистра AL вычитается 6, а из регистра AH вычитается 1, флаги AF и CF устанавливаются в 1. Во всех случаях команда AAS устанавливает в 0 левую шест.цифру в регистpе AL. Умножение в ASCII-формате Команда AAM (ASCII Adjust for Multiplication — коррекция для умножения ASCII-кодов) выполняет корректировку результата умножения ASCII-кодов в регистре AX. Однако, шест. цифры должны быть очищены от троек и полученные данные уже не будут являться действительными ASCII-кодами. Например, число в ASCII-формате 31323334 имеет распакованное десятичное представление 01020304. Кроме этого, надо помнить, что коррекция осуществляется только для одного байта за одно выполнение, поэтому можно умножать только oдно-байтовые поля; для более длинных полей необходима организация цикла. Команда AAM делит содержимое регистра AL на 10 (шест.0A) и записывает частное в регистр AH, а остаток в AL. Предположим, что в регистре AL содержится шест.35, а в регистре CL — шест.39. Следующие команды умножают содержимое регистра AL на содержимое CL и преобразуют результат в ASCII-формат: AX: AND CL,0FH ;Преобразовать CL в 09 AND AL,0FH ;Преобразовать AL в 05 0005 MUL CL ;Умножить AL на CL 002D AAM ;Преобразовать в распак.дес. 0405 OR AX,3030H ;Преобразовать в ASCII-ф-т 3435 Команда MUL генерирует 45 (шест.002D) в регистре AX, после чего команда AAM делит это значение на 10, записывая частное 04 в регистр AH и остаток 05 в регистр AL. Команда OR преобpазует затем распакованное десятичное число в ASCII-формат. Деление в ASCII-формате Команда AAD (ASCII Adjust for Division — коррекция для деления ASCII-кодов) выполняет корректировку ASCII-кода делимого до непосредственного деления. Однако, прежде необходимо очистить левые тройки ASCII-кодов для получения распакованного десятичного формата. AX: AND CL,0FH ;Преобразовать CL в распак.дес. AND AX,0F0FH ;Преобразовать AX в распак.дес. 0208 AAD ;Преобразовать в двоичный 001C DIV CL ;Разделить на 7 0004 Команда AAD умножает содержимое AH на 10 (шест.0A), прибавляет pезультат 20 (шест.14) к регистру AL и очищает регистр AH. Значение 001C есть шест. представление десятичного числа 28. Делитель может быть только однобайтовый от 01 до 09. Двоично-десятичный формат (BCD) В предыдущем примере деления в ASCII-формате было получено частное 00090204. В случае, если сжать это значение, сохраняя только правые цифры каждого байта, то получим 0924. Такой формат называется двоично-десятичным (BCD — Binary Coded Decimal) (или упакованным). Заметим, однако, что десятичное число 0924 имеет основание 10 и, будучи преобразованным в основание 16 (то есть, в шест. представление), даст шест.039C. Можно выполнять сложение и вычитание чисел в двоично-десятичном представлении (BCD-формате). Для этих целей имеются две корректиpующих команды: uDAA (Decimal Adjustment for Addition — десятичная коррекция для сложения) uDAS (Decimal Adjustment for Subtraction — десятичная коррекция для вычитания) Обработка полей также осуществляется по одному байту за одно выполнение. Преобразование ASCII-формата в двоичный формат Выполнение арифметических операций над числами в ASCII или BCD форматах удобно лишь для коротких полей. В большинстве случаев для арифметических операций используется преобразование в двоичный формат. Практически проще преобразование из ASCII-формата непосредственно в двоичный формат, чем преобразование из ASCII- в BCD-формат и, затем, в двоичный формат: Метод преобразования базируется на том, что ASCII-формат имеет основание 10, а компьютер выполняет арифметические операции только над числами с основанием 2. 1. Начинают с самого правого байта числа в ASCII-формате и обрабатывают справа налево. 2. Удаляют тройки из левых шест.цифр каждого ASCII-байта. 3. Умножают ASCII-цифры на 1, 10, 100 (шест.1, A, 64) и так далее и складывают результаты. Преобразование двоичного формата в Для того, чтобы напечатать или отобразить на экране арифметический pезультат, необходимо преобразовать его в ASCII-формат. Данная операция включает в себя процесс обратный предыдущему. Вместо умножения используется деление двоичного числа на 10 (шест.0A) пока результат не будет меньше 10. Остатки, которые лежат в границах от 0 до 9, образуют число в ASCII-формате. Сдвиг и округление Рассмотрим процесс округления числа до двух десятичных знаков после запятой. В случае, если число равно 12,345, то необходимо прибавить 5 к отбрасываемому разряду и сдвинуть число вправо на один десятичный разряд: Число: 12,345 Плюс 5: +5 — Округленное число: 12,350 = 12,35 В случае, если округляемое число равно 12,3455, то необходимо прибавить 50 и сдвинуть на два десятичных разряда. 12,3455 12,34555 +50 +500 — 12,3505 = 12,35 12,35055 = 12,35 К числу, имеющему шесть знаков после запятой, необходимо прибавить 5000 и сдвинуть на четыре десятичных разряда и так далее. Поскольку данные представляются в компьютере в двоичном виде, то 12345 выглядит как шест.3039. Прибавляя 5 к 3039, получим 303E, что соответствует числу 12350 в десятичном представлении. Пока все хорошо. Но вот сдвиг на одну двоичную цифру дает в результате шест.181F, или 1675 — то есть, сдвиг на одну двоичную цифру просто делит число пополам. Но нам необходим такой сдвиг, который эквивалентен сдвигу вправо на одну десятичную цифру. Такой сдвиг можно осуществить делением на 10 (шест.A): Шест.303E : Шест.A = 4D3 или дес.1235 Преобразование шест.4D3 в ASCII-формат дает число 1235. Теперь oстается лишь вставить запятую в правильную позицию числа 12,35, и можно выдать на экран округленное и сдвинутое значение. Таким образом можно округлять и сдвигать любые двоичные числа. Для трех знаков после запятой необходимо прибавить 5 и разделить на 10, для четырех знаков после запятой: прибавить 50 и pазделить на 100. Возможно вы заметили модель: фактор округления (5, 50, 500 и так далее) всегда составляет половину фактора сдвига (10, 100, 1000 и так далее). Конечно, десятичная запятая в двоичном числе только подpазумевается. Отрицательные величины Некоторые применения программ допускают наличие отрицательных величин. Знак минус может устанавливаться после числа, например, 12,34-, или перед числом -12,34. Программа может проверять наличие минуса при преобразовании в двоичный формат. Можно оставить двоичное число положительным, но установить соответствующий индикатор исходной отрицательной величины. После завершения арифметических операций знак минус при необходимости может быть вставлен в ASCII поле. В случае, если необходимо, чтобы двоичное число было также отрицательным, то можно преобразовать, как обычно, ASCII-формат в двоичный. Важно: uASCII-формат требует один байт на каждый символ. В случае, если поле содержит только цифры от 0 до 9, то замена старших троек в каждом байте на нули создает распакованный десятичный формат. Сжатие числа до двух цифр в байте создает упакованный десятичный формат. uПосле ASCII-сложения необходимо выполнить коррекцию с помощью команды AAA; после ASCII-вычитания — коррекция с помощью команды AAS. uПрежде чем выполнить ASCII-умножение, необходимо преобразовать множимое и множитель в «распакованный десятичный» формат, обнулив в каждом байте левые тройки. После умножения необходимо выполнить коррекцию результата с помощью команды AAM. uПрежде чем выполнить ASCII-деление, необходимо: uДля большинства арифметических операций используйте преобразование чисел из ASCII-формата в двоичной формат. В процессе такого преобразования проверяйте на корректность ASCII-символы: они должны быть от шест.30 до шест.39, могут содержать десятичную запятую (точку) и, возможно, знак минус. Лекция 5. ⇐ Предыдущая45678910111213Следующая ⇒ Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… |
Джонс на арифметике BCD
Джонс на арифметике BCD Часть
Сборник учебных пособий по арифметике Авторское право © 1999, Дуглас. У. Джонса, с основными изменениями, внесенными в 2002 г. Это произведение может быть передано или сохранено в электронном виде на любом компьютер, подключенный к Интернету или всемирной паутине, если это уведомление включено в копию. Физические лица могут изготавливать единичные экземпляры для собственного использования. Все остальные права защищены. |
Индекс
- Введение
- BCD Представительства
- Упакованный BCD Арифметический
- 6-битная двоично-десятичная арифметика
- ASCII-арифметика
- Аппаратная поддержка
- Прочие базы номеров
Входит в число 50 лучших сайтов по версии
Небеса программиста
по состоянию на февраль 2002 г. |
Двоично-десятичная арифметика потеряла популярность среди современных разработчиков аппаратного обеспечения, и он плохо поддерживается в большинстве современных программ. языков, но иногда это все еще уместно. Например, когда числовое поле записи в текстовом файле должно быть увеличено, методы представленное здесь, будет значительно быстрее, чем преобразование текстового значения в двоичное целое число, увеличивающееся, а затем преобразующееся обратно в текст.
Для программистов с извращенным чувством юмора эти методы могут оказаться очень опасными. эффективный способ запутать код на таких языках, как C. Эти методы также имеют историческое значение. DEC (позже Compaq, затем HP) Альфа-архитектура и более поздние расширения Intel MMX для Архитектура 80×86 обе поддержка манипулирования векторами небольших объектов, таких как упакованные пиксели в 64-битные слова; мотив для этого можно найти в гораздо более старых идеях описано здесь.
В следующих разделах предполагается, что вся арифметика выполняется в 32-битном формате. регистров (алгоритмы легко адаптируются к другим длинам слов) и
ни перенос, ни переполнение не считаются значительными. Код написан
для ясности, используя нотацию C для операторов и констант, с именованными
временные переменные всякий раз, когда цитируется подвыражение в вычислении
в тексте. Практические реализации, скорее всего, будут использовать гораздо меньше
временные переменные.
регистров (алгоритмы легко адаптируются к другим длинам слов) и
ни перенос, ни переполнение не считаются значительными. Код написан
для ясности, используя нотацию C для операторов и констант, с именованными
временные переменные всякий раз, когда цитируется подвыражение в вычислении
в тексте. Практические реализации, скорее всего, будут использовать гораздо меньше
временные переменные.
Все обсуждаемые здесь числовые представления являются беззнаковыми, хотя операция вычитания основана на использовании арифметики с дополнением до десятков, а это, в свою очередь, предполагает использование операции дополнения до десятков для отрицание. В этом случае число со старшей цифрой больше 5 можно интерпретировать как отрицательные числа.
Для беззнаковых десятичных чисел (или для чисел в дополнении до 10 с тем же
знак), обычные беззнаковые бинарные операторы сравнения остаются
применимо с этими десятичными представлениями. Таким образом, если А и
B — десятичные числа без знака, и если > — это
обычный беззнаковый оператор больше для двоичных чисел,
A>B даст правильные результаты для сравнения этих чисел.
Тем, кто интересуется происхождением описываемых здесь методов, следует прочитать очень краткое примечание и пример, показывающий, как добавлять числа BCD в двоичный файл компьютер найден на странице 66 IBM 7040 и IBM 7044 Система обработки данных Текст для учащихся, опубликовано IBM в 1963 году. Семейство компьютеров 7040 не предлагало аппаратного обеспечения. поддержка двоично-десятичной арифметики и представленный здесь материал по выполнению 6-битных Арифметика BCD практически такая же, как и в 1963 году.
Программист, заинтересованный в эффективном преобразовании BCD в двоичный, также должен ознакомьтесь с кодом в приложении I.5 документа «Супероптимизатор — Взгляд на самую маленькую программу» Генри Массалин, Проц. Второй междунар. конф. на арх. Поддержка прог. Ланг. и соч. Сис. (АСПЛОС II) опубликовано как Computer Architecture News 15 , 5 (октябрь 1987 г.).
Двоично-кодированные десятичные числа могут быть представлены несколькими способами.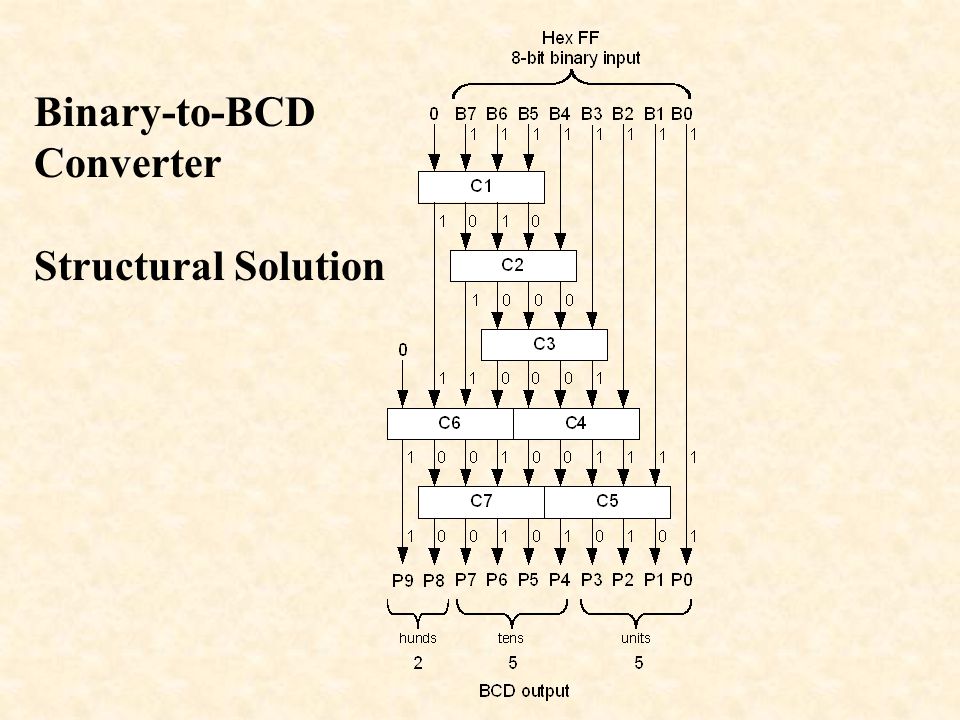 наиболее очевидным является упакованный BCD, , где каждая десятичная цифра представлена
4-битное поле, а цифры упаковываются последовательно в компьютер
слово. Эта схема позволяет упаковать 4 цифры в 16-битное слово или
8 цифр в 32-битное слово, как показано ниже.
наиболее очевидным является упакованный BCD, , где каждая десятичная цифра представлена
4-битное поле, а цифры упаковываются последовательно в компьютер
слово. Эта схема позволяет упаковать 4 цифры в 16-битное слово или
8 цифр в 32-битное слово, как показано ниже.
B31 B15 B0
|_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _|_ _ _ _ _ _ _ _ _ _ _ _ _ _ _|
|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ |_|_|_|_|_|_|_|
| Д7 | Д6 | Д5 | Д4 | Д3 | Д2 | Д1 | Д0 |
Помимо своей эффективности, этот формат полезен тем, что он совместим
с использованием шестнадцатеричных процедур ввода/вывода. Традиционно упакованный BCD был
рассматривается как требующее использования специального оборудования для выполнения двоично-десятичных арифметических операций, но в
на самом деле можно сложить два упакованных числа BCD, используя короткую последовательность
обычные бинарные и логические операторы. Многие ранние компьютеры использовали 6-битных двоично-десятичных кодов , где каждая двоично-десятичная цифра была
дополнен до 6 бит. Это было совместимо с используемыми 36, 48 и 60-битными словами.
на многих компьютерах в 1950-х и 1960-х годах, а также на 36-битных IBM 704-709
серия машин (вплоть до 7044 и 7094) и 60-битная серия CDC 6600,
этот формат использовался для выполнения двоично-десятичных арифметических операций без какой-либо специальной аппаратной поддержки.
На современной 16- или 32-битной машине это позволяет использовать 3 или чуть более 5 десятичных разрядов.
цифр в слове соответственно.
Это было совместимо с используемыми 36, 48 и 60-битными словами.
на многих компьютерах в 1950-х и 1960-х годах, а также на 36-битных IBM 704-709
серия машин (вплоть до 7044 и 7094) и 60-битная серия CDC 6600,
этот формат использовался для выполнения двоично-десятичных арифметических операций без какой-либо специальной аппаратной поддержки.
На современной 16- или 32-битной машине это позволяет использовать 3 или чуть более 5 десятичных разрядов.
цифр в слове соответственно.
B31 B15 B0
|_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _|_ _ _ _ _ _ _ _ _ _ _ _ _ _ _|
|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ |_|_|_|_|_|_|_|
| D5|0 0| D4 |0 0| Д3 |0 0| Д2 |0 0| Д1 |0 0| Д0 |
В 32-битном формате можно продуктивно использовать дробную цифру D5.
для обнаружения переноса и распространения в арифметике повышенной точности
операции. Следует отметить, что в наиболее исторически важном 6-битном двоично-десятичном кодировании
последовательности, все цифры, кроме нуля, были представлены, как показано выше,
в то время как ноль иногда представлялся двоичным кодом 1010, что позволяло
6-битный код 000000 для пробела. Единицы в двух наиболее значимых
биты каждого 6-битного байта использовались в кодах букв и знаков препинания.
Метки. Смотрите материал на
коды перфокарт
для более подробной информации по этому вопросу.
Единицы в двух наиболее значимых
биты каждого 6-битного байта использовались в кодах букв и знаков препинания.
Метки. Смотрите материал на
коды перфокарт
для более подробной информации по этому вопросу.
Обсуждаемые здесь методы могут быть распространены на другие системы заполнения в очевидные способы. Например, 6 5-битных полей можно упаковать в 32-битный слово с одним битом заполнения между двоично-десятичными цифрами. Альтернативно, 3 бита между цифрами может быть добавлено заполнение, так что 32-битное слово содержит 4 полных 7-битные поля плюс 4 бита, которые можно использовать для 5-й цифры BCD.
Заполнение каждой двоично-десятичной цифры для заполнения 8-битного байта вполне практично, но это неэффективное представление не особенно интересно, за исключением особый случай, когда каждая цифра непосредственно представлена своим Код ASCII следующим образом:
B31 B15 B0
|_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _|_ _ _ _ _ _ _ _ _ _ _ _ _ _ _|
|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ |_|_|_|_|_|_|_|
|0 0 1 1| D3 |0 0 1 1| D2 |0 0 1 1| D1 |0 0 1 1| Д0 |
Конечно, тот же подход можно использовать и для EBCDIC, используя 0xF для
цифра дополнения вместо 0x3. Довольно практично заниматься арифметикой
операции непосредственно над всеми этими представлениями!
9т2
t4 = t3 и 0x11111110
если t4 ненулевое, a недопустимо Этот код намеренно игнорирует D7, самую значащую цифру, потому что
Представленные здесь арифметические операторы позволяют этой цифре содержать значения до 15.
Чтобы понять этот код, обратите внимание, что двоичное добавление 6 к каждой цифре,
для получения t1, приведет к тому, что любая цифра со значением больше 9 будет
генерировать перенос в следующую более высокую цифру.
Довольно практично заниматься арифметикой
операции непосредственно над всеми этими представлениями!
9т2
t4 = t3 и 0x11111110
если t4 ненулевое, a недопустимо Этот код намеренно игнорирует D7, самую значащую цифру, потому что
Представленные здесь арифметические операторы позволяют этой цифре содержать значения до 15.
Чтобы понять этот код, обратите внимание, что двоичное добавление 6 к каждой цифре,
для получения t1, приведет к тому, что любая цифра со значением больше 9 будет
генерировать перенос в следующую более высокую цифру.t2 подобен t1 в том смысле, что похоже на добавление. Два будут равны в битах, где не было переноса в эту позицию, но они будут отличаться в битах, где был перенос. Следовательно, t3 содержит единицу везде, где был перенос в бит t1 и t4 содержат 1 везде, где был перенос в BCD цифра t1. Поскольку добавка, используемая для получения t1, должна не создавать такие переносы для действительного числа BCD, t4 должен быть равен нулю! 9а t3 = t2 и 0x11111110 если t3 ненулевое, a недопустимо
Вышеупомянутое улучшение было предложено Джоном Мертусом из Университета Брауна;
Здесь обратите внимание, что добавление 6 к 4-битному полубайту приводит к переносу.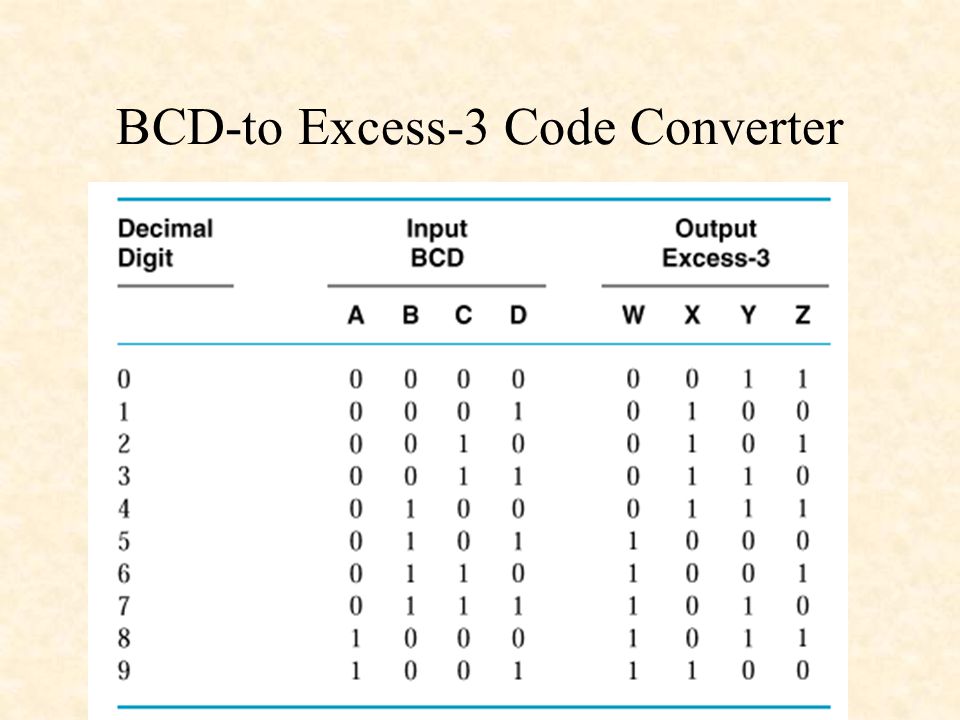 из этого полубайта, если полубайт недействителен, но также добавление 6 не
изменить младший значащий бит. Эксклюзивным объединением результата в t1
с a, чтобы сделать t2, младший бит каждого полубайта
сравнивается с оригиналом. Наконец, мы игнорируем все остальные биты и
требовать, чтобы все младшие значащие биты были равны нулю, что указывает на отсутствие переноса из
предыдущие битовые позиции.
из этого полубайта, если полубайт недействителен, но также добавление 6 не
изменить младший значащий бит. Эксклюзивным объединением результата в t1
с a, чтобы сделать t2, младший бит каждого полубайта
сравнивается с оригиналом. Наконец, мы игнорируем все остальные биты и
требовать, чтобы все младшие значащие биты были равны нулю, что указывает на отсутствие переноса из
предыдущие битовые позиции.
Антуан Швейцер-Шапут предложил альтернативную проверку достоверности мне. Обратите внимание, что все цифры BCD формы 0xxx действительны, как и цифры вида х00х. Следовательно, если d — двоично-десятичная цифра, мы можем проверить это для действительности с:
действительный (г)
если (d & 0x8) равно нулю или (d & 0x6) равно нулю
Майкл Видекинг из MATHEMA Software GMBH расширил это до упакованного BCD следующим образом:
действительный (а)
t1 = а & 0x08888888
т2 = а >> 3
t3 = t1 - t2
т4 = т3 | т1
t5 = а и t4
t6 = t5 и 0x06666666
если t6 ненулевое, a недействительно
Здесь t1 будет 1000, а t2 будет 0001 для всех цифр. больше 8 и ноль в противном случае. В результате t3 будет 0111
для всех цифр больше 8, а t4 будет 1111.
Таким образом, t6 включает только те цифры, которые были больше 8.
допустимые цифры больше 8 — это 1000 и 1001, а недопустимые цифры содержат
единицы в средних двух битах, как указано в t6.
больше 8 и ноль в противном случае. В результате t3 будет 0111
для всех цифр больше 8, а t4 будет 1111.
Таким образом, t6 включает только те цифры, которые были больше 8.
допустимые цифры больше 8 — это 1000 и 1001, а недопустимые цифры содержат
единицы в средних двух битах, как указано в t6.
В отличие от первых двух тестов на валидность, представленных выше, этот тест никогда не заставляет
перенос любой позиции цифры, поэтому его можно легко расширить для проверки
достоверность старшей цифры D7. Все, что нужно, это
расширьте каждую из двух 7-значных масок до полных 8 цифр.
9т3
t5 = ~ t4 и 0x11111110
t6 = (t5 >> 2) | (t5 >> 3)
возврат t2 — t6 Здесь добавление, используемое для формирования t1, не должно давать никаких переносов,
так как мы предполагаем, что t1 верно. Дополнение, используемое для образования
t2 произведет перенос точно тогда, когда десятичное сложение двух
цифры в операндах будут производить перенос, и это переносы, которые мы
обеспокоены.
В t2 цифры в каждой позиции, производящей перенос, будут иметь правильное значение, но цифры в позициях не производили перенос будет содержать лишние 6. Таким образом, проблема состоит в том, чтобы удалить лишние 6 из каждая цифра, которая не генерировала перенос.
Обратите внимание, что t2 и t3 различаются везде, где был перенос, поэтому t4 записывает все переносы в позиции в сумме. Следовательно, t5 содержит инверсию каждого из 7 переносов между последовательными десятичные цифры суммы. Эта битовая комбинация используется для генерации t6, где каждая цифра либо 6, где соответствующие цифры суммы сделали не генерировать перенос или 0 там, где они это сделали. Вычитая это из t2 дает правильную сумму BCD.
Обратите внимание, что старшая цифра суммы будет больше 9если там должно
были выполнять эту позицию. Кроме того, нет простого способа
чтобы обнаружить этот перенос! Значения вне диапазона в старшей цифре могут быть
ограниченное использование, но, как правило, старшая двоично-десятичная цифра должна использоваться только для
аккумулирует 7-разрядные двоично-десятичные операнды. Если его использование ограничено в
таким образом, числа всегда будут положительными и никогда не будут давать двойки.
переполнение комплемента.
Если его использование ограничено в
таким образом, числа всегда будут положительными и никогда не будут давать двойки.
переполнение комплемента.
Вычитание
Чтобы вычесть два числа, следует использовать дополнение до 10. Вычислить дополнение числа до 10, вычесть его цифра за цифрой из 99999999 (десятичное число), а затем добавьте 1 следующим образом:
тенкомп (а)
t1 = 0xF9999999 - а
вернуть добавить( t1, 0x00000001 )
Здесь t1 (в основном) является дополнением аргумента до 9, за исключением
что самая верхняя цифра является дополнением до 15 из-за избыточности
допускается в этой позиции цифры.
В этом коде есть место для оптимизации! В качестве первого шага
код для добавления был заменен на место (с соответствующими
переименование переменных).
тенкомп (а)
т1 = 0xF9т3
t5 = ~ t4 и 0x11111110
t6 = (t5 >> 2) | (t5 >> 3)
возврат t2 - t6
Проверка достоверности
Все 5 полных цифр 6-битного двоично-десятичного числа можно проверить на достоверность следующим образом:
действительный (а)
t1 = а + 006666666666
т2 = т1 и 006060606060
если t2 = 006060606060, a действительно
Чтобы понять этот код, обратите внимание, что двоичное добавление 066 к каждой цифре,
для получения t1 вызовет любую цифру со значением больше 9к
генерировать перенос в следующую более высокую цифру. Нижняя 6 заставляет выполнять
любой цифры больше 9, в то время как старшие 6 устанавливают биты заполнения и позволяют
перенос для распространения до следующей более высокой позиции цифры.
Нижняя 6 заставляет выполнять
любой цифры больше 9, в то время как старшие 6 устанавливают биты заполнения и позволяют
перенос для распространения до следующей более высокой позиции цифры.t2 содержит только биты дополнения в результате t1. Где нет перенос был распространен при вычислении t1, они будут установлены, в то время как перенос был распространен через заполнение, они будут сброшены. Действительный 6-битный двоично-десятичный код не должен генерировать никакого переноса, поэтому все биты должны быть установлены!
Дополнение
Код для добавления двух 5-значных 6-битных двоично-десятичных чисел должен решить проблему распространение переносов от одной двоично-десятичной цифры к другой, и логика выполнения поэтому основывается на только что представленных механизмах:
добавить (а, б)
т1 = а + б + 006666666666
т2 = т1 и 006060606060
вернуть t1 - (t2 >> 3)
Здесь добавление, используемое для формирования t1, добавляет дополнительные 6 к каждой двоично-десятичной цифре,
принудительный перенос этой цифры, если сумма превышает 9, и та же константа
также включает единицы в каждом бите пэда, чтобы заставить этот карри распространяться
до следующей старшей цифры.
В t1 цифры в каждой позиции, производящей перенос, будут иметь правильное значение, но цифры в позициях не производили перенос будет содержать лишнюю 6. Проблема состоит в том, чтобы удалить эту 6 из каждая цифра, которая не генерировала перенос.
t2 содержит только биты дополнения из суммы. Для тех цифр, которые не произвел перенос, биты заполнения все равно будут установлены в единицу. Для тех цифры, вызвавшие перенос, биты дополнения будут установлены в ноль распространение керри.
Сдвиг t2 на 3 позиции вправо дает 6 в каждой позиции цифры, которая не генерировал перенос и ноль в другом месте. Вычитание этого из t1 производит необходимую коррекцию!
Вынос из 5-значной двоично-десятичной суммы появится в неполной цифре D5, т.е. занимает верхние 2 бита 32-битного числа.
Вычитание
Чтобы вычесть два числа, следует использовать дополнение до 10. Вычислить дополнение до 10 5-значного 6-битного двоично-десятичного числа, вычесть его цифра за цифрой от 99999 (десятичное), а затем добавьте 1 следующим образом:
тенкомп (а)
t1 = 001111111111 - а
вернуть добавить( t1, 000000000001 )
Здесь t1 — дополнение аргумента до 9 (обратите внимание, что 11 восьмеричных
это 9 десятичных). Здесь есть большой простор для оптимизации!
Подставив определение add и переименовав переменные, чтобы избежать
столкновения, получаем:
Здесь есть большой простор для оптимизации!
Подставив определение add и переименовав переменные, чтобы избежать
столкновения, получаем:
тенкомп (а)
t1 = 001111111111 - а
t2 = t1 + 000000000001 + 006666666666
т3 = т2 и 006060606060
вернуть t2 - (t3 >> 3)
Перестановка терминов и переименование временных дает:
тенкомп (а)
t1 = (001111111111 - а)
+ 000000000001
+ 006666666666
т2 = т1 и 006060606060
вернуть t1 - (t2 >> 3)
Что упрощает:
тенкомп (а)
t1 = 010000000000 - а
т2 = т1 и 006060606060
вернуть t1 - (t2 >> 3)
Проверка достоверности
Чтобы убедиться, что 4-значная строка ASCII содержит только действительные коды BCD, методы аналогичны тем, которые используются для упакованного BCD, и можно использовать 6-битный BCD:
действительный (а)
t1 = а + 0xC6C6C6C6
t2 = t1 и 0xF0F0F0F0
если t2 = 0xF0F0F0F0, a допустимо
Чтобы понять этот код, обратите внимание, что двоичное добавление 0xC6 к каждому
цифра, для получения t1, приведет к тому, что любая цифра со значением больше
чем 9, чтобы сгенерировать перенос на следующую более высокую цифру.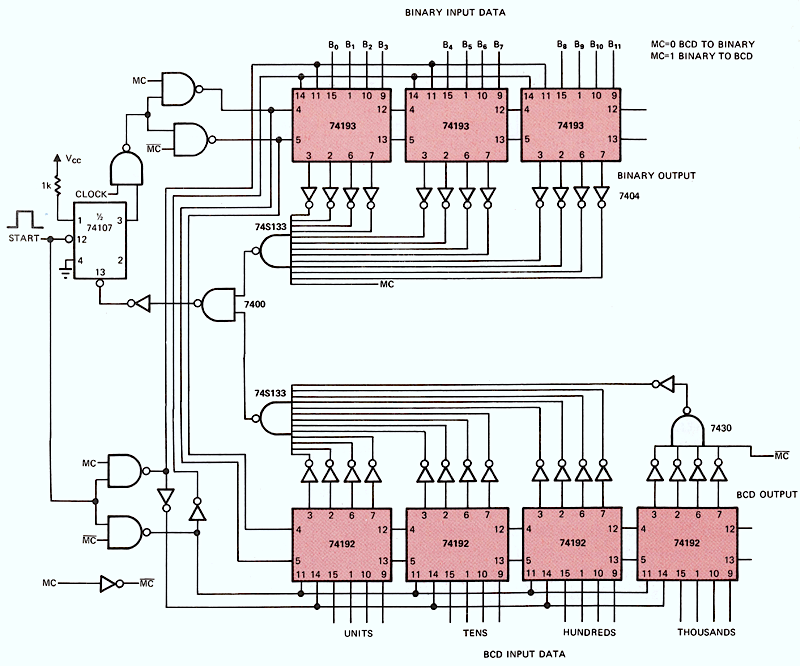 Нижние 6 сил
перенос любой цифры больше 9, в то время как более высокий 0xC устанавливает эти пэды
биты, которые еще не были установлены в ASCII-представлении цифры,
таким образом позволяя переносу распространяться до следующей более высокой позиции цифры.
Нижние 6 сил
перенос любой цифры больше 9, в то время как более высокий 0xC устанавливает эти пэды
биты, которые еще не были установлены в ASCII-представлении цифры,
таким образом позволяя переносу распространяться до следующей более высокой позиции цифры.t2 содержит только биты заполнения из t1. Где не нести были распространены при вычислении t1, они будут установлены, в то время как там, где был распространен перенос, они будут сброшены. Действительный 6-битный двоично-десятичный номер не должен был генерировать никакого переноса, поэтому все биты заполнения должны быть установлены!
Проверка достоверности усложняется, если пробел и ноль взаимозаменяемы. и еще сложнее, если допускаются только начальные пробелы. С другой рука, oring 0x10101010 с потенциальным числом преобразует все пробелы в нули, а также преобразовывать некоторые знаки препинания в другие цифры. В некоторых приложениях это может быть разумным способом работы с пробелами.
Дополнение
Код для добавления двух 4-значных номеров ASCII должен решить проблему распространение переносов от одной двоично-десятичной цифры к другой, и логика выполнения поэтому основывается на только что представленных механизмах:
добавить (а, б)
т1 = а + б + 0x96969696
t2 = t1 и 0x30303030
t3 = t1 - (t2 >> 3)
возврат (t3 и 0x0F0F0F0F) | 0x30303030
Здесь добавление, используемое для формирования t1, добавляет дополнительные 6 к каждой двоично-десятичной цифре,
принуждение к переносу этой цифры, если сумма превышает 9. Кроме того, он устанавливает
те биты заполнения, которые еще не были бы установлены дополнением, включенным в ASCII
для каждого персонажа. Эти силы распространяются до следующего старшего разряда.
Кроме того, он устанавливает
те биты заполнения, которые еще не были бы установлены дополнением, включенным в ASCII
для каждого персонажа. Эти силы распространяются до следующего старшего разряда.В t1 цифры в каждой позиции, производящей перенос, будут иметь правильное значение, но цифры в позициях не производили перенос будет содержать избыток 6.
t2 содержит два младших бита заполнения из сумма; эти биты будут равны 1, если перенос не распространялся, поэтому их можно сдвинуть из соседней цифры суммы вычесть лишние 6. Это исправлено сумма в t3 по-прежнему содержит неверные значения в полях заполнения. Независимо от того, что мы делаем, для восстановления требуется две дополнительные бинарные операции. поля pad к их правильным значениям.
Выполнение из 4-значной суммы ASCII может быть извлечено из битов заполнения. любой из временных переменных, использованных выше, поэтому цифры не тратятся впустую. ASCII-арифметика повышенной точности.
Во что бы то ни стало, если вашей целью является написание запутанного кода, и если вы язык программирования позволяет это, замените литералы ASCII на шестнадцатеричный константы везде, где это возможно, следующим образом:
добавить (а, б)
т1 = а + б + 0x96969696
t2 = t1 & '0000'
t3 = t1 - (t2 >> 3)
возврат (t3 и 0x0F0F0F0F) | '0000'
Вычитание
Чтобы вычесть два числа, следует использовать дополнение до 10. Вычислить
дополнение числа до 10, вычесть его по цифре из 9999
(десятичное число), а затем добавьте 1 следующим образом:
Вычислить
дополнение числа до 10, вычесть его по цифре из 9999
(десятичное число), а затем добавьте 1 следующим образом:
тенкомп (а)
т1 = 0x69696969 - а
вернуть добавить( t1, 0x30303031 )
Здесь t1 — дополнение аргумента до 9; сложный аспект
в данном случае заключается в том, что биты заполнения аргумента не равны нулю, поэтому константа
9999 должны быть дополнены странным образом, чтобы получить правильные результаты.
В любом случае, в этом коде есть значительный простор для оптимизации!
Подстановка кода для добавления и переименования временных дает:
тенкомп (а)
т1 = 0x69696969 - а
т2 = т1 + 0x30303031 + 0x96969696
t3 = t2 и 0x30303030
t4 = t2 - (t3 >> 3)
возврат (t4 и 0x0F0F0F0F) | 0x30303030
Объединение терминов, переименование и упрощение результата дает
следующий странный фрагмент кода:
тенкомп (а)
t1 = 0x30303030 - а
t2 = t1 и 0x30303030
t3 = t1 - (t2 >> 3)
возврат (t3 и 0x0F0F0F0F) | 0x30303030
Конечно, если ваша цель — написать обфусцированный код, обязательно
замените литералы ASCII на шестнадцатеричные константы везде, где это возможно, создав:
тенкомп (а)
t1 = '0000' - а
t2 = t1 & '0000'
t3 = t1 - (t2 >> 3)
возврат (t3 и 0x0F0F0F0F) | '0000'
Большая часть сложности приведенного выше кода обусловлена вычислениями, которые
определить перенос каждой цифры двоично-десятичной суммы. Аппаратное обеспечение, позволяющее
перенос переноса от бита к биту сумматора должен быть прерван в
выбранные точки могут значительно ускорить эти вычисления. Оба ОИК
(позже Compaq) Alpha и расширения Intel MMX для семейства 80×86
предусмотреть это, позволяя разделить 64-битные слова на множество подполей,
с прерванным распространением переноса от поля к полю и с
носители захвачены в форме, позволяющей ими манипулировать. Эти объекты
не подвергаются программисту на языке высокого уровня, но они
интенсивно используется в тщательно созданных вручную программах на языке ассемблера
для обычных векторных операций, таких как операции с пикселями
графических изображений.
9т3
t5 = ~ t4 и 0x55555554
t6 = (t5 >> 2)
возврат t2 — t6
Аппаратное обеспечение, позволяющее
перенос переноса от бита к биту сумматора должен быть прерван в
выбранные точки могут значительно ускорить эти вычисления. Оба ОИК
(позже Compaq) Alpha и расширения Intel MMX для семейства 80×86
предусмотреть это, позволяя разделить 64-битные слова на множество подполей,
с прерванным распространением переноса от поля к полю и с
носители захвачены в форме, позволяющей ими манипулировать. Эти объекты
не подвергаются программисту на языке высокого уровня, но они
интенсивно используется в тщательно созданных вручную программах на языке ассемблера
для обычных векторных операций, таких как операции с пикселями
графических изображений.
9т3
t5 = ~ t4 и 0x55555554
t6 = (t5 >> 2)
возврат t2 — t6
К сожалению, как и в случае с BCD, мы не можем использовать старшие биты для хранения еще одного цифра, потому что арифметические модели языка высокого уровня не позволяют нам зафиксировать выполнение этих битов.
Эта идея получила более полное развитие
здесь,
где дана довольно полная библиотека C, поддерживающая как беззнаковые, так и
сбалансированная тернарная арифметика.
Спасибо Сергею Фику, который 25.11.2015 указал на ошибку в оптимизированной версии алгоритма дополнения десятков BCD ASCII.
Двоично-десятичный или BCD | Brilliant Math & Science Wiki
Ариндам Кумар Пол, Грег Кевин, а также Махиндра Джайн предоставлено
Содержание
- Определение
- Примеры
- Типы
- Различия между BCD и простым двоичным представлением
- Использование двоично-десятичных чисел
BCD или двоично-десятичный — это особый вид представления десятичного числа в двоичных числах.
В двоично-десятичном коде каждая отдельная цифра числа преобразуется в двоичное число, а затем, объединяя их все, генерируется двоично-десятичный код. Но всегда помните, что десятичное число в двоичном коде не является двоичным представлением десятичного числа.
BCD или двоично-десятичное число числа 15 равно 00010101. 0001 — это двоичный код 1, а 0101 — двоичный код 5.
Любое одиночное десятичное число [0-9] может быть представлено четырехбитным шаблоном. Процедура кодирования цифр называется «Естественное двоично-десятичное число» (NBCD) , где каждая десятичная цифра представлена соответствующим ей четырехбитным двоичным значением.
Обычно BCD бывает двух видов: неупакованный и упакованный.
Распакованный двоично-десятичный код: В случае неупакованного двоично-десятичного числа каждая четырехбитная двоично-десятичная группа, соответствующая десятичной цифре, сохраняется в отдельном регистре внутри машины.
В таком случае, если размер регистров составляет восемь бит или больше, пространство регистра тратится впустую.
Упакованные числа BCD: В случае упакованных чисел BCD две цифры BCD хранятся в одном восьмибитном регистре. Процесс объединения двух двоично-десятичных цифр для их хранения в одном восьмибитном регистре включает сдвиг числа в верхнем регистре влево 4 раза, а затем сложение чисел в верхнем и нижнем регистрах.
Есть еще один, который на самом деле не считается BCD:
Invalid BCD: Некоторые числа не считаются BCD. Это 1010, 1011, 1100, 1101, 1110, 1111.
В простом двоичном представлении любого числа мы просто преобразуем целое число в его двоичную форму, многократно деля 2 снова и снова. Но в случае с BCD этого делать не нужно. Если кто знает двоичное представление чисел от 0 до 9, он/она может составить двоично-десятичный код любого числа, потому что в двоично-десятичном коде мы просто преобразуем каждую отдельную цифру любого числа в двоичное число, а затем записываем их вместе.
В случае 946 двоичное представление этого числа равно 01110110010. Здесь мы преобразуем общее число в его двоичную форму. Но когда мы формируем BCD код числа 946, это будет
9=1001,4=0100,6=0110⇒100101000110,9 = 1001, 4 = 0100, 6 = 0110 \Rightarrow 100101000110.9=1001,4=0100,6=0110⇒100101000110.
Использование BCD можно резюмировать следующим образом:
- BCD занимает больше места и больше времени, чем стандартная двоичная арифметика.
- Он широко используется в приложениях, работающих с валютой, поскольку представления с плавающей запятой по своей сути неточны. Системы управления базами данных
- предлагают множество вариантов хранения числовых значений; «Десятичный» означает, что числа хранятся внутри либо как BCD, либо как целые числа с фиксированной точкой .
- BCD предлагает относительно простой способ обойти ограничения размера в целочисленной арифметике.
Сколько битов потребуется для кодирования десятичных чисел от 0 до 9999 в прямом двоичном и двоично-десятичном кодах? Каким будет двоично-десятичный эквивалент десятичного числа 27 в 16-битном представлении?
- Общее количество десятичных знаков для представления = 10 000 = 104 = 213 29.
- Следовательно, количество битов, необходимых для прямого двоичного кодирования, = 14.
- Количество битов, необходимых для двоично-десятичного кодирования = 16,
- двоично-десятичный эквивалент числа 27 в 16-битном представлении = 0000000000100111 .
Найдите десятичное число, которое может быть представлено только единицами без нулей в двоичном формате и занимает 4 бита в двоичном формате. Другими словами, если вы преобразуете это десятичное число в двоичное, оно не может быть похоже на 10101, которое содержит 0. Он должен содержать только определенное количество единиц.
Введите ответ в виде суммы цифр двоично-десятичного числа этого десятичного числа.
Информацию о двоично-десятичном кодировании читайте в вики Binary-Coded Decimal.
Цитировать как: Двоично-десятичный код или BCD. Brilliant.org .
Извлекаются из
https://brilliant. org/wiki/binary-coded-decimal-or-bcd/
org/wiki/binary-coded-decimal-or-bcd/
BCD, ASCII И ДРУГИЕ ПРИКЛАДНЫЕ ПРОГРАММЫ
РАЗДЕЛ 6.5: BCD, ASCII И ДРУГИЕ ПРИКЛАДНЫЕ ПРОГРАММЫ
В этом В разделе мы приводим несколько реальных примеров использования арифметических и логических инструкций. Мы увидим их применение в реальных устройствах, описанных в следующих главах. Например, многие новые микроконтроллеры имеют часы реального времени (RTC), в которых время и дата сохраняются даже при выключенном питании. Эти микроконтроллеры обеспечивают время и дату в BCD. Однако для их отображения их необходимо преобразовать в ASCII. Далее мы покажем применение логики и команд ротации при преобразовании BCD и ASCII.
Таблица 6-5: Код ASCII для цифр 0–9 компьютер. Точно так же 31H (011 0001) предоставляется для клавиши «1» и т. д., как показано в Таблице 6-5.
Следует отметить, что хотя ASCII является стандартом в Соединенных Штатах (и многих других странах), числа BCD являются универсальными. Поскольку клавиатура, принтеры и мониторы используют ASCII, как данные преобразуются из ASCII в BCD и наоборот? Это темы, о которых пойдет речь далее.
Поскольку клавиатура, принтеры и мониторы используют ASCII, как данные преобразуются из ASCII в BCD и наоборот? Это темы, о которых пойдет речь далее.
Преобразование упакованного BCD в ASCII
Многие системы имеют так называемые часы реального времени (RTC). Часы реального времени постоянно отображают время суток (час, минута, секунда) и дату (год, месяц, день), независимо от того, включено питание или выключено (см. главу 16). Однако эти данные представлены в упакованном BCD. Чтобы эти данные отображались на таком устройстве, как ЖК-дисплей, или распечатывались на принтере, они должны быть в формате ASCII.
Чтобы преобразовать упакованный BCD в ASCII, его необходимо сначала преобразовать в неупакованный BCD. Затем распакованный BCD маркируется Oil 0000 (30H). Ниже показано преобразование из упакованного BCD в ASCII. См. также пример 6-34.
Преобразование ASCII в упакованный BCD
Чтобы преобразовать ASCII в упакованный BCD, он сначала преобразуется в неупакованный BCD (чтобы избавиться от 3), а затем объединяется для создания упакованного BCD. Например, для 4 и 7 клавиатура выдает 34 и 37 соответственно. Цель состоит в том, чтобы произвести 47H или «0100 0111», который упакован BCD. Этот процесс проиллюстрирован далее.
Например, для 4 и 7 клавиатура выдает 34 и 37 соответственно. Цель состоит в том, чтобы произвести 47H или «0100 0111», который упакован BCD. Этот процесс проиллюстрирован далее.
После этого преобразования обрабатываются упакованные двоично-десятичные числа, и результат будет в упакованном двоично-десятичном формате. Как мы видели ранее в этой главе, специальная инструкция «DA A» требует, чтобы данные были в упакованном двоично-десятичном формате. Пример 6-34. Это широко используемая концепция взаимодействия клавиатуры с микроконтроллером. Это показано в примере 6-35.
Пример 6-35
Предположим, что младшие три бита PI подключены к трем переключателям. Напишите программу для отправки следующих символов ASCII на P2 в зависимости от состояния коммутаторов.
Байт контрольной суммы в ПЗУ
Чтобы обеспечить целостность содержимого ПЗУ, каждая система должна выполнять вычисление контрольной суммы. Процесс контрольной суммы обнаружит любое повреждение содержимого ПЗУ. Одной из причин повреждения ПЗУ является скачок тока либо при включении системы, либо во время работы. Чтобы обеспечить целостность данных в ПЗУ, процесс контрольной суммы использует так называемый байт контрольной суммы. Байт контрольной суммы — это дополнительный байт, помеченный в конце последовательности байтов данных. Чтобы вычислить байт контрольной суммы последовательности байтов данных, можно предпринять следующие шаги.
Процесс контрольной суммы обнаружит любое повреждение содержимого ПЗУ. Одной из причин повреждения ПЗУ является скачок тока либо при включении системы, либо во время работы. Чтобы обеспечить целостность данных в ПЗУ, процесс контрольной суммы использует так называемый байт контрольной суммы. Байт контрольной суммы — это дополнительный байт, помеченный в конце последовательности байтов данных. Чтобы вычислить байт контрольной суммы последовательности байтов данных, можно предпринять следующие шаги.
Сложите байты вместе и отбросьте переносы.
Взять дополнение до 2 от общей суммы; это байт контрольной суммы, который
становится последним байтом серии.
Для выполнения операции с контрольной суммой добавьте все байты, включая байт контрольной суммы. Результат должен быть нулевым. Если он не равен нулю, один или несколько байтов данных были изменены (испорчены). Чтобы прояснить эти важные концепции, см.
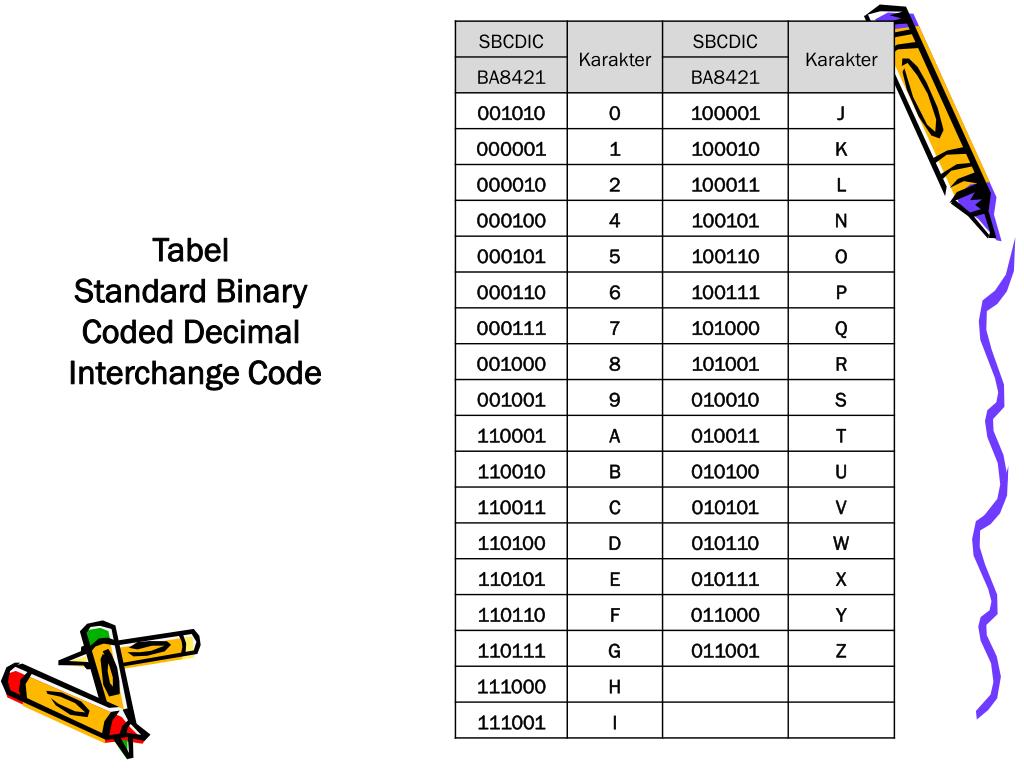 пример 6.36.
пример 6.36.
Пример 6-36
Предположим, что у нас есть 4 байта шестнадцатеричных данных: 25H, 62H, 3FH и 52H. (a) Найдите байт контрольной суммы, (b) выполните операцию проверки контрольной суммы, чтобы гарантировать целостность данных, и (c) если второй байт 62H был изменен на 22H, покажите, как контрольная сумма обнаруживает ошибку.
Программа контрольной суммы в модулях
Программа генерации и проверки контрольной суммы представлена в модульном виде. Мы разделили программу на несколько модулей (подпрограмм или подпрограмм). Разделение программы на несколько модулей (называемых функциями в программировании на C) позволяет нам использовать ее модули в других приложениях. Обычной практикой является разделение программы на несколько модулей, тестирование каждого модуля и помещение их в библиотеку. Показанная далее программа контрольной суммы состоит из трех модулей: она (а) получает данные из ПЗУ кода, (б) вычисляет байт контрольной суммы и (в) проверяет байт контрольной суммы на наличие ошибок в данных. Каждый из этих модулей можно использовать в других приложениях.
Каждый из этих модулей можно использовать в других приложениях.
Программа контрольной суммы
Преобразование двоичного (шестнадцатеричного) кода в ASCII
Многие микросхемы АЦП (аналогово-цифровой преобразователь) выдают выходные данные в двоичном (шестнадцатеричном) формате. Чтобы отобразить данные на ЖК-дисплее или экране ПК, нам нужно преобразовать их в ASCII. В следующем коде показана программа преобразования двоичного кода в ASCII. Обратите внимание, что подпрограмма получает байт 8-битных двоичных (шестнадцатеричных) данных из PI и преобразует их в десятичные цифры, а вторая подпрограмма преобразует десятичные цифры в цифры ASCII и сохраняет их. Мы сохраняем младшую цифру в ячейке с более низким адресом и старшую цифру в ячейке с более высоким адресом. Это называется соглашением Little-Endian, то есть от младшего байта к младшему и от старшего байта к старшему. Все продукты Intel используют соглашение Little-Endian.
Программа преобразования двоичных данных в ASCII
ОБЗОР
делая диапазон от 0 до 255 десятичных знаков. Подписанные данные используют 7 бит для данных и 1 для знакового бита, что составляет диапазон от -128 до +127 десятичных знаков.
Двоично-десятичные данные (BCD) представляют цифры от 0 до 9. Обсуждались как упакованные, так и неупакованные форматы BCD. 8051 содержит специальные инструкции для арифметических операций с данными BCD.
При кодировании арифметических инструкций для 8051 особое внимание следует уделить возможности переноса или переполнения.
В этой главе также определены логические инструкции И, ИЛИ, исключающее ИЛИ и дополнение. Кроме того, были описаны инструкции на языке ассемблера 8051 для этих функций. Также были описаны инструкции сравнения и перехода. Эти функции часто используются для обработки битов.
Команды поворота и перестановки 8051 используются во многих приложениях, таких как устройства с последовательным интерфейсом. В этой главе также описана проверка байтовых данных контрольной суммы, форматы BCD и ASCII и преобразования.
В этой главе также описана проверка байтовых данных контрольной суммы, форматы BCD и ASCII и преобразования.
ME Labs, Inc. | 1-719-520-5323 |
ME Labs, Inc. | 1-719-520-5323 || ME Labs, Inc. 719-520-5323 |
| Теперь вы должны быть знакомы с двоичным файлом,
Десятичный и
Шестнадцатеричная система счисления. Преобразование десятичного числа в двоично-десятичное выполняется просто. Вы просто присвоить каждой цифре десятичного числа байт и преобразовать от 0 до 9 в от 00000000 до 00001001, но вы не можете выполнить повторное деление на 2 как вы сделали, чтобы преобразовать десятичное число в двоичное. Посмотрим, как это работает. Определите значение BCD для десятичное число 5319. Поскольку в нашем десятичном числе четыре цифры, четыре байта в нашем двоично-десятичном числе. Они:
Так как память компьютера требует минимум 1 байт, вы можете видеть, что старший полубайт каждого числа BCD тратится впустую. БКД по-прежнему взвешенная позиционная система счисления, поэтому вы можете выполнять математику, но мы должны использовать специальные приемы для получения правильного ответа. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
УПАКОВАННЫЙ BCD Поскольку хранение в ОЗУ очень ценно, мы хотели бы
чтобы устранить это потраченное впустую хранилище.
Вот некоторый код PBP для упаковки 4 цифр данных BCD в 2 байта
Память. BCD1000 = 5 долларов СШАBCD100 = 3 долларов СШАBCD10 = 1 долларов СШАBCD1 = 9 долларов СШАPACKED_HIGH = (BCD1000<<4) + BCD100 PACKED_LOW = (BCD10<<4) + BCD1
|
Как выполнить преобразование упакованного BCD в ASCII?
Содержание
Как выполнить преобразование упакованного BCD в ASCII? Многие компьютерные системы или устройства имеют часы реального времени (RTC). Эти часы фактически используются для отображения времени (часы, минуты, секунды) и даты (год, месяц, день). Даже если питание включено или выключено, эта информация обрабатывается, но в двоично-десятичном формате. Для отображения этой информации на экранах устройств, ЖК-дисплеях или семи сегментах их необходимо преобразовать в формат ASCII.
Сначала упакованный двоично-десятичный код преобразуется в неупакованный двоично-десятичный, затем маскируется с помощью 30H и, наконец, преобразуется в ASCII.
Как выполнить преобразование упакованных BCD в ASCII и наоборот? Binary Coded Decimal — это система кодирования, в которой десятичные числа от 0 до 9 представлены в двоичной форме.
десятичные числа Распакованный и упакованный BCD:В байтовой ориентации двоично-десятичный код делится на две системы:
Неупакованный BCD:Неупакованный BCD — это система кодирования, в которой каждой цифре соответствует свой байт. Эта система обычно используется в современных компьютерах для точной обработки данных.
Пример: Распакованный BCD из 12 = 00000001 & 00000010
Распакованный BCD из 27 = 00000010 & 00000111
Также проверьте:
Как определить переполнение чисел со знаком и без знака?
Упакованный двоично-десятичный код: Упакованный двоично-десятичный код — это система кодирования, в которой две цифры закодированы в байте, одна цифра является старшим полубайтом, а другая цифра — младшим полубайтом.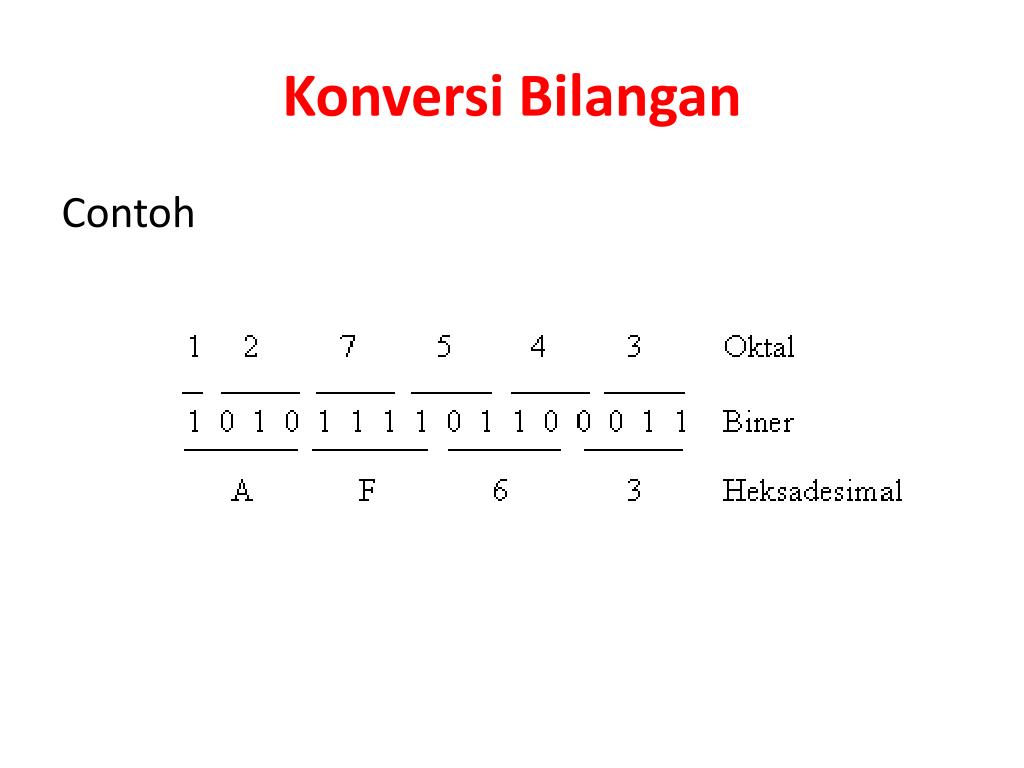
Пример: Упакованный BCD из 12 = 00010010
Упакованный BCD из 27 = 00100111
Код ASCII:
или символы. Стандартное представление этого шаблона было установлено в 1960 году, кто называет ASCII, что означает Американский стандартный код для обмена информацией. Большим преимуществом этой системы является то, что она используется на большинстве компьютеров, поэтому информация легко передается другим компьютерам. Код ASCII назначает двоичный шаблон от 0 до 9во всех алфавитах английского языка как в верхнем, так и в нижнем регистре. В системе ASCII для представления кода требуется семь битов.
Пример: 100 0010 = B
110 0011 = C
Нуль помещается в позицию старшего бита, чтобы код был восьмибитным. Код ASCII от 0 до 9:
Код ASCII Преобразование: Многие новые микроконтроллеры имеют часы реального времени (RTC), в которых данные хранятся независимо от того, включено или выключено питание. Эти микроконтроллеры предоставляют данные в BCD. Поэтому для отображения их данных на экране нам необходимо преобразовать их в ASCII.
Эти микроконтроллеры предоставляют данные в BCD. Поэтому для отображения их данных на экране нам необходимо преобразовать их в ASCII.
Часы реального времени (RTC) показывают время (часы: минуты: секунды) и дату (год: месяц: день) непрерывно, независимо от того, включено или выключено питание в современных микроконтроллерах. Однако данные предоставляются в упакованном формате BCD. Чтобы представить эти данные на экране или распечатать на принтере, они должны быть в формате ASCII. Итак, нам нужно сначала преобразовать упакованный BCD в распакованный BCD, а затем преобразовать в ASCII.
Например:
| Компенсатор плавучести в упаковке | Компенсатор плавучести без упаковки | ASCII |
| 35ч 0011 0101 | 03H и 05H 0000 0011 и 0000 0101 | 33H и 35H 0011 0011 и 0011 0101 |
| 49Х 0100 1001 | 04H и 09H 0000 0100 и 0000 1001 | 34H и 39H 0011 0100 и 0011 1001 |
Как преобразовать упакованные числа BCD в ASCII на MPLAB с помощью микроконтроллера PIC?
Here is the code first
#INCLUDE
HB1 EQU 0X06
LB1 EQU 0X07
HB2 EQU 0X32
LB2 EQU 0X33
BCD1 EQU 0X76
BCD2 EQU 0X87
ORG 0X00
MOVLW BCD1
ANDLW 0X0F
IORLW 0X30
MOVWF LB1
MOVLW BCD1
ANDLW 0XF0
SWAPF WREG,W
IORLW 0X30
MOVWF HB1
MOVLW BCD2
ANDLW 0X0F
IORLW 0X30
MOVWF LB2
MOVLW BCD2
ANDLW 0XF0
SWAPF WREG,W
IORLW 0X30
MOVWF HB2
END
Output on MPLAB
packed BCD to ASCII conversion ASCII to Packed BCD Conversion:Это обратный процесс преобразования BCD в ASCII. Сначала нам нужно преобразовать ASCII в неупакованный BCD, а затем неупакованный конвертируется в упакованный BCD.
Например:
| ASCII | Компенсатор плавучести без упаковки | Компенсатор плавучести в упаковке |
| 37H и 38H 0011 0111 и 0011 1000 | 07H и 08H 0000 0111 и 0000 1000 | 78ч 0111 1000 |
| 39H и 31H 0011 1001 и 0011 0001 | 09H и 01H 0000 1001 и 0000 0001 | 91H 1001 0001 |
ASCII в упакованное преобразование BCD в PIC на MPLAB
Код языка сборки
#include
MYBCD 0x20
ORG 0x00
MOVLW A
и MyBCF 0X.
MYBS
и MyBCF
и MyBCF
и MyBCF
и MyBCF
и MyBCF
. F
MOVLW A’2′
ANDLW 0X0F
IORWF MYBCD,F
END
BCD (двоично-десятичная система счисления)
BCD (двоично-десятичная система счисления)| Эрик Остергаард — BCD (двоично-десятичная система счисления) |
| Внизу этой страницы |
Система счисления BCD
Теперь вы должны быть знакомы с двоичным, десятичным
и шестнадцатеричная система счисления. Если мы рассмотрим однозначные значения для
hex, числа 0 — F, они представляют значения 0 — 15 в десятичном виде,
и занять кусок. Часто мы хотим использовать двоичный эквивалент
десятичная система. Эта система называется двоично-десятичной или двоично-десятичной.
также занимает откусывать. В BCD двоичные шаблоны с 1010 по 1111 делают
не представляют действительные числа BCD и не могут использоваться.
Если мы рассмотрим однозначные значения для
hex, числа 0 — F, они представляют значения 0 — 15 в десятичном виде,
и занять кусок. Часто мы хотим использовать двоичный эквивалент
десятичная система. Эта система называется двоично-десятичной или двоично-десятичной.
также занимает откусывать. В BCD двоичные шаблоны с 1010 по 1111 делают
не представляют действительные числа BCD и не могут использоваться.
Преобразование десятичного числа в двоично-десятичное выполняется просто. Ты просто назначьте каждую цифру десятичного числа байту и преобразуйте 0 через 9 до 0000 0000 до 0000 1001, но вы не можете выполнить повторное деление на 2, как вы делали для преобразования десятичного числа в двоичное.
Давайте посмотрим, как это работает. Определите значение BCD для десятичное число 5319. Так как в нашей десятичной дроби четыре цифры число, в нашем двоично-десятичном числе четыре байта. Они:
| Тысячи | Сотни | Десятки | Единицы |
| 5 | 3 | 1 | 9 |
| 0 0 0 0 0 1 0 1 | 0 0 0 0 0 0 1 1 | 0 0 0 0 0 0 0 1 | 0 0 0 0 1 0 0 1 |
Поскольку для хранения компьютера требуется как минимум 1
байт, вы можете видеть, что старший полубайт каждого числа BCD тратится впустую
хранилище. BCD по-прежнему является взвешенной позиционной системой счисления, поэтому вы можете
заниматься математикой, но мы должны использовать специальные методы, чтобы
получить правильный ответ.
BCD по-прежнему является взвешенной позиционной системой счисления, поэтому вы можете
заниматься математикой, но мы должны использовать специальные методы, чтобы
получить правильный ответ.
УПАКОВКА BCD
Поскольку хранение на диске и в ОЗУ очень ценно, мы хотел бы устранить это потраченное впустую хранилище. Это может быть выполнено путем упаковки чисел BCD. В упакованном двоично-десятичном коде каждый полубайт имеет взвешенная позиция, начиная с десятичной точки. Поэтому вместо требующих 4 байта для хранения числа BCD 5319, мы бы только требуется 2 байта, половина хранилища. Старший полубайт старшего байта нашего числа будет храниться значение ТЫСЯЧИ, в то время как нижний полубайт старшего байта будет хранить значение СОТНИ. Аналогично, чем ниже байт будет хранить значение ДЕСЯТКИ в старшем полубайте и цифру ЕДИНИЦ в нижнем клевете. Следовательно, наш предыдущий пример будет таким:
| Тысячи — сотни | Десятки — Единицы |
| 53 | 19 |
| 0 1 0 1 0 0 1 1 | 0 0 0 1 1 0 0 1 |
ПОДПРОГРАММА ДЛЯ УПАКОВКИ 2-БАЙТНОГО BCD НОМЕРА
Предположим, что буфер с именем NUMBUF содержит
двухзначный номер BCD, хранящийся в двух байтах, и мы хотим упаковать BCD
число в один байт. Мы создадим подпрограмму с именем PACKIT.
упаковать номер BCD. Давайте разработаем алгоритм для упаковки BCD
количество.
Мы создадим подпрограмму с именем PACKIT.
упаковать номер BCD. Давайте разработаем алгоритм для упаковки BCD
количество.
ПАКЕТ ПОДПРОГРАММ
При въезде:
- Регистр B содержит старший байт числа BCD.
- Регистр C содержит младший байт числа BCD.
На выходе:
- Регистр А содержит упакованный номер BCD.
Для упаковки номера мы должны:
- А <= (Б)
- Повернуть A влево 4 раза
- А <= (А) + (С)
Вот и все. Мы могли бы улучшить нашу рутину, проверив чтобы убедиться, что первое число равно нулю. Если это так, нам не нужно вращать 4 раза. Кроме того, эта подпрограмма предполагает, что число находится в формате BCD. Если мы не уверены, мы должны проверить, действительны ли числа BCD числа.
Это не сработает, если номер в ASCII. Если мы
вводили значения с клавиатуры в буфер, мы бы имели
удалить ASCII, занимающий старший полубайт, а также
проверьте допустимый номер BCD. Это довольно просто. значения ASCII для
числа, начинающиеся с 30H и заканчивающиеся на 39H.
Это довольно просто. значения ASCII для
числа, начинающиеся с 30H и заканчивающиеся на 39H.
ПАКЕТ ПОДПРОГРАММЫ ДЛЯ ЗНАЧЕНИЙ ASCII
При въезде:
- Регистр B содержит старший байт числа BCD в ASCII.
- Регистр C содержит младший байт числа BCD в ASCII.
На выходе:
- Регистр А содержит упакованный номер BCD.
Таким образом, поскольку условия входа и выхода нашей подпрограммы одинаковы, наш алгоритм теперь будет выглядеть следующим образом:
Чтобы упаковать значения ASCII в RP BC в упакованный номер BCD, мы должны:
- A <= (B) (скопировать номер в A)
- A <= (A) - 30H (проверьте, встречается ли он до 0)
- Переход по минусу к процедуре ошибки (недопустимый номер)
- Сравните с 0AH (см. выше 9)
- Переход при положительном результате к процедуре ошибки (недопустимый номер)
- Повернуть влево 4 раза, чтобы вставить верхний полубайт
- B <= (A) (сохранить старший полубайт в правильном формате)
- A <= (C) (получить младший полубайт)
- A <= (A) - 30H (проверьте, встречается ли он до 0)
- Переход по минусу к процедуре ошибки (недопустимый номер)
- Сравните с 0AH (см.
 выше 9)
выше 9) - Переход при положительном результате к процедуре ошибки (недопустимый номер)
- ADD A <= (A) + (B) (теперь запаковано)
- RET (возврат к основному состоянию после завершения подпрограммы)
Помните, что подпрограммы располагаются после нашей процедуры EXIT. в исходном коде. Теперь, когда мы увидели, как упаковать число, давайте посмотрите, что мы должны сделать в MAIN, чтобы упаковать 4-значное число. Мы просто звоните ПАКИТ. Вы бы использовали правильный алгоритм для чисел BCD или ASCII. в зависимости от того, какой формат использует ваша программа.
МОДУЛЬ ДЛЯ УПАКОВКИ A 4-ЗНАЧНЫЙ BCD НОМЕР
При входе в этот МОДУЛЬ,
- Номер находится в хранилище в 4-байтовом буфере с именем INBUF
- Упаковка будет выполняться подпрограммой PACKIT .
- Результат будет сохранен в двухбайтовом буфере с именем PAKBUF
- HL — адресный указатель на INBUF .
- DE — указатель адреса на PAKBUF .
- B содержит номер верхнего BCD
- C содержит нижний номер BCD

Алгоритм модуля
- HL <= INBUF инициализировать указатель адреса
- DE <= PAKBUF инициализировать указатель адреса
- B <= (M) на основе HL
- HL <= (HL) + (1) Увеличение точки HL до следующей цифры
- C <= (M) на основе HL
- HL <= (HL) + 1 Приращение HL к следующей цифре
- Обмен HL и DE, чтобы мы могли использовать MOV вместо STAX
- ПАКЕТ ВЫЗОВА
- M <= (A) Сохраните упакованный номер
- HL <= (HL) + 1 Увеличение точки HL до следующей цифры
- Замена HL и DE Возврат в исходное положение
- B <= (M) на основе второго запуска HL
- HL <= (HL) + 1 Приращение HL к следующей цифре
- C <= (M) на основе HL
- HL <= (HL) + 1 Приращение HL к следующей цифре
- Обмен HL и DE, чтобы мы могли использовать MOV вместо STAX
- ПАКЕТ ВЫЗОВА
- M <= (A) Сохраните упакованный номер
- HL <= (HL) + 1 Приращение HL к следующей цифре
- Поменять местами HL и DE Вернуть в исходное положение
Эти примеры специально предназначены для использования при программировании на
язык ассемблера.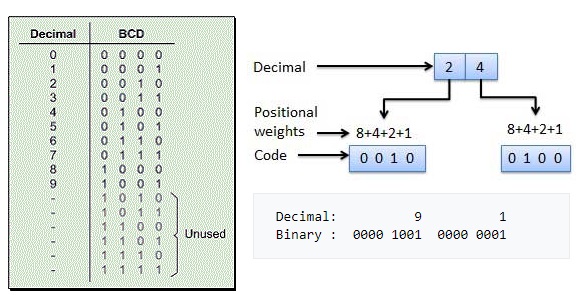
Мои источники / Мой киллер
Источники: Различные книги, Интернет, и различные энциклопедии.
Номер: Forskellige bøger, Internettet и Forskellige Leksikoner.
Компьютерное представление данных и системы счисления / Компьютерное представление данных и систематизация
- Бит(ы) и байт(ы) Преобразование / Omregn бит(ы) и байт(ы)
- Расчет примерного времени загрузки файла / Beregn anslået fil download-tid
- Термины в битах и байтах / Биты и байты udtryk
- Квантификаторы — префиксы SI (Système International) вместе с соответствующими бинарными интерпретациями.
- Пета-принцип — Статья Джима Биндера за июль-сентябрь 1994 г. Сбор/разброс.
- Этимология единиц
- Data Powers of Ten — Эти примеры
проиллюстрировать различные носители данных в зависимости от того, сколько данных
они могут хранить от одного бита до йоттабайта.


 Выполним их сложение
Выполним их сложение
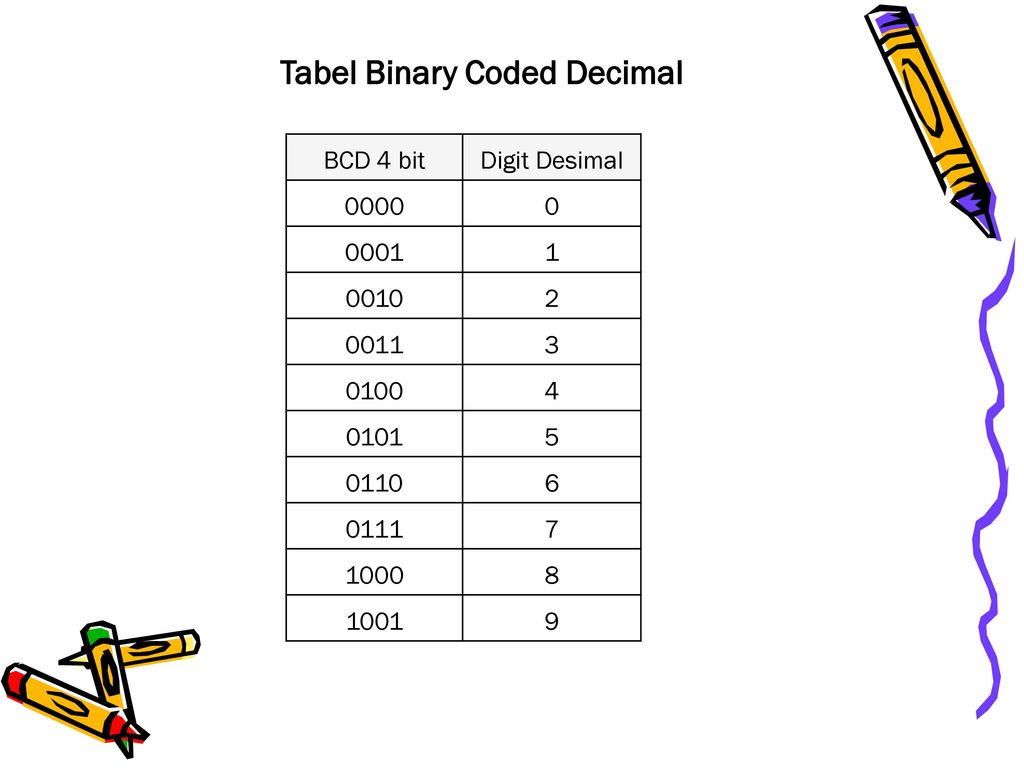 тетрады
тетрады Имеются две группы заданий стандартной (варианты 1–5) и повышенной сложности (варианты 6–8), выберите самостоятельно любой вариант из какой–либо группы.
Имеются две группы заданий стандартной (варианты 1–5) и повышенной сложности (варианты 6–8), выберите самостоятельно любой вариант из какой–либо группы.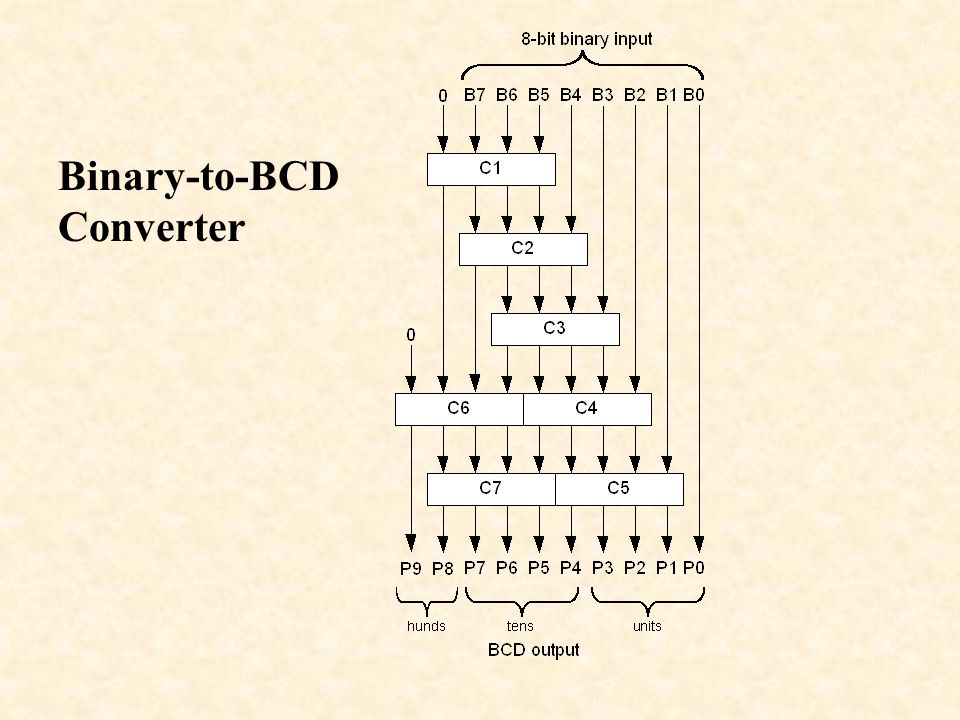

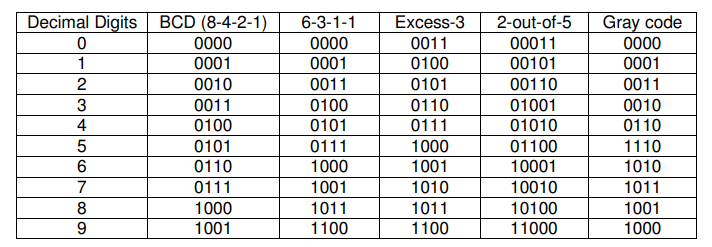
 При этом в двойном слове младшее слово содержит смещение, старшее слово — сегмент из адреса подпрограммы.
При этом в двойном слове младшее слово содержит смещение, старшее слово — сегмент из адреса подпрограммы.
 Удобно для адресации параметров описать соответствующую структуру данных.
Удобно для адресации параметров описать соответствующую структуру данных. Это позволяет вызывающей программе не заботиться об удалении параметров из стека. Для нашего примера команда возврата из подпрограммы может выглядеть следующим образом:
Это позволяет вызывающей программе не заботиться об удалении параметров из стека. Для нашего примера команда возврата из подпрограммы может выглядеть следующим образом: ниже). Однако такое статическое распределение памяти под локальные переменные не соответствует понятию локальных переменных в блочных языках типа Pascal или C, поскольку время существования таких переменных – время существования программы. Для того чтобы решить данную проблему, т.е. обеспечить динамическое распределение памяти под локальные переменные, следует выделять для них память в стеке (как это делается в Pascal или C).
ниже). Однако такое статическое распределение памяти под локальные переменные не соответствует понятию локальных переменных в блочных языках типа Pascal или C, поскольку время существования таких переменных – время существования программы. Для того чтобы решить данную проблему, т.е. обеспечить динамическое распределение памяти под локальные переменные, следует выделять для них память в стеке (как это делается в Pascal или C). . .
. .
 ..
..
 Этот формат не вызывает особых трудностей, если данные определены в самой программе. Во многих случаях новые данные вводятся программой с клавиатуры в виде ASCII символов в деcятичном формате. Аналогично вывод информации на экран осуществляется в кодах ASCII. Например, число 23 в двоичном представлении выглядит как 00010111 или шест.17; в коде ASCII на каждый cимвол требуется один байт и число 25 в ASCII-коде имеет внутpеннее представление шест.3235.
Этот формат не вызывает особых трудностей, если данные определены в самой программе. Во многих случаях новые данные вводятся программой с клавиатуры в виде ASCII символов в деcятичном формате. Аналогично вывод информации на экран осуществляется в кодах ASCII. Например, число 23 в двоичном представлении выглядит как 00010111 или шест.17; в коде ASCII на каждый cимвол требуется один байт и число 25 в ASCII-коде имеет внутpеннее представление шест.3235. 31323334. Во многих случаях формат алфавитных данных, например, имя человека или описание статьи, не меняется в программе. Но для выполнения арифметических операций над числовыми значениями, такими как шест.31323334, требуется специальная обработка.
31323334. Во многих случаях формат алфавитных данных, например, имя человека или описание статьи, не меняется в программе. Но для выполнения арифметических операций над числовыми значениями, такими как шест.31323334, требуется специальная обработка.
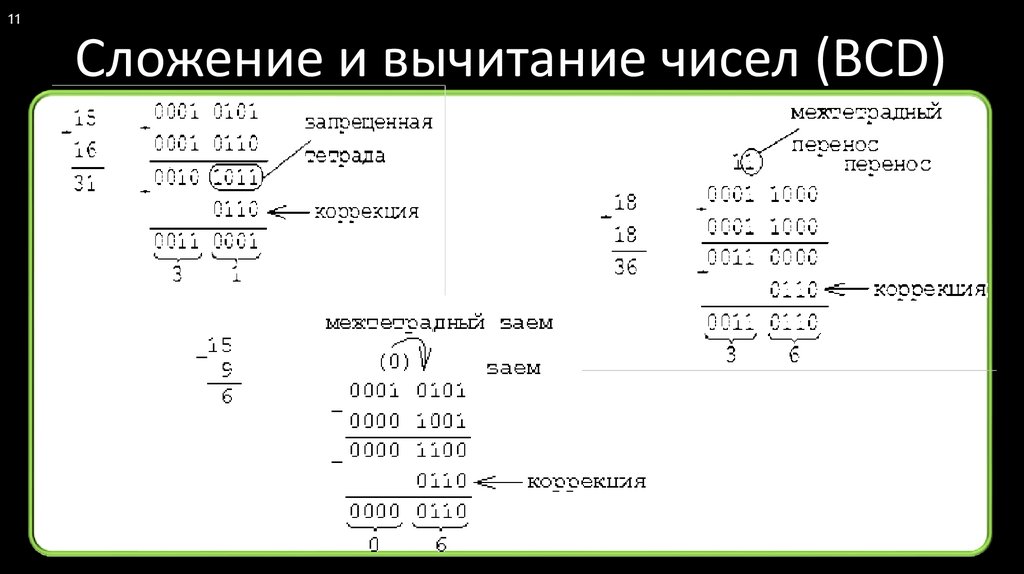 Команда AAD может оперировать с двухбайтовыми делимыми в регистре AX. Предположим, что регистр AX содержит делимое 3238 в ASCII-формате и регистр CL содержит делитель 37 также в ASCII-формате. Следующие команды выполняют коррекцию для последующего деления:
Команда AAD может оперировать с двухбайтовыми делимыми в регистре AX. Предположим, что регистр AX содержит делимое 3238 в ASCII-формате и регистр CL содержит делитель 37 также в ASCII-формате. Следующие команды выполняют коррекцию для последующего деления: Он содержит только десятичные цифры от 0 до 9. Длина двоично-десятичного представления в два раза меньше ASCII-представления.
Он содержит только десятичные цифры от 0 до 9. Длина двоично-десятичного представления в два раза меньше ASCII-представления. Процедура преобразования заключается в следующем:
Процедура преобразования заключается в следующем: Для 12,34555 необходимо прибавить 500 и сдвинуть на три десятичных разряда:
Для 12,34555 необходимо прибавить 500 и сдвинуть на три десятичных разряда:
 Будьте внимательны при использовании команд IMUL и IDIV для обработки знаковых данных. Для округления отрицательных чисел следует не прибавлять, а вычитать фактор 5.
Будьте внимательны при использовании команд IMUL и IDIV для обработки знаковых данных. Для округления отрицательных чисел следует не прибавлять, а вычитать фактор 5.
 Джонс
Джонс 
 Если мы рассмотрим однозначные значения для шестнадцатеричного числа, числа 0
— F, они представляют значения от 0 до 15 в десятичном виде и занимают полубайт. Часто мы
хотите использовать двоичный эквивалент десятичной системы. Эта система называется
Двоично-десятичный код или BCD, который также занимает полубайт. В BCD двоичный файл
шаблоны с 1010 по 1111 не представляют действительные числа BCD и не могут быть
использовал.
Если мы рассмотрим однозначные значения для шестнадцатеричного числа, числа 0
— F, они представляют значения от 0 до 15 в десятичном виде и занимают полубайт. Часто мы
хотите использовать двоичный эквивалент десятичной системы. Эта система называется
Двоично-десятичный код или BCD, который также занимает полубайт. В BCD двоичный файл
шаблоны с 1010 по 1111 не представляют действительные числа BCD и не могут быть
использовал.
 Это может быть достигнуто путем упаковки компенсатора плавучести.
числа. В упакованном двоично-десятичном числе каждый полубайт имеет взвешенную позицию, начинающуюся с
с десятичной точки. Поэтому вместо того, чтобы требовать 4 байта для хранения BCD
номер 5319, нам потребуется всего 2 байта, половина памяти. Верхний откус
старшего байта нашего числа будет хранить значение ТЫСЯЧИ, в то время как нижний
часть старшего байта будет хранить значение СОТНИ. Аналогично, чем ниже
байт будет хранить значение ДЕСЯТКИ в старшем полубайте и цифру ЕДИНИЦ в
нижний клев. Таким образом, наш предыдущий пример будет таким:
Это может быть достигнуто путем упаковки компенсатора плавучести.
числа. В упакованном двоично-десятичном числе каждый полубайт имеет взвешенную позицию, начинающуюся с
с десятичной точки. Поэтому вместо того, чтобы требовать 4 байта для хранения BCD
номер 5319, нам потребуется всего 2 байта, половина памяти. Верхний откус
старшего байта нашего числа будет хранить значение ТЫСЯЧИ, в то время как нижний
часть старшего байта будет хранить значение СОТНИ. Аналогично, чем ниже
байт будет хранить значение ДЕСЯТКИ в старшем полубайте и цифру ЕДИНИЦ в
нижний клев. Таким образом, наш предыдущий пример будет таким: Четыре цифры BCD хранятся в байтовых переменных: BCD1000,
BCD100, BCD10, BCD1. Используйте следующее для упаковки в байтовые переменные:
PACKED_HIGH и PACKED_LOW.
Четыре цифры BCD хранятся в байтовых переменных: BCD1000,
BCD100, BCD10, BCD1. Используйте следующее для упаковки в байтовые переменные:
PACKED_HIGH и PACKED_LOW.