Упакованный bcd формат: Page not found

Содержание

Смешанный десятично-двоичный формат vs IEEE754 / Хабр

В предыдущем топике был рассмотрен новый формат представления десятичных чисел с плавающей точкой, который мы назвали смешанным десятично-двоичным форматом (СДДФ).

Данный формат позволяет производить арифметические вычисления на компьютере без использования BCD с такой же точностью, как если бы вычисления велись вручную.
Напомним, что смешанным десятично — двоичным форматом (СДДФ) называется формат представления десятичных чисел с плавающей точкой двоичным кодом, в котором целочисленная мантисса является двоичным эквивалентом своего десятичного значения, а экспонента является двоичным эквивалентом степени числа 10. Вещественное число в СДДФ представляется в виде

где и e — целые двоичные числа. Под двоичным эквивалентом десятичного числа подразумевается двоичный код этого десятичного числа в выбранном формате. Под десятичным эквивалентом двоичного числа подразумевается десятичный код этого двоичного числа.

Сравним основные свойства чисел с плавающей точкой, которые представлены в стандарте IEEE754 и СДДФ. Для простоты рассмотрим 16-разрядное машинное слово. Это так называемый формат половинной точности. Результаты сравнения легко можно масштабировать на случай формата обмена одинарной и двойной точности.

16-разрядное двоичное слово разобьем на следующие поля: S,e,m. Где S-разряд знака числа, e — 5 разрядов смещенной экспоненты, m — 10 разрядов двоичного эквивалента десятичной мантиссы числа. Максимальное двоичное значение смещенной экспоненты, записанной в 5-ти разрядный регистр, будет равно emax=11111, или в десятичном виде emax=31. Смещение в этом случае равно 15.

Итак

1. Мантисса упакованного числа в IEEE754 содержит дробную часть мантиссы числа.

Мантисса числа в СДДФ представляет собой двоичное целое число.

2. Нормализованная мантисса IEEE в распакованном виде имеет вид 1.xxxxxxxxxx. Где x — любая двоичная цифра.

Поскольку мантисса нормализована, ее целая часть в распакованном виде всегда равна 1. Эту единицу можно не хранить в памяти машины. Таким образом, в распакованном виде, с учетом виртуальной единицы, мантисса будет иметь 11 бит.

Нормализованная мантисса в СДДФ является целым двоичным числом равным эквиваленту десятичного числа, которое в нашем случае представлено тремя цифрами: UХХ. Где U — любая десятичная цифра не равная нулю. Х — любая десятичная цифра.

В 10 битах мантиссы может быть представлено максимальное десятичное число 1023. Все целые числа меньше 1023 могут быть гарантировано представлены 10 битами. Следовательно, все целые десятичные числа с мантиссой ≤ 999 могут быть точно представлены 10 битами мантиссы.

3. В IEEE754 максимальная нормализованная двоичная мантисса равна Mmax=1.1111111111= 1.9990234375

Гарантированое количество верных цифр, которое можно представить двоичной 11-ти битной мантиссой равно 3.

Максимальная нормализованная десятичная мантисса в СДДФ равна Mmax=999 или в двоичном виде Mmax= 1 111 100 111. -13

12. В IEEE754 функция зависимости значения десятичного эквивалента числа Fd от его двоичного значения не является равномерной, т.к. для изменения на 1 младшего разряда десятичной мантиссы числа, как правило, необходима сумма нескольких h, равная машинному Ɛ.
Так, например, если e=0, для Fd1=1.0=1.0000000000 и Fd2=1.1≈1.0001100110 будем иметь
Fd2- Fd1=1.0001100110 -1.0000000000= 0.0001100110= 0.099609375
0.0001100110/h=0.0001100110/0.0000000001=1100110= 102=Ɛ

В СДДФ функция зависимости значения десятичного эквивалента числа Fd от его двоичного значения равномерна. Любое изменение на h двоичного эквивалента мантиссы десятичного числа влечет за собой изменение на 1 младшего разряда десятичного эквивалента числа. Здесь машинное Ɛ=1. Действительно.

Если e=0,
Fd1=100= 0001100100
Fd2=200 =0011001000
Fd2- Fd1=0011001000-0001100100= 0001100100=100= h
В заключение приведем основные характеристики представления вещественных чисел в стандарте IEEE754 и СДДФ для формата обмена, состоящего из 32 разрядов (single-precision в стандарте IEEE754). -57
Точность представления вещественных десятичных чисел равна 7 значащим десятичным цифрам.
1.4. Представление данных | Электронная библиотека
Информатика и вычислительная техника / Организация ЭВМ и систем / 1.4. Представление данных
При рассмотрении организации памяти ЭВМ данные трактовались с точки зрения их разрядности. Здесь мы рассмотрим логическую интерпретацию типов данных.

Целые числа
Система команд ЭВМ поддерживает работу с числами, находящимися в байте, слове или двойном слове. Различаются числа без знака и числа со знаком.
Целые числа без знака представляются в двоичном виде. Каждое такое число состоит из k бит, где k=8,16 или 32.
Например, байт   представляет число 2⁷+2⁵+2³+2²=172, а слово
представляет число 7*16³+7*16²+9=30473.
Самое большое число, которое можно представить байтом, равно 255, словом — 2¹⁶-1=65535.
Целые числа со знаком представляются в виде байта, слова и двоичного слова. Диапазоны значений равны:
· байт                        -128 £ x £ 127

· слово          -32768 £ x £ 32767
· двойное слово       -2147483648 £ x £ 2147483647
Числа со знаком записываются в дополнительном коде: положительное число записывается как беззнаковое, а отрицательное число – x, при x > 0, представляется как 2^k-x, где k – количество разрядов в ячейке памяти, отведенной под число (k=8,16 или 32). Ясно, что если в этой ячейке записано некоторое беззнаковое число z, старший бит которого равен 1, то это число представляет знаковое число –(2^k-z).
Например, в байте будет записано беззнаковое число z = 172, которое превращается в число –(256-172)=-84, если рассматривать его как число со знаком.
Таким образом, представление отрицательного числа –x будет равно 2^k-x. Это представление можно получить с помощью следующих действий:
1) выписать двоичное представление числа x,
2) равные единицам разряды заменить нулями, а нули – единицами,
3) к полученному числу прибавить 1.

Например, для числа –84, производятся действия:
1) 84=2⁶+2⁴+2²z
2) инвертируем биты:
3) прибавляем 1:
Двоично-десятичные числа
Иногда затраты на перевод чисел из десятичной формы записи в двоичную, и наоборот, велики. С учетом этого предусмотрено специальное представление целых чисел, при котором эти числа представляются в виде десятичных чисел. Оно строится по следующему принципу: берется десятичная запись числа и каждая его цифра заменяется на четыре двоичные цифры. Например, число 326 заменяется на последовательность бит 001100. Этот формат называется BCD-форматом. Различают неупакованный и упакованный BCD-форматы.
Неупакованный BCD-формат. Для каждой десятичной цифры отводится один байт. Значение байта равно значению его младшей тетрады (четырех бит). Для обозн

ачения знака применяются неиспользованные тетрады. Если использовать ASCII-коды для представления цифр и знаков, то число будет состоять из символов:
            00110000=’0’,                       00110110=’6’,
            00110001=’1’,                       00110111=’7’,
            00110010=’2’,                       00111000=’8’,
            00110011=’3’,                       00111001=’9’,
            00110100=’4’,                       01=’+’,
            00110101=’5’,                       01=’-‘.
Например, число -326 будет представляться как последовательность байт ‘6’,’2’,’3’,’-‘. Это записывается как db    ‘623-‘
Неупакованный BCD-формат может состоять из произвольного фиксированного числа байт. При выполнении арифметических операций отрицательные числа могут быть представлены в дополнительном коде:- если число байт формата равно n, то отрицательное число 10
n-x. Например, при n=4, число –326 будет представляться символьной строкой ‘4769’.
Упакованный BCD-формат.

В каждом байте записаны две десятичные цифры. Число состоит из 20 цифр и занимает 10 байт. Число определяется с помощью директивы DT. Например, число x=12345 будет определено как
x    dt   12345
и состоять из двадцати цифр 00000000000000012345, каждая из которых записана в виде четырех бит. В этом случае цифры располагаются в памяти как последовательность байт 01, 01, 00000001, 00000000, 00000000, …
Первый байт будет иметь смещение (относительный адрес) x, второй – x+1, третий – x+2, и т.д.

Самый старший бит десятого байта используется для хранения знака числа.
Например,
x    dt   -12345
будет транслироваться как строка, старший байт которой равен 80, затем идут шесть нулевых байтов, а затем – байты 01,23 и 45.
Замечание. Для форматов BCD применяется также противоположный порядок хранения байтов в памяти.
Числа с плавающей точкой
Число задает значения знака, порядка и мантиссы. В частности, если под число отводится 4 байта, то эти значения записываются в поля, размеры которых равны:
· знак S – 1 бит,
· порядок E – 8 бит,
· мантисса M – 23 бита.
В этом случае 32 бита
представляют число с плавающей точкой, значение которого равно
(-1)ⁿ×2^E-127×1.M.
Следовательно, наибольшее и наименьшее значения этого числа равно

±2^255-127×(2-2^-23). Наименьшее положительное число равно 2^-127.
Например, число 1 будет представлено битами:
1=(-1)⁰*2^127-127*1.0
Напомним, что дробное число переводится в двоичную форму записи следующим образом: сначала целая часть переводится в двоичную форму, затем ставится точка и вычисляются разряды дробной части. С этой целью дробная часть сравнивается с ½, ¼, ⅛, … Если она больше или равна, то ставится 1 и из дробной части вычитается это число, а если меньше – ставится 0. Затем сравнивается со следующим числом.
Например, пусть x=. Сравниваем x с ½. Ставим 0. Сравниваем с ¼. Ставим 1 и производим действие x=—=. Сравниваем с . Ставим 0. Сравниваем с . Ставим 1 и производим действие x=—, и т.д. Получим =0.0101…
Символьные данные
Обычно в ЭВМ используются восьмиразрядные коды символов ASCII. Отметим следующие особенности:
1) Коды латинских букв упорядочены согласно алфавиту и идут без пропусков. В частности, если к коду буквы ‘a’ прибавить 1, то получится код буквы ‘b’, а ‘a’+2 будет равно ‘c’ и т.д.
2) Коды цифр упорядочены по возрастанию и идут без пропусков, значит все х, лежащие в пределах ‘0’ £ x £ ‘9’ будут цифрами.
Представление данных сопроцессора
Сопроцессор может обрабатывать 7 типов:
1) Целое число со знаком, 16 бит.
2) Короткое целое со знаком, 32 бита.
3) Длинное целое со знаком, 64 бита.
4) Целое число в упакованном BCD-формате, 10 байт.
5) Короткое вещественное число, 32 бита.
6) Длинное вещественное число, 64 бита.
7) Временное (или расширенное) вещественное число, 10 байт.
Диапазоны изменения чисел типов 1,2,3 равны соответственно
–215 £ x £ 215-1, -231 £ x £ 231-1, -263 £ x £ 263-1.
Поскольку в формате BCD старший байт отводится под знак, то в этом формате число состоит из 18 десятичных цифр и, значит, изменяется в пределах –1018 £ x £ 1018.
Короткое вещественное число занимает 32 бита, и было описано выше. Для длинного формата порядок E состоит из 11 бит, мантисса M из 53 бит. Его значение равно (-1)S*2E-1023*1.M. Для расширенного формата порядок состоит из 15 бит, мантисса M — из 64 бит, x = (-1)S*2E-16383.
Десятичный формат — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1

Спецификаторы стандартных шаблонов числовых данных в NET. [1]
Десятичный формат, используемый для отображения только целых типов. Отображает десятичные цифры, а для отрицательных чисел перед ними записывается символ минуса. Если задан спецификатор точности, то он указывает минимальное число отображаемых цифр. Если в числе больше цифр, то все они отобразятся. А если в числе меньше цифр, то слева от числа отобразятся нули. [2]
Фиксированный десятичный формат при вводе, десятичных разрядов ( Fixed decimals) — позволяет ввести в поле со счетчиком количество десятичных знаков после запятой при вводе на листе числовых констант. После задания положительного числа, запятая передвигается влево, а после задания отрицательного числа, запятая передвигается вправо. Если значение в поле со счетчиком десятичных разрядов осталось пустым или содержит нулевое значение, то десятичную запятую необходимо установить вручную. [3]
Двоично-кодированный десятичный формат представления BCD ( binary coded decimal) представляет собой числа в позиционной десятичной системе, где каждая цифра числа занимает 4 бита. Арифметические операции с BCD-числами требуют применения специального математического аппарата, малоэффективны в сравнении с обычным двоичным представлением. Но, с другой стороны, BCD оказывается очень удобным при организации клавиатурного ввода и индикации. [4]
Можно рассматривать упакованный десятичный формат как компактный способ выражения общепринятых символьно — фор — матизованных десятичных величин. Каждый байт упакованных десятичных цифр будет содержать две числовые цифры, за исключением младшего байта, который обычно будет содержать одну числовую цифру и одну цифру для изображения знака числа. Примеры десятичных величин вместе с соответствующими им упакованными форматами длиной 4 байта приведены в табл. 4.1. Хотя длины полей этих величин в каждом примере равны 4 байтам, достаточно иметь длину, равную такому количеству байтов, чтобы вместить крайнюю левую значащую ( ненулевую) упакованную десятичную цифру. Заметим, что знаковая цифра для показанных на иллюстрации величин различна для аналогичных положительных или отрицательных конфигураций.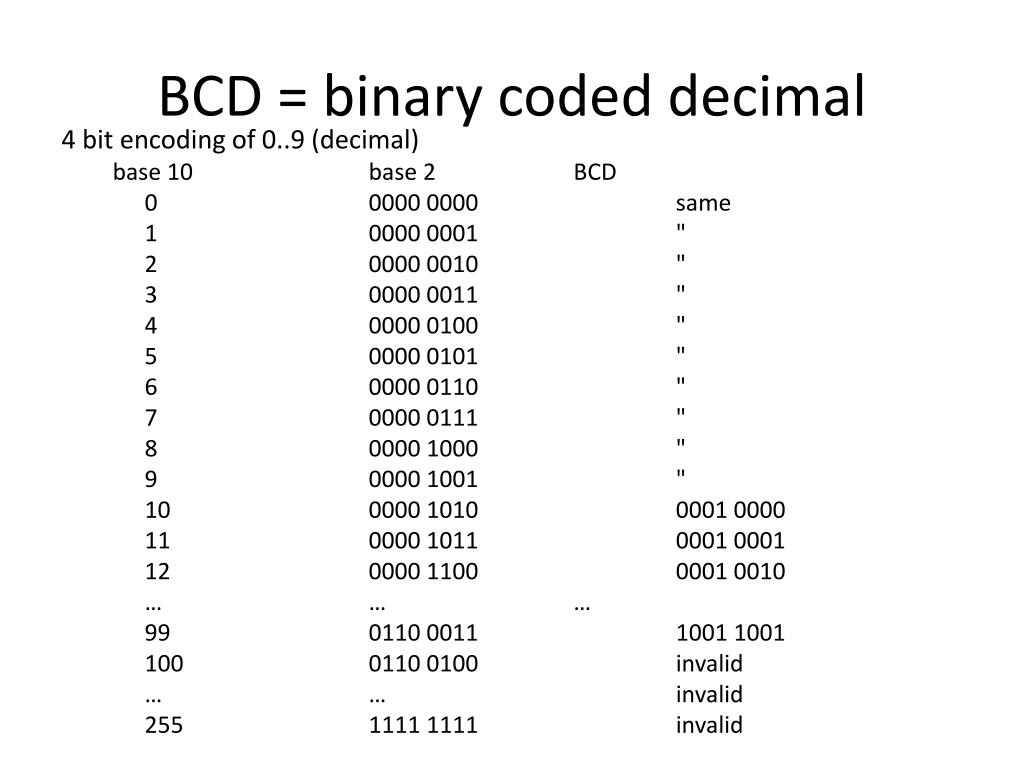 Правильный знак плюс можно представить шестнадцатеричны-ми буквенными цифрами А, С, Е или F; правильный отрицательный знак может быть представлен в виде D или В. [5]
По умолчанию принимается десятичный формат. Все разряды группы, специфицированной символами z и х, принимают такое состояние. [6]
Например, упакованный десятичный формат, предназначенный для хранения целых чисел с 18 значащими цифрами и занимающий в памяти 10 байт ( старший из которых знаковый), использует именно этот вариант. [7]
Числа в упакованном десятичном формате представляются полем из 1 или более байтов, в котором каждый отдельный полубайт содержит десятичную величину, выраженную в форме шестнадцатеричной цифры. [8]
Второй операнд имеет упакованный десятичный формат. Он проверяется на допустимость кодов знака и цифр. Наличие недопустимых кодов фиксируется как особый случай, относящийся к данным, и вызывает программное прерывание. Десятичный операнд занимает в памяти 8 байтов. Четыре младших бита поля используются для представления знака. Остальные 60 битов содержат 15 цифр в двоично-десятичном коде. Упакованный формат десятичных данных описан в гл. [9]
По умолчанию считается заданным десятичный формат для счетчиков и символьный формат для всех остальных памятей. Если длина не задана, то ее значение берется из дескриптора памяти, а для счетчика длина устанавливается равной 4 байтам. [10]
Если в поле упакованного десятичного формата содержится больше цифр, чем может поместиться в поле зонного формата, то избыточные старшие цифры теряются. [11]
Первый операнд представлен в упакованном десятичном формате. Сдвигаются только цифры операнда, знак в сдвиге не участвует. Освобожденные десятичные позиции заполняются нулями. [12]
Десятичные команды обрабатывают данные, имеющие десятичный формат, команды с плавающей точкой — данные / имеющие формат с плавающей точкой. [13]
Они преобразуются командой PACK в упакованный десятичный формат. [14]
Сравнивается содержимое первого операнда в упакованном десятичном формате с содержимым второго операнда в упакованном десятичном формате. Сравнение производится справа налево по всем цифрам обоих операндов. Если указатели длины двух операндов не равны между собой, то более короткое поле расширяется нулями со стороны старших разрядов до длины более протяженного. Двоичная конфигурация самых правых полубайтов каждого поля проверяется только с целью определения вида знака — плюс или минус. Все допустимые коды знака плюс рассматриваются как совпадающие; аналогично рассматриваются допустимые коды знака минус. Конфигурация содержимого операндов не изменяется в процессе выполнения сравнения. Максимальная подразумеваемая или явная длина для любого из сравниваемых полей равна 16 байтам. [15]
Страницы: 1 2 3 4
Двоично-десятичные числа
Другой системой счисления, которая иногда встречается, является двоично-десятичная система счисления. В этой системе числа представлены в десятичной форме, однако каждая десятичная цифра кодируется с использованием четырехбитного двоичного числа.
Двоично-десятичные числа

Другой системой счисления, которая иногда встречается, является двоично-десятичная система счисления. В этой системе числа представлены в десятичной форме, однако каждая десятичная цифра кодируется с использованием четырехбитного двоичного числа.
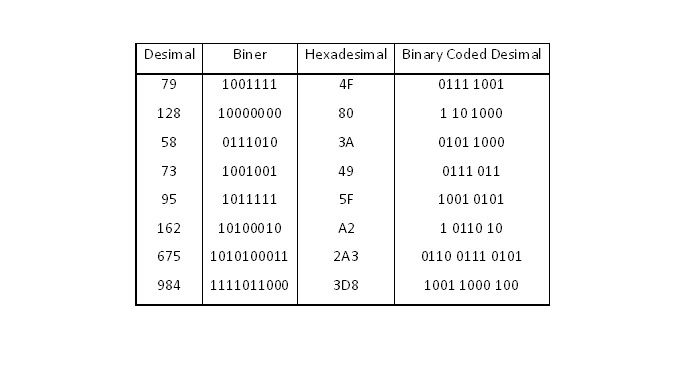
Десятичное число 136 будет представлено в BCD следующим образом: 136 = 0001 0011 0110
1 3 6
Преобразование чисел между десятичным и BCD довольно проста. Чтобы преобразовать десятичную систему в двоично-десятичную, просто запишите четырехбитный двоичный код для каждой десятичной цифры. Чтобы преобразовать двоично-десятичный формат в десятичный, разделите число на группы по 4 бита и запишите соответствующую десятичную цифру для каждой 4-битной группы.

Существует несколько вариантов представления BCD, а именно упакованный и неупакованный. В распакованном двоично-десятичном числе в каждом байте данных хранится только одна десятичная цифра. В этом случае десятичная цифра будет в младших четырех битах, а старшие 4 бита байта будут равны 0. В упакованном двоично-десятичном представлении в каждый байт помещаются две десятичные цифры. Как правило, старшие биты байта данных содержат более значащую десятичную цифру.

6. Ниже приведено 16 -битное число, кодируемое в упакованном формате BCD:
01010110 10010011
.
5 6 9 3 Значение составляет 5693 Десятиц
7. Такое же число в БКД (требуется 32 бита)
00000101 00000110 00001001 00000011
0101 00000110 00001001 00000011
00000101 00000110 00001001 00000011
00000101 00000110 00001001 000011

5          6            9            3

Использование двоично-десятичных кодов не так эффективно, как двоичная система, для представления чисел в компьютерах не так распространена. В упакованном BCD используются только 10 из 16 возможных битовых комбинаций в каждом 4-битном блоке. В распакованном BCD используется только 10 из 256 возможных битовых комбинаций в каждом байте. 16-битная величина может представлять диапазон 0-65535 в двоичном формате, 0-9999 в упакованном двоично-десятичном коде и только 0-9.9 в распакованном BCD. Мы не учитывали максимальный размер числа. Мы предположили, что доступно столько битов, сколько необходимо для представления числа. В большинстве компьютерных систем это не так. Числа в компьютерах обычно представляются с использованием фиксированного количества битов. Эти размеры обычно составляют 8 бит, 16 бит, 32 бит, 64 бит и 80 бит. Эти размеры обычно кратны 8, так как память большинства компьютеров организована на основе 8-битных байтов. Числа, в которых для представления значения используется определенное количество битов, называются числами с фиксированной точностью. Когда для представления числа используется определенное количество битов, это определяет диапазон возможных значений, которые могут быть представлены. Например, существует 256 возможных комбинаций из 8 битов, поэтому 8-битное число может представлять 256 различных числовых значений, а диапазон обычно составляет от 0 до 255. Любое число больше 255 не может быть представлено с использованием 8 бит. Точно так же

16 бит позволяют использовать диапазон от 0 до 65535.

Когда используются числа с фиксированной точностью (как это происходит практически во всех компьютерных вычислениях), необходимо учитывать концепцию переполнения. Переполнение происходит, когда результат вычисления не может быть представлен количеством доступных битов. Например, при сложении двух восьмибитных величин: 150 + 170 получается 320. Это выходит за пределы диапазона 0-255, поэтому результат не может быть представлен с использованием 8 бит. Результат превысил доступный диапазон. Когда происходит переполнение, младшие биты результата остаются действительными, но старшие биты теряются. В результате получается значение, которое значительно меньше правильного результата.

Выполняя арифметические операции с фиксированной точностью (которую включает вся компьютерная арифметика), необходимо помнить о возможности переполнения при вычислениях.

Числа со знаком и без знака.

мы рассмотрели только положительные значения для двоичных чисел. Когда двоичное число фиксированной точности используется для хранения только положительных значений, оно называется беззнаковым. В этом случае диапазон положительных значений, которые могут быть представлены, составляет 0 — 2n-1, где n — количество используемых битов. Также можно представлять числа со знаком (как отрицательные, так и положительные) в двоичном формате. В этом случае часть общего диапазона значений используется для представления положительных значений, а остальная часть диапазона используется для представления отрицательных значений.

Существует несколько способов представления чисел со знаком в двоичном виде, но наиболее распространенное сегодня представление называется дополнением до двух.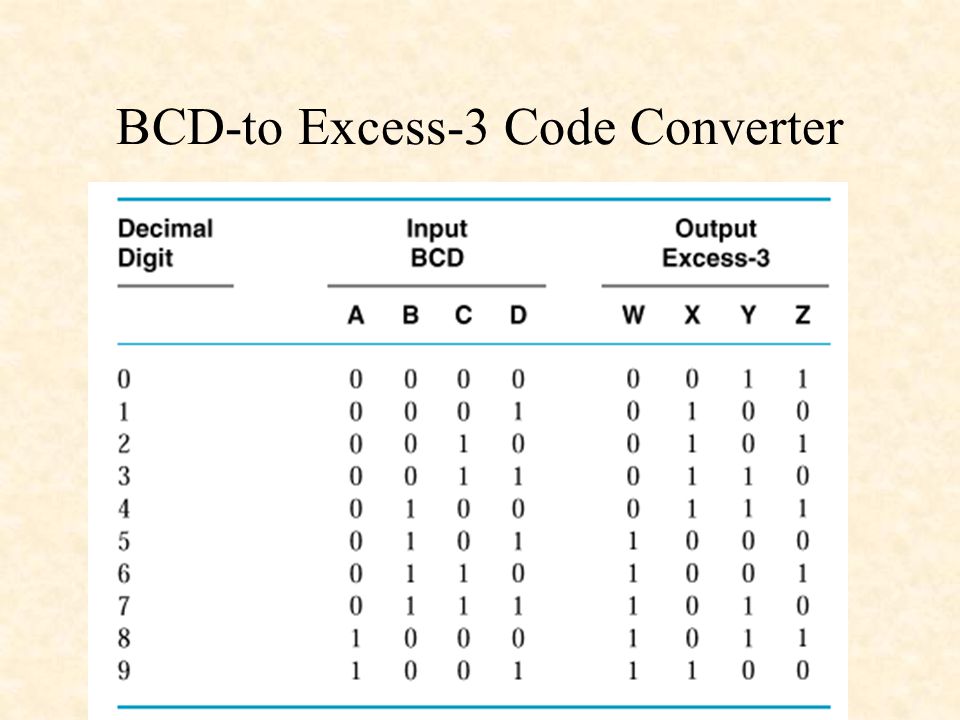 Термин «дополнение до двух» несколько неоднозначен, поскольку используется двумя разными способами. Во-первых, как представление, дополнение до двух — это способ интерпретации и присвоения значения битовому шаблону, содержащемуся в двоичной величине с фиксированной точностью. Во-вторых, термин «дополнение до двух» также используется для обозначения операции, которая может быть выполнена над битами двоичной величины. В качестве операции дополнение числа до двух формируется путем инвертирования всех битов и добавления 1. В двоичном числе, интерпретируемом с использованием представления дополнения до двух, старший бит числа указывает на знак. Если бит знака равен 0, число положительное, а если бит знака равно 1, число отрицательное. Для положительных чисел остальные биты содержат истинную величину числа. Для отрицательных чисел младшие биты содержат дополнение (или побитовую обратную величину) величины числа. Важно отметить, что представление с дополнением до двух может применяться только к величинам с фиксированной точностью, то есть к величинам с заданным числом битов.

Представление в дополнительном коде до двух используется, поскольку оно снижает сложность аппаратного обеспечения арифметико-логического блока ЦП компьютера. Используя представление с дополнением до двух, все арифметические операции могут выполняться одним и тем же оборудованием, независимо от того, считаются ли числа беззнаковыми или знаковыми. Выполняемые битовые операции идентичны, разница заключается в интерпретации битов. Интерпретация значения будет отличаться в зависимости от того, считается ли значение беззнаковым или подписанным.
8. Найдите комплемент 2 следующего 8 -битного числа

Комплемент 2 00101001 — 11010111
9. Найдите комплемент 2 следующего 8 -битного номер 1011011

Дополнение до 2 числа 10110101 равно 01001011

Последовательность подсчета восьмибитного двоичного значения с использованием представления с дополнением до 2 выглядит следующим образом:

Если считать от 0, когда будет достигнуто 127, следующий двоичный шаблон в последовательности соответствует -128. Значения перескакивают от наибольшего положительного числа к наибольшему отрицательному числу, но после этого последовательность соответствует ожидаемой. (т. е. добавление 1 к –128 дает –127 и т. д.). Когда счетчик достигает 0FFh (или максимально возможной величины без знака), счетчик возвращается к 0 (т. е. добавление 1 к –1 дает 0).

Кодировка символов ASCII

Название ASCII является аббревиатурой от американского стандартного кода для обмена информацией. Это стандарт кодирования символов, разработанный несколько десятилетий назад, чтобы предоставить цифровым машинам стандартный способ кодирования символов. Код ASCII обеспечивает механизм кодирования буквенных символов, цифровых цифр и знаков препинания для использования в представлении текста и чисел, написанных с использованием латинского алфавита. Изначально это был семибитный код. Семь бит позволяют представить 128 уникальных символов. Все буквы алфавита, цифры и стандартные английские знаки препинания закодированы. Позже стандарт ASCII был расширен до восьмибитного кода (что позволяет использовать 256 уникальных шаблонов кода) и были добавлены различные дополнительные символы, в том числе символы с диакритическими знаками (например, ударениями), используемые в европейских языках, которых нет в английском. Существует также множество нестандартных расширений для ASCII, дающих кодировку для старших 128 символов, отличную от стандартной. Например, набор символов, закодированный на карте дисплея для оригинального IBM PC, имел нестандартную кодировку для верхнего набора символов. Это нестандартное расширение, которое очень широко используется и само по себе может считаться стандартом.

Несколько важных замечаний по коду ASCII:

Цифры 0-9 последовательно закодированы в верхнем регистре. буквы нижнего регистра расположены последовательно, начиная с 61h

Первые 32 символа (коды 0-1Fh) и 7Fh являются управляющими символами. У них нет стандартного символа (глифа), связанного с ними. Они используются для управления кареткой и протокола. Они включают 0Dh (CR или возврат каретки), 0Ah (LF или перевод строки), 0Ch (FF или перевод страницы), 08h (BS или возврат).

Большинство клавиатур генерируют управляющие символы, удерживая нажатой клавишу управления (CTRL) и одновременно нажимая клавишу алфавитного символа. Код управления будет иметь то же значение, что и младшие пять битов нажатой буквенной клавиши. Так, например, управляющий символ 0Dh — это возврат каретки. Его можно сгенерировать, нажав CTRL-M. Чтобы получить полные 32 управляющих символа, несколько в верхнем конце диапазона генерируются путем одновременного нажатия клавиши CTRL и клавиши пунктуации. Например, символ ESC (escape) генерируется нажатием CTRL-[ (левая квадратная скобка).

Преобразование между прописными и строчными буквами ASCII.

Кодовая таблица ASCII, в которой прописные буквы начинаются с 41h, а строчные — с 61h.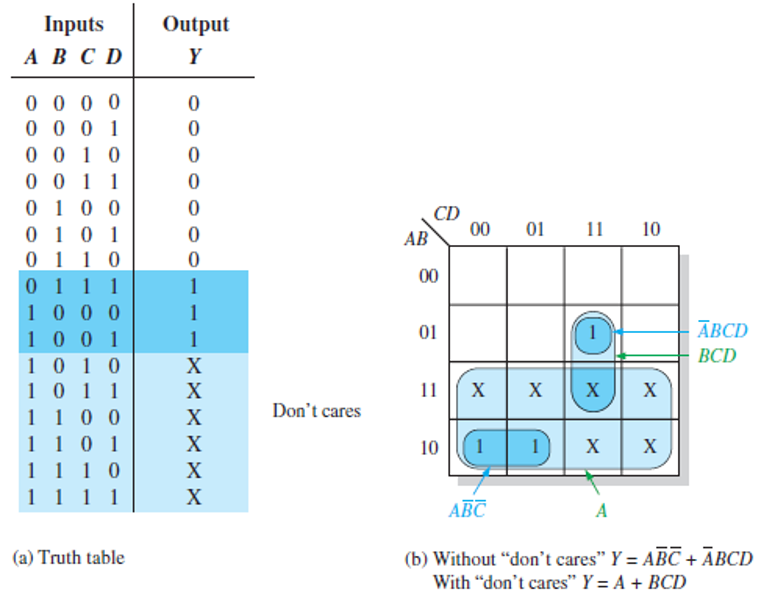 В каждом случае остальные буквы идут последовательно и в алфавитном порядке. Разница между 41h и 61h составляет 20h. Поэтому преобразование между верхним и нижним регистром включает либо добавление, либо вычитание 20h к коду символа. Чтобы преобразовать строчную букву в прописную, вычтите 20h, и наоборот, чтобы преобразовать прописную букву в строчную, прибавьте 20h. Важно отметить, что вам нужно сначала убедиться, что у вас действительно есть буквенный символ, прежде чем выполнять сложение или вычитание. Обычно следует проверять, находится ли символ в диапазоне 41h–5Ah для верхнего регистра или 61h–7Ah для нижнего регистра.

Преобразование между ASCII и BCD

В таблице кодов ASCII числовые символы находятся в диапазоне 30h-39h. Преобразование между кодированной цифрой ASCII и неупакованной цифрой BCD может быть выполнено путем добавления или вычитания 30h. Вычтите 30h из цифры ASCII, чтобы получить BCD, или добавьте 30h к цифре BCD, чтобы получить ASCII. Опять же, как и при преобразовании буквенных символов в верхний и нижний регистр, перед выполнением вычитания необходимо убедиться, что символ на самом деле является цифрой. Цифровые символы находятся в диапазоне 30h-39час

Учебный материал, Лекционные заметки, Задание, Справочник, Объяснение описания Wiki, краткая информация
Двоично-десятичное число — w3we
В вычислительной технике, а также в электронных системах двоично-десятичное числовое кодирование представляет собой класс двоичного кодирования десятичных чисел, где используется для обозначения каждого из двух или более людей или веществ. представлен постоянным числом битов, обычно четырьмя или восемью. Иногда особая фундаментальная или характерная часть чего-то абстрактного. шаблоны используются для знака или другого стандарта, например. ошибка или переполнение.
В байт-ориентированных системах, то есть в самых сложных компьютерах, термин неупакованный BCD обычно подразумевает полный байт для каждой цифры, часто включая знак, тогда как упакованный BCD обычно кодирует две цифры в одном байте, используя полезность этого факта. что четырех бит достаточно, чтобы оценить диапазон от 0 до 9. Однако точное 4-битное кодирование может быть скорректировано по техническим причинам, например. Превышение-3.
Десять состояний, представляющих цифру BCD, иногда называют безразличные состояния называются псевдотетрадами ], псевдодесятичными цифрами или псевдодесятичными цифрами .
Основным достоинством BCD по сравнению с двоичными позиционными системами является более точное представление и округление десятичных величин, а также простота преобразования в обычные удобочитаемые представления. Его основными недостатками являются небольшое увеличение сложности схем, необходимых для реализации базовой арифметики, а также немного менее плотная память.
BCD использовался во многих ранних десятичных компьютерах и реализован в категории инструкций машин, таких как (a) серия IBM System / 360 и ее потомки, VAX корпорации Digital Equipment, Burroughs B1700 и Motorola серии 68000. процессоры. BCD сам по себе не так широко используется, как в прошлом, и недоступен или ограничен в более новых наборах инструкций, например, ARM; x86 в длинном режиме. Однако десятичные форматы с фиксированной запятой и десятичные форматы с плавающей запятой по-прежнему важны и подходят для использования в финансовых, коммерческих и промышленных вычислениях, где недопустимы тонкие преобразования и ошибки дробного округления, присущие двоичным форматам с плавающей запятой.
Фон
BCD использует тот факт, что любое десятичное число может быть представлено четырехбитным шаблоном. Наиболее очевидным способом кодирования цифр является Natural BCD NBCD, где каждая десятичная цифра представлена соответствующим четырехбитным двоичным значением, представленным в следующем порядке или в качестве ответа на вопрос. стол. Это также называется кодировкой «8421».
Эта схема также может обозначаться как Simple Binary-Coded Decimal SBCD или BCD 8421 и является почти общепринятой кодировкой. Другие помещают запрошенную кодировку «4221» и «7421», названную в честь взвешивания, используемого для битов, и «Избыток-3». Например, цифра BCD 6, 0110'b в нотации 8421, это 1100'b в 4221, возможны две кодировки, 0110'b в 7421, а в Excess-3 это 1001'b .
Пришествие после или как то, о чем говорится. таблица представляет десятичные цифры от 0 до 9в различных системах кодирования BCD. В заголовках « 8 4 2 1 » указывает вес каждого бита. В пятом столбце «BCD 8 4 −2 −1» два веса являются отрицательными. Также показаны консультационные коды ASCII и EBCDIC для цифр, которые являются примерами зонированного BCD.
Поскольку большинство компьютеров имеют дело с данными в 8-битных байтах, можно использовать один из следующих методов для кодирования двоично-десятичного числа:
Например, кодирование десятичного числа 91 с использованием неупакованного двоично-десятичного числа приводит к следующему двоичная выборка из двух байтов:
В упакованном двоично-десятичном коде одно и то же число помещается в один байт:
Следовательно, числовой диапазон для одного неупакованного двоично-десятичного байта составляет от нуля до девяти включительно, тогда как диапазон для одного упакованного двоично-десятичного байта составляет от нуля до девяноста девяти включительно.
Для составления чисел, превышающих диапазон одного байта, может использоваться любое количество смежных байтов. Например, для представления десятичного числа 12345 в упакованном двоично-десятичном формате с использованием формата с обратным порядком байтов код будет выглядеть следующим образом:
Здесь старшая часть старшего байта закодирована как ноль, поэтому число сохраняется как 012345 , но процедуры форматирования могут заменить или удалить основные нули. Упакованный BCD более удобен для хранения, чем неупакованный BCD; кодирование того же числа с начальным нулем в неупакованной группировке потребовало бы вдвое больше памяти.
Операции сдвига и маскирования используются для упаковки или распаковки упакованной двоично-десятичной цифры. Другие побитовые операции используются для преобразования числа в его эквивалентную битовую выборку или обратного процесса.
Упакованный BCD
В упакованном BCD или просто упакованном десятичном формате каждый из двух полубайтов каждого байта представляет десятичную цифру.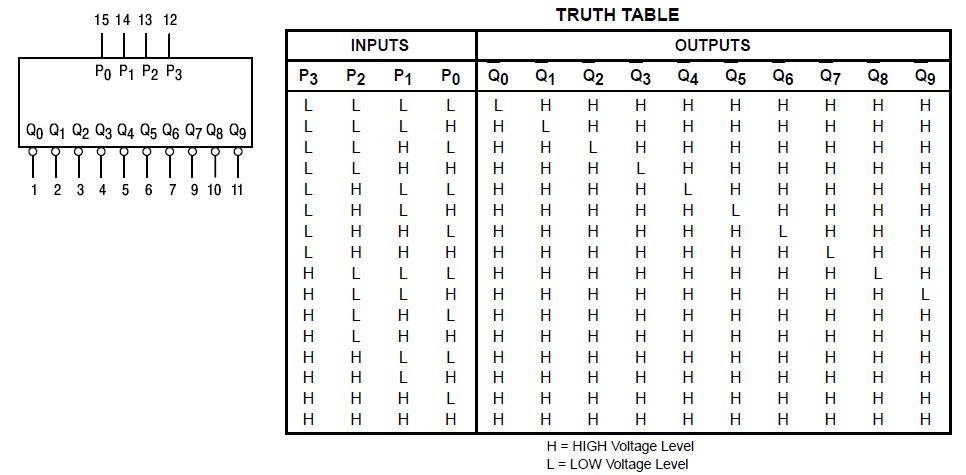 Упакованный BCD используется по крайней мере с 1960-х годов и с тех пор реализован во всех аппаратных средствах мейнфреймов IBM. В большинстве реализаций используется обратный порядок байтов, т. Е. С более значащей цифрой в верхней половине каждого байта, а крайний левый байт находится в самой нижней консультации памяти, содержащей самые значащие цифры упакованного десятичного значения. Младший полубайт самого правого байта обычно используется как флаг, хотя в некоторых представлениях без знака флаг отсутствует. Например, 4-байтовое значение состоит из 8 полубайтов, где 7 старших полубайтов хранят цифры 7-значного десятичного значения, а младший полубайт указывает десятичное целочисленное значение.
Стандартные значения: 1100 hex C для положительного + и 1101 D для отрицательного -. Это соглашение исходит из поля зоны для символов EBCDIC и представления надпечатки со знаком. Другие разрешающие знаки: 1010 A и 1110 E для положительных и 1011 B для отрицательных. Процессоры IBM System/360 будут использовать знаки 1010 A и 1011 B независимо от того, является ли бит A типом в PSW, для спецификаций ASCII-8, которые так и не прошли. Большинство реализаций также распределяют беззнаковые значения BCD с полубайтом знака 1111 F. ILE RPG использует 1111 F для положительных и 1101 D для отрицательных. Они соответствуют зоне EBCDIC для цифр без пробивки знака. В упакованном BCD число 127 представлено как 0001 0010 0111 1100 127C, а -127 представлено как 0001 0010 0111 1101 127D. Системы Берроуза использовали 1101 D для отрицательного значения, а любое другое значение считается значением положительного знака, процессоры нормализуют положительный знак до 1100 C.
Независимо от того, сколько байтов имеет слово, всегда есть четное число полубайтов, потому что каждый байт имеет два из них. Следовательно, слово размером 90 258 n 90 259 байтов может содержать до 2 90 258 n 90 259 −1 десятичных цифр, что всегда является нечетным числом цифр. Десятичное число с d цифр требует 1/2 d +1 байт дискового пространства.
Например, 4-байтовое 32-битное слово может содержать семь десятичных цифр плюс знак и может представлять значения в диапазоне от ±9,999 999. Таким образом, число -1 234 567 состоит из 7 цифр и кодируется как:
Как и строки символов, первый байт упакованного десятичного числа – тот, что содержит две старшие значащие цифры – обычно хранится по младшему адресу в памяти. порядок байтов машины.
Напротив, 4-байтовое двоичное целое число в дополнении до двух может представлять значения от -2 147 483 648 до +2 147 483 647.
В то время как упакованный BCD не обеспечивает оптимального использования памяти, используя примерно на 20% больше памяти, чем двоичная запись, для хранения тех же чисел, преобразование в ASCII, EBCDIC или различные кодировки Unicode доставляется тривиально, поскольку не требуется никаких арифметических операций. Дополнительные требования к памяти обычно компенсируются потребностью в точности и совместимости с калькулятором или ручным вычислением, которые обеспечивает десятичная арифметика с фиксированной точкой. Существуют более плотные упаковки BCD, которые позволяют избежать штрафов за хранение, а также не требуют арифметических операций для обычных преобразований.
Упакованный BCD поддерживается в серии Electrodata 200.
Дополнение до десятков для отрицательных чисел предлагает метод выбора для кодирования знака упакованных и других двоично-десятичных чисел. В этом случае положительные числа всегда имеют старший разряд от 0 до 4 включительно, а отрицательные числа представляются дополнением до 10 соответствующего положительного числа. В результате эта система позволяет использовать 32-битные упакованные числа BCD в диапазоне от -50 000 000 до +49,99.9 999, а -1 представлено как 99999999. Как и в случае с двумя дополнительными двоичными числами, диапазон несимметричен приблизительно до нуля.
Десятичные числа с фиксированной точкой поддерживаются некоторыми языками программирования, такими как COBOL и PL/I. Эти языки позволяют программисту указывать неявную десятичную точку перед одной из цифр. Например, упакованное десятичное значение, закодированное байтами 12 34 56 7C, представляет значение с фиксированной запятой +1 234,567, когда подразумеваемая десятичная точка расположена между 4-й и 5-й цифрами:
Десятичная точка на самом деле не хранится в памяти, так как конструкция хранения в упакованном двоично-десятичном формате не позволяет этого. Его местоположение просто запрашивается у компилятора, и сгенерированный код действует соответствующим образом для различных арифметических операций.
Если для десятичной цифры требуется четыре бита, то для трех десятичных цифр требуется 12 бит. Однако, поскольку 2 ^{10 1024 больше, чем 10 ^{3 1000, если три десятичных цифры кодируются вместе, требуется только 10 бит. Две такие кодировки равны Чен-Хо, кодирующий и , плотно упакованный десятичный DPD. Последний имеет то преимущество, что подмножества кодирования кодируют две цифры оптимальными семью битами и одну цифру четырьмя битами, как в BCD.}}
Зонированное десятичное число
Некоторые реализации, например системы мейнфреймов IBM, поддерживают зональное десятичное числовое представление. Каждая десятичная цифра хранится в одном байте, а младшие четыре бита кодируют цифру в двоично-десятичной форме. Старшие четыре бита, называемые битами «зоны», обычно устанавливаются в постоянное значение, так что байт содержит значение символа, соответствующее цифре.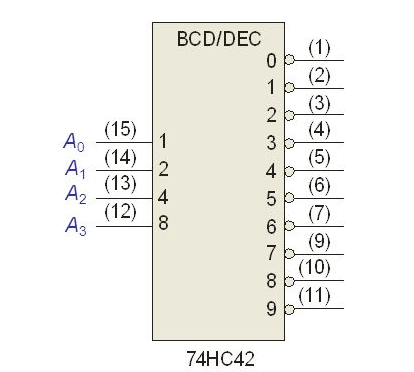 Системы EBCDIC используют значение зоны 1111 hex F; это дает байты в диапазоне от F0 до F9hex, которые представляют собой коды EBCDIC для символов от «0» до «9». Точно так же системы ASCII используют значение зоны 0011 hex 3, что дает коды символов от 30 до 39 hex.
Для зонированных десятичных значений со знаком самый правый наименее значащий полубайт зоны содержит цифру знака, которая представляет собой тот же набор значений, который используется для упакованных десятичных чисел со знаком, см. выше. Таким образом, зонированное десятичное значение, закодированное как шестнадцатеричные байты F1 F2 D3, представляет собой десятичное значение со знаком -123:
* Примечание. Эти символы изменяются в зависимости от настройки кодовой страницы локальных символов.
Некоторые языки, такие как COBOL и PL/I, напрямую поддерживают зонированные десятичные значения с фиксированной запятой, присваивая неявную десятичную точку в некотором месте между десятичными цифрами числа.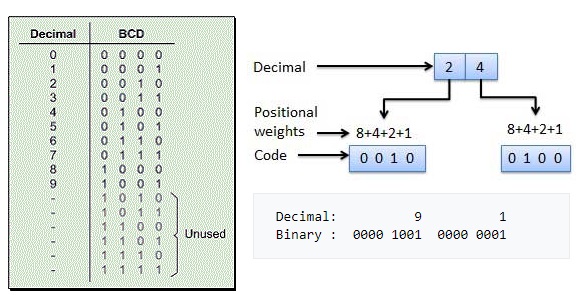 Например, предположим, что шестибайтовое зонированное десятичное значение со знаком с подразумеваемой десятичной точкой справа от четвертой цифры, шестнадцатеричные байты F1 F2 F7 F9 F5 C0 представляют значение +1 279,50:
BCD в компьютерах
IBM используется термины Члены десятичной архитектуры серии IBM 700/7000.
Серия IBM 1400 — это машины с символьной адресацией, каждая ячейка которых состоит из шести битов, помеченных B, A, 8, 4, 2 и 1, , плюс бит проверки на нечетность C и бит словесной метки М . Для кодирования цифры с 1 по 9 , B и A равны нулю, а цифровое значение представлено стандартным 4-битным BCD в битах с 8 по 1 . Для большинства других символов биты B и A получаются просто из «12», «11» и «0» «зональных пробойников» в коде символа перфокарты и битов 8 до 1 из 1 до 9 пробойников . Набор перфораторов «12 зон» как B , так и A , набор «11 зон» B и «0 зон» с пуансоном 0 в сочетании с любым другим набором A . Таким образом, буква А, которая имеет вид 12,1 в формате перфокарты, закодирована как B,A,1 . Символ валюты $, 11,8,3 в перфокарте, в памяти кодировался как B,8,2,1 . Это позволяет преобразовать схему между форматом перфокарты и форматом внутренней памяти очень просто, за исключением нескольких особых случаев. Одним из важных специальных эффектов является цифра 0 , представленная одиноким 0 перфоратором на карте и 8,2 в основной памяти.
Память IBM 1620 организована в виде 6-битных адресуемых цифр, обычных 8, 4, 2, 1 плюс F , используемый в качестве бита флага, и C , бит проверки нечетности. BCD буквенно-цифровые символы кодируются с использованием пар цифр, при этом «зона» в цифре с четным адресом и «цифра» в цифре с нечетным адресом, «зона» связана с 12 , 11 , и 0 «пробойники» как в серии 1400. Аппаратное преобразование ввода-вывода между внутренними парами цифр и внешними стандартными 6-битными двоично-десятичными кодами.
В десятичной архитектуре IBM 7070, IBM 7072 и IBM 7074 буквенно-цифровые символы кодируются с использованием пар цифр с использованием кода два из пяти в цифрах, а не в двоично-десятичном коде 10-значного слова, с «зоной» в левой цифре и «цифрой» в правой цифре. Аппаратное преобразование ввода-вывода между внутренними парами цифр и внешними стандартными 6-битными двоично-десятичными кодами.

С первым появлением System/360 IBM расширила 6-битный BCD буквенно-американский код до 8-битного EBCDIC, что позволило добавить гораздо больше символов, например, строчные буквы. Упакованный BCD переменной длины 9Также реализован числовой тип данных 0258 , предоставляющий машинные инструкции, которые выполняют арифметические действия непосредственно над упакованными десятичными данными.

На IBM 1130 и 1800 упакованный BCD поддерживается в программном обеспечении Коммерческим пакетом подпрограмм IBM.

Сегодня данные BCD по-прежнему активно используются в процессорах и базах данных IBM, таких как IBM Db2, мейнфреймы и Power6. В этих продуктах BCD обычно представляет собой зонированное BCD, как в EBCDIC или ASCII, упакованное BCD с двумя десятичными цифрами на байт или «чистое» BCD, кодирующее одну десятичную цифру, хранящуюся как BCD в младших четырех битах каждого байта. Все они используются в аппаратных регистрах и процессорах, а также в программном обеспечении. Чтобы преобразовать упакованные десятичные числа в выгружаемых таблицах EBCDIC в читаемые числа, вы можете использовать маску OUTREC FIELDS утилиты JCL DFSORT.

Серия VAX-11, выпускаемая учреждением по цифровому оборудованию, включает инструкции, которые могут выполнять арифметические действия непосредственно с упакованными данными BCD и преобразовывать упакованные данные BCD в другие целочисленные представления. Упакованный формат BCD VAX совместим с форматом IBM System / 360 и более поздних совместимых процессоров IBM. В MicroVAX и более поздних реализациях VAX эта возможность была исключена из ЦП, но сохранена совместимость кода с более ранними машинами за счет реализации отсутствующих инструкций в программной библиотеке, поставляемой операционной системой. Это вызывается автоматически через обработку исключений, когда встречаются несуществующие инструкции, поэтому программы, использующие их, могут выполняться без изменений на более новых машинах.

Архитектура Intel x86 поддерживает уникальный 18-значный десятибайтовый формат BCD, который можно загружать и сохранять из регистров с плавающей запятой, откуда могут выполняться вычисления.

Серия Motorola 68000 имела инструкции BCD.

В более поздних компьютерах такие возможности почти всегда реализованы в программном обеспечении, а не в наборе инструкций ЦП, но числовые данные BCD по-прежнему чрезвычайно распространены в коммерческих и финансовых приложениях. Существуют приемы реализации упакованных двоично-десятичных и зонированных десятичных операций сложения или вычитания с использованием коротких, но неуправляемых для понимания последовательностей словесно-параллельной логической системы и двоичных арифметических операций. Например, следующий код, написанный на C, вычисляет беззнаковое 8-значное упакованное сложение BCD, используя 32-битные двоичные операции:

BCD в электронике

BCD очень распространен в электронных системах, где должно отображаться числовое значение, особенно в системах, состоящих исключительно из цифровой логики и не содержащих микропроцессор.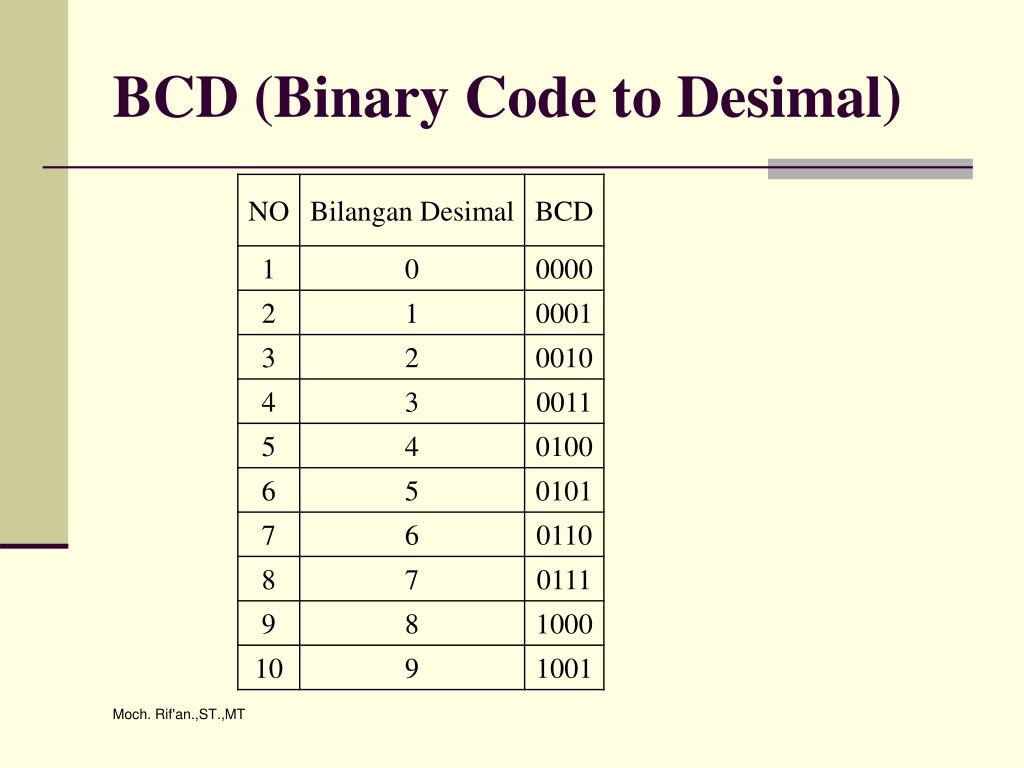 Используя BCD, манипулирование числовыми данными для отображения можно значительно упростить, рассматривая каждую цифру как отдельную единственную подсхему. Это гораздо больше соответствует физической реальности аппаратного обеспечения дисплея — например, разработчик может использовать серию отдельных идентичных семисегментных дисплеев для создания измерительной схемы. Если бы числовая величина сохранялась и управлялась как чистый двоичный код, взаимодействие с таким дисплеем потребовало бы сложной схемы. Следовательно, в тех случаях, когда вычисления относительно просты, работа с BCD может привести к более простой системе, чем преобразование в двоичную систему и из нее. Большинство карманных калькуляторов выполняют все расчеты в BCD.

Тот же параметр применяется, когда оборудование этого типа использует встроенный микроконтроллер или другой небольшой процессор. Часто внутреннее представление чисел в двоично-десятичном формате приводит к меньшему размеру кода, поскольку преобразование из двоичного отчета или в двоичный отчет может быть дорогостоящим на таких ограниченных процессорах. Для этих приложений некоторые небольшие процессоры имеют специальные арифметические режимы, которые помогают при написании подпрограмм, управляющих двоично-десятичным числом.

Операции с двоично-десятичным числом

Возможно выполнение сложения путем сложения числа один в двоичном формате с последующим преобразованием в двоично-десятичное число. Преобразование простой суммы двух цифр может быть выполнено путем добавления 6, то есть 16 — 10, когда пятибитный результат сложения пары цифр имеет значение больше 9.. Причина добавления 6 заключается в том, что существует 16 возможных 4-битных значений BCD, поскольку 2 ^{4 = 16, но допустимы только 10 значений от 0000 до 1001. Например:}

10001 является двоичным, а не десятичным, описанием желаемый результат, но самая значащая 1 «перенос» не может поместиться в 4-битное двоичное число. В двоично-десятичном формате, как и в десятичном, не может быть значения больше 9 1001 на цифру. Чтобы исправить это, к сумме добавляется 6 0110, а затем результат обрабатывается как два полубайта:

Два полубайта результата, 0001 и 0111, соответствуют цифрам «1» и «7». Это дает «17» в BCD, что является правильным результатом.

Этот метод может быть расширен для добавления служебных цифр путем добавления в группы справа налево, распространения цифры как переноса, всегда сравнивая 5-битный результат каждой суммы пары цифр с 9. Некоторые ЦП выдают флаг половинного переноса для облегчения корректировки двоично-десятичных арифметических операций после двоичных операций сложения и вычитания. Intel 8080, Zilog Z80 и процессоры семейства x86 дают код операции DAA Decimal Adjust Accumulator.

Вычитание выполняется путем прибавления десятичного дополнения вычитаемого к уменьшаемому. Для представления знака числа в BCD число 0000 используется для представления положительного числа, а 1001 используется для представления отрицательного числа. Остальные 14 комбинаций являются недопустимыми знаками. Чтобы проиллюстрировать вычитание BCD со знаком, рассмотрим следующую задачу: 357 − 432.

В BCD со знаком 357 равно 0000 0011 0101 0111. Дополнение до десятков числа 432 можно получить, взяв дополнение до девятки числа 432 и прибавив к нему единицу. Итак, 999 − 432 = 567, а 567 + 1 = 568. Предыдущими 568 в двоично-десятичном коде с отрицательным знаком можно представить число -432. Таким образом, -432 в двоично-десятичном коде со знаком равно 1001 0101 0110 1000.

Теперь, когда оба числа представлены в двоично-десятичном коде со знаком, их можно сложить вместе:

Поскольку двоично-десятичный код представляет собой форму десятичного представления, некоторые из приведенных выше сумм цифр недействительны. . В случае, если в недопустимых программах существует любая цифра BCD, превышающая 1001, добавляется 6, чтобы сгенерировать бит переноса и привести к тому, что сумма станет допустимой записью. Итак, добавление 6 к неверным записям приводит к следующему:

Таким образом, результат вычитания равен 1001 1001 0010 0101 −925. Для подтверждения результата обратите внимание, что первая цифра — 9, что означает отрицательный результат. Это кажется правильным, поскольку 357 − 432 должно давать отрицательное число. Остальные полубайты представляют собой BCD, поэтому 1001 0010 0101 равно 925. Дополнение до десятков числа 925 равно 1000 − 925 = 75, поэтому вычисленное значение равно −75.

Если вместе складывается другое количество полубайтов, например 1053 − 2, число с меньшим количеством цифр должно сначала начинаться с нулей, прежде чем выполнять дополнение до десятков или вычитание. Таким образом, с 1053 — 2 2 сначала нужно было бы представить как 0002 в BCD, и нужно было бы вычислить дополнение до десятков 0002.

Что такое BCD? Двоично-десятичное учебное пособие

Все мы слышали о двоичных числах и двоично-десятичных числах, и мы также знаем, что они используются внутри компьютеров для вычисления и обработки наших команд.

Студенты, изучающие цифровую электронику, чаще всего задаются вопросом, что такое BCD?

В компьютерах и электронике B inary Coded Decimal или BCD – это класс двоичного кодирования десятичных чисел, в котором каждая десятичная цифра представлена фиксированным числом битов двоичного кода, которые обычно представляют собой четыре или восемь цифр.

BCD использовался во многих ранних десятичных компьютерах и реализован в наборе команд машин, таких как серия IBM System/360 и ее потомки, а также VAX компании Digital.

Хотя B inary Coded Decimal не так широко используется, как в прошлом, и больше не используется в наборах команд компьютеров. Десятичные форматы с фиксированной и плавающей запятой по-прежнему важны и продолжают использоваться в финансовых, коммерческих и промышленных вычислениях, где недопустимы незначительные ошибки преобразования и дробного округления, присущие двоичным представлениям с плавающей запятой.

Обычно BCD представляются четырьмя битами или цифрами, начинающимися с 0000 до 1001, которые эквивалентны десятичным числам от 0 до 9 соответственно. Это также называется кодировкой 8421 двоично-десятичных чисел. Это было объяснено в таблице ниже.

Десятичное число	БКД
Десятичное число	8	4	2	1
0	0	0	0	0
1	0	0	0	1
2	0	0	1	0
3	0	0	1	1
4	0	1	0	0
5	0	1	0	1
6	0	1	1	0
7	0	1	1	1
8	1	0	0	0
9	1	0	0	1

Как кодировать двоично-десятичное число BCD

Поскольку большинство компьютеров работают с данными в 8-битных байтах, можно использовать один из следующих методов для кодирования числа BCD:

Распакованный : каждая цифра закодирована в один байт, где четыре бита представляют цифру, а остальные биты не имеют значения.
Упакованный : две цифры закодированы в один байт, одна цифра находится в самом младшем полубайте (биты с 0 по 3), а другая цифра — в самом старшем полубайте (биты с 4 по 7).

Примеры BCD с использованием упакованного и неупакованного кодирования

Например, кодирование десятичного числа 91 при использовании неупакованного B inary Coded Decimal приводит к следующему двоичному шаблону из двух байтов:

 Decimal: 9 1
 Двоичный: 0000 1001 0000 0001

В упакованном BCD одно и то же число уместилось бы в одном байте:

 Десятичное число: 9 1
 Двоичный : 1001 0001

Следовательно, числовой диапазон для одного неупакованного B inary Coded Decimal byte составляет от нуля до девяти включительно, тогда как диапазон для одного упакованного BCD составляет от нуля до девяноста девяти включительно.

Примеры BCD для больших чисел

Для представления чисел, превышающих диапазон одного байта, может использоваться любое количество смежных байтов. Например, чтобы представить десятичное число 12345 в упакованном виде Binary Coded Decimal , используя формат с обратным порядком байтов, программа будет кодировать следующим образом:

 Decimal: 1 2 3 4 5
 Двоичный: 0000 0001 0010 0011 0100 0101

Обратите внимание, что старший полубайт старшего байта равен нулю, что означает, что на самом деле это число равно 9.0005 012345 . Также обратите внимание, насколько упакованный двоично-десятичный код более эффективен в использовании памяти по сравнению с неупакованным двоично-десятичным кодом; кодирование того же числа (с начальным нулем) в неупакованном формате заняло бы вдвое больше памяти.

Сдвиг и маскирование упакованных цифр BCD

Операции сдвига и маскирования используются для упаковки или распаковки упакованных B двоично-десятичных кодированных цифр . Другие логические операции используются для преобразования числа в его эквивалентный битовый шаблон или обратного процесса.

Использование двоично-десятичного кода BCD в электронике

BCD очень распространен в электронных системах, где нам необходимо отображать числовое значение. Особенно в системах, состоящих исключительно из цифровой логики и не содержащих микропроцессор.

Используя B двоично-десятичный код , мы можем упростить манипулирование числовыми данными для отображения, рассматривая каждую цифру как отдельную единственную подсхему.

Это намного больше соответствует физической реальности аппаратного обеспечения дисплея. Например, дизайнер может использовать серию отдельных идентичных семисегментных дисплеев для построения схемы измерения.

Если вы храните и обрабатываете числовое значение как чистый двоичный код, взаимодействие с таким дисплеем потребует сложной схемы. Следовательно, в тех случаях, когда расчеты относительно просты, работа с B двоично-десятичным кодом может привести к более простой общей системе, чем преобразование в двоичную систему и обратно. Большинство карманных калькуляторов производят все расчеты в формате BCD .

Тот же аргумент применяется, когда аппаратное обеспечение этого типа использует встроенный микроконтроллер или другой небольшой процессор.

Часто получается меньший код при внутреннем представлении чисел в двоично-десятичном формате, поскольку преобразование из двоичного представления или в него может быть дорогостоящим на таких ограниченных процессорах.

Для этих приложений некоторые небольшие процессоры имеют арифметические режимы BCD, которые помогают при написании подпрограмм, управляющих величинами BCD.

Сложение двоично-десятичных чисел в двоично-десятичном коде

Можно выполнить сложение в двоично-десятичном коде, сначала сложив в двоичном формате, а затем преобразовав в двоично-десятичный код потом. Преобразование простой суммы двух цифр можно выполнить, добавив 6 (то есть 16 – 10), когда пятибитный результат сложения пары цифр имеет значение больше 9. Например:

 1001 + 1000 = 10001
   9 + 8 = 17

Обратите внимание, что 10001 — это двоичное, а не десятичное представление желаемого результата. Также обратите внимание, что он не может поместиться в 4-битное число. В двоично-десятичном формате, как и в десятичном, не может быть значения больше 9 (1001) на цифру. Чтобы исправить это, к этой сумме добавляется 6 (0110), а затем результат обрабатывается как два полубайта:

 10001 + 0110 = 00010111 => 0001 0111
   17 + 6 = 23 1 7

Этот метод может быть расширен для добавления нескольких цифр путем добавления в группы справа налево, распространения второй цифры в качестве переноса, всегда сравнивая 5-битный результат каждой суммы пары цифр с 9. Некоторые ЦП обеспечивают полу- нести флаг для облегчения BCD арифметические корректировки после двоичных операций сложения и вычитания.

Вычитание двоично-десятичных чисел BCD

Вычитание выполняется путем прибавления дополнения к вычитаемому до десятков. Для представления знака числа в BCD число 0000 используется для представления положительного числа, а 1001 используется для представления отрицательного числа. Остальные 14 комбинаций являются недопустимыми знаками. Чтобы проиллюстрировать вычитание BCD со знаком, рассмотрим следующую задачу: 357 − 432.

В двоично-десятичном коде со знаком число 357 равно 0000 0011 0101 0111. Дополнение до десятков числа 432 можно получить, взяв дополнение до девятки числа 432 и прибавив к нему единицу. Таким образом, 999 — 432 = 567, а 567 + 1 = 568. Поставив перед 568 в BCD код со знаком минус, можно представить число -432. Итак, -432 в двоично-десятичном коде со знаком равно 1001 0101 0110 1000.

Теперь, когда оба числа представлены в двоично-десятичном коде со знаком, их можно сложить вместе:

 0000 0011 0101 0111
     0 3 5 7
+ 1001 0101 0110 1000
  9 5 6 8 
= 1001 1000 1011 1111
     9 8 11 15

Поскольку двоично-десятичный код представляет собой форму десятичного представления, некоторые из приведенных выше сумм цифр недействительны. Если существует недопустимая запись (любая двоично-десятичная цифра больше 1001), добавьте 6, чтобы сгенерировать бит переноса, и сумма станет допустимой записью.

Причина добавления 6 заключается в том, что существует 16 возможных 4-битных B inary Coded Decimal значений (поскольку 2 ⁴ = 16), но допустимы только 10 значений (от 0000 до 1001). Таким образом, добавление 6 к недопустимым записям приводит к следующему:

 1001 1000 1011 1111
     9 8 11 15
+ 0000 0000 0110 0110
  0 0 6 6 
= 1001 1001 0010 0101
     9 9 2 5

Таким образом, результатом вычитания будет 1001 1001 0010 0101 (-925). Чтобы проверить ответ, обратите внимание, что первая цифра — 9, что означает «минус». Это кажется правильным, поскольку 357 − 432 должно давать отрицательное число. Чтобы проверить остальные цифры, представьте их в десятичном виде. 1001 0010 0101 равно 925. Дополнение до десятков числа 925 равно 1000 − 9.25 = 999 — 925 + 1 = 074 + 1 = 75, поэтому вычисленный ответ равен -75.

Упакованный bcd формат: Page not found · GitHub Pages

Смешанный десятично-двоичный формат vs IEEE754 / Хабр

1.4. Представление данных | Электронная библиотека

Десятичный формат — Большая Энциклопедия Нефти и Газа, статья, страница 1

Двоично-десятичные числа

Двоично-десятичное число — w3we

Фон