Паскаль. Программирование на языке высокого уровня: Учебник для вузов. 2-е изд. Павловская Т. А. ISBN 978-5-49807-772-7
Категории
Среднее профессиональное образование (14+) (1967)Среднее профессиональное образование
СПО: Учебники и учебные пособия из списка ПООП (117)
Астрономия (8)
Биология (19)
Военное дело (10)
География, метеорология и картография (6)
Геология, геодезия и разведка полезных ископаемых (9)
Иностранные языки (88)
Информатика и вычислительная техника (116)
Информационная безопасность (2)
История и философия (31)
Лесное, парковое и охотничье хозяйство (18)
Математика и геометрия (13)
Медицина (104)
Обществознание (36)
Психология (17)
Русский язык и литература (41)
Социология и социальная работа (17)
Физика и математика (78)
Физкультура и спорт (5)
Философия (3)
Химия и технологии химической промышленности (21)
Экология и природопользование (19)
Электроника, радио-, электро- и схемотехника (83)
Юриспруденция и правоведение (78)
Естествознание (2)
Технология деревообрабатывающих производств, столярное дело.
Мебельное производство. (6)
Укрупненная группа специальностей
01.00.00 Математика и механика (1048)
02.00.00 Компьютерные и информационные науки (3005)
03.00.00 Физика и астрономия (507)
04.00.00 Химия (352)
05.00.00 Науки о Земле (335)
06.00.00 Биологические науки (314)
07.00.00 Архитектура (385)
08.00.00 Техника и технологии строительства (385)
09.00.00 Информатика и вычислительная техника (3806)
10.00.00 Информационная безопасность (346)
11.00.00 Электроника, радиотехника и системы связи (1200)
12.00.00 Фотоника, приборостроение, оптические и биотехнические системы и технологии (305)
13.00.00 Электро- и теплоэнергетика (321)
14.00.00 Ядерная энергетика и технологии (125)
15.00.00 Машиностроение (486)
16.00.00 Физико-технические науки и технологии (1199)
17.00.00 Оружие и системы вооружения (69)
18.00.00 Химические технологии (232)
19.
00.00 Промышленная экология и биотехнологии (249)
20.00.00 Техносферная безопасность и природообустройство (303)
21.00.00 Прикладная геология, горное дело, нефтегазовое дело и геодезия (951)
22.00.00 Технологии материалов (334)
23.00.00 Техника и технологии наземного транспорта (159)
24.00.00 Авиационная и ракетно-космическая техника (155)
25.00.00 Аэронавигация и эксплуатация авиационной и ракетно-космической техники (159)
26.00.00 Техника и технологии кораблестроения и водного транспорта (75)
27.00.00 Управление в технических системах (391)
28.00.00 Нанотехнологии и наноматериалы (184)
29.00.00 Технологии легкой промышленности (363)
30.00.00 Фундаментальная медицина (252)
31.00.00 Клиническая медицина (491)
32.00.00 Науки о здоровье и практическая медицина (224)
33.00.00 Фармация (88)
34.00.00 Сестринское дело (45)
35.00.00 Сельское, лесное и рыбное хозяйство (366)
36.00.00 Ветеринария и зоотехния (136)
37.
00.00 Психологические науки (1875)
38.00.00 Экономика и управление (6167)
39.00.00 Социология и социальная работа (708)
40.00.00 Юриспруденция (4001)
41.00.00 Политические науки и регионоведение (896)
42.00.00 Средства массовой информации и информационно-библиотечное дело (278)
43.00.00 Сервис и туризм (113)
44.00.00 Образование и педагогические науки (3025)
45.00.00 Языкознание и литературоведение (3775)
46.00.00 История и археология (707)
47.00.00 Философия, этика и религиоведение (771)
48.00.00 Теология (165)
49.00.00 Физическая культура и спорт (462)50.00.00 Искусствознание (427)
51.00.00 Культуроведение и социокультурные проекты (566)
52.00.00 Сценические искусства и литературное творчество (74)
53.00.00 Музыкальное искусство (133)
54.00.00 Изобразительное и прикладные виды искусств (303)
55.00.00 Экранные искусства (114)
56.00.00 Военное управление (162)
57.00.00 Обеспечение государственной безопасности (64)
Остаться в выбранном разделе
Назад к каталогу
ISBN 978-5-49807-772-7
Авторы:
Павловская Т.
А.
Тип издания:
Учебник
Издательство:
Год:
2010
Аннотация
В учебнике рассматриваются структурная и объектно-ориентированная технологии программирования, методы проектирования и отладки программ и основные структуры данных. Книга содержит последовательное изложение основ программирования на примере языка Паскаль, практикум по всем разделам курса, полную справочную информацию, 260 индивидуальных заданий для лабораторных работ и полностью соответствует Государственному образовательному стандарту. Проверить правильность выполнения основных лабораторных работ, изучить электронный конспект лекций и пройти тесты на знание синтаксиса языка можно на сайте http://ips.ifmo.ru. Допущено Министерством образования и науки Российской Федерации в качестве учебника для студентов высших учебных заведений, обучающихся по направлению подготовки дипломированных специалистов «Информатика и вычислительная техника».
Библиографическое описание Скопировать библиографическое описание
Павловская Т. А. Паскаль. Программирование на языке высокого уровня: Учебник для вузов. 2-е изд. / Т.А. Павловская. — Санкт-Петербург : Питер, 2010. — 464 с. — ISBN 978-5-49807-772-7. — URL: http://m.ibooks.ru/bookshelf/21768/reading (дата обращения: 12.01.2023). — Текст: электронный.
Какой учебник по Turbo Pascal лучший? — Хабр Q&A
это вы хотите над кем то поиздеваться или этот процесс над вами уже идет?
7-ая версия TP вышла в 1994 году, почти 30 лет назад, книги по нему уже наверное в разряд исторических артефактов должны попадать и торговаться у коллекционеров а вам чеки подавай?
Вот продадут с чеком но это бу без дискеты, что логично, там еще одна есть
p.s. не знаю, кто сказал что обучение программированию на бумаге имеет какую то пользу и эффективность? по мне так глупость несусветная, вот обучать программированию на основе высокоуровневых языках и фреймворках — да, опасно и вредно, но это другое
upd.
есть сервисы, которые из электронной книги сделают бумажную — google: печать книги один экземпляр (цены порядка 2-3 т.р. может меньше, надо искать)
конторы, занимающиеся ксерокопированием с высокой вероятностью могут распечатать и брошурировать как тебе угодно, там вообще копейки получатся
Ответ написан
Комментировать
Этот объявленный устаревшим ООП зачем так нужен? Мне кажется, что времена, когда писатели дорвались до инфраструктуры коммерческого книгопечатания и платёжеспособного спроса, были временами, когда было достоверно известно, что развитие в дальнейшем (в Delphi) пошло по другому пути. Имело смысл писать о вечном, о записях и массивах, но не об ООП заброшенном. В Delphi 7, если написать object, это warning.
Extended syntax {$X+}, насколько я помню, позволяет не разыменовывать указатели на записи при обращении к их полям, и это распространяется и на методы тоже, так что кареток дополнительных в тексте будет не так уж много.
Отсутствие исключений в языке накладывает такой отпечаток, что конструктор без исключений писать тяжело, и чтоб это побороть, добавлена псевдопроцедура Fail, про которую надо почитать.
Ответ написан
Комментировать
Объяснение урока: Треугольник Паскаля | Nagwa
В этом объяснителе мы научимся решать задачи на треугольник Паскаля.
Треугольник Паскаля — одна из самых захватывающих структур, которые мы можем построить из простого числового шаблона. Удивительно видеть связи между такой простой конструкцией и многими другими областями математики.
Треугольник Паскаля можно составить, начав с единицы вверху и поместив две единицы внизу. Тогда каждый элемент строки равен сумме двух элементов выше. Таким образом, на рисунке ниже мы видим, что два являются суммой двух вышеперечисленных.
Чтобы завершить следующую строку, мы можем считать попарную сумму элементов этой строки. Первая запись будет 1. Мы можем думать об этом как о сумме 0 и 1, как показано.
Следующий элемент представляет собой сумму 1 и 2, как показано ниже.
Аналогично, следующий элемент представляет собой сумму 2 и 1, как показано.
Последний элемент, как и первый, можно представить как сумму 1 и 0 следующим образом.
Продолжая эту схему, мы приходим к так называемому треугольнику Паскаля.
Треугольник Паскаля
Треугольник Паскаля представляет собой треугольный массив чисел, удовлетворяющих тому свойству, что каждый элемент равен сумме двух элементы выше. Строки нумеруются сверху так, что первая строка имеет номер 𝑛=0.
Аналогично элементы каждой строки пронумерованы от 𝑘=0 до 𝑛. Первые восемь рядов треугольника Паскаля показаны ниже.
Хотя в большей части западного мира треугольник назван в честь французского математика Блеза Паскаля, на самом деле она была хорошо известна математикам за столетия до него в таких странах, как Китай, Персия и Индия. По сей день в этих местах он известен под разными именами.
Треугольник Паскаля обладает многими интересными свойствами. Мы начнем с рассмотрения некоторых простых паттернов, существующих в треугольнике.
Некоторые из наиболее очевидных шаблонов связаны с диагоналями: например, первая диагональ содержит только единицы, тогда как вторая содержит
последовательные целые числа.
Что еще интереснее, третья диагональ содержит треугольные числа, а четвертая содержит четырехгранные числа.
Кроме того, мы можем видеть отражательную симметрию относительно центра.
Пример 1. Элементы треугольника Паскаля
Какой второй элемент в 500-й строке треугольника Паскаля?
Ответ
Напомним, что вторые элементы каждой строки треугольника Паскаля — последовательные целые числа. В этот момент у нас может возникнуть соблазн немедленно прыгнуть к выводу, что, следовательно, будет 500. Однако нам нужно быть немного более осторожными, чем это. Напомним, что первая строка содержит только 1. Следовательно, второго элемента нет. Первая строка со вторым элементом — это вторая строка, состоящая из из двух. Следовательно, второй элемент в этой строке равен 1, а не 2. Значит, вторым элементом 500-й строки треугольника Паскаля будет 499.
Пример 2: закономерности в треугольнике Паскаля
Показан частично заполненный рисунок треугольника Паскаля.
Замечая закономерности или иным образом,
найдите значения 𝑎, 𝑏, 𝑐 и 𝑑.
Ответ
Начнем с рассмотрения элементов третьей диагонали. Существует четкая схема перехода от одного элемента к другому: чтобы перейти от первого ко второму, прибавляем два; затем, чтобы перейти от второго к третьему, мы добавляем 3.
Мы можем расширить этот шаблон следующим образом.
И 𝑎, и 𝑏 являются элементами в этой строке. Следовательно, 𝑎=10 и 𝑏=15.
Теперь рассмотрим элемент 𝑐. Этот элемент на самом деле тоже находится на третьей диагонали — той, что в другом направлении, — и он шестой элемент. Следовательно, 𝑐=21.
Наконец, мы видим, что 𝑑 находится на второй диагонали. Эта диагональ содержит последовательные положительные целые числа. Следовательно, поскольку это одиннадцатый элемент, его значение будет просто 11.
Следовательно, наш окончательный ответ: 𝑎=10, 𝑏=15, 𝑐=21 и 𝑑=11.
Пример 3: Суммы по диагоналям в треугольнике Паскаля
На рисунке показано сечение треугольника Паскаля.
Не используя калькулятор, найдите сумму выделенных элементов.
Ответ
Для этого вопроса мы могли бы просто суммировать отдельные элементы. Однако на самом деле мы можем использовать свойства треугольника Паскаля, чтобы быстро оценить сумму этих элементов. Мы начнем с наименьшего элемента в строке: 1. Очевидно, что сумма этого элемента равна 1, что, как мы видим, равно элемент ниже вправо, как показано на рисунке.
Теперь рассмотрим первые два элемента и заметим, что их сумма равна элементу, расположенному ниже второго элемента справа.
Аналогично, сумма первых трех элементов равна сумме первых двух элементов и третьего элемента. Из определяющего свойства треугольника Паскаля мы видим, что это элемент непосредственно под этими двумя.
Продолжая этот шаблон, мы видим, что сумма выделенных элементов будет элементом ниже последнего элемента справа, как показано.
Следовательно, сумма выделенных элементов равна 5 005.
Теперь обратим внимание на отношения между соседними элементами.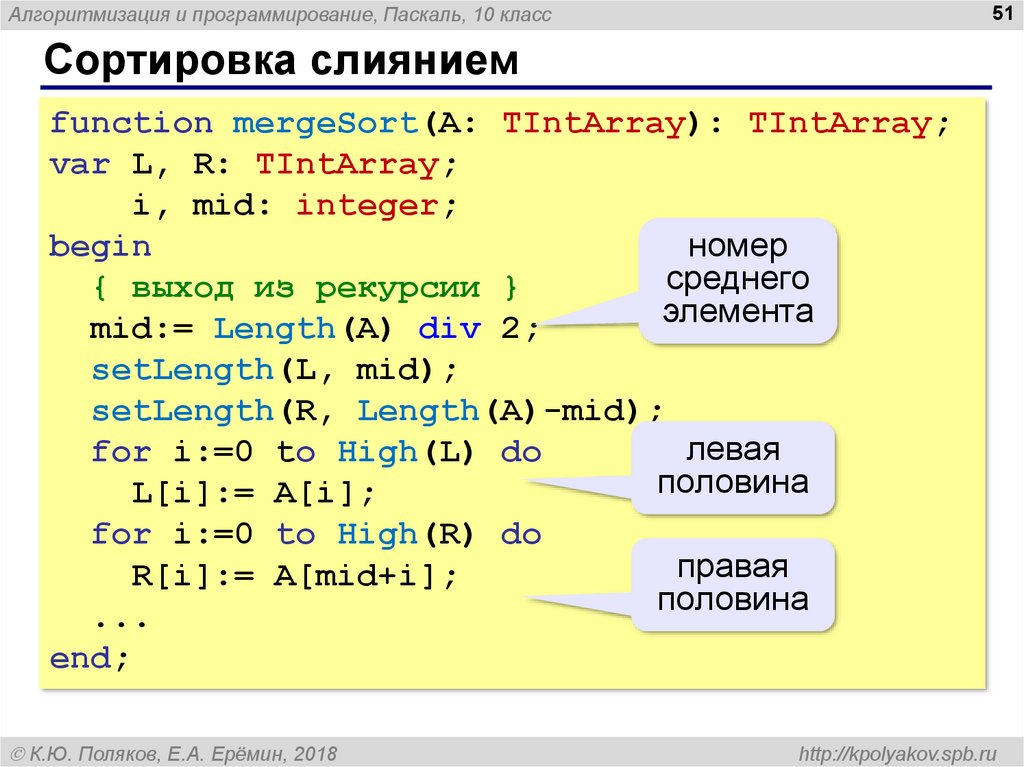
Ясно, что любой элемент является суммой двух указанных выше элементов. Однако,
существуют и другие отношения между этими тремя терминами. При обсуждении этого мы будем использовать перечисление строк, которое начинается с
𝑛=0. Точно так же в данной строке мы будем нумеровать элементы по 𝑘, где 𝑘=0 — первый элемент в строке.
Рассмотрим множители, связывающие члены на диагоналях между строками, пронумерованными 𝑛=5 и 𝑛=6. На рисунке ниже показан множитель, который берет нас из ряда 𝑛=5 к ряду 𝑛=6 по диагонали влево.
По-видимому, существует общая форма, связывающая эти термины, которую мы можем представить как умножение на
𝑛𝑘, где 𝑘 — нумерация элементов в строке 𝑛=6. На самом деле это правильное соотношение, которое выполняется для любых двух
элементы, связанные по левой диагонали. Обратите внимание, что и 𝑛, и 𝑘 относятся к нижним элементам. Точно так же мы можем посмотреть на
отношения между элементами на правой диагонали. На рисунке ниже показан множитель, который берет нас из
𝑛=5 ряд до 𝑛=6 ряда по диагонали вправо.
Снова появляется четкая закономерность, которую мы можем представить как умножение на 𝑛𝑛−𝑘. Это снова обобщается на любые два элемента, соединенных по правой диагонали. Опять же, и 𝑛, и 𝑘 относятся к нижним элементам.
Теперь рассмотрим связь между двумя последовательными элементами в одной строке. На рисунке ниже показан множитель, который берет нас из (𝑘−1)-й элемент в 𝑘-й элемент строки 𝑛=6.
Здесь снова четкая закономерность: чтобы перейти от (𝑘−1)-го элемента к 𝑘-ому, мы умножаем на 𝑛-𝑘+1𝑘.
Мы суммируем эти отношения на следующем рисунке.
Пример 4: Связь между соседними элементами в треугольнике Паскаля
На рисунке показаны 7 соседних элементов в треугольнике Паскаля.
Учитывая, что 5 985 — это 18-й элемент в 22-й строке, найдите 𝑎, 𝑏, 𝑐, 𝑑, 𝑒 и 𝑓.
Ответ
Во-первых, мы хотели бы записать значения 𝑛 и 𝑘 для данного элемента. Напомним, что мы начинаем перечисление
в 𝑛 и 𝑘 от нуля.
Следовательно, 18-й элемент — это элемент, для которого 𝑘=17, а 22-я строка — это строка для
что 𝑛=21.
Мы будем использовать отношения между последовательными элементами в треугольнике Паскаля. Мы представили мультипликаторы, которые соединяют соседние элементы на рисунке ниже.
Теперь займемся поиском 𝑎. Напомним, что в заданной строке для перехода от (𝑘−1)-го элемента к 𝑘й, умножаем на 𝑛−𝑘+1𝑘. Следовательно, чтобы перейти от 𝑘-го к (𝑘−1)-му элементу, мы умножаем по обратному: 𝑘𝑛−𝑘+1. Следовательно, 𝑎=1721−17+1×5985=175×5985=20349.
Теперь мы можем использовать соотношение между левыми диагоналями, чтобы найти 𝑏. Напомним, что для перемещения вниз по левой диагонали (от
(𝑘−1)-го элемента в (𝑛−1)-й строке до 𝑘-го элемента в 𝑛-й строке), мы умножаем на
𝑛𝑘. Следовательно, чтобы двигаться в обратном направлении, мы умножаем на обратную величину: 𝑘𝑛. Следовательно,
𝑏=1721×5985=4845.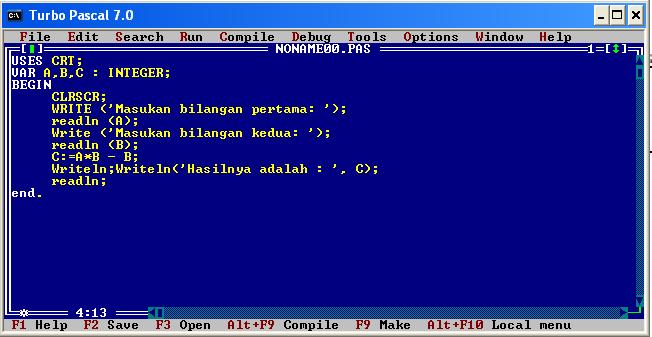
Точно так же, используя отношения между элементами на правой диагонали, мы можем найти 𝑐. Напомним, что для перемещения вниз по правой диагонали (от 𝑘-го элемента в (𝑛−1)-й строке к 𝑘-му элементу в 𝑛-й ряд), умножаем на 𝑛𝑛−𝑘. Следовательно, чтобы двигаться в обратном направлении, мы умножаем на взаимное: 𝑛−𝑘𝑛. Следовательно, 𝑐=421×5985=1140.
Стоит проверить, что 𝑏+𝑐=5985, так как, если бы это было не так, мы бы допустили ошибку. Проверяя это, мы находим, что наши три элемента удовлетворяют этому условию. Теперь рассмотрим 𝑑. Мы можем использовать отношения между элементами в одной строке и найти 𝑑, умножив на 418. Следовательно, 𝑑=418×5985=1330.
Наконец, мы можем найти 𝑒, используя определяющее свойство треугольника Паскаля: 5985+𝑑=𝑒. Следовательно, 𝑒=5985+1330=7315.
Точно так же мы можем найти 𝑓, вычислив 𝑎+5985=𝑓. Следовательно, 𝑓=20349+5985=26334.
Следовательно, окончательный ответ
𝑎=20349,𝑏=4845,𝑐=1140,𝑑=1330,𝑒=7315,𝑓=26334.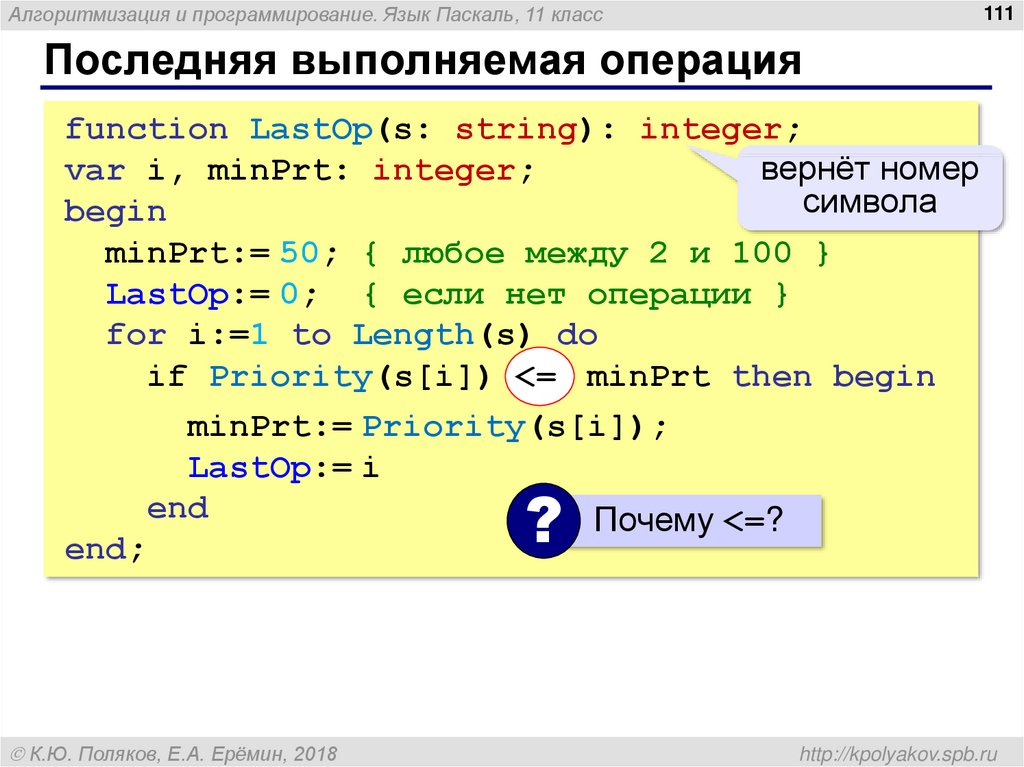
Используя эту связь между элементами, мы можем найти общую формулу элемента. Рассмотрим элемент, перечисленный 𝑘 в строке с номером 𝑛. Рассмотрим, как добраться до этого элемента из элемента at начало строки, которое всегда равно 1. Чтобы перейти ко второму элементу (𝑘=1), мы умножаем на 𝑛1. Затем, чтобы перейти к следующему элементу, мы умножаем на 𝑛−12. Следовательно, чтобы перейти от первого к третьему, мы умножаем на 𝑛(𝑛−1)2×1. Умножив это на множитель, чтобы перейти к следующему элементу, мы получим следующую формулу для четвертый элемент (в позиции 𝑘=3): 𝑛(𝑛−1)(𝑛−2)3×2×1.
Мы можем продолжать этот шаблон, пока не доберемся до элемента в позиции 𝑘, что дает нам формулу 𝑛(𝑛−1)(𝑛−2)×⋯×(𝑛−𝑘+1)𝑘×(𝑘−1)×⋯×2×1.
Используя факториал, мы можем написать это более кратко. Напомним, что факториал натурального числа
𝑛 — это произведение всех натуральных чисел, меньших или равных 𝑛. Обозначим факториал 𝑛 как 𝑛. Следовательно,
𝑛=𝑛×(𝑛−1)×(𝑛−2)×⋯×2×1.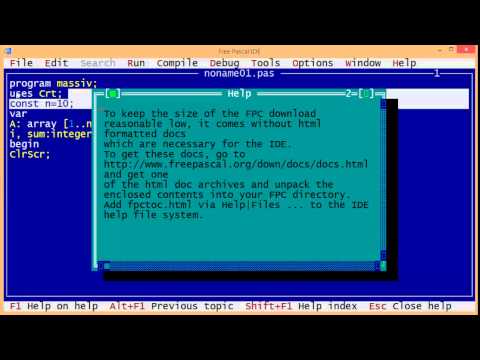
Используя факториал, мы можем переписать это как 𝑛(𝑛−1)(𝑛−2)×⋯×(𝑛−𝑘+1)𝑘×(𝑘−1)×⋯×2×1=𝑛(𝑛−1)(𝑛−2)×⋯×( 𝑛−𝑘+1)𝑘.
Умножая на 𝑛−𝑘𝑛−𝑘, имеем 𝑛(𝑛−1)(𝑛−2)×⋯×(𝑛−𝑘+1)𝑘=𝑛(𝑛−1)(𝑛−2)×⋯×(𝑛−𝑘+1)𝑘×(𝑛−𝑘 )!(𝑛−𝑘)!=𝑛𝑛−𝑘𝑘.
Эта формула может быть знакома, потому что на самом деле это формула для комбинация 𝐶, которую также иногда называют биномом коэффициент 𝑛𝑘. Таким образом, при нахождении общей формулы мы также продемонстрировали, что существует сильная Связь треугольника Паскаля с комбинаторикой. Кроме того, мы также показали, что треугольник Паскаля представляет собой треугольник, составленный из биномиальных коэффициентов (что, по сути, является альтернативным определением треугольника).
В оставшейся части этого объяснения мы потратим немного времени на изучение этих двух связей, начиная со связи между треугольником Паскаля и биномиальные коэффициенты.
Треугольник Паскаля можно использовать для нахождения коэффициентов членов разложения (𝑎+𝑏).
Рисунок демонстрирует это.
Это соотношение часто фиксируется в биномиальной теореме.
Биномиальная теорема
Для целого числа 𝑛, (𝑎+𝑏) = 𝐶𝑎+𝐶𝑎𝑏+𝐶𝑎𝑏+⋯+𝐶𝑎𝑏+⋯+𝐶𝑎𝑏+𝐶𝑏, куда 𝐶=𝑛𝑛−𝑟𝑟.
Иногда вместо 𝐶 используется следующее обозначение: 𝑛𝑟, 𝐶, 𝐶, 𝐶, и 𝐶(𝑛,𝑟).
Пример 5. Сумма строки треугольника Паскаля
Чему равна сумма членов 30-й строки треугольника Паскаля?
Ответ
Напомним, что 30-я строка треугольника Паскаля — это строка, которую мы пронумеровали 𝑛=29. Учитывая связь между элементами треугольника Паскаля и биномиальными коэффициентами, мы можем переформулировать это как проблему вычисления 𝐶+𝐶+𝐶+⋯+𝐶+𝐶.
Конечно, мы могли бы просто вычислить это с помощью калькулятора. Однако, используя биномиальную теорему,
(𝑎+𝑏) = 𝐶𝑎+𝐶𝑎𝑏+𝐶𝑎𝑏+⋯+𝐶𝑎𝑏+⋯+𝐶𝑎𝑏+𝐶𝑏,
мы можем серьезно упростить процесс вычисления этого выражения.
Обратите внимание, что если мы установим 𝑎=𝑏=1 и 𝑛=29, мы получим
2=𝐶+𝐶+𝐶+⋯+𝐶+𝐶.
Следовательно, сумма слагаемых в 30-й строке треугольника Паскаля равна 2.
Свойство, рассмотренное в последнем примере, не уникально для 30-й строки. В самом деле, сумма последовательных строк треугольника Паскаля является последовательными степенями двойки. В частности, строка с номером 𝑛 имеет сумму 2.
Пример 6. Сумма каждого второго элемента в строке треугольника Паскаля
Чему равна сумма всех остальных элементов в 1 000-й строке треугольника Паскаля?
Ответ
Напомним, что 1 тысячная строка треугольника Паскаля — это строка, которую мы перечисляем
𝑛=999. Очевидно, что для такого вопроса числа будут слишком большими, чтобы мы могли оценить их за один раз.
долгий путь. Поэтому нам нужно найти альтернативный путь. Во-первых, используя связь между
Треугольник Паскаля и биномиальные коэффициенты, мы можем переформулировать это как проблему вычисления
𝐶+𝐶+𝐶+⋯+𝐶+𝐶.
Обозначим эту сумму 𝑆. Кроме того, мы будем обозначать сумму остальных членов 𝑆. Следовательно, 𝑆=𝐶+𝐶+𝐶+⋯+𝐶+𝐶.
Мы знаем, что сумма всех слагаемых этой строки будет равно 2. Следовательно, 𝑆+𝑆=2. Теперь мы хотели бы найти другое выражение через 𝑆 и 𝑆, чтобы мы могли найти 𝑆. Используя биномиальную теорему, (𝑎+𝑏) = 𝐶𝑎+𝐶𝑎𝑏+𝐶𝑎𝑏+⋯+𝐶𝑎𝑏+⋯+𝐶𝑎𝑏+𝐶𝑏, мы можем найти такое выражение, установив 𝑎=1, 𝑏=−1 и 𝑛=999 следующим образом: 0=𝐶−𝐶+𝐶−𝐶+𝐶+⋯+𝐶−𝐶.
Мы можем переписать это как 0=𝑆−𝑆.
Поскольку 𝑆+𝑆=2, мы можем сложить эти два уравнения, чтобы получить 2𝑆=2.
Следовательно, 𝑆=2. Следовательно, сумма всех остальных элементов в 1 строке треугольника Паскаля равна 2.
Наконец, рассмотрим связь между треугольником Паскаля и комбинаторикой. Мы можем рассмотреть треугольник Паскаля
в виде графа, где каждая запись представляет узел.
В каждом узле у нас есть выбор: идти влево или вправо. Учитывая эту идею,
элементы в треугольниках Паскаля можно интерпретировать как количество различных путей, ведущих через граф
от верхнего элемента к данному элементу. Например, если мы рассмотрим третий элемент четвертой строки, мы увидим
есть три различных пути, чтобы добраться от вершины треугольника до данного элемента.
Мы можем использовать это свойство для решения комбинаторики и вероятностных задач, как будет показано в следующем примере.
Пример 7. Треугольник Паскаля и комбинаторика
Рами играет в игру, в которой мяч падает на ряд колышков с вертикально над верхним штифтом, и он отскакивает вниз к пронумерованным ведрам внизу.
Он получит приз только в том случае, если он попадет в ведро 3 или 7. Найдите вероятность того, что он получит приз, если существует даже вероятность того, что он упадет слева или справа от любого заданного колышка.
Ответ
Вероятность того, что шарик окажется в определенном ведре, будет равна числу возможных путей к этому ведру.
ведро, деленное на общее количество путей через массив. Напомним, что элементы треугольника Паскаля
можно интерпретировать как количество возможных путей через треугольник. Следовательно, количество путей к каждой корзине может быть
найти с помощью треугольника Паскаля. На данном рисунке у нас 9 ведер. Поэтому мы хотели бы рассмотреть девятую строку
Треугольник Паскаля, представляющий собой строку, для которой 𝑛=8. Мы можем записать эту строку, используя общую формулу для
записей или просто воспроизводя первые девять строк треугольника. Здесь мы будем использовать общую формулу.
Девятая строка треугольника Паскаля представлена ниже. 𝐶𝐶𝐶𝐶𝐶𝐶𝐶𝐶𝐶
Вычисление каждого из них может выразить элементы этой строки следующим образом. 18285670562881
Количество путей к каждому сегменту на диаграмме можно записать следующим образом.
Чтобы найти общее количество путей, мы могли бы сложить эти числа или использовать тот факт, что сумма элементов
(𝑛+1)-й строки равно 2.
Следовательно, общее количество путей через массив равно 2. Следовательно,
вероятность того, что шарик окажется в третьем ведре, равна 282=764. Сходным образом,
вероятность того, что шарик окажется в седьмом ведре, также равна 282=764. Следовательно,
вероятность того, что Рами выиграет приз, определяется как сумма этих чисел: 764+764=732.
Треугольник Паскаля обладает множеством других интересных закономерностей и свойств. Например, интересно изучить закономерности, которые мы получаем, рассматривая расположение всех нечетных чисел в треугольнике Паскаля или связь между треугольниками Паскаля и степенями числа 11.
Ключевые моменты
- Треугольник Паскаля можно определить двумя способами: свойство, что каждый элемент равен сумме двух элементов выше,
- треугольник биномиальных коэффициентов.
- Все элементы первой диагонали равны единице; во втором — последовательные положительные целые числа;
в третьем — треугольные числа; а в четвертом — четырехгранные числа.
- Каждый ряд симметричен относительно своей середины.
- Сумма элементов в (𝑛+1)-й строке равна 2.
- Переменная сумма любой строки равна нулю.
Tutorial Belajar Bahasa Pemrograman Pascal Bagi Pemula
Home
Tutorial Belajar Bahasa Pemrograman Pascal Bagi Pemula
Bagi kebanyakan mahasiswa ilmu komputer / teknik informatika, besar kemungkinan bahwa Pascal adalah bahasa pemrograman pertama yang anda pelajari.
Паскаль memiliki aturan pemrograman terstruktur sehingga cocok digunakan untuk mempelajari algoritma dan pemrograman komputer, terutama untuk pemula. Паскаль juga bahasa pemrograman янь pernah digunakan Dalam Olimpiade Sains Nasional bidang komputer.
Jika anda ingin mempelajari algoritma dan pemrograman komputer dari dasar, maka Паскаль adalah bahasa pemrograman янь tepat. Установил несколько структур, основанных на языке Pascal, а также на других языках C, C++, C# и Java.
Олег Карена ITU, duniailkom ingin menyajikan учебник belajar bahasa pemrograman Паскаль Ян ditujukan баги pemula. Dalam halaman ini, kami meng-index seluruh tutorial dan artikel Pascal di duniailkom:
Apabila anda serius ingin mempelajari Pascal dan butuh materi Pascal yang jauh lebih lengkap, Duniailkom telah menerbitkan eBook Паскаль Раскрыть .
Dengan Всего 453 halaman A4, buku JavaScript Раскрыть akan memandu rekan-rekan untuk menguasai bahasa pemrograman Pascal. Dalam buku ini akan dibahas mulai dari materi dasar Pascal hingga fitur lanjutan seperti процедура, функция, дан Pascal Unit.
Pascal Uncover bisa didapat dengan harga Rp.
50.000 . Untuk pemesanan silahkan kirim email ke [email protected] . Penjelasan lebih lanjut bisa ke: Pascal Uncover.
Pengertian dan Sejarah Bahasa Pemrograman Pascal
Untuk tutorial awal belajar pascal, kita akan berkenalan dengan bahasa pemrograman pascal, mulai dari pengertian bahasa pascal, sejarahnny dari awal kemunculan 197 ta 190.
- Учебное пособие Belajar Pascal Часть 1: Pengertian Bahasa Pemrograman Pascal
- Учебник Белахара Паскаля, часть 2: Седжара Бахаса Пемрограман Паскаль
Cara Install Free Pascal dan Turbo Pascal
Dalam 2 tutorial ini akan dibahas langkah demi langkah untuk mendownload dan menginstall aplikasi untuk menjalankan code program pascal, yakni Free Pascal dan Turbo Pascal 7.
- Tutorial Belajar Pascal Part 3: Cara MengPascal Part 02 Pascal 2 Freedownload dan Meng90
- Tutorial Belajar Pascal Part 4: Cara Mendownload dan Menginstall Turbo Pascal 7
Cara Penulisan дан Struktur Pascal
Bagian ini akan membahas tenang cara penulisan code Program Pascal, cara menjalankan code Program Pascal, Serta Struktur Dasar Kode Pascal.
- Учебник Belajar Pascal Часть 5: Cara Menjalankan Kode Program Pascal (Файл exe)
- Учебное пособие Belajar Pascal, часть 6: Aturan dan Cara Penulisan Kode Program Pascal
- Учебное пособие Belajar Pascal Часть 7: Struktur Dasar Kode Program Pascal
- Учебное пособие Belajar Pascal Часть 8: Pengertian Variabel Pascal dan Cara Penulisannya
- Учебник Belajar Pascal Часть 9: Pengertian Konstanta Pascal dan Cara Penulisannya
- Учебник Belajar Pascal Часть 10: Cara Penggunaan serta Perbedaan Write dan Writeln
- Учебник Belajar Pascal Часть 11: Cara Penggunaan serta Perbedaan Read dan Readln
Тип Data Pascal
Setelah memahami structur dasar bahasa pemrograman Pascal, dalam bagian ini kita akan membahas lebih jauh tenang tipe data yang ada di dalam Pascal. Pascal mendukung berbagai type data bawaan, yaitu: integer, real, char, boolean, dan строка .
Serta typee data bentukan: перечисление , поддиапазон, массив (ларик), запись и указатель .
- Учебное пособие Belajar Pascal Часть 12: Pengertian dan Cara Penggunaan Type Data Integer
- Учебное пособие Belajar Pascal, часть 13: Pengertian dan Cara Penggunaan Tipe Data Real
- Учебное пособие Belajar Pascal Часть 14: Pengertian dan Cara Penggunaan Тип данных Char
- Tutorial Belajar Pascal Part 15: Pengertian dan Cara Penggunaan Type Data String
- Tutorial Belajar Pascal Part 16: Pengertian dan Cara Penggunaan Типовые логические данные
- Учебное пособие Belajar Pascal Часть 17: Pengertian dan Cara Penggunaan Tipe Перечисленный
- Учебное пособие Belajar Pascal, часть 18: Pengertian dan Cara Penggunaan Typee Data Subrange
- Учебное пособие Belajar Pascal, часть 19: Pengertian dan Cara Penggunaan Тип массива данных
- Учебное пособие Belajar Pascal, часть 20: Cara Membuat Array 2 Dimensi Pascal
- Учебное пособие Belajar Pascal, часть 21: Pengertian dan Cara Membuat Array Dinamis
- Tutorial Belajar Pascal Part 22: Cara Membuat Array dari Type Data Bentukan
- Учебное пособие Belajar Pascal Часть 23: Pengertian dan Cara Penggunaan Типовая запись данных
- Учебное пособие Belajar Pascal, часть 24: Fungsi Perintah с записью данных типа pada
- Tutorial Belajar Pascal Part 25: Cara Membuat Array dari Struktur Data Record
- Учебное пособие Belajar Pascal, часть 26: Pengertian dan Cara Penggunaan Typee Data Set
- Учебное пособие Belajar Pascal, часть 27: Pengertian dan Cara Penggunaan Typee Data Pointer
- Учебное пособие Белахара Паскаля, часть 28: Дженис-Дженис Тип данных Далама Бахасы Паскаля
Оператор Паскаль
Pada sesi tutorial ini akan dibahas dengan lebih details tenang apa saja jenis-jenis operator di dalam bahasa pemrograman pascal.
- Учебное пособие Belajar Pascal Часть 29: Jenis-jenis Operator dalam Bahasa Pascal
- Tutorial Belajar Pascal Часть 30: Назначение оператора Jenis-jenis для Pascal
- Учебное пособие Belajar Pascal Часть 31: Jenis-jenis Operator Aritmatika dalam Pascal
- Tutorial Belajar Pascal Part 32: Jenis-Jenis Operator String для Паскаля
- Учебник Belajar Pascal Часть 33: Jenis-jenis Operator Perbandingan / Relasional Pascal
- Учебник Belajar Pascal Часть 34: Jenis-jenis Operator Logika dalam Pascal
- Учебное пособие Belajar Pascal Часть 35: Urutan Prioritas Operator dalam Bahasa Pascal
Struktur Kondisi dan Perulangan
Pada bagian ini akan dibahas perintah-perintah code pemrograman Pascal Yang digunakan untuk membuat percabangan code program atau dikenal juga dengan struktur kondisi / struktur logika. Di dalam pascal terdapat kondisi IF THEN , IF THEN ELSE , Вложенные IF THEN ELSE (если bersarang), dan structur CASE .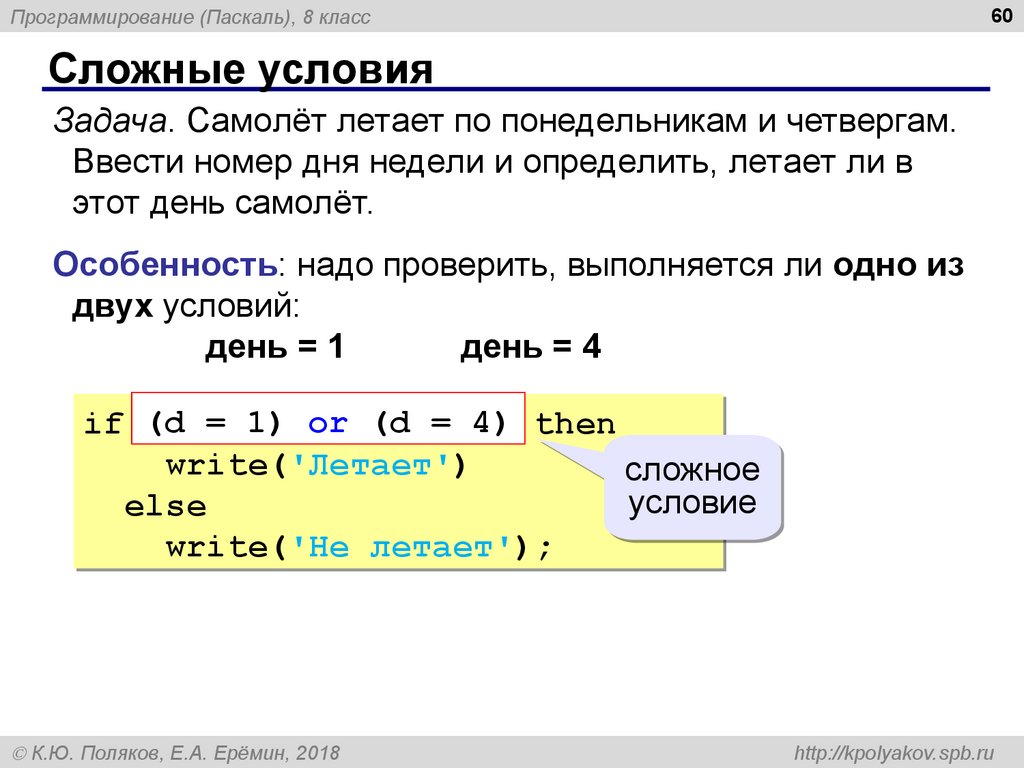
Setelah itu kita akan masuk ke perulangan. Perulangan atau Dalam bahasa inggris dikenal dengan istilah loop merupakan konsep pemrograman yang digunakan untuk mengulang baris perintah. Disini akan dibahas cara membuat perulangan di Pascal menggunakan perintah ДЛЯ ДО , ДЛЯ ДО , ПОКА ДЕЛАТЬ и ПОВТОРЯТЬ ДО .
- Tutorial Belajar Pascal Part 36: Percabangan Kondisi IF THEN dalam Pascal
- Tutorial Belajar Pascal Part 37: Percabangan Kondisi IF THEN ELSE dalam Pascal
- Tutorial Belajar Pascal Part 38: Percabangan Kondisi IF Bersarang dalam Pascal
- Tutorial Belajar Pascal Part 39: Struktur Percabangan CASE для Pascal
- Tutorial Belajar Pascal Part 40: Struktur Percabangan CASE ELSE dalam Pascal
- Учебник Belajar Pascal Часть 41: Perulangan FOR DO dalam Pascal
- Учебное пособие Belajar Pascal Часть 42: Перуланган FOR DOWNTO dalam Pascal
- Учебник Белахара Паскаля, часть 43: Перуланган, ПОКА ДЕЛАЕМ с Паскалем
- Учебник Белахара Паскаля Часть 44: Перуланган ПОВТОРЯТЬ ДО ДАЛАМА ПАСКАЛЯ
- Tutorial Belajar Pascal Part 45: Perulangan Bersarang (вложенный цикл) dalam Pascal (1)
- Учебное пособие Belajar Pascal Часть 46: Perulangan Bersarang (вложенный цикл) dalam Pascal (2)
- Учебное пособие Белаяр Паскаль, часть 47: Фунгси Перинтах BREAK Далам Перуланган Паскаль
- Учебное пособие Belajar Pascal Часть 48: Fungsi Perintah ПРОДОЛЖЕНИЕ Dalam Perulangan Pascal
Studi Kasus, Latihan dan Contoh Code Program Pascal
Bagian ini dikhususkan untuk tutorial lepas yang akan membahas studi kasus, latihan dan contoh code Program Bahasa Pascal.