Трехмерные координаты: HTTP 404 Resource not found

Трехмерные координаты для построения матрицы 4 * 4?

Как перевести точку в трехмерное пространство

Как мы должны трансгатировать точку в трехмерном пространстве? Ответ прост, нам нужно только добавить каждый компонент (x, y, z) в этой точке координат, и можно добавить расстояние перевода на соответствующую ось.
Например, точка P1 (x1, y1, z1) переводится Δx, Δy, Δz до новых точек p2 (x2, y2, z2) на оси x y y y и z-осью, то нам нужно только соответствовать Компонент, соответствующий координатам. Плюс эти приращения могут определить координаты точки P2. 
x2 = x1 + Δx 
y2 = y1 + Δy 
z2 = z1 + Δz

Это просто? Тогда давайте посмотрим на другое преобразование: поверните.

Поверните точку

Вращение переводимо, это будет немного сложнее. Поскольку нам необходимо указать следующие аспекты для описания вращения:
Роторный вал
повернись
Угол поворота

Здесь мы предполагаем, что точка P требует вращения β градусов вокруг оси Z.Как показано на этой сложной фигуре, наши точки P1 (x1, y1, z1) регулируются до точки p2 (x2, y2, z2) после вращения β-степени в осевой оси. Далее, давайте предположим, что происхождение P1 представляет собой биты расстояния P1, а угловые биты между осями P1 и Y, затем в соответствии с формулой треугольной функции, мы можем рассчитать специфические координаты точки P1:
x1 = L·sinα 
y1 = L·cosα

Поскольку он вращается вокруг оси Z, координата Z не изменилась, поэтому она не рассматривается.
Точно так же согласно треугольной формуле функции, мы можем продолжать рассчитать специфические координаты P2:
x2 = L·sin(α + β) 
y2 = L·cos(α + β)

Давайте помним содержание геометрической математики средней школы и вернув нас к учителю, чтобы научить нас в классе. Два угла и различия:
cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α+β)=sinα·cosβ+cosα·sinβsin(α-β)=sinα·cosβ-cosα·sinβ

После вспомогания учителя после знания учителя следующая комбинация представлений координат P1 может изменить координаты P2 к представлению.
x2 = L·(sinα·cosβ+cosα·sinβ) = cosβ·x1 + sinβ·y1 
y2 = L·(cosα·cosβ-sinα·sinβ) = cosβ·y1 — sinβ·x1 
z2 = z1

Следовательно, в случае известных координат точки P1 и угла вращения β, мы можем найти каждый компонент координат точки P2 в соответствии с вышеуказанной формулой. Если мы посмотрим на формулу точки в предыдущем разделе, мы можем обнаружить, что, по-видимому, нет необходимости в матрице, а преобразование координат может быть достигнуто только двумя наборами выражений. но……

Принесите удобную матрицу

Конечно, в теории мы можем реализовывать преобразования только через математические формулы, но фактические ситуации довольно сопоставимы, когда преобразование очень сложно, и она довольно сопоставима, напрямую с использованием математических выражений. Следовательно, на самом деле матрица (прямоугольный массив M × NBBS составлен) часто используется в реальности, что указывает на линейные преобразования, такие как перевод, вращение и увеличение. Еще одним интересным фактом является то, что когда завершение двух матриц преобразования A и B представляет собой P = AB, матрица P преобразования соответствует преобразованиям, представленным A и B. Например, если A — это матрица вращения, B — это матрица перевода, матрица P может реализовать вращение и трансформацию передачи. Однако следует отметить, что умножение матрицы не соответствует закону об обмене, поэтому AB и BA не равны. Как сказано так много, мы, кажется, не ответили, почему трехмерное пространство нуждается в матрице 4 × 4 для реализации преобразования? Ниже мы возьмем этот вопрос, посмотрите на матрицу 3 × 3 и матрицы 4 × 4.

Матрица и вращение

Во-первых, давайте сначала посмотрим на матрицу, умноженную на трехмерный вектор.Можно видеть, что матрица представляет собой матрицу 3 × 3, а правая сторона матрицы представляет собой координаты точки P1, а левая сторона матрицы — это координаты точки P2. Согласно этому выражению, мы можем найти значения x2, y2, z2:
x2 = a·x1 + b·y1 + c·z1 
y2 = d·x1 + e·y1 + f·z1 
z2 = g·x1 + h·y1 + i·z1

Чтобы подключить уравнение матрицы и математическое выражение предыдущего раздела, мы сделаем сравнение роторного выражения и уравнения матрицы.
x2 = a·x1 + b·y1 + c·z1x2 = cosβ·x1 + sinβ·y1 
y2 = d·x1 + e·y1 + f·z1y2 = cosβ·y1 — sinβ·x1 
z2 = g·x1 + h·y1 + i·z1z2 = z1

По сравнению x2 можно найти a = cosβ, b = sinβ, c = 0; сравнение y2, вы также можете найти d = -sinβ, e = cosβ, f = 0; конечное сравнение z2, может определить g = 0, h = 0, i = 1; принесите этот результат в предыдущую матрицу, наше уравнение может стать следующим:То есть через эту 3 × 3 трансформацию матрицы мы реализовали преобразование вращения трехмерного пространства. Так почему же нужно использовать матрицы 4 × 4?

Неожиданный перевод, 4 × 4 матрицы для спасения земли

Мы смогли получить преобразование вращения через матрицу 3 × 3. Очевидно, что если эта матрица 3 × 3 действительно прекрасно решает изменение, то он также должен быть подходит для других преобразований, таких как перевод. Но может ли это соответствовать трансляционным потребностям? Ниже мы ищем ответы со стороны сравнительных матричных уравнений и математических выражений.
x2 = a·x1 + b·y1 + c·z1x2 = x1 + Δx 
y2 = d·x1 + e·y1 + f·z1y2 = y1 + Δy 
z2 = g·x1 + h·y1 + i·z1z2 = z1 + Δz

Благодаря сравнению, мы обнаружили разницу между переводом и вращением, то есть трансляционное выражение имеет постоянную Δx, будь то вращающееся выражение или матричное уравнение, нет такой постоянной, чтобы соответствовать. Так что тогда у нас нет способа использовать матрицы 3 × 3, чтобы указать перевод. Как решить эту проблему? Ответ на самом деле очень простой, то есть используйте матрицу 4 × 4 для достижения. Но один из вопросов — это то, как сделать трехмерную координату и матрицу 4 × 4?

Координация

Чтобы решить проблему трехмерных векторов и матрицы 4 × 4, наша остроумность добавила четвертый компонент для трехмерных векторов, так что предыдущие трехмерные векторы (X, Y, Z) становятся четырехмерными ( X, Y, Z, W), который называется однородной координатой вектором, состоящим из четырех компонентов. Следует отметить, что координаты Qi (x, y, z, w) эквивалентны трехмерными координатам (x / w, y / w, z / w), так что до тех пор, пока значение компонента W составляет 1 Затем эта однородная координата его можно использовать в качестве трехмерной координаты, и координаты представления являются точки 3 значений X, Y, Z. Следовательно, для того, чтобы размножаться и 4 × 4 матрицы, наши координаты точки P1 становятся (x1, y1, z1, 1). Уравнение матрицы также стало следующим видом:Мы сравнили это новое уравнение матрицы и развивающееся математическое выражение:
x2 = a·x1 + b·y1 + c·z1 + dx2 = x1 + Δx 
y2 = e·x1 + f·y1 + g·z1 + hy2 = y1 + Δy 
z2 = i·x1 + j·y1 + k·z1 + lz2 = z1 + Δz 
1 = m·x1 + n·y1 + o·z1 + p

Сравнимом X2, мы можем найти a = 1, b = 0, c = 0, d = δx; контрастность y2, или его можно найти, что e = 0, f = 1, g = 0, h = Δy; снова сравнивать Z2, определяют i = 0, j = 0, k = 1, l = δz; наконец, в соответствии с выражением, m = 0, n = 0, o = 0, p = 1; Итак, мы найдем наши 4 × 4 Матрица перевода:

подводить итоги

Написав здесь, я не знаю, помню, что когда я ввел мультипликацию матрицы, я упомянул продукт P = ab двух матриц преобразования A и B, который эквивалентен преобразованиям, представленным A и B.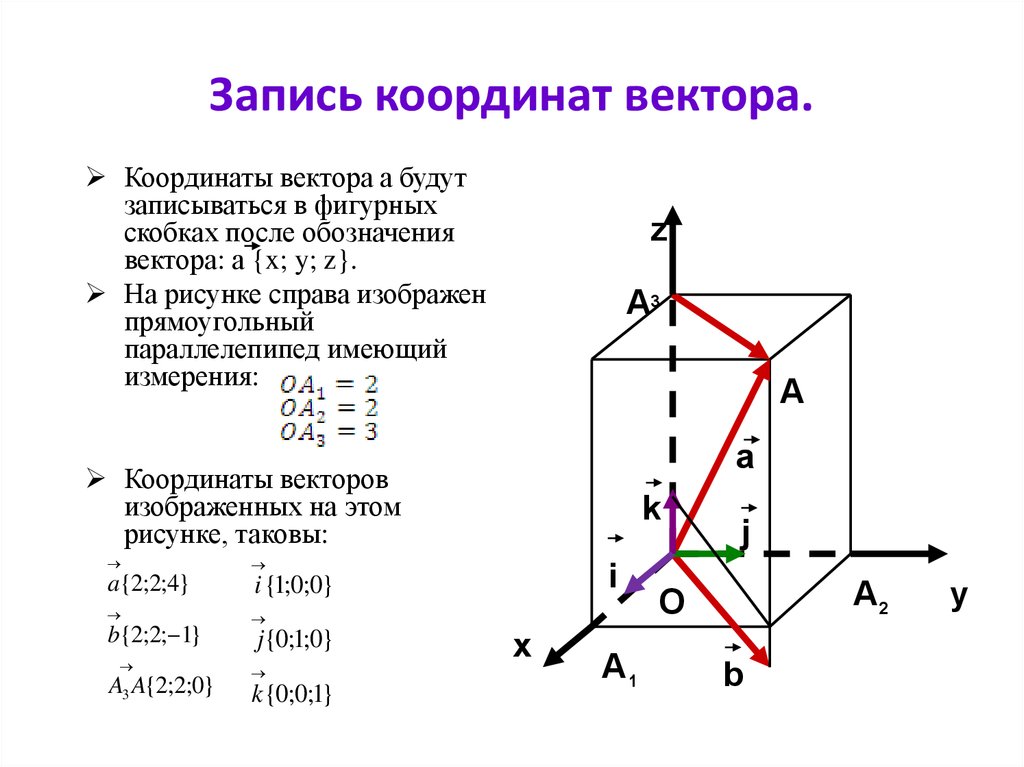 Фактически, в игровом программировании часто необходимо предварительно рассчитать серию преобразований в одну матрицу, так что в матрице нет 3 × 3 и матрицы 4 × 4. Матрица 3 × 3 расширяется до матрицы 4 × 4 или относительно легче. Таким образом, матрица перевода интегрирована, а матрица вращения интегрирована на матрицу 4 × 4.

Справочникhttp://www.cnblogs.com/murongxiaopifu/p/5149908.html

Прямоугольная система координат на плоскости и в пространстве. Трехмерные координаты

Двумерная система координат

Точка P имеет координаты (5,2).

Современная Декартова система координат в двух измерениях (также известная под названиемпрямоугольная система координат) задается двумя осями, расположенными под прямым углом друг к другу. Плоскость, в которой находятся оси, называют иногда xy-плоскости. Горизонтальная ось обозначается как x (ось абсцисс), вертикальная как y (ось ординат). В трехмерном пространстве до двух добавляется третья ось, перпендикулярная xy-плоскости — ось z. Все точки в системе декартовых координат, составляют так называемый Декартов пространство.

Точка пересечения, где оси встречаются, называется началом координат и обозначается как O. Соответственно, ось x может быть обозначена как

Ox, а ось y — как Oy. Прямые, проведенные параллельно каждой оси на расстоянии единичного отрезка (единицы измерения длины) начиная с начала координат, формируют координатную сетку.

Точка в двумерной системе координат задается двумя числами, которые определяют расстояние от оси Oy (абсцисса или х-координата) и от оси Ох (ордината или y-координата) соответственно. Таким образом, координаты формируют упорядоченную пару (кортеж) чисел (x, y). В трехмерном пространстве добавляется еще z-координата (расстояние точки от ху-плоскости), и формируется упорядоченная тройка координат (x, y, z).

Выбор букв x, y, z происходит от общего правила наименования неизвестных величин второй половиной латинского алфавита. Буквы первой его половины используются для именования известных величин.

Стрелки на осях отражают то, что они простираются до бесконечности в этом направлении.

Пересечение двух осей создает четыре квадранта на координатной плоскости, которые обозначаются римскими цифрами I, II, III, и IV. Обычно порядок нумерации квадрантов — против часовой стрелки, начиная с правого верхнего (т.е. там, где абсциссы и ординату — положительные числа). Значение, которых приобретают абсциссы и ординаты в каждом квадранте, можно свести в следующую таблицу:

Квадрант	x	y
I	> 0	> 0
II		> 0
III
IV	> 0

Трехмерная и n-мерная система координат

На этом рисунке точка P имеет координаты (5,0,2), а точка Q — координаты (-5, -5,10)

Координаты в трехмерном пространстве формируют тройку (x, y, z).

Координаты x, y, z для трехмерной декартовой системы можно понимать как расстояния от точки до соответствующих плоскостей: yz, xz, и xy.

Трехмерная Декартова система координат является очень популярной, так как соответствует привычным представлениям о пространственных измерения — высоту, ширину и длину (то есть три измерения). Но в зависимости от области применения и особенностей матиматичного аппарата, смысл этих трех осей может быть совсем другим.

Системы координат высших размерностей также применяются (например, 4-мерная система для изображения пространства-времени в специальной теории относительности).

Система декартовых координат в абстрактном n-мерном пространстве является обобщением изложенных выше положений и имеет n осей (по каждой на измерение), что является взаимоперпендикулярных. Соответственно, положение точки в таком пространстве будет определяться кортежем из

n координат, илиn-кой.

Уравнение прямой в (планиметрия) в каноническом

виде, параметрическом и общем виде.

Эти уравнения называются каноническими уравнениями прямой в пространстве.

могут быть равны нулю, это означает, что числитель соответствующей дроби тоже равен нулю.

Если в (1) ввести параметр t

x − x 0 l y − y 0 m z − z 0 n

то уравнения прямой можно записать в виде

При введении системы координат на плоскости или в трехмерном пространстве появляется уникальная возможность описания геометрических фигур и их свойств при помощи уравнений и неравенств. Это имеет иное название – методы алгебры.

Данная статья поможет разобраться с заданием прямоугольной декартовой системой координат и с определением координат точек. Более наглядное и подробное изображение имеется на графических иллюстрациях.

Чтобы ввести систему координат на плоскости, необходимо провести на плоскости две перпендикулярные прямые. Выбираем положительное направление , обозначая стрелочкой. Необходимо выбрать масштаб. Точку пересечения прямых назовем буквой O . Она считается началом отсчета . Это и называется прямоугольной системой координат на плоскости.

Прямые с началом O , имеющие направление и масштаб, называют координатной прямой или координатной осью .

Прямоугольная система координат обозначается O x y . Координатными осями называют О х и О у, называемые соответственно

ось абсцисс и ось ординат .

Изображение прямоугольной системы координат на плоскости.

Оси абсцисс и ординат имеют одинаковую единицу изменения и масштаб, что показано в виде штрихе в начале координатных осей. Стандартное направление О х слева направо, а O y – снизу вверх. Иногда используется альтернативный поворот под необходимым углом.

Прямоугольная система координат получила название декартовой в честь ее первооткрывателя Рене Декарта. Часто можно встретить название как прямоугольная декартовая система координат.

Трехмерное евклидовое пространство имеет аналогичную систему, только оно состоит не из двух, а из трех О х, О у, О z осей. Это три взаимно перпендикулярные прямые, где О z имеет название ось аппликат.

По направлению координатных осей делят на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке O , называемой началом. Каждая ось имеет положительное направление, которое указывается при помощи стрелок на осях. Если при повороте О х против часовой стрелки на 90 ° ее положительное направление совпадает с положительным О у, тогда это применимо для положительного направления О z . Такую систему считают правой. Иначе говоря, если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y , а средний за Z .

Аналогично образуется левая система координат. Обе системы совместить невозможно, так как соответствующие оси не совпадут.

Для начала отложим точку М на координатной оси О х. Любое действительное число x M равняется единственной точке М, расположенной на данной прямой. Если точка расположена на координатной прямой на расстоянии 2 от начала отсчета по положительному направлению, то она равна 2 , если — 3 , то соответственное расстояние 3 . Ноль – это начало отсчета координатных прямых.

Иначе говоря, каждая точка М, расположенная на O x , равна действительному числу x M . Этим действительным числом и является ноль, если точка M расположена в начале координат, то есть на пересечении O x и О у. Число длины отрезка всегда положительно, если точка удалена в положительном направлении и наоборот.

Имеющееся число x M называют координатой точки М на заданной координатной прямой.

Возьмем точку как проекцию точки M x на О х, а как проекцию точки M y на О у. Значит, через точку М можно провести перпендикулярные осям О x и О у прямые, где послучим соответственные точки пересечения M x и M y .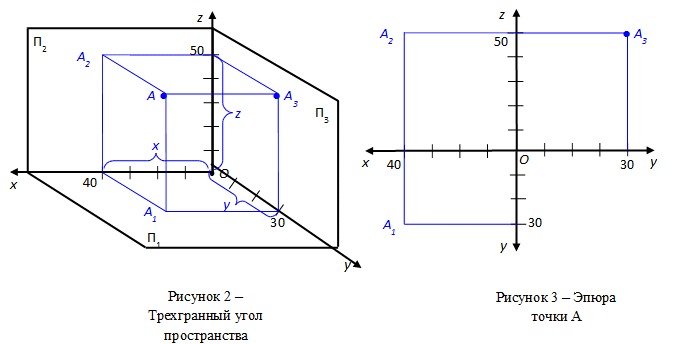

Тогда точка M x на оси О х имеет соответствующее число x M , а M y на О у — y M . На координатных осях это выглядит так:

Каждая точка M на заданной плоскости в прямоугольной декартовой системе координат имеет одну соответствующую пару чисел (x M , y M) , называемую ее координатами . Абсцисса M – это x M , ордината M – это y M .

Обратное утверждение также считается верным: каждая упорядоченная пара (x M , y M) имеет соответствующую заданную в плоскости точку.

Определение точки М в трехмерном пространстве. Пусть имеются M x , M y , M z , являющиеся проекциями точки М на соответствующие оси О х, О у, О z . Тогда значения этих точек на осях О х, О у, О z примут значения x M , y M , z M . Изобразим это на координатных прямых.

Чтобы получить проекции точки M , необходимо добавить перпендикулярные прямые О х, О у, О z продолжить и изобразит в виде плоскостей, которые проходят через M . Таким образом, плоскости пересекутся в M x , M y , M z

Каждая точка трехмерного пространства имеет свои данные (x M , y M , z M) , которые имеют название

координаты точки M , x M , y M , z M — это числа, называемые абсциссой, ординатой и аппликатой заданной точки M .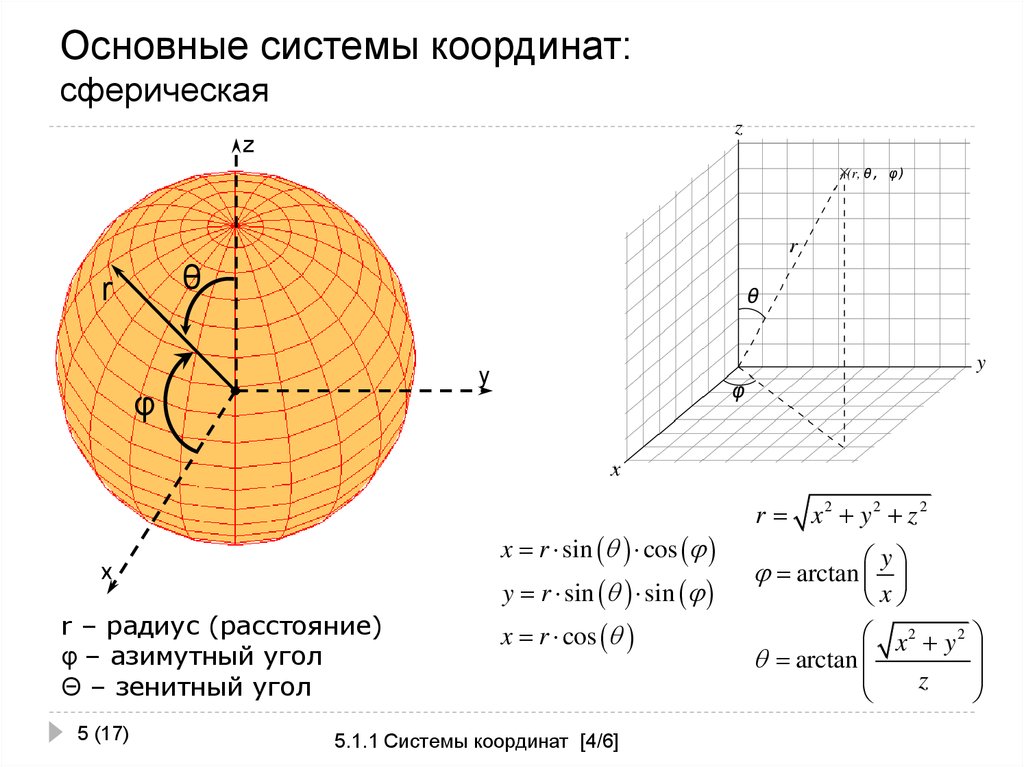 Для данного суждения верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (x M , y M , z M) в заданной прямоугольной системе координат имеет одну соответствующую точку M трехмерного пространства.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Если на плоскости или в трехмерном пространстве ввести систему координат, то мы получим возможность описывать геометрические фигуры и их свойства с помощью уравнений и неравенств, то есть, мы сможем использовать методы алгебры. Поэтому понятие системы координат очень важно.

В этой статье мы покажем как задается прямоугольная декартова система координат на плоскости и в трехмерном пространстве и выясним как определяются координаты точек. Для наглядности приведем графические иллюстрации.

Навигация по странице.

Прямоугольная декартова система координат на плоскости.

Введем прямоугольную систему координат на плоскости.

Для этого проведем на плоскости две взаимно перпендикулярные прямые, выберем на каждой из них положительное направление , указав его стрелочкой, и выберем на каждой из них масштаб (единицу измерения длины). Обозначим точку пересечения этих прямых буквой О и будем считать ее началом отсчета . Так мы получили прямоугольную систему координат на плоскости.

Каждую из прямых с выбранным началом отсчета О , направлением и масштабом называют координатной прямой или координатной осью .

Прямоугольную систему координат на плоскости обычно обозначают Oxy , где Ox и Oy – ее координатные оси. Ось Ox называют осью абсцисс , а ось Oy – осью ординат .

Сейчас условимся с изображением прямоугольной системы координат на плоскости.

Обычно единица измерения длины на осях Ox и Oy выбирается одинаковая и откладывается от начала координат на каждой координатной оси в положительном направлении (отмечается штришком на координатных осях и рядом записывается единица), ось абсцисс направляется вправо, а ось ординат – вверх. Все остальные варианты направления координатных осей сводятся к озвученному (ось Ox — вправо, ось Oy — вверх) при помощи поворота системы координат на некоторый угол относительно начала координат и взгляда на нее с другой стороны плоскости (при необходимости).

Прямоугольную систему координат часто называют декартовой, так как ее на плоскости впервые ввел Рене Декарт. Еще чаще прямоугольную систему координат называют прямоугольной декартовой системой координат, собирая все воедино.

Прямоугольная система координат в трехмерном пространстве.

Аналогично задается прямоугольная система координат Oxyz в трехмерном евклидовом пространстве, только берется не две, а три взаимно перпендикулярных прямых. Другими словами, к координатным осям Оx и Oy добавляется координатная ось Oz , которую называют осью аппликат .

В зависимости от направления координатных осей различают правую и левую прямоугольные системы координат в трехмерном пространстве.

Если смотреть с положительного направления оси Oz и кратчайший поворот от положительного направления оси Ox к положительному направлению оси Oy происходит против хода часовой стрелки, то система координат называется правой .

Если смотреть с положительного направления оси Oz и кратчайший поворот от положительного направления оси Ox к положительному направлению оси Oy происходит по ходу часовой стрелки, то система координат называется левой .

Координаты точки в декартовой системе координат на плоскости.

Сначала рассмотрим координатную прямую Ox и возьмем некоторую точку M на ней.

Каждому действительному числу соответствует единственная точка M на этой координатной прямой. К примеру, точке, расположенной на координатной прямой на расстоянии от начала отсчета в положительном направлении, соответствует число , а числу -3 соответствует точка, расположенная на расстоянии 3 от начала отсчета в отрицательном направлении. Числу 0 соответствует начало отсчета.

С другой стороны, каждой точке M на координатной прямой Ox соответствует действительное число . Это действительное число есть ноль, если точка M совпадает с началом отсчета (с точкой O ). Это действительное число положительно и равно длине отрезка OM в данном масштабе, если точка M удалена от начала отсчета в положительном направлении. Это действительное число отрицательно и равно длине отрезка OM со знаком минус, если точка M удалена от начала отсчета в отрицательном направлении.

Число называется координатой точки M на координатной прямой.

Теперь рассмотрим плоскость с введенной прямоугольной декартовой системой координат. Отметим на этой плоскости произвольную точку М .

Пусть — проекция точки M на прямую Ox , а — проекции точки M на координатную прямую Oy (при необходимости смотрите статью ). То есть, если через точку M провести прямые, перпендикулярные координатным осям Ox и Oy , то точками пересечения этих прямых с прямыми Ox и Oy являются соответственно точки и .

Пусть точке на координатной оси Ox соответствует число , а точке на оси Oy — число .

Каждой точке М плоскости в заданной прямоугольной декартовой системе координат соответствует единственная упорядоченная пара действительных чисел , называемых координатами точки M на плоскости. Координату называют абсциссой точки М , а — ординатой точки М .

Верно и обратное утверждение: каждой упорядоченной паре действительных чисел соответствует точка М плоскости в заданной системе координат.

Координаты точки в прямоугольной системе координат в трехмерном пространстве.

Покажем как определяются координаты точки М в прямоугольной системе координат, заданной в трехмерном пространстве.

Пусть и — проекции точки M на координатные оси Ox , Oy и Oz соответственно. Пусть этим точкам на координатных осях Ox , Oy и Oz соответствуют действительные числа и .

В предыдущих главах были рассмотрены приемы построения чертежей в плоскости XY. Положение любой точки в этой системе координат характеризуются двумя значениями – абсциссой и ординатой. Для выполнения построений в трехмерном пространстве к этим координатам добавляется третья величина, определяющая объем того или иного изделия. Речь идет о координате Z, придающей плоским объектам объем. Умение правильно задавать координаты трехмерных объектов способствует корректному моделированию пространственных деталей. Для этих целей AutoCAD располагает тремя типами систем отсчета: трехмерные декартовые, цилиндрические и сферические координаты.

ДЕКАРТОВЫЕ КООРДИНАТЫ

Для обозначения положения точки в трехмерном пространстве при помощи декартовых координат необходимо к значениям ее координат на плоскости XY добавить третье значение – координату Z. Так, например, на рис. 10.4 изображена точка, у которой координаты в плоскости XY равны 13.19, а по оси Z – 11 единиц.

При вводе координат в этой системе в первую очередь задается координата X, затем через запятую Y и только потом Z. Например: 13,19,11. Если числовое значение координаты дробное, то разделять целую и дробную части необходимо точкой. Кроме того, пробелы между числами и запятыми не допускаются.

Примечание. Если при вводе координат в трехмерном пространстве пропущено значение Z, AutoCAD автоматически присвоит ему значение по умолчанию, записанное в системной переменной ELEVATION и называемое возвышением.

При создании трехмерных объектов используются понятия возвышения (уровня плоскости XY) и высоты. Возвышение определяется Z-координатой плоскости XY, на которой объект построен. Понятно, что если возвышение равно нулю (значение по умолчанию), то уровень объекта (его плоскость) совпадает с плоскостью XY. При положительном возвышении объект находится выше плоскости XY, а при отрицательном – ниже. Что касается высоты трехмерных объектов, то она определяет расстояние, на которое объект смещен относительно возвышения.

Обычно к редактированию параметров возвышения и высоты прибегают в случае, когда необходимо построить несколько точек, у которых координата Z имеет одно и то же значение. Упрощение построений вызвано тем, что при этом достаточно будет вводить для каждой такой точки только два значения, определяющих ее положение в плоскости XY.

Как уже было отмечено, текущее значение возвышения хранится под именем системной переменной ELEVATION, а высоты – переменной THICKNEES. Для того чтобы изменить значение обоих параметров, присваиваемое вновь созданным объектам, нужно выполнить команду Elev и ответить на следующие вопросы:

Command: Elev
Specify new default elevation :
Specify new default thickness :

Также следует отметить, что значение высоты объекта можно менять из палитры Properties (Свойства).

ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ

Положение точки в цилиндрических координатах также определяется тремя величинами, однако одно из них – угловое.

Как известно, круговой цилиндр образуется путем вращения образующей 2-3 (рис. 10.5а) по окружности, описывая угол 360°. Именно этот принцип положен в концепцию цилиндрических координат. Определяя положение точки, необходимо задать вначале радиус цилиндра (0-1), затем угол вращения образующей (1-2) и, наконец, высоту цилиндра (2-3). Так, например, точка, изображенная на рис. 10.36, была построена относительно текущей ПСК после ввода в командную строку 23

Следует обратить внимание на правило знаков. Что касается линейных координат, то тут все просто – направление осей определяет положительные значения отсчета. При этом положительное направление оси Z можно контролировать правилом правой руки. Это правило заключается в следующем. Если большой палец правой руки совместить с осью X, а указательный – с осью Y, то остальные пальцы в изогнутом положении укажут положительное направление оси Z (рис. 10.56).

Для определения положительного направления вращения относительно любой оси нужно следовать следующему правилу. Если установить наблюдателя со стороны положительного направления оси, то положительное направление отсчета углов будет совпадать с движением против часовой стрелки (рис. 10.4). Таким образом, чтобы ввести направление угла по часовой стрелке, значение угла следует вводить со знаком минус.

СФЕРИЧЕСКИЕ КООРДИНАТЫ

Положение точки в сферических координатах определяется также тремя величинами, из которых одно линейное, а два остальных – угловые.

Как известно, сферическая поверхность представляет собой геометрическое место точек пространства, равноудаленных от одной точки – центра шара. Поэтому, чтобы определить положение точки, расположенной на поверхности сферы (рис. 10.7а), достаточно указать радиус окружности, вращением которой образуется шар (0-1), затем угол, образованный вращением окружности вокруг оси Z (1-2), и наконец, угол, образованный вращением окружности относительно оси X (2-3). Так, например, точка, изображенная на рис. 10.76, была построена относительно текущей ПСК после ввода в командную строку 25

ФИЛЬТРЫ ТОЧЕК

Координатные фильтры точек – это еще один способ ввода координат в трехмерном пространстве, отличительной чертой которого является зависимость от координат ранее введенных объектов. Другими словами, чтобы назначить координаты этим способом, нужно привязаться к узлам уже существующих объектов для автоматического извлечения из них заказанной вами координаты.

Примечание. Задание координат в трехмерном пространстве способом фильтрации точек может быть эффективно только при использовании режимов объектной привязки.

Упорядоченная система двух или трёх пересекающихся перпендикулярных друг другу осей с общим началом отсчёта (началом координат) и общей единицей длины называется прямоугольной декартовой системой координат .

Общая декартова система координат (аффинная система координат ) может включать и не обязательно перпендикулярные оси. В честь французского математика Рене Декарта (1596-1662) названа именно такая система координат, в которой на всех осях отсчитывается общая единица длины и оси являются прямыми.

Прямоугольная декартова система координат на плоскости имеет две оси, а прямоугольная декартова система координат в пространстве — три оси. Каждая точка на плоскости или в пространстве определяется упорядоченным набором координат — чисел в соответствии единице длины системы координат.

Заметим, что, как следует из определения, существует декартова система координат и на прямой, то есть в одном измерении. Введение декартовых координат на прямой представляет собой один из способов, с помощью которого любой точке прямой ставится в соответствие вполне определённое вещественное число, то есть координата.

Метод координат, возникший в работах Рене Декарта, ознаменовал собой революционную перестройку всей математики. Появилась возможность истолковывать алгебраические уравнения (или неравенства) в виде геометрических образов (графиков) и, наоборот, искать решение геометрических задач с помощью аналитических формул, систем уравнений. Так, неравенство z xOy и находящейся выше этой плоскости на 3 единицы.

С помощью декартовой системы координат принадлежность точки заданной кривой соответствует тому, что числа x и y удовлетворяют некоторому уравнению. Так, координаты точки окружности с центром в заданной точке (a ; b ) удовлетворяют уравнению (x — a )² + (y — b )² = R ² .

Прямоугольная декартова система координат на плоскости

Две перпендикулярные оси на плоскости с общим началом и одинаковой масштабной единицей образуют декартову прямоугольную систему координат на плоскости . Одна из этих осей называется осью Ox , или осью абсцисс , другую — осью Oy , или осью ординат . Эти оси называются также координатными осями. Обозначим через M x и M y соответственно проекции произвольной точки М на оси Ox и Oy . Как получить проекции? Проведём через точку М Ox . Эта прямая пересекает ось Ox в точке M x . Проведём через точку М прямую, перпендикулярную оси Oy . Эта прямая пересекает ось Oy в точке M y . Это показано на рисунке ниже.

x и y точки М будем называть соответственно величины направленных отрезков OM x и OM y . Величины этих направленных отрезков рассчитываются соответственно как x = x 0 — 0 и y = y 0 — 0 . Декартовы координаты x и y точки М абсциссой и ординатой . Тот факт, что точка М имеет координаты x и y , обозначается так: M (x , y ) .

Координатные оси разбивают плоскость на четыре квадранта , нумерация которых показана на рисунке ниже. На нём же указана расстановка знаков координат точек в зависимости от их расположения в том или ином квадранте.

Помимо декартовых прямоугольных координат на плоскости часто рассматривается также полярная система координат. О способе перехода от одной системы координат к другой — в уроке полярная система координат .

Прямоугольная декартова система координат в пространстве

Декартовы координаты в пространстве вводятся в полной аналогии с декартовыми координатами на плоскости.

Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом O и одинаковой масштабной единицей образуют декартову прямоугольную систему координат в пространстве .

Одну из указанных осей называют осью Ox , или осью абсцисс , другую — осью Oy , или осью ординат , третью — осью Oz , или осью аппликат . Пусть M x , M y M z — проекции произвольной точки М пространства на оси Ox , Oy и Oz соответственно.

Проведём через точку М Ox Ox в точке M x . Проведём через точку М плоскость, перпендикулярную оси Oy . Эта плоскость пересекает ось Oy в точке M y . Проведём через точку М плоскость, перпендикулярную оси Oz . Эта плоскость пересекает ось Oz в точке M z .

Декартовыми прямоугольными координатами x , y и z точки М будем называть соответственно величины направленных отрезков OM x , OM y и OM z . Величины этих направленных отрезков рассчитываются соответственно как x = x 0 — 0 , y = y 0 — 0 и z = z 0 — 0 .

Декартовы координаты x , y и z точки М называются соответственно её абсциссой , ординатой и аппликатой .

Попарно взятые координатные оси располагаются в координатных плоскостях xOy , yOz и zOx .

Задачи о точках в декартовой системе координат

Пример 1.

A (2; -3) ;

B (3; -1) ;

C (-5; 1) .

Найти координаты проекций этих точек на ось абсцисс.

Решение. Как следует из теоретической части этого урока, проекция точки на ось абсцисс расположена на самой оси абсцисс, то есть оси Ox , а следовательно имеет абсциссу, равную абсциссе самой точки, и ординату (координату на оси Oy , которую ось абсцисс пересекает в точке 0), равную нулю. Итак получаем следующие координаты данных точек на ось абсцисс:

A x (2; 0) ;

B x (3; 0) ;

C x (-5; 0) .

Пример 2. В декартовой системе координат на плоскости даны точки

A (-3; 2) ;

B (-5; 1) ;

C (3; -2) .

Найти координаты проекций этих точек на ось ординат.

Решение. Как следует из теоретической части этого урока, проекция точки на ось ординат расположена на самой оси ординат, то есть оси Oy , а следовательно имеет ординату, равную ординате самой точки, и абсциссу (координату на оси Ox , которую ось ординат пересекает в точке 0), равную нулю. Итак получаем следующие координаты данных точек на ось ординат:

A y (0; 2) ;

B y (0; 1) ;

C y (0; -2) .

Пример 3. В декартовой системе координат на плоскости даны точки

A (2; 3) ;

B (-3; 2) ;

C (-1; -1) .

Ox .

Ox Ox Ox , будет иметь такую же абсциссу, что и данная точка, и ординату, равную по абсолютной величине ординате данной точки, и противоположную ей по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно оси Ox :

A» (2; -3) ;

B» (-3; -2) ;

C» (-1; 1) .

Решить задачи на декартову систему координат самостоятельно, а затем посмотреть решения

Пример 4. Определить, в каких квадрантах (четвертях, рисунок с квадрантами — в конце параграфа «Прямоугольная декартова система координат на плоскости») может быть расположена точка M (x ; y ) , если

1) xy > 0 ;

2) xy

3) x − y = 0 ;

4) x + y = 0 ;

5) x + y > 0 ;

6) x + y

7) x − y > 0 ;

8) x − y

Пример 5. В декартовой системе координат на плоскости даны точки

A (-2; 5) ;

B (3; -5) ;

C (a ; b ) .

Найти координаты точек, симметричных этим точкам относительно оси Oy .

Продолжаем решать задачи вместе

Пример 6. В декартовой системе координат на плоскости даны точки

A (-1; 2) ;

B (3; -1) ;

C (-2; -2) .

Найти координаты точек, симметричных этим точкам относительно оси Oy .

Решение. Поворачиваем на 180 градусов вокруг оси Oy направленный отрезок, идущий от оси Oy до данной точки. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно оси Oy , будет иметь такую же ординату, что и данная точка, и абсциссу, равную по абсолютной величине абсциссе данной точки, и противоположную ей по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно оси Oy :

A» (1; 2) ;

B» (-3; -1) ;

C» (2; -2) .

Пример 7. В декартовой системе координат на плоскости даны точки

A (3; 3) ;

B (2; -4) ;

C (-2; 1) .

Найти координаты точек, симметричных этим точкам относительно начала координат.

Решение. Поворачиваем на 180 градусов вокруг начала координат направленный отрезок, идущий от начала координат к данной точке. На рисунке, где обозначены квадранты плоскости, видим, что точка, симметричная данной относительно начала координат, будет иметь абсциссу и ординату, равные по абсолютной величине абсциссе и ординате данной точки, но противоположные им по знаку. Итак получаем следующие координаты точек, симметричных этим точкам относительно начала координат:

A» (-3; -3) ;

B» (-2; 4) ;

C (2; -1) .

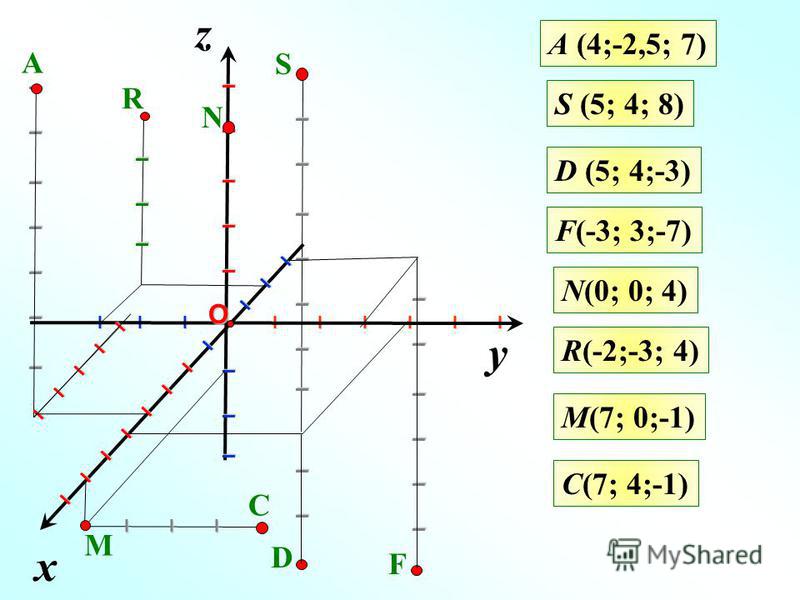
Пример 8.

A (4; 3; 5) ;

B (-3; 2; 1) ;

C (2; -3; 0) .

Найти координаты проекций этих точек:

1) на плоскость Oxy ;

2) на плоскость Oxz ;

3) на плоскость Oyz ;

4) на ось абсцисс;

5) на ось ординат;

6) на ось апликат.

1) Проекция точки на плоскость Oxy расположена на самой этой плоскости, а следовательно имеет абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxy :

A xy (4; 3; 0) ;

B xy (-3; 2; 0) ;

C xy (2; -3; 0) .

2) Проекция точки на плоскость Oxz расположена на самой этой плоскости, а следовательно имеет абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную нулю. Итак получаем следующие координаты проекций данных точек на Oxz :

A xz (4; 0; 5) ;

B xz (-3; 0; 1) ;

C xz (2; 0; 0) .

3) Проекция точки на плоскость Oyz расположена на самой этой плоскости, а следовательно имеет ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную нулю. Итак получаем следующие координаты проекций данных точек на Oyz :

A yz (0; 3; 5) ;

B yz (0; 2; 1) ;

C yz (0; -3; 0) .

4) Как следует из теоретической части этого урока, проекция точки на ось абсцисс расположена на самой оси абсцисс, то есть оси Ox , а следовательно имеет абсциссу, равную абсциссе самой точки, а ордината и апликата проекции равны нулю (поскольку оси ординат и апликат пересекают ось абсцисс в точке 0). Получаем следующие координаты проекций данных точек на ось абсцисс:

A x (4; 0; 0) ;

B x (-3; 0; 0) ;

C x (2; 0; 0) .

5) Проекция точки на ось ординат расположена на самой оси ординат, то есть оси Oy , а следовательно имеет ординату, равную ординате самой точки, а абсцисса и апликата проекции равны нулю (поскольку оси абсцисс и апликат пересекают ось ординат в точке 0). Получаем следующие координаты проекций данных точек на ось ординат:

A y (0; 3; 0) ;

B y (0; 2; 0) ;

C y (0; -3; 0) .

6) Проекция точки на ось апликат расположена на самой оси апликат, то есть оси Oz , а следовательно имеет апликату, равную апликате самой точки, а абсцисса и ордината проекции равны нулю (поскольку оси абсцисс и ординат пересекают ось апликат в точке 0). Получаем следующие координаты проекций данных точек на ось апликат:

A z (0; 0; 5) ;

B z (0; 0; 1) ;

C z (0; 0; 0) .

Пример 9. В декартовой системе координат в пространстве даны точки

A (2; 3; 1) ;

B (5; -3; 2) ;

C (-3; 2; -1) .

Найти координаты точек, симметричных этим точкам относительно:

1) плоскости Oxy ;

2) плоскости Oxz ;

3) плоскости Oyz ;

4) оси абсцисс;

5) оси ординат;

6) оси апликат;

7) начала координат.

1) «Продвигаем» точку по другую сторону оси Oxy Oxy , будет иметь абсциссу и ординату, равные абсциссе и ординате данной точки, и апликату, равную по величине апликате данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oxy :

A» (2; 3; -1) ;

B» (5; -3; -2) ;

C» (-3; 2; 1) .

2) «Продвигаем» точку по другую сторону оси Oxz на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oxz , будет иметь абсциссу и апликату, равные абсциссе и апликате данной точки, и ординату, равную по величине ординате данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oxz :

A» (2; -3; 1) ;

B» (5; 3; 2) ;

C» (-3; -2; -1) .

3) «Продвигаем» точку по другую сторону оси Oyz на то же расстояние. По рисунку, отображающему координатное пространство, видим, что точка, симметричная данной относительно оси Oyz , будет иметь ординату и апликату, равные ординате и апликате данной точки, и абсциссу, равную по величине абсциссе данной точки, но противоположную ей по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно плоскости Oyz :

A» (-2; 3; 1) ;

B» (-5; -3; 2) ;

C» (3; 2; -1) .

По аналогии с симметричными точками на плоскости и точками пространства, симметричными данным относительно плоскостей, замечаем, что в случае симметрии относительно некоторой оси декартовой системы координат в пространстве, координата на оси, относительно которой задана симметрия, сохранит свой знак, а координаты на двух других осях будут теми же по абсолютной величине, что и координаты данной точки, но противоположными по знаку.

4) Свой знак сохранит абсцисса, а ордината и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси абсцисс:

A» (2; -3; -1) ;

B» (5; 3; -2) ;

C» (-3; -2; 1) .

5) Свой знак сохранит ордината, а абсцисса и апликата поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси ординат:

A» (-2; 3; -1) ;

B» (-5; -3; -2) ;

C» (3; 2; 1) .

6) Свой знак сохранит апликата, а абсцисса и ордината поменяют знаки. Итак, получаем следующие координаты точек, симметричных данным относительно оси апликат:

A» (-2; -3; 1) ;

B» (-5; 3; 2) ;

C» (3; -2; -1) .

7) По аналогии с симметрии в случае с точками на плоскости, в случае симметрии относительно начала координат все координаты точки, симметричной данной, будут равными по абсолютной величине координатам данной точки, но противоположными им по знаку. Итак, получаем следующие координаты точек, симметричных данным относительно начала координат.

steps3D — Tutorials — Получение исходных 3D-координат по значениям из z-буфера.

За счет использования значений из буфера глубины (z-буфера) можно для каждого пиксела изображения восстановить исходные трехмерные координаты в пространстве наблюдателя (камеры).

Однако для этого сначала надо вспомнить как именно происходит преобразование координат в OpenGL. Для начала координаты задаются в системе координат объекта (object space). Умножение на модельно-видовую матрицу переводит координаты в систему координат наблюдателя/камеры (eye space). Далее, умножение на матрицу проектирования переводит координаты в систему координат отсечения (clip space). Перспективное деление (деление на w) переводит координаты в нормализованные координаты устройства (NDC).

Все три компоненты нормализованных координат устройства лежат в диапазоне [-1,1]. Для записи в буфер глубины z_NDC переводится из [-1,1] в [0,1] при помощи линейного преобразования (точно такого, какое переводит нормали в цвета для карт нормалей).

Рассмотрим теперь как можно восстановить координаты в системе координат наблюдателя, используя значение в буфере глубины.

Одним из способов достижения этого является приведение позиции фрагмента к кубу [-1,1]³ и последующем умножении на обращенную матрицу проектирования gl_ProjectionMatrixInverse. Ниже приводится реализующий это фрагментный шейдер (спасибо MrShoor) указавшему на этот способ.

Однако в ряде случаев можно избежать умножения на матрицы 4×4 (не говоря уже про ее обращение) и получить результат за меньшее число операций. Нам понадобится понимание того, как именно происходит вычисление значения, записываемого в буфер глубины.

Первым нашим шагом будет восстановление по значению из буфера глубины (d) значения z_eye — z-координаты в системе координат наблюдателя.

Для того, чтобы понять как это возможно, необходимо разобраться в работе стандартного перспективного проектирования в OpenGL. Оно производится при помощи следующей матрицы проектирования (задаваемой, например, командой gluPerspective):

Здесь использованы следующие обозначения:

Достаточно рассмотреть преобразования только двух последних координат — z и w при помощи соответствующей части матрицы проектирования.

После перспективного деления мы получаем значение z_NDC:

Однако следует иметь в виду, что стандартное перспективное преобразование в OpenGL использует в качестве направления взгляда отрицательное направление оси Oz и переводит усеченную пирамиду видимости в куб [-1,1]³. Поэтому полученное по предыдущей формуле значение z_NDC будет пробегать отрезок [-1,1] при z_eye пробегающем значения из отрезка [-zFar,zNear].

Соответственно значение d, действительно записываемое в буфер глубины, получается по следующей формуле:

Обратив эту формулу относительно z_eye получим следующую формулу:

Обратите внимание, что здесь через d обозначено значение глубины, прочитанное из буфера глубины и принимающее значение из отрезка [0,1].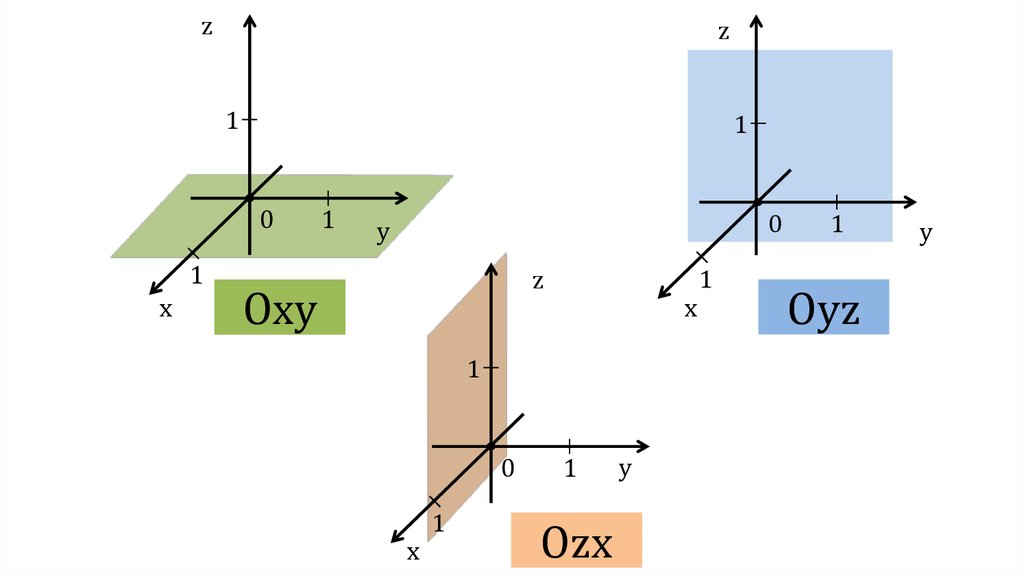 Подобную формулу можно найти, например здесь. Однако иногда встречаются и другие варианты этой же формулы.

Во-первых это связано с тем, какой знак z мы хотим получить — в OpenGL направление взгляда идет в сторону, противоположную оси Oz, что не всегда удобно. Поэтому иногда встречается вариант этой формулы, отличающийся знаком.

Другим вариантом этой же формулы является случай, когда мы используем не само значение, прочитанное из буфера глубины, а z_NDC, т.е. значение из отрезка [-1,1]. Для этого в исходную формулу просто подставляется преобразование, переводящее отрезок [-1,1] в [0,1] и в результате мы получаем следующую формулу (ее можно найти, например, здесь):

Таким образом, скопировав после первого прохода (а сейчас довольно часто рендеринг начинается с depth-only-прохода) буфер глубины в текстуру, на последующих проходах читая во фрагментном шейдере из этой текстуры значения глубины d можно легко восстановить соответствующие значения z_eye.

Осталось только восстановить две оставшиеся пространственные координаты x_eye и y_eye. Самым простым способом достижения этого является вывод прямоугольника с z_eye=1 границы которого соответствуют пересечению данной плоскости и (неусеченной) пирамиды видимости.

Переданные координаты вершин передаются через varying vec3-переменную во фрагментный шейдер и их достаточно просто умножить на вычисленное значение z_eye для получения полного набора пространственных координат (x_eye,y_eye,z_eye).

Ниже приводится соответствующий вершинный шейдер.

Декартовы координаты — Math Insight

Декартовы координаты позволяют задать положение точки на плоскости или в трехмерном пространстве. Декартовы координаты (также называемые прямоугольными координатами) точки представляют собой пару чисел (в двух измерениях) или тройку чисел (в трех измерениях), которые задают расстояния со знаком от оси координат.

Декартовы координаты на плоскости

Декартовы координаты на плоскости задаются относительно оси координат $x$ и оси координат $y$, как показано на рисунке ниже. Начало координат находится на пересечении осей $x$ и $y$. Декартовы координаты точки на плоскости записываются как $(x,y)$. Первое число $x$ называется $x$-координатой (или $x$-компонентой), так как это расстояние со знаком от начала координат в направлении вдоль оси $x$. Координата $x$ задает расстояние вправо (если $x$ положительное) или влево (если $x$ отрицательное) от оси $y$. Точно так же второе число $y$ называется $y$-координатой (или $y$-компонентой), так как это расстояние со знаком от начала координат в направлении вдоль оси $y$. Координата задает расстояние выше (если $y$ положительное) или ниже (если $y$ отрицательное) оси $x$. На следующем рисунке точка имеет координаты $(-3,2)$, так как точка находится на три единицы левее и две единицы вверх от начала координат.

Приведенный ниже апплет иллюстрирует декартовы координаты точки на плоскости. Он похож на рисунок выше, только позволяет менять точку.

Декартовы координаты на плоскости. Декартовы координаты $(x,y)$ синей точки задают ее положение относительно начала координат, которое является пересечением осей $x$ и $y$. Вы можете изменить положение точки, перетащив ее мышью.

Дополнительная информация об апплете.

Декартовы координаты трехмерного пространства

В трехмерном пространстве декартова система координат основана на трех взаимно перпендикулярных осях координат: оси $x$, оси $y$ и оси $z$- оси, показанной ниже. Три оси пересекаются в точке, называемой началом координат. Вы можете представить себе начало координат в точке, где стены в углу комнаты встречаются с полом. Ось $x$ — это горизонтальная линия, вдоль которой пересекаются стена слева от пола. Ось $y$ — это горизонтальная линия, вдоль которой пересекаются стена справа от пола. Ось $z$ — это вертикальная линия, по которой пересекаются стены. Части линий, которые вы видите, стоя в комнате, являются положительной частью каждой из осей, проиллюстрированной половинами каждой оси, помеченными $x$, $y$ и $z$ в апплете ниже. Отрицательная часть этих осей будет продолжением линий за пределами комнаты, что показано на немаркированных половинах каждой оси ниже.

Загрузка апплета

Трехмерные декартовы оси координат. Представление трех осей трехмерной декартовой системы координат. Положительная ось $x$, положительная ось $y$ и положительная ось $z$ — это стороны, помеченные $x$, $y$ и $z$. Начало — это пересечение всех осей. Ветвь каждой оси на противоположной стороне от начала координат (немаркированная сторона) является отрицательной частью. Вы можете перетащить фигуру с помощью мыши, чтобы повернуть ее.

Дополнительная информация об апплете.

С приведенными выше определениями положительных осей $x$, $y$ и $z$ результирующая система координат называется правой ; если согнуть пальцы правой руки от положительной оси $x$ к положительной оси $y$, большой палец правой руки будет указывать в направлении положительной оси $z$. Переключение положений положительной оси $x$ и положительной оси $y$ создает левостороннюю систему координат . Правосторонняя и левосторонняя системы координат представляют две одинаково действительные математические вселенные. Проблема в том, что переключение вселенных изменит знак в некоторых формулах. Поскольку эти страницы написаны в правосторонней вселенной, мы предлагаем вам жить в нашей вселенной, изучая эти страницы.

В дополнение к трем координатным осям мы часто имеем в виду три координатные плоскости. Плоскость $xy$ — это горизонтальная плоскость, натянутая на оси $x$ и $y$. Он идентичен двумерной координатной плоскости и содержит аналогию с полом в комнате. Точно так же $xz$-плоскость — это вертикальная плоскость, натянутая на оси $x$ и $z$ и содержащая аналогию с левой стеной в комнате. Наконец, $yz$-плоскость — это вертикальная плоскость, натянутая на оси $y$ и $z$ и содержащая аналогию с правой стеной в комнате.

Декартовы координаты точки в трех измерениях представляют собой тройку чисел $(x,y,z)$. Три числа или координаты определяют расстояние со знаком от начала координат по осям $x$, $y$ и $z$ соответственно. Их можно визуализировать, сформировав прямоугольник с краями, параллельными оси координат, и противоположными углами в начале координат и заданной точке, как показано в следующем апплете.

Загрузка апплета

Декартовы координаты точки в трех измерениях. Декартовы координаты $(x,y,z)$ точки в трех измерениях задают расстояние со знаком от начала координат по осям $x$, $y$ и $z$ соответственно. Прямоугольный прямоугольник имеет противоположные углы в начале координат и в синей точке. Три координаты синей точки представлены красными точками, которые являются углами прямоугольника вдоль каждой оси. Вы можете изменить точку, перетащив синюю точку с помощью мыши. Как вариант, вы можете самостоятельно изменить одну из координат, перетащив красную точку.

Дополнительная информация об апплете.

Учитывая приведенную выше аналогию с углом комнаты, мы могли бы сформировать декартовы координаты точки на макушке следующим образом. Представьте, что ваш рост составляет два метра, и вы проходите четыре метра от начала координат по оси $x$, затем поворачиваете налево и проходите параллельно оси $y$ три метра в комнату. Декартовы координаты точки на макушке будут $(4,3,2)$.

В отличие от других систем координат, таких как сферические координаты, декартовы координаты задают уникальную точку для каждой пары $(x,y)$ или тройки $(x,y,z)$ чисел, и каждая координата может принимать любые вещественные ценность.

Векторы и более высокие размерности

Декартовы координаты можно использовать не только для задания положения точек, но и для задания координат векторов. Декартовы координаты двух- или трехмерных векторов выглядят так же, как координаты точек на плоскости или в трехмерном пространстве.

Но нет причин останавливаться на трех измерениях. Мы могли бы определить векторы в четырех, пяти или более измерениях, просто указав четыре, пять или более декартовых координат. Мы не можем визуализировать эти более высокие измерения, как мы это делали с вышеупомянутыми апплетами, но мы можем легко записать список чисел для координат. Вы можете проверить примеры n-мерных векторов, чтобы убедиться, что разговоры о более высоких измерениях не являются полным безумием.

Трехмерная система координат – определение, методы построения графиков и примеры

Важно, чтобы мы понимали трехмерную систему координат при изучении векторов и тем более высокого исчисления. В прошлом мы имели дело с плоскостями и прямоугольными координатами. На этот раз мы рассмотрим компоненты и соглашения трехмерной системы координат.

Трехмерная система координат позволяет представить величину в пространстве, содержащем три взаимно перпендикулярные оси. С помощью трехмерной системы координат мы теперь можем визуализировать точки и поверхности по трем осям.

В этой статье мы рассмотрим все основы, необходимые для понимания того, как мы моделируем значения и системы в трехмерной системе координат. Мы также обсудим, как расширить наше понимание прямоугольной системы координат до графических уравнений в трехмерной системе координат.

Что такое трехмерная система координат?

Трехмерная система координат содержит начало координат (обычно обозначается $O$) и образована тремя взаимно перпендикулярными осями координат: осью $x$, осью $y$ и осью $z$ .

В прямоугольной системе координат мы можем найти точку, используя упорядоченную пару $(x, y)$, где $x$ представляет горизонтальное положение, а $y$ представляет вертикальное положение точки. Поскольку нам нужны только два направления, чтобы найти точку на плоскости, мы называем эту систему двумерной системой координат.

Теперь, если мы хотим найти точку в пространстве, нам понадобятся три числа: $x$, $y$ и $z$. Мы называем $\boldsymbol{(x, y,z)}$, упорядоченную тройку . Вот как мы установили начало трехмерной системы координат. Вместо двух осей у нас теперь есть три оси координат , которые взаимно перпендикулярны друг другу. В трехмерных системах координат мы обычно рассматриваем оси $\boldsymbol{x}$ и $\boldsymbol{y}$ как две горизонтальные оси, перпендикулярные друг другу . $\boldsymbol{z}$ -ось становится единственной вертикальной осью в трех измерениях.

Чтобы установить направление третьей оси, $z$-оси, мы можем применить 9{\circ}$ против часовой стрелки, наши пальцы будут двигаться от положительной оси $x$ к оси $y$. Положение большого пальца показывает положительное направление оси $z$.

Раньше мы работали только с одной плоскостью в системе координат $xy$. Для трехмерной системы координат у нас есть три координатные плоскости .

• Назовем плоскость, образованную осями $x$ и $y$, $\boldsymbol{xy}$ -плоскостью .
• Аналогично, плоскость, образованная осями $y$ и $z$, называется $\boldsymbol{yz}$ -самолет .
• $\boldsymbol{xz}$ -плоскость содержит оси $x$ и $z$.

Вот отличное умственное упражнение на случай, если вам все еще нужна помощь в визуализации трехмерной системы координат. Представьте, что вы находитесь в комнате и сосредоточьтесь на одном углу.

Начало — это точка пересечения этих трех осей.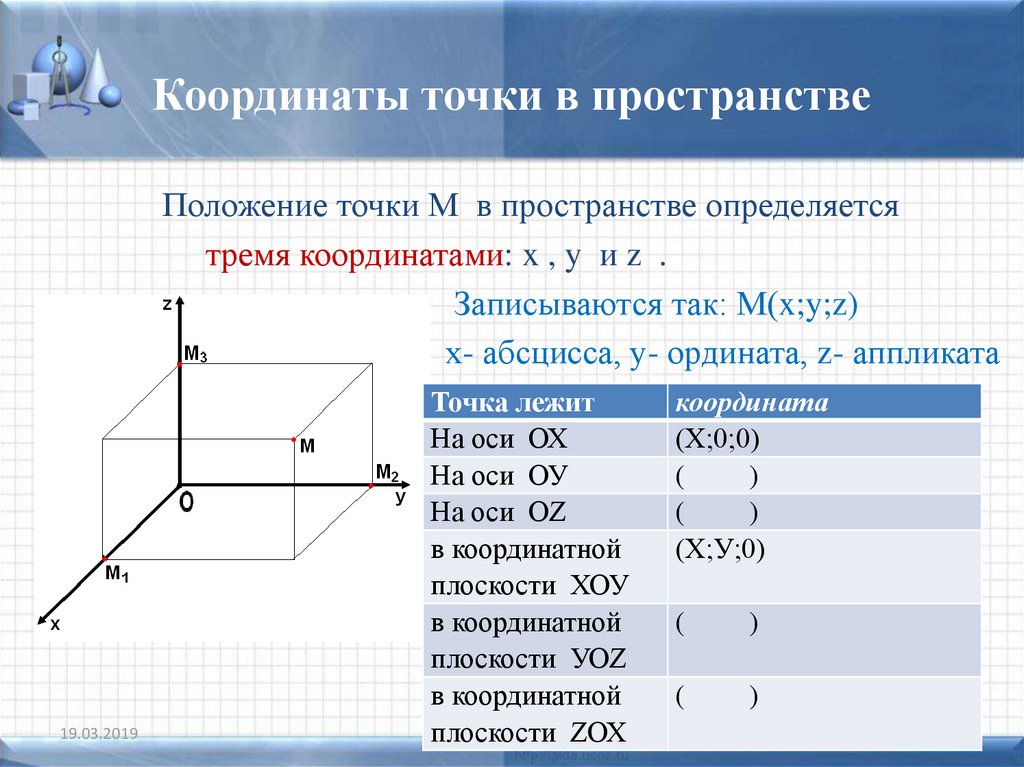 Представьте себе угол вашей комнаты, где пересекаются две стены — так мы можем изобразить положение начала координат.

Стена слева представляет плоскость $xz$, а стена справа представляет плоскость $yz$. Если стены представляют плоскости $xz$ и $yz$, то пол представляет собой плоскость $xy$. Расширив эти плоскости по их положительному и отрицательному направлениям, мы получим восемь «комнат», которые мы называем 9-ю.0061 октант . Трехмерная система координат будет иметь в общей сложности восемь октантов, которые все пересекаются в начале координат , $O$.

• Если двумерная система координат имеет четыре квадранта , то трехмерная система координат имеет восемь октантов .
• Первый октант будет положительным по трем координатам (подобно тому, как первый квадрант имеет положительные координаты $x$ и $y$).

Давайте теперь разберемся, как координаты представлены в трехмерных системах координат.

Координаты в трехмерной системе , поскольку наша точка теперь расположена в пространстве, точка $ p (x_o, y_o, z_o) $ будет расположена: · $ x_o $ units $yz$-плоскость ·         $y_o$ единиц из $xz$-плоскости ·         $z_o$ единиц из $xy$-плоскости Точка $P$, представленная упорядоченной тройкой, $(x_o , y_o, z_o)$, мы называем $x_o$, $y_o$ и $z_o$ координатами точки $P$. Как и в прямоугольной системе координат, мы называем $x_o$ координатой $x$, $y_o$ координатой $y$ и $z_o$ координатой $z$.

Вот положение $P(x_o, y_o, z_o)$: от начала отсчета $x_o$ единиц по оси $x$, от нашего счета по оси $x$, $ P$ — это $y_o$ единиц, параллельных оси $y$, и $z_o$ единиц, параллельных оси $z$.

Мы можем использовать точку $P$, чтобы построить прямоугольную коробку, как показано выше. Это выделяет проекций $\boldsymbol{P}$ на разные плоскости .

• Точка $Q(x_o, y_o, 0)$ является проекцией $\boldsymbol{P}$ на $\boldsymbol{xy}$ 93}$.

  Графики уравнений в 2D-системе координат называются кривыми , а уравнения в 3D-системе координат называются поверхностью .

  Теперь, когда у нас есть четкое представление о трехмерной системе координат, давайте сосредоточимся на изучении того, как графически отображать координаты и поверхности.

  Как построить график в 3D?

  Мы можем изобразить координату в трехмерной координате $P(x_o, y_o, z_o)$. система по:

  • Начните с исходной точки, затем переместите $x_o$ единиц вдоль оси $x$.
  • Точка должна находиться на расстоянии $y_o$ и $z_o$ от осей $y$ и $z$.
  • Спроецированный прямоугольный блок будет иметь размеры $x_o$, $y_o$ и $z_o$ единиц.

  Давайте попробуем нанести координатную точку $(-2, 4, 5)$ в нашу трехмерную прямоугольную систему координат.

  • Из исходной точки переместитесь на $-2$ единицы по оси $x$. Это означает, что точка будет позади первого октанта, где $x$ отрицательно.
  • Теперь точка должна быть параллельна $4$ единицам оси $y$ и $5$ единицам параллельно оси $z$.
  • Вы можете построить прямоугольную рамку, чтобы ориентироваться при построении $(-2, 4, 5)$.

  На этом графике показана точка $(-2, 4, 5)$ в трехмерной прямоугольной системе координат. Теперь в том же пространстве постройте график $(3, -2, 4)$, как показано ниже.

  Мы все еще можем измерить расстояние между двумя точками. Формула расстояния будет скорректирована с учетом третьей оси. Процесс аналогичен нахождению расстояния между двумя вершинами прямоугольной призмы. Следовательно, у нас есть следующая формула расстояния для трех измерений. 92}\\&= \sqrt{25 +36 +1}\\&= \sqrt{62}\end{aligned}

  Это означает, что расстояние между двумя точками равно $\sqrt{62}$ единицы.

  Мы можем изобразить поверхность в трехмерной системе координат. Самая основная поверхность, которую нам нужно изобразить, — это плоскость, представленная следующими уравнениями: $x= k$, $y = k$ или $z = k$.

  График $\boldsymbol{x = k}$

  График 93$. Построить горизонтальную плоскость, параллельную плоскости $xy$. Убедитесь, что горизонтальная плоскость находится на $4$ выше начала координат и вдоль оси $z$. Здесь показан график $z = 4$ в виде плоскости в трехмерной системе координат. Эта плоскость параллельна плоскости $xy$ и находится на $4$ выше оси $z$. Мы рассмотрели все основные понятия, необходимые для ознакомления с трехмерной системой координат. Еще лучше освойте эту тему, работая над примерами задач, которые мы подготовили для вас! Пример 1 Представьте, что вы начинаете с начала координат и перемещаете $3$ единиц вдоль положительной оси $x$. Затем вы перемещаете 3$ единиц в положительном направлении и 6$ единиц вверх. Каковы координаты, которые представляют ваше текущее положение? Решение Мы можем проследить движение, используя трехмерную систему координат. Переместите $3$ единиц вдоль оси $x$, затем переместите $3$ единиц и параллельно оси $y$. Затем переместите $6$ единиц вверх, чтобы найти окончательную позицию. Когда вы посмотрите на конечную позицию, у нас есть точка с координатой $(3, 3, 6)$. Пример 2 Нарисуйте следующие точки в одной пространственной или трехмерной системе координат: $A = (3, 2, 1)$ $B = (-3, 4, — 1)$ $C = (-4, 2, -4)$ Решение Процесс построения точки в трехмерном пространстве аналогичен ее нахождению. Давайте сначала разберем шаги построения графика каждой координаты: Для $A$ переместите $3$ единиц вдоль положительной оси $x$, затем переместите $2$ единиц и $1$ единиц параллельно осям $y$ и $z$. Вторая точка, $B$, имеет отрицательную координату $x$, поэтому, начиная с начала координат, переместите $-3$ единиц вдоль отрицательной оси $x$. Переместите на $4$ единицы в положительном направлении, затем на $1$ вниз. Наконец, для $C$ начните с исходной точки, затем переместите $-4$ единиц по оси $x$. Переместите $2$ единиц в положительном направлении и параллельно оси $y$, затем переместите $4$ единиц вниз. 93$ и в 3D системе координат. Решение Уравнение $y = 4$ представляет все точки, которые имеют $y$-координату $4$. Поверхность, представляющая это уравнение, представляет собой плоскость, параллельную плоскости $xz$ и отстоящую на $4$ единиц вдоль положительной оси $y$. Вот график плоскости, представляющий $ y = 4 $. Это также подтверждает тот факт, что он параллелен плоскости $xz$ и расположен на $4$ единицах от начала координат и вдоль оси $y$. 92}\\&= \sqrt{173} \end{aligned} Это означает, что расстояние между $(-6, 5, 8)$ и $(-4, 10, -4)$ равно $ \sqrt{173}$ единиц. Практические вопросы 1. Представьте, что вы начинаете с начала координат и перемещаете $6$ единиц вдоль отрицательной оси $x$. Затем вы перемещаете 4$ единиц в положительном направлении и 8$ единиц вниз. Каковы координаты, которые представляют ваше текущее положение? 2. Нарисуйте следующие точки в одной пространственной или трехмерной системе координат: 93$ и в 3D системе координат. 4. Каково расстояние между точками $(-12, 12, 13)$ и $(-5, -8, 12)$, расположенными в одной системе координат? Ключ ответа 1. $(-6, 4, -8)$ 2. 3. 4. $15\sqrt{2}$ единиц Трехмерные изображения/математические чертежи создаются с помощью GeoGebra . Трехмерная координатная геометрия — уравнение плоскости Содержание Введение Параллельно координатным плоскостям Нормальный вектор и точка Прохождение через три точки Решение проблем Смотрите также Плоскость в трехмерном координатном пространстве определяется точкой и вектором, перпендикулярным плоскости. Пусть P0=(x0,y0,z0) P_{0}=(x_{0}, y_{0}, z_{0} ) P0​=(x0​,y0​,z0​) будет заданной точкой, и n→\overrightarrow{n} n ортогональный вектор. Кроме того, пусть P=(x,y,z) P=(x,y,z) P=(x,y,z) — любая точка на плоскости, а r rr и r0r_{0} r0 — векторы положения точек PPP и P0, P_{0}, P0​ соответственно. Теперь, если мы допустим n→=(a,b,c), \overrightarrow{n}=(a,b,c), n=(a,b,c), то, поскольку P0P→ \overrightarrow{P_{0 }P} P0​P​ перпендикулярна n→, \overrightarrow{n},n, имеем P0P→⋅n→=(r→−r0→)⋅n→=(x−x0,y−y0,z−z0)⋅(a,b,c)=a(x−x0)+b( y−y0)+c(z−z0)=0. \begin{выровнено} \overrightarrow{P_{0}P} \cdot \overrightarrow{n} &= (\overrightarrow{r}-\overrightarrow{r_{0}}) \cdot \overrightarrow{n} \\ &= (x-x_{0}, y-y_{0}, z-z_{0}) \cdot (a, b, c) \\ &= a(x-x_{0}) + b(y-y_{0}) + c(z-z_{0})\\ &=0. \end{выровнено} P0​P​⋅n​=(r−r0​)⋅n=(x−x0​,y−y0​,z−z0​)⋅(a,b,c)=a( x−x0​)+b(y−y0​)+c(z−z0​)=0.​ Мы также можем записать приведенное выше уравнение плоскости как ax+by+cz+d=0, ax+by+cz+d = 0,ax+by+cz+d=0, , где d=-(ax0+by0+cz0). d= -(ax_{0} + by_{0} + cz_{0}).d=-(ax0​+by0​+cz0​). Это не совсем работает, если один из a,b,ca, b, ca,b,c равен нулю. В этом случае вектор параллелен одной из координатных плоскостей. Скажем, c=0c = 0c=0, тогда вектор параллелен плоскости xyxyxy и уравнение требуемой плоскости равно a(x−x0)+b(y−y0)=0 a(x-x_{0}) + b(y-y_{0}) = 0a(x−x0​)+b(y−y0​)=0, что, конечно, является прямой линией в плоскости xyxyxy, а zzz не имеет ограничений. Аналогичные рассуждения применимы, если два из a,b,ca,b,ca,b,c равны нулю. Другой способ представить уравнение плоскости как сплющенный параллелепипед. Сплющенный параллелепипед, составленный из трех векторов a⃗=⟨x1,y1,z1⟩,b⃗=⟨x2,y2,z2⟩,c⃗=⟨x3,y3,z3⟩ \vec{a} = \left \langle x_{1 }, y_{1}, z_1 \right \rangle , \vec{b} = \left \langle x_2, y_2, z_2 \right \rangle, \vec{c} = \left \langle x_3, y_3, z_3 \right \rangle a=⟨x1​,y1​,z1​⟩,b=⟨x2​,y2​,z2​⟩,c=⟨x3​,y3​,z3​⟩, имеет объем 0. Мы можем использовать скаляр тройное произведение для вычисления этого объема: 0=a⃗⋅(b⃗×c⃗),0 = \vec{a} \cdot \big(\vec{b} \times \vec{c}\big), 0=a ⋅(б×в), где (b⃗×c⃗) \big(\vec{b} \times \vec{c}\big) (b×c) задает вектор, перпендикулярный плоскости. Предположим, что концы (b⃗×c⃗) \big(\vec{b} \times \vec{c}\big) (b×c) равны (x,y,z) ( x, y, z ) (x,y,z) и (x0,y0,z0) (x_0, y_0, z_0 )(x0​,y0​,z0​) и компоненты a⃗ \vec{a} a равны ⟨a,b, c⟩ \ влево \ langle a, b, c \ right \ rangle ⟨a, b, c⟩. Затем, взяв скалярное произведение, мы получим уравнение плоскости, которое имеет вид 0=a(x−x0)+b(y−y0)+c(z−z0). 0 = а (х-х_0) + б (у-у_0) + с (г-г_0). 0=a(x−x0​)+b(y−y0​)+c(z−z0​). Попробуйте решить задачу: (6,3,2)(6,3,2)(6,3,2) (2,3,6)(2,3,6)(2,3,6) (1,2,3)(1,2,3)(1,2,3) (3,2,1)(3,2,1)(3,2,1) Каков вектор нормали к плоскости, представленной x−11+y−22+z−33=0?\ dfrac{x-1}{1}+\dfrac{y-2}{2}+\dfrac{z-3}{3}=0 ?1x−1​+2y−2​+3z−3​=0 ? Уравнение плоскости, параллельной каждой из плоскостей xyxyxy, yzyzyz и zxzxzx и проходящей через точку A=(a,b,c) A=(a,b,c) A=( а,б,в) определяется следующим образом: 1) Уравнение плоскости, параллельной плоскости xyxyxy, имеет вид z=c. z=c .z=c. 2) Уравнение плоскости, параллельной плоскости ызызыз, есть x=a. х=а .х=а. 3) Уравнение плоскости, параллельной плоскости zxzxzx, равно y=b. у=б.у=б. Вот пример, основанный на вышеизложенном: Каково уравнение плоскости, проходящей через точку B=(4,1,0) B=(4,1,0) B=(4,1,0) и параллельной плоскости ызызыз? Поскольку xxx-координата BBB равна 4, уравнение плоскости, проходящей через BBB параллельно плоскости yzyzyz, равно х=4. □х=4. \_\squarex=4. □​ Попробуйте решить следующую задачу: y=0y=0y=0 -x-z=0-x-z=0-x-z=0 у=-2 у=-2 у=-2 Ничего из вышеперечисленного Найдите уравнение плоскости, проходящей через точку (−1,0,−1)(-1,0,-1)(−1,0,−1), параллельную плоскости xzxzxz. Если мы знаем вектор нормали к плоскости и точку, проходящую через плоскость, уравнение плоскости установлено. Таким образом, уравнение плоскости через точку A=(x1,y1,z1) A=(x_{1}, y_{1}, z_{1} )A=(x1​,y1​,z1​ ), вектор нормали которого равен n→=(a,b,c) \overrightarrow{n} = (a,b,c)n=(a,b,c) is a(x−x1)+b(y −y1)+c(z−z1)=0. a(x-x_{1}) + b(y-y_{1}) + c(z-z_{1}) = 0 .a(x-x1​)+b(y-y1​)+c( z−z1​)=0. Ознакомьтесь со следующими примерами: Если плоскость проходит через точку A=(1,3,2) A=(1,3,2) A=(1,3,2) и имеет вектор нормали n→=(3,2,5), \overrightarrow{n} = (3,2,5),n=(3,2,5), то какое уравнение плоскости? Уравнение плоскости, проходящей через A=(1,3,2) A=(1,3,2) A=(1,3,2) и имеющей вектор нормали n→=(3,2,5 ) \overrightarrow{n} = (3,2,5) n=(3,2,5) равно 3(x−1)+2(y−3)+5(z−2)=03x−3+2y−6+5z−10=03x+2y+5z−19=0. □ \begin{выровнено} 3(х-1) + 2(у-3) + 5(z-2) &= 0 \\ 3х — 3 + 2у — 6 + 5з — 10&=0\ 3х + 2у + 5з — 19&=0. \ _\площадь \end{выровнено} 3(x−1)+2(y−3)+5(z−2)3x−3+2y−6+5z−103x+2y+5z−19​=0=0=0. □​​ Если плоскость проходит через точку A=(5,6,2) A=(5,6,2) A=(5,6,2) и имеет вектор нормали n→=(−1,3,−7 ), \overrightarrow{n} = (-1,3,-7),n=(−1,3,−7), то каково уравнение плоскости? Уравнение плоскости, проходящей через точку A=(5,6,2) A=(5,6,2) A=(5,6,2) и имеющей вектор нормали n→=(−1, 3,−7) \overrightarrow{n} = (-1,3,-7) n=(−1,3,−7) равно -1(x-5)+3(y-6)-7(z-2)=0-x+5+3y-18-7z+14=0-x+3y-7z+1=0. □ \begin{выровнено} -1 (x-5) + 3 (y-6) -7 (z-2) &= 0 \\ -x+5+3y-18-7z+14 &= 0 \\ -x+3y-7z+1 &=0. \ _\площадь \end{выровнено} −1(x−5)+3(y−6)−7(z−2)−x+5+3y−18−7z+14−x+3y−7z+1​=0= 0=0. □​​ Попробуйте решить следующую задачу: x+2y+3z=4x+2y+3z=4x+2y+3z=4 3x+2y+z=43x+2y+z=43x+2y+z=4 3x+2y+z=-43x+2y+z=-43x+2y+z=-4 х+2у+3г=-4х+2у+3г=-4х+2у+3г=-4 Найдите уравнение плоскости, проходящей через (−4,3,−2)(-4,3,-2)(−4,3,−2) и имеющей вектор нормали n⃗=(1,2,3) \vec n = (1,2,3)n=(1,2,3). Зная три точки на плоскости, мы можем найти уравнение плоскости, решив одновременные уравнения. Пусть ax+by+cz+d=0 ax+by+cz+d=0ax+by+cz+d=0 — уравнение плоскости, на которой находятся следующие три точки: A=(1,0 ,2),В=(2,1,1), А=(1,0,2), В=(2,1,1),А=(1,0,2),В=(2,1 ,1) и C=(−1,2,1).C=(-1,2,1). С=(−1,2,1). Тогда уравнение плоскости устанавливается следующим образом: У нас уже есть уравнение плоскости с 4 неизвестными константами: ax+by+cz+d=0. (1)ax + by + cz +d = 0. \qquad (1) ax+by+cz +d=0.(1) Мы также получаем следующие 3 уравнения, подставляя координаты A,B,A, B,A,B и CCC в (1):(1):(1): a⋅1+b⋅0+c⋅2+d=0a⋅2+b⋅1+c⋅1+d=0a⋅(−1)+b⋅2+c⋅1+d=0, \begin {выровнено} а \cdot 1 + b \cdot 0 + c \cdot 2 + d &= 0 \\ а \cdot 2 + b \cdot 1 + c \cdot 1 + d &= 0 \\ a \cdot (-1) + b \cdot 2 + c \cdot 1 +d &= 0, \end{выровнено} a⋅1+b⋅0+c⋅2+da⋅2+b⋅1+c⋅1+da⋅(−1)+b⋅2+c⋅1+d​=0=0 = 0, , что дает b=3a,c=4a,d=-9a.(2)b=3a, c=4a, d=-9a. \qquad (2)b=3a,c=4a,d=−9a.(2) Подставляя (2) (2) (2) в (1), (1), (1), получаем ax+3ay+4az-9a=0x+3y+4z-9=0. \begin{выровнено} топор + 3ay + 4az -9a &= 0 \\ х + 3у + 4г — 9 &=0. \end{aligned} ax+3ay+4az−9ax+3y+4z−9​=0=0.​ Следовательно, уравнение плоскости, проходящей через три точки A=(1,0,2),B =(2,1,1), A=(1,0,2), B=(2,1,1),A=(1,0,2),B=(2,1,1) и С=(-1,2,1)С=(-1,2,1) С=(-1,2,1) равно х+3у+4г-9=0. х + 3у + 4z — 9 = 0 .х + 3у + 4z-9 = 0. Используя этот метод, мы можем найти уравнение плоскости, если мы знаем три точки. Вот пара примеров: Если плоскость проходит через три точки A=(0,0,2),B=(1,0,1), A=(0,0,2), B=(1,0,1),A =(0,0,2),B=(1,0,1) и C=(3,1,1),C=(3,1,1),C=(3,1,1), тогда что такое уравнение плоскости? Пусть уравнение плоскости будет ax+by+cz+d=0.(1) ax+by+cz+d=0. \qquad (1)ax+by+cz+d=0.(1) Тогда, поскольку эта плоскость включает в себя три точки A=(0,0,2),B=(1,0,1), A=(0,0,2), B=(1,0,1),A =(0,0,2),B=(1,0,1) и C=(3,1,1),C=(3,1,1),C=(3,1,1), у нас есть a⋅0+b⋅0+c⋅2+d=0a⋅1+b⋅0+c⋅1+d=0a⋅3+b⋅1+c⋅1+d=0, \begin{выровнено} а \cdot 0 + b \cdot 0 + c \cdot 2 + d &= 0 \\ а \cdot 1 + b \cdot 0 + c \cdot 1 + d &= 0 \\ а \cdot 3 + b \cdot 1 + c \cdot 1 +d &= 0, \end{выровнено} a⋅0+b⋅0+c⋅2+da⋅1+b⋅0+c⋅1+da⋅3+b⋅1+c⋅1+d​=0=0=0, , что дает b=-2a,c=a,d=-2a.(2)b=-2a, c=a, d=-2a. \qquad (2)b=−2a,c=a,d=−2a.(2) Подставляя (2) (2) (2) в (1), (1), (1), получаем ax+−2ay+az−2a=0x−2y+z−2=0. \begin{выровнено} топор + -2ау + аз -2а &= 0 \\ х-2у + z-2&=0. \end{выровнено} ax+−2ay+az−2ax−2y+z−2​=0=0.​ Отсюда уравнение плоскости, проходящей через три точки A=(0,0,2),B=(1,0,1) A=(0,0,2), B=(1,0,1 )A=(0,0,2),B=(1,0,1) и C=(3,1,1)C=(3,1,1) C=(3,1,1) равно х-2у+г-2=0. □x -2y + z — 2 =0. \ _\квадрат x−2y+z−2=0. □​ Если плоскость проходит через три точки A=(3,1,2),B=(6,1,2), A=(3,1,2), B=(6,1,2),A =(3,1,2),B=(6,1,2) и C=(0,2,0),C=(0,2,0),C=(0,2,0), тогда каково уравнение плоскости? Пусть уравнение плоскости будет ax+by+cz+d=0.(1) ax+by+cz+d=0. \qquad (1)ax+by+cz+d=0.(1) Тогда, поскольку эта плоскость включает в себя три точки A=(0,0,2),B=(1,0,1), A=(0,0,2), B=(1,0,1),A =(0,0,2),B=(1,0,1) и C=(3,1,1),C=(3,1,1),C=(3,1,1), у нас есть a⋅3+b⋅1+c⋅2+d=0a⋅6+b⋅1+c⋅2+d=0a⋅0+b⋅2+c⋅0+d=0, \begin{выровнено} а \cdot 3 + b \cdot 1 + c \cdot 2 + d &= 0 \\ а \cdot 6 + b \cdot 1 + c \cdot 2 + d &= 0 \\ а \cdot 0 + b \cdot 2 + c \cdot 0 +d &= 0, \end{выровнено} a⋅3+b⋅1+c⋅2+da⋅6+b⋅1+c⋅2+da⋅0+b⋅2+c⋅0+d​=0=0=0, , что дает a=0,c=12b,d=-2b. (2)a=0, c=\frac{1}{2}b, d=-2b . \qquad (2)a=0,c=21​b,d=−2b.(2) Подставляя (2) (2) (2) в (1), (1), (1), получаем 0x+-by+12bz-2b=0x-y+12z-2=02x-2y+z-4=0. \begin{выровнено} 0x + -by + \frac{1}{2}bz -2b &= 0 \\ x -y + \frac{1}{2}z — 2 &=0 \\ 2x — 2y +z-4 &=0. \end{выровнено} 0x+-by+21bz-2bx-y+21z-22x-2y+z-4​=0=0=0.​ Следовательно, уравнение плоскости, проходящей через три точки A=(0,0,2),B=(1,0,1), A=(0,0,2), B=(1,0, 1),А=(0,0,2),В=(1,0,1) и С=(3,1,1)С=(3,1,1) С=(3,1,1) ) составляет 2x−2y+z−4=0. □2x — 2y +z-4 =0. \ _\квадрат 2x−2y+z−4=0. □​ Попробуйте решить следующую задачу: x=1x=1x=1 х+у=3х+у=3х+у=3 у-х=1у-х=1у-х=1 Ничего из вышеперечисленного Найдите уравнение плоскости, проходящей через (1,2,3)(1,2,3)(1,2,3) и (1,−3,2)(1,-3, 2)(1,−3,2) и параллельно оси zzz. Этот раздел предназначен для улучшения ваших навыков решения проблем с помощью нескольких задач. 9{3}R3? Правда Ложь Верно или неверно? Четыре точки (0,−1,0),(2,1,−1),(1,1,1),(0,-1,0), (2,1,-1), (1,1,1),(0,−1,0),(2,1,−1),(1,1,1) и (3,3,0)(3,3,0)( 3,3,0) компланарны. 31 \sqrt{31}31 ​ 41 \sqrt{41}41 ​ 51 \кв{51}51 ​ 61 \sqrt{61}61 ​ Если плоскость 6x+4y+3z=126x+4y+3z=126x+4y+3z=12 пересекает оси xxx, yyy и zzz в точках A, BA, BA, B и CCC соответственно, найдите площадь ΔABC\Delta ABCΔABC. Бесконечный столбец с центром по оси zzz. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт