Объединение малых матриц в большую MatLab
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
1278 0
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- Главная /
- База знаний /
- CAD / CAM /
Урок 2. Установка системы и первые навыки работы
Установка и файловая система MATLAB
Запуск MATLAB и работа в режиме диалога
Новый и старый
облик системы MATLAB 6.0
Операции строчного редактирования
Команды управления окном
MATLAB в роли суперкалькулятора
О переносе строки в
сессии
Основные объекты MATLAB
Понятие о математическом выражении
Действительные
и комплексные числа
Константы и системные переменные
Текстовые комментарии
Переменные и присваивание им значений
Уничтожение
определений переменных
Операторы и функции
Применение оператора : (двоеточие)
Сообщения об ошибках
и исправление ошибок
Форматы чисел
Формирование векторов и матриц
Особенности задания
векторов и матриц
Объединение малых матриц в большую
Операции с рабочей областью и текстом сессии
Дефрагментация рабочей области
Сохранение рабочей области сессии
Ведение дневника
Загрузка рабочей области сессии
Завершение вычислений и работы с системой
Завершение вычислений
Завершение работы с системой
Что нового мы узнали?
Описанный способ задания матриц позволяет выполнить операцию
конкатенации
—
объединения малых матриц в большую.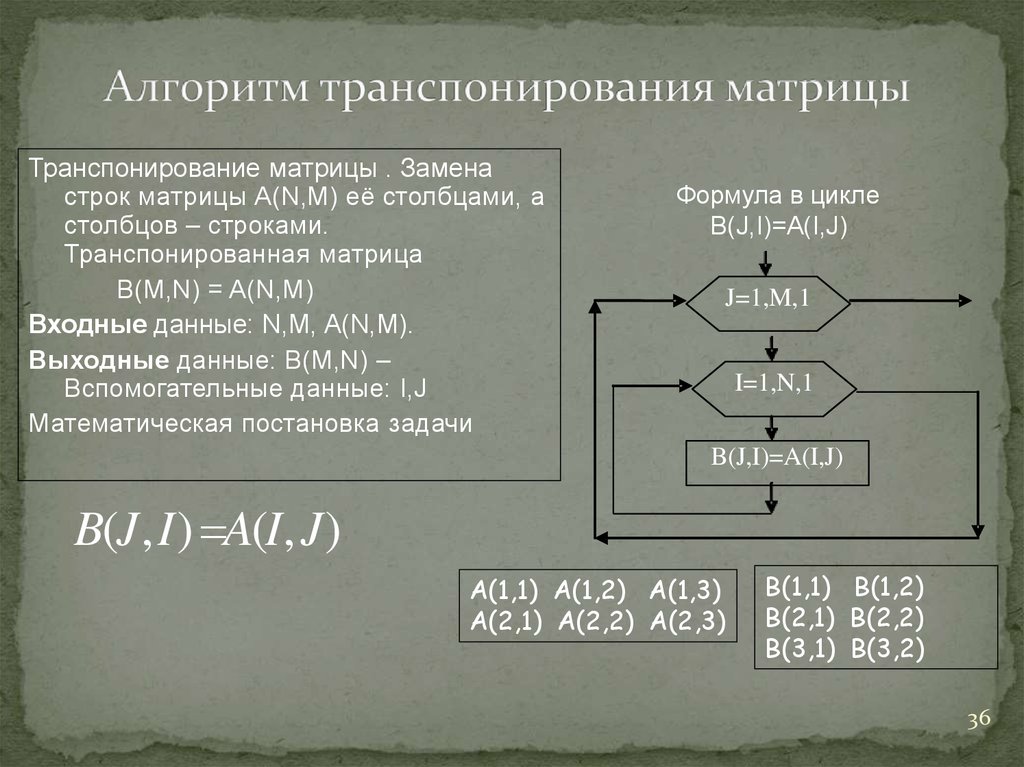 Например, создадим вначале магическую
матрицу размера 3×3:
Например, создадим вначале магическую
матрицу размера 3×3:
» A=magic(3)
А=
|
8
|
1
|
6
|
||
|
3
|
5
|
7
|
||
|
4
|
9
|
2
|
||
Теперь можно
построить матрицу, содержащую четыре матрицы:
» В-[А А+16:А+32 А+16]
В =
|
8
|
1
|
6
|
24
|
17
|
22
|
||
|
3
|
5
|
7
|
19
|
21
|
23
|
||
|
4
|
9
|
2
|
20
|
25
|
18
|
||
|
40
|
33
|
38
|
24
|
17
|
22
|
||
|
35
|
37
|
39
|
19
|
21
|
23
|
||
|
36
|
41
|
34
|
20
|
25
|
18
|
Полученная
матрица имеет уже размер 6×6. Вычислим сумму ее столбцов:
Вычислим сумму ее столбцов:
» sum(B)
ans
=
126 126 126
126 126 126
Любопытно, что она одинакова для всех столбцов. А для вычисления суммы стро!
используем команду
» sum(B.’)
ans =
78 78 78 174
174 174
» D=magic(6)
D=
|
35
|
1
|
6
|
26
|
19
|
24
|
||
|
3
|
32
|
7
|
21
|
23
|
25
|
||
|
31
|
9
|
2
|
22
|
27
|
20
|
||
|
8
|
28
|
33
|
17
|
10
|
15
|
||
|
30
|
5
|
34
|
12
|
14
|
16
|
||
|
4
|
36
|
29
|
13
|
18
|
11
|
||
»
sum(D)
ans=
111 111 111 111 111 111
» sum(D. ‘)
‘)
ans=
111 111 111 111 111 111
Более того, для магической матрицы одинаковой является и сумма элементов по
основным диагоналям (главной диагонали и главной антидиагонали).
Нравится
Твитнуть
Теги MatLab САПР
Сюжеты MatLab
Знакомство с матричной лабораторией MATLAB MatLab
8152 0
Визуализация и графические средства MatLab
9654 0
Техническая документация по системе MatLab
6165 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster.ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2377 s
| Государственное образовательное учреждение высшего профессионального образования московской области Международный университет природы, общества и человека «Дубна» Кафедра «Персональная электроника» Лабораторная работа №1 по дисциплине «Основы автоматических систем управления»
Выполнил: студент группы 4142 Зернин Н.Д.
Дубна, 2010 г. Цель работы: Знакомство с принципами работы в интерактивной компьютерной среде MATLAB ( программирование, построение графиков ). Введение.
Независимо от того, к какой платформе принадлежит ваш компьютер или какую операционную систему вы используете, большинство инструкций, функций и команд MATLAB применяются совершенно одинаково. В данном приложении на этот момент обращается особое внимание. Обычно при работе в среде MATLAB пользователь взаимодействует с компьютером с помощью четырех основных объектов. Это инструкции и переменные, матрицы, графические изображения и скрипты. MATLAB интерпретирует и обрабатывает входные данные в виде одного или нескольких этих объектов. Цель данного приложения — рассмотреть каждый из перечисленных объектов, чтобы читатель получил начальную подготовку по решению в среде MATLAB задач анализа и синтеза систем управления. Способ взаимодействия MATLAB с конкретной операционной системой зависит от платформы, к которой принадлежит компьютер. Специфичными для каждой платформы являются инсталляция MATLAB, файловая структура, получение твердой копии графических изображений, вызов программы и выход из нее, а также распределение памяти. Дальнейший материал приложения сгруппирован в четыре раздела соответственно четырем типам перечисленных выше объектов. В первом разделе мы рассмотрим основы понятий инструкций и переменных. Следующий раздел посвящен матрицам. Третий раздел содержит введение в графику, а в четвертом обсуждаются важные понятия, скриптов и М-файлов.
жүктеу/скачать 186 Kb. Достарыңызбен бөлісу: |
Транспонировать матрицу Matlab | Как мы можем транспонировать матрицу в Matlab?
В этой статье мы узнаем о Transpose Matrix Matlab. Если строки выходной матрицы равны входным столбцам, а столбцы выходной матрицы равны строкам входной матрицы, то выходная матрица называется «транспонированием матрицы». Эта буква «T» представляет собой транспонирование матрицы. Предположим, что есть две матрицы: одна — входная матрица «I», а вторая — выходная матрица «O». Количество строк входной матрицы равно «Irow». Количество столбцов во входной матрице — «Idol», а количество строк в выходной матрице — «Orow». Количество столбцов в выходной матрице равно «Ocol», затем транспонирование матрицы удовлетворяет двум условиям: Icol=Orow и Irow=Ocol. (строки входной матрицы = столбец выходной матрицы и столбцы входной матрицы = строки выходной матрицы)
Если строки выходной матрицы равны входным столбцам, а столбцы выходной матрицы равны строкам входной матрицы, то выходная матрица называется «транспонированием матрицы». Эта буква «T» представляет собой транспонирование матрицы. Предположим, что есть две матрицы: одна — входная матрица «I», а вторая — выходная матрица «O». Количество строк входной матрицы равно «Irow». Количество столбцов во входной матрице — «Idol», а количество строк в выходной матрице — «Orow». Количество столбцов в выходной матрице равно «Ocol», затем транспонирование матрицы удовлетворяет двум условиям: Icol=Orow и Irow=Ocol. (строки входной матрицы = столбец выходной матрицы и столбцы входной матрицы = строки выходной матрицы)
Как мы можем транспонировать матрицу в Matlab?
Есть два способа узнать транспонирование матрицы в Matlab:
- С помощью оператора
- С помощью команды
1. С помощью оператора
В этом методе оператор точки используется для нахождения транспонирования матрицы (. ’). Это один из самых простых и простых способов транспонирования. Единственным ограничением этого метода является высокая вероятность синтаксической ошибки из-за оператора.
’). Это один из самых простых и простых способов транспонирования. Единственным ограничением этого метода является высокая вероятность синтаксической ошибки из-за оператора.
Синтаксис:
Выходная матрица=входная матрица . ’
Шаги:
- Принять входную матрицу, используя квадратную матрицу (Ввод = [ 23 , 32 , 11 ; 22 3 2 ; 16 39 21 ; 32 4 1 ]
- Применить оператор к входной матрице (выходная матрица=входная матрица.’)
- Показать выходную матрицу.
2. С помощью команды
В этом методе команда «транспонировать» используется для определения транспонирования матрицы. Этот метод менее сложен и прост в реализации по сравнению с предыдущим методом. И меньше шансов ошибиться во время реализации.
Синтаксис:
Выходная матрица=транспонировать (входная матрица)
Шаги:
- Принять входную матрицу, используя квадратную матрицу (Ввод = [ 6 3 , 2 3 ; 2 3 , 1 32 21;32 4 1]
- Применить команду к входной матрице (выходная матрица = транспонировать (входная матрица))
- Отображение выходной матрицы.

Примеры для транспонирования матрицы Matlab
Ниже приведены примеры реализации матрицы Matlab:
Пример #1
Рассмотрим входную матрицу как mat1;
Код:
mat1 =
23 32 11
22 3 2
16 39 21
32 4 1
В следующей таблице показан код Matlab с использованием оператора by для примера 1.
| Редактор Matlab | Командное окно (вывод) |
мат1 = [ 23 , 32 , 11 ; 22 3 2 ; 16 39 21 ; 32 4 1 ] мат3 = мат1 . | мат1 = 23 32 11 22 3 2 16 39 21 32 4 1 мат3 = 23 22 16 32 32 3 39 4 11 2 21 1 |
Вывод:
В следующей таблице показан код Matlab для примера 1 с использованием команды транспонирования:
| Редактор Matlab | Командное окно (вывод) |
| мат1 = [ 23 , 32 , 11 ; 22 3 2 ; 16 39 21 ; 32 4 1 ] мат2=транспонировать(мат1) | мат1 = 23 32 11 22 3 2 16 39 21 32 4 1 мат2 = 23 22 16 32 32 3 39 4 11 2 21 1 |
Пример #2
Предположим, что входной матрицей является mat1 в форме магической команды.
MAT1 =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
Следующая таблица иллюстрирует код MATLAB, например, 1 с помощью оператора транспонирования.
| Редактор Matlab | Командное окно (вывод) |
мат1 = магия(4) мат2 = мат1.’ | мат1 = 16 2 3 13 5 11 10 8 9 7 6 12 4 14 15 1 мат2 = 16 5 9 4 2 11 7 14 3 10 6 15 13 8 12 1 |
В следующей таблице показан код Matlab для примера 2 с использованием команды транспонирования.
| Редактор Matlab | Командное окно (Вывод) |
| mat1 = magic ( 4 )%no 4 представляет количество строк и столбцов% мат2=транспонировать(мат1) | мат1 = 16 2 3 13 5 11 10 8 9 7 6 12 4 14 15 1 мат2 = 16 5 9 4 2 11 7 14 3 10 6 15 13 8 12 1 |
Пример #3
Теперь рассмотрим одну входную матрицу с комплексными числами.
MAT1 =
1.0000 - 3.0000 I 4.0000 + 4.0000 I 8.0000 + 0,0000 I 2.0000 - 5,0000 I
5,0000 + 0,0000 I 3.0000 + 0,0000 I 6,0000 + 8,0000 I 4.0000 + 4.0000 I
0,0000 + 1,0000 I 7,0000 + 8,0000 + +
0,0000 + 1,0000 I 7,0000 + 8,0000 + 9,0000 +
0,0000 + 1,0000 + 8,0000 + 9,0000 +
0,0000 + 1,0000 + 8,0000 I 4,0000 + 9,0000 i 10,0000 + 0,0000 i
| Редактор Matlab | Командное окно (Вывод) |
| мат1 = [ 1 – 3 я , 4 + 4 я , 8 , 2 – 5 я ; 5 , 3 , 6 + 8 я , 4 + 4 я ; я, 7 + 8 я, 9 + 9 я, 10] мат2=мат1.’ | мат1 = 1.0000 – 3.0000i 4.0000 + 4.0000i 8.0000 + 0.0000i 2.0000 – 5.0000i 5,0000 + 0,0000i 3,0000 + 0,0000i 6,0000 + 8,0000i 4,0000 + 4,0000i 0,0000 + 1,0000i 7,0000 + 8,0000i 9,0000 + 9,0000i 10,0000 + 0,0000i мат2 = 1,0000 – 3,0000i 5,0000 + 0,0000i 0,0000 + 1,0000i 4. 8.0000 + 0.0000i 6.0000 + 8.0000i 9.0000 + 9.0000i 2,0000 – 5,0000i 4,0000 + 4,0000i 10,0000 + 0,0000i |
| Редактор Matlab | Командное окно (Вывод) |
| мат1=[1-3i,4+4i,8,2-5i;5,3,6+8i,4+4i;i,7+8i,9+9i,10] мат2=транспонировать(мат1) | мат1 = 1.0000 – 3.0000i 4.0000 + 4.0000i 8.0000 + 0.0000i 2.0000 – 5.0000i 5,0000 + 0,0000i 3,0000 + 0,0000i 6,0000 + 8,0000i 4,0000 + 4,0000i 0,0000 + 1,0000i 7,0000 + 8,0000i 9,0000 + 9,0000i 10,0000 + 0,0000i мат2 = 1,0000 – 3,0000i 5,0000 + 0,0000i 0,0000 + 1,0000i 4.0000 + 4.0000i 3.0000 + 0.0000i 7.0000 + 8.0000i 8,0000 + 0,0000i 6,0000 + 8,0000i 9.0000 + 9.0000i 2,0000 – 5,0000i 4,0000 + 4,0000i 10,0000 + 0,0000i |
Заключение
Транспонирование матрицы — один из важных терминов, используемых при работе с матрицами. В этом разделе мы увидели, как узнать транспонирование матрицы, используя два метода: один — с помощью оператора, а другой — с помощью команды транспонирования. Наряду с различными методами мы видели различные матрицы в качестве входных данных для проверки системы (действительные числа, случайные числа и комплексные числа).
В этом разделе мы увидели, как узнать транспонирование матрицы, используя два метода: один — с помощью оператора, а другой — с помощью команды транспонирования. Наряду с различными методами мы видели различные матрицы в качестве входных данных для проверки системы (действительные числа, случайные числа и комплексные числа).
Рекомендуемые статьи
Это руководство по транспонированию матрицы Matlab. Здесь мы обсудим примеры реализации транспонированной матрицы Matlab с помощью оператора и команды. Вы также можете ознакомиться с другими нашими статьями по теме, чтобы узнать больше —
- Цвета в Matlab
- Графики рассеяния в Matlab
- 3D Матрица в MATLAB
- Возможности Matlab
- Руководство по работе с градиентом в Matlab
- Руководство по различным примерам обратной функции Matlab
Транспонирование Matlab | Различные примеры транспонирования Matlab
Транспонирование используется в математике для замены строк и столбцов входной матрицы. Итак, если у нас есть матрица 2 x 3 на входе, функция транспонирования даст нам матрицу 3 x 2 на выходе. В Matlab мы используем «функцию транспонирования» для вычисления транспонирования матрицы или вектора. Для вектора с «n» элементами функция транспонирования дает в качестве выходных данных матрицу «n x 1» («n» строк и 1 столбец).
Итак, если у нас есть матрица 2 x 3 на входе, функция транспонирования даст нам матрицу 3 x 2 на выходе. В Matlab мы используем «функцию транспонирования» для вычисления транспонирования матрицы или вектора. Для вектора с «n» элементами функция транспонирования дает в качестве выходных данных матрицу «n x 1» («n» строк и 1 столбец).
Синтаксис транспонированной функции:
T = транспонирование (M)
T = M. '
Обследование:
- T = Transpose (M) используется для Comput входная матрица ‘M’, т. е. он поменяет местами строки и столбцы матрицы ‘M’.
- T = M.’ — это еще один способ вычисления транспонирования. Это даст тот же результат, что и приведенный выше синтаксис.
Примеры Matlab Transpose
Ниже приведены примеры транспонирования Matlab:
Пример #1
В этом примере мы будем использовать функцию транспонирования для вычисления транспонирования реальной матрицы 2 x 2.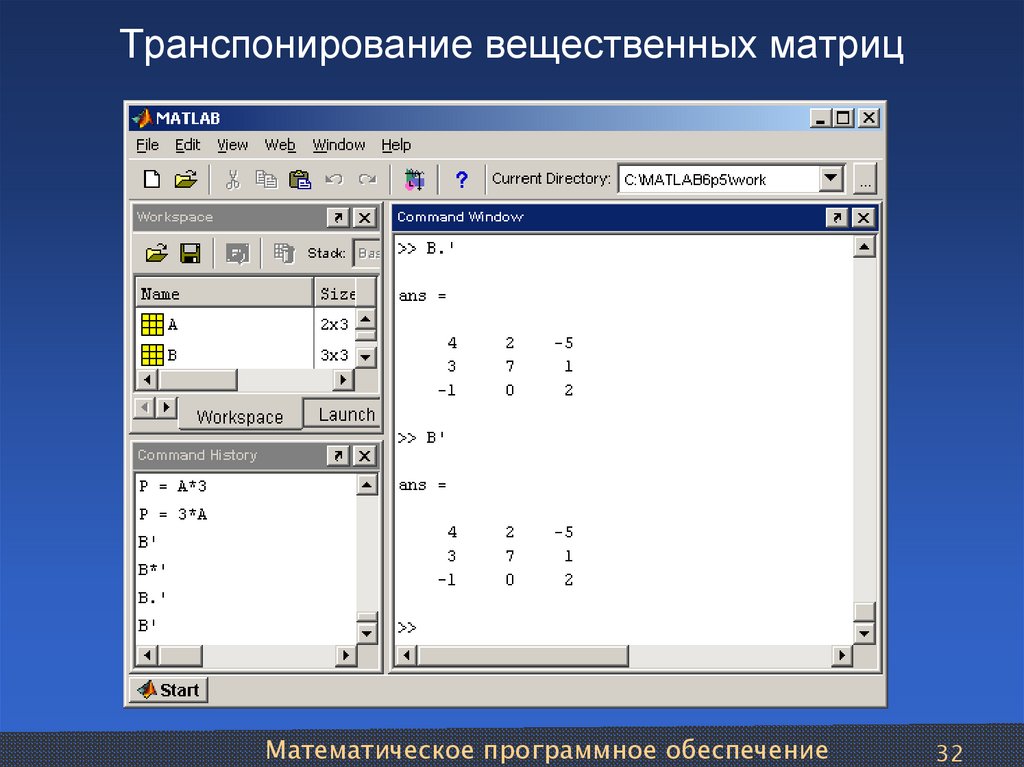
Ниже приведены шаги, которые необходимо выполнить:
- Инициализировать входную матрицу.
- Передайте эту входную матрицу в качестве аргумента функции транспонирования.
Код:
М = [6 -5; 1 6] [Инициализация входной матрицы 2 x 2]
T = транспонировать (M)
[Использование функции транспонирования для вычисления транспонирования входной матрицы]
Вход:
Выход:
Перед транспонированием:
После транспонирования:
Как мы можем увидеть на выходе. столбцы нашей входной матрицы.
Пример #2
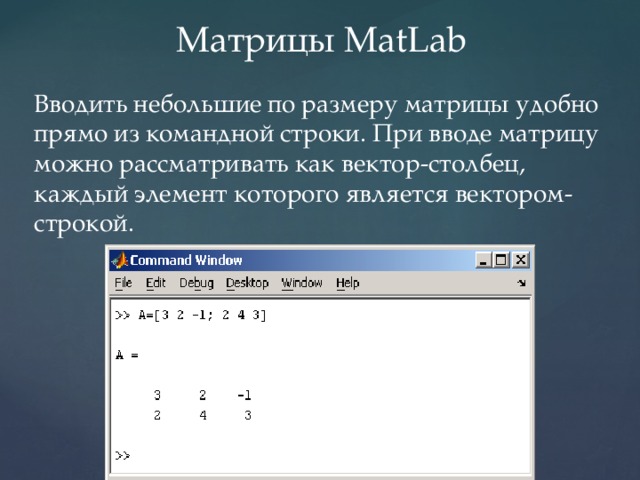
В этом примере мы будем использовать функцию транспонирования для вычисления транспонирования вещественной матрицы 3 x 3.
Ниже приведены шаги, которые необходимо выполнить:
- Инициализировать входную матрицу.
- Передайте эту входную матрицу в качестве аргумента функции транспонирования.
Код:
М = [2 -1 4; 1 16 2; 0 -4 3] [Инициализация входной матрицы 3 x 3]
T = транспонирование (M)
[Использование функции транспонирования для вычисления транспонирования входной матрицы]
Ввод:
Выход:
Перед транспонированием:
После транспонирования:
Как видно из вывода, функция транспонирования поменяла местами строки и столбцы нашей входной матрицы.
В приведенных выше 2 примерах наша входная матрица состояла из реальных элементов.
Далее, давайте возьмем пример, где наша входная матрица также будет иметь сложные элементы.
Пример #3
В этом примере мы будем использовать функцию транспонирования для вычисления транспонирования комплексной матрицы 3 x 3.
Ниже приведены шаги, которые необходимо выполнить:
- Инициализировать входную матрицу со сложными элементами.

- Передайте эту входную матрицу в качестве аргумента функции транспонирования.
Код:
М = [2+3i 1-4i 1; 1+3i 0 3-2i; 0 3 2] [Инициализация входной матрицы 3 x 3 со сложными элементами]
T = транспонирование (M)
[Использование функции транспонирования для вычисления транспонирования входной матрицы]
Ввод:
Выход:
Перед транспонированием:
После транспонирования:
Как мы можем видеть на выходе, транспонированная функция сдерживала Rows и колонны нашего входного комплексного матрикса.
В приведенных выше 3 примерах мы использовали квадратную матрицу в качестве входных данных.
Далее мы будем использовать неквадратную матрицу в качестве входных данных для функции транспонирования.
Пример #4
В этом примере мы будем использовать функцию транспонирования для вычисления транспонирования вещественной матрицы 2 x 3.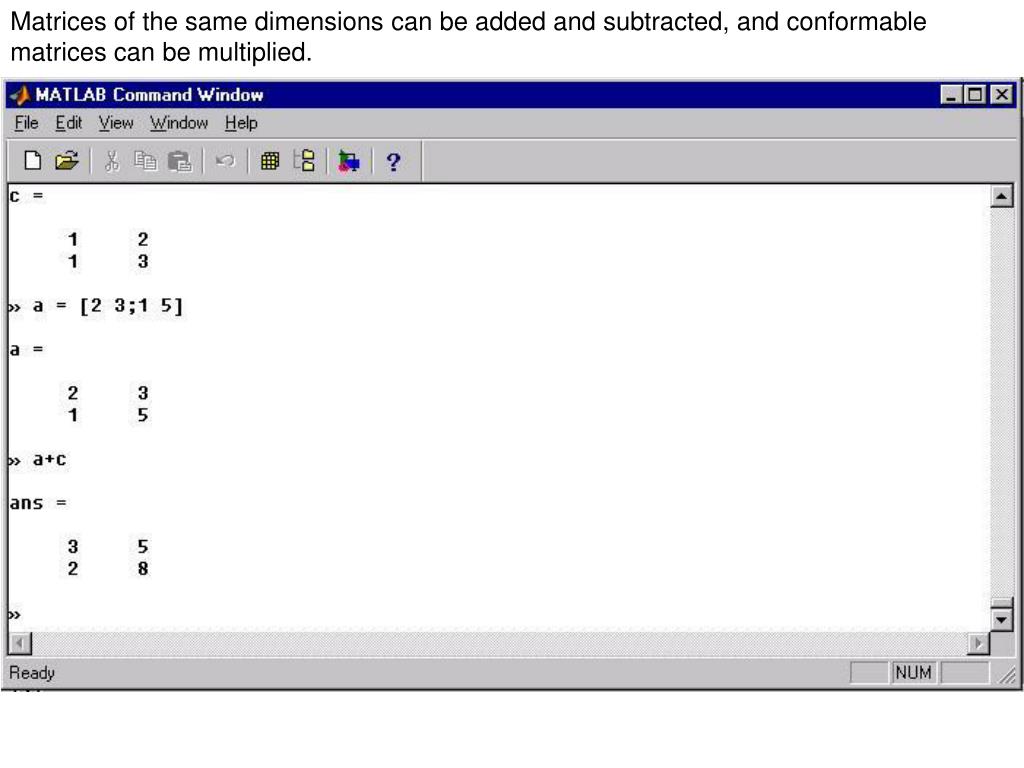
Ниже приведены шаги, которые необходимо выполнить:
- Инициализировать входную матрицу.
- Передайте эту входную матрицу в качестве аргумента функции транспонирования.
Код:
М = [1 6 4; 1 4 -2] [Инициализация входной матрицы 2 x 3]
T = транспонирование (M)
[Использование функции транспонирования для вычисления транспонирования входной матрицы]
Ввод:
Выход:
До транспонирования:
После транспонирования:
Как видно из вывода, функция транспонирования поменяла местами строки и столбцы нашей неквадратной входной матрицы.
В приведенных выше 4 примерах мы использовали матрицу в качестве входных данных для функции транспонирования.
Далее мы будем использовать функцию транспонирования для вычисления транспонирования входного вектора.
Пример #5
В этом примере мы будем использовать функцию транспонирования для вычисления транспонирования вектора с 5 элементами.
Ниже приведены шаги, которые необходимо выполнить:
- Инициализировать входной вектор с 5 элементами.
- Передайте этот входной вектор в качестве аргумента функции транспонирования.
Код:
М = [8 -11 4 5 7] [Инициализация входного вектора с 5 элементами]
T = транспонирование (M)
[Использование функции транспонирования для вычисления транспонирования входного вектора]
Обратите внимание, что поскольку наш ввод имеет 5 столбцов и 1 строку, наш вывод будет иметь 5 строк и 1 столбец.
Вход:
Выход:
Перед транспонированием:
После транспонирования:
Как можно увидеть на выходе. строки и столбцы.
Заключение
Мы используем функцию транспонирования, чтобы вычислить транспонирование матрицы, т. е. поменять местами ее строки и столбцы. Функция транспонирования может использоваться как для вещественных, так и для комплексных матриц.

 Эти специфичные для каждой платформы вопросы в данном приложении не рассматриваются. Это вовсе не означает, что они не являются существенными, однако вместо того, чтобы останавливаться на них в данной книге, мы предлагаем читателю для получения необходимой информации воспользоваться каким-либо руководством для пользователей MATLAB или обратиться за консультацией к специалисту.
Эти специфичные для каждой платформы вопросы в данном приложении не рассматриваются. Это вовсе не означает, что они не являются существенными, однако вместо того, чтобы останавливаться на них в данной книге, мы предлагаем читателю для получения необходимой информации воспользоваться каким-либо руководством для пользователей MATLAB или обратиться за консультацией к специалисту.
 0000 + 4.0000i 3.0000 + 0.0000i 7.0000 + 8.0000i
0000 + 4.0000i 3.0000 + 0.0000i 7.0000 + 8.0000i