Критерий Уилкоксона — Википедия. Что такое Критерий Уилкоксона
Т-критерий Вилкоксона — непараметрический статистический тест (критерий), используемый для проверки различий между двумя выборками парных или независимых измерений. Впервые предложен Фрэнком Уилкоксоном[1]. Другие названия — W-критерий Вилкоксона[2], критерий знаковых рангов Вилкоксона, критерий Уилкоксона для связных выборок[3]. Тест Вилкоксона для независимых выборок также называется критерием Манна-Уитни[4].
Назначение критерия
Критерий предназначен для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить не только направленность изменений, но и их выраженность, то есть способен определить, является ли сдвиг показателей в одном направлении более интенсивным, чем в другом.
Описание критерия
Критерий применим в тех случаях, когда признаки измерены, по крайней мере, в порядковой шкале.
Суть метода состоит в том, что сопоставляются абсолютные величины выраженности сдвигов в том или ином направлении. Для этого сначала все абсолютные величины сдвигов ранжируются, а потом суммируются ранги. Если сдвиги в ту или иную сторону происходят случайно, то и суммы их рангов окажутся примерно равны. Если же интенсивность сдвигов в одну сторону больше, то сумма рангов абсолютных значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть при случайных изменениях.
Минимальное значение величины: W=n(n+1)/2{\displaystyle W=n(n+1)/2}, где n — объём второй выборки. Максимальное значение величины W=n(n+1)/2+mn{\displaystyle W=n(n+1)/2+mn}, где n — объём второй выборки, m — объём первой выборки.
Ограничения критерия
Уверенно критерий Уилкоксона можно использовать при объёме выборки до 25 элементов [5] . Это объясняется тем, что при большем числе наблюдений распределение значений данного критерия стремительно приближается к нормальному. Поэтому в случае с большими выборками прибегают к преобразованию критерия Уилкоксона в величину z (z-score)[5]. Примечательно, что программа SPSS конвертирует критерий Уилкосона в величину z всегда независимо от размеров выборки[5].
Нулевые сдвиги исключаются из рассмотрения. (Это требование можно обойти, переформулировав вид гипотезы. Например: сдвиг в сторону увеличения значений превышает сдвиг в сторону их уменьшения и тенденцию к сохранению на прежнем уровне.
Сдвиг в более часто встречающемся направлении принято считать «типичным», и наоборот.
Есть также урезанный вариант для сравнения одной выборки с известным значением медианы.
Алгоритм
- Составить список испытуемых в любом порядке, например, алфавитном.
- Вычислить разность между индивидуальными значениями во втором и первом замерах. Определить, что будет считаться типичным сдвигом.
- Согласно алгоритму ранжирования, проранжировать абсолютные величины разностей, начисляя меньшему значению меньший ранг, и проверить совпадение полученной суммы рангов с расчетной.
- Отметить каким-либо способом ранги, соответствующие сдвигам в нетипичном направлении. Подсчитать их сумму Т.
- Определить критические значения Т для данного объема выборки. Если Т-эмп. меньше или равен Т-кр. – сдвиг в «типичную» сторону достоверно преобладает.
Фактически оцениваются знаки значений, полученных вычитанием ряда значений одного измерения из другого.
Если в результате количество снизившихся значений примерно равно количеству увеличившихся, то гипотеза о нулевой медиане подтверждается.
П
Область применения. Критерий Уилкоксона применяется в той же ситуации, что и критерий Манна-Уитни. В отличие от этого критерия и критерия знаков, он имеет дело не со знаками некоторых случайных величин, а с их рангами. Исторически критерий Уилкоксона был одним из первых критериев, основанных на рангах (о рангах см. п. 3).
Рассмотрим ранги элементов объединения двух выборок И . ДЛЯ получения рангов совокупность всех наблюдений следует упорядочить в порядке возрастания. (Напомним, что если функции распределения
Пусть, например, первая выборка состоит из чисел 6, 17 и 14, вторая — из чисел 5 и 12.
Тогда ранги величин первой группы есть 2, 5, 4, второй — 1, 3.
Нетрудно понять, что последовательность рангов совокупности oБъема Т+N является некоторой перестановкой чисел 1,…, M+N. Верно и обратное: любая перестановка чисел 1,…, M + П может оказаться ранговой последовательностью. Так что множество возможных ранговых последовательностей — это совокупность перестановок чисел 1, 2,…, M+n. Их общее число равно (M+N)!.
Зная распределения случайных величин и , мы можем (по крайней мере, теоретически) вычислить вероятность того, что результат их ранжирования будет заданной перестановкой. ПоэтоМу Каждое распределение случайных величин и поРождает некоторое распределение вероятностей на указанном множесТве Перестановок. Ясно, что если исходные данные однородны (И в совокупности являются независимыми и одинаково Распределенными случайными величинами), то в качестве Последовательности рангов с равными шансами может появиться любая Перестановка Чисел от 1 до M+N.
Число таких перестановок равно (M+N)!, поэтоМу Вероятность каждой равна . Заметим, что этот результ никак не зависит от распределения самих наблюдений.
Посмотрим, как изменяется распределение вероятностей среди ранговых последовательностей (т. е. среди перестановок) при отступлениях от однородности выборок. В качестве нарушений однородности мы будем рассматривать те же ситуации, что и при обсуждении критерия Манна-Уитни в предыдущем пункте: левосторонние альтернативы и правосторонние альтернативы
Таким образом, ранги в какой-то мере способны характеризовать, например, положение одной выборки по отношению к другой и в то же время они не зависят от неизвестных нам распределений выборок Х и У. Это обстоятельство и легло в основу ранговых методов, широко применяемых в настоящее время в различных задачах. Вернемся к непосредственному обсуждению критерия Уилкоксона.
Назначение. Критерий Уилкоксона используется для проверки Гипотезы об однородности двух выборок. Нередко одна из выборок ПреДСтавляет характеристики объектов, подвергшихся перед тем какому-то воздействию (обработке). В этом случае гипотезу однородности можно назвать Гипотезой об Отсутствии эффекта обработки.
Данные. Рассматриваются две выборки и , объемов M и П. Обозначим закон распределения первой выборки через F, а второй — через G.
Допущения. 1. Выборки и независимы между собой.
Гипотеза. В введенных выше обозначениях гипотезу об однородности выборок можно записать в виде Н : F = G.
Метод. 1. Рассмотрим ранги игреков в общей совокупности выборок Х и У. Обозначим их через .
2. Вычислим величину
,
Называемую статистикой Уилкоксона.
3. Зададим уровень значимости A или выберем метод, связанный с определением наименьшего уровня значимости, приведенный ниже.
4. Для проверки Н на уровне значимости A против правосторонних альтернатив найдем по таблице верхнее критическое значение W(A, M, N), т. е. такое значение, для которого
Гипотезу следует отвергнуть против правосторонней альтернативы при уровне значимости A, если .
5. Для проверки H на уровне значимости A против левосторонних альтернатив , необходимо вычислить нижнее критическое значение статистики W. В силу симметричности распределения W Нижнее критическое значение есТЬ N(M+N+1)—W(A, m, п). Гипотеза H должна быть отвергнута на уровне значимости A против левосторонней альтернативы, если .
6. Гипотеза H отвергается на уровне 2A против двусторонней альтернативы , если
или .
Напомним, что альтернативы должны выбираться из содержательных соображений, связанных с условиями получения экспериментальных данных.
7. Более гибкое правило проверки Н связано с вычислением наименьшего уровня значимости, на котором гипотеза Н может быть отвергнута. Для разных альтернатив речь идет о вычислении вероятностей:
Гипотеза отвергается, если соответствующая вероятность оказывается малой.
Приближение для больших выборок. На практике часто приходится сталкиваться с ситуацией, когда объемы выборок Т и П выходят за пределы, приведенные в таблицах. В этом случае используют аппроксимацию распределения W предельным распределением статистики W при и . Перейдем от величины W к . Ниже будет показано, что . Так же можно показать, что . Доказано, что в условиях H, при допущениях 1 и 2 и при больших Т, п случайная величина W* распределена приблизительно по нормальному закону с параметрами (0, 1).
Обозначим через ZA верхнее критическое значение стандартного нормального распределения. Его можно найти с помощью таблицы квантилей нормального распределения для любого 0 < A < 0.5. Благодаря симметрии распределения нижнее критическое значение равно — ZA. Правило проверки H перефразируем так:
• отвергнуть H на уровне A против альтернативы , есЛИ ;
• отвергнуть H на уровне A против альтернативы , ЕСли ;
• отвергнуть H на уровне 2A против альтернативы , если .
Правило, связанное с вычислением наименьшего уровня значимости, при использовании нормального приближения выглядит так: отвергнуть H (против соответствующих альтернатив), если оказывается малой вероятность для альтернативы , дЛЯ альтернативы , и длЯ Альтернативы , где Ф(U) — функция нормального распределения (функция Лапласа), равная
.
Функция нормального распределения и ей обратная, которая Называется функцией квантилей стандартного нормального распределЕния, подробно табулированы. Упомянутое ранее верхнее критическое значение ZA С помощью функции Ф можно определить как решение уравнения
Замечание. Указанное выше нормальное приближение для вычисления критических значений статистики W хорошо действует даже для небольших значений M и П, если только A не слишком мало. (Так, для Т = П = 8 приближенные квантили практически не отличаются от точных.
)
Обсуждение. Рассмотрим подробнее свойства статистики W и соображения положенные в основу критерия Уилкоксона.
ОблаСТь опредеЛЕния. Случайная величина W может принимать все целые значения от минимального значения до максимального . Минимальное значение W мы получаем, когда рангами игреков служат (в той или иной последовательности) числа 1, 2,… ,П. Максимальное значение W возникает, когда этими рангами служат M+1, M+2,…, Т+п.
Заметим, что W не изменится, если произвольно переменить порядок следования чисел, служащих рангами игреков (как не изменится и при перенумерации самих игреков). Чтобы упростить обсуждение, можно поэтому говорить далее о рангах игреков, упорядоченных по возрастанию. Пусть Обозначают именно упорядоченные ранги, так что .
Распределение вероятностей. Статистика Уилкоксона была определена нами как сумма (упорядоченного) набора рангов игреков .
Вероятность каждого такого упорядоченного набора при выдвинутой гипотезе Н — Одна и та же и равна . Таким образом, при гипотезе Н распределение W не зависит от закона распределения выборок х и У, так как от них не зависит распределение упорядоченной последовательности рангов. Для каждой пары (M, N) распределение W можно рассчитать. Покажем на примере, как это делается.
Пусть M = 3 и N = 2. Вычислим число всех возможных пар рангов игреков. Оно равно Следовательно, вероятность каждого упорядоченного набора рангов равна 0.1. Выпишем всевозможные наборы рангов S1, S2 и соответствующую им сумму:
|
S1, S2 |
1.2 |
1.3 |
1.4 |
1.5 |
2.3 |
2.4 |
2. |
3.4 |
3.5 |
4.5 |
W |
3 |
4 |
5 |
6 |
5 |
6 |
7 |
7 |
8 |
9 |
5Таким образом, получаем следующее распределение W:
W |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
P(W) |
0.1 |
0.1 |
0.2 |
0.2 |
0. |
0.1 |
0.1 |
2Отметим, что распределение W симметрично относительно точки — середины отрезка . Из этого свойства легко вывести, что .
Рассмотрим случайную величину . Согласно симметрии закона распределения относительно точки , вероятность , что эта величина примет некоторое значение K, равна вероятности , что она примет значение —K. Согласно определению математического Ожидания, . Учитывая, Что Математическое ожидание разности равно разности математических Ожиданий, а математическое ожидание константы равно самой константе, получаТ .
РаспредеЛЕние статистики W при нарушении гипотезы. ЧтоБы Оправдать сделанный выше выбор критических событий (критериев) для ПроВерки Н против рассмотренных альтернатив, надо изучить распределение стаТистик U и W при этих альтернативах. Когда F и G не одинаковы, распределеНия U и W уже не свободны от их влияния.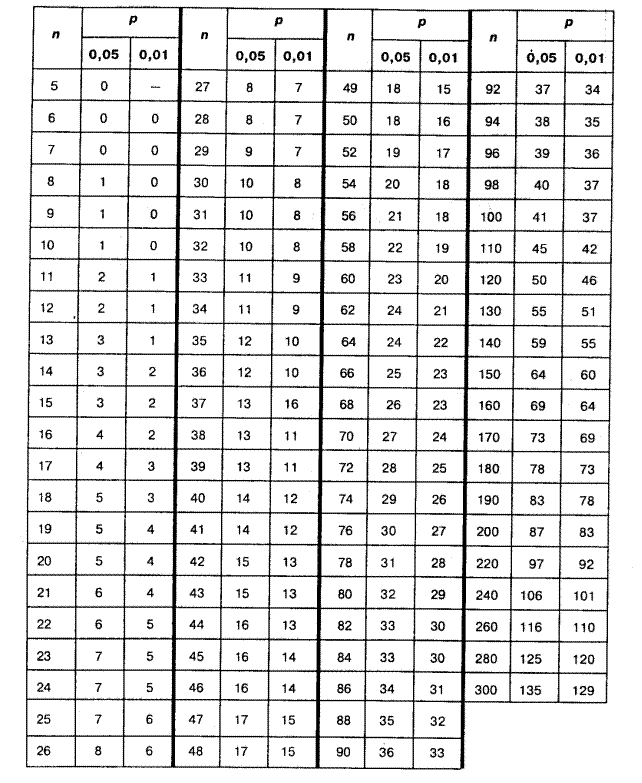
Поэтому точно вычислить и Указать Распределения U и W можно (в принципе) только для каждой конкретной Пары F и G. Тем не менее, характер изменения распределений статистик U и W при переходе от гипотезы к альтернативам — не всем, но некоторым, — установИть Можно. Это легко сделать для односторонних альтернатив. Например, Когда (правосторонняя альтернатива), распределение вероятноСтей W «перетекает» от середины к правому концу того множества значений, которОе Может принимать W. Для левосторонних альтернатив аналогичное «перетеКание» вероятности происходит влево — тем сильнее, чем больше Отличается от 0.5.
На рис. 1 мы попытались наглядно представить это положение, Условно Представляя распределение статистики W при гипотезе и при альтернативаХ с Помощью плотностей, — хотя искомые распределения дискретны и плотноСтей Не имеют. Но так получается выразительнее. (При желании можно считаТь, Что нарисованные непрерывные кривые изображают что-то вроде Огибающих Графиков дискретных вероятностей.
)
Рис. 1
Из рис. 1 ясно, что гипотеза Н должна отвергаться при слишком большЕ Или при слишком малых значениях W в зависимости от того, какие альтернативы мы рассматриваем. При том выборе критериев, который был описан выШе Их мощность возрастает при удалении от 0.5. Это правило и лежит в основе описанного выше метода.
Связь со статистикой Манна-Уитни. Нетрудно проверить, что для всех M, N: . Это соотношение показывает эквивалентноСть Статистик U и W. Поэтому их применения приводят к одинаковым результатам.
СоВПадения. Мы описали критерий Уилкоксона для проверки гипотезы об однородности двух выборок в условиях, когда функции распределений Данных Непрерывны и, тем самым, в выборках не должно быть совпадающих наблюдений. Однако на практике совпадающие наблюдения — не редкость. Чаще всего это происходит не потому, что нарушается условие непрерывности, а из-за ограниченной точности записи результатов измерений (например, рост человека обычно измеряется с точностью до 1 см).
Применение критерия Уилкоксона к таким данным приводит к приближенным выводам, точность которых тем ниже, чем больше совпадающих значений.
Когда среди наблюдений встречаются одинаковые, им приписываются Средние ранги. По определению, средний ранг числа в совокупности чисел есть среднее арифметическое из тех рангов, которые были бы назначены и всем остальным значениям, совпадающим с , если бы они оказались различными. После такого назначения рангов применяются описанные ранее процедуры.
Упомянутые группы одинаковых наблюдений называют Связками. Количество элементов в связке называют ее размером. Наличие связей влияет на асимптотические распределения статистики Уилкоксона. Так, при использовании нормальной аппроксимации следует в формуле для вычисления W* заменить DW на
,
Где — размеры наблюденных связок среди игреков, G — общее число связок среди игреков. Наблюдение, не совпавшее с каким-либо другим наблюдением, рассматривается как связка размера 1, и в формуле, заменяющей DW не учитывается.
При больших по размеру связках и (или) большом их числе применение критерия Уилкоксона сомнительно.
| < Предыдущая | Следующая > |
|---|
Метод расчета критерия Вилкоксона — МегаЛекции
Сейчас мы переходим к ознакомлению со следующим непараметрическим критерием. Он называется критерий Вилкоксона в честь ученого, который его разработал (иногда его фамилию переводят с английского как Уилкоксон).
Данный критерий называют «ранговым» критерием потому, что он опирается на расчет рангов, которые присваиваются полученным в эксперименте данным. Критерий Вилкоксона применяется обычно для сравнения двух рядов данных, которые не подчиняются закону нормального распределения, а проявляют себя как непрерывно возрастающие функции. При этом сравнению подлежат не сами данные, а степень быстроты их возрастания, иными словами, сравниваются «скорости» (интенсивности) возрастания величин показателей в одной и в другой группах.
Подобного рода задача может быть поставлена, например, в эксперименте, где изучаются две методики обучения профессиональному английскому языку. Такой профессиональный английский «жаргон» используют пилотами в радиопереговорах с зарубежными авиадиспетчерами.
В первой методике расширения словарного запаса у пилотов используются традиционный способ обучения – учебные занятия, а во второй методике применяется нетрадиционный способ – игровые занятия. Насколько интенсивно идет прирост словарного запаса при обучении по первой и второй методике, отражают два ряда (группы) данных. Быстрота нарастания показателей словарного запаса может иметь свою специфику в каждом ряду данных. Например, если показатели в одной группе данных меняются быстро, т.е. возрастают сразу на большое количество единиц, а в другой группе данных наблюдается медленный рост показателей, то можно говорить о достоверных различиях в эффективности обучения между двумя методиками.
Далее в таблице отражены темпы возрастания словарного запаса, т.
е. количества активно используемых пилотами слов от занятия к занятию.
| Номера занятий | Словарный запас при 1-й методике | Словарный запас при 2-й методике | Разницы между словарн. запасами |
| +2 | |||
| +3 | |||
| +1 | |||
| -2 | |||
| +1 | |||
| -1 | |||
| -1 | |||
| +2 | |||
| -3 | |||
| +1 |
Существует две формулы для критерия Вилкоксона: одна используется для малых по численности выборок, а другая – для больших по численности выборок.
Мы последовательно рассмотрим обе формулы.
Формула критерия Вилкоксона для малых выборок: Т=∑Rредк. знака
Здесь показатель критерия Т определяется как сумма рангов редкого знака. Чтобы вычислить данную величину на материале рассматриваемого примера с расширением словарного запаса у пилотов, необходимо проделать сначала следующие процедуры:
- вычислить разницу между парами значений (соответствующими одному и тому же занятию) в разных методиках, т.е. вычесть из значений второй графы значения первой графы в таблице;
- все полученные разницы (они представлены со знаками «+» или «-» в третьей графе) выписать в отдельную строку, но без знаков;
- проставить первоначальные ранги для выписанных разниц по мере возрастания их величин, а затем заново присвоить ранги с учетом того, что некоторые разницы повторяются (значит, они должны иметь один и тот же ранг) – для этого определяется средний арифметический ранг для подгруппы одинаковых разниц.
Выполнение данных процедур показано ниже: в верхней строке выписаны величины разниц без знаков, во второй строке им присвоены первичные ранги, а в нижней строке им присвоены уже окончательные ранги, где одинаковые величины разниц имеют теперь и одинаковые ранги.
| 1-й ранг | 2-й ранг | 3-й ранг | 4-й ранг | 5-й ранг | 6-й ранг | 7-й ранг | 8-й ранг | 9-й ранг | 10-й ранг |
| 3-й ранг | 3-й ранг | 3-й ранг | 3-й ранг | 3-й ранг | 7-й ранг | 7-й ранг | 7-й ранг | 9,5-й ранг | 9,5-й ранг |
Теперь надо определить, какой знак среди разниц является более редким.
Из таблицы, где разницы записаны со своими знаками, видно, что знак «-» встречается реже, чем знак «+»: четыре минуса, а плюсов – шесть. Следовательно, далее нам нужно посчитать сумму рангов, которая приходится на разницы с редким знаком «-». В число таких разниц попали следующие величины разниц: -1 (6-е занятие), еще раз -1 (7-е занятие), -2 (4-е занятие) и -3 (9-е занятие). Эти разницы получили согласно процедуре ранжирования такие ранги: 3-й ранг, еще один 3-й ранг, 7-й ранг и 9,5 ранг. Сумма данных рангов составляет 22,5 –это и есть величина критерия Вилкоксона для малых групп данных, т.е сумма рангов редкого знака «-». Достоверные различия будут иметь место лишь в том случае, если Тэксп ≤ Ткрит. Как и для других критериев предусмотрены два критических значения: один уровень значимости составляет р=0,05 (то есть 5% уровень ошибочности вывода о достоверных различиях), а другой уровень значимости составляет р=0,01 (то есть 1% ошибочности вывода о достоверных различиях между данными).
Из ниже приведенной таблицы критических значений видно, что для 10 сравниваемых пар (n=10) Ткрит равно 10 при р=0,05 и равно 5 при р=0,01.
Тэксп оказалось больше этих величин, значит, различия недостоверные.
Таблица критических значений критерия Вилкоксона для малых выборок.
| Число сравниваемых пар (n) | Уровень значимости (р) | Число сравниваемых пар (n) | Уровень значимости (р) | ||
| 0,05 | 0,01 | 0,05 | 0,01 | ||
| — | |||||
| — | |||||
Однако в статистических программах, которые предназначены для обсчета больших выборок, используют не выше указанная формула, а ее модифицированный вариант.
Данный модифицированный вариант критерия Вилкоксона разработали ученые Манн и Уитни для больших выборок. Причем в этой новой формуле рассмотренный выше показатель – сумма рангов редкого знака, — тоже применяется, но только в качестве одного из составных элементов большой формулы. Формула критерия Вилкоксона для больших выборок по сути является универсальной и может применяться в том числе и выборкам среднего размера. Она выглядит так:
В данной формуле показатель n означает количество сравниваемых пар значений двух групп (пары, между которыми вычисляются разницы). Эта же формула заложена и в программу SPSS. Но произведем расчет экспериментального значения критерия по данной формуле вручную, а затем уже в компьютерной программе.
Итак, в эксперименте по сравнению эффективности двух методик для обучения пилотов словарному запасу мы посчитали, что сумма рангов редкого знака «плюс» составила ∑Rредк. знака= 22,5, а количество сравниваемых пар n=10. Подставим эти цифры в формулу критерия:
Тэксп = [22,5 – (10·11):4] : √ (10∙11·21) : 24= 5: 9,8= 0,51
Критическое значение для данное критерия (если берутся средние или большие по численности группы) является единственным и соответствует числу Ткрит =1,96.
Чтобы иметь основание говорить о наличии достоверных различий при сравнении темпов возрастания значений в двух группах данных, необходимо, чтобы Тэксп ≥ Ткрит. Здесь действует обратное правило в соотношении экспериментального и критического значения, чем в ситуации с малыми группами! Полученные экспериментальные значения сравниваются по модулю.
Поскольку полученное экспериментальное значение меньше критического значения 1,96 для данного критерия, следовательно, нельзя говорить о наличии достоверных различий между традиционной и игровой методиками расширения английских запаса у пилотов. Как видим, выводы о достоверности совпали, хотя мы сравнивали по двум разным формулам (для малых и больших групп данных). Разберем пример с вычислением этого критерия в программе SPSS.
Предположим, мы наблюдали за соревнованиями двух групп эрудитов на интеллектуальном шоу. За каждый правильный ответ с учетом сложности вопроса каждая группа получала определенное количество баллов.
Судья производил суммирование баллов, полученных за каждый вопрос, и наблюдал темп прироста общей суммы баллов отдельно в первой и второй группах. Чтобы сделать судейство более справедливым, он задался вопросом: можно ли считать темп набора (роста суммы) баллов в двух группах одинаковым? Будучи уже ознакомленными с критерием Вилкоксона, вы вполне можете дать ответ на поставленный судьей вопрос.
Сейчас вам раздали таблицу, где напечатаны данные двух групп по мере возрастания сумм баллов, которые накапливались по ходу игры за выдачу правильных ответов.
Рассмотрим, как делается расчет критерия Вилкоксона с помощью программы SPSS. Входим в программу известным способом. Набираем в базе данных сами «сырые» значения (не разницы и не ранги!), которые были получены в каждой группе, таким образом, формируются две переменные. Программа сама рассчитывает разницы, присваивает им ранги, выбирает редкий знак, подсчитывает сумму рангов редкого знака и выполняет все остальные расчеты согласно формуле.
Для этого нажимаем команду Analyze, в представленном меню действий выбираем строку, где написано Nonparametric tests, после чего появится список критериев, где надо нажать на строку «2 Related Samples». В появившемся окне следует проверить, активирована ли позиция, в которой указана фамилия Wilcoxon (там должна высвечиваться точка), далее указать путем выбора из списка, с какими переменными произвести расчет критерия.
В примере с эрудитами расчеты в SPSS дали следующие показатели:
z (что соответствует обозначению Тэксп) = — 0,778, sig= 0,436
Здесь следует добавить, что под таблицей с показателем критерия (z) приводятся комментарии, обозначенные буквами «а» и «в». Буквой «а» обозначена та тенденция, которая встречалась редко, т.е. тенденция редкого знака — она учитывалась при расчете показателя критерия Вилкоксона. Буквой «в» обозначается противоположная тенденция (по отношению к редкой), иными словами, доминирующая тенденция. Напомним, что Критерий Вилкоксона, хотя и опирается в расчетах на выраженность редкой тенденции, тем не менее, оценивает достоверность преобладания именно доминирующей тенденции, т.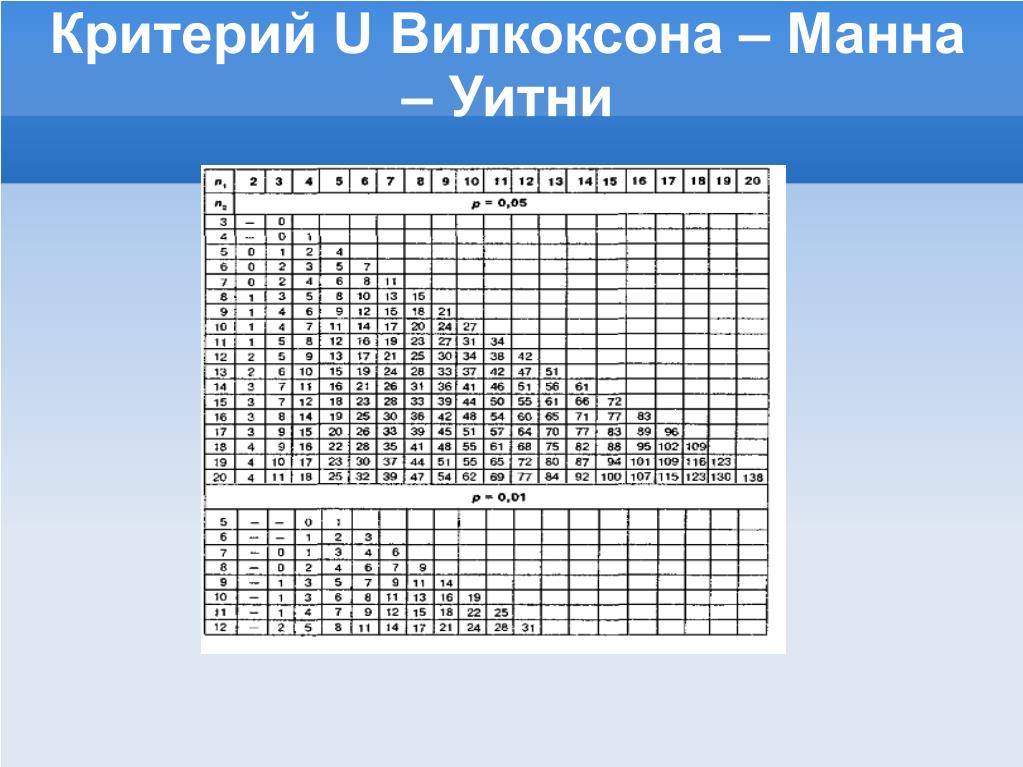
е. тенденции популярного знака, который фигурировал среди разниц, полученных при попарном вычитании V2 — V1. В этой связи вывод по критерию Вилкоксона делается по тенденции, обозначенной буквой «в», а не буквой «а», где указано, на базе каких рангов (положительных или отрицательных) производился расчет данного критерия.
В рассмотренном примере расчеты делались на базе отрицательных рангов, о чем говорится в комментарии под буквой «а». Следовательно, сам критерий надо рассматривать применительно к противоположной тенденции – к положительной (она соответствует «в»).
Если при вычитании из второй переменной первой переменной в большинстве пар получаются в основном знаки «+», значит, 2-я переменная нарастает круче. Но насколько достоверна эта тенденция указывает величина полученного критерия. Поскольку она оказалась меньше критического значения, равного 1,96, то делается вывод об отсутствии достоверных различий между темпами нарастания данных в двух сравниваемых группах.
Этот вывод подтверждается и тем фактом, что уровень ошибочности гипотезы о достоверных различиях составляет 43,6%, — такую гипотезу принять нельзя. Значит, принимаем гипотезу об отсутствии достоверных различий между темпами нарастания результатов в группах участников шоу.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
II. Описание критерия Т Вилкоксона. — Мегаобучалка
Критерий позволяет установить, является ли сдвиг показателей в каком-то направлении более интенсивным, чем в другом.
Значения признака должны варьировать в достаточно большом диапазоне, чтобы можно было говорить об интенсивности.
Суть метода состоит в том, что сопоставляем выраженность сдвигов в том или ином направлении по абсолютной величине.
Для этого 1) находят разность между индивидуальными значениями в первой и во второй выборке, 2) определяют типичный сдвиг и 3) формулируют гипотезы.
Но интенсивность («разница») у типичных может быть меньше, чем у нетипичных сдвигов.
4) Затем абсолютные значения этих разностей ранжируют. Если интенсивность сдвига в одном из направлений больше, то и сумма рангов в этом направлении будет выше.
Тэмп – сумма рангов для нетипичных сдвигов, Тэмп =ΣRi.
Ткр находим по таблице критических значений в зависимости от n. Далее с помощью оси значимости определяем, какую гипотезу принять, а какую отвергнуть. Но так как, чем меньше Тэмп, тем более достоверны различия, зоны на оси значимости поменяются местами. Этот критерий – исключение.
зона значимости зона неопределенности зона незначимости
Н1 р≤0,01 р≤0,05 Н0
Ткрит Ткрит
Ограничения Т-критерия Вилкоксона:
1. Объем выборки должен быть 5≤n≤50.
2. Если количество типичных сдвигов равно количеству нетипичных, то критерий не применяется.
3. Нулевые сдвиги из рассмотрения исключаются.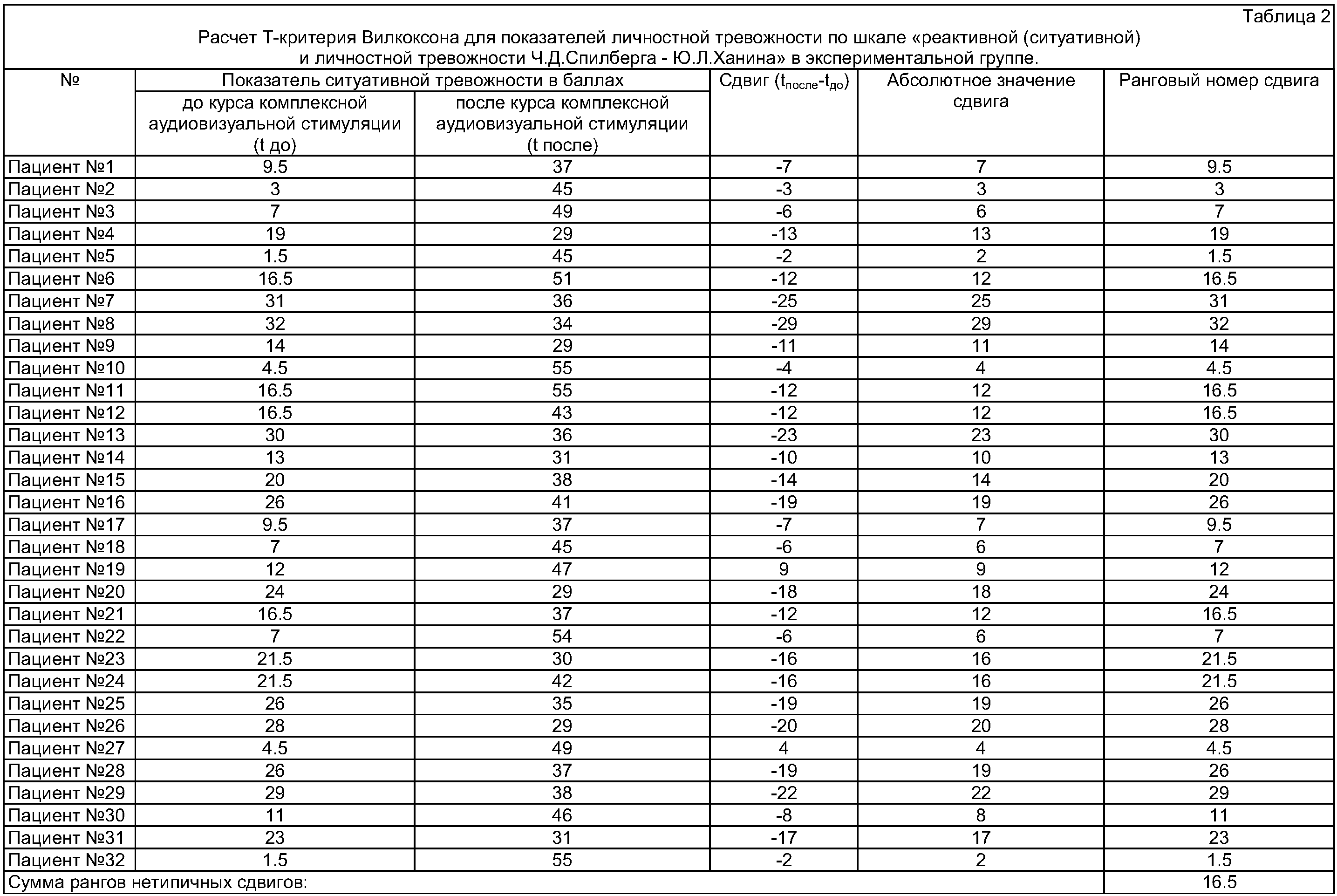
Пример. Психолог проводит групповой тренинг по снижению уровня тревожности. Вопрос: эффективен ли данный вариант тренинга для его участников?
Исследователь дважды выявлял с помощью теста Тейлора уровень тревожности у 14 участников до тренинга и после.
| уровень тревожности до тренинга | уровень тревожности после тренинга | сдвиг | абсол. величина сдвига | ранги |
| -14 +4 +1 +3 -10 -13 -9 -11 -8 +1 +7 -9 -7 | 1,5 8,5 1,5 5,5 8,5 5,5 |
Подсчитывая сдвиги, получаем n0=1, n+=5, n_=8.
Значит, типичные сдвиги – это отрицательные, а нетипичные – положительные.
H0 – уровень тревожности у участников тренинга не снизился.
H1 — уровень тревожности у участников тренинга снизился.
1. Применим критерий G знаков.
Gэмп=5, n=14 – 1=13.
3 (р≤0,05)
G кр=
1 (р≤0,01)
По оси значимости делаем вывод, что принимается гипотеза H0 — уровень тревожности в группе после тренинга не снизился, т.е. данный метод снижения тревожности не эффективен.
Н1 р≤0,01 р≤0,05 Н0
1 3 5
2. Применим критерий Т Вилкоксона.
Сформулируем гипотезы:
H0 – интенсивность сдвигов в сторону уменьшения уровня тревожности не превосходит интенсивности сдвигов в сторону увеличения.
H1 – интенсивность сдвигов в сторону уменьшения уровня тревожности превосходит интенсивности сдвигов в сторону увеличения.
Проранжируем абсолютные значения сдвигов, найдем сумму рангов ΣR=91. Сверим с расчетной суммой Σ R = N(N+1)/2=13(13+1)/2=91.
Выделим нетипичные сдвиги и найдем их сумму рангов.
Тэмп=4+1,5+3+1,5+5,5=15,5.
Для n=13
21 (р≤0,05)
Ткр=
12 (р≤0,01)
По оси значимости делаем вывод, что с уровнем значимости р≤0,05 можно принять гипотезу H1 — уровень тревожности в группе после тренинга не снизился.
Н1 р≤0,01 р≤0,05 Н0
12 21
Таким образом, видим, что когда диапазон значений достаточно большой, то лучше использовать критерий Т.
3. Критерии Фридмана и L Пейджа применяются для сопоставления показателей, измеренных в трех или более условий на одной и той же выборке испытуемых. Но если критерий позволяет установить, что величины показателей от условия к условию изменяются, то критерий L выявляет тенденцию в изменении величин признака при переходе от условия к условию.
Данные выборок для этих критериев должны быть представлены в порядковой, интервальной или шкале отношений.
Гипотезы:
H0 – между показателями, полученными в разных условиях, различия случайны.
H1 – между показателями, полученными в разных условиях, различия не случайны.
Для критерия L их лучше формулировать следующим образом:
H0 – возрастание показателей признака при переходе от первого замера ко второму, от второго к третьему и т.д. случайно.
H1 – возрастание показателей признака при переходе от первого замера ко второму, от второго к третьему и т.д. не случайно.
I. Описание критерия .
Данный критерий является распространением критерия Т на более двух выборок. Но здесь 1) ранжируются не модули сдвигов, а сами индивидуальные значения во всех замерах для каждого испытуемого в отдельности. 2) Затем находятся суммы рангов для каждого условия в отдельности.
Если различия между значениями признака в каждом замере случайны, то и суммы рангов не будут особенно отличаться друг от друга. В противном случае, суммы рангов будут достоверно различаться между собой. Эмпирическое значение указывает на то, насколько различаются суммы рангов, т.е. чем оно больше, тем более существенные различия сумм рангов он отражает.
Правильность ранжирования проверяем, сверяя общую сумму рангов с расчетной Σ R = n , где п- объем выборки, с – число замеров.
Эмпирическое значение находим по формуле
эмп= ΣRi2 — 3n(с+1).
Ограничения -критерия:
1. с≥3, n≥2.
2. Критические значения кр находят по двум таблицам: при с=3, n≤9 и при с=4, n≤4. В других случаях используют таблицу критических значений для распределения χ2 для числа степеней свободы ν=с – 1. Это объясняется тем, что имеет распределение, сходное с распределением χ2.
Подписанный ранговый тест Вилкоксона в сравнении с парным t-критерием Стьюдента
Набор данных сна
Рассмотрим набор данных о сне.
Набор данных противопоставляет эффект двух снотворных препаратов (также известных как снотворные), обеспечивая изменение количества часов сна после приема препарата по сравнению с исходным уровнем:
data (sleep) # загрузить набор данных сна
печать (сон) ## дополнительный идентификатор группы
## 1 0,7 1 1
## 2 -1,6 1 2
## 3 -0,2 1 3
## 4 -1.2 1 4
## 5 -0,1 1 5
## 6 3,4 1 6
## 7 3,7 1 7
## 8 0,8 1 8
## 9 0,0 1 9
## 10 2,0 1 10
## 11 1.9 2 1
## 12 0,8 2 2
## 13 1.1 2 3
## 14 0,1 2 4
## 15 -0,1 2 5
## 16 4,4 2 6
## 17 5,5 2 7
## 18 1,6 2 8
## 19 4,6 2 9
## 20 3,4 2 10 extra указывает увеличение / уменьшение (положительные / отрицательные значения) сна по сравнению с исходным измерением, группа обозначает лекарство, а ID дает идентификатор пациента.Чтобы было понятнее, я переименую группу в лекарство :
. colnames (сон) [which (colnames (sleep) == "group")] <- "drug" Обратите внимание, что набор данных о сне содержит два измерения для каждого пациента.
Таким образом, он подходит для демонстрации парных тестов, таких как те, с которыми мы имеем дело.
Для чего мы тестируем?
Предположим, мы работаем в фармацевтической компании, и это данные, которые были только что получены в ходе клинических испытаний.Теперь мы должны решить, какой из двух препаратов вы должны выпустить на рынок. Разумным способом выбора препарата будет определение препарата, который действует лучше. Более конкретно, вопрос заключается в следующем: связано ли одно из лекарств с более высокими значениями дополнительных , чем другое лекарство?
Чтобы получить интуитивное представление об эффективности двух препаратов, нанесем на график их соответствующие значения:
График показывает, что среднее увеличение времени сна для лекарства 1 близко к 0, в то время как среднее увеличение для лекарства 2 близко к 2 часам.Итак, на основании этих данных кажется, что препарат 2 более эффективен, чем препарат 1. Однако нам все еще необходимо определить, является ли наш результат статистически значимым.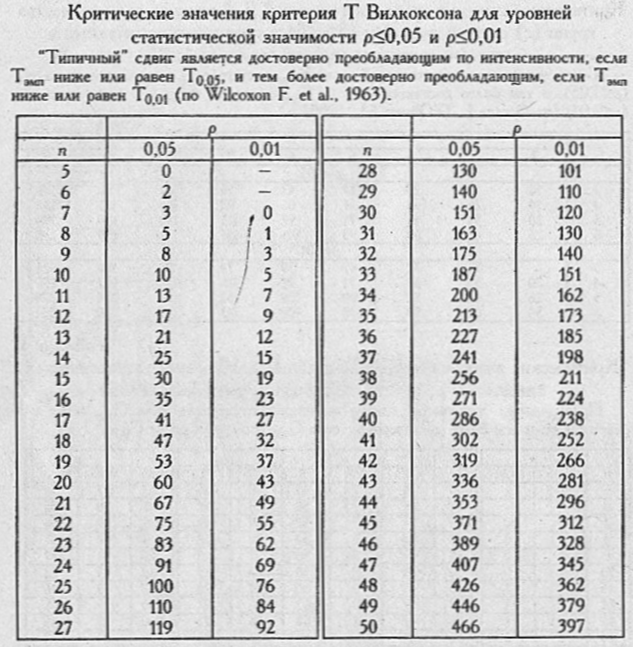
Нулевая гипотеза
Нулевая гипотеза теста состоит в том, что нет никакой разницы в дополнительном времени сна между двумя препаратами. Поскольку мы хотим выяснить, превосходит ли лекарство 2 лекарство 1, нам нужен не двусторонний тест (проверка того, обладает ли какое-либо из лекарств лучшими характеристиками), а односторонний тест.{{N}} [\ operatorname {sgn} (x _ {{2, i}} - x _ {{1, i}}) \ cdot R_ {i}] \]
Здесь \ (i \) - я из \ (N \) пар измерений обозначена \ (x_i = (x_ {1, i}, x_ {2, i}) \) и \ (R_ {i} \ ) обозначает ранг пары. Ранг просто представляет позицию наблюдения в упорядоченном списке \ (| x_ {2, i} - x_ {1, i} | \). Смысл тестовой статистики состоит в том, что пары с большими абсолютными различиями будут иметь большие ранги \ (R_ {i} \). Таким образом, эти пары являются определяющими факторами \ (W \), в то время как пары, демонстрирующие небольшие абсолютные различия, имеют низкое значение \ (R_ {i} \) и, следовательно, мало влияют на результат теста.
Поскольку статистика теста основана на рангах, а не на самих измерениях, знаковый ранговый критерий Вилкоксона можно рассматривать как проверку сдвигов в средних значениях между двумя группами.
Для выполнения теста в R мы можем использовать функцию wilcox.test . Однако мы должны явно установить аргумент парный , чтобы указать, что мы имеем дело с совпадающими наблюдениями. Чтобы указать односторонний тест, мы устанавливаем для аргумента альтернативный значение больше .Таким образом, альтернативой теста является то, связано ли лекарство 2 с большим увеличением продолжительности сна, чем лекарство 1.
x <- sleep $ extra [sleep $ drug == 2]
y <- sleep $ extra [sleep $ drug == 1]
res <- wilcox.test (x, y, paired = TRUE,
альтернатива = "больше") ## Предупреждение в wilcox.test.default (x, y, paired = TRUE, alternate = "больше"):
## не может вычислить точное значение p со связями ## Предупреждение в Уилкоксе. test.default (x, y, пара = ИСТИНА, альтернатива = "больше"):
## не может вычислить точное значение p с нулями 
test.default (x, y, пара = ИСТИНА, альтернатива = "больше"):
## не может вычислить точное значение p с нулями Расследование предупреждений
Прежде чем перейти к результатам, мы должны изучить два предупреждения, возникших в результате выполнения теста.
Предупреждение 1: связи
Первое предупреждение возникает из-за того, что тест ранжирует различия в дополнительных значений пар. Если две пары имеют одинаковую разницу, во время ранжирования возникают ничьи. В этом можно убедиться, вычислив разницу между парами
х - у ## [1] 1.2 2,4 1,3 1,3 0,0 1,0 1,8 0,8 4,6 1,4 и обнаружив, что пары 3 и 4 имеют одинаковую разницу в 1,3. Почему галстуки - проблема? Ранг, присваиваемый связям, основан на среднем рангах, которые они занимают. Таким образом, если имеется много связей, это снижает выразительность статистики теста, делая тест Вилкоксона неуместным. Поскольку у нас здесь только одна ничья, это не проблема.
Предупреждение 2: нулевые значения
Второе предупреждение относится к парам, в которых разница равна 0.В наборе данных о сне это относится к паре от 5-го пациента (см. Выше). Почему проблема с нулями? Помните, что нулевая гипотеза заключается в том, что различия пар сосредоточены вокруг 0. Однако наблюдение различий, когда значение равно 0, не дает нам никакой информации для отклонения нулевого значения. Следовательно, эти пары отбрасываются при вычислении статистики теста. Если это так для многих пар, статистическая мощность теста значительно упадет.Опять же, это не проблема для нас, так как присутствует только одно нулевое значение.
Исследование результатов
Основным результатом теста является его p-значение, которое можно получить через:
res $ p.value ## [1] 0,004545349 Поскольку p-значение меньше 5% уровня значимости, это означает, что мы можем отклонить нулевую гипотезу.
Таким образом, мы были бы склонны принять альтернативную гипотезу, согласно которой лекарство 2 превосходит лекарство 1.
Парный t-критерий Стьюдента
Парный t-критерий Стьюдента - это параметрический тест на основе парных количественных измерений в двух группах. Здесь параметрический означает, что t-критерий предполагает, что средняя разница между выборками распределена нормально. Тест основан на определении того, превышает ли средняя разница измерений в двух группах \ (\ bar {X} _ {D} \) \ (\ mu_D \), где \ (\ mu_D \) обычно устанавливается равным 0, чтобы узнать, есть ли разница.Тест-статистика,
\ [\ displaystyle t = {\ frac {{\ bar {X}} _ {D} - \ mu _ {0}} {\ frac {s_ {D}} {\ sqrt {n}}}}, \ ]
нормализовано с использованием стандартного отклонения разностей \ (s_D \) и количества пар \ (n \). Путем нормализации в соответствии с \ (\ frac {s_D} {\ sqrt {n}} \) тестовая статистика регулирует значение тестовой статистики в соответствии с количеством выборок (\ (| t | \) увеличивается с увеличением количества выборок) и стандартное отклонение разностей (\ (| t | \) уменьшается, если отклонение увеличивается).
В R мы можем выполнить парный t-тест с функцией t.test . Обратите внимание, что t.test предполагает, что дисперсии генеральной совокупности неравны. В этом случае тест также называется t-тест Велча . Чтобы получить исходный t-тест, который предполагает, что дисперсии генеральной совокупности равны, мы можем просто установить для параметра equal.var значение TRUE . Здесь мы просто будем использовать значение по умолчанию:
t.result <- t.test (x, y, пара = ИСТИНА, альтернатива = "больше")
печать (т.результат $ p.value) ## [1] 0,001416445 Опять же, p-значение меньше 0,05. Таким образом, мы были бы склонны принять альтернативную гипотезу: препарат 2 связан с большим увеличением средней продолжительности сна, чем препарат 1.
Проверка предположений t-критерия Стьюдента
t-критерий требует, чтобы средние выборки были распределены нормально.
Согласно центральной предельной теореме, средние значения выборок из совокупности приближаются к нормальному распределению для достаточного количества выборок.Следовательно, предположение о t-критерии выполняется даже для нестандартных измерений, если имеется достаточное количество образцов. Поскольку данные о сне содержат только 10 парных измерений, должны быть основания для беспокойства. Таким образом, мы должны проверить, нормально ли распределены различия между измерениями, чтобы проверить, действителен ли t-тест:
diff.df <- data.frame (diff = sleep $ extra [sleep $ drug == 1] - sleep $ extra [sleep $ drug == 2])
ggplot (diff.df, aes (x = diff)) + geom_histogram () ## `stat_bin ()` с использованием `bins = 30`.Выберите лучшее значение с помощью binwidth. Глядя на гистограмму, данные кажутся скорее равномерно распределенными, чем обычно. Для более детального изучения мы сравниваем различия со значениями, которые можно было бы ожидать от нормального распределения, используя график Q-Q (квантиль-квантиль):
require (car) # load car package, чтобы использовать qqp вместо встроенной функции qqplot ## Загрузка необходимого пакета: вагон ## Загрузка необходимого пакета: carData qqp (разн. df $ diff) 
df $ diff) ## [1] 9 5 График Q-Q показывает, что различия достаточно хорошо соответствуют нормальной модели, за исключением тяжелых хвостов. Из этого мы могли сделать вывод, что предположение t-критерия выполнено в достаточной степени. Тем не менее, у нас остается чувство неуверенности в том, был ли t-тест наиболее подходящим выбором для этих данных.
Резюме: знаковый ранговый критерий Уилкоксона против парного t-критерия Стьюдента
В этом анализе и знаковый ранговый критерий Вилкоксона, и парный t-критерий Стьюдента привели к отклонению нулевой гипотезы.Однако в целом, какой тест более уместен? Ответ: это зависит от нескольких критериев:
- Гипотеза: t-критерий Стьюдента - это критерий сравнения, тогда как критерий Уилкоксона проверяет порядок данных. Например, если вы анализируете данные со многими выбросами, такими как личное богатство (когда несколько миллиардеров могут сильно повлиять на результат), тест Вилкоксона может быть более подходящим.
- Интерпретация: Хотя доверительные интервалы также могут быть вычислены для теста Вилкоксона, может показаться более естественным спорить о доверительном интервале среднего значения в t-критерии, чем о псевдомедиане для критерия Вилкоксона.
- Выполнение предположений: Предположения t-критерия Стьюдента могут не выполняться для малых размеров выборки. В этом случае зачастую безопаснее выбрать непараметрический тест. Однако, если предположения t-критерия выполняются, он имеет большую статистическую мощность, чем критерий Вилкоксона.
Из-за небольшого размера выборки набора данных о сне я предпочел бы для этих данных тест Вилкоксона.
Какой тест вы бы использовали? В общем, вы бы предпочли один тест другому?
Знаковый ранговый тест Уилкоксона| R Учебник
Две выборки данных совпадают, если они получены в результате повторных наблюдений одного и того же
тема.Используя знаковый ранговый тест Вилкоксона, мы можем решить,
соответствующие распределения совокупности данных идентичны, не предполагая, что они
следуйте нормальному распределению.
Пример
Во встроенном наборе данных immer урожай ячменя в 1931 и 1932 гг. то же поле записываются. Данные об урожайности представлены в столбцах Y1 фрейма данных. и Y2.
> Библиотека (MASS) # загружаем пакет MASS> головка (погружная)
Loc Var Y1 Y2
1 UF M 81.0 80,7
2 УФ S 105,4 82,3
.....
Проблема
Не предполагая, что данные имеют нормальное распределение, проверьте уровень значимости 0,05 если урожайность ячменя 1931 и 1932 годов в наборе данных immer имеет одинаковые данные раздачи.
Решение
Нулевая гипотеза состоит в том, что урожайность ячменя за два выборочных года одинакова. населения. Чтобы проверить гипотезу, мы применяем функцию wilcox.test для сравнения совпадающие образцы. Для парного теста мы устанавливаем аргумент «парный» как ИСТИНА.Поскольку p-значение оказывается равным 0,005318, что меньше уровня значимости 0,05, мы отклоняем нулевая гипотеза.
> Wilcox.
test (immer $ Y1, immer $ Y2, paired = TRUE) знаковый ранговый тест Вилкоксона с поправкой на непрерывность
данные: погрузите $ Y1 и погрузите $ Y2
V = 368,5, p-значение = 0,005318
альтернативная гипотеза : True location shift не равен 0
Предупреждающее сообщение:
In wilcox.test.default (immer $ Y1, immer $ Y2, paired = TRUE):
не может вычислить точное p-значение со связями
Ответ
На уровне значимости 0,05 мы заключаем, что урожайность ячменя 1931 и 1932 гг. immer набора данных - это неидентичные популяции.
Mann-Whitney U ve Wilcoxon T Testleri
Ki-Kare Baımsızlık Analizi
Ki-Kare Baımsızlık Analizi Dr.
Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Ki-Kare Baımsızlık Analizi Kikare bağımsızlık analizi, isimsel ya da scıralı 9000 öl
Детайлы
BİYOİSTATİSTİK PARAMETRİK TESTLER
BİYOİSTATİSTİK PARAMETRİK TESTLER Doç. Доктор Махмут АКБОЛАТ * Бир testin kullanılabilmesi için belirli şartların sağlanması gerekir. * Бир тестин, уйгуланабилмеси ичин герекли шартлар; ne kadar çok veya güçlü
ДетайлыSPSS UYGULAMALARI-II Dr.Сехер Ялчин 1
SPSS UYGULAMALARI-II 27.12.2016 Д-р Сехер Ялчин 1 Нормальный Дагилым Варсайыминын Инчеленмеси Чарпиклык ве Басиклык Катсайынын Инчеленмеси Анализировать описательную статистику Descriptive tıklanır. Ачылан пенсереде,
ДетайлыOrtalamaların karşılaştırılması
Parametrik ve Parametrik Olmayan Testler Ortalamaların karşılaştırılması t testleri, ANOVA Mann-Whitney U Testi Wilcoxon İşaretli Sıra Testi Kruskal Wallis Testi BBY606 Araştırma Yöntemlean Güleda Do Детайлы
ÇND BİYOİSTATİSTİK EĞİTİMİ
ÇND BİYOİSTATİSTİK EĞİTİMİ Yrd.
Доктор Гёкмен ЗАРАРСИЗ Эрджиес Юниверситези, Тип Факюльтеси, Бийоистатистик Анабилим Дали, Кайсери Туркоса Аналитик özümlemeler Ltd Şti, Кайсери [email protected]
HİPOTEZ TESTLERİ. Yrd. Doç. Д-р Эмре АТИЛГАН
HİPOTEZ TESTLERİ Yrd. Doç. Доктор Эмре АТИЛГАН Хипотез Недир? HİPOTEZ: параметр hakkındaki bir inanıştır. Parametre hakkındaki inanışı test etmek için hipotez testi yapılır. Hipotez testleri sayesinde örneklemden
ДетайлыParametrik Olmayan İstatistiksel Yöntemler
Parametrik Olmayan İstatistiksel Yöntemler IST-4035 2.Ders DEÜ İstatistik Bölümü 208 Güz One Sample Tests İçerik Непараметрическая статистика Номинальный порядковый интервал Биномиальный тест Тест Колмогрова-Смирнова
ДетайлыФреканы. Гемоглобин Дюзейи
GRUPLARARASI VE GRUPİÇİ KARŞILAŞTIRMA YÖNTEMLERİ Uzm.
Derya ÖZTUNA Yrd. Doç. Д-р Атилла Халил ЭЛЬХАН 1. ÖNEMLİLİK (HİPOTEZ) TESTLERİ Önemlilik testleri, araştırma sonucunda elde edilen değerlerin ya da
İstatistik ve Olasılık
İstatistik ve Olasılık Ders 8: проф.Д-р Таним Хипотез, бир вейа даха фазла анакютле хаккинда илери сурюлен, анджак доğрулугу önceden bilinmeyen iddialardır. Ортая атылан иддиаларин, örnekten elde edilen
ДетайлыSPSS de Tanımlayıcı İstatistikler
SPSS de Tanımlayıcı İstatistikler Doç. Доктор Эртугрул ЧОЛАК Эскишехир Османгази Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı SPSS programında belirtici istatistikler 4 farklı menüden yararlanılarak
ДетайлыПАРАМЕТРИК ОЛМАЯН ТЕСТЛЕР
PARAMETRİK OLMAYAN TESTLER Daha önce incelediğimiz testler, normal dağılmış ana kütleden örneklerin rassal seçilmesi varsayımına dayanmaktaydı ve параметрик testler kullanılmıştı.
Параметрик олмаян тестлер
0.04.03 Standart Hata İstatistikte hesaplanan her istatistik değerin mutlaka hatası da hesaplanmalıdır. Çünkü hesaplanan istatistikler, tahmini bir değer olduğu için mutlaka hataları da vardır. Стандарт
ДетайлыİSTATİSTİKSEL TAHMİNLEME VE HİPOTEZ TESTİ
İSTATİSTİKSEL TAHMİNLEME VE HİPOTEZ TESTİ Bu bölümdeki yötemler, bilimeye POPULASYON PARAMETRE değeri hakkıda; TAHMİN yapmaya yöelik ve, KARAR vermekle ilgili, olmak üzere iki grupta icelemektedir.Параметр
ДетайлыPARAMETRİK OLMAYAN İSTATİSTİKSEL TEKNİKLER 8
ПАРАМЕТРИК ОЛМАЯН İSTATİSTİKSEL TEKNİKLER 8 Проф. Д-р Али ШЕН Ики Популасыонун Каршилаштырилмаси: Эшлештирилмиш Örnekler için Wilcoxon İşaretli Mertebe Testi -RÜNIÜK Детайлы
BİYOİSTATİSTİK TABLO VE FRAFİK YAPIMI
BİYOİSTATİSTİK TABLO VE FRAFİK YAPIMI B Doç.
Д-р Махмут АКБОЛАТ * Табло, араштырма сонукунда старейшина Эдилен билгилерин сайисал оларак * анлашилабилир бир нителикте сунулмасины саğлайан бир арачтыр. * Таблода
İstatistik Yöntemleri ve Hipotez Testleri
Sağlık Araştırmalarında Kullanılan Temel İstatistik Yöntemleri ve Hipotez Testleri Yrd. Doç. Доктор Эмре АТИЛГАН BİYOİSTATİSTİK İstatistiğin biyoloji, tıp ve diğer sağlık bilimlerinde kullanımı biyoistatistik
ДетайлыHipotez Testleri.Параметрик Тестлер
Hipotez Testleri Parametrik Testler Hipotez Testide Adımlar Bir araştırma sorusuu belirlemesi Araştırma sorusua dayaa istatistiki hipotezleri oluşturulması (H 0 ve H A) Hedef populasyoda öreklemi elde
elde ДетайлыПараметрик Олмаян Тестлер
Araştırma Yöntemleri Parametrik Olmayan Testler Parametrik Olmayan Testler Verilerin normal dağılmış olması gerekmiyor Veriler sınıflama ya da sıralama ölçme düzeyinde toplanmış olacak Da eşı aralık Детайлы
OLASILIK ve İSTATİSTİK Hipotez Testleri
OLASILIK ве İSTATİSTİK Hipotez Testleri Yrd.
Док. Pınar YILDIRIM Okan Üniversitesi Mühendislik ve Mimarlık Fakültesi Bilgisayar Mühendisliği Bölümü Hipotezler ve Testler Hipotez, kitleye (yığına) ait
İstatistik ve Olasılık
İstatistik ve Olasılık Ders 9: Проф. Д-р Ирфан КАЙМАЗ Таним Хипотез, бир вейа даха фазла анакютле хаккинда илери сурюлен, анджак догрулугу önceden bilinmeyen iddialardır. Ортая атылан iddiaların, örnekten
ДетайлыBÖLÜM 13 HİPOTEZ TESTİ
1 BÖLÜM 13 HİPOTEZ TESTİ Bilimsel yöntem aşamalarıyla tanımlanmış sistematik bir bilgi üretme biçimidir.Bilimsel yöntemin aşamaları aşağıdaki gibi sıralanabilmektedir (Карасар, 2012 г.): 1. Бир проблема
ДетайлыТекрарлы Олчюмлера ANOVA
Tekrarlı Ölçümler ANOVA Повторные измерения ANOVA Aynı veya ilişkili örneklemlerin tekrarlı ölçümlerinin ortalamalarının aynı olup olmadığını test eder.
Farklı zamanlardaki ölçümlerde aynı (ilişkili) kişiler
İSTATİSTİK II.Hipotez Testleri 1
İSTATİSTİK II Hipotez Testleri 1 1 Hipotez Testleri 1 1. Hipotez Testlerinin Esasları 2. Ortalama ile ilgili bir iddianın testi: Büyük örnekler 3. Ortalama ile ilgili bir iddianın testi: Küneçük 9000 ör5000 Детайлы
Parametrik Olmayan İstatistik
Parametrik Olmayan İstatistik 2 Anakütlenin Karşılaştırılması İki Anakütlenin Karşılaştırılması Bağımsız Örnekler Eşleştirilmiş Örnekler Вилкоксона Mertebe Toplam Тести Тести İşaret Вилкоксона İşaretli Mertebe
ДетайлыBÖLÜM 12 STUDENT T DAĞILIMI
1 BÖLÜM 12 СТУДЕНТ Т ДАГИЛИМИ 'Студент т дагылымы' я да кышача 'т дагилими'; normal dağılım ve Z daılımının da içerisinde bulunduğu 'sürekli olasılık dağılımları' ailesinde yer alan dağılımlardan bir
ДетайлыMerkezi Yıılma ve Daılım Ölçüleri
1.
11.013 Merkezi Yıılma ve Dağılım Ölçüleri 4.-5. hafta Merkezi eğilim ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, Hangi değer etrafında toplandığını gösteren ve veri grubunu
İkiden Çok Grup Karşılaştırmaları
İkiden Çok Grup Karşılaştırmaları Bir onkoloji kliniğinde göğüs kanseri tanısı almış kadınlar arasından histolojik evrelerine göre 17 şer kadın seçilerek sağkalım sürelerını.HİSTLOJİK EVRE
ДетайлыТЕМЕЛ КАВРАМЛАР Тест -1
ТЕМЕЛ КАВРАМЛАР Тест -1 1. 6 () 4 A) B) 3 C) 4 D) 5 E) 6 5. 4 [1 (3). (8)] A) 4 B) C) 0 D) E) 4. 48: 8 5 A) 1 B) 6 C) 8 D) 1 E) 16 6. 4 7 36: 9 18: 3 A) 1 Б) 8 В) Г) 4 Д) 8 3. (4: 3 + 1): 4 А) 3 Б) 5
ДетайлыPARAMETRİK OLMAYAN İSTATİSTİKSEL TEKNİKLER 6
ПАРАМЕТРИК ОЛМАЯН İSTATİSTİKSEL TEKNİKLER 6 Проф.
Д-р Али ШЕН 1 ики populasyon karşılaştırılırken her iki örneklemin hacmi n1 ve n2, 10 дан büyükse TA nın dağılışı ortalaması ve varansı aşağıdaki gösterilen
İçindekiler. Ön Söz ... xiii
İçindekiler Ön Söz ............................................... ..... xiii Bölüm 1 İstatistiğe Giriş ....................................... 1 1.1 Гириш ...................................................... 1
ДетайлыParametrik Olmayan İstatistiksel Yöntemler
Parametrik Olmayan İstatistiksel Yöntemler IST-4035 1. Ders DEÜ İstatistik Bölümü 2018 Güz 1 Dersin Amacı Yaygın olarak kullanılan параметрик olmayan istatistiksel yöntemleri tanıtmaktı. Темел каврамларин
ДетайлыSÜREKLĠ OLASILIK DAĞILIMLARI
SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır.
Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
Знаковый ранговый тест Вилкоксона - Справочник по биологической статистике
⇐ Предыдущая тема | Следующая тема ⇒
Содержание
Сводка
Используйте знаковый ранговый тест Уилкоксона, если вы хотите использовать парный тест t , но различия сильно не распределены нормально.
Когда использовать
Используйте знаковый ранговый критерий Уилкоксона, когда есть две номинальные переменные и одна переменная измерения.Одна из номинальных переменных имеет только два значения, например «до» и «после», а другая номинальная переменная часто представляет людей. Это непараметрический аналог парного t –теста, и вы должны использовать его, если распределение различий между парами сильно отличается от нормального.
Например, Laureysens et al. (2004) измерили содержание металлов в древесине 13 клонов тополя, произрастающих на загрязненной территории, один раз в августе и один раз в ноябре.
Концентрации алюминия (в микрограммах Al на грамм древесины) показаны ниже.
| Клон | август | ноябрь | август-ноябрь | ||
|---|---|---|---|---|---|
| Река Колумбия | 18,3 | 12,7 | -5,6 | Fritz4 | 4 9037 9037 | 4 | Hazendans | 16,5 | 15,3 | -1,2 |
| Primo | 12,6 | 12,7 | 0,1 | ||
| Raspalje | 9.5 | 10,5 | 1,0 | ||
| Hoogvorst | 13,6 | 15,6 | 2,0 | ||
| Шпилька бальзама | 8,1 5,3 | 11,2 | 8,1 2,1 | ||
| Beaupre | 10,0 | 16,3 | 6,3 | ||
| Unal | 8,3 | 15,5 | 7,2 | ||
| Trichobel | 9 | 19,9 | 12,0 | ||
| Gaver | 8,1 | 20,4 | 12,3 | ||
| Wolterson | 13,4 | 36,8 | 4 23,4 905 из двух или ноябрь) и клон тополя (Columbia River, Fritzi Pauley и т. д.) и одну переменную измерения (микрограммы алюминия на грамм древесины). Различия несколько искажены; клон Wolterson, в частности, имеет гораздо большее различие, чем любой другой клон.На всякий случай авторы проанализировали данные с помощью знакового рангового теста Уилкоксона, и я буду использовать его в качестве примера.Нулевая гипотезаНулевая гипотеза состоит в том, что медианная разница между парами наблюдений равна нулю. Обратите внимание, что это отличается от нулевой гипотезы парного t –теста, которая заключается в том, что среднее значение разницы между парами равно нулю, или от нулевой гипотезы знакового теста, заключающейся в том, что количество различий в каждом направлении равны. Как это работает Оцените абсолютное значение различий между наблюдениями от наименьшего к наибольшему, причем наименьшее различие получит ранг 1, затем следующее большее различие получит ранг 2 и т. Д. Присвойте средние ранги связям. ПримерыГолова индейки.Buchwalder и Huber-Eicher (2004) хотели узнать, будут ли индейки менее агрессивными по отношению к незнакомым особям, если их содержат в больших загонах. Они протестировали 10 групп по три индейки, которые были выращены вместе, представив незнакомую индейку и затем подсчитав, сколько раз ее клевали в течение периода тестирования.Каждую группу индеек тестировали в маленьком и большом загоне. Есть две номинальные переменные, размер загона (маленький или большой) и группа индюков, и одна переменная измерения (количество клевков за тест). Медианная разница между количеством клевков за тест в маленькой ручке и большой ручке была значительно больше нуля (W = 10, P = 0,04). Ho et al. (2004) вставили пластмассовый имплантат в мягкое небо 12 хронических храпящих людей, чтобы посмотреть, уменьшит ли он громкость храпа.Громкость храпа оценивалась спящим партнером храпящего по субъективной 10-балльной шкале. Есть две номинальные переменные: время (до операций или после операции) и индивидуальный храпящий, а также одна переменная измерения (громкость храпа). Один человек покинул исследование, и имплант выпал из неба у двух человек; у оставшихся девяти человек среднее изменение громкости храпа значительно отличалось от нуля (W = 0, P = 0,008). Графическое изображение результатовВы должны изобразить данные для знакового рангового теста Уилкоксона таким же образом, как и данные для парного теста t , гистограммы с рядом значений для каждой пары или различиями в каждой пара. Подобные тестыВы можете анализировать парные наблюдения измеряемой переменной с помощью парного t –теста, если нулевая гипотеза состоит в том, что средняя разница между парами наблюдений равна нулю, а различия распределены нормально. Если у вас есть большое количество парных наблюдений, вы можете построить гистограмму различий, чтобы увидеть, выглядят ли они нормально распределенными. Парный тест t не очень чувствителен к ненормальным данным, поэтому отклонение от нормального должно быть довольно значительным, чтобы сделать парный тест t неприемлемым. Используйте знаковый тест, когда нулевая гипотеза состоит в том, что существует равное количество различий в каждом направлении, и вас не волнует размер различий. Как сделать тестТаблицаЯ подготовил электронную таблицу для проведения знакового рангового теста Вилкоксона. Он будет обрабатывать до 1000 пар наблюдений. Интернет-страницаСуществует веб-страница, на которой выполняется тест Уилкоксона с ранговым знаком. Вы можете ввести свои парные номера прямо на веб-страницу; будет проще, если вы сначала введете их в электронную таблицу, а затем скопируете и вставите на веб-страницу. RSalvatore Mangiafico R Companion содержит образец программы R для знакового рангового теста Вилкоксона. SASЧтобы выполнить знаковый ранговый тест Уилкоксона в SAS, вы сначала создаете новую переменную, которая представляет собой разницу между двумя наблюдениями. Затем вы запускаете PROC UNIVARIATE для разницы, которая автоматически выполняет тест Уилкоксона с ранговыми знаками вместе с несколькими другими. Вот пример с использованием данных тополя сверху: СООБЩЕНИЯ ДАННЫХ; INPUT clone $ augal noval; diff = augal - новаль; ДАТАЛИНЫ; Бальзам Шпиль 8.1 11,2 Бопре 10,0 16,3 Хазенданс 16,5 15,3 Хугворст 13,6 15,6 Распалье 9,5 10,5 Унал 8,3 15,5 Columbia_River 18,3 12,7 Fritzi_Pauley 13,3 11,1 Трихобель 7,9 19,9 Гавер 8,1 20,4 Гибек 8,9 14,2 Primo 12,6 12,7 Уолтерсон 13,4 36,8 ; ОБЪЕДИНЕННЫЕ ДАННЫЕ ПРОЦЕССА = тополя; VAR diff; БЕЖАТЬ; PROC UNIVARIATE возвращает набор описательной статистики, которая вам не нужна; результат знакового рангового теста Вилкоксона показан в строке "Знаковый ранг":
Тесты для определения местоположения: Mu0 = 0
Test -Statistic- ----- Значение p ------
Студенческий т т -2.3089 Pr> | t | 0,0396
Знак М -3,5 Pr> = | M | 0,0923
Знаковый ранг S -29,5 Pr> = | S | 0,0398
Список литературыИзображение головы индейки из 4-H Poultry Университета штата Огайо. Buchwalder, T., and B. Huber-Eicher. 2004. Влияние увеличения площади пола на агрессивное поведение самцов индеек ( Melagris gallopavo ). Прикладная наука о поведении животных 89: 207-214. Хо, В.К., В.И. Вэй, К.Ф. Чанг.2004. Управление тревожным храпом с помощью небных имплантатов: пилотное исследование. Архивы отоларингологии хирургии головы и шеи 130: 753-758. Laureysens, I., R. Blust, L. De Temmerman, C. Lemmens и R. Ceulemans. 2004. Клональные вариации в накоплении тяжелых металлов и производстве биомассы в культуре тополя под поросльем. I. Сезонные колебания концентрации листьев, древесины и коры. Загрязнение окружающей среды 131: 485-494. ⇐ Предыдущая тема | Следующая тема ⇒ |
Сложите ранги всех различий в одном направлении, затем сложите ранги всех различий в другом направлении. Меньшая из этих двух сумм - это тестовая статистика W (иногда обозначается символом T s ). В отличие от большинства статистических данных тестов, меньших значений W менее вероятны при нулевой гипотезе.Для примера алюминия в древесине среднее изменение с августа по ноябрь (3,1 микрограмма Al / г древесины) значительно отличается от нуля (W = 16, P = 0,040).