Тест манна уитни онлайн: Расчет критерия Манна-Уитни

Содержание

Онлайн расчет критерия U-Манна-Уитни

Онлайн калькулятор непараметрического критерия U Манна-Уитни позволяет получить расчет сразу на сайте. Итоговое описание состоит из таблиц, графиков и текстовых выводов. Его можно сказать в формате Word, а таблицы в Excel.

Шаг 1. Введите название исследуемой шкалы

Шаг 1.1. Вы можете внести несколько названий шкал для исследования критерия Манна-Уитни

Шаг 2. Внесите название ПЕРВОЙ группы, количество человек в ней и нажмите на кнопку «Внести данные»

Шаг 2.1. Появится таблица с пустыми ячейками

Шаг 2.2. Внесите исходные данные группы

Вы можете внести данные для расчета критерия U-Манна-Уитни поочередно вручную или скопировать их из вашего Excel файла.

Шаг 3. Внесите название ВТОРОЙ группы, количество человек в ней и нажмите на кнопку «Внести данные»

Шаг 3.1. Появится таблица с пустыми ячейками

Шаг 3.2. Внесите исходные данные группы

Вы можете внести данные поочередно вручную или скопировать их из вашего Excel файла.

Шаг 4. Проверяем исходные данные

Именно по ним будет осуществляться, расчет всех показателей. В случае необходимости можно вернуться на предыдущие шаги и изменить данные.

Шаг 5. Краткий отчет по Манна-Уитни

Для незарегистрированных пользователей доступен только краткий отчет-таблица в которой указано — эмпирическое значение критерия и уровень значимости.

Если вы разбираетесь в статистике, этих данных хватит вам, чтобы сделать вывод о наличии/отсутствии различий между группами.

Шаг 5.1. Регистрация / Авторизация

Для того, чтобы получить более полный отчет с информацией о средних значениях с указание различий нужно зарегистрироваться в сервисе.

Вы можете зарегистрироваться используя свою почту или профиль ВКонтакте.

Шаг 6. Обычный отчет

После регистрации вам станет доступен более полный отчет в котором содержится информация о:

средних значениях в каждой группе
эмпирическое значении критерия
уровне значимости критерия
звездочкой в таблице указаны шкалы, по которым есть различия (в нашем примере это «Интеллект» и «Физическая агрессия»).

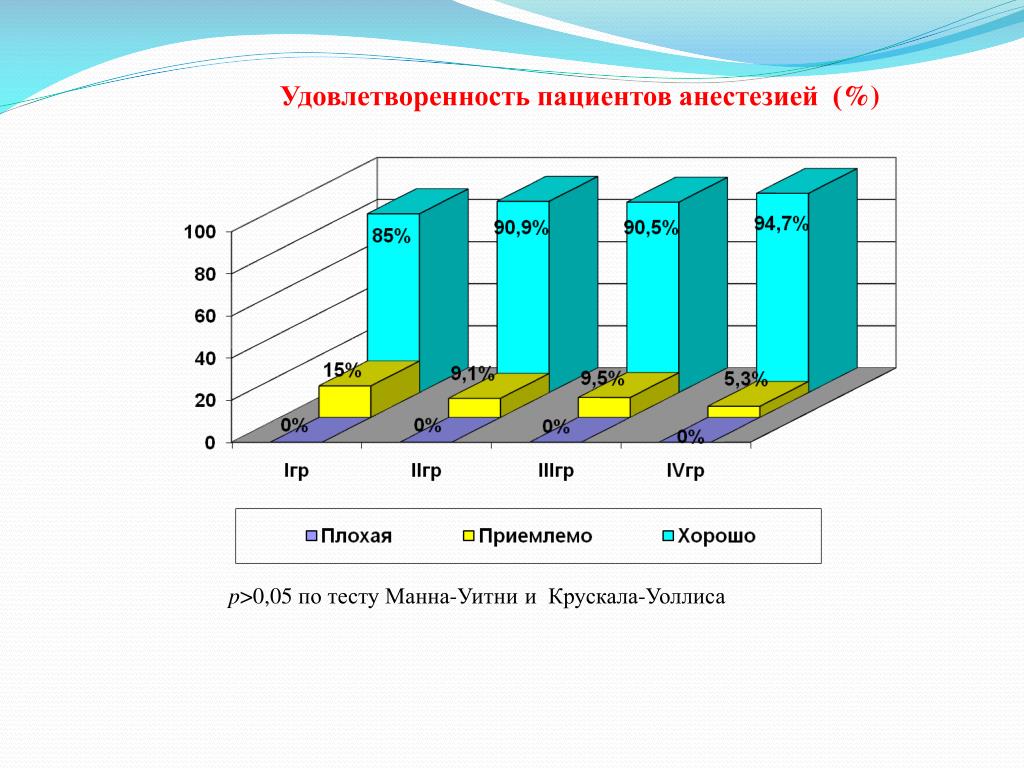
Также вы можете скачать итоговую таблицу в формате Excel.

Вы также можете получить подробный отчет в котором будут графики и нужные текстовые описания, для этого нужно оплатить работу сервиса.

Шаг 7. Полный статистический отчет

После оплаты, в течении суток, вы сможете неограниченное количество раз запускать калькулятор и получать итоговые расчеты.

В полном отчете доступно:

названия шкал,
средние значения по каждой шкале,
эмпирические значения критерия,
уровень значимости с отметкой о наличии различий,
описание различий,
описание выраженности значений в каждой группе,
графики «ящики-усы»
возможность скачать результаты одним файлом Word c указанием всех таблиц, графиков и описаний

В случае, если результаты расчетов вас не устроят, мы гарантируем, что бесплатно внесем все необходимые правки в вашу работу.

БиоСтатистика — 07. Тема 4 (продолжение). Непараметрические критерии для сравнения выборок

4.8. Непараметрические аналоги параметрических методов

Параметрические критерии, которые мы рассматривали до сих пор, основаны на том, что сравниваемые выборки можно охарактеризовать двумя параметрами: средним и стандартным отклонением (или какой-то иной мерой изменчивости). А что делать, если распределение в выборках (или, точнее, в той генеральной совокупности, откуда были получены эти выборки) является совсем иным?

Если численность каждой из сравниваемых выборок достаточно велика (больше ста), параметрические критерии можно использовать все равно. Какое бы распределение ни имели эти выборки, их средние «ведут себя» примерно так же, как средние выборок с нормальным распределением. Однако если численность выборок более низкая, следует использовать непараметрические критерии.

Например, непараметрическим аналогом t-критерия Стьюдента является U-критерий Манна-Уитни. Критерий Стьюдента построен на основе распределения, которое описывает отклонения среднего значения выборки определенной численности вокруг генеральной средней нормально распределенной величины . Чем сильнее отклонение от , тем ниже вероятность того, что оно получилось в силу случайности при формировании выборки. А как действовать, если мы ничего не знаем о характере распределения генеральных совокупностей?

Рассмотрим достаточно простой пример, поясняющий, как работает большая группа непараметрических методов, — ранговые критерии. У нас есть две выборки. Расположим их элементы в порядке возрастания: первая — a1, a2, a3, a4, a5; вторая — b1, b2, b3, b4, b5, b6. Составим из элементов этих выборок общий ряд, построенный в порядке возрастания их значений. Сравним три разных случая:
№ 1: a1, a2, a3, a4, a5, b1, b2, b3, b4, b5, b6;
№ 2: a1, a2, a3, a4, b1, a5, b2, b3, b4, b5, b6;
№ 3: b1, a1, b2, a2, b3, a3,b4, b5, a4, a5, b6.

В случае № 1 все элементы одной выборки расположены с одной стороны общего ряда, а все элементы другого ряда — с другой стороны. В случае № 2 одной перестановки (элементов b1 и a5) было бы достаточно, чтобы порядок элементов стал, как в случае № 1. Наконец, в случае № 3 элементы двух выборок перепутаны, и чтобы выстроить их в ряд, где будут сначала стоять одни, а потом — другие, надо сделать 5 перестановок. Нам нужно выбрать между альтернативной гипотезой (согласно которой выборки a и b взяты из разных совокупностей) и нулевой гипотезой (согласно которой эти выборки взяты из одной совокупности). Одинаковы ли вероятности альтернативной и нулевой гипотез для показанных нами трех разных случаев? Нет; альтернативная гипотеза более вероятна в первом случае, а нулевая — в третьем.

Идея рангового непараметрического критерия состоит в том, что мы можем использовать количество необходимых перестановок как меру для оценки нулевой и альтернативной гипотезы. Конкретные величины, которые высчитываются при применении непараметрических критериев, оказываются иными, но логика сравнения примерно соответствует рассмотренному нами примеру.

Итак, благодаря применению остроумных подходов, для параметрических методов сравнения выборок подобраны их непараметрические аналоги (табл. 4.8.1). Чаще всего непараметрические методы обладают меньшей мощностью (т.е. чаще отвергают альтернативную гипотезу в той ситуации, когда она на самом деле верна), но зато позволяют работать с разнообразно распределенными данными и менее чувствительны к малой численности сравниваемых выборок.

Таблица 4.8.1. Непараметрические аналоги параметрических методов

Тип сравнения	Параметрические методы	Непараметрические методы
Сравнение значений величины в двух независимых выборках	t-критерий Стьюдента; Дисперсионный анализ (ANOVA)	U-критерий Манна-Уитни; Критерий серий Вальда-Вольфовица; Двухвыборочный критерий Колмогорова-Смирнова
Сравнение значений величины в двух зависимых выборках	t-критерий Стьюдента для парных сравнений	Критерий знаков Критерий Вилкоксона
Сравнение значений величины в нескольких независимых выборках	Дисперсионный анализ (ANOVA)	Ранговый дисперсионный анализ Краскела-Уоллиса; Медианный тест

4.

9. U-критерий Манна-Уитни

Чтобы рассмотреть применение критерия Манна-Уитни на нашем файле-примере Pelophylax_example.sta нам придется использовать несколько искуственный пример. В качестве примера величины, распределение которой сильно отличается от нормального, мы можем использовать признак, который называется DNA — содержание ДНК на клетку (в пикограммах, пг), измеренное с помощью проточной ДНК-цитометрии.

Рис. 4.9.1. Признак «DNA» имеет распределение, резко отличающееся от нормального

Выясним, отличаются ли по значению этого признака самки и самцы Pelophylax esculentus. Чтобы воспользоваться критерием Манна-Уитни перейдем в меню Statistics / Nonparametrics. Обратите внимание на пиктограммы в меню: они соответствуют тем, которые используются для аналогичных сравнений с помощью t-теста.

Рис. 4.9.2. U-критерий Манна-Уитни вычисляется здесь

В диалоговом окне надо указать зависимую (Dependent) и группирующую (Grouping) переменные; если группирующая переменная имеет более двух значений, надо выбрать те два значения, которым будут соответствовать сравниваемые выборки.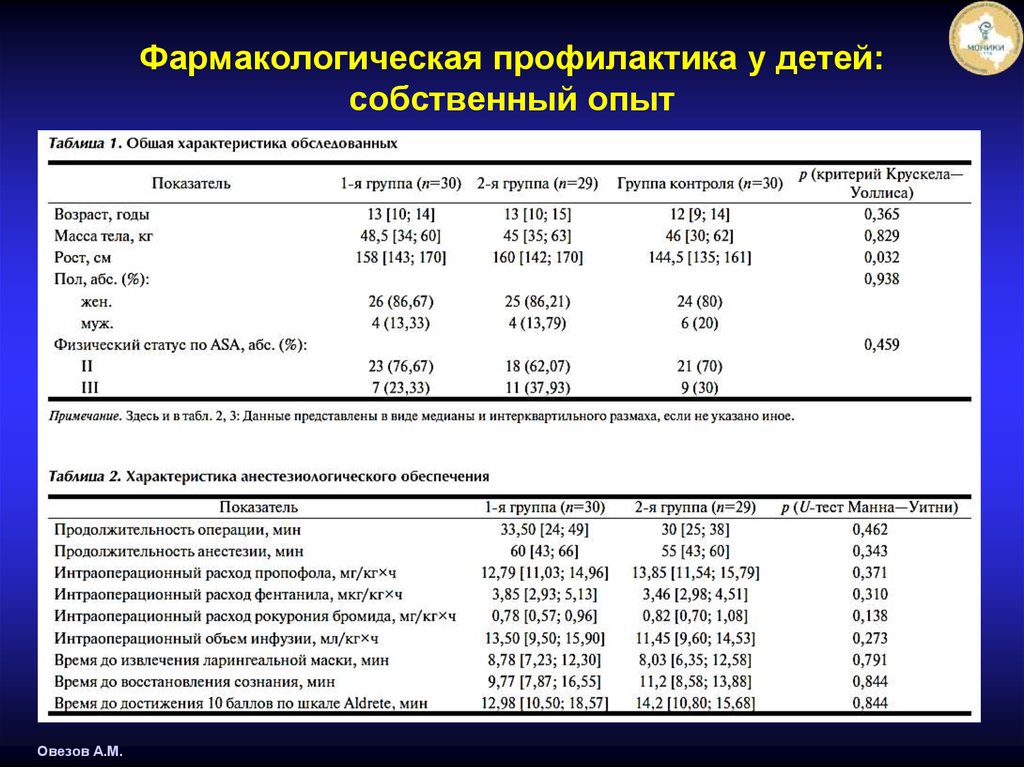 Чтобы выбрать только представителей Pelophylax esculentus, воспользуемся окошком Select cases и используем текстово-цифровые обозначения, введенные в пункте 3.1, при описании файла-примера.

Рис. 4.9.3. Установки, выбираемые для описываемого сравнения

Вы можете увидеть, что Statistica вычисляет все три упомянутых в табл. 4.9.1. критерия, которые используются для сравнения двух независимых выборок, но «рекомендует» (запускает с кнопки, расположенной в левом верхнем углу) критерий Манна-Уитни. Вычислим его и убедимся, что отличия между самками и самцами по количеству ДНК, приходящемуся на клетку, статистически незначимы.

Рис. 4.9.4. Результат сравнения по Манну-Уитни

Если нас не интересует односторонний критерий, целесообразно использовать значение p, вычисленное с поправкой (то, которое находится после столбца «Z adjusted, т.е. 0,906780). Эта поправка повыщает мощность критерия в случае выборок, численность которых превышает 20. Так или иначе, никакой сколь-нибудь существенной разницы между самцами и самками не обнаружено.

Использованный нами диалог для сравнения по Манну-Уитни предусматривает возможность построения коробчатых графиков. Поскольку мы используем непараметрический метод, на графике не тражаются параметры выборки (например, ее среднее значение), а используются непараметрические меры — медиана и квартили (значения, «отрезающие» по четвертой части распределения).

Рис. 4.9.5. Графическое сравнение распределений значения признака DNA для самок и самцов Pelophylax esculentus

Может показаться странным, почему первая (от Min до 25%) и последняя (от 75% до Max) четверти настолько уже, чем вторая и третья? Чтобы это понять, построим категоризованную гистограмму.

Рис. 4.9.6. Гистограмма, показывающая распределения значения признака DNA, зарегистрированные для самок и самцов Pelophylax esculentus

Становится понятно, что удивившее нас свойство показанных на предыдущем рисунке распределений является следствием бимодальности рассматриваемого нами признака.

4.10. Критерий знаков для парных сравнений

В нашем файле-примере Pelophylax_example.sta отсутствуют данные, которые требуют сравнения значений двух связанных выборок, поэтому мы создадиим их искусственно. Представим себе, что выборку из 25 лягушек измерили два человека. Их результаты измерений находятся в столбцах First и Second. Размерное распределение в данной выборке изначально было далеким от нормального.

Рис. 4.10.1. Распределение размеров лягушек (в 0,1 мм) по данным измерений, выполненных двумя людьми на одном и том же материале

Тем не менее, для многих из лягушек результаты измерений, сделанных первым и вторым исследователем, отличаются. Наша задача — установить, одинаково ли измеряют длину лягушек два исследователя. Для поиска ответа на этот вопрос воспользуемся критерием знаков.

Рис. 4.10.2. Использование критерия знаков для сравнения результатов измерений, сделанных двумя разными исследователями

Критерий знаков попросту определяет долю случаев, в которых значение из одной выборки больше, чем значение из другой выборки.

Рис. 4.10.3. Отличия статистически значимы!

Мы можем установить, что второй исследователь статистически значимо чаще завышал результаты измерений по сравнению с первым исследователем.

Сравним полученный результат с результатом от использования параметрического метода — t-критерия для парных выборок.

Рис. 4.10.4. Параметрический метод дал тот же результат, но с несколько большей надежностью

Более низкое значение p, определенное с помощью параметрического критерия, вполне согласуется с упомянутым выше фактом, что параметрические методы обладают большей мощностью, чем непараметрические. Но правомочно ли мы использовали параметрический критерий? На самом деле, правомочно. Парные сравнения рассматривают не совокупность значений в первой и второй выборке, а разницу по каждому элементу между первой и второй выборкой. Построим распределение разницы между выборками First и Second.

Рис. 4.10.5. Распределение разницы между измерениями двух исследователей

Можно увидеть, что отклонение распределения разницы между двумя измерениями от нормального является статистически незначимым. Использование параметрического теста было вполне правомочным.

А могли ли мы использовать методы для сравнения независимых выборок? В случае сравнения независимых выборок то, что распределение интересующих нас величин сильно отличается от нормального, оказывается важным. Таким образом, мы должны использовать не t-критерий, а U-критерий. Для того, чтобы использовать U-критерий Манна-Уитни, файл с данными придется перестроить: все измерения должны находиться в одном столбце, а второй столбец станет группирующим.

Рис. 4.10.6. По Манну-Уитни результаты измерений, выполненных двумя разными людьми, не отличаются

Как пояснить такое отличие? Как и во многих других случаях, первое, что нужно сделать в случае какого-то непонимания — надо посмотреть на распределение интересующих нас величин.

Рис. 4.10.7. Распределения результатов измерений, выполненных двумя людьми, практически одинаковы. Но, все-таки, как свидетельствует рис. 4.10.3, для 75% лягушек результаты измерения второго исследователя оказываются большими, чем результаты измерения первого исследователя!

Конечно, полученный результат вполне закономерен. Используя критерий Манна-Уитни вместо критерия знаков (или критерия Вилкоксона), мы утратили важнейшую информацию, характеризующую закономерности изменений рассматриваемой нами величины.

Кстати, использованные нами данные были сгенерированы искусственно. Столбец First был фрагментом из файла Pelophylax_example.sta, куда попали в основном самые мелкие и самые крупные особи, а столбец Second был получен с помощью формулы =Trunc(First-2,4+Rnd(8)). Вам ведь понятно, что и как «делает» эта формула?

4.11. Ранговый дисперсионный анализ Краскела-Уоллиса

До нестоящего времени мы использовали только попарные сравнения выборок. Сейчас мы рассмотрим метод, позволяющий сравнивать друг с другом одновременно несколько выборок. Тест Краскела-Уоллиса является непараметрическим аналогом дисперсионного анализа (ANOVA), который подробно обсуждается в следующем разделе нашего пособия. С вычислительной точки зрения он является многомерным обобщением теста Манна-Уитни. Хотя тест Краскела-Уоллиса в некоторых отношениях и уступает дисперсионному анализу (например, в том, что не позволяет одновременно оценивать действия двух или большего количества факторов), он является мощным инструментом, который оказывается пригодным для решения многих задач.

Покажем действие теста Краскела-Уоллиса на примере нашего файла Pelophylax_example.sta (см. пункт 3.1). Нам надо выяснить, отличаются ли представители разных генотипов по длине внутреннего пяточного бугра статистически значимо. Это вполне осмысленная задача, ведь размер и форма внутреннего пяточного бугра являются важным диагностическим признаком, полезным для определения разных форм зеленых лягушек.

Рис. 4.11.1. Обратите внимание на выделенную пиктограмму, соответствующую сравнению нескольких независимых групп

Естественно, что зависимой переменной является длина пяточного бугра (Ci), а группирующей — генотип.

Рис. 4.11.2. Установки выбраны. Если надо сравнивать не все значения группирующей переменной, следует воспользоваться диалогом, который вызывает кнопка Code

Нажав на кнопку Summary, вы получите результаты сразу двух тестов: непараметрического дисперсионного анализа Краскела-Уоллиса и медианного теста, который основан на методе Пирсона. Использование подробнее обсуждается в одной из следующих глав данного пособия, а здесь достаточно сказать, что этот метод используется для непараметрического сравнения распределений. Если распределения зависимой величины для разных групп, выделенных по значению группирующего признака, оказываются различными, это свидетельствует о том, что группирующая и зависимая переменная связаны. Метод же Краскела-Уолиса, как вы помните, относится к ранговым непараметрическим методам. Эти два метода работают по разным принципам и часто дают достаточно сильно отличающиеся результаты.

Рис. 4.11.3. Оба метода демонстрируют статистически значимое влияние группирующей переменной на зависимую переменную. Метод Краскела-Уоллиса дает p=0,0047, а медианный тест — p=0,0112

Обратите внимание: в силу какого-то непонятного снобизма в некоторых окнах программы Statistica 0 перед десятичным разделителем (при используемых настройках операционной системы — запятой) не ставится.

Нажав на кнопку Multiple comparisons of mean ranks for all groups можно получить результаты попарного сравнения всех групп. Фактически, это эквивалентно выполнению сравнения по Манну-Уитни для всех возможных пар групп. Программа при этом выводит два окна: значения величины z, используемой в вычислениях по Манну-Уитни, и расчитанный для каждой пары уровень статистической значимости различий.

Рис. 4.11.4. Попарные сравнения групп в диалоге теста Краскела-Уоллиса эквивалентны множественным сравнениям с помощью критерия Манна-Уитни

Обратите внимание на то, что при проведении множественных сравнений появляется опасность совершить статистическую ошибку I рода (принять альтернативную гипотезу в то время, когда верна нулевая). Чтобы избежать этой опасности, следует использовать описанную выше поправку на множественные сравнения.

Наконец, кнопка Box & whisker позволяет зримо сравнить распределения разных групп.

Рис. 4.11.

5. Сравнение распределений длины пяточного бугра у представителей разных генотипов

Еще одна из «графических» кнопок обсуждаемого диалога позволяет построить категоризованные гистограммы для сравниваемых групп; с точки зрения автора, этот способ вывода результатов является менее наглядным.

U-критерий Манна-Уитни Калькулятор

U-критерий Манна-Уитни — это тип непараметрического теста, в котором для проверки используется ранг. И U, и Z рассматриваются в качестве тестовой статистики для U-критерия Манна-Уитни. Каждый шаг обеспечен, как будто он решен вручную. Вы можете узнать, как рассчитать U-критерий Манна-Уитни, отправив любые образцы значений. Статистика U и p-значение вычисляются и отображаются ниже.0003

$$ \displaylines{—} $$

$$ \displaylines{ \mathbf{\color{Green}{H_{0}:\;две\;популяции\;равны\;}} \\\\ \mathbf{\color{Green}{H_{a}:H_{0}\;is\;false}} \\\\ } $$

$$ Образец \; 1 $$	$$ Образец \; 2 $$
$$ 1 0003	9	$$ 10003	9 $$ 1 0003	9	$ $ $
$$ 2 $$	$$ 3 $$
$$ 3 $$	$$ 4 $$
$$ 4 $$	$ 4 $
9 000 000 000 000 000 000 000 9000 000 000 000 000 000 000 000 000 000 000 000 000
9 9000 9000 3
$ 4.	$$ 3 $$
$$ — $$	$$ 7 $$
$$ — $$	$$ 4 $$

$$ \displaylines{} $$

$$ \displaylines{\\ \\ \mathbf{\color{Green}{Теперь\;мы\;должны\;создать\;ранг\;каждого\;значения}} \\\\ \mathbf{\color{Green}{Если\;2\;или\;более\;значения\;равны\;\;Взять\;среднее\;и\;дать\;равный\;ранг}} \\\\ } $$

599999999

$$ Values $$	$$ Sample $$	$$ rank $$
$$ 1 $$	$$ Sample\ ; 1 $$	$$ 1,5 $$
$$ 2 $$	$$ Образец \; 1 $$	$ 3,0 $ 9 0003922

	$ 3,0 $ 9 0003929925999999
$ 3,0 $ 9 00032 9003	$ 3,0. $$ 3 $$	$$ Образец\;1 $$	$$ 5.0 $$
$$ 4 $$	$$ Sample\;1 $$	$$ 8.5 $$
$$ 5 $$	$$ Образец \; 1 $$	$$ 11,0 $$
$ $ 1 $$ 9003	$ $. $$ 1,5 $$
$$ 3 $$	$$ Образец\;2 $$	$$ 5.0 $$
$$ 4 $$	$$ Sample\;2 $$	$$ 8.5 $$
$$ 4 $$	$$ Образец \; 2 $$	$$ 8,5 $$
$$ 3 $$ 9003	$ $. $$ 5,0 $$
$$ 7 $$	$$ Образец\;2 $$	$$ 12.0 $$
$$ 4 $$	$$ Sample\;2 $$	$$ 8. 5 $$

$$ \ displaylines{} $$

$$ \displaylines{ \mathbf{\color{Green}{Теперь\;замените\;исходное\;значение\;на\;ранг}} \\\\ } $$

$$ $$	$$ Проба\;1 $$	$$ Проба\;2 $$
$$ $$	$$ 1.5 $$	$$ 1.5 $$
$$ $$	$$ 3.0 $$	$$ 5,0 $$
$$ $$	$$ 5,0 $$	$$ 8,5 $
$$
$$
, 8,5 $$	$$ 8,5 $$
$$ $$	$$ 11.0 $$	$$ 5.0 $$
$$ $$	$$ — $$	$ $ 12,0 $$
$$ $$	$$ — $$	$$ 8,5 $$ 9003
$ $ $$ 29,0 $$	$$ 49,0 $$
$$ n_{i}\; $$	$$ 5 $$	$$ 7 $$

$$ \displaylines{} $${\een

$$ \displaylines{{f$ \displaylines{{f$ \displaylines{} Где \;R_{i}\;является\;суммой\;всех\;рангов\;в\;выборке}} \\\\ \mathbf{\color{Green}{n_{i}\;это\;общее\;количество\;\;значений\;в\;а\;обработке}} \\\\ U_{1} = R_{1} — \left\{\frac{n_{1}(n_{1}+1)}{2} \right\} \\ \\ \Правая стрелка 29,0 — \влево\{\разрыва{5(5+1)}}{2} \вправо\} \\ \\ \Правая стрелка 14,0 \\\\ U_{2} = R_{2} — \left\{\frac{n_{2}(n_{2}+1)}{2} \right\} \\ \\ \Правая стрелка 49. 0 — \ влево \ {\ гидроразрыва {7 (7 + 1)} {2} \ вправо \} \\ \\ \Правая стрелка 21,0 \\\\ U\;=\;минимум\;из\;U_{1},U_{2} \\ \\ \Правая стрелка мин \слева\{14.000000,21.000000 \справа\} \\ \\ \Правая стрелка 14,0 \\\\ \mu = \frac{n_{1}*n_{2}}{2} \\ \\ \Правая стрелка \фракция{5*7}{2} \\ \\ \Правая стрелка 17,5 \\\\ \sigma = \sqrt{\frac{n_{1}*n_{2}*(n_{1}+n_{2}+1)}{12}} \\ \\ \Правая стрелка \ sqrt {\ гидроразрыва {5 * 7 * (5 + 7 + 1)} {12}} \\ \\ \Правая стрелка 6.157651 \\\\ Z= \frac{U-\mu+C}{\sigma} \\\\ \mathbf{\color{Green}{C\;это\;непрерывность\;коррекция}} \\\\ \mathbf{\color{Зеленый}}{когда\;U\;>

\;\mu:\;C\;=\;-0,5,\;когда\;U\;

Тест Манна-Уитни

Логика и вычислительные детали теста Манна-Уитни
описаны в Подглаве 11a Концепций и приложений.

Для n _a = n _b =
Чтобы применить критерий Манна-Уитни, необработанные данные из образцов A и B необходимо сначала объединить в набор из

N=n _a +n _b

элементов, которые затем ранжируются от низшего к высшему, включая при необходимости ранговые значения.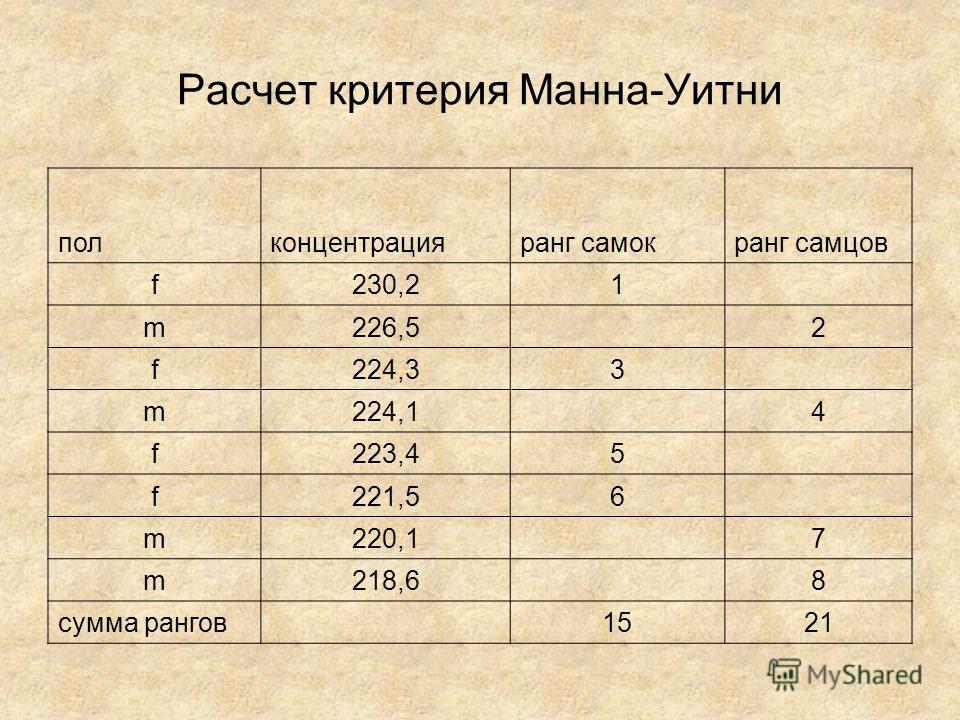

Эти рейтинги затем пересортировываются в две отдельные выборки.

Если ваши данные уже были ранжированы, эти ранги можно ввести прямо в ячейки, озаглавленные меткой «Ранги». В этом случае обратите внимание, что сумма всех рангов для образцов A и B вместе взятых должна быть равна [N(N+1)]/2. Если это равенство не выполняется, вы получите сообщение с просьбой проверить ввод данных на наличие ошибок.

Если ваши данные еще не ранжированы таким образом, их можно ввести в ячейки с надписью «Необработанные данные», и ранжирование будет выполнено автоматически. Ниже также есть опция для импорта необработанных данных из электронной таблицы.

После ввода данных нажмите одну или другую кнопку «Рассчитать» в зависимости от того, начинаете ли вы с рангов или исходных данных.

Опция для импорта необработанных данных с помощью копирования и вставки: _Т
В приложении для работы с электронными таблицами или другом источнике данных выберите и скопируйте столбец данных для образца А.

Затем вернитесь в веб-браузер, щелкните курсором в текстовой области для образца А и выполните операцию «Вставить» из окна «Редактировать». меню. Выполните ту же процедуру для образца B. При импорте необработанных данных в критерий Манна-Уитни абсолютно необходимо, чтобы количество элементов данных для образцов A и B точно совпадало со значениями n _a и n _b, которые вы указали при настройке этой страницы. Для каждого образца убедитесь, что за последней записью в списке не следует возврат каретки. Чтобы выполнить эту проверку, щелкните курсор справа от последней записи в списке, а затем нажмите клавишу со стрелкой вниз. Если присутствует дополнительная строка, курсор переместится вниз. Дополнительные строки можно удалить, нажимая клавишу со стрелкой вниз до тех пор, пока курсор не перестанет двигаться, а затем нажимая клавишу «Backspace» (на платформе Mac «удалить»), пока курсор не станет сразу справа от последней записи. _T

Импорт необработанных данных _T

Образец А	Образец В	Импорт данных в ячейки данных Очистить A Прозрачный В

Ввод данных: _T

	разрядов для		Необработанные данные для
количество	Образец А	Образец В	Образец А	Образец В

Средние ранги для
Образец А	Образец В		У _А =			P ₍₁₎	P ₍₂₎

Обратите внимание, что средние ранги приведены только в описательных целях.

Они
не являются частью теста Манна-Уитни. ~ Обратите также внимание, что z-коэффициент равен
рассчитывается, только если n _a и n _b равны или больше чем 5.

Критические интервалы U _A для _Q

	Уровень значимости для
	Тест направления
	.05	.025	.01
	Ненаправленный тест
	—	.05	.02
нижний предел
верхний предел

Наблюдаемое значение U _A является значимым на установленном уровне или за его пределами, если оно равно или меньше указанного нижнего предела для этого уровня или равно или больше верхнего предела.