Тангенс в матлабе – … MATLAB

Иллюстрированный самоучитель по MatLab › Операторы и функции › Гиперболические и обратные им функции [страница — 204] | Самоучители по математическим пакетам

Гиперболические и обратные им функции

Наряду с тригонометрическими функциями в математических расчетах часто используются и гиперболические функции. Ниже приводится список таких функций, определенных в системе MATLAB. Функции вычисляются для каждого элемента массива. Входной массив допускает комплексные значения. Все углы в тригонометрических функциях измеряются в радианах.

• acosh(X) – возвращает гиперболический арккосинус для каждого элемента X. Пример:

>>Y= acosh (0.7)

Y =

0 + 0.7954i

• acoth(X) – возвращает гиперболический арккотангенс для каждого элемента X. Пример:

>>Y = acoth (0.1)

Y=

0.1003

+ 1.5708i

• acsch(X) – возвращает гиперболический арккосеканс для каждого элемента X. Пример:

>> Y = acsch(1)

Y =

0.8814

• asech(X) – возвращает гиперболический арксеканс для каждого элемента X. Пример:

>> Y = asech(4)

Y =

0 + 1.3181i

• asinh(X) – возвращает гиперболический арксинус для каждого элемента X. Пример:

>> Y = asinh (2.456)

Y =

1.6308

• atanh(X)
  – возвращает гиперболический арктангенс для каждого элемента X. Пример:

>> X=[0.84 0.16 1.39];

>> atanh (X)

ans =

1.2212 0.1614 0.9065 + 1.5708i

• cosh(X) – возвращает гиперболический косинус для каждого элемента X. Пример:

>> X=[1 23];

>> Cosh(X)

ans =

1.5431 3.7622 10.0677

• coth(X) – возвращает гиперболический котангенс для каждого элемента X. Пример:

>

> Y = coth(3.987)

Y =

1.0007

• csch(x) – возвращает гиперболический косеканс для каждого элемента X. Пример:

>> X=[2 4.678 5:0.987 1 3];

>> Y = csch(X)

Y =

0.2757 0.0186 0.0135

0.8656 0.8509 0.0998

• sech(X) – возвращает гиперболический секанс для каждого элемента X. Пример:

>> X=[pi/2 pi

/4 pi/6 pi];

>> sech(X)

ans =

0.3985 0.7549 0.8770 0.0863

• sinh(X) – возвращает гиперболический синус для каждого элемента X. Пример:

>> X=[pi/8 pi/7 pi/5 pi/10];

>> sinh(X)

ans =

0.4029 0.4640 0.6705 0.3194

• tanh(X) – возвращает гиперболический тангенс для каждого элемента X. Пример:

>>

X=[pi/2 pi/4 pi/6 pi/10];

>>tanh(X)

ans =

0.9172 0.6558 0.4805 0.3042

Следующий m-файл-сценарий строит графики ряда гиперболических функций:

syms x

subplot(2.2.1).ezplot(sinh(x).[-4 4]).xlabel('').grid on

subplot(2.2.2).ezplot(cosh(x).[-4 4]).xlabel('').grid on

subplot(2.2.3).ezplot(tanh(x).[

-4 4]).grid on

subplot(2.2.4).ezplot(sech(x).[-4 4]).grid on

Нетрудно заметить, что гиперболические функции в отличие от тригонометрических не являются периодическими. Выбранные для графического представления функции дают примеры характерных нелинейностей.

В другом файле использованы команды для построения графиков ряда обратных гиперболических функций:

syms x

subplot(2.2.1).ezplot(asinh(x).[-4 4]).xlabel('').grid on

subplot(2.2.2).ezplot(acosh(x).[0 4]).xlabel('').grid on

subplot(2.2.3).ezplot(atanh(x).[

-1 1]).grid on

subplot(2.2.4).ezplot(asech(x).[0 1]).grid on

На этих графиках хорошо видны особенности данного класса функций. Такие функции, как обратный гиперболический синус и тангенс, «ценятся>> за симметричный вид их графиков, дающий приближение к ряду типовых нелинейностей.

samoychiteli.ru

02 Основы работы в MATLAB

2- Основы работы в Matlab

2.1.Работа в командном окне, арифметические операции, форматы чисел, константы в Матлаб

2.2.Стандартные функции в MATLAB, специальные функции пользователя

2.3.Векторы, поэлементные и матричные операции, вычисление сложных функции от данного вектора,

2.4.Матрицы как двумерные массивы, обработка матриц и операции с матрицами

2.1 — Работа в командном окне, арифметические операции, форматы чисел, константы в Матлаб

Основные арифметические операторы, сложение, вычитание, умножение, деление, возведение в степень + — * / ^

Следующие операции можно выполнять в командном окне:

>>x = 2+7 x = 9

>>x = 3*15 x = 45

>>x = 4^4 x = 64

>>x = 100/8 x= 12.5

>>x = (17 — 9) * 6 / 6 x = 8

Форматы чисел;

format short	1.3333	0.0000
format short e	1.3333E+000	1.2345E-6
format long	1.333333333333338	0.000001234500000
format long e	1.333333333333338 E+000	1.234500000000000E-006
format bank	1.33	0.00

>> x=pi	>> format long e
x =	>> x
3.1416	x =
>> format long	3.141592653589793e+000
>> x	>> format bank
x =	>> x
3.141592653589793	x =
	3.14
>> format short e
>> x
x =
3.1416e+000

3

Константы и переменные в Matlab

>> pi

ans = 3.1416 (какой формат ?)

>> e = exp (1)

e = 2.7183e+000 (Какой формат ?)

Здесь exp( ) встроенная функция, вычисляет экспоненты.

eps − ε = 2.2204e-016 (самое малое число, которое отличает двух чисел друг от друга)

ans − результат последней операции без знака присвивания i, j − мнимая единица ( −1)

inf − машинный символ бесконечности

NaN − неопределенный результат (0/0, ∞/ ∞, 1∞, и т.д.)

Знак процента % используется при вводе комментарий в любом месте в листинге кода, в начале операции или между строками.

4

2.2. Стандартные функции в MATLAB, специальные функции пользователя

Тригонометрические	Описание функции
Функции
sin(x) / sind(x)	синус числа х (радиан) / синус числа х (градус)
cos(x) / cosd(x)	косинус числа х (радиан) / косинус числа х (градус)
tan(x) / tand(x)	тангенс числа х (радиан) / тангенс числа х (градус)
cot(x) / cotd(x)	котангенс числа х (радиан)	/ котангенс числа х (градус)
sec(x) / secd(x)	секанс числа х (радиан) /	секанс числа х (градус)
csc(x) / cscd(x)	косеканс числа х (радиан) / косеканс числа х (градус)
asin(x) / asind(x)	арксинус чилса х (радиан) / арксинус чилса х (градус)
acos(x) / acosd(x)	арккосинус числа х (радиан) / арккосинус числа х (градус)
atan(x) / atand(x)	арктангенс числа х (радиан) / арктангенс числа х (градус)
acot(x) / acotd(x)	арккотангенс числа х (радиан) / арккотангенс числа х
	(градус)
asec(x) / asecd(x)	арксеканс числа х (радиан)	/ арксеканс числа х (градус)
acsc(x) / acscd(x)	арккосеканс числа х (радиан) / арккосеканс числа х
	(градус)

Замечание о тригонометрических функциях

>>sin(30) ans =

-0.99

>>Sin(pi()*30/180) ans =

0.50

>> sind(30) ans =

0.50

Неправильно (Вычисляется sin(30) в радианах)

правильно

правильно

studfiles.net

Иллюстрированный самоучитель по MatLab › Операторы и функции › Тригонометрические и обратные им функции [страница — 201] | Самоучители по математическим пакетам

Тригонометрические и обратные им функции

В системе MATLAB определены следующие тригонометрические и обратные тригонометрические функции. Функции вычисляются для каждого элемента массива. Входной массив допускает комплексные значения. Напоминаем, что все углы в функциях задаются в радианах.

• acos (X) – возвращает арккосинус для каждого элемента X. Для действительных значений X в области [-1, 1] acos(X) возвращает действительное значение из диапазона диапазона [0, р], для действительных значений X вне области [-1, 1] acos(X) возвращает комплексное число.

Примеры:

>>Y = acos (0.5)

1.0472

>> acos([0.5 1 2])

ans =

1.0472 0 0 + 1.31701

• acot (X) – возвращает арккотангенс для каждого элемента X. Пример:

>> Y=acot(0.l)

y =

1.4711

• acsc(X) – возвращает арккосеканс для каждого элемента X. Пример:

• asec(X) – возвращает арксеканс для каждого элемента X. Пример:

>> Y=asec(0.5)

Y =

0 + 1.31701

• asin(X) – возвращает арксинус для каждого элемента X. Для действительных значений X в области [-1, 1] asin(X) возвращает действительное число из диапазона [-р/2, р/2], для действительных значений X вне области [-1, 1] asin(X) возвращает комплексное число. Пример:

>> Y= asin (0.278)

Y =

0.2817

• atan(X) – возвращает арктангенс для каждого элемента X. Для действительных значений X atan(X) находится в области [-р/2, р/2]. Пример:

• atan2 (Y, X) – возвращает массив Р той же размерности, что X и Y, содержащий поэлементно арктангенсы отношения вещественных частей Y и X. Мнимые части игнорируются. Элементы Р находятся в интервале [-р, р]. Специфический квадрант определен функциями sign(Y) и sign(X). Это отличает полученный результат от результата atan(Y/X), который ограничен интервалом [-л/2, л/2].

Пример:

>> atan2(1,2)

ans =

0.4636

• cos(X) – возвращает косинус для каждого элемента X. Пример:

>>X=[123];

>> cos(X)

ans =

0.5403-0.4161-0.9900

• cot(X) – возвращает котангенс для каждого элемента X. Пример:

>> Y = cot(2)

Y =

-0.4577

• csc(X) – возвращает косеканс для каждого элемента X. Пример:

>> X=[2 4.678 5:0.987 1 3];

>> Y = csc(X)

Y =

1.0998-1.0006-1.0428

1.1985 1.1884 7.0862

Если Вы заметили ошибку, выделите, пожалуйста, необходимый текст и нажмите CTRL + Enter, чтобы сообщить об этом редактору.

samoychiteli.ru

Тригонометрические и обратные им функции MatLab

Арифметические операторы и функции
Операторы отношения и их функции
Логические операторы

Специальные символы
Системные переменные и константы
Функции поразрядной обработки
Функции обработки множеств
Функции времени и даты
Элементарные функции
Алгебраические и арифметические функции
Тригонометрические и обратные им функции
Гиперболические и обратные им функции
Функции округления и знака
Функции комплексного аргумента
Что нового мы узнали?

В системе MATLAB определены следующие тригонометрические и обратные тригонометрические функции. Функции вычисляются для каждого элемента массива. Входной массив допускает комплексные значения. Напоминаем, что все углы в функциях задаются в радианах.

Э acos (X) — возвращает арккосинус для каждого элемента X. Для действительных значений X в области [-1, 1] acos(X) возвращает действительное значение из диапазона диапазона [0, р], для действительных значений X вне области [-1, 1] acos(X) возвращает комплексное число.

Примеры:

»Y = acos (0.5)

1.0472

» acos([0.5 1 2]) 

ans =

1.0472 0     0 + 1.31701

acot (X) — возвращает арккотангенс для каждого элемента X. Пример:

» Y=acot(0.l)

у =

1.4711

acsc(X) — возвращает арккосеканс для каждого элемента X. Пример:

» Y= acsc(3)

0.3398

asec(X) — возвращает арксеканс для каждого элемента X. Пример:

» Y=asec(0.5)

Y =

0 + 1.31701

asin(X) — возвращает арксинус для каждого элемента X. Для действительных значений X в области [-1, 1] asin(X) возвращает действительное число из диапазона [-р/2, р/2], для действительных значений X вне области [-1, 1] asin(X) возвращает комплексное число. Пример:

» Y= asin (0.278) 

Y =

0.2817

atan(X) — возвращает арктангенс для каждого элемента X. Для действительных значений X atan(X) находится в области [-р/2, р/2]. Пример:

» Y=atan(1)

Y =

0.7854

atan2 (Y, X) — возвращает массив Р той же размерности, что X и Y, содержащий поэлементно арктангенсы отношения вещественных частей Y и X. Мнимые части игнорируются. Элементы Р находятся в интервале [-р, р]. Специфический квадрант определен функциями sign(Y) и sign(X). Это отличает полученный результат от результата atan(Y/X), который ограничен интервалом [-л/2, л/2].

Пример:

» atan2(l,2) 

ans = 

0.4636

cos(X) — возвращает косинус для каждого элемента X. Пример:

»Х=[123]; 

» cos(X) 

ans =

0.5403     -0.4161    -0.9900

cot(X) — возвращает котангенс для каждого элемента X. Пример:

» Y = cot(2) 

Y =

-0.4577

csc(X) — возвращает косеканс для каждого элемента X. Пример:

» Х=[2 4.678 5:0.987 1 3]; 

» Y = csc(X) 

Y =

1.0998     -1.0006    -1.0428

1.1985     1.1884     7.0862

sec(X) — возвращает массив той же размерности что и X, состоящий из секансов элементов X. Пример:

» X=[pi/10 pi/3 pi/5]; 

» sec(X) 

ans =

1.0515     2.0000     1.2361

sin(X) — возвращает синус для каждого элемента X. Пример:

» X=[pi/2 pi/4 pi/6 pi];

» sin(X)

ans =

1.0000     0.7071     0.5000     0.0000

tan(X) — возвращает тангенс для каждого элемента X.

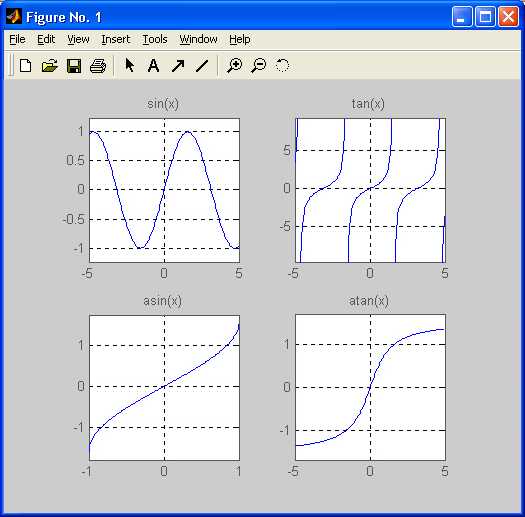
Рис. 8.2. Графики четырех тригонометрических функций

Пример:

» Х=[0.08 0.06 1.09]

X=

0.0800 0.0600 1.0900 

» tan(X)

ans=

0.802     0.0601     1.9171

Следующий файл-сценарий позволяет наблюдать графики четырех тригонометрических функций (рис. 8.2):

syms xsubplot(2.2.1).ezplot(sin(x),[-5 5]).xlabel(«),gnd on

subplot(2.2.2),ezp»lot(tan(x).[-5 5]).xlabel(«).grid on 

subplot(2,2,3),ezplot(asin(x),[-1 1]).grid on 

subplot(2.2.4),ezplot(atan(x).[-5 5]),grid on

Поскольку многие тригонометрические функции периодичны, появляется возможность формирования из них любопытных комбинаций, позволяющих создавать типовые тестовые сигналы, используемые при моделировании радиоэлектронных устройств. Следующий файл-сценарий строит графики для таких комбинаций, создающих из синусоиды три наиболее распространенных сигнала — прямоугольные, пилообразные и треугольные импульсы:[ В пакете расширения Signal Processing Toolbox есть специальные функции для генерации таких сигналов — square и sawtooth. — Примеч. ред. ]

х=-10:0.01:10;

subplot(2,2.1).plot(x.0.8*sin(x))

.x label(‘0.8*sin(x)’) 

subplot(2.2,2).plot(x,0.8*sign(sin(x)))

.x1abel(‘0.8*sgn(sin(x))’) 

subplot(2.2.3),plot(x.atan(tan(x/2)))

.xlabel(‘atan(tan(x/2))’) 

subplot(2.2.4),plot(x,asin(sin(x)))

.xlabel(‘asin(sin(x))’)

Соответствующие графики представлены на рис. 8.3.

Рис. 8.3. Графики синусоиды, прямоугольных, пилообразных и треугольных колебаний

Дополнительный ряд графиков, полученных комбинациями элементарных функций, показан на рис. 8.4. Эти графики строятся следующим файлом-сценарием:

х=-10:0.01:10;

subplot(2.2.1).plot(x.sin(x). ^A 3).x1abel(‘sin(xr3’)

subplot(2.2.2).plot(x,abs(s1n(x)))

.xlabel(‘abs(sin(x))’).axis([-10 10 -1 1]),

subplot(2.2,3),plot(x,tan(cos(x)))

.xlabel(‘tanCcos(x))’) 

subplot(2.2.4).plot(x.csch(sec(x))),xlabeK’csch(sec(x))’)

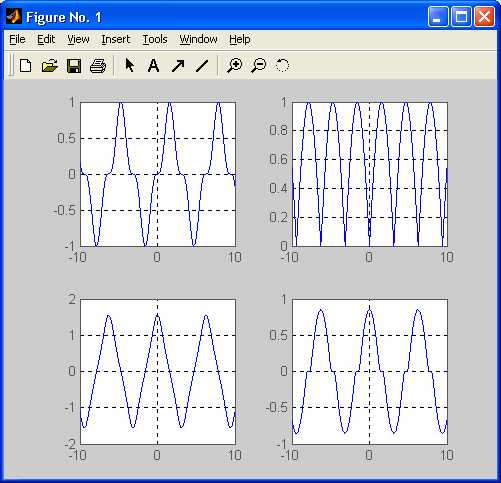
Рис. 8.4. Графики периодических сигналов без разрывов

Эти графики неплохо моделируют сигналы, получаемые при выпрямлении синусоидального напряжения (или тока) и при прохождении синусоидальных сигналов через нелинейные цепи.

 

radiomaster.ru