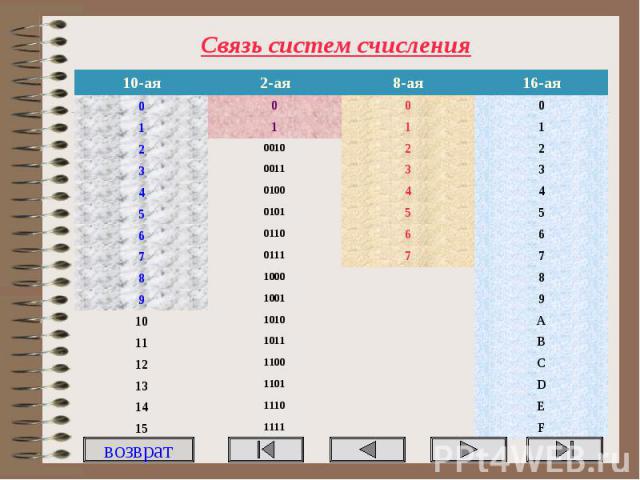
3.3.4. Взаимосвязь систем счисления используемых в вычислительной технике.
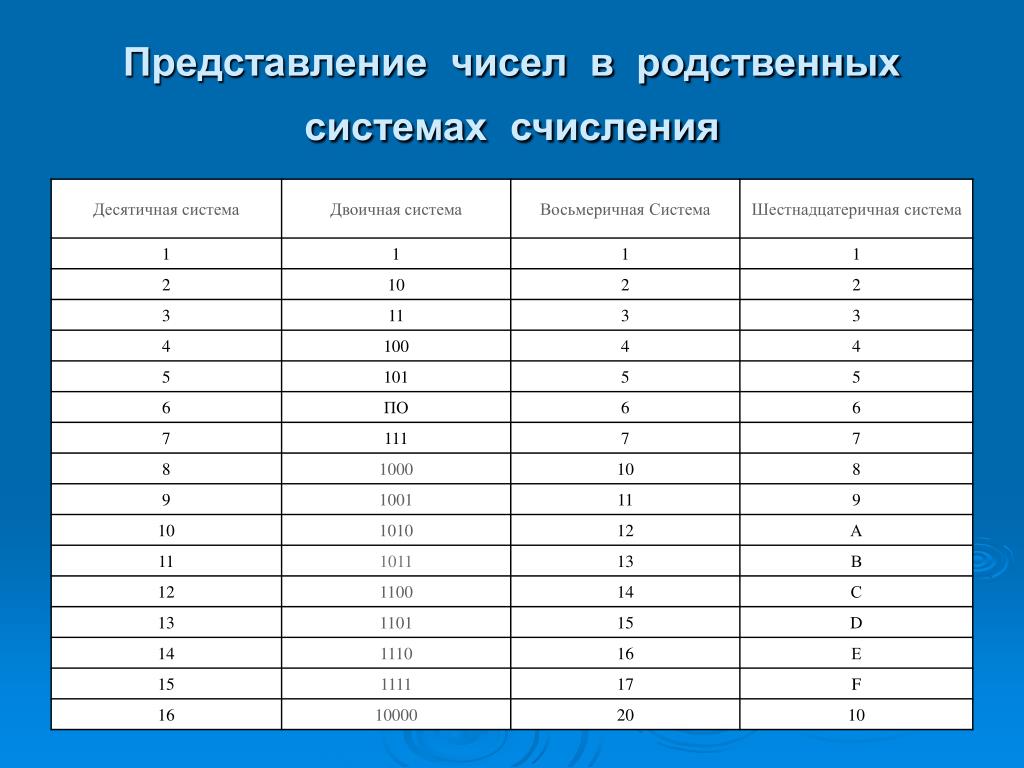
Двоичная система счисления, используемая элементами вычислительной техники имеет один недостаток – это громоздкость записи. Для того, чтобы записать число 255(10)требуется целых восемь разрядов 11111111(2). Для уменьшения разрядности при записи информации требовалось разработать системы счисления, в которые было бы легко переводить информацию из двоичной системы счисления, и при этом запись была бы менее громоздкой. Сначала была разработана восьмеричная система счисления, в которой тоже самое число 255(10)представлялось в виде 377(8), а затем шестнадцатеричная, это же число в которой имеет видFF(16). Перевод между этими системами счисления можно осуществлять при помощи таблицы 2.
Таблица 2.
Двоичная | Восьмеричная | |
0000 | 0 | 0 |
0001 | 1 | 1 |
0010 | 2 | 2 |
0011 | 3 | 3 |
0100 | 4 | 4 |
0101 | 5 | 5 |
| 0110 | 6 | 6 |
0111 | 7 | 7 |
1000 | 10 | 8 |
1001 | 11 | 9 |
1010 | 12 | A |
1011 | 13 | B |
1100 | C | |
1101 | 15 | D |
1110 | 16 | E |
1111 | 17 | F |
3.
 4. Перевод из одной системы счисления в другую.
4. Перевод из одной системы счисления в другую.Существует три способа перевода чисел из одной системы счисления в другую, это:
Перевод с использованием формулы разложения по степени основания;
Перевод целых чисел делением на основание;
Поразрядные способы перевода (переводы с использованием таблиц).
3.4.1. Перевод с использованием формулы разложения по степени основания.
В основе способа перевода лежит использование веса разрядов чисел. Перевод с использованием формулы разложения по степеням основания удобен для перевода в десятичную систему счисления, так как в процессе преобразования действия выполняются в новой системе счисления.
Алгоритм перевода из одной системы счисления в другую представлен на рисунке 7.
Рассмотрим процесс перевода с использованием формулы разложения по степени основания на примерах:
Пример 1.
Дано A(2)=10011. НайтиA(10). Решение примера приведено на рисунке 7.
Пример 2.
Дано A(8)=257. НайтиA(10).
Решение:
A(8)= a2a1
A(10)= 2*64+5*8+7*1=128+40+7
A(10)=175
Пример 3.
Дано A(16)=1EF6. НайтиA(10).
Решение:
A(16)= a3a2a1a0= a3*163+a2*162+a1*161+a0*160
A(10)= 1*4096+14*256+15*16+6*1=4096+3584+240+6
A(10)=7926
3.
 4.2. Перевод целых чисел делением на основание.
4.2. Перевод целых чисел делением на основание.Правило заключается в деление числа на основание с остатком, если остаток больше основания то он снова делиться на основание, до тех пор, пока остаток не станет меньше основания.
При этом способе перевода действия выполняются в исходной системе счисления, поэтому это способ удобен для перевода из десятичной системы счисления в остальные системы счисления.Пример 1.
Дано A(10)=43. НайтиA(2).
Ответ A(2)=101011
Пример 2.
Дано A(10)=132. НайтиA(8).
Ответ A(8)=204
Пример 3.
Дано A(10)=213. НайтиA(16).
Ответ A(16)=D5
3.
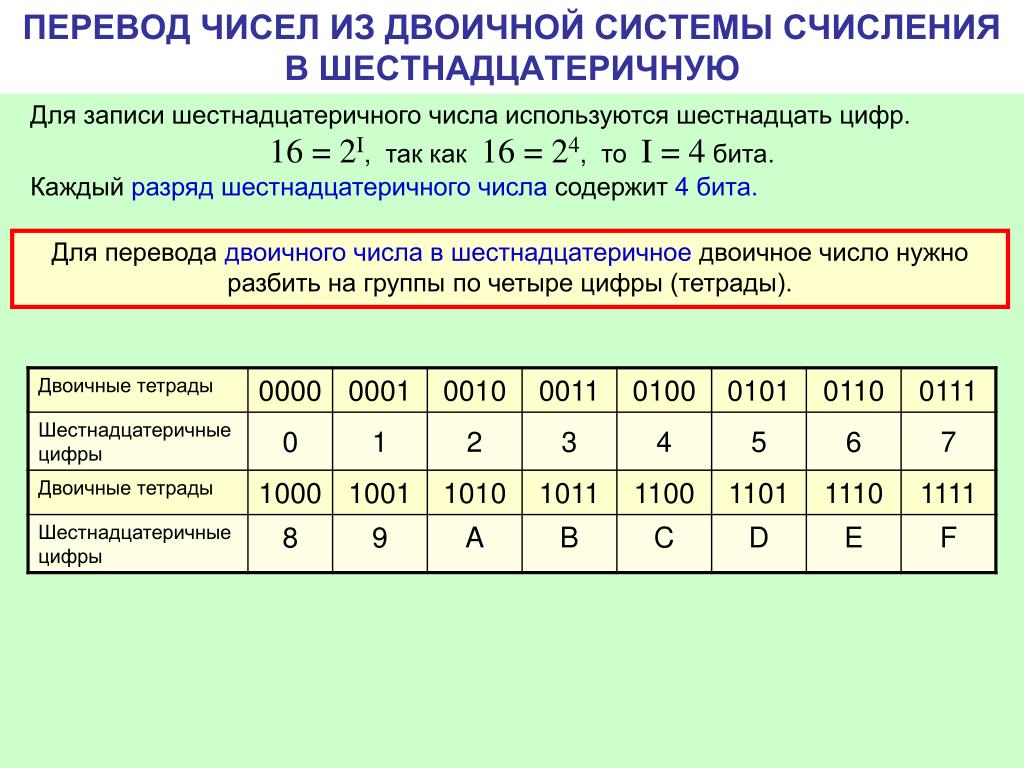 4.3. Поразрядные способы перевода.
4.3. Поразрядные способы перевода.Перевод чисел упрощается, если основание старой системы счисления pи новой системы счисленияqсвязаны отношением:
p=qk илиq=pk,
где:
q– основание результирующей системы счисления;
k – целое число.
Для систем счисления используемых в вычислительной технике значениеkприведено в таблице 3.
Таблица 3.
Исходная система счисления | Результирующая система счисления | Значение k |
Восьмеричная | Двоичная | 3 |
Двоичная | Восьмеричная | 3 |
Шестнадцатеричная | Двоичная | 4 |
Двоичная | Шестнадцатеричная | 4 |
При такой связи систем счисление перевод
осуществляется с помощью таблиц 4 и 5.
Таблица 4.
Взаимосвязь восьмеричной и двоичной систем счисления.
Двоичная | Восьмеричная |
000 | 0 |
001 | 1 |
010 | |
011 | 3 |
100 | 4 |
101 | 5 |
110 | 6 |
111 | 7 |
Таблица 5.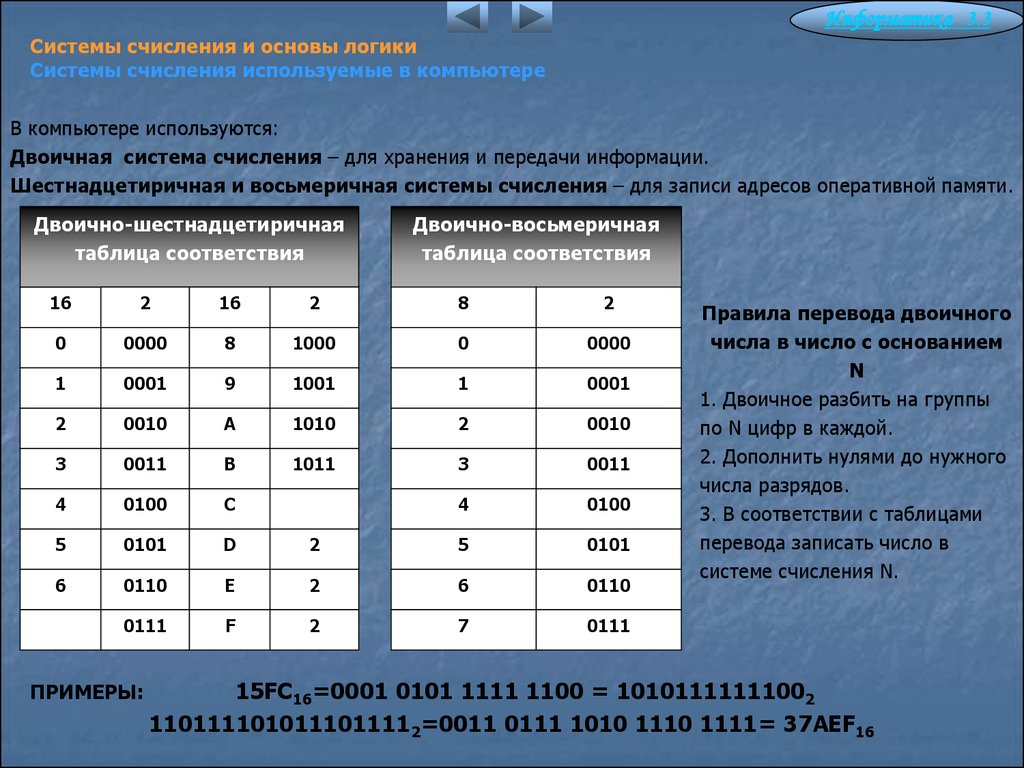
Взаимосвязь шестнадцатеричной и двоичной систем счисления.
Шестнадцатеричная | Восьмеричная |
0000 | 0 |
0001 | 1 |
0010 | 2 |
0011 | 3 |
0100 | 4 |
0101 | 5 |
0110 | 6 |
0111 | 7 |
1000 | |
1001 | 9 |
1010 | A |
1011 | B |
1100 | C |
1101 | D |
1110 | E |
1111 | F |
Алгоритм поразрядного
перевода из двоичной системы счисления
в восьмеричную заключается в дроблении
двоичного числа по три разряда с права
на лево и замене соответствующими
цифрами восьмеричной системы счисления
из таблицы 4. Если в конце дробления
остается меньше трех разрядов, то
двоичное число дополняют с лева нулями.
Алгоритм перевода представлен на рисунке
8.
Если в конце дробления
остается меньше трех разрядов, то
двоичное число дополняют с лева нулями.
Алгоритм перевода представлен на рисунке
8.
Обратный перевод из восьмеричной в двоичную систему счисления осуществляется по этому же алгоритму но в обратном порядке. Один разряд восьмеричной системы счисления заменяется тремя разрядами двоичной систем счисления.
Алгоритм перевода из двоичной в шестнадцатеричную систему счисления аналогичен алгоритму перевода в восьмеричную, за исключением того, что число дробиться не по три, а по четыре разряда и соответствия подбираются из таблицы 5.
Пример 1.
Дано A(2)=1001101. НайтиA(8).
Решение:
Ответ:
A(8)=115
Пример 2.
Дано A(8)=27. НайтиA(2).
НайтиA(2).
Решение:
A(8)=2’7
Ответ:
A(2)=010111=10111
Пример 3.
Дано A(2)=1101101. НайтиA(16).
Решение:
Ответ:
A(16)=6D
Пример 2.
Дано A(16)=F4. НайтиA(2).
Решение:
A(16)=F’4
Ответ:
A(2)=11110100
3.3.4. Взаимосвязь систем счисления используемых в вычислительной технике.
Двоичная система счисления, используемая
элементами вычислительной техники
имеет один недостаток – это громоздкость
записи.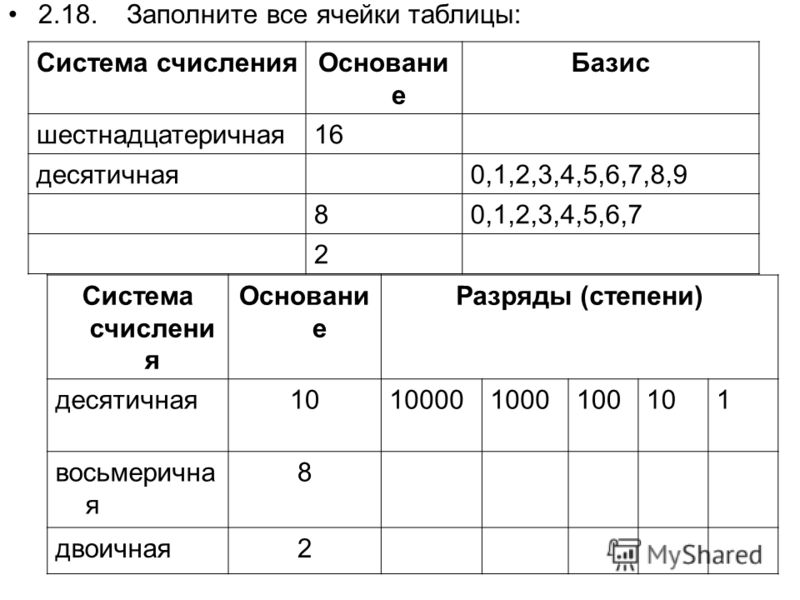 Для того, чтобы записать число
255(10)требуется целых восемь
разрядов 11111111(2). Для уменьшения
разрядности при записи информации
требовалось разработать системы
счисления, в которые было бы легко
переводить информацию из двоичной
системы счисления, и при этом запись
была бы менее громоздкой. Сначала была
разработана восьмеричная система
счисления, в которой тоже самое число
255(10)представлялось в виде 377(8),
а затем шестнадцатеричная, это же число
в которой имеет видFF(16).
Перевод между этими системами счисления
можно осуществлять при помощи таблицы
2.
Для того, чтобы записать число
255(10)требуется целых восемь
разрядов 11111111(2). Для уменьшения
разрядности при записи информации
требовалось разработать системы
счисления, в которые было бы легко
переводить информацию из двоичной
системы счисления, и при этом запись
была бы менее громоздкой. Сначала была
разработана восьмеричная система
счисления, в которой тоже самое число
255(10)представлялось в виде 377(8),
а затем шестнадцатеричная, это же число
в которой имеет видFF(16).
Перевод между этими системами счисления
можно осуществлять при помощи таблицы
2.
Таблица 2.
Двоичная | Восьмеричная | Шестнадцатеричная |
0000 | 0 | 0 |
0001 | 1 | 1 |
0010 | 2 | 2 |
0011 | 3 | 3 |
0100 | 4 | 4 |
0101 | 5 | 5 |
0110 | 6 | 6 |
0111 | 7 | 7 |
1000 | 10 | 8 |
1001 | 11 | 9 |
1010 | 12 | A |
1011 | 13 | B |
1100 | 14 | C |
1101 | 15 | D |
1110 | 16 | E |
1111 | 17 | F |
3.
 4. Перевод из одной системы счисления в другую.
4. Перевод из одной системы счисления в другую.Существует три способа перевода чисел из одной системы счисления в другую, это:
Перевод с использованием формулы разложения по степени основания;
Перевод целых чисел делением на основание;
Поразрядные способы перевода (переводы с использованием таблиц).
3.4.1. Перевод с использованием формулы разложения по степени основания.
В основе способа перевода лежит использование веса разрядов чисел. Перевод с использованием формулы разложения по степеням основания удобен для перевода в десятичную систему счисления, так как в процессе преобразования действия выполняются в новой системе счисления.
Алгоритм перевода из одной системы счисления в другую представлен на рисунке 7.
Рассмотрим процесс перевода с использованием формулы разложения по степени основания на примерах:
Пример 1.
Дано A(2)=10011. НайтиA(10). Решение примера приведено на рисунке 7.
Пример 2.
Дано A(8)=257. НайтиA(10).
Решение:
A(8)= a2a1a0=a2*82+a1*81+a0*80
A(10)= 2*64+5*8+7*1=128+40+7
A(10)=175
Пример 3.
Дано A(16)=1EF6. НайтиA(10).
Решение:
A(16)= a3a2a1a0= a3*163+a2*162+a1*161+a0*160
A(10)= 1*4096+14*256+15*16+6*1=4096+3584+240+6
A(10)=7926
3.
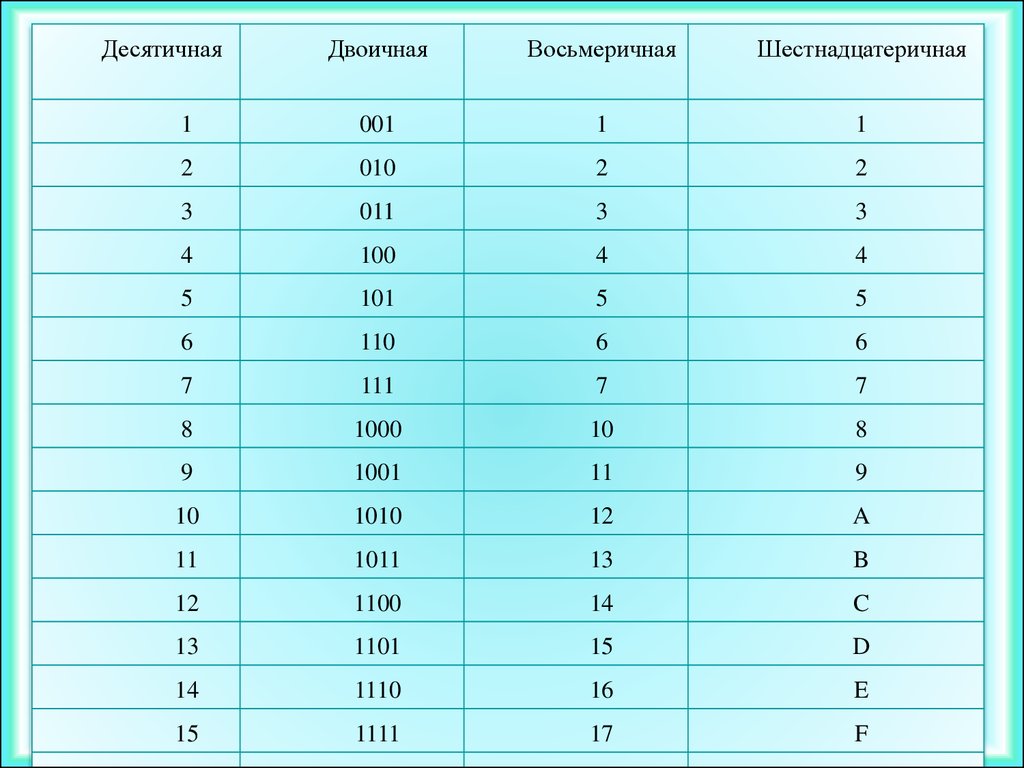 4.2. Перевод целых чисел делением на основание.
4.2. Перевод целых чисел делением на основание.Правило заключается в деление числа на основание с остатком, если остаток больше основания то он снова делиться на основание, до тех пор, пока остаток не станет меньше основания.
При этом способе перевода действия выполняются в исходной системе счисления, поэтому это способ удобен для перевода из десятичной системы счисления в остальные системы счисления.
Пример 1.
Дано A(10)=43. НайтиA(2).
Ответ A(2)=101011
Пример 2.
Дано A(10)=132. НайтиA(8).
Ответ A(8)=204
Пример 3.
Дано A(10)=213. НайтиA(16).
Ответ A(16)=D5
3.
 4.3. Поразрядные способы перевода.
4.3. Поразрядные способы перевода.Перевод чисел упрощается, если основание старой системы счисления pи новой системы счисленияqсвязаны отношением:
p=qk илиq=pk,
где:
p– основание исходной системы счисления;
q– основание результирующей системы счисления;
k – целое число.
Для систем счисления используемых в вычислительной технике значениеkприведено в таблице 3.
Таблица 3.
Исходная система счисления | Результирующая система счисления | Значение k |
Восьмеричная | Двоичная | 3 |
Двоичная | Восьмеричная | 3 |
Шестнадцатеричная | Двоичная | 4 |
Двоичная | Шестнадцатеричная | 4 |
При такой связи систем счисление перевод
осуществляется с помощью таблиц 4 и 5.
Таблица 4.
Взаимосвязь восьмеричной и двоичной систем счисления.
Двоичная | Восьмеричная |
000 | 0 |
001 | 1 |
010 | 2 |
011 | 3 |
100 | 4 |
101 | 5 |
110 | 6 |
111 | 7 |
Таблица 5.
Взаимосвязь шестнадцатеричной и двоичной систем счисления.
Шестнадцатеричная | Восьмеричная |
0000 | 0 |
0001 | 1 |
0010 | 2 |
0011 | 3 |
0100 | 4 |
0101 | 5 |
0110 | 6 |
0111 | 7 |
1000 | 8 |
1001 | 9 |
1010 | A |
1011 | B |
1100 | C |
1101 | D |
1110 | E |
1111 | F |
Алгоритм поразрядного
перевода из двоичной системы счисления
в восьмеричную заключается в дроблении
двоичного числа по три разряда с права
на лево и замене соответствующими
цифрами восьмеричной системы счисления
из таблицы 4.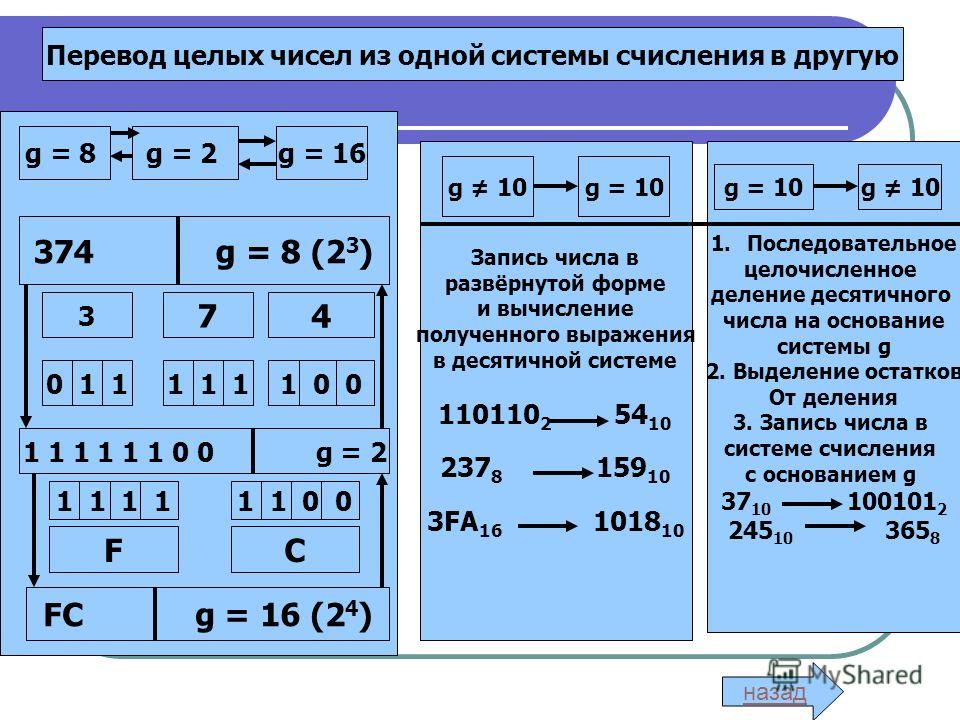 Если в конце дробления
остается меньше трех разрядов, то
двоичное число дополняют с лева нулями.
Алгоритм перевода представлен на рисунке
8.
Если в конце дробления
остается меньше трех разрядов, то
двоичное число дополняют с лева нулями.
Алгоритм перевода представлен на рисунке
8.
Обратный перевод из восьмеричной в двоичную систему счисления осуществляется по этому же алгоритму но в обратном порядке. Один разряд восьмеричной системы счисления заменяется тремя разрядами двоичной систем счисления.
Алгоритм перевода из двоичной в шестнадцатеричную систему счисления аналогичен алгоритму перевода в восьмеричную, за исключением того, что число дробиться не по три, а по четыре разряда и соответствия подбираются из таблицы 5.
Пример 1.
Дано A(2)=1001101. НайтиA(8).
Решение:
Ответ:
A(8)=115
Пример 2.
Дано A(8)=27. НайтиA(2).
НайтиA(2).
Решение:
A(8)=2’7
Ответ:
A(2)=010111=10111
Пример 3.
Дано A(2)=1101101. НайтиA(16).
Решение:
Ответ:
A(16)=6D
Пример 2.
Дано A(16)=F4. НайтиA(2).
Решение:
A(16)=F’4
Ответ:
A(2)=11110100
Таблица двоичных восьмеричных и шестнадцатеричных чисел — dj-sensor.ru
Содержание
- Двоичная система счисления
- Восьмеричная система счисления
- Шестнадцатеричная система счисления
- Двоично-восьмеричные и двоично-шестнадцатеричные преобразования
- Двоичная система счисления
- Восьмеричная система счисления
- Шестнадцатеричная система счисления
Двоичная система счисления
Для представления чисел в микропроцессоре используется двоичная система счисления .
При этом любой цифровой сигнал может иметь два устойчивых состояния: «высокий уровень» и «низкий уровень». В двоичной системе счисления для изображения любого числа используются две цифры, соответственно: 0 и 1. Произвольное число x=anan-1..a1a,a-1a-2…a-m запишется в двоичной системе счисления как
где ai — двоичные цифры (0 или 1).
Восьмеричная система счисления
В восьмеричной системе счисления базисными цифрами являются цифры от 0 до 7. 8 единиц младшего разряда объединяются в единицу старшего.
Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления базисными цифрами являются цифры от 0 до 15 включительно. Для обозначения базисных цифр больше 9 одним символом кроме арабских цифр 0…9 в шестнадцатеричной системе счисления используются буквы латинского алфавита:
Например, число 17510 в шестнадцатеричной системе счисления запишется как AF16.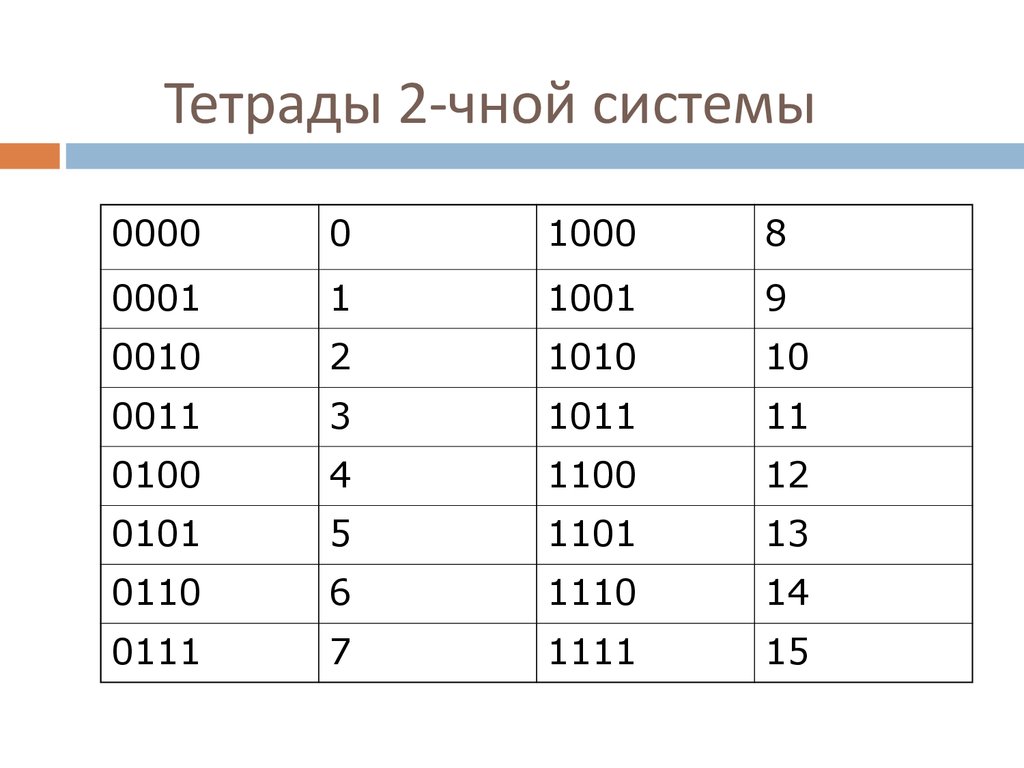 Действительно,
Действительно,
10·16 1 +15·16 0 =160+15=175
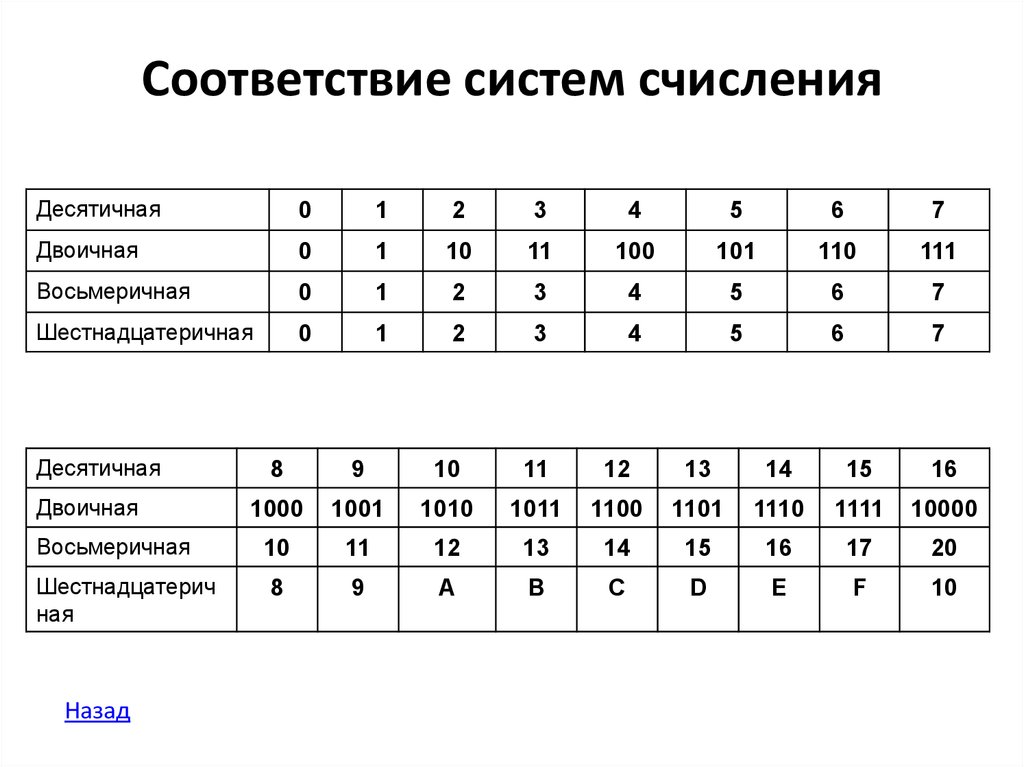
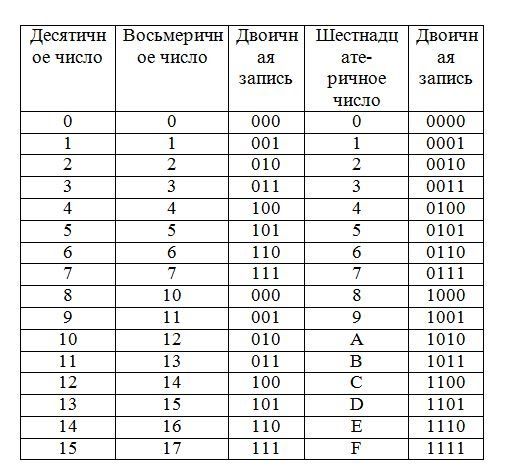
В таблице представлены числа от 0 до 16 в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
Двоично-восьмеричные и двоично-шестнадцатеричные преобразования
Двоичная система счисления удобна для выполнения арифметических действий аппаратными средствами микропроцессора, но неудобна для восприятия человеком, поскольку требует большого количества разрядов. Поэтому в вычислительной технике помимо двоичной системы счисления широкое применение нашли восьмеричная и шестнадцатеричная системы счисления для более компактного представления чисел.
Поэтому в вычислительной технике помимо двоичной системы счисления широкое применение нашли восьмеричная и шестнадцатеричная системы счисления для более компактного представления чисел.
Три разряда восьмеричной системы счисления реализуют все возможные комбинации восьмеричных цифр в двоичной системе счисления: от 0 (000) до 7(111). Чтобы преобразовать двоичное число в восьмеричное, нужно объединить двоичные цифры в группы по 3 разряда (триады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от него тоже можно добавить незначащие нули до заполнения всех триад. Затем каждая триада заменяется восьмеричной цифрой.
Читайте также: Тесты по javascript с ответами
Пример: Преобразовать число 1101110,012 в восьмеричную систему счисления.
Объединяем двоичные цифры в триады справа налево. Получаем
Чтобы перевести число из восьмеричной системы в двоичную, нужно каждую восьмеричную цифру записать ее двоичным кодом:
Четыре разряда шестнадцатеричной системы счисления реализуют все возможные комбинации шестнадцатеричных цифр в двоичной системе счисления: от 0 (0000) до F(1111). Чтобы преобразовать двоичное число в шестнадцатеричное, нужно объединить двоичные цифры в группы по 4 разряда (тетрады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от нее тоже нужно добавить незначащие нули до заполнения всех тетрад. Затем каждая тетрада заменяется шестнадцатеричной цифрой.
Чтобы преобразовать двоичное число в шестнадцатеричное, нужно объединить двоичные цифры в группы по 4 разряда (тетрады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от нее тоже нужно добавить незначащие нули до заполнения всех тетрад. Затем каждая тетрада заменяется шестнадцатеричной цифрой.
Пример: Преобразовать число 1101110,112 в шестнадцатеричную систему счисления.
Объединяем двоичные цифры в тетрады справа налево. Получаем
Чтобы перевести число из шестнадцатеричной системы в двоичную, нужно каждую шестнадцатеричную цифру записать ее двоичным кодом:
Данные системы счисления относятся к позиционным.
Двоичная система счисления
Эта система счисления свое название получила в результате того, что содержит в своем основании всего две цифры – $0$ и $1$. Таким образом, число $2$ и его степени $2, 4, 8$ и т.д.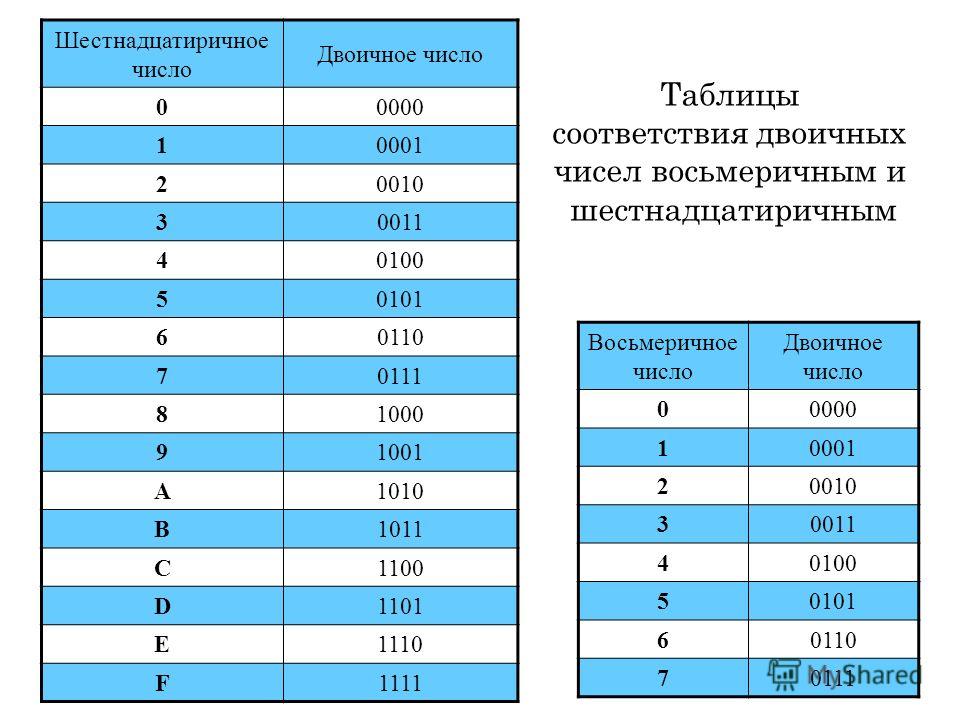 играют особую роль. Самая правая цифра числа показывает число единиц, следующая – число двоек, следующая — число четверок и т.д.
играют особую роль. Самая правая цифра числа показывает число единиц, следующая – число двоек, следующая — число четверок и т.д.
В двоичной системе счисления для формирования числа используются всего две цифры: $0$ и $1$. Пределом разряда является $1$, и как только при счете разряд достигает своего максимального значения, он обнуляется, а при этом образуется новый разряд. Ниже в таблице приведены соответствия двоичных и десятичных чисел.
Используя двоичную систему счисления, можно закодировать любое натуральное число, представляя его как последовательность нулей и единиц. В двоичном виде можно представить не только числа, но и любую другую информацию: тексты, изображения, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что оно легко реализуется технически.
Читайте также: Считается ли отсыпной выходным днем
Попробуй обратиться за помощью к преподавателям
Именно на принципе двоичного кодирования работает вся вычислительная техника: $1$ означает, что электрический сигнал прошел, а $0$ – сигнал отсутствует.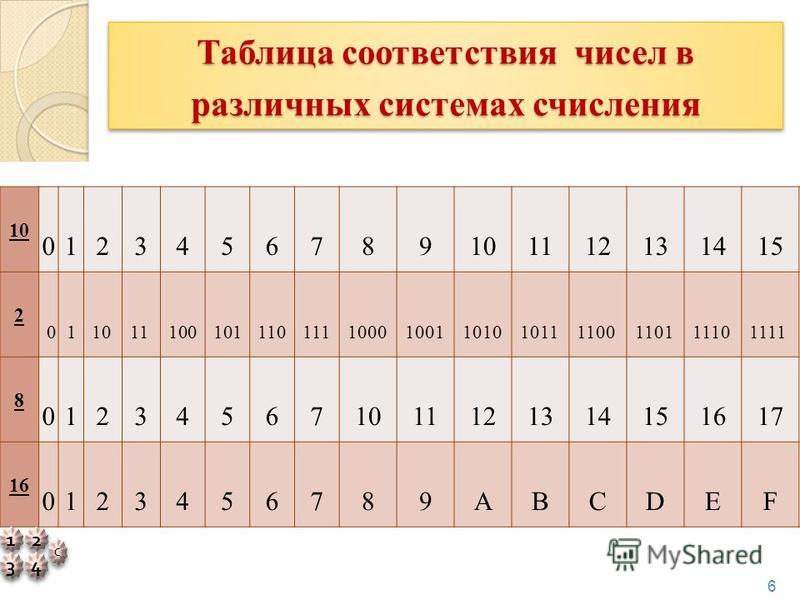 Наглядно это можно рассмотреть на примере перфокарт, которые использовались в вычислительных машинах первых поколений. Как уже упоминалось выше: в перфокартах пробивались отверстия в соответствующих рядах и столбцах цифр, таким образом, кодировались и сохранялись программы, поскольку жестких дисков, и тем более оптических, в те времена не было. Затем программы считывались при помощи электрического сигнала, который, если проходил в отверстие, значит, это был код $1$ и, наоборот, если не проходил сигнал – это был код $0$. Аналогичным способом в настоящее время записываются оптические диски при помощи лазерного луча, прожигающего невидимые микроотверстия на поверхности специальных дисков. Принцип считывания закодированной информации с диска аналогичен предыдущему.
Наглядно это можно рассмотреть на примере перфокарт, которые использовались в вычислительных машинах первых поколений. Как уже упоминалось выше: в перфокартах пробивались отверстия в соответствующих рядах и столбцах цифр, таким образом, кодировались и сохранялись программы, поскольку жестких дисков, и тем более оптических, в те времена не было. Затем программы считывались при помощи электрического сигнала, который, если проходил в отверстие, значит, это был код $1$ и, наоборот, если не проходил сигнал – это был код $0$. Аналогичным способом в настоящее время записываются оптические диски при помощи лазерного луча, прожигающего невидимые микроотверстия на поверхности специальных дисков. Принцип считывания закодированной информации с диска аналогичен предыдущему.
Из всего вышесказанного можно сделать вывод, что компьютер «понимает» всего два числа: $0$ и $1$. И именно один двоичный разряд и является минимальной единицей измерения памяти компьютера, которая называется «бит», т. е. бит – это ячейка памяти компьютера, в которую можно записать $1$ или $0$.
е. бит – это ячейка памяти компьютера, в которую можно записать $1$ или $0$.
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Другой единицей измерения информации является байт.
Байт – это восемь подряд расположенных битов. Общее количество комбинаций двоичных значений в байте равно $28 = 256$.
$1 байт = 8 битам$; $1 Кб = 210 байта = 1024 байта$; $1 Мб = 210 Кбайт = 1024 Кбайта$; $1 Гб = 210 байта = 1024 килобайта$; $1 Тб = 210 гигабайта = 1024 гигабайта$.
Достоинства двоичной системы счисления заключаются в ее простоте, благодаря которой она широко используется в технике. Устройства, работающие в двух состояниях (включено, выключено), наиболее помехоустойчивы, и, как следствие, более надежны.
Восьмеричная система счисления
В основе данной системы счисления находятся $8$ цифр: от $0$ до $7$. Цифра $1$, указанная в самом младшем разряде, означает, как и в десятичном числе просто $1$. Та же цифра $1$ в следующем разряде означает $8$, в следующем $64$ и т.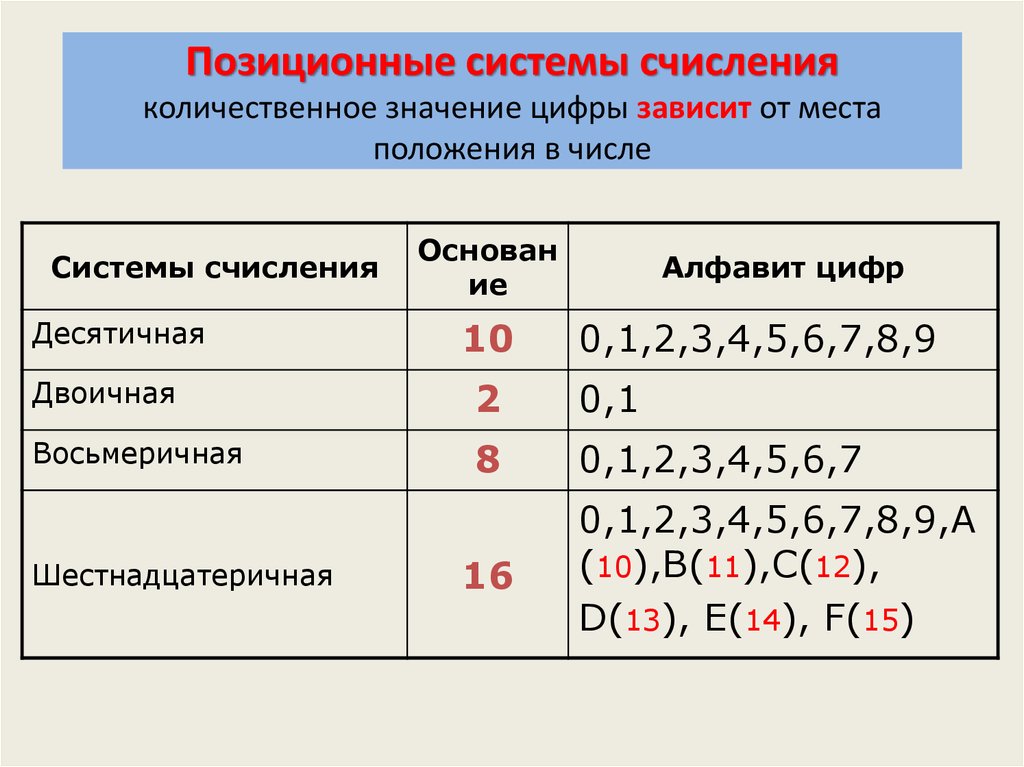 д. Число $100$ (восьмеричное) – это число $64$ (десятичное). Чтобы перевести в двоичную систему, например, число $611$ (восьмеричное), необходимо каждую цифру числа заменить эквивалентной тройкой двоичных чисел. Для перевода многозначного двоичного числа в восьмеричную систему счисления необходимо разбить его на тройки по правую сторону и по левую и заменить каждую тройку соответствующей восьмеричной цифрой.
д. Число $100$ (восьмеричное) – это число $64$ (десятичное). Чтобы перевести в двоичную систему, например, число $611$ (восьмеричное), необходимо каждую цифру числа заменить эквивалентной тройкой двоичных чисел. Для перевода многозначного двоичного числа в восьмеричную систему счисления необходимо разбить его на тройки по правую сторону и по левую и заменить каждую тройку соответствующей восьмеричной цифрой.
Читайте также: Чит на невидимость в слизарио
В таблице приведены соответствия чисел в восьмеричной и десятичной системах.
В технике данная система находит широкое применение, так с помощью нее можно компактно записывать двоичные числа.
Шестнадцатеричная система счисления
Запись числа в восьмеричной системе счисления достаточно компактная, но еще компактнее она выглядит в шестнадцатеричной системе. В основу данной системы входят цифры от $0$ до $9$ и первые буквы латинского алфавита: $A$, $B$, $C$, $D$, $E$, $F$.
Цифра $1$, записанная в самом младшем разряде, означает просо единицу.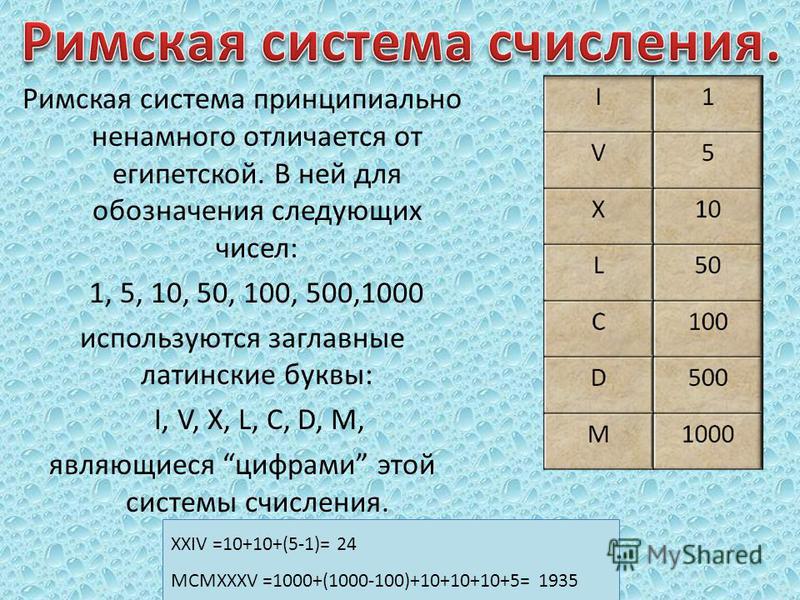 Цифра $1$ в следующем разряде – $16$ (десятичное число), в следующем – $256$ и т.д. Цифра, обозначенная латинской буквой $F$, расположенная в самом младшем разряде означает $15$ ( десятичное число).
Цифра $1$ в следующем разряде – $16$ (десятичное число), в следующем – $256$ и т.д. Цифра, обозначенная латинской буквой $F$, расположенная в самом младшем разряде означает $15$ ( десятичное число).
В таблице приведены соответствия чисел в шестнадцатеричной и десятичной системах.
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является $8$-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы $IBM/360$, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с $8$-битными символами, как, например, $PDP-11$ или $БЭСМ-6$) использовали восьмеричную систему.
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
Таблица соответствия десятеричного от 1 до 255 (decimal), двоичного (binary) и шестнадцатеричного (hexadecimal) представлений чисел.
- Автор: Мария Сухоруких
- Распечатать
Оцените статью:
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
Системы счисления — Умскул Учебник
На этой странице вы узнаете- В каких случаях 10 не равно 10?
- Как купить шоколадку у инопланетянина?
Привычная нам система счисления называется десятичной, потому что нам с детства удобно считать 10 пальцев на руках. Но так было не всегда: раньше людям было удобнее считать до 12, по количеству фаланг на пальцах одной руки. Для них и для нас число “10” имеет совершенно разное значение.
Виды систем счисленияСистема счисления — это модель, которая позволяет записывать числа по определенным правилам.
Основных типов систем счисления две:
- позиционные,
- непозиционные.
Непозиционные системы счисления основываются на том, что значение цифр никак не зависит от того, на какой позиции в числе они находятся.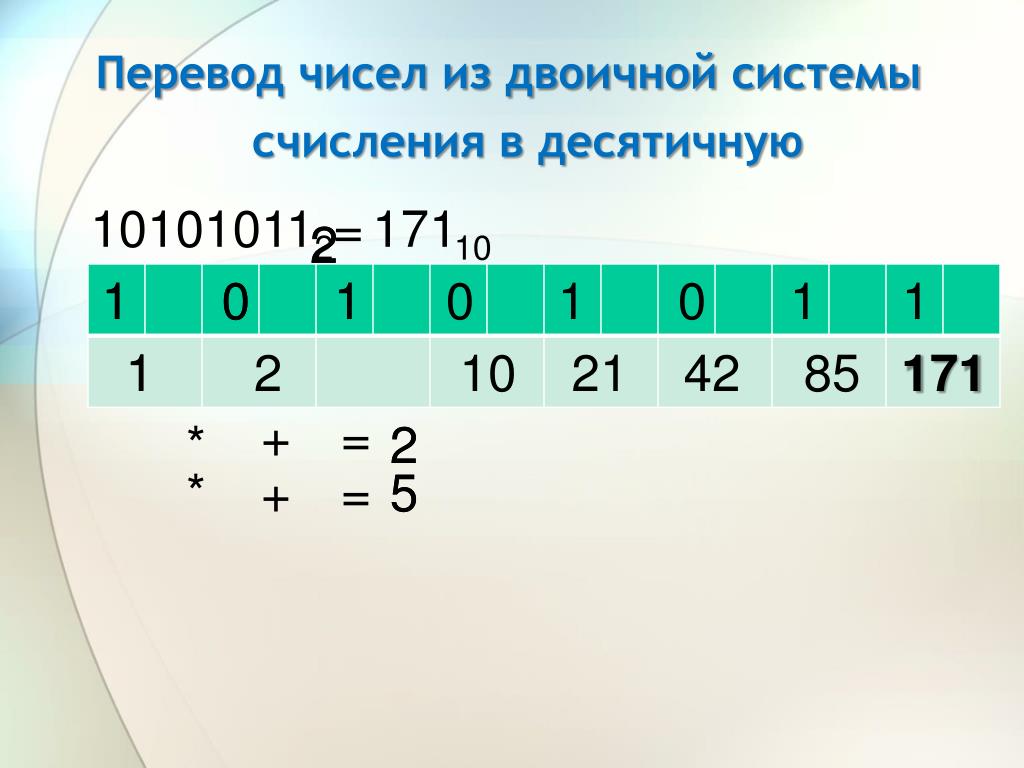
Возьмем фермера и его овец. Какой способ записать количество овец — самый удобный? Самый простой пример — подсчет с помощью одной насечки. Тогда мы подсчитываем овец в своем стаде поштучно, обозначая при записи каждую отдельной засечкой.
Очевидно, что это неудобно. В наших интересах размножать овец. Но чем их больше, тем менее читаема такая запись. Когда мы добьемся невиданных высот в скотоводстве, и у нас станет 2796 голов, их подсчет с помощью одной засечки будет невозможен.
Римская система счисления — еще один известный пример непозиционной системы счисления. В ней уже появляются символы для обозначения отдельных чисел. Но в какой бы позиции символ ни стоял, он все еще значит только самого себя:
- I — 1;
- V — 5;
- X — 10 и так далее.
Римская система счисления упрощает запись чисел, но не решает проблему неудобства чтения полностью. Например, число 2796 в римской записи будет выглядеть как MMDCCXCVI.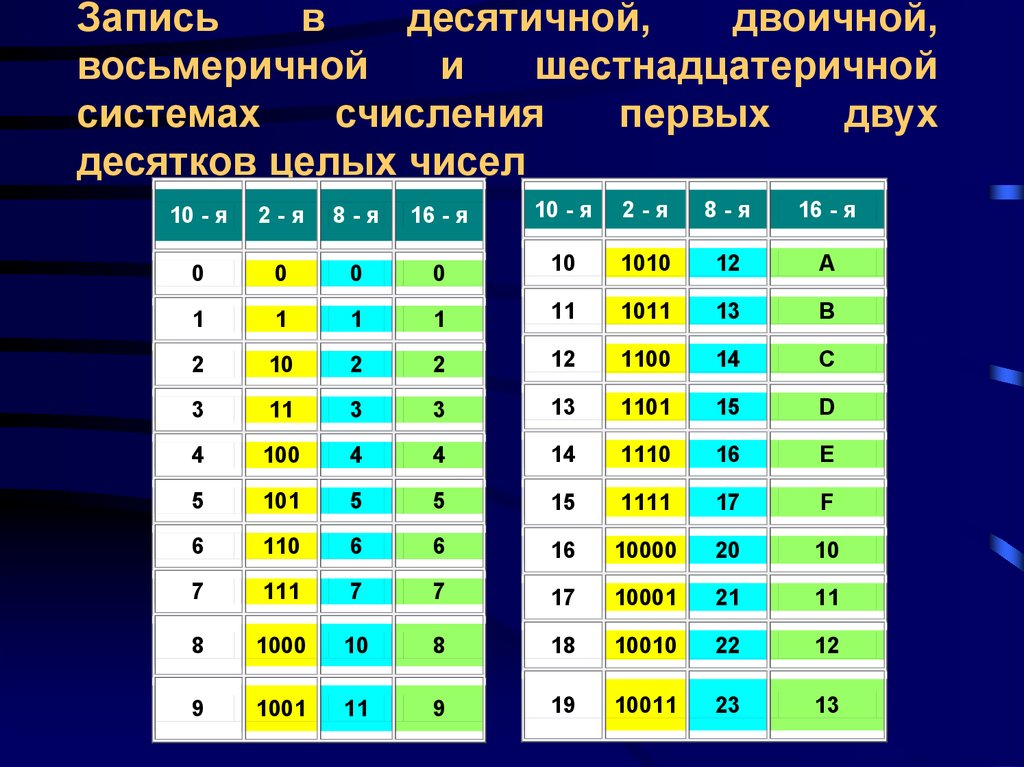 Уже неприятно.
Уже неприятно.
В позиционных системах счисления значение цифры зависит от того, на какой позиции она стоит.
На примере нашей родной десятичной системы счисления, мы с вами понимаем, что в числе 1234:
- 1 — количество тысяч, и обозначает не 1, а 1000;
- 2 обозначает количество сотен и понимается как 200;
- 3 отвечает за количество десятков и означает 30;
- 4 стоит на самой последней позиции и означает количество единиц, поэтому в данном случае 4 — это 4.
Это сильно упрощает чтение чисел любого размера, так как меняется сам принцип их чтения:
- В непозиционной системе счисления (на примере римской): СХХIII = 100 + 10 + 10 + 1 + 1 + 1 = 123.
- В позиционной: 123 = 100 + 20 + 3.
Именно позиционную систему счисления выберет грамотный фермер, чтобы подсчитать количество овечек.
Основание позиционной системы счисленияПозиционная система счисления характеризуется ее основанием — количеством цифр, которые она использует для записи чисел.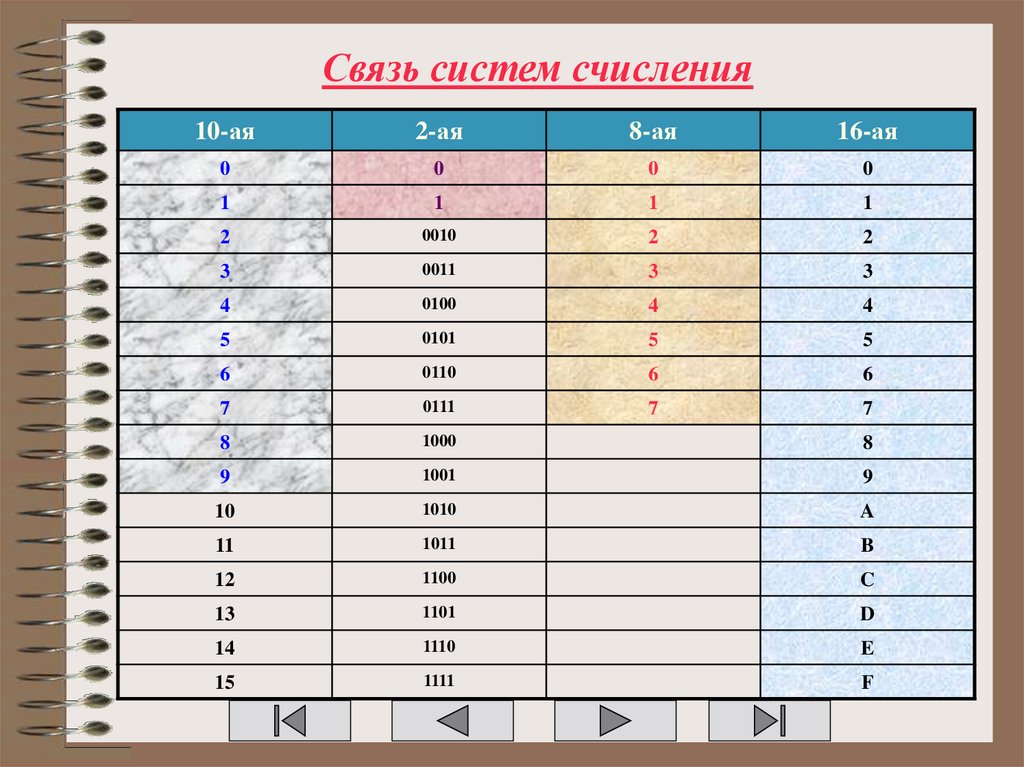
- Десятичная система счисления (10сс) использует 10 цифр — от 0 до 9, с ней мы знакомы с детства.
- Компьютеру роднее двоичная система счисления (2сс), которая использует 2 цифры — 1 и 0.
- В двенадцатеричной системе счисления (12сс) помимо цифр 0–9 необходимы еще два символа. Для удобства заменим их буквами: A = 10, B = 11. Теперь имеем 12 символов от 0 до B.
- Также небезызвестная система счисления — шестнадцатеричная. Для нее кроме цифр 0–9 нужно еще больше символов, чтобы обозначить все цифры. Происходит это по аналогии — каждая новая буква отвечает за большее значение: A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
| В каких случаях 10 не равно 10? Мы используем числа тогда, когда кончаются цифры. Привычная нам система счисления называется десятичной, потому что использует 10 цифр — от 0 до 9. Для записи значений больше 9, мы начинаем строить числа из цифр. Первое такое число — 10. Если бы мы использовали другое количество цифр, всё выглядело бы иначе. |
Построение числа в непривычных нам системах счисления происходит точно так же, как и в 10сс:
- Увеличиваем значения единиц, используя доступные цифры.
- Как только цифры закончились, значение единиц обнуляется. Появляется новый разряд десятков, который также увеличивается от 1 до предела системы счисления.
- Когда любой разряд числа принимает значение максимальной цифры — разряд выше увеличивается на 1, а текущий разряд обнуляется.
Например:
- В 10сс число 88 будет увеличиваться так:
88 → 89 → 90 → 91 → 92 → … 99 → 100;
- В 2сс разряды будут появляться быстрее из-за маленького количества цифр:
1 → 10 → 11 → 100 → 101 → 110 → 111 → 1000;
- В 12сс чуть медленнее, так как цифр больше:
8 → 9 → A → B → 10 → 11 → … 18 → 19 → 1A → 1B → 20 → … 99 → 9A → 9B → A0 → A1 → … AA → AB → B0 → B1 → … BA → BB → 100.
Арифметика, как и построение числа, во всех системах счисления одинакова:
- Изменение разрядов происходит с единиц.
- При сложении избыток суммы увеличивает разряд выше (то самое “6 пишем, 1 в уме”).
- В вычитании при необходимости занимаем значение из старшего разряда, уменьшая его на 1.
| Как купить шоколадку у инопланетянина? Уметь переводить числа из 10сс в другие и обратно важно для того, чтобы торговать с инопланетянами. |
Подсчитав количество пальцев на руках продавца шоколадок, важно научиться переводить числа из одной системы счисления в другую.
Полная запись числа a1a2a3…ai, где ai — цифра числа под номером i, состоящей из k символов и с основанием системы счисления n, будет выглядеть как:
a1a2a3…ai…ak = a1 * nk — 1 + a2 * nk — 2 + … + ai * nk — i + … + ak * n0.
На примерах:
- 123 в 10сс расписывается как: 1 * 102 + 2 * 101 + 3 * 100;
- 1010 в 2сс: 1 * 23 + 0 * 22 + 1 * 21 + 0 * 20;
- A9B в 12сс: 10 * 122 + 9 * 121 + 11 * 120.
Такой записи числа достаточно, чтобы перевести значение числа из любой системы счисления в 10сс — нужно посчитать значение составленной записи:
- 10102 = 1 * 23 + 0 * 22 + 1 * 21 + 0 * 20 = 8 + 0 +2 + 0 = 1010;
- 5259 = 5 * 92 + 2 * 91 + 5 * 90 = 5 * 81 + 2 * 9 + 5 * 1 = 42810;
- A9B12 = 10 * 122 + 9 * 121 + 11 * 120 = 10 * 144 + 9 * 12 + 11 * 1 = 155910.
Принцип деления с остатком поможет переводить числа в другую сторону — из 10сс в любую другую систему счисления.
Алгоритм перевода следующий:
- Делим исходное число на основание новой системы счисления.
- Остаток от деления — новая найденная цифра числа.
- Целую часть от деления снова делим на основание. Записываем остаток как новую цифру искомой записи, а целую часть от деления — как цель следующего деления. Снова делим целую часть на основание.
- Деление происходит до тех пор, пока целая часть от деления не станет равна 0.
- Полученные в качестве остатков от деления цифры нового числа читаются в обратном порядке.
Для примера давайте переведем число 2589 в 7сс:
- На первом шаге делим исходное число на 7, записывая остаток от деления как новую цифру и целую часть как оставшееся значение.
- На втором шаге делаем то же самое, но с целой частью предыдущего деления — теперь делим ее на 7.

- И так до тех пор, пока целая часть от деления не будет равна 0.
Интересующее нас значение находится в самом правом столбце и читается снизу вверх.
258910 = 103567
Перевод в системы счисления с основанием, больше 10, происходит так же. Просто надо не забывать, что цифры больше 9, будут обозначаться соответствующими буквами.
Например, таблица перевода десятичного числа 48406 в 16сс будет выглядеть следующим образом:
И искомое значение будет BD16.
ЛайфхакМежду 2сс и системами счисления, в основании которых стоит степень двойки (4сс, 8сс, 16сс), есть связь, которую можно использовать для быстрого перевода из 2сс в них и обратно. Для этого используется следующая таблица:
Алгоритм перевода состоит в следующем:
- Вычисляется степень, в которую нужно возвести 2, чтобы получить основание необходимой системы счисления.

- Используется количество столбцов таблицы, равное этой степени. Отсчет ведем с правого столбца.
- При переводе из 2сс весь код разбивается на кодовые слова длиной, равной степени — при необходимости в начало записи добавляются нули. Отдельные кодовые слова подставляются в нижнюю строку таблицы. Цифра записи числа в новой системе счисления будет равна сумме цифр верхней строки, под которыми стоит 1 кодового слова.
- При переводе в 2сс каждая цифра представляется как сумма цифр верхней строки таблицы. Цифрам, которые используются в сумме, соответствуют 1 кодового слова 2сс, а не использующимся — 0.
На примере:
- Для перевода между 2сс и 4сс используется часть таблицы:
- Перевод из 2сс в 4сс:
110001 = 11.00.01 = (2 + 1).(0 + 0).(0 + 1) = 3.0.1 = 301
- Перевод из 4сс в 2сс:
103 = 1.0.3 = (0 + 1).(0 + 0).(2 + 1) = 01.00.11 = 10011
- Для перевода между 2сс и 8сс используется часть таблицы:
- Перевод из 2сс в 8сс:
10101011100 = 010. 101.011.100 = (0 + 2 + 0).(4 + 0 + 1).(0 + 2 + 1).(4 + 0 + 0) = 2.5.3.4 = 2534
101.011.100 = (0 + 2 + 0).(4 + 0 + 1).(0 + 2 + 1).(4 + 0 + 0) = 2.5.3.4 = 2534
- Перевод из 8сс в 2сс:
1753 = 1.7.5.3 = (0 + 0 + 1).(4 + 2 + 1).(4 + 0 + 1).(0 + 2 + 1) = 001.111.101.011 = 1111101011
- Для перевода между 2сс и 16сс используется вся таблица:
- Перевод из 2сс в 16сс:
101101111000001 = 0101.1011.1100.0001 = (0 + 4 + 0 + 1).(8 + 0 + 2 + 1).(8 + 4 + 0 + 0).(0 + 0 + 0 + 1) = 5.11.12.1 = 5BC1
- Перевод из 16сс в 2сс:
F87A = 15.8.7.10 = (8 + 4 + 2 + 1).(8 + 0 + 0 + 0).(0 + 4 + 2 + 1).(8 + 0 + 2 + 0) = 1111.1000.0111.1010 = 1111100001111010
Перевод больших чисел между системами счисления вручную неудобен и может занимать много времени. Иногда выгоднее было бы написать программу.
Перевод из 10сс в другие будем выполнять по описанному выше алгоритму. Пока исходное число больше 0, делим его на основание системы счисления. Записываем остаток от деления как новую цифру числа. Искомое число — остатки от деления, записанные в обратном порядке.
Записываем остаток от деления как новую цифру числа. Искомое число — остатки от деления, записанные в обратном порядке.
- Основным циклом программы будет while, который работает, пока исходное число больше 0.
- Новую цифру числа берем как остаток от деления исходного числа на основание новой системы счисления с помощью оператора %. Новые цифры будем записывать в новую строку, в которой и будет храниться искомая запись. Чтобы не переворачивать число в конце, можем сразу заносить каждую новую цифру не в конец, а в начало строки.
- Уменьшаем само число, деля его нацело на основание с помощью оператора //.
Например, перевод числа 258936 в 5сс.
number = 258936 n = 5 new_number = "" while number > 0: d = number % n new_number = str(d) + new_number number //= n print(new_number) Вывод: 31241221
Перевод в 10сс из других систем счисления будем производить по описанной выше формуле:
a1a2a3…ai…ak = a1 * nk — 1 + a2 * nk — 2 + … + ai * nk — i + … + ak * n0.
- Главный цикл программы — for. Он будет перебирать цифры исходного числа, а точнее, их индексы, с помощью диапазона range по длине исходного числа.
- На каждом шаге цикла цифру ai числа будем умножать на основание системы счисления этого числа n в степени, равной разности длины числа k и порядкового номера текущей цифры i — ai*nk — i . Не забываем, что индексация строки начинается с 0, а не с 1, поэтому порядковый номер цифры — на 1 больше ее индекса.
Например, переведем число 31241221 из 5сс обратно в 10сс.
number = "31241221" n = 5 new_number = 0 k = len(number) for i in range(k): new_number += int(number[i]) * n ** (k - i - 1) print(new_number) Вывод: 258936
Лайфхаки по переводу между системами счисления программой:
- для перевода числа из 10сс в 2сс, 8сс и 16сс есть встроенные команды: bin, oct и hex соответственно
- bin(123) — “0b1111011”
- oct(123) — “0o173”
- hex(123) — “0x7b”
Важно заметить, что первые два символа в записи числа окажутся лишними в нашем случае — они будут обозначать идентификатор системы счисления, в которую мы перевели число.
Чтобы сразу от него избавиться, при переводе можно использовать срез, который будет учитывать все число без этого идентификатора:
- bin(123)[2:] — “1111011”
- oct(123)[2:] — “173”
- hex(123)[2:] — “7b”
- перевести число из любой системы счисления в 10сс можно с помощью команды int. Ей необходимо передать два параметра: исходное число в виде строки и основание его системы счисления:
- int(«31241221», 5) — 258936
- int(«7b», 16) — 123
- В позиционных системах счисления, в отличие от непозиционных, значение цифры зависит от ее положения в числе.
- Основание позиционной системы счисления определяет количество используемых в ней цифр для записи чисел.
- Для перевода из 10сс в любую другую: берем остаток от деления на основание новой системы счисления в качестве цифр нового числа и записываем их в обратном порядке.
- Для перевода из любой системы счисления в 10сс: умножаем каждую цифру числа на основание его системы счисления, возведенную в степень разности длины числа и порядкового номера данной цифры.
Задание 1.
Какая цифра не может использоваться в 8сс?
- 0
- 3
- 7
- 8
Задание 2.
Для записи цифр 10-15 в 16сс используются …
- буквы A-F
- буквы А-Д
- буквы U-Z
- любые символы по договоренности
Задание 3.
Десятичное число 101 в 2сс будет выглядеть как…
- 101
- 101101
- 1100101
- 1010011
Задание 4.
Шестнадцатеричное число FBA000 в 10сс будет выглядеть как …
- 16490496
- 69409461
- 61400900
- Это некорректная запись числа в 16сс
Задание 5.
Что сделает запись на языке Python — int(“777”, 8)?
- Переведет число 777 из 10сс в 8сс
- Переведет число 8 из 10сс в 777сс
- Переведет число 777 из 8сс в 10сс
Ответы: 1. — 4; 2. — 1; 3. — 3; 4. — 1; 5. — 3.
— 4; 2. — 1; 3. — 3; 4. — 1; 5. — 3.
Системы счисления | Образовательная социальная сеть
Всероссийская интернет-выставка достижений учащихся
Раздел — учебные проекты
математика
Системы счисления
Авторы: Семакина Маргарита Сергеевна
Исаева Аида Мукаиловна
ученицы 5Г класса
МБОУ «Средняя
общеобразовательная школа
№ 6» г. Когалым ХМАО-Югра
Руководитель: Плашевская Светлана
Григорьевна
учитель математики
МБОУ «Средняя общеобразовательная школа № 6» г. Когалым
Когалым
ХМАО-Югра
г. Когалым, 2013
Оглавление
Введение | стр.2 |
| стр.2 |
| стр.3 |
2.1 Непозиционные системы счисления | стр.3 |
2.2 Позиционные системы счисления | стр.3 |
3. Практическая часть | |
3.1 Сложение и вычитание | стр.4 |
| стр.4 |
| стр.5 |
Заключение | стр.7 |
Список используемой литературы | стр. |
Приложение | стр.8 |
1
Введение
На протяжении всей своей жизни мы сталкиваемся с числами и выполняем над ними арифметические действия. Нас это не удивляет. Мы воспринимаем это, как факт, как само собой разумеющееся. А откуда возникли числа и счет? Что такое система счисления? Где сейчас мы сталкиваемся с ними? Нам стало очень интересно, и мы решили изучить эту тему.
Данная тема нам интересна еще и потому, что в настоящее время двоичная система счисления приобрела большое значение в связи с ее применением в электронных вычислительных машинах. Системы счисления с основанием 8 и 16 применяются в программировании различных процессов на вычислительной технике.
Мы поставили перед собой цель: познакомиться с историей возникновения счета и систем счисления, изучить перевод чисел из одной системы в другую и арифметические действия в различных системах счисления.
1. Из истории
В древности людям приходилось считать на пальцах. Кроме пальцев считать нужно было много предметов, к счету привлекали больше участников. Один считал единицы, второй – десятки, третий – сотни. Очевидно, такой счет лег в основу системы счисления, принятой почти у всех народов, она называется десятичной системой. Счет с основанием десять применяли и у восточных славян.
Кроме пальцев считать нужно было много предметов, к счету привлекали больше участников. Один считал единицы, второй – десятки, третий – сотни. Очевидно, такой счет лег в основу системы счисления, принятой почти у всех народов, она называется десятичной системой. Счет с основанием десять применяли и у восточных славян.
Где люди ходили босиком, по пальцам легко было считать до 20. Сохранились следы использования при счете основания двадцать. Например, во французском языке число 80 в дословном переводе на русский язык звучит как «четырежды двадцать».
Так же был распространен счет дюжинами, то есть счет, при котором пользовались системой с основанием 12 (приложение 1). Её происхождение связано с 12 фалангами на четырёх пальцах руки (кроме большого). Еще и сейчас некоторые предметы принято считать дюжинами. Столовые приборы состоят из полудюжины или дюжины комплектов.
В древнем Вавилоне, где математика была очень высоко развита, существовала весьма сложная шестидесятеричная система счисления. В наше время мы тоже используем эту систему. Например: 1 час=60 минут; 1 минута=60 секунд.
В наше время мы тоже используем эту систему. Например: 1 час=60 минут; 1 минута=60 секунд.
Самой древней из пальцевых систем счисления считается пятеричная. Эта система зародилась, и наибольшее распространение получила в Америке. Ее создание относится к эпохе, когда человек считал по пальцам одной руки. До последнего времени у некоторых племен пятеричная система счисления сохранилась еще в чистом виде.
2
Все системы (пятеричная, двенадцатеричная, двадцатеричная) связаны с тем или иным способом счёта по пальцам рук (или рук и ног). Переход человека к пальцевому счету привел к созданию различных систем счисления.
2. Система счисления
Система счисления — это способ записи чисел с помощью цифр.
Цель создания системы счисления — выработка наиболее удобного способа записи количественной информации.
Системы счисления, которые использовали ранее, и которые используются в настоящее время можно разделить на две большие группы: позиционные и непозиционные.
2.1. Непозиционные системы счисления.
В настоящее время и в технике и в быту широко используются как позиционные, так и непозиционные системы счисления.
В непозиционных системах счисления вес цифры не зависит от позиции, которую она занимает в числе. Пример непозиционной системы счисления – римская система счисления (приложение 2). Возникшая в древнем Риме она просуществовала до наших дней. Традиционно применяют ее при нумерации веков или при составлении оглавлений печатных трудов. Римские цифры можно встретить на циферблатах часов.
В современной жизни наиболее яркий вариант использования непозиционной системы счисления — это денежные отношения. Мы с ними сталкиваемся каждый день. Здесь никому не приходит в голову, что сумма, которую мы выкладываем в магазине за продукты, может зависеть от того, в каком порядке мы расположим монеты на столе. Номинал монеты не зависит от того, в каком порядке она была вынута из кошелька. Это классический пример непозиционной системы счисления.
2.2. Позиционные системы счисления.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число. Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание можно принять любое натуральное число — два, три, четыре, шестнадцать и т.д. Следовательно, возможно бесконечное множество позиционных систем: двоичная, состоящая из цифр 0 и 1; троичная, состоящая из цифр 0,1,2; и так далее.
3
Позиционные системы удобны тем, что они позволяют записывать большие числа с помощью небольшого числа знаков, просто и легко выполняются арифметические действия.
3. Практическая часть.
Для чисел, записанных в десятичной системе, мы пользуемся правилами сложения и умножения чисел «столбиком», деления – «углом». Эти же правила полностью применимы и для чисел, записанных в любой другой позиционной системе. Считать мы будем в каждой системе своей меркой. Например в троичной системе мерка 3, в пятеричной мерка 5, в восьмеричной мерка 8.
Считать мы будем в каждой системе своей меркой. Например в троичной системе мерка 3, в пятеричной мерка 5, в восьмеричной мерка 8.
3.1 Сложение и вычитание. | ||
Пример 1 4435 + 345; Решение: 4435 345 10325 | Пример2 2478 + 6538; Решение 2478 6538 11228
| Пример 3 75428 – 7568; Решение: 75428 7568 65648 |
3.2 Умножение и деление. При умножении и делении, можно использовать мерки, но для более быстрого счета мы составили таблицы умножения ( приложения 3; 4; 5; 6; 7 ). | ||
Пример 1 2458 ∙ 318; Решение: 2458 318 245 757 100358 | Пример 2 6337 ∙ 2547; Решение: 6337 2547 3465 4431 1566 2410057 4 | Пример 3 2234 ∙ 324; Решение: 2234 324 1112 2001 211224 |
Пример 4 14126 : 356; Решение: 14126 356 114 246 232 232 0
| Пример 5 130325 : 145; Решение: 130325 145
43 33 102 102 0 | Пример 6 3228 : 168; Решение: 3228 168 16 178 142 142 0 |
3. 3. Перевод чисел из одной системы в другую
3. Перевод чисел из одной системы в другую
Как перевести число, записанное в одной системе, например в четверичной, в десятичную?
Любое число можно разложить по разрядам и каждый разряд измеряется своей меркой. В десятичной системе у единиц мерка 1, у десятков 10, у сотен 100. Следовательно, в четверичной системе счисления, у единиц мерка 1, у десятков – 4, у сотен – 16, у тысяч – 64,
у восьмеричной системы мерками будут 1; 8; 64 и так далее.
Пример 1 Пример 2
Перевести 1378 в десятичную систему. Перевести 3124 в десятичную систему.
Решение: Решение:
1378 = 1 ∙ 64 + 3 ∙ 8 + 7 ∙ 1 = 95. 3124 = 3 ∙ 16 + 1 ∙ 4 + 2 ∙ 1 = 54.
Пример 3
Перевести 1011012 в десятичную систему.
1011012 = 1∙ 32 + 1 ∙8 + 1 ∙ 4 + 1 = 45.
Пример 4
Перевести число 860 в восьмеричную систему счисления.
В данном примере мы воспользуемся меркой 8. Но если при переводе в десятичную систему мы умножали каждый разряд, то теперь будем делить число на мерку. Если частное больше мерки, то мы частное опять делим на мерку и так делим, пока частное не
5
станет меньше мерки. Остатки от деления как раз и есть разряды в данной системе счисления. Первый остаток – это разряд единиц, второй остаток – это разряд десятков и так далее.
Решение:
- 8 860 = 15348
- 107 8
60 8 13 8
56 27 8 1
4 24 5
3
Пример 5 Пример 6.
425 = 1156 382 = 30125
Решение: Решение:
- 6 382 5
- 7 6 35 76 5
5 6 1 32 5 15 5
1 30 26 15 3
2 25 0
1
При переводе чисел из троичной системы счисления в семеричную, мы сразу переводили из троичной в десятичную, а потом в семеричную. Этот способ занимает больше времени. Мы предположили, а что если при переводе из одной системы в другую сразу считать мерками той системы, в которую переводим. Проверили на нескольких примерах, и оказалось, что наше предположение верно. Тогда мы записали правило перевода.
Этот способ занимает больше времени. Мы предположили, а что если при переводе из одной системы в другую сразу считать мерками той системы, в которую переводим. Проверили на нескольких примерах, и оказалось, что наше предположение верно. Тогда мы записали правило перевода.
Чтобы перевести число из одной системы счисления в другую, нужно каждый разряд считать той меркой, в которую переводим данное число.
Пример 7.
Перевести 1425 в семеричную систему.
1425 = (3 ∙ 7 + 4 ) + (2 ∙ 7 + 6) + 2 = 30 + 20 + 15 = 657;
Число 15 считаем следующим образом: 4 + 6 + 2 =12 = 157.
Проверка: 1425 = 1∙ 25 + 4 ∙ 5 + 2 = 47; 47 : 7 = 657
Пример 8.
Перевести 3234 в шестеричную систему.
3234 = (8 ∙ 6 + 0) + (1 ∙ 6 +2) + 3 = 120 + 10 + 5 = 1356;
6
Проверка: 3234 = 3 ∙ 16 + 2 ∙ 4 + 3 = 59; 59 = 1356
- 6
54 9 6
5 6 1
3
Пример 9.
Перевести 689 в пятеричную систему.
689 = (10 ∙ 5 + 4) + (1∙ 5 + 3) = 200 + 10 + 12 = 2225
Проверка: 689 = 6 ∙ 9 + 8 = 62; 62 : 5 = 2225
- 5
5 12 5
12 10 2
10 2
2
Заключение
При выполнении данной работы мы самостоятельно изучили математические операции сложения, вычитания, умножения и деления в различных системах счисления. Составили таблицы, которые помогают гораздо быстрее умножать и делить числа.
Составили таблицы, которые помогают гораздо быстрее умножать и делить числа.
Познакомившись с системами счисления, мы узнали очень много нового и полезного, и считаем, что эта наука необходима для развития общества. Сложно представить мир без вычислительной техники. Ведь именно двоичная система получила широкое распространение в различных областях техники, в особенности в современных вычислительных машинах и компьютерах.
Числа правят миром.
Пифагор
Список литературы
- Виленкин Н.Я., Шибалов Л.П, Шибалова З.Г. За страницами учебника математики. М. Просвещение. АО Учебная литература 1996г.
- Выгодский Н.Я. Справочник по элементарной математике. М.Наука 1972г.
- Математика и программирование. «Универсальная энциклопедия школьников». Минск ТОО «ХАРВЕСТ», 1996г.
- Энциклопедический словарь юного математика. Составитель Савин А.П., М.Педагогика 1989г.
7
Приложение 1
8
Приложение 2
1 | 5 | 10 | 50 | 100 | 500 | 1000 |
I | V | X | L | C | D | M |
Примеры римских чисел.
7 | VII |
13 | XIII |
27 | XXVII |
45 | VL |
90 | XC |
120 | CXX |
9
Приложение 3
Таблица умножения в четверичной системе счисления.
Х | 2 | 3 |
2 | 104 | 124 |
3 | 124 | 214 |
10
Приложение 4
Таблица умножения в пятеричной системе счисления.
х | 2 | 3 | 4 |
2 | 45 | 115 | 135 |
3 | 115 | 145 | 225 |
4 | 135 | 225 | 315 |
11
Приложение 5
Таблица умножения в шестеричной системе счисления.
х | 2 | 3 | 4 | 5 |
2 | 46 | 106 | 126 | 146 |
3 | 106 | 136 | 206 | 236 |
4 | 126 | 206 | 246 | 326 |
5 | 146 | 236 | 326 | 416 |
12
Приложение 6
Таблица умножения в семеричной системе счисления.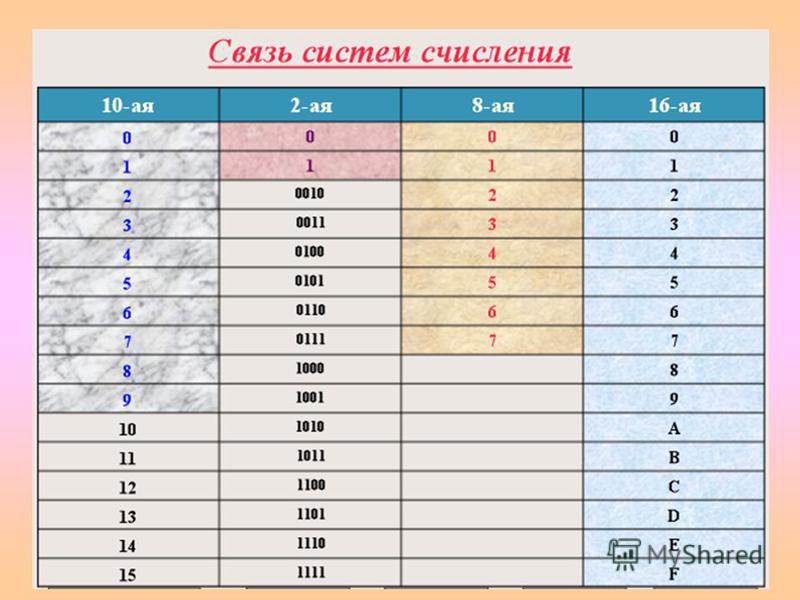
х | 2 | 3 | 4 | 5 | 6 |
2 | 47 | 67 | 117 | 137 | 157 |
3 | 67 | 127 | 157 | 217 | 247 |
4 | 117 | 157 | 227 | 267 | 337 |
5 | 137 | 217 | 267 | 347 | 427 |
6 | 157 | 247 | 337 | 427 | 517 |
13
Приложение 7
Таблица умножения в восьмеричной системе счисления.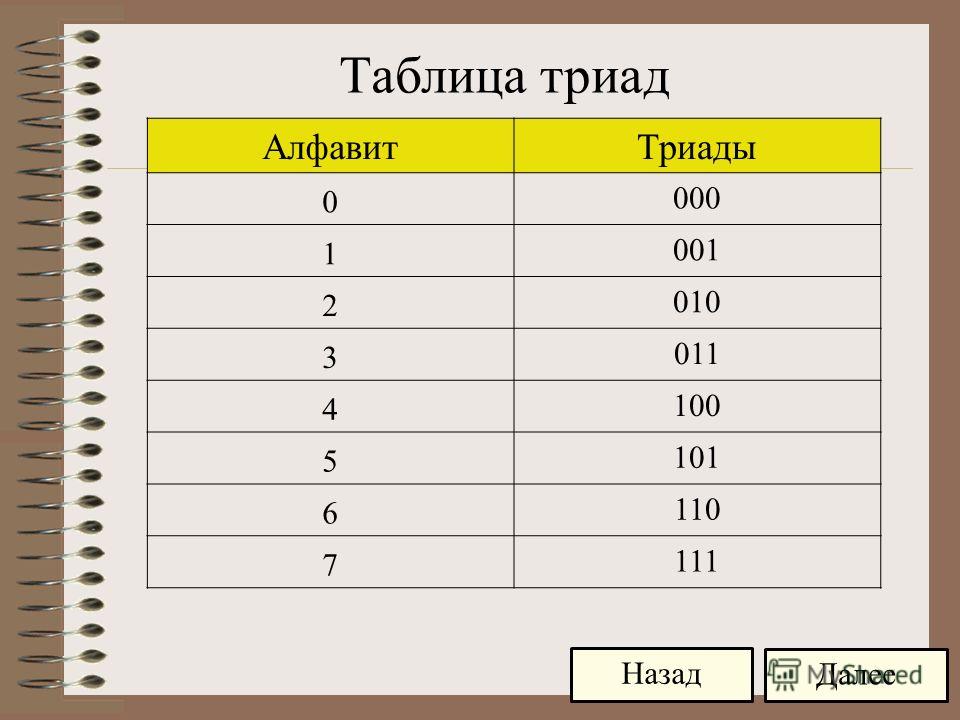
х | 2 | 3 | 4 | 5 | 6 | 7 |
2 | 48 | 68 | 108 | 128 | 148 | 168 |
3 | 68 | 118 | 148 | 178 | 228 | 258 |
4 | 108 | 148 | 208 | 248 | 308 | 348 |
5 | 128 | 178 | 248 | 318 | 368 | 438 |
6 | 148 | 228 | 308 | 368 | 448 | 528 |
7 | 168 | 158 | 348 | 438 | 528 | 618 |
14
Приложение 8
Таблица умножения в девятеричной системе счисления.
х | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
2 | 49 | 69 | 89 | 119 | 139 | 159 | 179 |
3 | 69 | 109 | 139 | 169 | 209 | 239 | 269 |
4 | 89 | 139 | 179 | 229 | 269 | 319 | 359 |
5 | 119 | 169 | 229 | 279 | 339 | 389 | 449 |
6 | 139 | 209 | 269 | 339 | 409 | 469 | 539 |
7 | 159 | 239 | 319 | 389 | 469 | 549 | 629 |
8 | 179 | 269 | 359 | 449 | 539 | 629 | 719 |
15
Официальный сайт МБОУ «ОШ №10»
Дата урока 8 апреля
Тема урока: Представление числовой информации с помощью систем счисления.
Ход урока
- Посмотрите видеоурок https://www.youtube.com/watch?v=qkhPtM4ZT8g
- Запишите тему урока в тетрадь. Прочитайте текст.
Историческая справка
Люди научились считать еще в незапамятные времена. Сначала они просто различали один предмет перед ними или нет. Если предмет был не один, то говорили «много». Постепенно появилось слово для обозначения двух предметов. Счет парами очень удобен.
Наиболее древней и простой «счетной машиной» издавна являются пальцы рук и ног. И даже в наше время еще пользуются этим «счетным прибором», который всегда при нас. На пальцах можно решать примеры не только в пределах десяти. В древние времена люди ходили босиком. Поэтому они могли пользоваться для счета пальцами как рук, так и ног.
Записывали числа поначалу совсем просто: делали зарубки на куске дерева или кости. На этой кости тридцать тысяч лет назад сделаны нарезки, они показывают, что уже тогда наши предки умели не только считать, но и записывать результаты счета!
Когда понадобилось записывать большие числа, то для пятерок и десяток стали придумывать новые знаки.
Запомнить большие числа трудно, поэтому к «счетной машине» рук и ног добавляли механические приспособления. Веревочные счеты с узелками применялись и в России, и во многих странах Европы. Остатками этого способа является практикуемое еще до сих пор завязывание узелков на носовых платках «на память». Так, одни пользовались для запоминания чисел камешками, зернами, веревкой с узелками, другие — палочками с зарубками. Это были первые счетные приборы, которые в конце концов привели к образованию различных систем счисления
Система счисления — это совокупность правил и приемов записи чисел с помощью набора цифровых знаков.
- позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
- непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.
Непозиционные СС. Единичная система счисления. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): зарубок, черточек, точек. Позже значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня (счетные палочки для обучения счету; полоски, нашитые на рукаве, означают на каком курсе учится курсант военного училища). Неудобства такой системы записи чисел и ограниченность ее применения очевидны: чем большее число надо записать, тем длиннее строка из палочек.
Позже значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня (счетные палочки для обучения счету; полоски, нашитые на рукаве, означают на каком курсе учится курсант военного училища). Неудобства такой системы записи чисел и ограниченность ее применения очевидны: чем большее число надо записать, тем длиннее строка из палочек.
Римская система счисления является непозиционной системой. В ней для записи чисел используются буквы латинского алфавита. При записи чисел в римской системе счисления значением числа является алгебраическая сумма цифр, в него входящих. При этом цифры в записи числа следуют, как правило, в порядке убывания их значений, и не разрешается записывать рядом более трех одинаковых цифр. В том случае, когда за цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в целом является отрицательным.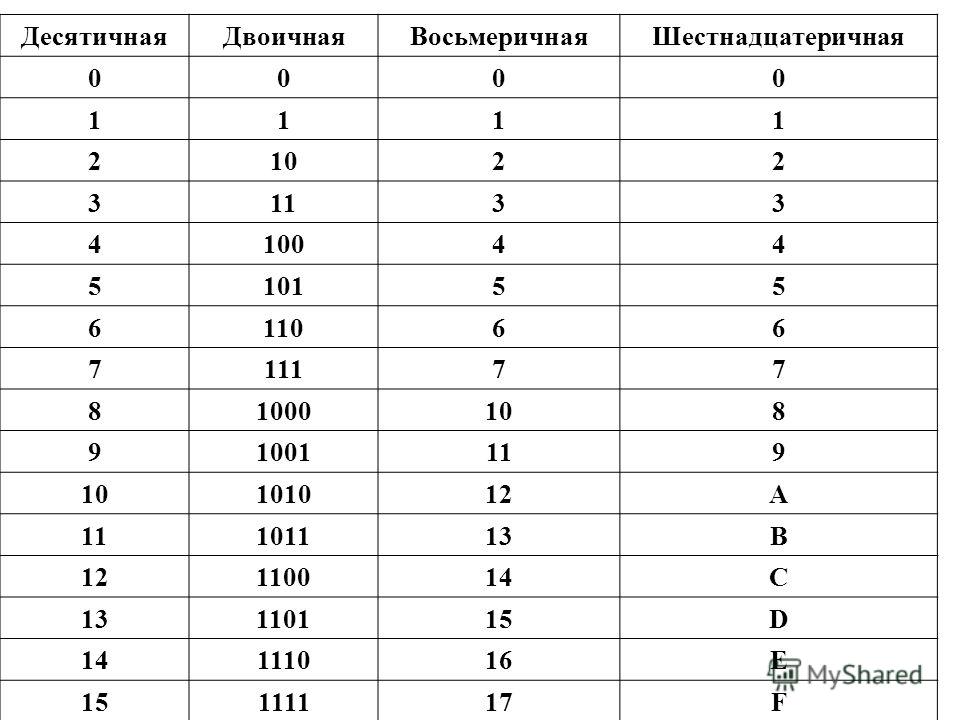 Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.
Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.
Таблица 1. Запись чисел в римской системе счисления
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 50 | 100 | 500 | 1000 |
I | II | III | IV | V | VI | VII | VIII | IX | X | L | C | D | M |
Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами. По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.
По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.
Мы с вами более подробно рассмотрим позиционные системы счисления.
В позиционной системе счисления основными понятиями являются понятие алфавита и основания системы счисления.
Алфавитом системы счисления называется совокупность всех цифр.
Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: 7810, 110001012, AF1216 и т. д.
Количество цифр, составляющих алфавит, называется его мощностью.
В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места(разряда), где он расположен.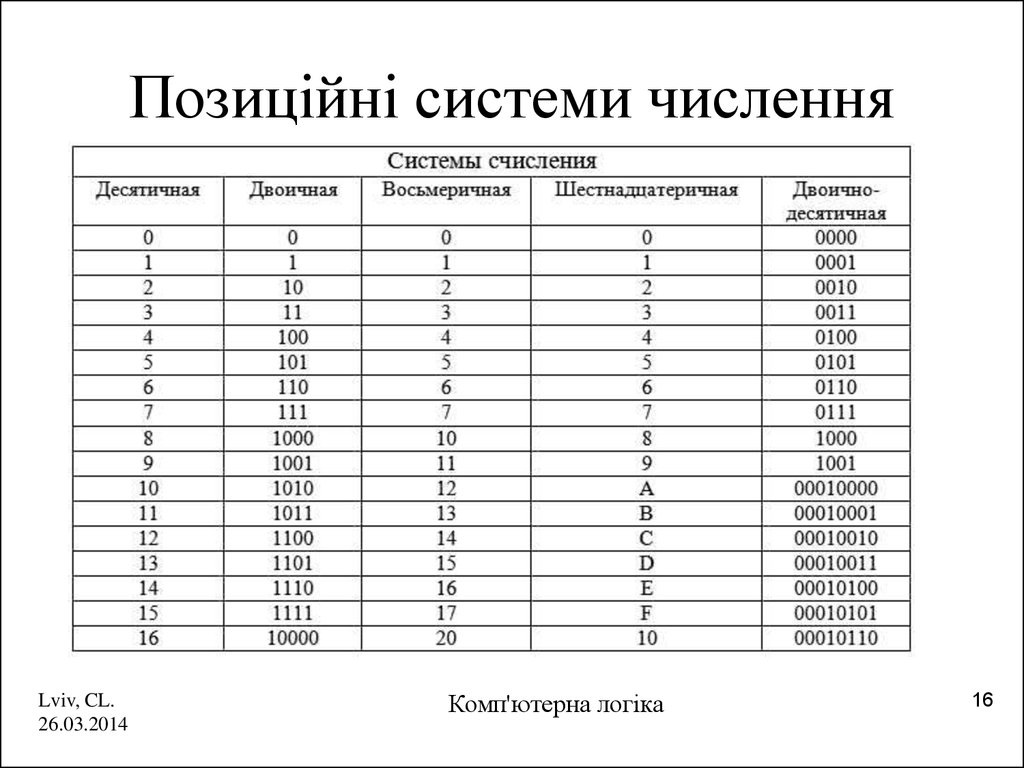 Разряд — номер позиции в числе. Нумеруются справа налево, начиная с нуля.
Разряд — номер позиции в числе. Нумеруются справа налево, начиная с нуля.
Пример. Число618410 запишется в форме многочлена следующим образом:
618410 = 6*10 3 +1*10 2 +8*10 1 +4*10 0
Виды систем счисления.
В компьютерах принято использовать 4 основные системы счисления – двоичную, восьмеричную, десятичную и шестнадцатеричную. Именно их подробно рассмотрим.
Десятичная система счисления – в настоящее время наиболее известная и используемая. Древнее изображение десятичных цифр не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 — углов нет, 1 — один угол, 2 — два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.
Десятичная система впервые появилась в Индии примерно в VI веке новой эры. Индийская нумерация использовала девять числовых символов и нуль для обозначения пустой позиции
Десятичная система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.
Если взять правило, по которым строятся числа в десятичной системе счисления, заменив основание 10 на натуральное число N, можно построить позиционную систему счисления с основанием N.
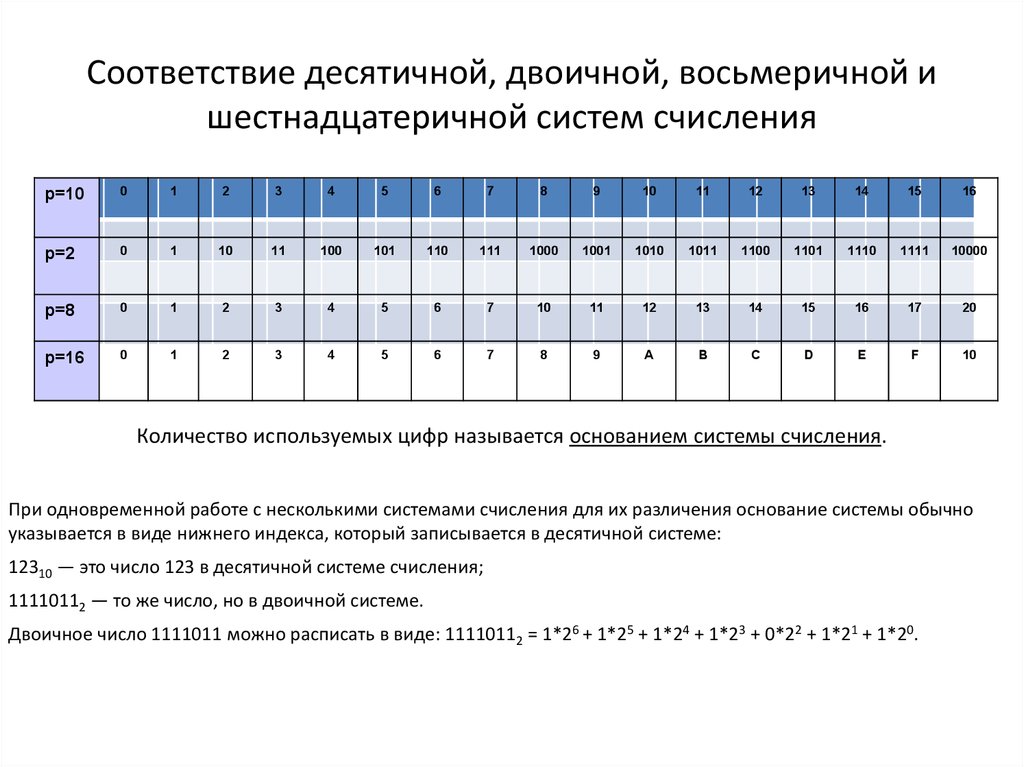
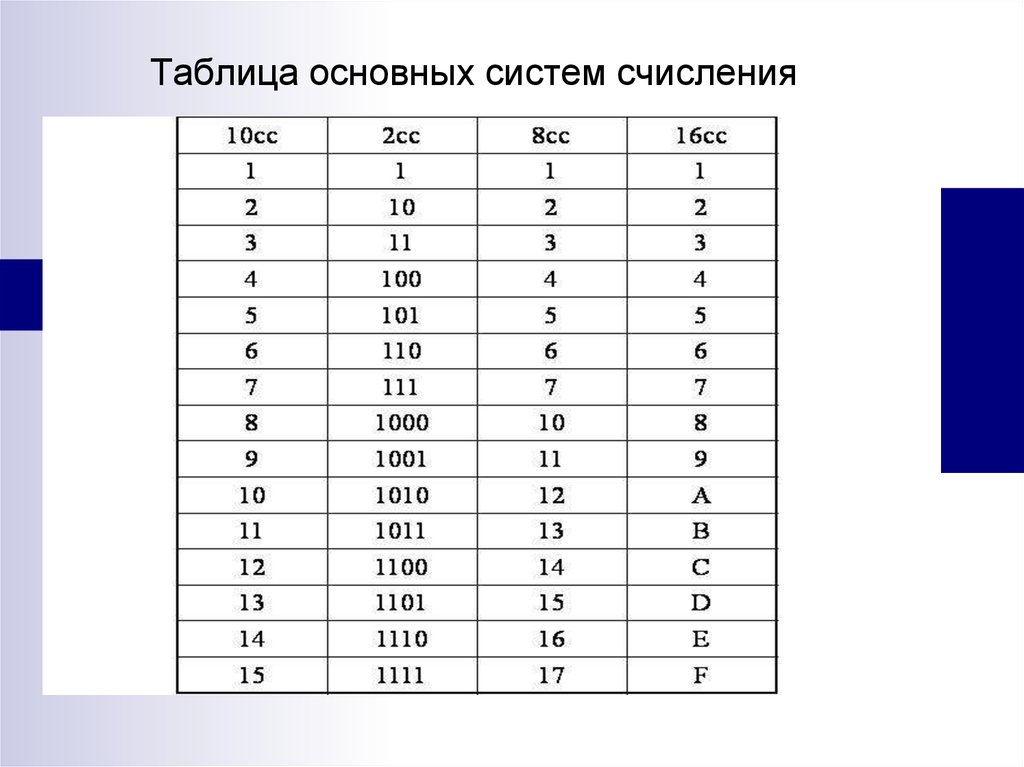
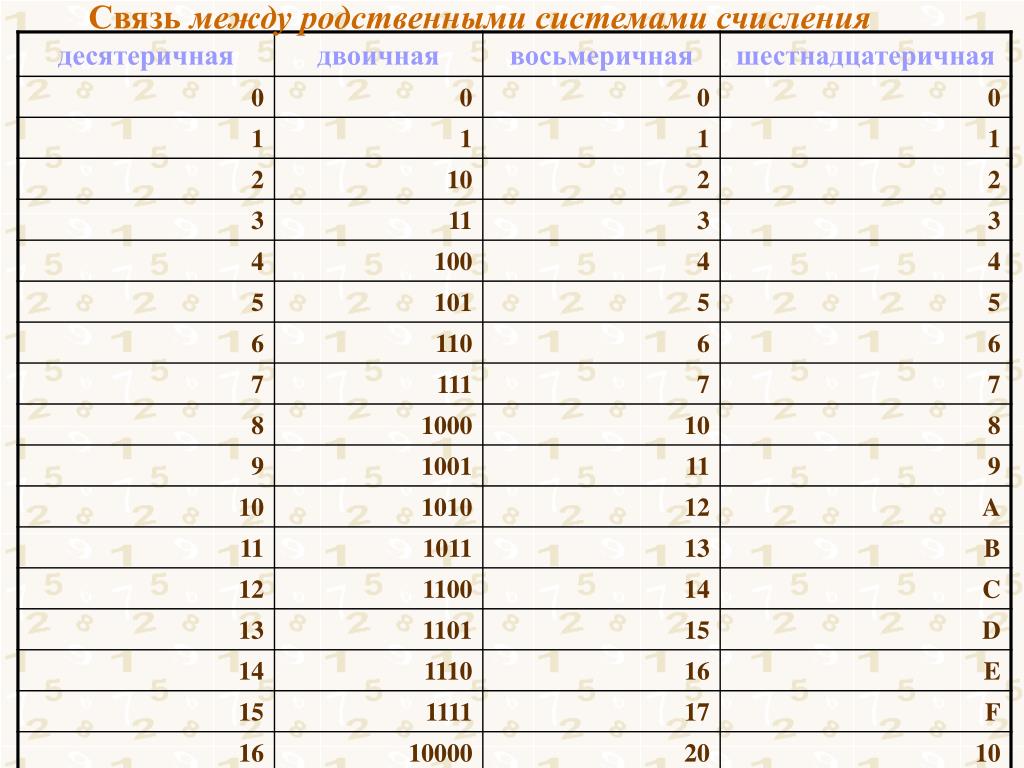
В вычислительных машинах используется двоичная система счисления, её основание — число 2. Для записи чисел в этой системе используют только две цифры — 0 и 1. Двоичная система счисления была придумана математиками и философами задолго до появления компьютеров, еще в ХVII — ХIХ веках. Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной — восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост. Ниже приведена таблица соответствия чисел, записанных в разных системах.
Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост. Ниже приведена таблица соответствия чисел, записанных в разных системах.
Учащиеся заполняют таблицу в тетрадях
Правила перевода чисел из одной системы счисления в другую
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
1. При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.
Числа 101001102 , 7038 , 23FA116 перевести в десятичную систему счисления.
101001102=1*27+0*26+1*25+0*24+0*23+1*22+1*21+0*20=128+32+4+2=16610
7038=7*82+0*81+3*80=448+3=44710
23FA116=2*164+3*163+15*162+10*161+1*160=131072+12288+3840+160+1=147361
2.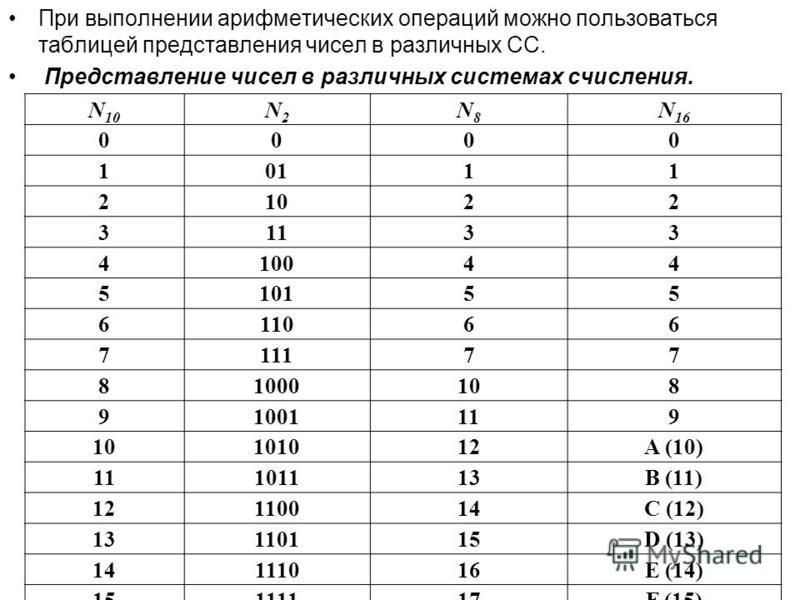 Правило перевода из десятичной системы счисления в систему с основанием q:
Правило перевода из десятичной системы счисления в систему с основанием q:
1. Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.
2. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).
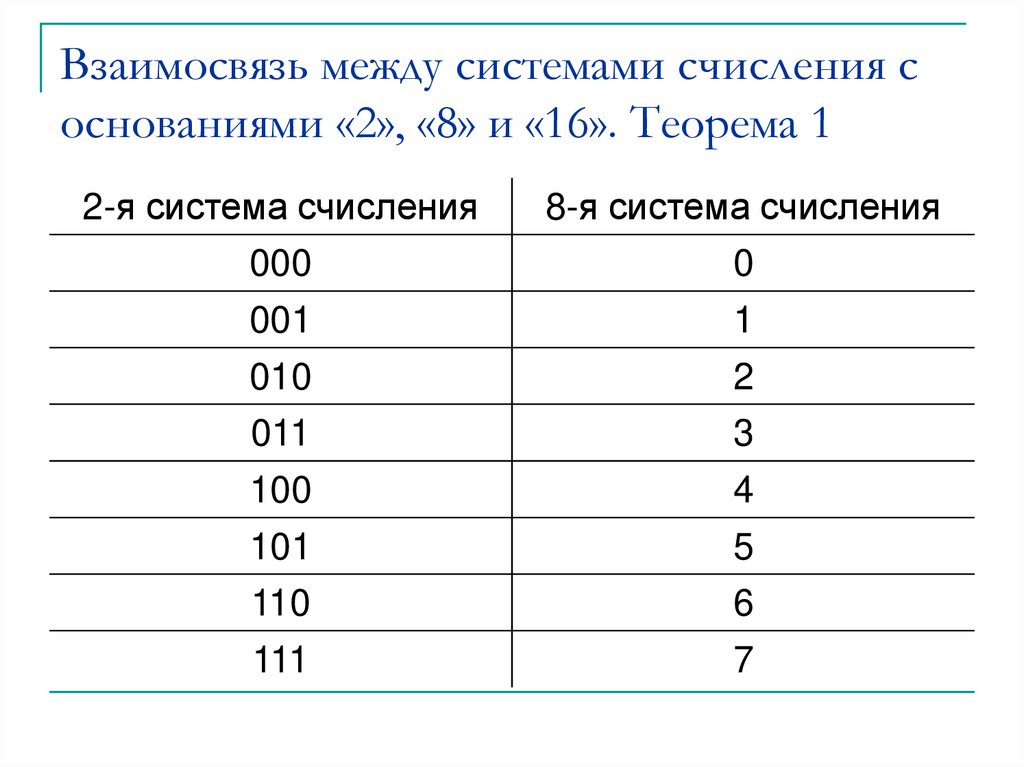
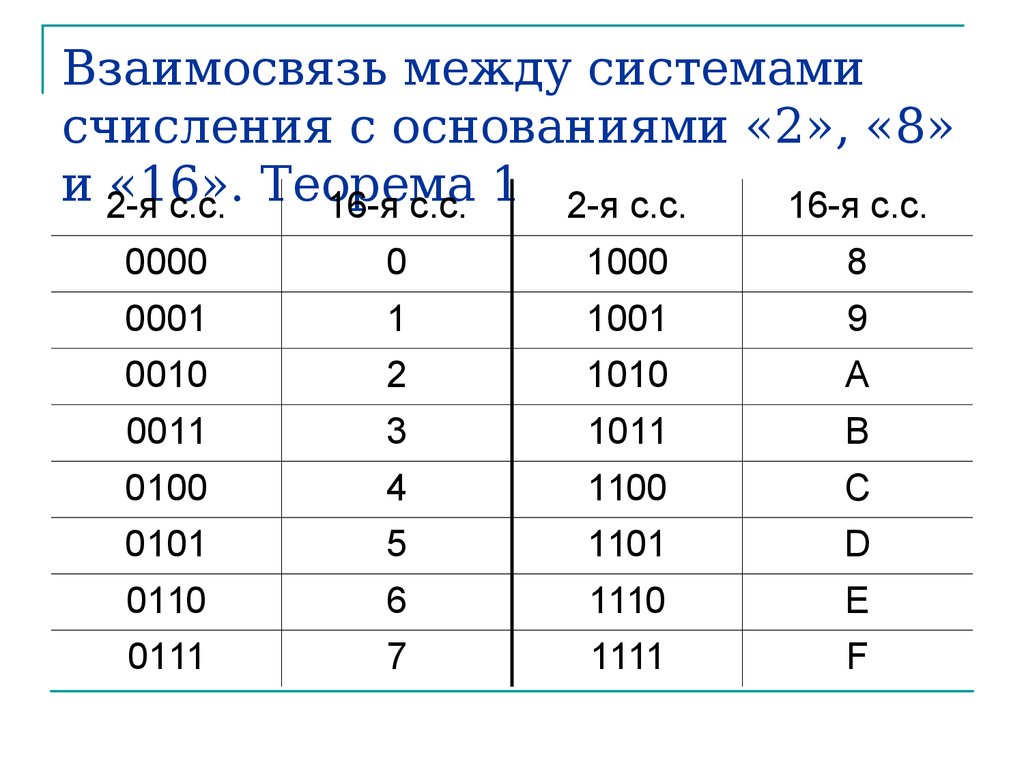
3. Чтобы перевести число из двоичной системы в восьмеричную (шестнадцатеричную), его нужно разбить на триады (тетрады), начиная с младшего разряда (справа налево), в случае необходимости дополнив старшую триаду (тетраду) нулями, и каждую триаду (тетраду) заменить соответствующей восьмеричной (шестнадцатеричной) цифрой (табл.).
Число 100101101112 перевести в восьмеричную и в шестнадцатеричную системы счисления.
4. Для перевода восьмеричного (шестнадцатеричного) числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой (тетрадой).
Числа 7268 и 74С16 перевести в двоичную систему счисления.
7268= 111 010 1102
74С16 = 0111 0100 11002 (при записи числа первый 0 не пишется)
5. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
Число FAE16 перевести в восьмеричную систему счисления.
FAE16=1111101011102
111 110 101 1102=76568
Число 6358 перевести в шестнадцатеричную систему счисления.
6358 =1100111012
1 1001 11012=19D16
- Составьте опорный конспект в виде таблиц, графиков, схем. На листе А4 (можно на листе в клетку)
- Домашнее задание. Задайте к прочитанному тексту 6 вопросов. Запишите их в тетрадь.
- Запишите дату своего рождения в римской системе счисления.
открытых учебников | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Объяснение систем нумерации | Library.Automationdirect.com
Существует несколько типов систем нумерации, обычно используемых в оборудовании автоматизации: двоичная, шестнадцатеричная, восьмеричная, двоично-десятичная и с плавающей запятой (действительная). Как их использовать может быть запутанным. В этой статье с нашей веб-страницы технической поддержки объясняются различные системы нумерации.
Компьютеры, включая ПЛК, используют систему нумерации с основанием 2, называемую двоичной или логической. В базе 2 есть только две допустимые цифры: 0 и 1 (ВЫКЛ и ВКЛ). Вы могли бы подумать, что система счисления, построенная на базе 2 только с двумя возможными значениями, будет сложной, но это можно сделать с помощью кодирования, используя несколько цифр.
Каждая цифра в системе счисления по основанию 2, на которую ссылается компьютер, называется битом. Когда четыре бита сгруппированы вместе, они образуют то, что известно как полубайт. Восемь бит или два полубайта — это байт. Шестнадцать бит – или два байта – это слово (таблица 1). Тридцать два бита или два слова — это двойное слово.
Когда четыре бита сгруппированы вместе, они образуют то, что известно как полубайт. Восемь бит или два полубайта — это байт. Шестнадцать бит – или два байта – это слово (таблица 1). Тридцать два бита или два слова — это двойное слово.
Двоичные числа не являются для нас «естественными», так как мы выросли, используя систему счисления с основанием 10, в которой используются числа 0-9. В этой статье различные базы будут показаны в виде числа с индексом. Например, десятичное число 10 будет равно 10 9.1112 10 .
В таблице 2 показано, как числа с основанием 2 соотносятся с их десятичными эквивалентами.
Часть 1001 2 будет равна десятичному числу 9 или (1*2 3 + 1*2 0 ) или (8 10 + 1
10 9). Байт 11010101 2 будет равен 213 10 или (1*2 7 + 1*2 6 + 1*2 4 + 1*2 2 + 1*2 0. ) или (128 10 + 64 10 + 16 10 + 4 10 +1 10 ).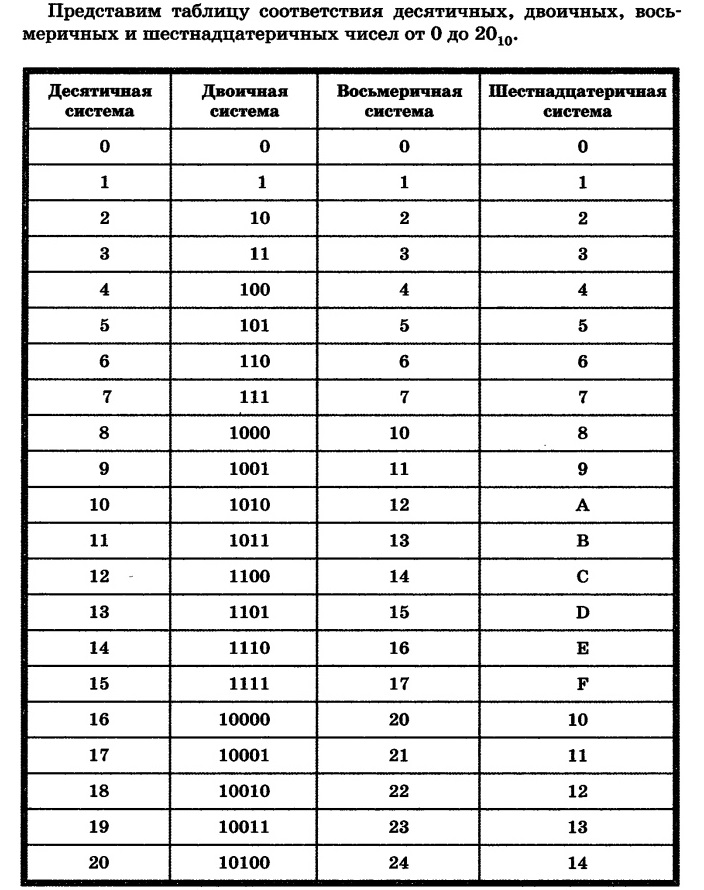
Как вы, наверное, заметили, двоичную систему счисления не очень легко интерпретировать. Для нескольких битов это легко, но большие числа обычно занимают много места при их записи, и трудно отслеживать позицию бита при преобразовании. Вот где использование альтернативной системы нумерации может быть преимуществом. Одной из первых используемых систем счисления была шестнадцатеричная или сокращенно Hex.
HEX-это система нумерации, которая использует базу 16. Числа 0-9 10 представлены нормально, но число 10 10 по 15 9111-это нормально, но число 10 10 по 15 9111. 10 представлены буквами от A до F соответственно (таблица 3). Это хорошо работает с двоичной системой, так как каждый полубайт (1111 2 ) равен 15 10 . Следовательно, для 16-битного слова у вас может быть возможное шестнадцатеричное значение FFFF 9. 1112 16 . См. пример в Таблице 4.
1112 16 . См. пример в Таблице 4.
Преобразование шестнадцатеричных чисел в десятичные работает почти так же, как и двоичные. C2 16 будет равно 194 10 или (12*16 1 + 2*16 0 ) или (192 10 +2 13 9111). A6D4 16 будет равен 42708 10 или (10*16 3 +6*16 2 +13*16 1 +4*16 0 ) или (40960 10 +1536120 0 ) Или (40960 10 +153660 0 ) или (40960 10 +1536120 0 ) или (40960 10 +153620) 10 + 208 10 +4 10 ).
Восьмеричные числаВосьмеричная система счисления аналогична шестнадцатеричной системе в интерпретации битов (Таблица 5). Разница заключается в том, что максимальное значение восьмеричного числа равно 7, так как это основание 8.
Например, 63 8 равно 51 10 или (6*8 1 + 3*8 0 ) или (48 10 +3 10 ).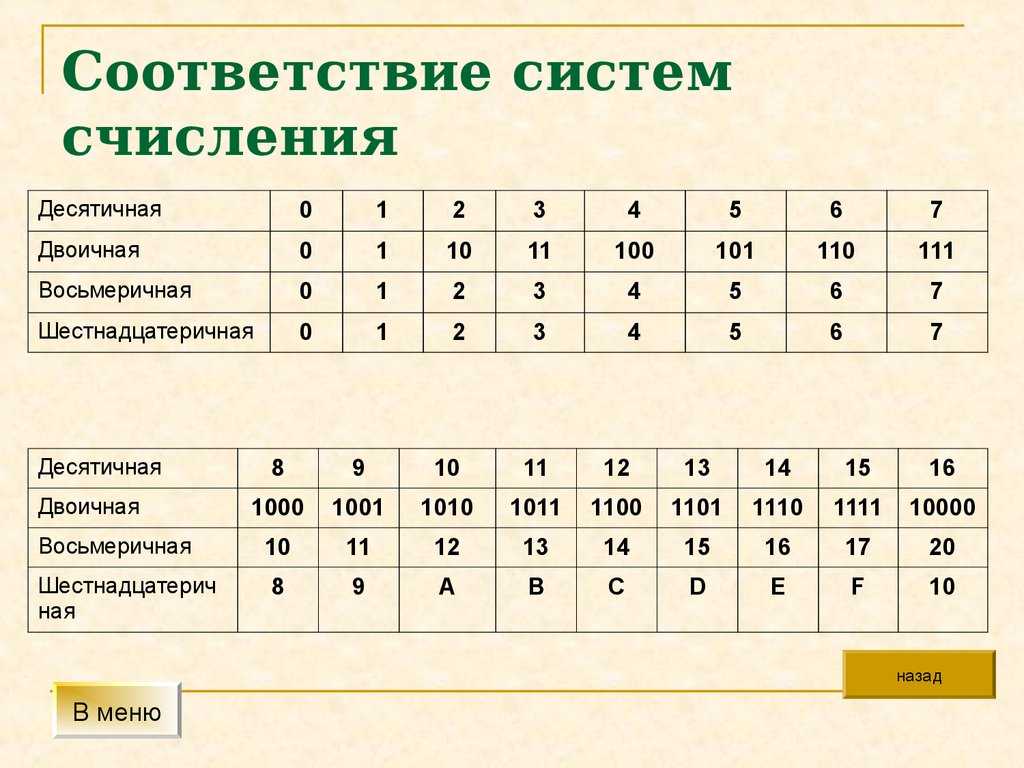
Система счисления в двоично-десятичной системе счисления, как и восьмеричная и шестнадцатеричная, основана на данных, закодированных битами (таблица 6). Это основание 10 (десятичное), но это двоично-десятичное число. Как мы увидим позже, между BCD и Binary существует большая разница.
Одним из преимуществ двоично-десятичного кода является то, что он читается как десятичное число, тогда как 867 двоично-десятичных означает 867 десятичное число. Преобразование не требуется. Однако, как и во всем, что связано с компьютером, есть проблемы, о которых стоит беспокоиться.
Вещественные числа (с плавающей запятой)Термины «Вещественное» и «Плавающая запятая» описывают числа с плавающей запятой IEEE-754. Большинство ПЛК используют 32-битный формат для чисел с плавающей запятой (действительных) (таблица 7).
Формула и раскладка номера следующая:
Число = 1. M*2(E-127)
M*2(E-127)
Число = число, которое необходимо преобразовать в число с плавающей запятой
M = мантисса
E = показатель степени
Вычисление формата вещественного числа является очень сложной операцией. Если вас интересует процесс преобразования, в Интернете есть множество документов, в которых подробно описаны все детали.
Возможно, вы заметили, что для формата действительных чисел не указано ни минимальное, ни максимальное значение. Диапазон от отрицательной бесконечности до положительной бесконечности. Сказав это и заметив, что для создания каждого числа можно использовать только 32 бита, легко предположить, что не все числа могут быть представлены. Это на самом деле так. Формату Real присуща степень погрешности.
Я уверен, вам интересно, сколько ошибок может существовать, и если ошибок много, то почему используется этот формат? Это действительно зависит от приложения. Для большинства приложений ПЛК, если вы не стремитесь к 100% точности, формат Real не вызовет особых проблем.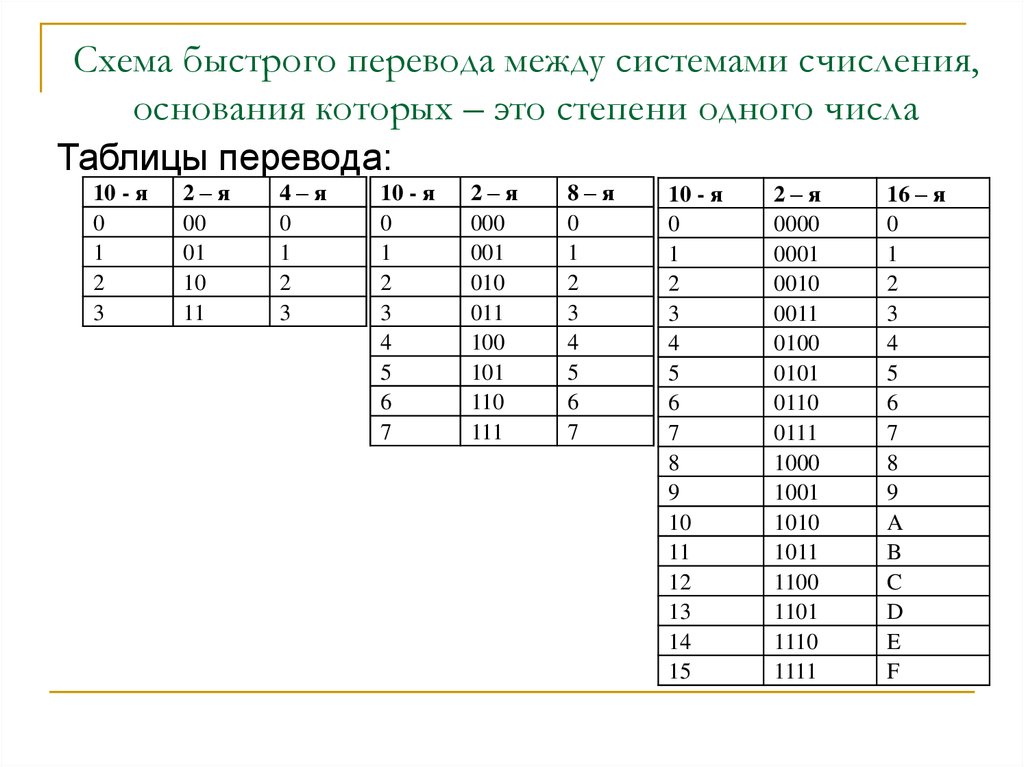 В большинстве случаев внутреннюю ошибку можно игнорировать, но важно знать, что она существует.
В большинстве случаев внутреннюю ошибку можно игнорировать, но важно знать, что она существует.
Иногда возникает путаница в связи с различиями между типами данных, используемыми в ПЛК. Хотя данные хранятся одинаковым образом (0 и 1), существуют различия в том, как их интерпретирует ПЛК.
Хотя все форматы основаны на системе нумерации по основанию 2 и данных с битовым кодированием, формат данных отличается. В таблице 8 показаны битовые комбинации и значения для различных форматов.
Несоответствие типов данных Несоответствие типов данных является распространенной проблемой при использовании интерфейса оператора. Диагностика может быть сложной задачей, пока вы не определите симптомы. Поскольку ПЛК использует двоично-десятичный формат в качестве собственного формата, многие люди склонны думать, что он взаимозаменяем с двоичным форматом (целое число без знака).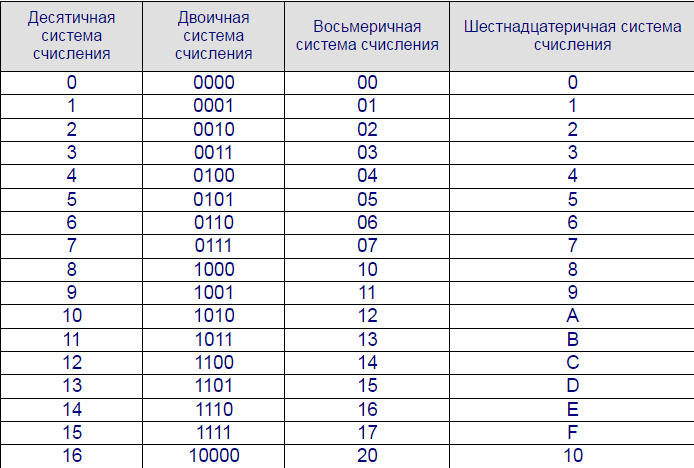 В какой-то степени это верно, но не в данном случае. Таблица 9показывает, как различаются двоично-десятичные и двоичные числа.
В какой-то степени это верно, но не в данном случае. Таблица 9показывает, как различаются двоично-десятичные и двоичные числа.
Как видно из таблицы, BCD и Binary используют один и тот же битовый шаблон, пока вы не дойдете до десятичного числа 10. Как только вы дойдете до 10, битовый шаблон изменится. Битовая комбинация BCD для десятичного числа 10 фактически равна значению 16 в двоичном формате, что приводит к скачку числа на шесть цифр при просмотре в виде BCD. При больших числах ошибка увеличивается. Двоичные значения от 10 до 15 Decimal фактически недействительны для типа данных BCD.
Давайте посмотрим на большее число, показанное в Таблице 10.
В качестве двоично-десятичного числа значение равно 4096. Если мы интерпретируем преобразованное двоично-десятичное число как двоичное, десятичное значение будет 16534. Точно так же, если мы интерпретируем двоичное число как двоично-десятичное, десятичное значение будет 1000.
До сих пор мы имели дело только с беззнаковыми типами данных.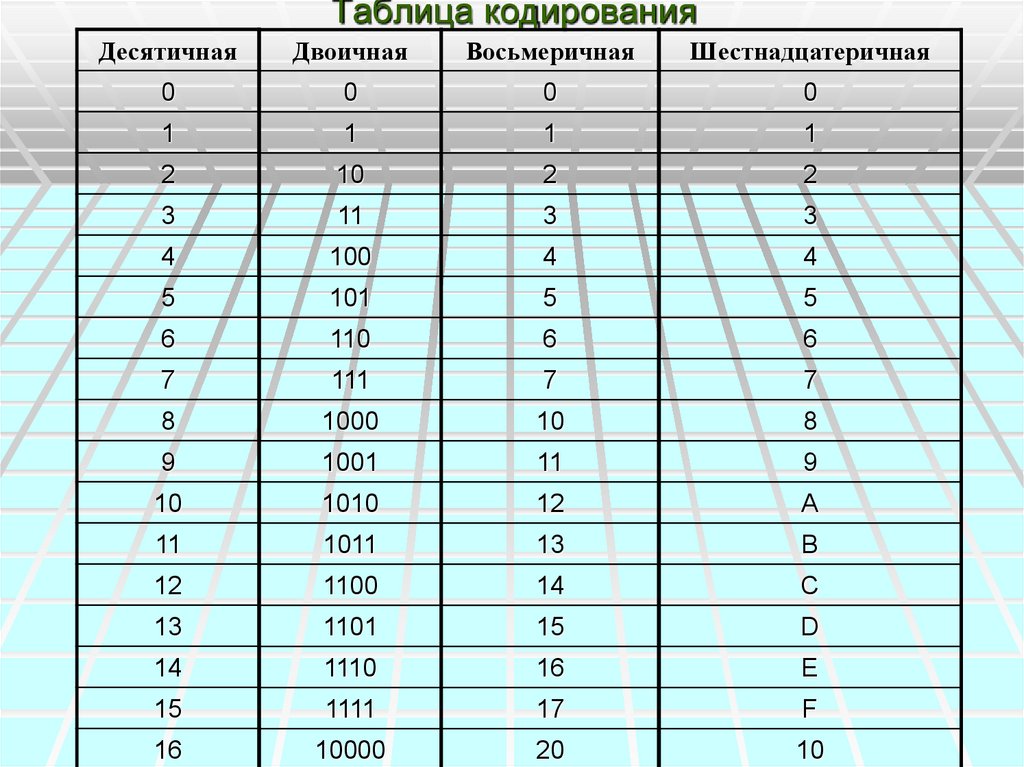 Теперь поговорим о знаковых типах данных (отрицательных числах). Представление BCD нельзя использовать для подписанных типов данных.
Теперь поговорим о знаковых типах данных (отрицательных числах). Представление BCD нельзя использовать для подписанных типов данных.
Чтобы указать, что число отрицательное или положительное, мы должны присвоить ему бит. Обычно это старший значащий бит (MSB), как показано в таблице 11. Для 16-битного числа это бит 15. Это означает, что для 16-битных чисел мы имеем диапазон от -32 767 до 32 767.
У нас есть два способа кодирования отрицательного числа: дополнение до двух и знак величины плюс. Эти два метода несовместимы.
Пока значение положительное (бит 15 выключен), правила работают аналогично двоичному. Если бит 15 включен, то мы должны знать, какой метод кодирования использовался.
Знак Величины Плюс расшифровать проще всего. В основном отрицательное число имеет тот же формат, что и положительное число, за исключением того, что бит 15 включен (таблица 12).
Дополнение до двух немного сложнее. Формула состоит в том, чтобы инвертировать двоичное значение и добавить единицу (таблица 13).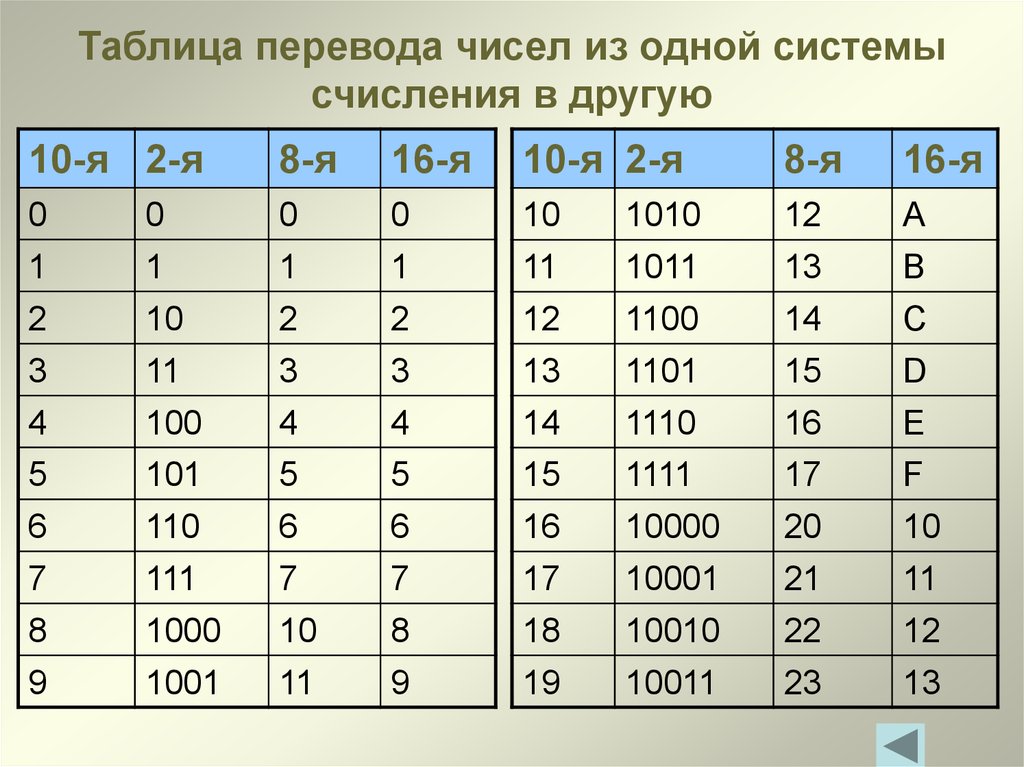
Очевидно, что системы нумерации различаются и в то же время схожи. Очень важно знать, какая система используется, чтобы правильно запрограммировать приложение. Методический и логический подход к пониманию используемой системы счисления делает интерпретацию данных менее сложной.
Первоначально опубликовано: 1 сентября 2005 г. / Пересмотрено 22 января 2021 г.
Системы счисления — определение, типы систем счисления, правила преобразования
Системы счисления — это системы в математике, которые используются для выражения чисел в различных формах и понимаются компьютерами. Число — это математическое значение, используемое для подсчета и измерения объектов, а также для выполнения арифметических вычислений. Числа имеют различные категории, такие как натуральные числа, целые числа, рациональные и иррациональные числа и так далее. Точно так же существуют различные типы систем счисления, которые имеют разные свойства, такие как двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления.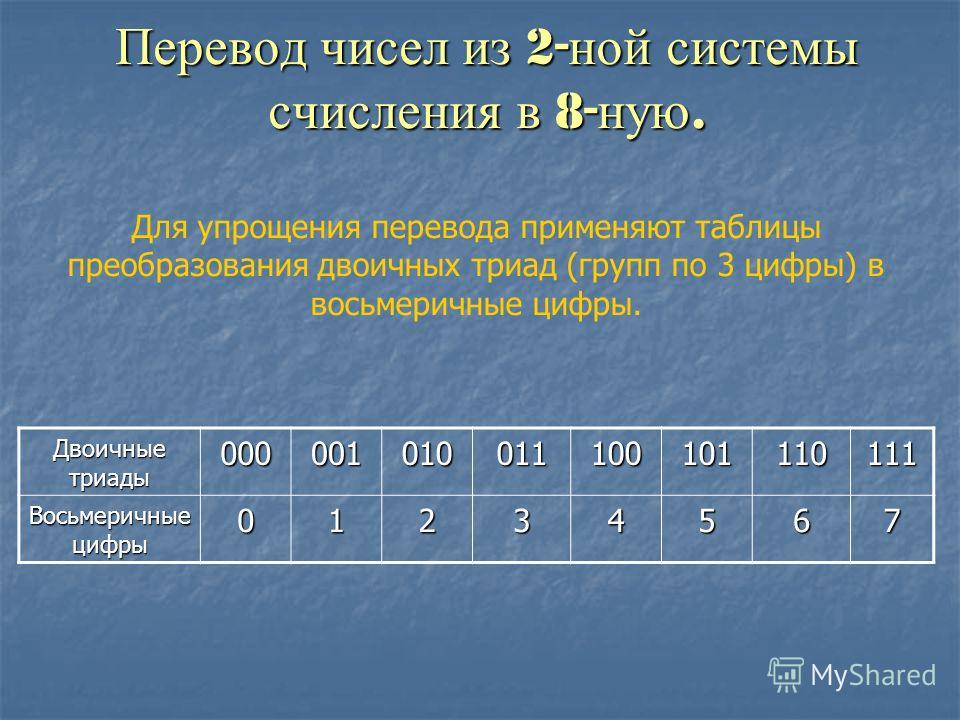
В этой статье мы рассмотрим различные типы систем счисления, которые мы используем, такие как двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления. Мы изучим преобразования между этими системами счисления и решим примеры для лучшего понимания концепции.
| 1. | Что такое системы счисления? |
| 2. | Типы систем счисления |
| 3. | Двоичная система счисления |
| 4. | Восьмеричная система счисления |
| 5. | Десятичная система счисления |
| 6. | Шестнадцатеричная система счисления |
| 7. | Правила преобразования систем счисления |
| 8. | Часто задаваемые вопросы о системах счисления |
Что такое системы счисления?
Система счисления — это система представления чисел.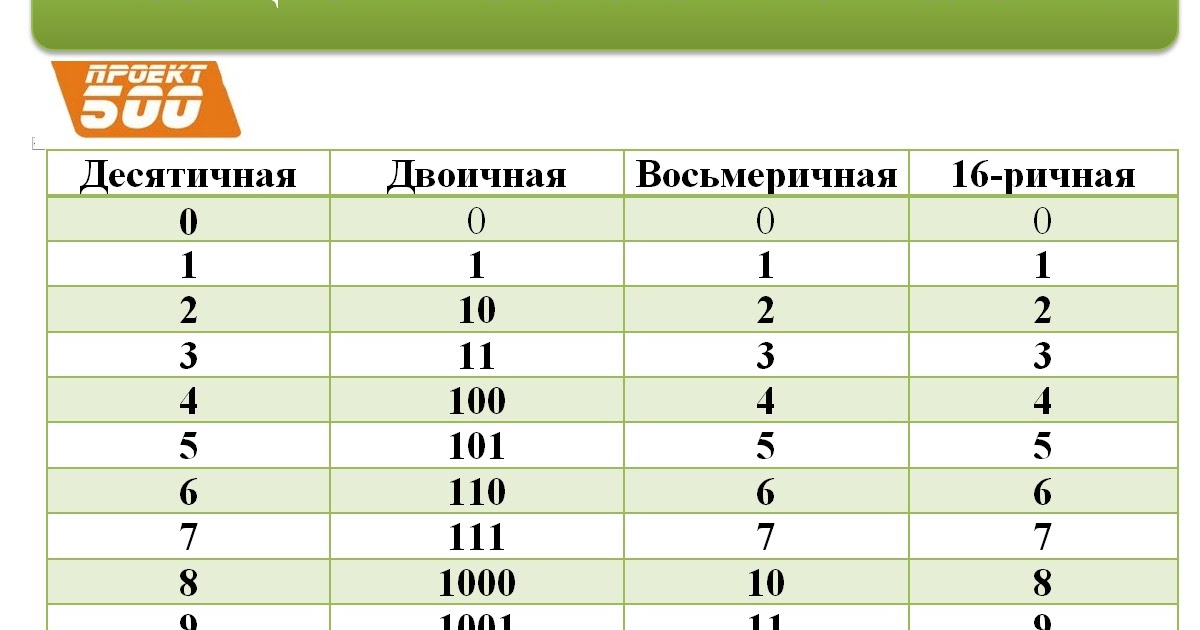 Ее также называют системой счисления, и она определяет набор значений для представления количества. Эти числа используются как цифры, и наиболее распространенными из них являются 0 и 1, которые используются для представления двоичных чисел. Цифры от 0 до 9 используются для представления других типов систем счисления.
Ее также называют системой счисления, и она определяет набор значений для представления количества. Эти числа используются как цифры, и наиболее распространенными из них являются 0 и 1, которые используются для представления двоичных чисел. Цифры от 0 до 9 используются для представления других типов систем счисления.
Системы счисления Определение
Система счисления определяется как представление чисел с помощью последовательного использования цифр или других символов. Значение любой цифры в числе может быть определено цифрой, ее положением в числе и основанием системы счисления. Числа представлены уникальным образом и позволяют нам выполнять арифметические операции, такие как сложение, вычитание и деление.
Типы систем счисления
Существуют различные типы систем счисления, в которых четыре основных типа следующие.
- Двоичная система счисления (основание — 2)
- Восьмеричная система счисления (основание — 8)
- Десятичная система счисления (основание — 10)
- Шестнадцатеричная система счисления (основание — 16)
Мы подробно изучим каждую из этих систем одну за другой после изучения следующей схемы системы счисления.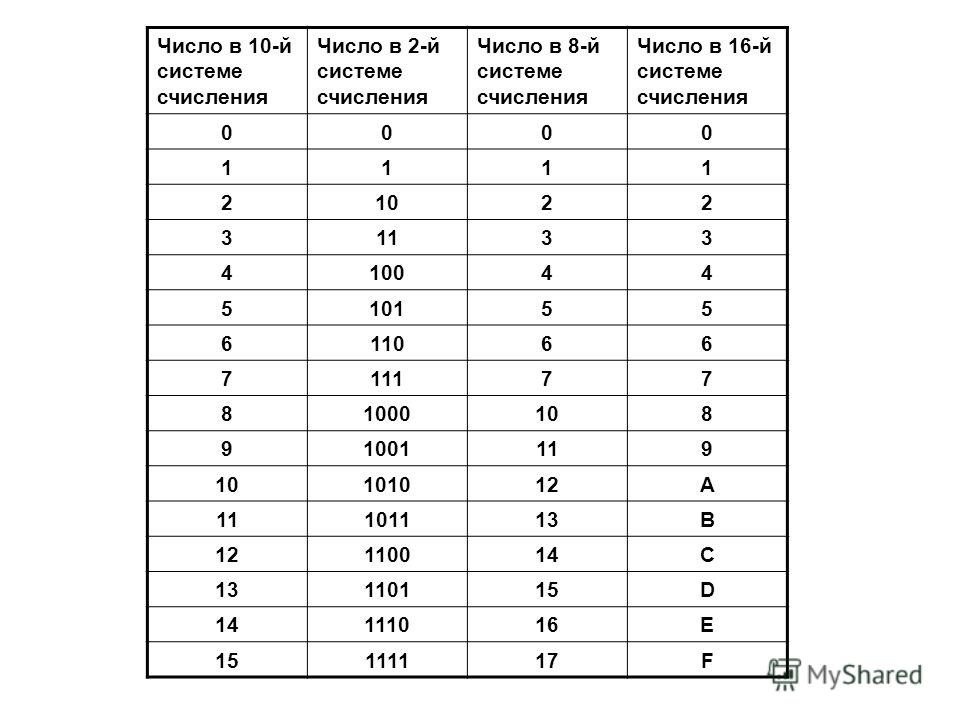
Таблица системы счисления
Ниже приведена таблица основных четырех типов системы счисления, которые мы используем для представления чисел.
Двоичная система счисления
В двоичной системе счисления используются только две цифры: 0 и 1. Числа в этой системе имеют основание 2. Цифры 0 и 1 называются битами, а 8 битов вместе составляют байт. Данные в компьютерах хранятся в виде битов и байтов. Двоичная система счисления не работает с другими числами, такими как 2,3,4,5 и так далее. Например: 10001 2 , 111101 2 , 1010101 2 — некоторые примеры чисел в двоичной системе счисления.
Восьмеричная система счисления
Восьмеричная система счисления использует восемь цифр: 0,1,2,3,4,5,6 и 7 с основанием 8. Преимущество этой системы в том, что в ней меньше цифр по сравнению с некоторыми другими системами, поэтому , было бы меньше вычислительных ошибок. Такие цифры, как 8 и 9, не входят в восьмеричную систему счисления. Как и двоичная, в миникомпьютерах используется восьмеричная система счисления, но с цифрами от 0 до 7. Например: 35 8 , 23 8 , 141 8 — некоторые примеры чисел в восьмеричной системе счисления.
Как и двоичная, в миникомпьютерах используется восьмеричная система счисления, но с цифрами от 0 до 7. Например: 35 8 , 23 8 , 141 8 — некоторые примеры чисел в восьмеричной системе счисления.
Десятичная система счисления
Десятичная система счисления использует десять цифр: 0,1,2,3,4,5,6,7,8 и 9 с базовым числом 10. Десятичная система счисления – это система, которую мы обычно используем для представления чисел. в реальной жизни. Если какое-либо число представлено без основания, это означает, что его основание равно 10. Например: 723 10 , 32 10 , 4257 10 — некоторые примеры чисел в десятичной системе счисления.
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления использует шестнадцать цифр/алфавитов: 0,1,2,3,4,5,6,7,8,9 и A,B,C,D,E,F с базовым числом 16. Здесь A-F шестнадцатеричной системы счисления означают соответственно числа 10-15 десятичной системы счисления. Эта система используется в компьютерах для сокращения больших строк двоичной системы. Например, 7B3 16 , 6F 16 , 4B2A 16 — некоторые примеры чисел в шестнадцатеричной системе счисления.
Эта система используется в компьютерах для сокращения больших строк двоичной системы. Например, 7B3 16 , 6F 16 , 4B2A 16 — некоторые примеры чисел в шестнадцатеричной системе счисления.
Правила преобразования систем счисления
Число может быть преобразовано из одной системы счисления в другую с помощью формул системы счисления. Подобно тому, как двоичные числа могут быть преобразованы в восьмеричные числа и наоборот, восьмеричные числа могут быть преобразованы в десятичные числа и наоборот, и так далее. Давайте посмотрим, какие шаги необходимы для преобразования систем счисления.
Шаги для преобразования двоичной системы счисления в десятичную
Чтобы преобразовать число из двоичной в десятичную систему, мы используем следующие шаги.
- Шаг 1: Умножьте каждую цифру данного числа, начиная с самой правой, на показатели степени основания.
- Шаг 2: Показатель степени должен начинаться с 0 и увеличиваться на 1 каждый раз, когда мы движемся справа налево.

- Шаг 3: Упростите каждый из вышеперечисленных продуктов и добавьте их.
Давайте разберемся с шагами с помощью следующего примера, в котором нам нужно преобразовать число из двоичной в десятичную систему счисления.
Пример: Преобразовать 100111 2 в десятичную систему.
Решение:
Шаг 1: Определите основание данного числа. Здесь основание 100111 2 равно 2.
Шаг 2: Умножьте каждую цифру данного числа, начиная с самой правой, на показатели степени основания. Показатели должны начинаться с 0 и увеличиваться на 1 каждый раз, когда мы движемся справа налево. Поскольку основание здесь равно 2, мы умножаем цифры данного числа на 2 0 , 2 1 , 2 2 и так далее справа налево.
Шаг 3: Мы просто упрощаем каждый из вышеперечисленных продуктов и добавляем их.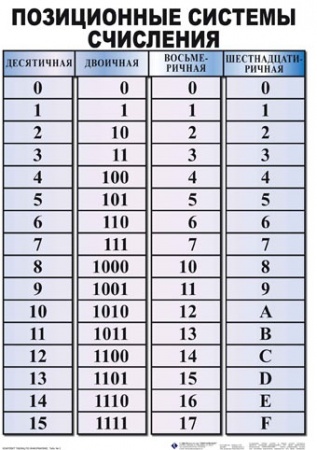
Здесь сумма является числом, эквивалентным данному числу в десятичной системе счисления. Или мы можем использовать следующие шаги, чтобы упростить этот процесс.
100111 = (1 × 2 5 ) + (0 × 2 4 ) + (0 × 2 3 ) + (1 × 2 2 ) + (1 × 2 1 ) + (1 × 2 0 )
= (1 × 32) + (0 × 16) + (0 × 8) + (1 × 4) + (1 × 2) + (1 × 1) )
= 32 + 0 + 0 + 4 + 2 + 1
= 39
Таким образом, 100111 2 = 39 10 .
Преобразование десятичной системы счисления в двоичную/восьмеричную/шестнадцатеричную систему счисления
Чтобы преобразовать число из десятичной системы счисления в двоичную/восьмеричную/шестнадцатеричную систему счисления, мы используем следующие шаги. Пошагово показано, как преобразовать число из десятичной системы в восьмеричную.
Пример: Преобразовать 4320 10 в восьмеричную систему.
Решение:
Шаг 1: Определите основание нужного числа. Так как мы должны преобразовать данное число в восьмеричную систему, основание искомого числа равно 8.
Так как мы должны преобразовать данное число в восьмеричную систему, основание искомого числа равно 8.
Шаг 2: Разделите данное число на основание требуемого числа и запишите частное и остаток в форма частно-остатка. Повторяем этот процесс (снова деля частное на основание), пока не получим частное меньше основания.
Шаг 3: Данное число в восьмеричной системе счисления получается простым чтением всех остатков и последнего частного снизу вверх.
Следовательно, 4320 10 = 10340 8
Преобразование из одной системы счисления в другую
Чтобы преобразовать число из одной из двоичных/восьмеричных/шестнадцатеричных систем в одну из других систем, мы сначала преобразуем его в десятичную систему, а затем мы преобразуем его в требуемые системы, используя вышеупомянутые процессы.
Пример: Преобразовать 1010111100 2 в шестнадцатеричную систему.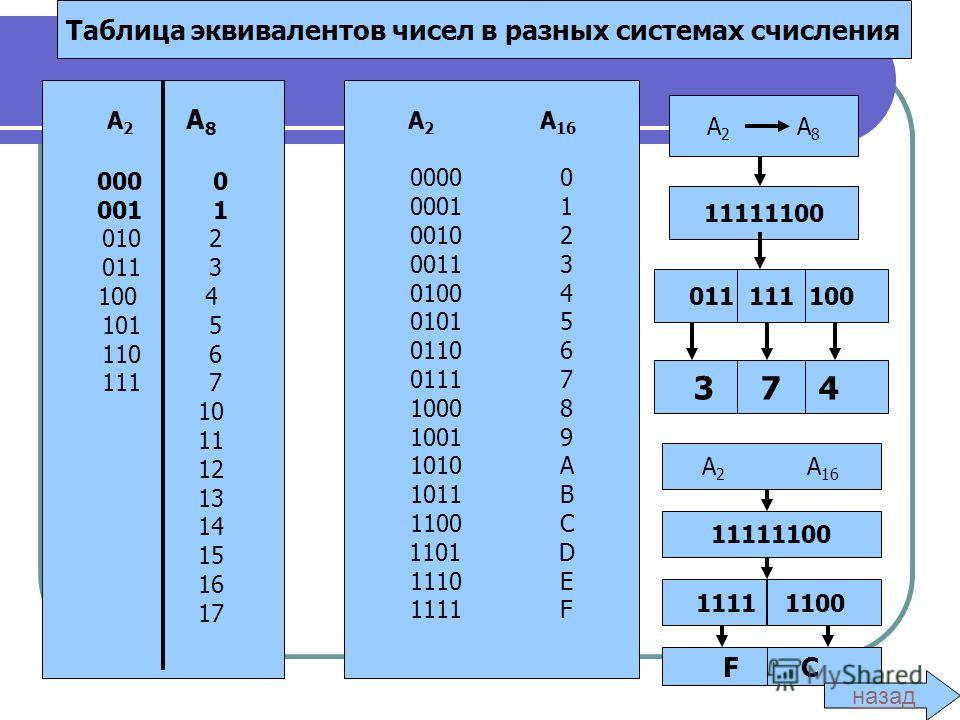
Решение:
Шаг 1: Преобразуйте это число в десятичную систему счисления, как описано выше.
Таким образом, 1010111100 2 = 700 10 → (1)
Шаг 2: Преобразуйте вышеуказанное число (которое находится в десятичной системе) в требуемую систему счисления (шестнадцатеричную).
Здесь мы должны преобразовать 700 10 в шестнадцатеричной системе, используя вышеупомянутый процесс. Следует отметить, что в шестнадцатеричной системе числа 11 и 12 записываются как B и C соответственно.
Таким образом, 700 10 = 2BC 16 → (2)
Из уравнений (1) и (2) 1010111100 2 = 2BC 6 903 6 9111 3 1 ☛ Связанные статьи
- Индийская система счисления
- Международная система счисления
- Двоичный калькулятор
- Преобразование двоичного кода в восьмеричный
- Восьмеричное в двоичное
- Преобразование десятичного числа в двоичное
- Двоичный код в десятичный
- Десятичный в шестнадцатеричный
- Шестнадцатеричный в десятичный
Часто задаваемые вопросы о системах счисления
Что такое системы счисления с примерами?
Система счисления — это система записи или выражения чисел. В математике числа представлены в заданном наборе с помощью цифр или символов определенным образом. Каждое число имеет собственное уникальное представление, и числа также могут быть представлены в арифметической и алгебраической структуре. Существуют различные типы систем счисления, которые имеют разные свойства, такие как двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления. Некоторые примеры чисел в разных системах счисления: 10010 2 , 234 8 , 428 10 и 4BA 16 .
В математике числа представлены в заданном наборе с помощью цифр или символов определенным образом. Каждое число имеет собственное уникальное представление, и числа также могут быть представлены в арифметической и алгебраической структуре. Существуют различные типы систем счисления, которые имеют разные свойства, такие как двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления. Некоторые примеры чисел в разных системах счисления: 10010 2 , 234 8 , 428 10 и 4BA 16 .
Какие существуют 4 типа систем счисления?
Существует четыре основных типа систем счисления:
- Двоичная система счисления (основание — 2)
- Восьмеричная система счисления (основание — 8)
- Десятичная система счисления (основание — 10)
- Шестнадцатеричная система счисления (основание — 16)
Каковы правила преобразования систем счисления?
Чтобы преобразовать число из двоичной/восьмеричной/шестнадцатеричной системы счисления в десятичную систему счисления, мы используем следующие шаги:
- Умножьте каждую цифру данного числа, начиная с самой правой цифры, на показатели степени основания.
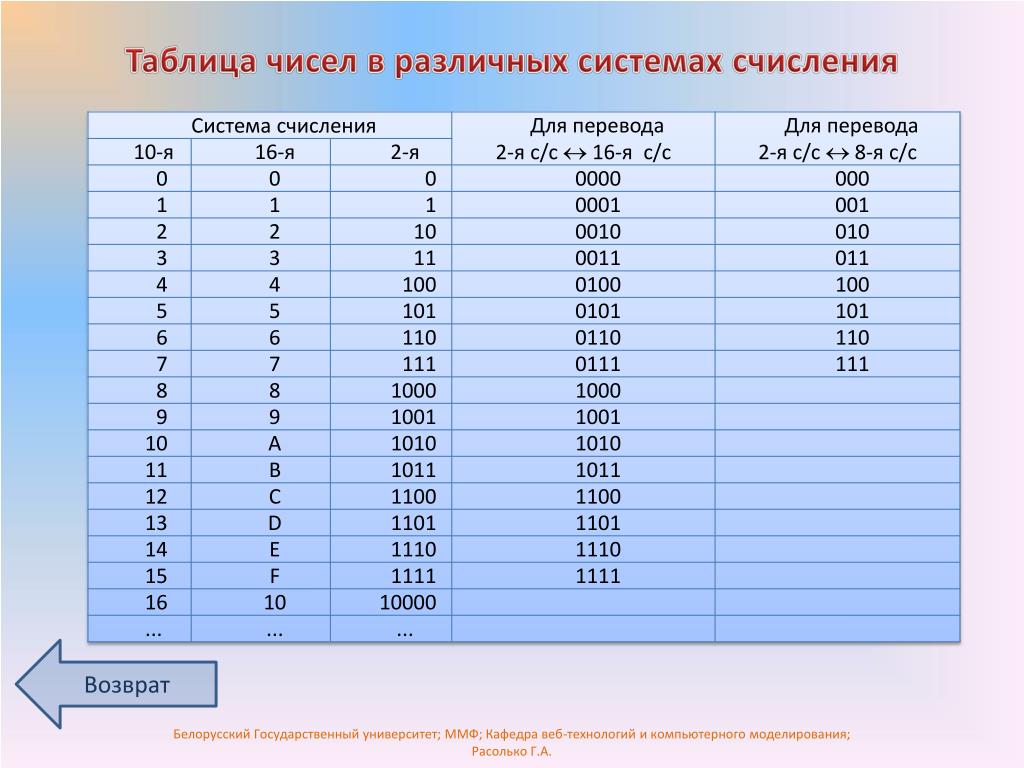
- Показатель степени должен начинаться с 0 и увеличиваться на 1 при каждом движении справа налево.
- Упростите каждый из вышеперечисленных продуктов и добавьте их.
Чтобы преобразовать число из десятичной системы в двоичную/восьмеричную/шестнадцатеричную систему, мы используем следующие шаги:
- Разделите данное число на основание требуемого числа и запишите частное и остаток в «частном- форма «остаток».
- Повторяем этот процесс (снова деля частное на основание), пока не получим частное меньше основания.
- Данное число в десятичной системе счисления получается простым чтением всех остатков и последнего частного снизу вверх.
Чтобы преобразовать число из одной из двоичных/восьмеричных/шестнадцатеричных систем в одну из других систем:
- Сначала мы преобразуем его в десятичную систему.
- Потом конвертируем в нужную систему.
Каково использование каждой системы счисления?
Каждая система счисления предназначена для разных целей, например:
- Двоичная система счисления используется для хранения данных в компьютерах.
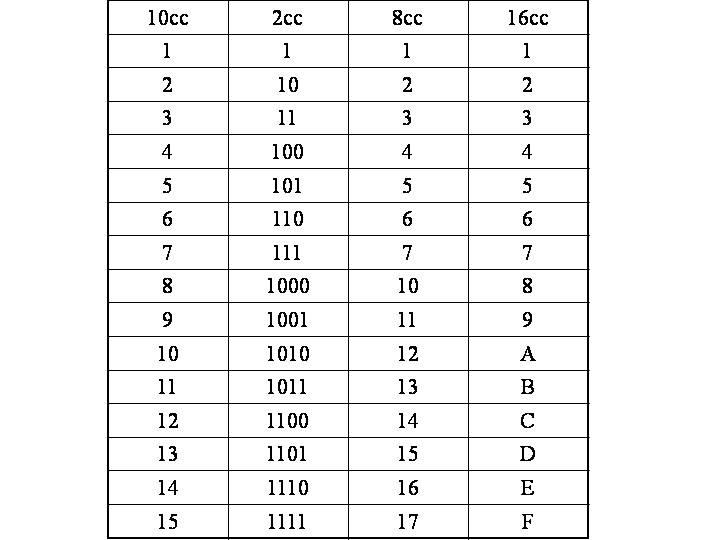
- Преимущество восьмеричной системы счисления состоит в том, что в ней меньше цифр по сравнению с некоторыми другими системами счисления, следовательно, будет меньше вычислительных ошибок.
- Десятичная система счисления — это система, которую мы используем в повседневной жизни.
- Шестнадцатеричная система счисления используется в компьютерах для сокращения больших строк двоичной системы счисления.
В чем важность систем счисления?
Системы счисления помогают представлять числа в небольшом наборе символов. Двоичные числа в основном используются в компьютерах, которые используют такие цифры, как 0 и 1, для вычисления простых задач. Системы счисления также помогают преобразовать одну систему счисления в другую.
Как классифицируются системы счисления?
Системы счисления можно разделить в основном на две категории: позиционные и непозиционные системы счисления. В позиционных системах счисления каждая цифра связана с весом, и ее примерами являются двоичные, восьмеричные, десятичные и т.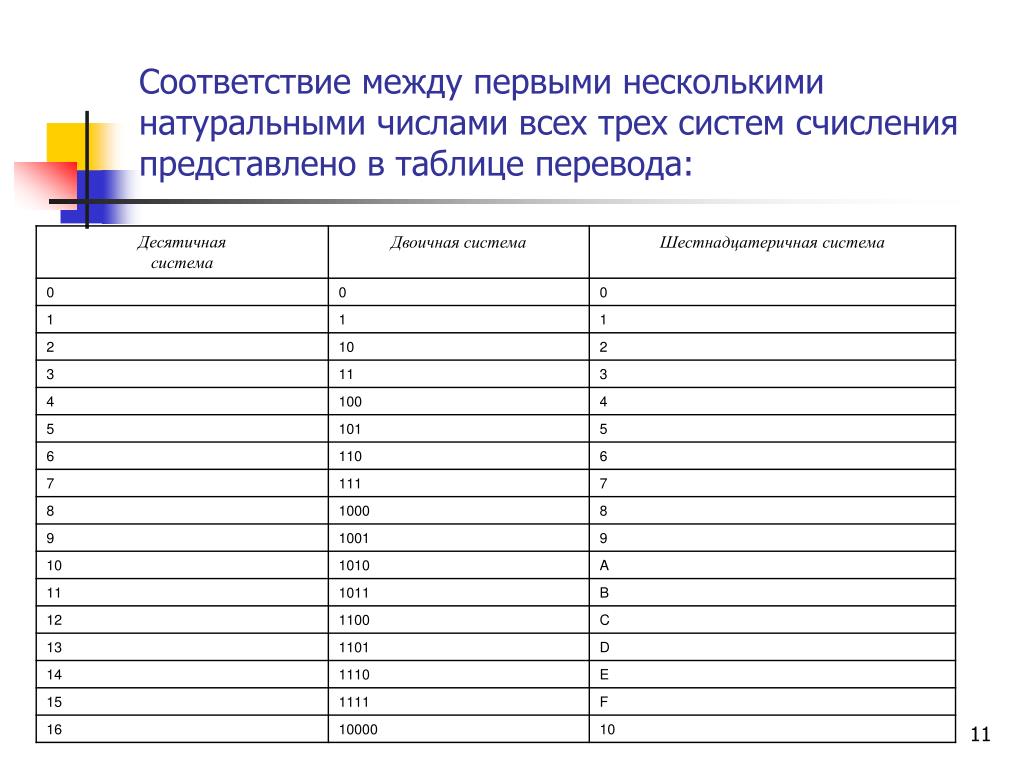 д. В непозиционных системах счисления значения цифр не зависят от их позиций, и их примерами являются код Грея, циклический код, ароматический код. код и т. д.
д. В непозиционных системах счисления значения цифр не зависят от их позиций, и их примерами являются код Грея, циклический код, ароматический код. код и т. д.
Почему в компьютерах используются разные системы счисления?
Компьютеры не понимают человеческих языков, поэтому для понимания команд и инструкций, данных компьютерам программистами, используются различные системы счисления, такие как двоичная, восьмеричная, десятичная и т. д.
Сколько существует типов систем счисления?
Система счисления включает в себя различные типы чисел, например, простые числа, нечетные числа, четные числа, рациональные числа, целые числа и т. д. Эти числа могут быть выражены в виде цифр или слов соответственно. Например, такие числа, как 40 и 65, выраженные в виде цифр, также могут быть записаны как сорок и шестьдесят пять.
A Система счисления или Система счисления определяется как элементарная система для выражения чисел и цифр.
Это уникальный способ представления чисел в арифметической и алгебраической структуре.
Числа используются в различных арифметических значениях, применимых для выполнения различных арифметических операций, таких как сложение, вычитание, умножение и т. д., которые применяются в повседневной жизни для целей вычислений. Значение числа определяется цифрой, ее разрядностью в числе и основанием системы счисления. Числа, как правило, также известные как числа, представляют собой математические значения, используемые для подсчета, измерений, маркировки и измерения основных величин.
Типы чиселЧисла — это математические значения или цифры, используемые для измерения или вычисления величин. Он представлен цифрами 2, 4, 7 и т. д. Некоторые примеры чисел: целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.
Существуют разные типы чисел классифицируются на наборы по системе счисления. Типы описаны ниже,
Типы описаны ниже,
- Натуральные числа: Натуральные числа — это положительные числа, которые считаются от 1 до бесконечности. Набор натуральных чисел представлен ‘N’. I t — это числа, которые мы обычно используем для счета. Набор натуральных чисел можно представить как N = 1, 2, 3, 4, 5, 6, 7,…
- Целые числа: Целые числа — это положительные числа, включая ноль, который считается от 0 до бесконечности. Целые числа не включают дроби или десятичные дроби. Набор целых чисел представлен «W». Пример: W = 0, 1, 2, 3, 4, 5,…
- Целые числа: Целые числа представляют собой набор чисел, включающий все положительные числа, нуль, а также все отрицательные числа, которые считаются от отрицательной бесконечности. до положительной бесконечности. В наборе нет дробей и десятичных знаков. Набор целых чисел обозначается «Z». Пример: Z = …..,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,…
- Десятичные числа: Любое числовое значение, состоящее из десятичная точка — это десятичное число.
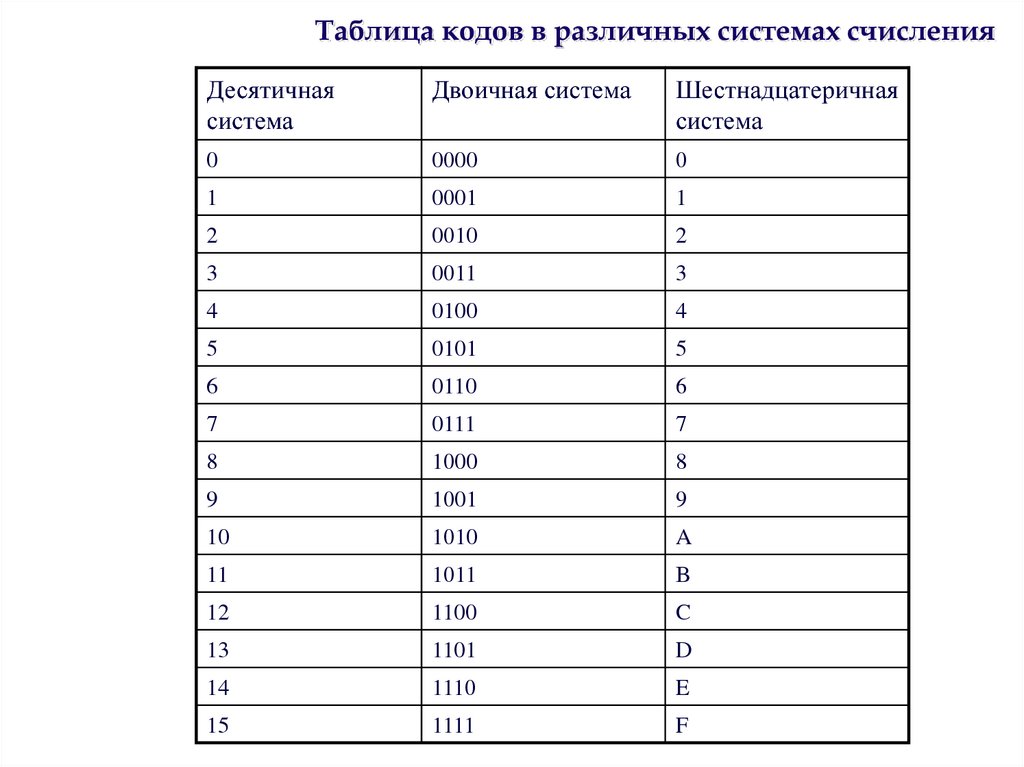 Его можно выразить как 2,5, 0,567 и т. д.
Его можно выразить как 2,5, 0,567 и т. д. - Вещественный номер: Вещественные числа — это заданные числа, не содержащие мнимых значений. Он включает в себя все положительные целые числа, отрицательные целые числа, дроби и десятичные значения. Обычно он обозначается «R».
- Комплексный номер: Комплексные числа — это набор чисел, включающий мнимые числа. Его можно выразить как a+bi, где «a» и «b» — действительные числа. Обозначается «С».
- Рациональные числа: Рациональные числа — это числа, которые можно представить как отношение двух целых чисел. Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается цифрой ‘В’.
- Иррациональные числа: Иррациональные числа — это числа, которые не могут быть выражены дробями или отношениями целых чисел. Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой.
 Обозначается «P».
Обозначается «P».
Система счисления — это метод записи чисел, представляющий собой математический способ представления чисел данного набора с использованием чисел или символов математическим способом.
Система записи для обозначения чисел с использованием цифр или символов в логическом порядке определяется как система счисления. Система счисления Представляет полезный набор чисел, отражает арифметическую и алгебраическую структуру числа и обеспечивает стандартное представление. Из цифр от 0 до 9 можно составить все числа.
С помощью этих цифр любой может создавать бесконечные числа. Например, 156,3907, 3456, 1298, 784859 и т. д.
Типы систем счисленияВ зависимости от базового значения и количества разрешенных цифр существует множество типов систем счисления. The four common types of Number systems are:
- Decimal Number System
- Binary Number System
- Octal Number System
- Hexadecimal Number System
Decimal Number System
Number system с базовым значением 10 называется десятичной системой счисления. Он использует 10 цифр, т.е. 0-9для создания номеров. Здесь каждая цифра в числе находится в определенном месте, а разрядное значение является произведением различных степеней 10. Здесь разрядное значение обозначается справа налево как первое разрядное значение, называемое единицами, второе слева как десятки и т. д. Сотни, тысячи и т. д. Здесь единицы имеют разрядное значение как 100, десятки имеют разрядное значение как 101, сотни как 102, тысячи как 103 и так далее.
Он использует 10 цифр, т.е. 0-9для создания номеров. Здесь каждая цифра в числе находится в определенном месте, а разрядное значение является произведением различных степеней 10. Здесь разрядное значение обозначается справа налево как первое разрядное значение, называемое единицами, второе слева как десятки и т. д. Сотни, тысячи и т. д. Здесь единицы имеют разрядное значение как 100, десятки имеют разрядное значение как 101, сотни как 102, тысячи как 103 и так далее.
Например, 12265 имеет следующие разрядные значения:
(1 × 10 4 ) + (2 × 10 3 ) + (2 × 10 2 ) + (6 × 10 1 ) + (5 × 10 0 )
= (00) + (10) + (10) 2 × 1000) + (2 × 100) + (6 × 10) + (5 × 1)
= 10000 + 2000 + 200 + 60 + 5
= 12265
с базовым значением 2 называется двоичной системой счисления. Он использует 2 цифры, то есть 0 и 1 для создания чисел. Числа, образованные из этих двух цифр, называются двоичными числами. Двоичная система счисления очень полезна в электронных устройствах и компьютерных системах, потому что ее можно легко реализовать, используя всего два состояния ВКЛ и ВЫКЛ, то есть 0 и 1.
Двоичная система счисления очень полезна в электронных устройствах и компьютерных системах, потому что ее можно легко реализовать, используя всего два состояния ВКЛ и ВЫКЛ, то есть 0 и 1.
Десятичные числа 0-9 представлены в двоичном виде как: 0, 1, 10, 11, 100, 101, 110, 111, 1000 и 1001
Например, 14 можно записать как 1110, 19 можно записать как 10011, 50 можно записать как 110010.
Пример 14 в бинарной системе
Бинарный один, в котором базовое значение равно 8. Он использует 8 цифр, т.е. 0-7, для создания восьмеричных чисел. Восьмеричные числа можно преобразовать в десятичные значения, умножив каждую цифру на разрядное значение, а затем сложив результат. Здесь значения мест равны 80, 81 и 82. Восьмеричные числа полезны для представления чисел UTF8. Пример,
(81) 10 can be written as (121) 8
(125) 10 can be written as (175) 8
Hexadecimal Number System
Number System with базовое значение 16 называется шестнадцатеричной системой счисления.
Он использует 16 цифр для создания своих номеров. Цифры от 0 до 9 воспринимаются как цифры в десятичной системе счисления, но цифры от 10 до 15 представлены как A-F, т.е. 10 представлен как A, 11 как B, 12 как C, 13 как D, 14 как E и 15 как F. Шестнадцатеричные числа полезны для обработки адресов памяти. Примеры,
(185) 10 можно записать как (B9) 16
(5440) 10 может быть написано как (1540) 16
(4265) 10
. 10A9) 16
Hexadecimal 0 1 2 3 4 5 6 7 8 9 A B C D E F Decimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Примеры вопросов
Вопрос 1: Преобразовать 4525 8 в десятичное число?
Решение:
4525 8 = 4 × 8 3 + 5 × 8 2 + 2 × 8 1 + 5 × 8 0
= 4 × 512 + 5 × 64 + 2 × 8 + 5 ×
= 2048 + 320 + 16 + 5
= 2389 10
Вопрос 2.
Преобразовать (17) 10 9111 в двоичное число?
Решение:
двоичный 17
Следовательно (17) 10 = (10001) 2
Вопрос 3: Преобразование (1011110) 2 в восьмеричное число .
Solution:
Given (1011110) 2 a binary number, to convert it into octal number
Octal Number Binary Number 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111 .
Итак, (1011110) 2 в восьмеричном числе равно (136) 8
Системы счисления | Определение, примеры, типы систем, преобразование
ВведениеСчет, а также измерение объектов обычно выполняется с использованием чисел. Числа также являются целыми числами для выполнения различных арифметических вычислений. Мы узнали о различных наборах чисел, таких как натуральные числа, целые числа, действительные числа и т. д. Подобно различным наборам чисел, у нас также есть разные системы счисления, которые имеют уникальные характеристики и используются для различных целей. Познакомимся с различными системами счисления.
ОпределениеСистема счисления — это система, которая используется для представления чисел. Другое название, которое используется для систем счисления, — система счисления. Другими словами, система счисления определяется как представление чисел с помощью последовательного использования цифр или других символов.
Типы систем счисленияКакие наиболее распространенные системы счисления используются? Давайте узнаем.
Наиболее распространенные системы счисления –
- Десятичная система счисления
- Двоичная система счисления
- Восьмеричная система счисления
- Шестнадцатеричная система счисления
Давайте узнаем больше об этих системах счисления одну за другой.
Десятичная система счисленияДесятичная система счисления состоит из 10 цифр или символов. Слово «Дека» означает 10, поэтому эта система известна как десятичная система счисления. Что это за 10 числительных, составляющих десятичную систему счисления? Это цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.. Используя эти цифры, можно представить любое число или количество. В десятичной системе счисления используется основание 10. Это означает, что 654 10 , 125 10 являются примерами чисел, представленных в десятичной системе счисления.
Следовательно, каждая позиция в десятичной системе счисления показывает определенную степень основания (10).
Давайте разберемся на примере.
Пример
Представьте число 2512 в десятичной системе счисления.
Решение
Нам дано число 2512 и мы должны представить его в десятичной системе счисления. Число 2512, в десятичной системе счисления будет равно
2512 = 2 х 10 3 + 5 х 10 2 + 1 х 10 1 + 2 х 10 0
3 Рассмотрим другое пример.
Пример
Представьте число 4168,23 в десятичной системе счисления.
Раствор
Нам дано число 4168,23 и мы должны представить его в десятичной системе счисления. Важно понимать, что десятичная точка отделяет положительные степени числа 10 от отрицательных степеней числа 10. Следовательно, число 4168,23 в десятичной системе счисления будет равно
4 x 10 3 + 1 x 10 2 + 6 x 10 1 + 8 x 10 0 + 2 x 10 -1 + 3 x 10 -2
Двоичная система счисленияВ двоичной системе счисления есть только два возможных значения цифр, 0 и 1.
По этой причине двоичная система счисления также известна как система счисления с основанием – 2. Это также позиционная система значений, в которой каждая двоичная цифра имеет собственное значение или вес, выраженный как степень числа 2. На самом деле цифры 0 и 1 называются битами, а 8 битов вместе составляют байт. Данные в компьютерах хранятся в виде битов и байтов. Например, 101101 2 и 1011 2 являются примерами двоичной системы счисления. Давайте разберемся на примере.
Пример
Представьте двоичное число 1110 2 в виде десятичного эквивалента.
Решение
Нам дано двоичное число 1110 2 , и мы должны найти его десятичный эквивалент. Десятичный эквивалент двоичного числа 1110 2 будет равен –
1110 2 = ( 1 x 2 3 ) + ( 1 x 2 2 ) + ( 1 x 2 x 1 ) + 91 1 1 . 2 0 )
⇒ 1110 2 = 8 + 4 + 2 + 1
⇒ 1110 2 = 14
Следовательно, десятичный эквивалент 1110 2 будет (14) 9 будет (14) 9 .
Восьмеричная система счисления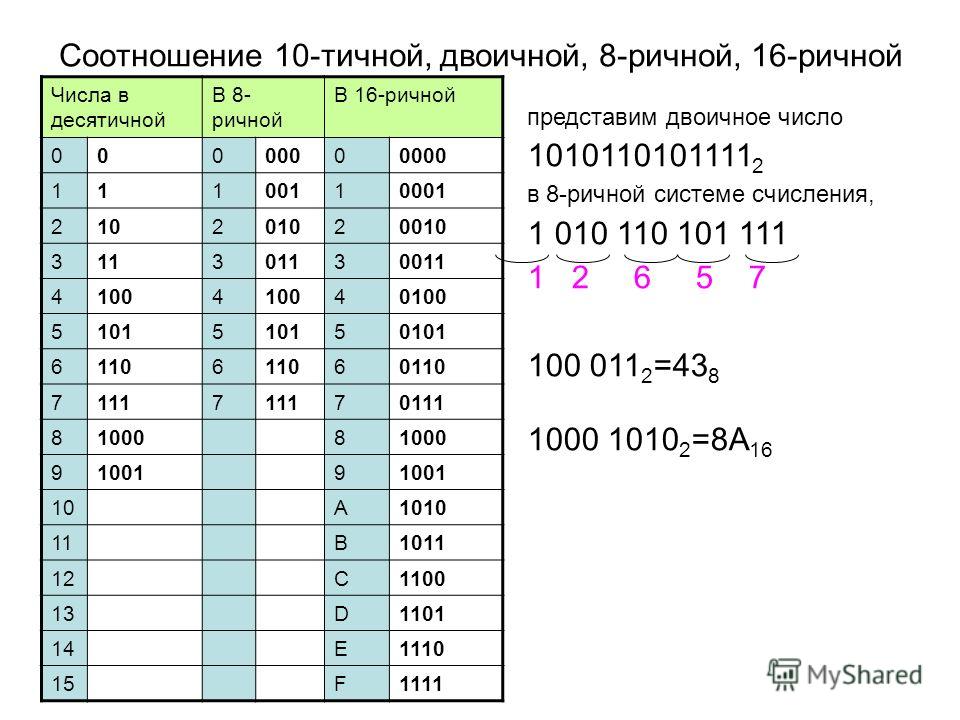
Восьмеричная система счисления имеет основание 8, что означает, что она имеет 8 уникальных символов. Эти 8 символов — 0, 1, 2, 3, 4, 5, 6 и 7. Таким образом, каждая цифра восьмеричного числа может иметь любое значение от 0 до 7. Цифры вроде 8 и 9не входят в восьмеричную систему счисления.
Восьмеричная система счисления также является позиционной системой значений, в которой каждая цифра имеет свое собственное значение или вес, выраженный степенью числа 8. Знаки слева от восьмеричной точки представляют собой положительные степени числа 8, а знаки справа — отрицательные степени. из 8. Давайте разберемся на примере. Как и двоичная, в миникомпьютерах используется восьмеричная система счисления, но с цифрами от 0 до 7.
Давайте разберемся на примере.
Пример
Представьте восьмеричное число 3721.2406 8 в виде десятичного эквивалента.
Решение
Нам дано восьмеричное число 3721.
2406 8 , и мы должны найти его десятичный эквивалент. Десятичный эквивалент восьмеричного числа 3721,2406 8 будет равен –
3721,2406 8 = ( 3 x 8 3 ) + ( 7 x 8 2 1 ) 1 1 x 0 8 . х 8 -1 ) + ( 4 х 8 -2 ) + (0 х 8 -3 ) + ( 6 х 10 -4 )
⇒ 3721,2406 8 = 3 х 512 + 7 х 512 + 7 8 + 2 x 0.125 + 4 x 0.015625 + 0 + 6 x 0.000244
⇒ 3721.2406 8 = 1536 + 448 + 16 + 1 + 0.25 + 0.0625 + 0 + 0.001464
⇒ 3721.2406 8 = 2001.313964 10
Следовательно, десятичным эквивалентом восьмеричного числа 3721,2406 8 будет 2001,313964 10
Шестнадцатеричная система счисленияШестнадцатеричная система счисления использует основание 16. Таким образом, она имеет 16 возможных цифровых символов.
Он использует цифры от 0 до 9 вместе с буквами A, B, C, D, E и F в качестве 16-значных символов. Подобно восьмеричной системе счисления, шестнадцатеричная система счисления также является позиционной системой значений, в которой каждая цифра имеет свое собственное значение или вес, выраженный в степени 16. Знаки слева от шестнадцатеричной точки представляют собой положительные степени числа 16, а места до справа — отрицательные степени числа 16.
Шестнадцатеричная система счисления используется в компьютерах для указания адресов памяти длиной 16 и 32 бита. Например, адрес памяти 110101101010111 — это большой двоичный адрес, но в шестнадцатеричном формате это D6F, который легче запомнить. Шестнадцатеричная система счисления также используется для представления цветовых кодов, например, (FF, FF, FF) представляет белый цвет в значении RGB, а (80, 80, 80) представляет серый цвет в значении RGB.
Связь между различными системами счисленияThe following tables demonstrates the relationship between the binary, decimal, octal and hexagonal number systems –
Hexadecimal Number System Octal Number System Decimal Number System Binary Number System 0 0 0 0 0 0 0 1 1 1 0 0 0 1 2 2 2 0 0 1 0 3 3 3 0 0 1 1 4 4 4 0 1 0 0 5 5 5 0 1 0 1 6 6 6 0 1 1 0 7 7 7 0 1 1 1 8 1 0 8 1 0 0 0 9 1 1 9 1 0 0 1 A 1 2 1 0 1 0 1 0 B 1 3 1 1 1 0 1 1 C 1 4 1 2 1 1 0 0 D 1 5 1 3 1 1 0 1 E 1 6 1 4 1 1 1 0 F 1 7 1 5 1 1 1 1 Теперь, когда мы знаем взаимосвязь между различными системами счисления, как нам преобразовать число из системы счисления в число? Давайте узнаем.
Преобразование десятичной системы счисления в двоичнуюРаспространенным методом преобразования десятичной системы счисления в двоичную является метод повторного деления. В этом методе число последовательно делится на 2 и записывается его остаток. Окончательный двоичный результат получается путем объединения всех остатков, при этом последний остаток является старшим битом (MSB).
Давайте разберемся на примере.
Предположим, мы хотим найти двоичный эквивалент десятичного числа 17. Сначала мы разделим 17 на 2 следующим образом —
Затем мы запишем остатки в порядке от последнего к первому, как показано ниже —
Таким образом, это означает что 17 в десятичной системе счисления эквивалентно 10001 в двоичной системе. Следовательно,
5 10 = 10001 2
Преобразование десятичной системы счисления в восьмеричнуюДесятичное целое число может быть преобразовано в восьмеричную систему счисления с помощью метода повторного деления точно так же, как десятичное число преобразуется в двоичное число.
Однако единственная разница здесь в том, что мы используем коэффициент деления 8 вместо 2. Разберемся на примере.
Пример
Преобразование десятичного числа 266 в восьмеричное.
Решение
Нам дано десятичное число 266, и нам нужно найти его эквивалентное восьмеричное число. У нас будет
Обратите внимание, что первый остаток становится младшей значащей цифрой ( L S B ) восьмеричного числа, а последний остаток становится старшей значащей цифрой ( M S B ) восьмеричного числа. Таким образом,
Десятичное число 266 2 будет равно 142 8 в восьмеричной системе счисления.
Преобразование десятичной системы счисления в шестнадцатеричную систему счисленияДесятичное целое число можно преобразовать в шестнадцатеричную систему счисления с помощью метода повторного деления точно так же, как десятичное число преобразуется в двоичное число.
Однако единственная разница здесь в том, что мы используем коэффициент деления 16 вместо 2. Разберемся на примере.
Пример
Преобразование десятичного числа 423 2 к шестнадцатеричному числу
Решение
Нам дано десятичное число 423 2 , и мы должны найти его шестнадцатеричный эквивалент. У нас будет
Обратите внимание, что первый остаток становится младшей значащей цифрой ( L S B ) шестнадцатеричного числа, а последний остаток становится старшей значащей цифрой ( M S B ) шестнадцатеричного числа. Таким образом,
Десятичное число 423 2 будет равно 1A7 16 в шестнадцатеричной системе счисления.
Преобразование двоичной системы счисления в десятичную систему счисленияМы знаем, что двоичная система счисления является позиционной системой счисления, в которой каждая двоичная цифра (бит) имеет определенный вес.
Любое двоичное число можно преобразовать в его десятичный эквивалент, просто суммируя веса различных позиций в двоичном числе, которые его содержат. Давайте разберемся на примере.
Пример
Найдите десятичный эквивалент двоичного числа 11011 2
Решение
Нам дано двоичное число 11011 2 9111, и мы должны найти его десятичный эквивалент. Данное двоичное число можно записать как
. Складываем значения позиций каждой цифры данного двоичного числа. У нас будет,
11011 2 = 1 х 2 4 + 1 х 2 3 + 0 х 2 2 + 1 х 2 1 + 1 х 2 0
⇒ 11011 2 = 1 х 16 + 1 х 8 + 0 х 4 + 1 х 2 + 1 х 9 ⇒ 1
3
= 16 + 8 + 0 + 2 +1⇒11011 2 = 27
Следовательно, десятичный эквивалент двоичного числа 11011 2 будет 27
113
.Преобразование двоичной системы счисления в восьмеричную систему счисления
Для преобразования двоичных целых чисел в восьмеричные целые числа биты двоичного целого группируются в группы по три бита, начиная с младшего значащего бита ( L S B ). Затем каждая группа преобразуется в восьмеричный эквивалент. Давайте разберемся с этим на примере.
Пример
Преобразование двоичного числа 100111010 2 в восьми номеры
Решение
нам нужно преобразовать бинарный номер 100111010 2 на октальный номер
HED 10011111113. 2 в восьмеричной системе счисления будет 472 8
Преобразование двоичной системы счисления в шестнадцатеричную систему счисленияДвоичные числа можно преобразовать в шестнадцатеричные, сгруппировав их по четыре, начиная с двоичной точки.
Давайте разберемся на примере.
Пример
Преобразование двоичного числа 10110110101 2 в шестнадцатеричный номер
Решение
нам нужно преобразовать бинарный номер 10110110101 2 на гекад. У нас будет
Следовательно, двоичное число 10110110101 2 В системе шестнадцатеричных чисел будет DB 16
Преобразование системы октальных чисел в десятичное число. восьмеричная цифра по ее позиционному весу.Давайте разберемся на примере.
Пример
Преобразование восьмеричного числа 372 8 в двоичное число
Решение
Нам нужно преобразовать двоичное число 372 8 в двоичное число. У нас будет,
372 8 = 3 х 8 2 + 7 х 8 1 + 2 х 8 0
⇒ 372 8 372 х 6 4 + 27 х 6 4 + 27 х 6 4 + 2 7 х 6 4 + 2 7 х 6 4 + 2 7 х 6 4 + 2 7 х 6 8 911 8 911
⇒ 372 8 = 250 10
Следовательно, октальное число 372 8 в системе десятимального числа будет 250
2 10 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 919 9 9 .
Ключевые факты и резюме1113 .
- Система счисления — это система, которая используется для представления чисел.
- Десятичная система счисления состоит из 10 цифр или символов. Это числа 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.
- Каждая позиция в десятичной системе счисления показывает определенную степень основания (10).
- В двоичной системе счисления есть только два возможных значения цифр, 0 и 1. По этой причине двоичная система счисления также известна как система счисления с основанием – 2.
- В двоичной системе счисления есть только два возможных значения цифр, 0 и 1.
- Восьмеричная система счисления имеет основание 8, что означает, что она имеет 8 уникальных символов. Эти 8 символов 0, 1, 2, 3, 4, 5, 6 и 7.
- Шестнадцатеричная система счисления использует основание 16. Таким образом, она имеет 16 возможных цифровых символов. Он использует цифры от 0 до 9 вместе с буквами A, B, C, D, E и F в качестве 16-значных символов.
- Распространенным методом преобразования десятичного числа в двоичное является метод повторного деления. В этом методе число последовательно делится на 2 и записывается его остаток. Окончательный двоичный результат получается путем объединения всех остатков, при этом последний остаток является старшим битом (MSB).
- Любое двоичное число можно преобразовать в его десятичный эквивалент, просто суммируя веса различных позиций в двоичном числе, которые его содержат.
- Десятичное целое число может быть преобразовано в восьмеричную систему счисления с помощью метода многократного деления точно так же, как десятичное число преобразуется в двоичное число. Однако единственная разница здесь в том, что мы используем коэффициент деления 8 вместо 2.
- Десятичное целое число может быть преобразовано в шестнадцатеричную систему счисления с помощью метода повторного деления точно так же, как десятичное число преобразуется в шестнадцатеричное число. двоичное число. Однако единственная разница здесь в том, что мы используем коэффициент деления 16 вместо 2,9.
0010
- Для преобразования двоичных целых чисел в восьмеричные целые числа биты двоичного целого числа группируются в группы по три бита, начиная с младшего значащего бита ( L S B ). Затем каждая группа преобразуется в восьмеричный эквивалент.
Целые числа (на тему Дня мертвых) Рабочие листы по математике
Связывание чисел: задачи со словами (на тему Всемирного дня животных) Рабочие листы по математике
Сравнение чисел (на тему Дня благодарения) Рабочие листы по математикеПросмотреть все рабочие листы
Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Системы счисления в цифровой электронике
- Изучив этот раздел, вы должны уметь:
- Знать основные значения широко используемых систем счисления.
- • Десятичный
- • Двоичный.
- • Восьмеричный.
- • Шестнадцатеричный.
- Понимать методы расширения области применения систем счисления.
- • Экспоненты.
- • Представление с плавающей запятой.
- • Нормализованная форма.
- Знать, как числовые значения могут храниться в электронных системах
- • Биты.
- • Байты.
- • Слова.
- • Регистры.
Системы счисления
Большинство систем счисления следуют общему шаблону для записи значения числа: достигнуто максимальное значение в системе подсчета. Количество числовых значений, используемых системой, называется базой системы. Например, десятичная система имеет 10 числовых знаков и поэтому имеет основание 10:9.0003
0 1 2 3 4 5 6 7 8 9
Для записи чисел больше 9 слева добавляется второй столбец, и этот столбец имеет в 10 раз больше значения столбца справа от него.
Поскольку системы счисления, обычно используемые в цифровой электронике, имеют базовые значения, отличные от десятичной системы счисления, они выглядят менее знакомыми, но работают по существу одинаково.
Десятичный, (база 10)
Десятичный имеет десять значений от 0 до 9. Если требуются значения больше 9, слева добавляются дополнительные столбцы. Значение каждого столбца в десять раз превышает значение столбца справа от него. Например, десятичное число двадцать два записывается как 22 (2 десятка + 2 единицы).
Двоичный, (с основанием 2)
Двоичный имеет только два значения 0 и 1. Если требуются значения больше 1, дополнительные столбцы добавляются слева. Значение каждого столбца теперь в два раза превышает значение столбца справа от него. Например, десятичное значение три записывается как 11 в двоичном виде (1 два + 1 один).
Восьмеричный, (основание 8)
Восьмеричный имеет восемь значений от 0 до 7. Если требуются значения больше 7, слева добавляются дополнительные столбцы.
Значение каждого столбца теперь в 8 раз превышает значение столбца справа от него. Например, десятичное число двадцать семь записывается как 33 в восьмеричной форме (3 восьмерки + 3 единицы).
Шестнадцатеричный, (основание 16)
Шестнадцатеричный имеет шестнадцать значений от 0 до 15, но чтобы все эти значения были в одном столбце, 16 значений (от 0 до 15) записываются как от 0 до F с использованием букв от A до F для представления чисел от 10 до 15, избегая использования второго столбца. Опять же, если требуются значения выше 15 (F в шестнадцатеричном формате), используются дополнительные столбцы слева. Значение каждого столбца в шестнадцать раз превышает значение столбца справа от него. Например, десятичное число шестьдесят восемь записывается как 44 в шестнадцатеричном формате (4 шестнадцати + 4 единицы).
Каждая из этих различных систем счисления работает одинаково, просто каждая система имеет различное основание, и значения столбцов в каждой системе увеличиваются на кратное основному числу по мере добавления столбцов слева.
Поскольку этот модуль описывает несколько различных систем счисления, важно знать, какая система описывается. Поэтому, если есть сомнения, к какой системе относится число, для идентификации системы счисления используется основание системы, записываемое в виде нижнего индекса сразу после значения.
Например:
10 10 представляет десятичное число десять. (1 десяток + 0 единиц)
10 2 представляет двоичное значение два. (1 два + 0 единиц)
10 8 представляет восьмеричное число восемь. (1 восемь + 0 единиц)
10 16 представляет собой шестнадцатеричное число шестнадцать. (1 шестнадцать + 0 единиц)
Система счисления
Основа системы, более правильно называемая RADIX, представляет собой количество различных значений, которые могут быть выражены с помощью одной цифры. Следовательно, десятичная система имеет основание 10, восьмеричная система имеет основание 8, шестнадцатеричная система счисления — 16, а двоичная система счисления — 2.
Диапазон числовых значений в различных системах счисления показан в таблице 1.1.2. Обратите внимание, что, поскольку шестнадцатеричная система должна выражать 16 значений, используя только один столбец, в ней используются буквы A B C D E и F для представления чисел от 10 до 15.
Точка основания.
При записи числа используемые цифры задают его значение, но число «масштабируется» по его RADIX POINT.
Например, 456,2 10 в десять раз больше, чем 45,62 10 , хотя цифры те же.
Также обратите внимание, что при использовании нескольких систем счисления используется термин «RADIX-точка» вместо «DECIMAL-точка». При использовании десятичных чисел используется десятичная точка, но если используется другая система, было бы неправильно называть точку десятичной точкой, ее нужно было бы называть «Двоичная точка» или «Восьмеричная точка» и т. д. Самый простой способ обойти это — обратиться к точке в любой системе (которая, конечно, будет иметь свое значение, помеченное своим основанием) как RADIX POINT.
Экспоненты
Десятичное число, такое как 456,2 10 , можно рассматривать как сумму значений его отдельных цифр, где каждая цифра имеет значение, зависящее от ее положения в числе (значение столбца):
= 456,2 10
Каждая цифра в числе умножается на систему счисления, возведенную в степень, в зависимости от ее положения относительно точки счисления. Это называется ЭКСПОНЕНТ. Цифра непосредственно слева от точки счисления имеет показатель степени 0, примененный к ее основанию, и для каждого места слева показатель степени увеличивается на единицу. Первое место справа от точки счисления имеет показатель -1 и так далее, положительные показатели слева от точки счисления и отрицательные показатели справа.
Этот способ записи чисел широко используется в электронике с десятичными числами, но может использоваться с любой системой счисления. Только основание другое.
шестнадцатеричные показатели 98,2 16 = (9 x 16 1 ) + (8 x 16 0 ) + (2 x 16 -1 )
Восьмидесявые экспоненты 56,2 8 = (5 x 8
1 ) + (6 x 8 0 ) + (2 x 8 -1 )
Двоичные показатели 10,1 2 = (1 x 2 1 ) + (0 x 2 0 ) + (1 x 2 -1 )
При использовании вашего калькулятора для приведенных выше примеров вы можете обнаружить, что он не любит системы счисления ни в каком другом виде, кроме десятичного.
Это характерно для многих электронных калькуляторов.
Обозначение с плавающей запятой
Если электронные калькуляторы не могут использовать точки счисления, отличные от десятичных, это может быть проблемой. К счастью, для каждой проблемы есть решение. Показатель степени счисления также можно использовать для устранения точки счисления без изменения значения числа. В приведенном ниже примере посмотрите, как значение остается неизменным при перемещении точки счисления. Все это делается путем изменения показателя системы счисления.
102,6 10 = 102,6 x 10 0 = 10,26 x 10 1 = 1,026 x 10 2 = .1026 x 10 3
Перемешается одно место влево путем увеличения от увеличения в рамках увеличения от увеличения в показатель на единицу.
Также можно переместить точку счисления вправо, уменьшив показатель степени. Таким образом, точку счисления можно расположить там, где это необходимо, в любой системе счисления, просто изменив показатель степени.
Это называется записью с плавающей запятой, и именно так калькуляторы обрабатывают десятичные точки в вычислениях.
Нормализованная форма
Поставив точку счисления перед числом и сохранив ее там, изменив показатель степени, расчеты становятся проще выполнять в электронном виде в любой системе счисления.
Электронное хранилище номеров.
Считается, что число, записанное (или сохраненное) таким образом, с точкой счисления слева от старшего разряда, находится в НОРМАЛИЗОВАННОЙ ФОРМЕ. Например, .11011 2 x 2 3 — это нормализованная форма двоичного числа 110,11 9.1112 2 . Поскольку числа в электронных системах хранятся в виде двоичных цифр, а двоичная цифра может быть только 1 или 0, невозможно сохранить точку счисления в числе. Поэтому число хранится в его нормализованной форме, а показатель степени хранится отдельно. Затем показатель степени повторно используется для восстановления точки счисления в правильное положение при отображении числа.
В электронных системах одна двоичная цифра называется битом (сокращение от Binary DigIT), но поскольку использование одной цифры серьезно ограничило бы математические операции, двоичные биты обычно используются группами.
4 бита = 1 полубайт
8 бит = 1 байт 32-битное слово. Длина слова зависит от того, сколько битов может физически обрабатываться или храниться системой одновременно.
4-битное двоичное представление
Когда число сохраняется в электронной системе, оно сохраняется в ячейке памяти с фиксированным числом двоичных битов. Некоторые из этих ячеек памяти используются для общего хранения, в то время как другие, имеющие некоторые специальные функции, называются регистрами. Где бы ни хранилось число, оно будет храниться в той или иной двоичной форме и всегда должно иметь заданное количество битов. Поэтому десятичное число, такое как 13, которое может быть выражено четырьмя двоичными битами как 1101 2 становится 00001101 2 при сохранении в восьмибитном регистре.
Это достигается путем добавления четырех НЕЗНАЧАЮЩИХ НУЛЕЙ слева от старшей значащей цифры «1».
В этой системе двоичный регистр размером n бит может содержать 2 n значений.
Таким образом, 8-битный регистр может содержать 2 8 значений = 256 значений (от 0 до 255)
4-битный регистр может содержать 2 4 значений = 16 значений (от 0 до 15) 16-БИТНЫЙ РЕГИСТР УДЕРЖАН?
Введите десятичное число.
Заполнение регистра незначащими нулями допустимо — если число меньше максимального значения, регистр удержится, но как насчет больших чисел? С ними необходимо справиться, разделив двоичное число на группы по 8 бит, каждая из которых может храниться в однобайтовой ячейке, и используя несколько ячеек для хранения разных частей общего значения. То, как число делится, зависит от конструкции используемой электронной системы.
Резюме:
- • В электронных системах могут использоваться различные системы счисления (например, десятичная, шестнадцатеричная, восьмеричная, двоичная).
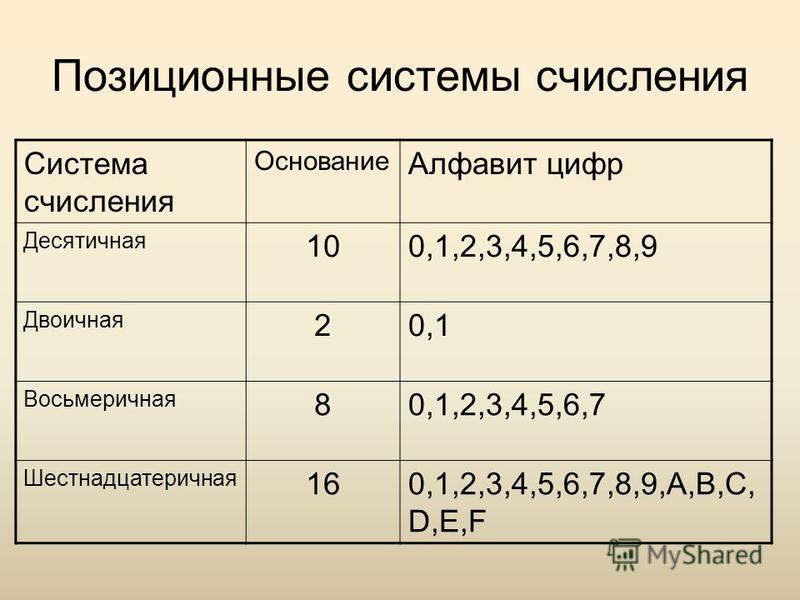 При использовании цифр от 0 до 6, нам пришлось бы строить числа уже для записи значений, больше 6. В таком случае 10 будет равно 7, но эти значения будут записаны в разных системах счисления.
При использовании цифр от 0 до 6, нам пришлось бы строить числа уже для записи значений, больше 6. В таком случае 10 будет равно 7, но эти значения будут записаны в разных системах счисления.
 7
7