Онлайн калькулятор систем счисления с решением онлайн
Переведем целую часть 12 числа 12.310 в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.| 12 | : | 2 | = | 6 | остаток: 0 |
| 6 | : | 2 | = | 3 | остаток: 0 |
| 3 | : | 2 | = | 1 | остаток: 1 |
| 1 | : | 2 | = | 0 | остаток: 1 |
1210 = 11002
Переведем дробную часть 0.3 числа 12.310 в 2-ичную систему счисления, при помощи последовательного умножения на 2, до тех пор, пока в дробной части произведения не получиться ноль или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.
В результате будет получено число из целых частей произведений, записанное слева направо.
| 0.3 | · | 2 | = | 0.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.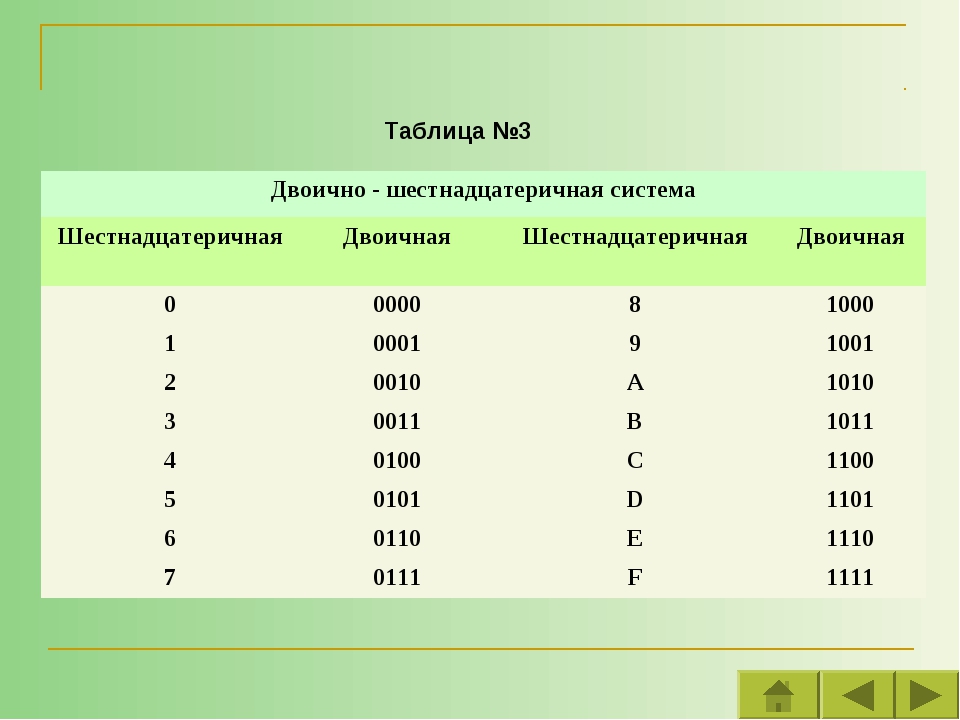 2 2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.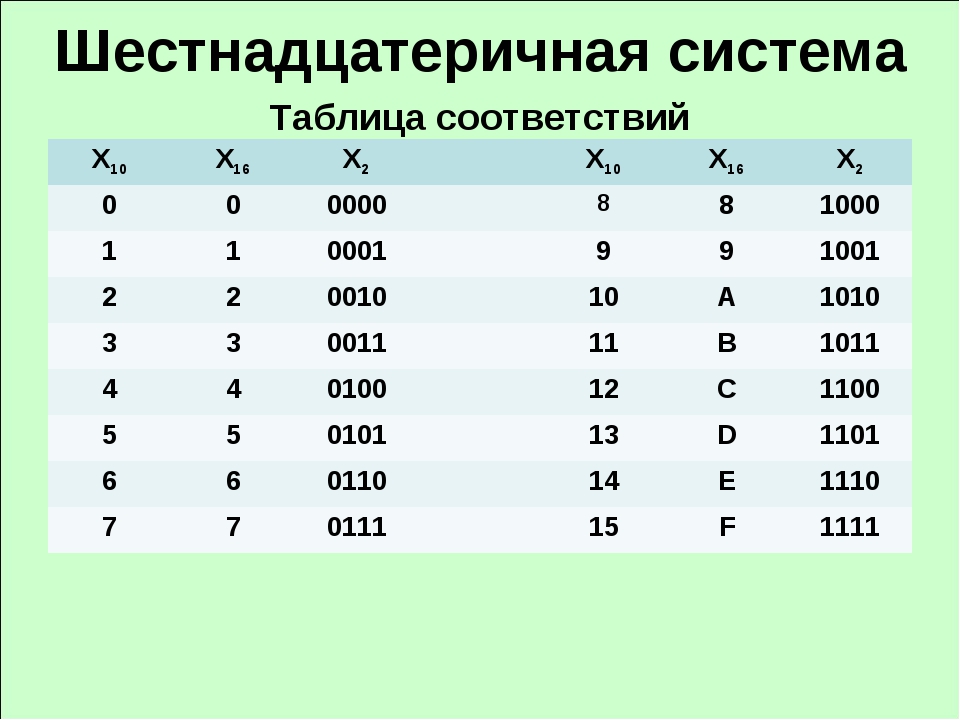 2 2 |
0.310 = 0.0100110011001100110011001100112
12.310 = 1100.0100110011001100110011001100112
Шестеричная система счисления
Содержание:Что такое шестеричная система счисления
Как перевести целое десятичное число в шестеричную систему счисления
Как перевести десятичную дробь в шестеричную систему счисления
Как перевести число из шестеричной системы счисления в десятичную
Как перевести дробное шестеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в шестеричной системе счисления
Что такое шестеричная система счисления
Шестеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в шестеричной системе счисления используется шесть цифр 0, 1, 2, 3, 4 и 5. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется основанием системы счисления.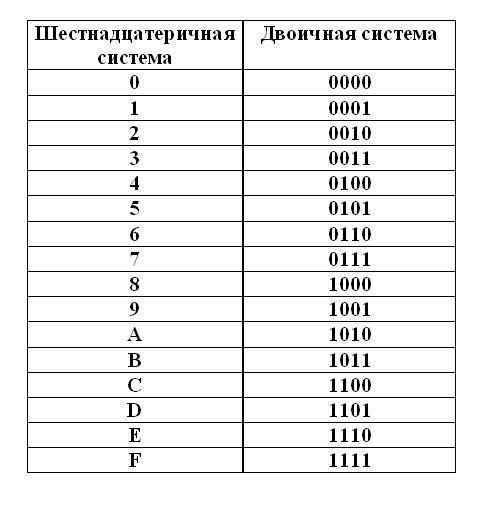 Например, 3353
Например, 3353Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.
Как перевести целое десятичное число в шестеричную систему счисления
Для того, чтобы перевести целое десятичное число в шестеричную систему счисления нужно десятичное число делить на 6 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.Например, переведем число 11510 в шестеричную систему счисления:
115 : 6 = 19 остаток: 1
19 : 6 = 3 остаток: 1
3 : 6 = 0 остаток: 3
11510 = 3116
Как перевести десятичную дробь в шестеричную систему счисления
Для того чтобы перевести десятичную дробь в шестеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в шестеричную систему счисления, а затем дробную часть, последовательно умножать на 6, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число) или не будет достигнуто необходимое количество знаков после запятой.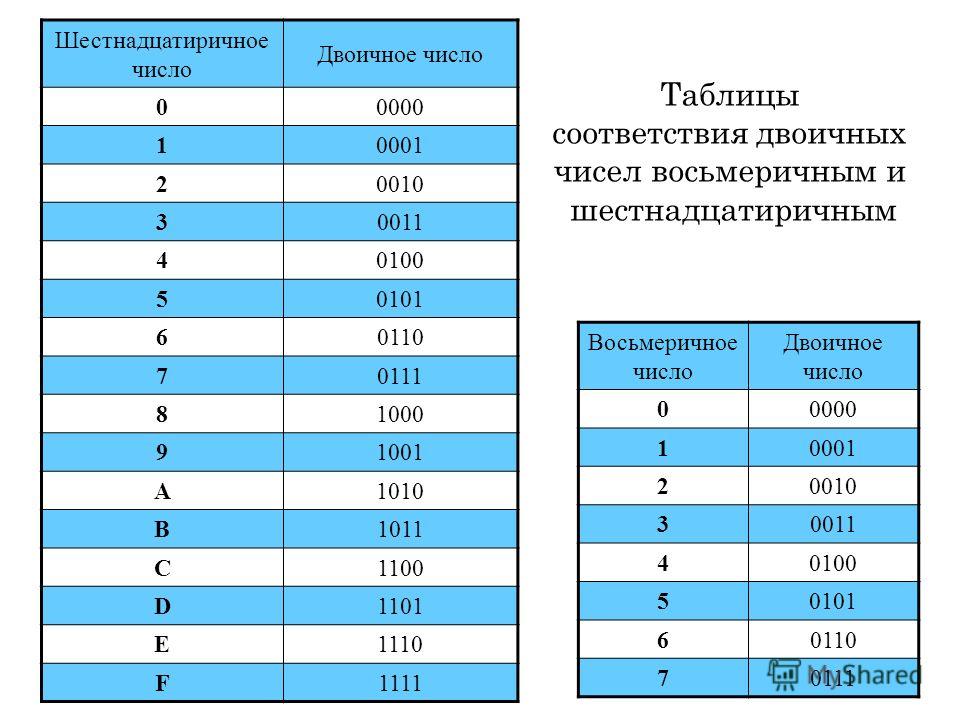 Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль.
В результате будет получено число из целых частей произведений, записанное слева направо.
Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль.
В результате будет получено число из целых частей произведений, записанное слева направо.Например, переведем десятичное число 95.3610 в шестеричную систему счисления:
Переведем целую часть
95 : 6 = 15 остаток: 5
15 : 6 = 2 остаток: 3
2 : 6 = 0 остаток: 2
9510 = 2356
Переведем дробную часть
0.36 · 6 = 2.16
0.16 · 6 = 0.96
0.96 · 6 = 5.76
0.76 · 6 = 4.56
0.56 · 6 = 3.36
0.36 · 6 = 2.16
0.16 · 6 = 0.96
0.96 · 6 = 5.76
0.56 · 6 = 3.36
0.3610 = 0.20543205436
95.3610 = 235.20543205436
Шестеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной шестеричной. В данном примере получается бесконечная периодическая шестеричная дробь, поэтому умножение на 6 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю.
В данном случае десятичная дробь 95.36 не может быть точно представлена в шестеричной системе счисления.
К примеру, дробь 2.510 может быть представлена в двоичной системе счисления в виде конечной 2.510 = 2.32.
В данном примере получается бесконечная периодическая шестеричная дробь, поэтому умножение на 6 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю.
В данном случае десятичная дробь 95.36 не может быть точно представлена в шестеричной системе счисления.
К примеру, дробь 2.510 может быть представлена в двоичной системе счисления в виде конечной 2.510 = 2.32.
Как перевести число из шестеричной системы счисления в десятичную
Для того, чтобы перевести число из шестеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля. Каждая позиция цифры будет степенью числа 6, так как система счисления 6-ичная. Необходимо последовательно умножить каждое число на 6 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции. Например, переведем число 504216 в десятичную систему счисления:
Например, переведем число 504216 в десятичную систему счисления:| Позиция в числе | 4 | 3 | 2 | 1 | 0 |
| Число | 5 | 0 | 4 | 2 | 1 |
504216 = 5 ⋅ 64 + 0 ⋅ 63 + 4 ⋅ 62 + 2 ⋅ 61 + 1 ⋅ 60 = 663710
Как перевести дробное шестеричное число в десятичное
Для того, чтобы перевести дробное шестеричное число в десятичное, необходимо записать дробное шестеричное число, убрав точку и затем сверху расставить индексы. Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию. Каждая позиция цифры (индекс) будет степенью числа 6, так как система счисления 6-ичная. Необходимо последовательно умножить каждое число на 6 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Например, переведем дробное шестеричное число 13.536 в десятичное:
| Позиция в числе | 1 | 0 | -1 | -2 |
| Число | 1 | 3 | 5 | 3 |
13.536 = 1 ⋅ 61 + 3 ⋅ 60 + 5 ⋅ 6 -1 + 3 ⋅ 6-2 = 9.916666666666666666666666666910
Таблица значений десятичных чисел от 0 до 100 в шестеричной системе счисления
| Значение числа в десятичной системе счисления | Значение числа в шестеричной системе счисления |
| 010 | 06 |
| 110 | 16 |
| 210 | 26 |
| 310 | 36 |
| 410 | 46 |
| 56 | |
| 610 | 106 |
| 710 | 116 |
| 810 | 126 |
| 910 | 136 |
| 1010 | 146 |
| 1110 | 156 |
| 1210 | 206 |
| 1310 | 216 |
| 1410 | 226 |
| 1510 | 236 |
| 1610 | 246 |
| 1710 | 256 |
| 1810 | 306 |
| 1910 | 316 |
| 2010 | 326 |
| 336 | |
| 2210 | 346 |
| 2310 | 356 |
| 2410 | 406 |
| 2510 | 416 |
| 2610 | 426 |
| 2710 | 436 |
| 2810 | 446 |
| 2910 | 456 |
| 3010 | 506 |
| 3110 | 516 |
| 3210 | 526 |
| 3310 | 536 |
| 3410 | 546 |
| 3510 | 556 |
| 3610 | 1006 |
| 3710 | 1016 |
| 3810 | 1026 |
| 3910 | 1036 |
| 4010 | 1046 |
| 4110 | 1056 |
| 4210 | 1106 |
| 4310 | 1116 |
| 4410 | 1126 |
| 4510 | 1136 |
| 4610 | 1146 |
| 4710 | 1156 |
| 4810 | 1206 |
| 4910 | 1216 |
| 5010 | 1226 |
| Значение числа в десятичной системе счисления | Значение числа в шестеричной системе счисления |
| 5110 | 1236 |
| 5210 | 1246 |
| 5310 | 1256 |
| 5410 | 1306 |
| 5510 | 1316 |
| 5610 | 1326 |
| 5710 | 1336 |
| 5810 | 1346 |
| 5910 | 1356 |
| 6010 | 1406 |
| 6110 | 1416 |
| 6210 | 1426 |
| 6310 | 1436 |
| 6410 | 1446 |
| 6510 | 1456 |
| 6610 | 1506 |
| 6710 | 1516 |
| 6810 | 1526 |
| 6910 | 1536 |
| 7010 | 1546 |
| 7110 | 1556 |
| 7210 | 2006 |
| 7310 | 2016 |
| 7410 | 2026 |
| 7510 | 2036 |
| 7610 | 2046 |
| 7710 | 2056 |
| 7810 | 2106 |
| 7910 | 2116 |
| 8010 | 2126 |
| 8110 | 2136 |
| 8210 | 2146 |
| 8310 | 2156 |
| 8410 | 2206 |
| 8510 | 2216 |
| 8610 | 2226 |
| 8710 | 2236 |
| 8810 | 2246 |
| 8910 | 2256 |
| 9010 | 2306 |
| 9110 | 2316 |
| 9210 | 2326 |
| 9310 | 2336 |
| 9410 | 2346 |
| 9510 | 2356 |
| 9610 | 2406 |
| 9710 | 2416 |
| 9810 | 2426 |
| 9910 | 2436 |
| 10010 | 2446 |
Системы счисления
Что это такое?
Есть много способов для представления одного и того же числового значения.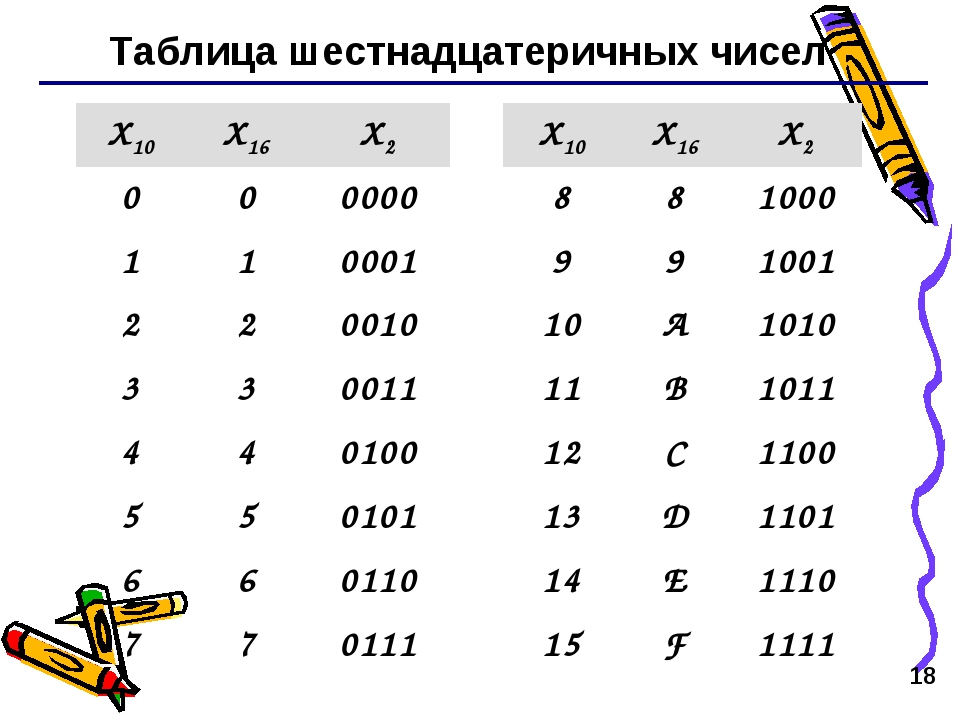 В давние времена люди использовали палочки для подсчета. Позднее научились
рисовать палочки на земле и в конечном счете на бумаге. Так что число 5 вначале
представлялось как: | | | | | (пять палочек).
В давние времена люди использовали палочки для подсчета. Позднее научились
рисовать палочки на земле и в конечном счете на бумаге. Так что число 5 вначале
представлялось как: | | | | | (пять палочек).Еще позднее римляне начали использовать различные символы для большого количества палочек:| | | означало три палочки, а V означало пять палочек, и наконец X использовалось для представления 10-ти палочек!
Использование палочек для счета было хорошей идеей для того времени.
А использование символов вместо реальных палочек было еще лучше. Одним из наиболее удобных современных способов представления чисел
является десятичная система. Почему? Потому что она использует основное свое
достижение — идею использования символа для подсчета ничего.
Около 1500 лет назад в Индии ноль (0) был впервые использован как число!
Позднее он был использован на Ближнем Востоке как арабский sifr. И наконец, представлен на западе как латинский zephiro. Вскоре вы увидите, какое большое значение имеет эта идея во всех
современных системах счисления.
И наконец, представлен на западе как латинский zephiro. Вскоре вы увидите, какое большое значение имеет эта идея во всех
современных системах счисления.
Десятичная система
Большинство людей сегодня используют десятичное представление числа. В десятичной системе 10 цифр:0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Этими цифрами можно представить любое значение, например:
754.
Значение формируется путем суммирования всех цифр, умноженных на основание (в нашем случае основание равно 10, т.к. в десятичной системе 10 цифр) в степени, равной позиции цифры (отсчет ведется с нуля):
Позиция каждой цифры — очень важный фактор! Например, если вы поместите «7» в конец:
547
то это будет уже другое значение:
Важное замечание: любое число в нулевой степени равно единице,
даже ноль в нулевой степени равен 1:
Двоичная система
Компьютеры не такие умные, как люди (во всяком случае пока). Легко сделать электронную машину с двумя состояниями: включено и выключено, или 1 и 0.
Легко сделать электронную машину с двумя состояниями: включено и выключено, или 1 и 0.Компьютеры используют двоичную систему, которая использует всего две цифры:
0, 1
И поэтому основание в двоичной системе равно 2.
Каждая цифра в двоичном числе называется БИТ, 4 бита — это ПОЛУБАЙТ, 8 битов это БАЙТ, два байта — это СЛОВО, два слова — это ДВОЙНОЕ СЛОВО (используется редко):
В конец двоичного числа принято добавлять букву «b». Таким образом мы можем определить, что 101b — это двоичное число, которое соответствует десятичному значению 5.
Двоичное число 10100101b эквивалентно десятичному значению 165:
Шестнадцатиричная система
Шестнадцатиричная система использует 16 цифр:0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
И поэтому основание в шестнадцатиричной системе равно 16.
Шестнадцатиричные числа являются компактными и легкими для чтения.
Их легко преобразовать в двоичную систему и наборот. Каждый полубайт
(4 бита) можно преобразовать в шестнадцатиричную цифру, пользуясь этой таблицей:
|
Принято в конец шестнадцатиричного числа добавлять букву «h»,
таким образом мы можем определить, что 5Fh — это шестнадцатиричное число,
которому соответствует десятичное значение 95.
Мы также добавляем «0» (ноль) в начало шестнадцатиричного числа,
если оно начинается с буквы (A..F), например 0E120h.
Шестнадцатиричное число 1234h эквивалентно десятичному 4660:
Преобразование значений десятичной системы в другие
Чтобы преобразовать число из десятичной системы в какую-либо другую, необходимо выполнить целое деление десятичного значения на основание нужной системы счисления. Получим результат и остаток. Затем будем делить результат на основание системы, пока результат не будет равен нулю.Остатки используются для представления значения в новой системе счисления.
Давайте преобразуем число 39 (основание 10) в шестнадцатиричную систему (основание 16):
Вы видите, что мы получили шестнадцатиричное число 27h.
Все остатки в этом примере меньше 10, поэтому мы не используем буквы.
Здесь приведен пример перевода числа с большим количеством цифр:
Давайте преобразуем десятичное число 43868 в шестнадцатиричную форму:
Результат получаем такой: 0AB5Ch, используя описанную выше таблицу
для преобразования остатков больше 9 в соответствующую букву.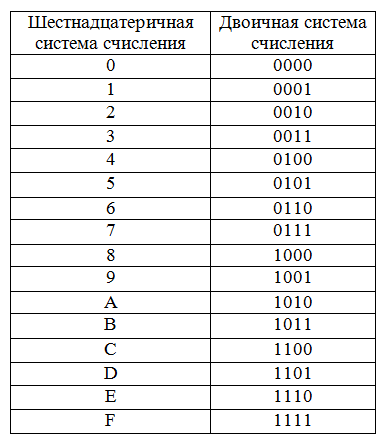
Используя тот же принцип мы можем преобразовать число в двоичную форму (используя 2 как делитель), или преобразовать шестнадцатиричное число в двоичное число, используя описанную выше таблицу:
Вы видите, что мы получили следующее двоичное число: 1010101101011100b
Числа со знаком
Нет никакой уверенности в том, каким является шестнадцатиричное число 0FFh — отрицательным или положительным. Оно может быть представлено двумя десятичными значениями: «255» или «— 1«.8 бит можно использовать для создания 256 комбинаций (включая ноль), поэтому мы просто предполагаем, что первые 128 комбинаций (0..127) будут представлять положительные числа, а следующие 128 комбинаций (128..256) будут представлять отрицательные числа.
Чтобы получить число «— 5«, мы должны вычесть 5 из
максимально возможного числа комбинаций (256). Так мы получим: 256 — 5 = 251.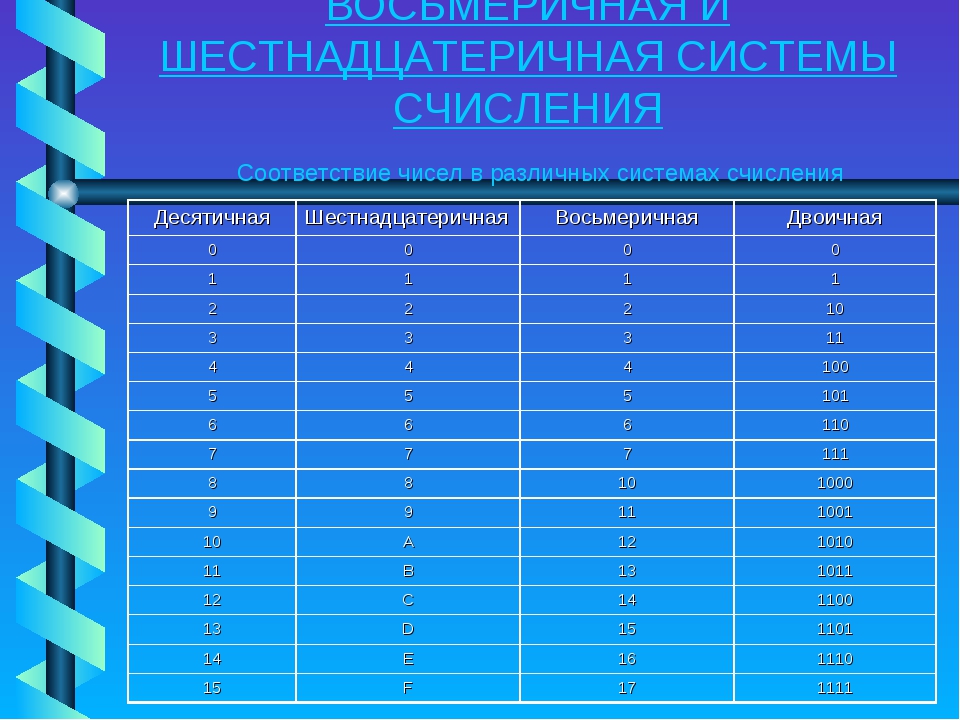
Использование этого способа для представления отрицательных чисел имеет
определенный смысл. В математике, если вы прибавите «— 5» к «5«,
вы должны получить ноль.
То же самое случается, когда процессор складывает два байта: 5 и 251.
Результат превышает значение 255, поэтому из-за переполнения
процессор получает ноль!
Когда используется комбинация 128..256, то старший бит всегда равен 1. Это используется для определения знака.
Тот же самый принцип используется для слов (16-ти битовых значений). С шестнадцатью битами можно создать 65536 комбинаций, первые 32768 комбинаций (0..32767) используются для представления положительных чисел, а следующие 32768 комбинаций (32767..65535) представляют отрицательные числа.
В Emu8086 имеются некоторые удобные инструменты для преобразования чисел и вычисления любых числовых выражений. Все их можно увидеть, выбрав пункт меню Math:
Number Convertor — преобразователь чисел позволяет вам преобразовывать
числа из любой системы в любую систему. Просто напечатайте значение
в любом текстовом поле и это значение будет автоматически преобразовано
во все другие системы. Вы можете работать как с 8-ми битовыми, так
и с 16-ти битовыми значениями.
Просто напечатайте значение
в любом текстовом поле и это значение будет автоматически преобразовано
во все другие системы. Вы можете работать как с 8-ми битовыми, так
и с 16-ти битовыми значениями.
Expression Evaluator — вычисление выражений может быть использовано
для вычислений выражений, в котороых имеются числа, представленные в
различных системах счисления, и преобразования чисел из одной системы в другую.
Напечатайте выражение и нажмите ENTER. Результат появится в выбранной системе счисления.
Вы можете работать со значениями до 32 битов. Если установлен
флажок Signed, то программа будет считать все значения
знаковыми (+ или -), кроме десятичных чисел и двойных слов.
Двойное слово всегда расценивается как знаковое значение, поэтому 0FFFFFFFFh преобразуется в -1.
Например, вы хотите вычислить: 0FFFFh * 10h + 0FFFFh
(максимальное местоположение памяти, доступное процессору 8086).
Если вы установите флажки Signed и Word, вы получите
-17 (потому что выражение будет вычислено
как (-1) * 16 + (-1) .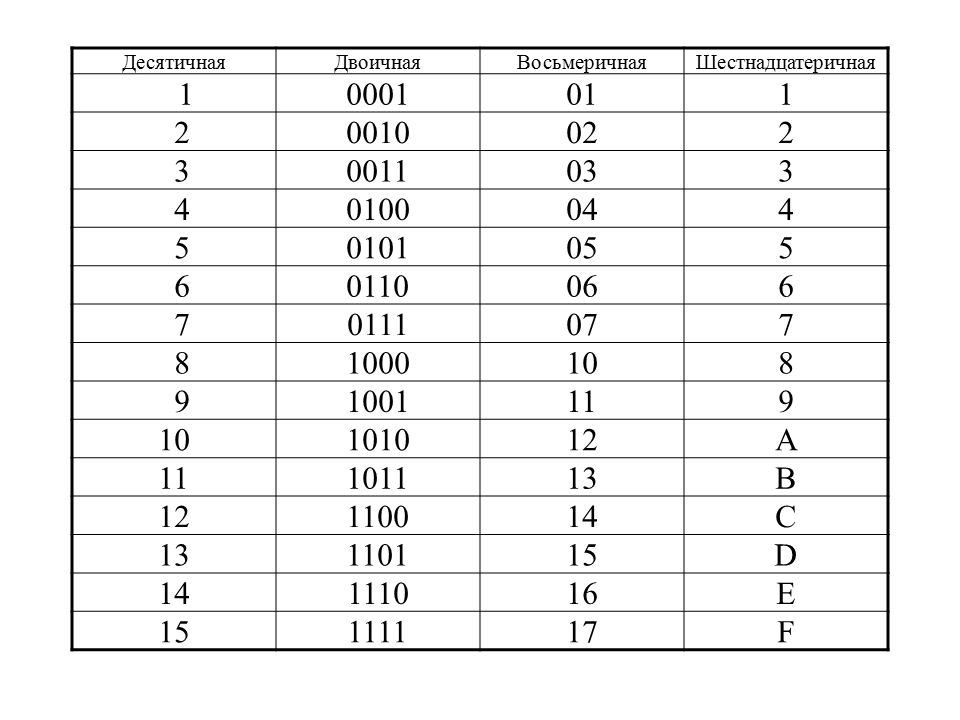 исключающее ИЛИ.
| логическое ИЛИ.
исключающее ИЛИ.
| логическое ИЛИ.
Двоичные числа должны иметь суффикс «b«, например:
00011011b
Шестнадцатиричные числа должны иметь суффикс «h«, и начинаться с нуля
если первая цифра — это буква (A..F), например:
0ABCDh
Восмеричные (основа 8) числа должны иметь суффикс «o«, например:
77o
>>> Следующий урок >>>
Шестнадцатеричное кодирование. Шестнадцатеричная нумерация и адресация
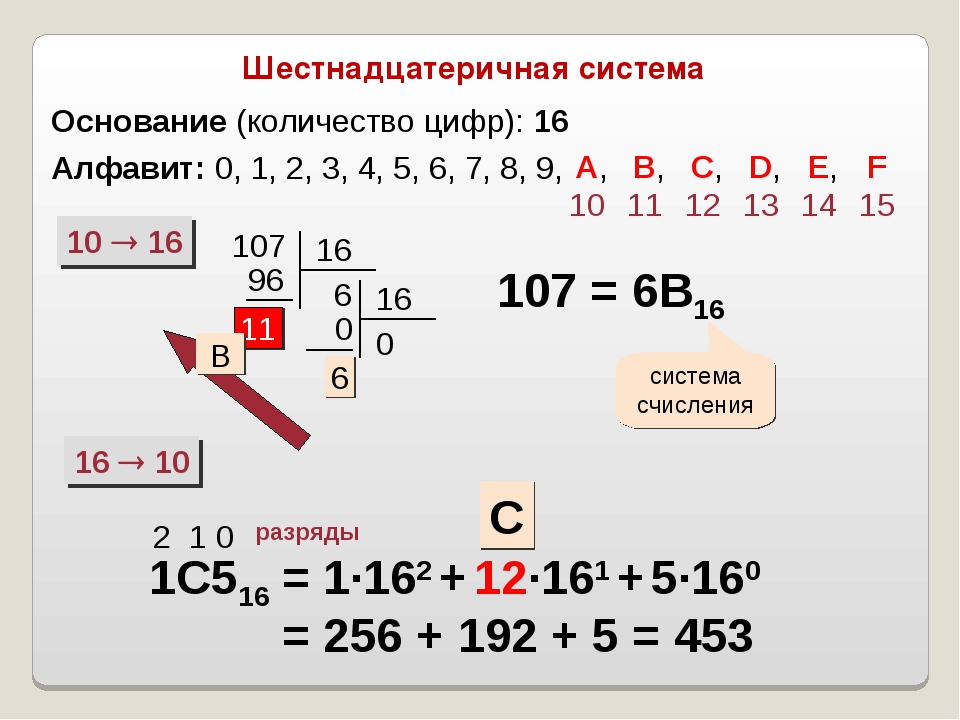
Шестнадцатеричная система счисления (также — шестнадцатеричный код) является позиционной системой счисления с целочисленным основанием 16. Иногда в литературе также используется термин hex (произносится «хекс», сокращение от англ. hexadecimal). Цифрами данной системы счисления принято использовать арабские цифры 0—9, а также первые символы латинского алфавита A—F. Буквы соответствуют следующим десятичным значениями:
- * A —10;
- * B —11;
- * C —12;
- * D —13;
- * E — 14;
- * F — 15.
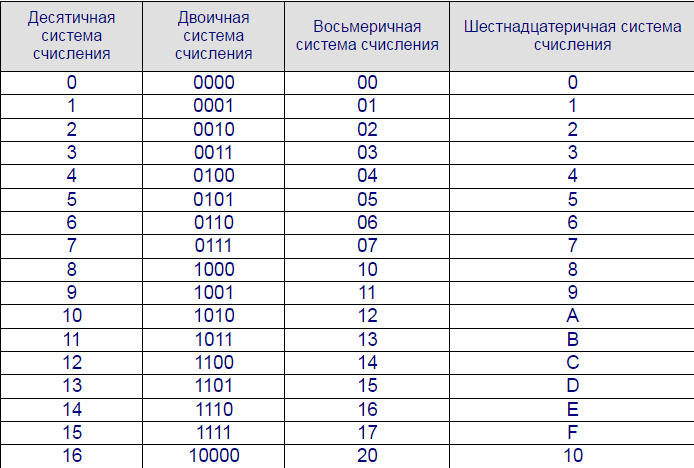
Таким образом, десять арабских цифр вкупе с шестью латинскими буквами и составляют шестнадцать цифр системы.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн .
Применение . Шестнадцатеричный код широко применяется в низкоуровневом программировании, а также в различных компьютерных справочных документах. Популярность системы обоснована архитектурными решениями современных компьютеров: в них в качестве минимальной единицы информации установлен байт (состоящий из восьми бит) — а значение байта удобно записывать с помощью двух шестнадцатеричных цифр. Значение байта может ранжироваться с #00 до #FF (от 0 до 255 в десятичной записи) — другими словами, используя шестнадцатеричный код , можно записать любое состояние байта, при этом не остаётся «лишних» не используемых в записи цифр.
В кодировке Юникод для записи номера символа используется четыре шестнадцатеричных цифры. Запись цвета стандарта RGB (Red, Green, Blue — красный, зелёный, синий) также часто использует шестнадцатеричный код (например, #FF0000 — запись ярко-красного цвета).
Запись цвета стандарта RGB (Red, Green, Blue — красный, зелёный, синий) также часто использует шестнадцатеричный код (например, #FF0000 — запись ярко-красного цвета).
Способ записи шестнадцатеричного кода.
Математический способ записи . В математической записи основание системы записывают в десятичном виде в нижнем индексе справа от числа. Десятичную запись числа 3032 можно записать как 3032 10 , в шестнадцатеричной системе данное число будет иметь запись BD8 16 .
В синтаксисе языков программирования . Синтаксис различных языков программирования по-разному устанавливает формат записи числа, использующего шестнадцатеричный код :
* В синтаксисе некоторых разновидностей языка ассемблера используется латинская буква «h», которая ставится справа от числа, например: 20Dh. Если число начинается с латинской буквы, то перед ним ставится ноль, например: 0A0Bh. Это сделано для того, чтобы отличать от констант значения, использующие шестнадцатеричный код ;
* В прочих разновидностях ассемблера, а также в Pascal (и его разновидностях, таких как Delphi) и некоторых диалектах Basic, применяют префикс «$»: $A15;
* В языке разметки HTML, а также в каскадных файлах CSS, для указания цвета в формате RGB с шестнадцатеричной системой записи, используется префикс «#»: #00DC00.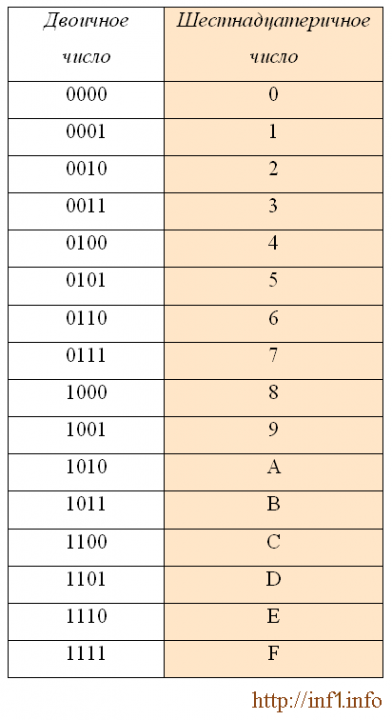
Как перевести шестнадцатеричный код в другую систему?
Перевод из шестнадцатеричной системы в десятичную. Для совершения операции перевода из шестнадцатеричной системы в десятичную, требуется представить исходное число как сумму произведений цифр в разрядах шестнадцатеричного числа на степень основания.
Двоичная СС | шестнадцатеричная СС |
Например, требуется выполнить перевод шестнадцатеричного числа A14: в нём три цифры. Используя правило, запишем его в виде суммы степеней с основанием 16:
Используя правило, запишем его в виде суммы степеней с основанием 16:
A14 16 = 10.16 2 + 1.16 1 + 4.16 0 = 10.256 + 1.16 + 4.1 = 2560 + 16 + 4 = 2580 10
Перевод чисел из двоичной в шестнадцатеричную систему и наоборот.
Для перевода используется таблица тетрад. Чтобы выполнить перевод числа из двоичной в десятичную систему, необходимо произвести разбиение его на отдельные тетрады справа налево, после чего, используя таблицу, выполнить замену каждой тетрады на соответствующую шестнадцатеричную цифру. При этом, если количество цифр не кратно четырём, то необходимо добавить соответствующее количество нулей справа от числа, для того, чтобы общее число двоичных цифр стало кратно четырём.
Таблица тетрад для перевода.
Для перевода из шестнадцатеричной системы в двоичную, необходимо выполнить обратную операцию: выполнить замену каждой цифры на тетраду из таблицы.
Двоичная СС | Восьмеричная СС |
Пример перевода из шестнадцатеричной системы в двоичную : A5E 16 = 1010 0101 1110 = 101001011110 2
Пример перевода из двоичной системы в шестнадцатеричную : 111100111 2 = 0001 1110 0111 = 1E7 16
В этом примере количество цифр в исходном двоичном числе не было равным четырём (9), поэтому были добавлены незначащие нули — общее число цифр стало 12.
Автоматический перевод
Шестнадцатеричный калькулятор онлайн
Если вам необходимо произвести математические операции в шестнадцатеричной системе счисления воспользуйтесь нашим онлайн калькулятором:
Просто введите шестнадцатеричные числа, выберите операцию и получите результат.
Калькулятор может производить следующие действия:
- сложение +
- вычитание −
- умножение ×
- деление ÷
- логическое И (AND)
- логическое ИЛИ (OR)
- исключающее ИЛИ (XOR)
Сложение в шестнадцатеричной системе счисления
Сложение двух шестнадцатеричных чисел производится столбиком, как и в десятичной системе, но по следующим правилам:
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 8 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 9 | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| A | A | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| B | B | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A |
| C | C | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B |
| D | D | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C |
| E | E | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C | 1D |
| F | F | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1B | 1C | 1D | 1E |
Пример
Для примера сложим F4240 и 7A120:
| + | F | 4 | 2 | 4 | 0 | |
| 7 | A | 1 | 2 | 0 | ||
| 1 | 6 | E | 3 | 6 | 0 | |
F424016 + 7A12016 = 16E36016
(1 000 00010 + 500 00010 = 1 500 00010)
Вычитание в шестнадцатеричной системе счисления
Правила вычитания шестнадцатеричных чисел обратны правилам сложения (см. таблицу выше).
таблицу выше).
Пример
Для примера вычтем из числа 16E360 число F4240:
| – | 1 | 6 | E | 3 | 6 | 0 |
| F | 4 | 2 | 4 | 0 | ||
| 7 | A | 1 | 2 | 0 | ||
16E36016 − F424016 = 7A12016
(1 500 00010 − 1 000 00010 = 500 00010)
Умножение чисел в шестнадцатеричной системе счисления
Умножение шестнадцатеричных чисел производится по следующим правилам:
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 2 | 0 | 2 | 4 | 6 | 8 | A | C | E | 10 | 12 | 14 | 16 | 18 | 1A | 1C | 1E |
| 3 | 0 | 3 | 6 | 9 | C | F | 12 | 15 | 18 | 1B | 1E | 21 | 24 | 27 | 2A | 2D |
| 4 | 0 | 4 | 8 | C | 10 | 14 | 18 | 1C | 20 | 24 | 28 | 2C | 30 | 34 | 38 | 3C |
| 5 | 0 | 5 | A | F | 14 | 19 | 1E | 23 | 28 | 2D | 32 | 37 | 3C | 41 | 46 | 4B |
| 6 | 0 | 6 | C | 12 | 18 | 1E | 24 | 2A | 30 | 36 | 3C | 42 | 48 | 4E | 54 | 5A |
| 7 | 0 | 7 | E | 15 | 1C | 23 | 2A | 31 | 38 | 3F | 46 | 4D | 54 | 5B | 62 | 69 |
| 8 | 0 | 8 | 10 | 18 | 20 | 28 | 30 | 38 | 40 | 48 | 50 | 58 | 60 | 68 | 70 | 78 |
| 9 | 0 | 9 | 12 | 1B | 24 | 2D | 36 | 3F | 48 | 51 | 5A | 63 | 6C | 75 | 7E | 87 |
| A | 0 | A | 14 | 1E | 28 | 32 | 3C | 46 | 50 | 5A | 64 | 6E | 78 | 82 | 8C | 96 |
| B | 0 | B | 16 | 21 | 2C | 37 | 42 | 4D | 58 | 63 | 6E | 79 | 84 | 8F | 9A | A5 |
| C | 0 | C | 18 | 24 | 30 | 3C | 48 | 54 | 60 | 6C | 78 | 84 | 90 | 9C | A8 | B4 |
| D | 0 | D | 1A | 27 | 34 | 41 | 4E | 5B | 68 | 75 | 82 | 8F | 9C | A9 | B6 | C3 |
| E | 0 | E | 1C | 2A | 38 | 46 | 54 | 62 | 70 | 7E | 8C | 9A | A8 | B6 | C4 | D2 |
| F | 0 | F | 1E | 2D | 3C | 4B | 5A | 69 | 78 | 87 | 96 | A5 | B4 | C3 | D2 | E1 |
Пример
Для примера перемножим числа 1F4 и 2D:
| × | 1 | F | 4 | ||
| 2 | D | ||||
| + | 1 | 9 | 6 | 4 | |
| 3 | E | 8 | |||
| 5 | 7 | E | 4 | ||
1F416 × 2D16 = 57E416
(50010 × 4510 = 2250010)
Деление шестнадцатеричных чисел
Деление шестнадцатеричных чисел выполняется по тому же принципу, что и деление десятичных, например:
Пример
Для примера разделим число 7D0 на 2:
7D016 ÷ 216 = 3E816
(200010 ÷ 210 = 100010)
См.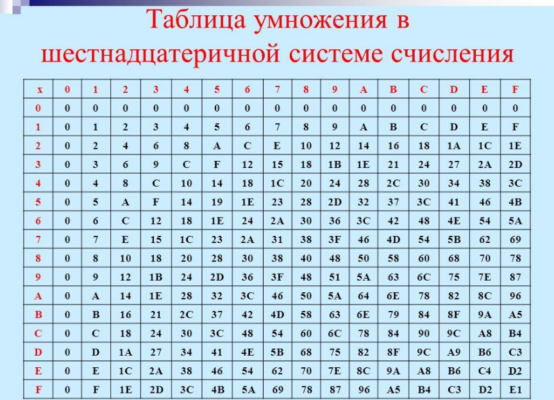 также
также
Перевод чисел из одной системы счисления в любую другую онлайн
Данный перевод возможен двумя способами: прямой перевод и через десятичную систему.
Сначала выполним прямой перевод.
Выполним прямой перевод из шестнадцатиричной в двоичную вот так:
EE816 = E E 8 = E(=1110) E(=1110) 8(=1000) = 1110111010002
Окончательный ответ: EE816 = 1110111010002
Теперь выполним перевод через десятичную систему счисления.
Выполним перевод в десятичную систему счисления вот так:
14∙162+14∙161+8∙160 = 14∙256+14∙16+8∙1 = 3584+224+8 = 381610
Получилось: EE816 =381610
Переведем число 381610 в двоичное вот так:
Целая часть числа находится делением на основание новой системы счисления:
| 3816 | 2 | ||||||||||||
| -3816 | 1908 | 2 | |||||||||||
| 0 | -1908 | 954 | 2 | ||||||||||
| 0 | -954 | 477 | 2 | ||||||||||
| 0 | -476 | 238 | 2 | ||||||||||
| 1 | -238 | 119 | 2 | ||||||||||
| 0 | -118 | 59 | 2 | ||||||||||
| 1 | -58 | 29 | 2 | ||||||||||
| 1 | -28 | 14 | 2 | ||||||||||
| 1 | -14 | 7 | 2 | ||||||||||
| 0 | -6 | 3 | 2 | ||||||||||
| 1 | -2 | 1 | |||||||||||
| 1 | |||||||||||||
В результате преобразования получилось:
381610 = 1110111010002
Окончательный ответ: EE816 = 1110111010002
Hexadezimalsystem — Википедия
шестигранник. | Двойная система | Dez. | |||||||
| 0 | 0 | 0 | 0 | 0 | 00 | ||||
| 1 | 0 | 0 | 0 | 1 | 01 | ||||
| 2 | 0 | 0 | 1 | 0 | 02 | ||||
| 3 | 0 | 0 | 1 | 1 | 03 | ||||
| 4 | 0 | 1 | 0 | 0 | 04 | ||||
| 5 | 0 | 1 | 0 | 1 | 05 | ||||
| 6 | 0 | 1 | 1 | 0 | 06 | ||||
| 7 | 0 | 1 | 1 | 1 | 07 | ||||
| 8 | 1 | 0 | 0 | 0 | 08 | ||||
| 9 | 1 | 0 | 0 | 1 | 09 | ||||
| А | 1 | 0 | 1 | 0 | 10 | ||||
| B | 1 | 0 | 1 | 1 | 11 | ||||
| С | 1 | 1 | 0 | 0 | 12 | ||||
| D | 1 | 1 | 0 | 1 | 13 | ||||
| E | 1 | 1 | 1 | 0 | 14 | ||||
| F | 1 | 1 | 1 | 1 | 15 | ||||
Im Hexadezimalsystem werden Zahlen in einem Stellenwertsystem zur Basis 16 dargestellt. «Шестнадцатеричный» (фон griech. hexa «sechs» и лат. decem «zehn») ist ein lateinisch-griechisches Mischwort; eine andere korrekte, jedoch seltener verwendete Bezeichnung ist sedezimal (von lat. sedecim «sechzehn»). Eine weitere alternate Bezeichnung ist hexadekadisch (griechisch). Falsch hingegen ist der Ausdruck hexa ges imal, der synonym zu sexa ges imal ist und das Zahlensystem zur Basis 60 bezeichnet.
«Шестнадцатеричный» (фон griech. hexa «sechs» и лат. decem «zehn») ist ein lateinisch-griechisches Mischwort; eine andere korrekte, jedoch seltener verwendete Bezeichnung ist sedezimal (von lat. sedecim «sechzehn»). Eine weitere alternate Bezeichnung ist hexadekadisch (griechisch). Falsch hingegen ist der Ausdruck hexa ges imal, der synonym zu sexa ges imal ist und das Zahlensystem zur Basis 60 bezeichnet.
In der Datenverarbeitung wird das Hexadezimalsystem sehr oft verwendet, da es sich hierbei letztlich um eine komfortablere Verwaltung des Binärsystems handelt. Die Datenwörter bestehen in der Informatik meist aus Oktetten, die statt als achtstellige Binärzahlen auch als nur zweistellige Hexadezimalzahlen dargestellt werden können. Im Gegensatz zum Dezimalsystem eignet sich das Hexadezimalsystem mit seiner Basis als vierte Zweierpotenz (16 = 2 4 ) zur einfacheren Notation der Binärzahlen, da stets eine feste Anzahl Zeicabeird des Wiedergwens. Nibbles können exakt mit einer hexadezimalen Ziffer und Bytes mit zwei hexadezimalen Ziffern dargestellt werden.
Nibbles können exakt mit einer hexadezimalen Ziffer und Bytes mit zwei hexadezimalen Ziffern dargestellt werden.
In den 1960er und 1970er Jahren wurde in der Informatik häufig auch das Oktalsystem mit seiner Basis als dritte Zweierpotenz (8 = 2 3 ) verwendet, da es mit den üblichen Ziffern von 0 7. Es findet aber heute seltener Anwendung, beispielsweise zur Darstellung von Zeichen in der Programmiersprache C. Auch gibt es noch weitere Zahlensysteme mit verschiedenen Basiswerten. [1]
Wir sind es gewohnt, im Dezimalsystem zu rechnen. Das bedeutet, unser indiarabisches Zahlensystem verwendet zehn Symbole zur Notation der Ziffern ( 0 bis 9 ). Das Hexadezimalsystem enthält dagegen sechzehn Ziffern. Seit Mitte der 1950er Jahre werden zur Darstellung der sechs zusätzlichen Ziffern die Buchstaben A bis F или a bis f as Zahlzeichen verwendet. Dies geht auf die damalige Praxis der IBM-Informatiker zurück.
Um hexadezimale von dezimalen Zahlen unterscheiden zu können, existieren mehrere Schreibweisen. Üblicherweise werden hexadezimale Zahlen mit einem Index oder Präfix versehen.
Verbreitete Schreibweisen sind: 72 16 , 72 hex , 72h, 72H, 72 H , 0x72, $ 72, «72 и X’72 ‘, wobei das Präfix 0x und das Suffix insbes h in der Programmierung und Technischen Informatik Verwendung finden. Das Anhängen eines h an die Hex-Zahl ist auch als Intel-Konvention geläufig.Die Schreibweise mit dem Dollar-Präfix ist in den Assemblersprachen bestimmter Prozessorfamilien üblich, insbesondere bei Motorola, zum beispiel beim Motorola 68xx and 68xxx, aber auch beim MOS 65xx; die Schreibweise X’72 ‘ist in der Welt der IBM-Großrechner üblich, wie in REXX.
Der Übersicht dienende Trennpunkte können bei Hexadezimalzahlen all vier Stellen gesetzt werden, trennen также Gruppen von jeweils sechzehn Bit. Die Bedeutung der 1.0000 16 = 65. 536 10 unter den hexadezimalen Zahlen entspricht также jener der 1.000 10 unter den dezimalen Zahlen.
536 10 unter den hexadezimalen Zahlen entspricht также jener der 1.000 10 unter den dezimalen Zahlen.
Zum Vergleich ein voller Vierundsechzig-Bit-Bus mit und ohne Trennpunkte: FFFF.FFFF.FFFF.FFFF und FFFFFFFFFFFFFFFF
Dezimale Zahlen werden, wo sie nicht der zu erwartende Normalfall sind, indiziert: 114 10
Gezählt wird wie folgt:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | B | С | D | E | F |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 1A | 1Б | 1С | 1D | 1E | 1F |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 2А | 2Б | 2C | 2D | 2E | 2F |
. .. .. | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | FA | FB | FC | FD | FE | FF |
| 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 10A | 10Б | 10C | 10D | 10E | 10F |
| … | … | … | … | … | … | … | … | … | … | … | . .. .. | … | … | … | … |
| FF0 | FF1 | FF2 | FF3 | FF4 | FF5 | FF6 | FF7 | FF8 | FF9 | FFA | FFB | FFC | FFD | FFE | FFF |
| 1000 | 1001 | 1002 | 1003 | 1004 | 1005 | 1006 | 1007 | 1008 | 1009 | 100A | 100B | 100C | 100D | 100E | 100F |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| FFF0 | FFF1 | FFF2 | FFF3 | FFF4 | FFF5 | FFF6 | FFF7 | FFF8 | FFF9 | FFFA | FFFB | FFFC | FFFD | FFFE | FFFF |
| 10000 | 10001 | 10002 | 10003 | 10004 | 10005 | 10006 | 10007 | 10008 | 10009 | 1000A | 1000B | 1000C | 1000D | 1000E | 1000F |
. .. .. | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
Für die hexadezimalen Ziffern und Zahlen sind keine eigenständigen Namen gebräuchlich. Hexadezimalzahlen werden daher meist Ziffer für Ziffer gelesen.
Beispiele:
- 10 sprich: «eins-null» (продавец: «zehn»),
- 1E sprich: „eins-E“,
- F112 sprich: «F-eins-eins-zwei».
Es lässt sich jedoch auch analog die Zählweise des Dezimalsystems verwenden, ohne dass der Einsatz des Hexadezimalsystems bei jeder Zahl gehört werden kann und sich dann zum Beispielbenus dem Kontext.
Beispiele:
- 10 sprich: „zehn“,
- 1E sprich: «E-zehn»,
- BD sprich: «D-und-B-zig»,
- F2A sprich: «F-hundert-A-undzwanzig»,
- F112 sprich: «F-tausendeinhundertzwölf».
Пример: 2 • 5 = A
Von der Spalte mit dem Wert 2 vertikal hinunter gehen bis Schnittpunkt der Zeile mit Wert 5.Эргебнис: А
| * | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | С | D | E | Ф | 10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | B | С | D | E | F | 10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 2 | 4 | 6 | 8 | А | С | E | 10 | 12 | 14 | 16 | 18 | 1A | 1С | 1E | 20 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 3 | 6 | 9 | С | F | 12 | 15 | 18 | 1Б | 1E | 21 | 24 | 27 | 2А | 2D | 30 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 4 | 8 | С | 10 | 14 | 18 | 1С | 20 | 24 | 28 | 2C | 30 | 34 | 38 | 3C | 40 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 5 | А | F | 14 | 19 | 1E | 23 | 28 | 2D | 32 | 37 | 3C | 41 | 46 | 4Б | 50 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 6 | С | 12 | 18 | 1E | 24 | 2А | 30 | 36 | 3C | 42 | 48 | 4E | 54 | 5A | 60 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 7 | E | 15 | 1С | 23 | 2А | 31 | 38 | 3F | 46 | 4D | 54 | 5Б | 62 | 69 | 70 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 8 | 10 | 18 | 20 | 28 | 30 | 38 | 40 | 48 | 50 | 58 | 60 | 68 | 70 | 78 | 80 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 9 | 12 | 1Б | 24 | 2D | 36 | 3F | 48 | 51 | 5A | 63 | 6C | 75 | 7E | 87 | 90 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| А | А | 14 | 1E | 28 | 32 | 3C | 46 | 50 | 5A | 64 | 6E | 78 | 82 | 8C | 96 | A0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Б | B | 16 | 21 | 2C | 37 | 42 | 4D | 58 | 63 | 6E | 79 | 84 | 8F | 9A | A5 | B0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| К | С | 18 | 24 | 30 | 3C | 48 | 54 | 60 | 6C | 78 | 84 | 90 | 9C | A8 | B4 | C0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| D | D | 1A | 27 | 34 | 41 | 4E | 5Б | 68 | 75 | 82 | 8F | 9C | A9 | B6 | C3 | D0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| E | E | 1С | 2А | 38 | 46 | 54 | 62 | 70 | 7E | 8C | 9A | A8 | B6 | C4 | D2 | E0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ф. {n}}, displaystylei B { } die dezimale Basis 16 и n {\ displaystyle n} die Position der jeweiligen Nachkommastelle ist.{3}} = {1 \ over 4096}} и так weiter. {n}}, displaystylei B { } die dezimale Basis 16 и n {\ displaystyle n} die Position der jeweiligen Nachkommastelle ist.{3}} = {1 \ over 4096}} и так weiter.Da die Zahl 16 nur über den einzigen Primfaktor 2 verfügt, ergibt sich bei allen gekürzten Brüchen, deren Nenner keine Zweierpotenz ist, eine periodische Kommadarstellung im Hexadezimalsystem:
Негатив Zahlen lassen sich ebenfalls darstellen. Информатика [Bearbeiten | Quelltext Bearbeiten]Das Hexadezimalsystem eignet sich sehr gut, um Folgen von Bits (verwendet in der Digitaltechnik) darzustellen. Vier Stellen einer Bitfolge (ein Nibble, auch Tetrade genannt) представлял собой двойную интерпретацию и предсказание таким образом, чтобы Ziffer des Hexadezimalsystems, от 16 die vierte Potenz von 2 ist.Die Hexadezimaldarstellung der Bitfolgen ist leichter zu lesen und schneller zu schreiben: Binär Hexadezimal Dezimal
1111 = F = 15
1.1111 = 1F = 31
11.0111.1100.0101 = 37C5 = 14.277
1010.1100.1101.1100 = ACDC = 44.252
1.0000.0000.0000.0000 = 1.0000 = 65.536
1010.1111.1111.Der Punkt dient bei dieser Darstellung lediglich der Zifferngruppierung. Software stellt daher Maschinensprache oft auf diese Weise dar. Mathematik [Bearbeiten | Quelltext Bearbeiten]Seit die Bailey-Borwein-Plouffe-Formel zur Berechnung von π im Jahr 1995 entwickelt wurde, ist das Hexadezimalsystem auch jenseits der Informatik von Bedeutung.Diese Summenformel kann jede trustbige Hexadezimalstelle von π berechnen, ohne die vorhergehenden Stellen dafür zu benötigen. Viele Taschenrechner, aber auch die genauso genannten Hilfsprogramme auf Personal Computern, bieten Umrechnungen zum Zahlbasiswechsel an. Insbesondere rechnen die Windows- и macOS-Program «Rechner» Binär-, Hexadezimal- и Oktalzahlen в Dezimale und zurück, wenn man unter «Ansicht» (Windows) bzw. «Darstellung» (macOS) из меню «Programmierer» auswählt.В системе Linux-Distributionen ist ein Taschenrechner-Hilfsprogramm vorinstalliert, das eine solche «Programmierer-Option» beinhaltet, или человек может быть использован как Kommandozeile die Anweisung printf (als eingzenebauten bashder-Beinhaltet). Umwandlung von Dezimalzahlen in Hexadezimalzahlen [Bearbeiten | Quelltext Bearbeiten]Eine Möglichkeit, eine Zahl des Dezimalsystems в eine Zahl des Hexadezimalsystems umzurechnen, ist die Betrachtung der Divisionsreste, die entstehen, wenn die Zahl durch die Basis 16 geteilt wird, die Methode wird genfahrentauch. Im Beispiel der 1278 10 sähe das so aus: 1278 : 16 = 79 Остальное: 14 (= E ) (№: 1278- (79 * 16) = 14)
79 : 16 = 4 Остальное: 15 (= F ) (№: 79- (4 * 16) = 15)
4 : 16 = 0 Остальное: 4 (№: 4- (0 * 16) = 4)
Die Hexadezimalzahl wird von unten nach oben gelesen und ergibt somit 4.F.E . Umwandlung von Hexadezimalzahlen in Dezimalzahlen [Bearbeiten | Quelltext Bearbeiten] Um eine Hexadezimalzahl in eine Dezimalzahl umzuwandeln, muss man die einzelnen Ziffern mit der jeweiligen Potenz der Basis multiplizieren. Umwandlung Hexadezimal nach Oktal [Bearbeiten | Quelltext Bearbeiten]Um Zahlen zwischen dem vor allem früher in der Informatik verbreiteten Oktalsystem und dem heute gebräuchlichen Hexadezimalsystem umzuwandeln, ist es zweckmäßig, den Zwischenschritt über das Binärsystem zu gehen.Dies gelingt recht einfach, da sowohl die Basis 8, als auch die Basis 16 Zweierpotenzen sind.
Beispiel für 8D53 16 : [8D53] 16 = 1000.1101.0101.00112 = 1′000′110′101′010′0112 = 1065238 {\ displaystyle [8D53] _ {16} = 1000.1101.0101.0011_ {2} = 1’000’110’101’010’011_ {2} = 106523_ {8}} Umwandlung Oktal nach Hexadezimal [Bearbeiten | Quelltext Bearbeiten]Genauso einfach erfolgt die Umwandlung von oktal nach hexadezimal, nur dass hier der Weg
gegangen wird. Ein- und zweihändiges Zählen mit den Fingerspitzen und Gelenken [Bearbeiten | Quelltext Bearbeiten]Wie auch das altbabylonische Sexagesimalsystem lässt sich auch das Hexadezimalsystem mit den Fingern abzählen.Mithilfe der folgenden Technik wird mit beiden Händen zusammen ein Byte dargestellt. Jede Hand repräsentiert dabei ein Nibble. Dessen oberes Crumb sich am benützten Finger zeigt, sein unteres Crumb dagegen am bezeigten Gelenk bzw. der Fingerspitze. Ein Bitflip ist durch Punktspiegelung der Daumenposition am Mittelpunkt der Fingerfläche herbeiführbar. Einhändiges Zählen von Null bis F 16 [Bearbeiten | Quelltext Bearbeiten] Benutzt man, wie schon die alten Babylonier, den Daumen as Zeiger und legt ihn an die Spitze des Zeigefingers wie beim OK-Zeichen der Taucher und Definiere dieses Zeichen als die Null.Dann lässt sich am oberen Gelenk des Zeigefingers die Eins festlegen, gefolgt von der Zwei am mittleren und schließlich der Drei am unteren Gelenk. Die beiden Crumbs des Nibbles werden dabei orthogonal auf der Hand abgebildet.Итак, dass die unteren beiden Bits an der Höhe des Daumens am jeweiligen Finger und die beiden oberen am benützen Finger abgelesen werden können. Das heißt, sowohl ein Daumen an der Fingerspitze, als auch am Zeigefinger steht für 00 2 im jeweiligen Crumb. Das obere Gelenk sowie der Mittelfinger stehen für 01 2 , das mittlere Gelenk und der Ringfinger für 10 2 und das untere Gelenk und der kleine Finger bedeuten 11 2 . Es müssen sich somit nur noch vier Kombinationen gemerkt werden, um mit der Hand zwischen Hexadezimal- und Binärsystem zu konvertieren, anstelle von 16. Ein Bitflip ist durch Punktspiegelung der Position des Daumens am Schnittpunkt der gedachten Achsen zwischen Ring- und Mittelfinger sowie der oberen und mittleren Gelenkreihe einfach zu erzielen. Ein Beispiel ist am Ende der folgenden Tabelle gegeben.
Zweihändiges Zählen von Null bis FF 16 [Bearbeiten | Quelltext Bearbeiten] Zählt man nun auf der linken Hand mit dem oben beschriebenen Verfahren wie oft man auf der rechten Hand bis F 16 gezählt hat, so lässt sich mit zwei Händen ein Byte darstellen.Da an jedem Finger vier Elemente gezählt werden ergibt sich, dass an den Fingerspitzen Vielfache von Vier auftreten. Dies bedeutet, dass wenn die Daumen der jeweiligen Hände an der jeweiligen Zeigefingerspitze bei Null zu zählen beginnen, so erhöht sich der Wert an den Spitzen der Finger der rechten Hand um vier wohingegen er sähils uim Zähler 90 16 bzw. 64 erhöht. Rückt man an der linken Hand nur um ein Fingerglied vor oder zurück, so ändert sich der dargestellte Wert um 10 16 bzw.
Hexadezimalsystem — Википедия
Im Hexadezimalsystem werden Zahlen in einem Stellenwertsystem zur Basis 16 dargestellt. In der Datenverarbeitung wird das Hexadezimalsystem sehr oft verwendet, da es sich hierbei letztlich um eine komfortablere Verwaltung des Binärsystems handelt. Die Datenwörter bestehen in der Informatik meist aus Oktetten, die statt als achtstellige Binärzahlen auch als nur zweistellige Hexadezimalzahlen dargestellt werden können. Im Gegensatz zum Dezimalsystem eignet sich das Hexadezimalsystem mit seiner Basis als vierte Zweierpotenz (16 = 2 4 ) zur einfacheren Notation der Binärzahlen, da stets eine feste Anzahl Zeicabeird des Wiedergwens. In den 1960er und 1970er Jahren wurde in der Informatik häufig auch das Oktalsystem mit seiner Basis als dritte Zweierpotenz (8 = 2 3 ) verwendet, da es mit den üblichen Ziffern von 0 7. Es findet aber heute seltener Anwendung, beispielsweise zur Darstellung von Zeichen in der Programmiersprache C. Auch gibt es noch weitere Zahlensysteme mit verschiedenen Basiswerten. [1] Wir sind es gewohnt, im Dezimalsystem zu rechnen. Das bedeutet, unser indiarabisches Zahlensystem verwendet zehn Symbole zur Notation der Ziffern ( 0 bis 9 ). Das Hexadezimalsystem enthält dagegen sechzehn Ziffern. Seit Mitte der 1950er Jahre werden zur Darstellung der sechs zusätzlichen Ziffern die Buchstaben A bis F или a bis f as Zahlzeichen verwendet. Dies geht auf die damalige Praxis der IBM-Informatiker zurück. Darstellung von HexadezimalzahlenBearbeitenUm hexadezimale von dezimalen Zahlen unterscheiden zu können, existieren mehrere Schreibweisen. Üblicherweise werden hexadezimale Zahlen mit einem Index oder Präfix versehen. Verbreitete Schreibweisen sind: 72 16 , 72 hex , 72h, 72H, 72 H , 0x72, $ 72, «72 и X’72 ‘, wobei das Präfix 0x und das Suffix insbes h in der Programmierung und Technischen Informatik Verwendung finden.Das Anhängen eines h an die Hex-Zahl ist auch als Intel-Konvention geläufig. Die Schreibweise mit dem Dollar-Präfix ist in den Assemblersprachen bestimmter Prozessorfamilien üblich, insbesondere bei Motorola, zum beispiel beim Motorola 68xx and 68xxx, aber auch beim MOS 65xx; die Schreibweise X’72 ‘ist in der Welt der IBM-Großrechner üblich, wie in REXX. Der Übersicht dienende Trennpunkte können bei Hexadezimalzahlen all vier Stellen gesetzt werden, trennen также Gruppen von jeweils sechzehn Bit. Zum Vergleich ein voller Vierundsechzig-Bit-Bus mit und ohne Trennpunkte: FFFF.FFFF.FFFF.FFFF und FFFFFFFFFFFFFFFF Dezimale Zahlen werden, wo sie nicht der zu erwartende Normalfall sind, indiziert: 114 10 Zählen im HexadezimalsystemBearbeitenGezählt wird wie folgt:
Aussprache der HexadezimalzahlenBearbeitenFür die hexadezimalen Ziffern und Zahlen sind keine eigenständigen Namen gebräuchlich. Hexadezimalzahlen werden daher meist Ziffer für Ziffer gelesen. Beispiele:
Es lässt sich jedoch auch analog die Zählweise des Dezimalsystems verwenden, ohne dass der Einsatz des Hexadezimalsystems bei jeder Zahl gehört werden kann und sich dann zum Beispielbenus dem Kontext. Beispiele:
Hexadezimale Multiplikationstafel (kleines Einmaleins) BearbeitenПример: 2 • 5 = A Von der Spalte mit dem Wert 2 vertikal hinunter gehen bis Schnittpunkt der Zeile mit Wert 5. Ergebnis: A
Каждая дополнительная цифра представляет все большее и большее количество.Это применимо как для Base 10, так и для других баз. Знание этого поможет вам лучше понять другие основы. двоичный Binary — это еще один способ сказать Base Two. Отсюда символов больше нет. Мы не переходим к 2, потому что в двоичном формате 2 не существует. Вместо этого мы используем 10.В двоичной системе 10 равно 2 в десятичной системе счисления. Мы можем считать дальше.

Однако, поскольку это основание два, числа не становятся такими большими, как в десятичном.Тем не менее, двоичное число из 10 цифр будет больше 1000 в десятичном. Двоичная система используется в информатике и электротехнике. Транзисторы работают от двоичной системы, и транзисторы можно найти практически во всех электронных устройствах. 0 означает отсутствие тока, а 1 означает разрешение тока. Когда различные транзисторы включаются и выключаются, сигналы и электричество отправляются для выполнения различных действий, например, для совершения звонка или вывода этих букв на экран. Компьютеры и электроника работают с байтами или восьмизначными двоичными числами. В каждом байте закодирована информация, которую компьютер способен понять. Многие байты объединяются в цепочки для формирования цифровых данных, которые можно сохранить для дальнейшего использования. восьмеричноеOctal — это еще одна система счисления, в которой используется меньше символов, чем в нашей традиционной системе счисления. Восьмеричный формат используется для Base Eight, что означает, что восемь символов используются для представления всех величин. Это 0, 1, 2, 3, 4, 5, 6 и 7.Когда мы считаем единицу из 7, нам нужно новое размещение, чтобы представить то, что мы называем 8, поскольку 8 не существует в Octal. Итак, после 7 будет 10.
Точно так же, как мы использовали степень десяти в десятичной системе и степень двойки в двоичной системе, для определения значения числа мы будем использовать степень восьмерки, поскольку это основание восемь.
Каждое дополнительное размещение слева имеет большую ценность, чем в двоичном формате. Третья цифра справа в двоичном формате представляет только 2 3-1 , то есть 4.В восьмеричном формате это 8 3-1 , что равно 64. ШестнадцатеричныйШестнадцатеричная система счисления — основание шестнадцати. Как следует из ее основания, эта система счисления использует шестнадцать символов для представления чисел. В отличие от двоичного и восьмеричного, шестнадцатеричный имеет шесть дополнительных символов, которые он использует помимо обычных, найденных в десятичном. Но что будет после 9? 10 — это не одна цифра, а две… К счастью, по соглашению, когда необходимы дополнительные символы, помимо обычных десяти, должны использоваться буквы.Таким образом, в шестнадцатеричном формате общий список используемых символов составляет 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. На цифровом дисплее , числа B и D строчные. При шестнадцатеричном счете вы считаете 0, 1, 2 и так далее. Однако, когда вы набираете 9, вы сразу переходите к A. Затем вы считаете B, C, D, E и F. Но что дальше? У нас закончились символы! Когда у нас заканчиваются символы, мы создаем новое расположение цифр и идем дальше. Итак, после F будет 10. Вы продолжаете считать, пока не дойдете до 19. После 19 следующее число будет 1A.Это продолжается вечно.
Цифры обозначают степень 16.Рассмотрим шестнадцатеричное число 2DB7.
Как видите, размещение в шестнадцатеричной системе счисления намного дороже, чем в любой из трех других систем счисления. Важно знать, что 364 в восьмеричном формате — это , а не , равное нормальному 364.Это похоже на то, как 10 в двоичном формате определенно не равно 10 в десятичном. 10 в двоичном формате (с этого момента будет записываться как 10 2 ) равно 2. 10 8 равно 8. Откуда мы это знаем? Что такое 20C.38F 16 и как нам узнать? Вот почему важно понимать, как работают системы счисления. Используя нашу степень основного числа, становится возможным превращать любое число в десятичное, а из десятичного — в любое. Десятичное основаниеИтак, мы знаем, что 364 8 не равно десятичному числу 364.{p-1} + … + v_1B + v_0 \ end {уравнение} Где V 10 — десятичное значение, v — цифра в расположении, p — это размещение справа от числа, предполагая, что крайнее правое размещение равно 0, а B — начальная база. Не пугайтесь формулы! Мы собираемся пройти через это шаг за шагом. Итак, допустим, у нас есть простое шестнадцатеричное число 2B. Мы хотим знать, что это за число в десятичной системе, чтобы лучше понять его. как нам это сделать? Воспользуемся формулой выше.Сначала определите каждую переменную. Мы хотим найти V 10 , так что это неизвестно. Число 2B 16 имеет две позиции, так как оно состоит из двух цифр. Следовательно, p на единицу меньше, поэтому p равно 1. Число в базе 16, поэтому B равно 16. Наконец, мы хотим знать, что такое v, но есть несколько v. У вас v 1 и v 0 . Это относится к значению цифры в позиции индекса. v 1 относится к цифре в первой позиции (вторая цифра справа).0) \\ V_ {10} = 2 (16) +11 (1) \\ V_ {10} = 32 + 11 \ V_ {10} = 43 \\ \ end {align} Следовательно, 2B 16 равно 43. Теперь позвольте мне объяснить, как это работает. Помните, как расположение цифр влияет на фактическое значение? Например, в десятичном числе 123 «1» представляет 100, что составляет 1 * 10 2 . «2» — это 20 или 2 * 10 1 . Аналогично, в числе 2B 16 «2» — это 2 * 16 1 , а B — 11 * 16 0 . Таким образом мы можем определить значение чисел.Для числа 364 8 мы сделаем диаграмму, которая показывает десятичное значение каждой отдельной цифры. Затем мы можем сложить их, чтобы получить целое. Число состоит из трех цифр, поэтому, начиная справа, у нас есть позиция 0, позиция 1 и позиция 2. Поскольку это основание восемь, мы будем использовать степень 8. Теперь 8 2 равно 64. 8 1 равно 8. 8 0 равно 1. Что дальше? Помните, что мы сделали с десятичным числом 123? Мы взяли значение цифры , умноженное на соответствующей степени.Итак, учитывая это дальше… Теперь мы складываем значения вместе, чтобы получить 244. Следовательно, 364 8 равно 244 10 . Точно так же, как для 123, мы говорим, что есть одна группа по 100, две группы по 10 и три группы по 1, для восьмеричной системы и числа 364 существуют три группы по 64, шесть групп по 8 и четыре группы по 1. от десятичной дроби к основаниюТочно так же, как мы можем преобразовать из любого основания в десятичное, можно преобразовать десятичное в любое основание.p \\ (4) \ hspace {6pt} Повторяйте шаги \ hspace {4pt} с \ hspace {4pt} 1 \ hspace {4pt} через \ hspace {4pt} 3 \ hspace {4pt}, пока \ hspace {4pt} p = 0 \\ \ end {align} Этот алгоритм может сначала показаться запутанным, но давайте рассмотрим пример, чтобы увидеть, как его можно использовать. Мы хотим представить 236 в двоичном, восьмеричном и шестнадцатеричном формате. Итак, давайте сначала попробуем преобразовать его в двоичный код. Первый шаг — сделать p равным $ \ operatorname {int} (\ sqrt [B] {V}) $. B — это база, в которую мы хотим преобразовать 2.V — это число, которое мы хотим преобразовать, 236. По сути, мы извлекаем квадратный корень из 236 и игнорируем десятичную часть. В результате p становится равным 7. Шаг второй говорит, что пусть v равно нашему числу V, деленному на B p . B p равно 2 7 , или 128, а целая часть 236, деленная на 128, равна 1. Таким образом, наша первая цифра слева равна 1. Теперь мы фактически меняем V, чтобы стать V минус цифра, умноженная на В стр . Итак, V теперь будет 236-128 или 108. Мы просто повторяем процесс, пока p не станет равным нулю. Когда p становится равным нулю, мы завершаем шаги в последний раз, а затем заканчиваем. Итак, поскольку V теперь 108, p становится 6. P \ end {уравнение} На человеческом языке: значение шифра в числе равно значению самого шифра, умноженному на основание системы счисления в степень позиции шифра слева направо в числе, начиная с при 0.Прочтите это несколько раз и попытайтесь понять. Таким образом, значение цифры в двоичном формате удваивается каждый раз, когда мы перемещаемся влево. (см. таблицу ниже) Из этого следует, что каждый шестнадцатеричный шифр можно разделить на 4 двоичных разряда. На компьютерном языке: кусочек. Теперь взгляните на следующую таблицу:
Еще один интересный момент: посмотрите на значение в верхней части столбца.Затем посмотрите на значения. Вы понимаете, о чем я? Да, ты прав! Биты включаются и выключаются в зависимости от своего значения. Значение первой цифры (начиная справа) выглядит следующим образом: 0,1,0,1,0,1,0,1,0,1,… Вторая цифра: 0,0,1,1,0 , 0,1,1,0,0,1,1,0,0… Третья цифра (значение = 4): 0,0,0,0,1,1,1,1,0,0,0,0 , 1,1,1,1,… И так далее… А как насчет больших чисел? Поэтому нам понадобится дополнительная цифра. (но я думаю, что вы догадались сами). Для значений начиная с 16 наша таблица выглядит так:
В последней теме я объяснил логику двоичной, шестнадцатеричной и восьмеричной систем счисления.Теперь я объясню кое-что более практичное. Если вы полностью поняли предыдущее, можете пропустить эту тему. Из десятичного числа в двоичное
Пример:
Из двоичного в десятичный
Пример:
Из десятичного в шестнадцатеричный.ЭТО ТОЛЬКО ОДИН ИЗ МНОГИХ СПОСОБОВ!
(вы можете добавить нули в начале, если количество битов не делится на 4, потому что, как и в десятичном, это не имеет значения) Пример:
Из шестнадцатеричного в десятичный* Проверьте формулу в первом абзаце и используйте ее для шифров в шестнадцатеричном числе. (это действительно работает для любого преобразования в десятичную систему счисления) Пример:
От десятичной к восьмеричной
Пример: преобразование 25 в восьмеричное число
От восьмеричного к десятичномуСнова применим формулу сверху Пример: преобразовать 42 в десятичное число
Хорошо, это может быть не на 100% «забавным», но тем не менее интересно.
Эта нотация чаще всего используется для перечисления адресов компьютеров, а это совсем другая история.
Вы все поняли? Если вы так думаете, проверьте себя:
Сделайте несколько упражнений самостоятельно, если хотите еще. Шестнадцатеричная таблица умноженияШестнадцатеричная таблица умноженияШестнадцатеричное Таблица умножения
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 Dazu wird in den meisten Fällen die Zweierkomplement-Darstellung verwendet. Durch ihre Auslegung braucht an den Mechanismen für Rechnungen in den Grundrechenarten keine Änderung vorgenommen zu werden.
Dazu wird in den meisten Fällen die Zweierkomplement-Darstellung verwendet. Durch ihre Auslegung braucht an den Mechanismen für Rechnungen in den Grundrechenarten keine Änderung vorgenommen zu werden.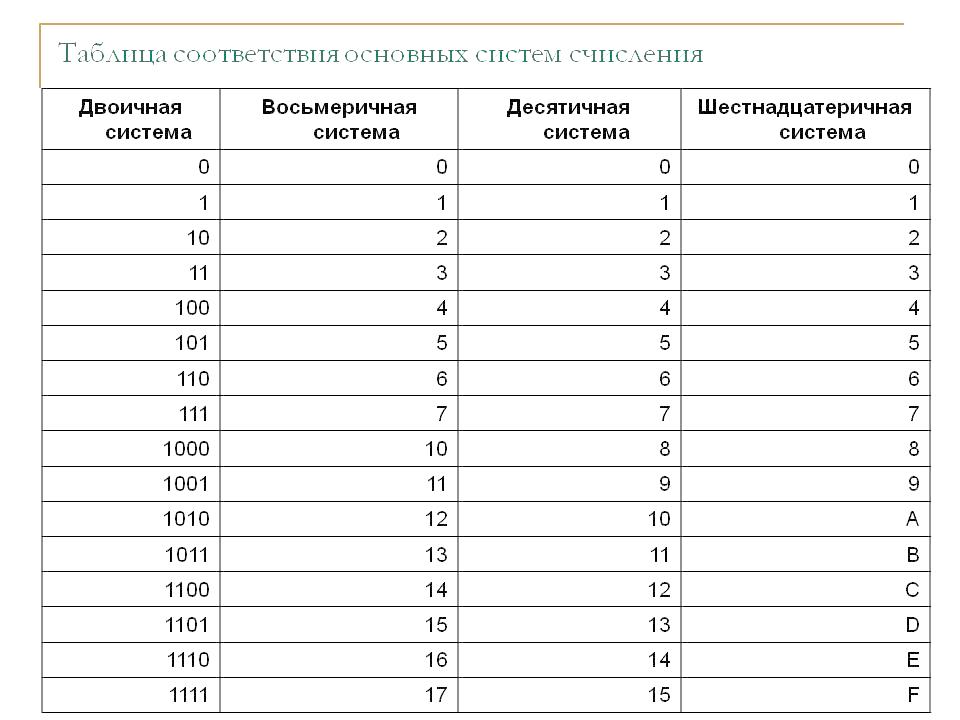 1110.0000.1000.0001.0101 = AFFE.0815 = 2.952.661.013
1110.0000.1000.0001.0101 = AFFE.0815 = 2.952.661.013

 {0} = [1278] _ {10}}
{0} = [1278] _ {10}} {i} \ qquad m, n \ in \ mathbb {N} \ quad h_ {i} \ in \ {0; 1; \ cdots; 9; A; \ cdots; F \}}
{i} \ qquad m, n \ in \ mathbb {N} \ quad h_ {i} \ in \ {0; 1; \ cdots; 9; A; \ cdots; F \}} Genauso fortgesetzt über die Vier an der Spitze des Mittelfingers, der Acht an der Spitze des Ringfingers und der Zwölf an der des Kleinen. Damit lässt sich dann bis 15 = F 16 zählen, wenn der Daumen das untere Gelenk des kleinen Fingers erreicht hat, da wo er angewachsen ist.
Genauso fortgesetzt über die Vier an der Spitze des Mittelfingers, der Acht an der Spitze des Ringfingers und der Zwölf an der des Kleinen. Damit lässt sich dann bis 15 = F 16 zählen, wenn der Daumen das untere Gelenk des kleinen Fingers erreicht hat, da wo er angewachsen ist.
 г. Gedachten Achsen
г. Gedachten Achsen 16.
16. «Шестнадцатеричный» (фон griech. hexa «sechs» и лат. decem «zehn») ist ein lateinisch-griechisches Mischwort; eine andere korrekte, jedoch seltener verwendete Bezeichnung ist sedezimal (von lat. sedecim «sechzehn»). Eine weitere alternate Bezeichnung ist hexadekadisch (griechisch). Falsch hingegen ist der Ausdruck hexa ges imal, der synonym zu sexa ges imal ist und das Zahlensystem zur Basis 60 bezeichnet.
«Шестнадцатеричный» (фон griech. hexa «sechs» и лат. decem «zehn») ist ein lateinisch-griechisches Mischwort; eine andere korrekte, jedoch seltener verwendete Bezeichnung ist sedezimal (von lat. sedecim «sechzehn»). Eine weitere alternate Bezeichnung ist hexadekadisch (griechisch). Falsch hingegen ist der Ausdruck hexa ges imal, der synonym zu sexa ges imal ist und das Zahlensystem zur Basis 60 bezeichnet. Nibbles können exakt mit einer hexadezimalen Ziffer und Bytes mit zwei hexadezimalen Ziffern dargestellt werden.
Nibbles können exakt mit einer hexadezimalen Ziffer und Bytes mit zwei hexadezimalen Ziffern dargestellt werden.
 Die Bedeutung der 1.0000 16 = 65.536 10 unter den hexadezimalen Zahlen entspricht также jener der 1.000 10 unter den dezimalen Zahlen.
Die Bedeutung der 1.0000 16 = 65.536 10 unter den hexadezimalen Zahlen entspricht также jener der 1.000 10 unter den dezimalen Zahlen. ..
.. ..
.. ..
..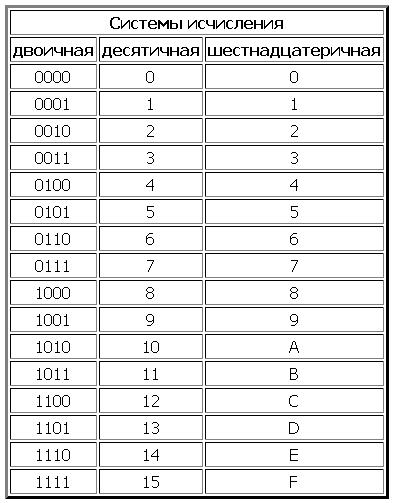
 {\ displaystyle B} die dezimale Basis 16 и n {\ displaystyle n} die Position der jeweiligen Nachkommastelle ist.{3}} = {1 \ over 4096}} и так weiter.
{\ displaystyle B} die dezimale Basis 16 и n {\ displaystyle n} die Position der jeweiligen Nachkommastelle ist.{3}} = {1 \ over 4096}} и так weiter. Dazu wird in den meisten Fällen die Zweierkomplement-Darstellung verwendet. Durch ihre Auslegung braucht an den Mechanismen für Rechnungen in den Grundrechenarten keine Änderung vorgenommen zu werden.
Dazu wird in den meisten Fällen die Zweierkomplement-Darstellung verwendet. Durch ihre Auslegung braucht an den Mechanismen für Rechnungen in den Grundrechenarten keine Änderung vorgenommen zu werden.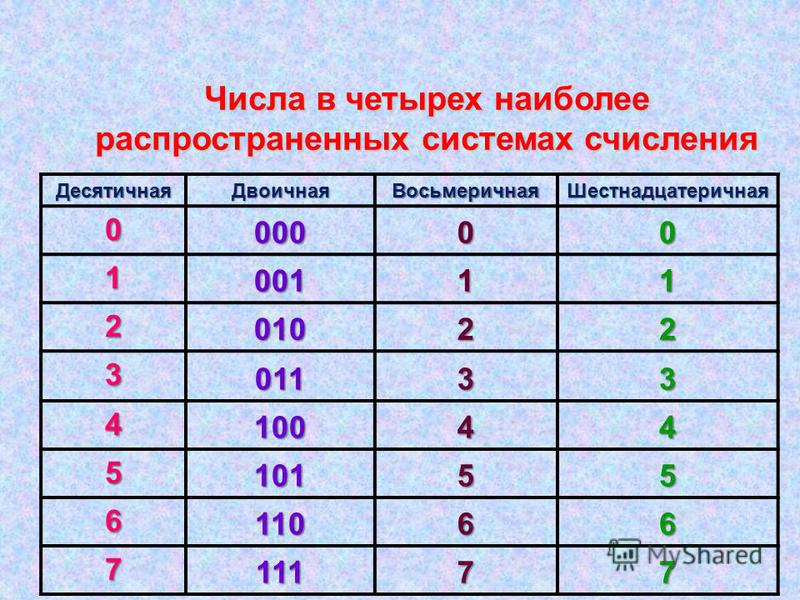 0815 = 2.952.661.013
0815 = 2.952.661.013

 {0} = [1278] _ {10}}
{0} = [1278] _ {10}} {i} \ qquad m, n \ in \ mathbb {N} \ quad h_ {i} \ in \ {0; 1; \ cdots; 9; A; \ cdots; F \}}
{i} \ qquad m, n \ in \ mathbb {N} \ quad h_ {i} \ in \ {0; 1; \ cdots; 9; A; \ cdots; F \}} Genauso fortgesetzt über die Vier an der Spitze des Mittelfingers, der Acht an der Spitze des Ringfingers und der Zwölf an der des Kleinen. Damit lässt sich dann bis 15 = F 16 zählen, wenn der Daumen das untere Gelenk des kleinen Fingers erreicht hat, da wo er angewachsen ist.
Genauso fortgesetzt über die Vier an der Spitze des Mittelfingers, der Acht an der Spitze des Ringfingers und der Zwölf an der des Kleinen. Damit lässt sich dann bis 15 = F 16 zählen, wenn der Daumen das untere Gelenk des kleinen Fingers erreicht hat, da wo er angewachsen ist.
 г. Gedachten Achsen
г. Gedachten Achsen 16.
16. Однако 10 в десятичной системе счисления представлено как A в шестнадцатеричной системе, 11 как B, 12 как C, 13 как D, 14 как E, 15 как F и 16 как 10. Итак, 16 цифр шестнадцатеричной системы счисления 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Однако 10 в десятичной системе счисления представлено как A в шестнадцатеричной системе, 11 как B, 12 как C, 13 как D, 14 как E, 15 как F и 16 как 10. Итак, 16 цифр шестнадцатеричной системы счисления 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. В таблице ниже обозначено представление шестнадцатеричной цифры в других формах.
В таблице ниже обозначено представление шестнадцатеричной цифры в других формах.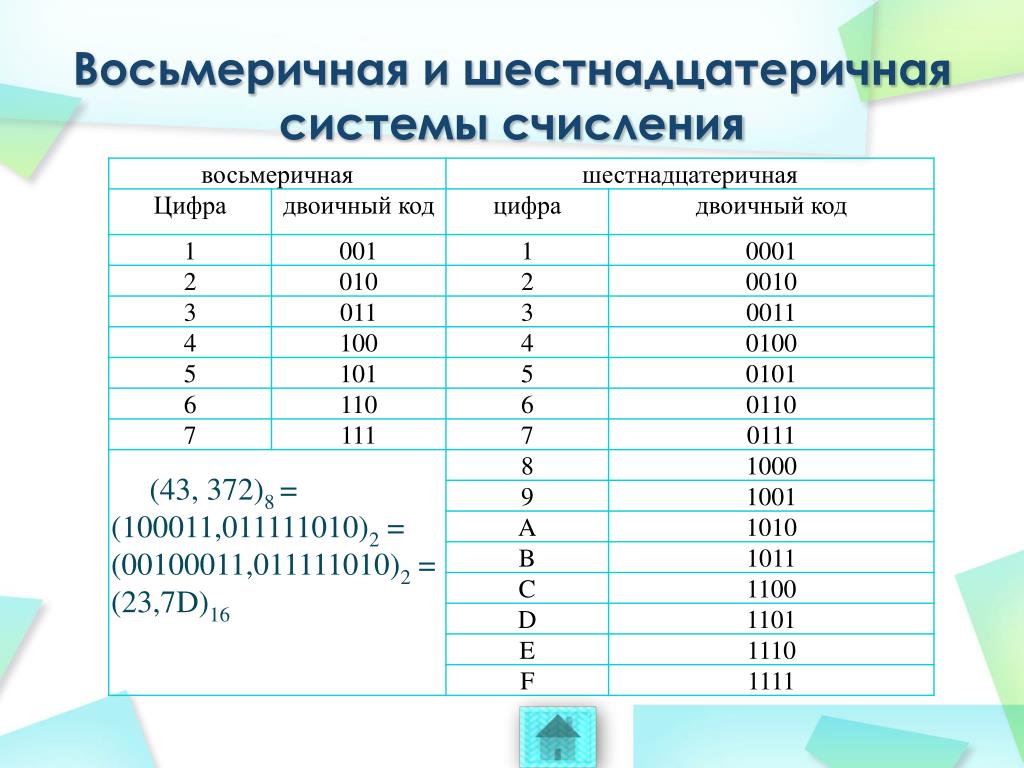 Полученное частное снова делится на 16 и записывается шестнадцатеричный эквивалент остатка. Деление продолжается до тех пор, пока частное не станет равным 0. Число в шестнадцатеричной форме — это остаток, записанный снизу вверх.
Полученное частное снова делится на 16 и записывается шестнадцатеричный эквивалент остатка. Деление продолжается до тех пор, пока частное не станет равным 0. Число в шестнадцатеричной форме — это остаток, записанный снизу вверх. Ее шестнадцатеричный эквивалент (28B) 16
Ее шестнадцатеричный эквивалент (28B) 16 путем умножения каждой цифры на ее позиционные значения 16.
путем умножения каждой цифры на ее позиционные значения 16.
 Затем двоичное число делится на группы из трех цифр, и их восьмеричный эквивалент записывается с использованием приведенной выше таблицы преобразования.
Затем двоичное число делится на группы из трех цифр, и их восьмеричный эквивалент записывается с использованием приведенной выше таблицы преобразования.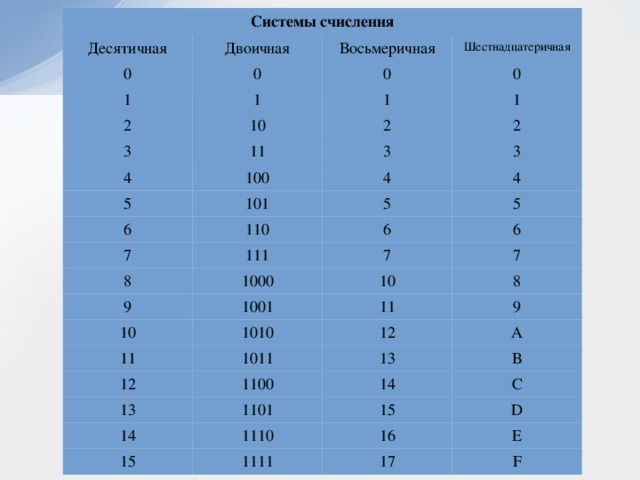 .. d 3 d 2 d 1 d 0
.. d 3 d 2 d 1 d 0 
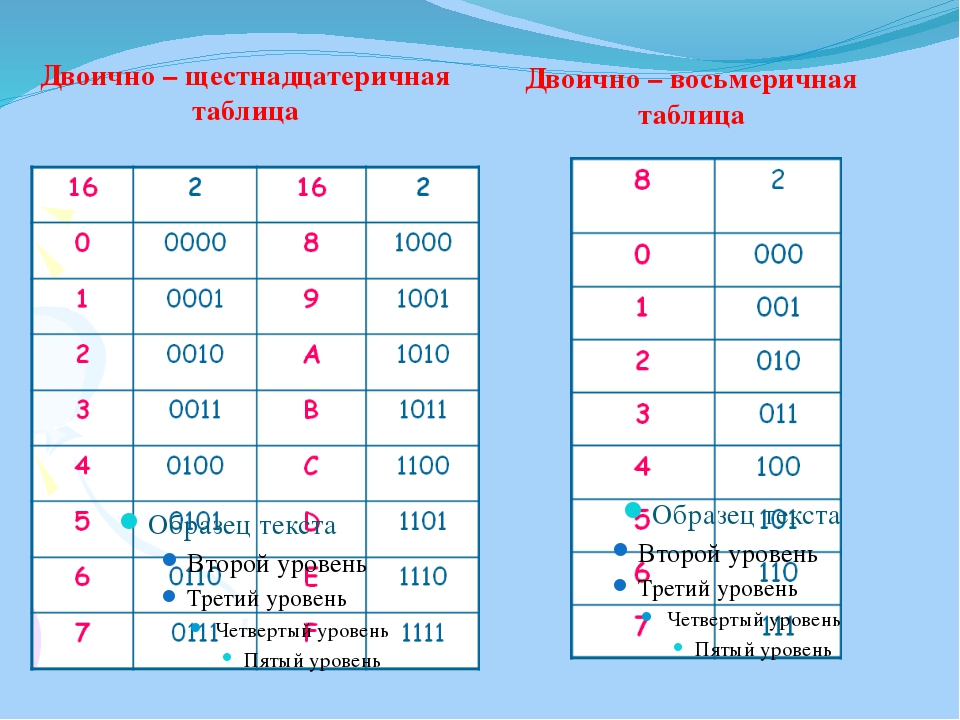 Также
Также  Итак, мы будем считать в двоичном формате 0, 1, 10, 11, 100, 101 и так далее.
Итак, мы будем считать в двоичном формате 0, 1, 10, 11, 100, 101 и так далее. Итак, после 99 мы переходим к 100.
Итак, после 99 мы переходим к 100. Итак, в двоичной системе счисления для представления чисел используются только два символа: 0 и 1. Когда мы считаем от нуля в двоичной системе счисления, символы заканчиваются гораздо чаще.
Итак, в двоичной системе счисления для представления чисел используются только два символа: 0 и 1. Когда мы считаем от нуля в двоичной системе счисления, символы заканчиваются гораздо чаще.
 Рассмотрим число 3623 по основанию восемь.
Рассмотрим число 3623 по основанию восемь.