Критерий согласия Пирсона χ2 (Хи-квадрат)
До конца XIX века нормальное распределение считалась всеобщим законом вариации данных. Однако К. Пирсон заметил, что эмпирические частоты могут сильно отличаться от нормального распределения. Встал вопрос, как это доказать. Требовалось не только графическое сопоставление, которое имеет субъективный характер, но и строгое количественное обоснование.
Так был изобретен критерий χ2 (хи квадрат), который проверяет значимость расхождения эмпирических (наблюдаемых) и теоретических (ожидаемых) частот. Это произошло в далеком 1900 году, однако критерий и сегодня на ходу. Более того, его приспособили для решения широкого круга задач. Прежде всего, это анализ категориальных данных, т.е. таких, которые выражаются не количеством, а принадлежностью к какой-то категории. Например, класс автомобиля, пол участника эксперимента, вид растения и т.д. К таким данным нельзя применять математические операции вроде сложения и умножения, для них можно только подсчитать частоты.
Наблюдаемые частоты обозначим О (Observed), ожидаемые – E (Expected). В качестве примера возьмем результат 60-кратного бросания игральной кости. Если она симметрична и однородна, вероятность выпадения любой стороны равна 1/6 и, следовательно, ожидаемое количество выпадения каждой из сторон равна 10 (1/6∙60). Наблюдаемые и ожидаемые частоты запишем в таблицу и нарисуем гистограмму.
Нулевая гипотеза заключается в том, что частоты согласованы, то есть фактические данные не противоречат ожидаемым. Альтернативная гипотеза – отклонения в частотах выходят за рамки случайных колебаний, расхождения статистически значимы. Чтобы сделать строгий вывод, нам потребуется.
- Обобщающая мера расхождения между наблюдаемыми и ожидаемыми частотами.
- Распределение этой меры при справедливости гипотезы о том, что различий нет.
Начнем с расстояния между частотами. Если взять просто разницу О — E, то такая мера будет зависеть от масштаба данных (частот). Например, 20 — 5 =15 и 1020 – 1005 = 15. В обоих случаях разница составляет 15. Но в первом случае ожидаемые частоты в 3 раза меньше наблюдаемых, а во втором случае – лишь на 1,5%. Нужна относительная мера, не зависящая от масштаба.
Например, 20 — 5 =15 и 1020 – 1005 = 15. В обоих случаях разница составляет 15. Но в первом случае ожидаемые частоты в 3 раза меньше наблюдаемых, а во втором случае – лишь на 1,5%. Нужна относительная мера, не зависящая от масштаба.
Обратим внимание на следующие факты. В общем случае количество категорий, по которым измеряются частоты, может быть гораздо больше, поэтому вероятность того, что отдельно взятое наблюдение попадет в ту или иную категорию, довольно мала. Раз так, то, распределение такой случайной величины будет подчинятся закону редких событий, известному под названием закон Пуассона. В законе Пуассона, как известно, значение математического ожидания и дисперсии совпадают (параметр λ). Значит, ожидаемая частота для некоторой категории номинальной переменной Ei будет являться одновременное и ее дисперсией. Далее, закон Пуассона при большом количестве наблюдений стремится к нормальному. Соединяя эти два факта, получаем, что, если гипотеза о согласии наблюдаемых и ожидаемых частот верна, то, при большом количестве наблюдений, выражение
имеет стандартное нормальное распределение.
Важно помнить, что нормальность будет проявляться только при достаточно больших частотах. В статистике принято считать, что общее количество наблюдений (сумма частот) должна быть не менее 50 и ожидаемая частота в каждой группе должна быть не менее 5. Только в этом случае величина, показанная выше, имеет стандартное нормальное распределение. Предположим, что это условие выполнено.
У стандартного нормального распределения почти все значение находятся в пределах ±3 (правило трех сигм). Таким образом, мы получили относительную разность в частотах для одной группы. Нам нужна обобщающая мера. Просто сложить все отклонения нельзя – получим 0 (догадайтесь почему). Пирсон предложил сложить квадраты этих отклонений.
Это и есть статистика для критерия Хи-квадрат Пирсона. Если частоты действительно соответствуют ожидаемым, то значение статистики Хи-квадрат будет относительно не большим (отклонения находятся близко к нулю). Большое значение статистики свидетельствует в пользу существенных различий между частотами.
«Большой» статистика Хи-квадрат становится тогда, когда появление наблюдаемого или еще большего значения становится маловероятным. И чтобы рассчитать такую вероятность, необходимо знать распределение статистики Хи-квадрат при многократном повторении эксперимента, когда гипотеза о согласии частот верна.
Как нетрудно заметить, величина хи-квадрат также зависит от количества слагаемых. Чем больше слагаемых, тем больше ожидается значение статистики, ведь каждое слагаемое вносит свой вклад в общую сумму. Следовательно, для каждого количества независимых слагаемых, будет собственное распределение. Получается, что χ2 – это целое семейство распределений.
И здесь мы подошли к одному щекотливому моменту. Что такое число независимых слагаемых? Вроде как любое слагаемое (т.е. отклонение) независимо. К. Пирсон тоже так думал, но оказался неправ. На самом деле число независимых слагаемых будет на один меньше, чем количество групп номинальной переменной n. Почему? Потому что, если мы имеем выборку, по которой уже посчитана сумма частот, то одну из частот всегда можно определить, как разность общего количества и суммой всех остальных. Отсюда и вариация будет несколько меньше. Данный факт Рональд Фишер заметил лет через 20 после разработки Пирсоном своего критерия. Даже таблицы пришлось переделывать.
Почему? Потому что, если мы имеем выборку, по которой уже посчитана сумма частот, то одну из частот всегда можно определить, как разность общего количества и суммой всех остальных. Отсюда и вариация будет несколько меньше. Данный факт Рональд Фишер заметил лет через 20 после разработки Пирсоном своего критерия. Даже таблицы пришлось переделывать.
По этому поводу Фишер ввел в статистику новое понятие – степень свободы (degrees of freedom), которое и представляет собой количество независимых слагаемых в сумме. Понятие степеней свободы имеет математическое объяснение и проявляется только в распределениях, связанных с нормальным (Стьюдента, Фишера-Снедекора и сам Хи-квадрат).
Чтобы лучше уловить смысл степеней свободы, обратимся к физическому аналогу. Представим точку, свободно движущуюся в пространстве. Она имеет 3 степени свободы, т.к. может перемещаться в любом направлении трехмерного пространства. Если точка движется по какой-либо поверхности, то у нее уже две степени свободы (вперед-назад, вправо-влево), хотя и продолжает находиться в трехмерном пространстве. Точка, перемещающаяся по пружине, снова находится в трехмерном пространстве, но имеет лишь одну степень свободы, т.к. может двигаться либо вперед, либо назад. Как видно, пространство, где находится объект, не всегда соответствует реальной свободе перемещения.
Точка, перемещающаяся по пружине, снова находится в трехмерном пространстве, но имеет лишь одну степень свободы, т.к. может двигаться либо вперед, либо назад. Как видно, пространство, где находится объект, не всегда соответствует реальной свободе перемещения.
Примерно также распределение статистики может зависеть от меньшего количества элементов, чем нужно слагаемых для его расчета. В общем случае количество степеней свободы меньше наблюдений на число имеющихся зависимостей.
Таким образом, распределение хи квадрат (χ2) – это семейство распределений, каждое из которых зависит от параметра степеней свободы. Формальное определение следующее. Распределение χ2 (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
Далее можно было бы перейти к самой формуле, по которой вычисляется функция распределения хи-квадрат, но, к счастью, все давно подсчитано за нас. Чтобы получить интересующую вероятность, можно воспользоваться либо соответствующей статистической таблицей, либо готовой функцией в Excel.
Чтобы получить интересующую вероятность, можно воспользоваться либо соответствующей статистической таблицей, либо готовой функцией в Excel.
Интересно посмотреть, как меняется форма распределения хи-квадрат в зависимости от количества степеней свободы.
С увеличением степеней свободы распределение хи-квадрат стремится к нормальному. Это объясняется действием центральной предельной теоремы, согласно которой сумма большого количества независимых случайных величин имеет нормальное распределение. Про квадраты там ничего не сказано )).
Вот мы и подошли к проверке гипотез по методу хи-квадрат. В целом техника остается прежней. Выдвигается нулевая гипотеза о том, что наблюдаемые частоты соответствуют ожидаемым (т.е. между ними нет разницы, т.к. они взяты из той же генеральной совокупности). Если этот так, то разброс будет относительно небольшим, в пределах случайных колебаний. Меру разброса определяют по статистике Хи-квадрат. Далее либо полученную статистику сравнивают с критическим значением (для соответствующего уровня значимости и степеней свободы), либо, что более правильно, рассчитывают наблюдаемый p-value, т. е. вероятность получить такое или еще больше значение статистики при справедливости нулевой гипотезы.
е. вероятность получить такое или еще больше значение статистики при справедливости нулевой гипотезы.
Т.к. нас интересует согласие частот, то отклонение гипотезы произойдет, когда статистика окажется больше критического уровня. Т.е. критерий является односторонним. Однако иногда (иногда) требуется проверить левостороннюю гипотезу. Например, когда эмпирические данные уж оооочень сильно похожи на теоретические. Тогда критерий может попасть в маловероятную область, но уже слева. Дело в том, что в естественных условиях, маловероятно получить частоты, практически совпадающие с теоретическими. Всегда есть некоторая случайность, которая дает погрешность. А вот если такой погрешности нет, то, возможно, данные были сфальсифицированы. Но все же обычно проверяют правостороннюю гипотезу.
Вернемся к задаче с игральной костью. Рассчитаем по имеющимся данным значение статистики критерия хи-квадрат.
Теперь найдем критическое значение при 5-ти степенях свободы (k) и уровне значимости 0,05 (α) по таблице критических значений распределения хи квадрат.
То есть квантиль 0,05 хи квадрат распределения (правый хвост) с 5-ю степенями свободы χ20,05; 5 = 11,1.
Сравним фактическое и табличное значение. 3,4 (χ2) < 11,1 (χ20,05; 5). Расчетный значение оказалось меньшим, значит гипотеза о равенстве (согласии) частот не отклоняется. На рисунке ситуация выглядит вот так.
Если бы расчетное значение попало в критическую область, то нулевая гипотеза была бы отклонена.
Более правильным будет рассчитать еще и p-value. Для этого нужно в таблице найти ближайшее значение для заданного количества степеней свободы и посмотреть соответствующий ему уровень значимости. Но это прошлый век. Воспользуемся ЭВМ, в частности MS Excel. В эксель есть несколько функций, связанных с хи-квадрат.
Ниже их краткое описание.
ХИ2.ОБР – критическое значение Хи-квадрат при заданной вероятности слева (как в статистических таблицах)
ХИ2. ОБР.ПХ – критическое значение при заданной вероятности справа. Функция по сути дублирует предыдущую. Но здесь можно сразу указывать уровень α, а не вычитать его из 1. Это более удобно, т.к. в большинстве случаев нужен именно правый хвост распределения.
ОБР.ПХ – критическое значение при заданной вероятности справа. Функция по сути дублирует предыдущую. Но здесь можно сразу указывать уровень α, а не вычитать его из 1. Это более удобно, т.к. в большинстве случаев нужен именно правый хвост распределения.
ХИ2.РАСП – p-value слева (можно рассчитать плотность).
ХИ2.РАСП.ПХ – p-value справа.
ХИ2.ТЕСТ – по двум диапазонам частот сразу проводит тест хи-квадрат. Количество степеней свободы берется на одну меньше, чем количество частот в столбце (так и должно быть), возвращая значение p-value.
Давайте пока рассчитаем для нашего эксперимента критическое (табличное) значение для 5-ти степеней свободы и альфа 0,05. Формула Excel будет выглядеть так:
=ХИ2.ОБР(0,95;5)
Или так
=ХИ2.ОБР.ПХ(0,05;5)
Результат будет одинаковым – 11,0705. Именно это значение мы видим в таблице (округленное до 1 знака после запятой).
Рассчитаем, наконец, p-value для 5-ти степеней свободы критерия χ2 = 3,4. Нужна вероятность справа, поэтому берем функцию с добавкой ПХ (правый хвост)
Нужна вероятность справа, поэтому берем функцию с добавкой ПХ (правый хвост)
=ХИ2.РАСП.ПХ(3,4;5) = 0,63857
Значит, при 5-ти степенях свободы вероятность получить значение критерия χ2 = 3,4 и больше равна почти 64%. Естественно, гипотеза не отклоняется (p-value больше 5%), частоты очень хорошо согласуются.
А теперь проверим гипотезу о согласии частот с помощью теста хи квадрат и функции Excel ХИ2.ТЕСТ.
Никаких таблиц, никаких громоздких расчетов. Указав в качестве аргументов функции столбцы с наблюдаемыми и ожидаемыми частотами, сразу получаем p-value. Красота.
Представим теперь, что вы играете в кости с подозрительным типом. Распределение очков от 1 до 5 остается прежним, но он выкидывает 26 шестерок (количество всех бросков становится 78).
p-value в этом случае оказывается 0,003, что гораздо меньше чем, 0,05. Есть серьезные основания сомневаться в правильности игральной кости. Вот, как выглядит эта вероятность на диаграмме распределения хи-квадрат.
Статистика критерия хи-квадрат здесь получается 17,8, что, естественно, больше табличного (11,1).
Надеюсь, мне удалось объяснить, что такое критерий согласия χ2 (хи-квадрат) Пирсона и как с его помощью проверяются статистические гипотезы.
Напоследок еще раз о важном условии! Критерий хи-квадрат исправно работает только в случае, когда количество всех частот превышает 50, а минимальное ожидаемое значение для каждой группы не меньше 5. Если в какой-либо категории ожидаемая частота менее 5, но при этом сумма всех частот превышает 50, то такую категорию объединяют с ближайшей, чтобы их общая частота превысила 5. Если это сделать невозможно, или сумма частот меньше 50, то следует использовать более точные методы проверки гипотез. О них поговорим в другой раз.
Ниже находится видео ролик о том, как в Excel проверить гипотезу с помощью критерия хи-квадрат.
Скачать файл с примером.
Поделиться в социальных сетях:
Таблица критерия Пирсона χ2 (хи-квадрат) онлайн. Теория вероятностей и математическая статистика
Ниже представлена таблица значений критических точек распределения χ2 (хи-квадрат) критерия Пирсона, широко используемые в задачах математической статистики, таких как построение доверительных интервалов, проверка статистических гипотез и непараметрическое оценивание.
| Число степеней свободы k | Уровень значимости α | |||||
| 0,01 | 0,025 | 0,05 | 0,95 | 0,975 | 0,99 | |
| 1 | 6,6 | 5 | 3,8 | 0,0039 | 0,00098 | 0,00016 |
| 2 | 9,2 | 7,4 | 6 | 0,103 | 0,051 | 0,02 |
| 3 | 11,3 | 9,4 | 7,8 | 0,352 | 0,216 | 0,115 |
| 4 | 13,3 | 11,1 | 9,5 | 0,711 | 0,484 | 0,297 |
| 5 | 15,1 | 12,8 | 11,1 | 1,15 | 0,831 | 0,554 |
| 6 | 16,8 | 14,4 | 12,6 | 1,64 | 1,24 | 0,872 |
| 7 | 18,5 | 16 | 14,1 | 2,17 | 1,69 | 1,24 |
| 8 | 20,1 | 17,5 | 15,5 | 2,73 | 2,18 | 1,65 |
| 9 | 21,7 | 19 | 16,9 | 3,33 | 2,7 | 2,09 |
| 10 | 23,2 | 20,5 | 18,3 | 3,94 | 3,25 | 2,56 |
| 11 | 24,7 | 21,9 | 19,7 | 4,57 | 3,82 | 3,05 |
| 12 | 26,2 | 23,3 | 21 ,0 | 5,23 | 4,4 | 3,57 |
| 13 | 27,7 | 24,7 | 22,4 | 5,89 | 5,01 | 4,11 |
| 14 | 29,1 | 26,1 | 23,7 | 6,57 | 5,63 | 4,66 |
| 15 | 30,6 | 27,5 | 25 | 7,26 | 6,26 | 5,23 |
| 16 | 32 | 28,8 | 26,3 | 7,96 | 6,91 | 5,81 |
| 17 | 33,4 | 30,2 | 27,6 | 8,67 | 7,56 | 6,41 |
| 18 | 34,8 | 28,9 | 9,39 | 8,23 | 7,01 | |
| 19 | 36,2 | 32,9 | 30,1 | 10,1 | 8,91 | 7,63 |
| 20 | 37,6 | 34,2 | 31,4 | 10,9 | 9,59 | 8,26 |
| 21 | 38,9 | 35,5 | 32,7 | 11,6 | 10,3 | 8,9 |
| 22 | 40,3 | 36,8 | 33,9 | 12,3 | 11 | 9,54 |
| 23 | 41,6 | 38,1 | 35,2 | 13,1 | 11,7 | |
| 24 | 43 | 39,4 | 36,4 | 13,8 | 12,4 | 10,9 |
| 25 | 44,3 | 40,6 | 37,7 | 14,6 | 13,1 | 11,5 |
| 26 | 45,6 | 41,9 | 38,9 | 15,4 | 13,8 | 12,2 |
| 27 | 47 | 43,2 | 40,1 | 16,2 | 14,6 | 12,9 |
| 28 | 48,3 | 44,5 | 41,3 | 16,9 | 15,3 | 13,6 |
| 29 | 49,6 | 45,7 | 42,6 | 17,7 | 16 | 14,3 |
| 30 | 50,9 | 47 | 43,8 | 18,5 | 16,8 | 15 |
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Математический справочник/ / Теория вероятностей и статистика / / Хи квадрат-распределение. Распределение Пирсона. Квантили хи-квадрат распределения
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
: Вероятности хи-квадрата Таблица
: Вероятности хи-квадрата Области, указанные вверху, — это области справа от критического значения. Чтобы найти область
слева, вычтите его из единицы, а затем посмотрите вверх (т. е. 0,05 слева равно 0,95 справа).
справа)
е. 0,05 слева равно 0,95 справа).
справа)
| дф | 0,995 | 0,99 | 0,975 | 0,95 | 0,90 | 0,10 | 0,05 | 0,025 | 0,01 | 0,005 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | — | — | 0,001 | 0,004 | 0,016 | 2,706 | 3,841 | 5.024 | 6,635 | 7,879 |
| 2 | 0,010 | 0,020 | 0,051 | 0,103 | 0,211 | 4,605 | 5,991 | 7,378 | 9.210 | 10,597 |
| 3 | 0,072 | 0,115 | 0,216 | 0,352 | 0,584 | 6.251 | 7,815 | 9,348 | 11.345 | 12.838 |
| 4 | 0,207 | 0,297 | 0,484 | 0,711 | 1,064 | 7,779 | 9,488 | 11. 143 143 | 13.277 | 14.860 |
| 5 | 0,412 | 0,554 | 0,831 | 1,145 | 1,610 | 9.236 | 11.070 | 12.833 | 15.086 | 16.750 |
| 6 | 0,676 | 0,872 | 1,237 | 1,635 | 2,204 | 10,645 | 12.592 | 14.449 | 16.812 | 18.548 |
| 7 | 0,989 | 1,239 | 1,690 | 2,167 | 2,833 | 12.017 | 14.067 | 16.013 | 18.475 | 20,278 |
| 8 | 1,344 | 1,646 | 2,180 | 2,733 | 3,490 | 13.362 | 15.507 | 17.535 | 20.090 | 21.955 |
| 9 | 1,735 | 2,088 | 2.700 | 3,325 | 4,168 | 14. 684 684 | 16.919 | 19.023 | 21.666 | 23.589 |
| 10 | 2,156 | 2,558 | 3,247 | 3,940 | 4,865 | 15,987 | 18.307 | 20.483 | 23.209 | 25.188 |
| 11 | 2,603 | 3,053 | 3,816 | 4,575 | 5,578 | 17.275 | 19.675 | 21.920 | 24.725 | 26.757 |
| 12 | 3,074 | 3,571 | 4.404 | 5,226 | 6.304 | 18.549 | 21.026 | 23.337 | 26.217 | 28.300 |
| 13 | 3,565 | 4.107 | 5.009 | 5,892 | 7.042 | 19.812 | 22.362 | 24.736 | 27.688 | 29.819 |
| 14 | 4.075 | 4,660 | 5,629 | 6,571 | 7,790 | 21.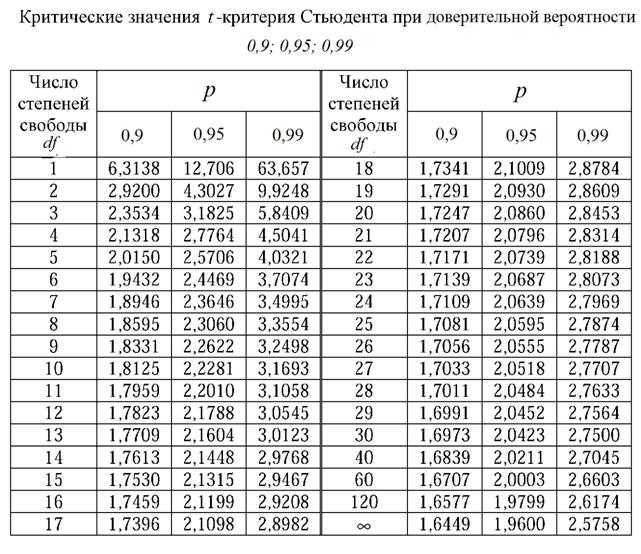 064 064 | 23.685 | 26.119 | 29.141 | 31.319 |
| 15 | 4.601 | 5.229 | 6,262 | 7,261 | 8,547 | 22.307 | 24,996 | 27.488 | 30,578 | 32.801 |
| 16 | 5.142 | 5,812 | 6.908 | 7,962 | 9.312 | 23.542 | 26.296 | 28.845 | 32.000 | 34,267 |
| 17 | 5,697 | 6.408 | 7,564 | 8,672 | 10.085 | 24.769 | 27.587 | 30.191 | 33.409 | 35,718 |
| 18 | 6,265 | 7.015 | 8.231 | 9.390 | 10,865 | 25,989 | 28.869 | 31,526 | 34.805 | 37,156 |
| 19 | 6,844 | 7,633 | 8. 907 907 | 10.117 | 11.651 | 27.204 | 30.144 | 32.852 | 36.191 | 38,582 |
| 20 | 7,434 | 8.260 | 9,591 | 10.851 | 12.443 | 28.412 | 31.410 | 34.170 | 37,566 | 39,997 |
| 21 | 8.034 | 8.897 | 10.283 | 11.591 | 13.240 | 29.615 | 32.671 | 35.479 | 38,932 | 41.401 |
| 22 | 8,643 | 9,542 | 10,982 | 12.338 | 14.041 | 30.813 | 33,924 | 36.781 | 40.289 | 42.796 |
| 23 | 9.260 | 10,196 | 11.689 | 13.091 | 14.848 | 32.007 | 35,172 | 38.076 | 41,638 | 44.181 |
| 24 | 9,886 | 10. 856 856 | 12.401 | 13.848 | 15.659 | 33.196 | 36.415 | 39,364 | 42,980 | 45,559 |
| 25 | 10,520 | 11.524 | 13.120 | 14.611 | 16.473 | 34.382 | 37,652 | 40.646 | 44.314 | 46,928 |
| 26 | 11.160 | 12.198 | 13.844 | 15.379 | 17.292 | 35,563 | 38.885 | 41,923 | 45.642 | 48.290 |
| 27 | 11.808 | 12.879 | 14.573 | 16.151 | 18.114 | 36.741 | 40.113 | 43,195 | 46,963 | 49,645 |
| 28 | 12.461 | 13,565 | 15.308 | 16,928 | 18,939 | 37.916 | 41.337 | 44.461 | 48.278 | 50,993 |
| 29 | 13. 121 121 | 14.256 | 16.047 | 17.708 | 19.768 | 39.087 | 42,557 | 45.722 | 49,588 | 52,336 |
| 30 | 13.787 | 14,953 | 16.791 | 18.493 | 20.599 | 40.256 | 43.773 | 46,979 | 50.892 | 53,672 |
| 40 | 20.707 | 22.164 | 24.433 | 26.509 | 29.051 | 51.805 | 55,758 | 59.342 | 63,691 | 66,766 |
| 50 | 27,991 | 29.707 | 32.357 | 34.764 | 37.689 | 63,167 | 67,505 | 71.420 | 76,154 | 79.490 |
| 60 | 35,534 | 37.485 | 40.482 | 43,188 | 46.459 | 74,397 | 79.082 | 83,298 | 88. 379 379 | 91,952 |
| 70 | 43,275 | 45.442 | 48.758 | 51,739 | 55,329 | 85,527 | 90.531 | 95.023 | 100.425 | 104.215 |
| 80 | 51.172 | 53,540 | 57,153 | 60.391 | 64,278 | 96,578 | 101.879 | 106.629 | 112.329 | 116.321 |
| 90 | 59,196 | 61,754 | 65,647 | 69,126 | 73.291 | 107,565 | 113,145 | 118,136 | 124,116 | 128,299 |
| 100 | 67,328 | 70.065 | 74.222 | 77,929 | 82,358 | 118.498 | 124,342 | 129,561 | 135.807 | 140,169 |
Содержание
1.3.6.7.4. Критические значения распределения хи-квадрат
1. 3.6.7.4. Критические значения хи-квадрата
Распределение
3.6.7.4. Критические значения хи-квадрата
Распределение | 1.
Исследовательский анализ данных 1.3. Методы ЭДА 1.3.6. Распределения вероятностей 1.3.6.7. Таблицы распределения вероятностей
| |||
| Как использовать эту таблицу | Эта таблица содержит критические значения
распределение хи-квадрат. Из-за
отсутствие симметрии распределения хи-квадрат, отдельные таблицы
предусмотрены верхний и нижний хвосты распределения. Тестовая статистика с ν степенями свободы вычисляется из
данные. Для односторонних тестов с верхним хвостом статистика теста сравнивается с
значение из таблицы верхних критических значений. Для двустороннего
тесты, статистика теста сравнивается со значениями из таблицы для
критические значения верхнего хвоста и таблица критических значений нижнего хвоста
ценности. Уровень значимости α показан на графике ниже показано распределение хи-квадрат с 3 степенями свободы для двусторонний тест на уровне значимости α = 0,05. Если тест статистика больше, чем критическое значение верхнего хвоста или меньше, чем критическое значение нижнего хвоста, мы отвергаем нулевую гипотезу. Специфический инструкции приведены ниже. Учитывая указанное значение α :
| ||
Верхние критические значения распределения хи-квадрат с ν степенями свободы
Вероятность меньше критического значения
ν 0,90 0,95 0,975 0,99 0,999
Критические значения нижнего хвоста распределения хи-квадрат с ν степень свободы
Вероятность меньше критического значения
ν 0,10 0,05 0,025 0,01 0,001
|
Хи-квадрат (Χ²) Таблица | Примеры и загружаемая таблица
Опубликован в
31 мая 2022 г. по
Шон Терни.
Отредактировано
9 июля 2022 г.
по
Шон Терни.
Отредактировано
9 июля 2022 г.
Таблица распределения хи-квадрата (Χ 2 ) представляет собой справочную таблицу, в которой перечислены критические значения хи-квадрата . Критическое значение хи-квадрат представляет собой порог статистической значимости для определенных проверок гипотез и определяет доверительные интервалы для определенных параметров.
Критические значения хи-квадрата рассчитываются из распределений хи-квадрат. Их трудно рассчитать вручную, поэтому большинство людей вместо этого используют справочную таблицу или статистическое программное обеспечение.
Скачать таблицу хи-квадрат (PDF)
Содержание
- Когда использовать таблицу распределения хи-квадрат
- Таблица распределения хи-квадрат (правосторонние вероятности)
- Как пользоваться таблицей
- Левосторонние и двусторонние вероятности
- Практические вопросы
- Часто задаваемые вопросы о таблицах хи-квадрат
Когда использовать таблицу распределения хи-квадрат
Вам понадобится критическое значение хи-квадрат, если вы хотите:
- Расчет доверительного интервала для дисперсии генеральной совокупности или стандартного отклонения
- Проверить, равна ли дисперсия или стандартное отклонение совокупности определенному значению (проверка одной дисперсии)
- Проверить, отличается ли частотное распределение категориальной переменной от ваших ожиданий (критерий согласия хи-квадрат)
- Проверить, связаны ли две категориальные переменные друг с другом (критерий независимости хи-квадрат)
- Проверка равенства пропорций двух тесно связанных переменных (критерий Макнемара)
Таблица распределения хи-квадрат (правосторонние вероятности)
Используйте приведенную ниже таблицу, чтобы найти критическое значение хи-квадрат для теста хи-квадрат или доверительного интервала, или загрузите таблицу распределения хи-квадрат (PDF).
В таблице представлены вероятности правого хвоста. Если вам нужны вероятности левого хвоста, вам нужно будет сделать небольшой дополнительный расчет.
Как пользоваться столом
Чтобы найти критическое значение хи-квадрат для проверки гипотезы или доверительного интервала, выполните следующие три шага.
Пример: исследование хи-квадрата. Представьте, что служба безопасности большого офисного здания устанавливает камеры видеонаблюдения на четырех входах в здание. Чтобы помочь им решить, где установить камеры, они хотят знать, как часто используется каждый вход. Они случайным образом выбирают 500 человек внутри здания и спрашивают их, через какой вход они вошли в здание.Команда хочет использовать критерий согласия хи-квадрат для проверки нулевой гипотезы ( H 0 ) о том, что четыре входа одинаково часто используются населением.
Чтобы узнать, следует ли отклонить нулевую гипотезу, им необходимо сравнить хи-квадрат Пирсона выборки с соответствующим критическим значением хи-квадрат.
Шаг 1. Расчет степеней свободы
Существует не одно распределение хи-квадрат — их много, и их формы различаются в зависимости от параметра, называемого «степенями свободы» (также называемого 9).1077 df или к ). Каждая строка таблицы распределения хи-квадрат представляет собой распределение хи-квадрат с различными df.
Вам необходимо использовать распределение с правильным df для вашего теста или доверительного интервала. В таблице ниже приведены уравнения для расчета df для нескольких распространенных процедур:
| Тест или процедура | Степени свободы ( df ) уравнение |
|---|---|
| Проверка одной дисперсии Доверительный интервал для дисперсии или стандартного отклонения | df = объем выборки − 1 |
| Хи-квадрат критерия согласия | df = количество групп − 1 |
| Критерий независимости хи-квадрат | df = (количество групп переменных 1 — 1) * (количество групп переменных 2 — 1) |
| Тест Макнемара | дф = 1 |
 Формула критерия согласия хи-квадрат выглядит следующим образом:
Формула критерия согласия хи-квадрат выглядит следующим образом:df = количество групп − 1
df = 4 − 1
df = 3
Шаг 2: Выберите уровень значимости
В столбцах таблицы распределения хи-квадрат указан уровень значимости критического значения. По соглашению уровень значимости (α) почти всегда равен 0,05, поэтому столбец для 0,05 выделен в таблице.
В редких случаях вы можете увеличить α, чтобы уменьшить частоту ошибок типа II, или уменьшить α, чтобы уменьшить частоту ошибок типа I.
Чтобы рассчитать доверительный интервал, выберите уровень значимости на основе желаемого уровня достоверности:
α = 1 − уровень достоверности
Наиболее распространенный доверительный уровень составляет 95% (0,95), что соответствует α = 0,05.
Пример: выбор уровня значимости Группа безопасности следует соглашению, выбирая уровень значимости 0,05.Шаг 3: Найдите критическое значение в таблице
Теперь у вас есть два числа, необходимые для нахождения критического значения в таблице распределения хи-квадрат:
- Степени свободы ( df ) перечислены в левой части таблицы.
 Найдите строку таблицы, соответствующую вычисленным вами степеням свободы.
Найдите строку таблицы, соответствующую вычисленным вами степеням свободы. - Уровни значимости (α) перечислены вверху таблицы. Найдите столбец, соответствующий выбранному вами уровню значимости.
- Ячейка таблицы, где встречаются строка и столбец, является вашим критическим значением.
Команда безопасности теперь может сравнить это критическое значение хи-квадрата с хи-квадратом Пирсона, рассчитанным для их выборки. Если критическое значение больше, чем хи-квадрат выборки, они могут отклонить нулевую гипотезу.
Левосторонние и двусторонние вероятности
В приведенной здесь таблице указаны вероятности правого хвоста. Вы должны использовать эту таблицу для большинства тестов хи-квадрат, включая критерий согласия хи-квадрат соответствия и критерий независимости хи-квадрат, а также критерий Макнемара.
Если вы хотите выполнить двусторонний или левосторонний тест, вам нужно будет сделать небольшой дополнительный расчет.
Левосторонние тесты
Наиболее распространенный левосторонний тест — это тест одной дисперсии при определении того, равна ли дисперсия совокупности или стандартное отклонение меньше, чем определенное значение.
Чтобы найти критическое значение левосторонней вероятности в приведенной выше таблице, просто используйте столбец таблицы для 1 − α.
Пример: левосторонний тестПредставьте, что вы подрабатываете печеньем в пекарне. Владелец пекарни говорит вам, что их печенье обычно различается по размеру со стандартным отклонением всего в 0,2 дюйма в диаметре.Вы гордитесь тем, что делаете все файлы cookie одинакового размера, поэтому решаете случайным образом отобрать 25 файлов cookie, чтобы проверить, не превышает ли их стандартное отклонение 0,2 дюйма.
Это левосторонний тест, потому что вы хотите знать, меньше ли стандартное отклонение определенного значения.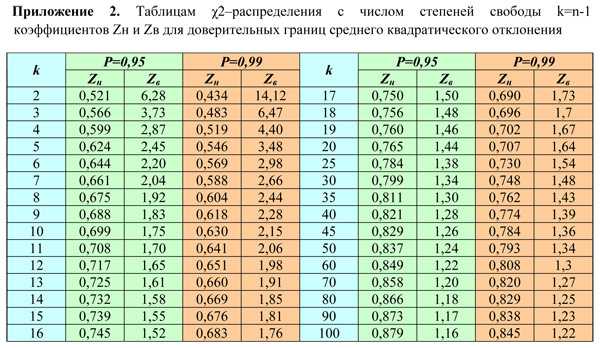 Вы ищете левостороннюю вероятность в правосторонней таблице, вычитая единицу из вашего уровня значимости: 1 — α = 1 — 0,05 = 0,95.
Вы ищете левостороннюю вероятность в правосторонней таблице, вычитая единицу из вашего уровня значимости: 1 — α = 1 — 0,05 = 0,95.
Критическое значение для df = 25 − 1 = 24 и α = 0,95 равно 13,848.
Если хи-квадрат вашей выборки больше этого критического значения, вы можете отклонить нулевую гипотезу о том, что ваши файлы cookie имеют стандартное отклонение в 0,2 дюйма в диаметре.
Двусторонние тесты
Наиболее распространенный левосторонний тест — это тест одной дисперсии при определении того, равна ли дисперсия или стандартное отклонение генеральной совокупности определенному значению.
Двусторонний тест имеет два критических значения. Чтобы найти критические значения, используйте столбцы таблицы для
и . Пример: двусторонний тест. Производитель детской одежды хочет спроектировать свои детские шапочки таким образом, чтобы они подходили любому шестимесячному ребенку с точностью до двух стандартных отклонений от среднего диаметра головы.
Они находят в медицинском учебнике, что стандартное отклонение диаметра головы шестимесячных младенцев составляет 1 дюйм, но хотят сами подтвердить это число. Они случайным образом выбирают 20 шестимесячных младенцев и измеряют их головы.
Это двусторонний тест, потому что они хотят знать, равно ли стандартное отклонение определенному значению. Они должны искать два критических значения в столбцах для:
- и
Критическое значение для df = 20 — 1 = 19 и α = 0,025 равно 32,852. Критическое значение для df = 19 и α = 0,975 равно 8,907.
Если хи-квадрат их выборки не находится между этими двумя критическими значениями, компания по производству одежды может отвергнуть нулевую гипотезу о том, что стандартное отклонение диаметра головы составляет 1 дюйм.
Практические вопросы
на базе Typeform
Часто задаваемые вопросы о таблицах хи-квадрат
- org/FAQPage»>
- Как найти критическое значение хи-квадрат в R?
Вы можете использовать функцию qchisq() , чтобы найти критическое значение хи-квадрат в R.
Например, чтобы вычислить критическое значение хи-квадрат для теста с df = 22 и α = 0,05:
qchisq(p = 0,05, df = 22, нижний.хвост = ЛОЖЬ)
- Как найти критическое значение хи-квадрат в Excel?
Вы можете использовать функцию CHISQ.INV.RT() , чтобы найти критическое значение хи-квадрат в Excel.
Например, чтобы вычислить критическое значение хи-квадрат для теста с df = 22 и α = 0,05, щелкните любую пустую ячейку и введите:
Источники в этой статье
Мы настоятельно рекомендуем учащимся использовать источники в своей работе.
 Распределение Пирсона. Квантили хи-квадрат распределения
Распределение Пирсона. Квантили хи-квадрат распределения ru:
ru: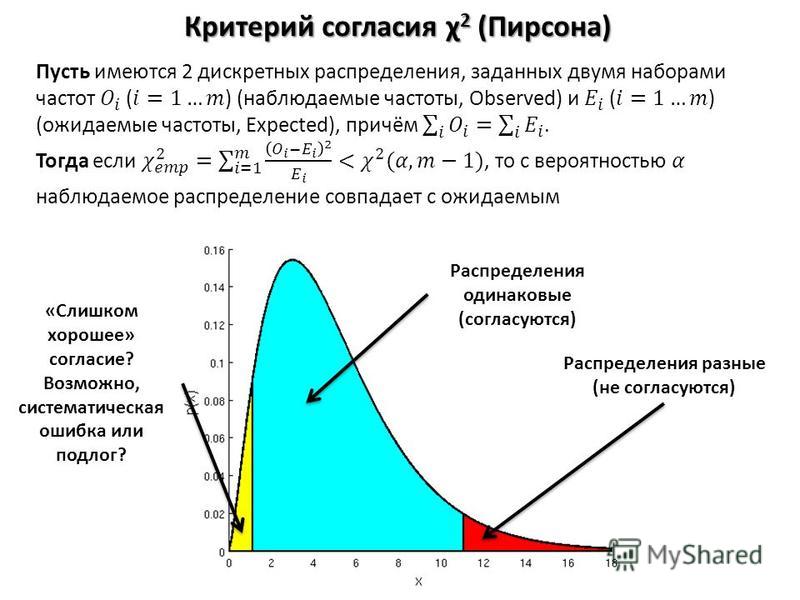
 и отклонить нулевую гипотезу, если статистика теста больше
чем табличное значение.
и отклонить нулевую гипотезу, если статистика теста больше
чем табличное значение. 919 19.023 21.666 27.877
10 15.987 18.307 20.483 23.209 29.588
11 17,275 190,675 21,920 24,725 31,264
12 18.549 21.026 23.337 26.217 32.910
13 19,812 22,362 24,736 27,688 34,528
14 21.064 23.685 26.119 29.141 36.123
15 22.307 24.996 27.488 30.578 37.697
16 23.542 26.296 28.845 32.000 39.252
17 24.769 27.587 30.191 33.409 40.790
18 25.989 28.869 31.526 34.805 42.312
19 27.204 30.144 32.852 36.191 43.820
20 28.412 31.410 34.170 37.566 45.315
21 290,615 32,671 35,479 38,932 46,797
22 30,813 33,924 36,781 40,289 48,268
23 32.007 35.172 38.076 41.638 49.728
24 33,196 36,415 39,364 42,980 51,179
25 34,382 37,652 40,646 44,314 52,620
26 35,563 38,885 41,923 45,642 54,052
27 36,741 40,113 43,195 46,963 55,476
28 37,916 41,337 44,461 48,278 56,892
29 39,087 42,557 45,722 490,588 58,301
30 40,256 43,773 46,979 50,892 59,703
31 41,422 44,985 48,232 52,191 61,098
32 42,585 46,194 49,480 53,486 62,487
33 43,745 47,400 50,725 54,776 63,870
34 44,903 48,602 51,966 56,061 65,247
35 46.
919 19.023 21.666 27.877
10 15.987 18.307 20.483 23.209 29.588
11 17,275 190,675 21,920 24,725 31,264
12 18.549 21.026 23.337 26.217 32.910
13 19,812 22,362 24,736 27,688 34,528
14 21.064 23.685 26.119 29.141 36.123
15 22.307 24.996 27.488 30.578 37.697
16 23.542 26.296 28.845 32.000 39.252
17 24.769 27.587 30.191 33.409 40.790
18 25.989 28.869 31.526 34.805 42.312
19 27.204 30.144 32.852 36.191 43.820
20 28.412 31.410 34.170 37.566 45.315
21 290,615 32,671 35,479 38,932 46,797
22 30,813 33,924 36,781 40,289 48,268
23 32.007 35.172 38.076 41.638 49.728
24 33,196 36,415 39,364 42,980 51,179
25 34,382 37,652 40,646 44,314 52,620
26 35,563 38,885 41,923 45,642 54,052
27 36,741 40,113 43,195 46,963 55,476
28 37,916 41,337 44,461 48,278 56,892
29 39,087 42,557 45,722 490,588 58,301
30 40,256 43,773 46,979 50,892 59,703
31 41,422 44,985 48,232 52,191 61,098
32 42,585 46,194 49,480 53,486 62,487
33 43,745 47,400 50,725 54,776 63,870
34 44,903 48,602 51,966 56,061 65,247
35 46. 059 49.802 53.203 57.342 66.619
36 47,212 50,998 54,437 58,619 67,985
37 48,363 52,192 55,668 59,893 69,347
38 490,513 53,384 56,896 61,162 70,703
39 50,660 54,572 58,120 62,428 72,055
40 51,805 55,758 59,342 63,691 73,402
41 52,949 56,942 60,561 64,950 74,745
42 54.090 58.124 61.777 66.206 76.084
43 55,230 59,304 62,990 67,459 77,419
44 56.369 60.481 64.201 68.710 78.750
45 57,505 61,656 65,410 69,957 80,077
46 58.641 62.830 66.617 71.201 81.400
47 590,774 64,001 67,821 72,443 82,720
48 60,907 65,171 69,023 73,683 84,037
49 62,038 66,339 70,222 74,919 85,351
50 63,167 67,505 71,420 76,154 86,661
51 64,295 68,669 72,616 77,386 87,968
52 65,422 69,832 73,810 78,616 89,272
53 66,548 70,993 75,002 79,843 90,573
54 67,673 72,153 76,192 81,069 91,872
55 68,796 73,311 77,380 82,292 93,168
56 69,919 74,468 78,567 83,513 94,461
57 71,040 75,624 79,752 84,733 95,751
58 72,160 76,778 80,936 85,950 97,039
59 73,279 77,931 82,117 87,166 98,324
60 74,397 79,082 83,298 88,379 99,607
61 75,514 80,232 84,476 89,591 100,888
62 76,630 81,381 85,654 90,802 102,166
63 77,745 82,529 86,830 92,010 103,442
64 78,860 83,675 88,004 93,217 104,716
65 79,973 84,821 89,177 94,422 105,988
66 81,085 85,965 90,349 95,626 107,258
67 82,197 87,108 91,519 96,828 108,526
68 83,308 88,250 92,689 98,028 109,791
69 84,418 89,391 93,856 99,228 111,055
70 85,527 90,531 95,023 100,425 112,317
71 86,635 91,670 96,189 101,621 113,577
72 87,743 92,808 97,353 102,816 114,835
73 88,850 93,945 98,516 104,010 116,092
74 89,956 95,081 99,678 105,202 117,346
75 91,061 96,217 100,839 106,393 118,599
76 92,166 97,351 101,999 107,583 119,850
77 93,270 98,484 103,158 108,771 121,100
78 94,374 99,617 104,316 109,958 122,348
79 95,476 100,749 105,473 111,144 123,594
80 96,578 101,879 106,629 112,329 124,839
81 97,680 103,010 107,783 113,512 126,083
82 98,780 104,139 108,937 114,695 127,324
83 99,880 105,267 110,090 115,876 128,565
84 100,980 106,395 111,242 117,057 129,804
85 102 079 107 522 112 393 118 236 131 041
86 103,177 108,648 113,544 119,414 132,277
87 104,275 109,773 114,693 120,591 133,512
88 105,372 110,898 115,841 121,767 134,746
89 106,469 112,022 116,989 122,942 135,978
90 107,565 113,145 118,136 124,116 137,208
91 108,661 114,268 119,282 125,289 138,438
92 109,756 115,390 120,427 126,462 139,666
93 110,850 116,511 121,571 127,633 140,893
94 111,944 117,632 122,715 128,803 142,119
95 113,038 118,752 123,858 129,973 143,344
96 114,131 119,871 125,000 131,141 144,567
97 115,223 120,990 126,141 132,309 145,789
98 116,315 122,108 127,282 133,476 147,010
99 117,407 123,225 128,422 134,642 148,230
100 118,498 124,342 129,561 135,807 149,449
100 118,498 124,342 129,561 135,807 149,449
059 49.802 53.203 57.342 66.619
36 47,212 50,998 54,437 58,619 67,985
37 48,363 52,192 55,668 59,893 69,347
38 490,513 53,384 56,896 61,162 70,703
39 50,660 54,572 58,120 62,428 72,055
40 51,805 55,758 59,342 63,691 73,402
41 52,949 56,942 60,561 64,950 74,745
42 54.090 58.124 61.777 66.206 76.084
43 55,230 59,304 62,990 67,459 77,419
44 56.369 60.481 64.201 68.710 78.750
45 57,505 61,656 65,410 69,957 80,077
46 58.641 62.830 66.617 71.201 81.400
47 590,774 64,001 67,821 72,443 82,720
48 60,907 65,171 69,023 73,683 84,037
49 62,038 66,339 70,222 74,919 85,351
50 63,167 67,505 71,420 76,154 86,661
51 64,295 68,669 72,616 77,386 87,968
52 65,422 69,832 73,810 78,616 89,272
53 66,548 70,993 75,002 79,843 90,573
54 67,673 72,153 76,192 81,069 91,872
55 68,796 73,311 77,380 82,292 93,168
56 69,919 74,468 78,567 83,513 94,461
57 71,040 75,624 79,752 84,733 95,751
58 72,160 76,778 80,936 85,950 97,039
59 73,279 77,931 82,117 87,166 98,324
60 74,397 79,082 83,298 88,379 99,607
61 75,514 80,232 84,476 89,591 100,888
62 76,630 81,381 85,654 90,802 102,166
63 77,745 82,529 86,830 92,010 103,442
64 78,860 83,675 88,004 93,217 104,716
65 79,973 84,821 89,177 94,422 105,988
66 81,085 85,965 90,349 95,626 107,258
67 82,197 87,108 91,519 96,828 108,526
68 83,308 88,250 92,689 98,028 109,791
69 84,418 89,391 93,856 99,228 111,055
70 85,527 90,531 95,023 100,425 112,317
71 86,635 91,670 96,189 101,621 113,577
72 87,743 92,808 97,353 102,816 114,835
73 88,850 93,945 98,516 104,010 116,092
74 89,956 95,081 99,678 105,202 117,346
75 91,061 96,217 100,839 106,393 118,599
76 92,166 97,351 101,999 107,583 119,850
77 93,270 98,484 103,158 108,771 121,100
78 94,374 99,617 104,316 109,958 122,348
79 95,476 100,749 105,473 111,144 123,594
80 96,578 101,879 106,629 112,329 124,839
81 97,680 103,010 107,783 113,512 126,083
82 98,780 104,139 108,937 114,695 127,324
83 99,880 105,267 110,090 115,876 128,565
84 100,980 106,395 111,242 117,057 129,804
85 102 079 107 522 112 393 118 236 131 041
86 103,177 108,648 113,544 119,414 132,277
87 104,275 109,773 114,693 120,591 133,512
88 105,372 110,898 115,841 121,767 134,746
89 106,469 112,022 116,989 122,942 135,978
90 107,565 113,145 118,136 124,116 137,208
91 108,661 114,268 119,282 125,289 138,438
92 109,756 115,390 120,427 126,462 139,666
93 110,850 116,511 121,571 127,633 140,893
94 111,944 117,632 122,715 128,803 142,119
95 113,038 118,752 123,858 129,973 143,344
96 114,131 119,871 125,000 131,141 144,567
97 115,223 120,990 126,141 132,309 145,789
98 116,315 122,108 127,282 133,476 147,010
99 117,407 123,225 128,422 134,642 148,230
100 118,498 124,342 129,561 135,807 149,449
100 118,498 124,342 129,561 135,807 149,449
 016 004 001 000 000
2. .211 .103 .051 .020 .002
3. .584 .352 .216 .115 .024
4. 1.064 .711 .484 .297 .091
5. 1,610 1,145 ,831 ,554 ,210
6. 2,204 1,635 1,237 ,872 ,381
7. 2,833 2,167 1,690 1,239 ,598
8. 3,490 2,733 2,180 1,646 ,857
9. 4,168 3,325 2,700 2,088 1,152
10. 4,865 3,940 3,247 2,558 1,479
11. 5,578 4,575 3,816 3,053 1,834
12. 6,304 5,226 4,404 3,571 2,214
13. 7,042 5,892 5,009 4,107 2,617
14. 7,790 6,571 5,629 4,660 3,041
15. 8,547 7,261 6,262 5,229 3,483
16. 9,312 7,962 6,908 5,812 3,942
17. 10.085 8.672 7.564 6.408 4.416
18. 10,865 9,390 8,231 7,015 4,905
19. 11.651 10.117 8.907 7.633 5.407
20. 12.443 10.851 9.591 8.260 5.921
21. 13.240 11.591 10.283 8.897 6.447
22. 14.041 12.338 10.982 9,542 6,983
23. 14.848 13.091 11.689 10.196 7.529
24. 15.659 13.848 12.401 10.856 8.085
25. 16.473 14.611 13.120 11.524 8.649
26. 17.292 15.379 13.844 12.198 9.222
27. 18.114 16.151 14.573 12.879 9.803
28. 18.939 16.928 15.308 13.565 10.391
29. 19.768 17.708 16.
016 004 001 000 000
2. .211 .103 .051 .020 .002
3. .584 .352 .216 .115 .024
4. 1.064 .711 .484 .297 .091
5. 1,610 1,145 ,831 ,554 ,210
6. 2,204 1,635 1,237 ,872 ,381
7. 2,833 2,167 1,690 1,239 ,598
8. 3,490 2,733 2,180 1,646 ,857
9. 4,168 3,325 2,700 2,088 1,152
10. 4,865 3,940 3,247 2,558 1,479
11. 5,578 4,575 3,816 3,053 1,834
12. 6,304 5,226 4,404 3,571 2,214
13. 7,042 5,892 5,009 4,107 2,617
14. 7,790 6,571 5,629 4,660 3,041
15. 8,547 7,261 6,262 5,229 3,483
16. 9,312 7,962 6,908 5,812 3,942
17. 10.085 8.672 7.564 6.408 4.416
18. 10,865 9,390 8,231 7,015 4,905
19. 11.651 10.117 8.907 7.633 5.407
20. 12.443 10.851 9.591 8.260 5.921
21. 13.240 11.591 10.283 8.897 6.447
22. 14.041 12.338 10.982 9,542 6,983
23. 14.848 13.091 11.689 10.196 7.529
24. 15.659 13.848 12.401 10.856 8.085
25. 16.473 14.611 13.120 11.524 8.649
26. 17.292 15.379 13.844 12.198 9.222
27. 18.114 16.151 14.573 12.879 9.803
28. 18.939 16.928 15.308 13.565 10.391
29. 19.768 17.708 16. 047 14.256 10.986
30. 20.599 18.493 16.791 14.953 11.588
31. 21.434 190,281 17,539 15,655 12,196
32. 22.271 20.072 18.291 16.362 12.811
33. 23.110 20.867 19.047 17.074 13.431
34. 23.952 21.664 19.806 17.789 14.057
35. 24.797 22.465 20.569 18.509 14.688
36. 25.643 23.269 21.336 19.233 15.324
37. 26.492 24.075 22.106 19.960 15.965
38. 27.343 24.884 22.878 20.691 16.611
39. 28.196 25.695 23.654 21.426 17.262
40. 290,051 26,509 24,433 22,164 17,916
41. 29.907 27.326 25.215 22.906 18.575
42. 30.765 28.144 25.999 23.650 19.239
43. 31.625 28.965 26.785 24.398 19.906
44. 32.487 29.787 27.575 25.148 20.576
45. 33.350 30.612 28.366 25.901 21.251
46. 34.215 31.439 29.160 26.657 21.929
47. 35.081 32.268 29.956 27.416 22.610
48. 35.949 33.098 30.755 28.177 23.295
49. 36.818 33.930 31.555 28.941 23.983
50. 37.689 34.764 32.357 29.707 24.674
51. 38.560 35.600 33.162 30.475 25.368
52. 39.433 36.437 33.968 31.246 26.065
53. 40.308 37.276 34.776 32.018 26.765
54. 41.183 38.116 35.
047 14.256 10.986
30. 20.599 18.493 16.791 14.953 11.588
31. 21.434 190,281 17,539 15,655 12,196
32. 22.271 20.072 18.291 16.362 12.811
33. 23.110 20.867 19.047 17.074 13.431
34. 23.952 21.664 19.806 17.789 14.057
35. 24.797 22.465 20.569 18.509 14.688
36. 25.643 23.269 21.336 19.233 15.324
37. 26.492 24.075 22.106 19.960 15.965
38. 27.343 24.884 22.878 20.691 16.611
39. 28.196 25.695 23.654 21.426 17.262
40. 290,051 26,509 24,433 22,164 17,916
41. 29.907 27.326 25.215 22.906 18.575
42. 30.765 28.144 25.999 23.650 19.239
43. 31.625 28.965 26.785 24.398 19.906
44. 32.487 29.787 27.575 25.148 20.576
45. 33.350 30.612 28.366 25.901 21.251
46. 34.215 31.439 29.160 26.657 21.929
47. 35.081 32.268 29.956 27.416 22.610
48. 35.949 33.098 30.755 28.177 23.295
49. 36.818 33.930 31.555 28.941 23.983
50. 37.689 34.764 32.357 29.707 24.674
51. 38.560 35.600 33.162 30.475 25.368
52. 39.433 36.437 33.968 31.246 26.065
53. 40.308 37.276 34.776 32.018 26.765
54. 41.183 38.116 35. 586 32.793 27.468
55. 42.060 38.958 36.398 33.570 28.173
56. 42.937 39.801 37.212 34.350 28.881
57. 43.816 40.646 38.027 35.131 290,592
58. 44.696 41.492 38.844 35.913 30.305
59. 45.577 42.339 39.662 36.698 31.020
60. 46.459 43.188 40.482 37.485 31.738
61. 47.342 44.038 41.303 38.273 32.459
62. 48.226 44.889 42.126 39.063 33.181
63. 49.111 45.741 42.950 39.855 33.906
64. 49.996 46.595 43.776 40.649 34.633
65. 50.883 47.450 44.603 41.444 35.362
66. 51.770 48.305 45.431 42.240 36.093
67. 52.659 49.162 46.261 43.038 36.826
68. 53,548 50,020 47,092 43,838 37,561
69. 54.438 50.879 47.924 44.639 38.298
70. 55.329 51.739 48.758 45.442 39.036
71. 56.221 52.600 49.592 46.246 39.777
72. 57.113 53.462 50.428 47.051 40.519
73. 58.006 54.325 51.265 47.858 41.264
74. 58.900 55.189 52.103 48.666 42.010
75. 59,795 56,054 52,942 49,475 42,757
76. 60.690 56.920 53.782 50.286 43.507
77. 61.586 57.786 54.623 51.097 44.258
78. 62.483 58.654 55.466 51.910 45.010
79. 63.380 59.522 56.
586 32.793 27.468
55. 42.060 38.958 36.398 33.570 28.173
56. 42.937 39.801 37.212 34.350 28.881
57. 43.816 40.646 38.027 35.131 290,592
58. 44.696 41.492 38.844 35.913 30.305
59. 45.577 42.339 39.662 36.698 31.020
60. 46.459 43.188 40.482 37.485 31.738
61. 47.342 44.038 41.303 38.273 32.459
62. 48.226 44.889 42.126 39.063 33.181
63. 49.111 45.741 42.950 39.855 33.906
64. 49.996 46.595 43.776 40.649 34.633
65. 50.883 47.450 44.603 41.444 35.362
66. 51.770 48.305 45.431 42.240 36.093
67. 52.659 49.162 46.261 43.038 36.826
68. 53,548 50,020 47,092 43,838 37,561
69. 54.438 50.879 47.924 44.639 38.298
70. 55.329 51.739 48.758 45.442 39.036
71. 56.221 52.600 49.592 46.246 39.777
72. 57.113 53.462 50.428 47.051 40.519
73. 58.006 54.325 51.265 47.858 41.264
74. 58.900 55.189 52.103 48.666 42.010
75. 59,795 56,054 52,942 49,475 42,757
76. 60.690 56.920 53.782 50.286 43.507
77. 61.586 57.786 54.623 51.097 44.258
78. 62.483 58.654 55.466 51.910 45.010
79. 63.380 59.522 56. 309 52.725 45.764
80. 64.278 60.391 57.153 53.540 46.520
81. 65.176 61.261 57.998 54.357 47.277
82. 66.076 62.132 58.845 55.174 48.036
83. 66.976 63.004 59.692 55.993 48.796
84. 67.876 63.876 60.540 56.813 490,557
85. 68.777 64.749 61.389 57.634 50.320
86. 69.679 65.623 62.239 58.456 51.085
87. 70.581 66.498 63.089 59.279 51.850
88. 71.484 67.373 63.941 60.103 52.617
89. 72.387 68.249 64.793 60.928 53.386
90. 73,291 69,126 65,647 61,754 54,155
91. 74.196 70.003 66.501 62.581 54.926
92. 75.100 70.882 67.356 63.409 55.698
93. 76.006 71.760 68.211 64.238 56.472
94. 76,912 72,640 69,068 65,068 57,246
95. 77.818 73.520 69.925 65.898 58.022
96. 78.725 74.401 70.783 66.730 58.799
97. 79,633 75,282 71,642 67,562 59,577
98. 80,541 76,164 72,501 68,396 60,356
99. 81.449 77.046 73.361 69.230 61.137
100. 82,358 77,929 74,222 70,065 61,918
309 52.725 45.764
80. 64.278 60.391 57.153 53.540 46.520
81. 65.176 61.261 57.998 54.357 47.277
82. 66.076 62.132 58.845 55.174 48.036
83. 66.976 63.004 59.692 55.993 48.796
84. 67.876 63.876 60.540 56.813 490,557
85. 68.777 64.749 61.389 57.634 50.320
86. 69.679 65.623 62.239 58.456 51.085
87. 70.581 66.498 63.089 59.279 51.850
88. 71.484 67.373 63.941 60.103 52.617
89. 72.387 68.249 64.793 60.928 53.386
90. 73,291 69,126 65,647 61,754 54,155
91. 74.196 70.003 66.501 62.581 54.926
92. 75.100 70.882 67.356 63.409 55.698
93. 76.006 71.760 68.211 64.238 56.472
94. 76,912 72,640 69,068 65,068 57,246
95. 77.818 73.520 69.925 65.898 58.022
96. 78.725 74.401 70.783 66.730 58.799
97. 79,633 75,282 71,642 67,562 59,577
98. 80,541 76,164 72,501 68,396 60,356
99. 81.449 77.046 73.361 69.230 61.137
100. 82,358 77,929 74,222 70,065 61,918