Svd разложение: Вычисление сингулярного разложения матриц

Содержание

Вычисление сингулярного разложения матриц

%PDF-1.6 % 1 0 obj > endobj 4 0 obj /Author /Creator (TeX) /Keywords /Producer (MiKTeX pdfTeX-1.40.17) /ModDate (D:20200419145631+07’00’) /Title >> endobj 2 0 obj > stream 2020-04-19T14:56:31+07:002020-04-19T14:55:24+07:002020-04-19T14:56:31+07:00TeXapplication/pdf

Вычисление сингулярного разложения матриц

Афанасьева А. А.

Публикации ТГУ

SVD–разложение

сингулярные числа

сжатие изображения.

uuid:3f21b630-8f4d-419b-b7bb-ef6baeff75b3uuid:05427aa8-3654-40e3-9606-94b0b1e8f28eMiKTeX pdfTeX-1.40.17SVD–разложение, сингулярные числа, сжатие изображения. endstream endobj 3 0 obj > endobj 5 0 obj > endobj 6 0 obj > endobj 7 0 obj > endobj 8 0 obj > endobj 9 0 obj > endobj 10 0 obj > endobj 11 0 obj > endobj 12 0 obj > stream x}V0+\&3Xd;-3PPߎcO@/;w»ؒx Z:ٰt̽&Ƒǯc{@y{-ZhQkU&_tCENcjEjU=*kݟJ

Сообщество Экспонента

Публикация
08. 01.2023

Глубокое и машинное обучение(ИИ)

🦾 Готовим для вас: Дайджесты новостей; Истории успеха; Анонсы ивентов. Присоединяйтесь!

Мы создали канал, чтобы помочь вам разобраться с лучшим подходам внедрения ИИ в промышленности и воплотить их в ваших проектах.

глубокое обучение
ИИ
Искусственный интеллект

08.01.2023

Публикация
08.01.2023

Цифровая обработка сигналов, Изображения и видео, Системы связи, Встраиваемые системы, Глубокое и машинное обучение(ИИ), Автоматизация испытаний, Робототехника и беспилотники, ПЛИС и СнК, Радиолокация, Системы управления, Биология, Математика и статистика, Финансы, Электропривод и силовая электроника, Верификация и валидация

📖 20 статей на Хабре. Если вам интересны ИИ, ЦОС, электроэнергетика, ПЛИС, то в нашем блоге на Хабр вы точно найдете занимательные статьи. 💻 15+ вебинаров о том, как внедрять инженерию моделей в образовании, в разработке ИИ, ЦОС и других систем, как генерирова…

🎄 Итоги 2022 года – делимся ключевыми событиями

Публикация
06.01.2023

Цифровая обработка сигналов, Автоматизация испытаний

Здравствуйте. Пишу сейчас диплом по программе спектрального анализа, одно из заданий — ускорение работы программы. 1/3-октавный анализ обычно длится около 10 минут, а 1/12-октавный 35+ минут, что при большом количестве записей очень затратно. С помощью Profile…

Программа спектрального анализа данных лётных испытаний по шуму на местности. В программе используется функция octaveFilter, но почему-то она не работает в цикле так, как должна

ЦОС
parallel
OCTAVE
октавный фильтр

06.01.2023

Публикация
04.01.2023

Другое, Изображения и видео, Математика и статистика

Графические построения «с помощью циркуля и линейки» являются критериями ПОДОБИЯ (графическими моделями), а не «натуральными Объектами», которые материально существуют «в окружающем пространстве Вселенной»!»Критерий подобия — безразмерная величина, соста. ..

Найдено ещё одно ГРАФИЧЕСКОЕ подтверждение того, что «число пи» является количественным соотношением двух натуральных чисел = 22/7 = 3+1/7.
Переводить это число в десятичную систему — НЕ РАЦИОНАЛЬНО!

https://www.math20.com/ru/forum/viewtopic.php?f=26&t=3326

Теория чисел

04.01.2023

вопрос
30.12.2022

Цифровая обработка сигналов

Доброго времени суток! Получил задание на разработку алгоритма и программы, реализующих преобразование ИКМ в ДИКМ(первого порядка). 1) Разработать методичку оценки сжатия; 2) Провести оценку степени с…

4 Ответа

вопрос
30.12.2022

Электропривод и силовая электроника, Цифровая обработка сигналов

Подскажите пожалуйста, может быть есть какой то блок, или уже написанная программа для загрузки файла осциллограммы формата COMTRADE в Simulink.

2 Ответа

MATLAB
Simulink

30.12.2022

вопрос
28.12.2022

Математика и статистика

Подскажите, пожалуйста, ссылки на видео и/или другую информацию (на русском) для того чтоб быстрее разобраться — как, после обучения модели и сохранив ее в виде скрипта , — использовать эт…

модель

28.12.2022

Публикация
24.12.2022

Системы связи

Скачать материалы семинара можно тут.

Недавно у нас в офисе прошел офлайн-семинар, который собрал на одной площадке специалистов данной тематики для обмена знаниями и опытом, чтобы вооружившись последними технологиями дать быстрый старт в развитии отечественного оборудования систем связи 5G.

5G
ИИ
Искусственный интеллект

24.12.2022

вопрос
23.12.2022

Глубокое и машинное обучение(ИИ), Робототехника и беспилотники, ПЛИС и СнК, Системы управления, Электропривод и силовая электроника, Радиолокация, Автоматизация испытаний, Системы связи, Цифровая обработка сигналов, Верификация и валидация, Математика и статистика, Изображения и видео

Здравствуйте! Есть такая вот статья. Мне в Matlab надо написать формулу, чтобы в результате получить диаграмму, как на рисунке 4 на статье. Только вот я не понимаю, какую формулу можно было бы написат…

3 Ответа

Отвеченный вопрос
21. 12.2022

Другое, Математика и статистика, Цифровая обработка сигналов

Есть массив экспериментальных данных (9 спектров при разных концентрациях), который я пытаюсь описать спектрами нескольких форм (в данном примере для упрощения только одна форма со спектром x(2,: ) и…

6 Ответов

Результаты поиска

Нет результатов поиска, попробуйте задать другие параметры.

Singular Value Decomposition (SVD) — GeeksforGeeks

SD 9003 9044 алгоритм Наивные способы расчета СВД | by Risto Hinno

Наивные способы расчета СВД

Источник

Цель этого поста — показать несколько простых и обучающих примеров, как вычислять разложение по сингулярным числам с помощью простых методов. Если вы заинтересованы в сильных отраслевых реализациях, вы можете найти это полезным.

Разложение по сингулярным числам (SVD) — это метод матричной факторизации, который обобщает собственное разложение квадратной матрицы (n x n) на любую матрицу (n x m) (источник).

Если вы не знаете, что такое собственное разложение или собственные векторы/собственные значения, погуглите или прочитайте этот пост. Этот пост предполагает, что вы знакомы с этими понятиями.

SVD аналогичен анализу главных компонентов (PCA), но имеет более общий характер. PCA предполагает, что входная квадратная матрица, SVD не имеет этого предположения. Общая формула SVD:

M = UΣV ᵗ, где:

M - исходная матрица, которую мы хотим разложить
U - левая сингулярная матрица (левый единственный столбец) . Столбцы U содержат собственные векторы матрицы MM ᵗ
Σ - диагональная матрица, содержащая сингулярные (собственные) значения
V - правая сингулярная матрица (столбцы - правые сингулярные векторы). Столбцы V содержат собственные векторы матрицы M ᵗ M

матрицы SVD (источник)

SVD является более общей, чем PCA. Из предыдущего рисунка видно, что SVD может обрабатывать матрицы с разным количеством столбцов и строк. СВД похожа на ППШ. Формула PCA: M = 𝑄 𝚲 𝑄 ᵗ, которая разлагает матрицу на ортогональную матрицу 𝑄 и диагональная матрица 𝚲. Просто это можно интерпретировать как:

изменение базиса со стандартного базиса на базис 𝑄 (с использованием 𝑄 ᵗ)
применение матрицы преобразования 𝚲, которая изменяет длину, а не направление, поскольку это диагональная матрица
изменение база из базы 𝑄 в стандартную базу (с использованием 𝑄 )

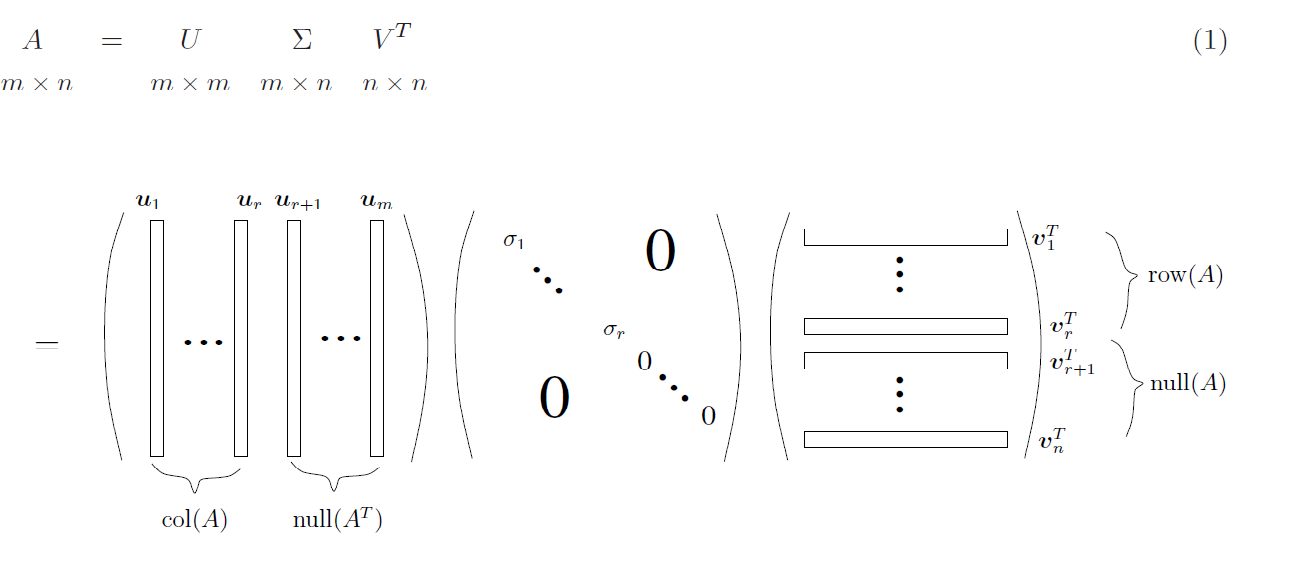SVD делает то же самое, но не возвращается к той же базе, с которой мы начали преобразования. Он не мог этого сделать, потому что наша исходная матрица M не является квадратной матрицей. На следующем рисунке показано изменение основы и преобразования, связанные с SVD.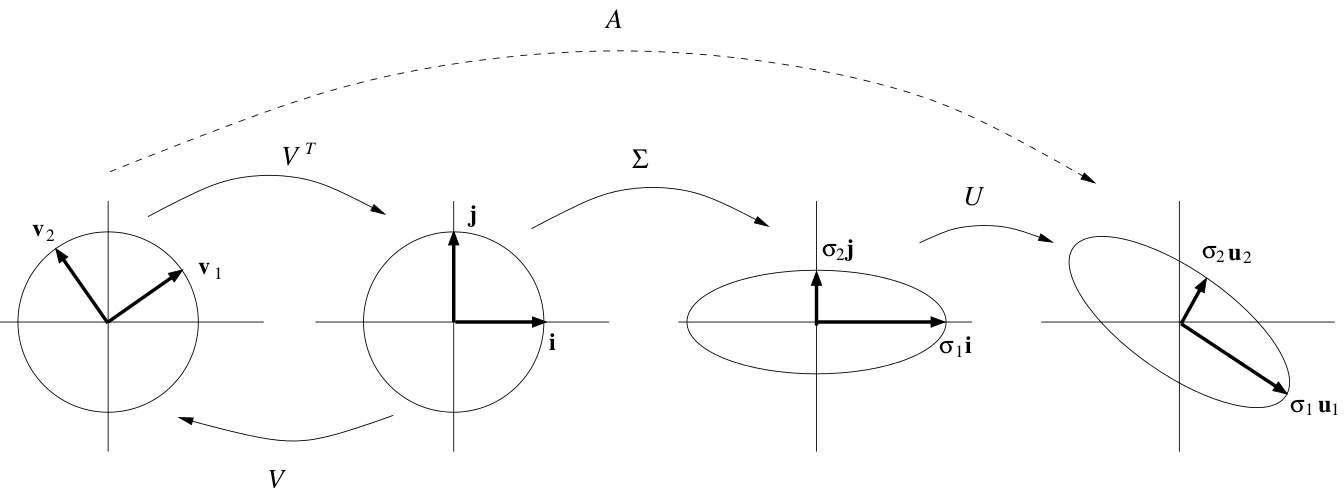

Преобразования СВД и смена базы. (исходник)

Из графика видно, что СВД делает следующие шаги:

изменение базы со стандартной базы на базу V (используя V ᵗ). Обратите внимание, что на графике это показано как простое вращение
с применением преобразования, описанного матрицей Σ . Это масштабирует наш вектор в базисе V
изменение базиса с V на базис U. Поскольку наша исходная матрица M не квадратная, матрица U не может иметь те же размеры, что и V, и мы не можем вернуться к нашей исходной стандартной основе (см. рисунок «Матрицы СВД»)

Существует множество вариантов СВД и способов расчета СВД. Я покажу лишь несколько способов его расчета.

Если вы хотите сами попробовать кодировать примеры, используйте этот блокнот, в котором есть все примеры, использованные в этом посте.

Итерация мощности

Итерация мощности начинается с b ₀, что может быть случайным вектором. На каждой итерации этот вектор обновляется по следующему правилу:

Источник

Сначала умножаем b ₀ на исходную матрицу A ( Abₖ ) и делим результат на норму (|| Abₖ ||). Мы будем продолжать, пока результат не сойдется (обновления меньше порогового значения).

Степенной метод имеет несколько допущений:

b ₀ имеет ненулевую составляющую в направлении собственного вектора, связанного с доминирующим собственным значением. Инициализация b ₀ случайным образом сводит к минимуму вероятность невыполнения этого предположения
матрица A имеет доминирующее собственное значение, которое имеет строго большую величину, чем другие собственные значения (источник).

Эти предположения гарантируют, что алгоритм сходится к приемлемому результату. Чем меньше разница между доминирующим собственным значением и вторым собственным значением, тем больше времени может потребоваться для сходимости.

Очень простой пример силового метода можно найти здесь. Я сделал пример, который также находит собственное значение. Как видите, ядром этой функции является итерация мощности.

Для простого примера мы используем набор данных о пиве (который доступен здесь). Мы построим ковариационную матрицу и попытаемся определить доминирующее сингулярное значение набора данных. Полный пример с обработкой данных доступен в записной книжке.

 #construct data 
 df=pd.read_csv('data/beer_dataset.csv') 
 X = np.array([df['Temperatura Maxima (C)'], 
 df['Consumo de cerveja (litros)' ]]).T 
 C = np.cov(X, rowvar=False)eigen_value, eigen_vec = svd_power_iteration(C)

Мы можем построить доминирующий собственный вектор с исходными данными.

Доминантный главный компонент/собственный вектор данных о пиве

Как видно из графика, этот метод действительно нашел доминирующее сингулярное значение/собственный вектор. Похоже, это работает. Вы можете использовать блокнот, чтобы увидеть, что результаты очень близки к результатам реализации svd, предоставленной numpy . Далее мы увидим, как получить больше, чем просто первые доминирующие сингулярные значения.

Степенная итерация для n сингулярных значений

Чтобы получить больше, чем просто наиболее доминирующее сингулярное значение из матрицы, мы все еще можем использовать степенную итерацию. Мы реализуем новую функцию, которая использует нашу предыдущую функцию svd_power_iteration . Найти первое доминирующее сингулярное значение несложно. Мы могли бы использовать ранее упомянутую функцию. Но как найти второе единственное число?

Мы должны удалить доминирующее направление из матрицы и повторить поиск наиболее доминирующего сингулярного значения (источник). Чтобы сделать это, мы могли бы вычесть предыдущий компонент (ы) собственных векторов из исходной матрицы (используя сингулярные значения и левый и правый сингулярные векторы, которые мы уже вычислили):

A_next = A-(singular_value₁)(u₁)(v₁)ᵗ

Вот пример кода (заимствован отсюда, с небольшими изменениями) для вычисления нескольких собственных значений/собственных векторов.

Когда мы применяем к нашему набору данных о пиве, мы получаем два собственных значения и собственные векторы.

Принципиальные компоненты/собственные векторы данных пива

Обратите внимание, что этот пример работает также с матрицами, в которых столбцов больше, чем строк, или строк больше, чем столбцов. Результаты сопоставимы с реализацией numpy svd. Вот один пример:

 mat = np.array([[1,2,3], 
 [4,5,6]]) 
 u, s, v = np.linalg.svd(mat, full_matrices=False) 
 значения, left_s , rigth_s = svd(mat)np.allclose(np.absolute(u), np.absolute(left_s)) 
 #True 
 np. allclose(np.absolute(s), np.absolute(values)) 
 #True 
 np.allclose(np.absolute(v), np.absolute(rigth_s)) 
 #True

Чтобы сравнить результаты нашего пользовательского решения с реализацией numpy svd, мы берем абсолютные значения, поскольку знаки в матрицах могут быть противоположными. Это означает, что векторы указывают противоположные направления, но все еще лежат на одной прямой и, следовательно, все еще являются собственными векторами.

Теперь, когда мы нашли способ вычисления нескольких сингулярных значений/сингулярных векторов, мы можем спросить, можем ли мы сделать это более эффективно?

Блочная версия степенного метода

Эта версия также имеет такие названия, как одновременная степенная итерация или ортогональная итерация. Идея этой версии довольно проста (источник):

другие собственные векторы ортогональны доминирующему
мы можем использовать степенной метод и заставить второй вектор быть ортогональным первому
алгоритм сходится к двум различным собственным векторам
делаем это для многих векторов, а не только для двух из них шаг мы нормализуем векторы, используя QR-разложение. QR-разложение разлагает матрицу на следующие компоненты:
A=QR, где
- A-исходная матрица, которую мы хотим разложить
- Q-ортогональная матрица
- R-верхняя треугольная матрица
Если алгоритм сходится, то Q будет собственными векторами и собственными значениями R. Вот пример кода:
Из кода видно, что вычисление сингулярных векторов и значений — это небольшая часть кода. Большая часть кода посвящена работе с матрицами различной формы.
Если мы применим эту функцию к набору данных о пиве, мы должны получить такие же результаты, как и в предыдущем подходе.
Принципиальные компоненты/собственные векторы данных пива из svd_simultaneous_power_iteration
Собственные векторы указывают противоположные направления по сравнению с предыдущей версией, но они находятся на той же прямой (с небольшой ошибкой) и, следовательно, являются одними и теми же собственными векторами. В блокноте у меня есть примеры, которые сравнивают вывод с реализацией numpy svd.
Навигация по записям
Как создать игру онлайн на андроид: Как создать игру на Андроид с нуля самому в 2022 году
Sony а6500: Sony A6500 — Цифровые фотоаппараты
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт
Найти:
Рубрики
2019 © Все права защищены. Карта сайта

from skimage.color import rgb2gray

from skimage import data

import matplotlib. pyplot как plt

импорт numpy как np

из scipy.linalg импорт 0009 svd

X = np.array([[ 3 , 3 , 2 ], [ 2 , 3 , - 2 ]])

print (X)

U, singular, V_transpose = svd(X)

print ( "У:" 9{T}" , V_transpose)

singular_inv = 1. 0 / singular

s_inv = np.zeros(A.shape)

s_inv[ 0 ][ 0 ] = singular_inv[ 0 ]

s_inv[ 1 ][ 1 ] = singular_inv[ 1 ]

M = np.dot(np.dot(V_transpose.T, s_inv.T), U.T)

print ( M)

cat = data.chelsea()

plt. imshow(cat)

gray_cat = rgb2gray(cat)

U, S, V_T = svd(gray_cat, full_matrices = False )

S = np.diag(S)

fig, ax = Plt.Subplots ( 5 , 2 , Рис. = ( 8 , 20 )

   ) 
     999999999999999999999999999999999999999999999999999999999999999999999999999999008    )))  0 
  for   r   in   [   5   ,   10   ,   70   ,   100   ,   200   ]: 
    CAT_APPROX   =   U [:: R] @ S [  0  : r ,: r] @ v_t [: r,:] 
    [Curr_fig] [
    [curr_fig] [  0   ]. imshow(  256   -   cat_approx) 
         ax[curr_fig][   0   ].set_title(   "k = "   +   str   (r)) 
    AX [Curr_FIG,   0  ]. Осис (  'OFF'  ) 
    AX [Curr_FIG] [  1  ] .set_TITL  ) 
         ax[curr_fig][   1   ].imshow(gray_cat) 
         ax[curr_fig,   1   ].axis(   'off'   ) 
         curr_fig   +   =   1 
  plt. show()

Вычисление сингулярного разложения матриц

Сообщество Экспонента

Результаты поиска

Singular Value Decomposition (SVD) — GeeksforGeeks

Наивные способы расчета СВД

Итерация мощности

Степенная итерация для n сингулярных значений

Блочная версия степенного метода

Добавить комментарий Отменить ответ