Как выполнить тест Колмогорова-Смирнова в Excel
Редакция Кодкампа
читать 2 мин
Критерий Колмогорова-Смирнова используется для определения нормальности распределения выборки.
Этот тест широко используется, потому что многие статистические тесты и процедуры предполагают , что данные распределены нормально.
В следующем пошаговом примере показано, как выполнить тест Колмогорова-Смирнова для образца набора данных в Excel.
Шаг 1: введите данныеВо-первых, давайте введем значения для набора данных с размером выборки n = 20:
Шаг 2: Расчет фактических и ожидаемых значений из нормального распределенияДалее мы рассчитаем фактические значения по сравнению с ожидаемыми значениями из нормального распределения:
Вот формула, которую мы использовали в различных ячейках:
- B2 : =СТРОКА() – 1
- C2 : = B2 /COUNT( $A$2:$A$21 )
- D2 : =( B2 -1)/СЧЁТ( $A$2:$A$21 )
- E2 : =ЕСЛИ( C2 <1, НОРМ.
С.ОБР( C2 )»,») - F2 : =НОРМ.РАСП( A2 , $J$1 , $J$2 , ИСТИНА)
- G2 : =ABS( F2 – D2 )
- J1 : =СРЕДНЕЕ( A2:A21 )
- J2 : =СТАНДОТКЛОН.С( A2:A21 )
- J4 : =МАКС( G2:G21 )
С.ОБР( C2 )»,»)В тесте Колмогорова-Смирнова используются следующие нулевая и альтернативная гипотезы:
- H 0 : Данные нормально распределены.
- H A : Данные не распределены нормально.
Чтобы определить, должны ли мы отклонить или не отклонить нулевую гипотезу, мы должны обратиться к максимальному значению на выходе, которое оказывается равным 0,10983 .
Это представляет собой максимальную абсолютную разницу между фактическими значениями нашей выборки и ожидаемыми значениями нормального распределения.
Чтобы определить, является ли это максимальное значение статистически значимым, мы должны обратиться к таблице критических значений Колмогорова-Смирнова и найти число, равное n = 20 и α = 0,05.
Критическое значение оказывается равным 0,190 .
Поскольку наше максимальное значение не превышает этого критического значения, мы не можем отвергнуть нулевую гипотезу.
Это означает, что мы можем предположить, что наши выборочные данные нормально распределены.
Дополнительные ресурсыВ следующих руководствах объясняется, как выполнять другие распространенные статистические тесты в Excel:
Как выполнить корреляционный тест в Excel
Как выполнить тест Дарбина-Ватсона в Excel
Как выполнить тест Харке-Бера в Excel
Как выполнить тест Левена в Excel
Тест Колмогорова-Смирнова в R (с примерами)
Тест Колмогорова-Смирнова используется для проверки того, происходит ли выборка из определенного распределения.
Чтобы выполнить одновыборочный или двухвыборочный тест Колмогорова-Смирнова в R, мы можем использовать функцию ks.test() .
В этом руководстве показан пример использования этой функции на практике.
Предположим, у нас есть следующие образцы данных:
#make this example reproducible seed(0) #generate dataset of 100 values that follow a Poisson distribution with mean=5 data <- rpois(n= 20 , lambda= 5 )
Связанный: Руководство по dpois, ppois, qpois и rpois в R
В следующем коде показано, как выполнить тест Колмогорова-Смирнова для этой выборки из 100 значений данных, чтобы определить, является ли она результатом нормального распределения:
#perform Kolmogorov-Smirnov test ks.test(data, " pnorm ") One-sample Kolmogorov-Smirnov test data: data D = 0.97725, p-value < 2.2e-16 alternative hypothesis: two-sided
Из вывода мы видим, что статистика теста равна 0,97725 , а соответствующее значение p равно 2,2e-16.Поскольку p-значение меньше 0,05, мы отвергаем нулевую гипотезу. У нас есть достаточно доказательств, чтобы сказать, что данные выборки не имеют нормального распределения.
Этот результат не должен вызывать удивления, поскольку мы сгенерировали выборочные данные с помощью функции rpois() , которая генерирует случайные значения, соответствующиераспределению Пуассона .
Пример 2. Двухвыборочный критерий Колмогорова-СмирноваПредположим, у нас есть следующие два примера набора данных:
#make this example reproducible seed(0) #generate two datasets data1 <- rpois(n= 20 , lambda= 5 ) data2 <- rnorm( 100 )
В следующем коде показано, как выполнить тест Колмогорова-Смирнова для этих двух образцов, чтобы определить, получены ли они из одного и того же дистрибутива:
#perform Kolmogorov-Smirnov test ks.test(data1, data2) Two-sample Kolmogorov-Smirnov test data: data1 and data2 D = 0.99, p-value = 1.299e-14 alternative hypothesis: two-sided
Из вывода мы видим, что статистика теста равна 0,99 , а соответствующее значение p равно 1,299e-14.Поскольку p-значение меньше 0,05, мы отвергаем нулевую гипотезу.
У нас есть достаточно доказательств, чтобы сказать, что два выборочных набора данных не происходят из одного и того же распределения.
Этот результат также не должен вызывать удивления, поскольку мы сгенерировали значения для первой выборки, используя распределение Пуассона, и значения для второй выборки, используя нормальное распределение .
Как выполнить тест Шапиро-Уилка в R
Как выполнить тест Андерсона-Дарлинга в R
Как выполнять многомерные тесты на нормальность в R
ТЕСТ КОЛМОГОРОВА–СМИРНОВА. Необходимый инструмент в вашей науке о данных… | by Marc-Olivier Arsenault
Необходимый инструмент в вашем наборе инструментов для обработки и анализа данных
В последнее время на работе нам приходилось проводить много неконтролируемой классификации. По сути, нам нужно было выделить N классов из выборки. У нас было приблизительное представление о том, сколько классов присутствует, но ни в чем нельзя было быть уверенным.
Мы обнаружили, что тест Колмогорова-Смирнова является очень эффективным способом определить, существенно ли отличаются два образца друг от друга.
Я расскажу вам немного о тесте Колмогорова-Смирнова и расскажу об одной задаче, которую мы решили с его помощью.
Исходное сообщение на coffeeanddata.ca
Отклонение нулевой гипотезы. Звучит как болезненное воспоминание из университетского курса статистики, но на самом деле это именно то, что мы хотим сделать здесь. Мы хотим исключить возможность того, что два образца взяты из одного и того же дистрибутива. Давайте посмотрим на очень высокий уровень, не математический, обзор некоторых доступных тестов. Если вы хотите получить хорошее представление о математике, лежащей в основе всех этих тестов, воспользуйтесь ссылкой на Википедию, представленной во всех разделах.
T-ТЕСТ СТЬЮДЕНТА
T-тест Стьюдента, вероятно, является наиболее известным способом отклонения нулевой гипотезы. Этот тест вычисляет P-значение выборки по сравнению с нормальной популяцией или по сравнению с другой выборкой.
Результат, P-значение, говорит вам, насколько вероятно, что эти выборки взяты из одного и того же распределения.
Полученное значение P можно сравнить со статистической значимостью порогового вызова (например, 0,05). Если значение P меньше, нулевые гипотезы можно отклонить.
Возникла проблема с Т-критерием Стьюдента, выборки должны быть нормальными (имеющими нормальное распределение). Для нас это проблема, потому что мы много работаем с распределениями Пуассона.
ТЕСТ КОЛМОГОРОВА-СМИРНОВА
Тест Колмогорова-Смирнова (тест КС) немного сложнее и позволяет обнаруживать закономерности, которые невозможно обнаружить с помощью Т-критерия Стьюдента.
Из Википедии:
«Статистика Колмогорова–Смирнова количественно определяет расстояние между эмпирической функцией распределения выборки и кумулятивной функции распределения эталонного распределения или между эмпирическими функциями распределения двух выборок».
Вот пример, который показывает разницу между T-тестом Стьюдента и тестом KS.
stackexchange.comПоскольку среднее значение выборки и стандартное отклонение очень похожи, T-критерий Стьюдента дает очень высокое значение p. KS Test может обнаружить дисперсию. В этом случае красное распределение имеет слегка биномиальное распределение, которое обнаруживает KS. Другими словами:
- Т-критерий Стьюдента говорит, что существует 79,3% шансов, что две выборки взяты из одного и того же распределения.
- Тест KS говорит, что существует 1,6% вероятность того, что два образца взяты из одного и того же дистрибутива.
ДРУГИЕ ТЕСТЫ
Существует множество других тестов и алгоритмов для выполнения такой работы. Тест Шапиро-Уилка и тест Андерсона-Дарлинга — два теста, которые считаются более мощными, чем тест КС. У этих двух тестов есть существенный недостаток: они не позволяют сравнивать две выборки, они всегда сравнивают выборку со стандартным распределением.
Редактировать: Мой коллега показал мне, что Андерсон-Дарлинг можно также использовать для двустороннего тестирования (сравнение образцов).
«Тест K–S для двух выборок — один из наиболее полезных и общих непараметрических методов сравнения двух выборок» — Википедия.
Для этого конкретного задания нам нужно было определить, какой пользователь использует конкретное устройство. Каждое устройство использовалось одним или несколькими разными пользователями, и нам нужно было придумать метод, чтобы определить, был ли это один пользователь или несколько. В случае с несколькими пользователями мы хотели определить, какое использование было выполнено тем или иным пользователем.
НАША СТРАТЕГИЯ
Мы решили использовать сочетание графовой сети и теста KS для выявления потенциальных кластеров. Идея этой демонстрации состоит в том, чтобы представить графовую сеть, в которой каждый узел (выборка) был связан с каждым другим узлом (выборкой).
Вершины или связь между этими узлами будут мне KS Test , другими словами, насколько близки эти два узла. Таким образом, два узла с низким P-значением KS будут близки, а два с высоким P-значением — далеко. Мы надеемся, что это создаст различимые кластеры.
НАБОР ДАННЫХ
Вот как выглядят наши данные:
Как видите, вся наша выборка выглядит как нормальное распределение с очень низким стандартным отклонением. Мы протестировали все 82 различных сеанса использования этого устройства.
Прямо из этой картинки видно, что есть разные узоры. Вся выборка не имеет одинакового распределения гистограмм. Это очень хорошее начало. После этого мы посмотрели на очевидный кластер распространения.
Для этого мы создали матрицу KS, которая состоит из двухстороннего теста KS для каждого распределения выборки по сравнению с любой другой выборкой. Быстрый просмотр тепловой карты матрицы KS не дает очевидных результатов (как вы можете видеть на рисунок справа от вас).
После такой иерархической кластеризации мы уже получили несколько лучших результатов. (Как вы можете видеть на следующем рисунке.)
На этих двух визуализациях дендрограмм мы можем видеть несколько потенциальных (3) кластеров. После просмотра эти кластеры снова оказались незначительными.
СЕТЕВОЙ ГРАФИК
После неудачной кластеризации дендрограммы мы попробовали предложенный графовый подход. Цель здесь, как объяснялось ранее, состоит в том, чтобы отобразить все возможные узлы и вершины. Длина вершин является тестовым значением KS. Пришлось убрать самореференцию (которая всегда была 0 (очевидно, вы совершенно похожи на себя)9.0005
Затем мы получили сетевой граф, в котором все были связаны со всеми остальными, что не особенно полезно.
Следующим шагом является сохранение только значимой ссылки (ниже определенного порога)
Как мы видим на этой картинке, мы получили очень впечатляющий результат. Мы можем ясно видеть два отдельных кластера и три выброса.
Это идеально подходит для нашей модели, большой кластер должен быть основным пользователем, а второй кластер может быть альтернативным пользователем.
После проверки правильности мы обнаружили, что кластер определил некоторую разницу между использованием кластеров 1 и 2, но не ту, которую мы искали. Другими словами, он не решил нашу проблему, но фактически нашел другой шаблон, который может быть полезен в другом контексте.
После этой работы мы пришли к выводу, что KS Test — это очень мощный способ автоматически различать образцы из разных дистрибутивов. Это не совсем решило нашу проблему, но показало, что его можно легко использовать в контексте науки о данных.
Сегодня я представил вам одну из задач, которые мы решили с помощью KS Test, но мы также использовали его для решения других задач. KS Test действительно становится хорошим тестом в нашем швейцарском ноже по науке о данных.
Следите за мной в моем блоге: coffeeanddata.ca
Подписанный тест Колмогорова-Смирнова: почему его не следует использовать
- Список журналов
- Гигасайенс
- т. 4; 2015
- PMC4342197
4; 2015Гигасайнс. 2015 г.; 4: 9.
Опубликовано онлайн 2015 Feb 27. DOI: 10.1186/S13742-015-0048-7
1, 2
АВТОР. выборочный критерий Колмогорова-Смирнова (КС) часто используется для определения того, имеют ли две случайные выборки одинаковое статистическое распределение. Популярная модификация теста KS заключается в использовании подписанной версии статистики KS, чтобы сделать вывод, являются ли значения одной выборки статистически большими, чем значения другой. Гипотезы, лежащие в основе теста KS, по своей сути несовместимы с этим подходом, и тест может давать ложноположительные результаты, подтверждаемые чрезвычайно низкими p-значениями. Это потенциально делает подписанный тест KS инструментом p-взлома, который следует пресекать, заменяя его стандартными тестами, такими как t-тест, и предоставляя доверительные интервалы вместо p-значений.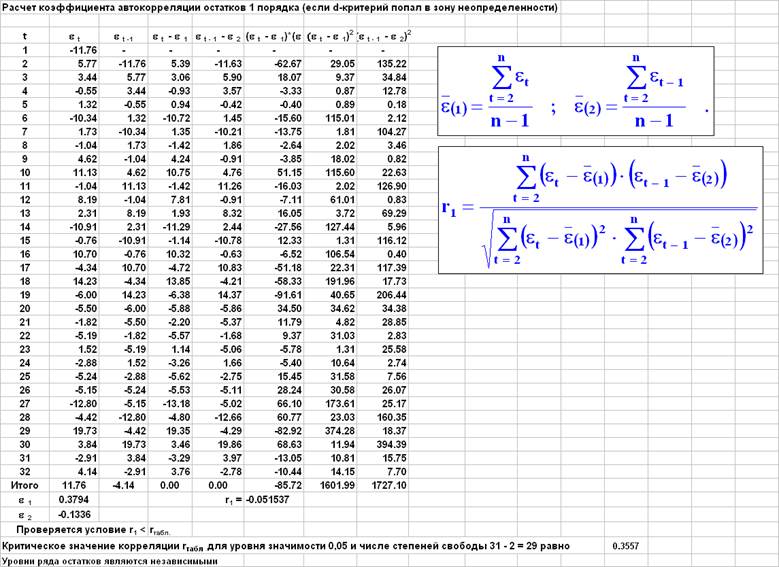
Ключевые слова: Критерий Колмогорова-Смирнова, Статистика, P-значение, P-взлом взяты из того же дистрибутива. Нулевая гипотеза теста KS заключается в том, что оба распределения идентичны, без каких-либо дополнительных предположений относительно их местоположения и формы, что делает тест KS широко применимым. Статистика теста KS представляет собой расстояние между двумя эмпирическими распределениями, рассчитанное как максимальная абсолютная разница между их кумулятивными кривыми. В нескольких исследованиях в области геномики (таких как [1-5]) было предложено использовать разность со знаком между кумулятивными кривыми. Согласно этой точке зрения, знак статистики указывает, какое из двух распределений имеет большее значение. Эта процедура не имеет официального названия; для ясности я буду называть его «подписанный тест КС» (тест сКС).
Аргумент в пользу использования теста sKS лучше всего представлен графически. На рисунке А показан пример двух распределений, сравниваемых с помощью теста sKS для двух случайных выборок бесконечно большого размера.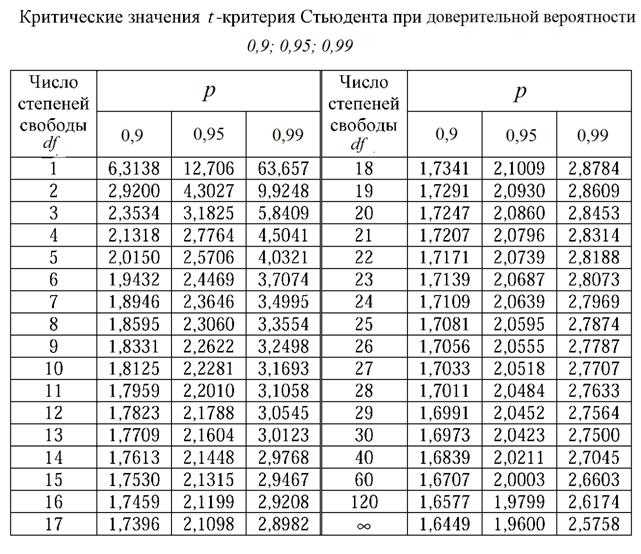
Красная стрелка указывает максимальную разницу между кумулятивными кривыми. Взяв за основу жирную кривую, стрелка указывает вниз, что означает, что знак статистики sKS отрицательный. Если бы тонкая кривая находилась слева от жирной кривой, тогда стрелка указывала бы в противоположном направлении, и статистика sKS была бы положительной. Следовательно, знак статистики sKS, по-видимому, указывает на выборку со статистически самыми высокими значениями.
Открыть в отдельном окне
Сравнение идеальных образцов по подписанному тесту КС. (A) Дистрибутивы расположены в разных местах. Линии представляют эмпирические кумулятивные распределения каждого образца (эталонный образец показан жирной линией). Статистика KS представляет собой максимальное расстояние по вертикали между кривыми и обозначена вертикальной красной линией. Поскольку эталонный образец находится слева, стрелка указывает вниз, поэтому статистика отрицательна. (Б) Распределения имеют разную дисперсию.
Однако этот аргумент делает неявное предположение, которое не обязательно выполняется. На рисунке А показаны две кривые одинаковой формы, а это значит, что они могут отличаться только своим расположением, т. е. сдвигом влево или вправо. Однако тест KS различает распределения, когда они различаются либо своим местоположением, либо формой.
На рисунке B показан еще один идеальный пример двух распределений, сравниваемых с помощью теста sKS, но на этот раз они отличаются только своей дисперсией. Есть две позиции, в которых кумулятивные кривые различаются больше всего, поэтому нарисованы две стрелки. Что еще более важно, одна стрелка указывает вверх, тогда как другая указывает вниз, так что знак статистики sKS не определен. В конечных выборках распределения никогда не бывают идеально симметричными, поэтому одна из этих стрелок будет самой длинной, и каждая будет иметь вероятность 0,5.
Этот идеальный пример никогда не встречается на практике. Распределения биологических образцов обычно различаются по форме и местоположению, поэтому ситуация, показанная на рисунке B, нереалистична. В реальном примере разница между формами распределения повысит значимость теста sKS, давая низкие значения p, даже если разница в местоположении незначительна или отсутствует.
Чтобы привести конкретный пример, на рисунке 4 (панель C) из Lara-Astiaso et al. [1] представляет собой тепловую карту, показывающую обогащение мотивов факторов транскрипции, рассчитанное с помощью теста sKS. Авторы сравнили баллы HOMER [6] для 205 мотивов в энхансерах, которые были активны в клеточной линии, и в энхансерах, которые были неактивны. Следуя указаниям авторов [1], я воспроизвел данные, на которых проводились тесты sKS, и выбрал два примера из 3485 (обратите внимание, что я использовал количество h4K27ac в качестве показателя активности, поскольку количество ATAC не было предоставлено).
Открыть в отдельном окне
Использование подписанного теста КС на реальных данных. Наилучшие оценки HOMER [6] для двух мотивов рассчитывают для энхансеров линии крови, и активные энхансеры сравнивают с неактивными энхансерами в двух типах клеток.
Если распределения имеют одинаковую форму (как на рисунке А), то критерий sKS имеет смысл, но все равно нет причин его использовать, поскольку он менее эффективен, чем t-критерий и даже критерий Уилкоксона-Манна–Уитни. тест. Другими словами, t-критерий и критерий Уилкоксона-Манна-Уитни имеют больше шансов обнаружить сдвиг, когда он существует (Гаррет Дженкинсон приводит анализ мощности в своем обзоре этой статьи, доступном в истории до публикации).
Эта проблема частично связана с эффектами нижнего и верхнего пределов, а это означает, что статистика теста sKS будет небольшой, если она находится в одном из хвостов распределения.
Таким образом, удивительно, что нетрадиционный подход, такой как тест sKS, может быть использован вместо установленного стандарта, такого как t-тест. Среди других причин это может быть частью ошибочной практики, называемой «p-hacking», которая заключается в проверке одной и той же статистической гипотезы различными способами до тех пор, пока не будет получено целевое значение p. Неправильное представление, лежащее в основе р-хакинга, заключается в том, что более высокая статистическая значимость влечет за собой большую биологическую реакцию (рисунок B является примером обратного). Замена теста сКС более стандартными вариантами была бы улучшением, но можно использовать и лучший метод.
При использовании статистического теста для оценки значимости ответа важно в заключение указать величину эффекта.
Доверительные интервалы — это естественная проверка, которая должна помочь исследователям отличить статистическую значимость от биологической значимости. Например, в примере, показанном на рисунке A, t-критерий дает p-значение ниже 2,2 × 10 -16 , что предполагает, что в В-клетках оценки Spi1 HOMER различаются между активными и неактивными энхансерами. Однако, давая (0,36, 0,53) как 95% доверительный интервал для этой разницы более информативен, потому что это конкретное утверждение о величине, которое позволяет читателю решить, является ли оно биологически релевантным.
В настоящее время, когда область геномики постепенно стандартизируется, важно обеспечить определенную статистическую строгость. SKS непоследовательна и менее мощна, чем t-критерий и критерий Уилкоксона-Манна-Уитни, поэтому нет причин использовать его, если нет тщательного обоснования. В более общем плане тестирование статистического ответа должно включать некоторую информацию о величине эффекта, например, в виде доверительного интервала.
Такая практика предоставила бы исследователям ценную информацию и препятствовала бы взлому.
Я благодарю Garrett Jenkinson и Desmond D Campbell за их полезные и конструктивные комментарии.
| KS test | Kolmogorov-Smirnov test |
| sKS | signed Kolmogorov-Smirnov test |
Competing interests
The author declares that he has no competing interests.
1. Лара-Астиасо Д., Вайнер А., Лоренцо-Вивас Э., Зарецкий И., Джайтин Д.А., Дэвид Э. и соавт. Динамика состояния хроматина при кроветворении. Наука. 2014;345:943–9. doi: 10.1126/science.1256271. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
2. Winter EE, Goodstadt L, Ponting CP. Повышенная скорость секреции белков, эволюция и заболевания среди тканеспецифических генов. Геном Res. 2004; 14:54–61. doi: 10.1101/gr.1924004. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
3.