Способы вращения и плоскопараллельного перемещения: Способ плоскопараллельного перемещения

Содержание

Способы вращения и плоскопараллельного переноса

Суть метода вращения состоит в том, что при неизменном положении основных плоскостей проекций изменяется положение заданных геометрических образов относительно них путем вращения объектов вокруг некоторой оси до тех пор, пока объекты не занимают частное положение в исходной системе плоскостей.

В качестве осей вращения удобнее принимать проецирующие прямые или прямые уровня, причем точки геометрических объектов вращаются в плоскостях, параллельных или перпендикулярных заданным плоскостям проекций. При повороте какого-либо геометрического образа радиус поворота у каждой его точки свой, а угол поворота для всех точек одинаков. На комплексном чертеже при использовании метода вращения принято показывать положение оси вращения.

При вращении вокруг горизонтально-проецирующей прямой i горизонтальная проекция А₁ точки А перемещается по окружности, а фронтальная (А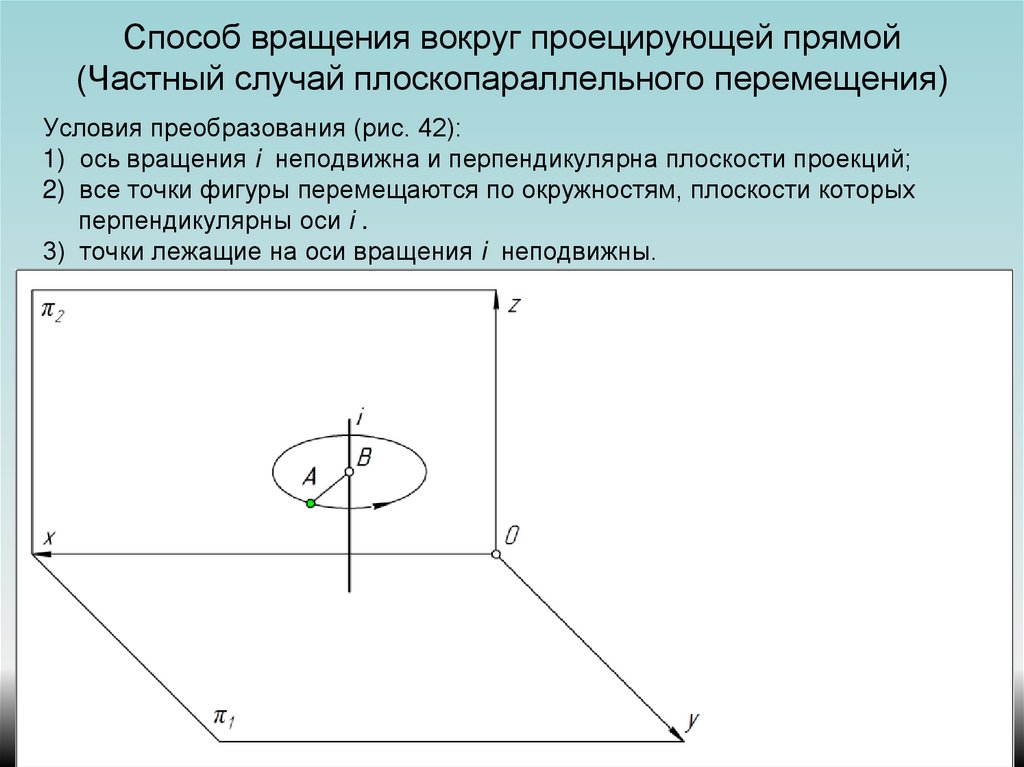

2) — по прямой, представляющей собой проекцию окружности той плоскости, в которой вращается точка А (рис.

38).

Отметим, что проекции точек на фронтальной плоскости проекций лежат на прямых, перпендикулярных исходным линиям связи. Используя это, можно не задаваться изображением оси вращения и не устанавливать величину его радиуса, на чем и основан метод плоскопараллельного перемещения как частный случай метода вращения. Рассмотрим способ плоскопараллельного переноса на примере решения задачи об определении натуральной величины треугольника ABC (рис. 39).

Решение. Заданный треугольник надо расположить так, чтобы горизонтальная проекция горизонтали плоскости треугольника оказалась перпендикулярной оси X. Поскольку горизонталь плоскости треугольника после такого преобразования станет фронтально-проецирующей прямой, а все горизонтали плоскости параллельны, плоскость треугольника ABC станет фронтально-проецирующей. Сущность следующего преобразования – сделать плоскость треугольника параллельной горизонтальной плоскости проекций.

Для этого линию А₂⁼В₂⁼ нужно расположить параллельно оси X. Тогда треугольник A₁⁼B₁⁼C₁⁼ станет представлять натуральную величину треугольника ABC.

Четыре исходные задачи преобразования чертежа

Подавляющее большинство метрических задач рассматривает прямые и плоскости. Если заранее известно, какие построения нужно выполнить, чтобы прямая (или плоскость) общего положения заняла частное, решение многих метрических задач значительно облегчается.

Частных положений, как у прямой, так и у плоскости — два (прямая (плоскость) уровня и проецирующая). Это означает, что существуют четыре исходные задачи преобразования чертежа, в результате которых: прямая общего положения становится прямой уровня; прямая общего положения становится проецирующей; плоскость общего положения переходит в проецирующую; плоскость общего положения становится плоскостью уровня.

Для решения подобных задач воспользуемся методом замены плоскостей проекций, хотя каждая из них может решаться как способом вращения, так и способом плоскопараллельного переноса.

Задача 1. Преобразовать прямую общего положения (АВ) в прямую уровня (рис. 40). Для решения задачи введем новую фронтальную плоскость проекций П₄, расположенную параллельно горизонтальной проекции A₁B₁ прямой (АВ). Т.к. при введении новой фронтальной плоскости проекций координаты Z точек А и В не изменяются, дальнейшие построения ясны из

чертежа, причем проекция А₄В₄ представляет собой натуральную величину отрезка [АВ]. Таким образом, решение рассмотренной задачи преобразования комплексного чертежа представляет собой еще один способ нахождения натуральной величины отрезка прямой общего положения.

Задача 2. Прямую общего положения необходимо преобразовать в положение проецирующей прямой (рис. 41).

Решение. Задача решается путем двух преобразований, поскольку нужно сделать две замены плоскостей проекций: первой прямая общего положения переводится в положение прямой уровня, а второй полученная прямая уровня переводится в проецирующую. Первое преобразование представляет собой решение рассмотренной выше задачи. Т.к. вводимая во втором преобразовании плоскость проекций (П

5) является новой горизонтальной плоскостью проекций, точка А₅ располагается на линии проекционной связи А₄А₅ на расстоянии, равном величине координаты Y точки А в системе плоскостей проекций П₁-П₄.

Овладев алгоритмом решения приведенной задачи, можно легко найти расстояния между параллельными и скрещивающимися прямыми, от точки до плоскости, а также натуральную величину двугранного угла (представив линию пересечения двух плоскостей в виде проецирующей прямой).

Задача 3. Перевести плоскость общего положения, заданную треугольником ABC, в проецирующую (рис. 42).

Решение. Плоскость, заданная любым способом, представима как множество соответствующих прямых уровня — либо ее горизонталей, либо фронталей. Поэтому преобразования нужно проводить так, чтобы прямые уровня плоскости спроецировались в точки. Тогда плоскость спроецируется в совокупность точек, расположенных на одной прямой. Следовательно, если в заданной плоскости общего положения провести прямые какого-либо уровня, то, расположив новую плоскость проекций перпендикулярно горизонтальной проекции горизонтали или фронтальной проекции фронтали плоскости, можно получить соответствующую проецирующую плоскость (рис. 42).

Такой подход позволяет находить расстояния от точки до прямой, между плоскостью и параллельной ей прямой, между параллельными плоскостями.

Задача 4. Плоскость общего положения, заданную треугольником ABC, перевести в положение плоскости уровня (рис.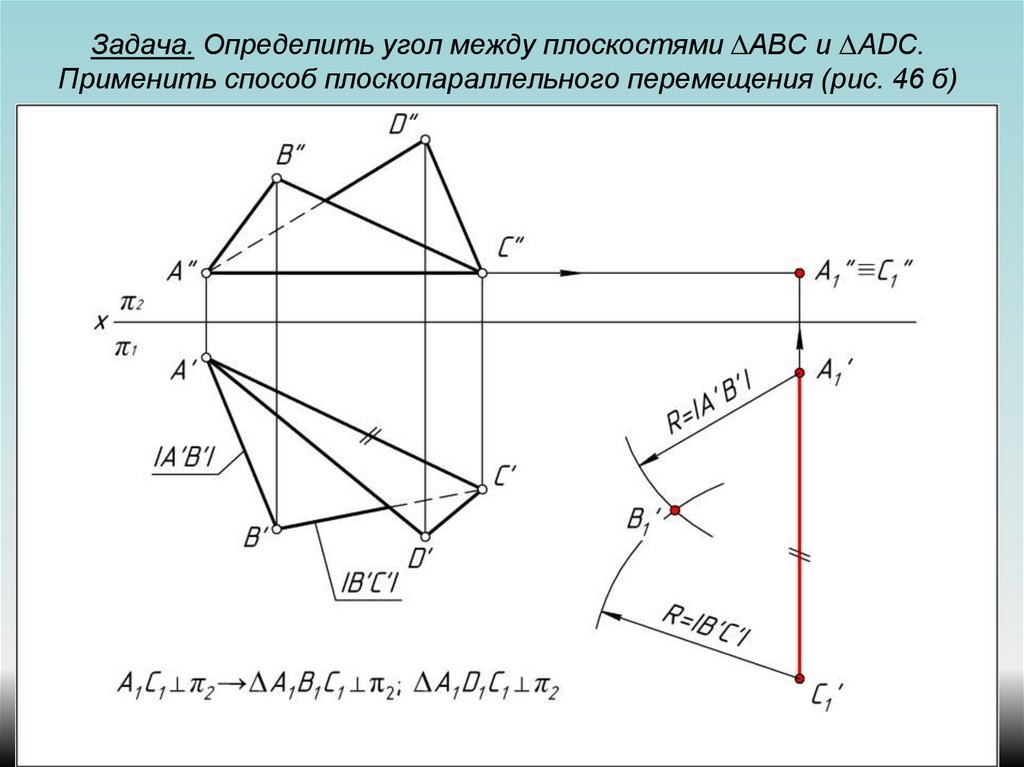 43).

Решение. Задача решается с помощью двух преобразований. Первым плоскость общего положения переводится в положение проецирующей (решение исходной задачи 3, изложенное выше), а вторым полученная проецирующая плоскость переводится в положение плоскости уровня (на рис. 42 это плоскость горизонтального уровня). Точки А

5, В₅ и C_sрасположены от оси X, разделяющей плоскости П₄ и П₅, на расстояниях, равных величинам координат Y для точек А, В и С в системе плоскостей проекций П₁-П₄.

Решение рассмотренной задачи позволяет находить натуральные величины плоских фигур (следовательно, сторон многоугольников и плоских углов). Решение этой же задачи методом плоскопараллельного переноса приведено на рис. 39.

Способ плоскопараллельного перемещения — Студопедия

При использовании способа вращения фигур иногда происходит наложение изображений.

Этого можно избежать, применяя способ плоскопараллельного перемещения.

Сущность этого способа заключается в том, что все точки геометрической фигуры перемещаются в плоскостях, параллельных одной из плоскостей проекций.

Следовательно, точки движутся в плоскостях уровня, и одна из проекций геометрической фигуры перемещается без изменения формы и размеров, а на другой проекции траектории движения точек параллельны оси x.

Рассмотрим преобразование отрезка АВ прямой общего положения в проецирующую прямую (рис. 5.10). Первоначально преобразуем прямую АВ во фронталь, переместив проекцию А₁В₁ без изменения размеров параллельно оси x (в произвольном месте). Точки прямой АВ перемещаются параллельно плоскости p₁. На фронтальной проекции траектории точек параллельны оси x. Новые фронтальные проекции определяем на пересечении линий связи от

А В с траекториями движения точек.

x). На горизонтальной проекции точки движутся параллельно оси x, и отрезок АВ преобразуется в горизонтально проецирующую прямую.

Пример 7. Определить расстояние от точки S до плоскости АВС (рис. 5.11) способом плоскопараллельного перемещения.

Решение. Для решения этой задачи необходимо преобразовать плоскость общего положения в проецирующую. Если одна из проекций плоскости будет преобразована в прямую линию, то можно опустить перпендикуляр из точки S и определить расстояние. Перемещаем плоскость АВС перпендикулярно плоскости p₂.

Рис. 5.11

Располагаем новую горизонтальную проекцию прямоугольника А В С без изменения формы и размера так, чтобы горизонталь h оказалась перпендикулярной плоскости p

2. На фронтальной проекции точки перемещаются параллельно оси x. Новая фронтальная проекция треугольника А В С преобразуется в прямую линию.

Опускаем перпендикуляр из перемещенной точки S на новую фронтальную проекцию треугольника.

Перемещение плоскопараллельное — Энциклопедия по машиностроению XXL

Параболоид соприкасающийся 82 Параллель поверхности вращения 67 Перемещение плоскопараллельное 33 Перспектива [c.316]

К числу законов, по которым перемещается в пространстве образующая линия, могут быть отнесены перемещение по некоторым другим неподвижным линиям, называемым направляющими, вращательное движение вокруг неподвижной оси, винтовое перемещение, плоскопараллельное перемещение и др. [c.140]

Профиль является элементом упругой лопатки. Вследствие ее деформации под действием силы Ру профиль перемещается и занимает некоторое равновесное состояние. Считаем согласно условию задачи, что перемещение плоскопараллельное, т. е. поворота профиля не происходит.

[c.278]

На рис.

243, а показана схема для исследования объекта 4, расположенного в пучках параллельных лучей между компонентами 2 и 6. Для изменения спектрального состава излучения источника 1 в схеме предусмотрен светофильтр 3. При выделении узкого спектрального интервала необходимо применение интерференционного светофильтра, который целесообразно устанавливать в параллельных пучках лучей. Приемник излучения 7 может быть размещен либо в плоскости изображения источника (или вблизи нее), либо в плоскости выходного зрачка оптической системы. Для изменения потока излучения в оптической схеме используют компенсатор 5—5, выполненный, например, в виде двух клиньев, образующих при их взаимном перемещении плоскопараллельную пластину переменной толщины. Это позволяет получить нейтральный свето- фильтр переменной плотности. [c.316]

Исследуя плоскопараллельное движение вязкой жидкости, Ньютон нашел опытным путем, что величина силы Т, необходимой для перемещения одного слоя жидкости параллельно другим, равна [c. 230]

Укажите последовательность приемов определения натуральной величины отсека плоскости способом плоскопараллельного перемещения. [c.103]

Согласно теореме, изложенной в разделе Плоскопараллельные перемещения , любое перемещение плоской фигуры в ее плоскости из начального положения в некоторое [c.324]

Поэтому при перемещении горизонтальная проекция треугольника свою форму не меняет. Следовательно, справедлива теорема при плоскопараллельном движении фигуры относи тельно горизонтальной плоскости проекций фронтальные проекции ее точек перемещаются по прямым, пер пендикулярным линиям связи, а гори зонтальная проекция фигуры остается конгруэнтной самой себе. [c.85]

Выполним плоскопараллельное перемещение прямой ЛВ относительно горизонтальной плоскости проекций. [c.86]

Таким образом, область применения всех рассмотренных преобразований одна и та же. Использование их в каждом конкретном случае зависит от дополнительных условий. Например, способ плоскопараллельного перемещения позволяет удобно располагать проекции фигуры на всем поле чертежа и избежать наложения проекций В способе замены плоскостей проекций проекция фигуры и ее образа на одной плоскости проекций тождественны (совпадают), что уменьшает число вспомогательных построений. В способе вращения вокруг проецирующей прямой также выбором положения оси вращения удается уменьшить число вспомогательных построений. [c.91]

Перемещение, при котором все точки системы движутся в параллельных плоскостях, называют плоскопараллельным. [c.49]

Мы назвали эти манипуляции плоскопараллельным перемещением объекта вместе с натуральной системой координат. [c.51]

В п.5.4, мы использовали плоскопараллельное перемещение и определили это понятие. [c.110]

При плоскопараллельном перемещении объекта [АВ] относительно горизонтальной плоскости проекций все его точки (А и В) движутся в горизонтальных плоскостях уровня (а и Р).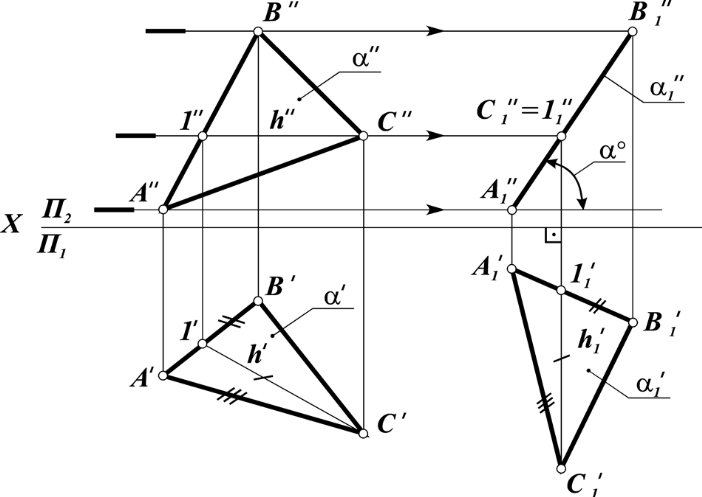 Это значит, что отрезок [АВ] может перемещаться в любое положение, но фронтальные проекции Аг и Вз его концов могут перемещаться только по проекциям аз и Рз горизонтальных плоскостей уровня (рис. 114, а), линии которых одновременно служат горизонтальными линиями связи. [c.110]

Рис.114. Условия плоскопараллельного перемещения объекта

При плоскопараллельном перемещении относительно фронтальной плоскости проекций все точки объекта движутся во фронтальных плоскостях (а и 5) уровня, при этом горизонтальные проекции точек (С1 и П]) перемещаются по прямым (ст1 и 81), перпендикулярным вертикальным линиям связи, а фронтальная проекция объекта (СаПа) может перемещаться произвольно, сохраняя свои размеры и форму. [c.111] Недостатком способа плоскопараллельного перемещения является необходимость построения свободно перемещаемой проекции в новом положении.

Зато этот способ позволяет более удобно размещать новые проекции. [c.113]

Для определения длины линии, например, длины трубопровода, проложенного в сложных условиях, или длины сварного шва в сложных изделиях, пользуются способом хорд и преобразованием чертежа способом плоскопараллельного перемещения. Дтя этого на одной проекции линию заменяют ломаной. На рис. 123 горизонтальная проекция разбита на участки с равными хордами. Точки через одну помечены цифрами. По линиям связи отмечаем фронтальные проекции точек. Проводим прямую параллельно оси проекций и на ней [c.120]

Проиллюстрируем применение способа плоскопараллельного перемещения на примере построения проекций куба по направлению одной из его диагоналей АВ (черт. 148). [c.65]

Первым плоскопараллельным перемещением относительно плоскости П, диагональ А В куба преобразуется в прямую уровня А В И U.2). Вершины А и В в этом случае движутся в горизонтальных плоскостях а и / (а 3/4, / э5).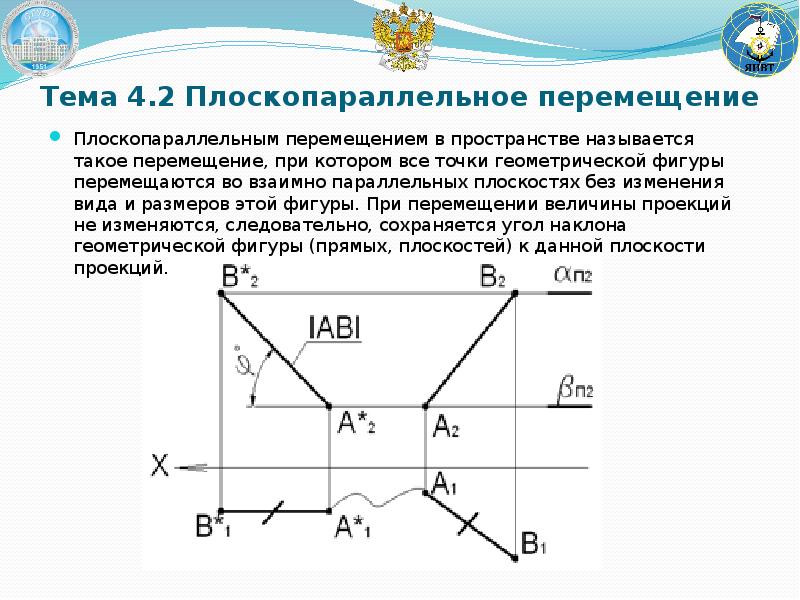 Проекция куба на П,, сохраняя свою форму, лишь меняет ориентировку, при которой горизонтальная проекция А В диаго- [c.65]

Итак, поставим одно из ребер пирамидальной поверхности, например ребро S3, в положение, перпендикулярное, скажем, к горизонтальной плоскости проекций. При выполнении этой части решения задачи способом плоскопараллельного перемещения требуется поставить ребро SB сначала в положение, параллельное фронтальной плоскости проекций (рис. 55), а затем вторым перемещением поставить это ребро в положение, перпендикулярное горизонтальной плоскости проекций (рис. 56). Горизонтальной проекцией пирамидальной поверхности будет треугольник аЬс. [c.63]

Построение этих углов осуществляем, приме)шв для этого способ плоскопараллельного перемещения. Эту часть решения задачи можно выполнить с меньшим количеством перемещений, чем это было сделано при решении предыдущих задач. [c.91]

Плоскопараллельным движением фигуры в пространстве называется такое ее перемещение, при котором все точки фигуры перемещаются в параллельных плоскостях.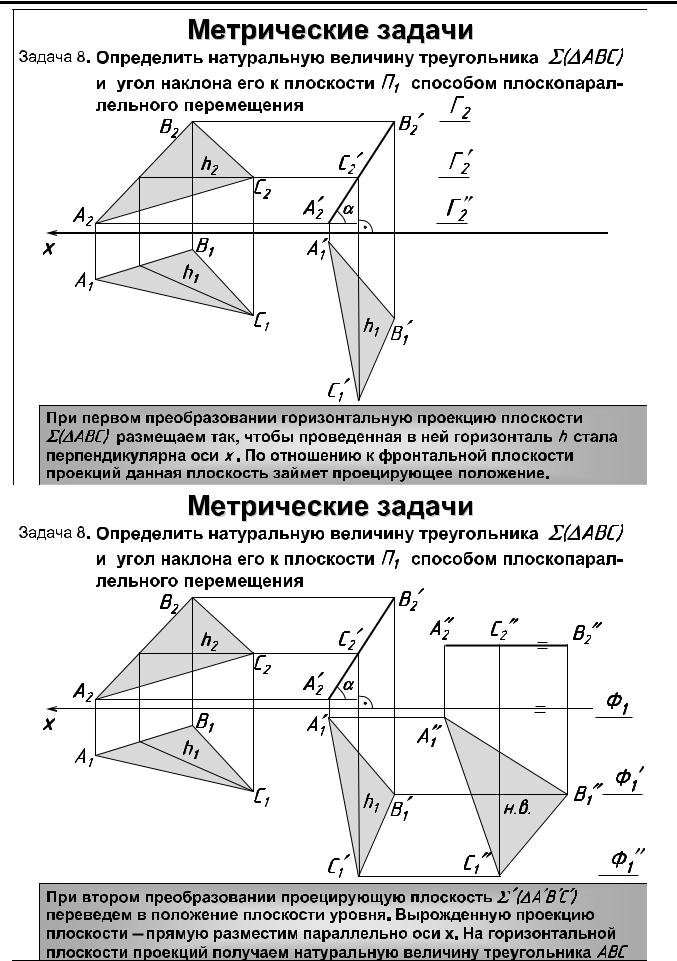 [c.57]

Справедлива аналогичная теорема о плоскопараллельном перемещении относительно 112. при плоскопараллельном движении фигуры относительно фронтальной плоскости проекций горизонтальные проекции ее точек перемещаются по прямым, перпендикулярным линиям связи, а фронтальная проекция фигуры остается конгруэнтной самой себе. [c.57]

Первый путь лежит в основе способа плоскопараллельного перемещения второй — составляет теоретическую базу способа замены плоскостей проекций. Рассмотрим каждый из этих способов в отдельности. [c.48]

Изменение взаимного положения проецируемой фигуры и плоскостей проекций способом плоскопараллельного перемещения осуществляется путем перемещения геометрической фигуры в новое положение так, чтобы траектории перемещения ее точек находились в параллельных плоскостях. [c.48]

Плоскопараллельное перемещение можно рассматривать как вращение вокруг не-выявленных проецирующих прямых. Здесь псе точки геометрического обра М переме-нцпогся во взаимно параллс]п.ных плоское [ях. [c.86]

Плоскопараллельное перемещение имеег перед вращением некоторое преимущесгво оно позволяет более свободно располагать проекции геометрических форм, исключать оси вращения и вспомогательные дуги однако чертеж занимает больщую площадь. [c.87]

В отличие от споеоба замены плоскостей проекций, которым данная фигура преобразуется в фигуру частного положения путем изменения системы отнесения,способом плоскопараллельного движения фигура приводится в частное положение в результате ее перемещения в пространстве относительно неподвижной системы отнесения, В теории преобразований показывается, что движение / фигуры в пространстве можно представить как композицию двух алоскопараллсльных [c.85]

Справедлива аналогичная теорема о плоскопараллельном перемещении относительно П2 при плоскопара.т лельном движении фигуры относи тельно фронтальной плоскости проек ций горизонтальные проекции ее то чек перемещаются по прямым, пер пендикулярным линиям связи, а фронтальная проекция фигуры оста ется конгруэнтной самой себе. [c.85]

На рис. 117, а изображена горизонтально проецирующая прямая /(г ь h) X П1 и горизонталь [AO](AiO , А2О2) X i. Если точку А вращать вокруг прямой то она будет совершать плоскопараллельное перемещение по окружности радиуса R = АО = А 0 с центром в точке О, плоскость которой перпен- [c.113]

Из приведенного определения следует, что вращательное движение фигуры является частным случаем плоскопараллельного, а способ врапгения — частный случай способа плоскопараллельного перемещения. [c.64]

Для этого необходимо, применив один из способов преобразования комплексного чертежа, например способ плоскопараллельного перемещения, поставить призматическую поверхность в положение, при котором ребра ее станут перпендикулярными к горизонтальной плоскости проекций. При выполнении этих построений горизонтальная проекция призматической поверхности изобразится в виде треугольника abid, фронтальные проекции ребер призматической поверхности изобразятся в виде прямых, перпендикулярных оси х.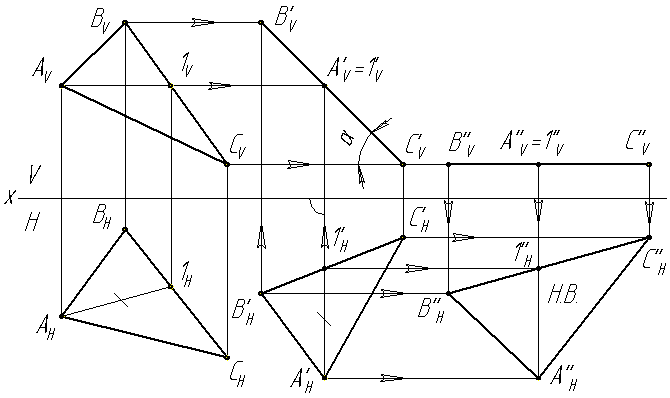 [c.71]

В противоположность способу замены плоскостей проекций, где данная фигура приводилась в частное положение путем изменения системы отнесения, в способе тоскопараллельного движения фигура приводится в частное положение путем ее перемещения в пространстве относительно неподвижной системы отнесения. В теории преобразований показывается, что движение / фигуры в пространстве можно гфед-ставить как композицию двух плоскопараллельных движений /, / относительно взаимно перпендикулярных плоскостей. [c.57]

Параллельный перенос, вращение плоскости и подобные треугольники

Содержание этой страницы:

— урок «Параллельный перенос» представлен на примере решения задач 145 — 148;
— в рабочих листах под номерами 149 — 154 данного учебного пособия по математике учитывается поворот плоскости вокруг точки на угол;
— пересмотр геометрии 9 степени в решениях приведен в примерах 155 — 173:

— углы треугольника,

— площадь треугольника через катеты и гипотенузу,

— углы треугольника расчет радиуса описанной окружности,

— сторона ромба,

— аналогичные треугольники.

Параллельный перенос

Определение:

Параллельный перенос на вектор — это отображение плоскости на себя, если выполняются следующие условия: каждая точка M отображается в точку M ₁, так что два вектора равны.

***

Задача 145.

Дано:

вектор

сегмент AB

Сборка:

AB → A ₁ B ₁

A → A ₁: =

B → B ₁: =

***

Теорема :

При параллельном переносе в вектор расстояние между точками сохраняется, т.е.е. параллельная передача — это движение .

Дано:

f — параллельный перенос к вектору

MM ₁

NN ₁

Докажите:

f — движение (MN = M ₁ N ₁)

Доказательство:

Точка M перемещается в точку M ₁ с условием равенства двух векторов: MM ₁: = MM ₁

Точка N перемещается движением к точке N ₁ с условием равенства двух векторов: NN ₁: = NN ₁

Следовательно, полученные отрезки параллельны MM ₁ || NN ₁ и построенные отрезки равны MM ₁ = NN ₁

Следовательно, четырехугольник MM ₁ N ₁ N является параллелограммом.

Следовательно, MN = M ₁ N ₁, тогда f — движение.

***

Задача 146.

треугольник ΔABC

AA ₁:

BB ₁:

CC ₁:

треугольник ΔABC

AA ₁: =

BB ₁:

***

Задача 147.

Дано:

треугольник ΔABC

AB = BC

точка D лежит на AC: DAC

точка C лежит на AD:

CAD

BC B ₁ D

a) Построить : B ₁ D

b) Докажите: ABB ₁ D — равнобедренная трапеция

Построение:

1) проведите линию a из точки B параллельно вектору: a ||

2) точка B перемещается движением в точку B ₁

3) проведите линию B ₁ D параллельно отрезку BC:

B ₁ D || BC

***

Доказательство:

Рассмотрим четырехугольник BB ₁ DC.

С баз ББ ₁ || CD и боковые стороны BC || BD параллельны, видим, что BB ₁ DC — параллелограмм (по определению)

По свойству параллелограмма:

основания BB ₁ = CD и боковые стороны BC = BD равны, но AB = BC, тогда AB = B ₁ D

Поскольку BB ₁ || AD параллельны, а AB B ₁ D не параллельны, поэтому ABB ₁ D — трапеция (по определению).

Поскольку AB = B ₁ D, мы видим, что ABB ₁ D — трапеция (по определению).

***

Задача 148.

Дано:

треугольник ΔABC

EFPQ — это трапеция

круг (O; R)

вектор

Build

круг (O; R) круг (O ₁; R ₁)

ΔABC ΔA ₁ B ₁ C ₁

EFPQ

E ₁ F ₁ P ₁ Q ₁

Конструкция:

как показано на картинке.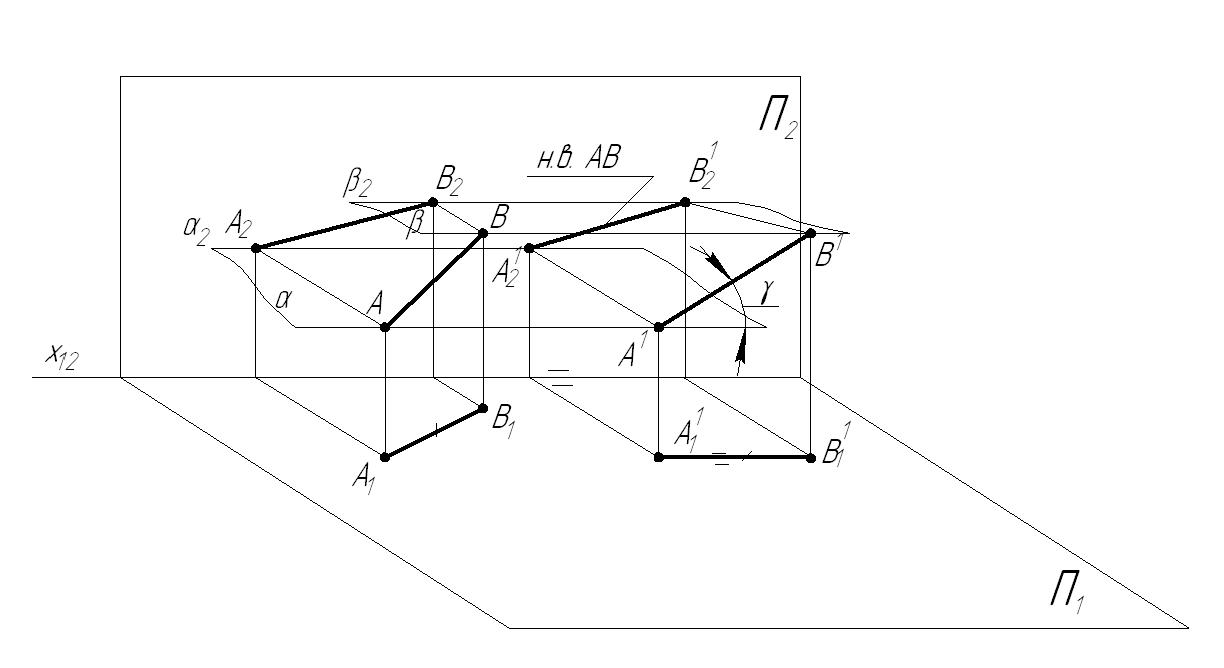

***

К началу

Поворот плоскости вокруг точки на угол

Определение:

Поворот плоскости вокруг точки O на угол α is отображение плоскости на себя так, что каждая точка M отображается на точку M ₁, так что угол поворота

MOM ₁ = α и OM ₁ = OM.

O — центр вращения

α — угол поворота

***

Задача 149.

Дано:

α = 75 ° (против часовой стрелки)

O — центр вращения

AB — сегмент

Сборка:

A ₁ B ₁

Строительство :

1) AA ₁;

AOA ₁ = 75 °

OA = OA ₁

2) BB ₁;

BOB ₁ = 75 °

OB = OB ₁

***

Теорема:

Вращение — это движение.

Дано:

f — поворот

α — угол поворота (против часовой стрелки)

точка O — центр вращения

MN — сегмент

Доказательство:

f — движение, MN = M ₁ N ₁

Доказательство:

Пусть M → M ₁; N → N ₁

Тогда треугольники равны ΔOMN = ΔOM ₁ N ₁ по двум сторонам и углу между ними:

OM = OM ₁

ON = ON ₁

MON = M ₁ ON ₁

Тогда MN = M ₁ N ₁, следовательно, f — движение..

***

Задача 150.

Дано:

точка O — центр вращения

α = 180 °

AB — сегмент

AB → A ₁ B ₁

Сборка:

A ₁ B ₁

Строительство:

1) AA ₁;

AOA ₁ = 180 °

OA = OA ₁

2) BB ₁;

BOB ₁ = 180 °

OB = OB ₁

***

Задача 151.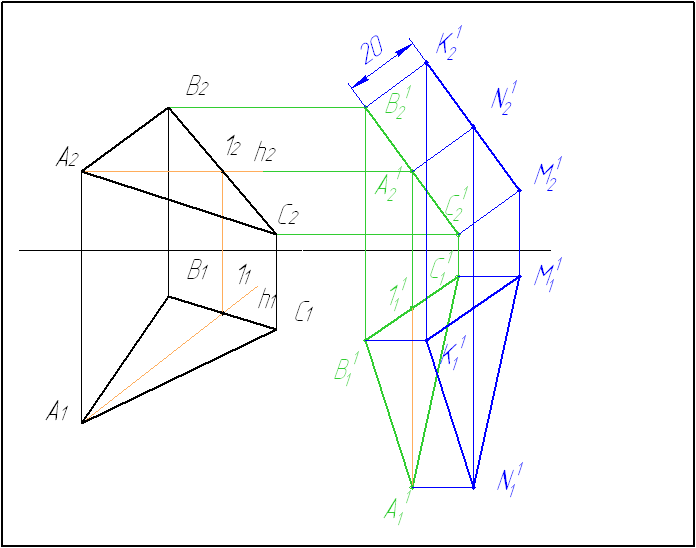

Дано:

треугольник ΔABC

точка A — центр вращения

α = 160 ° (против часовой стрелки)

ΔABC → ΔAB ₁ C ₁

Построить: ΔAB ₁ C ₁

Конструкция:

1) BB ₁;

BAB ₁ = 160 °

BA = B ₁ A

2) CC ₁;

CAC ₁ = 160 °

CA = AC ₁

***

Проблема 152.

Дано:

точка O — центр вращения

α = 120 °

AB — сегмент

AB → A ₁ B ₁

Сборка:

A ₁ B ₁

Строительство:

1) AA ₁;

AOA ₁ = 120 °

OA = OA ₁

2) BB ₁;

BOB ₁ = 120 °

OB = OB ₁

***

Задача 153.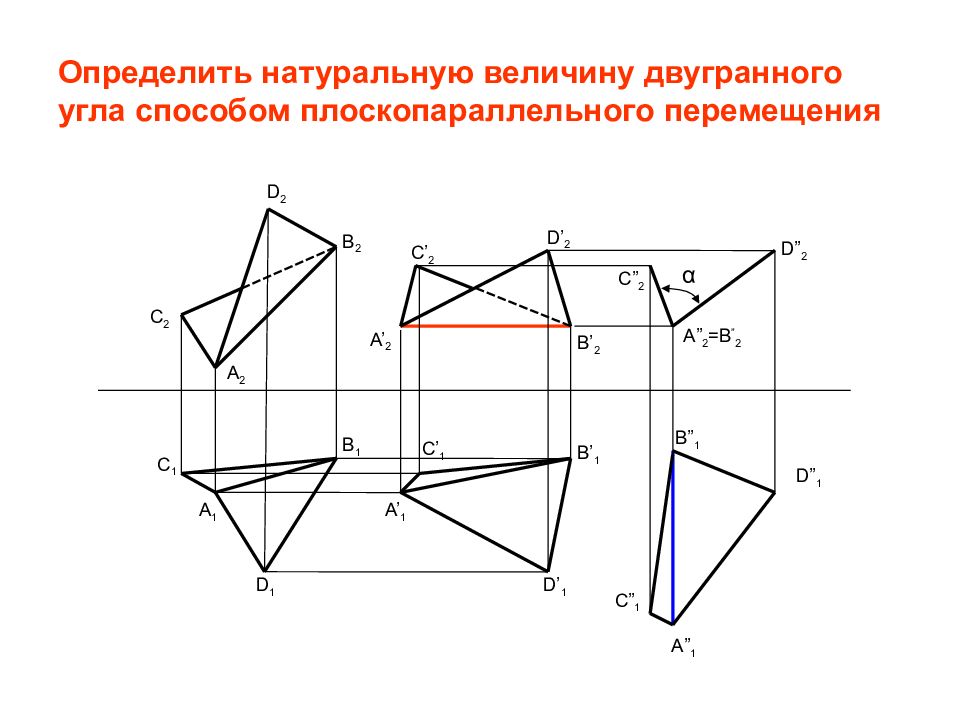

Дано:

точка C — центр окружности (C; R)

точка O — центр вращения

угол поворота α = 60 ° (против часовой стрелки)

a) точка C и точка O не совпадают

б) точка C и точка O совпадают

Строение:

круг (C ₁; R)

Строительство:

1) рисуем луч CO

2) CC ₁;

COC ₁ = 60 °

CO = C ₁ O

Поскольку точка O как центр вращения и точка C как центр окружности совпадают, мы видим, что круги (C; R) и (C ₁; R) также будут совпадать.

***

Задача 154.

Дано:

Δ ABC — равнобедренный равносторонний треугольник

D — точка пересечения биссектрис

D — центр вращения

угол поворота α = 120 °

Доказательство:

ΔABCΔABC

Доказательство:

Поскольку Δ ABC — правильный треугольник, мы видим, что все его углы равны 60 °.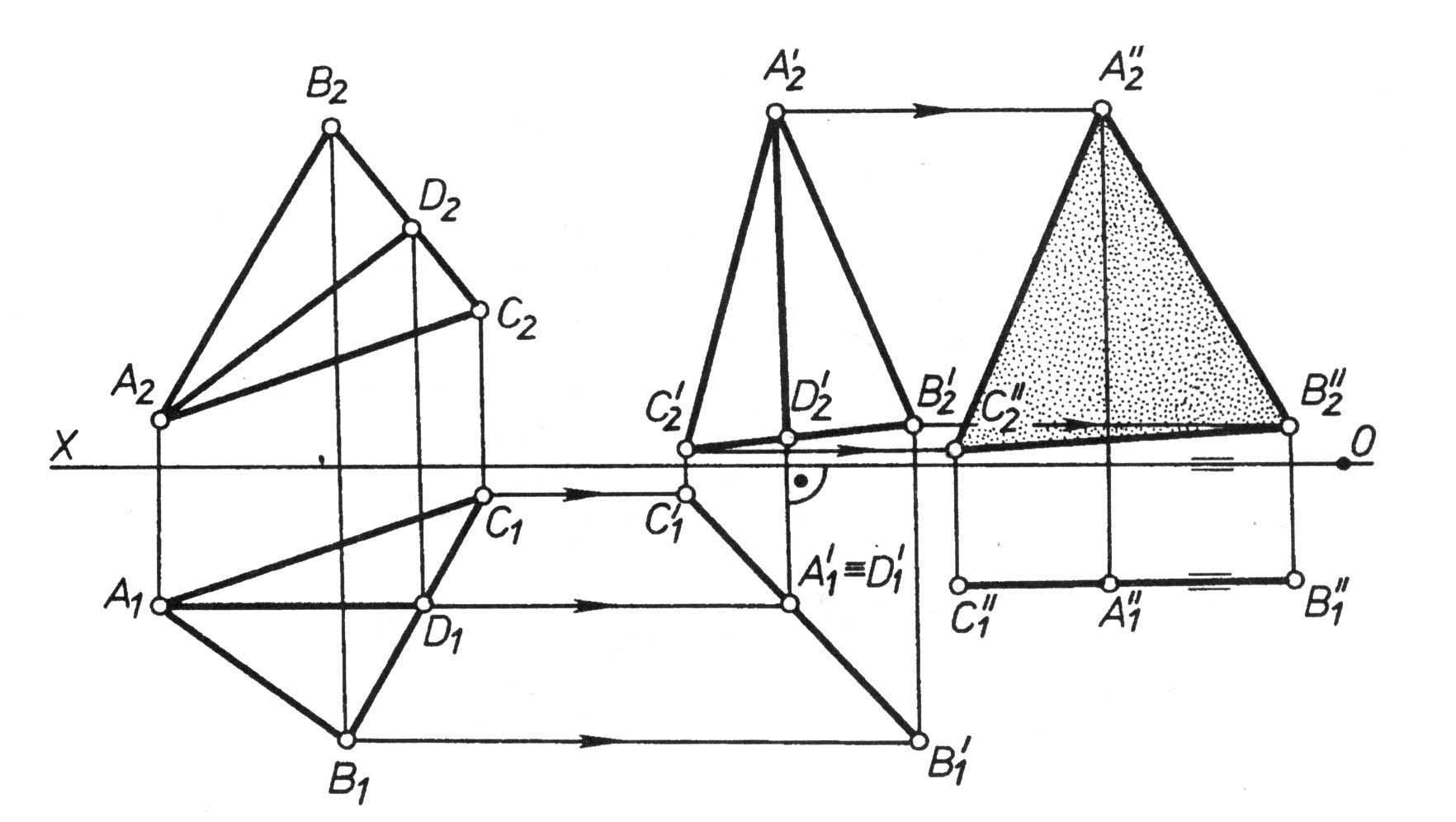

Поскольку точка D является центром описанной и вписанной окружности, мы видим, что

AD = BD = DC = R.

Δ ABD = Δ BDC = Δ DAC (по трем сторонам).

Следовательно,

ADB = BDC = CDA

Следовательно,

То есть. ΔABC → ΔBCA.

Итак, Δ ABC отображается в себя.

***

Пересмотр.

Задача 155.

Дано:

треугольник ΔABC

отношение углов

ABC: BCA: CAB = 3: 7: 8

Найти: наибольший угол треугольника

Решение:

Пусть x будет коэффициентом пропорциональности.Зная, что сумма углов в треугольнике равна 180 °, составляем и решаем уравнение:

3x + 7x + 8x = 180

18x = 180

x = 10

Наибольший угол равен

CAB = 8 • 10 = 80 °

Ответ: 80 °.

***

Задача 156.

Дано:

треугольник ΔABC является равнобедренным треугольником,

один угол больше другого:

ABC> BAC на 60 °

Найти: угол в основании треугольника

Решение:

Пусть x ° будет углом в основании треугольника.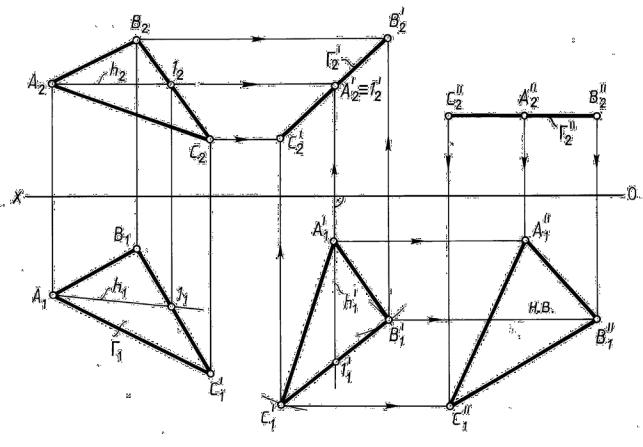 Зная, что сумма углов в треугольнике равна 180 °, составим и решим уравнение:

(x + 60 °) + x + x = 180 °

3x = 180-60

3x = 120

x = 40

Следовательно,

ВАС = 40 °.

Ответ: 40 °.

***

Задача 157.

Дано:

треугольник ΔABC правый

c = 26 см — гипотенуза

отношение катетов:

a: b = 5: 12

Найти: большую ногу b

Решение:

Пусть x будет коэффициентом пропорциональности.По теореме Пифагора составляем и решаем уравнение:

(5x) ² + (12x) ² = 26 ²

25x ² + 144x ² = 676

169x = 676

x ² = 4

x = 2

b = 12 • 2 = 24 (см)

Ответ: 24 см.

***

Задача 158.

Дано:

треугольник ΔABC,

C = 90 °

b = 5 — катет

c = 13 — гипотенуза

Найти: площадь треугольника S _Δ _ABC =?

Решение:

По теореме Пифагора получаем:

a ==== 12

Тогда площадь треугольника

S _Δ _ABC = • ab = =

= 30 (квадратных единиц)

Ответ: 30 квадратных единиц.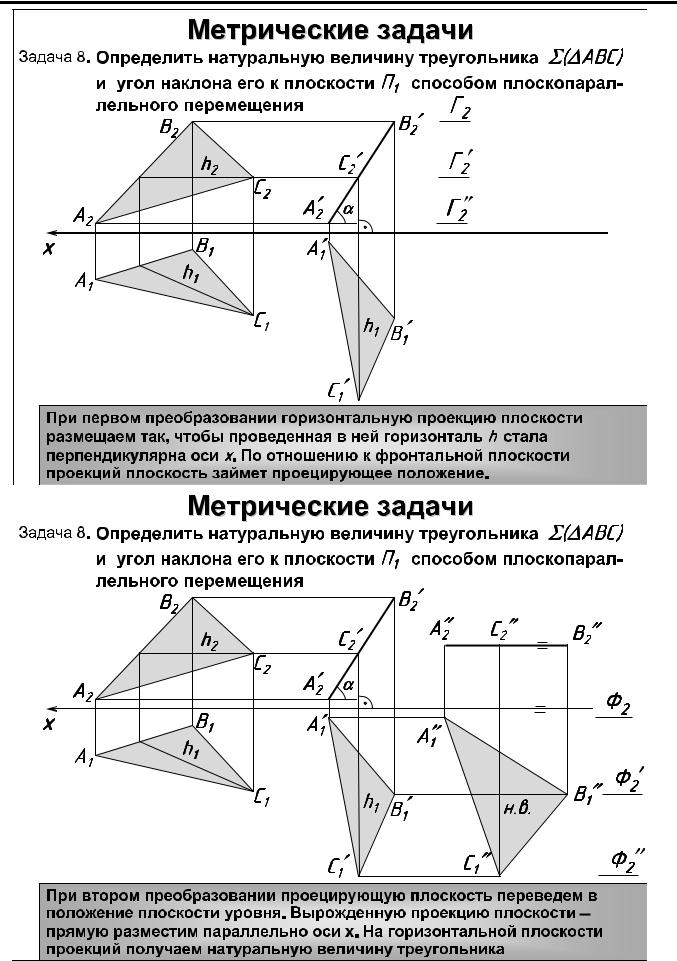

***

Задача 159.

Дано:

треугольник ΔABC равнобедренный,

C = 90 °

c = 4 — гипотенуза

треугольника S _Δ _ABC =?

Решение:

S _Δ _ABC = • ab

Поскольку Δ ABC равнобедренная, мы видим, что углы в основании 45 ° и ног равны a = b .

По теореме Пифагора получаем:

c ² = a ² + b ² = a ² + a ^{9024 a = 2903 2}

Тогда (4) ² = 2 a ²

a ² = 16

a = 4 (единица)

Тогда площадь треугольника

S _Δ _ABC = • ab = =

= 8 (квадратных единиц)

Ответ: 8 квадратных единиц.

***

Задача 160.

Дано:

треугольник ΔABC,

A = 90 °

AH — медиана

a = 6

b b

Найти: радиус описанной окружности R =?

Решение:

Поскольку AH — это медиана, мы видим, что CH = c

По теореме Пифагора получаем:

c ² = a ² + 90 b

c ² = 36 + 64

c = 10 (единицы)

Тогда CH = c = = 5 (единицы)

Точка H — центр описанной окружности

AH = BH = CH = R

Поскольку R = AH, мы видим, что R = AH = CH = 5 единиц.

Ответ: 5 шт.

***

Задача 161.

Дано:

треугольник ΔABC,

C = 90 °

отношение острых углов

ABC:

CAB = 1: 2
AC = 4
Найти: радиус описанной окружности R =?
Решение:
Пусть x будет коэффициентом пропорциональности. Зная, что сумма углов в треугольнике равна 180 °, составим и решим уравнение:
x + 2x + 90 = 180
3x = 90
x = 30
Тогда CAB = 30 °,
ABC = 2 • 30 ° = 60 °
Следовательно, BC = AB
По теореме Пифагора получаем:
AC ² + BC ² = AB ²
AC ² + = AB ²
AC ² = AB ²
AB ² 9 = 9 = 9246 единиц )
R = AD = BD = 8: 2 = 4 (шт.)
Ответ: 4 шт.
***
Задача 162.
Дано:
треугольник ΔABC,
C = 90 °
BC = 3
радиус описанной окружности
R = 2,5
Найти: AC =?
Решение:
R = AH = BH = 2,5
Тогда AB = 2,5 • 2 = 5
По теореме Пифагора получаем:
AC = = = 4 (единицы)
Ответ: 4.
***
Задача 163.
Дано:
треугольник ΔABC,
C = 90 °
tg A = 0,6
BC = 3
Найти: AC =?
Решение:
tgA =
0,6 =; AC = 3 • = 5 (единицы)
Ответ: 5.
***
Задача 164.
Дано:
треугольник ΔABC,
A = 90 °
AH = AC
Найти: ABC =?
Решение:
Поскольку AH = AC, мы видим, что Δ AHC равнобедренная.
Точка H — это радиус вписанной окружности, поэтому AH = CH, но AH = AC, следовательно, AH = CH = AC.
Тогда Δ AHC равносторонняя.
Следовательно, HAC = AHC = HCA = 60 °.
ABC = 180 ° — (90 ° + 60 °) = 30 °.
Ответ: 30 °.
***
Задача 165.
Дано:
треугольник Δ ABC правильный, равносторонний,
площадь треугольника
S _Δ _ABC = квадратные единицы
Найти: длина биссектрисы BH =?
Решение:
Поскольку Δ ABC — регулярно, мы видим, что все углы равны 60 °.
Считаем Δ ABC равнобедренным, где
BAC = BCA = 60 °.
Тогда BH — это медиана, высота.
Следовательно, сегменты перпендикулярны: BH
AC.
Рассмотрим треугольники Δ ABH и Δ BHC.
AB = BC, по данной гипотезе.
AH = CH, BH — медиана.
BH — общая сторона.
Следовательно, треугольники равны Δ ABH = Δ BHC.
Площадь треугольника S _Δ _ABC = 2S _Δ _ABH
I.е. S _Δ _ABH =
S _Δ _ABC = • = (квадратные единицы)
S _Δ _ABH = AH • BH
Рассмотрим треугольник Δ ABH.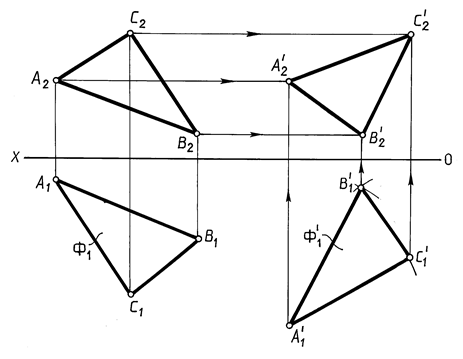
Поскольку BH — биссектриса, мы видим, что угол ABH = 30 °, поэтому
AH =
AB
S _ΔABH = AB • BH =
AB • BH = (*)
По теореме Пифагора получаем:
AB ² = AH ² + BH ²
AB ² = AB ² + BH ²
BH ^{2 900 = AB}
AB (**)
Используя результат (**) в уравнении (*), мы получаем
AB •
AB =
AB ² =
AB =
Тогда AB • BH = • BH =
BH = 1 (единица)
Ответ: BH = 1 единица
***
Задача 166.
Дано:
треугольник Δ ABC правильный, равносторонний,
радиус описанной окружности
R =
Найти: площадь треугольника
S _Δ _ABC =?
Решение:
Рассмотрим Δ ABO (AO = BO = R) Δ ABO — равнобедренный треугольник.
Проведем высоту OH от вершины O до AB.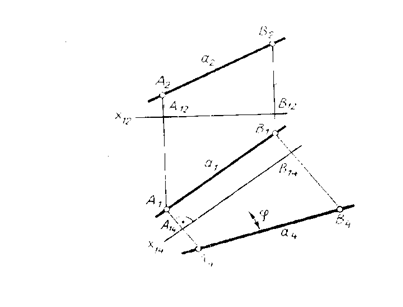
Рассмотрим Δ AOH, где AHO = 90 °.
Поскольку HAO = 30 °, мы видим, что OH =
AO OH = R
OH = • =
По теореме Пифагора получаем:
OH ² + AH ² = OA ²
OH ² + AH ² = R ²
+ AH ² = () ² + AH ² =
=
AH ² = — =
=
Тогда площадь треугольника
S _Δ _AOH =
AH • OH = •• = =
Следовательно, S _Δ _ABO = 2 • S _Δ _AOH = 2 • = ( квадратов)
Тогда площадь треугольника
S _Δ _ABC = 3 • S _Δ _ABO = 3 • = = 2 = 2.25 (квадратных единиц)
Ответ: 2,25 квадратных единиц
***
Задача 167.
Дано:
площадь ромба равна S _ABCD = 384
отношение диагоналей ромб:
AC: BD = 3: 4
Находим: сторона ромба AB =?
Решение:
площадь ромба
S _ABCD = AC • BD
Пусть x будет коэффициентом пропорциональности.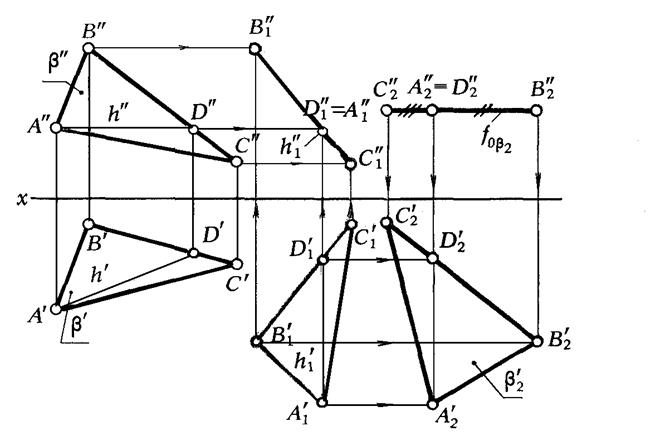 Тогда
S _ABCD = 3x • 4x
384 = 6x ²
x ² = 64
x = 8
Следовательно, диагональ BD = 4x = 4 • 8 = 32
AC = 3x = 3 • 8 = 24
AC = 2AO
BD = 2BO
Следовательно, половина диагонали AO = AC = • 24 = 12
BO =
BD = • 32 = 16
По теореме Пифагора мы получаем:
AO ² + BO ² = AB ²
Сторона ромба равна AB = == 20
Ответ: 20.
***
Задача 168.
Дано:
треугольник Δ ABD равнобедренный,
основание AD = 16
сторона AB = 10
Найти: площадь треугольник
S _Δ _ABD =?
Решение:
площадь треугольника
S _Δ _ABD = AD • BH
Проведем высоту BH к основанию AD.
По свойству равнобедренного треугольника:
BH — это медиана, биссектриса, высота.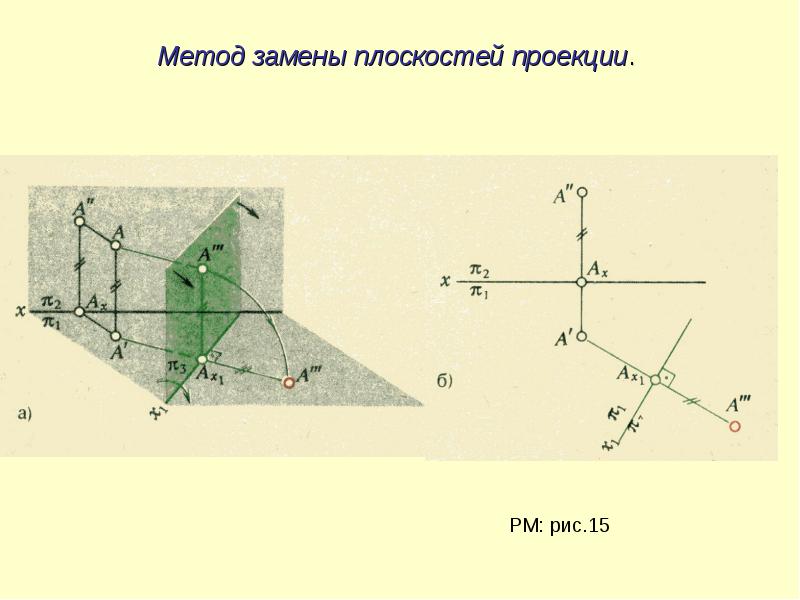
Поскольку BH — это медиана, мы видим, что AH = DH = 16: 2 = 8 (единица измерения)
Рассмотрим треугольник Δ ABH, где угол
AHB = 90 °.
По теореме Пифагора получаем:
AB ² = AH ² + BH ²
BH = = == 6 (единица)
Тогда площадь треугольника
S _Δ _ABD = AD • BH = • 16 • 6 = 48 (квадратных единиц)
Ответ: площадь треугольника S _Δ _ABD = 48 квадратных единиц
***
Задача 169 .
Дано:
треугольник Δ ABC равнобедренный,
высота BH = 15
основание AC больше высоты BH на 15: AC> BH на 15
Найти: основание AC = ?
Решение:
Поскольку треугольник Δ ABC равнобедренный, мы видим, что BH — это высота, медиана и биссектриса.
Следовательно, AH = CH.
Тогда AC = AH + CH = AH + AH = 2 AH
Рассмотрим Δ ABH — прямоугольный треугольник.
Пусть AC = ( x ) единица AH = () единица
Тогда AB = ( x -15) единица (по заданному условию).
По теореме Пифагора решаем уравнение:
(x — 15) ² = () ² + 15 ² x ² — 30x + 225 = + 225
4 (x ² — 30x) = x ²
4x ² — 120x = x ²
3x ² — 120x = 0 | : x
3x = 120
x = 40
Итак, 40 единиц — это длина основания.
Ответ: AC = 40 единиц
***
Вернуться к началу
Подобные треугольники
Задача 170.
Дано:
треугольник Δ ABC, два угла
A = 54 °
B = 18 °
CH — биссектриса угла C
Доказательство: подобие треугольников
Δ BHC Δ ABC
Доказательство:
C = 180 ° — (A + B)
C = 180 ° — (54 ° + 18 °) = 108 °
Поскольку CH является биссектрисой угла C, мы видим, что
углы равны
BCH = HCA = 108 °: 2 = 54 °
Рассмотрим Δ BHC
HBC = B = 18 °
BCH = A = 54 °
Тогда
CHB = C = 108 °
Следовательно, треугольники подобны Δ BHC Δ ABC.
***
Задача 171.
Дано:
ABCD — трапеция,
верхнее основание BC = 4 см
нижнее основание AD = 10 см
диагональ BD = 8 см
Найдите:
часть диагонали BO =?
отношение периметров треугольников
=?
Решение:
Углы равны CBO = ODA, как и поперечные углы на параллельных прямых BC и AD и секущей BD.
Углы равны BCO = OAD, как и поперечные углы на параллельных прямых BC и AD и секущей AC.
Тогда треугольники подобны Δ BCO Δ AOD.
= = = =
=. Тогда 4AO = 10BO
BO = AO
= = 0,4 = k
Пусть BO = x, AO = 8 — x. Тогда 10x = 4 • (8 — x)
10x = 32 — 4x
14x = 32
x = 2 (см)
Следовательно, BO = 2 см.
= k = 0,4
Ответ: БО = 2см, = 0.4.
***
Задача 172.
Дано:
аналогичные треугольники
ΔABC ΔA ₁ B ₁ C ₁,
AB = 12 дм,
BC = 16 дм,
AC = 20 дм,
периметр треугольника:
P (ΔA ₁ B ₁ C ₁) = 60 дм
Найти:
сторон треугольника ΔA ₁ B ₁ C ₁
A ₁ B ₁, A ₁ C ₁, B ₁ C ₁ =?
Решение:
периметр треугольника
P (ΔABC) = 12 +16 + 20 = 48 (дм)
Поскольку треугольники подобны, мы видим, что
==
=== k ( *)
Тогда отношение периметров треугольников
= k (**)
Из равенств (*) и (**) следует
=
=
B ₁ C ₁ = = 20 (дм)
Тогда
=
=
A ₁ B ₁ = = 15 (дм)
A ₁ C ₁ = P (ΔA ₁ B ₁ C ₁) — B ₁ C ₁ — A ₁ B ₁ = 60 — 20 — 15 = 25 (дм).
Ответ: A ₁ C ₁ = 25 дм, A ₁ B ₁ = 15 дм, B ₁ C ₁ = 20 дм.
***
Задача 173.
Дано:
ABCD — трапеция,
стороны трапеции пересекаются в точке M:
AB ∩ CD = M,
BC = 5 см,
AD = 8 см,
AB = 3,9 см,
CD = 3,6 см
Найти:
MB, MC =?
Решение:
Рассмотрим треугольники ΔAMD и ΔBMC:
BAD = MBC как соответствующие углы на параллельных прямых BC и AD и секущей AB.
MCB = MDA, как соответствующие углы на параллельных прямых BC и AD и секущей CD.
Тогда согласно первой теореме подобия треугольников:
треугольники подобны Δ AMD Δ BMC.
Следовательно,
= =
=,
, но AM = AB + BM = 3,9 + BM
Тогда
8 • BM = 5 (3,9 + BM)
8BM — 5BM = 19,5
3BM = 19,5
BM = 6,5 (см)
=,
, но MD = CD + MC = 3. 6 + MC
8 • MC = 5 (3,6 + MC)
3MC = 18
MC = 6 (см)
Ответ: 6,5 см, 6 см.
***

Понимание упражнений: плоскости, оси и движение
Самолеты и оси движения
Создать эффективную фитнес-программу не так просто, как может показаться. Это больше, чем просто составление списка упражнений, определение количества повторений и определение количества подходов. Он включает в себя выбор комбинации упражнений, разработанных для проверки всех возможных движений тела.Наше тело делает больше, чем просто движется вперед и назад или из стороны в сторону. Тело также может скручиваться, поворачиваться, прыгать и вращаться (при этом часто возникают травмы). Осложняя все аспекты движения, тело может добиться оптимальных результатов (например, развитие мышц, равновесие, гибкость, координация и т. Д.). Лучшая фитнес-программа — это та, которая не только дает физические результаты, но и обеспечивает прочность тела и защиту от возможных травм и вреда.
Понимание движений тела
Все физические нагрузки становятся возможными благодаря различным движениям и движениям.Каждое движение происходит в одной из трех плоскостей движения (сагиттальной, фронтальной или поперечной / горизонтальной) и вокруг одной из трех осей (сагиттальной, фронтальной или вертикальной).
Самолеты движения
Сагиттальная плоскость — вертикальная плоскость тела, которая проходит спереди назад, разделяя тело на две симметричные половины.
Фронтальная плоскость — плоскость тела, проходящая из стороны в сторону под прямым углом к сагиттальной плоскости; также называется корональной плоскостью.
Поперечная плоскость — любая горизонтальная плоскость тела, параллельная диафрагме; также называется горизонтальной плоскостью.
Оси движения
Сагиттальная горизонтальная ось — ось тела, проходящая спереди назад, лежащая под прямым углом к фронтальной плоскости.
Фронтальная горизонтальная ось — ось тела, проходящая горизонтально из стороны в сторону под прямым углом к сагиттальной плоскости.
Вертикальная ось — ось тела, проходящая от головы до стопы под прямым углом к поперечной плоскости.
Типы движения
Движение — это не только плоскости и оси. Есть несколько «типов» движения, которые далее разбиваются на следующие категории:
Сгибание и разгибание
Аддукция и похищение
Вращение
Обращение
Сгибание и разгибание
Первый и наиболее распространенный тип движения происходит в сагиттальной плоскости и вокруг фронтальной горизонтальной оси.Эти движения также известны как сгибание и разгибание.
Сгибание происходит, когда угол между двумя костями, прикрепленными к поражаемому суставу, уменьшается. Когда вы сгибаете коленный сустав, угол между бедром или бедром и большой / малоберцовой или голени уменьшается. Боковое сгибание — это боковой изгиб позвоночника и шеи.
Примеры сгибания:
Прыжок с группировкой
Подъем гантелей спереди
Сгибание рук на бицепс
Разгибание противоположно сгибанию.Расширение происходит, когда угол между двумя костями увеличивается. Когда вы разгибаете или разгибаете коленный сустав, угол между верхней и нижней частью ноги увеличивается.
Примеры расширения:
Становая тяга с прямыми ногами
Жим на трицепс вниз
Военная пресса
Если какая-то часть тела, например сустав, чрезмерно растянута или «согнута назад» из-за чрезмерного разгибания, это называется гиперэкстензией. Этот тип движения создает значительную нагрузку на связки сустава.Это не всегда произвольное движение и может происходить в результате несчастных случаев, падений или других причин травм.
Аддукция и похищение
Следующими наиболее распространенными движениями являются приведение и отведение. Эти два движения выполняются во фронтальной плоскости и вокруг сагиттальной горизонтальной оси.
Приведение — это движение в противоположном направлении к центру вашего тела. Когда вы возвращаете ногу из отведенного положения обратно в нормальное положение стоя, вы сводите ногу.
Примеры приведения включают:
Кроссовер кабеля вниз
Полеты гантелей лежа на спине
Аппарат отведения бедра
Отведение — это движение в сторону от середины тела. Из положения стоя, когда вы отводите ногу в сторону от середины тела, вы отводите ногу.
Примеры похищения:
Подъем гантелей в стороны на прямой руке
Звездный прыжок
Аппарат для отведения бедра
Вращение
Последнее движение — вращение.Вращение происходит в горизонтальной плоскости. Когда вы поворачиваете голову из стороны в сторону, вы поворачиваете голову в горизонтальной плоскости вокруг позвоночника, которая действует как вертикальная ось. С головой и туловищем есть только один вид вращения. Когда вы работаете с конечностями, есть два вида вращения — внутреннее и внешнее.
Внутреннее вращение происходит, когда передняя часть вашей руки или ноги поворачивается к середине (средней линии) вашего тела. Когда вы поворачиваете колени друг к другу в положении стоя, вы внутренне вращаете ноги.Внешнее вращение — противоположное направление. Если вы в положении стоя поворачиваете колени друг от друга, вы поворачиваете ноги наружу.
Примеры вращения включают:
Качели для гольфа
Метание бейсбольного мяча
Горные лыжи (поворот налево и направо)
Обращение
Есть еще один тип движения, с которым вам следует ознакомиться. Это комбинация движений в двух или трех плоскостях, которая называется циркумдукцией.Пример циркумдукции — это движение ваших рук вокруг тела, как мельница.
Общее движение относительно плоскостей и осей
Сгибание, разгибание и гиперэкстензия происходят в основном в сагиттальной плоскости и фронтальной оси тела (т. Е. Шее, плече, позвоночнике, бедре, коленях и лодыжках).
Боковое сгибание и латеральное разгибание происходят в основном во фронтальной плоскости и сагиттальной оси тела (то есть в шее и позвоночнике).
Аддукция и отведение также происходят в основном во фронтальной плоскости-сагиттальной оси тела (т.е.е. плечо и бедро).
Внутреннее и внешнее вращение, горизонтальное сгибание и разгибание, супинация и пронация — все это происходит в основном в поперечной плоскости и вертикальной оси.
Разработка программ с использованием плоскостей и осей движения
В будущих статьях вы узнаете, как разрабатывать программы для всего тела, которые включают упражнения, требующие сгибания, разгибания и вращения всего тела безопасными и эффективными способами для достижения оптимальных результатов.
Дополнительная информация о плоскостях и осях движения
Объяснение
плоскостей движения | Блог ACE
Ваше тело не движется в одном измерении.Если бы это было так, вы бы не смогли отвести ногу от себя, к вам, впереди и позади вас. Ваше тело движется в трех измерениях, и программы тренировок, которые вы разрабатываете для своих клиентов, должны это отражать. Разработка программы упражнений, в которой используются все плоскости движения, поможет вашим клиентам тренировать свое тело так же, как оно движется в реальной жизни.
Есть три различных плоскости движения: сагиттальная, фронтальная и поперечная. В каждой плоскости в суставах происходит несколько различных движений.Вот краткое изложение различных типов движения, которые происходят в каждой плоскости:
Сагиттальный
Сгибание : уменьшение угла между двумя костями
Расширение : увеличение угла между двумя костями
Тыльное сгибание: Перемещение верхней части стопы к голени (только в области лодыжки)
Подошвенный сгибание: смещение подошвы стопы вниз (указывая пальцами ног)
Фронтальный
Аддукция : движение к средней линии
Отведение : Движение от средней линии тела
Высота : перемещение в верхнее положение (только на лопатке)
Депрессия : Переход в нижнее положение (только на лопатку)
Инверсия : поднятие медиального края стопы
Eversion : Подъем боковой границы стопы
Поперечный
Вращение — Внутренний (внутрь) или внешний (наружу) поворот вокруг вертикальной оси кости
Пронация — Поворот кисти и запястья медиально от кости
Супинация -Поворот кисти и запястья в сторону от кости
Горизонтальное сгибание (приведение) — Из положения руки, отведенной под углом 90 градусов, плечевая кость сгибается (приводится) по направлению к средней линии тела в поперечной плоскости
Горизонтальное разгибание (отведение) — Возврат плечевой кости после горизонтального сгибания
Давайте рассмотрим каждую плоскость более подробно
Разделив тело на левую и правую половины с помощью воображаемой линии, мы получим сагиттальную плоскость .Любое движение вперед и назад параллельно этой линии происходит в сагиттальной плоскости .
Этой же воображаемой линией разделите тело на переднюю и заднюю половины, и вы получите фронтальную плоскость. Любое боковое (боковое) движение параллельно линии будет происходить во фронтальной плоскости .
И последнее, но не менее важное: у нас есть поперечная плоскость, которая разделяет тело на верхнюю и нижнюю половины. Движение параллельно талии, иначе известное как вращательное движение, происходит в поперечной плоскости .
Для более четкого понимания, мы можем просмотреть плоскости, как они относятся к упражнениям, выполняемым во время тренировки. Ниже приведены несколько упражнений, выполняемых в каждой плоскости.
Как только вы поймете концепцию движения в трех плоскостях, разработка клиентской программы станет бесшовной. Для получения дополнительной информации о плоскостях движения во время изучения вы можете просмотреть это видео.
Ось вращения
Если у вас возникли проблемы с пониманием концепции оси вращения, вот упрощенное объяснение.Эта концепция основана на понимании плоскостей движения и различных типов движений в суставах, поэтому обязательно изучите их в первую очередь, прежде чем переходить к трем осям вращения.
Понятие оси вращения может быть трудным для понимания, потому что это воображаемый объект. Применительно к анатомии человека ось вращения — это воображаемая линия, которая проходит через точку поворота / вращения в суставе (например, ось вращения для сгибания и разгибания руки проходит через локтевой сустав).Каждое движение в трех плоскостях движения (т. Е. Сагиттальной, фронтальной и поперечной) происходит вокруг оси вращения. Само движение — которое, конечно, не является воображаемым — происходит в воображаемой плоскости движения, перпендикулярной воображаемой оси вращения. Это означает, что оба воображаемых компонента — плоскость и ось — пересекаются, образуя прямой (90 °) угол. В примере с локтем предплечье движется в сагиттальной плоскости движения, когда локтевой сустав (через который проходит ось вращения) сгибается и разгибается.То есть рука движется в сагиттальной плоскости движения вокруг оси вращения, которая происходит в локте, что позволяет сгибать и разгибать руки. Поскольку сгибание и разгибание происходят в переднем и заднем направлении, соответственно, ось вращения перпендикулярна ей и проходит через сустав в медиолатеральном или поперечном направлении. Следовательно, для локтя движение происходит в сагиттальной плоскости (как сгибание и разгибание) вокруг медиолатеральной оси вращения.
Так же, как есть три плоскости движения, есть три оси вращения: передне-задняя ось, медиолатеральная ось и продольная ось.Суставы вращаются в этих осях, позволяя перемещаться в плоскостях.
Переднезадняя ось
, также известная как сагиттальная ось или переднезадняя ось
Представьте себе штифт, который проходит через сустав спереди назад (спереди и сзади), эффективно прижимая сустав, чтобы ограничить его потенциальную свободу движения. Например, вы можете представить себе булавку, входящую в переднюю часть тазобедренного сустава и выходящую из задней.Из-за положения штифта единственное движение вокруг этой оси — это боковое движение (отведение или приведение) во фронтальной плоскости.
Медиолатеральная ось
также известна как поперечная ось
Медиолатеральный означает, что мы берем воображаемый штифт и вводим его из бокового или бокового доступа. Как и в предыдущем примере с локтем, ось выступает из медиальной стороны сустава и выходит за боковую сторону.Положение штифта допускает только движение вперед и назад (сгибание и разгибание) в сагиттальной плоскости вокруг этой оси.
Продольная ось
Если мы вставим наш штифт в шарнир сверху вниз, он позволит перемещаться только в поперечной плоскости (то есть вращение). Представьте, что длинная булавка входит в верхнюю часть шейного отдела позвоночника и выходит из поясничного отдела позвоночника. Штифт эффективно предотвратит изгиб позвоночника вперед, назад или из стороны в сторону, но позволит позвоночнику скручиваться в поперечной плоскости.
Соединения вращаются по этим осям, позволяя перемещаться в плоскостях. Некоторые вращаются только по одной оси, а другие вращаются по нескольким осям.
Одноосные или одноплоскостные шарниры (также называемые шарнирными соединениями) вращаются по одной оси, что позволяет перемещаться в одной плоскости. Локтевой сустав является шарнирным, поскольку он допускает движение вперед и назад (сгибание и разгибание) только в сагиттальной плоскости.
Двухосные или двухплоскостные шарниры вращаются в двух осях, что позволяет перемещаться в двух плоскостях.Стопа и рука являются примерами двухосных / двухплоскостных суставов. Они оба движутся в стороны или из стороны в сторону во фронтальной плоскости и вперед и назад (сгибание и разгибание) в сагиттальной плоскости.
Многоплоскостные или трехосные шарниры вращаются по всем трем осям, обеспечивая перемещение во всех трех плоскостях. Плечевой сустав является примером многоплоскостного / трехосного сустава. Он допускает движение вперед и назад в сагиттальной плоскости, поперечное или из стороны в сторону во фронтальной плоскости, а также внутреннее и внешнее вращение в поперечной плоскости.
плоскостей движения — сагиттальная плоскость, поперечная плоскость, фронтальная плоскость
перейти к содержанию
Главное меню
Спортивные тренировки Переключить меню
Легкая атлетика Переключить меню
Спринтерская тренировка на 100 м / 200 м
Препятствия
Среднее расстояние
Прыжок с шестом
Прыжки в длину
Прыжки в высоту
Тройной прыжок
Толкание ядра
Метание диска
Метание копья
Молот
Бадминтонные упражнения и навыки
Баскетбол
Футбол (Футбол)
Тренировки и тренировки по нетболу
Регби
Теннис
Анатомия и физиология Переключить меню
Скелет и кости Переключить меню
Скелет человека
Структура кости
Осевой и аппендикулярный
Кости черепа
Типы соединений
Типы костей
Самолеты движения
Мышцы человека Переключить меню
Теория скользящей нити
Типы мышц
Типы мышечных сокращений
Анатомия и структура мышц
Формы скелетных мышц
Типы мышечных волокон
Система кровообращения Переключатель меню
Сердце человека
Структура системы кровообращения
Частота сердечных сокращений и сердечные объемы
Сердцебиение
Система сердцебиения и сердечной проводимости
Артериальное давление
Энергетические системы в спорте Переключить меню
Пищеварительная система человека
Реакция человеческого тела на упражнение
Влияние упражнений на тело
Кислородный долг и возврат
Клеточное дыхание
Анаэробное дыхание
Цикл Кребса и аэробные упражнения
Дыхательная система и дыхание Переключатель меню
Анатомия дыхательной системы
Механика и механизм дыхания
Газообмен в легких
Объемы дыхания
VO2 макс.