Спираль архимеда в декартовых координатах: Как построить параметризированную геометрию спирали Архимеда

Содержание

Как построить параметризированную геометрию спирали Архимеда

Спирали Архимеда широко используются при построении геометрий для катушек индуктивности, спиральных теплообменников и микрогидродинамических устройств. В этой заметке мы покажем, как построить спираль Архимеда, используя аналитические выражения и их производные для задания необходимых кривых. Сначала мы создадим двухмерную геометрию, а затем, задав нужную толщину, преобразуем её в трёхмерную с помощью операции Extrude (Вытягивание).

Что такое спираль Архимеда?

Широко распространённые в природе спирали или завитки используются во многих инженерных конструкциях. Например, в электротехнике и электронике с помощью проводников спиралевидной формы наматывают катушки индуктивности или проектируют геликоидные антенны. В машиностроении спирали используются при проектировании пружин, косозубых цилиндрических передач или даже механизмов часов, один из которых изображён ниже.

Пример спирали Архимеда, которая используется в часовом механизме. Изображение представлено Greubel Forsey. Доступно по лицензии CC BY-SA 3.0 из Wikimedia Commons.

В данной статье мы разберём только один вид спирали, а именно, спираль Архимеда, которая изображена в механизме выше. Спираль Архимеда – это особый вид спирали с постоянным расстоянием между витками. Благодаря этому свойству она широко распространена при проектировании катушек и пружин.

Уравнение спирали Архимеда в полярной системе координат записывается, как:

r=a+b\theta

где a и b — параметры, определяющие начальный радиус спирали и расстояние между витками, которое равно 2 \pi b. Обратите внимание, что спираль Архимеда также иногда называют арифметической спиралью. Это имя связывают с арифметической зависимостью расстояния от начала кривой до точек спирали, находящихся на одной радиальной линии.

Задание параметризированной геометрии спирали Архимеда

Теперь, когда вы уже знаете, что такое спираль Архимеда, давайте приступим к параметризации и созданию геометрии в COMSOL Multiphysics.

Спираль Архимеда может быть задана как в полярных, так и в декартовых координатах.

Для начала необходимо преобразовать уравнение спирали из полярной системы координат в декартову и выразить каждое уравнение в параметрической форме:

\begin{align*} x_{component}=rcos(\theta) \\ y_{component}=rsin(\theta) \end{align*}

После преобразования уравнения спирали в параметрической форме в декартовой системе координат примут вид:

\begin{align*} x_{component}=(a+b\theta)cos(\theta) \\ y_{component}=(a+b\theta)sin(\theta) \end{align*}

В COMSOL Multiphysics необходимо определить набор параметров, с помощью которых будем задавать геометрию спирали. В нашем случае — это начальный и конечный радиусы спирали a_{initial} и a_{final}, соответственно, и количество витков n. Показатель роста спирали b находится, как:

b=\frac{a_{final}-a_{initial}}{2 \pi n}

Также необходимо определить начальный и конечный углы спирали — theta_0 и theta_f, соответственно. Давайте с них и начнём — theta_0=0 и theta_f=2 \pi n. Исходя из заданной информации, определяем параметры для построения геометрии спирали.

Параметры, которые используются для построения геометрии спирали.

Начнём наше построение, выбрав трёхмерную задачу (3D Component) и создадим Work Plane (Рабочую плоскость) в разделе Geometry (Геометрия). В геометрии для Work Plane добавляем Parametric Curve (Параметрическую кривую) и записываем параметрические уравнения, описанные выше, чтобы задать двухмерную геометрию спирали Архимеда. Данные уравнения можно сразу вписать в соответствующие поля во вкладке Expression либо сначала можно задать каждое уравнение отдельной Аналитической функцией (Analytic function):

\begin{align*} X_{fun}=(a+bs)cos(s) \\ Y_{fun}=(a+bs)sin(s) \\ \end{align*}

Выражение для X-компоненты уравнения спирали Архимеда, заданное аналитической функцией.

Аналитическая функция затем может использоваться в качестве выражения в узле Parametric Curve. Во вкладке Parameter задаём параметр s от начального угла, theta_0, до его конечного значения, theta_f=2 \pi n.

Настройки для Parametric Curve (Параметрической кривой).

Как только вы зададите все параметры и нажмёте на кнопку «Build Selected», будет построена кривая, изображённая на скриншоте выше. Теперь давайте зададим толщину спирали, чтобы получить твёрдотельную (solid) двухмерную фигуру.

До этого момента параметрами нашей кривой были начальный (a_{initial}) и конечный (a_{final}) радиусы и количество витков n. Теперь мы хотим добавить ещё один – толщину спирали.

Ещё раз напомним главное свойство спирали — расстояние между витками постоянно и равно 2 \pi b. Что эквивалентно \frac{a_{final}-a_{initial}}{n}. Чтобы добавить толщину в наши уравнения, представляем расстояние между витками суммой толщины спирали и зазора thick+gap.

Расстояние между витками определяется толщиной спирали и величиной зазора.

Чтобы ввести параметр толщины и сохранить постоянное расстояние между витками, последнее перепишем, как:

\begin{align*} distance=\frac{a_{initial}-a_{final}}{n} \\ gap=distance-thick \end{align*}

После этого выражаем показатель роста спирали через толщину:

\begin{align*} distance=2\pi b \\ b=\frac{gap+thick}{2\pi} \end{align*}

Также нужно выразить конечный угол спирали через начальный угол и конечный радиус:

\begin{align*} \theta_{final}=2 \pi n \\ a_{final}=\text{total distance}+a_{initial} \\ a_{final}=2 \pi bn+a_{initial} \\ n=\frac{a_{final}-a_{initial}}{2 \pi b} \\ \theta_{final}=\frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \\ \theta_{final}=\frac{a_{final}-a_{initial}}{b} \end{align*}

Хотите задать отличный от нуля начальный угол спирали? Если так, то его надо будет добавить в выражение для определения конечного угла: theta_f=\frac{a_{final}-a_{initial}}{b}+theta_0. 2 }} \end{align*}
где N_x и N_y определяются аналитическими функциями в COMSOL Multiphysics, аналогично X_{fun} и Y_{fun} в первом примере. Внутри функции используется оператор производной, d(f(x),x), как показано на скриншоте ниже.

Примеры оператора производной, который используется в аналитической функции
Функции X_{fun}, Y_{fun}, N_x, и N_y могут быть использованы в выражениях для задания параметрической кривой, как с одной стороны:
\begin{align*} x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\ y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2} \end{align*}
Так и с другой:
\begin{align*} x_{upper}=X_{fun}(s)-N_x(s)\frac{thick}{2} \\ y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2} \end{align*}

Выражения для второй смещённой параметрической кривой.
Чтобы соединить концы, добавим ещё две параметрические кривые, используя незначительные изменения уравнений выше. Для кривой, которая будет соединять спираль в центре, необходимо задать X_{fun}, Y_{fun}, N_x, и N_y для начального значения угла, theta. Для кривой, которая будет соединять концы, необходимо задать конечное значение theta. Исходя из этого, уравнения кривой в центре:
\begin{align*} X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{thick}{2} \\ Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2} \end{align*}
Уравнения кривой на конце:
\begin{align*} X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot\frac{thick}{2} \\ Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2} \end{align*}
В этих уравнениях параметр s изменяется от -1 до 1, как показано на скриншоте ниже.

Уравнения кривой, соединяющей спираль в центре.
В итоге, мы имеем пять кривых, которые определяют осевую линию спирали и её четыре стороны. Осевую линию можно отключить (функция disable) или даже удалить, так как она не является необходимой. Добавив узел Convert to Solid, создаём единый геометрический объект. Последним шагом является вытягивание данного профиля с помощью операции Extrude и создание трёхмерного объекта.

Полная геометрическая последовательность и вытянутая (экструдированная) трёхмерная геометрия спирали.
Краткие выводы по моделированию спирали Архимеда в COMSOL Multiphysics
В данной заметке мы разобрали основные шаги по созданию параметрической спирали Архимеда. С помощью данной модели вы можете сами экспериментировать с различными значениями параметров, а также попробовать решить с использованием данной параметризации оптимизационную задачу. Надеемся, что данная статья оказалась полезной и вы будете применять данную технику в своих последующих моделях.
Дополнительные ресурсы по проектированию и расчёту спиралей
Для улучшения навыков моделирования спиралей, ознакомьтесь со следующими учебными моделями:
Спирально-щелевая антенна
Познакомьтесь с опытом одного из наших пользователей: Анализ спиральных резонаторных фильтров
Уравнение кривых в полярных координатах
Благодаря радиальной природе полярной системы координат, некоторые кривые могут быть достаточно просто описаны полярным уравнением, тогда как уравнение в прямоугольной системе координат были бы намного сложнее. Среди самых известных кривых: полярная роза, архимедова спираль, Лемниската, улитка Паскаля и кардиоида.
Окружность
Круг, заданный уравнением .
Общее уравнение окружности с центром в () и радиусом имеет вид:
Это уравнение может быть упрощено для частных случаев, например
является уравнением, определяющим окружность с центром в полюсе и радиусом .
[15]
Прямая
Радиальные прямые (те, которые проходят через полюс) определяются уравнением
где  — угол, на который прямая отклоняется от полярной оси, то есть, где  — наклон прямой в прямоугольной системе координат. Нерадиальная прямая, перпендикулярно пересекает радиальную прямую в точке определяется уравнением
Полярная роза
Полярная роза задана уравнением .
Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:
для произвольной постоянной (включая 0). Если  — целое число, то это уравнение будет определять розу с лепестками для нечётных , либо с лепестками для чётных . Если  — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная определяет длину лепестков.

Если считать, что радиус не может быть отрицательным, то при любом натуральном мы будем иметь — лепестковую розу. Таким образом, уравнение будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.
Спираль Архимеда
Одна из ветвей спирали Архимеда, задаваемая уравнением для .
Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:
Изменения параметра приводят к повороту спирали, а параметра  — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для а другую для . Две ветви плавно соединяются в полюсе. Зеркальное отображение одной ветви относительно прямой, проходящей через угол 90°/270°, даст другую ветвь. Эта кривая интересна тем, что была описана в математической литературе одной из первых, после конического сечения, и лучше других определяется именно полярным уравнением.

Конические сечения
Эллипс.
Коническое сечение, один из полюсов которого находится в полюсе, а другой где-то на полярной оси (так, что малая полуось лежит вдоль полярной оси) задаётся уравнением:
где  — эксцентриситет, а  — фокальный параметр. Если , это уравнение определяет гиперболу; если , то параболу; если , то эллипс. Отдельным случаем является , определяющее окружность с радиусом .
86. Вычисление определенного интеграла. Применение его к вычислению площадей плоских фигур, длины дуги кривой.
Вычисление площадей и длин дуг кривых в декартовых координатах
Пусть на плоскости x0y задана область, ограниченная снизу кривой y=f₁(x) , заданной в декартовых координатах, сверху – кривой y=f₂(x) , слева – прямой x=a (ее может и не быть, если f
1(a)=f₂(a) ), справа – прямой x=b.
Исходя из геометрического смысла определенного интеграла, площадь этой области можно вычислить по формуле
Здесь не нужно заботиться, какая из функций и где положительная, а какая отрицательная. Если, например, f₁(x)<0, то формула сама прибавит нужную площадь. Более сложные области всегда можно разбить так, чтобы выполнялись указанные условия.
Пусть на отрезке [a,b] уравнением y=f(x) задана плоская кривая. Ее длина вычисляется по формуле
Пример 1 ::  Вычисление площадей и длин дуг в декартовых координатах
Вычислим площадь области, ограниченной кривыми   и длину границы этой области.
Вычисление площадей и длин дуг при параметрическом задании кривых

Если область на плоскости снизу ограничена кривой, заданной параметрически, то есть
при этом   x₁()=b, x₁()=b, а сверху – кривой
Тогда площадь такой плоской фигуры вычисляем по формуле
Эта формула совпадает с формулой вычисления площади в декартовых координатах, если учесть, что x'(t)dt=dx.
Пусть кривая на плоскости задана параметрически
Тогда длина этой кривой вычисляется по формуле
Пример 2 ::  Вычисление площадей и длин дуг при параметрическом задании кривых.
Вычислим площадь фигуры, ограниченной кривыми   ,   , . Вычислим длину дуги циклоиды  ,  .
Вычисление площадей и длин дуг кривых в полярных координатах
Когда кривая, ограничивающая область, задана в
полярных координатах  =(), то площадь этой области вычисляем по формуле
Основная трудность в использовании этой формулы заключается в определении пределов интегрирования   ,  . Здесь нужно понимать, что кривая  =() определена только, если  >0. Поскольку в формуле присутствует ² , то она учтет и не существующую площадь, когда . Решив уравнение ()=0 , найдем пределы интегрирования.
Если кривая, ограничивающая область, задана в полярных координатах  =(), то ее длина вычисляется по формуле
Пределы интегрирования определяются из тех же соображений, что и при вычислении площади.
Архимедова спираль
Три 360 ° петли одного плеча спирали Архимеда
В Архимедова спираль (также известный как арифметическая спираль) это спираль назван в честь III века до нашей эры Греческий математик Архимед. Это локус точек, соответствующих местоположениям во времени точки, удаляющейся от фиксированной точки с постоянной скоростью вдоль линии, которая вращается с постоянной угловая скорость. Эквивалентно в полярные координаты (р, θ) его можно описать уравнением
р=а+бθ{ Displaystyle г = а + б тета}
с действительные числа а и б. Изменение параметра а перемещает центральную точку спирали наружу от начала координат (положительный а к θ = 0 и отрицательный а к θ = π), пока б контролирует расстояние между петлями.
Таким образом, из приведенного выше уравнения можно утверждать: положение частицы от начальной точки пропорционально углу θ по прошествии времени.
Архимед описал такую спираль в своей книге. На спиралях. Конон Самосский был его другом и Паппус заявляет, что эта спираль была открыта Кононом.^[1]
Содержание
1 Вывод общего уравнения спирали.
2 Характеристики
3 Общая архимедова спираль
4 Приложения
5 Код для создания спирали Архимеда
6 Смотрите также
7 Рекомендации
8 внешняя ссылка
Вывод общего уравнения спирали.
Смотрите также: Круговое движение
А физический подход используется ниже для понимания понятия спиралей Архимеда.
Предположим, что точечный объект движется в Декартова система с постоянным скорость v направлен параллельно Икс-оси относительно ху-самолет. Пусть на время т = 0, объект находился в произвольной точке (c, 0, 0). Если ху самолет вращается с постоянной угловая скорость ω о z-оси, то скорость точки относительно z-axis можно записать как:
В ху плоскость поворачивается на угол ωt (против часовой стрелки) о происхождении во времени т. {2}}} v_ {x} & = v cos omega t- omega (vt + c) sin omega t v_ {y} & = v sin omega t + omega (vt + c) cos omega t end { выровнен}}}
Здесь vt + c модуль вектор положения частицы в любое время т, v_Икс — компонента скорости вдоль Иксось и v_у компонент вдоль у-ось. Рисунок, показанный рядом, объясняет это.
∫vИксdт=Икс∫vуdт=у{ displaystyle { begin {align} int v_ {x} , dt & = x int v_ {y} , dt & = y end {align}}}
Приведенные выше уравнения можно интегрировать, применяя интеграция по частям, что приводит к следующим параметрическим уравнениям:
Икс=(vт+c)потому что⁡ωту=(vт+c)грех⁡ωт{ Displaystyle { begin {выровнено} x & = (vt + c) cos omega t y & = (vt + c) sin omega t end {align}}}
Возведение двух уравнений в квадрат с последующим сложением (и некоторыми небольшими изменениями) приводит к декартову уравнению
Икс2+у2=vω⋅арктан⁡уИкс+c{ displaystyle { sqrt {x ^ {2} + y ^ {2}}} = { frac {v} { omega}} cdot arctan { frac {y} {x}} + c}
(используя тот факт, что ωt = θ и θ = arctan у/Икс) или же
загар⁡((Икс2+у2−c)⋅ωv)=уИкс{ displaystyle tan left ( left ({ sqrt {x ^ {2} + y ^ {2}}} — c right) cdot { frac { omega} {v}} right) = { frac {y} {x}}}
Его полярная форма
р=vω⋅θ+c{ Displaystyle г = { гидроразрыва {v} { omega}} cdot theta + c}
Характеристики
Архимедова спираль обладает тем свойством, что любой луч из начала координат пересекает последовательные повороты спирали в точках с постоянным разделительным расстоянием (равным 2πb если θ измеряется в радианы ), отсюда и название «арифметическая спираль». В отличие от этого, в логарифмическая спираль эти расстояния, а также расстояния до точек пересечения, измеренные от начала координат, образуют геометрическая прогрессия.
Оскулирующие круги архимедовой спирали. Сама спираль не рисуется: мы видим ее как геометрическое место точек, в которых круги особенно близки друг к другу.
Спираль Архимеда имеет два рукава, одно для θ > 0 и один для θ < 0. Два плеча плавно соединены в начале координат. На прилагаемом графике показана только одна рука. Сделав зеркальное отображение этой руки через у- ось уступит другую руку.
Для больших θ точка движется с хорошо приближенным равномерным ускорением по спирали Архимеда, в то время как спираль соответствует положениям во времени точки, удаляющейся от фиксированной точки с постоянной скоростью вдоль линии, которая вращается с постоянной угловой скоростью^[2] (см. вклад Михаила Гайченкова).
По мере роста архимедовой спирали ее эволюционировать асимптотически приближается к окружности радиуса |v|/ω. { frac {1} {c}}.}
Нормальная архимедова спираль возникает, когда c = 1. К другим спиралям, попадающим в эту группу, относятся: гиперболическая спираль (c = −1), Спираль Ферма (c = 2), а литуус (c = −2). Практически все статические спирали, встречающиеся в природе, являются логарифмические спирали а не архимедовы. Многие динамические спирали (например, Спираль Паркера из Солнечный ветер, или узор, сделанный Екатерининское колесо ) архимедовы.
Приложения
Один метод квадрат круга, согласно Архимеду, использует спираль Архимеда. Архимед также показал, как можно использовать спираль для разрезать угол. Оба подхода ослабляют традиционные ограничения на использование линейки и циркуля в древнегреческих геометрических доказательствах.^[3]
Механизм спирального компрессора
Спираль Архимеда имеет множество практических применений. Спиральные компрессоры, используемые для сжатия газов, имеют роторы, которые могут быть выполнены из двух чередующихся архимедовых спиралей, эвольвенты круга такого же размера, как спирали Архимеда,^[4] или гибридные кривые. Архимедовы спирали можно найти в спиральная антенна, который может работать в широком диапазоне частот. Катушки смотреть пружины баланса и канавки очень ранних грампластинки образуют архимедовы спирали, делая канавки равномерно расположенными (хотя позже было введено переменное расстояние между дорожками, чтобы максимально увеличить количество музыки, которую можно было нарезать на пластинку).^[5] Попросить пациента нарисовать спираль Архимеда — это способ количественной оценки человеческого тремор; эта информация помогает в диагностике неврологических заболеваний. Архимедовы спирали также используются в цифровая обработка света (DLP) проекционные системы для минимизации «эффект радуги «, создавая впечатление, что несколько цветов отображаются одновременно, хотя на самом деле красный, зеленый и синий чередуются чрезвычайно быстро.^[6] Кроме того, спирали Архимеда используются в пищевой микробиологии для количественного определения концентрации бактерий с помощью спирального диска. Walser, H .; Hilton, P .; Pedersen, J .; Математическая ассоциация Америки (2000). Симметрия. Математическая ассоциация Америки. п.27. ISBN 9780883855324. Получено 2014-10-06.
внешняя ссылка
Джонатан Мэтт делает интересную спираль Архимеда — Видео: Удивительная красота математики — TedX Talks, Зеленые фермы
Вайсштейн, Эрик В. «Спираль Архимеда». MathWorld.
архимедова спираль в PlanetMath.
Страница с приложением Java для интерактивного изучения спирали Архимеда и связанных с ней кривых
Онлайн-исследование с использованием JSXGraph (JavaScript)
Архимедова спираль на «математической кривой»
Архимедова спираль — Archimedean spiral
Три 360 ° петли одного плеча спирали Архимеда
Резьб (также известный как арифметическая спираль ) представляет собой спираль, названной в честь третьего века до нашей эры греческого математика Архимеда .

Это геометрическое место, соответствующее местоположениям во времени точки, удаляющейся от фиксированной точки с постоянной скоростью вдоль линии, которая вращается с постоянной угловой скоростью . Эквивалентно, в полярных координатах ( r, θ ) его можно описать уравнением
рзнак равноа+б⋅θ{\ Displaystyle г = а + б \ cdot \ theta}
с действительными числами a и b . Изменение параметра a перемещает центральную точку спирали наружу от начала координат (положительное значение a в направлении θ = 0 и отрицательное значение a в сторону θ = π ) по существу за счет вращения спирали, в то время как b контролирует расстояние между петлями.
Таким образом, из приведенного выше уравнения можно утверждать: положение частицы от точки старта пропорционально углу θ с течением времени.
Архимед описал такую спираль в своей книге «
О спиралях» . Конон Самосский был его другом, и Папп утверждает, что эту спираль открыл Конон.
СОДЕРЖАНИЕ
1 Вывод общего уравнения спирали
2 Длина дуги, кривизна
3 Характеристики
4 Генеральная архимедова спираль
5 приложений
6 См. Также
7 ссылки
8 Внешние ссылки
Вывод общего уравнения спирали.
См. Также: Круговое движение
Ниже используется физический подход для понимания понятия спиралей Архимеда.
Предположим, что точечный объект движется в декартовой системе с постоянной скоростью v, направленной параллельно оси x относительно плоскости xy . Пусть в момент времени t = 0 объект находился в произвольной точке ( c, 0, 0) . Если плоскость xy вращается с постоянной угловой скоростью ω вокруг оси z, то скорость точки относительно оси z может быть записана как:
В ху плоскость поворачивается на угол ωt (против часовой стрелки) вокруг начала координат в времени т . ( c, 0) — положение объекта при t = 0 . {2}}} \\ v_ {x} & = v \ cos \ omega t- \ omega (vt + c) \ sin \ omega t \\ v_ {y} & = v \ sin \ omega t + \ omega (vt + c) \ cos \ omega t \ end { выровнено}}}
Здесь vt + c — модуль вектора положения частицы в любой момент времени t, v _x — составляющая скорости вдоль оси x, а v _y — составляющая вдоль оси y . Рисунок, показанный рядом, объясняет это.
∫vИксdтзнак равноИкс∫vуdтзнак равноу{\ displaystyle {\ begin {align} \ int v_ {x} \, dt & = x \\\ int v_ {y} \, dt & = y \ end {align}}}
Вышеупомянутые уравнения можно интегрировать, применяя интегрирование по частям, что приводит к следующим параметрическим уравнениям:
Иксзнак равно(vт+c)потому что⁡ωтузнак равно(vт+c)грех⁡ωт{\ displaystyle {\ begin {align} x & = (vt + c) \ cos \ omega t \\ y & = (vt + c) \ sin \ omega t \ end {align}}}
Возведение двух уравнений в квадрат с последующим сложением (и некоторыми небольшими изменениями) приводит к декартову уравнению
Икс2+у2знак равноvω⋅арктан⁡уИкс+c{\ displaystyle {\ sqrt {x ^ {2} + y ^ {2}}} = {\ frac {v} {\ omega}} \ cdot \ arctan {\ frac {y} {x}} + c}
(используя тот факт, что ωt = θ и θ = arctgу/Икс) или
загар⁡((Икс2+у2-c)⋅ωv)знак равноуИкс{\ displaystyle \ tan \ left (\ left ({\ sqrt {x ^ {2} + y ^ {2}}} — c \ right) \ cdot {\ frac {\ omega} {v}} \ right) = {\ frac {y} {x}}}
Его полярная форма
рзнак равноvω⋅θ+c{\ Displaystyle г = {\ гидроразрыва {v} {\ omega}} \ cdot \ theta + c}
Длина дуги, кривизна
Учитывая параметризацию в декартовых координатах
ж:θ↦(рпотому что⁡θ,ргрех⁡θ)знак равно(бθпотому что⁡θ,бθгрех⁡θ){\ Displaystyle е \ двоеточие \ тета \ mapsto (г \, \ соз \ тета, г \, \ грех \ тета) = (б \, \ тета \, \ соз \ тета, Ь \, \ тета \, \ грех \ theta)}
длина дуги от до составляет θ1{\ displaystyle \ theta _ {1}}θ2{\ displaystyle \ theta _ {2}}
б2[θ1+θ2+пер⁡(θ+1+θ2)]θ1θ2{\ displaystyle {\ frac {b} {2}} \ left [\ theta \, {\ sqrt {1+ \ theta ^ {2}}} + \ ln \ left (\ theta + {\ sqrt {1+ \ theta ^ {2}}} \ right) \ right] _ {\ theta _ {1}} ^ {\ theta _ {2}}}
или эквивалентно
б2[θ1+θ2+арсин⁡θ]θ1θ2. {\ frac {3} {2}}}}}
Характеристики
Архимедова спираль обладает тем свойством, что любой луч из начала координат пересекает последовательные повороты спирали в точках с постоянным разделительным расстоянием (равным 2 πb, если θ измеряется в радианах ), отсюда и название «арифметическая спираль». В отличие от этого в логарифмической спирали эти расстояния, а также расстояния до точек пересечения, измеренные от начала координат, образуют геометрическую прогрессию .
Оскулирующие круги спирали Архимеда. Сама спираль не рисуется: мы видим ее как геометрическое место точек, где окружности особенно близки друг к другу.
Спираль Архимеда имеет два рукава: одно для θ > 0 и одно для θ <0 . Два плеча плавно соединены в начале координат. На прилагаемом графике показана только одна рука. Если сделать зеркальное отображение этого плеча поперек оси Y, получится другое плечо.
Для больших θ точка движется с хорошо аппроксимированным равномерным ускорением вдоль спирали Архимеда, в то время как спираль соответствует положениям во времени точки, удаляющейся от фиксированной точки с постоянной скоростью вдоль линии, которая вращается с постоянной угловой скоростью (см. {\ frac {1} {c}}.}
Нормальная архимедова спираль возникает при c = 1 . Другие спирали, попадающие в эту группу, включают гиперболическую спираль ( c = −1 ), спираль Ферма ( c = 2 ) и литуус ( c = −2 ). Практически все статические спирали, встречающиеся в природе, являются логарифмическими, а не архимедовыми. Многие динамические спирали (например, Parker спирали от солнечного ветра, или рисунка, сделанного колеса Екатерины ) являются архимедова.
Приложения
В одном из методов квадрата круга, предложенном Архимедом, используется архимедова спираль. Архимед также показал, как спиралью можно разрезать угол пополам . Оба подхода ослабляют традиционные ограничения на использование линейки и циркуля в древнегреческих геометрических доказательствах.
Механизм спирального компрессора
Спираль Архимеда имеет множество практических применений. Спиральные компрессоры, используемые для сжатия газов, имеют роторы, которые могут быть изготовлены из двух чередующихся архимедовых спиралей, эвольвент круга одинакового размера, которые почти напоминают спирали Архимеда, или гибридных кривых. Архимедовы спирали можно найти в спиральной антенне, которая может работать в широком диапазоне частот. Катушки пружин баланса часов и канавки на очень ранних граммофонных пластинках образуют архимедовы спирали, делая канавки равномерно расположенными (хотя позже было введено переменное расстояние между дорожками, чтобы максимально увеличить количество музыки, которую можно было нарезать на пластинку). Попросить пациента нарисовать спираль Архимеда — это способ количественной оценки человеческого тремора ; эта информация помогает в диагностике неврологических заболеваний. Архимедовы спирали также используются в проекционных системах с цифровой обработкой света (DLP), чтобы минимизировать « эффект радуги », создавая впечатление, что несколько цветов отображаются одновременно, тогда как на самом деле красный, зеленый и синий чередуются чрезвычайно быстро. . Кроме того, спирали Архимеда используются в пищевой микробиологии для количественного определения концентрации бактерий с помощью спирального диска. Они также используются для моделирования узора, который появляется на рулоне бумаги или ленты постоянной толщины, намотанной вокруг цилиндра.
Смотрите также
Винт архимеда
Спираль Эйлера
Спираль Ферма
Золотая спираль Фибоначчи
Гиперболическая спираль
Список спиралей
Логарифмическая спираль
Спираль Теодора
Символ тройной спирали
использованная литература
внешние ссылки
Джонатан Мэтт делает спираль Архимеда интересной — Видео: Удивительная красота математики — TedX Talks, Green Farms
Вайсштейн, Эрик В. «Спираль Архимеда» . MathWorld .
архимедова спираль в PlanetMath .
Страница с приложением Java для интерактивного изучения спирали Архимеда и связанных с ней кривых
Онлайн-исследование с использованиемXGraph (JavaScript)
Спираль Архимеда на «математической кривой»
<img src=»//en. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»»>
Архимедова спираль — no-regime.com
Архимедова спираль
Архимедова спираль в полярной системе координат
Резьб (также арифметическая спиральная ) является самым простым из всех спиралей. Она возникает, когда радиус возрастает пропорционально до угла поворота во время вращательного движения : р{\ displaystyle r} φ{\ displaystyle \ varphi}
рзнак равноа⋅φ{\ Displaystyle г = а \ cdot \ varphi}
с . а>0{\ displaystyle a> 0}
Оглавление
1 недвижимость
1.1 «Расстояние намотки»
1.2 Касательное свойство
2 Возведение круга в квадрат и деление углов
3 исторические
4 обобщения
5 приложений
6 литературы
7 веб-ссылок
8 индивидуальных доказательств
характеристики
Представление в виде кривой параметров в декартовых координатах :
ж:φ↦(рпотому что⁡φ,ргрех⁡φ)знак равно(аφпотому что⁡φ,аφгрех⁡φ){\ Displaystyle е \ двоеточие \ varphi \ mapsto (r \, \ cos \ varphi, r \, \ sin \ varphi) = (a \, \ varphi \, \ cos \ varphi, a \, \ varphi \, \ sin \ varphi)}. {2}}} {a}} \ right) = {\ frac {y} {x}}}
«Расстояние между обмотками»
Каждый луч, исходящий из начала координат, пересекает последовательные витки архимедовой спирали в точках с постоянным расстоянием (см. Рисунок справа). Отсюда и появился термин «арифметическая спираль». рзнак равноаφ{\ Displaystyle \ г = а \, \ varphi \} а⋅2π{\ Displaystyle а \ cdot 2 \, \ пи \}
Касаясь спирали, красные дорожки имеют одинаковую длину.
Это особое свойство спирали Архимеда часто выражается в том, что шаг ее витков постоянен. Однако такой способ выражения легко может быть неправильно понят, поскольку речь идет не о постоянном расстоянии между кривыми в смысле параллельных кривых . Спираль которого витки на самом деле имеет постоянное расстояние в последнем смысле была бы эвольвентная окружность .
Касательная собственность
Есть точка P с соответствующим радиусом OP и углом поворота . Касательной к спирали через Р затем пересекает перпендикулярную к OP, установленной в О в точке Т. {\ circ} \, \ Rightarrow \, | {\ widehat {PQ}} | = | OT |}
Возведение круга в квадрат и разделение углов
Угловое деление на три (n = 3): βзнак равноα3{\ displaystyle \ beta = {\ tfrac {\ alpha} {3}}}
Круговая квадратура по Архимеду
Квадратура круга: F (круг (M, r)) = F (ABCD) = F (CJHG)
→ Основная статья : Квадрат круга
→ Основная статья : Трисекция угла
Благодаря своему определению, согласно которому расстояние точки кривой от начала координат пропорционально углу поворота, спираль Архимеда подходит для деления угла на n равных частей и для возведения окружности в квадрат . Следовательно, это и трисектриса (n = 3), и квадрикс . Обе проблемы не могут быть решены с помощью циркуля и линейки, но если спираль Архимеда допущена в качестве единственной дополнительной помощи, то они могут быть решены.
Чтобы разделить угол BAC на n равных частей, сначала создается спираль Архимеда над его участком AB. Нога здесь действует как ось x с угловым наконечником A как начало координат . Расстояние от острия уголка до точки D пересечения спирали с другим участком угла теперь разделено на n частей равной длины. С помощью теоремы о лучах это можно сделать только с помощью циркуля и линейки, так как для этого проводят следующий луч от углового наконечника A и проводят на n равных расстояниях от углового наконечника с помощью циркуля. Затем соединяют конечную точку последнего пути с точкой D и отрезками угла и проводят параллели этому маршруту через n-1, дальнейший путь заканчивается на балке угловой вершины A. Точки пересечения параллелей с отрезком угла AC разделите отрезок AD на n отрезков равной длины. Теперь вы строите n-1 окружностей, которые имеют точку угла A в качестве центра и проходят через n-1 конечные точки сегментов AD. Наконец, соединяют n-1 точек пересечения n-1 окружностей со спиралью с угловым наконечником A, и, таким образом, получается разделение угла BAC на n равных углов.
Чтобы возвести окружность в квадрат с радиусом r, сначала постройте две взаимно перпендикулярные оси координат через его центральную точку M и создайте спираль Архимеда в этой системе координат . В спираль пересекает ось у в точке Е, а длина в сегменте МЕ является единицы длины, так как связанного угла поворота спирали есть. Тогда прямоугольник с диаметром окружности 2r имеет длину и | ME | та же площадь, что и круг . Затем с помощью теоремы Евклида о высоте прямоугольник можно преобразовать в квадрат той же площади .рπ2{\ displaystyle {\ tfrac {r \ pi} {2}}}π2{\ displaystyle {\ tfrac {\ pi} {2}}}
Сам Архимед использовал другой метод, чтобы возвести круг в квадрат . Сначала он построил спираль за один полный оборот в системе координат с началом O, так что эта положительная половина оси x пересекается в P. Тангенс спирал в точке Р пересекает ось ординат в Т и прямоугольный треугольник OPT равен по площади к окружности с центральной O и радиусом OP. Этот треугольник можно легко преобразовать в прямоугольник той же площади, разделив пополам один из двух катетов, который можно преобразовать в квадрат с той же площадью, что и выше, с помощью теоремы Евклида о высотах .
Исторический
Архимед описал названную в его честь спираль в 225 г. {\ tfrac {1} {d}}}d∈Р.{\ displaystyle d \ in \ mathbb {R}}dзнак равно1,бзнак равно0{\ displaystyle d = 1, \, b = 0}dзнак равно2,бзнак равно0{\ displaystyle d = 2, \, b = 0}dзнак равно-2,бзнак равно0{\ displaystyle d = -2, \, b = 0}dзнак равно-1,бзнак равно0{\ displaystyle d = -1, \, b = 0}

Приложения
Лакричные улитки в форме архимедовой спирали
Рекорды как приложение спиралей Архимеда
Многие носители информации используют, по крайней мере, приблизительно принцип архимедовой спирали, поэтому ленты для хранения (например, аудио- и видеокассеты ) сворачиваются в виде спирали. Дорожки на пластинках или компакт-дисках также расположены в форме архимедовой спирали, что позволяет считывающей головке читать любой объем данных линейно ( последовательно ), не прерывая смены дорожки .
Жесткие диски для произвольного доступа, однако использовать с начала блоков / круговых сегментов на концентрически расположенных кругах .
литература
Д. Д. Соколов: Спираль Архимеда . В энциклопедии математики, том 1, с. 240
Клауди Альсина, Роджер Б. Нельсен: Очаровательные доказательства: Путешествие в элегантную математику . MAA 2010, ISBN 978-0-88385-348-1, стр. 145-146 ( отрывок () )
Янош Акзель, Клауди Альсина: Трисекция углов, классические кривые и функциональные уравнения . Математический журнал, Том 71, № 3 (июнь 1998 г.), стр. 182-189 ( 2691201 )
Александр Остерманн, Герхард Ваннер: Геометрия по ее истории . Springer, 2012, ISBN 978-3-642-29163-0, стр. 81-82
Мидхат Дж. Газале: Гномон: от фараонов до фракталов . Princeton University Press, 1999, ISBN 978-0-691-00514-0, стр. 168-171
Мартин Гарднер: Неожиданное зависание и другие математические отклонения . University of Chicago Press, 1969, стр. 103-107.
веб ссылки
Commons : спираль Архимеда — коллекция изображений, видео и аудио файлов
Эрик В. ^A^b Клауди Альсина, Роджер Б. Нельсен: Очаровательные доказательства: Путешествие в элегантную математику . MAA 2010, ISBN 978-0-88385-348-1, стр. 145-146 ( отрывок () )
↑ Жан-Поль Делахай: π — История . Springer, 2013 г., ISBN 978-3-0348-5085-8, стр. 75
<img src=»//de.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»»>
Связь между декартовыми и полярными координатами
Главная | Обратная связь

⇐ ПредыдущаяСтр 3 из 3
Пару полярных координат r и можно перевести в Декартовы координаты x и y путём применения тригонометрических функций синуса и косинуса:
x = rcos φ,
y = rsin φ,
в то время как две декартовы координаты x и y могут быть переведены в полярную координату r:
r² = y² + x² (по теореме Пифагора).
Для определения угловой координаты следует принять во внимание два следующие соображения:
Для , может быть произвольным действительным числом.
Для , чтобы получить уникальное значение , следует ограничиться интервалом в 2π. Обычно выбирают интервал или .
Для вычисления в интервале , можно воспользоваться такими уравнениями (arctg обозначает обратную функцию к тангенсу):
Для вычисления в интервале , можно воспользоваться такими уравнениями:^[14]
Учитывая, что для вычисления полярного угла не достаточно знать отношение y к x, а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо функции atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты x.
Уравнение кривых в полярных координатах
Благодаря радиальной природе полярной системы координат, некоторые кривые могут быть достаточно просто описаны полярным уравнением, тогда как уравнение в прямоугольной системе координат были бы намного сложнее. Среди самых известных кривых: полярная роза, архимедова спираль, Лемниската, улитка Паскаля и кардиоида.
Окружность
Круг, заданный уравнением .
Общее уравнение окружности с центром в ( ) и радиусом a имеет вид:
Это уравнение может быть упрощено для частных случаев, например
r(φ) = a
является уравнением, определяющим окружность с центром в полюсе и радиусом a.^[15]
Прямая
Радиальные прямые (те, которые проходят через полюс) определяются уравнением
φ = θ,
где θ — угол, на который прямая отклоняется от полярной оси, то есть, где m — наклон прямой в прямоугольной системе координат. Нерадиальная прямая, перпендикулярно пересекает радиальную прямую φ = θ в точке определяется уравнением
r(φ) = r₀sec(φ − θ).
Полярная роза
Полярная роза задана уравнением .
Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:
r(φ) = acos(kφ + θ₀)
для произвольной постоянной θ₀ (включая 0). Если k — целое число, то это уравнение будет определять розу с k лепестками для нечётных k, либо с 2k лепестками для чётных k. Если k — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная a определяет длину лепестков.
Если считать, что радиус не может быть отрицательным, то при любом натуральном k мы будем иметь k — лепестковую розу. Таким образом, уравнение r(φ) = cos(2φ) будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.
Спираль Архимеда
Одна из ветвей спирали Архимеда, задаваемая уравнением для .
Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:
r(φ) = a + bφ.
Изменения параметра a приводят к повороту спирали, а параметра b — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для φ > 0 а другую для φ < 0. Две ветви плавно соединяются в полюсе. Зеркальное отображение одной ветви относительно прямой, проходящей через угол 90°/270°, даст другую ветвь. Эта кривая интересна тем, что была описана в математической литературе одной из первых, после конического сечения, и лучше других определяется именно полярным уравнением.
[править] Конические сечения
Эллипс.
Коническое сечение, один из полюсов которого находится в полюсе, а другой где-то на полярной оси (так, что малая полуось лежит вдоль полярной оси) задаётся уравнением:
где e — эксцентриситет, а — фокальный параметр. Если e > 1, это уравнение определяет гиперболу; если e = 1, то параболу; если e < 1, то эллипс. Отдельным случаем является e = 0, определяющее окружность с радиусом .
Комплексные числа
Пример комплексного числа , нанесённого на комплексную плоскость.
Пример комплексного числа, нанесённого на график, с использованием формулы Эйлера.
Каждое комплексное число может быть представлено точкой на комплексной плоскости, и, соответственно, эта точка может определяться в декартовых координатах (прямоугольная или декартова форма), либо в полярных координатах (полярная форма). Комплексное число z может быть записано в прямоугольной форме так:
z = x + iy,
где i — мнимая единица, или в полярной (см. формулы преобразования между системами координат выше):
и отсюда:
z = reⁱ^φ,
где e — число Эйлера. Благодаря формуле Эйлера, оба представления эквивалентны^[16] (Следует отметить, что в этой формуле, подобно остальным формулам, содержащим возведения в степень углов, угол задан в радианах)
Для перехода между прямоугольным и полярным представлением комплексных чисел, могут использоваться указанные выше формулы преобразования между системами координат.
Операции умножения, деления и возведения в степень с комплексными числами, как правило, проще проводить в полярной форме. Согласно правилам возведения в степень:
Умножение:
Деление:
Возведение в степень (формула Муавра):
(reⁱ^φ)ⁿ = rⁿeⁱⁿ^φ.

Векторный анализ
Для полярных координат можно применить элементы векторного анализа. Любое векторное поле можно записать в полярной системе координат, используя единичные векторы:
в направлении , и
Связь между декартовыми компонентами поля F_x и F_y и его компонентами в полярной системе координат задаётся уравнениями:
F_x = F_rcos φ − F_φsin φ;
F_y = F_rsin φ + F_φcos φ.

⇐ Предыдущая123

©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.
исчисление — Дифференцировать спираль Архимеда
спросил 7 лет, 9 месяцев назад
Изменено 5 лет, 5 месяцев назад
Просмотрено 4к раз
$\begingroup$
Я читал, что единственная задача дифференциального исчисления, решенная Архимедом, заключалась в построении касательной к его спирали, $$r = а + b\тета$$ Я хотел бы дифференцировать это, но я мало знаю о дифференциации полярных функций и не могу найти эту конкретную проблему в Интернете. Как можно вычислить касательную к кривой в точке $\theta$, не читая мне полный курс дифференциальной геометрии?
исчисление
дифференциальная геометрия
$\endgroup$
7
$\begingroup$
Пусть $r(\theta)=a+b\theta$ уравнение архимедовой спирали.
Декартовы координаты точки с полярными координатами $(r,\theta)$ равны $$\влево\{\begin{выравнивание} х (г, \ тета) & = г \ соз \ тета \\ у(г,\тета)&=г\грех\тета \end{выравнивание}\right. $$ значит точка на спирали имеет координаты $$\влево\{\begin{выравнивание} х (\ тета) & = г (\ тета) \ соз \ тета = (а + б \ тета) \ соз \ тета \\ у(\тета)&=г(\тета)\грех\тета=(а+б\тета)\грех\тета \end{выравнивание}\right. $$ Отличие у нас есть $$ \ влево \ {\ начать {выравнивание} х'(\тета)&=b\cos\тета-(а+b\тета)\грех\тета\\ у'(\тета)&=b\sin\тета+(а+b\тета)\cos\тета \end{выравнивание}\right. $$ Параметрическое уравнение прямой, касательной к спирали в точке $(r(\theta_0),\theta_0)$, имеет вид $$ \ влево \ {\ начать {выравнивание} x(\theta)&=x(\theta_0)+x'(\theta_0)(\theta-\theta_0)=x(\theta_0)+[b\cos\theta_0-(a+b\theta_0)\sin\ тета_0](\тета-\тета_0)\\ y(\theta)&=y(\theta_0)+y'(\theta_0)(\theta-\theta_0)=x(\theta_0)+[b\sin\theta_0+(a+b\theta_0)\cos\theta_0 ](\тета-\тета_0) \end{выравнивание}\right. $$ или в декартовой форме $$ y(\theta)-y(\theta_0)=\frac{y'(\theta_0)}{x'(\theta_0)}[x(\theta)-x(\theta_0)]=\frac{b\sin \theta_0+(a+b\theta_0)\cos\theta_0}{b\cos\theta_0-(a+b\theta_0)\sin\theta_0}[x(\theta)-x(\theta_0)] $$ где наклон линии $$ \frac{y'(\theta)}{x'(\theta)}=\frac{{\operatorname{d}y}{\operatorname{d}x}=\frac{b\sin\theta+(a+b \theta)\cos\theta}{b\cos\theta-(a+b\theta)\sin\theta}=\frac{b\tan\theta+(a+b\theta)}{b-(a+ б\тета)\загар\тета} $$
$\endgroup$
$\begingroup$
Типичная точка на кривой $(x,y)=((a+b\theta)\cos\theta,(a+b\theta)\sin\theta)$.
По правилу произведения имеем \начать{выравнивать} dx & = (b\cos\theta-(a+b\theta)\sin\theta)\,d\theta, \\ dy & = (b\sin\theta+(a+b\theta)\cos\theta)\,d\theta. \end{выравнивание} Таким образом, наклон в $(x,y)$ равен $$ \frac{dy}{dx} = \frac{b\sin\theta+(a+b\theta)\cos\theta}{b\cos\theta-(a+b\theta)\sin\theta}. $$
В случае $a=0$ становится $$ \ гидроразрыва {\ гидроразрыва у \ тета + х} {\ гидроразрыва х \ тета — у} = \ гидроразрыва {у + \ тета х} {х- \ тета у}. \тег{$*$} $$ На самом деле я не знаю, полезна ли эта последняя форма для рисования графика.
Можно также написать $(*)$ как $$ \ frac {\ frac y x + \ theta} {1 — \ theta \ frac y x} = \ frac {\ tan \ theta + \ theta} {1- \ theta \ tan \ theta} = \ frac {\ tan \ tan \ eta + \tan\eta}{1-\tan\eta\tan\tan\eta} = \tan(\eta+\tan\eta) $$ где $\тета=\тан\эта$.
$\endgroup$
3
$\begingroup$
Вы можете параметризовать его в декартовой плоскости как $$s(t)=\begin{pmatrix}bt\cos(t-a/b)\\bt\sin(t-a/b)\end{pmatrix}$$ Таким образом, направление касательной в точке $s(t)$ определяется выражением $$s'(t)=\begin{pmatrix}b\cos(t-a/b)-bt\sin(t-a/b)\\b\sin(t-a/b)+bt\cos(t-a/b)\ конец{pmatrix}$$
$\endgroup$
8
$\begingroup$
Это гораздо легче проглотить в сложных переменных. Пусть 9{-1}\frac{\mathfrak{Im}(\dot z)}{\mathfrak{Re}(\dot z)}$$
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Как построить параметризованную геометрию архимедовой спирали
Архимедовы спирали часто используются при анализе катушек индуктивности, спиральных теплообменников и микрожидкостных устройств. Сегодня мы продемонстрируем, как построить спираль Архимеда, используя аналитические уравнения и их производные для определения набора спиральных кривых. Затем на основе этих кривых мы создадим 2D-геометрию определенной толщины, выдавливая ее в полноценную 3D-геометрию.
Краткое введение в архимедовы спирали
Широко распространенные в природе спирали или спирали используются во многих технических проектах. Например, как инженер-электрик, вы можете наматывать катушки индуктивности по спирали и проектировать спиральные антенны. Как инженер-механик, вы можете использовать спирали при проектировании пружин, косозубых шестерен или даже часового механизма, показанного ниже.

Пример использования спирали Архимеда в часовом механизме. Изображение Гребеля Форси. Лицензия CC BY-SA 3.0, через Wikimedia Commons.
Здесь мы сосредоточимся на конкретном типе спирали, который представлен в показанном выше механизме: спирали Архимеда. Спираль Архимеда — это разновидность спирали с фиксированным расстоянием между последовательными витками. Это свойство позволяет широко использовать его в конструкции плоских катушек и пружин.
Мы можем описать архимедову спираль следующим уравнением в полярных координатах: последнее из которых равно 2 \pi b. Обратите внимание, что спираль Архимеда также иногда называют спиралью 9.0102 арифметическая спираль . Это название происходит от арифметической прогрессии расстояния от начала координат до точки на том же радиале.
Проектирование параметризованной геометрии архимедовой спирали
Теперь, когда мы познакомились с архимедовыми спиралями, давайте посмотрим, как параметризовать и создать такой дизайн для анализа в COMSOL Multiphysics.

Спираль Архимеда может быть описана как в полярных, так и в декартовых координатах.
Для начала нам нужно преобразовать уравнения спирали из полярной в декартову систему координат и выразить каждое уравнение в параметрической форме:
\begin{align*}
x_{component}=rcos(\theta) \\
y_{component}=rsin(\theta)
\end{align*}
Это преобразование позволяет нам переписать спираль Архимеда уравнение в параметрической форме в декартовой системе координат:
\begin{align*}
x_{component}=(a+b\theta)cos(\theta) \\
y_{component}=(a+b\ theta)sin(\theta)
\end{align*}
В COMSOL Multiphysics необходимо выбрать набор параметров, которые будут определять спиральную геометрию. Этими параметрами являются начальный радиус спирали a_{initial}, конечный радиус спирали a_{final} и желаемое количество витков n. Тогда скорость роста спирали b может быть выражена как:
b=\frac{a_{final}-a_{initial}}{2 \pi n}
Далее нам нужно определить начальный угол спирали theta_0 и конечный угол theta_f. Начнем со значений theta_0=0 и theta_f=2 \pi n. С помощью этой информации мы можем определить набор параметров для геометрии спирали.

Параметры, используемые для построения спиральной геометрии.
Чтобы построить эту спираль, мы начнем с 3D-компонента и создадим рабочую плоскость в Геометрия филиал. Затем в геометрию Work Plane мы добавляем параметрическую кривую и используем упомянутые выше параметрические уравнения с переменным углом, чтобы нарисовать 2D-версию спирали Архимеда. Эти уравнения можно ввести непосредственно в поле Expression параметрической кривой, или мы можем сначала определить каждое уравнение в новой функции Analytic следующим образом:
\begin{align*}
X_{fun}=(a+bs) cos(s) \\
Y_{fun}=(a+bs)sin(s) \\
\end{align*}

X-компонент уравнения спирали Архимеда, заданный в Аналитической функции.
Функцию Analytic можно использовать в выражениях для параметрической кривой. В этой параметрической кривой мы изменяем параметр s от начального угла спирали, theta_0, до конечного угла спирали, theta_f=2 \pi n.

Настройки функции «Параметрическая кривая».
Уравнения параметрической спирали, используемые в функции «Параметрическая кривая», приведут к получению спирали, представленной кривой. Теперь давайте возьмем за основу эту геометрию, увеличив ее толщину, чтобы создать 2D-тело.
До этого момента наша спираль была параметризована с точки зрения начального радиуса a_{начальный}, конечного радиуса a_{конечный} и желаемого количества витков n. Теперь мы должны включить толщину в качестве еще одного управляющего параметра в уравнение спирали.
Начнем с основного свойства спирали, которое гласит, что расстояние между витками спирали равно 2 \pi b. Это также эквивалентно \frac{a_{final}-a_{initial}}{n}. Чтобы включить толщину, мы представляем расстояние между каждым последующим витком спирали как сумму толщины спирали и оставшегося зазора между витками, толщина+зазор.

Расстояние между витками спирали определяется параметрами толщины спирали и зазора.
Для контроля толщины и получения одинакового расстояния между витками это расстояние можно выразить следующим образом:
\begin{align*}
Distance=\frac{a_{initial}-a_{final}}{n} \\
gap=distance-thick
\end{align*}
После определения толщины и выражения зазора между витками через толщину и постоянное расстояние между центральными линиями спирали мы можем переписать параметр роста спирали через толщину как:
\begin{align*}
Distance=2\pi b \\
b=\frac{gap+thick}{2\pi}
\end{align*}
Мы также хотим выразить конечный угол спирали с точки зрения ее начального и конечного радиусов:
\begin{align*}
\theta_{final}=2 \pi n \\
a_{final}=\text{общее расстояние}+a_{initial} \\
a_{final}=2 \pi bn+a_{initial} \\
n=\frac{a_{final}-a_{initial}}{2 \pi b} \\
\theta_{final}= \frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \\
\theta_{final}=\frac{a_{final}-a_{initial}}{b}
\end{align*}
Хотите начать спираль под углом, отличным от нуля? Если это так, вам нужно будет добавить этот начальный угол к вашему конечному углу в выражении для параметра: theta_f=\frac{a_{final}-a_{initial}}{b}+theta_0.
Дважды дублируя существующую спиральную кривую и размещая эти кривые со смещением -\frac{thick}{2} и +\frac{thick}{2} относительно исходной спиральной кривой, мы можем построить спираль с толщина. Чтобы правильно расположить верхнюю и нижнюю спирали, мы должны убедиться, что смещенные спирали перпендикулярны исходной спиральной кривой. Этого можно добиться, умножив расстояние смещения \pm\frac{thick}{2} на единичный вектор, перпендикулярный спиральной кривой. Уравнения векторов нормали к кривой в параметрической форме таковы: 92 }}
\end{align*}
, где каждый N_x и N_y определяется с помощью функции Analytic в COMSOL Multiphysics, аналогично тому, как мы определили X_{fun} и Y_{fun} для первой параметрической кривой. Внутри функции мы используем оператор дифференцирования d(f(x),x) для получения производной, как показано на следующем снимке экрана.

Примеры оператора производной, используемого в Аналитической функции .
Функции X_{fun}, Y_{fun}, N_x и N_y можно использовать непосредственно в выражениях параметрической кривой для кривой с одной стороны:
\begin{align*}
x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\
y_{lower}=Y_{fun}(s)+ N_y(s)\frac{thick}{2}
\end{align*}
Функции также можно использовать для кривой на другой стороне:
\begin{align*}
x_{upper}=X_ {fun}(s)-N_x(s)\frac{thick}{2} \\
y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2}
\end {align*}

Уравнения для второй из двух параметрических кривых смещения.
Чтобы соединить концы двух кривых, мы добавляем еще две параметрические кривые, используя небольшую модификацию уравнений, упомянутых выше. Для кривой, соединяющей центр спирали, мы должны оценить X_{веселье}, Y_{веселое}, N_x и N_y для начального значения угла, тета. Для кривой, соединяющей внешнюю сторону спирали, мы должны оценить конечное значение тета. Следовательно, кривая соединения в центре:
\begin{align*}
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{thick}{2} \\
Y_{fun}(theta_0)+s\cdot N_y( theta_0)\cdot\frac{thick}{2}
\end{align*}
Между тем внешняя кривая соединения:
\begin{align*}
X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot\frac{thick}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
В обоих приведенных выше уравнениях s изменяется от -1 до +1, как показано на снимке экрана ниже.

Уравнения для кривой, соединяющей один конец спирали.
Теперь у нас есть пять кривых, которые определяют осевую линию спирали и все четыре стороны профиля. Мы можем отключить (или даже удалить) кривую, описывающую осевую линию, так как она на самом деле не нужна, оставив только контур спирали. Определив контур нашей спирали, можно использовать операцию Convert to Solid для создания единого геометрического объекта. Эта 2D-спираль, наконец, может быть выдавлена в 3D с помощью Операция вытягивания .

Полная последовательность геометрии и экструдированная трехмерная спиральная геометрия.
Заключительные замечания по моделированию архимедовых спиралей в COMSOL Multiphysics
Мы провели вас через этапы создания полностью параметризованной архимедовой спирали. С помощью этой спиральной геометрии вы можете изменить любой из параметров и поэкспериментировать с различными конструкциями или даже использовать их в качестве параметров в исследовании оптимизации. Мы рекомендуем вам использовать этот метод в ваших собственных процессах моделирования, продвигая анализ вашего конкретного инженерного проекта на основе спирали.
Дополнительные ресурсы по проектированию и анализу спиралей
Чтобы изучить дополнительные возможности моделирования при проектировании спиральных моделей, попробуйте эту учебную модель: Спиральная щелевая антенна
Прочтите соответствующую историю пользователя: «Анализ спиральных резонаторных фильтров»
Полярная сила | plus.maths.org
Декартовы координаты.
Большинство из нас знакомы с декартовой системой координат, которая присваивает каждой точке плоскости две координаты. Чтобы найти, вы начинаете с точки и проходите расстояние по горизонтальной оси и расстояние по вертикальной оси (см. изображение справа).
Но есть и другой способ нахождения точек на плоскости, тоже очень удобный. Каждой точке присвойте пару чисел , где расстояние от до вдоль прямой радиальной линии, а угол, образованный этой радиальной линией и положительной осью, измеренный против часовой стрелки от -оси до линии. Эти новые координаты называются полярными координатами , потому что вы рассматриваете точку пересечения осей как полюс, от которого исходит все.
На изображении ниже щелкните точку и перетащите ее, чтобы увидеть, как меняются ее полярные координаты (градусы измеряются в радианах).
Как выразить простые формы в полярных координатах? Как видно из интерактивности выше, луч, начинающийся в точке, задается определенным значением угла. Например, положительная -ось описывается уравнением

, а луч, который делит вдвое угол между положительной и -осями, задается уравнением

Обычно уравнение

описывает луч, который начинается и образует угол с положительной осью.
А круги? Окружность с центром в радиусе состоит из всех точек, которые лежат на расстоянии от . Таким образом, мы можем описать окружность в полярных координатах, используя уравнение

Это выражение намного проще, чем уравнение окружности в декартовых координатах, которое равно

Полярные уравнения, описывающие прямые, не проходящие через точку (0,0), и окружности, не имеющие центра в (0,0), сложнее, чем их декартовы версии (см. здесь). Но есть фигуры, описание которых с использованием полярных координат намного проще, чем их декартовы аналоги. Вот три наших любимых примера.
Спирали Архимеда
Рассмотрим все точки, полярные координаты которых удовлетворяют уравнению

другими словами смотрим точки с полярными координатами Где они?
Анимация ниже показывает луч, соответствующий углу, в диапазоне от 0 до . Точка, отмеченная на луче, имеет координаты. По мере увеличения точка перемещается дальше от (Щелкните значок воспроизведения в нижнем левом углу или используйте ползунок для изменения.)
У нас начало спирали!
Но зачем останавливаться на ? Вы можете продолжать поворачивать радиальную линию более чем на один полный оборот, через полтора оборота (), два оборота () и так далее, по кругу. Затем при еще одном полном обороте от до расстояние до точки с координатами увеличивается еще больше, от до . Отпуск от до дает нам еще один полный оборот с перемещением точек еще дальше. Анимация ниже показывает спираль, которую вы получаете, изменяя значение от 0 до 9.0005
Увеличение до бесконечности дает спираль, которая закручивается бесконечное количество раз:

Эта красивая форма называется спиралью Архимеда, названной в честь великого греческого математика Архимеда, открывшего ее в третьем веке до нашей эры. Как видно из рисунка, витки спирали расположены равномерно: если провести радиальную линию из , то расстояние между двумя последовательными точками пересечения со спиралью всегда равно .
Существуют и другие спирали Архимеда, все они характеризуются тем, что радиальная линия пересекает спираль через равные промежутки времени. Их можно охарактеризовать уравнением

для положительного действительного числа. Поэкспериментировав с различными значениями for, вы можете убедиться, что они контролируют, насколько плотно закручена спираль, и, следовательно, расстояние между последовательными точками пересечения вдоль радиальной линии. Для получения психоделического опыта (или чтобы вызвать у себя головную боль) попробуйте анимацию ниже, показывающую спирали Архимеда с изменением от 5 до 0,9.0005
Если вы предпочитаете физическую интерпретацию, спираль Архимеда — это то, что вы получите, если проследите траекторию точки, удаляющейся от центра с постоянной скоростью вдоль линии, вращающейся с постоянной угловой скоростью.
Логарифмические спирали
Теперь рассмотрим все точки, полярные координаты которых удовлетворяют уравнению

где — основание натурального логарифма, .
При , получаем

Итак, наша фигура содержит точку с полярными координатами (декартовы координаты которой также равны ). На анимации ниже показана радиальная линия, соответствующая углу при изменении его от до. Точка с координатами также отмечена. Снова мы видим начало спирали, но на этот раз другой.
Опять же, мы можем оставить диапазон за пределами , через , и так далее, получая спираль, которая закручивается любое количество раз. Однако на этот раз петли спирали расположены неравномерно.

Это пример логарифмической спирали . Он носит такое название, потому что вместо

можно написать

где натуральный логарифм по основанию.
(Существует также более общая форма логарифмической спирали, задаваемая уравнением
где и — положительные действительные константы. )
Но здесь мы можем сыграть еще одну хитрость: мы можем позволить углу стать отрицательным! Чтобы найти точку с отрицательной второй полярной координатой, нужно измерить угол от положительной -оси в другом направлении: по часовой стрелке . Например, точка с полярными координатами лежит на отрицательной части оси -.
Что это означает для нашей логарифмической спирали? По мере движения от к отрицательной бесконечности радиальная линия задается поворотами по часовой стрелке через один, два, три и любое количество оборотов. Точки с координатами

лежат на этой радиальной линии. Но теперь по мере убывания к отрицательной бесконечности точки движутся внутрь, к
, так что если очень отрицательное, то это очень большое число, поэтому оно положительное и очень близко к 0. 0005
Диапазон от отрицательной до положительной бесконечности создает спираль, бесконечную в обоих направлениях, у нее нет ни начала, ни конца.
Полная логарифмическая спираль.

Но подождите секунду. Это изображение выглядит почти так же, как и то, которое вы видите на анимации выше, хотя оси x и y здесь охватывают гораздо меньший диапазон, как вы можете видеть из меток! Это иллюстрирует очень интересное свойство логарифмических спиралей. Если вы увеличиваете или уменьшаете изображение логарифмической спирали, изображение, которое вы видите, выглядит точно так же, как и до увеличения. Эта функция называется самоподобие . Возможно, поэтому логарифмические спирали так распространены в природе. Их можно увидеть в изгибах раковины улитки, во многих растениях и даже в рукавах спиральных галактик. Математик XVII века Якоб Бернулли был настолько очарован этой прекрасной формой, что назвал ее «spiral mirabilis» (чудесная спираль) и попросил выгравировать ее на своем надгробном камне вместе с фразой «Хоть и изменившись, я восстану такой же. » К сожалению, граверы ошиблись, и вместо этого на его могиле осталась архимедова спираль.
Полярные розы
Для нашей окончательной формы или, скорее, семейства фигур, начнем с рассмотрения уравнения

(Символ || обозначает абсолютное значение , поэтому мы рассматриваем только положительные числа для .)
Чтобы понять, что здесь происходит, давайте сначала вспомним форму функции синуса, построенную по горизонтали ось против вертикальной:
Применение абсолютного значения означает, что части волны, находящиеся ниже горизонтальной оси (для которой отрицательное значение), переворачиваются, чтобы лежать над ней: максимум 1 (в ) и обратно до 0.
Теперь вернемся к нашим полярным координатам. Как колеблется от до , расстояние до наших точек

Теперь поднимем ставки и рассмотрим уравнение

Новый коэффициент 2 означает, что две петли, которые ранее появлялись для диапазона от до, теперь отображаются только для диапазона только от до . Это означает, что обе петли возникают в верхней полуплоскости и также становятся немного сплющенными. По мере продвижения от к значение колеблется от до Поскольку синусоидальная функция является периодической (она имеет то же значение для , что и для ), зеркальное отображение нашей пары петель также появляется в нижней полуплоскости:
У нас есть цветок с четырьмя лепестками!
Что произойдет, если мы рассмотрим уравнение

где любое положительное целое число? Вы угадали! У вас получится цветок с лепестками — ниже мы покажем вам результаты для и .. Удивительно, на что способны полярные координаты!
Об авторе
Марианна Фрейбергер является редактором Plus .
Визуализация данных на спиралях
Визуализация данных на спиралях
Цзугуан Гу ([email protected])
2022-07-26
Спираль Архимеда
Макет спирали
Создать треки
Графические функции
Очки
строк
сегментов
Прямоугольники
Бары
полигонов
Текст
Ось
Карта горизонта
Изображения
Стрелки
Изюминка
Дендрограммы и филогенетические деревья
Вспомогательные функции
Информация о сеансе
Эта виньетка создана с помощью Spiralize 1. 0.5.
В этой виньетке я описываю пакет Spiralize , который визуализирует данные по спирали Архимеда. Он имеет два основных преимущества для визуализации:
Позволяет визуализировать данные по очень длинной оси с высоким разрешением.
Для данных временных рядов эффективно выявлять периодические закономерности.
Спираль Архимеда
В полярных координатах ($r$, $\theta$) спираль Архимеда имеет следующий вид:
\[ r = b \cdot \theta \]
где \ (b\) управляет расстоянием между двумя петлями. Радиальное расстояние между двумя соседними петлями для данного $\theta$ равно:
\[ d(\theta) = r(\theta + 2\pi) — r(\theta) = b \cdot (\theta + 2\pi) — b \cdot \theta = b \cdot 2\pi \]
Это показывает, что радиальное расстояние между двумя соседними контурами не зависит от значения $\theta$ и является постоянным значением. На следующем рисунке показана архимедова спираль с 4 петлями ($\theta \in [0, 8\pi]$).
Примечание $\theta$ также могут быть отрицательными значениями, если спираль отражается по оси y (в декартовых координатах). В по спирали мы рассматриваем только $\theta$ как положительные значения. Зеркальную спираль можно установить с помощью 9Аргумент 0253 flip , который представлен позже в этой виньетке.
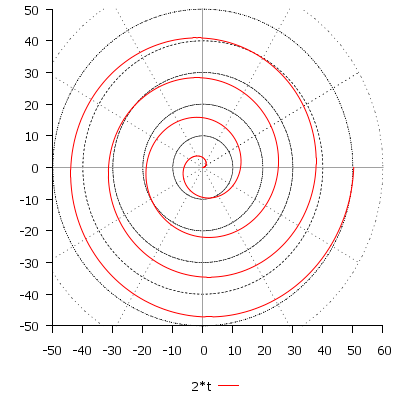
Поскольку расстояние между любыми двумя соседними петлями для любого заданного $\theta$ является постоянным, это идеальное место для размещения дорожек вдоль спирали, где дорожки везде имеют одинаковую радиальную высоту. Позже треки можно использовать в качестве виртуальных систем координат для сопоставления с данными. Вот почему пакет называется « Spiralize » (чтобы преобразовать обычную декартову систему координат в форму изогнутой спирали). Следующие два рисунка демонстрируют спираль с одной дорожкой и с двумя дорожками. Красная линия — это сама спираль. Спираль колеблется между $\pi/2$ и $6\pi$. Легко видеть, что верхняя граница каждой дорожки также является спиралью, но со смещением $a$:
\[ r = a + b \cdot \theta \]
где $a$ — это смещение относительно «основной спирали» (красная спираль на следующих графиках).
Обозначим максимальный радиус спирали как $d_{max} = b \cdot \theta_{max}$, а длину спирали обозначим как $l$ (которая имеет сложную форму, см. https://downloads.imagej.net/fiji/snapshots/arc_length.pdf), мы можем рассматривать $2d_{max}$ как разрешение визуализации, применяемой в обычной декартовой системе координат, а $l$ как разрешение визуализации, нанесенной на спираль. Тогда отношение двух разрешений равно: 92}}{4} \]
Когда $\theta$ становится большим,
\[ отношение \приблизительно \frac{\mathrm{ln}(\theta + \theta)}{4\theta} + \ frac{\theta}{4} \приблизительно \frac{\theta}{4} \]
Обозначим $k$ как количество петель, т.е. $\theta = 2\pi \cdot k$, тогда
\[отношение \приблизительно \frac{\theta}{4} = \frac{\pi}{2} \cdot k \]
Макет спирали
Для инициализации спирали используется функция Spiral_initialize() . Аргументы начинаются с и и управляют угловым диапазоном спирали. Здесь значения должны быть в градусах, и они внутренне конвертируются в радианы.
В спирализации параметр $b$ в уравнении спирали $r = b \cdot \theta$ устанавливается равным $b = 1/2\pi$, так что расстояние между двумя соседние петли равны $d = 1$. Обозначьте $\theta_e$ как конечный угол (в радианах) спирали, диапазоны окна просмотра (в графической системе сетки ) по осям x и y -оси, которые рисуют спираль, это $[-x, x]$ где
\[x = b \cdot \theta_e + d = 1/2\pi \cdot \theta_e + 1\]
На следующих двух графиках показаны разные значения start и end . Также, как показано в следующем примере кода, я предлагаю установить значения start и end в виде 360*a + b , например 360*4 + 180 , чтобы было просто узнать положения в полярных координатах и количество петель в спирали (я думаю, что люди должны чувствовать себя более естественно с градусами, чем с радианами).
 # левый участок
спираль_инициализировать (начало = 90, конец = 360)
спираль_трек()
# правильный сюжет
спираль_инициализировать (начало = 180, конец = 360 * 4 + 180)
Spiral_track() 
Аргумент flip определяет, как переворачивать спираль. Он принимает одно из четырех значений: "нет" / "горизонтальный" / "вертикальный" / "оба" . Примеры следующие. В примерах я дополнительно добавляю оси в дорожках, чтобы показать, в каком направлении распространяются данные по спирали. Я также вручную регулирую высоту гусеницы, чтобы было достаточно места для осей.
 # верхний левый график
spiral_initialize(flip = "none") # по умолчанию
спираль_трек (высота = 0,6)
ось_спирали()
# верхний правый график
спираль_инициализировать (флип = "горизонтально")
спираль_трек (высота = 0,6)
ось_спирали()
# нижний левый график
спираль_инициализировать (флип = "вертикальный")
спираль_трек (высота = 0,6)
ось_спирали()
# нижний правый график
спираль_инициализировать (флип = "оба")
спираль_трек (высота = 0,6)
спираль_ось() 
Более просто, вы можете напрямую установить по часовой стрелке = ИСТИНА , чтобы изменить ориентацию спирали. Сравните следующие графики:
 # верхний левый график
спираль_инициализировать (начало = 45 + 360) # по умолчанию
спираль_трек (высота = 0,6)
ось_спирали()
# верхний правый график
спираль_инициализировать (начало = 45 + 360, по часовой стрелке = ИСТИНА)
спираль_трек (высота = 0,6)
ось_спирали()
# нижний левый график
спираль_инициализировать (начало = 135 + 360)
спираль_трек (высота = 0,6)
ось_спирали()
# нижний правый график
спираль_инициализировать (начало = 135 + 360, по часовой стрелке = ИСТИНА)
спираль_трек (высота = 0,6)
спираль_ось() 
Аргумент scale_by управляет линейным масштабированием данных на спирали. Он допускает значение "угол" или "curve_length" (или для краткости "кривая" ). "угол" означает, что равная разница в данных соответствует равной разнице углов в полярных координатах. "curve_length" означает, что равная разница в данных соответствует равной разнице в длине спирали. Обратите внимание, как деления оси распределяются на следующих двух графиках. Также полярные линии удалены на scale_by = "длина_кривой" .
 # левый участок
spiral_initialize(scale_by = "угол") # по умолчанию
спираль_трек (высота = 0,6)
ось_спирали()
# правильный сюжет
спираль_инициализировать (масштаб_по = "curve_length")
спираль_трек (высота = 0,6)
спираль_ось() 
Следующие тепловые карты могут быть более четкими, чтобы продемонстрировать разницу между "угол" и "curve_length" . В этом примере каждая сетка имеет одинаковый размер ячейки данных.
Как вы можете видеть, когда scale_by установлено в "угол" , во внешних циклах, даже когда фактическая разница в данных одинакова, физическая ширина больше, чем во внутренних циклах. Тем не менее, когда данные представляют собой временные ряды или периодические данные, 90 253 «угол» 90 254 является правильным выбором, потому что легко напрямую сравнивать циклы, которые являются одними и теми же временными точками в разные периоды. Для сравнения, "curve_length" не будет предоставлять никакой периодической информации.
Спираль растет от внутренних циклов к внешним, таким образом, по умолчанию данные увеличиваются и от внутренних циклов. Это можно изменить, установив аргумент reverse = TRUE . См. следующий пример, а также обратите внимание на оси. Красные стрелки указывают направление осей.
 # левый участок
спираль_инициализация (обратное = ЛОЖЬ) # по умолчанию
спираль_трек()
спираль_стрелка (0,2, 0,8, gp = gpar (fill = "красный"))
ось_спирали()
# правильный сюжет
спираль_инициализировать (обратное = ИСТИНА)
спираль_трек()
спираль_стрелка (0,2, 0,8, gp = gpar (fill = "красный"))
спираль_ось() 
Для отображения данных на спираль необходимо задать аргумент xlim , который соответствует диапазону данных по оси x . Обратите внимание на оси на следующих графиках.
 # левый участок
спираль_инициализировать (xlim = c (0, 1000))
спираль_трек (высота = 0,6)
ось_спирали()
# правильный сюжет
спираль_инициализировать (xlim = c (-1000, 1000))
спираль_трек (высота = 0,6)
спираль_ось() 
В режиме «угол» количество циклов также можно контролировать с помощью аргумента период , который контролирует длину данных, которым соответствует цикл спирали. Обратите внимание, что в этом случае аргумент end игнорируется, а значение end пересчитывается внутри. См. следующий пример:
 # левый график
спираль_инициализировать (xlim = c (0, 1), период = 1/3)
спираль_трек (высота = 0,6)
# правильный сюжет
спираль_инициализировать (xlim = c (0, 1), период = 2)
спираль_трек (высота = 0,6) 
Создание дорожек
После инициализации спирали мы можем добавить вдоль нее дорожки. Аргумент height управляет высотой трека. Значение height — это значение от 0 до 1, которое представляет собой долю расстояния между двумя соседними витками в спирали. На следующем левом графике я добавляю к дорожке черную рамку, устанавливая аргумент background_gp .
 # левый участок
спираль_инициализировать ()
спираль_дорожка (высота = 1, background_gp = gpar (столбец = "черный"))
# правильный сюжет
спираль_инициализировать ()
спираль_трек (высота = 0,5) 
Несколько треков могут быть добавлены последовательно. Только учтите, что сумма высот всех дорожек не должна превышать 1.
 Spiral_initialize()
спираль_дорожка (высота = 0,4, background_gp = gpar (заполнение = 2))
спираль_дорожка (высота = 0,2, background_gp = gpar (заполнение = 3))
спираль_трек (высота = 0,1, background_gp = gpar (заполнение = 4)) 
Значение для высоты также может быть единицей объекта.
 спираль_инициализировать()
спираль_дорожка (высота = единица (1, "см")) 
Диапазон данных по оси y задается аргументом ylim . В следующем примере я также добавляю ось y с помощью Spiral_yaxis() .
 спираль_инициализировать()
спираль_трек (илим = с (0, 100))
Spiral_yaxis() 
Направление оси y по умолчанию указывает на внешнюю сторону спиралей. Это направление можно изменить, установив аргумент reverse_y = TRUE в Spiral_track() , но в приложениях это редко используется.
 спираль_дорожка (реверс_у = ИСТИНА) 
Графические функции
Треки создаются с диапазонами данных как по оси x , так и по оси y . Теперь треки можно рассматривать как обычные декартовы координаты. Существуют следующие низкоуровневые графические функции, так что сложные графики могут быть легко построены путем комбинирования этих низкоуровневых графических функций.
Точки
Подобно другим графическим функциям, например. точки() или grid.points() , «функции спиральной графики» также допускают расположение точек данных по осям x и y . Spiral_points() рисует точки на спиральной дорожке.
 Spiral_initialize() # по умолчанию xlim = c(0, 1)
спираль_трек() # по умолчанию ylim = c(0, 1)
Spiral_points(x = runif(1000), y = runif(1000)) 
Lines
Добавление строк с помощью Spiral_lines() также просто:
 x = sort(runif(1000))
у = runif(1000)
спираль_инициализировать ()
спираль_трек()
спираль_линии (х, у) 
Аргумент тип может быть установлен на "h" , чтобы вертикальные линии (или радиальные линии, если вы берете полярные координаты в качестве эталона) были проведены к базовой линии для каждой точки данных.
 # левый участок
спираль_инициализировать ()
спираль_трек()
спираль_линии (х, у, тип = «ч»)
# правильный сюжет
спираль_инициализировать ()
спираль_трек()
спираль_линии(х, у, тип = "h", базовая линия = 0,5, gp = gpar(col = ifelse(y > 0,5, "красный", "синий"))) 
Аргумент область может быть установлена на TRUE , чтобы область под линиями могла быть заполнена определенным цветом.
 спираль_инициализировать()
спираль_трек()
спираль_линии(x, y, area = TRUE, gp = gpar(fill = 2, col = NA)) 
Обратите внимание, что вы также можете установить базовую линию с областью = TRUE , однако вы не можете установить разные цвета для области выше базовой линии и ниже базовой линии. Рассмотрите возможность использования Spiral_Bars() или Spiral_horizon() для этого сценария.
Сегменты
Spiral_segments() рисует список сегментов.
 n = 1000
х0 = runif(n)
y0 = runif(n)
x1 = x0 + runif(n, мин.  = -0,01, макс. = 0,01)
у1 = 1 - у0
спираль_инициализировать (xlim = диапазон (с (х0, х1)))
спираль_трек()
спираль_сегменты (х0, у0, х1, у1,
    gp = gpar(col = circlize::rand_color(n, luminosity = "bright"), lwd = runif(n, 0.5, 3))) 
То же, что grid.segments() , вы также можете установите аргумент стрелка , чтобы добавить стрелки на сегменты.
 n = 100
х0 = runif(n)
y0 = runif(n)
x1 = x0 + runif(n, мин. = -0,01, макс. = 0,01)
у1 = 1 - у0
спираль_инициализировать (xlim = диапазон (с (х0, х1)))
спираль_трек()
спираль_сегменты (x0, y0, x1, y1, стрелка = стрелка (длина = единица (2, "мм")),
    gp = gpar(col = circlize::rand_color(n, luminosity = "bright"), lwd = runif(n, 0.5, 3))) 
Rectangles
Spiral_rect() рисует прямоугольники, т.е. базовая функция для рисования тепловых карт и гистограмм. Первые четыре аргумента — это координаты нижнего левого и верхнего правого прямоугольников.
 n = 1000
требовать (обвести)
спираль_инициализировать (xlim = c (0, n))
спираль_трек (высота = 0,9)
х1 = рунесли(п)
col1 = circlize::colorRamp2(c(0, 0. 5, 1), c("синий", "белый", "красный"))
спираль_рект(1:n - 1, 0, 1:n, 0,5, gp = gpar(fill = col1(x1), col = NA))
х2 = рунесли(п)
col2 = circlize::colorRamp2(c(0, 0.5, 1), c("зеленый", "белый", "красный"))
Spiral_rect(1:n - 1, 0.5, 1:n, 1, gp = gpar(fill = col2(x2), col = NA)) 
Bars
Spiral_bars() может рисовать столбцы просто из числовой вектор. Столбики также можно рисовать на базовой линии.
 x = seq(1, 1000, by = 1) - 0,5 # средние точки столбцов
у = runif(1000)
# левый сюжет
спираль_инициализировать (xlim = c (0, 1000))
спираль_трек (высота = 0,8)
спираль_бары (х, у)
# правильный сюжет
спираль_инициализировать (xlim = c (0, 1000))
спираль_трек (высота = 0,8)
Spiral_bars(x, y, baseline = 0.5, gp = gpar(fill = ifelse(y > 0.5, 2, 3), col = NA)) 
Spiral_bars() также может рисовать столбцы из матрицы, тогда каждый столбец в матрице соответствует одному набору столбцов.
 y = матрица (runif (3 * 1000), ncol = 3)
у = у/суммы строк(у)
спираль_инициализировать (xlim = c (0, 1000))
спираль_трек (высота = 0,8)
Spiral_bars(x, y, gp = gpar(fill = 2:4, col = NA)) 
Ширина полос может быть разной. Вы можете установить вектор в аргумент bar_width . Примечание. x всегда соответствует середине каждой полосы.
 w = runif(100)
w = w/sum(w) # ширина столбцов, сумма всех ширин равна 1
б = с (0, общая сумма (ш))
x = (b[1:100] + b[2:101])/2 # середина каждого бара
у = рун если (100)
спираль_инициализировать ()
спираль_трек()
спираль_бары(х, у, ширина_бара = w) 
Многоугольники
Spiral_polygon() рисует многоугольники. Обратите внимание, что полигон должен быть замкнутым, то есть последняя точка данных должна перекрываться с первой.
 x0 = сортировка (runif (200))
x0 = матрица (x0, ncol = 2, по строке = TRUE)
x1 = сортировка (runif (200))
x1 = матрица (x1, ncol = 2, по строке = TRUE)
спираль_инициализировать ()
спираль_трек()
для (я в 1:100) {
    pt1 = circlize:::get_bezier_points(x0[i, 1], 0, x1[i, 1], 1, xlim = c(0, 1), ylim = c(0, 1))
    pt2 = circlize:::get_bezier_points(x0[i, 2], 0, x1[i, 2], 1, xlim = c(0, 1), ylim = c(0, 1))
    спираль_полигон(
        c(x0[i, 1], x0[i, 2], pt2[ 1], rev(pt1[ 1]), x0[i, 1]),
        с(0, 0, pt2[ 2], обр(pt1[ 2]), 0),
        gp = gpar(fill = rand_color(1, luminosity = "яркий"), col = NA)
    )
} 
Текст
Spiral_text() рисует тексты. Аргумент напротив управляет поворотом текстов.
 х = последовательность (0,1, 0,9, длина = 26)
текст = strrep (буквы, 6)
# верхний левый график
спираль_инициализировать ()
спираль_трек()
спираль_текст(х, 0.5, текст, облицовка = "вниз") # по умолчанию
# нижний левый график
спираль_инициализировать ()
спираль_трек()
спираль_текст (х, 0,5, текст, облицовка = "внутри")
# нижний правый график
спираль_инициализировать ()
спираль_трек()
спираль_текст(х, 0,5, текст, облицовка = "снаружи") 
Текст также может быть установлен на "по часовой стрелке" или "назад_по часовой стрелке" :
 x = seq(0,1, 0,9, длина = 26)
# левый сюжет
спираль_инициализировать ()
спираль_трек()
спираль_текст (х, 0,5, "аааа", лицом = "по часовой стрелке")
# правильный сюжет
спираль_инициализировать ()
спираль_трек()
спираль_текст(х, 0.5, "аааа", облицовка = "реверс_по часовой стрелке") 
Для длинных текстов напротив можно установить на "curved_inside" или "curved_outside" , чтобы изогнутые тексты рисовались по спирали.
 х = последовательность (0,1, 0,9, длина = 10)
текст = rep (вставить (буквы, свернуть = ""), 10)
# левый сюжет
спираль_инициализировать ()
спираль_трек()
спираль_текст (х, 0,5, текст, облицовка = "curved_inside")
# правильный сюжет
спираль_инициализировать ()
спираль_трек()
спираль_текст(x, 0.5, текст, облицовка = "curved_outside") 
Вычисление положения букв изогнутого текста зависит от размера текущего графического устройства. Когда устройство изменит свой размер, положение букв будет неправильным, и вам нужно перегенерировать график. Также пользователи должны быть осторожны при использовании grid.grabExpr() для захвата графика. По умолчанию grid.grabExpr() захватывает вывод графики на устройство с размерами 7 дюймов x 7 дюймов. Пользователям может потребоваться вручную установить размер устройства, чтобы убедиться, что изогнутые тексты не затронуты.
В следующем примере я использую grid.grabExpr() для захвата двух спиральных графиков с изогнутыми текстами. Позже два графика объединяются с помощью пакета cowplot , а окончательный объединенный график сохраняется в формате PDF шириной 10 дюймов и высотой 5 дюймов. Я вручную установил размер устройства в двух grid.grabExpr() вызывает, чтобы размер места, где захвачена графика, был таким же, как размер места, где она окончательно рисуется.
 p1 = grid.grabExpr({
    спираль_инициализировать ()
    спираль_трек()
    спираль_текст (х, 0,5, текст, облицовка = "curved_inside")
}, ширина = 5, высота = 5)
p2 = grid.grabExpr({
    спираль_инициализировать ()
    спираль_трек()
    спираль_текст (х, 0,5, текст, облицовка = "curved_outside")
}, ширина = 5, высота = 5)
pdf(..., ширина = 10, высота = 5)
plot_grid (p1, p2)
dev.off() 
Последнее, что нужно сделать для рисования текста, это то, что аргумент nice_facing можно установить равным TRUE , чтобы автоматически регулировался поворот текстов, чтобы их было легко читать, т. е. все тексты всегда обращены к нижней части полярная система координат.
Ось
Spiral_aixs() рисует ось по спирали. Так что это x — ось данных.
 спираль_инициализировать()
спираль_трек (высота = 0,6)
спираль_ось() 
Аргумент major_at или просто at управляет точками разрыва на оси, а аргумент labels управляет соответствующими метками оси.
 # левый участок
спираль_инициализировать (xlim = c (0, 360 * 4), начало = 360, конец = 360 * 5)
спираль_трек (высота = 0,6)
ось спирали (major_at = seq (0, 360 * 4, by = 30))
# правильный сюжет
спираль_инициализировать (xlim = c (0, 12 * 4), начало = 360, конец = 360 * 5)
спираль_трек (высота = 0,6)
ось спирали (основной_ат = последовательность (0, 12 * 4, по = 1), метки = с ("", rep (название месяца, 4))) 
Если метки осей слишком длинные, аргумент curved_labels можно установить равным TRUE , чтобы метки были изогнуты по спирали.
 спираль_инициализировать()
спираль_трек (высота = 0,6)
ось спирали (at = c (0,1, 0,3, 0,6, 0,9), метки = strrep (буквы [1:4], 20), Curved_labels = ИСТИНА) 
ось спирали () рисует y -ось. Аргумент сторона контролирует, с какой стороны дорожки разместить оси и . сторона может быть установлена на "оба" , так что y -оси отрисовываются с двух сторон дорожки.
 # левый участок
спираль_инициализировать ()
спираль_трек (высота = 0,8)
спираль_yaxis (сторона = "начало")
ось спирали (сторона = «конец», at = c (0, 0,25, 0,5, 0,75, 1), метки = буквы [1: 5])
# правильный сюжет
спираль_инициализировать ()
спираль_трек (высота = 0,8)
спираль_yaxis(сторона = "оба") 
Карта горизонта
Дорожки вдоль спирали длинные, но высота дорожек обычно очень мала. Горизонтальная диаграмма — это эффективный способ визуализации распределений путем сворачивания графика распределения по вертикали, что позволяет визуализировать область построения с очень небольшой высотой.
В следующем примере я визуализирую разницу ggplot2 ежедневных загрузок со средним значением текущего года, между 01.01.2015 и 31.12.2020.
 # Данные можно загрузить следующей строкой. Объект данных уже сохранен в пакете Spiralize.
# df = cranlogs::cran_downloads("ggplot2", from = "2015-01-01")
df = readRDS (system.file («extdata», «ggplot2_downloads.rds», package = «spiralize»))
# для упрощения данных я беру только полные годы между 2015 и 2020 годами
df = df[df$date < as.Date("2021-01-01"), ]
day_diff = as.double(df$date[nrow(df)] - df$date[1], "дни")
year_mean = tapply(df$count, lubridate::year(df$date), function(x) mean(x[x > 0]))
df$diff = log2(df$count/year_mean[as.character(lubridate::year(df$date))])
df$diff[is.infinite(df$diff)] = 0
q = квантиль (abs (df $ diff), 0,99) # скорректировать выбросы
df$diff[df$diff > q] = q
df$diff[df$diff < -q] = -q
head(df) 
 ## дата подсчета пакетов diff
## 1 2015-01-01 817 ggplot2 -1.4789475
## 2 2015-01-02 1218 ggplot2 -1. 4789475
## 3 2015-01-03 1063 ggplot2 -1.4789475
## 4 2015-01-04 1106 ggplot2 -1.4789475
## 5 2015-01-05 2171 ggplot2 -1.1495651
## 6 2015-01-06 2455 ggplot2 -0.9722018 
Функция Spiral_horizon() рисует график горизонта по спирали. Входные переменные x -местоположения и y -местоположения данных. Чтобы выровнять недели по годам, каждый цикл содержит 364 (52 недели). На следующем графике красные области соответствуют тем дням, когда ежедневные загрузки превышают среднегодовые, а синие области соответствуют дням, когда ежедневные загрузки меньше среднегодовых.
 Spiral_initialize(xlim = c(0, nrow(df)), start = 360, end = 360*(day_diff/364) + 360) # круг из 52 недель
спираль_трек (высота = 0,9)
спираль_горизонт(1:nrow(df) - 0,5, df$diff) 
Бары можно использовать для наложения на каждый день, установив аргумент use_bar = TRUE :
 Spiral_initialize(xlim = c(0, nrow(df)), start = 360, end = 360*(day_diff/364 ) + 360)
спираль_трек (высота = 0,9)
спираль_горизонт(1:nrow(df) - 0. 5, df$diff, use_bars = TRUE) 
При использовании баров аргумент bar_width может быть установлен как вектор, если ширина баров не все равны.
Обратите внимание, что в этом примере объекты «время» можно напрямую использовать в качестве значения по оси x. Примеры см. виньетки «Инициализация спиралей специальными типами данных» и «Примеры из реальной жизни».
Реже используется, пользователи могут явно установить аргумент y_max на максимальное абсолютное значение для y . Это было бы полезно, когда есть несколько треков диаграммы горизонта, и сделать их сопоставимыми.
Изображения
Spiral_raster() добавляет изображения к спирали. В настоящее время он поддерживает форматы png/svg/pdf/eps/jpeg/jpg/tiff. Форматы могут быть смешанными.
 image = system.file("extdata", "Rlogo.png", package = "circlize")
х = последовательность (0,1, 0,9, длина = 10)
спираль_инициализировать ()
спираль_трек()
Spiral_raster(x, 0. 5, image) 
Подобно тексту, аргумент напротив может быть установлен для управления вращением изображений. Если nice_facing = TRUE , изображение с вращением вверх будет автоматически смещено вниз.
 # левый участок
спираль_инициализировать ()
спираль_трек()
спираль_растр (x, 0,5, изображение, облицовка = "внутри")
# правильный сюжет
спираль_инициализировать ()
спираль_трек()
спираль_растр (x, 0,5, изображение, облицовка = "внутри", nice_facing = ИСТИНА) 
Аргумент , обращенный к , может быть установлен на один из "curved_inside" или "curved_outside" , чтобы изображение заполнялось на дорожке. В этом случае аргументы ширина и высота могут быть установлены как значения, измеренные в координатах данных. Обратите внимание, что каждый пиксель изображения на самом деле рисуется как «спиральный прямоугольник», поэтому для больших изображений рисование будет медленным.
 # левый участок
спираль_инициализировать ()
спираль_трек()
спираль_растр (с (0,2, 0,4, 0,6, 0,8), 0,5, изображение, ширина = 0,05,
    высота = 1, облицовка = "curved_inside")
# правильный сюжет
спираль_инициализировать (scale_by = "кривая")
спираль_трек()
спираль_растр (с (0,2, 0,4, 0,6, 0,8), 0,5, изображение, ширина = 0,05,
    высота = 1, облицовка = "curved_outside") 
Стрелки
Spiral_arrow() рисует стрелки по спирали.
 спираль_инициализировать()
спираль_трек()
спираль_стрелка (0,3, 0,6, gp = gpar (fill = "красный", col = NA))
спираль_стрелка(0.8, 0.9, gp = gpar(fill = "синий"), хвост = "точка", arrow_position = "начало") 
Подсветка
Spiral_highlight() выделяет определенный участок спирали. Если для аргумента тип задано значение "rect" (по умолчанию), он выделяет раздел полупрозрачным прямоугольником, который охватывает весь диапазон на и -ось. Если для тип установлено значение "линия" , линия аннотации рисуется либо внизу, либо вверху дорожки.
 спираль_инициализировать()
спираль_трек()
спираль_хайлайт (0,4, 0,6)
спираль_хайлайт (0.1, 0.2, тип = "линия", gp = gpar (столбец = "синий"))
Spiral_highlight(0.7, 0.8, type = "line", line_side = "outside") 
Если для scale_by установлено значение угла (по умолчанию), пользователи также могут захотеть выделить конкретный интервал, но через несколько циклы, напр. с января по март с 2000 по 2010 год. Здесь функция Spiral_highlight_by_sector() рисует полупрозрачный сектор для выделения фиксированного интервала в течение нескольких циклов.
Первые четыре аргумента x1 , x2 , x3 и x4 в Spiral_highlight_by_sector() определяют позицию сектора. Если указаны только x 1 90 254 и 90 253 x 2 90 254, начальная окружность рассчитывается из 90 253 x 1 90 254 и 90 253 x 2 90 254, а конечная окружность является самой внешней. Если 9Также указаны 0253х3 и х4 , внешний круг вычисляется из х3 и х4 .
 Spiral_initialize(xlim = c(0, 360*4), начало = 360, конец = 360*5)
спираль_трек (высота = 0,6)
ось_спирали()
спираль_хайлайт_по_сектору (36, 72)
Spiral_highlight_by_sector (648, 684)
Spiral_highlight_by_sector(216, 252, 936, 972, gp = gpar(fill = "blue")) 
Дендрограммы и филогенетические деревья
визуализировать их. Есть две функции: спираль_дендрограмма() для дендрограмм объектов и спираль_фило() для фило объектов.
Обратите внимание, поскольку дендрограммы или филогенетические деревья не имеют «периодических паттернов», scale_by в Spiral_initialize() обычно устанавливается на «curve_length» .
Объект дендрограмма может быть визуализирован с помощью пакета dendextend . См. следующие примеры.
 dend = as.dendrogram(hclust(dist(runif(1000))))
# левый сюжет
спираль_инициализация (xlim = c (0, 1000), начало = 360, конец = 360 * 2 + 180, scale_by = "curve_length")
спираль_трек()
спираль_дендрограмма (денд)
# правильный сюжет
библиотека (дендекстенд)
dend = color_branches(dend, k = 4)
спираль_инициализация (xlim = c (0, 1000), начало = 360, конец = 360 * 2 + 180, scale_by = "curve_length")
спираль_трек()
спираль_дендрограмма (денд) 
Spiral_phylo() работает с объектом phylo . В следующем примере, чтобы разрезать филогенетическое дерево на несколько частей, объект phylo преобразуется в дендрограмму с помощью функции phylo_to_dendrogram() , позже применяется dendextend::cutree.dendrogram() для получения расколы.
 библиотека (обезьяна)
данные (hivtree.newick)
tree.hiv = read.tree (textConnection (hivtree.newick))
n = length(tree.hiv$tip.label) # количество листьев
спираль_инициализация (xlim = c (0, n), начало = 360, конец = 360 * 2 + 180, scale_by = "curve_length")
спираль_трек()
спираль_фило (дерево.  hiv)
split = dendextend::cutree(phylo_to_dendrogram(tree.hiv), k = 8)
tb = таблица (разделенная)
for(i in seq_along(tb)) {
    Spiral_highlight (сумма (tb [seq_len (i-1)]), сумма (tb [seq_len (i)]), gp = gpar (fill = i))
} 
Филогенетическое дерево также может быть непосредственно окрашено категориальной переменной. Мы используем переменную , разделенную на , сгенерированную в предыдущем примере.
 Spiral_initialize(xlim =c(0, n), start = 360, end = 360*2 + 180, scale_by = "curve_length")
спираль_трек()
Spiral_phylo(tree.hiv, group = split) 
Как дендрограммы, так и филогенетические деревья могут быть направлены наружу спирали, просто поменяв местами y -ось в Spiral_track() .
 Spiral_initialize(xlim =c(0, n), start = 360, end = 360*2 + 180, scale_by = "curve_length")
спираль_дорожка (reverse_y = ИСТИНА)
спираль_фило(tree.hiv) 
Вспомогательные функции
Существует несколько служебных функций, которые помогают получить информацию о текущем графике спирали. Spiral_info() выводит общую информацию о текущей спирали:
 Spiral_initialize(xlim = c(0, 100))
спираль_трек (илим = с (-1, 1))
Spiral_info() 
 ## Спираль Архимеда (r = b*theta) со следующими параметрами:
## б: 0,15
430
## расстояние между двумя соседними кругами: 1
## xlim: [0, 100]
## диапазон теты (в градусах): [360, 1800]
## Спиральная кривая линейно масштабируется по углу.
##
## дорожка 1:
## илим: [-1, 1]
## height: 0.8 (доля расстояния между двумя соседними петлями) 
Специальная переменная TRACK_META извлекает метаинформацию о текущей дорожке.
 TRACK_META 
 ## Пожалуйста, используйте в форме `TRACK_META$name`. Введите `names(TRACK_META)` для поддерживаемых имен. 
 имен(TRACK_META) 
 ## [1] "xlim" "xmin" "xmax" "xcenter" "xrange" "theta_lim"
## [7] "theta_min" "theta_max" "theta_center" "theta_range" "ylim" "ymin"
## [13] "ymax" "ycenter" "yrange" "abs_height" "rel_height" "track_index" 
Следующие две функции преобразуют координаты данных в полярные координаты или координаты холста (координаты, в которых наконец рисуется графика) .
xy_to_cartesian()
xy_to_polar()
Следующие три функции получают или устанавливают дорожки:
current_track_index()
set_current_track()
n_track()
Также есть еще одна функция, которая преобразует координаты холста в координаты данных. Точки данных назначаются ближайшим внутренним циклам. Для точки данных $P$ обозначим $r$ как расстояние до начала координат, $\theta$ - это угол к линии $x > 0, y = 0$ (против часовой стрелки угол). Предположим, что значение $\theta$ находится между 0 и $2\pi$ (что на самом деле не важно, если $\theta$ умножается на $2\pi$). Обозначим $r_k$ и $r_{k+1}$ — это радиусы двух петель спирали в точках $\theta + 2\pi \cdot a$ и $\theta + 2\pi \cdot (a+1)$, что ниже и выше точки данных (здесь $a$ - это целое число, которое следует правильно рассчитать, чтобы убедиться, что $p$ находится между петлей $k$ и $ k+1$), то точка данных $P$ назначается контуру $k$.
декартово_к_ху()
Существует интересное приложение для cartesian_to_xy() , предназначенное для наложения изображения на спираль. Если мы рассматриваем каждый пиксель как точку данных, то мы можем рисовать только те пиксели, которые находятся внутри дорожки на спирали. В следующем примере я сначала загружаю объект изображения:
 load(system.file("extdata", "doodle.RData", package = "circlize")) # загруженный объект `img_list`
img = img_list[[1]] # img_list содержит несколько изображений в качестве растровых объектов, здесь мы используем только первое.
img = apply(img, 1:2, function(x) rgb(x[1], x[2], x[3])) # преобразовать в цветные символы 
Сейчас img это матрица цветов. Обратите внимание, что первый элемент в img (то есть img[1, 1] ) соответствует верхнему левому пикселю изображения. В следующем коде я в основном проверяю, находятся ли пиксели на дорожке. Если они есть, позиции и соответствующие цвета сохраняются.
 номер = номер строки (изображение)
нк = нккол (изображение)
спираль_инициализировать (начало = 0, конец = 360*5, полярные_линии = ЛОЖЬ)
спираль_трек (фон = ИСТИНА)
s = текущая_спираль()
все_х = НУЛЬ
all_y = NULL
all_col = NULL
для (я в 1: номер) {
    for(j в 1:nc) {
        x = (j - nc/2)/nc*1,5*s$max_radius
        y = -(i - nr/2)/nr*1.5*s$max_radius
        df = декартово_к_ху (х, у)
        если (is_in_track (df $ x, df $ y)) {
            all_x = c(all_x, df$x)
            all_y = c(all_y, df$y)
            all_col = c(all_col, img[i, j])
        }
    }
}
Spiral_points(all_x, all_y, pch = 16, gp = gpar(col = all_col), size = unit(2, "pt")) 
Следующие два участка начерчены спиралями из 20 петель и 50 петель. Также не прорисовывается фон треков.
Гиперболическая спираль — HandWiki
Из HandWiki
Пространства имен
Стр.
Обсуждение
Подробнее
Подробнее
Языки
Страница
Читаясь
. Просмотр
9
.0019
Краткое описание : Спиральная асимптотика к прямой
Гиперболическая спираль: ветвь для φ > 0
Гиперболическая спираль: обе ветви
полярные координаты по уравнению
[math]\displaystyle{ r=\frac{a}{\varphi} }[/math]
гиперболы. Поскольку он может быть получен инверсией окружности спирали Архимеда, он называется 9.1536 Ответная спираль тоже. ^[1] ^[2]
Пьер Вариньон впервые изучил кривую в 1704 году. ^[2] Позднее над кривой также работали Иоганн Бернулли и Роже Котс.
Угол закрутки гиперболической спирали увеличивается с расстоянием от ее центра, в отличие от логарифмической спирали (в которой угол постоянен) или спирали Архимеда (в которой он уменьшается с расстоянием). По этой причине его использовали для моделирования формы спиральных галактик, которые в некоторых случаях также имеют увеличивающийся угол закрутки. Однако эта модель не дает хорошего соответствия формам всех спиральных галактик. ^[3] ^[4]
Содержание
1 В декартовых координатах
2 Геометрические свойства
2.1 Асимптота
2.2 Полярный склон
2.3 Кривизна
2.4 Длина дуги
2.5 Площадь сектора
2.6 Инверсия
2.7 Центральный выступ спирали
3 Каталожные номера
4 Внешние ссылки
В декартовых координатах
гиперболическая спираль с полярным уравнением
[math]\displaystyle{ r=\frac a \varphi ,\quad \varphi \ne 0 }[/math]
можно представить в декартовых координатах ( x = r cos φ 42 , y = r sin φ ) на
[математика] \ displaystyle { x = a \ frac {\ cos \ varphi} \ varphi, \ qquad y = a \ frac {\ sin \ varphi} \ varphi , \ quad \ varphi \ ne 0. } [/ math]
Гипербола имеет оси координат в плоскости rφ как асимптоты. Гиперболическая спираль (в плоскости xy) сближается на 92}}\справа) . }[/math]
Геометрические свойства
Асимптота
Потому что
[математика] \ displaystyle { \ lim _ {\ varphi \ to 0} x = a \ lim _ {\ varphi \ to 0} \ frac {\ cos \ varphi} \ varphi = \ infty, \ qquad \lim_{\varphi\to 0}y = a\lim_{\varphi\to 0} \frac{\sin \varphi} \varphi = a}[/math]
кривая имеет асимптоту с уравнением y = a .
Полярный наклон
Определение сектора (светло-голубой) и полярного угла наклона α
Из векторного исчисления в полярных координатах можно получить формулу tan α = r ′/ r для полярного наклона и его угла α между касательной кривой и касательной соответствующей полярной окружности.
Для гиперболической спирали r = a / φ полярный наклон равен
[математика]\displaystyle{ \tan\alpha=-\frac{1}{\varphi}. }[/math]
Кривизна
2}\, д\варфи\\ &= \frac{a}{2}\left(\frac{a}{\varphi_1}-\frac{a}{\varphi_2}\right)\\ &=\frac{a}{2}\bigl(r(\varphi_1)-r(\varphi_2)\bigr) . \end{align} }[/math]
Инверсия
Гиперболическая спираль (синяя) как изображение спирали Архимеда (зеленая) с инверсией окружности
Инверсия на единичной окружности имеет в полярных координатах простое описание: ( r , φ ) ↦ (1/ r , φ ).
Изображение спирали Архимеда r = φ / a с инверсией окружности является гиперболической спиралью с уравнением r = a / φ . При φ = a две кривые пересекаются в фиксированной точке на единичной окружности.
Соприкасающаяся окружность спирали Архимеда r = φ / a в начале координат имеет радиус ρ ₀ = 1/2 a (см. ρ ₀ ). Изображением этого круга является линия y = a (см. инверсию круга). Следовательно, прообразом асимптоты гиперболической спирали с инверсией архимедовой спирали является соприкасающаяся окружность архимедовой спирали в начале координат.
Пример: На диаграмме показан пример с a = π .
Центральная проекция спирали
Гиперболическая спираль как центральная проекция спирали
Рассмотрим центральную проекцию из точки C ₀ = (0, 0, d ) на плоскость изображения z = 0. Это отобразит точку ( x , y
, z ) до точки d / d − z ( x , y ).
Изображение под этой проекцией спирали с параметрическим представлением
[математика]\displaystyle{ (r\cos t, r\sin t, ct),\quad c\neq 0, }[/math]
кривая
[math]\displaystyle{ \frac{dr}{d-ct}(\cos t,\sin t)}[/math]
с полярным уравнением
[math]\displaystyle{ \rho=\frac{dr}{d-ct}, }[/math]
, который описывает гиперболическую спираль.
Для параметра t ₀ = d / c гиперболическая спираль имеет полюс и спираль пересекает плоскость z = d в точке a1 V
2 ₀ . Расчетным путем можно проверить, что изображение спирали при ее приближении к V ₀ является асимптотой гиперболической спирали.
Ссылки
↑ Баузер, Эдвард Альберт (1880), Элементарный трактат по аналитической геометрии: охват плоской геометрии и введение в геометрию трех измерений (4-е изд.), Д. Ван Ностранд, с. 232, https://books.google.com/books?id=g3cLAAAAYAAJ&pg=PA232
↑ ^2,0 ^2.1 Лоуренс, Дж. Деннис (2013), Каталог специальных плоских кривых , Dover Books on Mathematics, Courier Dover Publications, p. 186, ISBN 9780486167664, https://books.google.com/books?id=9rrFAgAAQBAJ&pg=PA186 .
↑ RC, Jr. Kennicutt (декабрь 1981 г.), «Формы спиральных рукавов вдоль последовательности Хаббла», The Astronomical Journal (American Astronomical Society) 86 : 1847, doi: 10. 1086/113064, Bibcode: 1981AJ. ....86.1847К
↑ Савченко С. С.; Решетников В. П. (сентябрь 2013 г.), «Вариации угла наклона спиральных галактик», Ежемесячные уведомления Королевского астрономического общества 436 (2): 1074–1083, doi: 10.1093 / mnras / stt1627
Ханс-Йохен Барч, Майкл Сакс: Taschenbuch mathematischer Formeln für Ingenieure und Naturwissenschaftler , Carl Hanser Verlag, 2018, ISBN: 3446457070, 9783446457072, S. 9016.
Кинко Цудзи, Стефан С. Мюллер: Спирали и вихри: в культуре, природе и науке , Springer, 2019, ISBN: 3030057984, 9783030057985, S. 96.
Пьер Вариньон: Новая формация де Спиралей – пример II , Mémoires de l’Académie des Sciences de l’Institut de France, 1704, стр. 94–103.
Friedrich Grelle: Analytische Geometrie der Ebene , Verlag F. Brecke, 1861 hyperbolische Spirale, S. 215.
Якоб Филипп Кулик: Lehrbuch der höhern Analysis, Band 2 г. , в комм. Бей Кронбергер у. Rziwnatz, 1844, Spirallinien, S. 222.
Внешние ссылки
Вайсштейн, Эрик В.. «Гиперболическая спираль». http://mathworld.wolfram.com/HyperbolicSpiral.html.
Онлайн-исследование с использованием JSXGraph (JavaScript)
2dcurves "гиперболическая спираль" страница
pt:Espiral logarítmica
Логарифмическая спираль - Словарь героев Википедии
"Spira mirabilis" перенаправляется сюда. Чтобы узнать об оркестре, см. Spira Mirabilis (оркестр) . Чтобы узнать об итальянском фильме, см. Spira Mirabilis (фильм) .
Логарифмическая спираль (шаг 10°)
Участок множества Мандельброта, следующий за логарифмической спиралью
A логарифмическая спираль , равноугольная спираль или спираль роста представляет собой самоподобную спиральную кривую, которая часто появляется в виде спиральной кривой природа. Первым, кто описал логарифмическую спираль, был Альбрехт Дюрер (1525 г.), назвавший ее «вечной линией» («ewige lini»). ^[1] Более чем столетие спустя кривая обсуждалась Декартом (1638 г.), а затем подробно исследовалась Якобом Бернулли, который назвал ее Spira mirabilis , «чудесная спираль».
Логарифмическую спираль можно отличить от архимедовой спирали тем, что расстояния между витками логарифмической спирали увеличиваются в геометрической прогрессии, а в архимедовой спирали эти расстояния постоянны.
Содержание
1 Определение
2 В декартовых координатах
3 Spira mirabilis и Якоб Бернулли
4 Свойства
5 Особые случаи и приближения
6 В природе
7 В технических приложениях
8 См. также
9 Ссылки
10 Внешние ссылки \displaystyle (r,\varphi )} логарифмическая спираль может быть записана как ^[2]
или
, где e{\displaystyle e} является основанием натуральных логарифмов, а a>0{\displaystyle a>0 }, k ≠ 0 {\ displaystyle k \ neq 0} - реальные константы. 9{i\varphi }=\cos \varphi +i\sin \varphi )}:
Spira mirabilis и Якоб Бернулли для логарифмической спирали. Хотя эта кривая уже была названа другими математиками, конкретное название («чудесная» или «дивная» спираль) ей дал Яков Бернулли, потому что он был очарован одним из ее уникальных математических свойств: размером спирали увеличивается, но его форма не меняется с каждой последующей кривой, свойство, известное как самоподобие. Возможно, в результате этого уникального свойства спира чудесная эволюционировала в природе, появляясь в определенных растущих формах, таких как раковины наутилуса и головки подсолнуха. Яков Бернулли хотел, чтобы такая спираль была выгравирована на его надгробии вместе с фразой «Eadem mutata resurgo» («Хотя я изменился, я восстану прежним»), но по ошибке вместо нее была помещена архимедова спираль. 9{k\varphi}\;,\;k\neq 0,} обладает следующими свойствами (см. Спираль):
Полярный наклон : tan⁡α=k(constant!){\displaystyle \tan\alpha = k \ quad ({\ color {red} {\ text {constant!}}})} с полярным углом наклона α {\ displaystyle \ alpha} (см. {2}}{4k}}} 9{\ circ }} соответственно. Все спирали не имеют общих точек (см. свойство комплексной экспоненциальной функции ).
Связь с другими кривыми: Логарифмические спирали конгруэнтны своим собственным эвольвентам, эволютам и педальным кривым, основанным на их центрах.
Комплексная экспоненциальная функция : Экспоненциальная функция точно отображает все линии, не параллельные действительной или мнимой оси на комплексной плоскости, во все логарифмические спирали на комплексной плоскости с центром в точке 0{\displaystyle 0}: угол наклона полярной оси α {\ displaystyle \ alpha} логарифмической спирали - это угол между прямой и воображаемой осью.
Особые случаи и приближения Его можно аппроксимировать «спиралью Фибоначчи», состоящей из последовательности четвертей кругов с радиусами, пропорциональными числам Фибоначчи.
В природе. Построенная спираль (штриховая синяя кривая) основана на параметре скорости роста b = 0,1759.
{\круг}}.
В некоторых природных явлениях можно найти кривые, близкие к логарифмическим спиралям. Вот несколько примеров и причин:
Приближение ястреба к своей добыче в классической погоне, предполагая, что добыча движется по прямой. Их самый острый взгляд находится под углом к направлению их полета; этот угол равен шагу спирали. ^[6]
Подход насекомого к источнику света. Они привыкли иметь источник света под постоянным углом к траектории полета. Обычно солнце (или луна для ночных видов) является единственным источником света, и полет таким образом приведет к практически прямой линии. ^[7]
Рукава спиральных галактик. ^[8] Наша галактика Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет собой логарифмическую спираль с шагом около 12 градусов. ^[9] Однако, хотя спиральные галактики часто моделируются как логарифмические спирали, спирали Архимеда или гиперболические спирали, их углы закрутки меняются с расстоянием от галактического центра, в отличие от логарифмических спиралей (у которых этот угол не меняется), и также в отличие от других математических спиралей, используемых для их моделирования. ^[10]
Нервы роговицы (то есть роговичные нервы субэпителиального слоя заканчиваются вблизи поверхностного эпителиального слоя роговицы в виде логарифмической спирали). ^[11]
Полосы тропических циклонов, таких как ураганы. ^[12]
Многие биологические структуры, включая раковины моллюсков. ^[13] В этих случаях причиной может быть построение из расширения подобных фигур, как в случае с многоугольными фигурами.
Логарифмические спиральные пляжи могут образовываться в результате преломления и дифракции волн на побережье. Half Moon Bay (Калифорния) является примером такого типа пляжа. ^[14]
В инженерных приложениях[править]
Логарифмические спиральные антенны представляют собой частотно-независимые антенны, то есть антенны, диаграмма направленности, импеданс и поляризация которых остаются практически неизменными в широкой полосе пропускания. ^[16]
При изготовлении механизмов на субтрактивных станках (таких как лазерные резаки) может быть потеря точности, когда механизм изготавливается на другом станке из-за различия удаляемого материала (т. ) каждой машиной в процессе резки. Чтобы приспособиться к этому варианту пропила, самоподобное свойство логарифмической спирали было использовано для разработки механизма устранения пропила для лазерных резаков. ^[17]
Логарифмические спирально-конические зубчатые колеса представляют собой спирально-конические зубчатые колеса, центральная линия зубьев которых представляет собой логарифмическую спираль. Логарифмическая спираль имеет то преимущество, что обеспечивает равные углы между осевой линией зуба и радиальными линиями, что придает зацеплению большую стабильность. ^[18]
См. также
Цзян, Цзяньфэн; Луо, Циншэн; Ван, Литинг; Цяо, Лицзюнь; Ли, Минхао (2020). «Обзор логарифмической спирально-конической передачи». Журнал Бразильского общества механических наук и инженерии . 42 (8): 400. doi:10.1007/s40430-020-02488-y. ISSN 1678-5878.
Вайсштейн, Эрик В. «Логарифмическая спираль».