Сопряжения • Блог архитектора
Очертания многих предметов представляют собой сочетание ряда линий, в большинстве своём плавно переходящих одна в другую.
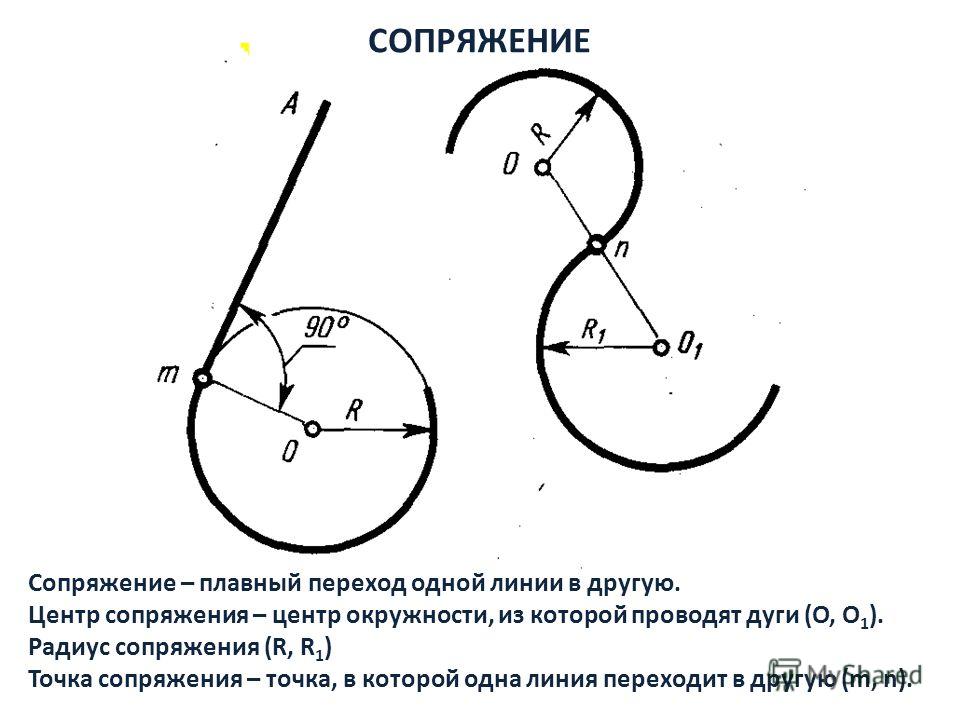
Плавный переход одной линии в другую называют касанием, а точку, в которой происходит касание, точкой касания или перехода (рис. 49).
Рис. 49Через любую точку касания можно провести общую касательную, которая будет перпендикулярна к радиусам дуг, проведенным в точку касания.
Плавный переход одной линии в другую при помощи промежуточной линии называют сопряжением. На рис. 50 такой линией является дуга АВ радиуса Rc. Её называют дугой сопряжения, радиус R c — радиусом сопряжения, а центр сопрягающей дуги – центром сопряжения.
Рис. 50При сопряжении всегда имеются две точки перехода и через каждую из них можно провести по одной общей касательной.
Таким образом, построение сопряжений основано на свойствах касательной к дуге окружности и касания двух дуг окружностей.
Построение касательной к окружности в заданной на ней точке.
 Рис. 51
Рис. 51Через точку А и центр О (рис. 51) проводят прямую и в точке А восстанавливают к ней перпендикуляр (построение перпендикуляра к прямой в заданной на ней точке рассмотрено на рис. 32).
рис. 32Построение касательной к окружности из точки А вне окружности.
Рис. 52Центр окружности О и точку А соединяют прямой (рис. 52). Отрезок OA принимают за диаметр вспомогательной окружности. Разделив отрезок OA пополам, получают точку О1 .
Из точки О1 описывают окружность радиусом O1 A, которая пересекает заданную окружность в точках касания В и С.
Построение касательных окружностей.
При внешнем касании окружностей центры О1 и О2 расположены на расстоянии R+r друг от друга. Точка касания лежит на прямой, соединяющей центры О1 и О2 , а общая касательная MN к этой прямой в точке А перпендикулярна (рис. 53а).
При внутреннем касании расстояние между центрами касающихся окружностей равно разности радиусов R-r.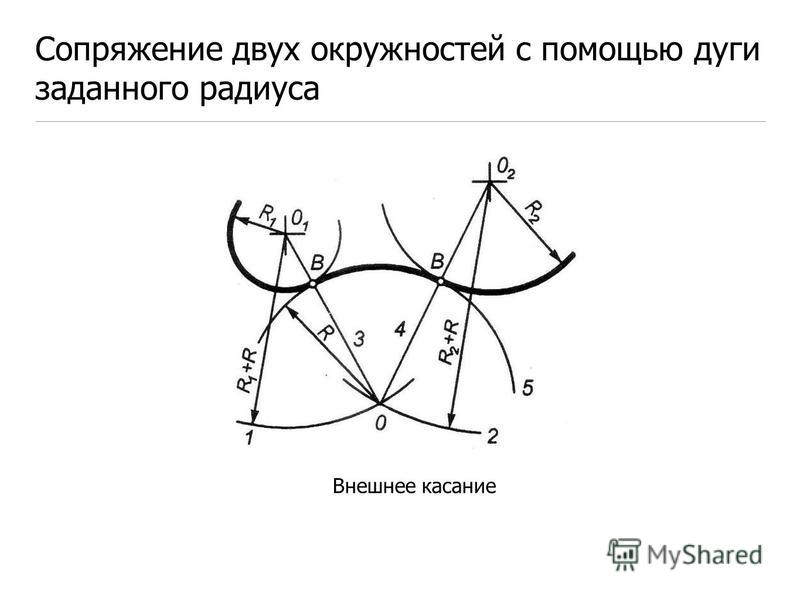 Точка касания А расположена на продолжении прямой, соединяющей центры О1 и О2 (рис. 53б).
Точка касания А расположена на продолжении прямой, соединяющей центры О1 и О2 (рис. 53б).
Построение общей внешней касательной к двум окружностям.
Из центра O 1 большей окружности описывают окружность радиусом R-r (рис. 54а).
Находят середину отрезка O1 O2 – точку О3 и из неё проводят окружность радиусом O1 O3 .
Обе проведенные окружности пересекаются в точках А и В. Точки O1 и В соединяют прямой и в пересечении её с окружностью радиуса R определяют точку касания D (рис. 54б). Из точки О 2 параллельно прямой O1 D проводят линию до пересечения с окружностью радиуса г и получают вторую точку касания С.
Рис. 54Построение общей внутренней касательной к двум окружностям.
Из центра любой окружности описывают окружность радиусом R+r (рис. 55а). Разделив отрезок O1 O2 пополам, получают точку O3. Из точки O3 описывают окружность радиусом O1O3 и отмечают точки А и В пересечения вспомогательных окружностей.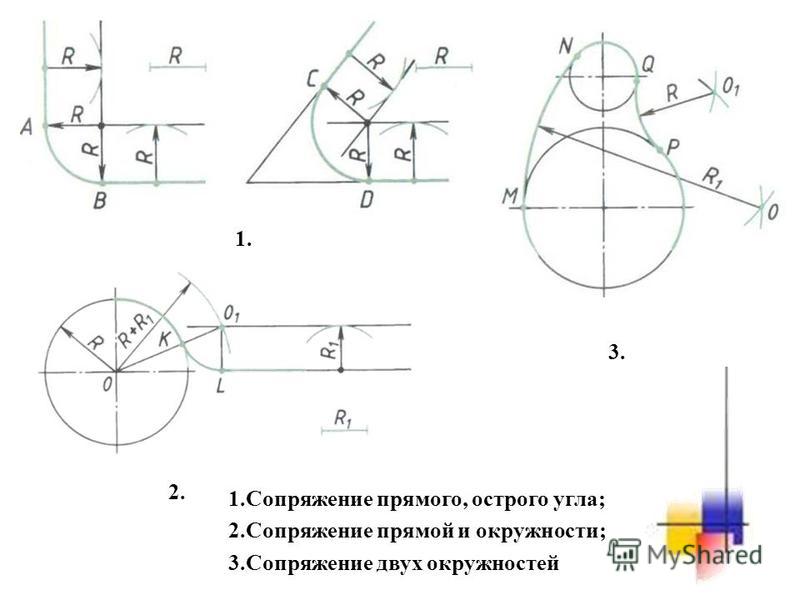 Соединив точки O1 и А прямой (рис. 55б), получают точку касания D. Через точку O2, проводят прямую, параллельную O1A, и получают вторую точку касания С.
Соединив точки O1 и А прямой (рис. 55б), получают точку касания D. Через точку O2, проводят прямую, параллельную O1A, и получают вторую точку касания С.
Сопряжение двух пересекающихся прямых дугой заданного радиуса.
Проводят две прямые, параллельные заданным и удалённые от них на величину радиуса Rc (рис. 56а). В пересечении отмечают точку О – центр сопряжения. Из точки О опускают перпендикуляры на заданные прямые и получают точки касания А и В дуги сопряжения. Такое построение справедливо для любого угла между заданными прямыми.
Для сопряжения сторон прямого угла можно воспользоваться способом, указанным на рис. 56б.
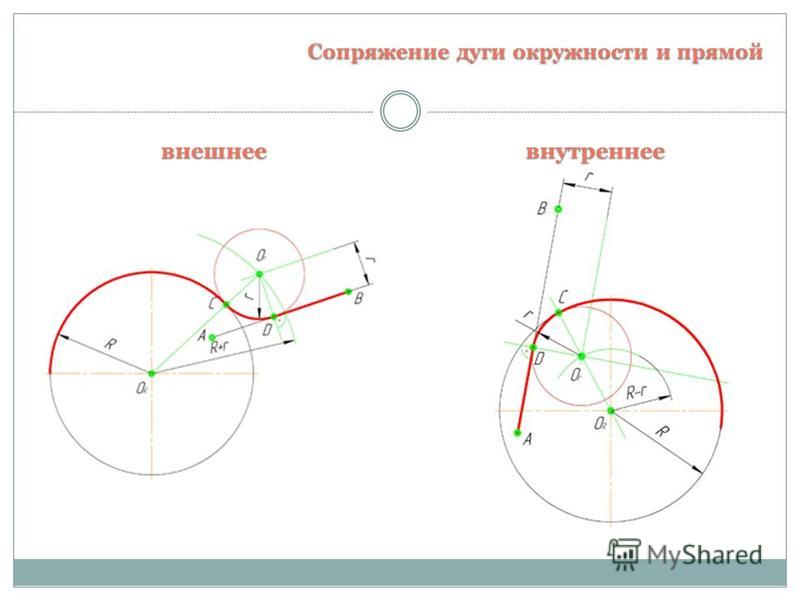
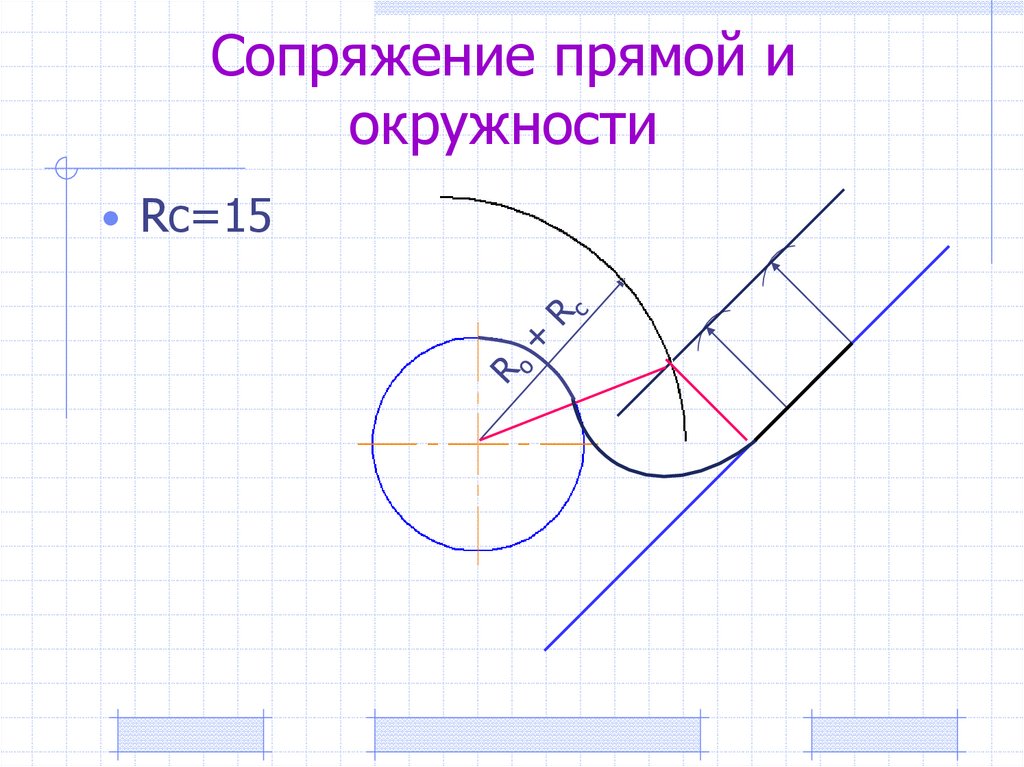
Рис. 56Сопряжение дуги и прямой дугой окружности заданного радиуса.
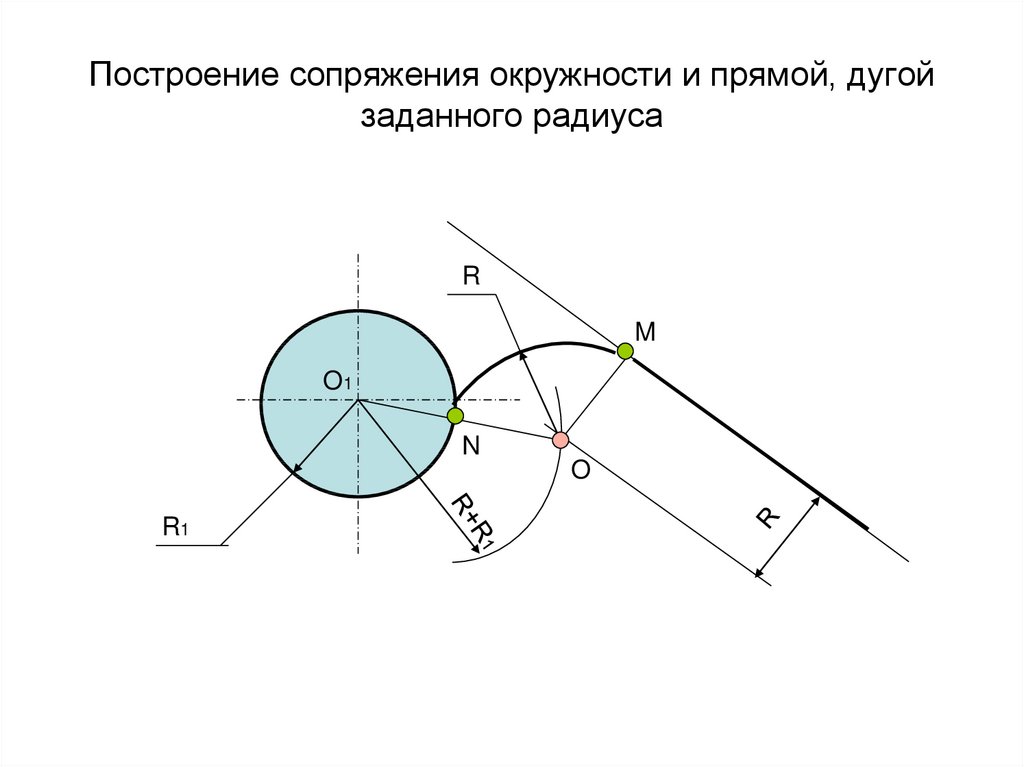
Может быть два случая такого сопряжения: внешнее касание сопрягающей дуги с заданной (рис. 57а) и внутреннее (рис. 57б). При внешнем касании из центра О1 проводят дугу радиусом R+R c и прямую, параллельную заданной, на расстоянии R c от неё.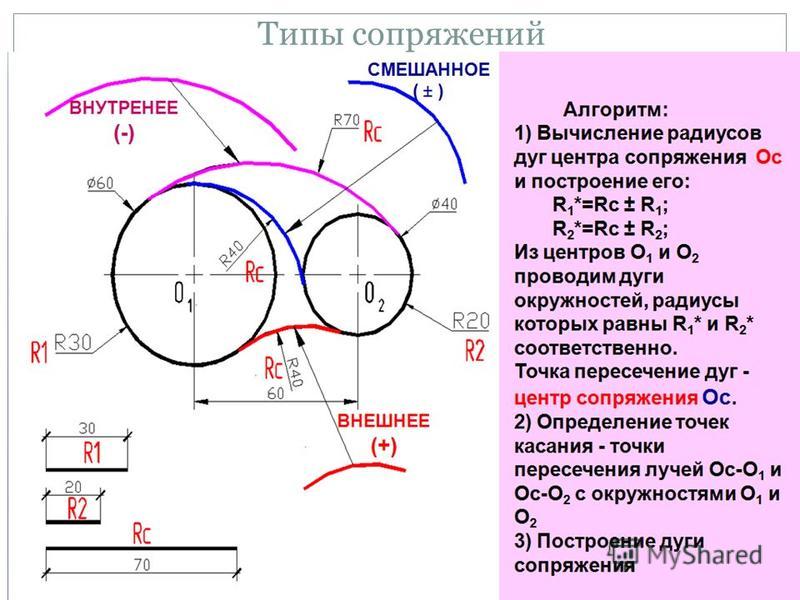 На пересечении получают точку О центра сопряжения. На прямой ОО1 отмечают точку касания А. Точку В касания получают, опустив перпендикуляр из центра О на заданную прямую.
На пересечении получают точку О центра сопряжения. На прямой ОО1 отмечают точку касания А. Точку В касания получают, опустив перпендикуляр из центра О на заданную прямую.
При внутреннем касании построения аналогичны, только радиус вспомогательной дуги равен Rс-R.
Сопряжение двух дуг дугой окружности заданного радиуса.
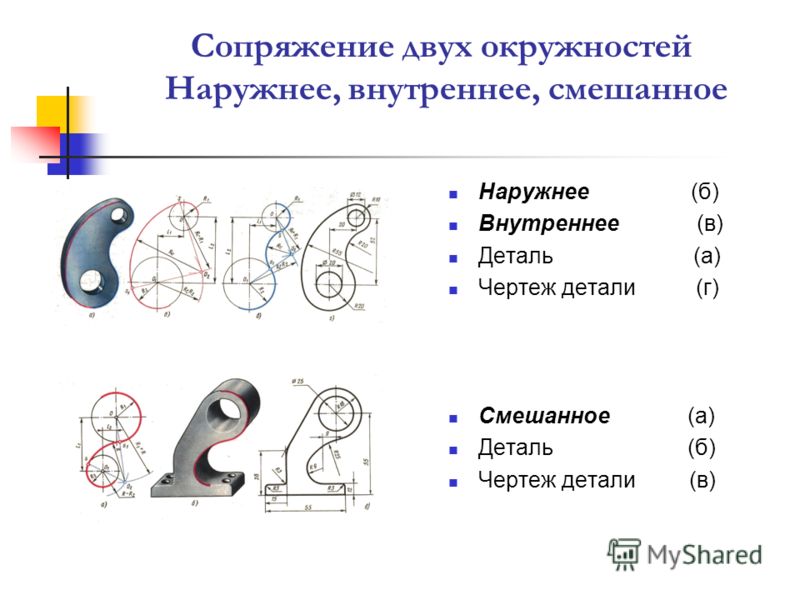
Различают три вида такого сопряжения: внешнее, внутреннее и смешанное.
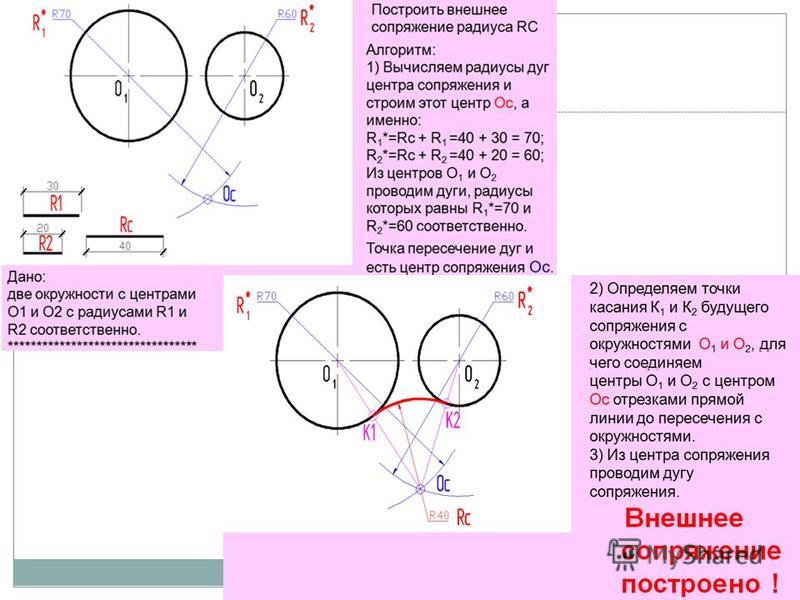
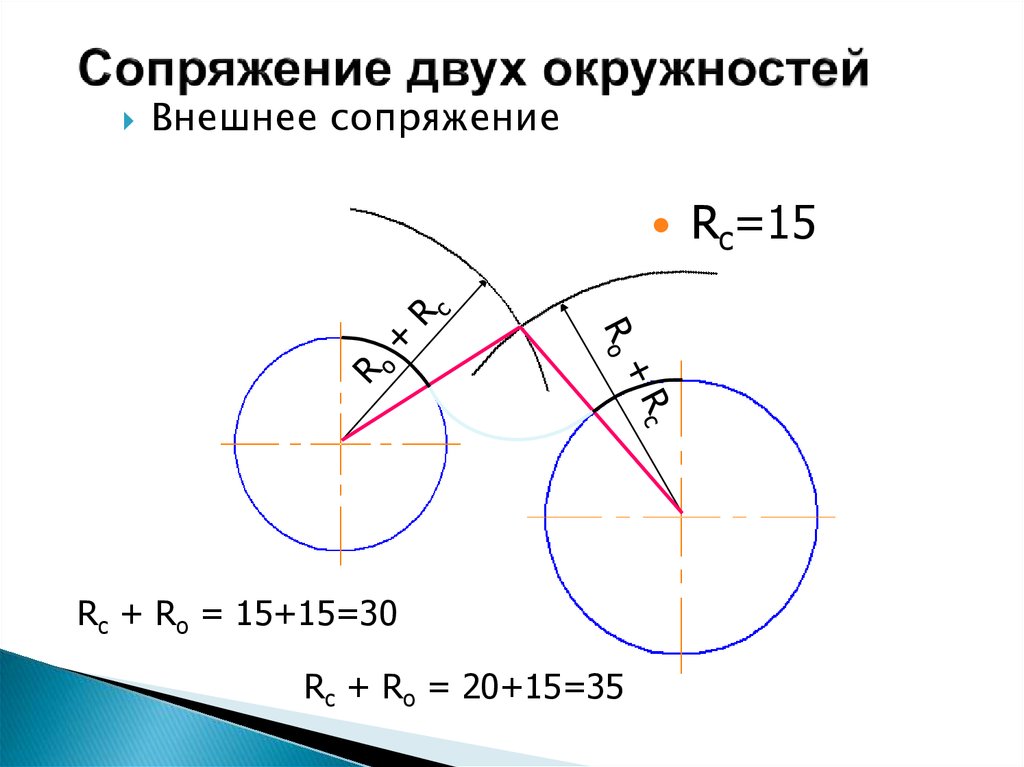
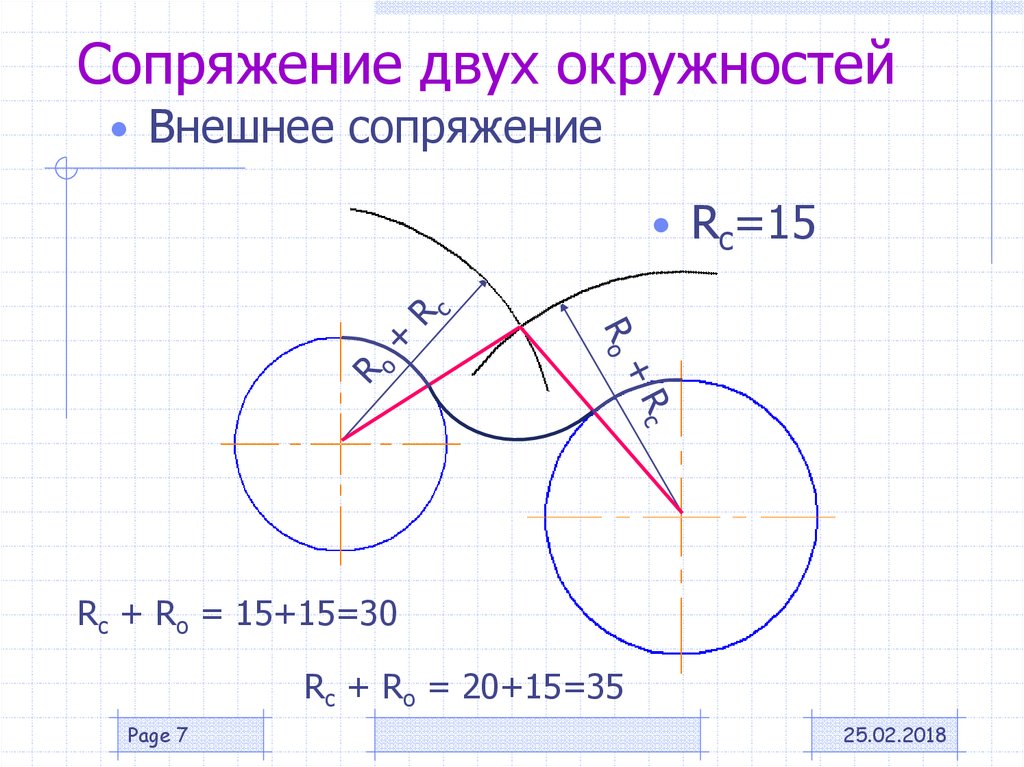
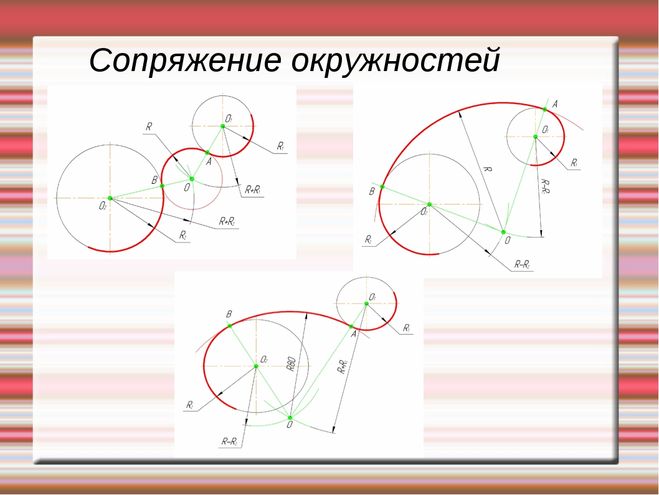
При внешнем сопряжении (рис. 58а) центр сопряжения О располагается на пересечении дуг радиусов R+R c и r+R c , проведенных из центров О1 и О2. Точки касания А и В определяются как точки пересечения заданных дуг с прямыми ОО1 и ОО2.
При внутреннем сопряжении (рис. 58б) проводят вспомогательные дуги радиусами R c -R и R c -r из центров О1 и О2. Через точки ОО1 и ОО2 проводят прямые до пересечения с заданными дугами и находят точки касания А и В.
При смешанном сопряжении (рис. 58в) построения аналогичны и ясны из чертежа.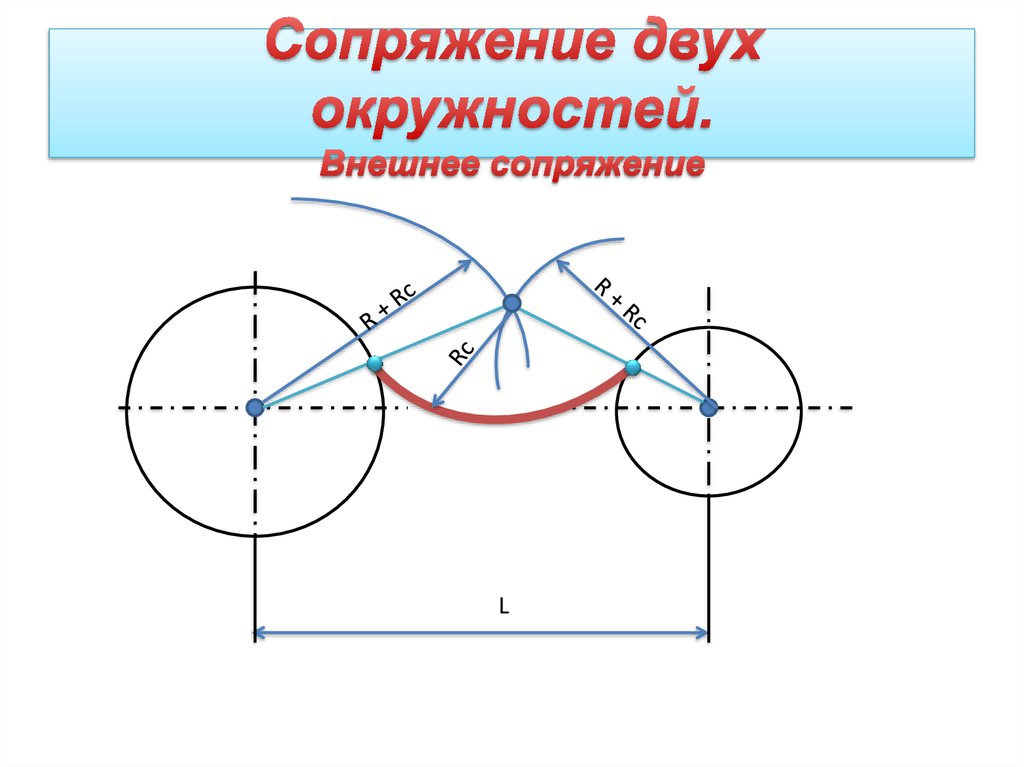
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает… Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров… Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Интересное: Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений. Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным… Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 8 из 12Следующая ⇒ На формате А4 вычертить контур технической детали с построением сопряжений и делением окружности на равные части. Сопряжением называется плавный переход одной линии в другую. Общая точка этих линий называется точкой сопряжения или точкой перехода. Приемы выполнения сопряжений показаны на рис. 80. Построение прямой, касающейся дуги окружности в данной точке. Для проведения касательной к окружности параллельно данной прямой MN нужно из центра Построение окружности, касательной к данной прямой. Геометрическим местом центров окружностей, касательных к данной прямой, является прямая, параллельная данной и отстоящая от нее на расстояние радиуса окружности R. Для определения точки касания из намеченного центра опускаем перпендикуляр на прямую и проводим окружность радиусом R (рис. Построение сопряжения двух дуг окружностей. Точки касания двух дуг окружностей находятся на линии центров ОО1или на продолжении этой линии центров (рис. 80, б, в). Дуги могут иметь внешнее (рис. 80, б) и внутреннее (рис. 80, в) касания. При внешнем касании расстояние между центрами ОО1равно сумме радиусов сопрягаемых дуг, при внутреннем — разности радиусов сопрягаемых дуг. Построение сопряжения двух параллельных прямых дугой. Для сопряжения параллельных прямых AB и CD (рис. 80, д) к ним проводят перпендикуляр EF. Прямая EF параллельные прямые в точках сопряжений n и n1. Поделив прямую nn1пополам, получаем центр сопряжения параллельных прямых. Построение сопряжения двух пересекающихся прямых дугой заданного радиуса. Построение сопряжения дуги окружности с прямой с помощью дуги заданного радиуса и точки сопряжения. Центр дуги сопряжения О1должен лежать на перпендикуляре к заданной прямой, восстановленном из точки сопряжения А (рис. 80, з). Центр дуги сопряжения лежит на пересечении прямых, одна из которых проходит через центр окружности О и точку сопряжения А, а вторая является биссектрисой угла, образованного данной прямой и касательной, проведенной через точку А.
Построение сопряжения двух дуг окружностей дугой сопряжения заданного радиуса R2. В случае внешнего сопряжения (рис. 80, и) из центров дуг О1и О2радиусами, равными R + R2и R1+ R2проводят дуги, пересечение которых определяет центр сопрягаемой дуги О. Точки сопряжений 1 и 2 находятся на линиях О1О и О2О, соответственно. В случае внутреннего сопряжения (рис. 80, к) из центров О1и О2радиусами, равными R2— R1и R2— R проводят дуги, точка пересечения которых определяет центр сопрягаемой дуги Построение сопряжения дугами окружностей четырех пересекающихся прямых. Произвольно выбранная точка Она биссектрисе угла между прямыми l и l1может служить первым центром сопряжения (рис.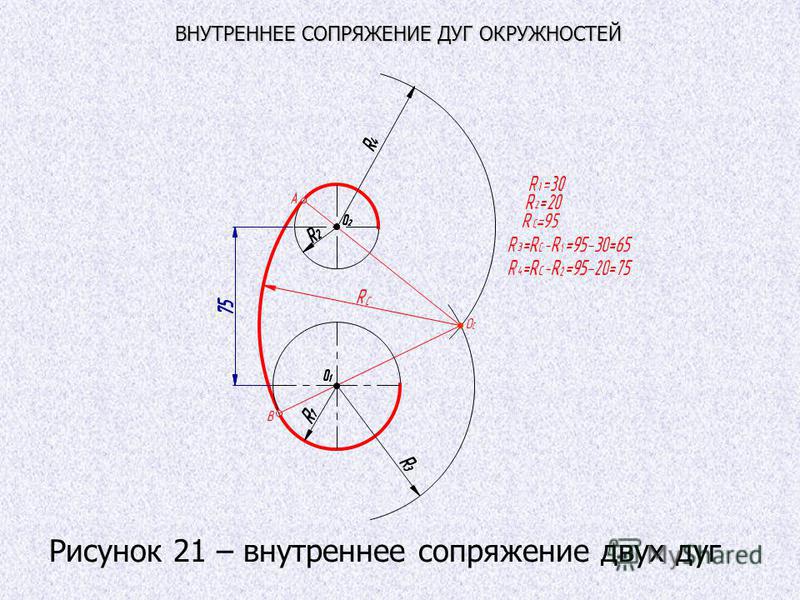 80, м). Перпендикуляры, опущенные из этого центра на прямые l и l1, дают точки сопряжений А и В. Второй центр дуги сопряжения О1находят на пересечении биссектрисы угла между прямыми l1и l2с продолжением перпендикуляра ВО. Третий центр дуги сопряжения О2определяют в точке пересечения биссектрисы угла между прямыми l2и l3с продолжением перпендикуляра О1С. 80, м). Перпендикуляры, опущенные из этого центра на прямые l и l1, дают точки сопряжений А и В. Второй центр дуги сопряжения О1находят на пересечении биссектрисы угла между прямыми l1и l2с продолжением перпендикуляра ВО. Третий центр дуги сопряжения О2определяют в точке пересечения биссектрисы угла между прямыми l2и l3с продолжением перпендикуляра О1С.
Задание 4
⇐ Предыдущая3456789101112Следующая ⇒ Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой. Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
Сопряжение окружностей (дуг) — МегаЛекции
Внешнее сопряжение дуг окружностей
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей (дуг) O1 ( радиус R 1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг (рис.5). Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
Рисунок 5. Внешнее сопряжение дуг окружностей
Внутреннее сопряжение дуг окружностей
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O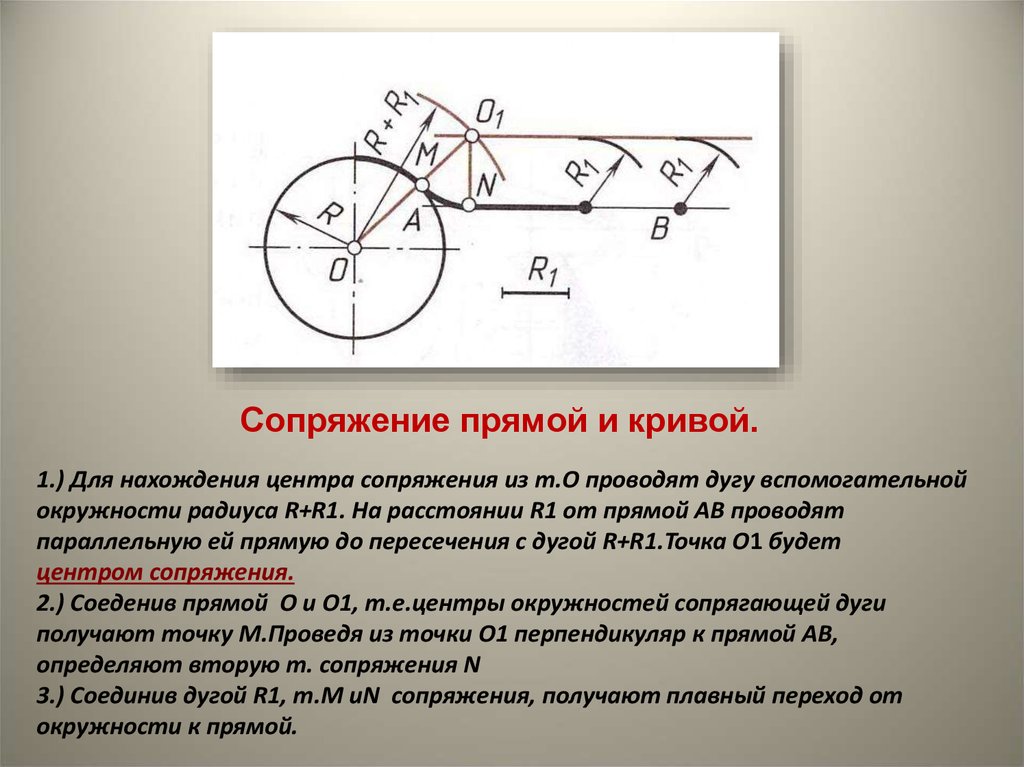
| Рисунок 6. Внутреннее сопряжение дуг окружностей | Рисунок 7.Смешанное сопряжение дуг окружностей |
Смешанное сопряжение дуг окружностей
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На рис.7 приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+ R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B.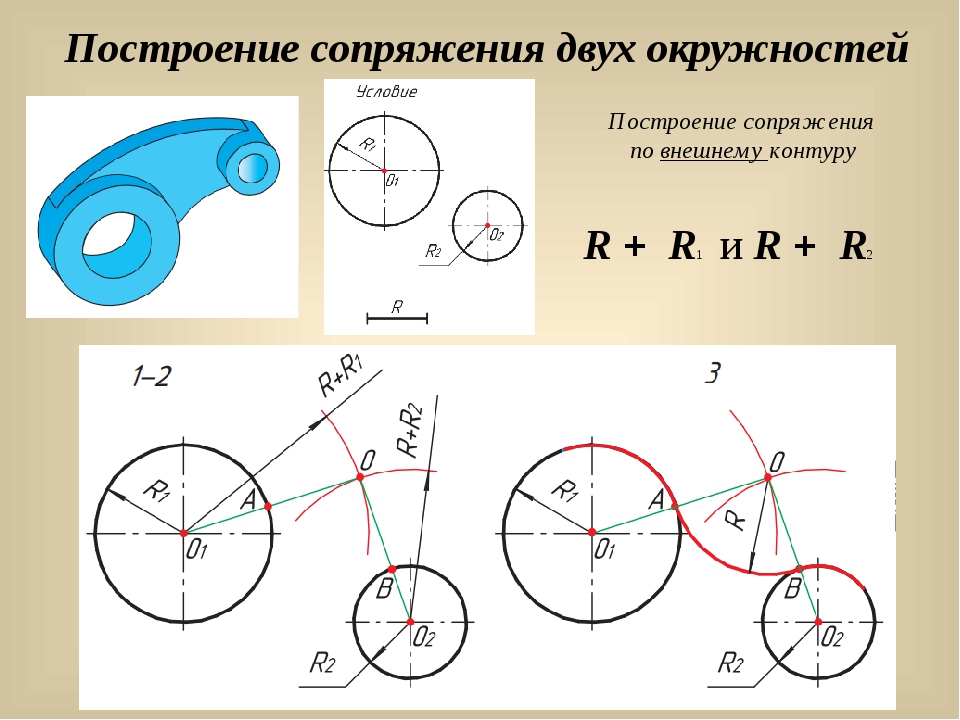 Затем строим сопряжение.
Затем строим сопряжение.
Построение кулачка
Построение очертания кулачка в каждом варианте следует начинать с нанесения осей координат Ох и Оу. Затем строят лекальные кривые по их заданным параметрам и выделяют участки, входящие в очертание кулачка. После этого можно вычертить плавные переходы между лекальными кривыми. При этом следует учесть, что во всех вариантах через точку D проходит касательная к эллипсу.
Обозначение Rx показывает, что величина радиуса определяется построением. На чертеже вместо Rx надо проставить соответствующее число со знаком «*».
Лекальной называют кривую, которую нельзя построить с помощью циркуля. Ее строят по точкам с помощью специального инструмента, называемого лекалом. К лекальным кривым относятся эллипс, парабола, гипербола, спираль Архимеда и др.
Среди закономерных кривых наибольший интерес для инженерной графики представляют кривые второго порядка: эллипс, парабола и гипербола, с помощью которых образуются поверхности, ограничивающие технические детали.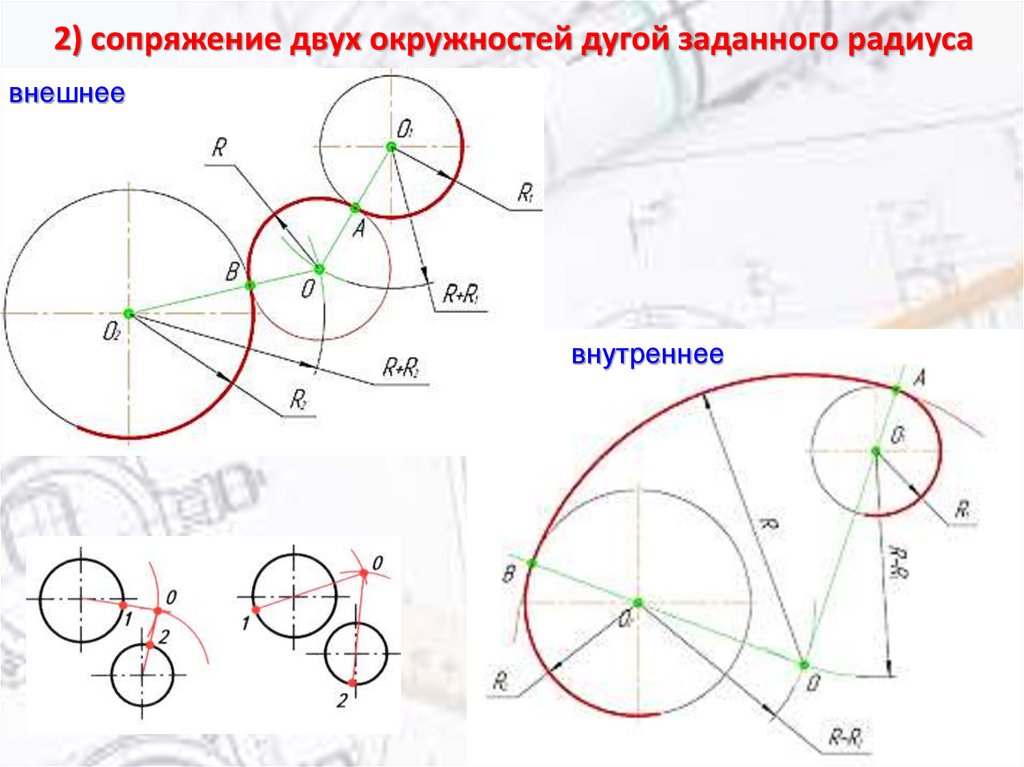
Эллипс — кривая второго порядка. Одним из способов построения эллипса является способ построения эллипса по двум осям рис.8. При построении проводим окружности радиусами r и R из одного центра О и произвольную секущую ОА. Из точек пересечения 1 и 2 проводим прямые, параллельные осям эллипса. На их пересечении отмечаем точку М эллипса. Остальные точки строим аналогично.
| Рисунок 8. Способ построения эллипса по двум осям | Рисунок 9. Построение параболы |
Параболой называется плоская кривая, каждая точка которой расположена на одинаковом расстоянии от заданной прямой, носящей название директрисы, и точки называемой фокусом параболы, расположенных в той же плоскости.
На рисунке 9 приведен один из способов построения параболы. Даны вершина параболы О, одна из точек параболы А и направление оси – ОС.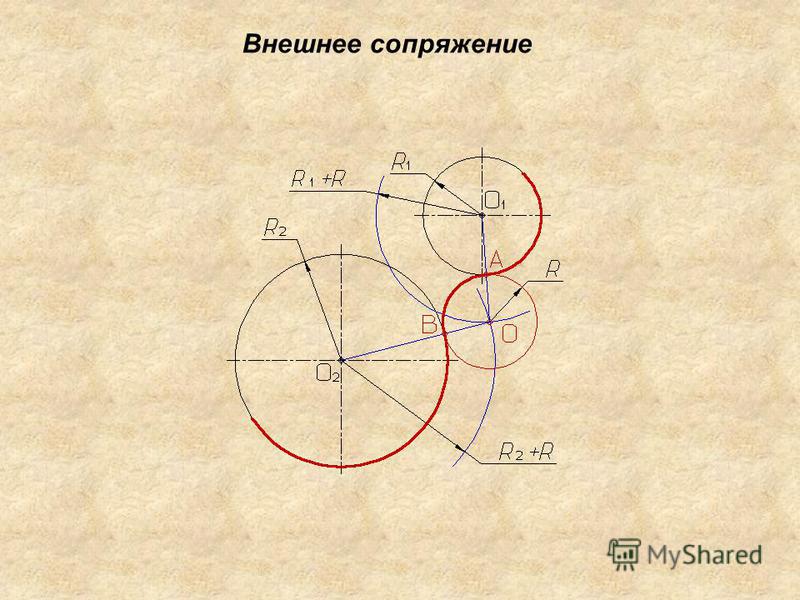 На отрезке ОС и СА строят прямоугольник, стороны этого прямоугольника в задании – А1 и В1, делят на произвольное одинаковое число равных частей и нумеруют точки деления 1, 2, 3, 4… 10. Вершину О соединяют с точками деления на А1, а из точек деления отрезка В1 проводят прямые параллельные оси ОС. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяют ряд точек параболы.
На отрезке ОС и СА строят прямоугольник, стороны этого прямоугольника в задании – А1 и В1, делят на произвольное одинаковое число равных частей и нумеруют точки деления 1, 2, 3, 4… 10. Вершину О соединяют с точками деления на А1, а из точек деления отрезка В1 проводят прямые параллельные оси ОС. Пересечение прямых, проходящих через точки с одинаковыми номерами, определяют ряд точек параболы.
Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 10) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2лR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.
Рисунок 10. Построение синусоиды
Эвольвентой называют плоскую кривую, являющуюся траекторией любой точки прямой линии, перекатываемой по окружности без скольжения.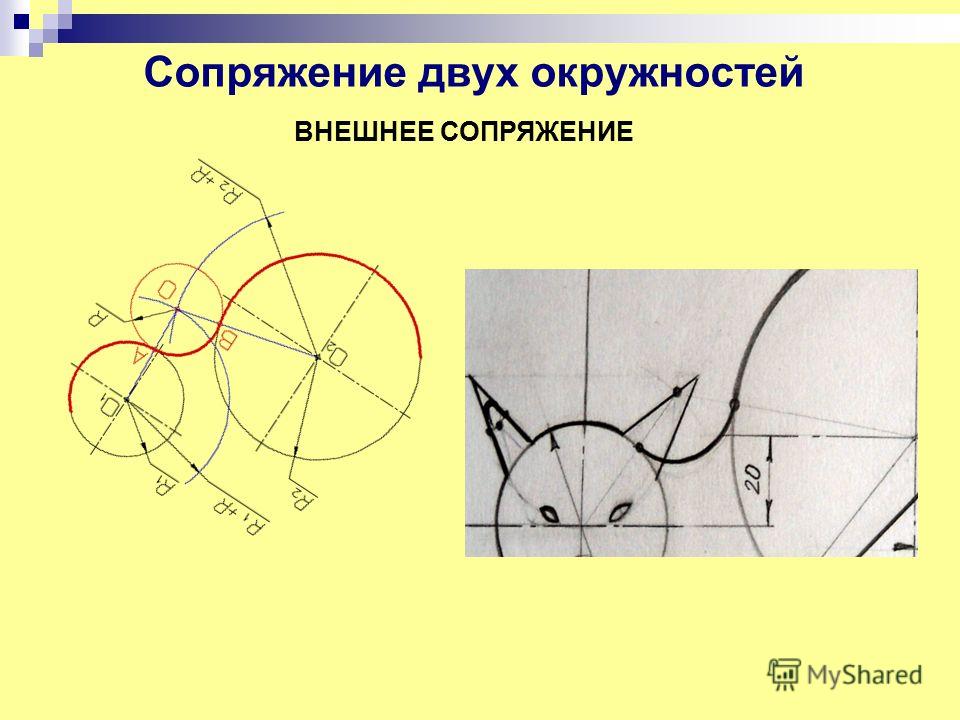 Построение эвольвенты выполняют в следующем порядке (рис.11): окружность делят на равные части; проводят касательные к окружности, направленные в одну сторону и проходящие через каждую точку деления; на касательной, проведенной через последнюю точку деления окружности, откладывают отрезок, равный длине окружности 2лR, который делят на столько же равных частей. На первой касательной откладывают одно деление 2лR/n, на второй – два и т.д.
Построение эвольвенты выполняют в следующем порядке (рис.11): окружность делят на равные части; проводят касательные к окружности, направленные в одну сторону и проходящие через каждую точку деления; на касательной, проведенной через последнюю точку деления окружности, откладывают отрезок, равный длине окружности 2лR, который делят на столько же равных частей. На первой касательной откладывают одно деление 2лR/n, на второй – два и т.д.
| Рисунок 11. Построение эвольвенты | Рисунок 12. Спираль Архимеда |
Спираль Архимеда – плоская кривая, которую описывает точка, движущаяся равномерно-поступательно от центра О по равномерно вращающемуся радиусу (рис.12).
Для построения спирали Архимеда задается шаг спирали – а, и центр О. Из центра О описывают окружность радиусом Р = а (0-8). Делят окружность на несколько равных частей, например, на восемь (точки 1, 2, …, 8).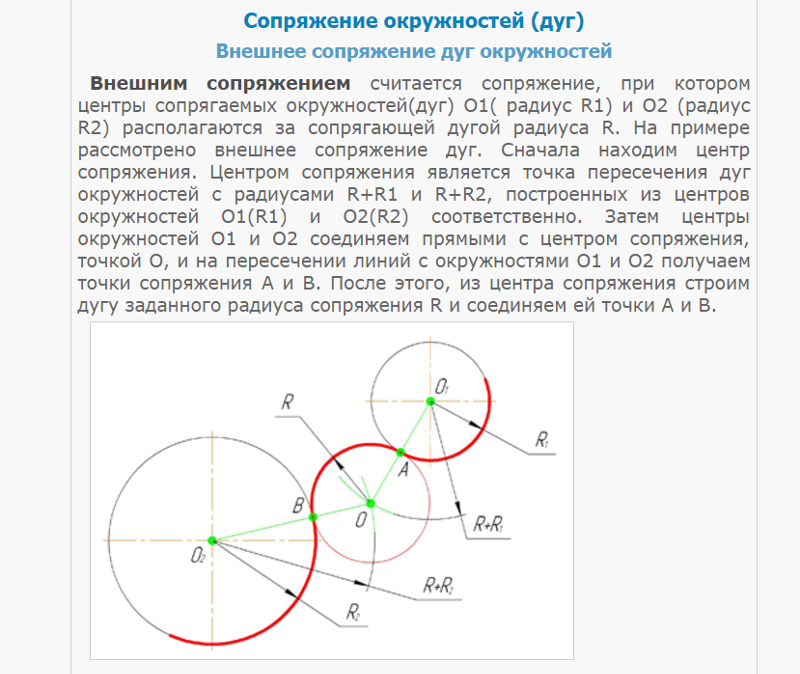 На столько же частей делят отрезок О8. Из центра О радиусами О1, О2, и т.д. проводят дуги окружностей, точки пересечения которых с соответствующими радиусами-векторами принадлежат спирали (I, II, …,YIII)
На столько же частей делят отрезок О8. Из центра О радиусами О1, О2, и т.д. проводят дуги окружностей, точки пересечения которых с соответствующими радиусами-векторами принадлежат спирали (I, II, …,YIII)
Таблица 2
Кулачок
| ||||||||||||||||||||||||||
Кулачок
|
Кулачок
| ||||||||||||||||||||||||||||
Кулачок
|
Кулачок
| ||||||||||||||||||||||||||||||
Кулачок
|
Кулачок
| ||||||||||||||||||||||||||||||
Кулачок
|
Кулачок
| ||||||||||||||||||||||||||
Кулачок
|
Кулачок
| ||||||||||||||||||||||||||
Кулачок
|
Кулачок
| ||||||||||||||||||||||||||||
Кулачок
|
Кулачок
| ||||||||||||||||||||||||||||||
Кулачок
|
Воспользуйтесь поиском по сайту:
Три свойства изогональных сопряжений – Подавляющая сила
В этом посте я расскажу о трех свойствах изогональных сопряжений, о которых мне стало известно совсем недавно.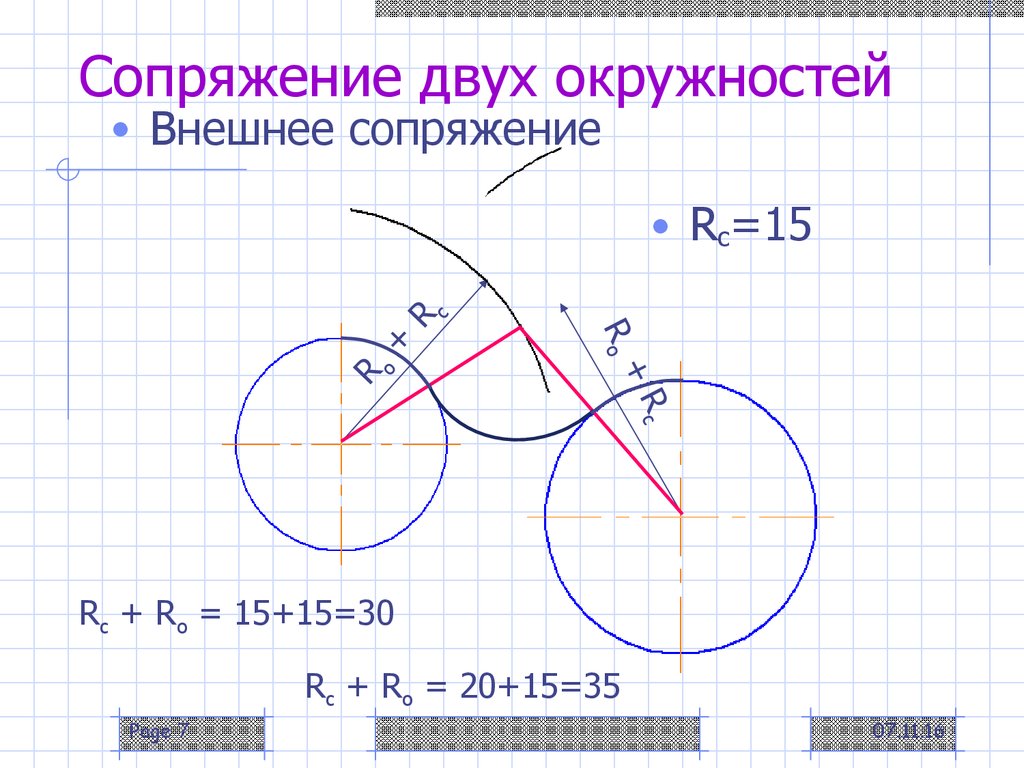 Эти свойства являются обобщением некоторых известных лемм, таких как лемма о вписанном/эксцентрическом центре и окружность с девятью точками.
Эти свойства являются обобщением некоторых известных лемм, таких как лемма о вписанном/эксцентрическом центре и окружность с девятью точками.
1. Определения
Позвольте быть треугольником с incenter , и пусть будет любая точка внутри . Тогда получим три строки , , . Тогда отражения этих линий от линий , , всегда совпадают в точке, которая называется изогональное сопряжение . (Доказательство этого совпадения легко следует из Trig Ceva.) Когда лежит внутри , то это точка, для которой и так далее.
Изогональное сопряжение иногда обозначается . Обратите внимание, что .
Примеры пар изогональных сопряжений включают следующее.
- Центр инцентрации является собственным изогональным сопряжением. Точно так же каждый эксцентр также является своим собственным изогональным сопряжением.
- Изогональное сопряжение центра описанной окружности является ортоцентром.
- Изогональное сопряжение центроида является симедианной точкой.
- Изогональное сопряжение точки Нагеля – это точка пересечения , , , где – точка касания –миктилинейной вписанной окружности. Доказательство этого результата, по сути, было дано в виде пятой задачи Европейской женской олимпиады по математике.
2. Обратные и описанные окружности
Возможно, вам уже известен знаменитый результат (который я всегда ласково называю «Фактом 5») о том, что центр описанной окружности является серединой дуги описанной окружности. Действительно, так же как и окружной центр треугольника , где -эксцентр.
На самом деле оказывается, что мы можем обобщить этот результат для произвольных изогональных сопряженных элементов следующим образом.
Теорема 1 Пусть и изогонально сопряжены. Тогда окружности и являются обратными по отношению к описанной окружности .
Доказательство: Это просто погоня за углом. Пусть и — искомые центры описанной окружности. Ясно, что оба и лежат на серединном перпендикуляре к . Погоня за углом позволяет нам вычислить, что
Пусть и — искомые центры описанной окружности. Ясно, что оба и лежат на серединном перпендикуляре к . Погоня за углом позволяет нам вычислить, что
Аналогично, . Но читатель может это проверить. Используя это, мы можем показать, что , так , как нужно.
Когда мы берем и быть (или ), мы восстанавливаем Факт 5, о котором мы упоминали выше. Когда мы принимаем за ортоцентр и за центр описанной окружности, мы находим, что центр окружности является обратным центром окружности . Но инверсия окружности является отражением над . Таким образом, мы получаем это и имеем описанные окружности, которые являются просто отражениями над .
3. Круги педалей
Возможно, вы уже знакомы с девятиконечным кругом, который проходит через середины и подошвы высот . На самом деле, мы можем получить такую окружность для любой пары изогональных сопряжений.
Теорема 2 Пусть и изогонально сопряжены внутри . Педали треугольников и делят описанную окружность.
Кроме того, центр этой окружности является серединой .
Берем и восстанавливаем девятиточечный круг. Конечно, вписанный круг — это особый случай!
Доказательство: Позвольте и быть педальными треугольниками. Мы предоставляем читателю проверить, что
Следовательно, точки , , , концикличны. Центр окружности этих четырех точек является пересечением серединных перпендикуляров сегментов и , что точно . Таким образом,
Аналогичная работа с другими вершинами показывает, что это действительно искомый центр описанной окружности.
Существует второй способ сформулировать эту теорему, взяв гомотетию в точке .
Следствие Если точка отражается относительно сторон , , и , то полученный треугольник имеет центр описанной окружности .
4. Эллипсы
Фактически из приведенной выше теоремы можно вывести следующий замечательный результат.
Теорема 3 В треугольник вписан эллипс. Тогда фокусы и изогонально сопряжены.
Конечно, вписанная окружность — это частный случай, когда эллипс — это окружность.
Доказательство: Мы выведем это из следствия. Пусть эллипс касается точек , , . При этом пусть отражение относительно сторон будет точками , , . По определению существует общая сумма с
Из-за условия касания точки , , лежат на одной прямой. Но теперь
и мы выводим
Таким образом, центр окружности . Следовательно, изогональное сопряжение .
Обратное утверждение этой теоремы также верно; заданы изогональные сопряжения и внутри мы можем построить подходящий эллипс. Кроме того, стоит отметить, что линии , , также параллельны; одно доказательство – проективное преобразование, превращающее эллипс в окружность.
Используя эту теорему, мы можем дать «морально правильное» решение следующей задачи, которая находится в списке IMO Shortlist 2000, Задача G3.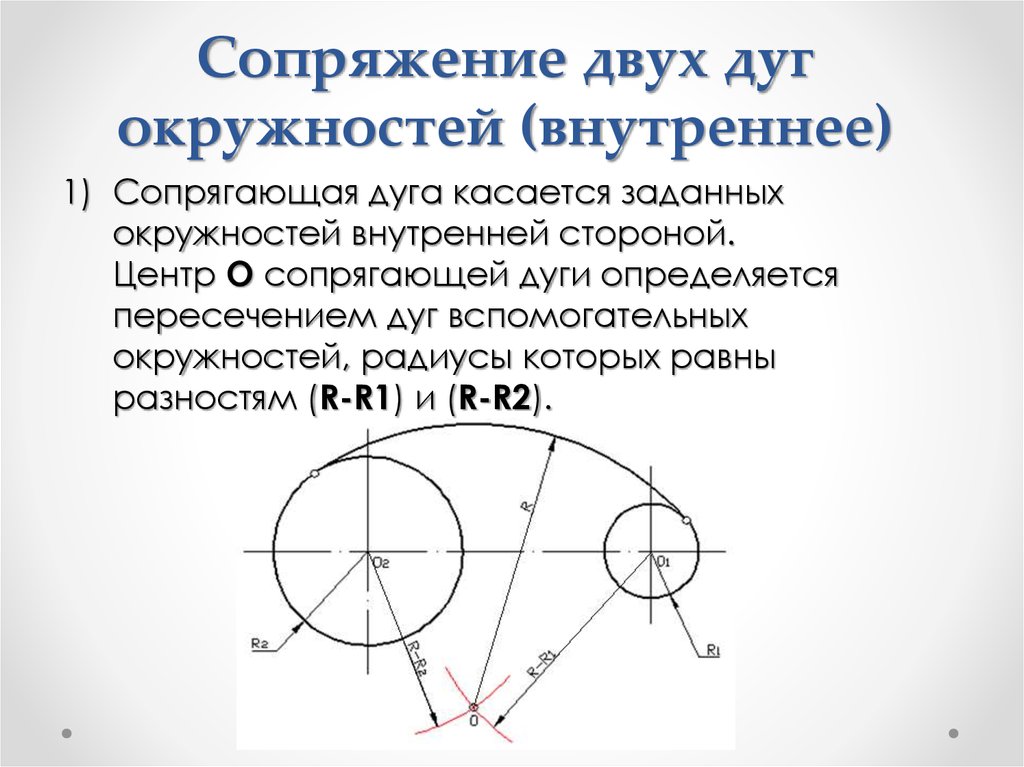
Задача Позвольте быть центром описанной окружности и ортоцентром острого треугольника. Покажите, что существуют точки , , и на сторонах , , и соответственно такие, что
и линии , , и параллельны.
Доказательство: Поскольку и изогонально сопряжены, мы можем построить эллипс, касающийся сторон в точках , откуда следуют оба условия.
5. Теорема Паскаля
Подробнее об изогональных сопряжениях см., например, Дарий Гринберг. Я закончу еще одним прекрасным применением изогональных конъюгатов, о котором мне сообщил М. Курал в августе прошлого года.
Теорема 4 (Паскаль) Пусть вписанным шестиугольником, как показано. Предположим, и . Тогда точки , , коллинеарны.
Доказательство: Обратите внимание, что , хотя треугольники имеют противоположные ориентации. Так как , и т. д., точки и соответствуют изогонально-сопряженным. Отсюда , что дает коллинеарность.
д., точки и соответствуют изогонально-сопряженным. Отсюда , что дает коллинеарность.
Спасибо R Alweiss и heron1618 за указание на несколько опечаток и Даниэлю Палеке за небрежное применение теоремы Брианшона.
Нравится:
Нравится Загрузка…
Анатомия, брюшная полость и таз, вход в таз — StatPearls ложный таз выше. Между мужским и женским тазом существуют ощутимые, генетические и гормональные различия, связанные с репродуктивной функцией.
В акушерстве вход в таз является входом в родовые пути. Головная конечность плода должна позиционироваться и адекватно адаптироваться, чтобы сравнить меньший диаметр с наибольшим диаметром пространства, ограниченного анатомической линией входа в таз матери.
Форма входного отверстия зависит от общей формы таза согласно традиционной классификации Колдуэлла и Молоя[1]. Размеры ее переднезаднего, косого и поперечного диаметров варьируют в зависимости от морфологического типа таза.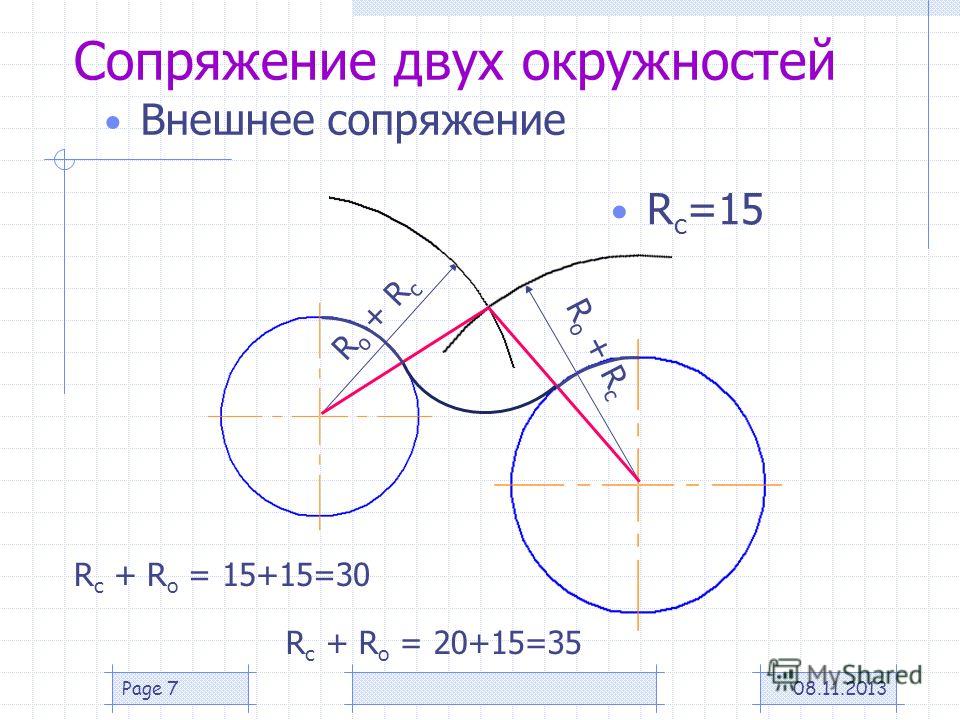 Пропорции формы внутренних тазовых пространств соответствуют пропорциям крестцовой области Михаэлиса.
Пропорции формы внутренних тазовых пространств соответствуют пропорциям крестцовой области Михаэлиса.
Имеются рентгенологические данные о том, что внутритазовое пространство изменяется в зависимости от положения субъекта. Положение, занимаемое испытуемым, влияет на значения поперечного и передне-заднего диаметров. Это доказательство чрезвычайно полезно для облегчения входа плода в истинный таз и способствует фазе расширения родов.[2]
Метод оценки диаметров внутритазовых пространств и их адаптируемости (подвижности) будет полезен для диагностики «узкого таза» и предотвращения последствий для здоровья матери и новорожденного, которые могут быть связаны с затяжными родами и оперативными родами .
Структура и функция
Анатомия костей
Вход в таз включает три из четырех частей, из которых состоит костный таз. Край таза включает первый крестцовый сегмент, подвздошную и лобковую части, но не седалищную кость.
Вход в таз очерчен костным гребнем, который определяет его границу (край таза), который позже относится к мысу крестца.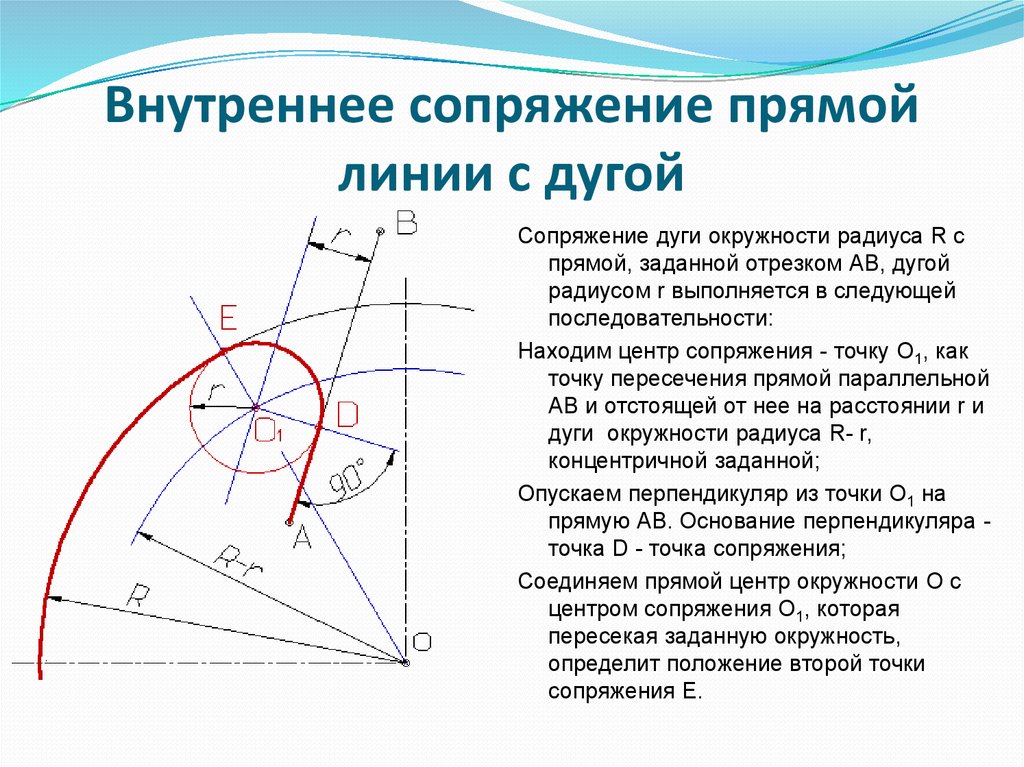 Продолжая движение вправо и влево в направлении вниз и латерально в направлении подвздошной кости, проходя по закругленному краю, отделяющему основания крестца от передней поверхности самого крестца: linea terminalis. Он продолжается вбок, поднимаясь над крестцово-подвздошными сочленениями, вдоль подвздошно-гребешковых линий в их начальной части (linea innominata, дугообразные линии) подвздошной кости (также называемой «безымянной») и продолжается по направлению к гребенчатой линии лобковой кости (гребни), и закрывается перед лобковым симфизом, проходя через верхне-задний край подвздошно-лобковых ветвей и лобковый бугорок.
Продолжая движение вправо и влево в направлении вниз и латерально в направлении подвздошной кости, проходя по закругленному краю, отделяющему основания крестца от передней поверхности самого крестца: linea terminalis. Он продолжается вбок, поднимаясь над крестцово-подвздошными сочленениями, вдоль подвздошно-гребешковых линий в их начальной части (linea innominata, дугообразные линии) подвздошной кости (также называемой «безымянной») и продолжается по направлению к гребенчатой линии лобковой кости (гребни), и закрывается перед лобковым симфизом, проходя через верхне-задний край подвздошно-лобковых ветвей и лобковый бугорок.
Глядя на внутреннюю поверхность подвздошной кости, видно, что дугообразная линия заканчивается за передним углом, разделяющим верхнюю и нижнюю части ушной поверхности, сочленяющейся с крестцом. Прослеживая воображаемую линию, которая продолжается назад, край таза продолжается к задней верхней подвздошной ости после прохождения через нижний подвздошный бугорок.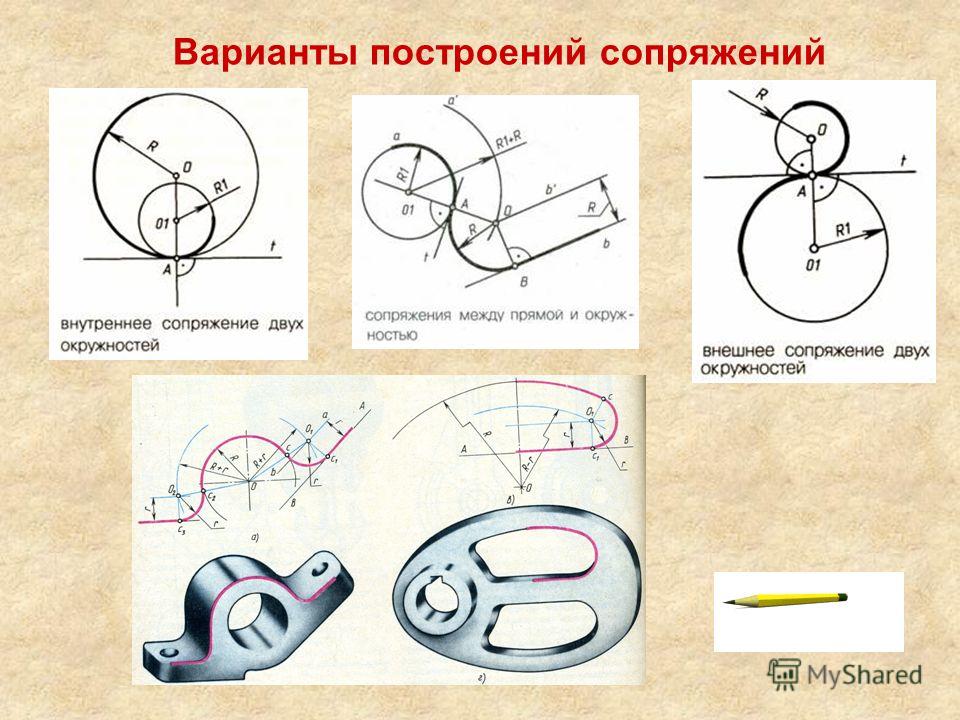 Таким образом, по аналогии, лобковый бугорок и пространство лобкового симфиза являются передним соединительным мостом двух половин входа в таз, а верхняя задняя подвздошная ость (SIPS) и пространство между подвздошными (крестцово-подвздошными суставами и передняя и задняя связки) являются краями заднего моста.
Таким образом, по аналогии, лобковый бугорок и пространство лобкового симфиза являются передним соединительным мостом двух половин входа в таз, а верхняя задняя подвздошная ость (SIPS) и пространство между подвздошными (крестцово-подвздошными суставами и передняя и задняя связки) являются краями заднего моста.
Висцеральные структуры
Сигма пересекает верхнюю узкую тазовую артерию с корнем мезосигмы (который находится на уровне левого крестцово-подвздошного сочленения), мочеточником и семявыносящим протоком. Иногда даже слепая кишка и червеобразный отросток опускаются в таз из правой подвздошной ямки, около правого крестцово-подвздошного сочленения. Купол мочевого пузыря имеет тенденцию выступать за пределы верхнего пролива, когда мочевой пузырь наполнен, вместе с медиальной пузырно-пупочной связкой (остатками урахуса) и медиальными пузырно-пупочными складками (остатками пупочных артерий). Наиболее глубокой париетальной структурой, пересекающей верхнетазовую узкую, оказывается париетальная брюшина.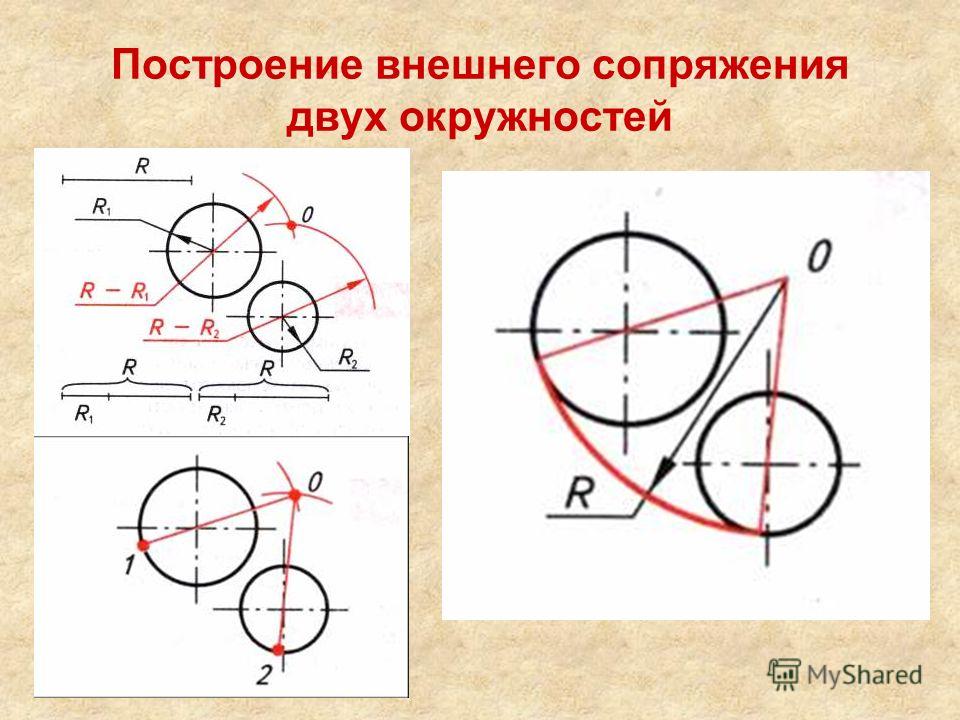
Эмбриология
Скелет таза формируется путем мезенхимального уплотнения и эндохондральной оссификации. Первый очаг окостенения развивается в подвздошной кости в раннем внутриутробном периоде. Множественные участки окостеневают и продолжают развиваться после рождения до подросткового возраста.
Таз плода, включая подлобковый угол, ширину и глубину седалищной вырезки, зависит от пола. Однако рост седалищной и лобковой костей и седалищно-лобковые индексы с возрастом не меняются. Половые различия в морфологии таза могут быть обнаружены у плодов через девять недель после оплодотворения (или через 11 недель после последней менструации) после активации половых хромосом.[3]
Соединения и сочленения хрящей в области таза необходимы для формирования тазового кольца в течение ограниченного периода времени: от 54 до 60 дней после оплодотворения, примерно через восемь недель эмбрионального периода или 10 недель беременности. Нормальный период необходим для начала эффективных движений плода, которые могут вызывать механические силы и влиять на нормальное развитие скелета. Движения плода также могут объяснить некоторые изменения формы таза, наблюдаемые позднее. Наблюдения, проведенные в более позднем периоде внутриутробного развития, показали, что наиболее частая форма входа в таз одинакова между полами: андроидный тип у 56% плодов мужского пола и 54% у плодов женского пола. Кажется, это указывает на важность факторов окружающей среды в определении формы таза.[3]
Движения плода также могут объяснить некоторые изменения формы таза, наблюдаемые позднее. Наблюдения, проведенные в более позднем периоде внутриутробного развития, показали, что наиболее частая форма входа в таз одинакова между полами: андроидный тип у 56% плодов мужского пола и 54% у плодов женского пола. Кажется, это указывает на важность факторов окружающей среды в определении формы таза.[3]
Кровоснабжение и лимфатическая система
Разделение подвздошных сосудов, общих для наружной и внутренней подвздошных костей, происходит перед крестцово-подвздошным сочленением. Внутренние подвздошные сосуды спускаются в таз, а наружные подвздошные сосуды проходят по медиальному брюшку поясничной мышцы параллельно верхнему краю таза. Также внутренние запирательные сосуды делают то же самое на нижнем крае.
Структура, которая наиболее тесно проходит вдоль тазового края краев таза, по-видимому, является остатком пупочной артерии, расположенным над обструктивным сосудисто-нервным пучком в контакте с костно-связочной плоскостью входа в таз.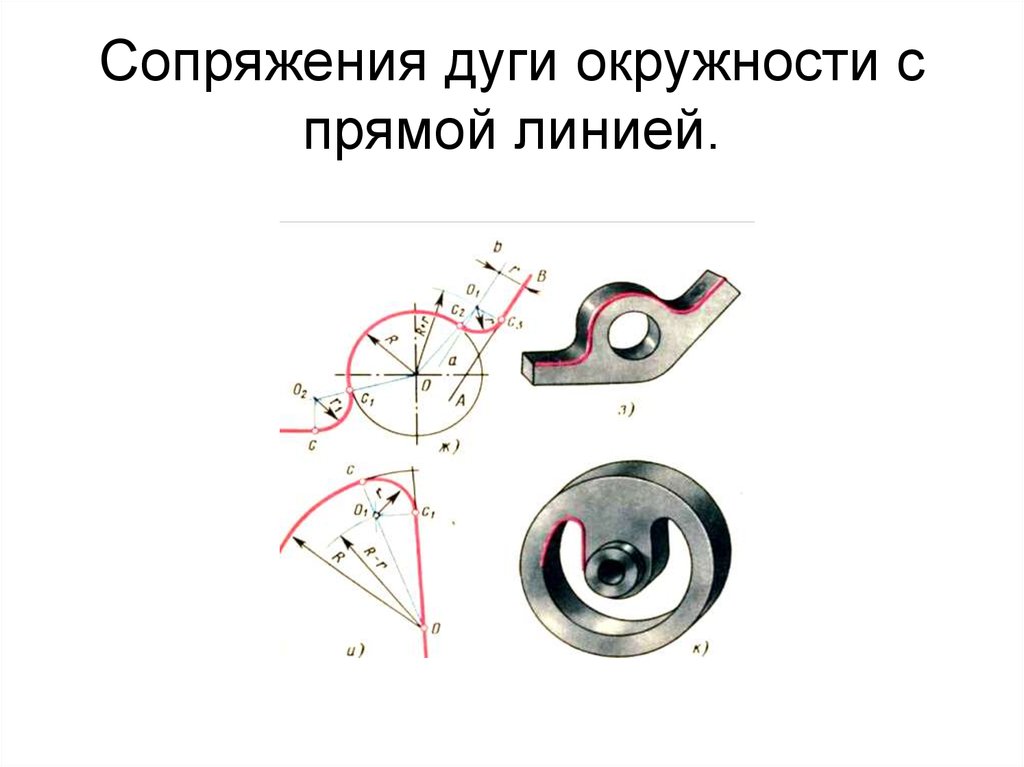 Средняя крестцовая артерия берет начало от брюшной аорты в углу, образованном отхождением общих подвздошных артерий, затем проходит над мысом крестца и спускается к копчику. Залобковая ветвь надчревной артерии (ветвь наружной подвздошной артерии) обходит края таза в своем переднем полуцикле.
Средняя крестцовая артерия берет начало от брюшной аорты в углу, образованном отхождением общих подвздошных артерий, затем проходит над мысом крестца и спускается к копчику. Залобковая ветвь надчревной артерии (ветвь наружной подвздошной артерии) обходит края таза в своем переднем полуцикле.
То же самое происходит и с сосудами яичника (но не яичковыми, входящими в паховый канал из внутреннего отверстия) и круглой связкой матки с ее сосудами.
Нервы
Запирательный нерв должен пересекать верхние тазовые сужения и четвертый и пятый поясничные корешки пояснично-крестцового сплетения. Кпереди от оснований крестца проходит латерально-позвоночная цепь ортосимпатической системы.
Верхнее (верхнее) подчревное сплетение проходит сначала кпереди от брюшной аорты, а затем впереди мыса крестца, опускается и смешивается своими волокнами с нижним внутритазовым подчревным сплетением. Соединение верхнего и нижнего сплетений обеспечивает иннервацию желудочно-кишечного тракта и половых органов в малом тазу.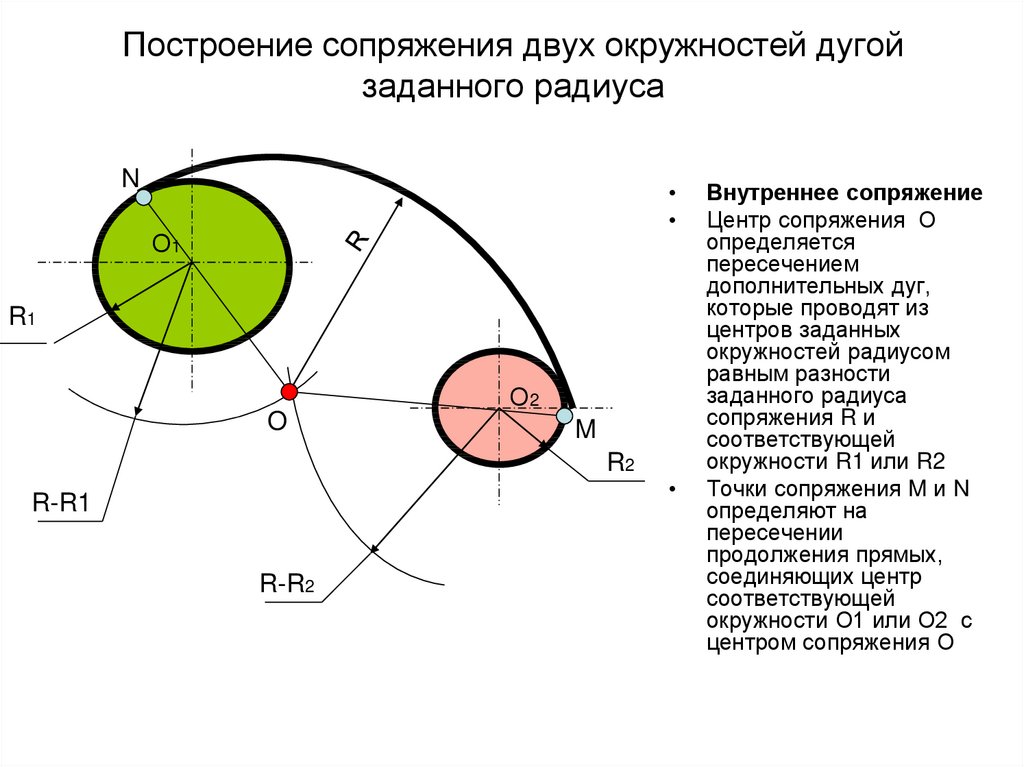 [4]
[4]
Мышцы
Несколько миофасциальных структур прикрепляются к костному краю входа в таз, в то время как его обходят многие сосудистые, нервные и висцеральные структуры, которые могут быть заинтересованы в компрессионных факторах, когда головка плода вот-вот войдет в таз на последней неделе беременности.
Мышечные структуры
На краю таза (крае таза) нижняя часть подвздошно-поясничной мышцы прикрепляется кзади, охватывая крестцово-подвздошный сустав, прежде чем мышечный желудок сдвинется вперед к лобку, скользя параллельно краю таза своим медиальным краем. Покрыта лентой, которая внизу продолжается после прохождения арочной линии на верхней вставке внутренняя запирательная мышца мышца. Гребневидная мышца берет начало впереди по отношению к лобково-гребенчатому гребню верхнего сужения таза. Малая поясничная мышца , непостоянная, может прикрепляться непосредственно к гребенчатой линии и ее связке.[5]
Связки и бандажи
Передняя продольная связка, которая проходит спереди по всей длине позвоночного столба, продолжается крестцовой надкостницей на уровне мыса.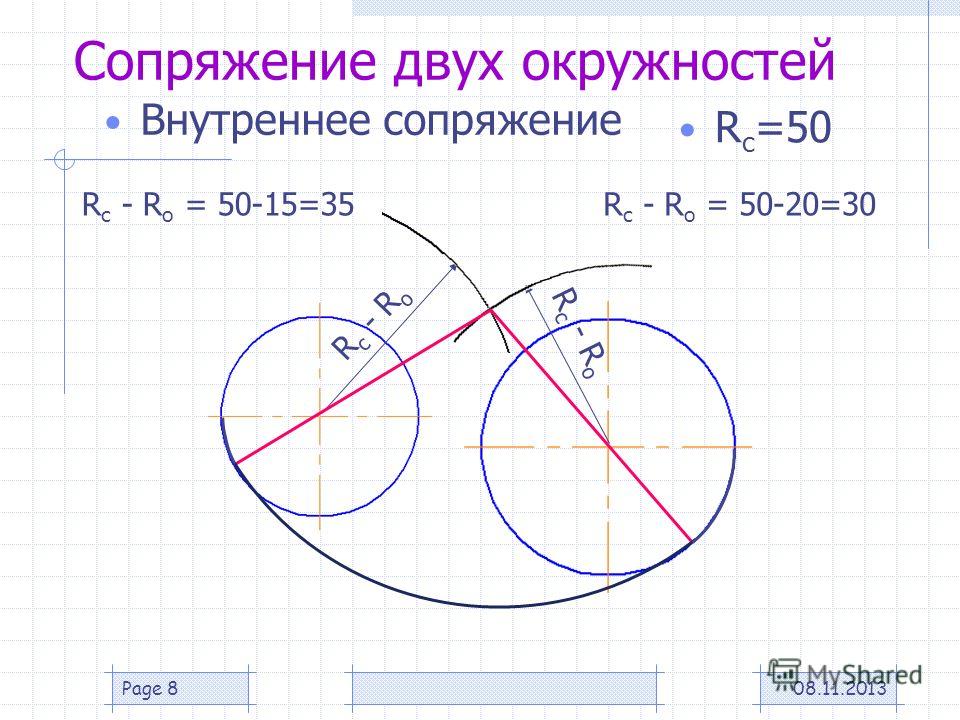 Небольшой пучок передней подвздошно-поясничной связки, который является частью фиброзной капсулы крестцово-подвздошного сустава, имеет криволинейное направление вниз и прикрепляется кпереди по дугообразной линии.[6] Паховая связка имеет основное передне-нижнее прикрепление к лобковому бугорку. Она продолжается лакунарной связкой, образуя сильное утолщение в виде подвздошно-гребешковой связки, которое находится на продолжении безымянная линия подвздошной кости.
Небольшой пучок передней подвздошно-поясничной связки, который является частью фиброзной капсулы крестцово-подвздошного сустава, имеет криволинейное направление вниз и прикрепляется кпереди по дугообразной линии.[6] Паховая связка имеет основное передне-нижнее прикрепление к лобковому бугорку. Она продолжается лакунарной связкой, образуя сильное утолщение в виде подвздошно-гребешковой связки, которое находится на продолжении безымянная линия подвздошной кости.
Паховая связка является продолжением фасции поперечной мышцы живота, которая берет начало кзади от поясничной области как продолжение грудопоясничной фасции. Подвздошно-поясничные связки утолщаются и продолжаются грудопоясничной фасцией на передней стороне латеральной поверхности позвоночника.
Физиологические варианты
Морфология входа в таз
Общая форма таза определена в исторической публикации 1930-х годов Колдуэлла и Молоя. Форма окружности таза узкая. Внутреннее пространство таза зависит от общей формы самого таза.
Форма женского таза была разделена на четыре класса Колдуэллом и Молоем, которые сообщают о следующих пропорциях в популяции из 147 случаев: гиноид — 41,4%; андроид, 32,5%; антропоидный — 23,5% и платипеллоидный — 2,6%. Каждый из них имеет особые характеристики, касающиеся ширины подлобкового угла, высоты таза, поперечных диаметров трех плоскостей таза (вход, средний таз, выход) и формы окружности верхнего сужения таза [1]. ].
Вход в гиноидный таз имеет овальную форму, поперечный диаметр чуть больше передне-заднего диаметра. Таз андроида имеет форму сердца, при этом наибольшая ширина поперечного диаметра смещена в сторону крестца. Акушерская конъюгата антропоидного таза значительно больше поперечного диаметра. В платипеллярном тазу вход широкий и очень узкий. Форма зависит как от генетических факторов, так и от факторов окружающей среды, таких как питание и образ жизни. Недостаток пищи или инфекционные заболевания приводят к деформации таза, которая, к счастью, осталась в прошлом.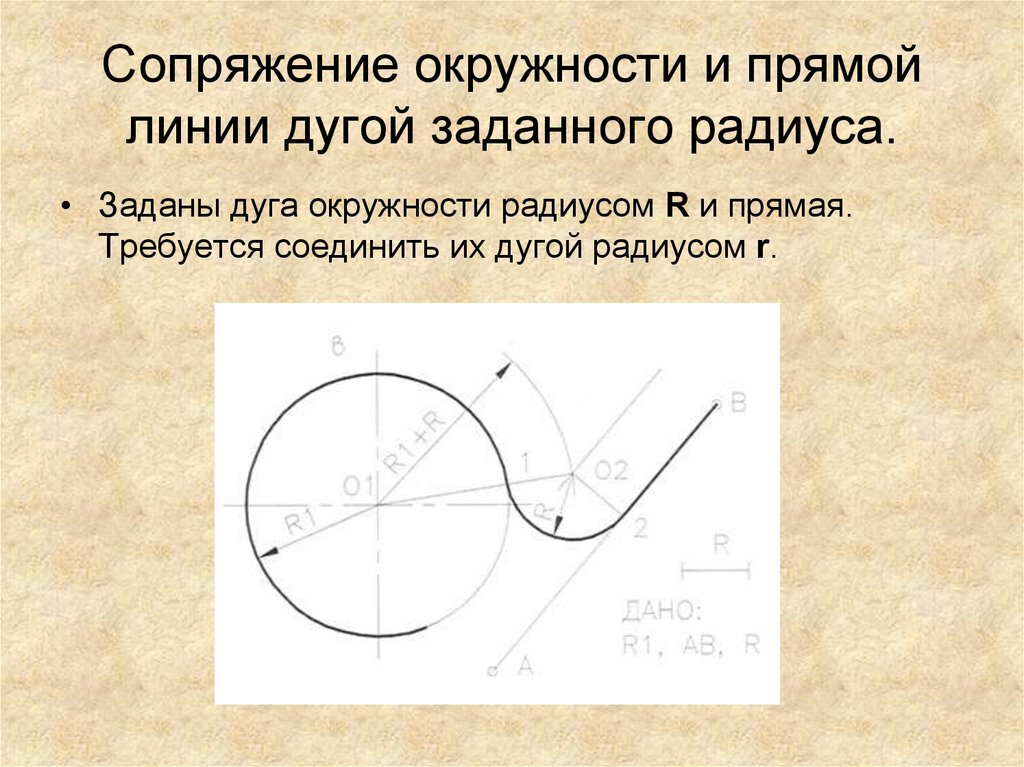 Тяжелые формы подросткового сколиоза могут влиять на морфологию таза, а также на врожденный вывих бедра и, вероятно, на положение плода в утробе (неопубликованные личные наблюдения).
Тяжелые формы подросткового сколиоза могут влиять на морфологию таза, а также на врожденный вывих бедра и, вероятно, на положение плода в утробе (неопубликованные личные наблюдения).
Исследование Abitbol, проведенное в 1996 году, связывает морфологию таза с такими факторами, как гормональный тонус, возраст, в котором достигается прямохождение и ходьба, и интенсивная спортивная активность в подростковом возрасте [7].
Ориентация входа в таз
Вход в таз имеет наклон примерно от 55 до 60 градусов относительно анатомической горизонтальной плоскости. Большой или малый углы означают ретроверсию или антеверсию таза и наклон таза назад или вперед. Общий наклон таза поддерживается балансовым напряжением между различными мышечными и фасциальными анатомическими компонентами. Грудно-поясничная фасция играет фундаментальную роль в статике и динамике таза и в его взаимоотношениях с плечевым поясом, необходимая для поддержания осанки, ходьбы и скоординированных движений конечностей.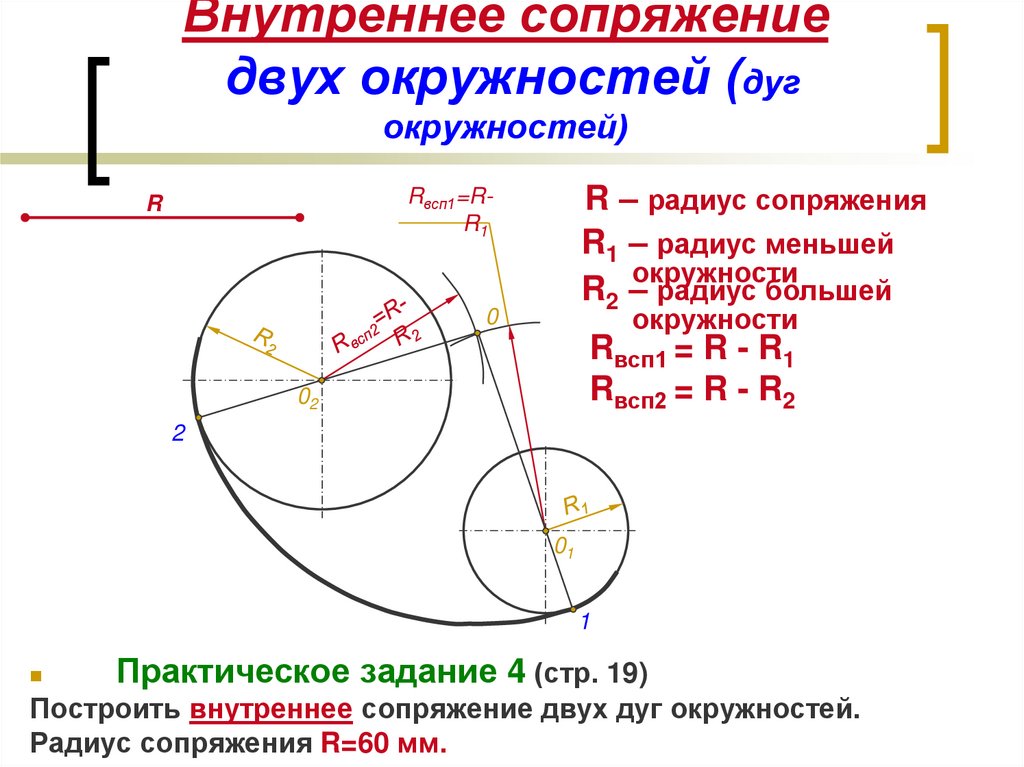 Согласно Коттингэму (1988), передний наклон соответствует общему ортосимпатическому тонусу, тогда как задний наклон таза соответствует относительному парасимпатическому тонусу.[8][9]
Согласно Коттингэму (1988), передний наклон соответствует общему ортосимпатическому тонусу, тогда как задний наклон таза соответствует относительному парасимпатическому тонусу.[8][9]
Мышцы, поддерживающие наклон, в основном относятся к абдоминальной «коробке»: передняя и латеральная мышцы живота (которые своими связками способствуют формированию паховой связки), паравертебральные мышцы, большая поясничная мышца и грушевидные мышцы; торакоабдоминальной диафрагмы и тазового дна. В группе мышц задней поверхности бедра biceps femoris мышца упоминается из-за ее проксимального прикрепления к седалищному бугру в продолжение крестцово-бугорной связки, которая является одним из основных утолщений крестцово-пояснично-грудного фасциального комплекса.
Клиническое значение
Внешняя морфология таза и вход в таз
Традиционная наружная тазовая метрия Боделока возникла из гипотезы о соответствии наружных форм и размеров таза внутренним. Текущая литература подтверждает корреляцию. [10]
[10]
Можно отследить и измерить косой диаметр, поперечный диаметр и передне-задний или сопряженный диаметр входа в таз. Форма входного отверстия регулируется относительными пропорциями между поперечным диаметром и акушерской конъюгатой.[11]
Область крестцового ромба внешне соответствует входу в таз: поперечный и продольный диаметры крестцовой области Михаэлиса будут иметь определенное реципрокное соотношение для каждого типа таза, соответствующее форме входа в таз. Поперечный диаметр крестцовой ромбовидной области Михаэлиса равен расстоянию между двумя задними верхними подвздошными остями (PSIS) [12]. Продольный диаметр описывают между верхушкой остистого отростка пятого поясничного позвонка вверху и верхней границей межъягодичной борозды, что соответствует четвертому-пятому крестцовому сегменту.
Два диаметра области крестцового ромба имеют одинаковые размеры, либо продольный больше поперечного (встречается редко), и они пересекаются в своей средней точке. Могло случиться так, что поперечный диаметр, пересекающий продольный на уровне второго крестцового сегмента, разделит последний на две неравные части: верхняя часть продольного диаметра короче нижней.
Динамика биомеханического движения будет разной в зависимости от морфологии таза по тому же принципу. Анатомия фасций боков крестцово-ромбовидной области, регулирующих ее форму и движение, соответствует фасциальным утолщениям, входящим в состав крестцового комплекса грудопоясничной фасции, которая окружает крестцово-подвздошные суставы как сзади, так и, со стороны подвздошно-поясничных связок, спереди. Биомеханические свойства полос будут иметь последствия изнутри наружу и наоборот.[6] Форма задней мышечной и жировой тканей, по-видимому, соответствует общей морфологии таза. Классификация следующая: гинекоидному тазу соответствует округлая форма ягодиц, платипеллоидному тазу — треугольная форма, антропоидному тазу — квадратная форма, а андроидному тазу — трапециевидная ягодичная форма.[13]
Диаметры крестцовой области использовались для выявления черепно-тазовой диспропорции с последующими осложненными родами и дистоцией, что привело к корреляции между поперечным диаметром и осложнениями во время родов. [12][10][14][15]
[12][10][14][15]
Диаметр входа в таз
Вход в таз неправильной формы; можно определить три диаметра.
Переднезадний (или «сопряженный») диаметр — это расстояние между лобковым симфизом и мысом крестца. Три дистанции:
Анатомическая конъюгата или истинная: измеряется между мысом крестца и верхним краем лобкового симфиза и имеет среднюю длину 11,0 см. задняя часть лобкового симфиза, расположенная примерно на 1 см ниже его верхней границы. В среднем он составляет 10,5 см; это меньший переднезадний диаметр.
Диагональная конъюгата: Измеряется между мысом крестца и нижним краем лобкового симфиза, средний размер 12,5.
Передне-задний диаметр также можно оценить с помощью наружной тазовой манометрии с использованием различных типов тазовых трубок. По классическому объяснению Бауделока, наружная конъюгата измеряется от верхнего края лобкового симфиза спереди до первого крестцового сегмента сзади («впадина на один сантиметр под остистым отростком пятого поясничного позвонка»), ее размеры составляют около 20 см.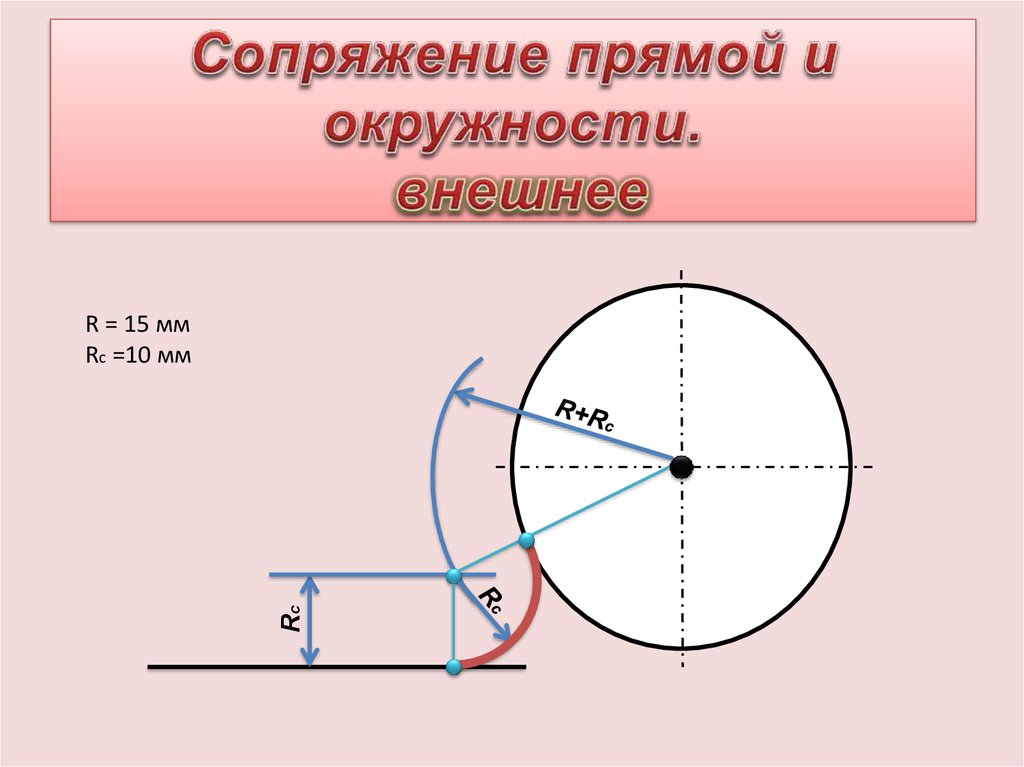 [10]
[10]
Косой диаметр самый большой из трех; это расстояние между дугообразной линией возле крестцово-подвздошного сустава сзади и лобково-гребешковой линией спереди. Это диаметр, на котором представлена головка плода; его размер около 12 см. Поперечный диаметр — это расстояние между двумя безымянными линиями в их самом широком месте и составляет примерно 13 см. Вход головки плода в полость таза в норме происходит путем поворота от косого диаметра к поперечному диаметру. Внешняя пельвиметрия также позволяет оценить поперечный диаметр путем измерения расстояния между двумя верхними задними подвздошными остями (PSIS). Среднее расстояние между двумя PSIS составляет около 11 см.[10]
Прочие вопросы
Эндотазовая биомеханическая динамика
Интересное лонгитюдное исследование 2016 года, появившееся на PNAS, показывает, что форма таза у обоих полов не статична, а изменяется с возрастом. Кажется, что морфология таза меняется каждые два десятилетия из-за формы ремоделирования, общего изменения формы костей.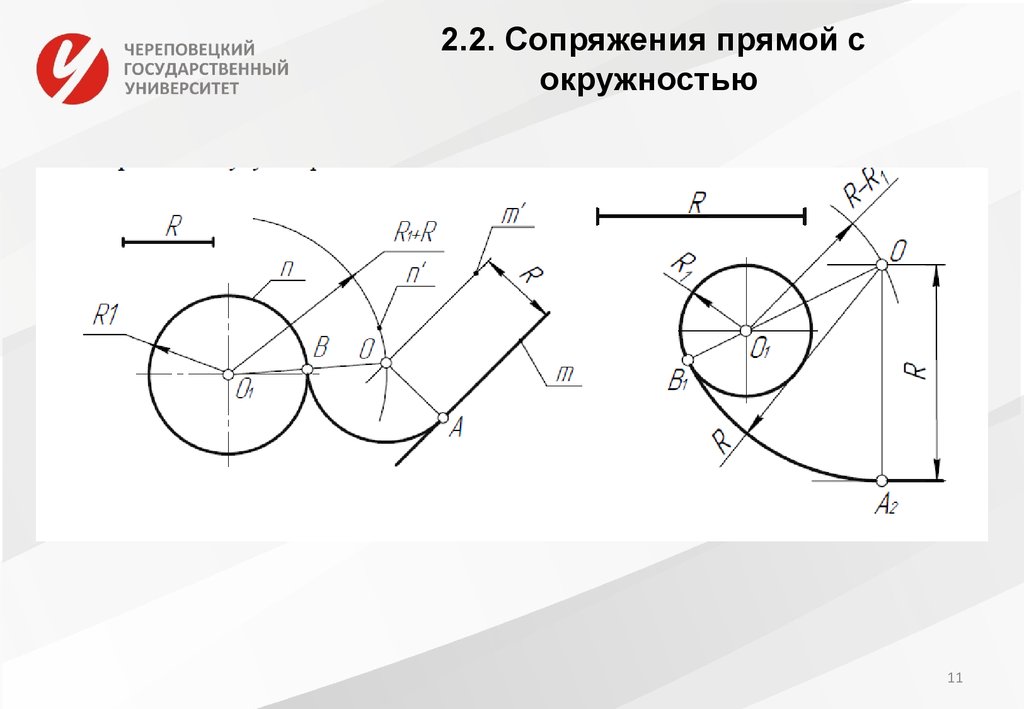 [16] У женщин тазовая форма, имеющая самые большие внутренние диаметры, присутствует между 20 и 40 годами: возраст половой зрелости и беременность с меньшим риском.
[16] У женщин тазовая форма, имеющая самые большие внутренние диаметры, присутствует между 20 и 40 годами: возраст половой зрелости и беременность с меньшим риском.
Два радиологических исследования с помощью МРТ изучали возможность оценки внутритазового диаметра субъектов, находящихся в различных позах: в положении лежа, на четвереньках (опираясь на руки и колени) и в приседаниях на коленях. Выявлены значительные изменения в изменении положения с уменьшением диаметров конъюгаты около 3 мм, увеличением переднезадних диаметров срединной плоскости и выхода на 4 и 5 мм, а поперечных диаметров показывают увеличение около 15 мм. Исследование проводилось на двух группах женщин: беременных и не беременных. Результаты были такими же. Вход в таз показал меньшую разницу, чем выход и середина таза: это может означать, что при изменении положения вход изменяет больше свою форму и наклон в горизонтальной плоскости, чем его поперечный диаметр.
В области клинического акушерства и остеопатии оценка качества заднего движения таза предлагается в качестве общего показателя возможности родоразрешения через естественные родовые пути.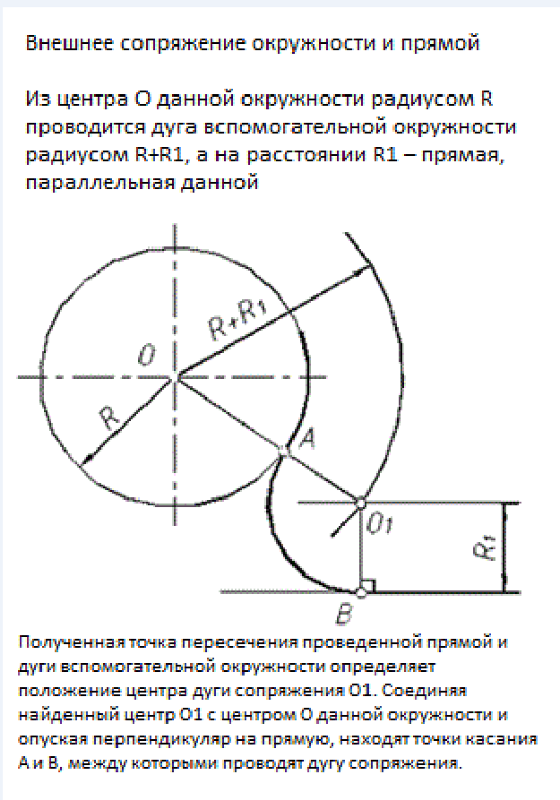 Диаметрами крестцовой области являются поперечный диаметр, лежащий между двумя задними верхними подвздошными остями (ЗВП), и продольный диаметр, натянутый между остистым отростком пятого поясничного позвонка и началом межъягодичной борозды («алмазный тест», «, которым десятилетиями обучают в остеопатической практике). Они должны увеличивать свою амплитуду при переходе беременных из положения стоя в положение сидя. В зависимости от возможного амплитудного ограничения диапазона движений сустава (крестцово-подвздошного, тазобедренного или лобкового) или можно предположить фасциальную/связочную дисфункцию [9].0003
Диаметрами крестцовой области являются поперечный диаметр, лежащий между двумя задними верхними подвздошными остями (ЗВП), и продольный диаметр, натянутый между остистым отростком пятого поясничного позвонка и началом межъягодичной борозды («алмазный тест», «, которым десятилетиями обучают в остеопатической практике). Они должны увеличивать свою амплитуду при переходе беременных из положения стоя в положение сидя. В зависимости от возможного амплитудного ограничения диапазона движений сустава (крестцово-подвздошного, тазобедренного или лобкового) или можно предположить фасциальную/связочную дисфункцию [9].0003
Тазовая метрия и акушерство: прошлое и настоящее
С наступлением технологической эры классическая наружная тазовая метрия, главным представителем которой в 18 веке был французский врач Боделок Ж.Л., была заброшена. Это была попытка объяснить причины родовой дистоции, не имея средств для ее решения.
В первые десятилетия двадцатого века рентгенологическое исследование дало новый импульс статической тазовой оценке с возможностью непосредственного измерения внутренних диаметров; однако и этот метод разочаровал.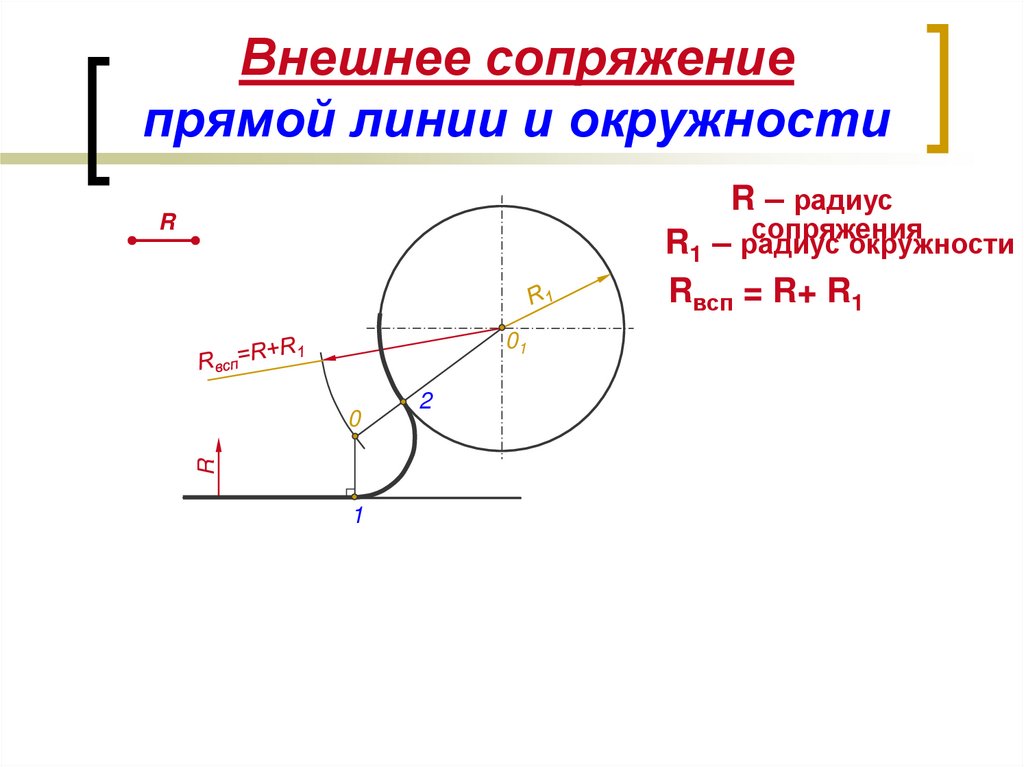 МРТ упростила измерения и сделала их более точными благодаря воспроизводимым сканам. Возможность записи изображений в движении позволила увидеть живые роды и подтвердить, что изменение положения роженицы изменяет внутренний диаметр таза.[2] Эта информация была интуитивно известна и использовалась акушерками на протяжении нескольких столетий.
МРТ упростила измерения и сделала их более точными благодаря воспроизводимым сканам. Возможность записи изображений в движении позволила увидеть живые роды и подтвердить, что изменение положения роженицы изменяет внутренний диаметр таза.[2] Эта информация была интуитивно известна и использовалась акушерками на протяжении нескольких столетий.
Доказательства, выявленные рентгенологическими исследованиями, дают рациональную поддержку исследованиям и определению клинического теста внешней тазовой метрии. Существующий качественный тест в пельвиометрии, который в настоящее время предлагается в акушерских и остеопатических учреждениях, имеет некоторые практические ограничения, такие как отсутствие стандартизации теста, трудность для большинства беременных женщин в ближайшем сроке беременности плавно опуститься в приседаниях и отсутствие эталонные кривые и пороговые значения.
Контрольные вопросы
Доступ к бесплатным вопросам с несколькими вариантами ответов по этой теме.
Комментарий к этой статье.
Рисунок
Таз, оси таза, плоскость входа, ось полости, плоскость выхода, вертикальный разрез. Предоставлено Grey’s Anatomy Plates
Ссылки
- 1.
SWENSON PC. Анатомические вариации женского таза; Классификация Колдуэлла-Молоя. Радиология. 1947 мая; 48(5):527. [PubMed: 20240130]
- 2.
Reitter A, Daviss BA, Bisits A, Schollenberger A, Vogl T, Herrmann E, Louwen F, Zangos S. Создает ли беременность и/или смена положения больше места в женской таз? Am J Obstet Gynecol. 2014 Декабрь;211(6):662.e1-9. [PubMed: 24949546]
- 3.
Okumura M, Ishikawa A, Aoyama T, Yamada S, Uwabe C, Imai H, Matsuda T, Yoneyama A, Takeda T, Takakuwa T. Формирование хрящей в тазовом скелете во время эмбриональный и раннеплодный период. ПЛОС Один. 2017;12(4):e0173852. [Бесплатная статья PMC: PMC5383024] [PubMed: 28384153]
- 4.
Ротлисбергер Р.
 , Аврора В., Бёмке С., Бангертер Х., Бергманн М., Тальманн Г.Н., Джонов В. Анатомия нижнего подчревного сплетения у мужчин: что мы должны знать для нервосберегающей хирургии. Клин Анат. 2018 сен; 31 (6): 788-796. [PubMed: 29577446]
, Аврора В., Бёмке С., Бангертер Х., Бергманн М., Тальманн Г.Н., Джонов В. Анатомия нижнего подчревного сплетения у мужчин: что мы должны знать для нервосберегающей хирургии. Клин Анат. 2018 сен; 31 (6): 788-796. [PubMed: 29577446]- 5.
Сиккарди М.А., Тарик М.А., Валле С. StatPearls [Интернет]. Издательство StatPearls; Остров сокровищ (Флорида): 11 августа 2021 г. Анатомия, костный таз и нижняя конечность, большая поясничная мышца. [В паблике: 30571039]
- 6.
Willard FH, Vleeming A, Schuenke MD, Danneels L, Schleip R. Грудно-поясничная фасция: анатомия, функция и клинические аспекты. Дж Анат. 2012 декабрь; 221(6):507-36. [Бесплатная статья PMC: PMC3512278] [PubMed: 22630613]
- 7.
Abitbol MM. Формы женского таза. Способствующие факторы. J Reprod Med. 1996 г., апрель; 41 (4): 242–50. [PubMed: 8728076]
- 8.
Cottingham JT, Porges SW, Richmond K. Изменения угла наклона таза и парасимпатического тонуса, вызванные манипуляциями с мягкими тканями Рольфинга.
 физ. тер. 1988 сент; 68 (9): 1364-70. [PubMed: 3420170]
физ. тер. 1988 сент; 68 (9): 1364-70. [PubMed: 3420170]- 9.
Cottingham JT, Porges SW, Lyon T. Влияние мобилизации мягких тканей (лифтинг таза Рольфинга) на парасимпатический тонус в двух возрастных группах. физ. тер. 1988 март; 68 (3): 352-6. [PubMed: 3279437]
- 10.
Liselele HB, Tshibangu CK, Meuris S. Связь между внешней тазовой метрией и осложнениями при родах у африканских женщин. Acta Obstet Gynecol Scand. 2000 г., август; 79 (8): 673-8. [В паблике: 10949233]
- 11.
Бетти Л., Маника А. Изменения формы родовых путей человека значительны и географически структурированы. Proc Biol Sci. 2018 Oct 24; 285 (1889) [PMC бесплатная статья: PMC6234894] [PubMed: 30355714]
- 12.
нерожавшие африканские женщины: когортное исследование. БЖОГ. 2000 г., август; 107 (8): 947-52. [В паблике: 10955423]
- 13.
Куэнка-Гуэрра Р., Кесада Дж. Что делает ягодицы красивыми? Обзор и классификация определяющих факторов красоты ягодичных мышц и хирургических методов их достижения.
 Эстетик Пласт Хирург. 2004 г., сен-октябрь; 28(5):340-7. [PubMed: 15666052]
Эстетик Пласт Хирург. 2004 г., сен-октябрь; 28(5):340-7. [PubMed: 15666052]- 14.
Bansal S, Guleria K, Agarwal N. Оценка крестцовых ромбовидных размеров для прогнозирования суженного таза: пилотное исследование индийских первобеременных. J Obstet Gynaecol Индия. 2011 Октябрь; 61 (5): 523-7. [Бесплатная статья PMC: PMC3257337] [PubMed: 23024521]
- 15.
Какома Д.Б. Показания к кесареву сечению и антропометрические параметры у руандийских нерожавших: предварительные результаты продольного исследования. Pan Afr Med J. 2016; 24:310. [Бесплатная статья PMC: PMC5267785] [PubMed: 28154665]
- 16.
Fischer B, Mitteroecker P. Ковариация между формой человеческого таза, ростом и размером головы облегчает акушерскую дилемму. Proc Natl Acad Sci U S A. 2015 May 05;112(18):5655-60. [Бесплатная статья PMC: PMC4426453] [PubMed: 258]
- 17.
Мишель С.К., Рейк А., Трейбер К., Зайферт Б., Шауи Р.
 , Хуч Р., Маринчек Б., Кубик-Хуч Р.А. МР-акушерская тазовая пельвиметрия: влияние положения при родах на размеры костей таза. AJR Am J Рентгенол. 2002 г., октябрь; 179 (4): 1063-7. [PubMed: 12239066]
, Хуч Р., Маринчек Б., Кубик-Хуч Р.А. МР-акушерская тазовая пельвиметрия: влияние положения при родах на размеры костей таза. AJR Am J Рентгенол. 2002 г., октябрь; 179 (4): 1063-7. [PubMed: 12239066]
Транг Чо — Дьен Дан Тоан Хок
01-09-2022
Gửi bởi bangbang1412 Чонг Тоан Хок Хьон Джи
Trong topic này mình muốn giới thiệu về K-lý thuyết Milnor (Milnor’s K-theory) và kết nối nó với một số lý thuyết đối đồng điều như đối đồng điều Galois, nhóm Bloch-Chow, đối đồng điều motivic. Về Mặt lịch Sử, Ban ầu k-lý thuyết ại số (алгебраический k-теория) chỉ ịnh nghĩa ược cho $ k_0, k_1, k_2 $ (grothendiec tạp rồi, về sau k-lý thuyết ại s chỉ ược ịnh nghĩa và nghiên cứu một cách có hệng từ sau quillen khi ô ưa ha ha ồ ồ ồ ồ ồ ồ ồ ồ ồ kh kh kha ọ kh kh kh hi hi hi hệ hệ hệ hệ hệ ọ ồ hệ hi hệ hệ hệ ọ ồ hệ hệ ngh nghy ô ư ư ư kha kh kh ha ư ư qu ượ ượ ượ ượ ị hệ h h gha ô Trước đ đt ịnh lý của matsumoto cho ta mô tả $ k_2 $ cụ thể dưới dạng phần tử sinh và quan hệ, milnor dựa trên ịnh nghĩa này ưa ra một ị ị n ọ ọ ọ ọ ọ ọ ị ọ ọ ọ ị ị kh kh kh kh kh kh kh kht hrết hrết hrết -lý thuyết milnor, nó chứa một phần thông tin của k-lý thuyết ại s s số (the nghĩa quillen + cổ điển) theo nghĩa sau khi tensor với $ \ так.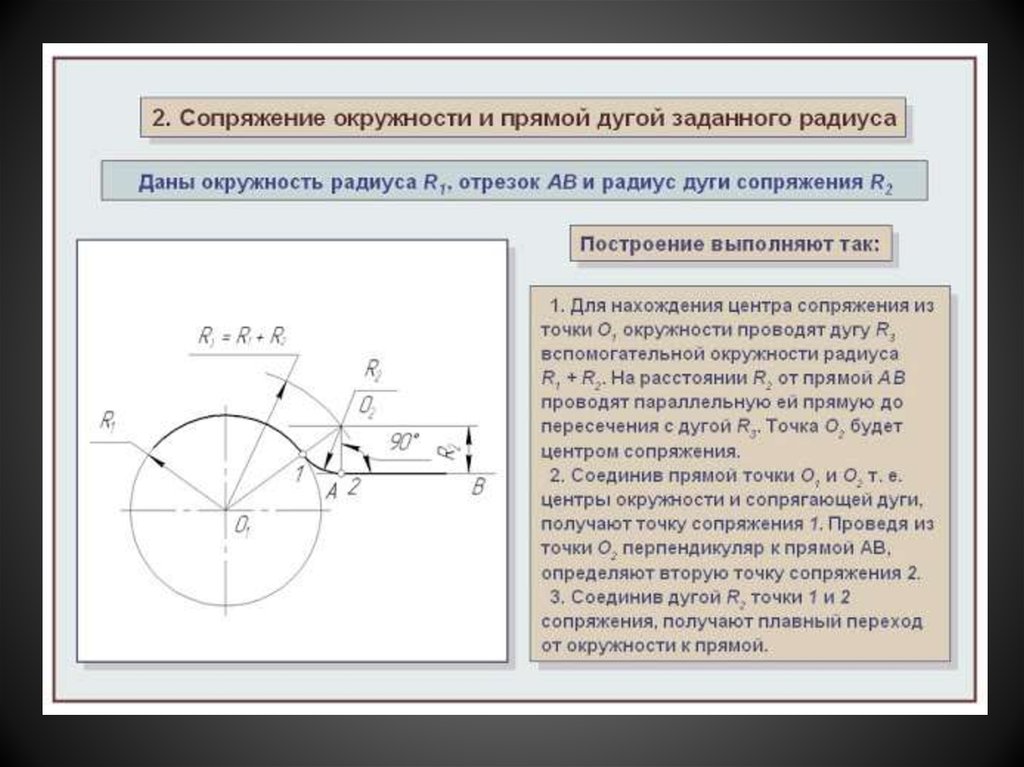 Ể thuận tiện cho người ọcc, mình sẽ ịnh nghĩa lại một số nhóm cổ điển $ k_0, k_1, k_2 $ và một số tính chất cơ bản (không chứng minh). Nhóm K_0 Cố định một vành $R$ (giao hoán có đơn vị). Nhắc lại rằng một модуль xạ ảnh la một hạng tử trực tiếp của một модуль tự do nào đó. Định nghĩa. Nhóm $K_0(R)$ được định nghia bởi công thức sau$$K_0(R) = \bigoplus \mathbb{Z}[P]/\sim,$$trong đó tổng trực tiếp lếy trån lớng cáp ấu $-модуль xạ ảnh hữu hạn sinh, quan hệ $\sim$ được cho bởi $[P] + [Q] = [P \oplus Q]$. Ta cũng có thể trang bị cho $K_0(R)$ một cấu t…
Ể thuận tiện cho người ọcc, mình sẽ ịnh nghĩa lại một số nhóm cổ điển $ k_0, k_1, k_2 $ và một số tính chất cơ bản (không chứng minh). Nhóm K_0 Cố định một vành $R$ (giao hoán có đơn vị). Nhắc lại rằng một модуль xạ ảnh la một hạng tử trực tiếp của một модуль tự do nào đó. Định nghĩa. Nhóm $K_0(R)$ được định nghia bởi công thức sau$$K_0(R) = \bigoplus \mathbb{Z}[P]/\sim,$$trong đó tổng trực tiếp lếy trån lớng cáp ấu $-модуль xạ ảnh hữu hạn sinh, quan hệ $\sim$ được cho bởi $[P] + [Q] = [P \oplus Q]$. Ta cũng có thể trang bị cho $K_0(R)$ một cấu t…
Подробнее
26-08-2022
Гуи бои bangbang1412 Чонг Тоан Хок Хьон Джи
Gửi mọi người một самостоятельная заметка của minh về đối đồng điều động lực (мотивная когомология) phát triển bởi Voevodsky. Ối ồng điều ộng lực ược dự đoán tồn tại bởi beillinson, cụ thể, ô ro dự đoán tồn tại một phức $ \ mathbb {z} nta nta ntố ntố ntố ntố ntố ntố ntố w ntố w ntố ntố nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta net *,n}(X,\mathbb{Z})=\mathbb{H}_{Zar}^*(X,\mathbb{Z}(n))$ mà khi hạn chế tại một số bậc đặc biệt thu được K-lý thuyết Milnor, nhóm Bloch-Chow bậc cao và đồng thời có một dãy phổ hội tụ về K-lý thuyết Quillen sao cho sau khi tensor với $\mathbb{Q}$ dãy phổ này suy biến về $\gamma $-lọc của K-lý thuyết Quillen.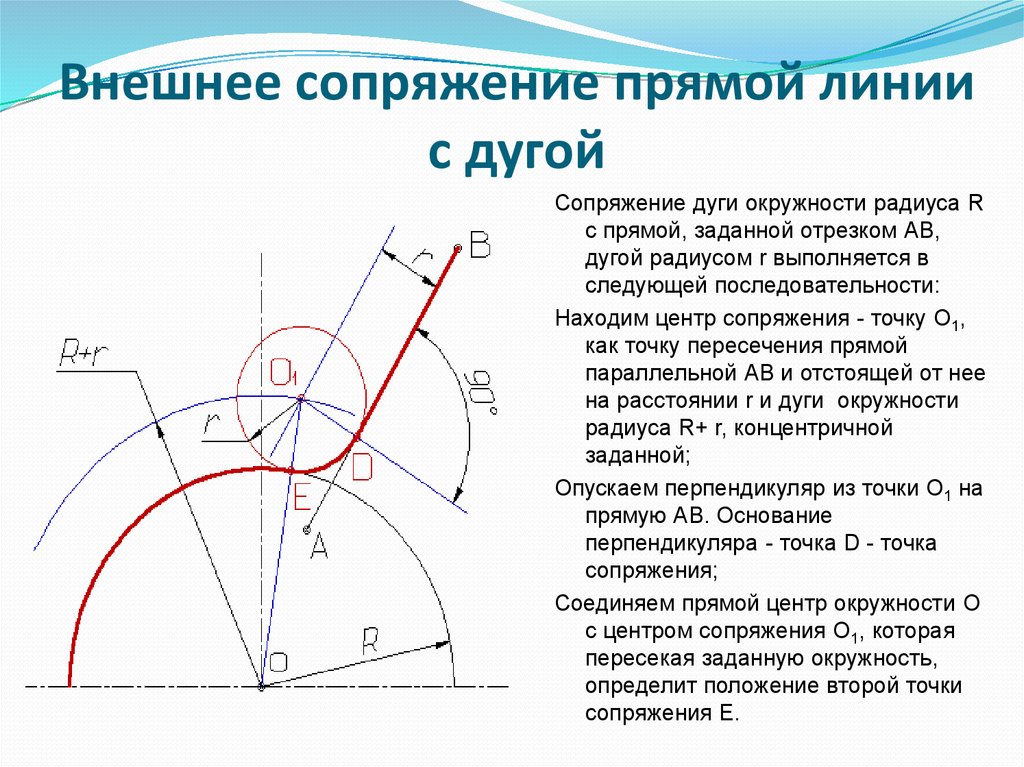 {\otimes q})$. Voevodsky sau đó đã được huy chương Fields vì chứng minh trọn vẹn giả thuyết Bloch-Kato bằng cách xây dựng một lớp đa tạha Rosdọa cựn trìn c. Với mình đ nhy là thành công ầu tiên hướng tới lý thuyết otive của grothendieck vì giả thuyế bloch-kato đ đ nối hai loại bấn biến: transcendental (nhómale). Đối đồng điều động lực tới nay có rất nhiều cách xây dựng, có thể kể đến: гиперкогомология Như trên Zarikis hoặc Nisnevich site. Như nhóm Bloch-Chow bậc cao. Như hom-set trong phạm trù мотив Hình Học $…
{\otimes q})$. Voevodsky sau đó đã được huy chương Fields vì chứng minh trọn vẹn giả thuyết Bloch-Kato bằng cách xây dựng một lớp đa tạha Rosdọa cựn trìn c. Với mình đ nhy là thành công ầu tiên hướng tới lý thuyết otive của grothendieck vì giả thuyế bloch-kato đ đ nối hai loại bấn biến: transcendental (nhómale). Đối đồng điều động lực tới nay có rất nhiều cách xây dựng, có thể kể đến: гиперкогомология Như trên Zarikis hoặc Nisnevich site. Như nhóm Bloch-Chow bậc cao. Như hom-set trong phạm trù мотив Hình Học $…
Подробнее
08.11.2022
Гуи бой Несбит trong Lịch sử toán học
[Nhan có bạn nhắc đến giả thuyết về cac số nguyên tố sinh đôi, xin chia sẻ một bài viết gần đay của GS. Vũ Hà Văn viết trên blog vào dịp Джеймс Мейнард nhận được Huy chương Fields năm nay. Giọng văn của giáo sư vẫn hài hước như mọi khi, đặc biệt là phần chốt hạ bằng hai câu thơ lục bát. ] Nhà toán học thứ hai được giải Fields năm nay là anh J. Maynard, vỡi những công trình về số nguyên tố . Số nguyên tố có lẽ la một trong nhung chủ đề lâu đời nhất và được chú ý tới nhất trong toán học. Cac nhà hiền triet Hy lập đáng kính đã nguyên cứu về nó, từ trước khi chúa Jesu ra đời. Rất có thể là trước cả khi Mỵ nương cưới Sơn tinh. Số nguyên tố la nhung số nguyên dương chỉ chia hết đươc cho chính nó. Ви до нхо 5; 6 không phải la số nguyên tố vì nó chia hết cho 2. Cac số nguyên tố nhỏ nhất la 2,3,5,7,11,13,17,19, 23,29, 31, 37….Số 1, thấp cổ be họng, không được vào hội. Это ra lý do sâu xa hơn là vì một ịnh lý, xưa như quả ất, là tất cả các số nguyên dương ều có thể viết dưới dạng tích của một s nguyn thểt dưới dạng tych nhi nhan nhan nhan nhan nhan nhan nhan nhan nhan nha nhan nhan nha nhan nha nhan nha nha nhun là nhân với 1 thì chả thêm vị gì, nên chàng đã bị loại. Từ thời Наполеон, người ta đã biết la có vô hạn số nguyên tố. Tức cái dãy 2,3,5…ở trên no sẽ kéo dài vô hạn. Một trong những câu hỏi nổi tiếng và trung tâm nhất của toán học, là cái sự kéo dai đó nó diễn ra như thế nào.
] Nhà toán học thứ hai được giải Fields năm nay là anh J. Maynard, vỡi những công trình về số nguyên tố . Số nguyên tố có lẽ la một trong nhung chủ đề lâu đời nhất và được chú ý tới nhất trong toán học. Cac nhà hiền triet Hy lập đáng kính đã nguyên cứu về nó, từ trước khi chúa Jesu ra đời. Rất có thể là trước cả khi Mỵ nương cưới Sơn tinh. Số nguyên tố la nhung số nguyên dương chỉ chia hết đươc cho chính nó. Ви до нхо 5; 6 không phải la số nguyên tố vì nó chia hết cho 2. Cac số nguyên tố nhỏ nhất la 2,3,5,7,11,13,17,19, 23,29, 31, 37….Số 1, thấp cổ be họng, không được vào hội. Это ra lý do sâu xa hơn là vì một ịnh lý, xưa như quả ất, là tất cả các số nguyên dương ều có thể viết dưới dạng tích của một s nguyn thểt dưới dạng tych nhi nhan nhan nhan nhan nhan nhan nhan nhan nhan nha nhan nhan nha nhan nha nhan nha nha nhun là nhân với 1 thì chả thêm vị gì, nên chàng đã bị loại. Từ thời Наполеон, người ta đã biết la có vô hạn số nguyên tố. Tức cái dãy 2,3,5…ở trên no sẽ kéo dài vô hạn. Một trong những câu hỏi nổi tiếng và trung tâm nhất của toán học, là cái sự kéo dai đó nó diễn ra như thế nào.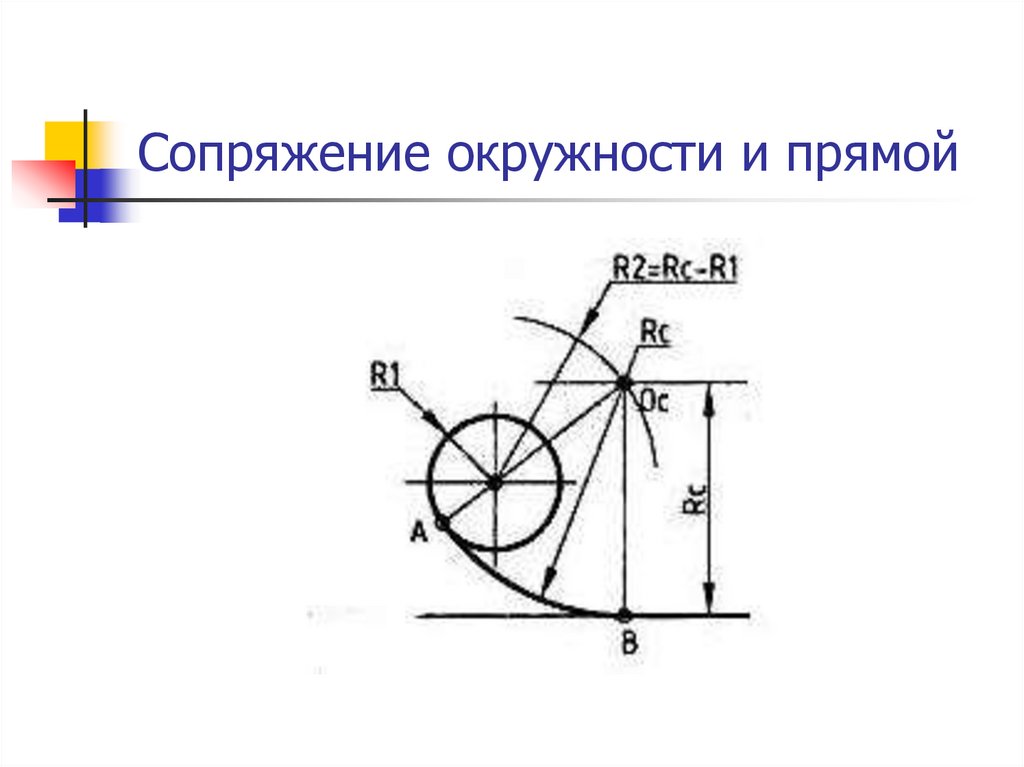 Chẳng hạn bạn thấy ở trên có tới 8 số nguyên tố giưã 1 và 20, nhưng giữa 21 và 40 chỉ còn 4 số. Tức tần suất xuất hiện của số nguyên tố ngày một giảm đi. Cũng như số lần …
Chẳng hạn bạn thấy ở trên có tới 8 số nguyên tố giưã 1 và 20, nhưng giữa 21 và 40 chỉ còn 4 số. Tức tần suất xuất hiện của số nguyên tố ngày một giảm đi. Cũng như số lần …
Подробнее
15.07.2022
Гуи бой Несбит trong Thi HSG Quốc gia và Quốc tế
Kì thi lần này đội tuyển chúng ta xếp thứ 4, sau Trung Quốc, Hàn Quốc, và Mỹ. Đây la thành tích rất cao. Thành tích cá nhân của đội Việt Nam như sau: Em Ngô Quý Đăng là một trong 10 thí sinh giành được điểm tuyệt đối 42/42. Đây cũng là HCV thứ hai của em (HCV đầu tiên giành được năm 2020 lúc đang học lớp 10, rất tiếc la năm 2021 lại rng vÛt).
Подробнее
07.12.2022
Гуи бои хоангвипмесси97 trong Thi HSG Quốc gia và Quốc tế
Ngày thi thứ nhấtBài 1: Ngân hàng Oslo có phát hành hai loại tiền xu: đồng vàng (kí hiệu bởi A) và đồng bạc (kí hiệu bởi B). 2 + x + k $ với $ x Biết rằng, hai cách xếp nhận được từ nhau qua phép quay và phép phản…
2 + x + k $ với $ x Biết rằng, hai cách xếp nhận được từ nhau qua phép quay và phép phản…
Подробнее
07.09.2022
Гои бои nmlinh26 Чонг Тоан Хок Хьон Джи
Gửi cac thành viên trên diễn đàn ghi chú của minh về định lý phân loại mặt đóng, một định lý cơ bản của tô pô. Học sinh phổ thông có thể đọc được ghi chú này.https://drive.google…iew?usp=sharing
Подробнее
07.06.2022
Гуйбуи Э. Галуа trong Dành cho giáo viên các cấp
SKKN: Hướng dẫn học sinh giải bài toán tổ hợp tạo số bằng lập trình PASCAL
Подробнее
07.05.2022
Гуи бой Несбит trong Tin tức — Vấn đề — Sự kiện
Ngày 07. 05.2022, Hội Toán học Thế giới đã trao Huy chương Fields 2022 cho bốnhà Toán học: Hugo Duminil-Copin (Pháp), June Huh (Hàn Quoc, Mỹ), James Maynard (Anhiazov), vàska (Украина). Buổi lễ trao giải được diễn ra tại Đại học Aalto (thành phố Helsinki, thủ đô của Phần Lan), và được прямая трансляция trực tiep. Thông tin về giải thưởng: https://www.mathunio…lds-medals-2022. Фото предоставлено: Твиттер.
05.2022, Hội Toán học Thế giới đã trao Huy chương Fields 2022 cho bốnhà Toán học: Hugo Duminil-Copin (Pháp), June Huh (Hàn Quoc, Mỹ), James Maynard (Anhiazov), vàska (Украина). Buổi lễ trao giải được diễn ra tại Đại học Aalto (thành phố Helsinki, thủ đô của Phần Lan), và được прямая трансляция trực tiep. Thông tin về giải thưởng: https://www.mathunio…lds-medals-2022. Фото предоставлено: Твиттер.
Подробнее
21-06-2022
Гуи бой Несбит trong Hội thợo, Hội nghị, Семинар
ICM 2022 sẽ дин ра vào ngày 6-14 tháng 7 năm 2022 dưới Hình thức виртуальная конференция. Lúc ầu icm 2022 ược dự ị ịnh tổ chức tại thành phố saint petersburg của nga, nhưng chỉ hi ngày sau khi nga xâm lược kraine (24/02) thì й -hran -hranga nonly no nanly no no nanly -hranga nanly -hrangang миен фи. Cac bạn có thể đăng ký tại đây: https://www.mathunio. ..rtual-icm-2022 Cảm ơn Nxb đã chia sẻ thong tin. Thảo luận tại đây: https://diendantoanh…90876-icm-2022/
..rtual-icm-2022 Cảm ơn Nxb đã chia sẻ thong tin. Thảo luận tại đây: https://diendantoanh…90876-icm-2022/
Подробнее
05.12.2022
Гуи бои Nxb trong Tin tức — Vấn đề — Sự kiện
Bài viết của giáo sư Hoa về giáo sư Trung. Qui luật và ngẫu nhiên
Như các ngành khoa học khác, một trong những vấn ềc trung tâm trong toán học là đi tìm một hoặc một vài tính chất chung trong số vàn những ối ượ ố những ố ố Chẳng hạn, có vô số vòng tròn lớn nhỏ. Ngoai chuyện Hình dáng trông gieng gieng nhau, có vẻ chung chẳng có gì chung. Ấy thế mà từ lâu loài người đã đoán định rằng số giữa chu vi và đường kính la như nhau ở tất cả cac đưng. Mã ến khi khái niệm giới hạn xuất hiện ở kỷ thứ 16 thì điều đoán ịnh đ đi ược chứng minh chặt chẽ, và tên gọi số gấ như wệ π π π π π π π π π πt π Việc tìm ra số π chính la đã kham phá ra một qui luật. Джао Со Нго Вьет Трунг. Oái AM thay, tỷ số π này lại là một số không thể tính chính xac được! Cho đến hiện nay, người ta cũng không biết được các chữ số thập phân của p có xuất hiện theo một qui luật nào không, hay hoàn toàn ngẫu nhiên (theo nghĩa ta không đoán trước được cho đến khi tìm ra nó)? Qua ví dụ tưởng Như đơn giản là số π, ta co thể hiểu được, việc tìm ra qui luật nhiều khi khó khan và tốn thời gian nhượo! Một ví dụ cao cấp hơn la việc giải hệ phương trình đa thức (với hệ số trên một trường).
 80, г).
80, г).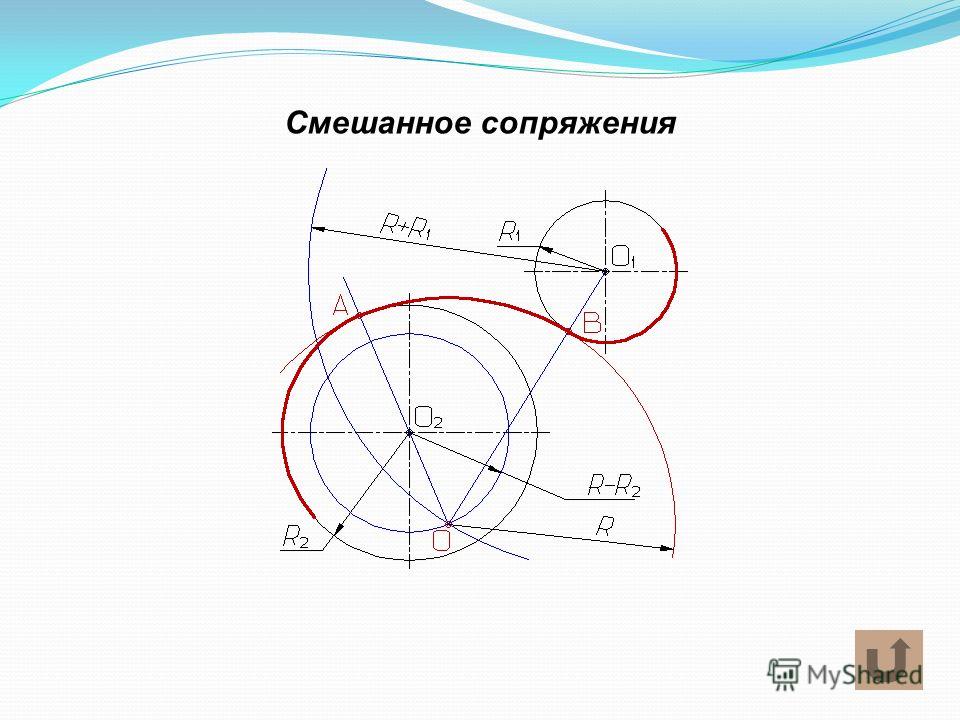 Такое сопряжение называют также скруглением углов. Центр скругления О находят в точке пересечения прямых, проведенных параллельно заданным прямым на расстоянии от них, равном радиусу скругления
Такое сопряжение называют также скруглением углов. Центр скругления О находят в точке пересечения прямых, проведенных параллельно заданным прямым на расстоянии от них, равном радиусу скругления 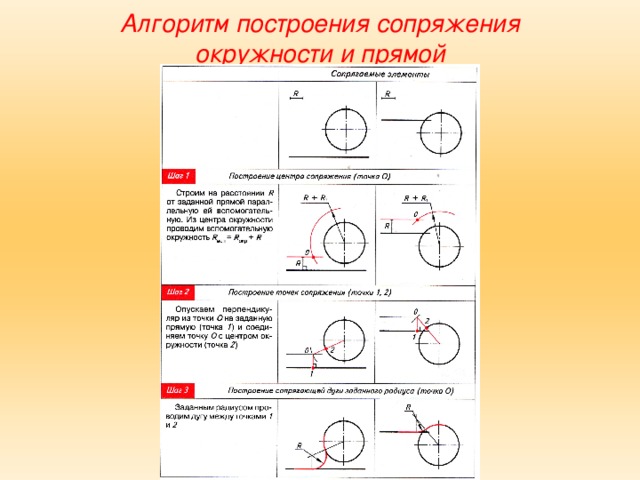
 Точки сопряжений 1 и 2 находятся на продолжениях линий, соединяющих центры ОО1и ОО2. В случае внутреннего и внешнего сопряжения (рис. 80, л) требуется провести дугу сопряжения радиуса RСтак, чтобы она имела с одной окружностью внутреннее, а с другой — внешнее сопряжение. Центр этой дуги находится в точке пересечения дуг, описанных из центра О1радиусом RC+ R и из центра О2радиусом RC— r. Точки сопряжений А и В лежат на линии ОО1и продолжении линии ОО2, соответственно.
Точки сопряжений 1 и 2 находятся на продолжениях линий, соединяющих центры ОО1и ОО2. В случае внутреннего и внешнего сопряжения (рис. 80, л) требуется провести дугу сопряжения радиуса RСтак, чтобы она имела с одной окружностью внутреннее, а с другой — внешнее сопряжение. Центр этой дуги находится в точке пересечения дуг, описанных из центра О1радиусом RC+ R и из центра О2радиусом RC— r. Точки сопряжений А и В лежат на линии ОО1и продолжении линии ОО2, соответственно. ..
..