Урок по черчению «Сопряжение сторон углов дугами» (9-й класс)
- Машункина Людмила Ивановна, учитель изобразительного искусства и черчения
Разделы: Технология
Класс: 9
Цели: развитие у учащихся аналитических умений, развитие логического мышления.
Задачи урока: познакомить учащихся с
применением сопряжений в технических формах,
предметах быта, научить строить сопряжение между
сторонами углов; развивать логическое мышление,
познавательный интерес, умение работать
чертежными инструментами; воспитывать точность
и аккуратность, внимательность и усидчивость.
Оборудование: таблица “Сопряжения”, технические детали, имеющие плавные переходы, карточки-задания.
Ход урока:
Проверка д.з.:
Задание: Проверка чертежей деталей (взаимопроверка учащихся).
Работа по карточкам:
Карточка 1.
расстояние от центра окружности до точки на
ней. |
Карточка 2.
|
Карточка 3.
|
Карточка 4.
|
Объяснение новой темы.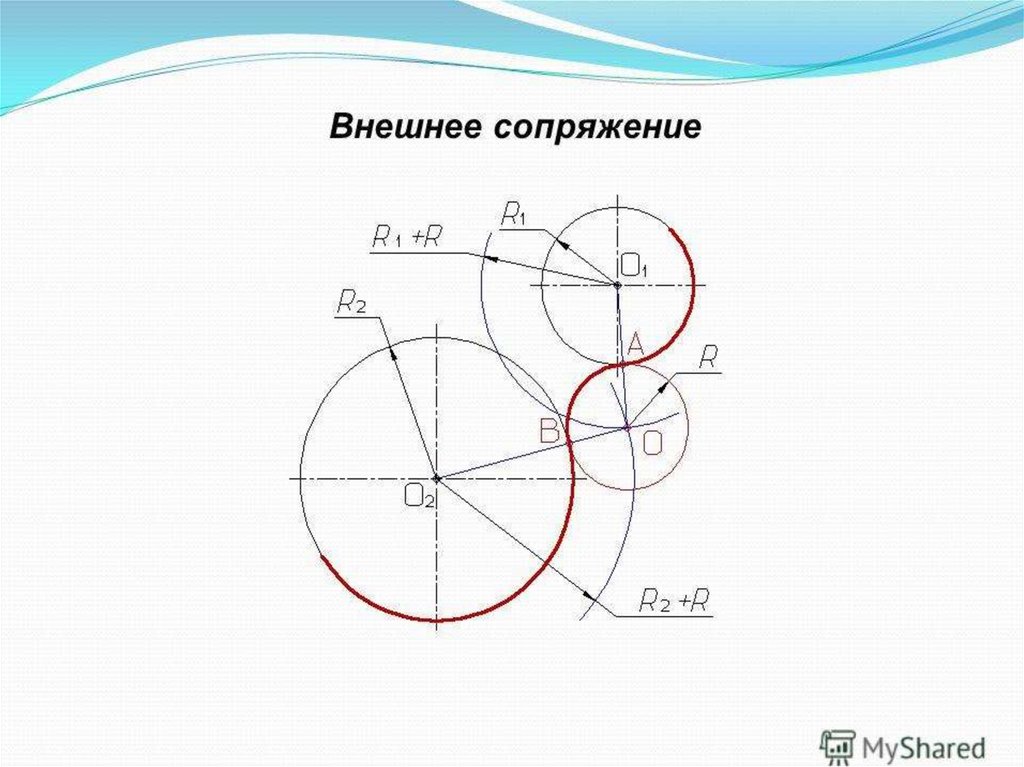
Сопряжением называется плавный переход от одной линии к другой.
Применение сопряжений настолько разнообразно и многопланово, что дать все примеры их использования просто невозможно.
Сопряжения в технических деталях, предметах, изделиях применяют с целью: увеличения прочности, удобного и безопасного обращения, уменьшения коррозийное деталей, учета эстетических требований.
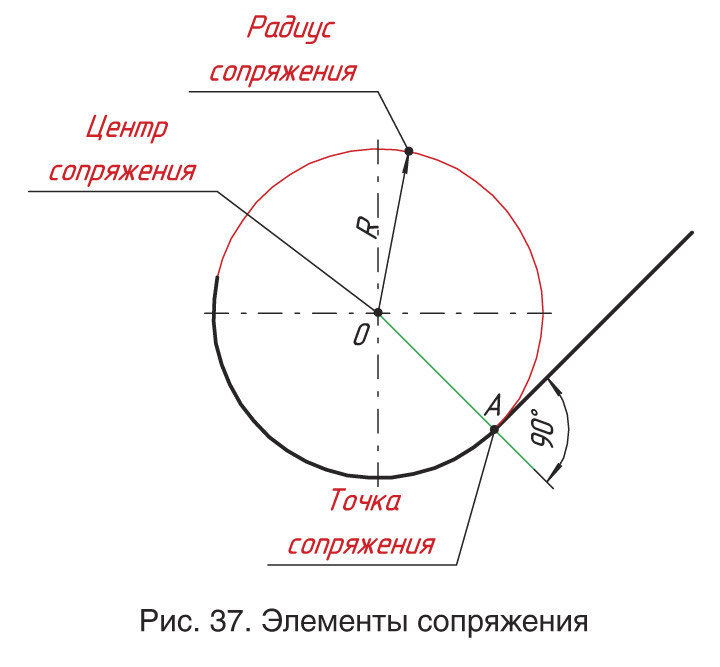
Построение сопряжений углов:
- Построение центра сопряжения
Строим на расстоянии R от заданных прямых параллельные им вспомогательные прямые. Точка пересечения прямых — центр сопряжения (точка О)
2. Построить точки сопряжения
Проводим перпендикуляры из центра сопряжения (точка О) к сопрягаемым прямым.
3. Построение сопрягающей дуги заданного
радиуса.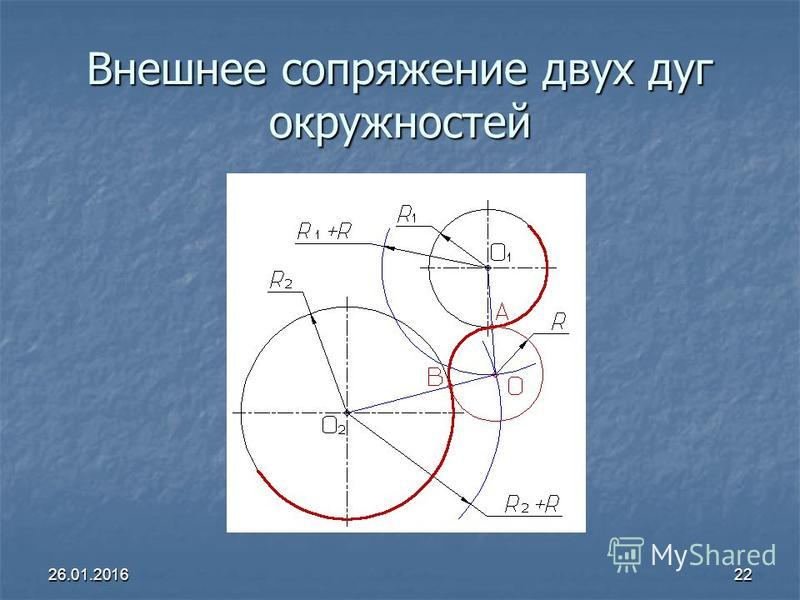
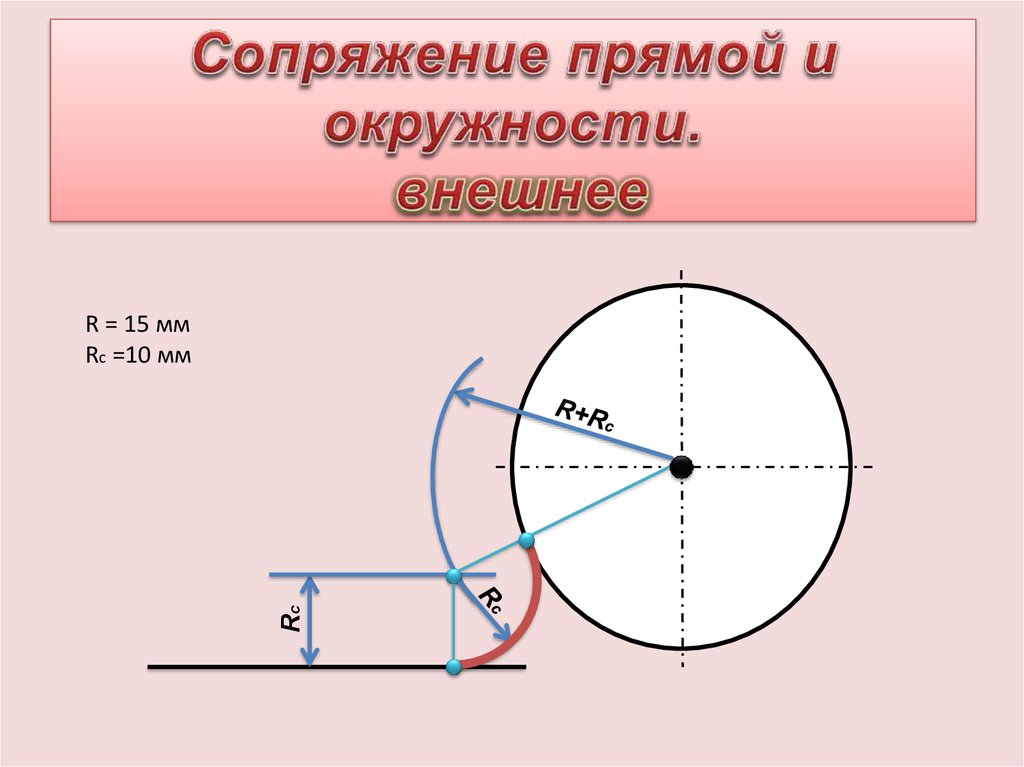
Алгоритм построения сопряжения окружности и прямой.
Сопрягаемые элементы
- Построение центра сопряжения
- Построение точек сопряжения (точки 1, 2)
Опускаем перпендикуляр из точки О на заданную прямую (точка /) и соединяем точку Ос центром окружности (точка 2)
Построение сопрягающей дуги заданного радиуса (точка О)
Заданным радиусом проводим дугу между точками 1 и 2.
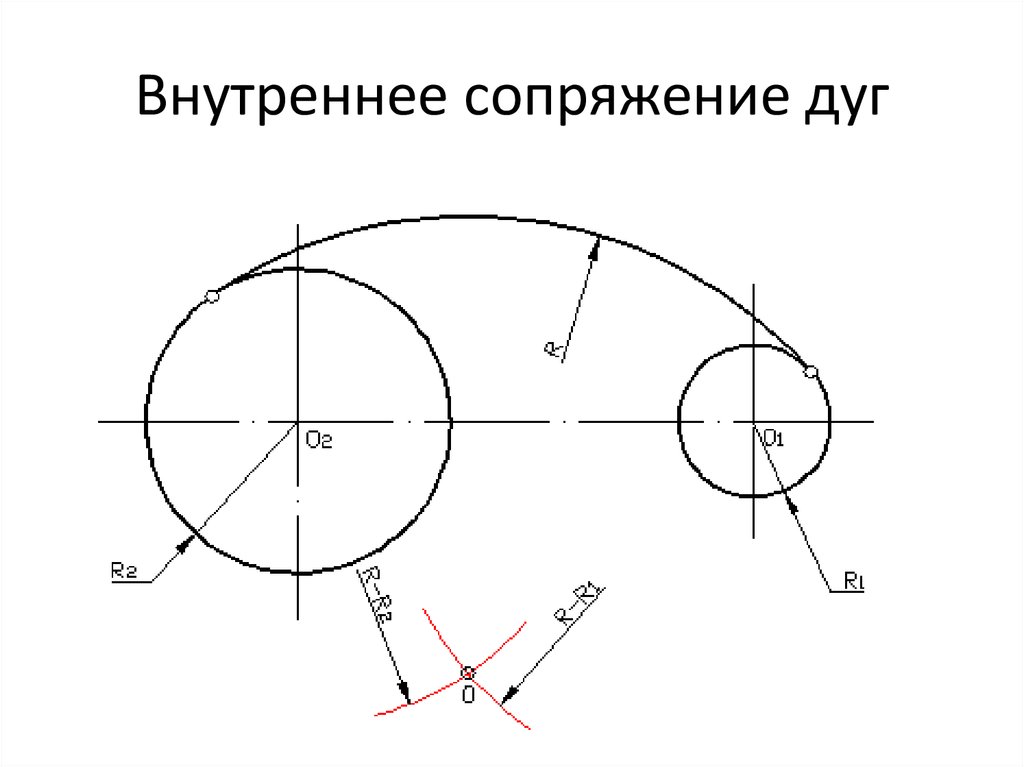
Алгоритм построения сопряжения двух окружностей
- Построение центра окружности
- Построение точек сопряжения
- Построение сопрягающей дуги заданного радиуса
Практическая работа: построить в тетради объемную звезду стр.
57. рис 98.
Итог урока:
— Что называется сопряжением?
— Перечислите основные элементы сопряжения.
Домашнее задание: §17 прочитать. На формате А4 начертить главный вид детали по карточке.
Инновационные технологии на уроках «Черчения». Презентация к уроку по теме «Сопряжение окружностей» | Презентация к уроку (8 класс):
Опубликовано 30.05.2016 — 15:19 — Гумарова Лариса Васильевна
Материал предназначен для объяснения нового учебного материала по разделу «Сопряжение. Слайды посвящены подтемам: «Сопряжение окружности и прямой», «Сопряжение двух окружностей» (внутреннее, внешнее и смешанное)
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Слайд 1
Сопряжение – плавный переход от одной линии к другой, выполненный при помощи циркуля
Слайд 2
Сопряжение – плавный переход от одной линии к другой, выполненный при помощи циркуля Сопряжения прямых линий и окружностей Детали (в, г, д) Построение сопряжений (а, б) Чертеж детали (е)
Слайд 3
Сопряжение прямой и окружности
Слайд 4
Сопряжение окружности и прямой
Слайд 5
Сопряжение двух окружностей Наружнее (б) Внутреннее (в) Деталь (а) Чертеж детали (г) Смешанное (а) Деталь (б) Чертеж детали (в)
Слайд 6
Сопряжение окружностей Алгоритм построения «Внешнего сопряжения» R 1 =10 R 2 =20 R с = 15 О1 и О2= 45 Ос R 3= R 1+ R с=10+15=25 R 4= R 2+ R с=20+15=35
Слайд 7
Алгоритм построения «Внутреннего сопряжения» R 1 =10 R 2 =20 R с = 50 О1 и О2= 45 Ос R 3= R с- R 1=50-10=40 R 4= R с- R с=50-20=30 Сопряжение окружностей R 1
Слайд 8
Сопряжение окружностей Алгоритм построения «Смешанного сопряжения» R 1 =10 R 2 =20 R с = О1 и О2= Ос R 3= R с + R 1 R 4= R с — R с
По теме: методические разработки, презентации и конспекты
Материалы инновационной деятельности «Открытые образовательные технологии на уроках русского языка и литературы», представленные на окружном семинаре по теме «Применение и результативность инновационных технологий на уроках русского языка и литературы»
Материалы обмена опытом инновационной деятельности «Открытые образовательные технологии на уроках русского языка и литературы», представленные на окружном семинаре по теме «Применение и результа. ..
..
Презентацияк уроку в 11 классе по литературе «Страшный мир А.Блока»
Данная презентация помогает более качественно провести урок….
11 класс «Давление света», конспект и презентацияк уроку.
11 классТема: «Давление света»Цели:Дидактическая: выяснить причины появления давления света на твердые поверхности и газ, с волновой и корпускулярной теории.Воспитательная: убедить учащихся…
Методическая разработка урока по волейболу в 5 классе на основе инновационной технологии спортивно-ориентированного физического воспитания. Методическая разработка урока по волейболу в 5 классе на основе инновационной технологии спортивно-ориентированн
урок по физической культуре с ипользованием инновационной технологии спортивно-ориентированного физического воспитания…
Использование инновационных технологий( оздоровительные системы) на уроке физкультуры.
Работа содержит План-конспект урока физической культуры с использованием инновационных технологий(оздоровительные системы).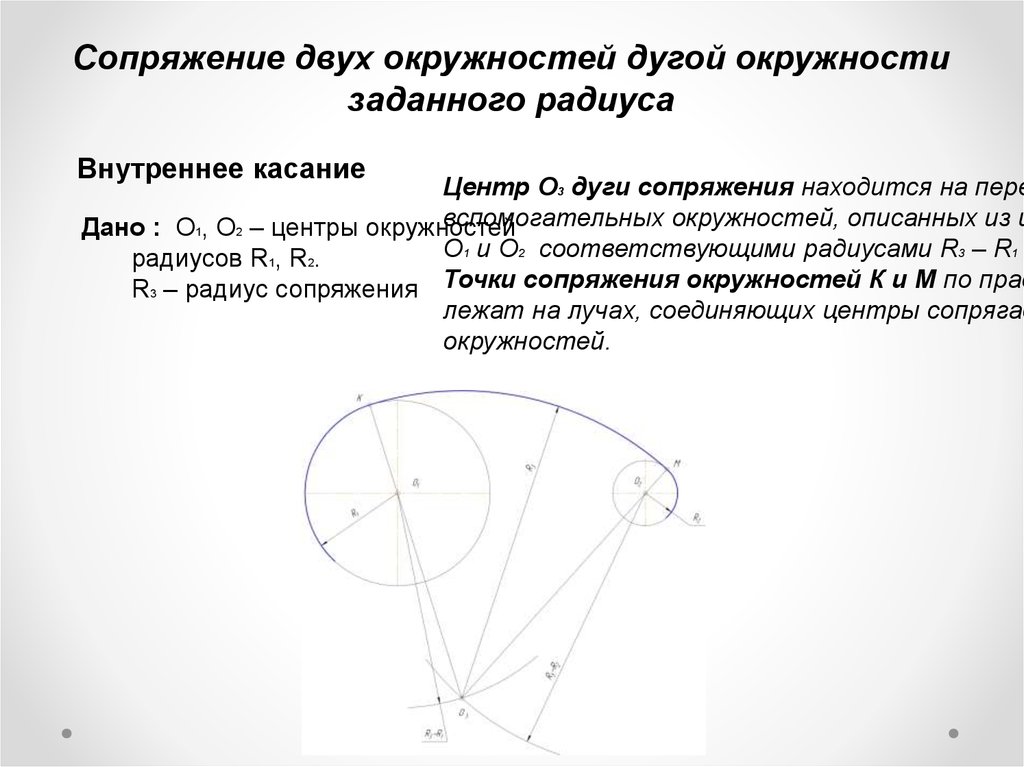 Урок с использованием элементов фитнеса и стретчинга….
Урок с использованием элементов фитнеса и стретчинга….
Использование инновационных технологий( оздоровительные системы) на уроке физкультуры.
Материал содержит план-конспект урока с использованием инновационных технологий(оздоровительные системы) на уроке физической культуры….
Презентацияк уроку «Задачи на процентную концентрацию»
Презентацияк уроку «Задачи на процентную концентрацию»…
Поделиться:
Научное объяснение того, о чем говорил Терренс Ховард на вручении премии «Эмми»
Изображения: Wikimedia, YouTube. Композиция Джордана Пирсона
За год громких заявлений на красной дорожке премии «Эмми», от комбинации кроссовок и платья Виолы Дэвис до страстных речей о правах трансгендеров и равной оплате труда, одному удалось выделиться на церемонии вручения наград на прошлой неделе: Звезда «Империи » Терренс Ховард глубоко погружается в геометрию, древнюю философию и квантовую физику.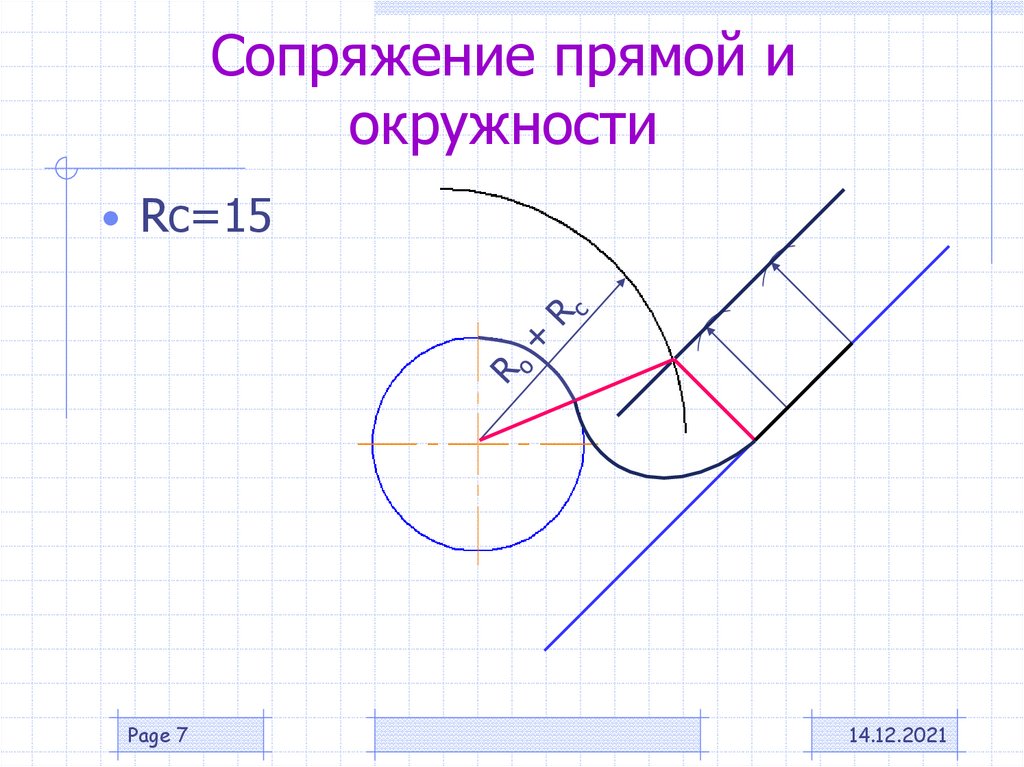
«Я сделал несколько открытий в своей личной жизни с помощью науки, которую, знаете, искал Пифагор, — сказал он очень сбитому с толку интервьюеру. — Я смог правильно раскрыть цветок жизни и найти настоящие волновые сопряжения, которые мы искали 10 000 лет».
Реклама
На этом можно было бы и закончить, но тут Говард перешел к науке:
«Вся энергия во Вселенной выражается в движении, все движение выражается в волнах, все волны кривые, так откуда же прямые линии берутся из платоновых тел? Прямых линий нет. Итак, когда я взял цветок жизни и открыл его должным образом, я обнаружил совершенно новые волновые сопряжения, которые обнажают промежуточные пространства. Это то, что держит нас всех вместе».
Ошеломляющий ответ Ховарда на случайный вопрос в интервью о том, что он бросит актерскую карьеру после того, как Empire закончится, был настолько примечателен, что на прошлой неделе клип стал вирусным в Твиттере.
Здесь есть что распаковать, но самое удивительное то, что это частично основано на реальной науке.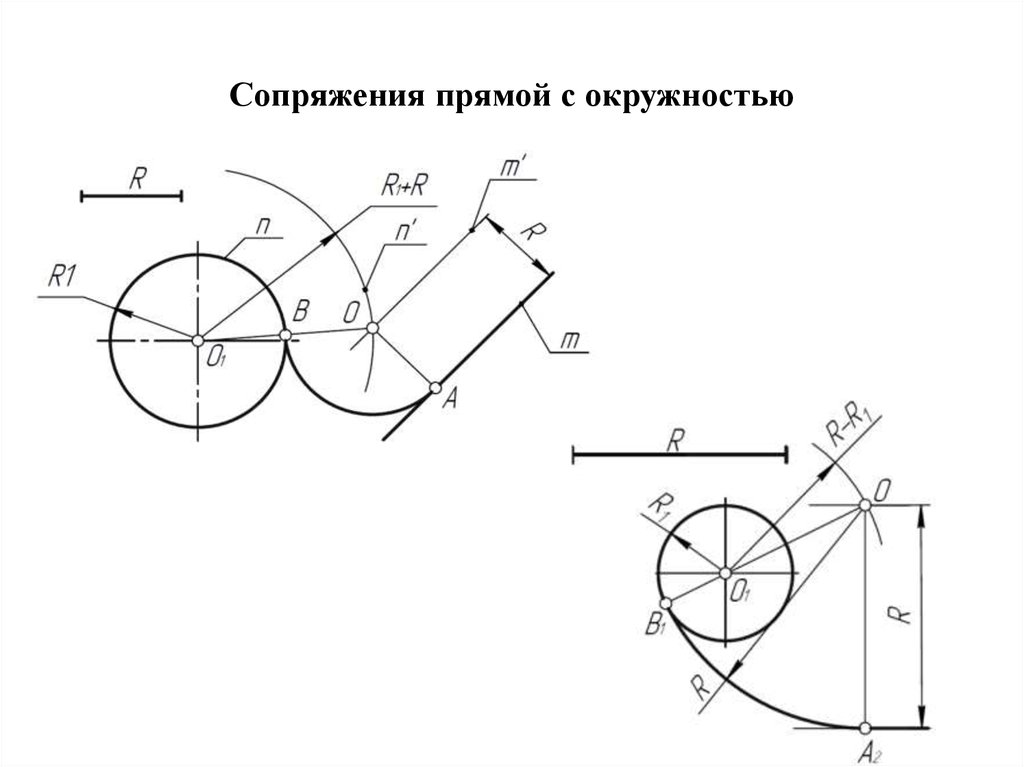 Когда дело доходит до прямых линий, он не ошибается .
Когда дело доходит до прямых линий, он не ошибается .
На самом деле прямых линий не существует
Это правда, что в физическом мире, который мы видим и ощущаем вокруг себя, нет прямых линий, но это имеет очень мало общего с кривизной волны или (ложным) утверждением Говарда что вся энергия выражается в движении. Вместо этого это причуда математики и логики из-за того, как мы определяем «прямой» и как мы определяем «линию».
Строго говоря, любая линия (прямая или изогнутая) имеет нулевую толщину — именно это мы имеем в виду в математических терминах, когда говорим о линии. Если «прямая» линия конечной длины вообще имеет толщину, то на самом деле это очень тонкий прямоугольник, а не линия.
Тогда должно быть очевидно, что физически не существует истинных линий; даже самая тонкая линия, которую мы можем нарисовать, имеет ширину больше нуля. Прямые линии — это идеализированное математическое понятие, и поэтому их, возможно, «не существует».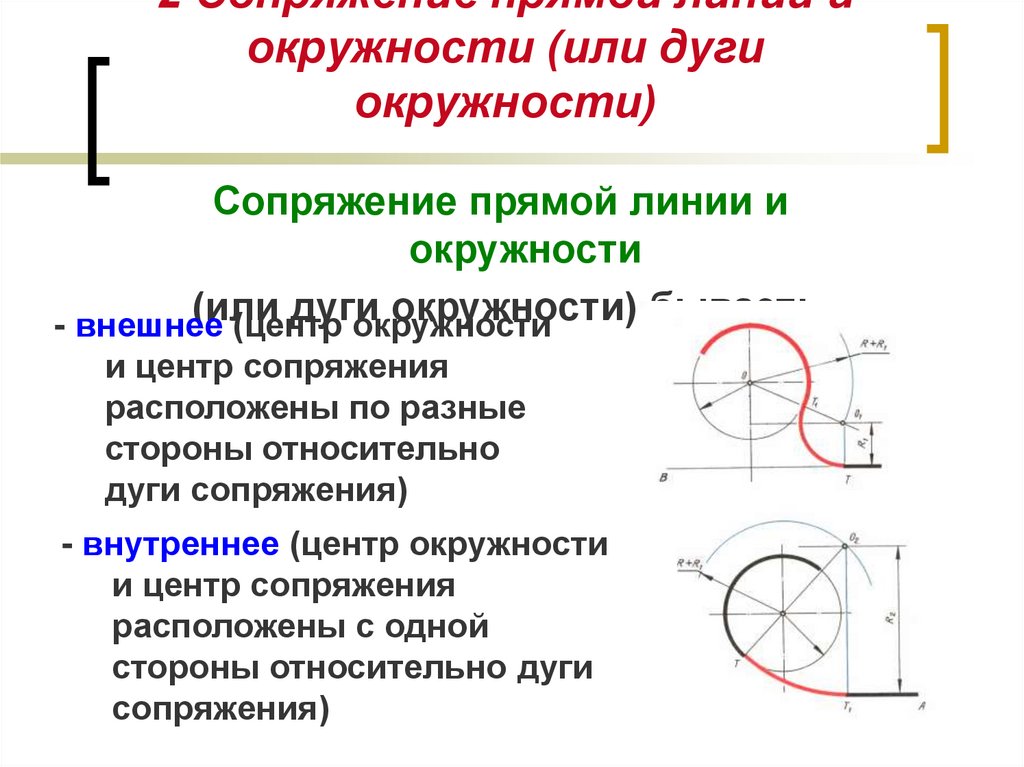
Реклама
Итак, мы можем доказать утверждение Ховарда, даже не касаясь вопроса о том, существуют ли в реальном мире объекты с прямыми линиями. Как оказалось, он и здесь что-то напутал.
Возьмите любой физический объект с идеально прямыми линиями. Чем внимательнее мы смотрим, тем больше мы видим дефектов или несоответствий в материалах, которые показывают, что существуют крошечные отклонения от идеальной прямолинейности.
Даже свет на самом деле не распространяется прямолинейно. В самом маленьком физическом масштабе квантовая физика вступает в действие, что означает, что все становится действительно странным. На квантовом уровне свет — это нечто большее, чем кажется на первый взгляд, поскольку он состоит из световых частиц (фотонов), которые иногда ведут себя как одна непрерывная волна, а иногда — как отдельные частицы.
Если бы мы не могли разложить свет на фотоны, то можно было бы сказать, что он движется по совершенно прямым линиям. Но у фотонов есть странное свойство: у них нет траекторий, которые мы можем рассчитать; они просто появляются в конечной точке, когда мы идем их измерять.
«Вся энергия — это движение, а всякое движение — это волна»
На данный момент Ховарду, возможно, было бы разумно не заниматься потенциальной карьерой профессора естественных наук после Empire .
Движение — это один из видов энергии (называемый кинетической энергией), но это, конечно, не единственный фундаментальный тип энергии. Все формы энергии можно разделить на два общих типа: кинетическую (движение) или потенциальную, которая представляет собой энергию, хранящуюся, когда на объект действуют силы, которые вызвали бы движение при правильных условиях, например запасенная электрическая энергия.
Реклама
В рамках двух основных видов энергии, другие формы включают электрическую энергию, тепловую энергию, радиацию, ядерную энергию и другие.
Техник
OK, WTF это кристалл времени?
Даниэль Оберхаус
Неверно и то, что всякое движение есть волна. На самом деле, я подозреваю, что Ховард хотел повернуть все это утверждение в обратном порядке: «Всякое движение — это энергия, а вся энергия — это волна». Это ближе к истине, но все же не соответствует действительности.
На самом деле, я подозреваю, что Ховард хотел повернуть все это утверждение в обратном порядке: «Всякое движение — это энергия, а вся энергия — это волна». Это ближе к истине, но все же не соответствует действительности.
Из-за квантовой физики все ведет себя странным образом, изменяя форму, когда вы спускаетесь на бесконечно малый уровень. Неподвижные частицы с массой преобразуют часть своей массы в энергию, чтобы иметь движение (эквивалентность энергии и массы), а энергичные частицы ведут себя как волны с частотой, и наоборот (двойственность волны и частицы).
Квантовая физика показывает, что свойства частиц (масса, энергия, движение, импульс, местоположение и т. д.) взаимозаменяемы со свойствами волн (частота, длина волны), но не говорит нам, что все состоит из изогнутых волн . На самом деле квантовая физика не дает нам делать такие категоричные утверждения.
Что такое Платоновые тела и цветок жизни?
Говард, вероятно, не сам придумал эти теории.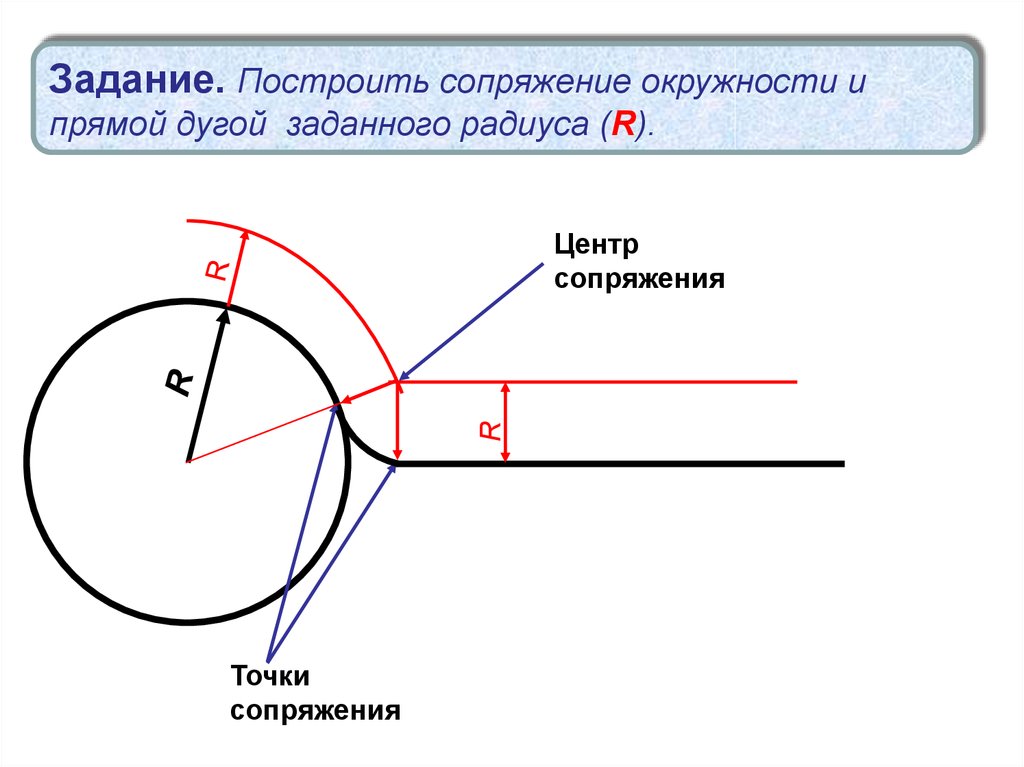 Он явно увлекается «сакральной геометрией», духовной практикой нового века, которая опирается на идеи древних философов и математиков, таких как Платон, Евклид и Пифагор.
Он явно увлекается «сакральной геометрией», духовной практикой нового века, которая опирается на идеи древних философов и математиков, таких как Платон, Евклид и Пифагор.
Платоновы тела представляют собой набор из пяти трехмерных фигур, все грани которых имеют одинаковую форму и размер, все ребра и углы правильные, а каждый угол объекта имеет одинаковое количество граней, сходящихся в этой точке. Примерами Платоновых тел являются кубы и тетраэдры.
Сакральная геометрия придает новое значение таким геометрическим объектам, как эти, и более сложным формам, таким как «цветок жизни» — геометрический узор, содержащий в себе все пять Платоновых тел, — используя их для соединения с различными «энергиями».
Сегодня эта идея кажется в лучшем случае лженаукой, но еще долго после того, как Платон и его современники пришли и ушли, «настоящие» ученые продолжали зацикливаться на том, как связать геометрию с физическим или природным миром.
Возьмем важный XVII век. физик Иоганн Кеплер, который пытался (и потерпел неудачу) использовать Платоновы тела для моделирования Солнечной системы.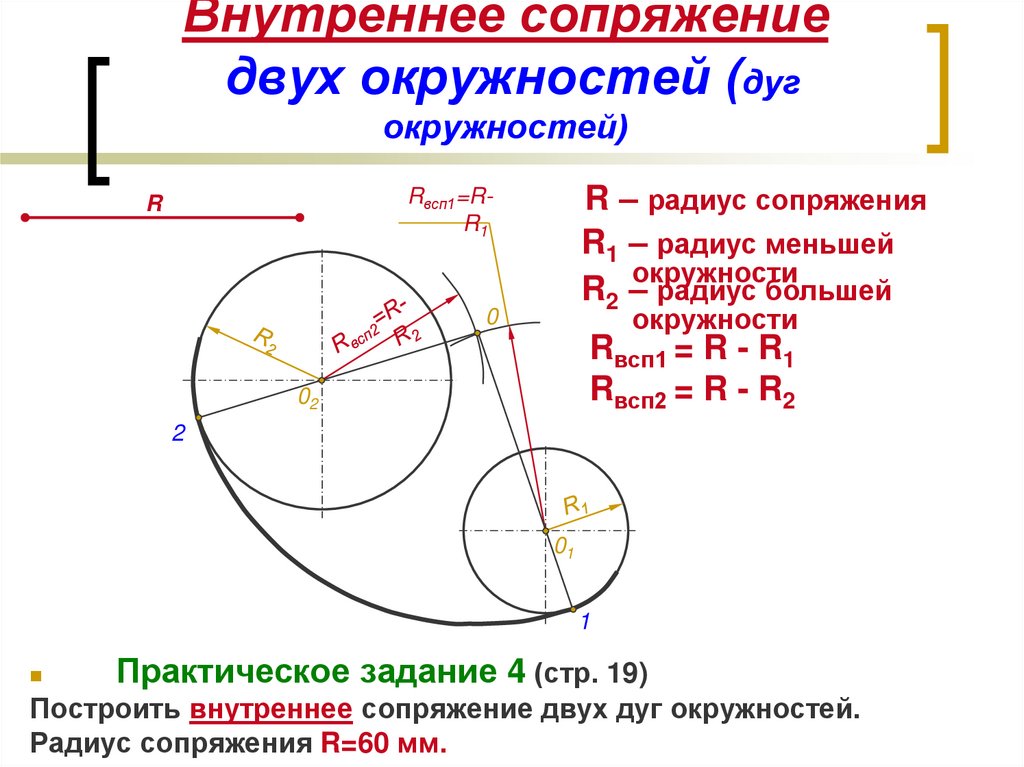 Несмотря на то, что он отказался от геометрической стороны своей работы, его оригинальные теории в конечном итоге породили революционные теории планетарных орбит, которые до сих пор используются для описания движение планет сегодня
Несмотря на то, что он отказался от геометрической стороны своей работы, его оригинальные теории в конечном итоге породили революционные теории планетарных орбит, которые до сих пор используются для описания движение планет сегодня
Итак, в некотором смысле Ховард оказался в хорошей компании. Но я все же не рекомендовал бы следовать его примеру и использовать устаревшие представления о неясных формах для принятия важных жизненных решений.
Плавное скругление углов в Adobe Illustrator | by sergey nikolaev
Возможно, вы знаете, что способ скругления углов по умолчанию — просто вставка фрагментов кругов — не лучший вариант.
Самое примитивное скругление угловЖелезнодорожники узнали об этом столетия назад, когда поезда падали с рельсов из-за внезапной центробежной силы при переходе с прямого участка на дуговой. Им нужно было найти кривые перехода, в которых кривизна (и центробежная сила) росли бы плавно.
В графическом дизайне такие задачи гораздо менее популярны, ведь присоединение кусочка круга к прямой линии в логотипе не приводит к катастрофе с жертвами, вы просто получаете некрасивый зад на стыке.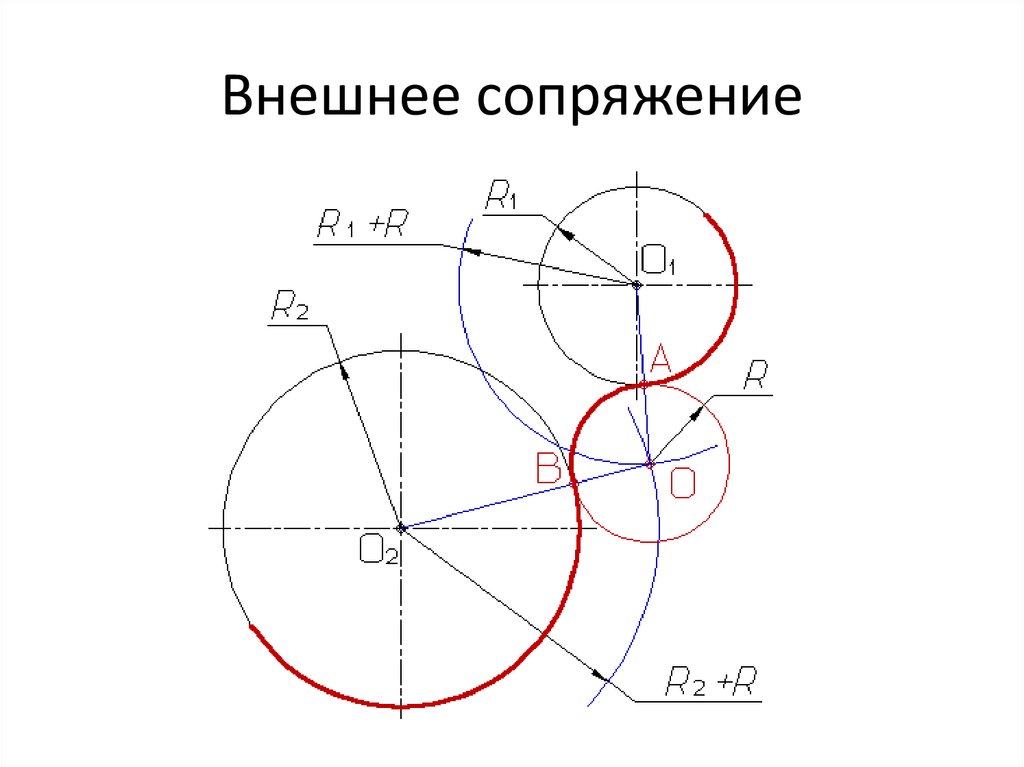 Но стоит обратить внимание на такую деталь, как перестать видеть ее невозможно — везде замечаешь эти неуклюжие соединения, они торчат, как кости в открытом переломе или как челюсти Гигачада.
Но стоит обратить внимание на такую деталь, как перестать видеть ее невозможно — везде замечаешь эти неуклюжие соединения, они торчат, как кости в открытом переломе или как челюсти Гигачада.
У дизайнеров также есть свои альтернативы переходным кривым, что позволяет им плавно скруглять углы. Самый популярный пример «правильного» плавного скругления углов — иконки приложений в iOS.
источник изображенияОни часто используются для объяснения проблемы закругленных углов. Например, вот типичная картинка из типичной статьи о форме значков Apple, показывающая, чем она отличается от обычно закругленного квадрата:
image sourceimage source Здесь форма значка называется Squircle (он же суперэллипс с параметрами n=4 , а = Ь = 1).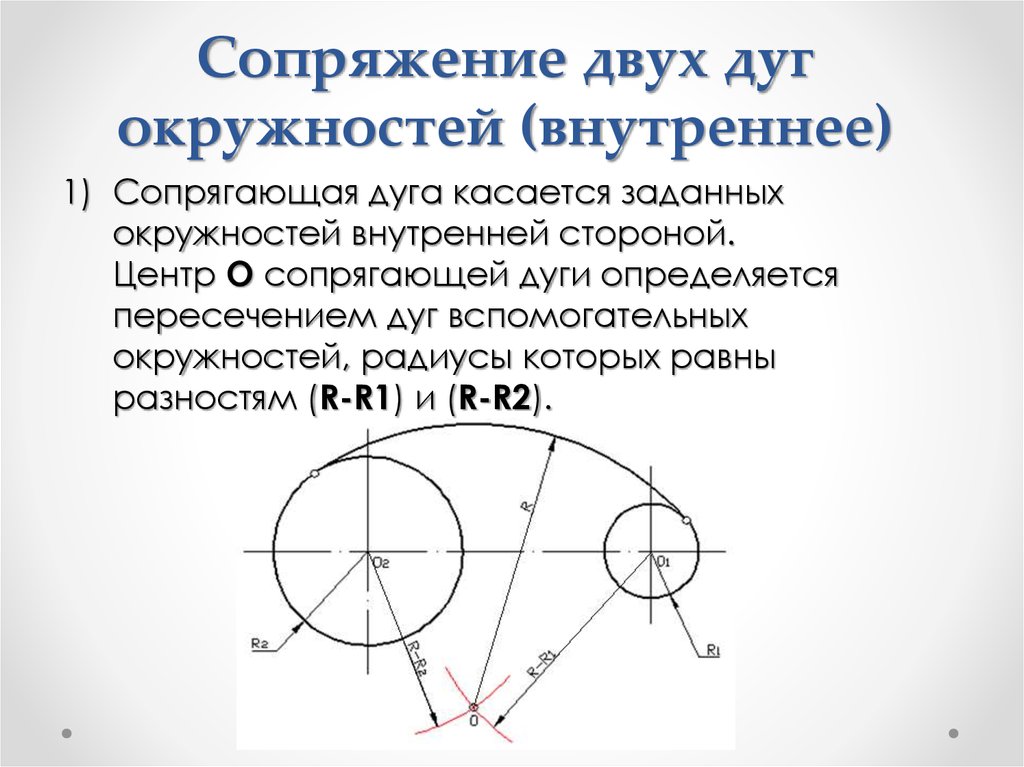 Если быть точным, то форма иконок в Apple на самом деле не кегли…сквиртл…сквиртл, и на самом деле все намного сложнее, но нас не особо интересуют эти поиски Святого Грааля. Важно понимать разницу между обычным закруглением и плавным закруглением: обычное закругление имеет резкий скачок кривизны в точке пересечения дуги окружности с прямой, и эта негладкость весьма заметна, глаза натыкаются на эту точку, как на незавершенный грубый шов. При плавном закруглении кривизна нарастает постепенно, без резких скачков, а переход прямой линии в дугу происходит плавно.
Если быть точным, то форма иконок в Apple на самом деле не кегли…сквиртл…сквиртл, и на самом деле все намного сложнее, но нас не особо интересуют эти поиски Святого Грааля. Важно понимать разницу между обычным закруглением и плавным закруглением: обычное закругление имеет резкий скачок кривизны в точке пересечения дуги окружности с прямой, и эта негладкость весьма заметна, глаза натыкаются на эту точку, как на незавершенный грубый шов. При плавном закруглении кривизна нарастает постепенно, без резких скачков, а переход прямой линии в дугу происходит плавно.
Вы также можете думать о закругленном углу как о траектории автомобиля, и тогда кривизна в точке кривой покажет, насколько повернут руль при прохождении этой части кривой. Очевидно, что рулевое колесо водителя не мгновенно перескакивает из положения «прямо вперед» в положение «90° вправо», а затем в мгновение ока обратно в положение прямо. В реальности руль плавно поворачивается от прямого до крайнего положения и обратно, без возможности пропустить какие-либо промежуточные углы поворота.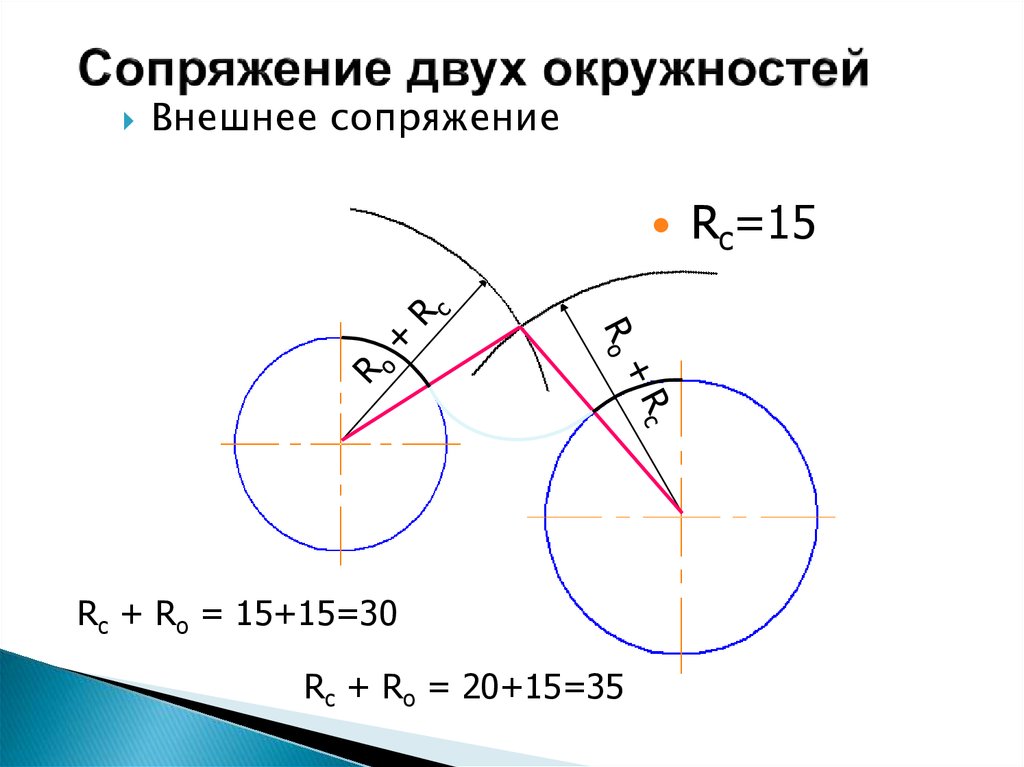 Естественное и приятное для глаз скругление углов содержит ту же плавную «траекторию» линии.
Естественное и приятное для глаз скругление углов содержит ту же плавную «траекторию» линии.
Говоря языком математики: обычное скругление встраиванием дуги обеспечивает непрерывность только для первой производной (кривая поворачивается плавно без скачков), а плавное скругление и для второй производной (скорость поворотов кривой изменяется плавно без скачков) .
Кстати, то же самое относится к трехмерному пространству и промышленным дизайнерам: сопряжение с непрерывностью кривизны первого порядка (G1, трехмерный эквивалент вложения дуги окружности) приводит к тому, что ребро на поверхность, собирающая неприятные блики.
Согласование поверхностей: положение, касательная, нормальная кривизна и кривизна второго порядка для перфекционистов. Источник Как вы уже поняли, Apple беспокоит непрерывность кривизны. sourceПлавное округление в графических редакторах — Figma и Sketch
Но вернемся к двухмерному пространству.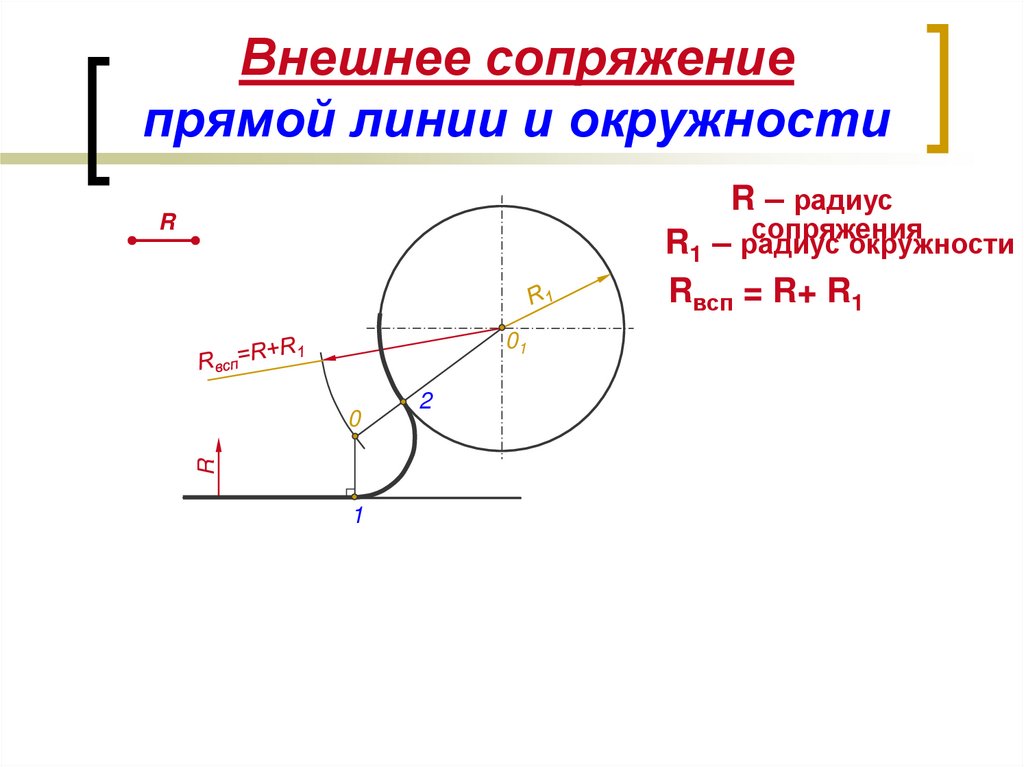 Часть проблемы сопряжения кривизны заключается в отсутствии надлежащего инструмента округления. Округление гораздо проще реализовать путем встраивания частей круга, поэтому этот метод доминирует везде, где требуется округление: графические редакторы, библиотеки графических программистов или CSS 9.0115 граница-радиус правило.
Часть проблемы сопряжения кривизны заключается в отсутствии надлежащего инструмента округления. Округление гораздо проще реализовать путем встраивания частей круга, поэтому этот метод доминирует везде, где требуется округление: графические редакторы, библиотеки графических программистов или CSS 9.0115 граница-радиус правило.
Только в 2017 году Sketch, а позже Figma (2018) представили возможность сглаживания углов. Если перейти к краткому анализу предложенных решений, то в Figma эта функция реализована гораздо лучше. Во-первых, Figma применила его к конкретному углу, а не ко всей фигуре, что позволяет применять плавное скругление к любым пользовательским путям, а не только к «стандартным» формам, таким как прямоугольники, треугольники и т. д., как это сделал Sketch.
В Sketch можно сгладить углы квадрата, но не нарисованный уголВо-вторых, в Figma степень округления регулируется ползунком, а в Sketch это бинарная опция: округление либо плавное, либо регулярное.
Интерфейс управления сглаживанием углов в Sketch и Figma Собственно, вся тема плавного скругления углов с математической точки зрения была полностью раскрыта в блоге Figma инженером, который занимался реализацией этой фичи. Из этого поста и самого интерфейса реализации еще раз видно, как разработчики и дизайнеры увлечены поиском perfect закругленный квадрат «как в значках iOS», хотя плавное закругление углов будет полезно везде, где есть закругленные углы, а не только в виде значков приложений, и угол в значке iOS не единственный, обеспечивающий сопряжение кривизны , это всего лишь один из возможных вариантов.
Из этого поста и самого интерфейса реализации еще раз видно, как разработчики и дизайнеры увлечены поиском perfect закругленный квадрат «как в значках iOS», хотя плавное закругление углов будет полезно везде, где есть закругленные углы, а не только в виде значков приложений, и угол в значке iOS не единственный, обеспечивающий сопряжение кривизны , это всего лишь один из возможных вариантов.
Идеального способа скруглить угол не существует, это дело вкуса, нет необходимости фетишизировать какую-то одну конкретную форму, выбранную Apple.
Плавное скругление в Adobe Illustrator
Что касается Adobe Illustrator, то здесь все печально: медленный и неповоротливый Adobe только добавил привычное скругление углов (радиус угла) в 2014 году, а про нативное плавное скругление и мечтать нечего. Но есть еще способы настроить скругление в Illustrator:
Конечно, вы можете вручную перемещать маркеры угловых точек по своему усмотрению.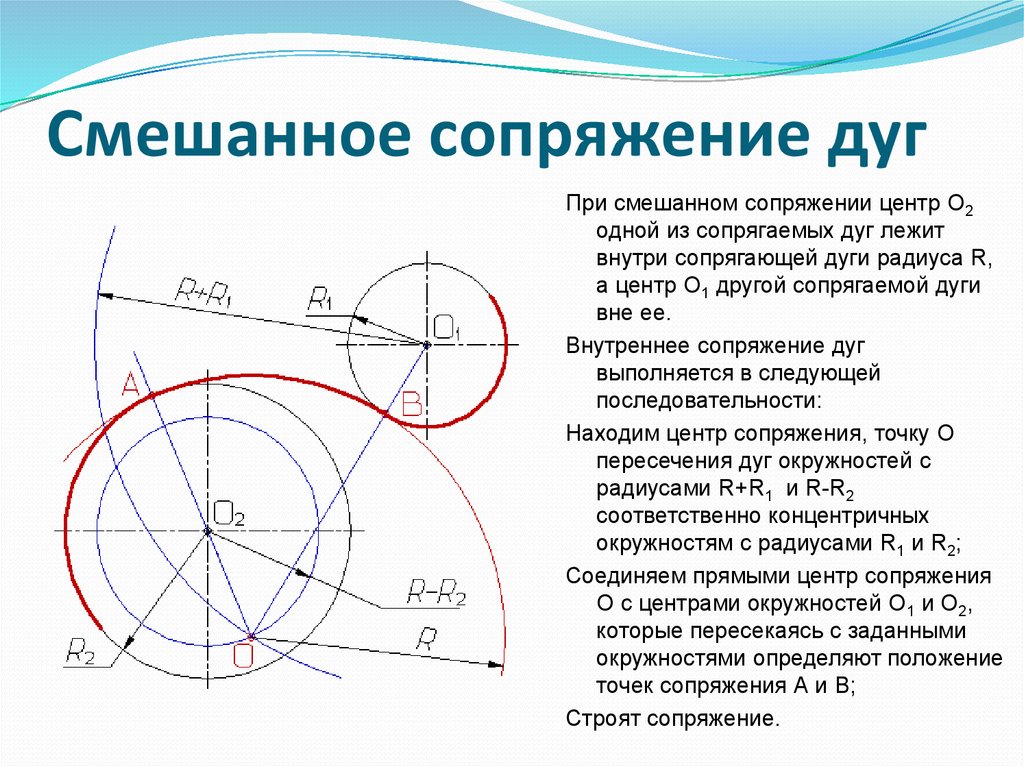 Минус здесь в ручной обработке каждого угла и в том, что это «как хочешь» нельзя зафиксировать, каждый угол будет исправляться немного по-своему.
Минус здесь в ручной обработке каждого угла и в том, что это «как хочешь» нельзя зафиксировать, каждый угол будет исправляться немного по-своему.
Сергей Стеблина предложил выделить ручки угловых базовых точек (но не точек привязки) и применить к ним масштабирование . Этот способ позволяет одинаково и достаточно быстро исправить все закругления, но все равно каждый угол нужно обрабатывать индивидуально. Также нельзя сдвинуть точки немного назад, чтобы компенсировать визуальное уменьшение радиуса угла.
Масштабирование ручек: сглажено закругление, но радиус скругления визуально уменьшенЕгор Чистяков открыл способ использования особой магии Внешности с комбинацией эффектов Деформации для получения из квадрата скворообразной формы.
ai-sourceТак же есть платный скрипт для рисования прямоугольников со сглаженными углами.
Наконец, последняя версия плагина VectorScribe включает режим Squircular округления, но без дополнительных настроек.
Мой скрипт плавного округления для Illustrator
Свой небольшой самописный скрипт для решения этой проблемы использую с 2016 года, и только сейчас нашел время довести его до относительно приемлемого состояния для публичного релиза.
Сам скрипт не скругляет углы, а настраивает существующие скругления по умолчанию. И позвольте мне сказать вам прямо, что мой сценарий не дает вам идеального округления , «как в значках iOS», просто потому, что после того, как вы применяете плавное округление «Apple» для достижения желаемой формы угла, он создает четыре точки кривой Безье на угол в Скетч и Фигма. Вектор в официальной библиотеке интерфейса Apple также содержит по четыре точки на угол:
Я не хотел, чтобы мой скрипт добавлял лишние точки, и ограничился аккуратной настройкой манипуляторов только уже существующих закругленных угловых точек. Именно поэтому скрипт делает ровно две вещи: немного оттягивает точки сопряжения линия-дуга от угла и немного выдвигает вперед их ручки. Это выглядит примерно так:
Это выглядит примерно так:
Поэтому в скрипте два параметра: насколько отодвинуть точку от угла (Anchors coef) и насколько отодвинуть манипулятор назад (Handles коэф.).
Даже без добавления дополнительных точек скрипт решает проблему: сглаживаются стыки и не так быстро растет кривизна. Двух переменных достаточно, чтобы охватить самые разные формы углов, от вялых до тугих, от тщательно подогнанных до совершенно новых форм:
По сути, два ползунка распределяют площадь профиля кривизны угла — равномерно распределяют по всему углу или собирают в горб.
Конечно, скрипт может обрабатывать все углы объекта сразу:
Или только выделенные:
Или даже все объекты сразу:
Я так понимаю, что два параметра в скрипте, которые не понятны влияют на результат не самые удобные или интуитивно понятные опции по сравнению с другими инструментами (один ползунок в Figma и переключатель вкл/выкл в Sketch и плагине Vectorscribe). Но я решил не пытаться объединить их в один параметр или чекбокс, воруя точность настройки. Этот скрипт, в конце концов, небольшой профессиональный инструмент, а не продукт.
Но я решил не пытаться объединить их в один параметр или чекбокс, воруя точность настройки. Этот скрипт, в конце концов, небольшой профессиональный инструмент, а не продукт.
Поэтому вместо кнопки «Сделай круто, как Apple» предлагаю поиграться с ползунками, подобрать нужные комбинации коэффициентов и сохранить их в пресеты. Например, разработчик транспортных схем может сделать различные предустановки скругления для всех встречающихся на схеме углов поворотов: 30°, 45°, 60°, 90°, 120°, 135°. Некоторые пресеты уже идут со скриптом, и вы можете удалить их, если они вам не нужны.
Так же я добавил галочку для запуска скрипта в тишине, чтобы панель настроек не раздражала вас, когда скрипт приходится запускать каждый раз с одними и теми же параметрами и ничего менять не надо. Затем скрипт выполняется без всплывающего окна с последними использованными значениями коэффициентов. Панель настроек появится при запуске скрипта с зажатой клавишей Shift.
UPD: Ранее здесь писалось как найти в коде переменную, отвечающую за отображение профиля кривизны. Начиная с версии 0.0.4 скрипта, выпущенной в октябре 2022 года, во всплывающее окно добавлен флажок отображения профиля кривизны.
Начиная с версии 0.0.4 скрипта, выпущенной в октябре 2022 года, во всплывающее окно добавлен флажок отображения профиля кривизны.
Остальные параметры в интерфейсе не ставил, но их можно изменить в коде.
Репозиторий GitHub: https://github.com/kefiijrw/Round-Corners-Customization-for-Illustrator.
GitHub — kefiijrw/Round-Corners-Customization-for-Illustrator: сценарий настройки скругления углов…
В настоящее время вы не можете выполнить это действие. Вы вошли в другую вкладку или окно. Вы вышли из системы на другой вкладке или…
github.com
Или просто ссылка для скачивания: https://kefiijrw.com/upload/Round Corner Customization for Illustator.zip
Пожалуйста, пишите отчеты об ошибках или предложения по адресу репозиторий, или, если вы не можете, то в телеграмму или по электронной почте [email protected].
Хорошо, это не должно было быть частью истории, но… использование скриптов в Illustrator по умолчанию довольно раздражает (и лениво).
Способ 1. «Ленив как черт, упрям как сатана»
Просто перетащите файл скрипта в окно Illustrator
Способ 2. «Веер диалоговых окон»
Нажмите Файл → Скрипты → Другой скрипт… и затем найдите файл скрипта в недрах файла система.
Способ 3. «Триумф воли»
Один раз заставить себя положить файл скрипта в /Applications/Adobe Illustrator [верс.]/Presets.localized/en_GB/Scripts (MacOS) или C: \Program Files\Adobe\Adobe Illustrator [версия] (64-разрядная версия)\Presets\en_RU\Scripts\