Сопряжение окружности и прямой внутреннее: Страница не найдена — НИЖНЕКАМСКИЙ ХИМИКО-ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

3.3.2 Сопряжение дуги и прямой дугой окружности заданного радиуса

Могут встретиться два случая такого сопряжения: внешнее касание сопрягающей дуги с заданной и внутреннее касание. В обоих случаях задача сводится к определению центра сопрягающей дуги и точек касания.

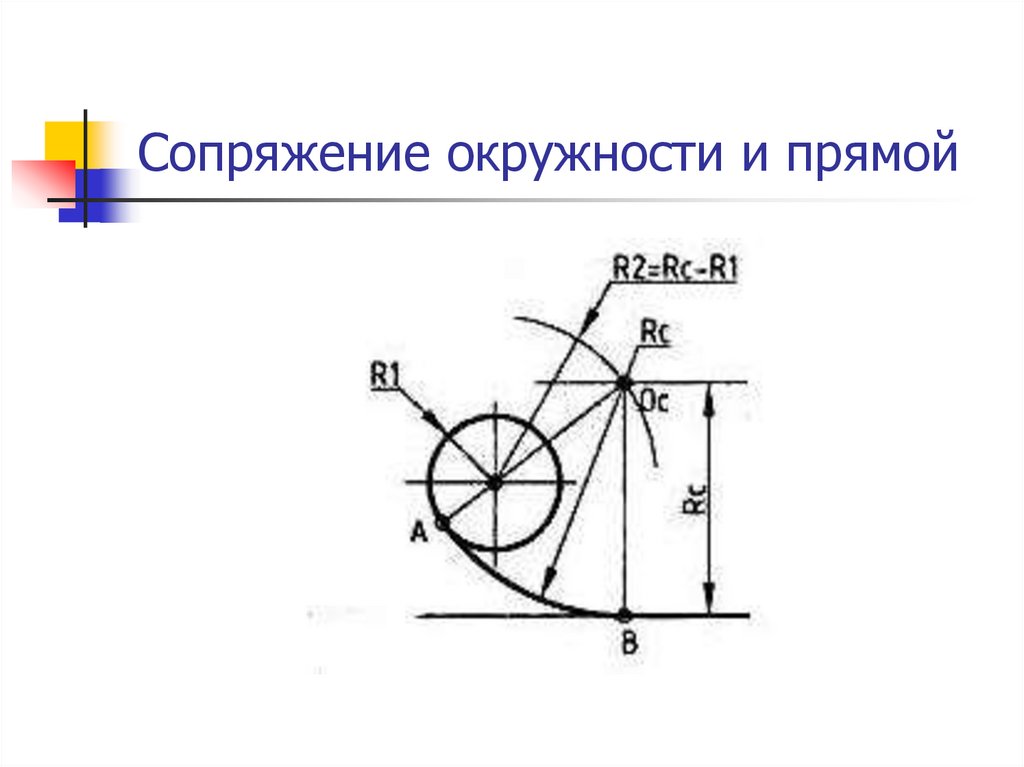
При внешнем касании (рисунок 52, а) из центра заданной дуги – точки O₁ проводят вспомогательную дугу радиусомR +R_с. На расстоянии, равном радиусуR_cсопрягающей дуги, параллельно заданной прямой проводят прямую. ТочкаОпересечения вспомогательной дуги и прямой есть центр сопрягающей дуги. На пересечении прямой, соединяющей точкиОиO₁с заданной дугой, отмечают точку касанияA. Вторую точку касанияВопределяют как точку пересечения заданной прямой с перпендикуляром, опущенным на нее из точки

О.

При внутреннем касании (рисунок 52, б) определение центра сопрягающей дуги и точек касания аналогичны предыдущему случаю с той лишь разницей, что радиус вспомогательной дуги равен R_c – R.

а б

Рисунок 52

3.3.3 Сопряжение двух дуг дугой окружности заданного радиуса

Различают три вида такого сопряжения:

1) внешнее сопряжение при внешнем касании сопрягающей дуги с двумя заданными;

2) внутреннее сопряжение при внутреннем касании сопрягающей дуги с двумя заданными;

3) смешанное сопряжение при внешнем касании сопрягающей дуги с одной заданной и внутреннем касании с другой.

При внешнем сопряжении(рисунок 53, а) центр сопрягающей дуги точка

O располагается в точке пересечения вспомогательных дуг радиусамиr +R_c иR +R_c, проведенных соответственно из центров сопрягаемых дуг – точекO₂ иO₁.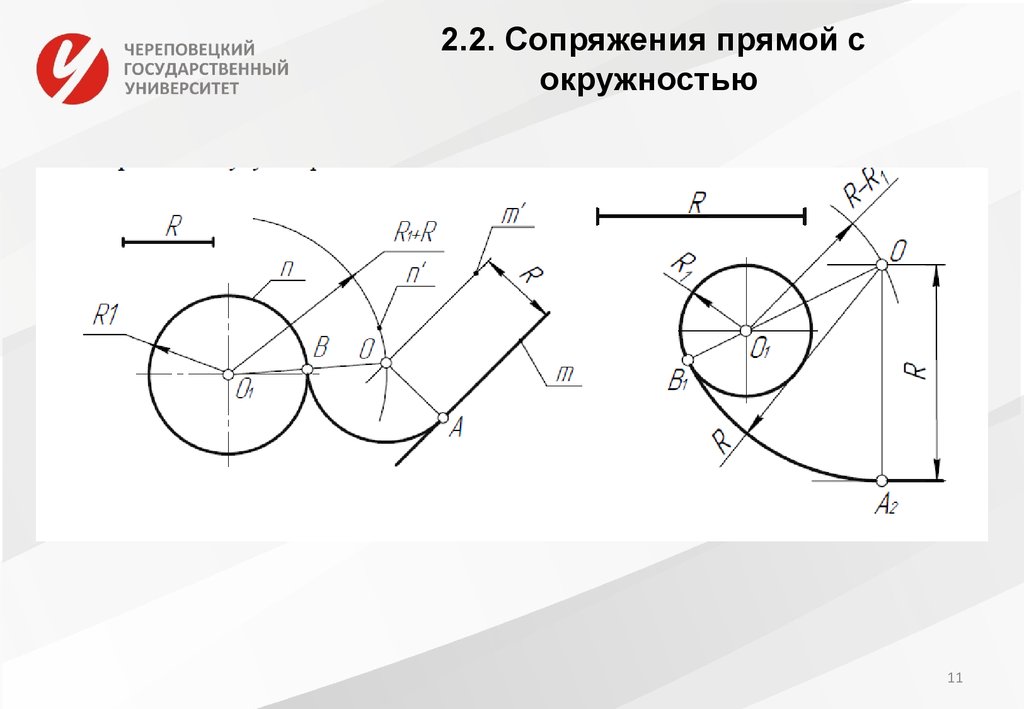 Точки касанияA иB определяются как точки пересечения заданных дуг с прямымиOO₁ иOO₂.

Внутреннее сопряжениедуг радиусамиr иR дугой радиусомR_cпоказано на рисунке 53, б. Для определения центра сопрягающей дуги – точки

Опроводят вспомогательные дуги радиусамиR_c–r иR_c–Rсоответственно из центров заданных дуг – точекO₂иO₁. ТочкаОпересечения этих дуг и явится центром сопрягающей дуги. Из точкиОчерез точкиO₁ иO₂проводят прямые до пересечения с заданными дугами и получают соответственно две точки касания –A иB.

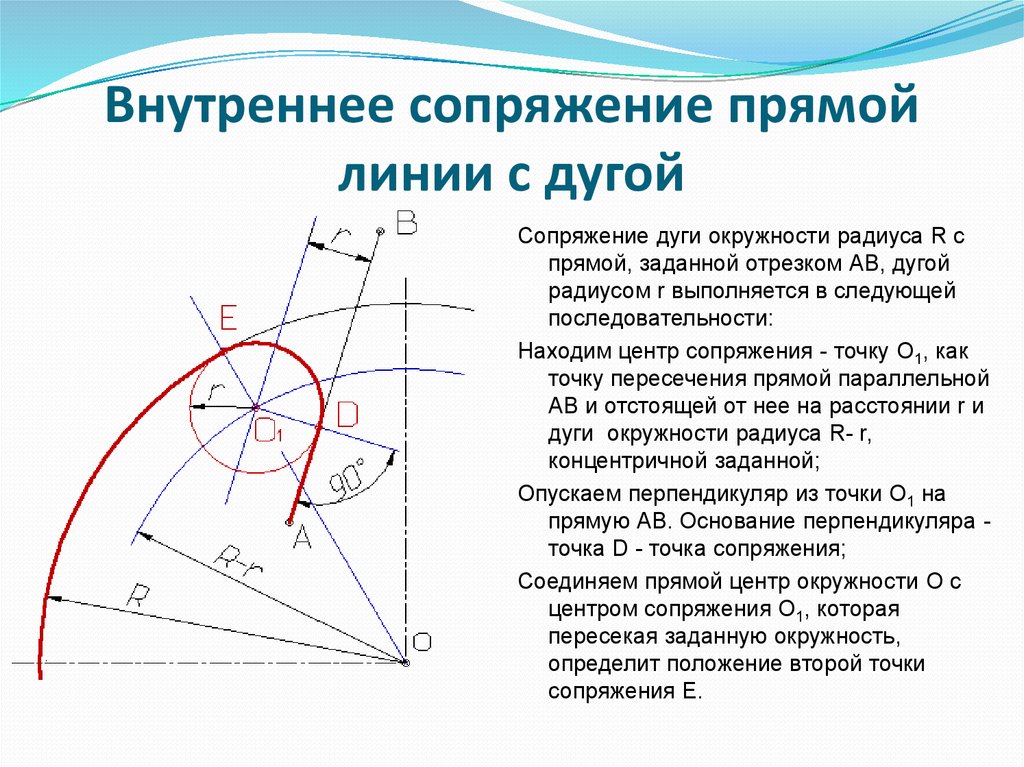
Рисунок 53

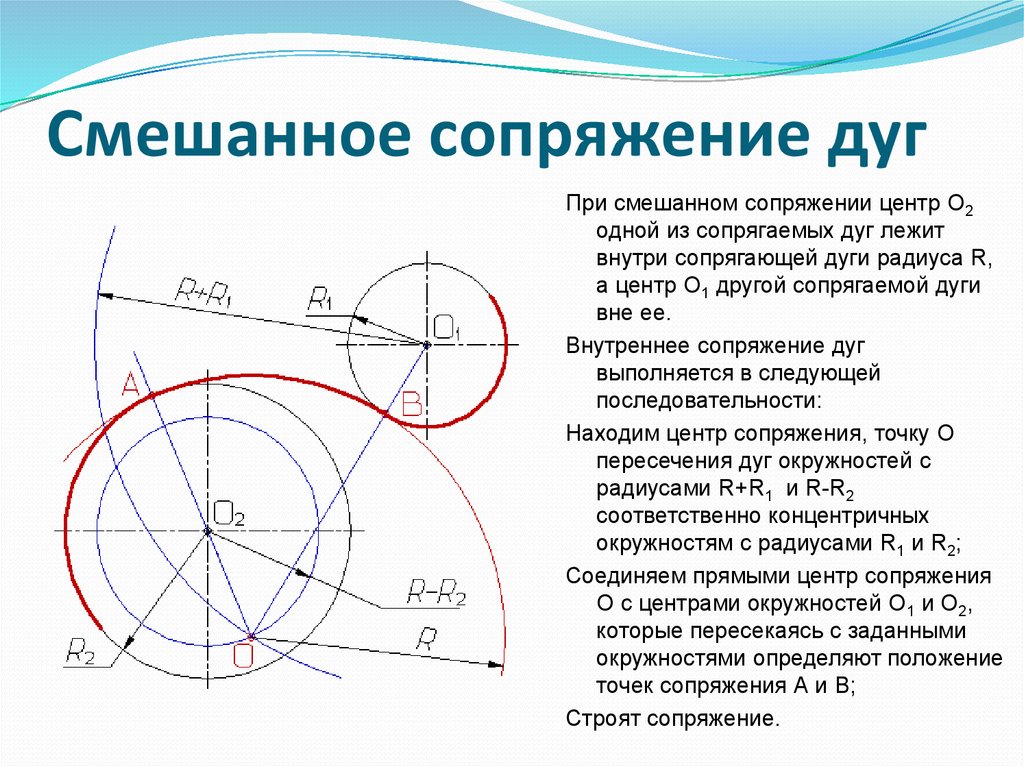
При смешанном сопряжении центр сопрягающей дуги – точка

Оопределяется как точка пересечения двух вспомогательных дуг радиусамиR_c+R иR_с–r (рисунок 53, в) илиR_с–R иR_с+r, проведенных соответственно из центров заданных дуг – точекO₁ иO₂. Для определения точек касания сопрягающей дуги с заданными проводят две прямые: одну через точкиО и O₁, другую через точки О и O₂. Точки пересечения каждой из них с заданными дугами дают искомые точки касания A и B.

3.3.4 Вычерчивание контуров деталей

Последовательность вычерчивания контуров деталей в основном зависит от их формы. Поэтому можно указать только на некоторые общие положения, справедливые для всех случаев.

Перед вычерчиванием любого контура необходимо установить, из каких линий и их сочетаний он состоит, а также решить, какие геометрические построения следует выполнить при вычерчивании контура. Только после подобного анализа можно приступать к построению контура.

Последовательность вычерчивания контура проследим на примере контура скобы (рисунок 54, а). Вычерчивание начинают с проведения осей симметрии (вертикальная ось на рисунке 54, б), осевой (горизонтальная ось на рисунке 54, б) и центровых линий контура. Затем проводят линии, связанные с горизонтальной осью (рисунок 54, в), и строят остальные основные линии контура (рисунок 54, г). Далее выполняют скругления углов (рисунок54, д) и вычерчивают внутренние очертания, не связанные с другими линиями (прорезь, рисунок 54, е).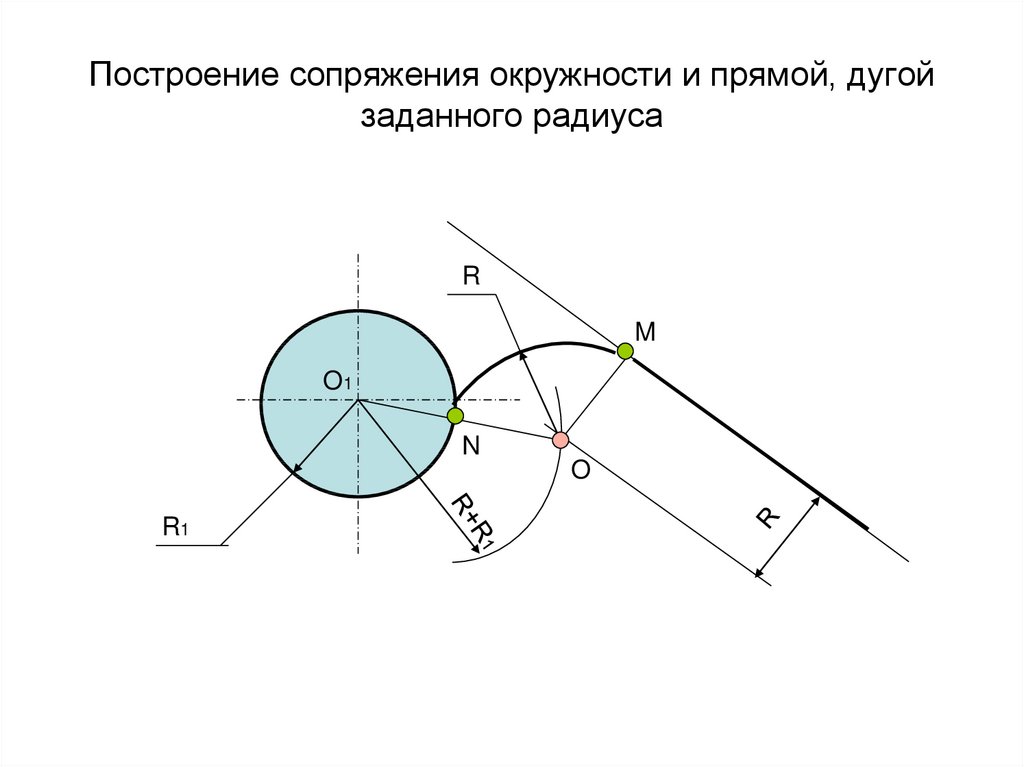

Последними вычерчивают контуры, не содержащие элементов сопряжения. Заканчивают построение проведением выносных и размерных линий с простановкой размеров (рисунок 54, а).

Рисунок 54

Дуга — сопряжение — Большая Энциклопедия Нефти и Газа, статья, страница 2

Cтраница 2

Если сопрягаемые отрезки находятся на одном слое, то дуга сопряжения помещается на этот же слой, в противном случае она помещается на текущий слой. Аналогичное правило действует на цвет и тип линии дуги сопряжения.  [16]

Важно: Задаваемый радиус служит основанием для определения центра дуги сопряжения или хорды соединения. Линии могут быть сопряжены / соединены в их средней части или на продолжении.  [17]

Фрезерование криволинейных поверхностей, состоящих из участков прямых и

дуг различных кривых и радиусных сопряжений на деталях типа автоматных копиров, производится в полярной системе координат на горизонтальном поворотном столе.  [18]

Чаще всего промежуточной линией является дуга окружности, называемая дугой сопряжения или сопрягающей дугой. Радиус сопрягающей дуги носит название радиуса сопряжения, а центр дуги — центра сопряжения. Дуга сопряжения касается одновременно двух сопрягаемых линий. При сопряжении всегда имеются две точки перехода ( на рис. 102 точки А и В), через каждую из них можно провести по одной общей касательной. Таким образом, построение сопряжений основано на свойствах касательной к дуге окружности и касания двух дуг окружностей.  [19]

Для сопряжения прямой линии и дуги необходимо, чтобы центр дуги сопряжения лежал на перпендикуляре к прямой, восстановленной из точки сопряжения ( фиг.  [20]

Дуги окружностей, при помощи которых выполняется сопряжение, называются дугами сопряжения. Для построения дуги сопряжения необходимо на чертеже выявить центр ее, радиус этой дуги и точки сопряжения, в которых дуга сопряжения переходит в сопрягаемые линии. Задаваясь одним из этих параметров, остальные можно определить графически.  [21]

Внешнее сопряжение окружности и прямой дугой заданного радиуса.| Внутреннее сопряжение окружности и прямой дугой заданного радиуса.  [22]

Точка пересечения проведенной прямой и дуги вспомогательной окружности определяет положение центра дуги сопряжения О. Соединяя найденный центр О с центром О данной окружности и опуская из О перпендикуляр на прямую, находят точки касания К и К, между которыми заключена дуга сопряжения.  [23]

Внешнее сопряжение окружности и прямой дугой заданного радиуса.| Внутреннее сопряжение окружности и прямой дугой заданного радиуса.  [24]

Точка пересечения проведенной прямой и дуги вспомогательной окружности определяет положение центра дуги сопряжения О, Соединяя найденный центр Ot с центром О данной окружности и опуская из Ot перпендикуляр на прямую, находят точки касания К и К, между которыми заключена дуга сопряжения.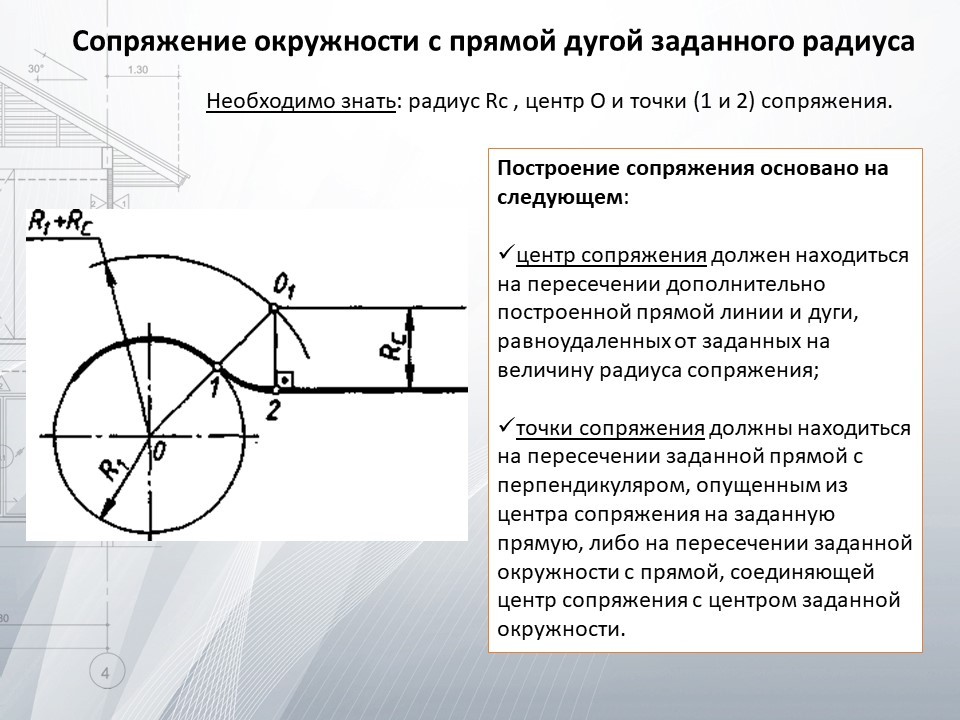  [25]

Из точек 02 и 03 как из центров радиусом R2 про-вздят дуги сопряжения.  [26]

Параллельно данной прямой проводят вспомогательную прямую на расстоянии, равном радиусу дуги сопряжения Rt. Из центра дуги О делают засечку радиусом, равным сумме радиусов данной дуги R и дуги сопряжения Rit до пересечения со вспомогательной прямой в точке О.  [27]

Чертеж, дополненный новыми конструктивными элементами при использовании.  [28]

Если оба отрезка располагаются на одном слое чертежа, то фаска или дуга сопряжения прямых помещается на этот же слой. В противном случае фаска ( дуга) размещается на текущем слое.  [29]

Из центров данных дуг делают циркулем засечки радиусом, равным сумме радиусов дуг сопряжения. Точка пересечения засечек О, является центром сопрягающей дуги.  [30]

Страницы:      1    2    3    4

Круги – объяснение и примеры

Одной из важных фигур в геометрии является круг.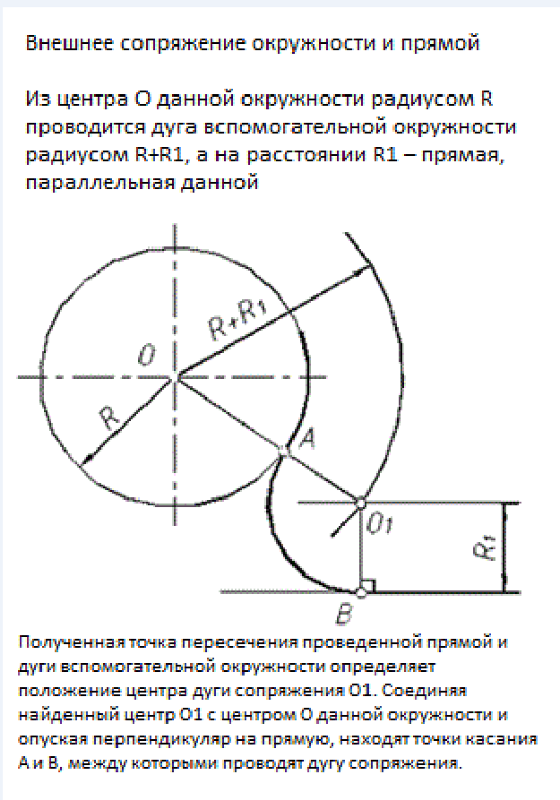 На экзамене по геометрии большинство вопросов будет состоять из прямоугольников, треугольников и кругов.

Все мы уже видели круги. У них идеально круглая форма, что делает их идеальными для хула-хупов! В этой статье объясняется, что такое круг, его свойства и составные части.

Что такое круг в геометрии?

Слово ‘ круг «происходит от греческого слова, означающего « обруч » или « кольцо «. В геометрии круг определяется как замкнутая двумерная фигура, в которой множество всех точек на плоскости равноудалено от данная точка называется « центр ».

Никогда не путайте круг с многоугольником. Круг не является многоугольником, потому что он состоит из кривых.

История круга древняя. Раньше люди верили, что луна, солнце и другие планеты имеют круглую форму, потому что не существовало представления о трехмерных формах — математики изучают круги, что помогло им развить исчисление и астрономию.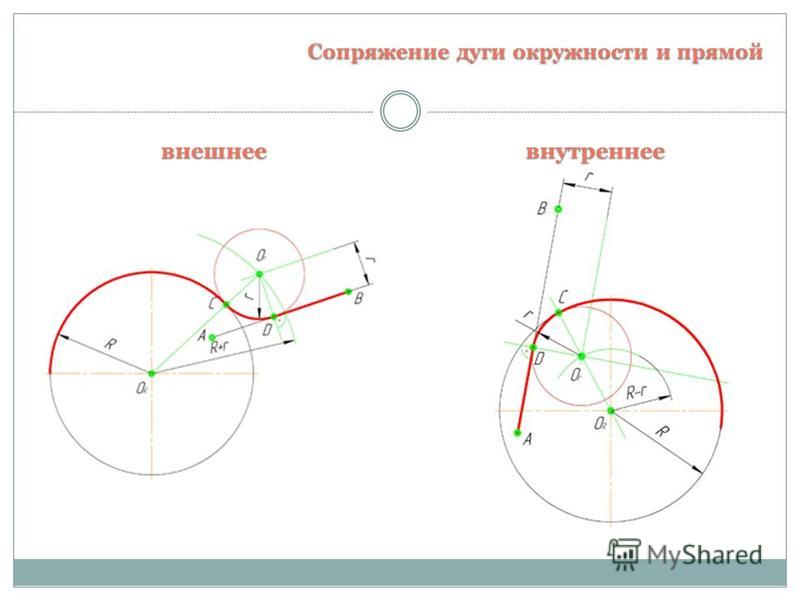

В 1700 г. до н.э. Райнд Папирус предложил метод нахождения площади круга. В то время значение числа пи не было точным. В 300 г. до н.э. Евклид в своей книге изложил свойства кругов. Наконец, в 1880 году нашей эры немецкий математик Линдеманн решил проблему со значением числа пи и доказал, что число пи является трансцендентным (не корнем какого-либо многочлена с рациональными коэффициентами).

Круги вокруг нас! Некоторые из реальных примеров кругов:

• Колесо велосипеда
• Монета
• Обеденная тарелка
• Настенные часы
• Колеса обозрения

Таким образом, круг является важной формой в области геометрии. Посмотрим на стороны и свойства окружности.

Части круга

• Центр: Центр — это середина круга. На приведенной выше диаграмме центр окружности указывает « O» .
• Радиус : Это отрезок от центра круга, соединяющий любую точку на самом круге. Радиус окружности обозначается либо буквой « r ” (строчные буквы) или “ R ” (верхние буквы).

Линия ОТ – это радиус описанной выше окружности.

• Диаметр : Диаметр круга — это отрезок, проходящий через центр круга и имеющий обе конечные точки круга. Математически диаметр в два раза больше радиуса окружности. Диаметр окружности обозначается « D » или «»

Линия PQ — это диаметр окружности.

• Хорда : Хорда представляет собой отрезок с обеими концами на окружности. Линия RS является хордой окружности выше. Диаметр окружности — самая длинная хорда.
• Секанс : Секанс представляет собой удлиненную хорду окружности.

Строка 2 ( l ₂ ) является секущей круга выше.

• Дуга : Дуга представляет собой кривую вдоль внешней линии окружности
• Касательная : Тангенс окружности — это прямая линия, которая снаружи касается окружности, внешней линии окружности. Линия 2 ( l ₂ ) является касательной окружности.
• Сегмент : Сегмент представляет собой область, ограниченную дугой и хордой.
• Сектор : Сектор представляет собой область по дуге и двум радиусам. Регион OTP — это сектор круга, как показано выше.
• Окружность : Окружность круга – это общее расстояние вокруг внешней линии круга
• Площадь круга : Область, ограниченная внешней линией круга
• Кольцо : Кольцо представляет собой кольцо -образный объект, образованный между двумя концентрическими (окружностями с общим центром) окружностями. Например, заштрихованная область в круге ниже называется кольцом.

Свойства круга

Существует несколько фактов о кругах. Эти факты о кругах известны как свойства круга. Давайте рассмотрим их.

• Окружности с равными радиусами или диаметрами конгруэнтны.
• Самая длинная хорда окружности называется диаметром.
• Диаметр круга в два раза больше радиуса самого круга.
• Диаметр делит круг на две равные половины.
• Внешняя линия круга равноудалена от центра.
• Независимо от меры радиуса или диаметра, все окружности подобны.
• Радиус представляет собой серединный перпендикуляр к хорде.
• Две или более хорды равны по длине, если все они равноудалены от центра окружности.
• Угол между радиусом и касательной всегда равен 90 градусов (прямой угол).
• Две касательные равны, если они имеют общую точку начала.
• Угол, образуемый в центре круга его окружностью, равен четырем прямым углам.
• Длина окружности двух или более различных кругов пропорциональна их соответствующим радиусам.
• Дуги одной и той же окружности пропорциональны соответствующим углам.
• Радиусы равных окружностей или одной и той же окружности равны.
• Равные круги имеют площадь и длину окружности.
• Расстояние между самой длинной хордой и центром окружности равно нулю.
• Перпендикулярное расстояние от центра окружности до хорды увеличивается по мере уменьшения длины хорды, и наоборот.
• Окружность может описывать многоугольники, такие как треугольник, трапеция, прямоугольник и т. д.
• Точно так же окружность может быть вписана внутрь многоугольника, такого как прямоугольник, воздушный змей, квадрат, трапеция и т. д.
• Касательные, проведенные на обоих концах диаметра, всегда параллельны друг другу.
• Два радиуса, соединяющие концы хорды с центром окружности, образуют равнобедренный треугольник.
• Равные дуги образуют равные углы в центре окружности.

Пример 1

Какой из следующих предметов имеет круглую форму?

1. Пицца
2. Футбол
3. Апельсин
4. Все это.

Решение

Все упомянутые формы имеют круглую форму.

Следовательно, правильный выбор D.

Пример 2

Круглая чаша имеет диаметр 9 дюймов. Каков радиус чаши?

Решение

Мы знаем, что радиус круга равен половине диаметра.

Следовательно,

Радиус = 9/2 = 4,5 дюйма

Пример 3

Какая из следующих частей окружности также может быть хордой окружности?

1. Радиус
2. Диаметр
3. Дуга
4. Сектор

Решение

Хорда — это отрезок, оба конца которого лежат на окружности. Диаметр окружности — самая длинная хорда.

 

Использование сопряжения в предложении

conjugate

• Advertisement

• Advertisement

• Advertisement

• Реклама

• Advertisement

• Advertisement

• Advertisement

• Advertisement

• Реклама

• Реклама

Приведенные выше примеры использования слов были собраны из различных источников, чтобы отразить текущее и историческое употребление.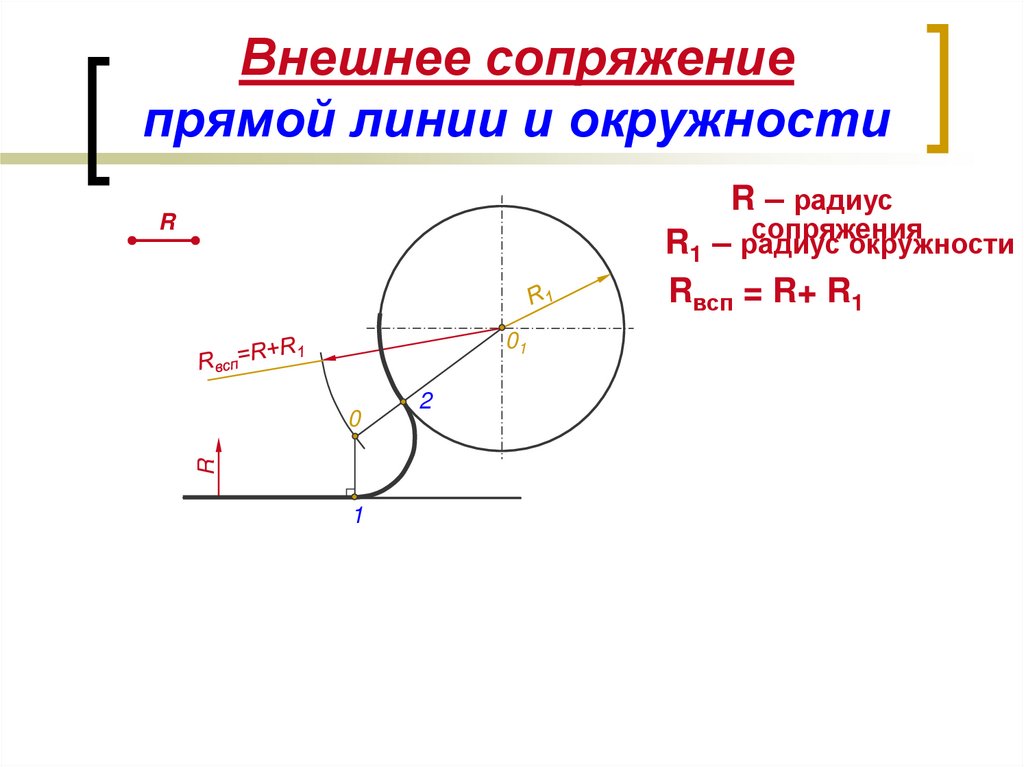 Они не отражают мнения YourDictionary.com.

Статьи по теме

• Что такое спрягаемый глагол?

  Если вы когда-либо посещали курсы второго языка, вы много слышали о спряженных глаголах и спряжениях глаголов. Короче говоря, спряженный глагол — это глагол, форма которого была изменена по сравнению с его основной формой; но, как и все, что связано с грамматикой, все немного сложнее. Давайте посмотрим, как спрягаются глаголы и какие разные вещи они сообщают, когда они спрягаются.

• Правила спряжения глаголов

  Спряжение глаголов сообщает читателю, когда происходит действие и кто его выполняет. Постоянное спряжение глаголов приводит к меньшему количеству недоразумений и недопонимания. Вам никогда не придется беспокоиться об ошибках в глаголах, если вы освоите несколько важных правил спряжения глаголов.