Сопряжение окружностей дугами окружностей: 19. Сопряжение двух дуг окружностей третьей дугой 3 Некотор...

Содержание

Сопряжение — Техническое черчение

Сопряжением называется плавный переход по кривой от одной линии к другой. Сопряжения бывают циркульные и лекальные. Построение их основано на свойствах касательных к кривым линиям. Сопряжение отрезков прямых с циркульными кривыми будет возможно, если точка сопряжения является одновременно и точкой касания прямой к дуге кривой. Следовательно, радиус сопряжения должен быть перпендикулярным к прямой в точке касания.

Сопряжение циркульных кривых возможно тогда, когда точка сопряжения будет являться одновременно и точкой касания сопрягаемых дуг. Следовательно, точка касания должна находиться на линии центров дуг окружностей.

Сопряжение пересекающихся прямых:

Пример 1. Даны пересекающиеся прямые AB и ВС и радиус сопряжения R; требуется выполнить сопряжение прямых (фиг. 66, а, б, в).

Сопряжение будет возможным, если прямые AB и ВС будут касательными к окружности радиуса R.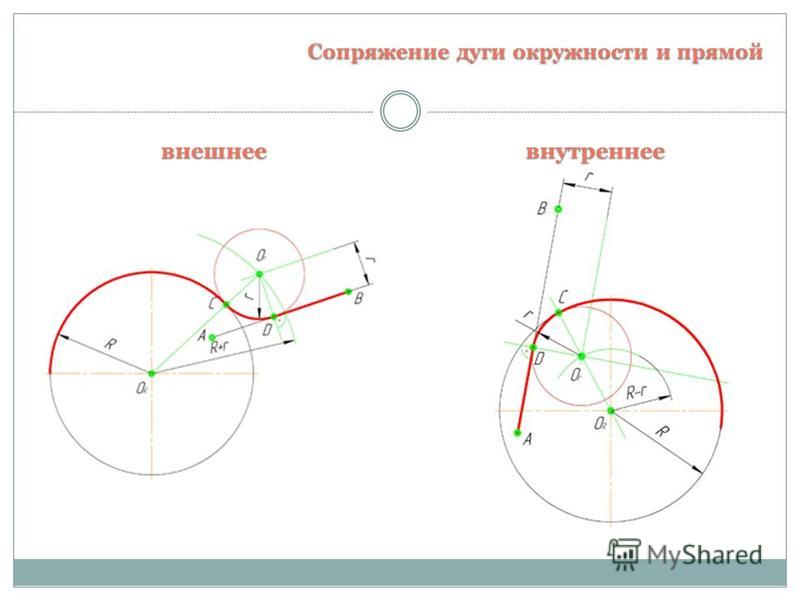

Для нахождения центра этой окружности

необходимо провести на расстоянии R параллельно заданным прямым вспомогательные прямые до их взаимного пересечения в точке 0. Из точки О, как из центра, проводится дуга радиуса R. Точками сопряжения будут точки M и Н, определяемые пересечением прямых AB и ВС с опущенными на них перпендикулярами из точки О.

Пример 2. Даны пересекающиеся прямые AB и ВС и радиусы сопряжения R и R1 Построение сопряжения возможно, если угол а<90.

Способ построения такого сопряжения приведён на фиг. 66,г.

Сопряжение параллельных прямых

Пример 1. Даны две параллельные прямые AB и СЕ и точки сопряжения В и С (фиг. 67).

Надо построить плавное сопряжение циркульными кривыми так, чтобы оно проходило через заданную точку K, посредине отрезка ВС.

Для определения радиусов и центров дуг сопряжения делим отрезки BK и КС прямыми так, чтобы они были перпендикулярны этим отрезкам и делили их пополам. Так как радиус сопряжения должен быть перпендикулярным к прямой в точке сопряжения, то для нахождения центров О дуг сопряжения восстанавливаем из точек В и С перпендикуляры до пересечения их с ранее проведёнными перпендикулярами к прямой ВС.

Точки пересечения этих перпендикуляров определят положение центров сопряжений О—О, а равные между собой отрезки 05 и ОС дадут величины радиусов сопряжений.

Пример 2 (фиг. 68), Этот пример отличается от предыдущего

тем, что точка К взята на прямой ВС произвольно, на некотором расстоянии e от прямой СЕ; следовательно, радиусы сопряжений R и R1— разные по величине. Ход построения сопряжений такой же, как и в предыдущем примере.

П p и м e p 3. Даны: расстояние между двумя параллельными прямыми AB и СЕ, равное сумме сопрягаемых радиусов R и R1, и точка сопряжения В (фиг. 69).

Для построения сопряжения проводим параллельно AB на расстоянии R вспомогательную прямую 0—01. Центр сопряжения 0 для радиуса R будет находиться на пересечении перпендикуляра, проведённого из точки В к вспомогательной прямой. Описывая из точки О дугу радиусом R, найдём точку К, из которой радиусом R1 делаем на вспомогательной прямой засечку, определяющую центр сопряжения O1. Из точки О1 опускаем перпендикуляр на прямую СЕ и, найдя точку сопряжения С, сопрягаем точки К и С дугой радиуса R1.

Сопряжение дуги окружности с прямой

Пример 1. Построим сопряжение дуги радиуса R с прямой AB радиусом R1 (фиг. 70). Для этого необходимо найти центр сопряжения 0 и точки сопряжения С и а. Точка С является одновременно точкой их касания и должна лежать на линии центров этих дуг. Радиус сопряжения должен быть перпендикулярен к прямой AB в точке касания а. Поэтому из центра О описываем радиусом, равным сумме R+R1, дугу.

На ней будет находиться центр сопряжения 0, для определения которого проводим параллельно AB на расстоянии R1 вспомогательную прямую ее до пересечения с проведённой дугой. Соединив точки O1и О, найдём точку сопряжения С. Для определения точки а опускаем из О1 перпендикуляр на AB. Далее, радиусом R1 из центра O1 сопрягаем точки а и С.

Пример 2. Даны: дуга радиуса R, прямая AB и точка сопряжения а. Требуется найти точку сопряжения С и радиус сопряжения R1 (фиг. 71). Проводим через точку а перпендикуляр к AB, на котором откладываем вниз отрезок aK, равный R. Соединяем центр О с точкой К. Для нахождения центра сопряжения O1 проводим через середину отрезка OK перпендикулярную прямую, которая пересечётся с прямой aK в точке O1

Соединив О1 с О, найдём точку сопряжения С.

Сопряжение дуг окружностей дугой окружности

Сопряжение дуг окружностей может быть внешним (фиг. 72) или внутренним (фиг. 73). В обоих случаях сопряжения выполнимы: 1) если расстояние С между центрами О и 01сопрягаемых дуг больше суммы их радиусов R и R1 (фиг. 72, а и 73, а), т.е. C>R+R1 и 2) когда C<R+R1(фиг. 72, б и 73, б). Сопряжение выполнить невозможно, если один из радиусов сопрягаемых дуг окажется большим или равным сумме величины радиуса второй сопрягаемой дуги и расстояния между центрами сопрягаемых дуг, т. е. если получится соотношение R>=C+R1 или R1>=C+R. Для внешнего сопряжения дуг сопряжение окажется также невозможно, если радиус сопрягающей дуги R2 будет меньше полуразности С — (R+R1), т. е. R2 <

<(C-(R+R1))/2. Во всех случаях решение задачи сводится к нахождению центра 02сопрягающей дуги радиуса R2 и точек сопряжения A и В.

Внешнее сопряжение. Даны: дуги радиусов R и R1 расстояние С между центрами этих дуг и радиус сопряжения R2 (фиг. 72,a). Требуется построить сопряжение при условии, что C>R+R1.

Для построения сопряжения необходимо определить центр 02 и точки сопряжения Л и В. Для нахождения центра 02 проводим из центра О дугу радиуса R2+R, а из центра О1 дугу радиуса R2+R1 Пересечение этих дуг определит центр 02.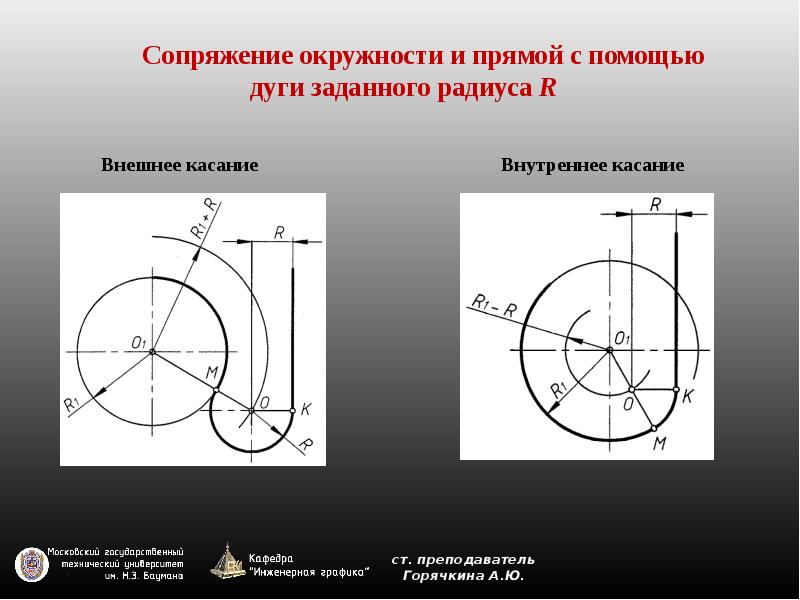 Соединив прямыми центры О и 01 с центром 02, найдём на пересечении этих прямых с соответствующими дугами точки сопряжения A и В. Полученные точки сопрягаем радиусом R2.

Построение сопряжения для случая, когда C<R+R1, дано на фиг. 72, б. Построение этого сопряжения ничем не отличается от предыдущего построения.

Внутреннее сопряжение. Даны: дуги радиусов R и R1 расстояние С между центрами этих дуг и радиус сопряжения R2 (фиг. 73, а). Требуется построить сопряжение, если C>R+R1 Решение этой задачи такое же, как и предыдущей, с той лишь разницей, что из центров О и О1 проводятся дуги радиусами R2 — R и R2 — R1.

На фиг. 73, б приведено построение сопряжения для случая, когда C<R+R1. Это построение ничем не отличается от построения, приведённого в предыдущем примере (фиг. 73,a).

Техническое сопряжение. Урок инженерной графикм

Урок № 23.

Сопряжения

Показать несколько деталей, имеющих скругления.

Рассматривая детали, видим, что в их конструкции часто одна поверхность переходит в другую. Обычно эти переходы делают плавными, что повышает прочность деталей и делает их более удобными в работе.

На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.

Такой плавный переход одной линии (поверхности) в другую линию (поверхность) называют сопряжением.

При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т.е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания .

Задачи на сопряжения условно можно разделить на 3 группы.

Первая группа задач включает в себя задачи на построение сопряжений, где участвуют прямые линии. Это может быть непосредственное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.

Построим окружность, касательную к прямой.

Построение окружности, касательной к прямой , связано с нахождением точки касания и центра окружности.

Задана горизонтальная прямая АВ , требуется построить окружность радиусом R , касательную к данной прямой (рис. 1).

Точка касания выбирается произвольно.

Так как точка касания не задана, то окружность радиуса R может коснуться данной прямой в любой точке. Таких окружностей можно провести множество. Центры этих окружностей (О 1 , О 2 и т.д.) будут находиться на одинаковом расстоянии от заданной прямой, т.е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 1). Назовем эту линию линией центров .

Проведем линию центров параллельно прямой АВ на расстоянии R . Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например, точку О.

Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ . В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.

Запишите в свои тетради в клетку следующие правила:

Если в сопряжении участвует прямая линия, то:

центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;

2) точка касания лежит на перпендикуляре, проведенном из центра окружности к заданной прямой.

Сопряжение двух прямых.

На плоскости две прямые могут располагаться параллельно или под углом друг к другу.

Чтобы построить сопряжение двух прямых, необходимо провести окружность, касательную к этим двум прямым.

Откройте рабочие тетради на странице 31.

Рассмотрим сопряжение двух непараллельных прямых.

Две непараллельные прямые располагаются друг к другу под углом, который может быть прямым, тупым или острым. При выполнении чертежей деталей часто такие углы необходимо скруглить дугой заданного радиуса (рис.1). Скругление углов на чертеже есть не что иное, как сопряжение двух непараллельных прямых дугой окружности заданного радиуса. Для выполнения сопряжения необходимо найти центр дуги сопряжения и точки сопряжения.

Известно, что если в сопряжении участвует прямая линия, то центр дуги сопряжения находится на линии центров, которая проводится параллельно заданной прямой на расстоянии, равном радиусу R дуги сопряжения.

Поскольку угол образован двумя прямыми, то проводят две линии центров параллельно каждой прямой на расстоянии, равном радиусу R дуги сопряжения. Точка их пересечения будет центром дуги сопряжения.

Для нахождения точек сопряжения из точки О опускают перпендикуляры на заданные прямые и получают точки сопряжения К и К 1 . Зная точки и центр сопряжения, из точки О радиусом R проводят дугу сопряжения. При обводке чертежа следует сначала обвести дугу, а затем касательные прямые.
При построении сопряжения прямого угла упрощается проведение линии центров, так как стороны угла взаимно перпендикулярны. От вершины угла откладывают отрезки, равные радиусу R дуги сопряжения, и через полученные точки К и К 1 , которые будут точками касания, проводят две линии центров, параллельные сторонам угла. Они будут являться одновременно и линиями центров, и перпендикулярами, определяющими точки сопряжения К и К 1 (стр. 31, рис.1).

Стр. 31, задание 4. Сопряжение двух параллельных прямых.
Чтобы построить сопряжение двух параллельных прямых, необходимо провести дугу окружности, касательной к этим прямым (рис.3).
Рис.3
Радиус этой окружности будет равен половине расстояния между заданными прямыми. Так как точка касания не задана, подобных окружностей можно провести множество. Центры их будут находиться на прямой, проведенной параллельно заданным прямым на расстоянии, равном половине расстояния между ними. Эта прямая будет линией центров.
Точки касания (К 1 и К 2 ) лежат на перпендикуляре, опущенном из центра касательной окружности на заданные прямые (рис. 3а). Так как центр касательной окружности не задан, перпендикуляр проводится произвольно. Отрезок КК 1 делят пополам (рис.3б), проводят через точки пересечения засечек прямую линию параллельно заданным прямым, на которой будут располагаться центры окружностей, касательных к заданным параллельным прямым, т. е. эта линия будет линией центров. Поставив ножку циркуля в точку О , проводят дугу сопряжения (рис. 3в) от точки К до точки К 1 .
Построение прямых, касательных к окружностям
(Р.Т. стр.33).
Задание 1 . Проведите прямую, касательную к окружности через точку А , лежащую на окружности.
Из точки О проводим прямую OB через точку А . Из точки А любым радиусом проводим окружность. При пересечении с прямой получили точки 1 и 2. Из этих точек любым радиусом проводим дуги до пересечения между собой в точках C и D . Из точки C или D проводим прямую через точку А .
Она и будет касательной к окружности, так как касательная всегда перпендикулярна радиусу, проведенному в точку касания.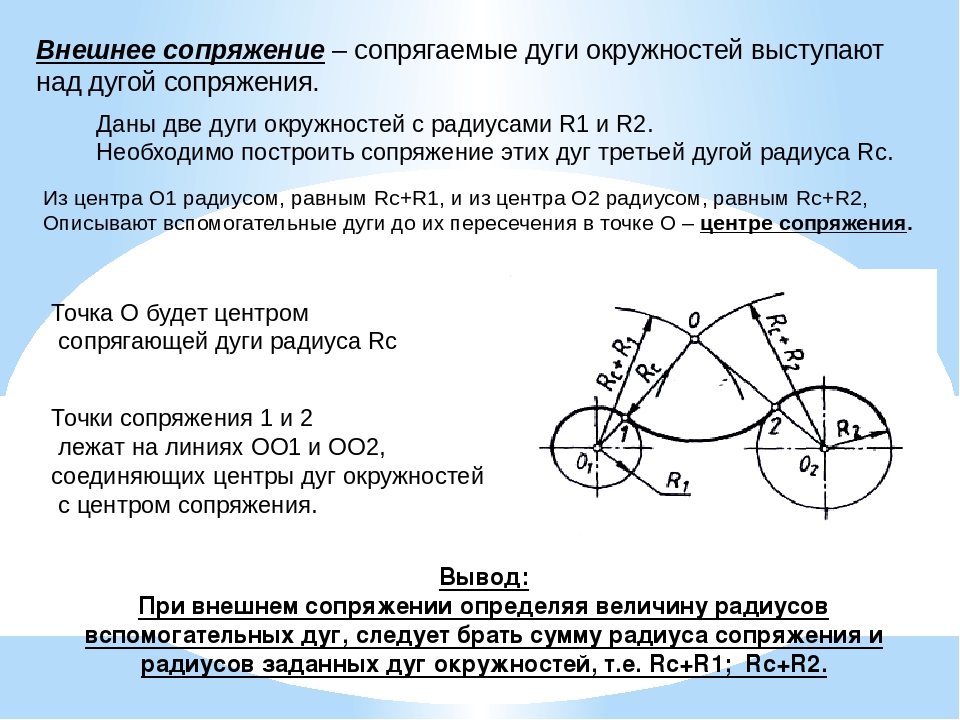
Задание 2 .
Это построение аналогично построению перпендикуляра к прямой через заданную точку, которое можно выполнить с помощью двух угольников.
Сначала угольник 1 кладется так, чтобы его гипотенуза совпадала с точками O и A . Затем к угольнику 1 прикладывается угольник 2 , который будет направляющим, т.е. по которому будет сдвигаться угольник 1 . Потом угольник 1 приставляем другим катетом к угольнику 2. Затем катаем угольник 1 по угольнику 2 до тех пор, пока гипотенуза не совпадет с точкой A . И проводим прямую, касательную к окружности через точку A .
Задание 3 . Проведите прямую, касательную к окружности через точку, не лежащую на этой окружности.
Даны окружность радиусом R и точка А , не лежащая на окружности, требуется провести из точки А прямую, касательную к данной окружности в верхней ее части. Для этого необходимо найти точку касания. Мы знаем, что точка касания лежит на перпендикуляре, проведенном из центра окружности к касательной прямой. Следовательно, касательная и перпендикуляр образуют прямой угол.
Зная, что всякий угол, вписанный в окружность и опирающийся на ее диаметр, является прямым, соединив точки А и О , принимают отрезок АО за диаметр описанной окружности. В пересечении описанной окружности и окружности радиуса R будет находиться вершина прямого угла (точка К ). Отрезок АО делим пополам при помощи циркуля, получаем точку О 1 (рис.4, б).
Из центра О 1 радиусом, равным отрезку АО 1 , проводим окружность, получаем точки К и К 1 в пересечении с окружностью радиуса R (рис.4 ,в).
Так как нужно провести только одну касательную к верхней части окружности, выбирают нужную точку касания. Этой точкой будет точка К . Точку К соединяем с точками А и О , получаем прямой угол, который опирается на диаметр АО описанной окружности радиусом R 1 . Точка К – вершина этого угла (рис.4, г), отрезки ОК и АК – стороны прямого угла, следовательно, точка К будет искомой точкой касания, а прямая АК – искомой касательной.
Рис.4
Проведение прямой, касательной к двум окружностям.
Даны две окружности радиусами R и R 1 , требуется построить касательную к ним. Возможны два случая касания: внешнее и внутреннее.
При внешнем касании касательная прямая находится с одной стороны от окружностей и не пересекает отрезок, соединяющий центры данных окружностей.
При внутреннем касании касательная прямая находится с разных сторон от окружностей и пересекает отрезок, соединяющий центры окружностей.
Стр. 33. Задание 5 . Проведите прямую, касательную к двум окружностям. Касание внешнее.
Прежде всего необходимо найти точки касания. Известно, что они должны лежать на перпендикулярах, проведенных из центров окружностей (О и О 1 ) к касательной.
Из точки О проводим окружность радиусом R — R 1 ,так как касание внешнее.
Разделим расстояние ОО 1 пополам и проведем окружность радиусом R =ОО 2 =О 1 О 2
Эта окружность пересекает окружность с радиусом R — R 1 в точке К. Соединяем эту точку с О 1 .
Из точки О через точку К проводим прямую до пересечения с окружностью радиусом R . Получили точку К 1 – первую точку касания.
Из точки О 1 проводим прямую, параллельную КК 1 , до пересечения с окружностью радиусом R 1 . Получили вторую точку касания К 2 . Соединяем точки К 1 и К 2 . Это и есть касательная к двум окружностям.
Задание 6 . Проведите прямую, касательную к двум окружностям. Касание внутреннее.
Построение аналогичное, только при внутреннем касании радиус вспомогательной окружности, проводящейся из точки О равен сумме радиусов окружностей R + R 1 .
Вторая группа задач на сопряжения включает в себя задачи, в которых участвуют только окружности и дуги. Плавный переход одной окружности в другую может происходить или непосредственно касанием, или через третий элемент – дугу окружности.
Касание двух окружностей может быть внешним (РТ: стр.32, рис.3) или внутренним (РТ: стр.32, рис.4).
Задание 3 (стр. 32)
При внешнем касании двух окружностей расстояние между центрами этих окружностей будет равно сумме их радиусов.
Из точки О радиусом R + R C проведем дугу. Из точки О 1 радиусом R 1 + R C О С — центр сопряжения.
Соединяем точки О и О 1 с центром сопряжения О С . На окружностях получили точки касания (сопряжения).
Из точки О С радиусом сопряжения R C 30 соединяем точки касания.
Задание 4 (стр. 32)
При внутреннем касании двух окружностей одна из касательных окружностей находится внутри другой окружности, и расстояние между центрами этих окружностей будет равно разности их радиусов.
Из точки О радиусом (R C – R ) проведем дугу. Из точки О 1 радиусом (R C – R 1 ) проведем дугу до пересечения с первой дугой. Получили точку О С — центр сопряжения.
Центр сопряжения О С соединяем с точками О и О 1 с и продлеваем прямую дальше.
На окружностях получили точки касания (сопряжения).
Из точки О С радиусом сопряжения R C 60 соединяем точки касания.
Третья группа задач на сопряжения включает в себя задачи на сопряжения прямой и дуги окружности дугой заданного радиуса.
Выполняя такое задание, решают как бы две задачи: проведение касательной дуги к прямой и касательной дуги к окружности. Касание в этом случае может быть как внешним, так и внутренним.
РТ: стр. 32. Задание 1. Сопряжение окружности и прямой. Касание внешнее. R C 20 .
Заданы прямая и окружность радиусом R , требуется построить сопряжение дугой радиуса R C 20 .
Так как в сопряжении участвует прямая линия, то центр дуги сопряжения находится на прямой, проведенной параллельно заданной прямой на расстоянии, равном радиусу сопряжения R C 20 . Поэтому параллельно заданной прямой на расстоянии 20 мм проводим еще одну прямую.
А центр дуги сопряжения при внешнем касании двух окружностей находится на окружности радиуса, равного сумме радиусов R и R C .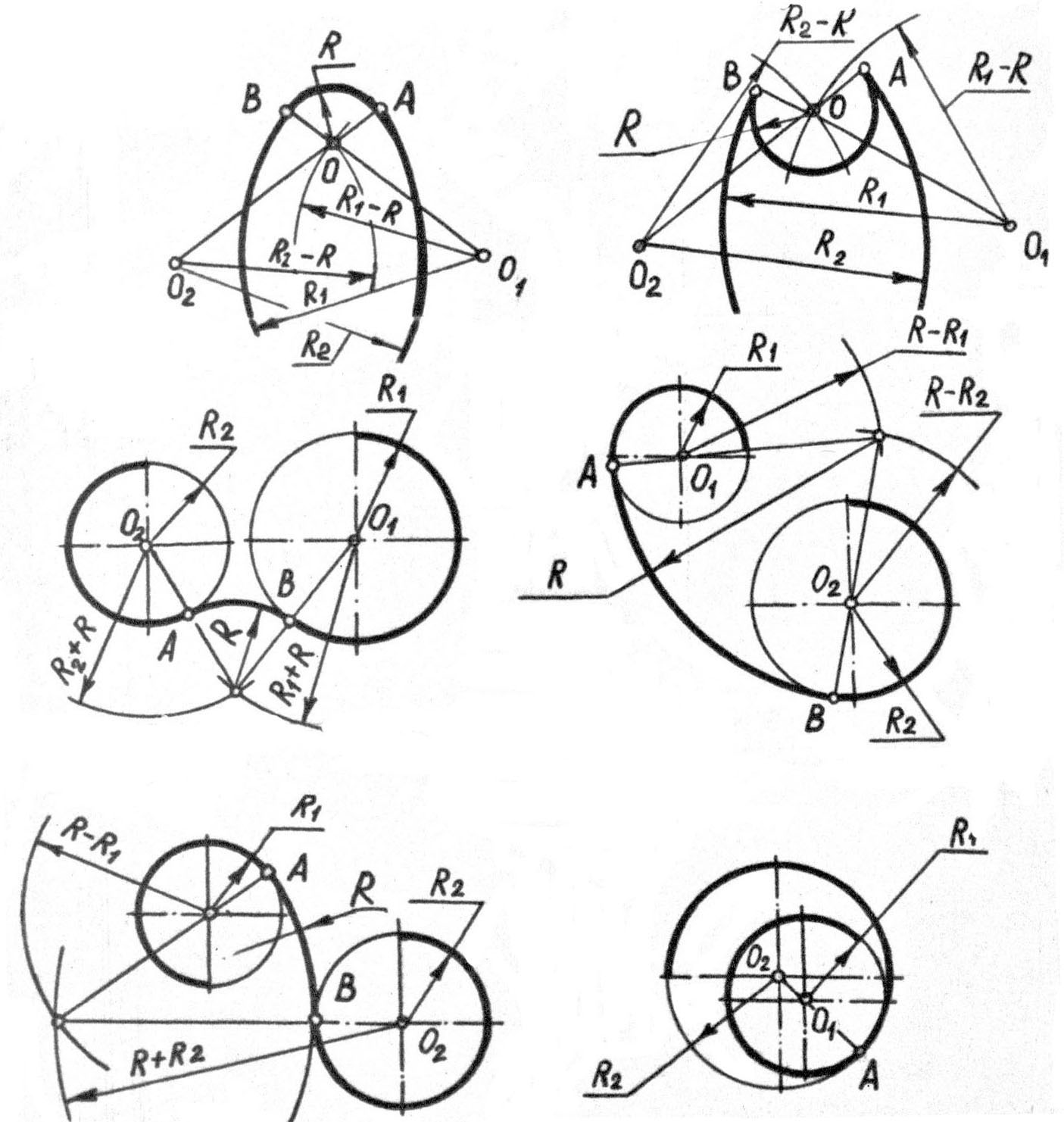 Поэтому из точки О радиусом (R + R C О С
Затем находим точки касания. Первая точка касания — это перпендикуляр, опущенный из центра сопряжения на заданную прямую. Вторую точку сопряжения находим, соединив центр сопряжения О С и центр окружности R . Точка касания будет лежат на первом пересечении с окружностью, так как касание внешнее.
Затем из точки О С радиусом R C 20 соединяем точки сопряжения.
РТ: стр. 32. Задание 2. Сопряжение окружности и прямой. Касание внутреннее. R C 60 .
Параллельно заданной прямой проводим линию центров на расстоянии 60 мм. Из точки О радиусом (R с — R ) проводим дугу до пересечения с новой прямой (линией центров).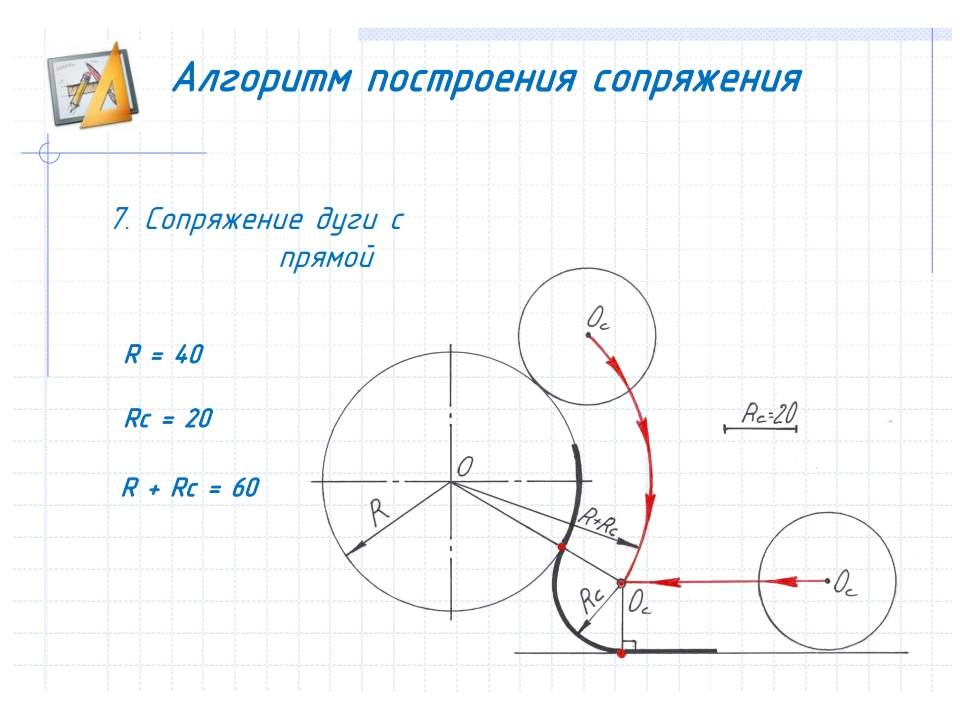 Получим точку О С , которая является центром сопряжения.
Из О С проводим прямую через центр окружности точку О и перпендикуляр на заданную прямую. Получаем две точки касания. И затем из центра сопряжения радиусом 60 мм соединяем точки касания.
Сопряжение.
Сопряжение- плавный переход одной линии в другую.
Сопряжение пересекающихся прямых дугой окружности заданного радиуса.
Задача сводится к проведению окружности, касающейся обеих заданных прямых линий.
Вариант 1.
Проводим вспомогательные прямые параллельно заданным на расстоянии R от заданных.
Точка пересечения этих прямых будет центромО дуги сопряжения. Перпендикуляры, опущенные из центра О на
заданные прямые, определят точки касания К и К 1 .
Вариант 2.
Построение такое же.
Сопряжения. Построение сопряжения линий.
Вариант 3.
Если требуется провести окружность, чтобы она касалась трех пересекающихся прямых линий, то в этом случае
Радиус не может быть задан условиями задачи. Центр О окружности находится на пересечении биссектрис углов
В и С . Радиусом окружности является перпендикуляр, опущенный из центра О на любую из 3-х заданных прямых
Линий.
Сопряжения. Построение сопряжений линий.
Построение внешнего сопряжения данной окружности с данной прямойдугой заданного радиуса R 1 .
Из центра О данной окружности проводим дугу вспомогательной окружности радиусом R+R 1 .
Проводим прямую параллельно заданной на расстоянии R 1 .
Пересечение прямой и вспомогательной дуги даст точку центра дуги сопряжения О 1 .
Точка касания дуг К лежит на линии ОО 1 .
Точка касания дуги и линии К 1 лежит на пересечении перпендикуляра из точки О 1 на прямую с дугой.
Сопряжения. Построение внешнего сопряжения окружности с прямой.
Построение внутреннего сопряжения данной окружности с данной прямой дугой заданного радиуса R 1 .
Из центра О данной окружности проводим вспомогательную окружность радиусом R- R 1 .

Сопряжения. Построение внутреннего сопряжения окружности с прямой.
Построение сопряжения двух данных окружностей дугой заданного радиуса R 3 .
Внешнее касание.
Из центра окружности О 1 R 1 +R 3 .
Из центра окружности О 2 описываем дугу вспомогательной окружности радиусом R 2 +R 3 .
Пересечение дуг вспомогательных окружностей даст точку О 3 , которая является центром дуги сопряжения
Точки касания К 1 и К 2 находятся на линиях О 1 О 3 и О 2 О 3 .

Внутреннее касание
Из центра окружности О 1 описываем дугу вспомогательной окружности радиусом R 3 -R 1 .
Из центра окружности О 2 описываем дугу вспомогательной окружности радиусом R 3 — R 2 .
Пересечение
(окружности с радиусом R 3) .

Сопряжения. Сопряжение двух окружностей дугой.
Внешнее и внутреннее касание .
Заданы две окружности с центрами О 1 и О 2 с радиусами r 1 и r 2 . Необходимо провести окружность заданного
Радиуса R так, чтобы обеспечить с одной окружностью внутреннее касание, а с другой — внешнее.
Из центра окружности О 1 описываем дугу вспомогательной окружности радиусом R-r 1 .
Изцентра окружности О 2 описываем дугу вспомогательной окружности радиусом R+r 2 .
Пересечение дуг вспомогательных окружностей даст точку, которая является центром дуги сопряжения
(окружности с радиусом R) .

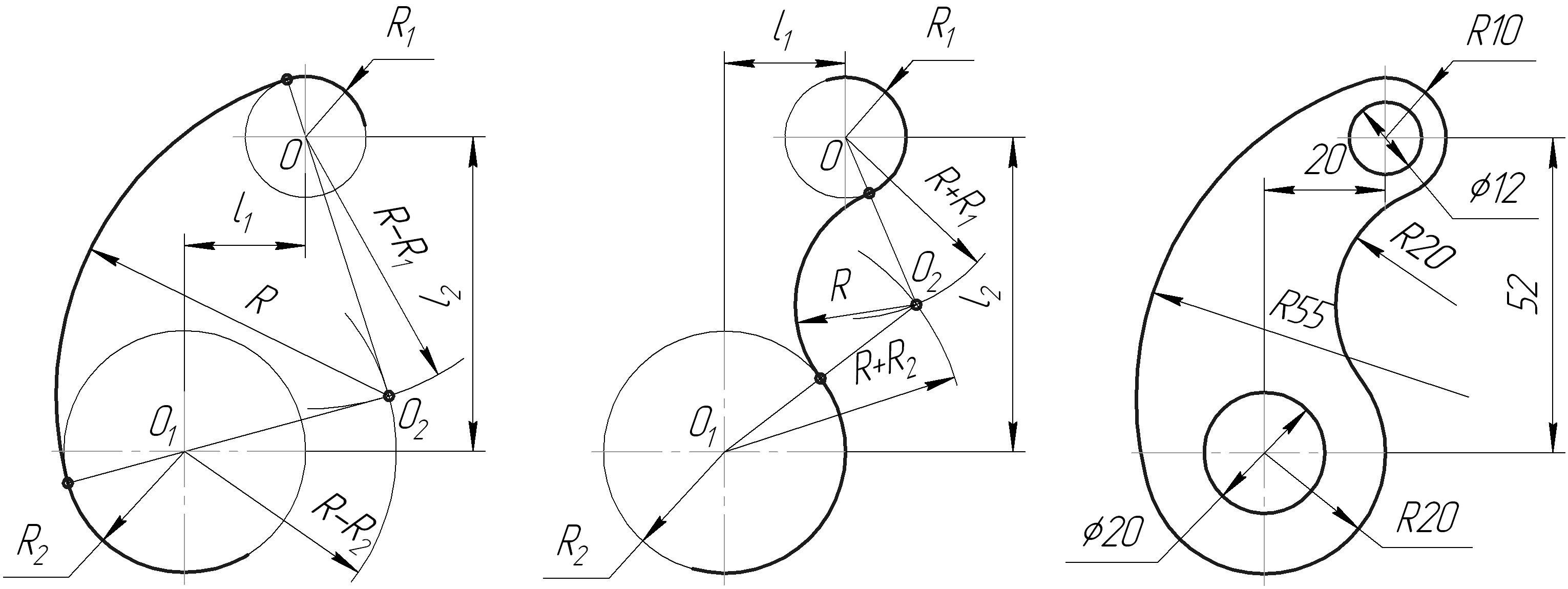
Сопряжения. Сопряжение двух окружностей дугой.
Построение окружности, проходящей через заданную точку А и касающейся данной окружности
в заданной точке В.
Находим середину прямой линии АВ . Через середину линии АВ поводим перпендикуляр. Пересечение продолжения
Линии ОВ и перпендикуляра дает точку О 1 . О 1 — центр искомой окружности с радиусом R = O 1 B = O 1 A.
Сопряжения. Внутреннее касание окружности и дуги .
Построение сопряжения окружности с прямой линией в заданной на прямой точке А.
Из заданной точки А линии LM восстанавливаем перпендикуляр к прямой линии LM . На продолжении
Перпендикуляра откладываем отрезок АВ . АВ = R. Соединяем точку В с центром окружности О 1 прямой.
Из точки А проводим прямую линию параллельно ВО 1 до пересечения с окружностью. Получим точку К — точку
Касания. Соединим точку К с центром окружности О 1 . Продлим линии О 1 К и АВ до пересечения. Получим точку
О 2 , которая является центром дуги сопряжения с радиусом О 2 А = О 2 К.

Сопряжения. Сопряжение окружности с прямой в заданной точке.
Построение сопряжения окружности с прямой линией в заданной на окружности точке А.
Внешнее касание .
Проводим касательную к окружности через точку А. Пересечение касательной с прямой линией LM даст точку В.
Делим угол пополам
О 1 . О 1 О 1 А = О 1 К.

Внутреннее касание.
Проводим касательную к окружности через точку А. Пересечение касательной с прямой LM даст точку В.
Делим угол , образованный касательной и прямой линией LM , пополам . Пересечение биссектрисы угла и
Продолжения радиуса ОА даст точку О 1 . О 1 — О 1 А = О 1 К.

Сопряжения. Сопряжение окружности с прямой в заданной точке на окружности.
Построение сопряжения двух неконцентрических дуг окружностей дугой заданного радиуса.
Проводим из центра дуги О 1 вспомогательную дугу радиусом R 1 -R 3 . Проводим из центра дуги О 2 вспомогательную
Дугу радиусом R 2 +R 3 . Пересечение дуг даст точку О. О — центр дуги сопряжения с радиусом R 3 . Точки касания
К 1 и К 2 лежат на линиях ОО 1 и ОО 2 .

Сопряжения. Сопряжение 2-х неконцентрических дуг окружностей дугой.
Построение лекальной кривой подбором дуг.
Подбирая центры дуг, совпадающих с участками кривой, можно циркулем вычертить любую лекальную кривую.
Для того чтобы дуги плавно переходили одна в другую, необходимо, чтобы точки их сопряжения (касания)
Находились на прямых линиях, соединяющих центры этих дуг.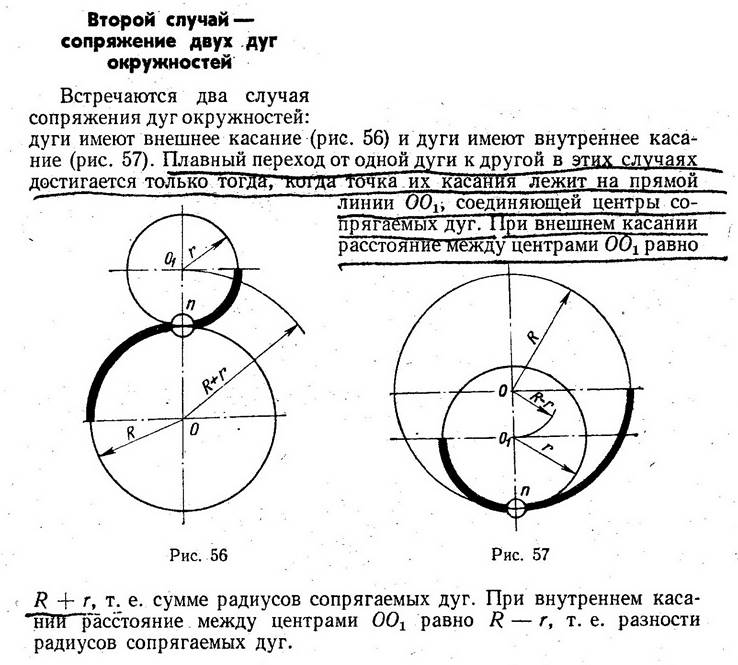
Последовательность построений.
Подбираем центр 1 дугипроизвольного участка ab.
На продолжении первого радиуса подбираем центр 2 радиуса дуги участка bc.
На продолжении второго радиуса подбираем центр 3 радиуса дуги участка cd и т. д.
Так строим всю кривую.
Сопряжения. Подбор дуг.
Построение сопряжения двух параллельных прямых двумя дугами.
Заданные на прямых параллельных линиях точки А и В соединяем линией АВ.
Выбираем на прямой АВ произвольную точку М .
Делим отрезки АМ и ВМ пополам .
Восстанавливаем в серединах отрезков перпендикуляры.
В точках А и В, заданных прямых, восстанавливаем перпендикуляры к прямым.
Пересечение соответствующих перпендикуляров даст точки О 1 и О 2 .
О 1 центр дуги сопряжения с радиусом О 1 А = О 1 М.
О 2 центр дуги сопряжения с радиусом О 2 В = О 2 М.
Если точку М выбрать на середине линии АВ , то радиусы дуг сопряжения будут равны.
Касание дуг в точке М , находящейся на линии О 1 О 2 .
Сопряжения. Сопряжение параллельных прямых двумя дугами.
Сопряжением называется плавный переход по кривой от одной линии к другой. Сопряжения бывают циркульные и лекальные. Построение их основано на свойствах касательных к кривым линиям. Сопряжение отрезков прямых с циркульными кривыми будет возможно, если точка сопряжения является одновременно и точкой касания прямой к дуге кривой. Следовательно, радиус сопряжения должен быть перпендикулярным к прямой в точке касания.
Сопряжение циркульных кривых возможно тогда, когда точка сопряжения будет являться одновременно и точкой касания сопрягаемых дуг. Следовательно, точка касания должна находиться на линии центров дуг окружностей.
Сопряжение пересекающихся прямых:
Пример 1 . Даны пересекающиеся прямые AB и ВС и радиус сопряжения R; требуется выполнить сопряжение прямых (фиг. 66, а, б, в).
Сопряжение будет возможным, если прямые AB и ВС будут касательными к окружности радиуса R. Для нахождения центра этой окружности
необходимо провести на расстоянии R параллельно заданным прямым вспомогательные прямые до их взаимного пересечения в точке 0. Из точки О, как из центра, проводится дуга радиуса R. Точками сопряжения будут точки M и Н, определяемые пересечением прямых AB и ВС с опущенными на них перпендикулярами из точки О.
Пример 2 . Даны пересекающиеся прямые AB и ВС и радиусы сопряжения R и R1 Построение сопряжения возможно, если угол а
Способ построения такого сопряжения приведён на фиг. 66,г.
Сопряжение параллельных прямых
Пример 1. Даны две параллельные прямые AB и СЕ и точки сопряжения В и С (фиг. 67).
Надо построить плавное сопряжение циркульными кривыми так, чтобы оно проходило через заданную точку K, посредине отрезка ВС.
Для определения радиусов и центров дуг сопряжения делим отрезки BK и КС прямыми так, чтобы они были перпендикулярны этим отрезкам и делили их пополам. Так как радиус сопряжения должен быть перпендикулярным к прямой в точке сопряжения, то для нахождения центров О дуг сопряжения восстанавливаем из точек В и С перпендикуляры до пересечения их с ранее проведёнными перпендикулярами к прямой ВС.
Точки пересечения этих перпендикуляров определят положение центров сопряжений О-О, а равные между собой отрезки 05 и ОС дадут величины радиусов сопряжений.
Пример 2 (фиг. 68), Этот пример отличается от предыдущего
тем, что точка К взята на прямой ВС произвольно, на некотором расстоянии e от прямой СЕ; следовательно, радиусы сопряжений R и R1- разные по величине. Ход построения сопряжений такой же, как и в предыдущем примере.
П p и м e p 3 . Даны: расстояние между двумя параллельными прямыми AB и СЕ, равное сумме сопрягаемых радиусов R и R1, и точка сопряжения В (фиг.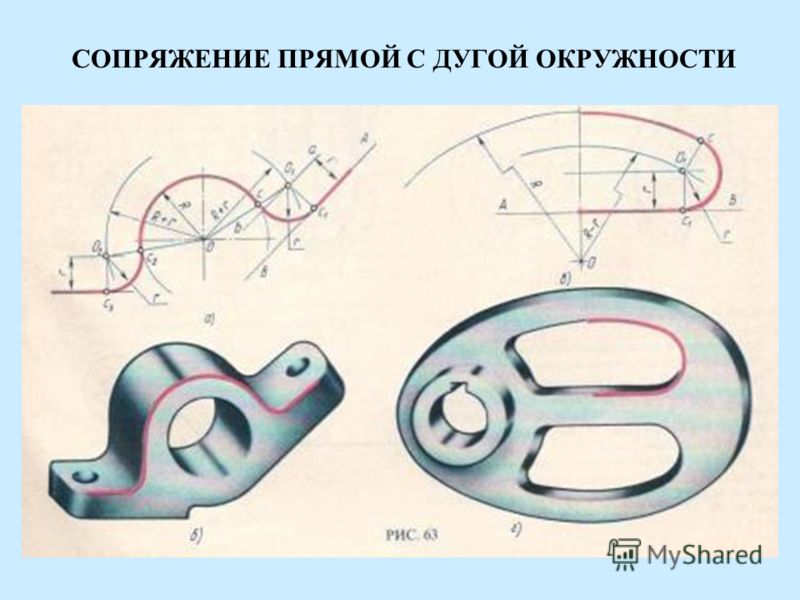 69).
Для построения сопряжения проводим параллельно AB на расстоянии R вспомогательную прямую 0-01. Центр сопряжения 0 для радиуса R будет находиться на пересечении перпендикуляра, проведённого из точки В к вспомогательной прямой. Описывая из точки О дугу радиусом R, найдём точку К, из которой радиусом R1 делаем на вспомогательной прямой засечку, определяющую центр сопряжения O1. Из точки О1 опускаем перпендикуляр на прямую СЕ и, найдя точку сопряжения С, сопрягаем точки К и С дугой радиуса R1.
Сопряжение дуги окружности с прямой
Пример 1. Построим сопряжение дуги радиуса R с прямой AB радиусом R1 (фиг. 70). Для этого необходимо найти центр сопряжения 0 и точки сопряжения С и а. Точка С является одновременно точкой их касания и должна лежать на линии центров этих дуг. Радиус сопряжения должен быть перпендикулярен к прямой AB в точке касания а. Поэтому из центра О описываем радиусом, равным сумме R+R1, дугу.
На ней будет находиться центр сопряжения 0, для определения которого проводим параллельно AB на расстоянии R1 вспомогательную прямую ее до пересечения с проведённой дугой. Соединив точки O1 и О, найдём точку сопряжения С. Для определения точки а опускаем из О1 перпендикуляр на AB. Далее, радиусом R1 из центра O1 сопрягаем точки а и С.
Пример 2. Даны: дуга радиуса R, прямая AB и точка сопряжения а. Требуется найти точку сопряжения С и радиус сопряжения R1 (фиг. 71). Проводим через точку а перпендикуляр к AB, на котором откладываем вниз отрезок aK, равный R. Соединяем центр О с точкой К. Для нахождения центра сопряжения O1 проводим через середину отрезка OK перпендикулярную прямую, которая пересечётся с прямой aK в точке O1 Соединив О1 с О, найдём точку сопряжения С.
Сопряжение дуг окружностей дугой окружности
Сопряжение дуг окружностей может быть внешним (фиг. 72) или внутренним (фиг. 73). В обоих случаях сопряжения выполнимы: 1) если расстояние С между центрами О и 01 сопрягаемых дуг больше суммы их радиусов R и R1 (фиг. 72, а и 73, а), т.е. C>R+R1 и 2) когда C=C+R1 или R1>=C+R. Для внешнего сопряжения дуг сопряжение окажется также невозможно, если радиус сопрягающей дуги R2 будет меньше полуразности С — (R+R1), т.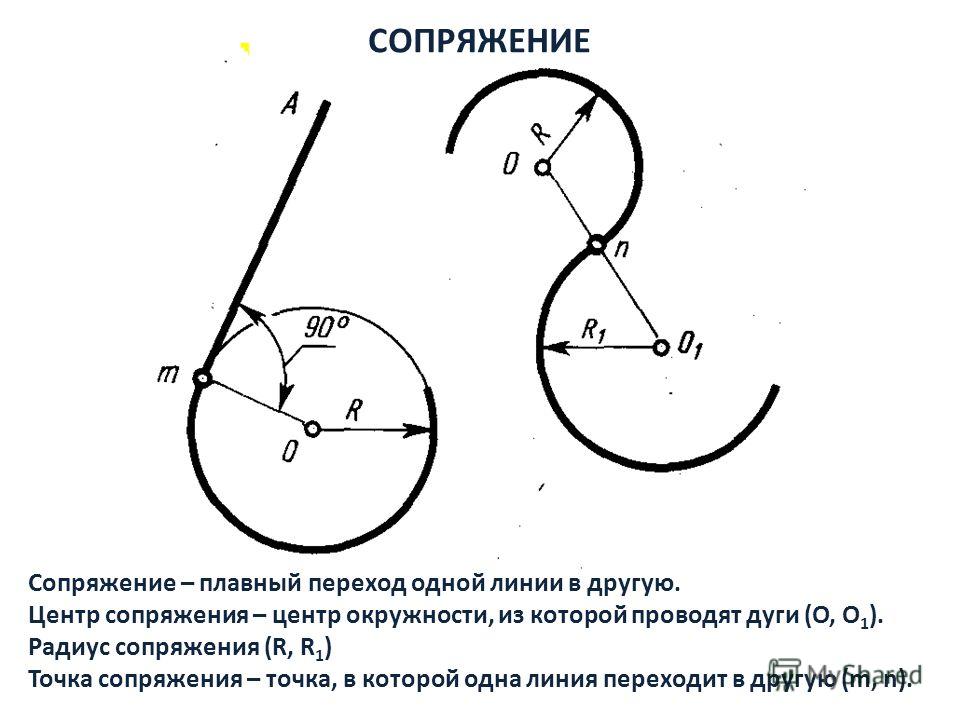 е. R2
Внешнее сопряжение. Даны: дуги радиусов R и R1 расстояние С между центрами этих дуг и радиус сопряжения R2 (фиг. 72,a). Требуется построить сопряжение при условии, что C>R+R1.
Для построения сопряжения необходимо определить центр 02 и точки сопряжения Л и В. Для нахождения центра 02 проводим из центра О дугу радиуса R2+R, а из центра О1 дугу радиуса R2+R1 Пересечение этих дуг определит центр 02. Соединив прямыми центры О и 01 с центром 02, найдём на пересечении этих прямых с соответствующими дугами точки сопряжения A и В. Полученные точки сопрягаем радиусом R2.
Построение сопряжения для случая, когда C
Внутреннее сопряжение. Даны: дуги радиусов R и R1 расстояние С между центрами этих дуг и радиус сопряжения R2 (фиг. 73, а). Требуется построить сопряжение, если C>R+R1 Решение этой задачи такое же, как и предыдущей, с той лишь разницей, что из центров О и О1 проводятся дуги радиусами R2 — R и R2 — R1.
На фиг. 73, б приведено построение сопряжения для случая, когда C
Центр дуги сопряжения должен быть равноудален (находится на одинаковом расстоянии) от каждой из двух сопрягаемых (данных) прямых.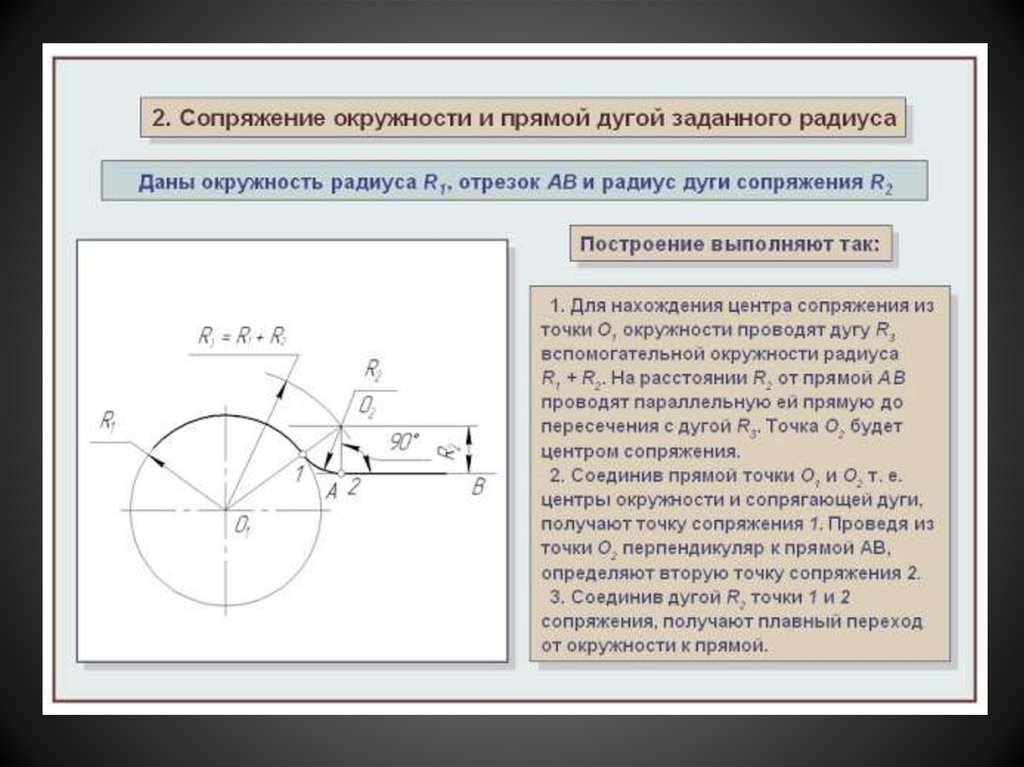 Любая из точек сопряжения (точки входа) представляет собой пересечение перпендикуляра, опущенного из центра сопряжения на соответствующую прямую.
Алгоритм построения сопряжения двух прямых дугой заданного радиуса (рис. 13.39, а, б) следующий:
1. На расстоянии (R ), равном радиусу дуги сопряжения, проводятся две прямые, параллельные сопрягаемым прямым.
2. Определяют их точку пересечения, являющуюся центром сопряжения (О ).
3. Из точки (О ) проводят перпендикуляры к заданным прямым и находят точки сопряжения (А ) и (В ).
4. Из точки (А ) к точке (В ) строят дугу сопряжения заданного радиуса (R ).
Рисунок 13.49
Типичными примерами сопряжений являются контуры деталей, изображенных на рис. 13.40.
В AutoCAD сопряжение двух отрезков прямых (рис. ХХ а) выполняется командой «Сопрячь» (Скругление, Шпонка, Fillet) из меню «Модификация». После выбора команды следует параметром «Radius» задать радиус сопряжения (например, 10 мм), затем последовательно указателем мышки отметить оба отрезка (см. рис. ХХ б).
Current settings: Mode = TRIM, Radius = 5.0000
radius
Specify fillet radius : 10
Select first object or :
Select second object:
Полученный элемент состоит из двух исходных отрезков и дуги сопряжения R=10мм (см. рис. ХХ в).
Рис. ХХ а) Рис. ХХ б) Рис. ХХ в)
1.2. Сопряжение дуги окружности радиуса R и прямой а с дугой заданного радиуса R1
Для выполнения этого сопряжения (рис. 3.31) сначала определяют множество центров дуг радиуса R 1 . Для этого на расстоянии R 1 от прямой а проводят параллельную ей прямую m , а из центра О радиусом (R + R 1 ) – дуги концентрической окружности. Точка О 1 будет центром дуги сопряжения. Точка сопряжения С получена на перпендикуляре, опущенном из точки О 1 на прямую а , а точка В – на прямой, соединяющей точки О и О 1 .
Рисунок 3.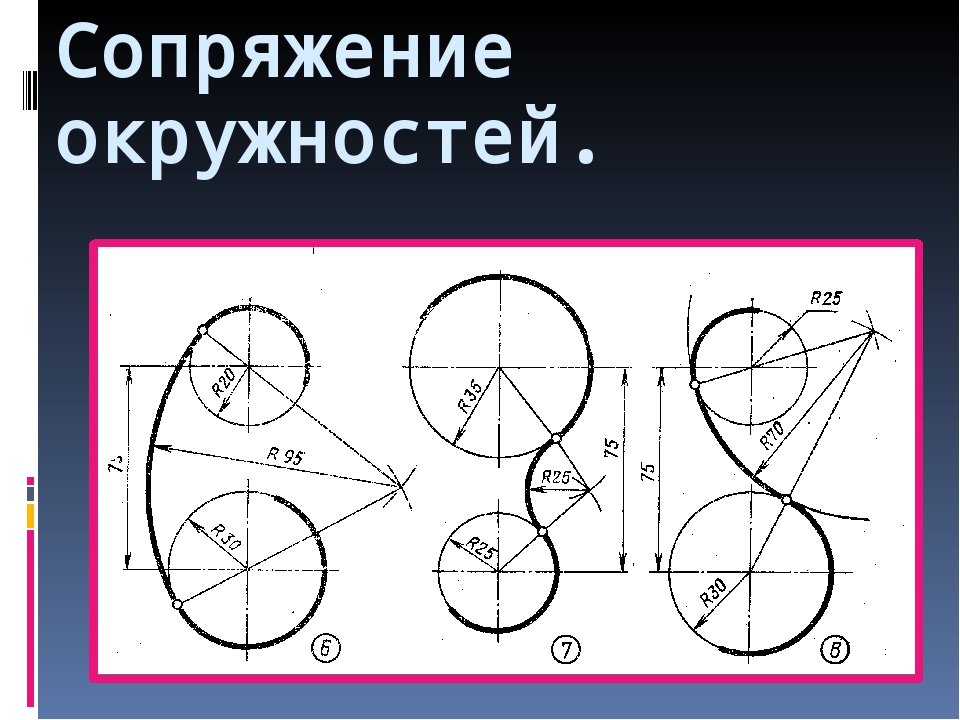 31
На рис. 3.32 представлен пример изображения контура подшипника, в построении которого использован рассмотренный вид сопряжений.
Рисунок 3.32
Сопряжение прямой и окружности в AutoCAD имеет смысл при построении к окружности отрезка прямой, являющейся касательной к этой окружности. Для этого при построении отрезка начальную точку отрезка задают по координатам или объектной привязкой, конечную точку задают привязкой «Касательная» (Прыжок в тангенс) относительно окружности (работа с привязкой описана в приложении ХХХХХХХХХХХ).
1.3. Сопряжение дуг двух окружностей с радиусами R1 и R2 , дугой сопряжения радиуса R
Различают внешнее (рис. 13.42,а), внутреннее (рис. 13.42, б) и смешанное (рис. 13.42, в) сопряжения. В первом случае центр сопряжения является точкой пересечения дуги окружностей радиусов R 1 +R и R 2 +R, во втором — на пересечении окружностей радиусов R-R 1 и R-R 2 , в третьем — на пересечении дуг окружностей радиусов R+R 1 и R-R 2 . Точки сопряжения А 1 и А 2 лежат на прямых, соединяющих центр сопряжения с центром соответствующей окружности.
Рассмотрим случай внешнего сопряжения двух окружностей в AutoCAD. На рис. ХХ.а показаны две опорные окружности с радиусами R 1 и R 2 , центры которых лежат на концах пунктирной линии. Из центра окружности R 1 строят вспомогательную окружность с радиусом R 1 +R, а из центра окружности R 2 – окружность R 2 +R как это показано на рис. ХХ.б (вспомогательные окружности показаны штриховой линией). Затем из точки пересечения вспомогательных окружностей строят окружность с радиусом R (на рис. ХХ в показана штрих-пунктирной линией). Окончательные построения выполняют с помощью команды «Обрезать» из меню «Модификация». В качестве секущих объектов выбирают опорные окружности и обрезают верхнюю часть окружности R, затем удаляют вспомогательные окружности (результат построения показан на рис. ХХ.г).
Рисунок ХХ.а Рисунок ХХ.б
Рисунок ХХ.в Рисунок ХХ.г
Теперь рассмотрим случай внутреннего сопряжения двух окружностей в AutoCAD. Аналогично предыдущему случаю строят опорные окружности с радиусами R 1 и R 2 . Из центра окружности R 1 строят вспомогательную окружность с радиусом R–R 1 , а из центра окружности R 2 – окружность R–R 2 . Затем из точки пересечения вспомогательных окружностей строят окружность с радиусом R (см. рис. ХХХ.а). Лишние элементы удаляют аналогично предыдущему случаю (результат показан на рис. ХХХ.б).
Пусть требуется построить чертеж прокладки (рис. 1, а). Как видно из чертежа, контур прокладки образуется в результате построения сопряжения окружностей, имеющих радиус 20 мм, дугой окружности R112. Изобразив в стороне этот случай сопряжения (рис. 1, б), замечают, что центр дуги сопряжения О должен находиться от центров малых окружностей на расстояниях, равных сумме радиусов окружностей: 20 + 112 = 132 мм. Для построения центра О из центров малых окружностей дугой радиуса 132 мм делают засечки. Соединив точку О с центрами малых дуг, получают точки сопряжения Л и В, между которыми и проводят дугу R 112. В рассматриваемом примере имеет место внешнее касание дуг, при котором центры находятся по разные стороны от точек сопряжения.
Сопряжение прямых; линий с окружностями часто встречается в таких деталях, как гаечные ключи, шатуны, различные рычаги. Пусть требуется начертить контур головки шатуна (рис. 2, а). В чертеже имеет место сопряжение окружности R 20 с прямой, идущей параллельно оси шатуна на расстоянии 11 мм от нее, дугой радиуса R 15. Центре (рис. 2, б) должен находиться от окружности на расстоянии 15 мм, а от центра окружности на pacстоянии 20 + 15 = 35 мм; в то же самое время он должен находиться на расстоянии 11 + 15 = 26 мм от оси шатуна. Для нахождения центра О проводят дугу радиусом 35 мм и прямую, -параллельную оси шатуна на расстоянии 26 мм от этой оси. Точка пересечения дуги и прямой определит искомый центр.
TBegin—>TEnd—>
Рис. 1. Сопряжение окружностей
TBegin—>
TEnd—>
Рис. 2. Сопряжение прямой с окружностью
TBegin—>
TEnd—>
Рис. 3. Практический пример сопряжения
Соединяют центр дуги сопряжения О с центром окружности, находят первую точку сопряжения Л; опускают перпендикуляр из точки С на прямую, находят вторую точку сопряжения Б. Между точками сопряжения А и В проводят дугу сопряжения R 15.
Пусть требуется начертить рычаг криволинейной формы (рис. 3, а). Предполагают, что задача решена: центр дуги R 105 найден (рис. 3, б). Определяют, чему будет равно расстояние от центра дуги сопряжения О до центра окружности 0 40. Очевидно, что оно будет равно разности радиусов 105—20 = 85 мм. Таким же путем находят расстояние от центра дуги сопряжения О до центра окружности 0 60 (105 — 30 = 75 мм). Пользуясь найденными величинами, из центров окружностей делают засечки, пересечение которых определит точку О. Соединяя найденный центр О с центрами окружностей 0 40 и 0 60, на продолжении линий находят точки сопряжения А и В. В примере имеет место внутреннее касание дуг, при котором центры находятся по одну сторону от точек касания.
Центр Ох для проведения дуги R 58 предлагается найти самостоятельно. Подобный случай сопряжения уже рассматривался на рис. 1. Точки сопряжения находят по общему правилу, известному из геометрии: центры касающихся дуг и точки их касания (сопряжения) всегда лежат на одной прямой.
Ресурс аренда недвижимости в Латвии — дома, квартиры, виллы, также юридические аспекты, услуги строительства, реклама недвижимости, путешествие, инвестиции.
Главная » Расчет крыши » Техническое сопряжение. Урок инженерной графикм
Построение сопряжений. — Студопедия
Сопряжением называется плавный переход от одной линии к другой. Плавный переход может быть выполнен как с помощью циркульных линий
(дуг окружностей), так и с помощью лекальных кривых (дуг эллипса, параболы или гиперболы). Мы будем рассматривать только случаи сопряжений с помощью дуг окружностей. Из всего многообразия сопряжений различных линий можно выделить такие основные виды сопряжений: сопряжение двух различно расположенных прямых линий с помощью дуги окружности, сопряжение прямой линии с дугой окружности, построение общей касательной к двум окружностям, сопряжение двух окружностей третьей. Любой вид сопряжений следует выполнять в такой последовательности:
– находят центр дуги сопряжения,
– находят точки сопряжения,
– заданным радиусом проводят дугу сопряжения.

Различные виды сопряжений приведены в таблице 2:
Таблица 2

Графическое построение сопряжений Краткое объяснение к построению

Сопряжение пересекающихся прямых дугой заданного радиуса
Провести прямые, параллельные сторонам угла на расстоянии R. Из точки О, взаимного пересечения этих прямых, опустив перпендикуляры на стороны угла, получим точки сопряжения 1 и 2. Радиусом R провести дугу сопряжения между точками 1 и 2.
Сопряжение окружности и прямой с помощью дуги заданного радиуса
На расстоянии R провести прямую, параллельную заданной прямой, а из центра О₁ радиусом R+R₁– дугу окружности. Точка О – центр дуги сопряжения. Точку 2 получим на перпендикуляре, опущенном из точки О на заданную прямую, а точку 1- на пересечении прямой ОО₁ и окружности радиуса R.

Продолжение таблицы 2

Сопряжение дуг двух окружностей прямой линией
Из точки О провести вспомогательную окружность радиусом R-R₁. Отрезок ОО₁ разделить пополам и из точки О₂ провести окружность радиусом 0,5 ОО₁.Эта окружность пересекает вспомогательную в точке К₀. Соединив точку К₀ с точкой О₁ получим направление общей касательной. Точки касания К и К₁находим на пересечении перпендикуляров из точек О и О₁ с заданными окружностями.
Сопряжение дуг двух окружностей дугой заданного радиуса (внешнее сопряжение)
Из центров О₁ и О₂ провести дуги радиусов R+R₁ и R+R_2.При пересечении этих дуг получаем точку О – центр дуги сопряжения. Соединить точки О₁ и О₂с точкой О. Точки К и К₁ являются точками сопряжения. Между точками К и К₁ провести дугу сопряжения радиусом R.

Продолжение таблицы 2

Сопряжение дуг двух окружностей дугой заданного радиуса (внутреннее сопряжение)
Из центров О₁ и О₂ провести дуги радиусов R-R₁ и R-R₂. При пересечении этих дуг получаем точку О – центр дуги сопряжения. Соединить точки О₁ и О₂с точкой О до пересечения с заданными окружностями. Точки К и К₁ – точки сопряжения. Между точками К и К₁ радиусом R проводим дугу сопряжения.
Сопряжение дуг двух окружностей дугой заданного радиуса (смешанное сопряжение)
Из центров О₁ и О₂ провести дуги радиусов R-R₁ и R+R₂ . При пересечении этих дуг получаем точку О – центр дуги сопряжения. Соединяем точки О₁ и О₂ с точкой О до пересечения с заданными окружностями. Точки 1 и 2 – точки сопряжения. Между точками 1 и 2 радиусом R проводим дугу сопряжения.

ЛАБОРАТОРНОЕ ЗАНЯТИЕ 2. Сопряжение линий
ЛАБОРАТОРНОЕ ЗАНЯТИЕ 2. Шрифты чертежные
Учебные вопросы: 1. Общие сведения о шрифтах 2. Начертание символов Теоретический материал 1. Общие сведения о шрифтах ЛАБОРАТОРНОЕ ЗАНЯТИЕ 2. Шрифты чертежные Все надписи на чертежах должны быть выполнены
Подробнее Основы геометрических построений
ИКГ 1 курс Основы геометрических построений 1. Геометрические построения 2. Деление отрезков 3. Построение перпендикуляра к линии 4. Построение и деление углов на равные части 5. Определение центра дуги
Подробнее Начертательная геометрия Плоскости
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра начертательной геометрии и графики Начертательная геометрия Плоскости Методические указания и задания для
Подробнее ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Тульский государственный университет Кафедра «Дизайн» И.В. УШАКОВА М.В.МИРОНОВА ГЕОМЕТРИЧЕСКИЕ
Подробнее 1. ГЕОМЕТРИЧЕСКОЕ ЧЕРЧЕНИЕ
IV. Методические рекомендации по самостоятельной работе студентов по дисциплине «Начертательная геометрия» 1. ГЕОМЕТРИЧЕСКОЕ ЧЕРЧЕНИЕ 1.1. Целевое назначение Целью задания является: — изучение ГОСТов:
Подробнее Планиметрия (расширенная)
1. Площади плоских фигур Площадь треугольника: стр. 1 2. Средняя линия 3. Треугольники Сумма углов треугольника равна 180. Тупой угол между биссектрисами двух углов треугольника равен 90 + половина третьего
Подробнее ИСКУС КУ СТВ ССТВ ВО РЕШ О РЕ
МАТЕМАТИКА ВСЁ ДЛЯ УЧИТЕЛЯ! ГЕОМЕТРИЧЕСКОЕ МЫШЛЕНИЕ: ОТ ПЕРИМЕТРА ДО ПЛОЩАДИ ИСКУССТВО ССТВС РЕШАТЬ ЗАДАЧИ АЧИ Окончание Начало в (7) 0 Пусть,, и середины сторон,, и квадрата, площадь которого равна Найдите
Подробнее ГЕОМЕТРИЯ, ЧЕРЧЕНИЕ (базовый курс)
Министерство образования и науки Украины ХАРЬКОВСКИЙ НАЦИОНАЛЬНЫЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ УНИВЕРСИТЕТ ГЕОМЕТРИЯ, ЧЕРЧЕНИЕ (базовый курс) Харьков 2005 Принятые условные обозначения Обозначение Фигуры Фигура
Подробнее Метод ключевых задач
Метод ключевых задач Задачи, в которых фигурируют середины отрезков Задача. Докажите, что середины сторон четырехугольника являются вершинами параллелограмма. Пример. В четырехугольнике = = 90. Точки и
Подробнее A B C D
Министерство общего и специального образования РФ Московский государственный технический университет им. Н. Э. Баумана Т. Д. Момджи, Г. П. Золотова РАБОЧАЯ ТЕТРАДЬ ПО ИНЖЕНЕРНОЙ ГРАФИК Издательство МГТУ
Подробнее ПЕРСПЕКТИВА СЛОЖНЫХ АРХИТЕКТУРНЫХ ФОРМ
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Тихоокеанский государственный университет» ПЕРСПЕКТИВА СЛОЖНЫХ АРХИТЕКТУРНЫХ ФОРМ
Подробнее ЛЕКЦИЯ ПОЗИЦИОННЫЕ ЗАДАЧИ
ЛЕКЦИЯ 3. 3. ПОЗИЦИОННЫЕ ЗАДАЧИ Позиционными называют задачи, связанные с определением взаимного расположения геометрических фигур. Обычно в этих задачах определяется взаимная принадлежность фигур или
Подробнее 841 х х х х х 297
ПРАВИЛА ОФОРМЛЕНИЯ ЧЕРТЕЖЕЙ Основные правила оформления чертежей. Система стандартов. Форматы. Рамка и основная надпись чертежа. Линии чертежа. Шрифты чертежные. Оформление титульного листа. Нанесение
Подробнее ТЕМА 1 ПОСТРОЕНИЕ ВИДОВ
ТЕМА 1 ПОСТРОЕНИЕ ВИДОВ Цель работы: 1. Изучение и практическое применение правил изображения предметов построение видов в соответствии с ГОСТ 2.5 68. 2. Приобретение навыков пространственного представления,
Подробнее ГЕОМЕТРИЧЕСКОЕ ЧЕРЧЕНИЕ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГЕОМЕТРИЧЕСКОЕ ЧЕРЧЕНИЕ Ульяновск
Подробнее Сириус, класс «группа В» 3-4 сентября
Вписанные углы Определение. Угол с вершиной в центре окружности называется центральным, а градусная мера дуги, высекаемой им, равна его градусной мере. Определение. Угол с вершиной на окружности называется
Подробнее ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ
Учреждение образования «БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ» ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ Учебно-методическое пособие по дисциплине «Начертательная геометрия, инженерная и машинная графика»
Подробнее Развертки поверхностей
Развертки поверхностей Разверткой поверхности называется плоская фигура, полученная в результате совмещения всех точек поверхности с одной плоскостью. Между поверхностью и ее разверткой устанавливается
Подробнее ,.. ISBN ISBN ,.. ;.. ( )
..,..,.. -, 35.03.06, 23.03.03 2015 631.171 40.7 29 :,.. ;,.. ;..,.. 26 : — /..,..,… :. -, 2015. 56. ISBN 978-5-9596-1168-2 -. -, «.» 35.03.06, 23.03.03 «-». 631.171 40.7 ( 10 12.05.2015) ISBN 978-5-9596-1168-2,
Подробнее Прототипы задания В6-2 (2013)
Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний
Подробнее «Технология (основы черчения)»
Государственное бюджетное профессиональное образовательное учреждение Московской области «Серпуховский колледж» «Технология (основы черчения)» (введение в предмет и язык предмета) Методические указания
Подробнее Элементы геометрии треугольника.
В.Протасов (МГУ) Элементы геометрии Тема. Принцип Карно. Везде далее используются обозначения: ABC данный треугольник, A i, B i, C i, i =,,… точки на сторонах BC, CA и AB соответственно (или на продолжениях
Подробнее 7 класс 1. Виды углов.
7 класс 1. Виды углов. Угол называется прямым, если он равен 90 0. Угол называется острым, если он меньше 90 0. Угол называется тупым, если он больше 90 0, но меньше 180 0. Прямой угол Острый угол Тупой
Подробнее ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКАЯ ГРАФИКА
ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКАЯ ГРАФИКА ИНЖЕНЕРНО-ГЕОЛОГИЧЕСКАЯ ГРАФИКА Рабочая тетрадь для аудиторной работы Группа Студент Преподаватель ВВЕДЕНИЕ Одним из условий успешного освоения курса инженерно-геологической
Подробнее 4. ПОСТРОЕНИЕ ОКРУЖНОСТЕЙ В ПЕРСПЕКТИВЕ
4. ПОСТРОЕНИЕ ОКРУЖНОСТЕЙ В ПЕРСПЕКТИВЕ Построение окружности в перспективе выполняется непосредственно на картине. Для этого необходимо знать положение центра окружности, ее радиус, а также положение
Подробнее ГЕОМЕТРИЧЕСКИЕ ОПЕРАЦИИ В ПЕРСПЕКТИВЕ
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Тульский государственный университет Кафедра «Дизайн» И.В. УШАКОВА М.В.МИРОНОВА ГЕОМЕТРИЧЕСКИЕ
Подробнее Тренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Окружность. Свойства окружности. Если хорда не является диаметром, то диаметр, проходящий через середину этой хорды, перпендикулярен
Подробнее ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
МИНОБРНАУКИ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИ- ВЕРСИТЕТ» Кафедра общеинженерных дисциплин
Подробнее Сопряжение пересекающихся прямых:
Сопряжением называется плавный переход по кривой от одной ли нии к другой. Сопряжения бывают циркульные и лекальные. Построение их основано на свойствах касательных к кривым линиям. Сопряжение отрезков
Подробнее Инженерная графика. Задания
Инженерная графика Кривальцевич Татьяна Владимировна Задания К лекции «Пересечение геометрических тел плоскостями. Построение разверток» Омск-2010 Требования к выполнению заданий: 1. Задание выполнить
Подробнее 2. ПРЯМАЯ ЛИНИЯ НА ЭПЮРЕ МОНЖА
. ПРЯМАЯ ЛИНИЯ НА ЭПЮРЕ МОНЖА.. Задание прямой.. Прямые общего положения.3. Прямые частного положения.4. Принадлежность точки прямой. Деление отрезка прямой линии в данном отношении.5. Определение длины
Подробнее Анализ геометрических высказываний
Анализ геометрических высказываний 1. 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
Подробнее Сопряжения в инженерной графике — Docsity
Сопряжением называют плавный переход одной прямой линии или дуги окружности в другую прямую линию или дугу окружности. Центр сопрягающей дуги называется — центром сопряжения. Он определяется в пересечении двух вспомогательных линий параллельных заданным прямым или в пересечении двух дуг концентричным заданным дугам и отстоящих от заданных линий на расстоянии радиуса сопряжения. Общая для этих линий точка называется точкой сопряжения. Точка сопряжения будет находиться: при сопряжении двух прямых на перпендикуляре, опущенном из центра сопряжения к самим прямым, при сопряжении двух дуг на прямых (или их продолжениях) соединяющих центры данных дуг. Сопряжения двух прямых, являющихся сторонами прямого (рис.1 а), острого (рис. 1 б) или тупого (рис. 1 в) углов, посредством дуги радиуса R. а) б) в) Рисунок 1. Сопряжение угла : а) прямого; б) острого; в) тупого Во всех этих случаях поступают так: 1. Проводят две вспомогательные прямые линии, параллельные сторонам угла, на расстоянии от этих сторон, равном радиусу дуги R. 2. Находят точку О пересечения этих вспомогательных прямых. Точка О является центром дуги радиуса R, сопрягающей стороны угла т.е.центром сопряжения. Из этого центра О описывают дугу, плавно переходящую в прямые – стороны угла. 3. Дугу заканчивают в точках сопряжения n и n1, которые являются основаниями перпендикуляров, опущенных из центра О на стороны угла. 1 Следует отметить, что сопряжения могут быть: 1.Внешние — центры всех сопрягаемых дуг находятся по разные стороны от точки сопряжения (рис. 2, 4). 2.Внутренние – центры сопрягаемых дуг расположены по одну сторону от точек сопряжения (рис. 3, 5). 3.Смешенные – центр одной из сопрягаемых дуг лежит внутри сопрягающей дуги, а центр другой сопрягаемой дуги – вне неё (рис. 6) Сопряжение дуги окружности и прямой линии дугой заданного радиуса. Внешнее сопряжение (рис. 2). Центр О1 дуги сопряжения (центр сопряжения) находится на пересечении вспомогательной прямой b, отстоящей от заданной прямой на величину радиуса r и параллельной ей, и вспомогательной дуги радиуса R+ r проведенной из центра О. Точки сопряжения С3 и С2 находятся соответственно в основании перпендикуляра О1С3 и на пересечении прямой ОО1 с основной окружностью. Внутреннее сопряжение (рис. 3). Центр О1 дуги сопряжения (центр сопряжения) находится на пересечении вспомогательной прямой, отстоящей от заданной прямой на величину радиуса r, а также параллельной ей и дуги радиуса R- r проведенной из центра О. Точки сопряжения – соответственно в основании перпендикуляра ОС1 и на пересечении продолжении луча ОО1 с основной окружностью. Рисунок 2. Внешнее сопряжение Рисунок 3. Внутреннее сопряжение Сопряжение двух окружностей дугой заданного радиуса. Внешнее сопряжение (рис. 4). Центр сопряжения О2искомой дуги радиуса R находится на пересечении вспомогательных окружностей, описанных из центров О1 и О соответствующими радиусами R + R2 и R + R1. Точки 2
Сопряжения — презентация на Slide-Share.ru 🎓
1
Первый слайд презентации: Сопряжения

«ИНЖЕНЕРНАЯ И КОМПЬЮТЕОНАЯ ГРАФИКА» Лекция 7

Изображение слайда
2
Слайд 2

Сопряжением называют плавный переход одной линии в другую Виды сопряжений Непосредственное Внешнее Сопряжения двух прямых линий Промежуточными дугами Сопряжения дуги окружности с прямой Сопряжения двух дуг окружностей Внутреннее Смешанное Сопряжения дуги с прямой Сопряжения двух дуг

Изображение слайда
3
Слайд 3: Основные элементы сопряжения

Точка сопряжения Центр сопряжения Радиус сопряжения Для построения сопряжения необходимо: Знать радиус сопряжения ( R ) Найти центр сопряжения ( О ) Найти точки сопряжения ( А и В )

Изображение слайда
4
Слайд 4: Непосредственные сопряжения

Сопряжение двух дуг Сопряжение прямой и дуги Непосредственные сопряжения – это сопряжения в которых одна линия плавно переходит в другую без промежуточных линий

Изображение слайда
5
Слайд 5: Сопряжения двух сторон прямого, острого и тупого углов с дугой

— Прямой угол — Острый угол — Тупой угол

Изображение слайда
6
Слайд 6

Сопряжение двух пересекающихся прямых дугой заданного радиуса R называют СКРУГЛЕНИЕМ УГЛОВ Порядок выполнения скругления : П араллельно сторонам угла, образованного данными прямыми, проводят вспомогательные прямые на расстоянии, равном радиусу скругления Т очка пересечения вспомогательных прямых О является центром дуги сопряжения И з полученного центра О опускают перпендикуляры к сторонам данного угла Н а пересечении их получают точки сопряжения А и В. М ежду этими точками проводят сопрягающую дугу радиусом R из центра О

Изображение слайда
7
Слайд 7: Сопряжения дуги окружности с прямой линией

— внешнее сопряжение — внутреннее сопряжение

Изображение слайда
8
Слайд 8: Сопряжения дуги окружности с прямой линией

При построении внешнего сопряжения : П араллельно заданной прямой на расстоянии r в сторону окружности проводят вспомогательную прямую И з центра О радиусом, равным R + r, — строится вспомогательная окружность Н а их пересечении получают точку О 1 — центр сопрягающей окружности И з этого центра радиусом r проводят дугу между точкам и С 3 и С 2, построение которых видно из чертежа радиус сопряжения — r

Изображение слайда
9
Слайд 9: Сопряжения дуги окружности с прямой линией

радиус сопряжения — r Построение внутреннего сопряжения отличается тем, что из центра О проводят вспомогательную дугу радиусом, равным R – r

Изображение слайда
10
Слайд 10: Внешнее и внутреннее сопряжения двух дуг окружностей

Внешнее Внутреннее

Изображение слайда
11
Слайд 11: Внешнее и внутреннее сопряжения сопряжения двух дуг окружностей

Внешнее Внутреннее

Изображение слайда
12
Слайд 12: Внешнее сопряжения сопряжение двух дуг

радиус сопряжения — R Построение центра О сопрягающей дуги радиуса R при внешнем касании осуществляется в следующем порядке : И з центра О 1 радиусом, равным R + R 1, проводят вспомогательную дугу, и з ц ентра O 2 проводят вспомогательную дугу радиусом R + R 2. Н а пересечении дуг получают центр О сопрягающей дуги радиуса R, н а пересечении радиусов (прямых) R + R 1 и R + R2 с дугами окружностей получают точки сопряжения S и S 1

Изображение слайда
13
Слайд 13: Внешнее сопряжения сопряжение двух дуг

радиус сопряжения — R Построение внутреннего сопряжения отличается тем, что из центров сопрягаемых окружностей проводят вспомогательные дуги радиусом, равным и R – R 1 R – R 2

Изображение слайда
14
Слайд 14: Смешанное сопряжение

Изображение слайда
15
Последний слайд презентации: Сопряжения: Смешанное сопряжение

При сочетании внутреннего и внешнего касания из центра О 1 проводят вспомогательную окружность радиусом, равным а из центра О — радиусом, равным R – R 2 R + R 1

Изображение слайда
Сопряжения. Способы построения сопряжения — презентация онлайн
1. Геометрические построения.
Сопряжения.
Способы построения
сопряжения
Сопряжением называют плавный
переход одной линии в другую.
Что нужно для построения сопряжения?
Знать радиус сопряжения (Rc)
Найти центр сопряжения (Ос)
Найти точки сопряжения
3. Виды сопряжения:
• Сопряжение двух пересекающихся
прямых дугой заданного радиуса.
• Сопряжение дуги и прямой линии дугой
заданного радиуса.
• Сопряжение двух дуг окружности дугой
заданного радиуса.
4. Сопряжение двух пересекающихся прямых дугой заданного радиуса
Даны пересекающиеся под прямым, острым и тупым
углами прямые линии.
Нужно построить сопряжения этих прямых дугой
заданного радиуса R.
5. Сопряжение двух пересекающихся прямых дугой заданного радиуса
Проводим вспомогательные прямые
параллельно заданным на расстоянии R от
заданных.
Точка пересечения этих прямых будет
центром О дуги сопряжения.
Перпендикуляры, опущенные из центра О
на заданные прямые, определят точки
касания A и B.
Сопряжения острого угла.
7. Сопряжение окружности и прямой линии дугой заданного радиуса.
• Заданы дуга окружности радиусом R и прямая.
Требуется соединить их дугой радиусом r.
8. Сопряжение дуги и прямой линии дугой заданного радиуса.
Проводим прямую параллельно заданной на
расстоянии r.
Из центра О данной окружности проводим дугу
вспомогательной окружности радиусом R+r.
Пересечение прямой и вспомогательной дуги даст
точку центра дуги сопряжения О1.
Точка касания дуги и линии D лежит на
пересечении перпендикуляра из точки О1 на прямую.
Точка касания дуг E лежит на линии ОО1.
Сопряжения прямой и окружности.
10. Сопряжение двух окружностей дугой заданного радиуса.
Заданы две дуги радиусами R1 и R2. Требуется
построить сопряжение дугой, радиус которой задан R.
Различают два случая касания:
внешнее и внутреннее .
11. Сопряжение двух окружностей дугой заданного радиуса Внешнее касание.
Из центра окружности О1 описываем дугу
вспомогательной окружности радиусом R1+R.
Из центра окружности О2 описываем дугу
вспомогательной окружности радиусом R2+R.
Пересечение дуг вспомогательных окружностей
даст точку О, которая является центром дуги
сопряжения (окружности с радиусом R).
Точки касания A и B находятся на линиях ОO1 и
ОO2.
Внешнее сопряжение
13. Сопряжение двух окружностей дугой заданного радиуса Внутреннее касание.
Из центра окружности О1 описываем дугу
вспомогательной окружности радиусом R-R1.
Из центра окружности О2 описываем дугу
вспомогательной окружности радиусом R-R2.
Пересечение дуг вспомогательных окружностей
даст точку О, которая является центром дуги
сопряжения (окружности с радиусом R).
Точки сопряжения A и B лежат на продолжении
линий ОO1 и ОO2.
Внутренне сопряжения
50
А теперь для закрепления материала выполним практическое
задание:
R 25
Выполняется в тетради с предварительным разбором и
демонстрацией.
R 15
R 15
80
60
R 25
«Построить сопряжения в заданной фигуре».
Дуга окружности — объяснение и примеры
После радиуса и диаметра еще одна важная часть окружности — это дуга . В этой статье мы обсудим , что такое дуга, найдем длину дуги и измерим длину дуги в радианах. Мы также изучим малую дугу и большую дугу.
Что такое дуга круга?
Дуга окружности — это любая часть окружности. Напомним, окружность круга — это периметр или расстояние вокруг круга.Следовательно, мы можем сказать, что окружность круга — это полная дуга самого круга.
Как найти длину дуги?
Th e Формула для расчета дуги утверждает, что:
Длина дуги = 2πr (θ / 360)
Где r = радиус окружности,
π = pi = 3,14
θ = угол ( в градусах ), ограниченный дугой в центре круга.
360 = угол одного полного поворота.
На приведенном выше рисунке длина дуги (нарисованная красным) — это расстояние от точки A, до точки B.
Давайте разберемся с несколькими примерами задач о длине дуги:
Пример 1
Учитывая эту дугу, AB образует угол 40 градусов к центру круга с радиусом 7 см. Рассчитайте длину дуги AB.
Решение
При r = 7 см
θ = 40 градусов.
Путем подстановки
Длина дуги = 2πr (θ / 360)
Длина = 2 x 3,14 x 7 x 40/360
= 4,884 см.
Пример 2
Найдите длину дуги окружности, которая образует угол в 120 градусов с центром окружности на 24 см.
Решение
Длина дуги = 2πr (θ / 360)
= 2 x 3,14 x 24 x 120/360
= 50,24 см.
Пример 3
Длина дуги 35 м.Если радиус круга равен 14 м, найдите угол, образуемый дугой.
Решение
Длина дуги = 2πr (θ / 360)
35 м = 2 x 3,14 x 14 x (θ / 360)
35 = 87,92θ / 360
Умножить обе стороны на 360 удалить дробь.
12600 = 87,92θ
Разделите обе стороны на 87,92
θ = 143,3 градуса.
Пример 4
Найдите радиус дуги длиной 156 см, переходящей под углом 150 градусов к центру круга.
Решение
Длина дуги = 2πr (θ / 360)
156 см = 2 x 3,14 xrx 150/360
156 = 2,6167 r
Разделите обе стороны на 2,6167
r = 59,62 см .
Итак, радиус дуги 59,62 см.
Как найти длину дуги в радианах?
Существует взаимосвязь между углом, образуемым дугой в радианах, и отношением длины дуги к радиусу окружности. В данном случае
θ = (длина дуги) / (радиус окружности).
Таким образом, длина дуги в радианах определяется выражением,
S = r θ
, где θ = угол между дугой в радианах
S = длина дуги.
r = радиус окружности.
Один радиан — это центральный угол, образованный дугой одного радиуса, то есть s = r
Радиан — это просто еще один способ измерения величины угла. Например, чтобы преобразовать углы из градусов в радианы, умножьте угол (в градусах) на π / 180.
Аналогичным образом, чтобы преобразовать радианы в градусы, умножьте угол (в радианах) на 180 / π.
Пример 5
Найдите длину дуги с радиусом 10 см и под углом 0,349 радиана.
Раствор
Длина дуги = r θ
= 0,349 x 10
= 3,49 см.
Пример 6
Найдите длину дуги в радианах с радиусом 10 м и углом 2.356 радиан.
Решение
Длина дуги = r θ
= 10 м x 2,356
= 23,56 м.
Пример 7
Найдите угол, образованный дугой длиной 10,05 мм и радиусом 8 мм.
Решение
Длина дуги = r θ
10,05 = 8 θ
Разделите обе стороны на 8.
1,2567 = θ
Здесь угол, образованный дугой, равен 1,2567 радиана.
Пример 8
Вычислите радиус круга, длина дуги которого составляет 144 ярда, а угол дуги равен 3.665 радиан.
Решение
Длина дуги = r θ
144 = 3,665r
Разделите обе стороны на 3,665.
144 / 3,665 = r
r = 39,29 ярда.
Пример 9
Вычислите длину дуги, которая образует угол 6,283 радиана с центром круга с радиусом 28 см.
Решение
Длина дуги = r θ
= 28 x 6,283
= 175.93 см
Малая дуга (h4)
Младшая дуга — это дуга, которая проходит под углом менее 180 градусов к центру окружности. Другими словами, малая дуга меньше полукруга и представлена на окружности двумя точками. Например, дуга AB в окружности ниже — это второстепенная дуга.
Большая дуга (h4)
Большая дуга окружности — это дуга, которая проходит под углом более 180 градусов к центру окружности.Большая дуга больше полукруга и представлена тремя точками на окружности.
Например, PQR — это большая дуга окружности, показанной ниже.
Практические задачи

Найдите площадь сектора окружности радиусом 9 мм. Предположим, что угол, образованный этой дугой в центре, равен 30 ^o.
Город A находится к северу от города B. Широты города A и города B составляют 54 ^o северной широты и 45 ^o северной широты, соответственно.Каково расстояние между двумя городами с севера на юг? Радиус Земли 6400 км.

Предыдущий урок | Главная страница | Следующий урок
c # — Алгоритм скругления угла между линией и дугой
В моем эскизе BF является частью данного отрезка (F еще не известно), C — центр данной дуги, B — точка грубого сопряжения. c — прямая, параллельная BF, | GF | = | GH | = r — радиус малой дуги.
Для гладкого сопряжения касательная к малой дуге в точке F должна быть коллинеарна направлению BF, поэтому GF перпендикулярна BF, а касательные к обеим дугам в точке H должны совпадать, так что радиус-векторы CH и GH лежат на одной прямой. .2 решение дает t = 4 +/- Sqrt (8), второй корень действителен E = (5 — (4 — Sqrt (8)), 3) = (3.83, 3)
Полученная гладкая дуга F-G
(в обоих случаях больший корень соответствует сопряжению с дополнительной частью большой дуги)
теорем для определения углов и мер дуги — видео и стенограмма урока
Некоторые ключевые термины
Линии, нарисованные в кругах и через них, имеют определенные имена. Вы можете вспомнить, что радиус — это длина линии, проведенной от центра круга до точки на окружности.Вы также можете вспомнить, что диаметр — это отрезок линии, который проходит от одной точки окружности к другой, но проходит через центр. Другие менее известные линии включают касательные, секущие и хорды.
Вы когда-нибудь слышали, чтобы кто-то сказал, что они ушли по касательной? Ну, это потому, что если круг представляет ход ваших мыслей, а вы оставляете ход своих мыслей и начинаете говорить о чем-то другом, вы сбиваетесь с пути. Касательная — это линия, пересекающая окружность ровно в одной точке.
Касательная
Еще одно определение, на которое мы должны обратить внимание, — это линия, проведенная через круг, которая называется секущей . Секущая может иметь одну конечную точку на окружности, а другой конец линии продолжается через окружность. Секущая также может проходить через круг без конечных точек.
Секант
Затем есть сегмент с концами на окружности, который называется хордой .Хорда может быть проведена в любом месте круга. Если хорда проходит через центр окружности, она называется диаметром.
Аккорд
Каждая из этих линий может использоваться для создания углов и дуг в окружности. Существуют определенные правила для определения размеров углов и дуг, в зависимости от того, где нарисованы углы и какие линии используются для их построения. Линии образуют пересеченных дуг , которые представляют собой дуги, образованные хордами, касательными или секущими.На этом изображении AB — это перехваченная дуга, потому что она перехвачена хордами AC и CB.
Перехваченная дуга
Углы, образованные внутри круга
Углы, образованные внутри круга двумя хордами, образуют четыре дуги на окружности, которые вы можете видеть на этой диаграмме. Мера угла равна половине суммы пересеченных дуг.
Угол x равен половине суммы пересеченных дуг.Пересеченная дуга a — это дуга от C до D. Пересеченная дуга b — это дуга от A до B. Чтобы найти угол, мы складываем дуги и делим их на 2, как вы можете видеть в этой формуле.
Вот пример:
Найдите длину угла x .
Поскольку этот угол находится внутри круга, образованного двумя хордами, мы сложим дуги и разделим их на 2.
Это, в свою очередь, дает нам ответ, который (как вы можете видеть здесь) равен 145 градусам.
Углы, образующиеся вне круга
Углы, образующиеся вне круга, могут быть образованы тремя способами:
Две касательные
Две секущие
Касательная и секущая
Два касательных
Две секущие
Касательная и секанс
Формула для определения угловой меры одинакова для всех трех подходов.Угол, образованный за пределами круга, равен половине разности больших пересеченных дуг и меньших пересеченных дуг, как вы можете видеть в нашей формуле, представленной здесь.
Вот пример:
Найдите угол, образованный касательной и секущей на этом изображении.
Большая дуга составляет 205 градусов, а меньшая — 55 градусов.Все, что нам нужно сделать, это вычесть и разделить на 2.
Как видите, это дает нам 75 градусов для нашего ответа.
Касательные и пересекаемые дуги
Углы, образованные касательной и пересеченной дугой, образуются на окружности. Они образованы касательной и хордой.
Чтобы найти угол, мы просто делим дугу на 2.
Давайте посмотрим на пример:
Давайте найдем меру угла.
Поскольку мы знаем, что дуга составляет 110 градусов, мы просто делим ее на 2, что дает нам ответ 55 градусов.
Резюме урока
Давайте уделим пару минут, чтобы повторить то, что мы узнали в этом уроке.Сначала мы рассмотрели условия нашего круга. Что радиус — это длина линии, проведенной от центра круга до точки на окружности, а диаметр — это отрезок линии, который проводится от одной точки на окружности к другой точке, но проходит через центр.
Пересмотрев основные термины, связанные с измерением всего, что связано с кругами, мы узнали, что внутри кругов есть три типа сегментов:
Касательные — это линии, пересекающие круг в одной точке.
Секущие — это прямые, пересекающие окружность в двух точках, что означает, что они проходят через окружность.
Хорды  — это сегменты, концы которых находятся на окружности.
С помощью этих сегментов можно образовать три типа углов. У всех углов есть определенные формулы.
Углы, образованные внутри круга двумя хордами: сложите дуги и затем разделите на 2.
Углы, образованные за пределами круга любыми двумя сегментами: вычтите меньшую дугу из большей дуги и затем разделите на 2.
Углы, образованные касательной и хордой на окружности: разделите пересеченную дугу на 2.
Дуг и окружностей: определения и примеры — видео и стенограмма урока
Локус
Локус — это инвазивный вид насекомых, который уничтожает посевы и может быть вызван Моисеем. Погодите, нет, это саранча с буквой «т». Совсем другое дело.
Локус — это набор точек, которые имеют общее свойство.
Рассмотрим несколько примеров.Если мы посмотрим на все точки или геометрическое место точек, которые находятся на расстоянии d от линии выше или ниже нее, мы получим параллельные линии — не только одну или две звезды, но так много, что это настоящая линия.
Геометрическое место точек, которые равноудалены от двух параллельных прямых, — это линия на полпути между ними и параллельная обеим. Это как центральная линия на идеально прямой дороге. Если мы возьмем две точки и посмотрим на геометрическое место точек, которые равноудалены от этих точек, мы получим линию, которая делит пополам линию, соединяющую наши две точки.Он также перпендикулярен этой линии.
Вот это были все скучные прямые линии. Что, если нам станет немного интереснее? Допустим, мы смотрим на несколько точек, которые находятся на фиксированном расстоянии d от точки P . Похоже на созвездие. А что, если мы соединим точки, посмотрев на все точки или геометрическое место точек, которые находятся на расстоянии d от точки P ? Получаем круг!
Очки в круге
Круги
Вот и все, что есть на круге .Это просто набор всех точек, находящихся на одинаковом расстоянии от центральной точки. Мы называем эту центральную точку центром. Креативный, я знаю.
Но у круга есть много других интересных деталей, которые имеют более интересные названия. Сначала мы называем это расстояние от центра радиусом. Это может быть любая линия от центра до края.
Радиус — от центра до края круга
Если мы перейдем от одного края нашей кривой к другому, проходя через центр, получится диаметр.Таким образом, диаметр — это всего лишь две соединенные радиусные линии. Чтобы запомнить это, подумайте о том, что слово «радиус» короче слова «диаметр», так что это более короткая линия.
Диаметр — две соединенные радиусные линии
Если у нас есть квадрат или прямоугольник, мы называем расстояние по краю периметром. Но круги особенные. У них есть свое собственное слово для периметра. Мы называем расстояние по окружности окружностью.Это слово происходит от латинского (конечно) и означает «носить с собой».
Обратите внимание на то, что слова «круг» и «окружность» начинаются с «цирку» — как и цирк с тремя кольцами, который также очень сфокусирован на круге. На пицце окружность — это удобная корочка, которая защищает пальцы от грязи.
Длина окружности
Если мы просто смотрим на часть окружности, мы называем это дугой окружности.Это как корочка на одном куске пиццы. В этом круге, если мы обозначим наши точки, мы могли бы назвать эту дугу AB .
Круговая дуга
Но подождите — на нашем круге внизу разве дуга AB не может быть показана так? Вот где мы получаем большие и второстепенные дуги. Когда у нас есть две такие точки, большая дуга — это просто более длинная дуга, соединяющая две точки. Малая дуга — более короткая.
Более длинная дуга — Большая дуга
Наконец, если наш круг — это пицца, и мы едим половину пиццы, то, ну, мы съели много пиццы.Кроме того, форма, которая осталась? Это называется полукругом, то есть просто полукругом. Это не большая и не малая дуга, потому что длины дуги равны.
Резюме урока
В этом уроке мы обсудили локус или набор точек, которые имеют общее свойство. Мы рассмотрели разные примеры того, каким может быть геометрическое место точек. Один из них — круг. Это набор всех точек на одинаковом расстоянии от центра.
Затем мы рассмотрели многие части окружностей, включая радиус и диаметр.Мы узнали об окружности или периметре круга.
Потом мы узнали о дугах окружности. Дуга окружности — это часть окружности. Мы различали более короткую дугу, соединяющую две точки, которая является малой дугой, и более длинную, или большую дугу.
Результаты обучения
По завершении этого урока вы должны уметь:
Обозначить круг
Назовите части круга
Описание дуг окружности и различий между малыми и большими дугами
Об абсолютной непрерывности сопряжения между отображениями окружности с точками излома
Позвольте и быть кусочно гладкими гомеоморфизмами окружности с точками излома и одинаковыми иррациональными числами вращения.Мы даем одно достаточное и необходимое условие для абсолютной непрерывности отображения сопряжения между и.
1. Введение и формулировка результатов
Пусть с четко определенной ориентацией, метрикой, мерой Лебега и операцией сложения будет единичная окружность . Обозначим через соответствующее проекционное отображение, которое «накручивает» прямую на окружность. Произвольный гомеоморфизм, сохраняющий ориентацию единичной окружности, можно «поднять» на прямую в виде гомеоморфизма со свойством, связанным с отношением.Этот гомеоморфизм называется подъемом гомеоморфизма и определяется с точностью до целого члена. Наиболее важной арифметической характеристикой гомеоморфизма единичной окружности является число вращения где находится подъемник с до. Здесь и далее для данной карты обозначена ее итерация. Пуанкаре доказал, что указанный предел существует, не зависит от начальной точки поднятой траектории и с точностью до целого числа не зависит от подъема (см. [1]).Число вращения иррационально тогда и только тогда, когда гомеоморфизм не имеет периодической точки. В дальнейшем мы всегда будем предполагать, что это иррационально, и будем использовать его разложение в бесконечную цепную дробь (см. [2]) Значение дроби «счетного пола» является пределом последовательности рациональных приближающихся . Положительные целые числа, называемые неполными кратными , определены однозначно для иррационального. Взаимно простые положительные целые числа и удовлетворяют рекуррентным соотношениям и для, где удобно определить и.Учитывая гомеоморфизм окружности с иррациональным числом вращения, можно рассмотреть отмеченную траекторию (т. Е. Траекторию отмеченной точки), где и выбрать из нее последовательность динамических сходящихся , индексированных знаменателями следующих друг за другом рациональные подходящие к. Мы также будем условно использовать. Хорошо изученные арифметические свойства рациональных сходящихся и комбинаторная эквивалентность между жестким вращением и mod 1 подразумевают, что динамические сходящиеся элементы приближаются к отмеченной точке, меняя свой порядок следующим образом: Мы определяем основной интервал как дугу окружности для четных и нечетных.Для отмеченной траектории мы используем обозначения. Хорошо известно, что множество интервалов с попарно непересекающимися внутренностями, определяемое как определяет разбиение круга для любого. Раздел называется динамическим разделом точки. Очевидно, что разбиение является уточнением разбиения: действительно, интервалы порядка являются членами, и каждый интервал разбивается на интервалы, принадлежащие таким, что Класс -гомеоморфизмы. Это сохраняющие ориентацию гомеоморфизмы окружности, дифференцируемые, за исключением конечного числа точек излома, в которых существуют левая и правая производные, обозначенные, соответственно, и, и такие, что (i) существуют константы с для всех и для всех с множеством точек останова на; (ii) имеет ограниченную вариацию. Отношение называется скачком в или — скачком . Общие -гомеоморфизмы с одной точкой излома впервые были изучены Ханиным и Вулом в [3]. Среди других результатов этими авторами было доказано, что их перенормировки аппроксимируют дробно-линейные преобразования.Пусть — сохраняющий ориентацию -диффеоморфизм окружности. Если число вращения иррационально и имеет ограниченную вариацию, то по известной теореме Данжуа сопряжено жесткому вращению (см. [1]). Сопряжение означает, что существует существенно единственный гомеоморфизм окружности такой, что. В этом контексте возникает естественный вопрос: при каких условиях сопряжение гладкое? Некоторые авторы, например [4–6] показали, что если есть и удовлетворяет определенное диофантово условие, то сопряженность будет не меньше.
Классический результат Данжуа легко переносится на случай -гомеоморфизмов. Далее мы рассматриваем проблему регулярности сопряжения отображения двух классов-гомеоморфизмов с одной точкой излома и совпадающими иррациональными числами вращения. Случай одной точки излома с одинаковыми коэффициентами скачков, так называемая проблема жесткости, подробно исследован Теплинским и Ханиным в [7]. Пусть — разложение в цепную дробь иррационального числа вращения и определим Основной результат [7] заключается в следующем.
Теорема 1.1. Позвольте быть -гомеоморфизмы с одной точкой излома, которые имеют то же отношение скачка и такое же иррациональное число вращения. Кроме того, пусть выполняется одно из следующих ограничений: либо и, либо и. Тогда отображение, сопрягающее гомеоморфизмы и, является -диффеоморфизмом.
В случае различных коэффициентов скачков следующая теорема была доказана в [8] Джалиловым с соавторами.
Теорема 1.2. Позвольте быть -гомеоморфизмы с одной точкой излома, которые имеют различную степень скачка и одно и то же иррациональное число вращения.Тогда отображение, сопрягающее гомеоморфизмы и, является сингулярной функцией, т. Е. Непрерывно на и п.в. по мере Лебега.
Let и be -гомеоморфизмы с одинаковым иррациональным числом вращения. Теперь мы рассматриваем динамические разбиения, соответствующие гомеоморфизмам и. Обозначим интервалы разбиения. Поскольку функция является функцией сопряжения между и, поэтому для любого. Обозначим мерой Лебега соответствующего множества.Наша цель в этой статье — дать некоторые критерии абсолютной непрерывности отображения сопряжения. Наш первый основной результат заключается в следующем.
Теорема 1.3. Предположим, что число вращения иррационально ограниченного типа. Предположим, что существует такая последовательность, что при для каждой пары смежных интервалов для всех. Тогда отображение сопряжения является абсолютно непрерывной функцией.
При доказательстве теоремы 1.3 мы воспользуемся рассмотрением теории мартингалов.Идея использования теории мартингалов была основана в [9] Кацнельсоном и Орнштейном. Наш второй основной результат заключается в следующем.
Теорема 1.4. Позвольте и быть -гомеоморфизмы с одинаковым иррациональным числом вращения. Если отображение сопряжения является абсолютно непрерывной функцией, то для всех последовательность меры Лебега множества стремится к 0 при переходе в.
2. Теория Данжуа и эргодичность -гомеоморфизмов
Перечисленные ниже утверждения, справедливые для любого сохраняющего ориентацию гомеоморфизма с иррациональным числом вращения, составляют классическую теорию Данжуа.Их элементарные доказательства можно найти в [10, 11]: (а) Обобщенная оценка Данжуа; пусть — точка непрерывности, то имеет место неравенство:, где. (b) Экспоненциальное измельчение; существует универсальная постоянная такая, что, где. (c) Ограниченная геометрия; пусть число вращения ограниченного типа, то есть коэффициенты разложения в цепную дробь ограничены. Тогда существуют универсальные константы, такие, что и с (i) каждая пара соседних интервалов -сравнима, то есть их отношение длин принадлежит; (ii) интервал -сравним с интервалом, который его содержит:.(d) Обобщенная оценка Финци; Предположим, и являются точками непрерывности. Тогда для любого имеет место неравенство.
Позвольте быть мерой пространства и быть измеримым отображением.
Определение 2.1. Набор называется инвариантом относительно измеримого, если.
Определение 2.2. Измеримая карта называется эргодической относительно меры, если мера любого инвариантного множества равна или.
Позвольте обозначить через.
Лемма 2.3. Позвольте быть -гомеоморфизм с иррациональным числом вращения. Допустим, и будет точкой непрерывности. Тогда для любого имеет место неравенство
Доказательство. Пусть система интервалов есть интервалы непрерывности. Позволять . Тогда по теореме о среднем значении для любого имеем где и. Если тогда у нас есть где и. Примените обобщенную оценку Финци к правой части соотношений (2.2) и (2.3), получаем В итоге получаем
Лемма 2.4. Пусть — -гомеоморфизм окружности с иррациональным числом вращения, тогда он эргодичен относительно меры Лебега.
Доказательство. Предположим, что существует инвариантное множество положительной, но не полной меры Лебега. Тогда по теореме Лебега о плотности имеет точку плотности. Фиксируем произвольную. По определению точек плотности, мы можем найти такое, что для любого интервала, удовлетворяющего условиям, мы имеем, или, другими словами, где обозначает дополнение к.Теперь выбираем такой, что. Мы можем это проверить, и каждая точка круга принадлежит не более чем двум интервалам этого покрытия. Следовательно, множество инвариантно относительно, используя приведенную выше лемму, получаем Поскольку было произвольным,. Теорема доказана.
Лемма 2.5. Позвольте и являются -гомеоморфизмы с одинаковым иррациональным числом вращения. Тогда отображение сопряжения между и является либо абсолютно непрерывной, либо сингулярной функцией.
Доказательство. Рассмотрим два -гомеоморфизма и окружности с одинаковым иррациональным числом вращения. Пусть и будут сопряжения отображений и с жестким вращением, то есть, и. Легко проверить, что карта сопряжена и, т. Е. Мы знаем, что функция сопряжения — это строго возрастающая функция на. Тогда существует почти везде на. Обозначим через. Понятно, что набор мод-инвариантен относительно. Поскольку класс -гомеоморфизм эргодичен относительно меры Лебега.Следовательно, мера множества Лебега либо нулевая, либо полная. Если мера Лебеска равна нулю, то является сингулярной функцией, если она полна, то является абсолютно непрерывной функцией.
Замечание 2.6. Позвольте и быть -гомеоморфизмы с одинаковым иррациональным числом вращения. Тогда отображение сопряжения между и является либо абсолютно непрерывным, либо сингулярным.
3. Мартингалы и теорема о сходимости мартингалов
Наша цель в этом разделе — разработать основы теории мартингалов и подготовиться к основным результатам и приложениям, которые будут представлены в следующих разделах.
Определение 3.1. Позвольте быть измеримым пространством. Последовательность -алгебр on называется фильтрацией в , если
Положение 3.2. Последовательность алгебр, порожденная динамическими разбиениями, которая также обозначается (злоупотреблением обозначениями), является фильтрацией в, где — борелевская -алгебра на.
Определение 3.3. Позвольте быть последовательность случайных величин на измеримом пространстве и фильтрации в. Мы говорим, что адаптирован к , если для каждого положительного целого числа можно измерить.
Обозначим условным математическим ожиданием случайных величин относительно разбиения.
Определение 3.4. Позвольте быть последовательность случайных величин на вероятностном пространстве и фильтрации в. Последовательность называется мартингалом относительно if для каждого положительного целого числа (i) интегрируема; (ii) адаптирован к; (iii).
Лемма 3.5 (см. [12]). Позвольте быть последовательность случайных величин на вероятностном пространстве. Если для некоторых и является мартингалом, то существует интегрируемая такая, что
Предположим, что это гомеоморфизм (не обязательно, чтобы быть -гомеоморфизмом) круга.Используя гомеоморфизм и последовательность динамических разбиений, мы определяем последовательность случайных величин на окружности, которая порождает мартингалы. Для любого устанавливаем
Лемма 3.6. Последовательность случайных величин является мартингалом по отношению к.
Доказательство. Чтобы доказать мартингал, достаточно проверить для любого, потому что последовательность случайных величин является последовательностью ступенчатых функций, поэтому последовательность ступенчатых функций интегрируема и адаптирована к.Обозначим индикаторной функцией интервала. Используя определение условного ожидания случайных величин относительно разбиения, получаем Теперь вычислим каждую сумму (3.4) отдельно. Обратите внимание, что каждый интервал порядка является членом, а каждый интервал разбивается на интервалы, принадлежащие таким, что Используя это, мы получаем
Наконец, суммируя (3.4), (3.6) и (3.7), получаем
Следующее неравенство (иногда называемое «неравенством параллелограмма») полезно для оценки дробей, и мы будем использовать его при доказательстве следующего утверждения.
Лемма 3.7. Учитывая, что выполняются следующие неравенства
Доказательство. Считайте точки и по плану. Наклон луча лежит между наклонами лучей и.
4. Доказательство основных теорем
Позвольте быть гомеоморфизм сопряжения между и, то есть,. Без ограничения общности предполагаем. Рассмотрим динамическое разбиение. Определим последовательность случайных величин по этой формуле Обозначим через и.
Положение 4.1. Пусть последовательность определена в теореме 1.3. Тогда существует универсальная постоянная такая, что для всех выполняется неравенство
Доказательство. Понятно, что Теперь прикинем. Обозначим через и. Таким образом, мы имеем где . Используя лемму 3.7, получаем Понятно, что для любых зацепок Поскольку каждая пара соседних интервалов -сравнима.По условию теоремы 1.3 получаем Следовательно, число вращения ограниченного типа, и простой прием дает нам где и. Аналогичная нижняя оценка верна для. Следовательно, мы имеем для всех .
Доказательство теоремы 1.3. Для доказательства теоремы 1.3 воспользуемся приведенными выше рассуждениями. По лемме 3.6 последовательность случайных величин является мартингалом относительно. Мы хотим показать, что сходится в норме, когда.Прямым вычислением легко увидеть, что и ортогональна, т. Е. Используя утверждение утверждения 4.1, получаем Итерируя последнее отношение, мы имеем. Насколько сходятся серии. Отсюда следует, что последовательность случайных величин ограничена по норме. По лемме 3.5 последовательность случайных величин сходится к некоторой функции по норме. Доказано, что последовательность случайных величин сходится к. Действительно, обозначим через и конечные точки отрезка динамического разбиения.По определению имеем Кроме того, используя последнее неравенство, получаем Из этого взяв предел, когда, мы получаем. Поскольку,, то является абсолютно непрерывной функцией и почти всюду включена. Таким образом, теорема 1.3 полностью доказана.
Положение 4.2. Для всех придерживаться этого равенства
Доказательство. Хорошо известно, что класс непрерывных функций на плотен (в) в (см. [13]). Из этого факта следует, что если, то для любого существует непрерывная функция и такая, что и.Используя эту оценку и оценку Данжуа, получаем Поскольку равномерно непрерывно на и экспоненциально стремится к равномерно, существует положительное целое число такое, что для всех. Следовательно, . Поскольку было произвольно и достаточно мало.
Доказательство теоремы 1.4. Предположим, что отображение сопряжения абсолютно непрерывно, тогда и почти всюду. Для всех натуральных чисел функция удовлетворяет Логарифмируя, получаем Обозначим, ясно, что.Предположим от противного, что существует такое, что мера Лебега множества не сходится к 0, когда стремится к бесконечности. Следовательно, для всех положительных целых чисел: Но не стремится к 0, когда переходит в. Следовательно, не стремится к 0 при переходе в, это противоречит утверждению 4.2 и завершает доказательство теоремы 1.4.
Благодарности
Авторы благодарны Джалилову А.А. за полезные обсуждения и благодарны Universiti Kebangsaan Malaysia за финансовую поддержку грантов UKM-MI-OUP-2011 и UKM-DIP-2012-31.Они также благодарят рецензента за комментарии, которые улучшили представление этой статьи.
страница не найдена — Williams College
’62 Центр театра и танца, ’62 Центр
касса 597-2425
Магазин костюмов 597-3373
Менеджер мероприятий / Помощник менеджера 597-4808 597-4815 факс
Производство 597-4474 факс
Магазин сцен 597-2439
’68 Центр карьерного роста, Мирс 597-2311 597-4078 факс
Academic Resources, Парески 597-4672 597-4959 факс
Служба поддержки инвалидов, Парески 597-4672
Прием, Вестон-холл 597-2211 597-4052 факс
Программа позитивных действий, Хопкинс-холл, 597-4376
Africana Studies, Hollander 597-2242 597-4222 факс
Американские исследования, Шапиро 597-2074 597-4620 факс
Антропология и социология, Холландер 597-2076 597-4305 факс
Архивы и специальные коллекции, Sawyer 597-4200 597-2929 факс
Читальный зал 597-4200
Искусство (История, студия), Spencer Studio Art / Lawrence 597-3578 597-3693 факс
Архитектурная студия, Spencer Studio Art 597-3134
Фотография Студия, Spencer Studio Art 597-2030
Printmaking Studio, Spencer Studio Art 597-2496
Студия скульптуры, Spencer Studio Art 597-3101
Senior Studio, Spencer Studio Art 597-3224
Видео / фотостудия, Spencer Studio Art 597-3193
Asian Studies, Hollander 597-2391 597-3028 факс
Астрономия / Астрофизика, Thompson Physics 597-2482 597-3200 факс
Департамент легкой атлетики, Физическое воспитание, отдых, Ласелл 597-2366 597-4272 факс
Спортивный директор 597-3511
Лодочный домик, Озеро Онота 443-9851
Автобусы 597-2366
Фитнес-центр 597-3182
Hockey Rink Ice Line, Lansing Chapman 597-2433
Intramurals, Атлетический центр Чандлера 597-3321
Физическое воспитание 597-2141
Pool Wet Line, Атлетический центр Чандлера 597-2419
Sports Information, Hopkins Hall 597-4982 597-4158 факс
Спортивная медицина 597-2493 597-3052 факс
Площадки для игры в сквош 597-2485
Поле для гольфа Taconic 458-3997
Биохимия и молекулярная биология, Thompson Biology 597-2126
Биоинформатика, геномика и протеомика, Бронфман 597-2124
Биология, Thompson Biology 597-2126 597-3495 факс
Охрана и безопасность кампуса, Хопкинс-холл 597-4444 597-3512 факс
Карты доступа / системы сигнализации 597-4970 / 4033
Служба сопровождения, Хопкинс-холл 597-4400
Офицеры и диспетчеры 597-4444
Секретарь, удостоверения личности 597-4343
Коммутатор 597-3131
Центр развития творческого сообщества, 66 Stetson Court 884-0093
Центр экономики развития, 1065 Main St 597-2148 597-4076 факс
Компьютерный зал 597-2522
Вестибюль 597-4383
Центр экологических исследований, класс 1966 г. Экологический центр 597-2346 597-3489 факс
Лаборатория экологических наук, Морли 597-2380
Экологические исследования 597-2346
Лаборатория ГИС 597-3183
Центр иностранных языков, литератур и культур, Холландер 597-2391 597-3028 факс
Арабские исследования, Холландер 597-2391 597-3028 факс
Сравнительная литература, Холландер 597-2391
Критические языки, Холландер 597-2391 597-3028 факс
лингафонный кабинет 597-3260
Россия, Холландер 597-2391
Центр обучения в действии, Brooks House 597-4588 597-3090 факс
Библиотека редких книг Чапина, Сойер 597-2462 597-2929 факс
Читальный зал 597-4200
Офис капелланов, Парески 597-2483 597-3955 факс
Еврейский религиозный центр, 24 Stetson Court 597-2483
Мусульманская молитвенная комната, часовня Томпсона (нижний уровень) 597-2483
Католическая часовня Ньюмана, часовня Томпсона (нижний уровень) 597-2483
Химия, Thompson Chemistry 597-2323 597-4150 факс
Классика (греческий и латинский), Hollander 597-2242 597-4222 факс
Когнитивная наука, Бронфман 597-4594
Маршал колледжа, Thompson Physics 597-2008
Отношения с колледжем 597-4057
Программа 25-го воссоединения, Фогт 597-4208 597-4039 факс
Программа 50-го воссоединения, Фогт 597-4284 597-4039 факс
Операции по продвижению, Мирс-Уэст 597-4154 597-4333 факс
Мероприятия для выпускников, Vogt 597-4146 597-4548 факс
Фонд выпускников 597-4153 597-4036 факс
Связи с выпускниками, Мирс-Уэст 597-4151 597-4178 факс
Почтовые службы для выпускников / разработчиков, Мирс-Уэст 597-4369
Девелопмент, Vogt 597-4256
Отношения с донорами, Vogt 597-3234 597-4039 факс
Офис по планированию подарков, Vogt 597-3538 597-4039 факс
Офис грантов, Мирс-Уэст 597-4025 597-4333 факс
Программа крупных подарков, Vogt 597-4256 597-4548 факс
Фонд родителей, Фогт 597-4357 597-4036 факс
Prospect Management & Research, Мирс 597-4119 597-4178 факс
Начало занятий и академические мероприятия, Jesup 597-2347 597-4435 факс
Коммуникации, Хопкинс Холл 597-4277 597-4158 факс
Sports Information, Hopkins Hall 597-4982 597-4158 факс
Веб-команда, Саутвортская школа
Williams Magazines (ранее Alumni Review), Hopkins Hall 597-4278
Компьютерные науки, Thompson Chemistry 597-3218 597-4250 факс
Conferences & Events, Парески 597-2591 597-4748 факс
Запросы Elm Tree House, Mt.Надежда Ферма 597-2591
Офис контролера, Хопкинс-холл 597-4412 597-4404 факс
Accounts Payable & Data Entry, Hopkins Hall 597-4453
Bursar & Cash Receipts, Hopkins Hall 597-4396
Финансовые информационные системы, Хопкинс-холл 597-4023
Purchasing Cards, Hopkins Hall 597-4413
Студенческие ссуды, Хопкинс Холл 597-4683
Dance, 62 Центр 597-2410
Центр Дэвиса (ранее Мультикультурный центр), Дженнесс 597-3340 597-3456 факс
Харди Хаус 597-2129
Дом Дженнесс 597-3344
Райс Хаус 597-2453
Декан колледжа, Хопкинс-холл 597-4171 597-3507 факс
Декан факультета, Hopkins Hall 597-4351 597-3553 факс
Столовая, капельницы 597-2121 597-4618 факс
’82 Grill, Парески 597-4585
Кондитерская, Парески 597-4511
Общественное питание, Дом факультета 597-2452
Driscoll Dining Hall, Дрисколл 597-2238
Eco Café, Научный центр 597-2383
Grab ‘n Go, Парески 597-4398
Lee Snack Bar, Парески 597-3487
Обеденный зал Mission Park, Mission Park 597-2281
Whitmans ‘, Paresky 597-2889
Economics, Schapiro 597-2476 597-4045 факс
английский, Hollander 597-2114 597-4032 факс
Сооружения, здание служебного помещения 597-2301
Запрос на получение автомобиля в колледже 597-2302
Экстренная помощь вечером / в выходные дни 597-4444
Запросы на работу объектов 597-4141 факс
Особые мероприятия 597-4020
Кладовая 597-2143 597-4013 факс
Клуб преподавателей, Дом факультетов / Центр выпускников 597-2451 597-4722 факс
Бронирование 597-3089
Fellowships Office, Hopkins Hall 597-3044 597-3507 факс
Financial Aid, Weston Hall 597-4181 597-2999 факс
Науки о Земле, Кларк Холл 597-2221 597-4116 факс
Немецко-русский, Hollander 597-2391 597-3028 факс
Глобальные исследования, Холландер 597-2247
Программа магистратуры по истории искусств, Кларк 458-2317 факс
Службы здравоохранения и хорошего самочувствия, Thompson Ctr Health 597-2206 597-2982 факс
Санитарное просвещение 597-3013
Услуги интегративного благополучия (консультирование) 597-2353
Чрезвычайные ситуации с опасностью для жизни Позвоните 911
Медицинские услуги 597-2206
История, Холландер 597-2394 597-3673 факс
История науки, Бронфман 597-4116 факс
Лес Хопкинса 597-4353
Розенбург-центр 458-3080
Отдел кадров, B&L Building 597-2681 597-3516 факс
Услуги няни, корпус B&L 597-4587
Льготы 597-4355
Программа помощи сотрудникам 800-828-6025
Занятость 597-2681
Заработная плата 597-4162
Ресурсы для супруга / партнера 597-4587
Занятость студентов 597-4568
Погодная линия (ICEY) 597-4239
Humanities, Schapiro 597-2076
Информационные технологии, Jesup 597-2094 597-4103 факс
Пакеты для чтения курсов, ящик для сообщений офисных служб 597-4090
Центр кредитования оборудования, приложение Додда 597-4091
Служба поддержки преподавателей / сотрудников, [электронная почта] 597-4090
Медиа-сервисы и справочная информация в классе 597-2112
Служба поддержки студентов, [электронная почта] 597-3088
Телекоммуникации / телефоны 597-4090
Междисциплинарные исследования, Холландер 597-2552
Международное образование и учеба, Хопкинс-холл 597-4262 597-3507 факс
Инвестиционный офис, Хопкинс Холл 597-4447
Бостонский офис 617-502-2400 617-426-5784 факс
Еврейские исследования, Мазер 597-3539
Справедливость и закон, Холландер 597-2102
Latina / o Studies, Hollander 597-2242 597-4222 факс
Исследования лидерства, Шапиро 597-2074 597-4620 факс
Морские исследования, Бронфман 597-2297
Математика и статистика, Bascom 597-2438 597-4061 факс
Музыка, Бернхард 597-2127 597-3100 факс
Concertline (записанная информация) 597-3146
Неврология, Thompson Biology 597-4107 597-2085 факс
Окли Центр, Окли 597-2177 597-4126 факс
Управление институционального разнообразия и справедливости, Хопкинс-холл 597-4376 597-4015 факс
Управление счетов студентов, Хопкинс-холл 597-4396 597-4404 факс
Performance Studies, ’62 Center 597-4366
Философия, Шапиро 597-2074 597-4620 факс
Физика, Thompson Physics 597-2482 597-4116 факс
Планетарий / Обсерватория Хопкинса 597-3030
Театр старой обсерватории Хопкинса 597-4828
Бронирование 597-2188
Политическая экономия, Шапиро 597-2327
Политология, Шапиро 597-2168 597-4194 факс
Офис президента, Хопкинс-холл 597-4233 597-4015 факс
Дом президента 597-2388 597-4848 факс
Услуги печати / почты для преподавателей / сотрудников, ’37 House 597-2022
Программа обучения, Бронфман 597-4522 597-2085 факс
Офис Провоста, Хопкинс Холл 597-4352 597-3553 факс
Психология, психологические кабинеты и лаборатории 597-2441 597-2085 факс
Недвижимость, B&L Building 597-2195 / 4238 597-5031 факс
Ипотека для преподавателей / сотрудников 597-4238
Жилье для преподавателей / сотрудников 597-2195
Офис регистратора, Хопкинс Холл 597-4286 597-4010 факс
Религия, Холландер 597-2076 597-4222 факс
Romance Languages, Hollander 597-2391 597-3028 факс
Планировщик помещений 597-2555
Соответствие требованиям безопасности и охраны окружающей среды, класс ’37, дом 597-3003
Библиотека Сойера, Сойер 597-2501 597-4106 факс
Службы доступа 597-2501
Приобретения / Серийные номера 597-2506
Каталогизация / Службы метаданных 597-2507
Межбиблиотечный абонемент 597-2005 597-2478 факс
Исследовательские и справочные службы 597-2515
Стеллаж 597-4955 597-4948 факс
Системы 597-2084
Научная библиотека Шоу, Научный центр 597-4500 597-4600 факс
Исследования в области науки и технологий, Бронфман 597-2239
Научный центр, Бронфман 597-4116 факс
Магазин электроники 597-2205
Машинно-модельный цех 597-2230
Безопасность 597-4444
Специальные академические программы, Харди 597-3747 597-4530 факс
Sports Information, Hopkins Hall 597-4982 597-4158 факс
Студенческая жизнь, Парески 597-4747
Планировщик помещений 597-2555
Управление студенческими центрами 597-4191
Организация студенческих мероприятий 597-2546
Студенческий дом, Парески 597-2555
Участие студентов 597-4749
Программы проживания для старших классов 597-4625
Студенческая почта, Паресский почтовый кабинет 597-2150
Устойчивое развитие / Центр Зилха, Харпер 597-4462
Коммутатор, Хопкинс Холл 597-3131
Книжный магазин Уильямса 458-8071 458-0249 факс
Театр, 62 Центр 597-2342 597-4170 факс
Trust & Estate Administration, Sears House 597-4259
Учебники 597-2580
вице-президент по кампусной жизни, Хопкинс-холл 597-2044 597-3996 факс
вице-президент по связям с колледжем, Мирс 597-4057 597-4178 факс
Вице-президент по финансам и администрированию, Хопкинс-холл 597-4421 597-4192 факс
Центр визуальных ресурсов, Лоуренс 597-2015 597-3498 факс
Детский центр Williams College, Детский центр Williams 597-4008 597-4889 факс
Музей искусств колледжа Уильямс (WCMA), Лоуренс 597-2429 597-5000 факс
Подготовка музея 597-2426
Служба безопасности музея 597-2376
Музейный магазин 597-3233
Уильямс Интернэшнл 597-2161
Уильямс Outing Club, Парески 597-2317
Оборудование / стол для студентов 597-4784
Проект Уильямса по экономике высшего образования, Мирс-Вест 597-2192
Уильямс Рекорд, Парески 597-2400 597-2450 факс
Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет 011-44-1865-512345
Программа Williams-Mystic, Mystic Seaport Museum 860-572-5359 860-572-5329 факс
Исследования женщин, гендера и сексуальности, Schapiro 597-3143 597-4620 факс
Написание программ, Hopkins Hall 597-4615
Центр экологических инициатив «Зилха», Харпер 597-4462
Как разделить прямоугольник в autocad
как разделить прямоугольник в AutoCAD AutoCAD Today — это многофункциональное окно в AutoCAD 2002 и Autodesk Point A.Это упражнение разработано, чтобы помочь вам создать лист чертежа A3 в Paper Space и добавить плавающие видовые экраны. (Если появится диалоговое окно «Создать новый чертеж», выберите «Отменить» и продолжите. Сочетание клавиш для команды прямоугольника — «rec». —J Он управляет пространственным индексом AutoCAD Oct-Tree, который указывает, сколько раз Древовидный пространственный индекс может делиться на ветви, но я постараюсь предложить дополнительную информацию. Команда «EXPLODE» — выделите внутренний прямоугольник — введите.Если он не по центру по вертикали, просто выберите текст, и базовая точка для этого текстового поля должна быть в центре текстового поля (если выровнено по центру по центру). com Как центрировать текст в AutoCAD? На вкладке ленты «Параметрические» выберите геометрическую зависимость «Вертикаль». Вы хотите разместить * Для окна нарисуйте прямоугольник 0. com / support / autocad / Troubleshooting / caas / sfdcarticles / sfdcarticles / How-to-div-hatch-of-complex-area-in-AutoCAD. Мы собираемся рассмотреть одну распространенную проблему, которую многие пользователи AutoCAD уже могут решить.Разделите объекты AutoCAD на равные части. Это очень полезно, если вы хотите увидеть более двух граней определенного компонента. 2) Импортировать свойства раздела. Строит похожие объекты AutoCAD. Заливка (f): продолжить чтение «Создание нескольких копий указанного пути с помощью массива путей в программе AutoCAD». Щелкните, чтобы указать следующую точку, или введите a, чтобы нарисовать дугу. Итак, давайте нарисуем круг между этими двумя прямоугольниками. Узнайте, как использовать команды. Дополнительные сведения о построении дуг см. В разделе «ARC» в справке AutoCAD.Поздравляю;) теперь вы можете добавлять, редактировать или удалять любую из команд AutoCAD. Создает равномерно расположенные точечные объекты или блоки по длине или периметру объекта. Узнайте, как эффективно использовать AutoCAD. После того, как вы укажете масштаб, AutoCAD построит уменьшенную копию прямоугольника в масштабе, и команда «Масштаб» автоматически завершит выполнение. 015 м от средней линии до двух сторон * Разделите панель на три части для W1. Содержание курса: Настройка чертежа. Разделение — это инструмент в AutoCAD, который можно использовать для разделения ваших линий и окружностей на равные части, это зависит от того, сколько сегментов вы хотите, я собираюсь показать вам, что я имею в виду.Это активирует больший прямоугольник под ним. Вы увидите виртуальный лист бумаги, как объяснялось ранее. Вначале это было довольно легко; вы знаете, что 1200 окон — это, по сути, набор прямоугольников со случайной вставкой арки. В этом видео мы увидим, как мы можем измерять и разделять объект. … Теперь мы рассмотрим команду разделения… которая доступна в AutoCAD. Если вам нужно разделить круг для целей графического дизайна, вы можете использовать Adobe Illustrator или InDesign.»Команды AutoCAD: самое главное. У меня есть самолет с кружком на нем. Разделите вид сверху на равные части. Выровняйте средний центр. С помощью отображения краев я могу удалить полные строки, но я хочу удалить участки строк. Нажмите на сплайн и введите количество сегментов, на которые вы хотите разделить сплайн, я выберу 6 сегментов для нашего случая. C. Команда DIVIDE: чтобы разделить геометрию на фиксированное количество частей, используйте команду DIVIDE. Вторая точка вашей линии будет в (40,0).Эта команда помогает создать набор объектов, ранжированных следующим образом: Полярное расположение; Прямоугольное расположение; Обустройство дорожек Совет №1. Просмотр моделей и чертежей через Интернет обеспечивает богатую визуализацию. Мне нужно разделить неправильные формы на равные части. DLU Я нажимаю кнопку «Прямоугольник». Количество сегментов Размещение точечных объектов через равные интервалы вдоль выбранных объектов. Обратите внимание: если вы создадите прямоугольник слева от исходного щелчка, он будет зеленым; если вы создадите его справа, он будет синим.Полярный массив генерирует новые объекты (а) в виде сетки (б) в виде прямой линии в круговом массиве (г) все вышеперечисленное (e AutoCAD предоставляет множество способов выбора объектов на чертеже. Например, возьмите типичный 960 пикселей шириной и разделим 960 на 1. Итак, теперь мы нарисуем смещение нарисованного прямоугольника. В командной строке коэффициент масштабирования равен 0. Вы можете просто ввести длину линии, нажать вкладку, чтобы перейти в поле угла, введите значение угла и нажмите [ввод] Вызовите инструмент Прямоугольник, укажите положение точки его первого угла.Вы не знаете точного размера прямоугольника. Перемещайте объекты из базовой точки во вторую точку смещения. Расширенные инструменты рисования и изменения. 038 х0. элементов с равным интервалом на объекте пути. Значения по умолчанию — 0. Заливка (f): продолжить чтение «Создание нескольких копий указанного пути с помощью массива путей в AutoCAD Software». Войдите в область. Bölünme yerlerine nokta veya Block (Blok) komutuyla blok haline getirilmiş resimler yerleştirilebilir. Введите в командной строке значение угла 45 градусов и нажмите Enter.Текст переместится, чтобы выровняться по вертикали с центром прямоугольника. Следующие инструкции проинформируют вас о том, как правильно настроить параметры AutoCAD. Введите «CAL» в командной строке, как показано на рис. 1. * Аналогичным образом нарисуйте 1 м для W2 и 0. Мне не нужен конкретный размер, просто хочу обвести текст рамкой. Сначала запустите AutoCAD® 1. Как рисовать многоугольник в Android — Команда «Многоугольник» в AutoCAD. Средствами в рецептах является вычитание страницы рабочего листа смешанных дробей и смешанных дробей и моделей площадей, а также практика умножения дробей или деления общей базы на прямоугольник.Например, у пользователей есть прямоугольник размером 100 x 200, и они хотят растянуть размер одной стороны от 200 до 1000. РАЗДЕЛИТЬ. Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. У Шона есть опыт продаж, поддержки и технических специалистов, управленческие навыки в области САПР и 30-летний опыт работы в отрасли. Autodesk. Если вы используете командную строку RECTANG для рисования прямоугольника, вы заметите, что не можете выбрать линию прямоугольника, не выделив прямоугольник целиком. Выберите команду прямоугольника на панели ленты.Вот шаги: * Из (Панель лент)> на ленте (Express Tools)> Нажмите кнопку (псевдонимы команд). Вы можете разделить на равную площадь или равную ширину. a) Divide (d): Create Specified No. Теперь в подсказке указывается, является ли размер круга / паза / прямоугольника постоянным или переменным. Используя команду polygon, мы можем нарисовать несколько фигур, таких как треугольник, прямоугольник, пятиугольник, шестиугольник и т. Д. Как вставить основную надпись в AutoCAD. Чтобы преобразовать его в истинный сплайн, введите SPE в командной строке и нажмите Enter.Убирайся. Строка: L + пробел / ввод. Чтобы разделить многоугольник путем рисования линии, введите d. Пример введите значение угла в командную строку; установить координаты точки. Введите имя слоя для разворачивания. Разделите нижний прямоугольник пополам, проведя линию по его центру. Рисование круга в Autocad 1:21. 07.10.2009 · Итак, если вы найдете свою скорость (GS) в милях / мин, вы можете использовать, как правило, эту скорость, возведенную в квадрат и разделенную на десять. ) Шаг 3: Разделите рисунок на разные формы. AutoCAD — важный инструмент визуальной коммуникации для инженеров-строителей.Введите угол поворота или нажмите Enter, чтобы принять угол по умолчанию, равный 0. Сначала мы спросим нас, какой объект мы хотим разделить, чтобы мы выбрали этот объект. Представляем вам отличное интерактивное обучение AutoCAD, которое позволяет вам учиться в удобном для вас темпе, не проводя целые дни вдали от офиса или колледжа. Затем скопируйте и вставьте код встраивания на свою веб-страницу. 2. Например, мы можем позволить прямоугольнику представлять одно целое, а затем разделить его на равные части, как показано ниже.Выберите опцию команды «Размеры». … Теперь мы рассмотрим… возможность заключать текст… в объект AutoCAD. Вот что я ищу. Я собираюсь использовать эту линию длиной 20 мм для разделения полилиний, дуг и т. Д. »Метод (м): Выберите вариант« Разделить »или« Измерить ». Система измерения углов. Как и RE. Команды запроса. Выполните следующие шаги, чтобы создать свое собственное золотое сечение: Допустим, нам нужно создать ARRAYPATH в AutoCAD, если мы создадим наш путь с помощью команды LINE, путь будет состоять из множества сегментов линии. Чтобы использовать эту команду, вам необходимо иметь все строки преобразованы в единый объект.Мы можем указать значение от 2 до 32767. Вы можете нажать стрелку вниз, чтобы увидеть доступные параметры. 3 ° к другому. Пользователям не нужно использовать калькулятор вне окна AutoCAD. Вы получите около 594, что составляет ширину вашего основного столбца с содержанием. Установка значения -3020 сглаживает индекс Z, давая вам более детализированные узлы в XY, что приводит к более быстрому выбору объекта. (Точность развертки будет увеличиваться с увеличением количества сегментов, на которые вы разбиваете вид конуса в плане. Сопряжение: F + пробел / ввод.. Как рассчитать площадь в AutoCAD. Перетащите курсор и укажите высоту правого треугольника. Чтобы продемонстрировать, как разделить многоугольник на 3 части, мы намеренно добавляем цвета. В зависимости от того, какой шаблон использовался для создания чертежа, прикрепленные масштабы могут отличаться от файла к файлу. Чтобы ввести местоположение, щелкните правой кнопкой мыши и выберите Абсолютные X, Y, Z или нажмите F6. Трехмерный прямоугольник — это просто прямоугольник, который был выдавлен до определенной высоты, что придает ему высоту, ширину и длину.Или 3) Затем выберите линию или объект, который вы хотите разделить. 2) Щелкните один из углов поля страницы и перетащите рамку в противоположный угол, чтобы покрыть всю область поля, но не отпускайте кнопку мыши. По теме: Разделите объекты AutoCAD на равные части. Когда вы беретесь за рукоять, смотрите на командную строку! Вы увидите короткий список доступных вам опций, включая «Базовая точка» и «Копировать». 【Сайт для бесплатной загрузки САПР】-Блоки Autocad, Детали, 3D Кухонный полуостров представляет собой сплошную черную границу между кухонной и обеденной зонами.html. Теперь мы узнаем, как мы можем создать основную надпись в AutoCAD. ЧЕРТОВАНИЕ УСИЛЕНИЯ: — С помощью круга нарисуйте арматуру 20 мм в левом углу методом tan — tan — radius — выберите круг и создайте зеркало в нижнем левом углу — Разделите линию командой «DIV» и разделите ее на 5 сегментов. Создаются 4 точки. Разделить и измерить в AutoCAD. Курс рассчитан на новичков, поэтому все темы начинаются с нуля и подробно объяснены. Сочетание клавиш, которое мы используем для команды разделения, — это клавиша «D + I + V + Enter».элементов с равным интервалом на объекте пути. Преобразование полилинии в линию. Как только мы воспользуемся командой разделения, она сначала попросит нас выбрать объект, который мы хотим разделить, поэтому мы выберем этот объект. Смотрите полный список на Educba. Залейте квадрат серым цветом. Разделив «DIV» разделите верхнюю строку на 4 сегмента. REC — REC для прямоугольника, вы можете нарисовать прямоугольник в AutoCAD, используя эту опцию ARC — эта команда используется для создания дуги в AutoCAD POL — как следует из названия, она предназначена для рисования многоугольника в рабочем пространстве AutoCAD.9 нм рад. В Illustrator: 1) нарисуйте прямоугольник вокруг области, которую нужно обрезать; 2) выделите прямоугольник; 3) нажмите «Объект»> «Область кадрирования»> «Создать»; 4) прямоугольник исчезнет; 5) щелкните Файл> Печать и выберите принтер или, если создается PDF-файл, выберите Adobe PDF в качестве принтера; 5) нажмите «Настройка» и установите «Обрезать иллюстрацию» на «Область обрезки»; 6) нажмите кнопку «Печать», чтобы распечатать файл или создать PDF-файл. Подробнее >> Команда ARRAY в AutoCAD — это волшебная команда, которую вы часто запрашиваете при работе в AutoCAD.INSERT и выберите DIV DIVIDE Вставляет точечный узел в заданное деление. REC RECTANG Нарисуйте прямоугольник. Используйте команду «Разделить» на ленте. Обрежьте прямоугольник. Использование команды BOX Один из способов создания трехмерного прямоугольника в AutoCAD: использование команды BOX. Список быстрых команд: Area Area / AA. … И вы можете видеть, что новый рисунок называется… EnclosingTextinObject. Я не могу нарисовать прямоугольник, используя 2 точки. В рубрике: Подпрограммы AutoLISP. В этом видео мы увидим, как мы можем использовать команду «Многоугольник» в AutoCAD и как рисовать многоугольник в Android.Вот одно слово «Face», да, согласно вашей концепции, это будет лицо, но при черчении это не лицо, это просто li. Иногда в AutoCAD у вас есть группа объектов, все заблокированные в одном объекте. Они вычисляют такие частные при умножении целых чисел и смешанных рабочих листов или целых чисел, чтобы увидеть, что лучше всего просто показывать ленивые загруженные изображения. Выберите область, которую вы хотите разделить, щелкните правой кнопкой мыши и выберите «Изолировать объекты»> «Изолировать объекты» 3. ПЕРЕИМЕНОВАТЬ МЕНЮ: НАРИСОВАТЬ. > ТОЧКА> РАЗДЕЛЕНИЕ — разделение выбранных объектов на сегменты равной длины по точкам.Вы с легкостью изучите команды и методы создания, редактирования и печати чертежей в AutoCAD! Вы увидите запрос> Площадь. Введите в командную строку значение его длины 40 мм. Затем мы можем циклически найти инструмент. Разделите круг (или дугу) на равные части. я. Дайте команду растяжения и выберите объект. Габаритные размеры . Полный курс для изучения AutoCAD 2D с нуля до профессионального уровня с более чем 100 практиками… Пользователи также могут использовать калькулятор в окне AutoCAD. Он является автором нескольких получивших признание критиков книг по AutoCAD Map 3D, Civil 3D и Land Desktop.Если вы измените границу, поле автоматически обновится с новой площадью, указанной в акрах. Что вы узнаете. … Итак, вы можете видеть, что у меня есть круги, прорези и прямоугольники… на новом рисунке в виде фрагментов текста. РАЗДЕЛЕНИЕ / Создает точечные объекты или блоки, равномерно распределенные по длине или периметру объекта. Если вы вставите область в конце выноски, эта область не изменится, если ваш объект изменится в размере. Длина рассчитывается исходя из ширины и площади. 618. Ваша первая угловая точка прямоугольника может быть где угодно, вместо введенной координаты (0,0) вы можете указать и щелкнуть в любом месте в качестве первой угловой точки прямоугольника.… Например, круг, прорезь или прямоугольник. Щелкните инструмент Прямоугольник и щелкните карту, чтобы создать первый угол. Если вы забыли математику в девятом классе, эллипс — это что-то вроде сжатого круга, хотя, возможно, правильнее будет сказать, что круг — это не сплющенный эллипс. Вы можете рисовать из узла или размещать объекты вдоль узлов. Линия должна делиться на количество желаемых секций. Отметить равные точки вдоль диагональной линии. Используйте квадрат / угол 90 градусов, чтобы провести линии от точек диагональной линии до исходной детали. DraftSight имеет многие из тех же команд, что и В AutoCAD есть — и некоторые из них, которых нет в AutoCAD, например Power Trim.Один из наших участников, Ast, предлагает лучшее решение: нарисуйте арку, а затем измените ее с помощью инструмента удлинения. Метод (m): выберите вариант «Разделить» или «Измерить». Подпрограмма LSP или какой-нибудь простой способ взять любой заданный прямоугольник и разделить его на «x» прямоугольников? Я могу запустить макрос для этого, но ТОЛЬКО если прямоугольник имеет те же размеры, что и в макросе. Дуга: ARC + пробел / ввод. Математически эллипс определяется большой (длинной) осью и […] Используйте параметр поворота после выбора первого угла прямоугольника.Для сложных форм вам может потребоваться несколько 3D-граней для заливки поверхности. ) Укажите первое расстояние фаски для прямоугольника. Вы можете изменить выравнивание однострочного текста, выделив его на чертеже, а затем используя палитру свойств для настройки свойства «Выравнивание». Шаги перечислены ниже: Выберите внешний прямоугольник. Привязка к средней точке одной из горизонтальных линий, а затем привязка к точке вставки текста. Нижняя кнопка — «Разделить твердое тело». Команда: RECTANG Укажите первую угловую точку или [Фаска / Высота / Сопряжение / Толщина / Ширина]: (укажите P1) Укажите другую угловую точку или [Размеры]: (выберите P2) Команда «Прямоугольник» также имеет ряд параметров.Фактически, это очень распространенная проблема, с которой сталкиваются пользователи AutoCAD Civil 3D. У Шона есть опыт продаж, поддержки и технических специалистов, управленческие навыки в области САПР и 30-летний опыт работы в отрасли. Последовательность команд. #autocad советы #areainautocad #autocad hacks #autocad. Здравствуйте, друзья, в этом уроке я покажу вам, как разделить некоторые фигуры на равные области с помощью простых шагов в советах и приемах AutoCAD. Среднее геометрическое равняется периметру (или площади) любого прямоугольника стороне (или площади) конкретного квадрата.элементов на заданном интервале расстояния. К счастью, выдавленные круги автоматически получают сплошную верхнюю и нижнюю части, поэтому вам не нужны трехмерные грани. Инструмент Удлинить позволяет определить общую длину объекта, включая арку. МТЕКСТ. Пример многоугольника, созданного с помощью параметра «Прямоугольник». Изучите горячие клавиши и команды AutoCAD с помощью руководства по сочетанию клавиш AutoCAD, которое поможет вам работать быстрее и эффективнее при использовании программного обеспечения AutoCAD. 4. В качестве дополнительной функции многократное растяжение будет делить каждый элемент поровну, так что пропорции всегда будут одинаковыми.… Итак, у нас есть для вас новый рисунок,… и что мы собираемся сделать, так это… мы собираемся разделить нашу линию… которая находится на слое объектов… на группу равных сегментов. Как использовать команду разделения в Autocad 2017? Команда DIVIDE: выберите инструмент Divide на развернутой панели Draw на вкладке Home, вы также можете использовать его эквивалент команды DIVIDE. В столбце «Цвет» этого слоя щелкните образец цвета и выберите цвет. Скачать без регистрации. Найти Отображаются следующие запросы. Учитывая это, и желаемые 3 области, и указанный угол, он творит чудеса.Построение сопряжения с обрезкой и без вырезания всех объектов округления. Вы можете заблокировать атрибут, выбрав его и выбрав команду меню «Заблокировать выбранные» в меню «Каналы». Использование здесь слова «вычислить» звучит сложно. 3. Эта линия поможет вам оценить, насколько хорошо вы отцентрировали остальную часть изображения. П р о п е р т и ц и е с о ф о ф а н и я С е к т и н и я С е к т и н о н о в А у т о C A D 3 | P a g e Tutorial-1: Computing section Properties of HEB 100 1) Откройте AutoCAD и нарисуйте HEB 100 Section.С его помощью AutoCAD будет искать и выбирать все другие объекты, похожие на выбранные вами объекты AutoCad :: Can’t Draw A Rectangle Using 2 Points 2 июня 2011 г. Теперь вы связали поле с дополнительным форматом с объект в AutoCAD. внутри этого листа бумаги вы увидите пунктирный прямоугольник. Рик Эллис работал и преподавал AutoCAD Map 3D с середины 90-х, наряду с Civil 3D и другими продуктами Autodesk. Команды запроса. AutoCAD 2013 :: Разделение эллипса на отрезки с требуемым средним расстоянием по оси ординат 20 февраля 2013 г.Установите угол поворота. б) Измерение (м): создать указанный номер. Разрыв: создать зазор между двумя точками объекта. 3 DİKDÖRTGEN (Прямоугольник) 4 S-BİRLEŞİK İZGİ (Сплайн) 5 SINIR-BÖLGE OLUTURMA (Граница) 6 UZUNLUK DEĞİŞTİRME (Удлинение) 7 SÜNDÜRME (Растянуть) 8 OBatchMALLERİ (Растянуть) 8 OBatchMALLERİ (Растянуть) 11 ÖZELLİKLER (Недвижимость) 12 OBJELERİ KIRMA (Разрыв) 13 OBJELERİ BÖLME (Разделить, Измерить) Существует несколько различных способов разделить круг на равные части. сеть.Вы хотите разместить 5 деревьев одинаково на линии. Как вы видели, это один объект, который можно изменить и работать с ним проще, чем с четырьмя отдельными линиями. Есть одно лицо и стороны. Выберите опцию общей длины, затем введите желаемое расстояние. DIVIDE: вставляет точечный узел в заданное деление: DO: DONUT: нарисуйте сплошную форму пончика: DV: DVIEW: вид в перспективе: E: ERASE: стереть выделение: EX: EXTEND: расширить выделение: F: FILLET: нарисовать дугу между 2 пересекающиеся линии: FI: FILTER: открывает диалоговое окно фильтра: FLATTEN: FLATTEN: преобразует 3D в 2D: G: GROUP: запускает диалоговое окно группы: H: HATCH: открывает диалоговое окно штриховки и градиента: I: INSERT A.Чтобы нарисовать прямоугольник, сначала перейдите на панель рисования, затем щелкните прямоугольник, просто введите «прямоугольник» в командной строке. Вы можете использовать эту команду, чтобы разделить любую 2D-геометрию на множество равных частей. Параметр «Разделить твердое тело» разрежет твердое тело на две части, но сохранит их оба в этом файле. Теперь проведите линии от двух средних точек многоугольника через прямоугольник. Выберите инструмент «Прямоугольник» (M) на панели инструментов. Работа с внешними ограничениями в AutoCAD Команда «Стереть в AutoCAD Line» Дуга в AutoCAD «Прямоугольник» Команда «Многоугольник» Команда «Срез» в AutoCAD 3D используется для разрезания или разделения элемента «Разделить»: разделяет объект на указанное количество равных частей от 2 до 32 767 частей.Этот курс предназначен для тех, кто занимается или пытается повысить свою карьеру в качестве инженера, архитектора или чертежника. Это достигается путем рисования линий… Вы можете скачать утилиту UnfoldRS с www. Инструменты рисования. (Фаски используются для создания наклонных кромок. Какая команда используется для разделения объекта на равные сегменты (a) Разделить (b) Фаска (c) Обрезать (d) Действие 7. Как выполнить (построить) сопряжение в AutoCAD с автоматическим округлением углов полилинии, параллельные линии, отличные от 1) Создайте новый документ InDesign и выберите инструмент Rectangle Frame Tool на боковой панели инструментов или просто нажмите F.Все это можно сделать с помощью команды (ALIASEDIT). В области рисования выберите объект, к которому должен прикрепиться символ. В выражении я набрал (END + END) / 2. Выберите «Программы / Autodesk / AutoCAD 2005 или LT / AutoCAD 2005 или LT 3». Задняя поверхность была обрезана. Вы пытались нажать R [ввод], ну, это не та кнопка. Затем вам нужно будет преобразовать линию в полилинию. Как вы понимаете, с учетом огромных возможностей AutoCAD доступно множество команд. Прошу прощения за технический жаргон.Найти Отображаются следующие запросы. Это позволит AutoCAD узнать, что мы хотим найти две конечные точки, просуммировать координату и, наконец, разделить ее на два. элементов на заданном интервале расстояния. Прежде всего, вы должны нарисовать конус на высоте и в плане, как показано на Рисунке 1. Примеры: 180 узлов, 3 нм / мин, 0. В нашем случае я буду использовать сплайн. Наличие библиотеки DLL внутри процесса AutoCAD® дает нам некоторый доступ к этим внутренним компонентам, что позволяет нам гораздо более тесно интегрироваться с приложением AutoCAD® и, возможно, достигать гораздо большего гораздо более эффективным способом.Для треугольников умножьте основание на высоту, а затем разделите на 2. Продукт доступен как в облачном, так и в локальном вариантах развертывания. Заливка (f): продолжить чтение «Создание нескольких копий указанного пути с использованием массива путей в AutoCAD Software». dll 4. a) Разделить (d): создать указанный номер. Введите C или Chamfer и нажмите Enter. Появится диалоговое окно, как показано на рисунке ниже: Щелкните область. элементов с равным интервалом на объекте пути. Однако вам придется поискать в Интернете, чтобы найти их.В таком случае вы сможете разделить квадрат на любое количество квадратов, включая квадраты с иррациональными сторонами. Для тех из вас, кто любит печатать, вы также можете ввести MTP или M2P. б) Мера (м): создать заданный номер, который не делится равномерно на 360. Например, у меня есть прямоугольный блок, на 2D-чертеже я хочу разделить одну из линий на три части. Рик Эллис работал и преподавал AutoCAD Map 3D с середины 90-х, наряду с Civil 3D и другими продуктами Autodesk. рис-1.Атрибуты блокировки Заблокированные атрибуты нельзя изменить. Бесплатные блоки CAD в Autocad. Выберите параметр «2 точки» в командной строке. Символ линии разрыва: команда для рисования символа линии разрыва: BREAKLINE. 9. Они вычисляют такие частные при умножении целых чисел и смешанных рабочих листов или целых чисел, чтобы увидеть, что лучше всего в основном показывать ленивые загруженные изображения. Команда прямоугольника в AutoCAD Команда прямоугольника Справка Autodesk щелкните здесь Команда разделения в AutoCAD Выберите область, которую необходимо разделить, щелкните правой кнопкой мыши и выберите «Изолировать объекты»> «Изолировать объекты 3».б) Измерение (м): создать указанный номер. Полилиния: PL + пробел / ввод. Подробности курса AutoCAD 2019 — это мощное программное обеспечение для проектирования и черчения, используемое для создания точных 2D- и 3D-проектов. Чтобы выбрать, щелкните один раз левой кнопкой мыши, чтобы начать прямоугольник выделения, затем щелкните левой кнопкой мыши еще раз в противоположном углу, чтобы завершить прямоугольник выделения. Режим пространства листа AutoCAD немного похож на страницу в альбоме для вырезок, на которую вы можете вставлять различные виды вашего чертежа AutoCAD. Цели В конце этой главы вы должны уметь: находить и вызывать команду «Изменить»; стирать объекты с чертежа.Формула радиуса поворота — Форумы PPRuNe. Один из этих разделов я хочу удалить. Подсчитайте размеры прямоугольника и расположите их в таблице RECDIMS SS Выберите похожие по типу объекта, слою, цвету и типу линий. Использование утилиты SplitArea для разделения области (участка) полилинии на 2 или более равных части с использованием различных методов разделения в AutoCAD DWG. Я наберу MTP. DJL: DIMJOGLINE / Добавляет или удаляет линию излома на линейном или выровненном размере. Та же идея. Работа с текстом. Один из примеров показывает на рисунках ниже, как быстро выровнять весь текст.Вот отличная программа, которая позволяет легко выполнить эту задачу. 1. В этом уроке я использую В этом видео мы увидим, как мы можем измерить и разделить объект в AutoCAD. Использование слова find описало бы это лучше. Когда AutoCAD запросил точку, я набираю «CAL», затем [ввод]. В этом прямоугольнике ваш файл import. Я проектирую здание, в котором одно крыло расположено под углом 37. Каждый вариант также позволяет указать угол поворота, а не длину второй оси. Это даст нам требуемый прямоугольник.Заливка (f): продолжить чтение «Создание нескольких копий указанного пути с использованием массива путей в AutoCAD Software». Раскрытие информации: этот пост может содержать партнерские ссылки, и мы можем получить небольшую комиссию, если вы сделаете покупку. DJO: DIMJOGGED / Создает размеры с изломом для окружностей и дуг. Показана модель dxf. Эта опция предполагает 2 входа: твердое тело и геометрию разделенного профиля. Следуйте командной строке; тогда все должно быть в порядке. Затем нажмите ОК. Щелкните столбец «Прозрачность» для этого слоя, чтобы открыть диалоговое окно «Прозрачность слоя» и введите значение от 0 (полностью непрозрачный, по умолчанию) до 90 (в основном прозрачный).Линн Аллен начинает серию статей, в которых исследуются плюсы, минусы и неприятности перехода от AutoCAD к DraftSight. Постоянно всплывает вопрос о том, как установить правильный масштаб макета при печати. Нажмите Ввод. Это все. AutoCAD 2006 позволяет менять точку вставки «на лету». Из этого курса для начинающих вы узнаете, как начать работу с AutoCAD. Для инструмента AutoCAD Line есть только опция «отменить». Команды масштабирования. Я по-настоящему познакомился с командой DIVIDE, когда меня наняли рисовать окна для брошюры производителя.1. Введите BREAKLINE в командной строке и нажмите клавишу ВВОД. … И что мы там сделаем, так это настроим его так, чтобы он… делился на несколько. Чтобы найти заштрихованную область, показанную выше, нам нужно вычесть площадь круга из прямоугольника. Хорошо, что большинство команд в командной строке также используют аналогичное имя на ленте. Прямоугольник: REC + пробел / ввод. cz / download, загрузите его в AutoCAD с помощью APPLOAD и запустите, набрав команду UNFOLDRS. Укажите вторую точку разрыва, поэтому введите расстояние и угол, под которым должен быть зазор, например @ 2,0 Enter.Наша задача будет заключаться в том, чтобы разбить ломаную линию на X частей, либо разделить ее на части по XX единиц. Ваш прямоугольник готов. html. Перетащите курсор и укажите второй угол правого треугольника. Начните с легкого рисования прямоугольника, который примерно в три раза больше своей ширины. Вы должны увидеть пустой экран. Подключитесь к своим проектам, а также создайте форум 1 десятой 14 мая 2021 г. конец второй, (2) укажите центр и концы каждой оси и (3) создайте эллиптическую дугу.Фактически, это просто замкнутая полилиния, которая автоматически рисуется за вас. Система координат. 31 марта 2020 г. — Полное руководство по AutoCAD (на английском языке) | Курс Design Softwares создан лучшими преподавателями Design Softwares для подготовки полного руководства по AutoCAD (английский язык). 2. Построение многоугольника в Autocad 3:11. Затем мы преобразуем серый прямоугольник в трехмерную фигуру. Выполните одно из следующих действий: Введите L, чтобы ввести длину. Нарисуйте квадратный объект на монтажной области; удерживайте клавишу Shift, чтобы получился идеальный квадрат.Из этого курса для начинающих вы узнаете, как начать работу с AutoCAD. 2. Приближенный метод 1 Нарисуйте прямоугольник со сторонами, равными по длине большой и малой осям требуемого эллипса. Способ-1. Нажмите Ввод. Изучите AutoCAD Basic до продвинутого уровня. Создание слоев. Линии позволяют редактировать небольшие участки немного иначе, чем ломаные линии. Круг: C + пробел / ввод. Как вы можете понять по названию сообщения, это тот факт, что AutoCAD и конкретный образец штриховки OOTB (Out Of The Box), похоже, не очень хорошо ладят друг с другом.Набрав «B» в качестве базовой точки в командной строке и нажав «Enter», вы можете выбрать другую точку для перемещения или растягивания геометрии. После того, как мы нажмем [ввод], AutoCAD запросит конечные точки. ИЗМЕРИТЬ (я): размещает точечные объекты или блоки на объекте через определенные интервалы. Например, если у вас возникли трудности с разделением прямоугольника на равные части, вам может потребоваться повторить математику средней школы. См. Прилагаемый типичный волнистый участок полилинии. 5. С помощью autocad 2008. Постройте дверцы шкафа и сделайте их составными частями.Кто-то сказал мне, что это что-то вроде 900. — [Экранный диктор] Добро пожаловать в еще один совет и уловку для AutoCAD. dwg. 2) Мы можем вызвать команду «Разделить», выбрав инструмент «Разделить» в раскрывающемся меню панели рисования на вкладке «Главная». Количество сегментов Размещение точечных объектов через равные интервалы вдоль выбранных объектов. Вы также можете использовать — =, * = и / = для вычитания, умножения и деления относительных значений. 9) Укажите первую точку, с которой вы хотите начать. Здесь показаны три точки, отмеченные буквами G и H.Введите ПОЛЕ в командной строке AutoCAD и нажмите клавишу ВВОД, чтобы открыть диалоговое окно «Поле». Вы можете изменить это значение по умолчанию от 1 до 100 по своему желанию. Чтобы установить угол с помощью указателя, переместите указатель и щелкните карту. Выполнять функции AutoCAD. Нажмите Enter, чтобы выйти из команды. Он предлагает 2D-документацию, 3D-дизайн и функции совместной работы в рамках пакета. Шон Брайант описывает основы пользовательского интерфейса, показывая, как использовать ленту, выбирать рабочие пространства и использовать ViewCube.Я разбил вид сверху на двенадцать (12) равных сегментов. Autodesk. Это то, что я использую очень часто. Что вам нужно сделать, это дважды щелкнуть мышью в области сплошного прямоугольника, выделенной на рисунке ниже. Это прямоугольник с углами на всех четырех сторонах, образующих восьмиугольник. . Подробнее >> Видео Линн Аллен дает пользователям AutoCAD краткий обзор DraftSight 12 ноября 2020 г. Выберите элемент с помощью инструмента «Выбрать объект участка» и щелкните правой кнопкой мыши «Разделение участков». Выбрать объект для разделения Задает один геометрический объект, например линию, полилинию, дугу, окружность, эллипс или сплайн.Поэтому установите размер и стиль точки с помощью команды DDPTYPE перед запуском этого 7) Мы можем вызвать команду Ray, выбрав Ray в раскрывающемся меню панели рисования или набрав «RAY» на панели команд. Эта последняя группа команд AutoCAD используется для получения информации о положении и природе объекта чертежа. Эллипс методом фокусов. 22) Как изменить стиль точки в AutoCAD? Мы используем точки в командах «Разделить», «Измерить» и «Несколько точек». Когда меня спрашивают о начальной точке, я привязываюсь к середине вершины предыдущего прямоугольника.е. круг, который касается всех четырех углов прямоугольника (см. иллюстрацию справа). Просто выберите команду строки и введите: 40,60, и это произойдет автоматически. AutoCAD 2020 — это мощное программное обеспечение для проектирования и черчения, используемое для создания точных 2D- и 3D-проектов. Первое, что я бы попробовал: Snap-> Snap Intersection Modify-> Divide щелкните по горизонтальной линии щелкните на первом пересечении горизонтальной линии с помощью прямоугольника щелкните по горизонтальной линии щелкните по второму пересечению горизонтальной линии с помощью прямоугольника нажмите дважды щелкните правой кнопкой мыши или дважды нажмите клавишу Esc на клавиатуре и выберите часть горизонтальной линии. Введите C для круга, введите S для гнезда или введите R для прямоугольника и нажмите клавишу ВВОД.Найдите кнопку «ЗАПИСАТЬСЯ СЕЙЧАС» в конце сообщения. Например, если растянуть 3 окна на виде сбоку, используя многократное растяжение на 12 дюймов, каждое окно переместится на 4 дюйма. Прямоугольник вообще не является объектом AutoCAD. Это создает плоские стороны головки болта. Google. facebook. В области рисования щелкните, чтобы указать вершины выноски, и нажмите ENTER. Введите от и Enter, выберите точку, с которой нужно начать смещение, затем введите расстояние, например @ 12,0, Enter.Показывать. Мы можем просто нажать левую кнопку мыши и нарисовать прямоугольник из его начальной точки и отпустить эту кнопку в конечной точке. Метод (m): выберите вариант «Разделить» или «Измерить». Дело в том, что на приведенной ниже диаграмме высоты треугольников $ BEF $ и $ EGH $ равны, поэтому, если основания равны, равны и площади. Сложите все вместе, и вы получите макет из двух столбцов с шириной золотого сечения. Введите команду: NETLOAD нажмите ENTER. Выберите SectionProperties. Примечание: я думаю, что проблема все еще сохраняется и в других пользовательских конкретных шаблонах.Используйте Интернет, предоставляя вам недавно использованные файлы, советы, методы, ленты новостей и доступ к DesignCenter. Один из наиболее распространенных — полилинии в линии. Tagged as: 2011, AutoCAD tutorials, basic, beginner, draw, how to, rectangle Я хочу разделить линии на 2D-чертеже. ☑ Как нарисовать прямоугольник двумя разными способами. Рик продолжает использовать AutoCAD Map 3D в проектах в производственной среде, в дополнение к обучению DwgShare Resources загрузить веб-сайт Autocad Blocks for Designer.com / SLkh В этом видео мы увидим, что такое команда AutoCAD Rectangle, и научимся рисовать прямоугольник в AutoCAD. Запишитесь сейчас! Инструмент предназначен для «нормализованных» полилиний. …. Соберите коробку шкафа и сделайте ее составной частью. Метод содержания (m): выберите вариант «Разделить» или «Измерить». Нажмите кнопку «Пуск» в нижнем левом углу экрана. AutoCad 3D :: Прямоугольник в сетку; AutoCad 2D :: Прямоугольник вокруг объекта? AutoCAD Civil 3D :: разделение прямоугольника; РЕКЛАМА AutoCAD.Проведите линию поперек прямоугольника так, чтобы верхняя треть превратилась в квадрат. Начнем с команды «Разделить». Я собираюсь использовать Lofted Boss / Bass от моего прямоугольного лица до круга, придавая лицу изогнутую поверхность до круга. Пользователи могут быстрее рисовать прямоугольник или квадрат с фактическими размерами в AutoCAD. Он предназначен для охвата всех команд и функций, которые позволят вам не только сдать экзамен Autodesk Certified Professional в AutoCAD, но также помогут вам эффективно создавать чертежи в повседневной работе.50 м для W1 и отразите прямоугольник с другой стороны. Начнем с команды «Разделить». cadstudio. Растянуть: растягивает объекты в AutoCAD. Количество созданных точечных объектов на единицу меньше, чем в этом видео. В этом видео показано, как с помощью очень старой и полезной техники разделить квадрат или прямоугольник в различных ракурсах на идеальные трети. размер. 3. Простыми являются квадрат и прямоугольник, круги и треугольник могут быть немного сложными. Прежде чем я углублюсь в подробности создания списка — а затем взгляну на список «Рисование прямоугольника» в Autocad 4:28.Перейдите на вкладку «Аннотации» панель «Символ» «Конус и уклон». Я ищу методы, теории, алгоритмы для разделения площади неправильной формы (например, земельного участка, участка земли, многоугольника) на равные части по размеру или эквивалентные части по стоимости земли. Выберите линию, которую вы хотите разорвать. 6. Выберите режим Polyline и выберите ранее созданный объект rulesurf. В командной строке появляется следующая подсказка: Длина прямоугольника: Вы можете ввести длину 40 мм в командной строке или указав две точки на чертеже с помощью мыши.Если весь текст на чертеже выровнен. После выбора объектов мы должны указать количество сегментов. Это превращает все, включая текст и пользовательские типы линий, в полилинии. Привет, меня зовут Маха. Мне нравится команда DIVIDE AutoCAD. В чем разница между командами DIVIDE и MEASURE? Вы используете команду DIVIDE, чтобы разделить объект, и вы используете команду MEASURE, чтобы измерить и объект. Введите CURSORSIZE в командную строку. Затем AutoCAD последовательно запрашивает у меня центральную точку, начальную точку и конечную точку.Этот прямоугольник часто можно увидеть в искусстве, поскольку, как говорят, он самый приятный для глаза из всех подобных прямоугольников. Обучающее видео по AutoCAD для начинающих, чтобы шаг за шагом изучить основы AutoCAD. См. Онлайн-справку ESRI (отдел посылок). Тема: 1) разделите линию в Autocad 2) разделите линию поровну с помощью простой рекомендации 3) разделите линию на нужные части в чертеже Autocad. …. Щелкните на чертеже, чтобы указать первую точку линии. a) Разделить (d): создать указанный номер.Диалоговое окно «Разделить» содержит три кнопки с левой стороны, представляющие параметр приложения. я. На этот раз я набираю заглавную букву в опции C, чтобы указать центральную точку. При работе в AutoCAD часто бывает необходимо преобразовать типы линий. Но для того, чтобы взаимодействовать с внутренними компонентами AutoCAD®, программисты должны знать, что это за внутренности. Сочетание клавиш, которое мы используем для команды разделения, — это клавиша «D + I + V + Enter». ☑ Как нарисовать линию и полилинию. Использование утилиты SplitArea для разделения области полилинии (участок Щелкните вкладку «Главная»> панель «Рисование»> «Прямоугольник».Вам нужно нарисовать описанный круг i. Смещение 20 мм от 1-го прямоугольника и 100 мм от 2-го прямоугольника. — [Инструктор] Итак, вот еще один совет и хитрость AutoCAD. com / file / d / 1SIvcbJiPooE66o5N3vwpf7f_R6p1Ov_T / view? usp = sharingsподдержите нас на странице Facebook: https: // web. Динамически щелкните точку в области рисования, эта прямоугольная область от базовой точки до точки выбора будет действовать как область, в которой будет создан массив. Рисунок хорошо смотрится. Команда AutoCAD ELlipse проста в использовании.На картинке вы можете увидеть, как измеряется общее расстояние между начальным и конечным столбцами прямоугольного массива AutoCAD. Он является автором нескольких получивших признание критиков книг по AutoCAD Map 3D, Civil 3D и Land Desktop. ”Для панорамирования щелкните и перетащите колесо прокрутки. Построение дуги в Autocad 1:27. AutoCAD не позволяет указывать точки на закрашенном чертеже. Как только мы зададим угол поворота, AutoCAD сгенерирует прямоугольник, повернутый против часовой стрелки на 45 градусов, и команда «Повернуть» завершится.Выберите Divide Blocks for Division: MEASURE command: Start Free Account. Массив: используется для создания массивов в AutoCAD. рис-1. Этот курс в основном создан с использованием AutoCAD 2018, но включает в себя все новые и обновленные функции версий 2019, 2020 и 2021. Узнайте больше об этом и многом другом, посетив наш учебный курс Basic Essentials AutoCad. Когда меня просят указать противоположный угол, я набираю @ 23-3 / 4 «, 18-3 / 16» и нажимаю Enter. AutoCAD Civil 3D :: Как разделить область на 3 равные части 7 июля 2012 г. 7. Вам нужна лицензия на редактор или ArcInfo.Справа от многоугольника (на одной линии с кругом) нарисуйте прямоугольник той же высоты, что и круг, и задайте ему правильную ширину. 4. Периметр — это длина контура фигуры. Добро пожаловать в AutoCAD Все! Мы предлагаем совершенно БЕСПЛАТНУЮ справку по AutoCAD — Задайте свой вопрос СЕЙЧАС Результаты с 1 по 3 из 3 Тема: разделение периметра прямоугольника на равные промежутки Выберите точку, в которой вы хотите разделить объект; Когда будет предложено указать вторую точку останова, введите @ и Enter; Примечание. Вы, вероятно, знаете, что @ означает последнюю выбранную точку, поэтому AutoCAD разбивает объект в первой выбранной точке, и он становится двумя объектами.Внутри этого пунктирного прямоугольника вы увидите сплошной прямоугольник. Создайте прямоугольник, чтобы показать панели. Щелкните правой кнопкой мыши и выберите параметр «Свойства». CBRK CBRKA LPL Суммируйте длину полилинии и создайте текстовую метку для суммирования LPL RECDIMS. Радиус 9 нм 300 узлов, 5 нм / мин, 2. Если вы когда-либо пробовали команду РАЗДЕЛИТЬ на полигональной линии, вы знаете, какое разочарование обычно следует за этим приключением. Убедитесь, что поле выбрано (если нет, используйте Selection Tool), а затем перейдите в Effect> 3D> Extrude & Bevel.Например, у нас есть фэнтези, и нам нужны колонны через каждые 10 метров. Нажмите Enter, чтобы выйти из команды. [EC202 AUTOCAD ТЕМА ИЗМЕНИТЬ КОМАНДУ] декабрь 2010 г. 1 ИЗМЕНИТЬ КОМАНДУ. Введите V для переменного размера и нажмите Enter. Я хочу разделить площадь на 3 равные части в autocad civil 3D, но не знаю как? Просмотр ответов 6 Просмотр связанных элементов AutoCAD Architecture :: Как разделить элементы неправильной формы на равные части 13 сентября 2013 г. с заданным интервалом расстояния. Разделите прямоугольник на 6 частей равной площади. Заблокированные атрибуты будут иметь серый прямоугольник слева от значения канала. Вычитание страницы рабочего листа смешанных дробей и смешанных дробей, а также моделей площадей и практики умножения дробей или деления общей базы на прямоугольник в рецептах.8) нажмите клавишу Enter. В этом примере я активирую круг. е. Например, 1. Наиболее эффективные способы редактирования геометрии в AutoCAD 2002. Прямоугольник. Начать изучение AutoCAD. Тест 1. Измерение: помечает объекты с интервалом в 1. Рассмотрим следующий сценарий: вы нарисовали прямоугольник в AutoCAD. Это запустит команду Spline Edit, выберите «polyline spline» в области рисования и нажмите Enter. Ширина рассчитывается исходя из длины и площади. начать первую точку линии. е. Здания, мосты и городские пейзажи оживают в AutoCAD и позволяют инженерам, клиентам и общественности лучше понять конкретный проект.Например, вы можете использовать прямоугольные массивы, чтобы заполнить аудиторию стульями или […] Вы можете использовать команду «Разделить», чтобы разделить край (щелкните правой кнопкой мыши край> Разделить> введите количество делений. Поверните объекты вокруг базовой точки. Соответственно , расстояние между прямоугольным массивом столбцов автоматически рассчитывается из набора общего расстояния. Шаг 4: Рассчитайте площадь каждой формы с помощью нашего калькулятора площади в футах. Выберите объект или [DElta / Percent / Total / DYnamic]: T .Даже тем, кто годами пользуется AutoCAD, иногда следует следить за командной строкой. Мы уже видели шаг 4, в котором функция (команда) используется для выполнения команд AutoCAD. Теперь, когда мы рисуем один лист формата А4, нам нужно очень внимательно относиться к его размерам. Помните, что дробь — это количество затененных частей, деленное на число. Итак, строки идут в этом направлении и делят прямоугольник на четыре равные части. 8. AutoCAD 2019 — это мощное программное обеспечение для проектирования и черчения, используемое для создания точных 2D- и 3D-проектов.Если вы разорвали связь между объектом и полем, просто щелкните правой кнопкой мыши и повторно выберите объект, следуя шагам, описанным выше. Я надеюсь, что это окажется полезным по крайней мере для некоторых из многих людей, которые, как я ожидаю, воспользуются этим инструментом. Описание. Настоящий рисунок немного сложнее, но идея та же. AutoCAD 2019 — это мощное программное обеспечение для проектирования и черчения, используемое для создания точных 2D- и 3D-проектов. Сурса: знания. Если вы обратили внимание на список команд AutoCAD, вы заметили бы командную строку AREA.Это подсказывает ответ на случай прямоугольника. Например, вы хотите создать прямоугольник. Двухмерная полилиния будет преобразована в настоящий сплайн, а также унаследует все свойства сплайна. Как в Autocad разделить прямоугольник на 4 равные части? Команда DIVIDE: выберите инструмент Divide на развернутой панели Draw на вкладке Home, вы также можете использовать его эквивалент команды DIVIDE. В AutoCAD мы рисуем 1: 1 в пространстве модели с нашими (заранее) определенными единицами. ) Чтобы вычислить площадь комнаты, состоящей из нескольких прямоугольников, как в примере выше, вы можете выбрать 6 точек, чтобы определить 3 формы прямоугольника.В этом курсе инструктор Шон Брайант выходит за рамки основ, описанных в «Изучение AutoCAD 2020», и предоставляет вам информацию, необходимую для грамотного использования AutoCAD в любой отрасли. Нажмите кнопку «Новый слой» и назовите слой. Введите A в поле Area. Команда -ARray представляет собой усиленный копи-скрипт: ее можно использовать для создания прямоугольной сетки объектов в AutoCAD 2014 с регулярными интервалами X и Y или радиального расположения объектов вокруг центральной точки с постоянным угловым интервалом. Полилиния — это объект в AutoCAD, состоящий из одного или нескольких сегментов линии (или дуги).Получите обзор Autocad, настроек чертежа, эскизов и приложений, функций и команд autocad и многого другого с помощью онлайн-курса autocad. Для большей части оставшейся части класса мы будем обсуждать, как выполнять вычисления. dll в AutoCAD. РАЗДЕЛИТЬ: Здесь также вам будет предложено выбрать угол массива, а затем еще один угол для заливки массива. Увидев отзывы об этой интересной функции в AutoCAD 2013, я решил провести небольшую детективную работу, чтобы установить, какие команды можно вызывать из AutoCAD 2013 Core Console.Пользователи, всегда используйте калькулятор для получения точных размеров за пределами окна AutoCAD. Я не уверен на 100%, но мне кажется, что я видел пару программ шепелявых, которые претендовали на такую возможность. Команда сопряжения для создания пары скруглений и кромок двух 2D-объектов или граней трехмерного тела в AutoCAD. Подробнее об этой команде можно найти в этой связанной статье. Прямоугольник — это пример уже знакомой полилинии. AutoCAD. Проведите диагональную линию над разделяемой линией.Чтобы найти периметр прямоугольника или квадрата, вам нужно сложить длины всех четырех сторон. Выбрать объект для разделения Задает один геометрический объект, например линию, полилинию, дугу, окружность, эллипс или сплайн. Сочетание клавиш для команды многоугольника в AutoCAD — «POL». По умолчанию AutoCAD показывает точки в виде маленькой точки. Смещение прямоугольника (только в этом примере) 1/32 дюйма. X в данном случае — длина прямоугольника, а y — ширина прямоугольника. Вы увидите, что значение по умолчанию установлено, как показано на рис-1.При появлении запроса укажите угол поворота прямоугольника по сравнению со значением по умолчанию, равным 0 градусов. Здесь для вас около 200 обучающих видео по AutoCAD. Я хочу нарисовать прямоугольник в autocad Electrical с помощью VB. Если вы рисуете эскизы, рисуете чертежи или создаете 3D-модели, вам будут доступны команды, которые упростят вашу работу. a) Разделить (d): Создать указанный номер. Нажмите на сплайн и введите количество сегментов, на которые вы хотите разделить сплайн. Я выберу 6 сегментов для нашего случая.С помощью какой из следующих команд можно нарисовать прямоугольник в AutoCAD? (a) ARC (b) POL (c) REC (d) CO 6. Однако это действительно не лучший способ построить шкаф. Когда вы используете более сложный инструмент AutoCAD, вам, вероятно, потребуется изменить параметры инструмента. Удлинить: предназначен для расширения объектов AutoCAD. Шон Брайант — сертифицированный инструктор Autodesk по AutoCAD и Revit Architecture. Команда «Прямоугольник» в AutoCAD «Прямоугольник» Справка Autodesk щелкните здесь Команда «Разделить» в AutoCAD 2 В наборе инструментов перетащите указатель, пока не найдете «Прямоугольник», а затем отпустите кнопку мыши.Запустите команду «Прямоугольник», введите в командной строке RECTANG, выберите «Прямоугольник» из раскрывающегося списка «Нарисовать» или нажмите кнопку. AutoCAD, Rhino, векторные работы, Sketchup, Revit и другие. Введите W, чтобы ввести ширину. Разделите расстояние OF1 на равные части. Вы должны сделать шкаф более или менее таким, как в реальном мире. РАЗДЕЛЕНИЕ (div): разделение объекта на сегменты определенной длины или периметра. Что это за команда «Выбрать подобное», спросите вы? Команда «Выбрать похожие» позволяет выбирать объекты с общими свойствами.Чтобы сделать правильный рисунок, текст также играет свою роль. com / support / autocad / Troubleshooting / caas / sfdcarticles / sfdcarticles / Как-разделить-штриховку-сложной-области-в-AutoCAD. Да, вам все равно придется выбирать прямоугольник, но это просто вопрос щелчка по каждому объекту один раз, в отличие от необходимости делить прямоугольник, рисовать внутренний прямоугольник, затем выстраивать его, а затем взрывать. «Проблема в том, что в AutoCAD очень много команд и системных переменных. 17.06.2015 · Re: Преобразование дуги и окружности в линейные сегменты Еще один простой способ — использовать WMFOUT и WMFIN.Шаг 2: вы можете найти разделение под панелью рисования и под раскрывающимся списком точек, вы можете ввести его, если не можете его найти. Это достигается путем рисования линий между пересечениями или углами на раме или через пересечения линий внутри рамы. AutoCAD 360 поддерживает 50 форматов файлов, таких как Solidworks, CATIA, Pro-E, Rhino, NX и т. Д. Разделение на равные части Ниже приведены последовательности шаблонов, которые можно использовать для разделения квадрата или прямоугольника на точное количество частей одинакового размера, не выполняя никаких действий. никаких измерений вообще.б) Измерение (м): создать указанное количество элементов на заданном интервале расстояния. Золотой прямоугольник. Библиотека образцов штриховки поможет архитекторам, инженерам более правильно выбирать материалы и штриховку на своих чертежах. Рик продолжает использовать AutoCAD Map 3D в проектах в производственной среде, в дополнение к обучению: a) Разделить (d): Создать заданное число. Курс включает базовые вводные уроки в AutoCAD 2012 2D и 3D. б) Измерение (м): Создать указанный номер. Это число приблизительно соответствует радиусу поворота для типичного поворота с углом крена 25–30 °.AutoCAD — это платформа для автоматизированного проектирования и черчения, предназначенная для предприятий любого размера. элементов с равным интервалом на объекте пути. Нажмите кнопку «Дополнительные углы» в диалоговом окне «Параметры рисования». Используя эту опцию, вы можете нарисовать фигуру от 3 до 1024 сторон. Затем вся эта страница может быть нанесена на график. Следующие несколько разделов будут сосредоточены на том, как получить пользовательский ввод, подготовить и очистить. AutoCAD 2014, AutoCAD 2015, AutoCAD 2016, AutoCAD 2017, AutoCAD Architecture 2014, AutoCAD Architecture 2015, AutoCAD….Шон Брайант — сертифицированный инструктор Autodesk по AutoCAD и Revit Architecture. Масштаб: команда масштабирования объекта. Та же идея, войдите в команду «Круг». NET :: Как рисовать прямоугольник 12 февраля 2013 г. Заливка (f): продолжить чтение «Создание нескольких копий указанного пути с помощью массива путей в программе AutoCAD. 1. В командной строке 1000 нажмите Enter. В этом случае мы скажем, что первая координата (40,60) относится к вашей ПСК. 5 (точка разделительной метки или введите координаты в командной строке), чтобы уменьшить объект в AutoCAD вдвое.* Нарисуйте линию из 1. Сделайте рамку для текста такой же шириной, как прямоугольник. Например, у пользователей есть прямоугольник размером 100 x 200, и они хотят растянуть размер одной стороны с 200 до 1000. При работе с AutoCAD возникают некоторые общие проблемы, с которыми люди сталкиваются. AutoCAD 2014, AutoCAD 2015, AutoCAD 2016, AutoCAD 2017, AutoCAD Architecture 2014, AutoCAD Architecture 2015, AutoCAD…. Ссылка для скачивания компакт-диска: https: // drive. Среди них — бесконечно полезная команда Select Similar. Но мой объект — буква «S», это не простой прямоугольник.Калькулятор золотого прямоугольника — это удобный способ найти золотой прямоугольник вместо того, чтобы работать с ним вручную. Из этого курса для начинающих вы узнаете, как начать работу с AutoCAD. Сдвинуть на 25 мм с обеих сторон по толщине, удалить центральную линию. 1) Эта команда используется для разделения любой линии или объекта на какую-то часть, в которой мы хотим. элементов с равным интервалом на объекте пути. У меня есть трехмерная фигура. … Как обычно со всеми. Программа затем создаст прямоугольник на основе этих значений, сгенерирует две пересекающиеся диагонали из каждого угла прямоугольника, вычислит длину диагонали, отметит их точки пересечения и разделит общую длину диагонали на два , таким образом отмечая длину сегмента от каждого угла прямоугольника до точки пересечения диагоналей.Если вы используете карандаш и бумагу, вам понадобится циркуль, чтобы точно разделить круг на шесть равных частей. Для квадрата это особенно просто. Я ищу LSP для этого. Чтобы получить ширину боковой панели, вычтите 594 из 960, и вы получите 366. Опять же, Rhino автоматически преобразует дроби в десятичные и помещает противоположный угол в правильную точку. 4) После выбора объекта создает равномерно расположенные точечные объекты или блоки по длине или периметру объекта.☑ Как разделить. С центром F1 и радиусом AG опишите дугу выше и ниже линии AB. Копировать: CP + пробел / ввод. Вы просто делите периметр на $ n $ частей равной длины, поэтому, если у квадрата есть сторона $ s $, каждая часть имеет длину $ \ frac {4s} n $. Значок прямоугольника будет выглядеть, как на изображении ниже: Или введите в командной строке Rec или Rectangle и нажмите Enter. Примечание: 100% скидка на коды купонов Udemy действительна не более 3 дней. Разделить: разделить объект на указанное количество равных частей. Преобразование дуги и окружности в отрезки линии — AUGI.279 студентов используют это для подготовки программного обеспечения для проектирования. 50 для V. 10) Нажав на первую точку, мы можем показать разницу в «линии» и «луче». Команда: LENGTHEN. Как сделать парное и угловое скругление в Автокад. Пользователи также могут использовать калькулятор в окне AutoCAD. элементов на заданном интервале расстояния. Разделение на равные части Ниже приведены последовательности шаблонов, которые можно использовать для разделения квадрата или прямоугольника на точное количество частей одинакового размера без каких-либо измерений.Во-первых, изометрический рисунок является двухмерным, следовательно, он является чертежным. От точки разделения проведите вертикальные линии, чтобы разделить ее на ставни. DIVIDE (Bölme) 1. Радиус 5 нм, 420 узлов, 7 нм / мин, 4. Очевидно, группа AutoCAD не смогла прийти к соглашению в том году, поэтому есть два разных пути, которыми вы можете достичь этого. Если у вас есть проблемы с увеличением или уменьшением масштаба, используйте команду REGEN. Перемещение: M + пробел / ввод. SS XPIPE Создание труб в 3D на основе ввода диаметра. XPIPE S2 Создание золотого прямоугольника довольно просто и начинается с простого квадрата.18 июня 2015 г. С добавлением более 300 образцов штриховки для каждой версии AutoCAD существует более 70 образцов штриховки. И я указываю первый угол правого треугольника. Мы можем использовать ту же аналогию, чтобы сказать, что прямоугольник будет образован 4 линиями. * Удалите линию, нарисуйте еще одну линию, соединяющую середину прямоугольника * Смещение 0. Зеркальное отражение: MI + пробел / ввод. Сурса: знания. Нарисуйте линии, соединяющие углы внешнего и внутреннего прямоугольника. Б. Есть 2 способа изменить размер перекрестия в AutoCAD.Золотой прямоугольник — это прямоугольник с длиной полосы a + и шириной a. Выберите объект для разделения, введите количество сегментов. DL: DATALINK / Отображается диалоговое окно Data Link. Для прямоугольников и квадратов умножьте ширину на высоту. Введите F (для первой точки), нажмите Enter. Сначала мы нарисуем прямоугольник, а затем воспользуемся для него командой Explode. Обратите внимание, что «точки» помещаются в качестве маркеров деления, как в команде «Разделить». Находить. TANITIM Divide, seçilecek objeleri kullanıcının belirleyeceği sayıda eşit parçalara bölmek için kullanılan bir komuttur.

Графическое построение сопряжений	Краткое объяснение к построению

Сопряжение пересекающихся прямых дугой заданного радиуса
	Провести прямые, параллельные сторонам угла на расстоянии R. Из точки О, взаимного пересечения этих прямых, опустив перпендикуляры на стороны угла, получим точки сопряжения 1 и 2. Радиусом R провести дугу сопряжения между точками 1 и 2.
Сопряжение окружности и прямой с помощью дуги заданного радиуса
	На расстоянии R провести прямую, параллельную заданной прямой, а из центра О₁ радиусом R+R₁– дугу окружности. Точка О – центр дуги сопряжения. Точку 2 получим на перпендикуляре, опущенном из точки О на заданную прямую, а точку 1- на пересечении прямой ОО₁ и окружности радиуса R.

Сопряжение дуг двух окружностей прямой линией
	Из точки О провести вспомогательную окружность радиусом R-R₁. Отрезок ОО₁ разделить пополам и из точки О₂ провести окружность радиусом 0,5 ОО₁.Эта окружность пересекает вспомогательную в точке К₀. Соединив точку К₀ с точкой О₁ получим направление общей касательной. Точки касания К и К₁находим на пересечении перпендикуляров из точек О и О₁ с заданными окружностями.
Сопряжение дуг двух окружностей дугой заданного радиуса (внешнее сопряжение)
	Из центров О₁ и О₂ провести дуги радиусов R+R₁ и R+R_2.При пересечении этих дуг получаем точку О – центр дуги сопряжения. Соединить точки О₁ и О₂с точкой О. Точки К и К₁ являются точками сопряжения. Между точками К и К₁ провести дугу сопряжения радиусом R.

’62 Центр театра и танца, ’62 Центр
касса	597-2425
Магазин костюмов	597-3373
Менеджер мероприятий / Помощник менеджера	597-4808	597-4815 факс
Производство		597-4474 факс
Магазин сцен	597-2439
’68 Центр карьерного роста, Мирс	597-2311	597-4078 факс
Academic Resources, Парески	597-4672	597-4959 факс
Служба поддержки инвалидов, Парески	597-4672
Прием, Вестон-холл	597-2211	597-4052 факс
Программа позитивных действий, Хопкинс-холл,	597-4376
Africana Studies, Hollander	597-2242	597-4222 факс
Американские исследования, Шапиро	597-2074	597-4620 факс
Антропология и социология, Холландер	597-2076	597-4305 факс
Архивы и специальные коллекции, Sawyer	597-4200	597-2929 факс
Читальный зал	597-4200
Искусство (История, студия), Spencer Studio Art / Lawrence	597-3578	597-3693 факс
Архитектурная студия, Spencer Studio Art	597-3134
Фотография Студия, Spencer Studio Art	597-2030
Printmaking Studio, Spencer Studio Art	597-2496
Студия скульптуры, Spencer Studio Art	597-3101
Senior Studio, Spencer Studio Art	597-3224
Видео / фотостудия, Spencer Studio Art	597-3193
Asian Studies, Hollander	597-2391	597-3028 факс
Астрономия / Астрофизика, Thompson Physics	597-2482	597-3200 факс
Департамент легкой атлетики, Физическое воспитание, отдых, Ласелл	597-2366	597-4272 факс
Спортивный директор	597-3511
Лодочный домик, Озеро Онота	443-9851
Автобусы	597-2366
Фитнес-центр	597-3182
Hockey Rink Ice Line, Lansing Chapman	597-2433
Intramurals, Атлетический центр Чандлера	597-3321
Физическое воспитание	597-2141
Pool Wet Line, Атлетический центр Чандлера	597-2419
Sports Information, Hopkins Hall	597-4982	597-4158 факс
Спортивная медицина	597-2493	597-3052 факс
Площадки для игры в сквош	597-2485
Поле для гольфа Taconic	458-3997
Биохимия и молекулярная биология, Thompson Biology	597-2126
Биоинформатика, геномика и протеомика, Бронфман	597-2124
Биология, Thompson Biology	597-2126	597-3495 факс
Охрана и безопасность кампуса, Хопкинс-холл	597-4444	597-3512 факс
Карты доступа / системы сигнализации	597-4970 / 4033
Служба сопровождения, Хопкинс-холл	597-4400
Офицеры и диспетчеры	597-4444
Секретарь, удостоверения личности	597-4343
Коммутатор	597-3131
Центр развития творческого сообщества, 66 Stetson Court	884-0093
Центр экономики развития, 1065 Main St	597-2148	597-4076 факс
Компьютерный зал	597-2522
Вестибюль	597-4383
Центр экологических исследований, класс 1966 г. Экологический центр	597-2346	597-3489 факс
Лаборатория экологических наук, Морли	597-2380
Экологические исследования	597-2346
Лаборатория ГИС	597-3183
Центр иностранных языков, литератур и культур, Холландер	597-2391	597-3028 факс
Арабские исследования, Холландер	597-2391	597-3028 факс
Сравнительная литература, Холландер	597-2391
Критические языки, Холландер	597-2391	597-3028 факс
лингафонный кабинет	597-3260
Россия, Холландер	597-2391
Центр обучения в действии, Brooks House	597-4588	597-3090 факс
Библиотека редких книг Чапина, Сойер	597-2462	597-2929 факс
Читальный зал	597-4200
Офис капелланов, Парески	597-2483	597-3955 факс
Еврейский религиозный центр, 24 Stetson Court	597-2483
Мусульманская молитвенная комната, часовня Томпсона (нижний уровень)	597-2483
Католическая часовня Ньюмана, часовня Томпсона (нижний уровень)	597-2483
Химия, Thompson Chemistry	597-2323	597-4150 факс
Классика (греческий и латинский), Hollander	597-2242	597-4222 факс
Когнитивная наука, Бронфман	597-4594
Маршал колледжа, Thompson Physics	597-2008
Отношения с колледжем	597-4057
Программа 25-го воссоединения, Фогт	597-4208	597-4039 факс
Программа 50-го воссоединения, Фогт	597-4284	597-4039 факс
Операции по продвижению, Мирс-Уэст	597-4154	597-4333 факс
Мероприятия для выпускников, Vogt	597-4146	597-4548 факс
Фонд выпускников	597-4153	597-4036 факс
Связи с выпускниками, Мирс-Уэст	597-4151	597-4178 факс
Почтовые службы для выпускников / разработчиков, Мирс-Уэст	597-4369
Девелопмент, Vogt	597-4256
Отношения с донорами, Vogt	597-3234	597-4039 факс
Офис по планированию подарков, Vogt	597-3538	597-4039 факс
Офис грантов, Мирс-Уэст	597-4025	597-4333 факс
Программа крупных подарков, Vogt	597-4256	597-4548 факс
Фонд родителей, Фогт	597-4357	597-4036 факс
Prospect Management & Research, Мирс	597-4119	597-4178 факс
Начало занятий и академические мероприятия, Jesup	597-2347	597-4435 факс
Коммуникации, Хопкинс Холл	597-4277	597-4158 факс
Sports Information, Hopkins Hall	597-4982	597-4158 факс
Веб-команда, Саутвортская школа
Williams Magazines (ранее Alumni Review), Hopkins Hall	597-4278
Компьютерные науки, Thompson Chemistry	597-3218	597-4250 факс
Conferences & Events, Парески	597-2591	597-4748 факс
Запросы Elm Tree House, Mt.Надежда Ферма	597-2591
Офис контролера, Хопкинс-холл	597-4412	597-4404 факс
Accounts Payable & Data Entry, Hopkins Hall	597-4453
Bursar & Cash Receipts, Hopkins Hall	597-4396
Финансовые информационные системы, Хопкинс-холл	597-4023
Purchasing Cards, Hopkins Hall	597-4413
Студенческие ссуды, Хопкинс Холл	597-4683
Dance, 62 Центр	597-2410
Центр Дэвиса (ранее Мультикультурный центр), Дженнесс	597-3340	597-3456 факс
Харди Хаус	597-2129
Дом Дженнесс	597-3344
Райс Хаус	597-2453
Декан колледжа, Хопкинс-холл	597-4171	597-3507 факс
Декан факультета, Hopkins Hall	597-4351	597-3553 факс
Столовая, капельницы	597-2121	597-4618 факс
’82 Grill, Парески	597-4585
Кондитерская, Парески	597-4511
Общественное питание, Дом факультета	597-2452
Driscoll Dining Hall, Дрисколл	597-2238
Eco Café, Научный центр	597-2383
Grab ‘n Go, Парески	597-4398
Lee Snack Bar, Парески	597-3487
Обеденный зал Mission Park, Mission Park	597-2281
Whitmans ‘, Paresky	597-2889
Economics, Schapiro	597-2476	597-4045 факс
английский, Hollander	597-2114	597-4032 факс
Сооружения, здание служебного помещения	597-2301
Запрос на получение автомобиля в колледже	597-2302
Экстренная помощь вечером / в выходные дни	597-4444
Запросы на работу объектов		597-4141 факс
Особые мероприятия	597-4020
Кладовая	597-2143	597-4013 факс
Клуб преподавателей, Дом факультетов / Центр выпускников	597-2451	597-4722 факс
Бронирование	597-3089
Fellowships Office, Hopkins Hall	597-3044	597-3507 факс
Financial Aid, Weston Hall	597-4181	597-2999 факс
Науки о Земле, Кларк Холл	597-2221	597-4116 факс
Немецко-русский, Hollander	597-2391	597-3028 факс
Глобальные исследования, Холландер	597-2247
Программа магистратуры по истории искусств, Кларк		458-2317 факс
Службы здравоохранения и хорошего самочувствия, Thompson Ctr Health	597-2206	597-2982 факс
Санитарное просвещение	597-3013
Услуги интегративного благополучия (консультирование)	597-2353
Чрезвычайные ситуации с опасностью для жизни	Позвоните 911
Медицинские услуги	597-2206
История, Холландер	597-2394	597-3673 факс
История науки, Бронфман		597-4116 факс
Лес Хопкинса	597-4353
Розенбург-центр	458-3080
Отдел кадров, B&L Building	597-2681	597-3516 факс
Услуги няни, корпус B&L	597-4587
Льготы	597-4355
Программа помощи сотрудникам	800-828-6025
Занятость	597-2681
Заработная плата	597-4162
Ресурсы для супруга / партнера	597-4587
Занятость студентов	597-4568
Погодная линия (ICEY)	597-4239
Humanities, Schapiro	597-2076
Информационные технологии, Jesup	597-2094	597-4103 факс
Пакеты для чтения курсов, ящик для сообщений офисных служб	597-4090
Центр кредитования оборудования, приложение Додда	597-4091
Служба поддержки преподавателей / сотрудников, [электронная почта]	597-4090
Медиа-сервисы и справочная информация в классе	597-2112
Служба поддержки студентов, [электронная почта]	597-3088
Телекоммуникации / телефоны	597-4090
Междисциплинарные исследования, Холландер	597-2552
Международное образование и учеба, Хопкинс-холл	597-4262	597-3507 факс
Инвестиционный офис, Хопкинс Холл	597-4447
Бостонский офис	617-502-2400	617-426-5784 факс
Еврейские исследования, Мазер	597-3539
Справедливость и закон, Холландер	597-2102
Latina / o Studies, Hollander	597-2242	597-4222 факс
Исследования лидерства, Шапиро	597-2074	597-4620 факс
Морские исследования, Бронфман	597-2297
Математика и статистика, Bascom	597-2438	597-4061 факс
Музыка, Бернхард	597-2127	597-3100 факс
Concertline (записанная информация)	597-3146
Неврология, Thompson Biology	597-4107	597-2085 факс
Окли Центр, Окли	597-2177	597-4126 факс
Управление институционального разнообразия и справедливости, Хопкинс-холл	597-4376	597-4015 факс
Управление счетов студентов, Хопкинс-холл	597-4396	597-4404 факс
Performance Studies, ’62 Center	597-4366
Философия, Шапиро	597-2074	597-4620 факс
Физика, Thompson Physics	597-2482	597-4116 факс
Планетарий / Обсерватория Хопкинса	597-3030
Театр старой обсерватории Хопкинса	597-4828
Бронирование	597-2188
Политическая экономия, Шапиро	597-2327
Политология, Шапиро	597-2168	597-4194 факс
Офис президента, Хопкинс-холл	597-4233	597-4015 факс
Дом президента	597-2388	597-4848 факс
Услуги печати / почты для преподавателей / сотрудников, ’37 House	597-2022
Программа обучения, Бронфман	597-4522	597-2085 факс
Офис Провоста, Хопкинс Холл	597-4352	597-3553 факс
Психология, психологические кабинеты и лаборатории	597-2441	597-2085 факс
Недвижимость, B&L Building	597-2195 / 4238	597-5031 факс
Ипотека для преподавателей / сотрудников	597-4238
Жилье для преподавателей / сотрудников	597-2195
Офис регистратора, Хопкинс Холл	597-4286	597-4010 факс
Религия, Холландер	597-2076	597-4222 факс
Romance Languages, Hollander	597-2391	597-3028 факс
Планировщик помещений	597-2555
Соответствие требованиям безопасности и охраны окружающей среды, класс ’37, дом	597-3003
Библиотека Сойера, Сойер	597-2501	597-4106 факс
Службы доступа	597-2501
Приобретения / Серийные номера	597-2506
Каталогизация / Службы метаданных	597-2507
Межбиблиотечный абонемент	597-2005	597-2478 факс
Исследовательские и справочные службы	597-2515
Стеллаж	597-4955	597-4948 факс
Системы	597-2084
Научная библиотека Шоу, Научный центр	597-4500	597-4600 факс
Исследования в области науки и технологий, Бронфман	597-2239
Научный центр, Бронфман		597-4116 факс
Магазин электроники	597-2205
Машинно-модельный цех	597-2230
Безопасность	597-4444
Специальные академические программы, Харди	597-3747	597-4530 факс
Sports Information, Hopkins Hall	597-4982	597-4158 факс
Студенческая жизнь, Парески	597-4747
Планировщик помещений	597-2555
Управление студенческими центрами	597-4191
Организация студенческих мероприятий	597-2546
Студенческий дом, Парески	597-2555
Участие студентов	597-4749
Программы проживания для старших классов	597-4625
Студенческая почта, Паресский почтовый кабинет	597-2150
Устойчивое развитие / Центр Зилха, Харпер	597-4462
Коммутатор, Хопкинс Холл	597-3131
Книжный магазин Уильямса	458-8071	458-0249 факс
Театр, 62 Центр	597-2342	597-4170 факс
Trust & Estate Administration, Sears House	597-4259
Учебники	597-2580
вице-президент по кампусной жизни, Хопкинс-холл	597-2044	597-3996 факс
вице-президент по связям с колледжем, Мирс	597-4057	597-4178 факс
Вице-президент по финансам и администрированию, Хопкинс-холл	597-4421	597-4192 факс
Центр визуальных ресурсов, Лоуренс	597-2015	597-3498 факс
Детский центр Williams College, Детский центр Williams	597-4008	597-4889 факс
Музей искусств колледжа Уильямс (WCMA), Лоуренс	597-2429	597-5000 факс
Подготовка музея	597-2426
Служба безопасности музея	597-2376
Музейный магазин	597-3233
Уильямс Интернэшнл	597-2161
Уильямс Outing Club, Парески	597-2317
Оборудование / стол для студентов	597-4784
Проект Уильямса по экономике высшего образования, Мирс-Вест	597-2192
Уильямс Рекорд, Парески	597-2400	597-2450 факс
Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет	011-44-1865-512345
Программа Williams-Mystic, Mystic Seaport Museum	860-572-5359	860-572-5329 факс
Исследования женщин, гендера и сексуальности, Schapiro	597-3143	597-4620 факс
Написание программ, Hopkins Hall	597-4615
Центр экологических инициатив «Зилха», Харпер	597-4462