Урок «Сопряжения», ФГОС
Сопряжения
Под сопряжением понимают плавный переход одной линии в другую. Чаще всего сопряжения представляют собой сочетания прямых и дуг окружностей. Например, изображенная на рис. 1 линия состоит из нескольких элементов: прямая АВ плавно переходит в дугу окружности радиусом R1, затем в дугу окружности радиусом R2 и заканчивается прямой DE. Плавность перехода достигается за счет того, что последовательно расположенные линии касаются друг друга. Прямая АВ касается окружности с центром в точке О1 в точке В, окружность с центром в точке О1 касается окружность с центром О2 в точке С, а окружность с центром в точке О2 касается прямой DE в точке D.
Если сопряжения состоят из прямых и дуг окружностей, то для правильного и точного их изображения необходимо определить их основные параметры: радиусы сопряжений (R1 или R2), центры сопряжений (точки О1 и О2) и точки сопряжений (точки В, С и D). | Рис. 1. |
Чаще всего радиусы сопряжений задаются, и решение задачи сводится к определению центров и точек сопряжения. В этом случае можно сформулировать общий план решения подобных задач.
Определить и провести на чертеже линию, предоставляющую собой множество точек плоскости, удаленную от одной заданной линии на расстояние, равное радиусу сопряжения.
Определить и провести на чертеже линию, представляющую собой множество точек плоскости, удаленную от другой заданной линии на расстояние, равное радиусу сопряжения.
Найти точку пересечения построенных линий, являющуюся центром сопряжения.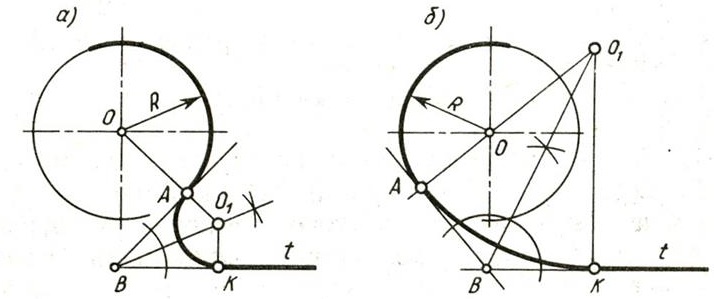
Построить точки сопряжения заданных линий с сопрягающей дугой окружности, т.е. точки касания заданной линии с окружностью.
Провести сопрягающую дугу окружности в пределах найденных точек сопряжения.
Сопряжение двух пересекающихся прямых линий
Пусть имеются прямые АВ (рис. 2) и CD, которые необходимо сопрячь окружностью радиусом Rс.
Множество точек плоскости, удаленных от прямой на расстоянии Rс, есть две прямые, параллельные заданной и стоящие от нее на расстоянии Rс. Выбираем на прямой АВ произвольную точку Е, восстановим из нее перпендикуляр к АВ, отложим на нем отрезок EF, равный Rс, и через точку F проведем одну из прямых, параллельно прямой АВ. Аналогичные построения выполним относительно прямойCD, взяв произвольную точку G и соответственно отрезок перпендикуляра GH= Rс. | Рис. |
Точка О пересечения прямых, проходящих через точки F и H, удалена на расстояние Rс как от прямой АВ, так и от прямой CD. Таким образом, точка О – центр окружности, касательной к прямым АВ и CD (центр сопряжения). Для того чтобы определить точки касания сопрягающихся окружностей и заданных прямых, следует опустить на них перпендикуляры к точке О. Точки К1 и К2 пересечения этих перпендикуляров с прямыми АВ и CD являются точками касания окружности с центром в точке О с заданными прямыми (точками сопряжения). Располагая всеми параметрами сопряжения, можно провести дугу окружности радиусом Rс с центром в точке О от точки К1 до точки К2.
Если использовать полные множества точек, удаленных от прямых АВ и CD (рис. 3) на расстоянии Rс, и провести по две прямых, параллельных заданным, можно построить четыре центра сопряжений О1, О2, О3 и О4 и получить четыре варианта решения поставленной задачи.
Сопряжение прямой линии с окружностью
Если радиус Rс сопряжения прямой линии и окружности радиусом R задан, то при определении параметров сопряжений следует исходить из следующих положений:
Рис.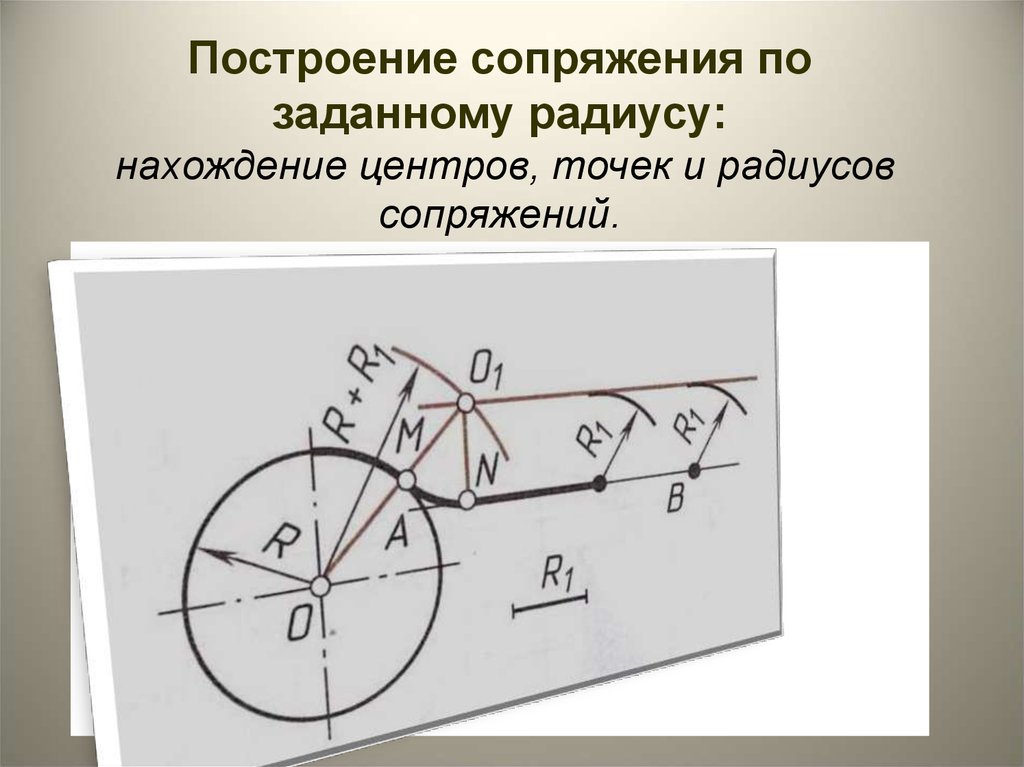 3
3
множество точек, удаленных от прямой на расстоянии Rс, есть две прямые, параллельные заданной прямой и отстоящие на расстоянии Rс от нее;
множество точек, удаленных от окружности на расстояние Rс, есть две концентрические окружности, радиусы которых ровны сумме или разности радиусов R и Rс;
точки пересечения множеств, указанных в пунктах «а» и «б», являются центрами сопряжений;
точки сопряжения в заданной прямой есть основание перпендикуляра, опущенного их центра сопряжения на прямую;
точка сопряжения с заданной окружностью расположена на прямой, соединяющей ее центр с центром сопряжения.
По положению центра заданной окружности и центра сопрягающей дуги относительно общей касательной различают внешнее и внутреннее сопряжения. Если центр окружности и центр сопряжения располагаются по разные стороны от касательной, то такое сопряжение считается внешним, а если центры располагаются по одну сторону от касательной, — внутренним.
Рассмотрим несколько примеров.
Пусть заданы окружность радиусом R1 (рис. 4) с центром в точке О и прямая АВ. Требуется выполнить внешнее сопряжение окружности и прямой дугой окружности радиусом Rс.
Выбрав на прямой АВ произвольную точку М, восстановим из нее перпендикуляр к прямой АВ и отложим на нем отрезок MN, ранее Rс. Через точку N проведем прямую, параллельную АВ (см. п. «а»).
Из точки О, как из центра, радиусом R2, равным сумме радиусов R1 и Rс, проведем дугу окружности (см. п. «б»).
Точка С пересечения прямой, проходящей через точку N, с дугой радиусом R2, является центром сопряжения (см. п. «в»).
Из точки С опустим перпендикуляр на прямую АВ. Основание К2 перпендикуляра и будет точкой сопряжения с прямой (см. п. «г»).
Соединим точки О и С прямой линией. Пересечение этой прямой с заданной окружностью определяет точку сопряжения К1 (см. п. «д»).
п. «д»).
Завершая построение, следует из центра С радиусом Rс провести дугу окружности от точки К1 до точки К2.
Рис. 4. Рис. 5.
Пусть заданы окружность радиусом R1 (рис. 5) с центром в точке О и прямая АВ. Требуется выполнить внутреннее сопряжение окружности и прямой дугой окружности радиусом Rс.
Требуемые построения не отличаются существенно от рассмотренных в предыдущем примере и имеют лишь две особенности. Множество точек плоскости, удаленных от заданной окружности на расстояние Rс, представляет собой концентрическую окружность, радиус которой R2 равен разности радиусов R1 и Rс. Точка К1 сопряжения располагается на продолжении прямой, соединяющей центры заданной и сопрягающей окружностей.
Пусть заданы окружность радиусом R1 (рис. 6) с центром в точке О и пряма АВ. Требуется выполнить внутреннее сопряжение окружности и прямой дугой окружности радиусом Rс.
Особенностью данной задачи по сравнению с предыдущей является то, что радиус сопряжения Rс больше, чем радиус R1 заданной окружности. В этом случае радиус R2 тоже определяют как разность радиусов сопряжения и заданной окружности, однако уменьшаемое и вычитаемое должны быть выбраны такими, чтоб эта разность была положительной.
Рис. 5. Рис. 6.
Сопряжение двух заданных окружностей
При решение задач на сопряжение двух окружностей следует учитывать, что множество точек плоскости, удаленных от окружностей на равные расстояния, представляет собой концентрические окружности, радиусы которых равны сумме или разности радиусов заданной окружности и сопряжения. Точка пересечения этих окружностей является центром сопряжения. Точки сопряжения определяются как точки пересечения прямых, соединяющих центры заданных окружностей с центром сопряжения.
Пусть заданы окружности с центром в точках О1 и О2 (рис.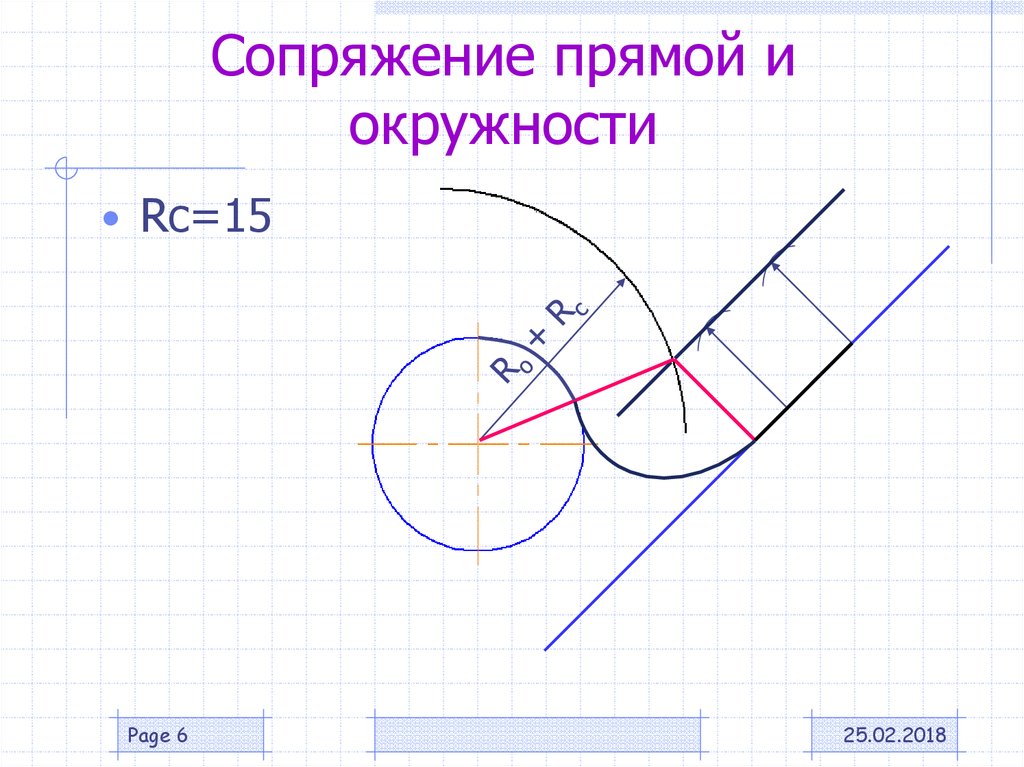 6), имеющие соответствующие радиусы R1 и R2. Требуется выполнить внутреннее сопряжение этих окружностей дугой окружности радиусом Rс.
6), имеющие соответствующие радиусы R1 и R2. Требуется выполнить внутреннее сопряжение этих окружностей дугой окружности радиусом Rс.
Из центра О1 проведем дугу окружности радиусом R3, равным сумме радиусов R1 и Rс, а из центра О2 – дугу окружности радиусом R4, равным сумме радиусов R2 и Rс. Точка с пересечения этих дуг является центром сопряжения, а точки К1 и К2 пересечения прямых О1С и О2С с соответствующими окружностями – точками сопряжения. Определив основные параметры сопряжения, модно из центра С и точками К1 и К2 провести дугу окружности радиусом Rс.
Если необходимо выполнить внутренне сопряжение окружностей с радиусами R1 и R2 и центрами в точках О1 и О2 (рис. 7), то для определения центра их сопряжения С нужно провести дуги окружностей радиусами R3 и R4, равными разностями радиуса сопряжения Rс и соответственно радиусов R1 и R2 заданных окружностей. При этом точки К1 и К2 сопряжения будут находится на продолжении прямых, соединяющих центр С сопряжений с центрами окружностей О1 и О2.
Рис. 7. Рис. 8.
Если же радиус сопряжения Rс задан (рис. 8) и для одной из окружностей (с центром О1 и радиусом R1) следует выполнит внутреннее сопряжение, а для другой (с центром О2 и радиусом R2) – внешнее, то для определения центра сопряжения С нужно из точки О1 провести дугу окружности радиусом R3, равным сумме радиусов сопряжения Rс и окружности R1, а из точки О2 дугу окружности радиусом R4, равным разности радиуса сопряжения Rс и окружности R2. При этом точка сопряжения К1 будет находиться на пересечении прямой О1С с окружностью радиусом R1, а точка сопряжения К2 – на пересечении окружности с радиусом R2 с продолжением прямой О2С.
Сопряжения — прочее, уроки
Тема урока: Сопряжения.
Цель урока: рассмотреть основные виды сопряжений ,узнать о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.
Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.
Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.
Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.
Ниже будут рассмотрены основные типы сопряжений.
Сопряжение углов (Сопряжение пересекающихся прямых)
Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения.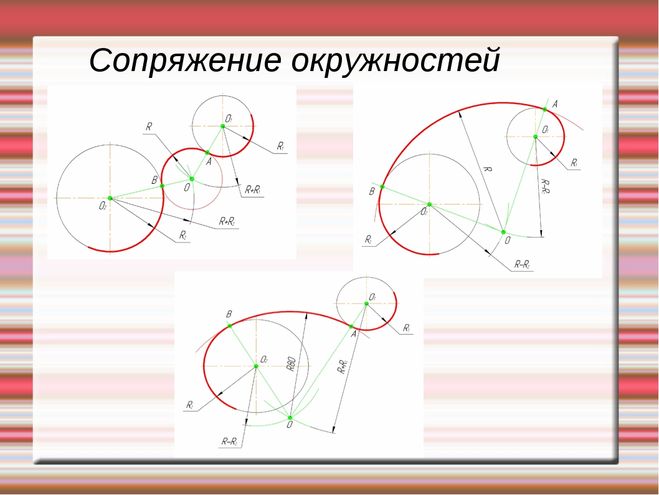
Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)
Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.
Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.
Сопряжение параллельных прямых линий
Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.
Сопряжение окружностей(дуг) с прямой линией
Внешнее сопряжение дуги и прямой линии
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.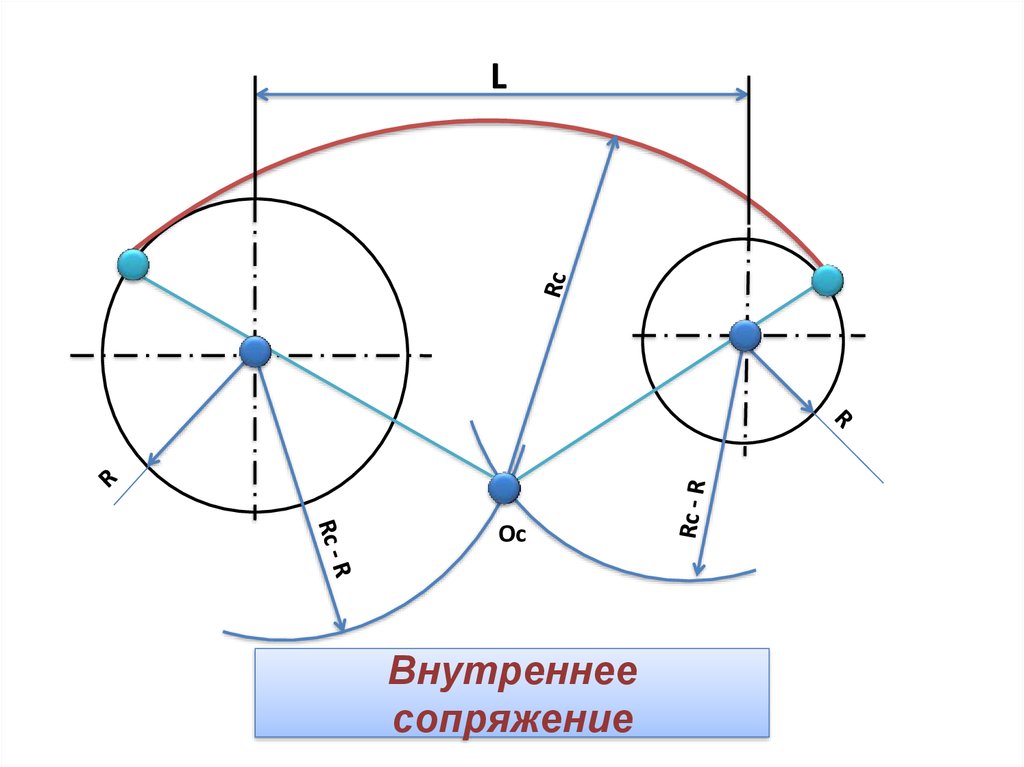
Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности OR радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой Оr.
Из центра сопряжения, точки Оr, опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности ОR и центр сопряжения Оr линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.
Внутреннее сопряжение прямой линии с дугой
По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности OR радиусом R-r.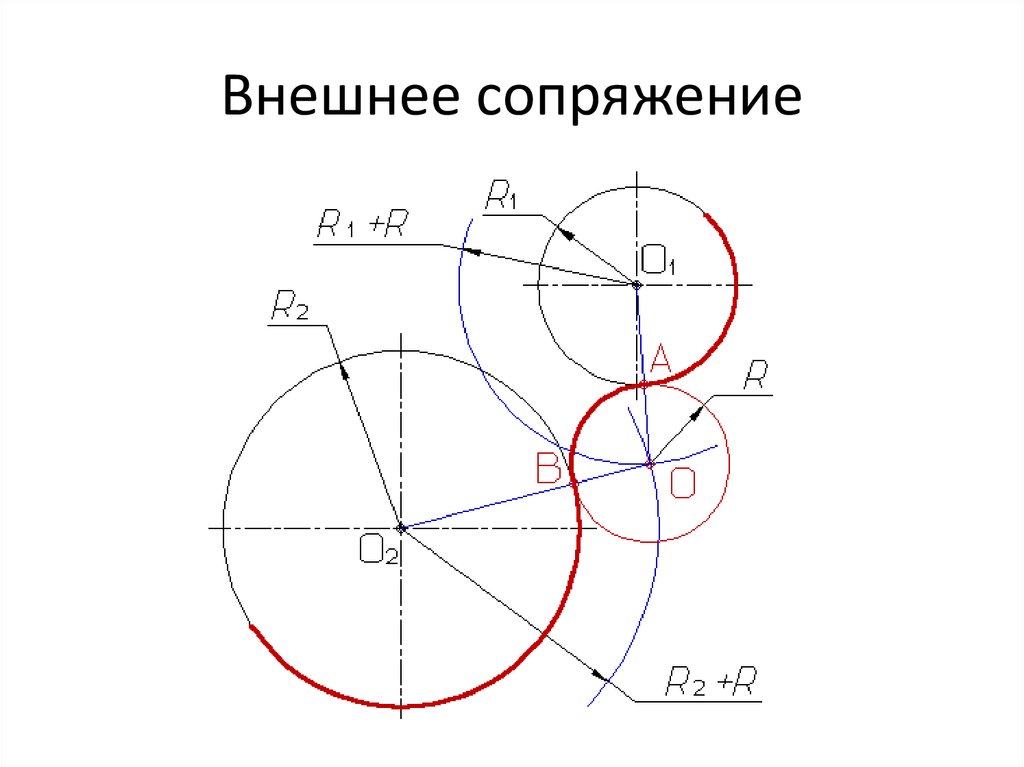
Из центра сопряжения(точка Оr) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.
Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности ОR прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки Оr, центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.
Сопряжение окружностей (дуг)
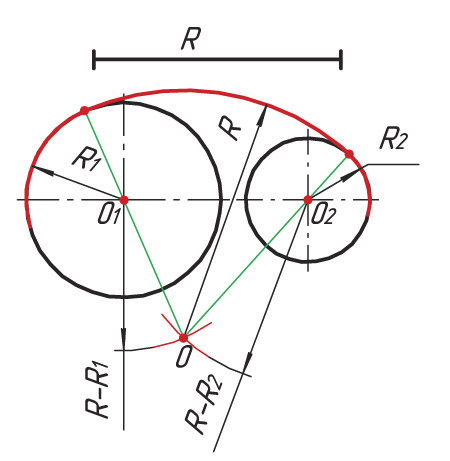
Внешнее сопряжение дуг окружностей
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно.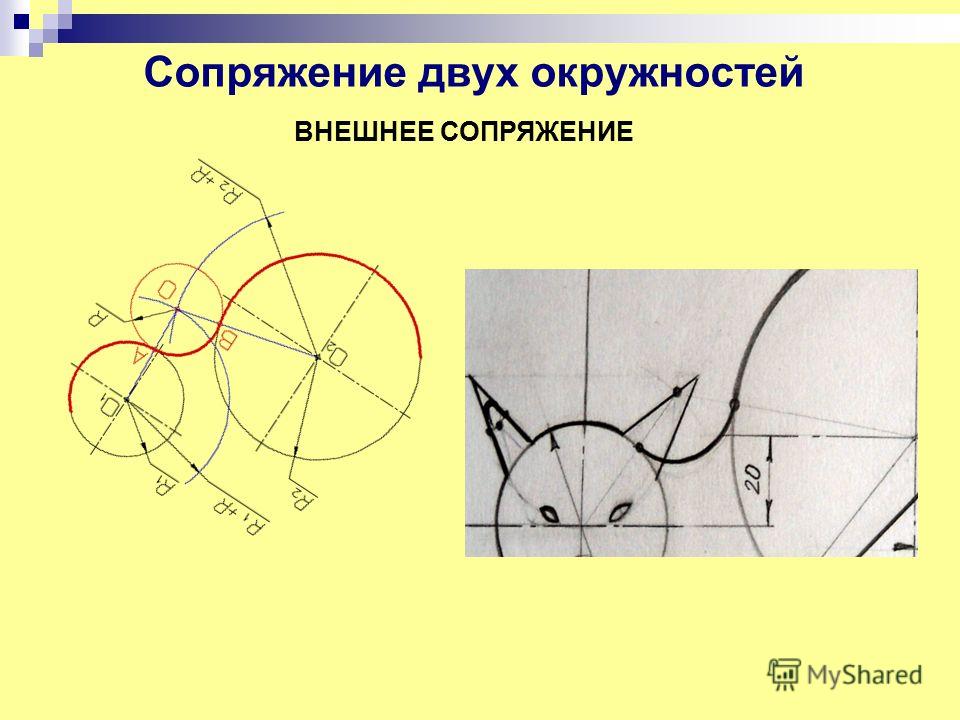
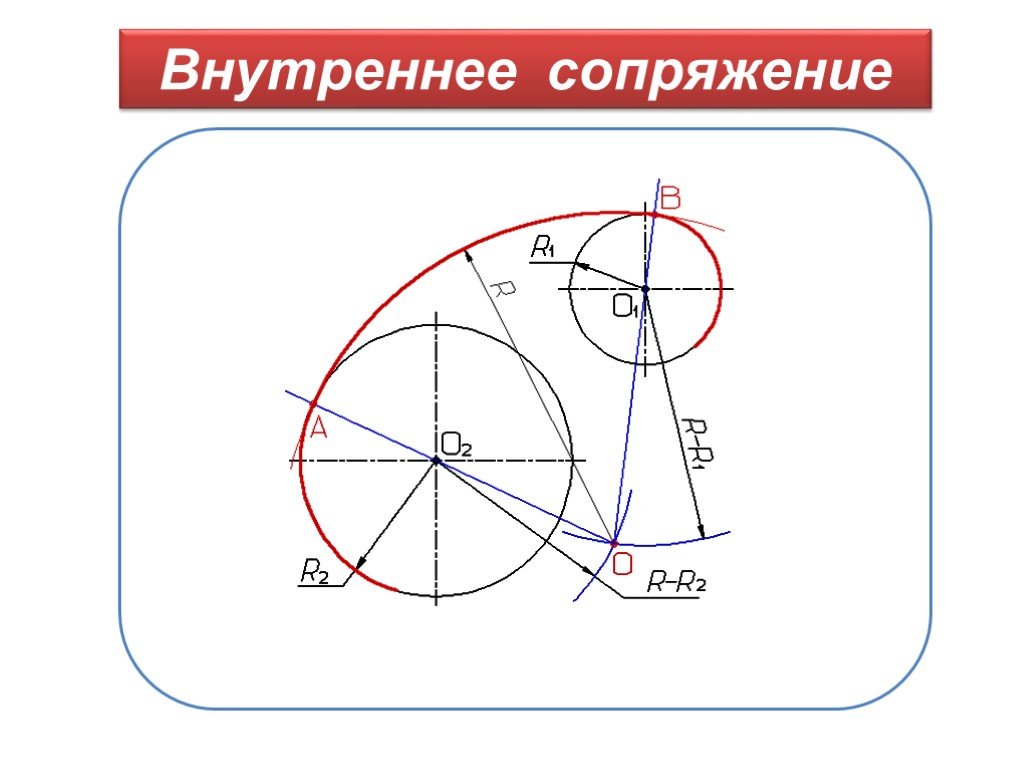
Внутреннее сопряжение дуг окружностей
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.
Смешанное сопряжение дуг окружностей
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.
Просмотр содержимого документа
«Сопряжения »
Тема урока: Сопряжения.
Цель урока: рассмотреть основные виды сопряжений ,узнать о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.
Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.
Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.
Ниже будут рассмотрены основные
Сопряжение углов (Сопряжение пересекающихся прямых) Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом.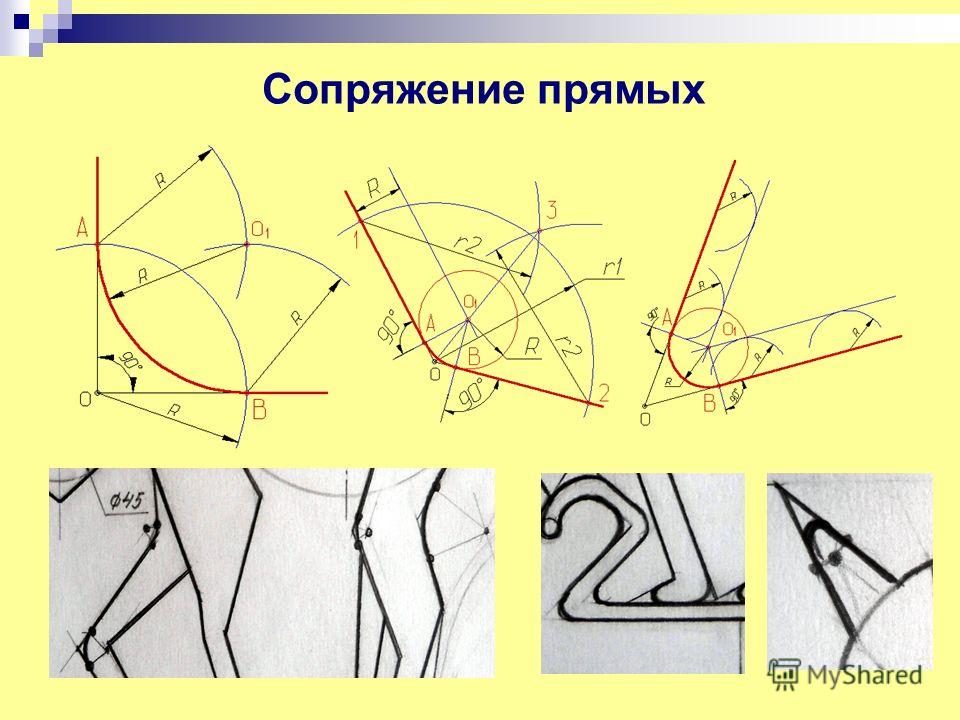 Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.
Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.
Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)
Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b. Сопряжение острого угла построено.
Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
Сопряжение тупого угла строится по аналогии с сопряжением острого угла.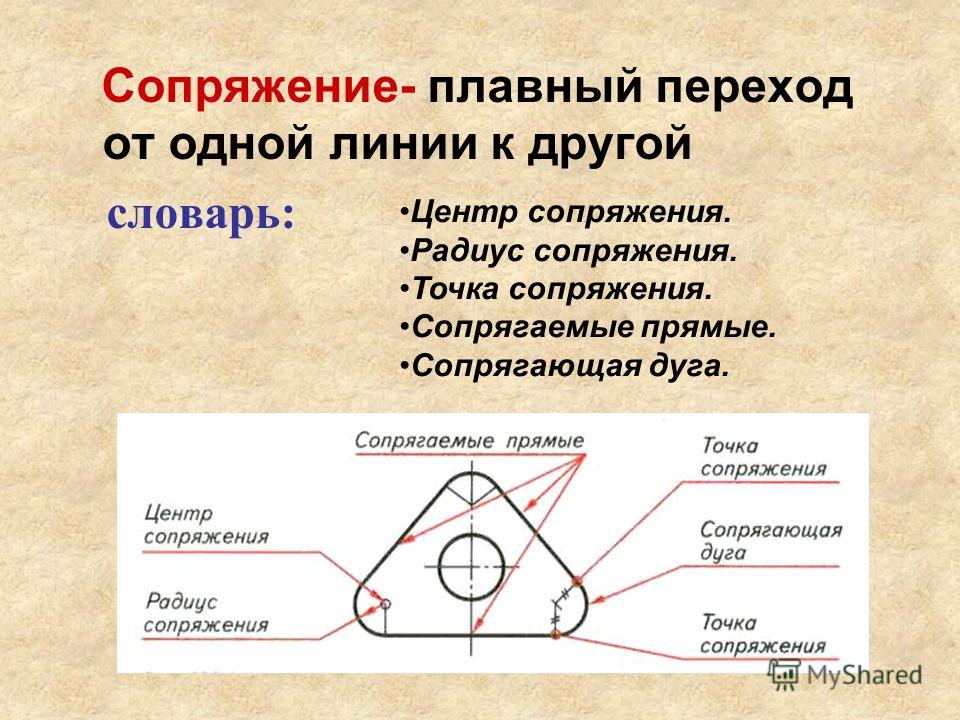
Сопряжение параллельных прямых линий
Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.
Сопряжение окружностей(дуг) с прямой линией Внешнее сопряжение дуги и прямой линии
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.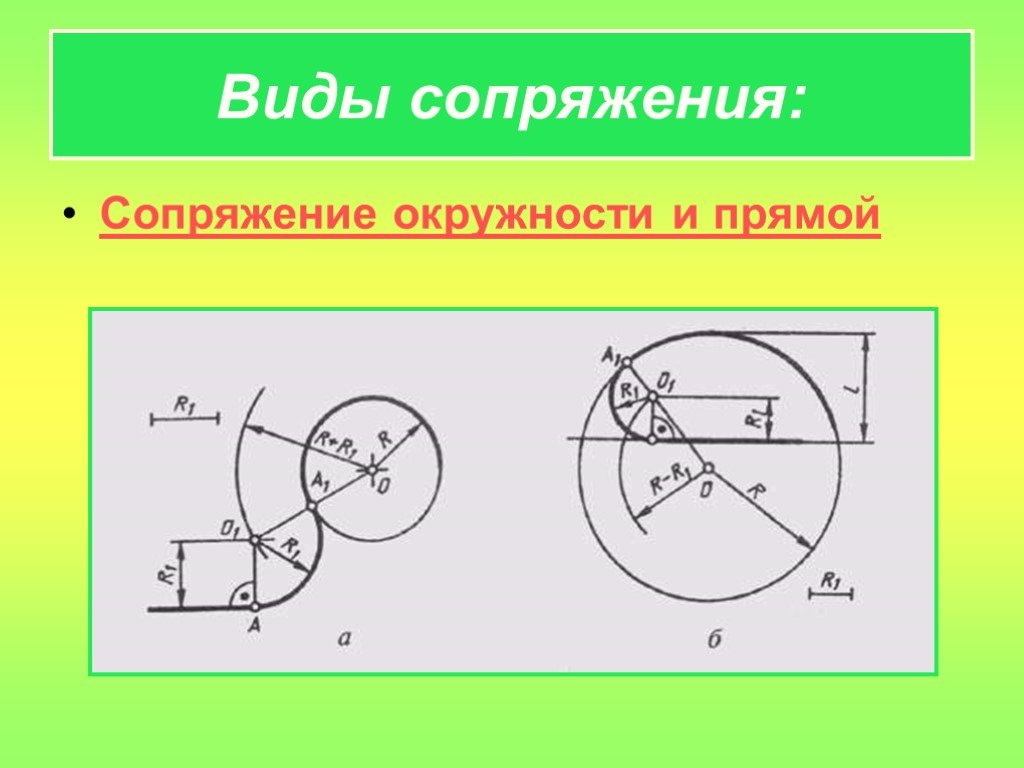
Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности OR радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой Оr.
Из центра сопряжения, точки Оr, опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности ОR и центр сопряжения Оr линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.
Внутреннее сопряжение прямой линии с дугой
По аналогии строится внутреннее сопряжение прямой линии с дугой. Рассмотрим пример построения сопряжения радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиуса R. Найдём центр сопряжения. Для этого построим прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса r, и дугу, из центра окружности OR радиусом R-r.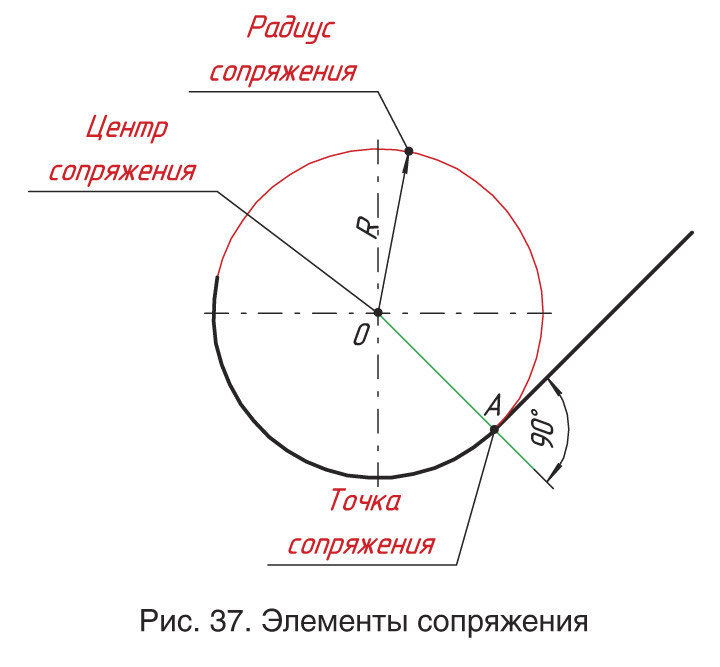 Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.
Точка Оr, полученная на пересечении прямой и дуги, и будет центром сопряжения.
Из центра сопряжения(точка Оr) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.
Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности ОR прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки Оr, центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.
Сопряжение окружностей (дуг) Внешнее сопряжение дуг окружностей
Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
Внутреннее сопряжение дуг окружностей
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.
Смешанное сопряжение дуг окружностей
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.
( ∑ p x Ha) есть уравнение pK(X6, P), которое подтверждает, что три гиперболы проходят через четыре упомянутых выше фокуса. В более общем случае, если Q = u : v : w — другая точка, ( ∑ u x Ha) — уравнение spK(Q, P), как в CL055. *** Преобразование Psi_P Psi_P(M) точки M является полюсом M в карандаше выше. Psi_P можно рассматривать как изогональное сопряжение в неправильном треугольнике, вершины которого являются вершинами диагонального треугольника четырех фокусов, а именно P и бесконечно удаленных круговых точек J1, J2. См. Таблицу 62 для других подобных преобразований. Отсюда следует, что Psi_P — квадратичная инволюция с особыми точками P, J1, J2 и неподвижными точками F1, F2, F’1, F’2. Если P не является центром в/эксцентра ABC, Psi_P(P*) лежит на описанной окружности (O): это изогональное сопряжение бесконечной точки линии PP*. Следовательно, Psi_P-образ (O) представляет собой окружность C_P, проходящую через P*, аналогичную окружности Брокара, полученной, когда P = X(2). Центр C_P является изображением Psi_P обратного P в (O). C_P также содержит Psi_P-образы Ap, Bp, Cp для A, B, C, которые являются вершинами треугольника (аналогичного второму треугольнику Брокара) в перспективе от P* до ABC. *** Поворотная кубическая Psi_P — это геометрическое место M, такое что M, Psi_P(M) и фиксированная точка Q лежат на одной прямой. Эта кубика является фокальной кубикой, проходящей через P, J1, J2, F1, F2, F’1, F’2, Q, бесконечную точку линии PQ (которая является ортопедической линией) и Psi_P(Q), которая является сингулярный фокус F. Полярной коникой F называется окружность, проходящая через F, P, Q. Когда Q = P*, эта фокальная кубика является изогональным nK, геометрическим местом фокусов инконик с центром на линии PP*. *** Пси2 При P = X(6) преобразование Psi_P равно Psi2, как упоминалось в K018, K1142 и на некоторых других страницах. Вот список пар {P, Psi2(P)}, составленный Питером Мозесом (обновлено 5 июня 2022 г.). {1, 5540}, {2, 111}, {3, 115}, {4, 112}, {5, 2079}, {11, 46408}, {13, 16}, {14, 15}, { 23, 6032}, {25, 1560}, {32, 6033}, {39, 12188}, {52, 39839}, {54, 13527}, {61, 6777}, {62, 6778}, {64, 13526}, {69, 36696}, {74, 6794}, {98, 34235}, {99, 14700}, {101, 6788}, {110, 6792}, {114, 5941}, {125, 35901}, {128, 15551}, {132, 46942}, {136, 50364}, {182, 11646}, {187, 381}, {265, 32761} , {352, 5640}, {353, 9140}, {378, 5523}, {389, 39849}, {399, 15544}, {403, 21397}, {427, 8428}, {574, 11632}, { 599, 28662}, {729, 6787}, {843, 9144}, {868, 8429}, {895, 48945}, {919, 10773}, {1083, 3125}, {1113, 8426}, {1114, 8427}, {1316, 3569}, {1326, 32431}, {1344, 8105}, {1345, 8106}, {1351, 5477}, {1379, 31862}, {1380, 31863}, {1511, 15538} , {1570, 39899}, {1587, 13283}, {1588, 13282}, {1593, 40234}, {1625, 31850}, {1637, 14685}, {1648, 9129}, {1691, 3818}, {1692, 18440}, {1879, 32762}, {1992, 10765}, {1995, 5913}, {2030, 47353}, {2076, 19130}, {2080, 5475}, {2088, 18332}, {2395, 46130}, {2453, 2492}, {2459, 6564}, {2460, 6565} , {2502, 9169}, {2549, 11579}, {2715, 11005}, {3003, 15928}, {3016, 41330}, {3018, 14687}, {3070, 49371}, {3071, 49372}, { 3098, 6034}, {3102, 35824}, {3103, 35825}, {3120, 46407}, {3124, 5108}, {3258, 50363}, {3269, 18338}, {3815, 33900}, {5000, 5001}, {5060, 45924}, {5091, 24290}, {5099, 50381}, {5104, 5476}, {5164, 45923}, {5166, 11188}, {5309, 35002}, {5355, 47618}, {5469, 10645} , {5470, 10646}, {5471, 5611}, {5472, 5615}, {5526, 5902}, {5622, 35902}, {5653, 35606}, {5870, 19115}, {5871, 19114}, { 5890, 13509}, {5912, 5968}, {5946, 45769}, {5971, 9465}, {6128, 15919}, {6141, 13636}, {6142, 13722}, {6566, 13665}, {6567, 13785}, {6644, 49123}, {6776, 10766}, {6785, 26714}, {7698, 9998}, {7737, 9970}, {7753, 9301}, {9721, 47391}, {10546, 11647} , {10605, 15341}, {10606, 44909}, {10657, 30440}, {10658, 30439}, {11472, 16303}, {11477, 41672}, {11650, 14431}, {13492, 31961}, {13530, 13531}, {13748, 49270} , {13749, 49271}, {14398, 47285}, {14899, 35609}, {15033, 15340}, {15048, 16010}, {16808, 39554}, {16809, 39555}, {18424, 38225}, { 18451, 50387}, {19780, 22797}, {19781, 22796}, {20998, 32525}, {21044, 46410}, {28343, 36990}, {30521, 31840}, {31861, 47322}, {32618, 32619}, {34288, 45019}, {35607, 35608}, {35903, 36202}, {35904, 36203}, {35906, 35909}, {35907, 35908}, {38940, 39024}, {39162, 39163}, {39164, 39165}, {41042, 41407}, {41043, 41406}, {45375, 50374}, {45376, 50375}, {45723, 50149}. | |
Комплексные числа: обратные, сопряженные и деление
Комплексные числа: обратные, сопряженные и деление Мы изучали сложение, вычитание и умножение. Теперь пришло время деления. Точно так же, как вычитание может быть составлено из сложения и отрицания, деление может быть составлено из умножения и взаимного обмена. Итак, мы поставили перед собой задачу найти 1/ z дано z. Другими словами, по заданному комплексному числу z = x + yi, найдите другое комплексное число w = u + vi , теперь мы можем сделать 4 w , yi такое, что что и алгебраически, и геометрически. Во-первых, алгебраически. Мы будем использовать формулу продукта, которую мы разработали в разделе об умножении. Он сказал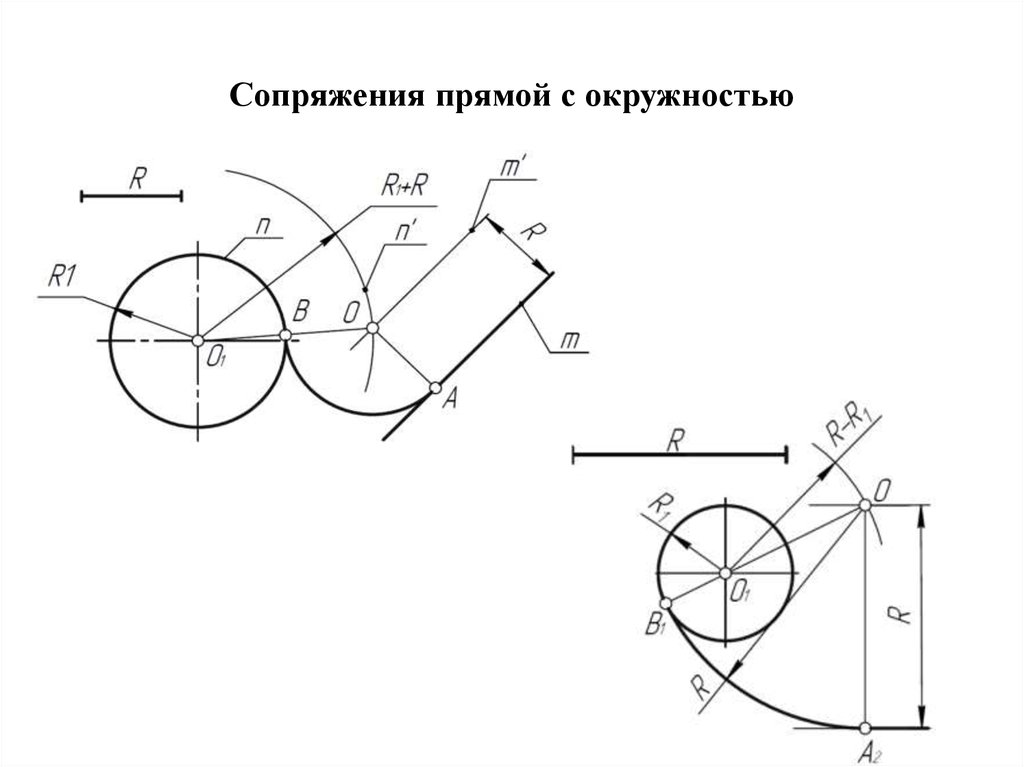
Теперь, если два комплексных числа равны, то их действительные части должны быть равны, и их мнимые части должны быть равны. Чтобы zw = 1, нам понадобится
Это дает нам два уравнения. Первый говорит, что действительные части равны:
а второй говорит, что мнимые части равны:
Теперь, в нашем случае, х было задано, а х было неизвестно, поэтому в этих двух уравнениях х и х даны, а х и х являются неизвестными для решения. Вы можете довольно легко решить за u и v в этой паре одновременных линейных уравнений. Когда вы это сделаете, вы найдете
Таким образом, обратное число z = x + yi равно числу w = u + vi , где u и .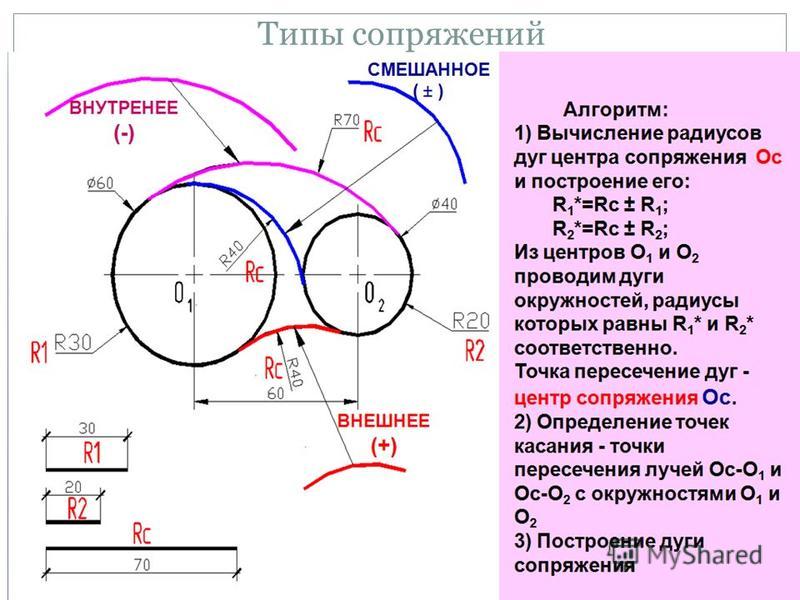 Таким образом, мы имеем следующую формулу взаимного обмена:
Таким образом, мы имеем следующую формулу взаимного обмена:
Обратные числа, выполненные геометрически, и комплексно-сопряженные числа.
Из того, что мы знаем о геометрии умножения, мы можем определить обратные геометрически. Если z и w обратны, то zw = 1, поэтому произведение их модулей равно 1, а сумма их аргументов (углов) равна 0.Это означает, что длина 1/ z является обратной величиной длины z. Например, если | из | = 2, как на схеме, то |1/ з | = 1/2. Это также означает, что аргумент для 1/ z является отрицанием аргумента для z. На диаграмме arg( z ) составляет около 65°, а arg(1/ z ) составляет около 65°.
Вы можете видеть на диаграмме еще одну точку, отмеченную чертой над z. Это называется комплексным сопряжением числа z. Имеет ту же действительную составляющую x, , но мнимая составляющая инвертирована. Комплексное сопряжение отрицает мнимую составляющую, поэтому преобразование плоскости C все точки отражаются на реальной оси (то есть точки выше и ниже реальной оси меняются местами). Конечно, точки на действительной оси не меняются, потому что комплексное сопряжение действительного числа есть само.
Комплексное сопряжение отрицает мнимую составляющую, поэтому преобразование плоскости C все точки отражаются на реальной оси (то есть точки выше и ниже реальной оси меняются местами). Конечно, точки на действительной оси не меняются, потому что комплексное сопряжение действительного числа есть само.
Комплексно-сопряженные числа дают нам еще один способ интерпретировать обратные числа. Вы можете легко проверить, что комплексное число z = x + yi , умноженное на его сопряженное x yi , является квадратом его абсолютного значения | г | 2 .
Таким образом, 1/ z является сопряженным z , деленным на квадрат его абсолютного значения | из | 2 .
На рисунке видно, что 1/| из | и сопряженные z лежат на том же луче от 0, но 1/| из | составляет только одну четвертую длины сопряжения z (и | г | 2 это 4).
 Радиусы и центры сопряжений характеризуют размеры и положение сопрягающих дуг окружностей. Точки сопряжений – это точки, общие для последовательно расположенных линий, или границы, отделяющие одну линию от другой.
Радиусы и центры сопряжений характеризуют размеры и положение сопрягающих дуг окружностей. Точки сопряжений – это точки, общие для последовательно расположенных линий, или границы, отделяющие одну линию от другой.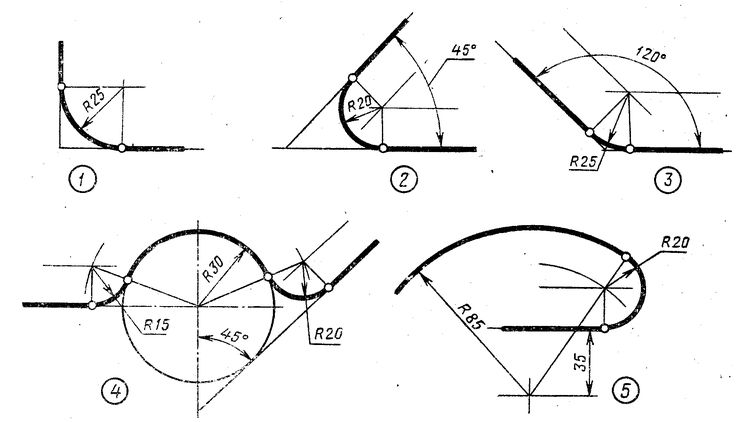 2.
2.
 Этот треугольник равносторонний тогда и только тогда, когда P = X(15) или X(16).
Этот треугольник равносторонний тогда и только тогда, когда P = X(15) или X(16).