Введение в программирование с MATLAB
Об этом курсе
Недавно просмотрено: 200 299
This course teaches computer programming to those with little to no previous experience. It uses the programming system and language called MATLAB to do so because it is easy to learn, versatile and very useful for engineers and other professionals. MATLAB is a special-purpose language that is an excellent choice for writing moderate-size programs that solve problems involving the manipulation of numbers. The design of the language makes it possible to write a powerful program in a few lines. The problems may be relatively complex, while the MATLAB programs that solve them are relatively simple: relative, that is, to the equivalent program written in a general-purpose language, such as C++ or Java. As a result, MATLAB is being used in a wide variety of domains from the natural sciences, through all disciplines of engineering, to finance, and beyond, and it is heavily used in industry.
Hence, a solid background in MATLAB is an indispensable skill in today’s job market.
Гибкие сроки
Назначьте сроки сдачи в соответствии со своим графиком.
Сертификат, ссылками на который можно делиться с другими людьмиСертификат, ссылками на который можно делиться с другими людьми
Получите сертификат по завершении
100% онлайн100% онлайн
Начните сейчас и учитесь по собственному графику.
Курс 1 из 3 в программе
Специализация MATLAB Programming for Engineers and Scientists
Начальный уровеньНачальный уровень
Часов на завершениеПрибл. 35 часов на выполнение
Доступные языкиАнглийский
Субтитры: Арабский, Французский, Португальский (Европа), Греческий, Итальянский, Вьетнамский, Корейский, Немецкий, Русский, Английский, Испанский
Будет ли вашей компании выгодно обучить сотрудников востребованным навыкам?
Попробуйте Coursera для бизнесаЧему вы научитесь
You will learn fundamental computer programming concepts such as variables, control structures, functions and many others.
You will learn about various data types and how to handle them in MATLAB.
You will learn the powerful support MATLAb provides for working with matrices.
You will learn about file input/output.
Приобретаемые навыки
- Computer Programming
- Problem Solving
- Matlab
- Programming Language
Гибкие сроки
Назначьте сроки сдачи в соответствии со своим графиком.
Сертификат, ссылками на который можно делиться с другими людьми
Получите сертификат по завершении
100% онлайн100% онлайн
Начните сейчас и учитесь по собственному графику.
СпециализацияКурс 1 из 3 в программе
Специализация MATLAB Programming for Engineers and Scientists
Начальный уровеньНачальный уровень
Часов на завершениеПрибл. 35 часов на выполнение
Доступные языкиАнглийский
Субтитры: Арабский, Французский, Португальский (Европа), Греческий, Итальянский, Вьетнамский, Корейский, Немецкий, Русский, Английский, Испанский
Будет ли вашей компании выгодно обучить сотрудников востребованным навыкам?
Попробуйте Coursera для бизнесаПреподаватели
Akos Ledeczi
Professor of Computer Engineering, Computer Science and Electrical Engineering
Department of Electrical Engineering and Computer Science
458 261 учащийся
3 курса
Mike Fitzpatrick
Professor Emeritus of Computer Science, Computer Engineering, Electrical Engineering, Neurosurgery, and Radiology
Electrical Engineering & Computer Science, Neurological Surgery, Radiology & Radiological Sciences
457 837 учащихся
2 курса
от партнера
Университет Вандербильта
Vanderbilt University, located in Nashville, Tenn.
, is a private research university and medical center offering a full-range of undergraduate, graduate and professional degrees.
Рецензии
4.8
Filled StarFilled StarFilled StarFilled StarFilled StarРецензии: 4345
5 stars
82,88 %
4 stars
14,75 %
3 stars
1,65 %
2 stars
0,26 %
1 star
0,43 %
Лучшие отзывы о курсе ВВЕДЕНИЕ В ПРОГРАММИРОВАНИЕ С MATLAB
Filled StarFilled StarFilled StarFilled StarStarот партнера SA26 июня 2020 г.
I didn’t like the assignment of echo. The description was not sufficient to understand the mechanism of putting echo by code. Except this, the assignments were exciting and the lectures were clear.
Filled StarFilled StarFilled StarFilled StarFilled Starот партнера A23 мая 2020 г.
The explanation of the topics was great. The assignments of the last week were challenging and I loved that.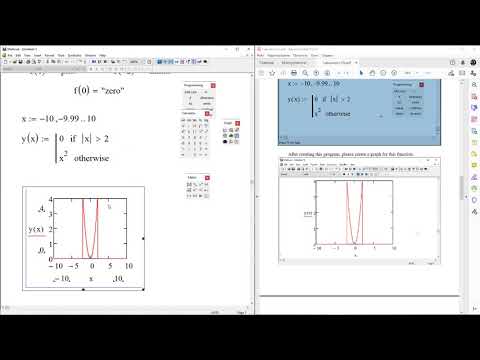
I learned a lot from this course. Thank you so much for sharing your knowledge with us.
от партнера MK25 сент. 2016 г.
There is much more to MATLAB than what the course can cover. But It has definitely provided me with the necessary skills and confidence to use it in tackling the practical problems in the real world.
Filled StarFilled StarFilled StarFilled StarFilled Starот партнера XL25 мая 2020 г.
I am at loss in rating this course. For me, it is 1000/100. Although I had some programming knowledge, this course had been mind-broadening. Professor is very humorous and enlightening in teaching!
Посмотреть все отзывы
Специализация MATLAB Programming for Engineers and Scientists: общие сведения
This Specialization aims to take learners with little to no programming experience to being able to create MATLAB programs that solve real-world problems in engineering and the sciences.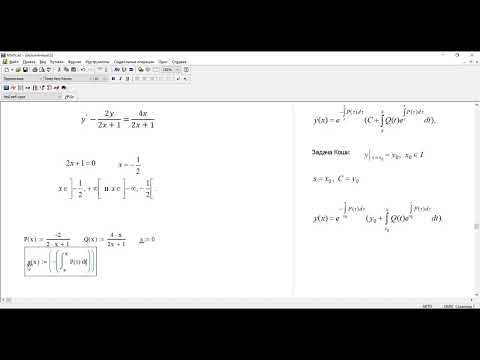
The focus is on computer programming in general, but the numerous language features that make MATLAB uniquely suited to engineering and scientific computing are also covered in depth. Topics presented range from basic programming concepts in the first course, through more advanced techniques including recursion, program efficiency, Object Oriented Programming, graphical user interfaces in the second course, to data and image analysis, data visualization and machine learning in the third course.
Часто задаваемые вопросы
Остались вопросы? Посетите Центр поддержки учащихся.
Обучайте сотрудников и добивайтесь отличных результатов в бизнесе
Откройте для себя Coursera для бизнесаMathCAD — это просто! Часть 9. Неравенства
MathCAD — это просто! Часть 9. Неравенства
Источник: http://www.nestor.minsk.by/kg
Неравенства бывают разные — это всем известно еще со школьной скамьи.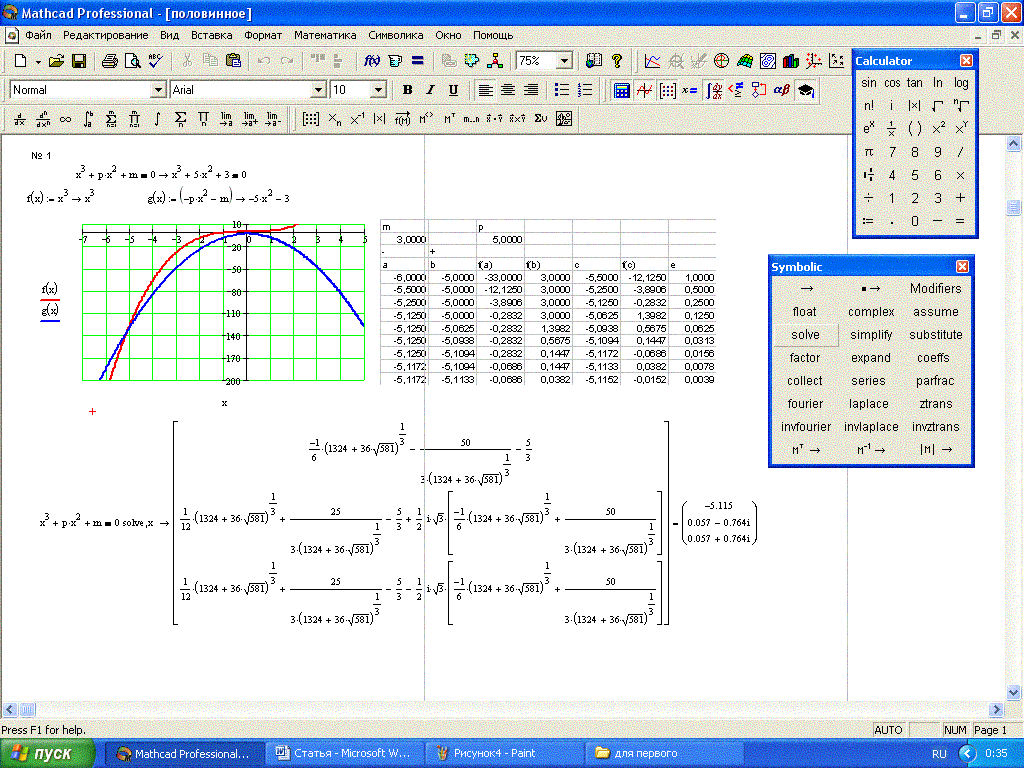
Я хотел рассказать о неравенствах уже давно, но как-то переключился на графики, а потому ушел немного в сторону. Сейчас мы с вами как бы вернемся немного назад, к уравнениям, и посмотрим, насколько решение неравенств в MathCAD’е отличается от решения уравнений. Надеюсь, что вы еще не совсем забыли, каким именно образом мы их решали — впрочем, даже если и так, всегда можно поднять подшивку КГ и посмотреть, что именно рассказывалось в любой из предыдущих частей серии «MathCAD — это просто». Ну и, конечно же, некоторые вещи я буду напоминать прямо по ходу дела. Так что не будем больше откладывать дело в долгий ящик, а примемся вместо этого, засучив рукава, упоенно решать, решать, решать неравенства.
Решение неравенств
Неравенство, вообще говоря, вещь более сложная, чем уравнение, в силу того простого факта, что мы часто имеем дело с необходимостью исследования функции на всей числовой оси. Поэтому особенно соблазнительно переложить на MathCAD столь нудную и неприятную работу. Думаю, для вас не станет откровением то, что использовать для решения неравенств можно solve — точно так же, как и для решения уравнений. Порядок действий совершенно аналогичен уже изученному нами ранее: записываем собственно неравенство (к примеру, пусть это будет x2+2x-5>0), нажимаем solve на панели Symbolic и, как говорится, наслаждаемся полученным результатом. На рисунке вы можете увидеть, что, как и следовало ожидать, то неравенство, которым мы загрузили MathCAD, он разгрыз как орешек.
Пожалуй, единственный минус, который можно назвать — это то, что функция solve выдает ответы в несколько непривычном виде. То есть результат она записывает в виде вектора элементарных неравенств в то время, как удобнее бывает его записать в виде двойного неравенства или в виде интервала.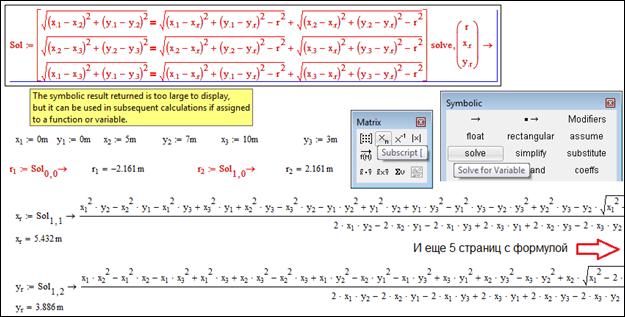
Однако, глядя на рисунок, думаю, вы согласитесь со мной в том, что привести результат в удобный для человеческого глаза вид не составит никакого труда. Нужно только иметь в виду, что, если в результате вычисления решения MathCAD пришел к выводу, что данному неравенству удовлетворяет любое рациональное число, то в ответе напишет просто обозначение той переменной, относительно которой мы решали неравенство — то есть в нашем случае MathCAD написал бы, если бы было нужно, просто x. При интерпретации решений нужно внимательно следить за тем, какой именно знак (знак точного неравенства или приблизительного, то есть с возможностью равенства) используется системой в ответе: даже если из всей числовой оси не подходит всего лишь одна-единственная точка, MathCAD не выдаст вам ответ в виде x?a, а напишет в столбик два неравенства: x<a и x>a.
Но если бы вывод результатов был единственным минусом всего процесса решения неравенств в MathCAD’е, то о нем, пожалуй, не стоило бы даже и вспоминать.
К сожалению, есть вещи гораздо более серьезные, которые не позволяют использовать результаты решения неравенств в MathCAD’е без их предварительной проверки. Дело в том, что MathCAD не умеет грамотно работать с областью определения той переменной, которая используется в неравенстве. Это, конечно, бывает не во всех случаях — например, когда область определения ограничивается тем фактом, что неравенство у нас записано в виде дроби, но при этом и числитель, и знаменатель содержат многочлены целых степеней, то MathCAD вполне успешно справляется с такими задачами. Однако уже наличие корней в неравенстве ставит MathCAD в тупик: программа вполне может выдать результат, для которого под корнем оказываются отрицательные значения переменных в то время, как на множестве рациональных чисел вычисление корня отрицательной величины не определено. За примером подобного случая далеко ходить не надо: давайте попробуем подсунуть функции solve неравенство (x1/2-2)(x-4)>0. В качестве результата MathCAD безо всяких зазрений совести выдает ответ, который можно записать как x?4 (см.
Другая проблема, которая может возникнуть при решении неравенств (как, впрочем, и в решении уравнений) — это громоздкость выдаваемых системой в ответе выражений. Правда, для тех случаев, когда мы записываем все коэффициенты в выражениях непосредственно в числовом виде, это менее заметно, поскольку и ответ система выдает в виде чисел. Однако, если перейти от конкретных чисел к общему виду неравенств, то получится все как-то уже не так весело и жизнерадостно. Чтобы не быть голословным, приведу, как издавна уже у нас с вами повелось, пример, иллюстрирующий последние высказывания. Эта иллюстрация показывает, как MathCAD решал неравенство x1/2-a>0.
Выражение, выдаваемое MathCAD’ом результате борьбы с этим неравенством, настолько громоздкое, что даже сложно сходу оценить его правильность.
В будущем мы с вами посмотрим, как можно бороться с громоздкостью выражений, используя мощь символьного процессора, встроенного в MathCAD его разработчиками, но заранее хочу сказать, что серьезно упростить с его помощью удается сравнительно небольшое число разнообразных выражений. Что это значит? Это значит, что с неравенствами лучше не увлекаться получением решения в общем виде, а решать, используя конкретные значения коэффициентов, и тогда работать с результатами решений, выдаваемыми MathCAD’ом, будет существенно проще и удобнее. Но самого грустного в песне о решении неравенств мы еще не касались. Оно же состоит в том, что даже не со всеми элементарными функциями MathCAD справляется успешно, не говоря уже о функциях специальных. Так, скажем, символьный процессор MathCAD, который и использует функция solve, «не дружит» с тригонометрическими функциями. Верится с трудом, но это так — при всей своей мощи MathCAD не может решить даже элементарное школьное неравенство sin(x)<0 (см. иллюстрацию).
Возможно, вас несколько утешит мысль о том, что с показательными и логарифмическими неравенствами MathCAD справляется все-таки неплохо (правда, и здесь есть ограничение — случаи, когда переменная, стоящая в основании степенной функции, в том или ином виде попадает и в показатель). Однако и с тригонометрическими неравенствами ведь что-то нужно делать, не так ли? Действительно, способ решить сложное тригонометрическое неравенство существует — это преобразовать его таким образом, чтобы оно содержало одноименные тригонометрические функции (обычно синусы или косинусы, хотя, возможно, также и тангенсы или котангенсы — это уже зависит от вашего вкуса и от вида конкретного неравенства), а затем уже решать, но не относительно x, а относительно той функции, которая является для вашего получившегося неравенства базовой. О преобразовании выражений встроенными средствами MathCAD мы, как я уже, кажется, обещал выше, поговорим, а пока просто имейте в виду, что можно применять такой прием борьбы с тригонометрическими неравенствами.
Системы неравенств
Неравенства могут быть записаны и в виде системы. Если вы помните, как мы справлялись с решением систем уравнений, то и работа с системами неравенств не должна показаться для вас особенно сложной, поскольку в большинстве случаев она совершенно аналогична работе с системами уравнений. Мы записываем систему неравенств виде вектор-столбца, который потом решаем с помощью функции solve совершенно аналогично тому, как решали одиночное неравенство.
Этот метод решения систем неравенств, безусловно, подкупает, прежде всего, своей простотой, однако, сами понимаете, у всего на свете есть свои минусы (или, как сказал герой фильма «В джазе только девушки», «У всех свои недостатки»). Бывают случаи, когда solve в бессилии опускает руки перед не самой сложной системой неравенств, и тогда приходится изобретать какие-то специальные методы, которые позволили бы нам получить решение нужной системы.
К счастью, ничего экстраординарного изобретать, на самом-то деле, не требуется, поскольку алгебраические неравенства обладают счастливым свойством, позволяющим нам разбить решение на несколько этапов. То есть мы можем решить каждое из неравенств системы по отдельности, а потом просто объединить результаты так, как этому учили еще в школе. То есть мы должны выбрать из всех результатов решения неравенств те промежутки, на которых наша переменная удовлетворяет каждому из наших неравенств. Сделать это, как правило, не так уж и сложно. Возможно, решение системы неравенств вторым, пошаговым, способом можно считать даже более предпочтительным путем, чем «скармливание» функции solve всей системы сразу, потому что путем преобразования мы всегда сможем добиться того, чтобы MathCAD справился с неравенством, а значит, что такой метод подходит для всех неравенств. Функция solve же, к сожалению, творческими задатками не обладает, а потому априори метод действия «в лоб», который мы применяем, используя ее ко всей системе, менее результативен, чем пошаговое решение каждого из неравенств с последующим объединением ответов.
Но, конечно, какой из методов использовать сразу — это все остается на ваше собственное усмотрение.
Итак, мы с вами познакомились с методами решения неравенств в среде MathCAD. Как видите, реализация решений их в MathCAD’е, скажем прямо, довольно-таки далека еще от совершенства, но, тем не менее, применяя природную смекалку и некоторые математические хитрости, можно успешно справляться с большинством видов неравенств и их систем (ну, разве что придется решать вручную простые тригонометрические неравенства — но это не так уж и страшно, на самом-то деле). Но в общем и целом, несмотря на все трудности, с которыми столкнется пользователь, пожелавший озадачить MathCAD неравенствами, без MathCAD’а решать их будет, как ни крути, дольше.
Kalyan Open 7 Pass — Google Suce
AllenewsvideosbildermapsshoppingBücher
Sucoptionen
GET Daily Kalyan Open Pass Direct — Satka Matka
Sattamatkaratan.
in Passaal все индийские пользователи. Карта Kalyan Open Pass может быть доступна из любого города или штата Индии. Наши советы высокого уровня …
Kalyan Open Pass — Satta Matka
sattamatkaratan.com › kalyan-open-pass
Kalyan Open Pass — Only Fix sm Matka игра, угадывание матки, Kalyan Open Pass Satta Matka, 100% числа Matka, Satta ka Matka, sattamatka, fix fix Matka …
Kalyan Open Pass, Satta Matka, Fix Matka, Kalyan Dpboss
sattamatka.rest › Kalyan Open Pass
Kalyan Open Pass — тип индийской лотереи, которая проводится после 10-летия независимости Индии. Kalyan Open Pass является частью индустрии MAtka …
KALYAN | САТТА МАТКА | МАТКА | КАЛЯН МАТКА | МАТКА…
kalyan-matka.net
Вам просто нужно ежедневно посещать наш сайт и получать еженедельные игры Lines, Kalyan Open, Matka Jodi Fix, Kalyan Final и принимать участие в игре Matka. Вы также можете получить Kalyan …
Kalyan Open Pass — Satta Matka Blue
sattamatka.
blue › kalyan-open-pass
Kalyan Open Pass является частью индийской системы азартных игр, которая действует в Индии после 90-х годов. . Из-за безработицы в Индии люди начинают зарабатывать деньги …
Kalyan matka — Kalyan open 7 pass — Facebook
www.facebook.com › posts › kalyan-open-7-pass
Kalyan matka · 24 февраля 2020 г., 11:18 · Facebook для Android ·. Кальян открыть 7 проход. Описание фото отсутствует. Загрузка… Повторите попытку.
Кальян Матка, Кальян Сатта | AFTER PASS AFTER PASS 8144750737
www.facebook.com › … › Кальян Матка, Калян Сатта | Facebook
Kalyan Special Game — 8374765680. 2 тыс. участников · 70 сообщений в день. Посетить группу · Групповое фото · KALYAN FREE JODI SATTA MATKA. 7 тыс. участников · 305 сообщений в день.
Бесплатный еженедельный джоди
studiomedicobulzomi.it › free-weekly-jodi
Мы используем наш опыт, чтобы помочь вам с Kalyan Matka никогда не проигрывать игры.
… Open Panna=680=4=Pass Kalyan Fix Single JODI Today Game=379=99=Pass Milan …
Kalyan Satta Matka Fix Ank OTC — Apps on Google Play
play.google.com › store › apps › подробности › id=apps.k…
Bewertung 4,9
(2.762) · Kostenlos · Android
Kalyan Matka Main Mumbai Satta Matka Результаты рынка Самое быстрое обновление в реальном времени. Запись диаграммы Кальяна В этом приложении у нас есть данные записи диаграммы Кальяна с 1974 по …
Ähnliche Fragen
Как рассчитывается число Сатта?
Законен ли Кальян Сатта?
Кто владелец Кальян Сатта?
Матка настоящая?
Кальян Результат | Новый Золотой день| Matkaone
www.matka1.com › kalyan-result-new-golden-day-…
Matka| Сатта матка | Калян Результат | матка живой результат| маткаоне, кальян… ОТКРЫТЫЙ 1 ПРОХОД. ДЕНЬ РАДЖАНИ. ОТКРЫТЬ 7 ПРОХОД. ЗАКРЫТЬ 0 ПРОХОД.
КАЛЯН. ОТКРЫТЬ 7 ПРОХОД.
ähnliche sucalfragen
Kalyan Open Pass
Kalyan Fix Open Pass
Kalyan Open Pass Result
Kalyan Open Pass
Kalyan Open Panna
Kalyan Open
Kalyan Open Open
Kalyan Open
Kalyan Open Open
40004 Kalyan Open
Kalyan Open Open
Kalyan Open.
Исправьте дизайны, темы, шаблоны и загружаемые графические элементы Matka на Dribbble
Посмотреть CarBee
CarBee
Посмотреть Пятиминутное исправление обратной связи
Пятиминутное исправление обратной связи
Посмотреть AE86
Просмотр устранения неполадок MSIX
Устранение неполадок MSIX
Посмотреть Получите больше за меньшие деньги
Получите больше за меньшие деньги
Смотреть Ничто не может исправить небольшая музыка
Нет ничего, что не исправила бы музыка
Посмотреть 1992 г.
