Смешанное сопряжение двух окружностей: Смешанное сопряжение дуг окружностей — Студопедия

Сопряжение двух дуг окружностей дугой заданного радиуса R

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

 

 

ИНЖЕНЕРНАЯ ГРАФИКА

 

Методические указания и контрольные задания

Для студентов строительных специальностей и направлений

Заочной формы обучения

 

 

Одобрено

редакционно-издательским советом

Балаковского института техники,

технологии и управления

 

 

Балаково 2012

 

ВВЕДЕНИЕ

Данные методические указания и контрольные задания составлены для студентов строительных специальностей и направлений заочной формы обучения.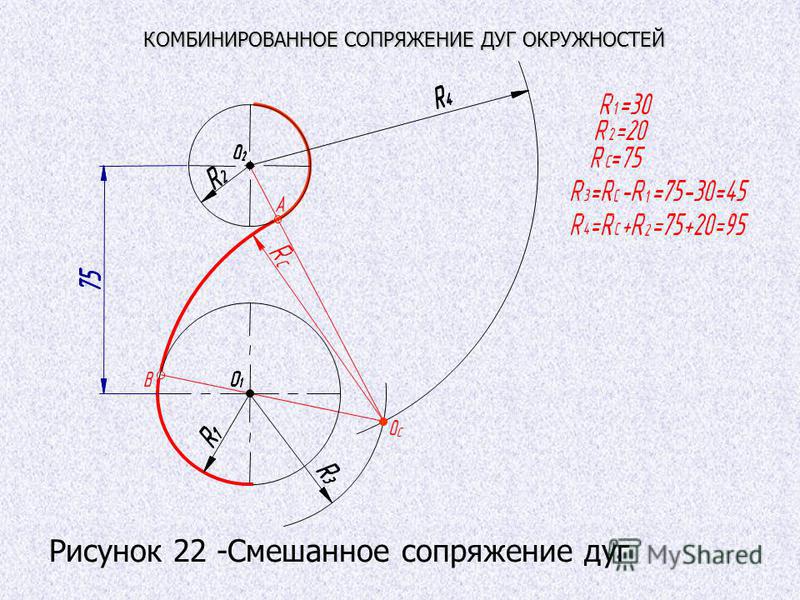

Включают задания по темам дисциплины «»Инженерная графика».

Контрольная работа выполняются на листах чертежной бумаги формата А3 (297х420 мм)

с помощью чертежных инструментов карандашом в заданном масштабе в соответствии с вариантом. Номер варианта задания соответствует последней цифре шифра студента. На рецензию контрольные работы предоставляются в полном объеме.

К экзамену допускают студентов, выполнивших практические, контрольные задания и прошедших собеседование.

Надписи и буквенно-цифровые обозначения на листах выполняют шрифтом по ГОСТ ЕСКД 2.304-81.

ЛИСТ 1

Задача 1. Перечертить крюк крана с рис. 1.

Задача 2. Начертить прокатный профиль. Данные для решения задачи взять из табл. 1. Пример оформления листа 1 приведен на рис. 2.

Указания к решению задач 1, 2

Сопряжением называется плавный переход прямой линии в дугу или одной дуги в другую.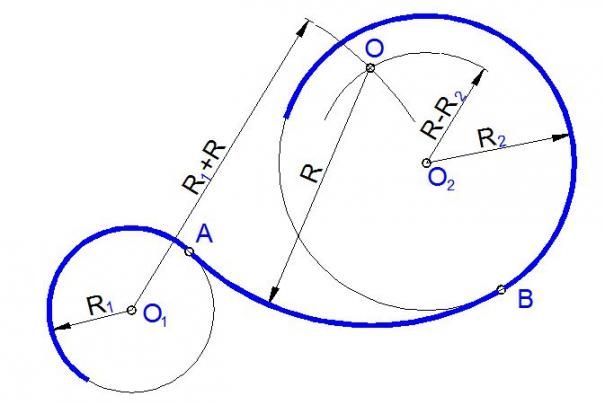

Сопряжение пересекающихся прямых дугой заданного радиуса R

Центр сопряжения О находится в точке пересечения двух прямых, проведенных параллельно сопрягаемым прямым на расстоянии, равном заданному радиусу сопряжения R. Точки сопряжения 1 и 2 получаются на пересечении перпендикуляров, проведенных из центра сопряжения О к сопрягаемым прямым (рис.3).

Рис.1. Крюк крана

Таблица 1

Таблица прокатных профилей

Рис 3. Примеры сопряжения пересекающихся прямых

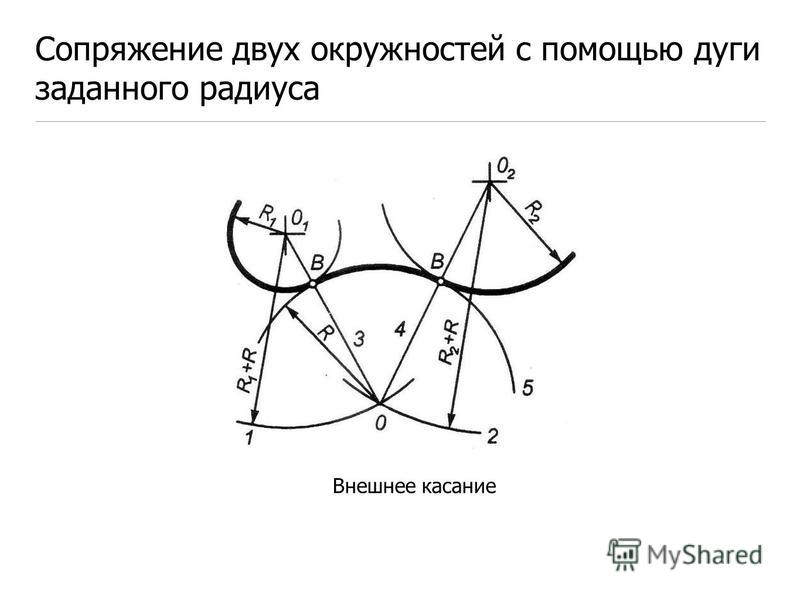
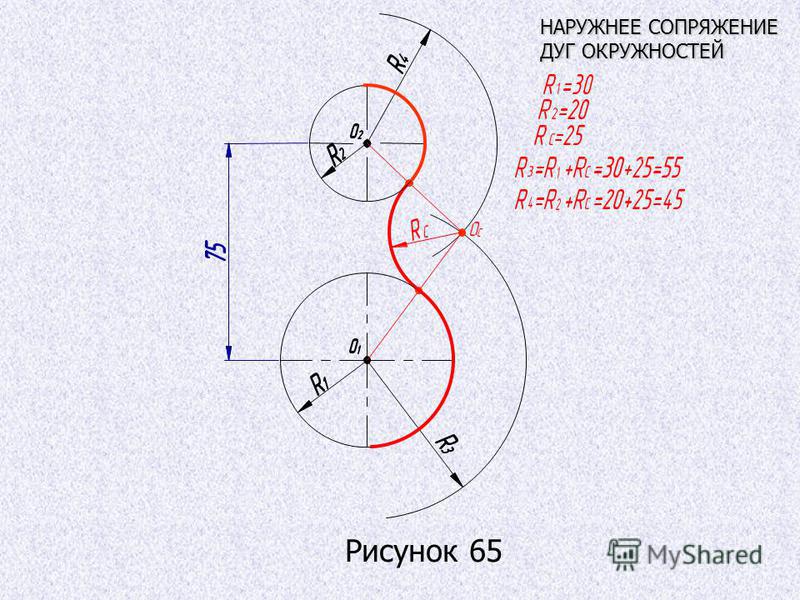
Сопряжение двух дуг окружностей дугой заданного радиуса R

Внешнее сопряжение. Под внешним сопряжением двух дуг понимается такое сопряжение, при котором сопрягаемые дуги и дуга сопряжения находятся по разные стороны от общей касательной, и дуга сопряжения является вогнутой относительно сопрягаемых дуг.

Из центров О₁ и О₂ радиусами, равными сумме радиусов R1 + R, R2+ R, проводятся дуги окружностей, пересечение которых определяет точку О – центр сопряжения. Центр сопряжения О соединяется с центрами сопрягаемых дуг окружностей О₁ и О₂, находятся точки сопряжения 1 и 2. Из центра сопряжения О проводится дуга радиусом R от точки 1 до точки 2 (рис.4а).

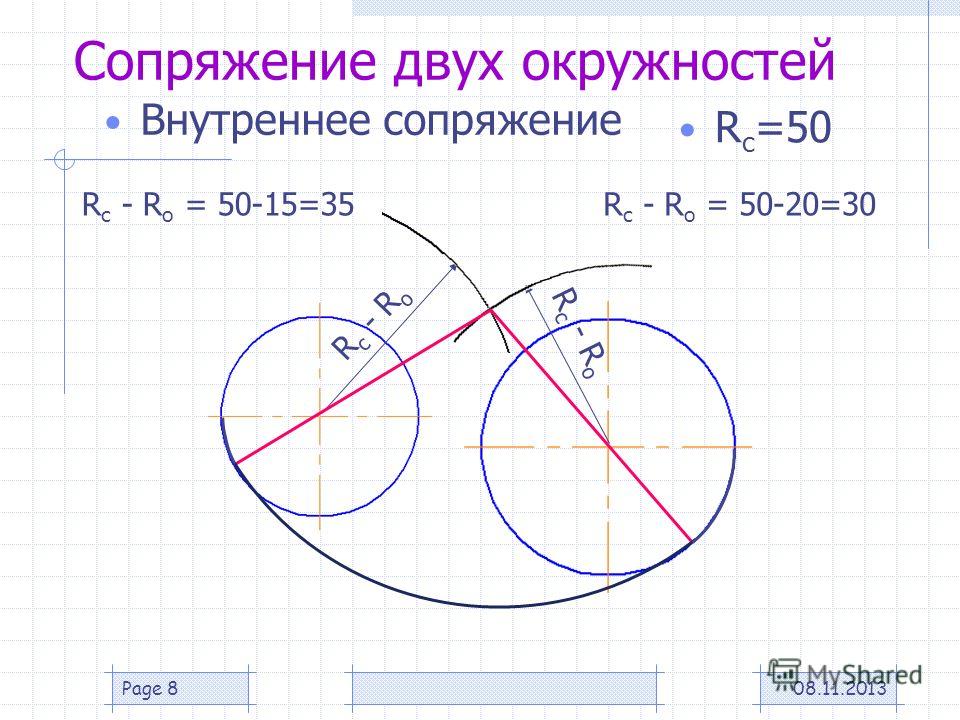
Внутреннее сопряжение. При внутреннем сопряжении дуга сопряжения и сопрягаемые дуги находятся по одну сторону от общей касательной и дуга сопряжения является выпуклой относительно сопрягаемых дуг.

Из центров О₁ и О₂ радиусами, равными разности радиусов R – R1, R- R2, проводятся дуги окружностей, пересечение которых определяет точку О – центр сопряжения. Центры сопрягаемых дуг О₁ и О₂ соединяются с центром сопряжения О, на дугах находят точки сопряжения 1 и 2. Из центра сопряжения О проводится дуга радиусом R от точки 1 до точки 2 (рис.4б).

Смешанное сопряжение. Смешанное сопряжение содержит элементы внешнего и внутреннего сопряжений. Из центров О₁ и О₂ радиусами, равными разности радиусов R – R1 и сумме радиусов R2+ R, проводятся дуги окружностей, пересечение которых определяет точку О – центр сопряжения.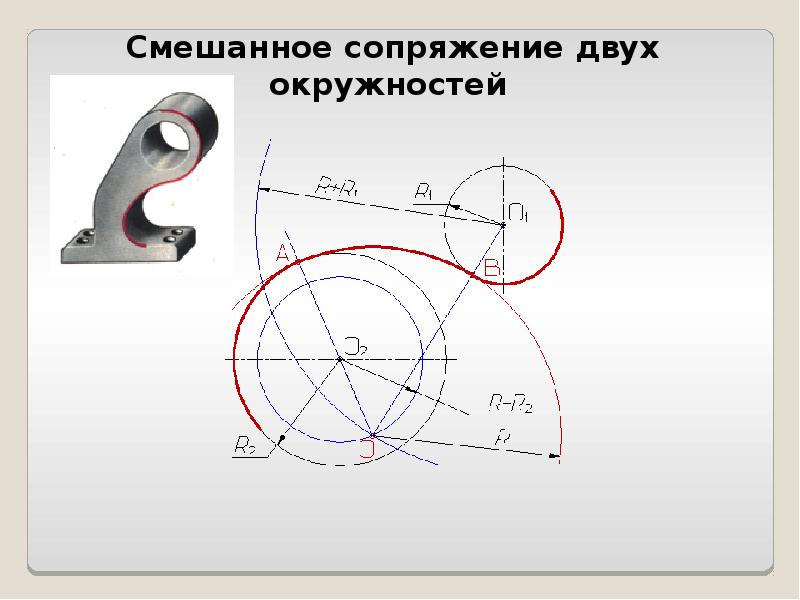 Центры сопрягаемых дуг О₁ и О₂ соединяются с центром сопряжения О, на дугах находят точки сопряжения 1 и 2. Из центра сопряжения О проводится дуга радиусом R от точки 1 до точки 2 (рис.4в).

Рис 4. Пример построения сопряжения двух дуг окружностей дугой заданного радиуса R: а- внешнее сопряжение; б- внутреннее сопряжение; в- смешанное сопряжение

ЛИСТ 2

Задача 3. Построить вид сверху и слева, выполнить фронтальный, горизонтальный, профильный разрезы, аксонометрическую проекцию.

Пример оформления листа представлен на рис. 5. Данные для решения задачи приведены в табл. 2.

Указания к решению задачи 3

Геометрическое тело в задаче имеет два сквозных отверстия: вертикальное и горизонтальное. Используя метод вспомогательных секущих плоскостей, строится линия пересечения наружной поверхности с горизонтальным отверстием, затем линия пересечения внутренней поверхности с горизонтальным отверстием.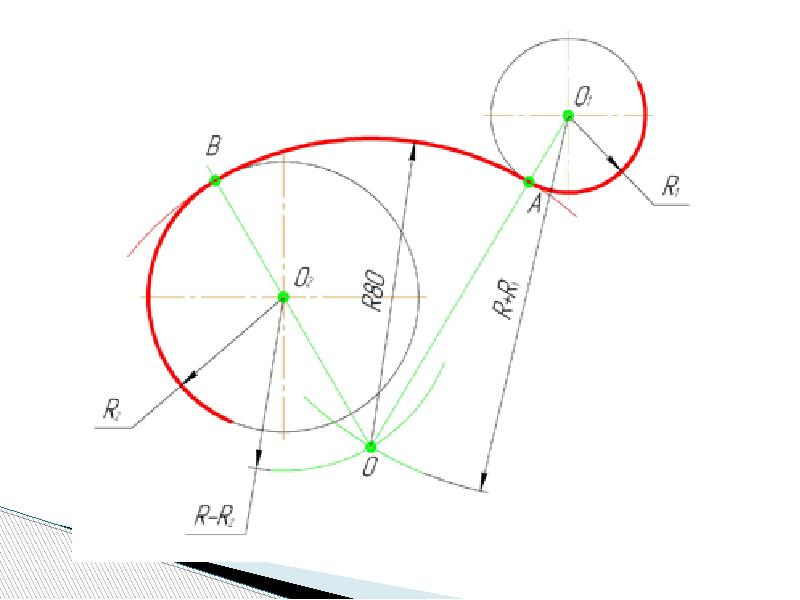 Вид слева рекомендуется строить в проекционной связи, используя правила начертательной геометрии.

 

 

После построения видов выполняют простые разрезы: фронтальный, горизонтальный, профильный, располагая их на месте соответствующих видов. Для симметричных деталей линией, разделяющей вид и разрез, является штрихпунктирная линия. В случае наличия ребра детали, совпадающего с осью симметрии – волнистая линия обрыва.

Для построения аксонометрии рекомендуется использовать диметрическую проекцию. В аксонометрии разрезы выполняют двумя секущими плоскостями.

ЛИСТ 3

Задача 4.Вычертить: 1) болт, гайку, шайбу по действительным размерам; 2) болтовое соединение по относительным размерам, используя заданный болт; 3) условное изображение болтового соединения. Пример выполнения листа приведен на рис.6. Варианты для выполнения задачи приведены в таблице 3.

Указания к решению задачи 4.

Изображения болта, гайки, шайбы и простановку размеров выполняются в соответствии с ГОСТ (таблицы 4, 5, 6).

Болтовое соединение вычерчивают по относительным размерам (рис. 7).

Исходными данными для построения являются длина болта и диаметр болта. Болты, гайки, шайбы в продольном разрезе показывают нерассеченными. Соединяемые детали штрихуют в разные стороны.

Упрощенное изображение болтового соединения выполняют в масштабе 1:4.

Задача 5. Перечертить условное обозначение стандартного шва сварного соединения, изображенного на рис.6.

Перед выполнением задачи следует изучить ГОСТ 2.312-72 «Условные изображения и обозначения швов сварных соединений».

 

Таблица 3

Варианты заданий к задаче 4

 

№ варианта	Резьба	Длина болта, мм	№ варианта	Резьба	Длина болта, мм
	М16х1,5			М16
	М20х1,5			М18
	М22х1,5			М20
	М24х2			М22
	М18х1,5			М24

 

Рис. 7. Изображение и расчет болтового соединения по относительным размерам

 

Таблица 4

Таблица 5

Таблица 6

ЛИСТ 4

Задача 6. По аксонометрическому изображению узла металлических конструкций вычертить:1) ортогональные проекции узла в масштабе 1: 10; 2) обозначить сварные швы; 3) составить и вычертить спецификацию металла на узел. Варианты заданий приведены на рис. 8. Пример выполнения задачи 6 приведен на рис. 9.

Указания к решению задачи 6.

Расположение видов элементов металлических конструкций отличается от расположения видов других конструкций. Вид сверху располагается в проекционной связи над главным видом, вид снизу – под главным видом, вид справа – справа от главного вида, вид слева – слева от главного вида. Над каждым видом, кроме главного, делают надпись по типу «А», а направление взгляда указывают стрелкой, обозначенной соответствующей буквой.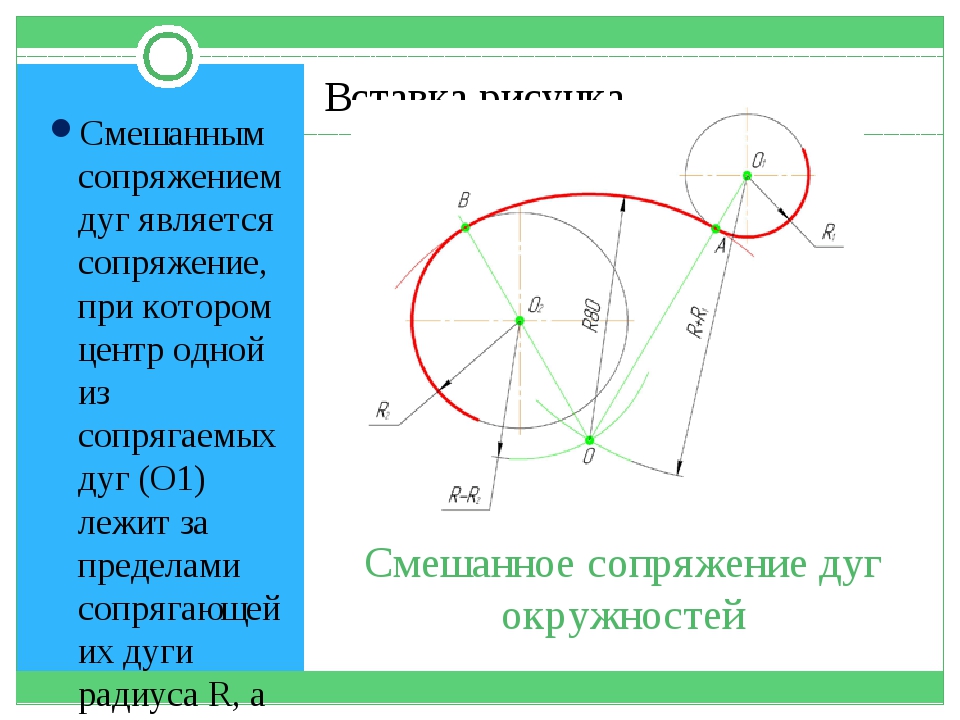

На чертежах металлических конструкций допускается условное обозначение и размеры профилей материалов указывать на изображениях деталей на полках линий – выносок. Размеры профиля или его номер и длину детали наносятся справа от условного обозначения, количество деталей указывается рядом с размерами детали через тире.

Сварные швы выполняются на чертеже по требованиям ГОСТ 2.312-72. При наличии одинаковых швов обозначение наносят у одного, а от изображений остальных швов проводят линии выноски с полками. Всем одинаковым швам присваивают один порядковый номер. При обозначении сварных швов рекомендуется принять ГОСТ 5264-80, катет шва – 8 мм.

 

Рис.8. Варианты заданий для задачи 6

ЛИСТ 5

Задача 7.Выполнить сборочный чертеж железобетонного фундаментного блока в масштабе 1:20 и спецификацию на железобетонный фундаментный блок. Данные для выполнения задачи 7 представлены на рис.

10 и в таблице 8. Пример оформления листа 5 приведен на рис. 11.

Рис.10. Эскиз фундамента

Таблица 8

Варианты заданий к задаче 7

 

№ варианта	Марка фундамента	Длина,мм l	Ширина,мм b	Высота,мм h	Расход бетона, м3	Вес изделия, т
1, 0	ФЛ 28.12-4				1,369	3,42
2, 9	ФЛ 24.12-4				1,138	2,85
3, 8	ФЛ 20.12-4				0,975	2,44
4, 7	ФЛ 16. 12-4				0,486	1,215
5, 6	ФЛ 16.8-4				0,32	0,8

 

Указания к решению задачи 7

Сборочные чертежи состоят из видов, разрезов, и схем армирования.

На видах, разрезах показываются контуры и габаритные размеры элемента, закладные детали, отверстия. Арматура изображается на схемах армирования, бетон условно считается прозрачным. Для несложных железобетонных конструкций схема армирования совмещается с видами. Контуры конструкции изображаются на схемах армирования тонкими линиями, арматуру – сплошной основной линией.

На видах и разрезах наносятся размеры, указания о характере соединения составных частей и другие требования, которые должны быть выполнены и проконтролированы по чертежу, размеры отдельных деталей, на которые не выпускаются чертежи.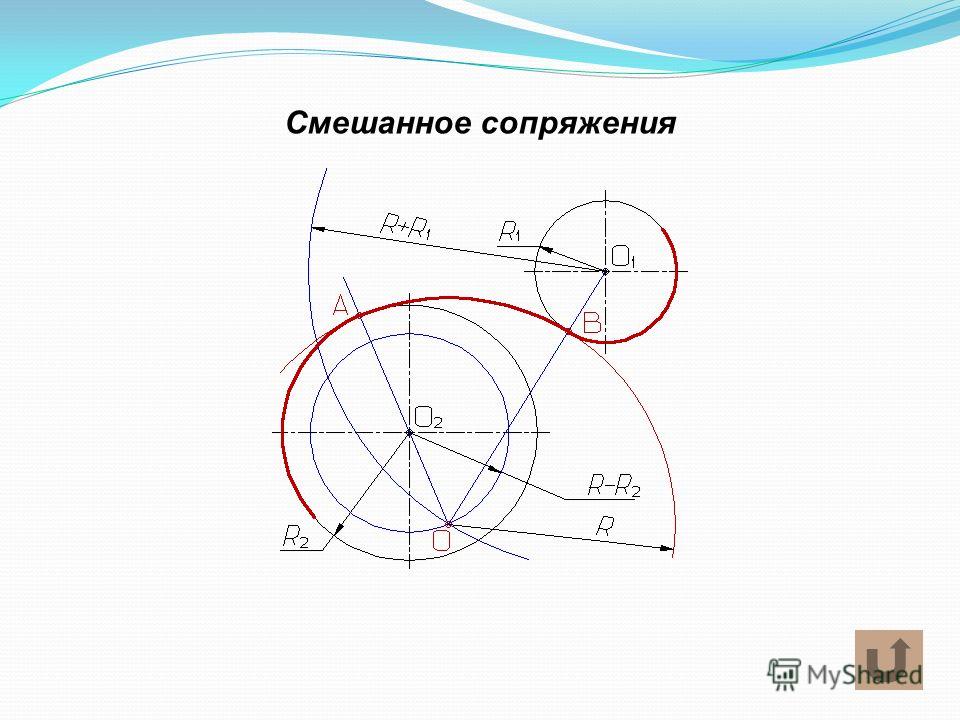

Все составные части конструкции нумеруются в соответствии с номерами позиций, указанными в спецификации.

Номера позиций на чертеже указываются, как правило, один раз. Номера позиций наносятся на полках линий-выносок, проводимых от видимых изображений элементов конструкции и располагаются вне контура изображения.

Спецификация на фундаментный блок выполняется в соответствии с ГОСТ 2.108-68*. Спецификация содержит разделы: документация, комплекс, сборочные единицы, детали, стандартные изделия, прочие изделия, материалы, комплекты. Наименование разделов указываются в виде заголовков, подчеркивают тонкой линией и выделяются пустыми графами.

В графе «Поз.» указывается порядковый номер составных частей, непосредственно входящих в специфицируемое изделие.

В графе «Обозначение», в разделе «Документация» указывается: обозначение настоящих методических указаний и обозначение сборочного чертежа изделия, в разделах «Сборочные единицы», «Детали» — обозначение чертежей.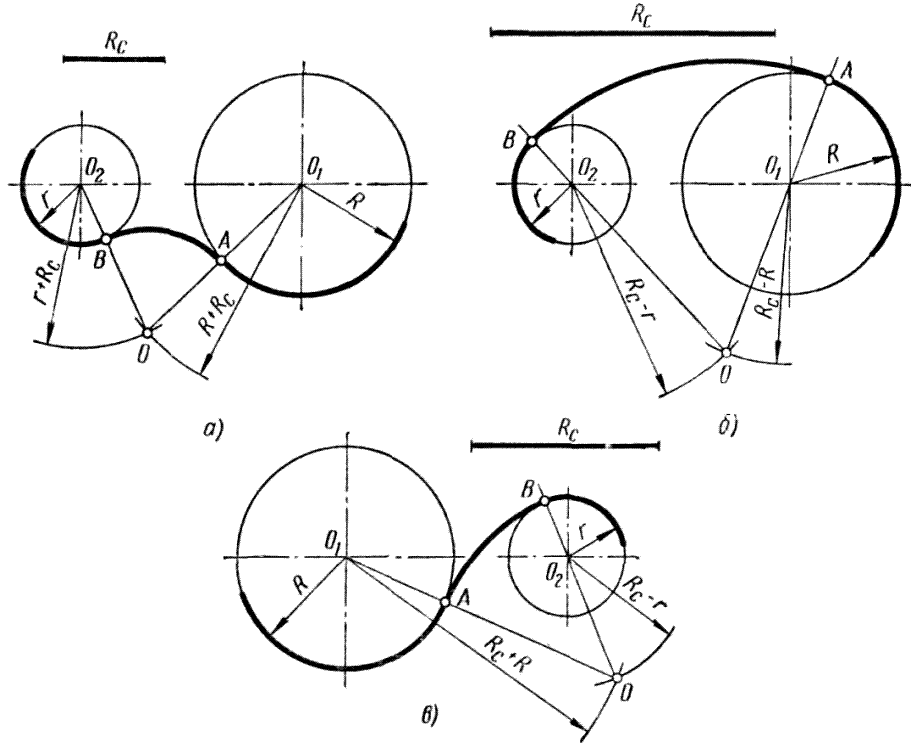

В графе «Наименование» указывается наименование документа или изделия. В данной графе для деталей, не имеющих чертежей, записывается вся информация, необходимая для изготовления и контроля, например ñ 10 А 300 ГОСТ 5781-82 =1150.

В графе «Кол.» указывается количество составных частей деталей, входящих в специфицируемое изделие. В разделе «Материалы» — общее количество материалов на одно специфицируемое изделие с указанием единиц измерения. Допускается единицы измерения записывать в графе «Примечание». В графе «Примечание» указываются дополнительные сведения, например, единицу измерения массы.

Как правило, спецификация выполняется на отдельных листах формата А4. Допускается совмещать спецификацию со сборочным чертежом. Такому совмещенному документу присваивается обозначение спецификации.

ЛИСТ 6

Задача 8. Перечертить план здания в масштабе 1: 100, изображенный на рис. 12. Нанести недостающие размеры.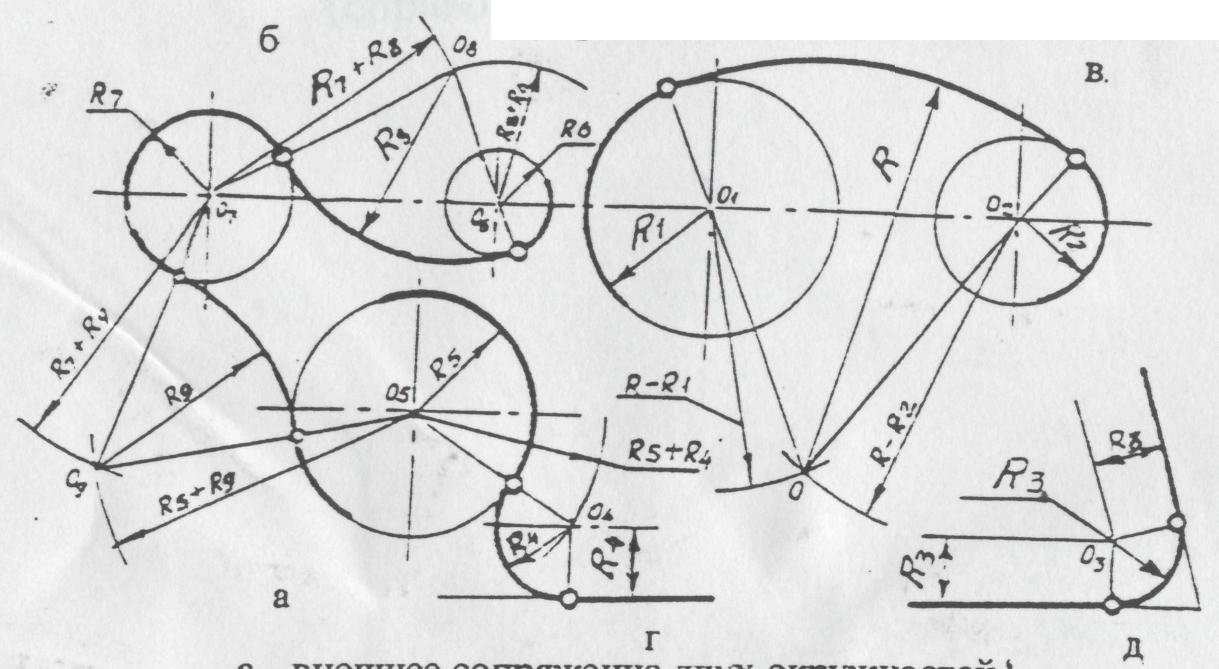

Указания к выполнению задачи 8

План здания — изображение здания, мысленно рассеченное горизонтальной плоскостью на уровне оконных и дверных проемов или на расстоянии 1м над изображаемым уровнем и спроецированное на горизонтальную плоскость проекций.

Положение всех конструктивных элементов на плане здания определяется привязкой к координационным осям.

Координационные оси выполняются штрихпунктирными линиями и обозначаются марками в кружках диаметром 6…12мм. Для маркировки используются арабские цифры и прописные буквы, за исключением букв З, Й, О, Х, Ы, Ъ, Ь. Цифрами маркируются оси по сторонам здания с большим количеством координационных осей. Размер шрифта марок осей должен быть на 1-2 номера больше размера шрифта на чертеже.

Последовательность маркировки осей принимают слева направо и снизу вверх. Маркировку осей, как правило, располагается по левой и нижней сторонам плана здания.

Линейные размеры наносятся в миллиметрах без обозначения единицы измерения в виде замкнутой цепи. Размеры допускается повторять.

На строительных чертежах вместо стрелок применяются засечки в виде короткой сплошной основной линии под углом 45⁰ к размерной линии.

Отметки уровней (высоты, глубины) на планах наносятся в прямоугольнике, контур которого обведен тонкой сплошной линией, или на полке линии-выноски. Перед размерным числом отметки обязательно ставится знак плюс или минус. Отметки указываются в метрах с тремя десятичными знаками, например +4,500.

На планах здания проводятся внешние размерные линии (от одной до четырех) обычно слева и снизу вне контура плана. При этом первую размерную линию проводят на расстоянии не менее 10 мм от контура плана.

На первой размерной линии наносятся размеры дверных и оконных проемов и простенков между ними, на второй — размеры между смежными осями и на третьей размеры между крайними осями.

Внутренние размеры помещений, толщины перегородок и внутренних стен проставляются на внутренних размерных линиях.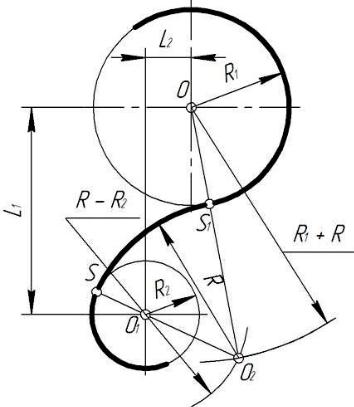

На планах этажей наносят и указывают:

1. Координационные оси здания, расстояния между ними и крайними осями.

2. Отметки участков плана, расположенные на разных уровнях.

 

3. Толщину стен и перегородок и их размерную привязку.

4. Все проемы и отверстия с необходимыми размерами и привязками.

Для проемов с четвертями размеры показывают по наименьшей величине проема. Размеры дверных проемов в перегородках на планах не показывают.

5. Площади помещений в квадратных метрах с двумя десятичными знаками приводят в нижнем правом углу плана и подчеркивают основной линией.

6. Тип заполнения проемов, ворот и дверей (в кружках диаметром 5мм).

7. Марки элементов зданий (например, лестниц, сантехкабин).

8. Номера помещений в кружках диаметром 5-7мм.

Последовательность вычерчивания плана следующая:

1. Проводят продольные и поперечные координационные оси.

2. Вычерчивают все наружные и внутренние стены и перегородки, колонны, если они имеются.

3. Производят разбивку оконных и дверных проемов в наружных и внутренних стенах и перегородках, условно показывают открывание дверей.

4. Вычерчивают санитарно-технические приборы. Наносят выносные и размерные линии.

5. Проставляют все размеры на чертеже и надписи.

6. Проверяют чертеж, выполненный в тонких линиях.

7. После исправлений и доработок приступают к окончательной обводке плана карандашом марки ТМ.

ЛИСТ 7

Задача 9. Перечертить фасад здания в масштабе 1 : 100, изображенный на рис. 13.

Указания к решению задачи.

Виды здания спереди, сзади, слева, справа называются фасадами.

 

 

Чертежи фасадов именуются по крайним координационным осям, например “Фасад 1-4” или по одной оси — “Фасад по оси А”.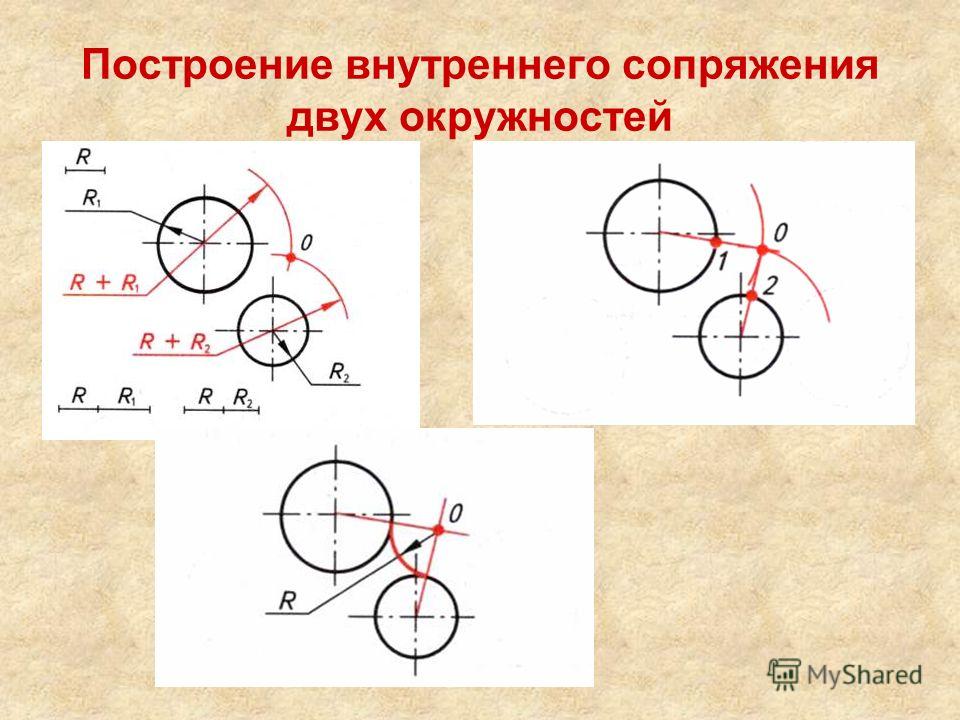

На фасаде наносят и указывают:

1. Координационные оси здания, проходящие в характерных местах фасадов. Размеры между ними не проставляют.

2. Отметки уровня земли, входных площадок, верха стен, низа и верха дверных проемов и расположенных на разных уровнях элементов фасадов.

3. Отметки, размеры и привязки проемов и отверстий.

4. Типы заполнения оконных проемов, если они не входят в состав элементов сборных конструкций стен.

5. Вид отделки отдельных участков стен, отличающихся от остальных. В крупноблочных и панельных зданиях показывают разрезки стен на блоки и панели.

6. Ссылки на фрагменты и узлы, а также на чертежи элементов зданий, не замаркированные на планах и разрезах.

Построения, связанные с вычерчиванием фасада, производятся в следующей последовательности:

1. Наносят координационные оси и чертят контур здания.

2. Вычерчивают оконные и дверные проемы, балконы, плиты козырьков над входами и другие архитектурные элементы фасада, вычерчивают оконные переплеты, двери, вентиляционные и дымовые трубы на крыше.

3. Проставляют знаки высотных отметок.

4. Проверяют соответствие фасада плану и разрезу.

5. Обводят изображения. Линию контура земли допускается проводить утолщенной линией, выходящей за пределы фасада.

ЛИСТ 8

Задача 10. Перечертить разрез здания в масштабе 1 : 100 с рис.14.

 

Указания к решению задачи

Разрезом называется изображение здания, мысленно рассеченного вертикальной плоскостью и спроецированного на плоскость проекций, параллельно секущей плоскости.

При выполнении разреза здания положение мнимой вертикальной плоскости разреза принимается с таким расчетом, чтобы в изображение попали проемы окон, наружных ворот и дверей. Из видимых элементов на разрезах изображаются только элементы конструкций здания, лестницы и площадки, находящиеся непосредственно за мнимой плоскостью разреза.

Секущие плоскости не проводятся по колоннам, вдоль прогонов и балок перекрытий и по стропилам.

Колонны, перегородки, прогоны, балки и стропила в продольном направлении всегда показываются нерассеченными.

Видимые линии контуров, не попадающие в плоскость сечения, выполняются сплошной тонкой линией.

Различают архитектурные (контурные) и конструктивные разрезы.

Архитектурные разрезы составляются на начальной стадии проектирования, чтобы выявить внутренний вид помещений и расположение архитектурных элементов интерьера. На архитектурных разрезах не показываются конструкции фундаментов, перекрытий, стропил и других элементов, но проставляются размеры и высотные отметки.

Конструктивные разрезы составляются на стадии разработки рабочих чертежей, на них показываются конструктивные элементы здания и их сопряжения.

На разрезах наносят и указывают:

1. Координационные оси здания, расстояния между смежными и крайними осями;

2. Отметки уровня земли, пола этажей и площадок;

3. Отметки низа несущих конструкций покрытия одноэтажных зданий и низа плит покрытия верхнего этажа многоэтажных зданий;

4. Отметку низа опорной части заделываемых в стены элементов конструкций;

5. Отметку верха стен, карнизов, уступов;

6. Размеры и привязку (по высоте) проемов, отверстий, ниш и т.п. в стенах и перегородках, для проемов с четвертями размеры указывают по наименьшему проему;

7. Толщину стен и их привязку к координационным осям здания;

8. Марки элементов зданий, не замаркированных на других изображениях;

9. Ссылки на узлы, а также на чертежи элементов здания, замаркированных на разрезах.

Пол на грунте изображается одной сплошной толстой линией, пол на перекрытии и кровлю изображается одной сплошной тонкой линией независимо от числа слоев в конструкции. Состав и толщина слоев покрытия указывается в выносной надписи.

Разрезы обозначаются буквами или цифрами по типу “Разрез 1-1” над изображением. Надпись не подчеркивается.

Отметки уровней на разрезе помещаются на выносных линиях или линиях контура. Отметки указываются метрах с тремя десятичными знаками после запятой.

Построение разреза на чертеже выполняется в следующей последовательности:

1. Проводят вертикальные координационные оси.

2. Перпендикулярно осям проводят горизонтальные линии уровней поверхности земли, пола всех этажей, условно верха чердачного пере-крытия, карниза.

3. Наносят тонкими линиями контуры наружных и внутренних стен, перегородок, а также высоты междуэтажных и чердачного перекрытий и конька крыши, отмечают и вычерчивают выноса карниза и цоколя, вычерчивают окаты крыши.

4. Намечают в наружных и внутренних стенах и перегородках оконные и дверные проемы.

5. Проводят выносные и размерные линии, кружки для маркировки координационных осей и знаки для простановки высотных отметок.

6. Окончательно обводят сечения, проставляют высотные отметки и размеры, делают поясняющие надписи.

ЛИТЕРАТУРА

1. ГОСТ 2.104-2006. Основная надпись. Введ.2006-09-01 -. М: Изд- во стандартов, 2006. – 5с.

2.ГОСТ 2.301-68. Форматы. Введ. 1971-01-01 — М.: Изд — во стандартов, 2005. – 2с.

3. ГОСТ 2.302-68. Масштабы. Введ. 1971-01-01 — М.: Изд — во стандартов, 2005. – 1с.

4. ГОСТ 2.303-68.Линии. Введ. 1971-01-01 – М.: Изд — во стандартов, 2005. – 6с.

5. ГОСТ 2.304-81.Шрифты чертёжные. Введ. 1982-01-01. – М.: Изд- во стандартов, 2005. – 21с.

6. ГОСТ 2.305-2008. Изображения-виды, разрезы, сечения. Введ.. 2009-07-01 – М.: Изд-во стандартов, 2009.-25с.

7. ГОСТ 2.306-68. Обозначения графических материалов и правила их нанесения на чертежах. – Введ.1971–01–01. –Изд-во стандартов,1995. – 8с.

8. ГОСТ 2.307-2011. Нанесение размеров и предельных отклонений.- Введ. 2011-07-01 – М.: Стандартинформ, 2011.-33с.

9. ГОСТ 2.311-68. «Изображение резьбы». – Введ.1971–01–01. –Изд-во стандартов,1995. – 6с.

10. ГОСТ 2.312-72. Условные изображения и обозначения швов сварных соединений. – Введ.1973–01–01. –Изд-во стандартов,1995. – 15с.

11. ГОСТ 2.315-68^*. Изображения упрощенные и условные крепежных деталей. – Введ.1971–01–01. –Изд-во стандартов,1995. – 15с.

12. ГОСТ 2.317-2011. Аксонометрические проекции. – Введ.2012–01–01. – Стандартинформ, 2012. – 15с.

13. ГОСТ 2-108-68^*. Спецификация. – Введ.1971–01–01. –Изд-во стандартов,1995. – 12с.

14. ГОСТ Р21.1101-2009. Система проектной документации для строительства. Основные требования к проектной и рабочей документации. – Введ.2010–07–01. –Изд-во стандартов, 2010. – 40с.

15. Короев Д.И. Черчение для строителей.– М.: ВШ, 2009.– 256с.

 

СОДЕРЖАНИЕ

	Введение
	Лист 1
	Лист 2
	Лист 3
	Лист 4
	Лист 5
	Лист 6
	Лист 7
	Лист 8
	Литература
	Содержание

 

ИНЖЕНЕРНАЯ ГРАФИКА

Читайте также:

Рекомендуемые страницы:

Поиск по сайту

Конспект Практического Занятия по Черчению: выполнение сопряжений

Практическая работа № 1.

Тема: Сопряжение прямой и окружности.

Цель: формирование у учащихся знаний и умений по выполнению сопряжений.

Задание: Выполнить сопряжения линий и окружностей.

Структура занятия:

1)Вступительная часть – 3-5 мин.

2)Изучение теоретической части – 15-20 мин.

3)Выполнение задания – 55-60 мин.

4)Заключительная часть – 5 мин.

Содержание занятия:

1) Приветствие.  Проверка посещаемости. Постановка цели и задач занятия.

2) Ознакомление с заданием на урок, выполнение сопряжений.

Сопряжения линий

Сопряжением называется плавный переход от одной линии к другой. Для построения любого сопряжения дугой заданного радиуса нужно найти:

1. Центр сопряжения – центр, из которого проводят дугу;
2. Точки сопряжения (касания) – точки, в которых одна линия переходит в другую.

Центр сопряжения находится от точек сопряжения на одинаковых расстояниях, равных радиусу сопряжения R.  Переход от прямой к окружности будет плавным в том случае, если прямая касается к окружности. Точка сопряжения К лежит на перпендикуляре, опущенном из центра О окружности к прямой (рис. 1)

рис. 1

Переход от одной окружности к другой будет плавным, если окружности касаются.

Различают два случая касания дуг окружностей: внешнее (рис. 2)  и внутреннее (рис.3). 

При внешнем касании центры окружностей лежат по разные стороны от их общей касательной L (рис. 2). Расстояние между их центрами ОО1 равно сумме радиусов окружностей R+R1 и точка касания лежит на прямой ОО1, соединяющей их центры.

При внутреннем касании центры окружностей лежат по одну сторону от их общей касательной L. Расстояние между их центрами ОО1 равно разности их радиусов  R-R1 и точка касания К окружностей лежит на продолжении прямой ОО1 (рис. 3).

рис. 2	рис. 3

Касание дуг окружностей:

рис. 2 – сопряжение двух окружностей (внешнее касание)

рис. 3 – сопряжение двух окружностей (внутреннее касание)

Сопряжение двух пересекающихся прямых

Даны пересекающиеся  под прямым, острым и тупым углами прямые линии.

Требуется построить сопряжения этих прямых дугой заданного радиуса R.

рис. 4

Для нахождения центра сопряжения проводят вспомогательные прямые, параллельные данным на расстоянии равном радиусу R. Точка пересечения этих прямых т.О и будет центом дуги сопряжения (рис. 4).

1. Перпендикуляры, опущенные из центра дуги сопряжения т.О на данные прямые, определяют точки касания К и N.
2. Из точки О, как центра, описывают дугу заданного радиуса R.

 

рис. 5

Примечание.Для прямых углов центр сопряжения удобнее находить с помощью циркуля (рис. 5).

Сопряжение дуги окружности и прямой линии дугой заданного радиуса.

Внешнее касание 

Дана окружность радиуса R  и прямая АВ. Требуется соединить их дугой радиусом  R1.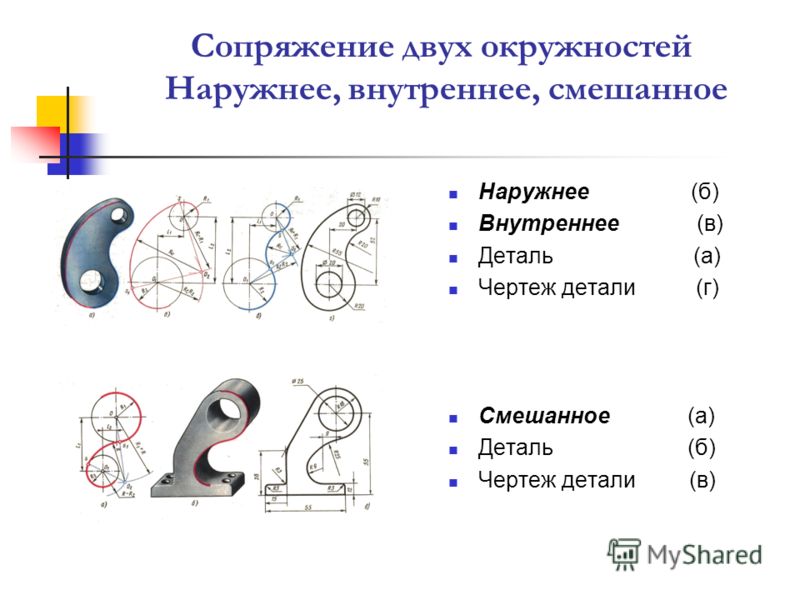

 

 рис. 6 

1. Для нахождения центра сопряжения из центра О заданной окружности проводят дугу m радиуса R + R1 и на расстоянии R1 – прямую n // AB. Точка  О1  пересечения прямой n и дуги m будет центром сопряжения.
2. Для получения точек сопряжения: К и К1  проводят линию центров ОО1 и восстанавливают к прямой АВ перпендикуляр ОК1.
3. Из центра сопряжения О1 между точками К и К1  проводят дугу сопряжения радиусом  R1

Внутреннее касание

 В случае внутреннего касания выполняют те же построения, но дугу m  вспомогательной окружности проводят радиусом R — R1.

рис. 7

Сопряжение двух окружностей дугой заданного радиуса 

Заданы две окружности радиусом R1 и R2. Требуется построить сопряжение дугой заданного радиуса R.

рис. 8

Внешнее касание

1. Для определения центра сопряжения О проводят вспомогательные дуги: из центра О1окружности радиусом  R + R1  и из центра О2 окружности радиуса R + R2. 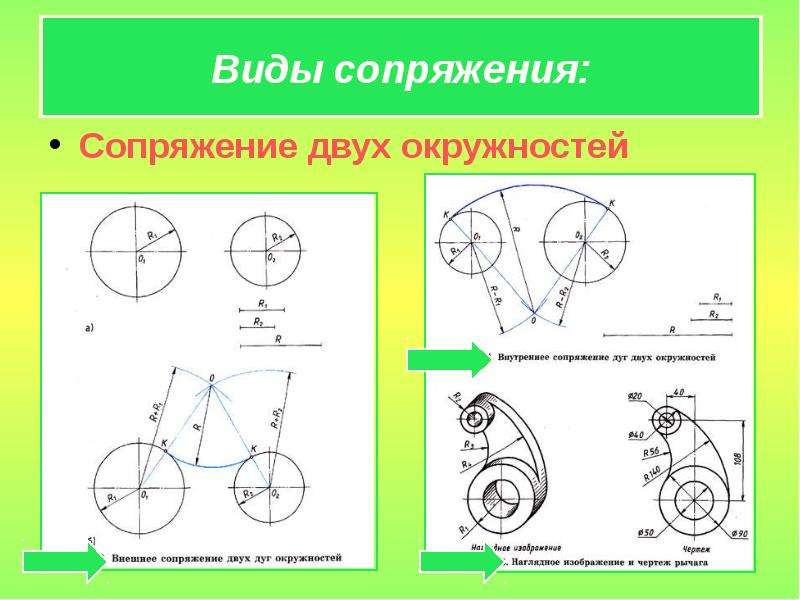Точка О пересечения этих дуг является центом сопряжения.
2. Соединяя центры О и О1, а так же О и О2 , определяют точки сопряжения (касания) К1  и  К2.
3. Из центра О радиусом R проводят дугу сопряжения между точками  К1  и К2

Внутреннее касание 

При внутреннем касании выполняют те же построения, но дуги проводят радиусами

R -R1  и R — R2.

рис. 9 

Смешанное касание

рис. 10

Центр сопряжения О находится в пересечении двух дуг, описанных из центра О1 радиусом R — R1 и из центра О2 радиусом R + R2

Примечание. При смешанном сопряжении центр О1 одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R , а центр О2 другой дуги – вне ее.

 

Частные случаи

 Нахождение центра дуги заданного радиуса.

Задана дуга радиусом R, соединяющая две параллельные прямые mи n и проходящая через точку А ∈ m (рис. 11). Требуется найти центр О заданной дуги.

 

рис. 11

В основу построения положено нахождение точки О, равноудаленной от заданных прямых (рис.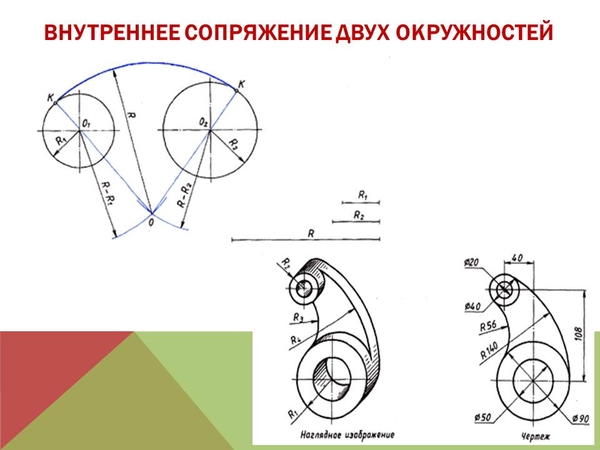 11).

1. Из точки А ∈ m, как из центра, проводят дугу вспомогательной окружности с заданным радиусом R.   
2. Проводят вспомогательную прямую l, параллельную прямой n, на расстоянии, равном заданному радиусу R.
3. Точка О – точка пересечения этих вспомогательных линий является центром заданной дуги. (рис. 12)

рис. 12

3) Подведение итогов занятия. Отметить отличившихся учащихся. Сообщить тему следующего занятия, домашнее задание.

Литература

1. Боголюбов С.К. Инженерная графика: Учебник для средних специальных учебных заведений. – 3-е изд., испр. И доп. — М.: Машиностроение, 2006. – с.392:  ил.
2. Куприков М.Ю. Инженерная графика: учебник для ССУЗов – М.: Дрофа, 2010 – 495 с.: ил.
3. Федоренко В.А., Шошин А.И. Справочник по машиностроительному черчению Л.: Машиностроение. 1976. 336 с.

Тема: «Сопряжения, овалы» | Поурочные планы по черчению

Тема: «Сопряжения, овалы»

23. 04.2014 4513 0

---

Тема: «Сопряжения, овалы»

Черчение 9 класс

Цели урока:

1.      Закрепить полученные знания по теме: «Сопряжения, овалы».

2.      Сформировать умение применять графические знания на практике.

3.      Развитие пространственных представлений учащихся, их наблюдательности, глазомера, измерительных навыков и образного мышления.

4.      Формирование у учащихся основ графической грамотности и навыков графической деятельности, умение анализировать чертёж и выполнять необходимые геометрические построения.

 

Оборудование:

1.      Рабочая тетрадь, учебник, чертёжные инструменты

2.      Карточки – задания для учащихся

 

Ход урока

I Организационный момент

 

Проверка готовности к уроку. Сообщение темы и задачи урока:

·         «Закрепление темы: «Сопряжения»

·         задача нашего урока закрепить полученные знания, выполнив ряд практических упражнений

II Повторение пройденного материала

Ребята, давайте вспомним, о каком графическом построении мы говорили с вами на прошлых уроках? (ответ учащихся)

— Сопряжения. Дайте, пожалуйста, определение (ответ учащихся)

— Сопряжение – это плавный переход одной линии в другую.

Что нужно для построения сопряжения?

• Знать радиус сопряжения (Rc)

• Найти центр сопряжения (Ос)
• Найти точки сопряжения
• Первое сопряжение, с которым мы с вами знакомились – это:

«Сопряжение двух прямых (угла) дугой заданного радиуса»

Даны две прямые, которые составляют прямой, острый и тупой углы, наша задача построить сопряжение: (ответ учащихся)

1.      Находим центр сопряжения, для этого из любых двух точек прямой откладываем расстояние равное радиусу сопряжения. Полученные точки соединяем, получили точку пересечения – это и есть центр сопряжения — точка Ос.

2.      Находим точки сопряжения, для этого из центра сопряжения опускаем перпендикуляры к заданным прямым и на прямых получили точки пересечения – это и есть точки сопряжения.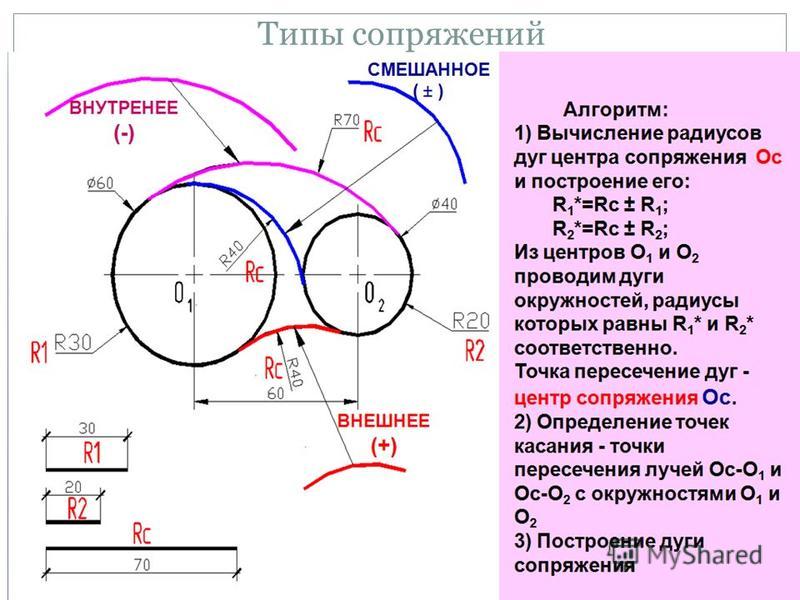

3.      Проводим дугу из центра сопряжения, радиусом равным радиусу сопряжения, соединяя точки сопряжения.Получили

сопряжение двух прямых дугой заданного радиуса.

 

• Следующее сопряжение, с которым мы с вами знакомились – это:

«Сопряжение прямой и окружности дугой заданного радиуса»

Даны прямая и окружность, наша задача построить сопряжение заданным радиусом.

1.                 Находим центр сопряжения, для этого из любых двух точек прямой  откладываем расстояние равное радиусу сопряжения. Полученные точки соединяем, получили прямую, параллельную данной.

2.                 Ставим ножку циркуля в центр окружности и проводим дугу радиусом  равным  радиус окружности + радиус сопряжения. Получили точку пересечения – это и есть центр сопряжения точка Ос.

3.      Находим точки сопряжения, для этого из центра сопряжения опускаем перпендикуляр к заданной прямой.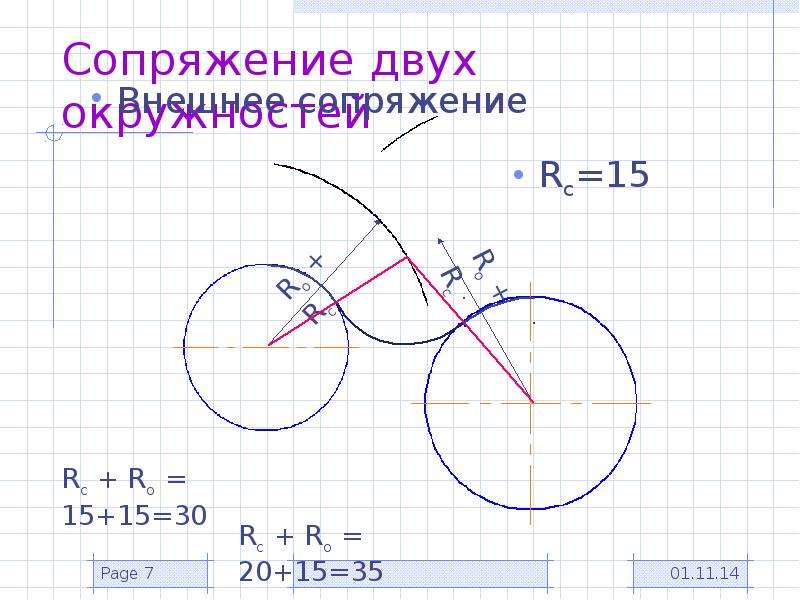 И на прямой получили точку пересечения – это и есть 1 точка сопряжения. 2 точка сопряжения лежит на дуге окружности, полученная при пересечении дуги окружности с прямой, соединяющей

центр окружности с центром сопряжения.

4.      Проводим дугу из центра сопряжения, радиусом равным радиусу сопряжения, соединяя точки сопряжения.Получили:

сопряжение прямой и окружности дугой заданного радиуса.

• Следующее сопряжение, которое мы научились строить – это:

«Сопряжение двух окружностей дугой заданного радиуса»

(внешнее)

Даны две окружности, наша задача построить внешнее сопряжение заданным радиусом.

1.      Находим центр сопряжения, для этого ставим ножку циркуля в центры окружностей и проводим дугу радиусом  равным  радиус окружности + радиус сопряжения. Получили точку пересечения – это и есть центр сопряжения точка Ос.

2.      Находим точки сопряжения, для этого соединяем центр сопряжения с центрами окружностей и на дугах окружностей получаем точки пересечения – это и есть точки сопряжения.

3. Проводим дугу из центра сопряжения, радиусом равным радиусу сопряжения, соединяя точки сопряжения.Получили:

внешнее сопряжение двух окружностей дугой заданного радиуса.

Последнее сопряжение, которое нам знакомо – это:

«Сопряжение двух окружностей дугой заданного радиуса»

(внутреннее)

Даны две  окружности, наша задача построить внутреннее сопряжение окружностей заданным радиусом.

1.                 Находим центр сопряжения, для этого ставим ножку циркуля в центры окружностей и проводим дугу радиусом  равным  радиус сопряжения — радиус окружности. Получили точку пересечения – это и есть центр сопряжения точка Ос.

2.                 Находим точки сопряжения, для этого соединяем центр сопряжения с центрами окружностей и на дальних дугах окружностей получаем точки пересечения – это и есть точки сопряжения.

 

3. Проводим дугу из центра сопряжения, радиусом равным радиусу сопряжения, соединяя точки сопряжения.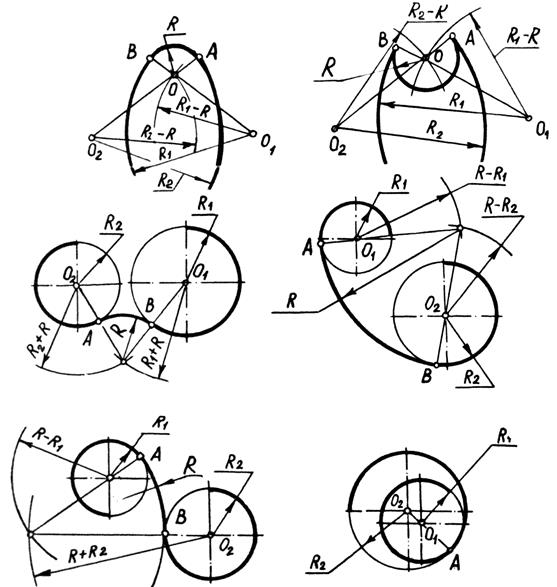 Получили:

внутреннее сопряжение двух окружностей дугой заданного радиуса.

 

Переходим к практической части нашего урока

III. Практическая работ

IV.  Проверка и взаимопроверка работ

 

·        После того, как вы внимательно проверили ещё раз свои работы, обменяйтесь работами с соседями. И теперь ваша задача, внимательно проверить работу одноклассника и оценить её.

 

V.  Подведение итога урока

 

VI Домашнее задание

·        Откройте дневники и запишите домашнее задание: повторить в учебнике стр. 104‑107, записи в тетради, принести формат А 4 (вертикально) и подобрать рисунок для творческой работы по теме: «Сопряжения».

Спасибо, за урок. Урок окончен.

Сопряжение окружностей (помогите)

← →
GibiW ©   (2009-04-06 00:37) [0]

Добрый день, Программисты! Я к вас с таким вот вопросом,может чуток глупым.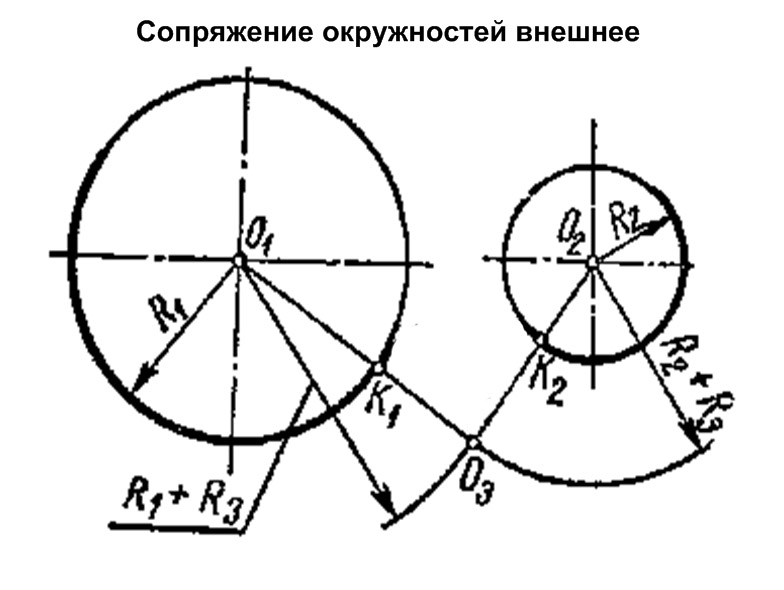 .. Помогите нарисовать в Делфи сопряжение двух окружностей разных радиусов. Это мой курсовой проект… Если у кого нить есть какие нить идеи по этому поводу, выложите код программы. Заранее благодарю!

---

← →
{RASkov} ©   (2009-04-06 00:48) [1]

> [0] GibiW ©   (06.04.09 00:37)
> Это мой курсовой проект…

Какая цена этим словам?

---

← →
AndreyV ©   (2009-04-06 00:49) [2]

А что именно не получается?

---

← →
Тимохов ©   (2009-04-06 00:50) [3]

тут любят студентов )

---

← →
boa_kaa ©   (2009-04-06 00:52) [4]

> GibiW ©   (06. 04.09 00:37)  
> Это мой курсовой проект…
> выложите код программы

блин, совесть когда-нибудь появится?
или так и будем всю жизнь других за свои решения просить отдуваться?
не можешь учиться — вали из института и не мешай тем, кто может и хочет

---

← →
boa_kaa ©   (2009-04-06 00:53) [5]

> AndreyV ©   (06.04.09 00:49) [2]
> А что именно не получается?

он же написал, что у него не получается

> выложите код программы

---

← →
{RASkov} ©   (2009-04-06 00:53) [6]

Студентам почему бы не помочь, а вот лоботрясам…. 🙂
там кстати я не о деньгах в [1]….)

---

← →
AndreyV ©   (2009-04-06 01:01) [7]

> [5] boa_kaa ©   (06.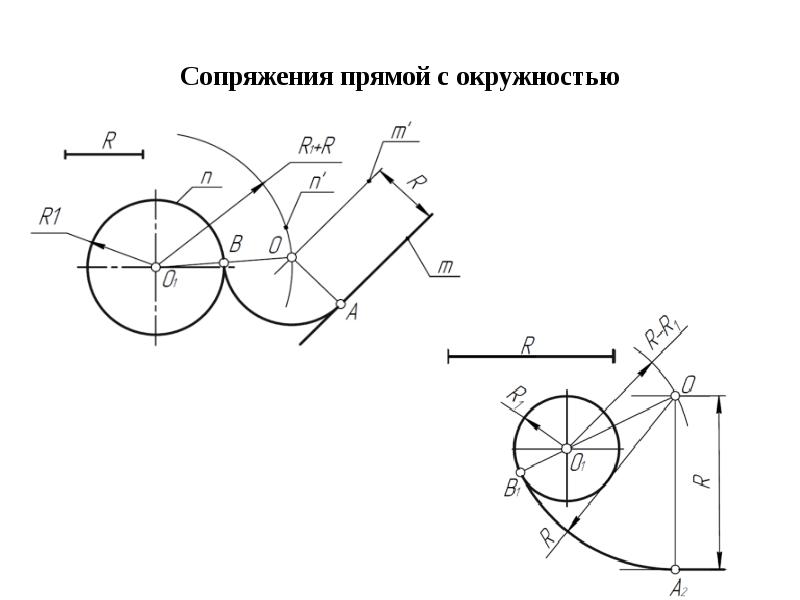 04.09 00:53)
> > А что именно не получается?
> он же написал, что у него не получается
> > выложите код программы

У автора ещё слово «помогите» втретилось — может чего и пробует сделать, хочется надеятся.:(

---

← →
Германн ©   (2009-04-06 01:22) [8]

> GibiW ©   (06.04.09 00:37)
>
> Добрый день, Программисты! Я к вас с таким вот вопросом,
> может чуток глупым… Помогите нарисовать в Делфи сопряжение
> двух окружностей разных радиусов. Это мой курсовой проект.
> ..

http://forum.sources.ru/index.php?showforum=149

---

← →
Petr V. Abramov ©   (2009-04-06 04:03) [9]

> У автора ещё слово «помогите» втретилось — может чего и
> пробует сделать

вполне может быть, но пока ответом на вопрос может быть только код программы, который не получается 🙂
P.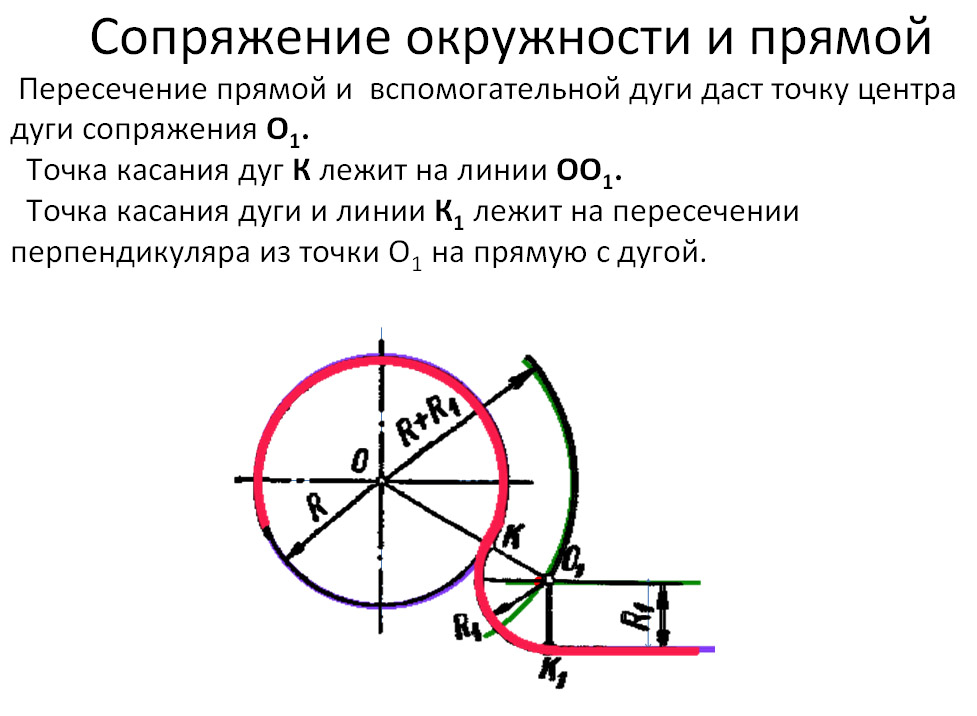 S.
я уверен, что в задании для проболевших лекции-семинары где-то сказано, что надо использовать ф-цию NarisivatiKrug(radius_kruga).
А не хватаеи идей, где и как круги расположить. А ведь не сказано, думай! Отлитчная задача, элемнтарная, но мосх включает.

---

← →
KilkennyCat ©   (2009-04-06 06:39) [10]

Оплачиваем мне путевку в Делфи, и  я там таких сопряженных окружностей нарисую!

---

← →
Немо ©   (2009-04-06 09:16) [11]

http://www.profstaff.info/fillet.html

---

← →
korneley ©   (2009-04-06 09:41) [12]

> Немо ©   (06.04.09 09:16) [11]

«Господа, вы звери! Господа!» (c) «Раба любви». Просили Дельфи-код, а дали ажтээмельный. .. Ну ладно, и так хорошо :)))

---

← →
TUser ©   (2009-04-06 09:54) [13]

Судяпо анкете — второе высшее чувак получает. Интересно, где?

---

← →
Немо ©   (2009-04-06 10:03) [14]

Молчу,молчу,не то по шее получу. И подвиг свой не совершу! (с) В бой идут одни старики

---

← →
Anatoly Podgoretsky ©   (2009-04-06 10:18) [15]

> Судяпо анкете — второе высшее чувак получает. Интересно,
>  где?

832000 это не 83 год рождения, а 8 марта 2000 года

---

← →
brother ©   (2009-04-06 11:06) [16]

> 832000 это не 83 год рождения, а 8 марта 2000 года

улыбнуло.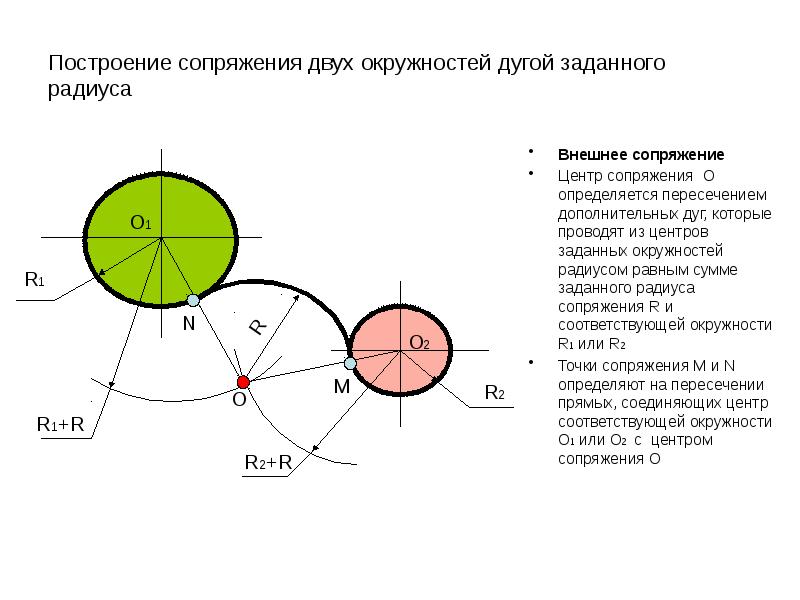

---

← →
GibiW ©   (2009-04-06 20:51) [17]

Я учусь заочно… школу закончил 9 лет назад, так что сами понимаете что забыл тригонометрию (высчитывать радиусы всякие). Мне на курсовой проект задали написать программу, которая после введения своих размеров, построила нужный чертеж. Чертеж полностью состоит из приблизительно 8-10 сопряжений.
  У кого есть время, и кто сможет помочь (потренироваться во всяком случае)прошу отписаться.

---

← →
atruhin ©   (2009-04-07 03:42) [18]

> Я учусь заочно… школу закончил 9 лет назад, так что сами
> понимаете что забыл тригонометрию

Повторить/освоить ВЕСЬ школьный курс тригонометрии можно за несколько часов. Все таки он на детей расчитан.

---

← →
KilkennyCat ©   (2009-04-07 06:55) [19]

> 832000 это не 83 год рождения, а

количество неудачных попыток зарегистрировать почтовый ящик минус один.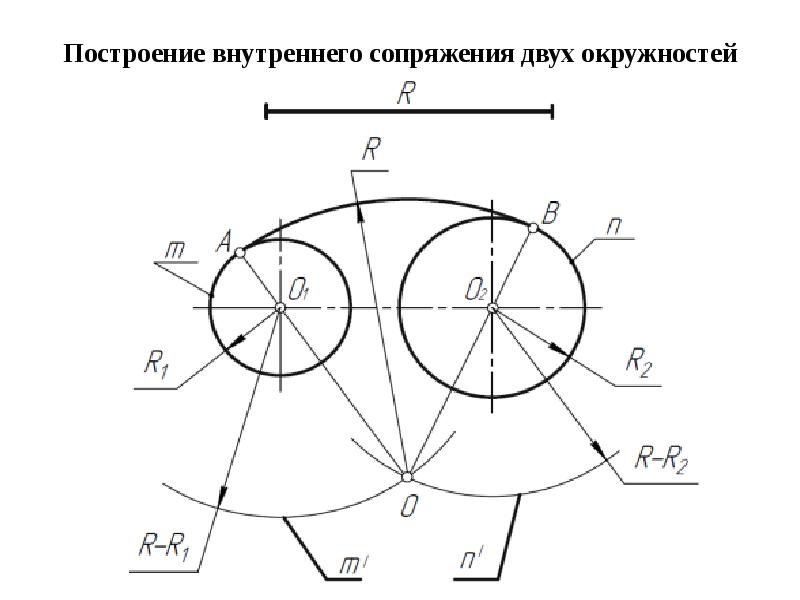

---

← →
KilkennyCat ©   (2009-04-07 06:56) [20]

Блин, пытался вспомнить, когда я закончил школу. Возникли сомнения…

---

← →
KilkennyCat ©   (2009-04-07 07:06) [21]

а вообще, есть проще способ, чем указано выше.
Рисуем окружность с радиусом, равный радиусу соряжения R.
из это-го же центра рисуем окружноcти радиусом R — R1 и R — R2
теперь можно , взяв любую точку внутренних окружностей за центр, нарисовать окружности R1 и R2 соответсвенно. независимо от расстояния между цетрами они всегда буду сопряжены. То же для обратного, только радиусы складываются.  вот с третим типом сложнее.. но и пофиг. А с точки зрения дизайнера мой способ удобнее.

---

← →
MBo ©   (2009-04-07 07:23) [22]

А что имеется в виду под сопряжением?

---

← →
palva ©   (2009-04-07 07:37) [23]

> А что имеется в виду под сопряжением?

По-моему, это что-то из области черчения. Там пытаются рисовать кривую кусками окружностей. Эти куски должны плавно переходить один в другой, т. е. в точке перехода соответствующие окружности должны иметь общую касательную. Вместо дуги окружности может использоваться отрезок. Тогда прямая, на которой он лежит, должна касаться окружностей, с кусками которой он стыкуется.
Но я школу кончил 42 года назад, значит тем более не помню точно.

---

← →
MBo ©   (2009-04-07 09:08) [24]

>palva ©   (07.04.09 07:37) [23]
В том-то и дело, что конкретика (мне) здесь непонятна. Может, общие касательные к двум окружностям надо построить, может, третью, касающуюся обоих, заданного радиуса, или касающуюся в данных точках  и т.д…

---

← →
tButton ©   (2009-04-08 06:18) [25]

> сопряжение двух окружностей разных радиусов

две окружности располагаются так чтобы расстояние между центрами было равно сумме радиусов. всё.

> Это мой курсовой проект…

лажа какая-то…

---

теорем о круге

Некоторые интересные вещи об углах и окружностях.

Угол с надписью

Прежде всего, определение:

Inscribed Angle : угол, образованный точками, лежащими на окружности круга.

A и C — «конечные точки»
B — «вершины»

Поиграйте с этим здесь:

Что происходит с углом, когда вы перемещаете точку «B»?

Теоремы о вписанных углах

Вписанный угол a ° равен половине центрального угла 2a °

(называется углом в центральной теореме )

И (с фиксированными конечными точками)…

… угол a ° всегда один и тот же ,
независимо от того, где он находится на той же дуге между конечными точками:

Угол а ° — то же .
(называется углов, подчиненных теореме о той же дуге )

Пример: Каков размер POQ Angle? (О — центр круга)

Угол POQ = 2 × Угол PRQ = 2 × 62 ° = 124 °

Пример: Какой размер Angle CBX?

Угол ADB = 32 ° также равен углу ACB.

А Angle ACB также равен углу XCB.

Итак, в треугольнике BXC мы знаем, что угол BXC = 85 °, а угол XCB = 32 °.

Теперь используем углы треугольника и прибавляем к 180 °:

Угол CBX + Угол BXC + Угол XCB = 180 °

Угол CBX + 85 ° + 32 ° = 180 °

Угол CBX = 63 °

Угол в полукруге (теорема Фалеса)

Угол вписанный поперек диаметра окружности всегда прямой угол:

(Конечные точки — это любой конец диаметра круга,
вершина может находиться в любом месте окружности.)

Почему? Потому что: Вписанный угол 90 ° составляет половину центрального угла 180 ° (с использованием «теоремы об углу в центре» выше)

Еще одна веская причина, почему это работает

Мы также можем повернуть фигуру на 180 °, чтобы получился прямоугольник!

Это — это прямоугольник, потому что все стороны параллельны и обе диагонали равны.

Итак, его внутренние углы прямые (90 °).

Итак, поехали! Независимо от , где этот угол равен
по окружности, всегда 90 °

Пример: Какой размер Angle BAC?

Угол в теореме о полукруге говорит нам, что угол ACB = 90 °

Теперь используйте углы треугольника и прибавьте к 180 °, чтобы найти угол ВАС:

.

Угол ВАС + 55 ° + 90 ° = 180 °

Угол ВАС = 35 °

В поисках центра круга

Мы можем использовать эту идею, чтобы найти центр круга:

• нарисуйте прямой угол из любого места на окружности круга, затем нарисуйте диаметр, в котором две ноги касаются круга
• сделайте то же самое, но для другого диаметра

Где крест диаметров — центр!

Циклический четырехугольник

«Циклический» четырехугольник имеет каждую вершину на окружности:
противоположных углов циклического четырехугольника складываются в 180 ° : а + с = 180 ° б + г = 180 °

Пример: Каков размер угла WXY?

Сумма противоположных углов вписанного четырехугольника дает 180 °

Угол WZY + Угол WXY = 180 °

69 ° + угол WXY = 180 °

Угол WXY = 111 °

Касательный угол Касательная линия просто касается окружности в одной точке. Всегда образует прямой угол с радиусом круга.

Кругов: Круги на координатной плоскости Учебное пособие

Мы можем описать окружность в координатной плоскости с помощью уравнения. Но прежде чем мы туда поедем, мы немного упростим задачу. Начнем с рассмотрения круга с центром в начале координат и радиусом 5 единиц. Вот он, на координатной плоскости.

Обратите внимание, что круг проходит через точки (5, 0), (0, 5), (-5, 0) и (0, -5).

Мы пытаемся найти уравнение, связывающее координаты общей точки на окружности ( x , y ). Обратите внимание, что по природе декартовой системы мы можем легко нарисовать прямоугольный треугольник на основе любой точки ( x , y ).

Одна нога горизонтальная и имеет длину x . Другая нога вертикальная и имеет длину х . Гипотенуза соединяет ( x , y ) и начало координат. Если ( x , y ) находится на окружности, а центр окружности находится в начале координат, тогда гипотенуза имеет длину, равную радиусу окружности. В данном случае это 5 единиц.

Пифагор говорит нам, что x ² + y ² = 5 ² .

Но радиус круга с центром в начале координат не обязательно должен быть 5 единиц. Это могло быть 6, 7, 50 или даже миллион единиц. Покроем все наши базы и назовем это r единиц. Итак, у нас есть уравнение x ² + y ² = r ² .

Вот и все.Теперь у нас есть уравнение, которое связывает координаты x и y любой точки на окружности с радиусом r с центром в начале координат. Разве это не было просто?

Вы можете заметить, что мы оставили члены x и y на одной стороне уравнения, вместо того чтобы решать для y , как мы обычно делаем для линейных уравнений. (Помните те из алгебры?) Формула со всеми переменными на одной стороне называется неявно , а формула, которая была решена для одной переменной через другую (например, y = mx + b ) называется явным .

Попробуйте решить наше неявное уравнение для y . В итоге вы получите беспорядочный плюс-минус квадратный корень. Мы будем придерживаться красивого, чистого и простого уравнения, которое у нас есть. Кроме того, это семейный сайт. Мы не хотим здесь никакого явного содержания.

Пример задачи

Какова формула для круга с центром в начале координат и окружностью 25,1 дюйма?

Мы знаем, что формула для круга: x ² + y ² = r ² .Все, что нам нужно для завершения, это длина радиуса, которую мы можем найти с помощью окружности. Если мы просто вспомним формулу C = 2π r , мы можем вставить 25,1 дюйма для C и решить для r ≈ 4 дюйма. Таким образом, наше окончательное уравнение: x ² + y ² = 4 ² или x ² + y ² = 16.

Наша формула определенно хороша, чистый и простой, но это полезно, только если наш круг находится в начале координат. Как мы можем описать такой круг за пределами Сиднея?

Мы все еще можем нарисовать прямоугольный треугольник, поэтому Пифагор все еще может нам помочь. Гипотенуза по-прежнему имеет длину, равную радиусу окружности, поскольку ее концы — это центр окружности и точка на окружности. Мы знаем, что радиус Сиднейского круга составляет 5 км.

Но длина ножек уже не просто старые x и y . Мы должны скорректировать «смещение» центра круга от начала координат.Таким образом, длины горизонтальных и вертикальных сторон нашего прямоугольного треугольника равны x — 4 и y — 3 соответственно. Теперь мы можем подставить эти длины в теорему Пифагора, чтобы получить ( x — 4) ² + ( y — 3) ² = 5 ² .

И вот наша формула для Сиднейского круга с x и y в километрах (потому что австралийцы, как и весь остальной мир, используют метрическую систему).

В общем случае неявная формула для окружности с центром ( h , k ) и радиусом r :

( x — h ) ² + ( y — k ) ² = r ²

Теперь у нас есть вся информация, необходимая для определения любого круга в красивой компактной формуле. Вы можете использовать его для описания чего угодно, от орбиты космического корабля до печенья на листе печенья. Совершенно верно: математическая технология, необходимая для вывода спутника на орбиту, не более сложна, чем та, которая необходима для изготовления сникердудлей в домашних условиях. Более или менее.

Пример задачи

Каково уравнение для окружности с центром (6, -2) и радиусом 18 единиц?

Неявная формула для окружности с центром ( h , k ) и радиусом r : ( x — h ) ² + ( y — k ) ² = r ² .Нам даны центр и радиус, поэтому все, что нам нужно сделать, это вставить информацию в нужные места. У нас должно получиться ( x — 6) ² + ( y — (-2)) ² = 18 ² , или ( x -6) ² + ( y + 2) ² = 324 в упрощенном виде.

Как построить (провести) две внешние касательные к двум заданным окружностям

На этой странице показано, как нарисовать один из двух возможных внешних общие касательные к двум заданным кругам с помощью циркуля и линейки или линейки. Эта конструкция предполагает, что вы уже знакомы с Построением серединного перпендикуляра отрезка линии.

Как это работает

На рисунке ниже представлена ​​окончательная конструкция с добавленной линией PJ. Строительство состоит из трех основных этапов:

1. Окружность OJS построена таким образом, что ее радиус равен разности радиусов двух данных окружностей. Это означает, что JL = FP.
2. Построим касательную PJ от точки P к окружности OJS. Это делается с помощью метода, описанного в Касательные через внешнюю точку.
3. Требуемая касательная FL параллельна PJ и смещена от нее на JL. Поскольку PJLF представляет собой прямоугольник, нам нужен лучший способ построить этот прямоугольник. Используемый здесь метод заключается в построении PF параллельно OL с использованием метода «углового копирования», как показано на Построение параллели через точку

Как показано ниже, таких касательных две, вторая построена таким же образом, но в нижней половине окружностей.

Проба

Это тот же рисунок, что и последний шаг в приведенной выше анимации, с добавленной линией PJ.

	Аргумент	Причина
1	PJ является касательной к внутреннему кругу O на J.	По конструкции. См. Построение касательной через внешнюю точку для метода и доказательства.
2	FP параллельно LJ	По конструкции. Раздел Построение параллели (метод копирования под углом) для метода и доказательства.	3	FP = LJ	QS был установлен из радиуса окружности P на этапах построения 2 и 3.	4	FPJL — прямоугольник	FP параллельна LJ из (2) и (3) и равна ей. ∠PJL = ∠PJO = 90 ° (касательная проходит под прямым углом к ​​радиусу)	5	∠FLJ = ∠LFP = 90 °	Внутренние углы прямоугольников 90 ° (4)
6	FL является касательной к окружности O и P	Касается круга в одном месте (F и L) и находится под прямым углом к ​​радиусу в точке контакта

— В. E.D

Пошаговые инструкции для печати

Вышеупомянутая анимация доступна как распечатываемый лист с пошаговыми инструкциями, который можно использовать для изготовления раздаточных материалов или когда компьютер недоступен.

Попробуйте сами

Щелкните здесь, чтобы распечатать касательные к двум кругам, чтобы попробовать их. Когда вы перейдете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Печатная продукция не защищена авторскими правами.

Другие конструкции, страницы на сайте

строк

Уголки

Треугольники

Правые треугольники

Центры треугольника

Окружности, дуги и эллипсы

Полигоны

Неевклидовы конструкции

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

Модель

Kachru «Три круга английского языка» — разновидности английского языка

На протяжении всей истории английского языка эксперты предлагали множество моделей, чтобы попытаться классифицировать его носителей. Однако не все лингвисты сходятся во мнении, какой из них лучший. В этом посте мы пытаемся взглянуть на модель Качру, предложенную четыре десятилетия назад. Но прежде чем приступить к объяснению какой-либо модели, мы должны осознавать тот факт, что это трехгрупповая модель.То есть тот, который классифицирует динамики как:

• ENL : Английский как родной язык, это носители языка, родившиеся в англоязычной стране, для которых этот язык является родным.
• ESL : английский как второй язык, это те люди, для которых английский не является родным, которые изучают английский почти одновременно со своим родным.
• EFL : Английский как иностранный язык, это те, для кого английский язык не является родным,
  они изучали английский в стране, где на английском обычно не говорят.

Хотя эта классификация показывает некоторые проблемы, такие как классификация двуязычных носителей и психологические проблемы, показанные в ENL для носителей нестандартных разновидностей и ESL для носителей, которым неудобно использовать язык в определенных ситуациях. Это основная классификация, которую лингвисты собираются учитывать при написании собственных моделей.

Для многих социолингвистов наиболее важной и точной моделью является модель, предложенная Брэджем Качру в 1988 г.Его «Модель с тремя кругами английского языка мира» утверждает, что есть три круга, внутри которых классифицируются разные говорящие. Различные круги:

• Inner Circle составлен на основе традиционных основ английского языка, и его носители отвечают за соблюдение норм. В этих местах создаются нормы и откуда они распространяются на другие круги. Некоторые из стран, которые соответствуют внутреннему кругу, — это США, Великобритания и Канада.
  
• Внешний круг представляет собой места, где они говорят на официальных неродных вариантах английского языка из-за их колониальной истории . Спикеры этих мест — это те, кто оспаривает нормы и развивает их, и в основном это ESL Некоторые из стран, которые принадлежат к этому кругу, — Индия, Пакистан и Египет.
• Расширяющийся круг состоит из носителей EFL , из которых обычно не говорят на английском языке
  . В этом круге говорящие должны следовать правилам, установленным Внутренним кругом и разработанным Внешним.Некоторые примеры стран, которые принадлежат к этому кругу, — Китай, Россия и Бразилия.

Видео «The Spread of English» предлагает расширенное объяснение того, как работает модель. Он показывает, как колонизация, история и политика сыграли роль в распространении английского языка в разных странах. Внутренний круг, как было объяснено ранее, составляют страны, которые принадлежат к первой диаспоре. В этих странах традиционно расположены языковые и культурные базы английского языка.Внешний круг соответствует второй диаспоре благодаря колонизации Британской империей различных мест в Азии и Африке. Одна из самых важных вещей, которые следует учитывать при рассмотрении этого круга, заключается в том, что английские разновидности, на которых говорят там, обычно находятся в постоянном контакте с другими языками.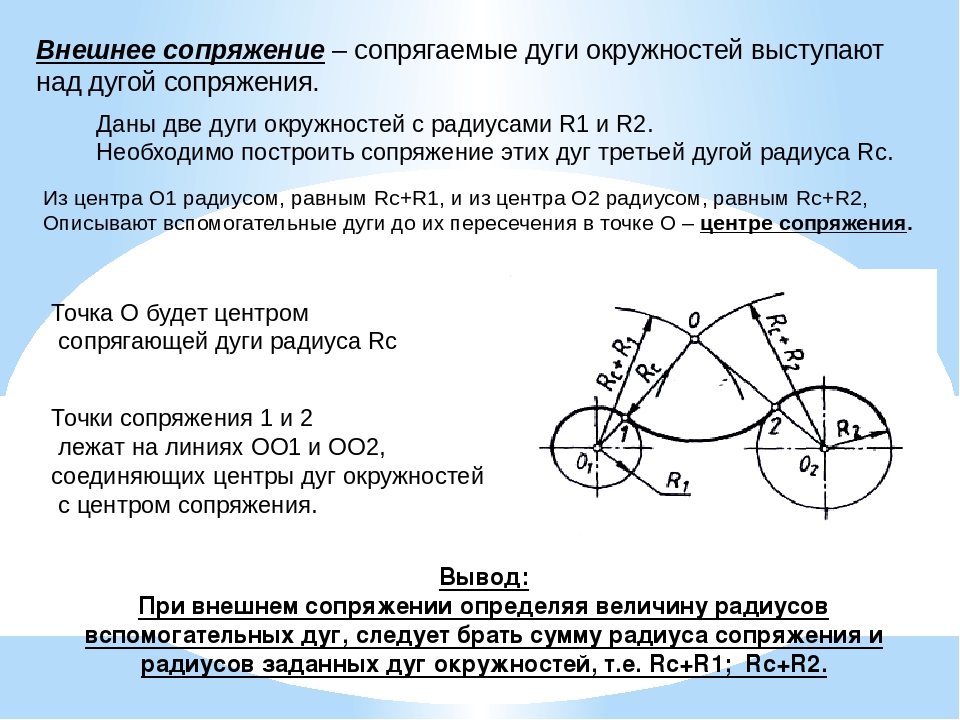 Это приводит к тому, что английское разнообразие зависит от этих других языков и в некоторых случаях включает некоторые их особенности. Вот почему Внешний Круг развивается в норме, потому что контакт с другими языками вызывает изменения в его словарном запасе, а иногда и в грамматике.Расширяющийся круг никогда не был колонией Британской империи, и поэтому английский язык не является языком, на котором говорит значительное количество людей в стране.

Однако мы также должны принять во внимание, что эта модель также представляет проблем , потому что она учитывает не экосистемы в своей классификации, а нации. По этой причине Kachru, например, включает только стандартный английский без анализа множества других разновидностей английского языка. То же самое и с Внешним Кругом.Во-вторых, у нас есть проблема в том, что он учитывает только пиджины и креолы, которые считаются официальными в своих странах. Это оставляет многих ораторов за пределами его модели. И, наконец, он не считает понятие владения важным, и поэтому носитель языка, который бросил школу в раннем возрасте и не знает многих грамматических правил языка, считается лучшим говорящим, чем, например, учитель английского языка. из Испании, который более подготовлен и знает все правила языка.

В целом, модель Качру имела большое значение в истории социолингвистики, однако она также показывает некоторые проблемы, которые необходимо решить, чтобы охватить всех носителей английского языка.

Библиография

• Handke, J. (25 июня 2013 г.). YouTube . Получено 7 ноября 2016 г. из The Spread of English: https://www.youtube.com/watch?v=KrsQmIVYrdg
.
• Венфанг, К. (2011, апрель). Различные модели английского языка как международного языка и их значение для преподавания неанглийских специальностей. Китайский журнал прикладной лингвистики , 5-17.

Me gusta esto:

Me gusta Cargando …

10 бесплатных упражнений по произношению английского языка: Практикуйте звуки английского языка

Издатель: All ESL | Последнее обновление: 31 декабря 2020 г.

Упражнения по произношению английского языка

Если вы являетесь носителем английского языка, одним из важнейших ваших активов для изучающих английский язык является ваше произношение.

Без сомнения, обучение звукам английского языка — это один из навыков, который вы можете привнести в свой класс.И есть множество способов научить произношению в классе.

Например, вы можете адаптировать эти упражнения по произношению английского языка как «повторять за мной», в парах или слушать учителя.

Независимо от того, какой способ обучения вы решите преподавать, эти упражнения по произношению английского языка станут отличной отправной точкой.

1 Звуки английского языка

Эти упражнения по произношению английского языка учит студентов, как правильно располагать языки, когда они говорят по слогам.

Например, звук / th / ставит кончик языка между зубами. В то время как звук / s / удерживает язык за зубами.

Звуки английского языка

Пирамида из 2 произношений

Во-первых, все начинают с вершины пирамиды. Далее учитель говорит на уровне ниже. Студенты индивидуально обводят слово, которое слышат.

До основания пирамиды учитель произносит слово, а ученики обводят то, что они слышат.Учитель также отслеживает спуск по пирамиде. Где закончить? Приятно смотреть.

Пирамида произношения

3 минимальные пары

Для каждой пары слова звучат очень похоже. Но они разные. Студенты должны внимательно следить за тем, что они слышат.

Пока учитель читает рамку по своему выбору, ученики обводят слово, которое они слышат. Когда вы пройдетесь по всем минимальным парам, проверьте их понимание, исправив бумаги.

Минимальные пары

Игровые карты с 4 минимальными парами

Перед этим учитель должен распечатать раздаточный лист. Они вырезают каждое слово и раскладывают по парам столов.

В парах ученики внимательно слушают учителя. Затем им нужно найти слово, которое они слышат, быстрее, чем их сосед. Наконец, тот ученик, который быстрее схватил карточку, сохраняет ее. В конце игры победителем становится ученик с наибольшим количеством карточек.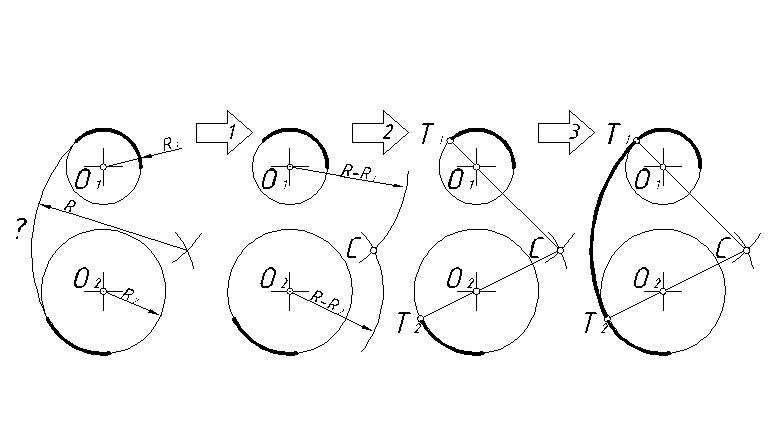

Минимальные пары карт ESL

5 скороговорок

Как ни странно, скороговорки — легкий способ научить студентов говорить.Я не могу понять, почему … но им, вероятно, нравится эта проблема.

Сначала ученики повторяют каждую строчку вслед за учителем. Далее педагог молниеносно демонстрирует скороговорку. Теперь попросите добровольцев попытаться сделать это быстрее.

Скороговорки

6 похожих предложений

Насколько ваши ученики обращают внимание на детали? Каждое предложение звучит одинаково, но они разные.

Вы можете сами прочитать каждое предложение.Или вы можете попросить своих учеников прочитать их. Могут ли они найти разницу между собой?

Подобные предложения

7 Тест на прослушивание

Это ваш основной тип теста на аудирование. Могут ли они различать каждый уникальный звук, когда вы их читаете?

Сначала смешайте звуки. Затем отслеживайте произносимые вами звуки. Наконец, исправьте их листы, чтобы проверить распознавание слогов.

Тест на прослушивание минимальных пар

8 Время рифмы

Сначала разделите учащихся на группы по 3 или 4 человека.Затем попросите учащихся придумать как можно больше рифм для каждой коробки.

Это классический конкурс «мозговой штурм». Возьмите секундомер, потому что побеждает группа с наибольшим количеством рифм.

Rhyme Time (Время рифмы)

Скороговорки 9

Как ни странно, скороговорки — легкий способ научить ваших учеников говорить. Практикуйте каждую скороговорку, и пусть ваши ученики попытаются продемонстрировать свои навыки английского языка.

Совет от профессионалов: им нравится, если вы можете сказать скороговорку на их родном языке.

Скороговорки

10 открыток ко Дню святого Валентина

На листе открыток ко Дню святого Валентина учащиеся заканчивают стих из классического стихотворения «Розы красные, фиалки синие…».

Сначала раздайте листок с примером стишка к стихотворению. Затем просмотрите его со своими учениками. Наконец, пусть ваши ученики сочинят рифму для «Розы красные, фиалки синие».

Открытки ко Дню святого Валентина

Упражнения по произношению английского языка

Говорить как истинный носитель английского языка — одна из целей изучающего английский язык.Хорошее начало для достижения этой цели — это тщательно изучать все звуки английского языка.

Конечно, важен и базовый разговор. Вот где вы можете попрактиковаться в разговорной теме 101 ESL, чтобы заставить их говорить.

Эти 10 упражнений по произношению английского языка можно переработать несколькими способами — парами, индивидуально или в классе.

Как вам нравится учить произношению? Что работает, а что нет? Пожалуйста, дайте нам знать, какие у вас упражнения на английское произношение, в разделе комментариев ниже.

Клин из двух окружностей — Topospaces

Определение

Абстрактное определение

Клин из двух окружностей (иногда также называемый восьмеркой ) определяется как сумма клиньев двух окружностей относительно любой базовой точки в обеих.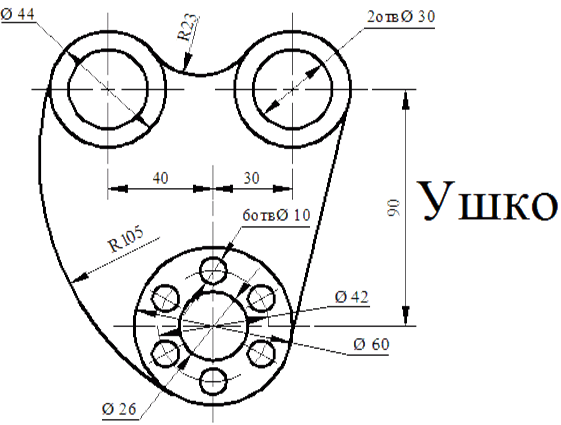 Обратите внимание: поскольку окружность является однородным пространством, выбор базовой точки не влияет на тип гомеоморфизма клина.

Обозначен клин из двух окружностей.

Определение как подмножество евклидова пространства

Клин ‘ из двух окружностей можно рассматривать конкретно как следующее подмножество евклидовой плоскости:

Здесь первый множитель соответствует окружности с центром и радиусом, а второй множитель соответствует окружности с центром и радиусом.Две окружности касаются друг друга в точке, где кружки скреплены между собой .

Эквивалентные места

Космос	Насколько сильно он эквивалентен клину двух окружностей?
Пространство, полученное удалением двух точек из евклидовой плоскости.	Гомотопический эквивалент
Пространство, полученное удалением трех точек из 2-сферы	Гомотопический эквивалент
фактор-пространство непересекающегося объединения двух квадратов путем идентификации одной стороны каждого.	Гомотопический эквивалент

Алгебраическая топология

Группы гомологий

Группы гомологии с коэффициентами в следующие: ,, и все высшие группы гомологии равны нулю.

В более общем смысле, группы гомологий с коэффициентами в любом модуле над коммутативным кольцом с единицей следующие:,, и все высшие группы гомологий равны нулю.

Эти результаты следует из вычисления гомологий для сфер (в частности, случая круга) и приведенной гомологии суммы клина относительно базовых точек с окрестностями, которые деформация ретранслирует к ним, является прямой суммой редуцированных гомологий (что, в свою очередь, следует из теории Майера-Вьеториса). последовательность гомологии).

Группы когомологий

Группы когомологий с коэффициентами в следующие: ,, и все высшие группы когомологий равны нулю.

В более общем смысле, группы когомологий с коэффициентами в коммутативном кольце с единицей следующие:,, и все высшие группы когомологий равны нулю.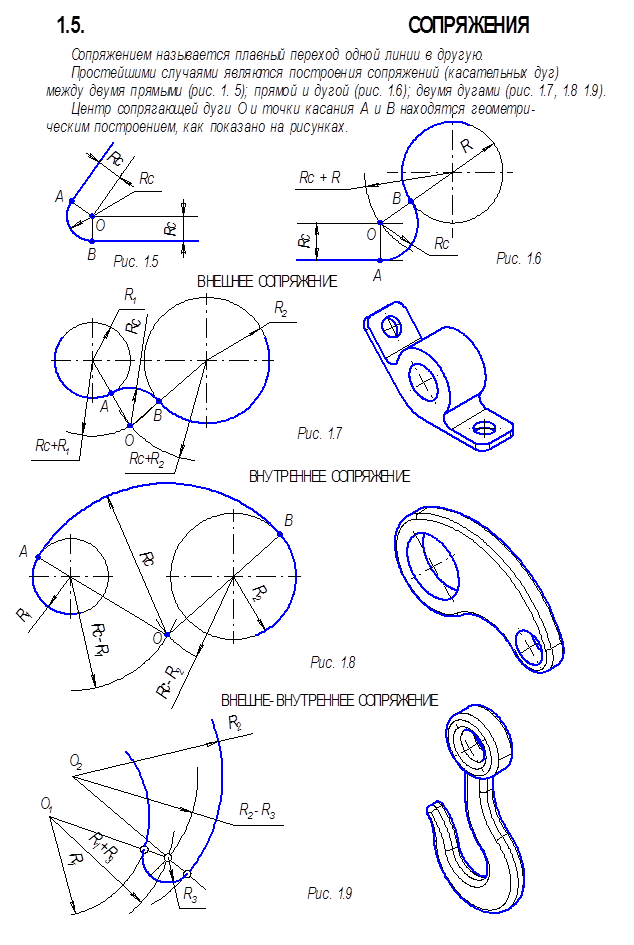 Группа когомологий — это где и являются базисом для свободного модуля над.

Гомотопические группы

Набор компонентов пути является одноточечным. Фундаментальная группа изоморфна свободной группе: F2 — это следует из того факта, что фундаментальная группа суммы клина относительно базовых точек с окрестностями, которые деформируют ретрансляции, является свободным произведением фундаментальных групп (что, в свою очередь, следует из формулы Зейферта-ван Кампена теорема).

.