Сложить два двоичных числа: Сложение двоичных чисел онлайн

Сложение двоичных чисел. — Энциклопедия современных знаний

Таблица сложения:

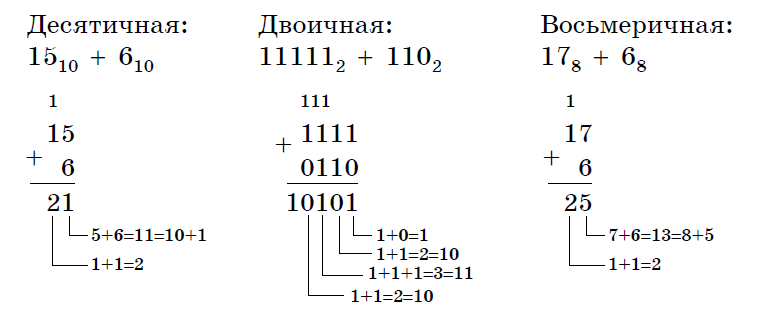
Сложение двоичных чисел удобно проводить столбиком. В случае, когда мы получаем число , единица переходит в старший разряд.

Пример:

Считаем справа налево:

• ;
• , единица переходит в старший разряд;
• + единица из предыдущего разряда , единица переходит в старший разряд;
• + единица из предыдущего разряда , единица переходит в старший разряд;
• + единица из предыдущего разряда , единица переходит в старший разряд;
• + единица из предыдущего разряда , единица переходит в старший разряд.

Вычитание двоичных чисел.

Вычитание двоичных чисел удобно проводить столбиком. Если нужно отнять от нуля, занимаем единицу в старшем разряде. В младший разряд она приходит как двоичное . Если имеются промежуточные разряды (содержащие нули), в них остаётся .

Пример:

Считаем справа налево:

• ;
• ;
• занимаем единицу в старшем разряде ;
• теперь в следующем разряде вместо единицы – ноль в старшем разряде – тоже ноль, занимаем единицу в следующем старшем разряде ;
• после того, как мы заняли в старшем разряде единицу – в следующем разряде вместо нуля – единица (этот ноль уже не записываем).

Для того чтобы сложить два отрицательных числа, нужно сложить их модули, а перед суммой поставить знак “минус”.

Для того чтобы сложить два числа с разными знаками, нужно из большего из двух модулей вычесть меньший, а перед полученной разностью поставить знак числа, модуль которого больше[1].

Пример:

Умножение двоичных чисел.

Таблица умножения:

Умножение двоичных чисел также удобно проводить столбиком.

Пример:

II. Действия с восьмеричными числами.

Сложение восьмеричных чисел.

При сложении восьмеричных чисел следует помнить, что после числа следует , т. е. .

и т. д.

Сложение восьмеричных чисел проводят столбиком. Сложение удобно проводить в десятичной системе, переводя результат в восьмеричную. Десятичные числа до соответствуют восьмеричным числам. Если же получено число больше , то из него вычитают , прибавляя единицу к старшему разряду.

Пример:

Считаем справа налево:

• , единица переходит в старший разряд;
• , + единица из предыдущего разряда , единица переходит в старший разряд;
• , + единица из предыдущего разряда , единица переходит в старший разряд;
• , + единица из предыдущего разряда ;
• ;
• .

Вычитание восьмеричных чисел.

Вычитание восьмеричных чисел удобно проводить столбиком. Если нужно отнять от меньшего числа большее, занимаем единицу в старшем разряде. В младший разряд она приходит как десятичное (восьмеричное ). Если имеются промежуточные разряды (содержащие нули), в них остаётся десятичное .

Пример:

Считаем справа налево:

• занимаем единицу в старшем разряде ;
• теперь в следующем разряде вместо семёрки – шестёрка занимаем единицу в старшем разряде ;
• в следующем разряде вместо шестёрки – пятёрка ;
• ;
• ;
• .

Сложение отрицательных чисел и чисел с разными знаками осуществляется так же, как и для двоичных чисел (см. выше, стр. 8).

III. Действия с шестнадцатеричными числами.

Сложение чисел в двоичной системе счисления. Лекция по информатике №4

Похожие статьи.

• Умножение двоичных чисел

• Сложение и вычитание дробей.

• Числа с плавающей точкой

• Модуль числа как расстояние

Python | Поразрядные операции с числами

Последнее обновление: 11.01.2022

Особый класс операций представляют поразрядные операции. Они выполняются над отдельными разрядами чисел типа int. Но чтобы понять природу поразрядных операций, надо понимать что вообще представляет число в двоичном представление.

Двоичное представление чисел

При двоичной системе каждый разряд числа может иметь только два значения — 0 и 1. Например, 0 в десятичной системе также будет равен 0 в двоичной системе, а 1 в десятичной системе будет соответствовать 1 в двоичной системе. Следующее число в десятичной системе — 2 в двоичной системе будет соответствовать 10. То есть, когда мы к 1 прибавляем 1, то результатом будет 10. И так далее.

Например, 5 в двоичном представлении 101 и имеет три разряда. Для вывода десятичного числа в двоичной системе можно применять спецификатор 0b:

number = 5 # в двоичной форме 101
print(f"number = {number:0b}")  # number = 101

Без указания спецификатора функция print() выводит число в десятичной системе.

При этом Python позволяет сразу определять число в двоичной форме. Для этого число в двоичной форме указывается после префикса 0b:

number = 0b101	# определяем число в двоичной форме
print(f"number = {number:0b}")  # number = 101
print(f"number = {number}")  # number = 5 - в десятичной системе

Еще несколько примеров сопоставления между двоичной и десятичной системами:

number1 = 1 # в двоичной системе 0b1
number2 = 2 # в двоичной системе 0b10
number3 = 3 # в двоичной системе 0b11
number4 = 4 # в двоичной системе 0b100
number5 = 5 # в двоичной системе 0b101
number6 = 6 # в двоичной системе 0b110

Логические операции

Логические операции выполняются над отдельными разрядами числа.

В Python есть следующие логические операции:

• &(логическое умножение)

  Умножение производится поразрядно, и если у обоих операндов значения разрядов равно 1, то операция возвращает 1, иначе возвращается число 0. Например:

  x1 = 2  # 010
  y1 = 5  # 101
  z1 = x1 & y1
  print(f"z1 = {z1}")   # z1 = 0
  
  x2 = 4  # 100
  y2 = 5  # 101
  z2 = x2 & y2
  print(f"z2 = {z2}")   # z2 = 4
  print(f"z2 = {z2:0b}")  # z2 = 100
  

  В первом случае у нас два числа 2 и 5. 2 в двоичном виде представляет число 010, а 5 — 101. Поразрядно умножим числа (0*1, 1*0, 0*1) и в итоге получим 000.

  Во втором случае у нас вместо двойки число 4, у которого в первом разряде 1, так же как и у числа 5, поэтому в итоге получим (1*1, 0*0, 0 *1) = 100, то есть число 4 в десятичном формате.

• | (логическое сложение)

  Похоже на логическое умножение, операция также производится по двоичным разрядам, но теперь возвращается единица, если хотя бы у одного числа в данном разряде имеется единица. y print(f»x = {x}») # x = 5 print(f»y = {y}») # y = 9

• ~(инверсия)

  Инвертирует число. Выражение ~x фактически аналогично -(x+1). Например:

  x = 5
  y = ~x;
  print(f"y: {y}")  # -6
  

Операции сдвига

Операции сдвига также производятся над разрядами чисел. Сдвиг может происходить вправо и влево.

• x<<y — сдвигает число x влево на y разрядов. Например, 4<<1 сдвигает число 4 (которое в двоичном представлении 100) на один разряд влево, то есть в итоге получается 1000 или число 8 в десятичном представлении.

• x>>y — сдвигает число x вправо на y разрядов. Например, 16>>1 сдвигает число 16 (которое в двоичном представлении 10000) на один разряд вправо, то есть в итоге получается 1000 или число 8 в десятичном представлении.

Таким образом, если исходное число, которое надо сдвинуть в ту или другую строну, делится на два, то фактически получается умножение или деление на два. Поэтому подобную операцию можно использовать вместо непосредственного умножения или деления на два. Например:

a = 16 # в двоичной форме 10000
b = 2  
c = a << b  # Сдвиг числа 10000 влево на 2 разряда, равно 1000000 или 64 в десятичной системе
print(c)   #64

d = a >> b  #Сдвиг числа  10000  вправо на 2 разряда, равно 100 или 4 в десятичной системе
print(d)   #4

При этом числа, которые участвую в операциях, необязательно должны быть кратны 2::

a = 22 # в двоичной форме 10110
b = 2
c = a << b  # Сдвиг числа 10110 влево на 2 разряда, равно 1011000 или 88 в десятичной системе
print(c)   # 88

d = a >> b  # Сдвиг числа 10110 вправо на 2 разряда, равно 101 или 5 в десятичной системе
print(d)   # 5

НазадСодержаниеВперед

Калькулятор двоичного сложения — Калькуляторы онлайн

Калькулятор двоичного сложения — Калькуляторы онлайн | Веб-расчет

Этот калькулятор двоичного сложения позволяет складывать два двоичных числа и отображать результат в двоичном формате. Он включает в себя пользовательский интерфейс, позволяющий вводить два двоичных числа, а также кнопку или другой механизм для запуска вычисления. Затем калькулятор выполняет алгоритм двоичного сложения и отображает результат.

Двоичный номер 1:
Двоичный номер 2:

Результат:

• Калькулятор процентов от числа
• Сколько процентов составляет одно число от другого
• Калькулятор продажной цены
• Изучите компьютерные науки на уровне
• Максимальное значение, основанное на количестве шестнадцатеричных цифр калькулятора

Сложение двоичных чисел — простой процесс, похожий на сложение десятичных чисел, с той лишь разницей, что основание системы счисления — 2 вместо 10. Вот шаги для сложения двоичных чисел:

1. Выровняйте два двоичных числа так, чтобы их младшие значащие цифры (крайние правые цифры) совпадали.
2. Начиная с самой правой цифры, сложите цифры обоих чисел вместе. Если сумма меньше 2, просто запишите сумму как соответствующую цифру в результате.
3. Если сумма двух цифр больше или равна 2, крайняя левая цифра суммы переносится в следующий столбец. Например, если сумма равна 10 (двоичная), крайняя левая цифра равна 1, а крайняя правая цифра — 0. Крайняя левая цифра переносится и добавляется к следующему столбцу.
4. Повторите шаги 2 и 3 для каждой цифры двоичного числа, работая справа налево.
5. Если после добавления последней цифры остался перенос, добавьте его в крайнее левое положение результата.
6. Конечным результатом является двоичное представление суммы двух двоичных чисел.

Например:
Сложим двоичные числа 1011 и 1101.

1 0 1 1
+ 1 1 0 1
———
1 0 0 1 0

Сложение выполняется справа налево, последняя цифра обоих чисел 1+1 = 10 (2 в десятичной дроби), перенос равен 1, а результат равен 0.
Вторая цифра обоих чисел 1+0 = 1.

Третья цифра обоих чисел 0+1 = 1.
Четвертая цифра обоих чисел 1+1 = 10 (2 в десятичном формате), перенос равен 1, а результат равен 0.
Сумма чисел равна 10110, что равно 22 в десятичном виде.

В этом примере результат такой же, как если бы мы сложили десятичные эквиваленты двоичных чисел 11 и 13, а затем преобразовали сумму обратно в двоичную.

Сложение двоичных чисел применимо только к положительным числам, для отрицательных чисел существует другой процесс, называемый дополнением до двух, который используется для выполнения арифметических операций над отрицательными числами.

Дополнительные проекты

Unit 6, стр. 2

Дополнительные проекты Unit 6, стр. 2

На этой странице вы мельком увидите, как компьютеры выполняют основные арифметические операции, такие как сложение, используя только двоичные числа и логические элементы.

Обзор: Добавление номеров

Когда вы складываете два числа в десятичной системе (с основанием 10), вы оцениваете каждый столбец сложения, принимая во внимание любые

переносы в значения из предыдущего столбца, а затем переходя к следующему столбцу любые переносы значение.

Точно такая же процедура выполняется при сложении двух чисел в двоичной системе (с основанием 2), как показано ниже.

Как вы можете видеть, чтобы выполнить сложение чисел, вы должны иметь возможность вводить перенос в значение и выводить значение выполнять .

Полусумба

Полусумматор складывает две двоичные цифры (без переноса в ) и сообщает сумму, а значение выполняет . Если вы посмотрите на столбец «SUM», вы заметите, что он идентичен выходному столбцу XOR, а если вы посмотрите на столбец «CARRY», вы заметите, что он идентичен выходному столбцу AND.

Если вам трудно разобраться в этой таблице, рассмотрите возможность добавления двоичных цифр:
0+0=0
0+1=1
1+0=1
1+1=2, что равно 10 в двоичном формате с цифрой единиц сумма 0 и перенос 1.

2. Осмотрите оснастку ! и все его спрайты. Для спрайтов SUM и CARRY соберите несколько блоков кода для имитации полусумматора.

Полный сумматор

Если вам трудно разобраться в этой таблице, рассмотрите возможность добавления трех двоичных цифр:

Например, 1+1+1=3, что равно 11 в двоичном формате с цифрой единиц 1 и значением переноса 1.

Полный сумматор использует два полусумматора для выполнения полного сложения двоичных цифр, вмещающих перенос

в значение . Он сообщает сумму и выполняет значение .

3. Изучите приведенную выше таблицу и схему полного сумматора, чтобы объяснить, как полный сумматор выполняет сложение двух двоичных чисел с перенесите , используя два полусумматора и вентиль ИЛИ.
5. Осмотрите оснастку ! и все его спрайты. Код для спрайтов CARRY IN , A и B , был написан для вас.