Сложение двоичных: Сложение двоичных чисел онлайн

Учимся вместе: Сложение в двоичной системе

 Вся числовая информация внутри компьютерной системы передается, хранится и обрабатывается только в двоичной системе счисления. Для удобства пользователя числовая информация переводится в десятичную (восьмеричную или шестнадцатеричную) систему счисления.

 Рассмотрим сложение в двоичной системе счисления. В его основе лежит таблица сложения двоичных чисел:

0 + 0 =  0

0 + 1 =  1

1 + 0 =  1

1 + 1 = 10

1 + 1 + 1 = 11

 

При сложении двух или трёх единиц производится перенос единицы в старший разряд. Приведём пример сложения двух  двоичных чисел:
 110112
+     112
 _____
 111102
 Проверка:
111102 =27₁₀

24	23	22	21	20
16	8	4	2	1

16	8	4	2	1
1	1		1	1

 16+8+2+1=27₁₀

 11₂ =3₁₀

21	20
2	1

              

2	1
1	1

 2+1=3

27+3=30

111102 =30₁₀

24	23	22	21	20
16	8	4	2	1

16	8	4	2	1
1	1	1	1

16+8+4+2=30

Пример сложения больших чисел:
    1011101100011012
+
_

   11000111100101

2 
  10001111011100102

 

	1	0	1	1	1	0	1	1	0	0	0	1	1	0	1
+
		1	1	0	0	0	1	1	1	1	0	0	1	0	1
1	0	0	0	1	1	1	1	0	1	1	1	0	0	1

       Проверить с помощью калькулятора

Параграф 5. Представление целых чисел в компьютере

Похожие презентации:

Представление чисел в памяти компьютера

Представление чисел в памяти компьютера (10 класс)

Арифметические основы цифровой техники

Системы счисления и действия в них

Перевод между СС и представление чисел

Представление чисел в памяти ЭВМ (Лекция 03)

Представление чисел в памяти компьютера. (Тема 5)

Системы счисления. Представление чисел в компьютере

Представление чисел в памяти компьютера. 9 класс

Представление чисел в компьютере

1. Представление чисел в памяти компьютера

Написать тему

2. Образ компьютерной памяти

Не писать
Образ компьютерной памяти

3. Главные правила представления данных в компьютере

Написать подтему

4. Правило 1

Данные (и программы) в памяти
компьютера хранятся в двоичном виде, т.
е. в виде цепочек единиц и нулей.
Написать всё

5. Правило 2

Представление данных в компьютере
дискретно.
Дискретное множество состоит из отделенных друг
от друга элементов.
Написать всё

6. Правило 3

Множество представимых в памяти
компьютера величин ограничено и
конечно.
МАТЕМАТИКА:
множество целых
чисел дискретно,
бесконечно,
не ограничено
ИНФОРМАТИКА:
множество целых
чисел дискретно,
конечно,
ограничено
Написать всё

7. Правило 4

В памяти компьютера числа хранятся в
двоичной системе счисления.
Написать всё

8. Числовые величины

Целые
(формат с
фиксированной запятой)
Вещественные
(формат с
плавающей запятой)
Написать всё
0 … 28-1 (0 … 255)
один байт
от 00000002 до 11111112
без
знака
0 … 216-1 (0 … 65 535)
два байта
Целые
числа
со
знаком
от 00000000 000000002
до 11111111 111111112
один байт
-27 . .. 27-1 (-128 … 127)
два байта
-215 … 215-1 (-32 768 … 32 767)
четыре
байта
-231 … 231-1
(-2 147 483 648 … 2 147 483 647)
Написать всё
Написать всё
• Число 3910 = 100111 2 в однобайтовом
формате: Номера
разрядов
7
Биты
числа
0 0 1 0 0 1 1 1
6
5
4
3
2
1
0
Число 3910 = 100111 2 в двубайтовом формате:
Номера разрядов
15
Биты
числа
0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
Число 65 53510 = 11111111 111111112 в двубайтовом
формате:
Номера разрядов
15
Биты
числа
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
«+»
0
«-»
1
Написать всё

12. Формы записи целых чисел со знаком

Прямой код
Обратный код
Дополнительный код
Написать всё

13. Формы записи чисел целых чисел со знаком

Написать всё
Положительное число
прямой
код
обратный
код
дополнительный
код
имеют одинаковое
представление
Число 1910=100112
Число 12710=11111112
прямой, обратный и дополнительный
код
прямой, обратный и дополнительный
код
0 0 0 1 0 0 1 1
0 1 1 1 1 1 1 1
«+»
«+»

14.

Формы записи чисел целых чисел со знакомНаписать всё
Отрицательное число
прямой
код
обратный
код
дополнительный
код
имеют разное
представление
Прямой код числа 19:
1 0 0 1 0 0 1 1
Прямой код числа 127:
1 1 1 1 1 1 1 1
«-»
«-»

15. Формы записи чисел целых чисел со знаком

Написать всё
Число -19:
Число -127:
Код модуля числа:
0 0010011
Обратный код числа: 1 1101100
Код модуля числа:
0 1111111
Обратный код числа: 1 0000000
1 1 1 0 1 1 0 0
1 0 0 0 0 0 0 0
«-»
«-»
Дополнительный
код
получается
образованием
обратного кода с последующим прибавлением единицы к
его младшему разряду.
Дополн. код числа -19:
1
«-»
1
1
0
1
1
0
1
Дополн. код числа -127:
1 0 0 0 0 0 0 1
«-»

16. Арифметические действия

В
большинстве
компьютеров
операция
вычитания не выполняется. Вместо неё
производится сложение уменьшаемого с
обратным
или
дополнительным
кодом
вычитаемого.
При сложении дополнительных кодов чисел
А и В имеют место четыре случая.
Написать всё

17. Арифметические действия

• 1) А и В положительные:
Десятичная
запись:
+
Двоичные коды:
5
Апк 0 0 0 0 0 1 0 1
7
Впк 0 0 0 0 0 1 1 1
12
Спк 0 0 0 0 1 1 0 0
Написать всё

18. Арифметические действия

• 2)
А
–
положительное,
отрицательное, |B|>|A|
В
–
Десятичная
Двоичные коды:
запись:
5
Апк 0 0 0 0 0 1 0 1
+
-12
Вдк 1 1 1 1 0 1 0 0
-7
Сдк 1 1 1 1 1 0 0 1
При переводе в прямой код биты цифровой части результата
инвертируются и к младшему разряду прибавляется единица:
10000110 + 1 = 10000111= -710
Написать всё

19. Арифметические действия

• 3)
А
–
положительное,
отрицательное, |B|<|A|
В
–
Десятичная
Двоичные коды:
запись:
12
Апк 0 0 0 0 1 1 0 0
+
-5
Вдк 1 1 1 1 1 0 1 1
7
Спк 0 0 0 0 0 1 1 1
Перенос отбрасывается
Единицу переноса
отбрасывает.
из
знакового
разряда
компьютер
Написать всё

20. Арифметические действия

• 4) А и В отрицательные
Десятичная
запись:
+
Двоичные коды:
-5
Адк 1 1 1 1 1 0 1 1
-7
Вдк 1 1 1 1 1 0 0 1
-12
Сдк 1 1 1 1 0 1 0 0
Перенос отбрасывается
При переводе в прямой код биты цифровой части результата
инвертируются и к младшему разряду прибавляется единица:
10001011+1= 10001100= -1210
Написать всё

21. Целые числа без знака

Для хранения целых неотрицательных чисел без знака
отводится одна ячейка памяти (8 битов).
7
6
5
4
3
2
1
0
Номера разрядов
0
1
1
0
1
1
0
1
Биты, составляющие
число
0
0
0
0
0
0
0
0
Минимальное число 0
1
1
1
1
1
1
1
1
Максимальное число 25510
111111112 = 1000000002 -1 = 28 – 1 = 25510
Для n-разрядного представления максимальное целое
неотрицательное число равно 2n – 1.
Написать всё

22. Целые числа без знака

Пример. Представить число 5110 в двоичном виде в
восьмибитовом представлении в формате целого
без знака.
Решение.
5110 = 1100112
0
0
1
1
0
0
1
1
Написать всё

23. Целые числа со знаком

Для хранения целых чисел со знаком отводится
две ячейки памяти (16 битов).
Старший разряд числа определяет его знак.
Если он равен 0, число положительное,
если 1, то отрицательное.
5110 = 1100112
0
0
1
1
0
0
1
1
— 5110 = — 1100112
1
0
1
1
0
0
1
1
Такое представление чисел в компьютере называется
прямым кодом.
Написать всё

24. Целые числа со знаком

Для n-разрядного представления со знаком (с учетом
выделения одного разряда на знак):
•минимальное отрицательное число равно
– 2n-1
•максимальное положительное число равно 2n-1 – 1,
Целые числа в памяти компьютера —
это дискретное, ограниченное и конечное
множество.
Написать всё

25. Целые числа со знаком

Написать всё
Целые числа со знаком
Для представления отрицательных целых чисел используется
дополнительный код.
Алгоритм получения дополнительного кода отрицательного
числа:
1. Число записать прямым кодом в n двоичных разрядах.
2. Получить обратный код числа, для этого значения всех
битов инвертировать, кроме старшего разряда.
3. К полученному обратному коду прибавить единицу.
Представить число -201410 в двоичном виде в шестнадцатибитном
представлении в формате целого со знаком.
Прямой код
-201410
10000111 110111102
Обратный код
Инвертирование
11111000 001000012
Прибавление единицы
11111000 001000012
00000000 000000012
Дополнительный код
11111000 001000102

26. Целые числа со знаком

Написать всё
Целые числа со знаком
Алгебраическое сложение двоичных чисел
1.
Положительные слагаемые представить в прямом коде.
2.
Отрицательные слагаемые – в дополнительном.
3.
Найти сумму кодов, включая знаковые разряды,
которые при этом рассматриваются как старшие
разряды. При переносе из знакового разряда единицу
переноса отбрасывают.
4.
В результате получают алгебраическую сумму в прямом
коде, если эта сумма положительная, и в
дополнительном, если сумма отрицательная.

27. Целые числа со знаком

Пример 1. Найти разность 1310 – 1210 в восьмибитном
представлении.
1310
– 1210
Прямой код
00001101
10001100
Обратный код
—
11110011
Дополнительный код
—
11110100
0 0001101
+
1 1110100
10 0 0 0 0 0 0 1
Так как произошел перенос из знакового разряда,
первую единицу отбрасываем, и в результате
получаем 00000001.
Написать всё

28. Целые числа со знаком

Пример 2. Найти разность 810 – 1310 в восьмибитном
представлении.
810
– 1310
Прямой код
00001000
10001101
Обратный код
—
11110010
Дополнительный код
—
11110011
+
0 0001000
1 1110011
1 1111011
Написать всё

29.

Целые числа со знакомНаписать всё
Целые числа со знаком
Пример 2. Найти разность 810 – 1310 в восьмибитном
представлении.
+
0 0001000
1 1110011
1 1111011
В знаковом разряде стоит 1, значит результат получен в
дополнительном коде. Прейдем от дополнительного кода к обратному,
вычтя единицу:
1 1110011
0 0000001
1 1111010
Прейдем от обратного кода к прямому, инвертируя все цифры, за
исключением знакового (старшего) разряда: 100001012 = 510.

30. Вещественные числа

Вещественные числа хранятся и обрабатываются в
компьютере в формате с плавающей запятой,
использующем экспоненциальную форму записи чисел.
n
A=M q
M – мантисса числа (правильная отличная от нуля дробь),
q – основание системы счисления,
n – порядок числа.
Диапазон ограничен максимальными значениями M и n.
Написать всё

31. Вещественные числа

Написать всё
Вещественные числа
Например, 123,45 = 0,12345 · 103
Порядок указывает, на какое количество позиций и в каком
направлении должна сместиться десятичная запятая в мантиссе.
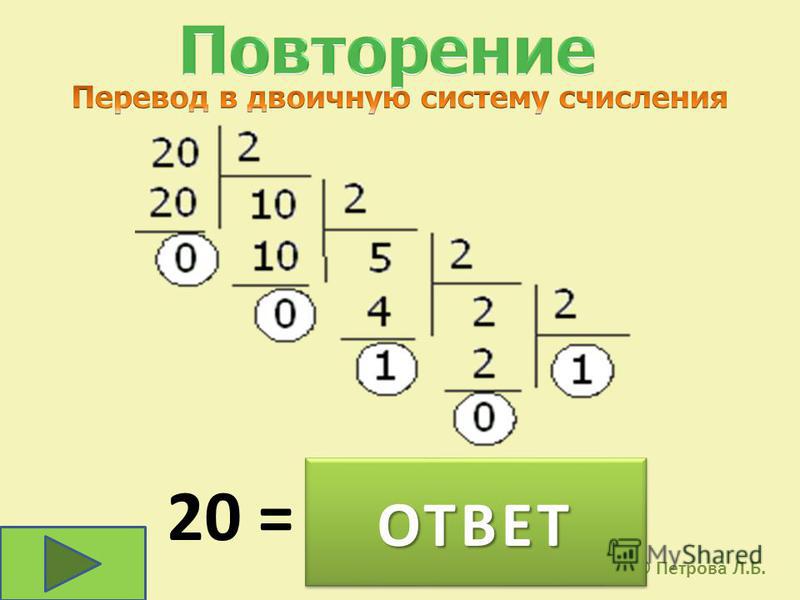
Число в формате с плавающей запятой может занимать
в памяти 4 байта (обычная точность) или 8 байтов
(двойная точность).
При записи числа выделяются разряды для хранения

знака мантиссы, знака порядка, порядка и мантиссы.
Мантисса M и порядок n определяют диапазон
изменения чисел и их точность.

English     Русский Правила

Калькулятор НОД и НОК с решением онлайн

0
AC		+/-	÷
7	8	9	×
4	5	6	—
1	2	3	+
0	00	,	=

При помощи данного калькулятора вы можете легко найти наибольший общий делитель НОД и наименьшее общее кратное НОК благодаря подробно расписанному решению.

Вы можете найти НОД и НОК для двух, трех и четырех чисел

Выберите количество чисел для НОД и НОК

2 числа

3 числа

4 числа

Вы так же можете воспользоваться:

калькулятором нахождения НОД и НОК по алгоритму Евклида калькулятором нахождения НОД и НОК для любого количества чисел

---

Наибольший общий делитель НОД

Наибольший общий делитель НОД(a, b) – это наибольшее натуральной число, на которое можно разделить без остатка числа a и b.

Если числа имеют только один общий делитель – единицу, то такие числа называют взаимно простыми.

Наибольший общий делитель НОД обозначают: НОД(a, b), (a, b), gcd(a, b), hcf(a, b).

Свойства НОД

1. Наибольший общий делитель чисел a и b делится на любой общий делитель этих чисел.
   Данное свойство означает, что если найти все общие делители чисел a и b, то НОД(a, b) будет делится на любой из этих делителей.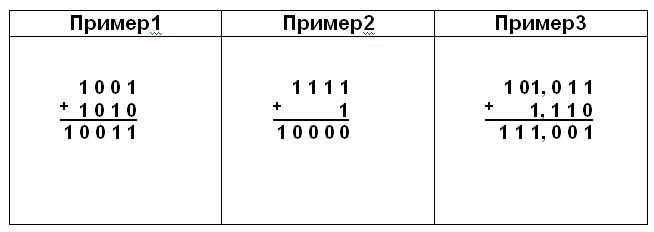
   Например, возьмём два числа 15 и 30 и найдем все общие делители этих чисел: 1, 3, 5, 15. Наибольший из этих делителей – число 15. Тогда число 15 делится на 1, 3, 5, 15.
2. Если число a делится на b, то НОД(a, b) = b.
   Например, число 20 делится на число 10, тогда НОД(20, 10) = 10.
3. При помощи наибольшего общего делителя можно привести дроби к несократимому виду.
   Например, дробь 5/30 можно привести к несократимому виду, если найти НОД(30, 5). НОД(30, 5) = 5, следовательно число 5 – самое больше число из возможных делителей числа 30 и 5 на которое можно разделить эти числа, тогда 30:5 = 6, 5:5 = 1. Получаем дробь 5/30 = 1/6.
   Любые действия с дробями и развернутое поэтапное решение можно вычислить, используя калькулятор дробей.

Как найти наибольший общий делитель НОД

Чтобы найти наибольший общий делитель НОД двух, трех и более чисел, необходимо:

1. Разложить числа на простые множители.
2. Найти общие множители чисел – такие числа, которые есть в разложении всех чисел и вычеркнуть их.
3. Перемножить оставшиеся множители.

---

Приведем пример, найдем наибольший общий делитель двух чисел 24 и 58.

Способ №1

1. Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением).

   58 — составное число

   Разложим число 24 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом

   24 : 2 = 12 — делится на простое число 2
   12 : 2 = 6 — делится на простое число 2
   

   6 : 2 = 3 — делится на простое число 2.
   Завершаем деление, так как 3 простое число

   Разложим число 58 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом

   58 : 2 = 29 — делится на простое число 2.
   Завершаем деление, так как 29 простое число

2. Выделим синим цветом и выпишем общие множители.

   24 = 2 ⋅ 2 ⋅ 2 ⋅ 3
   58 = 2 ⋅ 29

   У чисел (24, 58) только один общий множитель — 2 и он и будет наибольшим общим делителем этих чисел

   Ответ: НОД (24, 58) = 2

Способ №2

1. Найдем все возможные делители чисел (24, 58). Для этого поочередно разделим число 24 на делители от 1 до 24, число 58 на делители от 1 до 58. Если число делится без остатка, то делитель запишем в список делителей.

   Для числа 24 выпишем все случаи, когда оно делится без остатка:
   24 : 1 = 24;
   24 : 2 = 12;
   24 : 3 = 8;
   24 : 4 = 6;
   24 : 6 = 4;
   24 : 8 = 3;
   24 : 12 = 2;
   24 : 24 = 1;

   Для числа 58 выпишем все случаи, когда оно делится без остатка:
   58 : 1 = 58;
   58 : 2 = 29;
   58 : 29 = 2;
   58 : 58 = 1;

2. Выпишем все общие делители чисел (24, 58) и выделим зеленым цветом самый большой, это и будет наибольший общий делитель НОД чисел (24, 58)

   Общие делители чисел (24, 58): 1, 2

   Ответ: НОД (24, 58) = 2

---

Наименьшее общее кратное НОК

Наименьшее общее кратное НОК(a, b) – это наименьшее число, которое можно разделить на числа a и b без остатка.

Наименьшее общее кратное НОК обозначается: НОК(a, b), [a, b], LCM(a, b), lcm(a, b).

Как найти наименьшее общее кратное НОК

Чтобы найти НОК двух, трех и более чисел необходимо:

1. Разложить эти числа на простые множители.
2. Выписать множители одного из чисел и добавить к ним множители из разложения остальных чисел, которых нет в разложении.
3. Умножить получившиеся множители.

---

Приведем пример, найдем наименьшее общее кратное НОК для чисел 30 и 225.

Способ №1

1. Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением).
   225 — составное число
   30 — составное число

   Разложим число 225 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом

   225 : 3 = 75 — делится на простое число 3
   75 : 3 = 25 — делится на простое число 3
   25 : 5 = 5 — делится на простое число 5.
   Завершаем деление, так как 5 простое число

   Разложим число 30 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом

   30 : 2 = 15 — делится на простое число 2
   15 : 3 = 5 — делится на простое число 3.
   Завершаем деление, так как 5 простое число

2. Прежде всего запишем множители самого большого числа, а затем меньшего числа. Найдем недостающие множители, выделим синим цветом в разложении меньшего числа множители, которые не вошли в разложение большего числа.
   225 = 3 ∙ 3 ∙ 5 ∙ 5
   30 = 2 ∙ 3 ∙ 5

   3) Теперь, чтобы найти НОК нужно перемножить множители большего числа с недостающими множителями, которые выделены синим цветом

   НОК (225 ; 30) = 3 ∙ 3 ∙ 5 ∙ 5 ∙ 2 = 450

Способ №2

1. Найдем все возможные кратные чисел (225 ; 30). Для этого поочередно умножим число 225 на числа от 1 до 30, число 30 на числа от 1 до 225.

   Выделим все кратные числа 225 зеленым цветом: зеленым цветом:

   225 ∙ 1 = 225;   225 ∙ 2 = 450;   225 ∙ 3 = 675;   225 ∙ 4 = 900;
   225 ∙ 5 = 1125;   225 ∙ 6 = 1350;   225 ∙ 7 = 1575;   225 ∙ 8 = 1800;
   225 ∙ 9 = 2025;   225 ∙ 10 = 2250;   225 ∙ 11 = 2475;   225 ∙ 12 = 2700;
   225 ∙ 13 = 2925;   225 ∙ 14 = 3150;   225 ∙ 15 = 3375;   225 ∙ 16 = 3600;
   225 ∙ 17 = 3825;   225 ∙ 18 = 4050;   225 ∙ 19 = 4275;   225 ∙ 20 = 4500;
   225 ∙ 21 = 4725;   225 ∙ 22 = 4950;   225 ∙ 23 = 5175;   225 ∙ 24 = 5400;
   225 ∙ 25 = 5625;   225 ∙ 26 = 5850;   225 ∙ 27 = 6075;   225 ∙ 28 = 6300;
   225 ∙ 29 = 6525;   225 ∙ 30 = 6750;   

   Выделим все кратные числа 30 зеленым цветом:

   30 ∙ 1 = 30;   30 ∙ 2 = 60;   30 ∙ 3 = 90;   30 ∙ 4 = 120;
   30 ∙ 5 = 150;   30 ∙ 6 = 180;   30 ∙ 7 = 210;   30 ∙ 8 = 240;
   30 ∙ 9 = 270;   30 ∙ 10 = 300;   30 ∙ 11 = 330;   30 ∙ 12 = 360;
   30 ∙ 13 = 390;   30 ∙ 14 = 420;   30 ∙ 15 = 450;   30 ∙ 16 = 480;
   30 ∙ 17 = 510;   30 ∙ 18 = 540;   30 ∙ 19 = 570;   30 ∙ 20 = 600;
   30 ∙ 21 = 630;   30 ∙ 22 = 660;   30 ∙ 23 = 690;   30 ∙ 24 = 720;
   30 ∙ 25 = 750;   30 ∙ 26 = 780;   30 ∙ 27 = 810;   30 ∙ 28 = 840;
   30 ∙ 29 = 870;   30 ∙ 30 = 900;   30 ∙ 31 = 930;   30 ∙ 32 = 960;
   30 ∙ 33 = 990;   30 ∙ 34 = 1020;   30 ∙ 35 = 1050;   30 ∙ 36 = 1080;
   30 ∙ 37 = 1110;   30 ∙ 38 = 1140;   30 ∙ 39 = 1170;   30 ∙ 40 = 1200;
   30 ∙ 41 = 1230;   30 ∙ 42 = 1260;   30 ∙ 43 = 1290;   30 ∙ 44 = 1320;
   30 ∙ 45 = 1350;   30 ∙ 46 = 1380;   30 ∙ 47 = 1410;   30 ∙ 48 = 1440;
   30 ∙ 49 = 1470;   30 ∙ 50 = 1500;   30 ∙ 51 = 1530;   30 ∙ 52 = 1560;
   30 ∙ 53 = 1590;   30 ∙ 54 = 1620;   30 ∙ 55 = 1650;   30 ∙ 56 = 1680;
   30 ∙ 57 = 1710;   30 ∙ 58 = 1740;   30 ∙ 59 = 1770;   30 ∙ 60 = 1800;
   30 ∙ 61 = 1830;   30 ∙ 62 = 1860;   30 ∙ 63 = 1890;   30 ∙ 64 = 1920;
   30 ∙ 65 = 1950;   30 ∙ 66 = 1980;   30 ∙ 67 = 2010;   30 ∙ 68 = 2040;
   30 ∙ 69 = 2070;   30 ∙ 70 = 2100;   30 ∙ 71 = 2130;   30 ∙ 72 = 2160;
   30 ∙ 73 = 2190;   30 ∙ 74 = 2220;   30 ∙ 75 = 2250;   30 ∙ 76 = 2280;
   30 ∙ 77 = 2310;   30 ∙ 78 = 2340;   30 ∙ 79 = 2370;   30 ∙ 80 = 2400;
   30 ∙ 81 = 2430;   30 ∙ 82 = 2460;   30 ∙ 83 = 2490;   30 ∙ 84 = 2520;
   30 ∙ 85 = 2550;   30 ∙ 86 = 2580;   30 ∙ 87 = 2610;   30 ∙ 88 = 2640;
   30 ∙ 89 = 2670;   30 ∙ 90 = 2700;   30 ∙ 91 = 2730;   30 ∙ 92 = 2760;
   30 ∙ 93 = 2790;   30 ∙ 94 = 2820;   30 ∙ 95 = 2850;   30 ∙ 96 = 2880;
   30 ∙ 97 = 2910;   30 ∙ 98 = 2940;   30 ∙ 99 = 2970;   30 ∙ 100 = 3000;
   30 ∙ 101 = 3030;   30 ∙ 102 = 3060;   30 ∙ 103 = 3090;   30 ∙ 104 = 3120;
   30 ∙ 105 = 3150;   30 ∙ 106 = 3180;   30 ∙ 107 = 3210;   30 ∙ 108 = 3240;
   30 ∙ 109 = 3270;   30 ∙ 110 = 3300;   30 ∙ 111 = 3330;   30 ∙ 112 = 3360;
   30 ∙ 113 = 3390;   30 ∙ 114 = 3420;   30 ∙ 115 = 3450;   30 ∙ 116 = 3480;
   30 ∙ 117 = 3510;   30 ∙ 118 = 3540;   30 ∙ 119 = 3570;   30 ∙ 120 = 3600;
   30 ∙ 121 = 3630;   30 ∙ 122 = 3660;   30 ∙ 123 = 3690;   30 ∙ 124 = 3720;
   30 ∙ 125 = 3750;   30 ∙ 126 = 3780;   30 ∙ 127 = 3810;   30 ∙ 128 = 3840;
   30 ∙ 129 = 3870;   30 ∙ 130 = 3900;   30 ∙ 131 = 3930;   30 ∙ 132 = 3960;
   30 ∙ 133 = 3990;   30 ∙ 134 = 4020;   30 ∙ 135 = 4050;   30 ∙ 136 = 4080;
   30 ∙ 137 = 4110;   30 ∙ 138 = 4140;   30 ∙ 139 = 4170;   30 ∙ 140 = 4200;
   30 ∙ 141 = 4230;   30 ∙ 142 = 4260;   30 ∙ 143 = 4290;   30 ∙ 144 = 4320;
   30 ∙ 145 = 4350;   30 ∙ 146 = 4380;   30 ∙ 147 = 4410;   30 ∙ 148 = 4440;
   30 ∙ 149 = 4470;   30 ∙ 150 = 4500;   30 ∙ 151 = 4530;   30 ∙ 152 = 4560;
   30 ∙ 153 = 4590;   30 ∙ 154 = 4620;   30 ∙ 155 = 4650;   30 ∙ 156 = 4680;
   30 ∙ 157 = 4710;   30 ∙ 158 = 4740;   30 ∙ 159 = 4770;   30 ∙ 160 = 4800;
   30 ∙ 161 = 4830;   30 ∙ 162 = 4860;   30 ∙ 163 = 4890;   30 ∙ 164 = 4920;
   30 ∙ 165 = 4950;   30 ∙ 166 = 4980;   30 ∙ 167 = 5010;   30 ∙ 168 = 5040;
   30 ∙ 169 = 5070;   30 ∙ 170 = 5100;   30 ∙ 171 = 5130;   30 ∙ 172 = 5160;
   30 ∙ 173 = 5190;   30 ∙ 174 = 5220;   30 ∙ 175 = 5250;   30 ∙ 176 = 5280;
   30 ∙ 177 = 5310;   30 ∙ 178 = 5340;   30 ∙ 179 = 5370;   30 ∙ 180 = 5400;
   30 ∙ 181 = 5430;   30 ∙ 182 = 5460;   30 ∙ 183 = 5490;   30 ∙ 184 = 5520;
   30 ∙ 185 = 5550;   30 ∙ 186 = 5580;   30 ∙ 187 = 5610;   30 ∙ 188 = 5640;
   30 ∙ 189 = 5670;   30 ∙ 190 = 5700;   30 ∙ 191 = 5730;   30 ∙ 192 = 5760;
   30 ∙ 193 = 5790;   30 ∙ 194 = 5820;   30 ∙ 195 = 5850;   30 ∙ 196 = 5880;
   30 ∙ 197 = 5910;   30 ∙ 198 = 5940;   30 ∙ 199 = 5970;   30 ∙ 200 = 6000;
   30 ∙ 201 = 6030;   30 ∙ 202 = 6060;   30 ∙ 203 = 6090;   30 ∙ 204 = 6120;
   30 ∙ 205 = 6150;   30 ∙ 206 = 6180;   30 ∙ 207 = 6210;   30 ∙ 208 = 6240;
   30 ∙ 209 = 6270;   30 ∙ 210 = 6300;   30 ∙ 211 = 6330;   30 ∙ 212 = 6360;
   30 ∙ 213 = 6390;   30 ∙ 214 = 6420;   30 ∙ 215 = 6450;   30 ∙ 216 = 6480;
   30 ∙ 217 = 6510;   30 ∙ 218 = 6540;   30 ∙ 219 = 6570;   30 ∙ 220 = 6600;
   30 ∙ 221 = 6630;   30 ∙ 222 = 6660;   30 ∙ 223 = 6690;   30 ∙ 224 = 6720;
   30 ∙ 225 = 6750;

2. Выпишем все общие кратные чисел (225 ; 30) и выделим зеленым цветом самое маленькое, это и будет наименьшим общим кратным чисел (225 ; 30).

   Общие кратные чисел (225 ; 30): 450, 900, 1350, 1800, 2250, 2700, 3150, 3600, 4050, 4500, 4950, 5400, 5850, 6300, 6750

   Ответ: НОК (225 ; 30) = 450

Вам могут также быть полезны следующие сервисы

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N2 | Двоичная система счисления

N3 | Троичная система счисления

N4 | Четырехичная система счисления

N5 | Пятеричная система счисления

N6 | Шестеричная система счисления

N7 | Семеричная система счисления

N8 | Восьмеричная система счисления

N9 | Девятеричная система счисления

N11 | Одиннадцатиричная система счисления

N12 | Двенадцатеричная система счисления

N13 | Тринадцатеричная система счисления

N14 | Четырнадцатеричная система счисления

N15 | Пятнадцатеричная система счисления

N16 | Шестнадцатеричная система счисления

N17 | Семнадцатеричная система счисления

N18 | Восемнадцатеричная система счисления

N19 | Девятнадцатеричная система счисления

N20 | Двадцатеричная система счисления

N21 | Двадцатиодноричная система счисления

N22 | Двадцатидвухричная система счисления

N23 | Двадцатитрехричная система счисления

N24 | Двадцатичетырехричная система счисления

N25 | Двадцатипятеричная система счисления

N26 | Двадцатишестеричная система счисления

N27 | Двадцатисемеричная система счисления

N28 | Двадцативосьмеричная система счисления

N29 | Двадцатидевятиричная система счисления

N30 | Тридцатиричная система счисления

N31 | Тридцатиодноричная система счисления

N32 | Тридцатидвухричная система счисления

N33 | Тридцатитрехричная система счисления

N34 | Тридцатичетырехричная система счисления

N35 | Тридцатипятиричная система счисления

N36 | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Калькулятор двоичных сложений

Создано Ритой Рейн

Отзыв от Доминика Черниа, доктора наук и Стивена Вудинга

Последнее обновление: 24 сентября 2022 г.

Содержание:

• Что такое двоичная система?
• Как пользоваться калькулятором двоичного сложения?
• Каковы правила двоичного сложения?
• Двоичная сумма: сложение двоичных чисел
• Часто задаваемые вопросы

Этот калькулятор двоичного сложения суммирует числа, представленные нулями и единицами (вы можете сгенерировать их с помощью двоичного преобразователя).

Прочтите этот текст, чтобы узнать больше о языке компьютеров и о том, как складывать двоичные числа без двоичного математического калькулятора. Как только вы освоите сложение двоичных чисел, вы можете научиться вычитать их с помощью нашего калькулятора двоичного вычитания.

🔎 Помимо суммирования, вы можете вычитать, умножать и делить эти типы чисел с помощью нашего двоичного калькулятора.

Что такое двоичная система?

Чтобы понять двоичную систему, давайте сначала посмотрим на более привычную десятичную систему .

В десятичной системе мы используем десять цифр (0-9) и, в зависимости от их положения, умножаем их на соответствующие степени десяти. Например, давайте разберем число 1934 :

1934 = 1000 + 900 + 30 + 4

1934 = 1*1000 + 9*100 + 3*10 + 4*1

1934 = 1*10³ + 9*10² + 3*10¹ + 4*10⁰

Если бы мы составили формулу для 4-значного числа, она могла бы выглядеть так:

а₃а₂а₁а₀ = а₃ * 10³ + а₂ * 10² + а₁ * 10¹ + а₀ * 10⁰

Символ «а» здесь представляет цифру от 0 до 9. Индекс рядом с «а» обозначает место цифры счет от 0, справа налево).

Теперь, , двоичная система работает аналогично, но мы используем только две цифры и умножаем их на степени двойки. Таким образом, формула будет следующей:

а₃а₂а₁а₀ = а₃ * 2³ + а₂ * 2² + а₁ * 2¹ + а₀ * 2⁰

В этой системе мы умножаем две цифры (0 и 1), соответствующие степени 2, на 2 на свое место в номере.

Например, мы запишем «9» как «1001», потому что:

1001 = 1 * 2³ + 0 * 2² + 0 * 2¹ + 1 * 2⁰ = 8 + 0 + 0 + 1 = 9

Аналогично:

• «2» в двоичном формате равно «10», потому что 1 * 2¹ + 0 * 2⁰ = 2

• «3» в двоичном формате равно «11», потому что 1 * 2¹ + 1 * 2⁰ = 2 + 1 = 3

• «4» в двоичном формате равно «100», потому что 1 * 2² + 0 * 2¹ + 0 * 2⁰ = 4

Как пользоваться калькулятором двоичного сложения?

Чтобы двоичный математический калькулятор выполнял сложение двоичных чисел, выполните следующие действия:

1. Введите первое число в первое поле калькулятора двоичного сложения. Помните, что для используйте только нули и единицы . Вам не нужно вводить ведущие нули, например, для «00001111» вы можете ввести просто «1111».

2. Введите второе двоичное число во второй строке.

3. Калькулятор двоичного сложения отобразит результат в третьем поле .

4. В расширенном режиме (внизу) вы можете заставить калькулятор двоичного сложения печатать длинное сложение двоичных чисел.

Каковы правила двоичного сложения?

Существует четыре основных правила двоичного сложения:

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 10 (запишите «0» в столбце и перенесите 1 на следующий бит)

Приведенные выше уравнения работают так же, как и в десятичной системе, только здесь вам нужно перевести 1, когда сумма превышает 1 (в десятичной системе мы делаем это, когда она превышает 9).

Двоичная сумма: Сложение двоичных чисел

Как складывать двоичные числа? Вы всегда можете преобразовать двоичные числа в десятичные, сложить их, как обычно, и восстановить результат в двоичной форме.

Другой способ состоит в том, чтобы использовать приведенные выше правила двоичного сложения и выполнить длинное сложение . Давайте посмотрим на эту двоичную сумму:

перенос:    1    1 ___________              1001        +   1101 ___________        =10110\text{carry:} \ \ \ \ 1\ \ \ \ 1 \\\ \_\_\_\_\_\_\_\_\_\_\_ \\\ \\\\\\\\\\\\\1001\\\ \\\\\\\+\\\1101\\\ \_\_\_\_\_\_\_\_\_\_\_ \\\ \ \ \ \ \ \ \ = 10110carry:    1    1 ___________              1001        +   1101 ___________        =10110

🔎 Наш калькулятор длинных сложений может помочь понять описанную выше операцию.

В первом столбце справа 1 + 1 дает нам 2, поэтому нам нужно перенести 1 во второй столбец (1, помещенный во второй столбец, равен двум, потому что 1 * 2¹ = 2) и записать 0 в первый столбец. Во втором столбце 0 + 0 = 0 , поэтому мы просто записываем 1, которую мы перенесли. В третьем столбце справа 0 + 1 = 1 . В четвертом столбце у нас есть 1 + 1 , поэтому снова пишем 0 и переносим 1. Так как добавить больше нечего, пишем «1» в начале результата (слева).

Приложения двоичного сложения присутствуют во многих методах исправления и обнаружения ошибок, таких как бит четности и расстояние Хэмминга!

Часто задаваемые вопросы

Что такое двоичное сложение?

Двоичное сложение — это операция суммирования чисел в двоичной форме . Он работает как «обычное» (десятичное) сложение, но в числе могут быть только нули и единицы в качестве цифр, поэтому, если сумма превышает 1, вы должны перенести 1 в следующий бит. Например, 101 + 101 = 1010 .

Как решить двоичное сложение?

1. Чтобы решить двоичное сложение, выполните длинное сложение — расположите числа вертикально и добавьте цифры в столбцы, идущие справа налево.

2. Если сумма в столбце равна 2, перенести 1 в следующий столбец (слева). Если сумма равна 1 или 0, запишите ее и перейдите к следующему столбцу.

3. Продолжайте таким образом, пока не просуммируете все столбцы (включая переносимые числа).

Как обнаружить переполнение при двоичном сложении?

Проверить, имеет ли смысл сумма двоичных чисел. Если сумма двух отрицательных чисел положительна или сумма двух положительных чисел равна , что-то не так. Эта ошибка означает, что сумма переполняла — то есть двоичное представление результата не помещалось в выделенное количество бит.

Рита Рейн

Посмотреть 10 похожих бинарных калькуляторов 1️0️

Двоичное делениеДвоичная дробьДвоичное умножение… Еще 7

Двоичное сложение — правила, примеры, формулы, часто задаваемые вопросы числа по основанию 10. При двоичном сложении значения разрядов задаются как единицы, двойки, четверки, восьмерки, шестнадцати и т.

д. Сначала мы складываем цифры в столбце единиц, затем движемся влево, т. е. складываем цифры в столбце двоек, затем цифры в четвертом столбце и так далее. Единственная разница в том, что здесь мы делаем перегруппировку, когда сумма цифр становится больше 1. Давайте узнаем больше о двоичном сложении в этой статье.

1.	Что такое двоичное сложение?
2.	Двоичные правила сложения
3.	Как добавить двоичные числа?
4.	Двоичное сложение с использованием дополнения до 1
5.	Часто задаваемые вопросы о двоичном сложении

Что такое двоичное сложение?

Сложение двух или более двоичных чисел является одной из арифметических операций над двоичными числами или системами счисления с основанием 2. В десятичном сложении, когда мы складываем 3 + 2, мы получаем 5. Точно так же, когда мы складываем их двоичные эквиваленты, то есть (11) ₂ и (10) ₂ , мы получаем, (11) ₂ + ( 10) ₂ = (101) ₂ , что равно 5 по основанию 10. Результаты как двоичного, так и десятичного сложения дают нам один и тот же ответ, разница только в разрядных значениях цифр. Процесс двоичного сложения покажется вам очень знакомым, с той лишь разницей, что в десятичной системе счисления мы перегруппировываем следующее разрядное значение всякий раз, когда получаем сумму цифр больше 9.потому что в десятичной системе мы используем 10 цифр от 0 до 9. Но при добавлении двоичных чисел мы перегруппируем следующее разрядное значение, когда сумма цифр становится больше 1, поскольку в двоичной системе счисления можно использовать только две цифры. , а это 0 и 1.

Двоичные правила сложения

Четыре правила, которые применяются при сложении двух двоичных цифр, приведены ниже:

Теперь давайте воспользуемся этими правилами сложения двоичных чисел, чтобы изучить процесс сложения двоичных чисел.

Как добавить двоичные числа?

Двоичные числа используются в компьютерах для хранения и представления данных с помощью цифр 0 и 1. При изучении двоичного сложения возникают два случая, которые приведены ниже:

• Двоичное сложение без перегруппировки
• Сложение двоичных чисел с перегруппировкой

Двоичное сложение без перегруппировки

Когда сложение двух цифр дает 0 или 1, нам не нужно перегруппировывать при сложении двух или более двоичных чисел. Например, добавим (101) ₂ и (10) ₂ , которые являются двоичными эквивалентами 5 и 2 соответственно.

Шаг 1: Запишите все цифры обоих чисел в отдельные столбцы в соответствии с их разрядами.

1 0 1
+ 1 0
————
————

Шаг 2: Начните с цифр самого правого столбца, 1 и 0. Примените одно из правил двоичного сложения, согласно которому 1 + 0 = 1.

1 0 1
+ 1 0
————
1
————

Шаг 3: Переход к следующему столбцу слева. Здесь у нас есть две цифры 0 и 1. Посмотрите на приведенные выше правила и выясните, какое правило будет применяться здесь. Примените одно из правил двоичного сложения, согласно которому 0 + 1 = 1.

1 0 1
+ 1 0
————
1 1
————

Шаг 4: Теперь в последнем столбце у нас остался только 1, поэтому мы можем применить правило, 1 + 0 = 1,

1 0 1
+ 1 0
———-
1 1 1
———-

Таким образом, сложив (101) ₂ с (10) ₂ , мы получим (111) ₂ в качестве окончательного ответа.

Сложение двоичных чисел с перегруппировкой

Когда сложение двух цифр дает число больше 1, нам необходимо перегруппировать при сложении двух или более двоичных чисел. Например, добавим (1001) ₂ и (111) ₂ , которые являются двоичными эквивалентами 9и 7 соответственно.

• Шаг 1: Расположите числа, как показано ниже.
• Шаг 2: Следуйте правилам двоичного сложения, чтобы сложить числа. Сначала добавим цифры вместо единиц, то есть 1 + 1 = 0 (1 перенос). Здесь 1 + 1 равно 10, что является двоичным эквивалентом (2) ₁₀ , поэтому мы перегруппируем столбец двоек, взяв 1 в качестве переноса.
• Шаг 3: Теперь мы переходим к следующему разрядному значению влево, то есть к разряду двоек. Здесь у нас есть 0 + 1 + 1 (перенос) = 10. Итак, мы снова напишем 0 и возьмем 1 в качестве переноса на следующее разрядное значение. В следующем столбце у нас есть 0 + 1 + 1 = 10. Точно так же мы снова берем 1 в качестве переноса в следующий столбец. В последнем столбце слева имеем 1 + 1 (перенос) = 10,9.0010

Следовательно, (1001) ₂ + (111) ₂ = (10000) ₂ .

Двоичное сложение с использованием дополнения до 1

Дополнение числа до 1 можно найти, поменяв местами каждый 0 на 1 и каждый 1 на 0 в двоичном числе. Например, дополнение до 1 двоичного числа 110 равно 001. До сих пор мы изучали сложение всех положительных двоичных чисел, но, используя дополнение до 1, мы можем даже сложить два отрицательных двоичных числа и одно отрицательное с положительным числом. Во-первых, давайте научимся добавить положительное число к отрицательному числу .

Когда положительное число больше , мы находим дополнение отрицательного числа до 1. Сложите положительное число и дополнение до 1 отрицательного числа. Затем мы снова добавляем полный перенос суммы к результату, чтобы получить окончательный ответ. Например, добавим 1010 к (-1001). Во-первых, давайте найдем дополнение до 1 отрицательного двоичного числа (-1001), заменив 0 на 1 и 1 на 0. Таким образом, дополнение до 1 равно 0110. Теперь мы добавим 0110 к положительному числу, которое равно 1010.

1 0 1 0
+ 0 1 1 0
————-
1 0 0 0 0
————-

Здесь конечный перенос равен 1, поэтому мы снова добавляем его к остальной части числа, то есть 0000. Теперь 0000+1 = 0001. Итак, , 0001 — это ответ, когда мы добавляем положительное число 1010 к отрицательному числу (-1001).

Когда отрицательное число больше положительного числа , то сначала мы берем дополнение до 1 отрицательного числа, а затем прибавляем его к положительному числу. Теперь, в этом случае, не будет сквозного переноса. Таким образом, окончательный ответ получается путем добавления до 1 результирующего значения. Например, чтобы добавить 0111 и (-1000), мы сначала находим дополнение до 1 числа -1000, что равно 0111. Теперь мы добавляем дополнение до 1 к заданному положительному двоичному числу 0111.

0 1 1 1
+ 0 1 1 1
————-
1 1 1 0
————-

Теперь найдите дополнение до 1 числа 1110, которое равно 0001. Таким образом, 0001 является окончательным ответом после добавления 0111 к -1000.

В случае сложения двух отрицательных двоичных чисел , сначала мы представляем оба числа в 5-битном регистре, присоединяя необходимое количество нулей слева. Затем мы находим дополнение обоих чисел до 1 и складываем значения. Конечный перенос снова будет добавлен к остальной части номера. Обратите внимание, что в этом случае мы всегда будем получать переносную цифру. После сложения нужно найти дополнение до 1 для полученного числа. Это значение с отрицательным знаком будет окончательным ответом.

Например, добавим два отрицательных двоичных числа -1010 и -0101. Представив оба эти числа в 5-битном регистре, мы получим 01010 и 00101. Теперь нам нужно найти дополнение обоих до 1, заменив 1 на 0 и 0 на 1. Мы получим 10101 и 11010 соответственно. Получим 101111 после сложения обоих чисел. Здесь 1 в крайнем левом углу — это перенос в конце, и он снова будет добавлен к остальной части числа справа от него (01111). Теперь нам нужно найти дополнение 1 к 10000, что равно 01111. Следовательно, -01111 является окончательным ответом.

Связанные темы

Ознакомьтесь с интересными статьями, посвященными двоичному сложению.

• Двоичное вычитание
• Двоичный код в десятичный
• Двоично-десятичный калькулятор
• Преобразование десятичного числа в двоичное
• Двоичная система счисления

Часто задаваемые вопросы о двоичном сложении

Каковы правила двоичного сложения?

Существует 4 основных правила двоичного сложения, которые приведены ниже:

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 1 = 10 (результат — 0, перенос — 1)
• 1 + 1 + 1 = 11 (результат — 1, перенос — 1)

Как складывать двоичные числа?

Сложение двоичных чисел становится очень простым, если мы знаем приведенные выше правила сложения двоичных чисел. Например, если мы хотим прибавить 10 к 11, мы должны сначала начать с разрядов единиц обоих чисел. Складывая цифры в разряде единиц, 0 и 1, мы получаем 0 + 1 = 1. Теперь складываем цифры в разряде двоек, т.е. 1 и 1. Слева от разряда двоек в этих числах больше нет разрядов, так что нет необходимости брать перенос. В соответствии с правилом двоичного сложения 1 + 1 = 10. Таким образом, окончательный результат сложения 10 + 11 равен 101. Вот как мы складываем двоичные числа.

Как узнать, есть ли у двоичного дополнения переполнение?

Если при сложении двух двоичных чисел мы получаем число больше 1, то мы должны выполнить перенос на следующее разрядное значение слева. Это случай переполнения при двоичном сложении, поскольку у нас не может быть цифр, отличных от 0 и 1, в двоичной системе. Каждое число больше 1 выражается с использованием 2 или более битов, что приводит к переполнению.

Что такое 1+1+1 в двоичном сложении?

В двоичном сложении 1+1+1 равно 11. Так как 1 + 1 равно 10, и если мы прибавим 1, то получим 10 + 1, что равно 11.

Как сложить 4 двоичных числа?

Существует два способа сложения четырех двоичных чисел. Во-первых, мы можем сложить вместе любые три числа, а затем добавить четвертое число к полученному значению. Второй способ — сложить любые две пары чисел, а затем сложить получившиеся значения друг с другом. Например, если нам нужно сложить 10 + 11 + 101 + 1010, мы можем сначала сложить 10 и 101, что даст нам 101+10 = 111. Теперь складываем два других числа 11 и 1010. Мы знаем, что 1010 + 11 = 1101. Теперь сложите оба полученных значения, 1101 + 111 = 10100. Следовательно, 10100 — это окончательный ответ. Вот как мы можем сложить вместе четыре двоичных числа.

В чем разница между двоичным сложением и двоичным вычитанием?

Двоичное сложение и двоичное вычитание — это две арифметические операции, выполняемые над двоичными числами. При двоичном сложении мы находим сумму заданных двоичных чисел, а при двоичном вычитании находим разность обоих заданных чисел. Это то же самое, что и десятичная система счисления, с той лишь разницей, что здесь мы используем только две цифры 0 и 1. Таким образом, существует другой набор правил для двоичного сложения и двоичного вычитания, которые нам нужно применить, чтобы получить ответы.

Двоичное сложение с полными сумматорами

Бинарное сложение с полными сумматорами

Двоичное сложение — это простая математическая операция, используемая для сложения двух двоичных чисел. Логические правила этой операции реализованы в каждом цифровом компьютере через цифровые схемы, известные как сумматоры.

Сложение 1-битных двоичных чисел

Сложение двоичных чисел представляет собой несколько странный процесс, который поначалу может показаться слегка запутанным. Но на самом деле это очень похоже на сложение десятичных чисел, которому нас учат в рамках элементарной математики — за тем очевидным исключением, что мы работаем с двумя цифрами, а не с десятью!

Чтобы начать думать о сложении в двоичном виде, давайте рассмотрим двоичное сложение двух однобитовых значений — простейшую форму сложения, которую мы можем себе представить:

Рисунок 1: Двоичное сложение двух однобитных чисел.

В приведенной выше таблице представлены основные логические правила двоичного сложения. Числа в левой части таблицы представляют собой двоичные значения, которые мы пытаемся сложить, а числа в правой части представляют результат этого сложения. Это может иметь смысл, если не считать внезапно появившейся странной колонки переноса!

Столбец переноса обозначает результаты, в которых мы превысили количество, которое мы можем представить всего одним битом. Наличие дополнительного бита для представления этого действует как механизм для перемещения (или переноса) превышения значений в следующий столбец единиц (в двоичном формате эти столбцы единиц равны 1, 2, 4, 8… и т. д.) при вычислении сложения. Интуитивно вы можете думать об этом так же, как мы можем «переносить» десятичные значения в их следующий столбец единиц (1, 10, 1000… и т. д.) при вычислении десятичного сложения вручную.

А как насчет аппаратной реализации? Что ж, поскольку метод сложения использует базовую логику, его можно построить в виде цифровой схемы, представленной на блок-схеме ниже.

Рисунок 2. Блок-схема полусумматора

Эта схема принимает два однобитных двоичных значения в качестве входных данных (A и B), выводит результат (R) и значение переноса (поскольку перенос является выходом результата, который мы назовите это «выполнить», или сокращенно Cout). Именно такое поведение определяет «полусумматор» — механизм, позволяющий нам выполнять 1-битное двоичное сложение.

Сложение n-битных двоичных чисел

Сложение одиночных битов — несколько тривиальный пример, поэтому давайте рассмотрим нечто более сложное — сложение многобитных двоичных чисел или n-битных двоичных чисел.

Дополнительная сложность с n-битным сложением заключается в том, что бит переноса используется как механизм объединения нескольких однобитовых сложений.

Это требует, чтобы мы думали о бите переноса как о механизме ввода и вывода. Другими словами, вы можете ввести бит переноса в 1-битное сложение, которое было сгенерировано из вывода предыдущего 1-битного сложения. Мы можем свести эту логику в таблицу, как мы это сделали на рисунке 1, чтобы показать, как сложение представлено битом «переноса»:

Рисунок 3. Двоичное сложение двух 1-битных чисел с переносом.

Логическую таблицу и концепцию переноса можно понять более интуитивно, если мы вернемся к примеру на блок-диаграмме.

На рис. 4 ниже показана схема «полного сумматора». Это похоже на половинный сумматор, но включает дополнительный входной бит, позволяющий «перенос» из логической таблицы на рисунке 3.

Рисунок 4. Блок-схема полного сумматора

И, как мы увидим далее, эта схема действует как строительный блок для более сложного бинарного сложения.

n-бит Дополнения: Объединяем все вместе!

Теперь, когда мы представили двоичные 1-битные сложения как полный сумматор, мы можем начать понимать, как n-битные вычисления реализуются в виде цифровых схем. Если вы еще не догадались, полные сумматоры можно соединить вместе, соединив их выход переноса (C _из ) со следующим входом переноса полного сумматора (C _в )!

Рисунок 5. Объединение полных сумматоров в цепочку для выполнения 4-битного сложения.

На рис. 5 это показано в действии как 4-битный сумматор с A _x и B _x , представляющие 4-битные augend* и addend*, R _x , представляющие 4-битный результат, и C _в и C _out , представляющие перенос и перенос всего 4-битный сумматор.

*augend — это просто математический термин для числа, к которому прибавляется, а addend — это число, которое мы прибавляем к другому.