НОУ ИНТУИТ | Лекция | Двоичные числа и двоичная арифметика
Аннотация: Рассматривается двоичная система счисления как частный случай позиционной системы и основные правила двоичной арифметики.
Ключевые слова: вес, целое число, запись, аналогия, выражение, логический, основание, связь, восьмеричная система счисления, обратный код, дополнительный код, прямой, система счисления, сложение, вычитание
Принцип представления чисел в позиционных системах счисления
Позиционной называется система счисления, в которой вес разряда числа определяется его позицией в записи числа [1].
Вспомним нашу привычную десятичную систему счисления, в которой мы с детства производим все расчеты. Уже в начальной школе мы привыкли к терминам «единицы», «десятки», «сотни», «тысячи», «десятые», «сотые», «тысячные» и не задумываемся над тем, что они означают вес разряда, выраженный в виде числа, равного , где — целое число. Например, число 125, 46 можно представить в виде суммы:
Например, число 125, 46 можно представить в виде суммы:
сотни десятки единицы десятые доли сотые доли
Аналогично любое число в десятичной системе счисления можно представить в виде подобной суммы:
где — количество знаков в целой части числа, — количество знаков в дробной части числа, — вес -го разряда, — весовой коэффициент для -го разряда числа.
Количество возможных вариантов значения коэффициента в десятичной системе счисления равно , поскольку для записи чисел в ней используются десять знаков — арабские цифры «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9». Число является основанием системы счисления. Исторически сложилось, что десятичная система получила наибольшее распространение, хотя по этому принципу можно сделать аналогичную запись в любой другой системе счисления c любым другим основанием. В табл. 11.1 прослежива
ется аналогия между позиционными системами счисления.
Число является основанием системы счисления. Исторически сложилось, что десятичная система получила наибольшее распространение, хотя по этому принципу можно сделать аналогичную запись в любой другой системе счисления c любым другим основанием. В табл. 11.1 прослежива
ется аналогия между позиционными системами счисления.
Основание системы счисления — это число, равное количеству знаков, которые используются в этой системе для записи чисел.
Для числа в системе счисления с основанием выражение (11.1) преобразуется к виду:
| ( 11.2) |
| Название системы счисления | Основание системы счисления | Знаки, использующиеся для записи чисел |
|---|---|---|
| Двоичная | 2 | 0, 1 |
| Троичная | 3 | 0, 1, 2 |
| Четверичная | 4 | 0, 1, 2, 3 |
| … | … | … |
| Восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
| … | … | … |
| Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| … | … | … |
| Шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
| … | … | … |
intuit.ru/2010/edi»>С началом развития цифровой вычислительной техники большой интерес стала вызывать двоичная система, поскольку вычислительная машина любого поколения и любой степени сложности — это совокупность логических схем. Работа элементов этих схем основана на ключевом режиме работы транзистора, в котором он может быть только в двух состояниях, принимаемых за логический 0 и логическую 1.
Запись двоичного числа, как будет показано ниже, как правило, довольно длинна и громоздка, поэтому для более короткой записи двоичных чисел применяются восьмеричные и шестнадцатеричные числа. Выбор именно этих систем обусловлен тем, что их основания равны целой степени числа 2. Основание восьмеричной системы , а основание шеснадцатиричной системы — это . Для записи шестнадцатеричных чисел арабских цифр не хватает, поэтому используются первые шесть заглавных букв латинского алфавита.
Итак, далее мы подробно рассмотрим именно эти позиционные системы — двоичную, восьмеричную, шестнадцатеричную и их связь с привычной нам десятичной системой счисления.
Приведем примеры записи чисел в указанных системах и найдем их десятичные эквиваленты по формуле (11.2).
Для двоичного числа:
Здесь и далее будем придерживаться следующего правила: числа в двоичной, восьмеричной и шестнадцатеричной системах записываются с указанием основания, десятичные — без этой записи.
Для восьмеричного числа:
Для шестнадцатеричного числа:
Округление относится к дробной части числа, целая часть переводится точно. Особенностью перевода из шестнадцатеричного кода в десятичный код является то, что в качестве коэффициента используется десятичный эквивалент шестнадцатеричного знака в соответствии с таблицей 11.2. Для нашего примера вместо знака » » в расчетную формулу (11.2) подставляется десятичное число .
Из рассмотренных примеров видно, что общая формула (11.2) может использоваться для перевода числа из системы счисления с любым основанием в десятичную.
Перевод чисел из одной системы счисления в другую
Перевод из десятичной системы в любую другую. Перевод целых чисел
Целое десятичное число нужно поделить на основание новой системы счисления. Остаток от этого деления является самым младшим разрядом в новой записи числа. Результат деления вновь делится на основание. Остаток от этого деления будет следующим разрядом в новой записи числа, результат деления вновь делится на основание и т.д. до тех пор, пока в результате деления получится число, меньшее по величине, чем основание новой системы. Остаток этого последнего деления будет предпоследним разрядом в новой записи числа, а результат этого последнего деления — самым старшим разрядом в новой записи числа.
intuit.ru/2010/edi»>Проверка перевода осуществляется по формуле (11.2), так, как это показано ниже на примерах.
Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (П11.2).
| a) | б) | в) |
Проверка:
- в восьмеричном коде ;
- в шестнадцатеричном коде — .
В рассмотренном примере при переводе вместо коэффициента используется его десятичный эквивалент в соответствии с таблицей 11. 2.
2.
Перевод из двоичной системы в шестнадцатеричную (восьмеричную)
Как уже было сказано выше, шестнадцатеричный и восьмеричный коды используются для более компактной и удобной записи двоичных чисел. Так, программирование в машинных кодах осуществляется в большинстве случаев в шестнадцатеричном коде. Правила перевода для шестнадцатеричной и восьмеричной системы структурно одинаковы, отличия для восьмеричной системы отображаются в скобках.
Двоичная запись числа делится на группы по четыре ( три ) двоичных знака влево и вправо от запятой, отделяющей целые и дробные части Неполные крайние группы (если они есть) дополняются нулями до четырех ( трех ) знаков. Каждая группа заменяется одним шестнадцатеричным ( восьмеричным ) знаком в соответствии с кодом группы (табл. 11.2).| Двоичная группа | Шестнадцатеричный знак | Десятичный эквивалент | Двоичная группа | Восьмеричный знак |
|---|---|---|---|---|
| 0 | 0 | 000 | 0 | |
| 0001 | 1 | 1 | 001 | 1 |
| 0010 | 2 | 2 | 010 | 2 |
| 0011 | 3 | 3 | 011 | 3 |
| 0100 | 4 | 4 | 100 | 4 |
| 0101 | 5 | 5 | 101 | 5 |
| 0110 | 6 | 6 | 110 | 6 |
| 0111 | 7 | 7 | 111 | 7 |
| 1000 | 8 | 8 | ||
| 1001 | 9 | 9 | ||
| 1010 | A | 10 | ||
| 1011 | B | 11 | ||
| 1100 | C | 12 | ||
| 1101 | D | 13 | ||
| 1110 | E | 14 | ||
| 1111 | F | 15 |
intuit.ru/2010/edi»>Примеры:
- перевод в шестнадцатеричную систему:
- перевод в восьмеричную систему:
Перевод из шестнадцатеричной (восьмеричной) системы в двоичную
Обычно программы в машинных кодах записаны в шестнадцатеричной системе счисления, реже — в восьмеричной. При необходимости отдельные числа такой программы записываются в двоичном коде, например, при рассмотрении форматов регистров, кодов операции команд и т.п. В этом случае нужен обратный перевод из шестнадцатеричной (восьмеричной) системы счисления в двоичную по следующему правилу.
Каждая цифра (без всяких сокращений!) шестнадцатеричного ( восьмеричного ) числа заменяется одной двоичной группой из четырех ( трех ) двоичных знаков (табл. 11.2).
Примеры:
- intuit.ru/2010/edi»>для шестнадцатеричного числа: ;
- для восьмеричного числа: .
Как показано в примерах, крайние нули слева и справа при желании можно не писать, но такое сокращение делается уже после перевода в двоичную систему.
Lab_rab_2_Dvoichn_arifmetika
Лабораторная работа №122. Двоичная арифметика.
Цель работы. Научиться выполнять арифметические операции (сложение, вычитание, умножение и деления) с двоичными числами.
Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения.
Таблица двоичного сложения | Таблица двоичного вычитания | Таблица двоичного умножения |
0+0=0 0+1=1 1+0=1 1+1=10 | 0–0=0 1–0=1 1–1=0 10–1=1 | 0 0=0 0 1=0 1 0=0 1 1=1 |
Задание
1. Выполните
сложение чисел в двоичной системе
счисления 100100111,0012+100111010,1012
Выполните
сложение чисел в двоичной системе
счисления 100100111,0012+100111010,1012
Методические указания.
При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и цифры, переносимой из соседнего младшего разряда, если она имеется При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий разряд.
Примеры.
1) Выполнить сложение двоичных чисел X=1101, Y=111.
В приведенном
примере в младшем нулевом разряде две
единицы: 1+1=10 дают нуль в данном разряде
и единицу переноса в следующий. В первом
разряде: 0+1+1=10 (крайняя единица перенесена
из нулевого разряда) дают 0 и единицу
переноса в следующий. Во втором разряде
1+1+1=11(крайняя единицы перенесена из
первого разряда) дают 1 и единицу переноса
в следующий. В старшем третьем разряде
1 и единица переноса из предыдущего
разряда дают 1+1=10.
В старшем третьем разряде
1 и единица переноса из предыдущего
разряда дают 1+1=10.
Результат: 1101+111=10100.
2) Сложить три двоичных числа X=1101, Y=101, Z=111.
Результат: 1101+101+111=11001.
Задание 2. Выполните вычитание чисел в двоичной системе счисления: 1100110110,00112– 11111110,012.
Методические указания.
При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум единицам данного разряда, так как 10=1+1.
Примеры.
1) Заданы двоичные числа X=10010 и Y=101. Вычислить X–Y.
Результат: 100102 – 1012 = 11012.
Замечание. Число
100…002 можно представить в виде суммы
Число
100…002 можно представить в виде суммы
Данное разложение на слагаемые объясняет правило вычитания в столбик. Если вы занимаете 1 из ближайшего старшего разряда, тогда над всеми следующими за единицей нулями следует дописывать 1, а над крайним нулем, для которого произведен заем, 1+1 или 10.
2) Выполнить вычитание: 1100000011,0112 – 101010111,12
Результат: 1100000011,0112 – 101010111,12 = 110101011,1112.
Задание 3. Выполните умножение чисел 110012 и 10111002 в двоичной системе счисления.
Методические указания.
Правила умножения двоичных чисел такие же, как и для умножения десятичных чисел в столбик, с использованием двоичного умножения и сложения.
Пример. Найти произведение 10012 1012
1001
101
1001
+1001
101101
Результат: 10012 1012=1011012.
Задание 4. Выполните деление чисел 1111012 и 11102 в двоичной системе счисления.
Методические указания.
Деление двоичных чисел производится так же, как и десятичных чисел, при этом используется двоичное умножение и вычитание.
Пример. Найти частное от деления 1100,0112: 10,012
_110001,1 | 1001 |
1001 | 101,1 |
_1101 | |
1001 | |
_1001 1001 | |
0 |
Результат:
1100,0112:10,012=101,12.
Задания для самостоятельной работы
Вариант | Заданы двоичные числа X и Y. Вычислить X+Y и X–Y , если: | Заданы двоичные числа X и Y. Вычислить X*Y и X/Y , если: |
Х=100101,1012 Y=11101,112 | X=100101,0112 Y=110,12 | |
Х=101101,1012 Y=1101,1112 | X=110000,112 Y=2 | |
Х=110101,1012 Y=11101,112 | X=111001,00012 Y=1010,0112 | |
Х=1101111,1012 Y=10101,112 | X=111011,00012 Y=101,012 | |
Х=1000111,112 Y=11101,1112 | X=111100,0112 Y=101,112 | |
Х=1110001,1012 Y=10011,112 | X=110110,1012 Y=100,112 | |
Х=1010001,1012 Y=10011,112 | X=100110,00012 Y=111,012 | |
Х=1000011,1012 Y=10011,0112 | X=101011,1112 Y=110,112 | |
Х=1101001, 1012 Y=10111,112 | X=1010110,1012 Y=1000,012 | |
Х=1010001,1012 Y=1111,0112 | X=111111,012 Y=101,12 | |
Х=101001, 1012 Y=10111,1112 | X=1011010,1012, Y=111,012 | |
Х=1010111, 1012 Y=11100,1112 | X=1000101,00112, Y=110,112 | |
Х=110101,1012 Y=1111,112 | X=100101,0112, Y=110,12 | |
Х=101111,1012 Y=1101,1112 | X=100000,11012, Y=101,012 | |
Х=110101,0112 Y=10011,112 | Х=110111,112 Y=101,112 | |
Х=1001011,112 Y=10101,1012 | Х=100101,112 Y=111,012 | |
Х=100011,0112 Y=10011,1112 | Х=100011,012 Y=1011,12 | |
Х=1010001,1012 Y=1011,0112 | Х=100001,1012 Y=1001,012 | |
Х=110001,1012 Y=10111,112 | Х=111001,1012 Y=1101,112 | |
Х=1000111,0112 Y=11111,112 | Х=1010111,0112 Y=111,112 | |
Х=111001, 1012 Y=1110,1112 | Х=11100001, 1012 Y=110,112 | |
Х=100001,1012 Y=1111,1112 | Х=1000001,1012 Y=1111,012 | |
Х=1011101, 1012 Y=10111,0112 | Х=1010101, 1012 Y=100,0112 | |
Х=1111000, 1012 Y=101111,112 | Х=1111001, 0112 Y=1011,112 | |
Х=1100000, 1012 Y=1111,1112 | Х=1100011, 012 Y=11,1112 |
Контрольные
вопросы.
1. Каковы правила сложения двоичных чисел?
2. Каковы правила вычитания двоичных чисел?
3. Каковы правила умножения двоичных чисел?
4. Каковы правила вычитания двоичных чисел?
Как добавить двоичные номера с и без перегруппировки
Введение в двоичные номера
числа, также известные как системы счисления с основанием 2, представлены двумя цифрами, а именно 0 и 1. Числа в двоичной системе счисления выглядят следующим образом: 1100011010. Каждая цифра в двоичной системе счисления известна как «бит».
Все цифровые устройства используют в своих электронных схемах двоичную систему счисления. Вход 0 указывает на состояние OFF, а вход 1 указывает на состояние On. Из-за этих реализаций двоичные системы счисления наиболее широко используются в современных компьютерных технологиях. Прочтите статью ниже, чтобы узнать, как выполнить двоичное сложение с перегруппировкой и без нее.
Прочтите статью ниже, чтобы узнать, как выполнить двоичное сложение с перегруппировкой и без нее.
Они могут включать сложение, умножение, деление и вычитание. Каждая бинарная операция представлена отдельным символом. Помимо использования в математике, эти операции также играют важную роль в компьютерных технологиях. Они помогают нам создавать операционные системы и схемы для различных электрических устройств, таких как компьютеры, ноутбуки, смартфоны и т. д.
Основные двоичные арифметические операции
В этой статье мы подробно обсудим двоичное сложение вместе с примерами двоичного сложения, чтобы учащиеся могли выполнять вычисления быстрее.
Что такое двоичное сложение?
Двоичное сложение — это сумма двух или более двоичных чисел. Двоичное сложение очень похоже на десятичное сложение, даже немного проще. При десятичном сложении, если сумма двух чисел дает две цифры, мы переносим цифру в разряде десятков в следующий столбец слева. Точно так же в двоичном сложении, если сумма двух чисел больше 1, мы переносим цифру 2 в следующий столбец слева. Например, 1+ 1 = 10₂. В этом случае мы записываем цифру 1 (0) и переносим цифру 2, т. е. 1 результата, в следующий столбец слева. По этой причине бит, переносимый в следующий столбец, называется битом переноса.
Точно так же в двоичном сложении, если сумма двух чисел больше 1, мы переносим цифру 2 в следующий столбец слева. Например, 1+ 1 = 10₂. В этом случае мы записываем цифру 1 (0) и переносим цифру 2, т. е. 1 результата, в следующий столбец слева. По этой причине бит, переносимый в следующий столбец, называется битом переноса.
Правила сложения двоичных чисел
Сложение двух двоичных чисел так же просто, как и в десятичной системе счисления. Просто мы должны принять во внимание некоторые правила при сложении двух двоичных чисел. Есть четыре-пять правил, связанных с двоичным сложением. Правила бинарного сложения следующие.
Поскольку двоичные числа включают только две цифры, то есть 0 и 1, эти четыре правила являются всеми возможными условиями для сложения двоичных чисел.
Вот пошаговая процедура сложения двух двоичных чисел с перегруппировкой и без перегруппировки.
Двоичное сложение без перегруппировки
Когда сумма двух или более двоичных цифр дает 0 или 1, то в таких случаях перегруппировка не требуется. Давайте добавим двоичные числа \[101_{2}\] и \[10_{2}\], чтобы лучше понять это.
Давайте добавим двоичные числа \[101_{2}\] и \[10_{2}\], чтобы лучше понять это.
Шаг 1. Запишите все цифры обоих двоичных чисел в отдельный столбец в соответствии с их разрядами, как показано ниже. крайний правый столбец, добавьте 1 и 0. Следуйте правилам двоичного сложения, согласно которым 1 + 0 = 1.
1 0 1
+ 1 0
………..
1
Шаг 3. Перейдите к следующему столбцу слева, добавьте 0 и 1. Следуйте правилам двоичного сложения, которые говорят: 0 + 1 = 1.
1 0 1
+ 1 0
………..
1 1
………..
Шаг 4: Снова переходим к следующему столбцу, видим слева осталась только одна цифра, то есть 1. Следовательно, мы можем применить правило 1 + 0 = 1.
1 0 1
+ 1 0
………..
1 1 1
………. .
.
Следовательно, \[101_{2} + 10_{2} = 111_{2}\].
Двоичное сложение с перегруппировкой
Когда сумма двух или более двоичных цифр больше 0 или 1, то в таких случаях необходима перегруппировка. Давайте добавим двоичные числа 1001₂ и 111₂, чтобы лучше понять это.
Шаг 1: Запишите все цифры обоих двоичных чисел в отдельный столбец в соответствии с их разрядностью, как показано ниже
1 0 0 1
+ 1 1 1
………….
Шаг 2. Начиная с крайнего правого столбца, добавьте 1 и 1. Следуйте правилам двоичного сложения, согласно которым 1 + 1 = 10. Это эквивалентно 2₁₀. Следовательно, мы напишем 0 внизу, а два возьмем 1 в качестве переноса на следующее значение разряда.
1
1 0 0 1
+ 1 1 1
………….
0
Шаг 3. Перейдите к следующему столбцу слева. Следуйте правилам двоичного сложения, согласно которым 1 + 0 + 1 = 10. Это снова эквивалентно 2₁₀. Следовательно, мы напишем 0 внизу, а два возьмем 1 в качестве переноса на следующее значение разряда.
Следуйте правилам двоичного сложения, согласно которым 1 + 0 + 1 = 10. Это снова эквивалентно 2₁₀. Следовательно, мы напишем 0 внизу, а два возьмем 1 в качестве переноса на следующее значение разряда.
1 1
1 0 0 1
+ 1 1 1
………….
0 0
Шаг 4. Снова перейдите к следующему столбцу слева. Следуйте правилам двоичного сложения, согласно которым 1 + 1 + 0 = 10. Это снова эквивалентно 2₁₀.
1 1 1
1 0 0 1
+ 1 1 1
………….
0 0 0
Шаг 5. Снова перейдите к следующему столбцу слева. Следуйте правилам двоичного сложения, согласно которым 1 + 1 + 0 = 10. Это снова эквивалентно 2₁₀. Поскольку это последний оставшийся столбец, мы не будем брать 1 в качестве переноса, вместо этого мы напишем 10 в качестве результата внизу.
1 1 1
1 0 0 1
+ 1 1 1
…………….
1 0 0 0 0
…………….
Следовательно, \[1001_{2} + 111_{2} = 10000_{2}\]
Примеры двоичного сложения с решениями
Пример 1:
Добавить \[1010_{2} и 1111_{2}\]
Решение:
1 1
1 0 1 0
+ 1 1 1 1
——————————————
1 1 0 0 1
—————————
Пример 2:
Добавить: \[10011_{2} \, и \, 110001_{ 2}\]
Решение:
1 1 1
1 0 0 1 1
+ 1 1 0 0 0 1
— 90 ————
1 0 0 0 1 0 0
—————————- —
Практические задачи
1. Сложите двоичные числа — 11001+10111
Ответ: 0110000
2. Какова сумма 1111+0101?
Какова сумма 1111+0101?
Ответ: 010100
Резюме
Двоичное сложение означает сложение более одного двоичного числа. Это то же самое, что и десятичная система, и охватывает двоичные числа 0 и 1. Для сложных и быстрых вычислений мы можем использовать преобразователи двоичного сложения. Двоичные числа и их операции используются для различных целей, например, для создания схем электрических устройств. Кроме того, эти операции широко используются в компьютерных технологиях, где 0 указывает на выключенное состояние схемы, а 1 указывает на ее включенное состояние.
Сложение и вычитание двоичных чисел
Подготовьте ответы на приведенные ниже вопросы и заполните клеточки. Нажать на кнопку, чтобы узнать, правильно ли вы ответили. Если ты прав то появится, и вы должны перейти к следующему вопросу. Если появляется, то ваш ответ неверен. Нажмите на чтобы очистить свой первоначальный ответ и попробовать еще раз. Если вы не можете найти правильный ответ, нажмите на чтобы увидеть ответ.
Если вы не можете найти правильный ответ, нажмите на чтобы увидеть ответ.
Вычислить двоичные числа:
| (a) | 11 + 1 | |
| (b) | 11 + 11 | |
| (c) | 111 + 11 | |
| (d) | 111 + 10 | |
| (д) | 1110 + 111 | |
| (е) | 12 3 90 11090 +0213 | |
| (g) | 1111 + 10101 | |
| (h) | 1100 + 11001 | |
| (i) | 1011 + 1101 | |
| (j) | 1110 + 10111 | |
| (k) | 1110 + 1111 | |
| (l) | 11111 + 11101 |
Вычислить двоичные числа:
| (a) | 11 – 10 | |
| (b) | 110 – 10 | |
| (c) | 1111 – 110 | |
| (d) | 100 – 10 | |
| (e) | 100 – 11 | |
| (f) | 1000 – 11 | |
| (g) | 1101 – 110 | |
| (h) | 11011 – 110 | |
| (i) | 1111 – 111 | |
| (j) | 110101 – 1010 | |
| (k) | 11011 – 111 | |
| (l) | 11110 – 111 |
Вычислить двоичные числа:
| (a) | 11 + 11 | |
| (b) | 111 + 111 | |
| (c) | 1111 + 1111 | |
| (d) | 11111 + 11111 |
| Каким будет следующее число, которое будет соответствовать этому шаблону? |
Вычислить двоичные числа:
| (a) | 10 + 10 | |
| (b) | 100 + 100 | |
| (c) | 1000 + 1000 | |
| (d) | 10000 + 10000 |
| Какое следующее число продолжит ваш двоичный код? |
Решите следующие уравнения, где все числа, включая x , являются двоичными:
| (a) | x + 11 = 1101 | x = | |||||||||||||||||||||||||||||||||||||||||||
| (b) | x – 10 = 101 | x = | |||||||||||||||||||||||||||||||||||||||||||
| (в) | х – 1101 = 11011 | x = | |||||||||||||||||||||||||||||||||||||||||||
| (d) | x + 1110 = 10001 | x = | |||||||||||||||||||||||||||||||||||||||||||
| (e) | x + 111 = 11110 | х = | |||||||||||||||||||||||||||||||||||||||||||
| (е) | х – 1001 = 11101 | х = | 172188 Вопрос 6Вычислить двоичные числа:
Четырехзначное двоичное число имеет 2 нуля и 2 единицы. 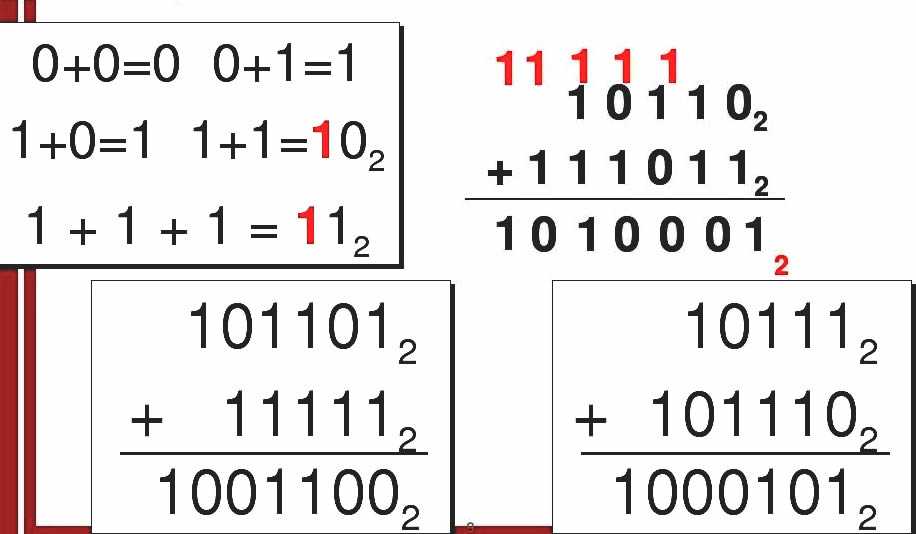
Двоичное число состоит из 8 цифр и должно быть преобразовано в основание 10.
Вот 3 двоичных числа:
|
 1.
Параметры позиционных систем счисления
1.
Параметры позиционных систем счисления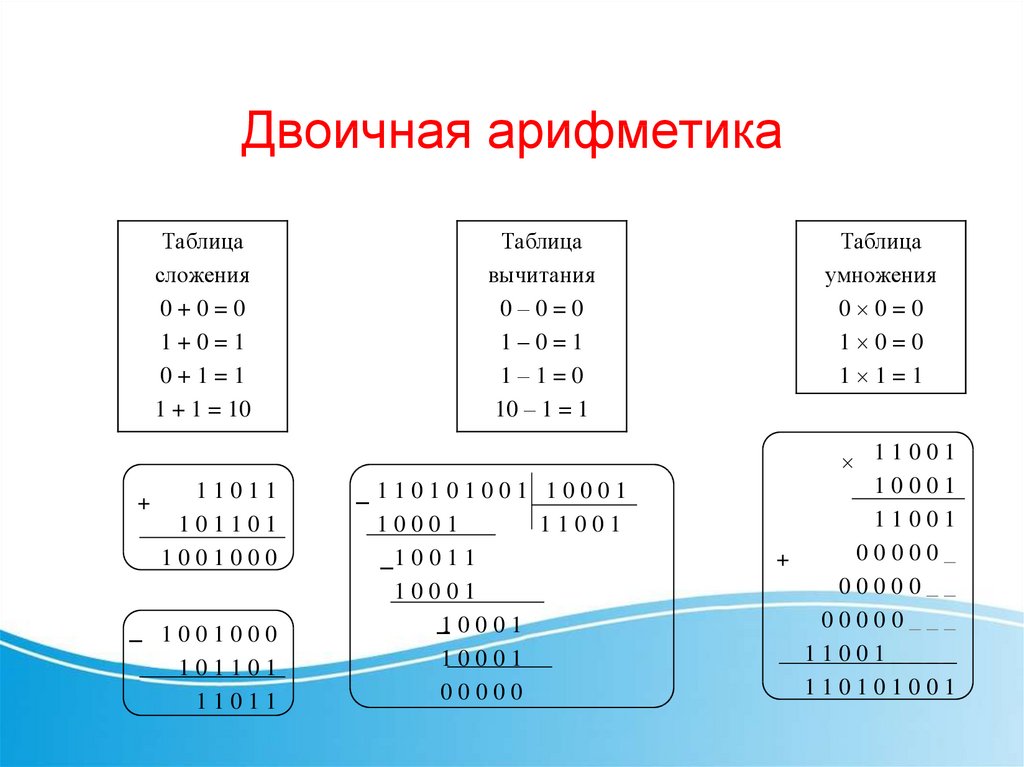 2.
Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков
2.
Соответствие двоичных групп, шестнадцатеричных и восьмеричных знаков