Сколько цифр в восьмеричной системе счисления: Сколько цифр в восьмеричной системе?

Содержание

Десятичная система счисления

Цифры и числа

Система счисления — это способ записи чисел при помощи письменных знаков. Системы счисления бывают позиционные, непозиционные и смешанные.

Позиционные системы счисления

Цифры и основание системы счисления

В позиционных системах счисления для записи чисел используются числовые знаки, они же — цифры.

Всем привычная десятичная система счисления — позиционная. Двоичная, восьмеричная, шестнадцатеричная системы счисления — это тоже позиционные системы счисления.

Позиционные системы счисления различаются между собой количеством используемых в них цифр. Например, в десятичной системе счисления используется десять цифр от 0 до 9. Собственно, система счисления называется десятичной потому, что в ней используется десять цифр. В двоичной — как следует из названия — используется только две цифры — это 0 и 1. В восьмеричной — восемь цифр от 0 до 7.

Количество используемых в системе счисления цифр называется основанием системы счисления.

Если основание системы счисления больше 10, то обычно используют буквы латинского алфавита, начиная с A. Так, в шестнадцатеричной системе счисления для записи чисел используются десятичные цифры от 0 до 9 (10 символов) и буквы от А до F (плюс ещё 6 недостающих символов) — всего шестнадцать разных цифр. Когда буквы используются при записи числа, то они тоже называются цифрами — например, цифра “A”.

Обычно из контекста понятно, в какой системе счисления записано число. Например, если Вы читаете новости на каком-нибудь сайте, и там написано, что «учёные установили, что длина экватора Земли равна примерно 40075.7 км», то Вам врядли покажется, что это число в восьмеричной или в шестнадцатеричной системе счисления. Обычно все числа записываются в десятичной системе счисления — и в данном случае по умолчанию считается, что число тоже записано в десятичной системе счисления.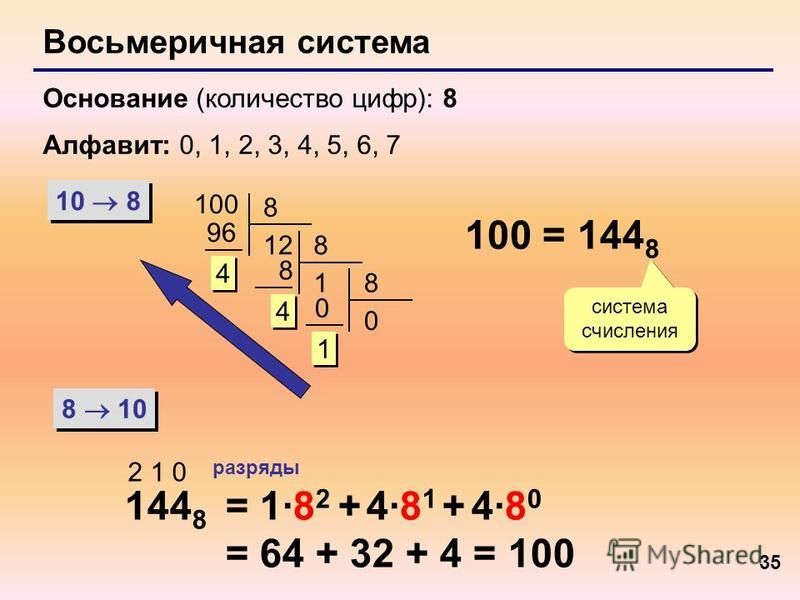

Но в некоторых случаях, чаще всего, когда используются числа в разных системах счисления, важно знать, в какой системе счисления записано это число. Чтобы отличать основания систем счисления, это основание записывается как нижний индекс после числа. Например “40075.7₁₀” — означает явно, что это число записано в десятичной системе счисления. Если бы было записано так: “40075.7₈”, то это число следовало бы интерпретировать как число в восьмеричной системе счисления.

Одна и та же цифра в позиционной системе счисления имеет разное значение в зависимости от того, где эта цифра находится в числе.

Например, число 175.3₁₀ в десятичной системе счисления содержит в себе четыре цифры — 1, 7, 5 и 3. В этом числе 3 — это десятые доли, 5 — это количество единиц, 7 — это количество десятков, а 1 — это количество сотен. Если перед единицей дописать ещё цифру, то это будут уже тысячи.

Значение, которое добавляет цифра в десятичной системе счисления во всё число, определяется по формуле: 10^{позиция}. Позиции нумеруются начиная с нуля, причём цифра, стоящая непосредственно перед десятичной точкой, всегда считается нулевой позицией. Влево номер позиции увеличивается, а вправо — уменьшается.

Перемножив и сложив, мы получим, собственно само число: 1*100+7*10+5+3/10=175.3₁₀.

Эта формула справедлива для абсолютно любых позиционных систем счисления, только в каждой системе счисления вместо 10 подставляется своё основание.

Восьмеричная система счисления

Например, в восьмеричной системе счисления число 327.4₈ — означает 3 64-ки, 2 восьмёрки, 7 единиц и 4 восьмых долей (то есть, в десятичной это было бы число 64*3+2*8+7+4/8=219.5

10):

Двоичная система счисления

Пример для числа 101.11₂ в двоичной системе счисления:

Число 101.11₂ в двоичной системе счисления означает одну четвёрку, одну единицу, одну половинку и одну четвертинку. Если сложить, получится всего 5.75₁₀.

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления содержит 16 цифр — это цифры от 0 до 9 (соответствуют десятичным цифрам) и буквы от A до F, соответствие которых десятичным эквивалентам можно запомнить, а можно каждый раз в уме подсчитывать (10₁₀ — это А₁₆, 11₁₀ — это B₁₆, 12₁₀ — это C₁₆, 13₁₀ — это D

16, 14₁₀ — это E₁₆, а 15₁₀ — это F₁₆).

Все остальные правила, по которым представляются числа в разных позиционных системах счисления — абсолютно одинаковые. Меняется только количество используемых цифр, всё остальное — точно так же, как во всем привычной десятичной системе счисления.

Поэтому, Вы можете считать, что Вы разобрались с системами счисления, если Вы разобрались не только в каких-то определённых системах счисления (например, только в двоичной, восьмеричной, десятичной и шестнадцатеричной), а если Вы разобрались в любой системе счисления. В том числе, в троичной, в девятиричной, в двенадцатеричной, в двадцатисемиричной — и вообще в любой.

И поэтому, если в данный момент Вам ещё не понятно что-то с шестнадцатеричной системой счисления, то я рекомендовал бы Вам ещё раз прочитать и поглубже разобраться с тем, что написано выше на этой странице.

Непозиционные системы счисления — это такой способ записи чисел, в которых значение знака зависит не от позиции, а от каких-то других правил. Пример непозиционной системы счисления — всем известная римская система счисления. Для записи чисел в римской системе счисления используются римские цифры.

Хотя, строго говоря, римская система счисления не является полностью непозиционной. Так, меньшая цифра, записанная перед большей, вычитается из неё, а записанная после большей — прибавляется (то есть, значение цифры всё-таки зависит от позиции). Например, IV_{римская}=4₁₀, в то время как VI_{римская}=6₁₀.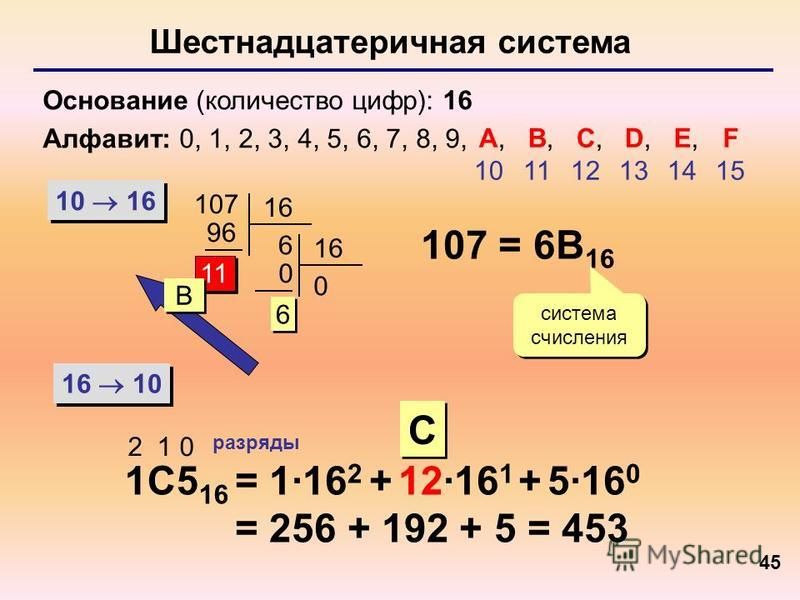

Числа, не зависимо от системы счисления, всегда означают количество чего-нибудь. Собственно, записать число (в любой системе счисления) — это всего лишь способ записать это количество. Поэтому, можно составить таблицу соответствия между числами в разных системах счисления:

Для практического применения имеет смысл запомнить первые 16 строк этой таблицы (для чисел от 0 до 15). Но если разобраться в том, как эта таблица устроена, можно не запоминать, а научиться легко вычислять соответствие в уме.

Десятичная		Двоичная	Восьмеричная	Шестнадцатеричная	Римская
0		0	0	0	отсутствует
1		1	1	1	I
2		10	2	2	II
3		11	3	3	III
4		100	4	4	IV
5		101	5	5	V
6		110	6	6	VI
7		111	7	7	VII
8		1000	10	8	VIII
9		1001	11	9	IX
10		1010	12	A	X
11		1011	13	B	XI
12		1100	14	C	XII
13		1101	15	D	XIII
14		1110	16	E	XIV
15		1111	17	F	XV
16		10000	20	10	XVI
17		10001	21	11	XVII
18		10010	22	12	XVIII
19		10011	23	13	XIX
20		10100	24	14	XX
И так далее
	Перевод чисел из десятичной системы счисления в любую другую

При переводе чисел из десятичной системы счисления в любую другую, всегда отдельно (по разным правилам) переводится целая и дробная части.

§12. Арифметические операции в позиционных системах счисления

Планирование уроков на учебный год (ФГОС)

Содержание урока:

12.1. — 12.2. Сложение и вычитание чисел в системе счисления с основанием q

12.3. Умножение чисел в системе счисления с основанием q

12.4. Деление чисел в системе счисления с основанием q

12.5. Двоичная арифметика

САМОЕ ГЛАВНОЕ. Вопросы и задания

Материалы к уроку

		12.5. Двоичная арифметика
	12. 4. Деление чисел в системе счисления с основанием q		САМОЕ ГЛАВНОЕ Вопросы и задания

12.5. Двоичная арифметика

Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения, вычитания и умножения:

Рассмотрим несколько простых, но очень важных примеров на сложение и вычитание в двоичной системе счисления.

Пример 1. Найдём количество единиц в двоичной записи числа, являющегося результатом десятичного выражения 2⁴⁰⁰⁰ + 4²⁰¹⁶ + 2²⁰¹⁸ — 8⁶⁰⁰ + 6

Представим все операнды исходного выражения в виде степеней двойки:

4²⁰¹⁶ = (2 • 2)²⁰¹⁶ = (2²)²⁰¹⁶ = 2^2•2016 = 2⁴⁰³²,

8⁶⁰⁰ = (2³)⁶⁰⁰ = 2¹⁸⁰⁰,

6 = 4 + 2 = 2² + 2¹.

Исходное выражение примет вид:

2⁴⁰⁰⁰ + 4²⁰¹⁶ + 2²⁰¹⁸ — 8⁶⁰⁰ + 6 = 2⁴⁰⁰⁰ + 2⁴⁰³² + 2²⁰¹⁸ — 2¹⁸⁰⁰ + 2² + 2¹

Перепишем выражение в порядке убывания степеней:

2⁴⁰³² + 2⁴⁰⁰⁰ + 2²⁰¹⁸ — 2¹⁸⁰⁰ + 2² + 2¹

Для работы с десятичными числами вида 2ⁿ полезно иметь в виду следующие закономерности в их двоичной записи:

2¹ = 10 = 1 + 1;
2² = 100 = 11 + 1;
2³ = 1000 = 111 + 1;
2⁴ = 10000 = 1111 + 1 и т. д.

В общем виде:

Для натуральных n и m таких, что n > m, получаем:

Эти соотношения позволят нам подсчитать количество единиц в нашем выражении, не прибегая к его вычислению.

Действительно, двоичные представления чисел 2⁴⁰³² и 2⁴⁰⁰⁰ внесут в двоичное представление суммы по одной единице. Разность 2²⁰¹⁸ — 2¹⁸⁰⁰ в двоичной записи представляет собой цепочку из 218 единиц и следующих за ними 1800 нулей. Слагаемые 2² и 2¹ дают ещё 2 единицы.

Итого: 1 + 1 + 218 + 1 + 1 = 222.

Пример 2. Найдём количество цифр в восьмеричной записи числа, являющегося результатом десятичного выражения 2²⁹⁹ + 2²⁹⁸ + 2²⁹⁷ + 2²⁹⁶.

Двоичное представление исходного числа имеет вид:

Всего в этой записи 300 двоичных символов. При переводе двоичного числа в восьмеричную систему счисления каждая триада исходного числа заменяется восьмеричной цифрой. Следовательно, восьмеричное представление исходного числа состоит из 100 цифр.

Cкачать материалы урока

Восьмеричная система счисления (определение, преобразование и примеры)

Система счисления с основанием (или основанием) восемь известна как восьмеричная система счисления .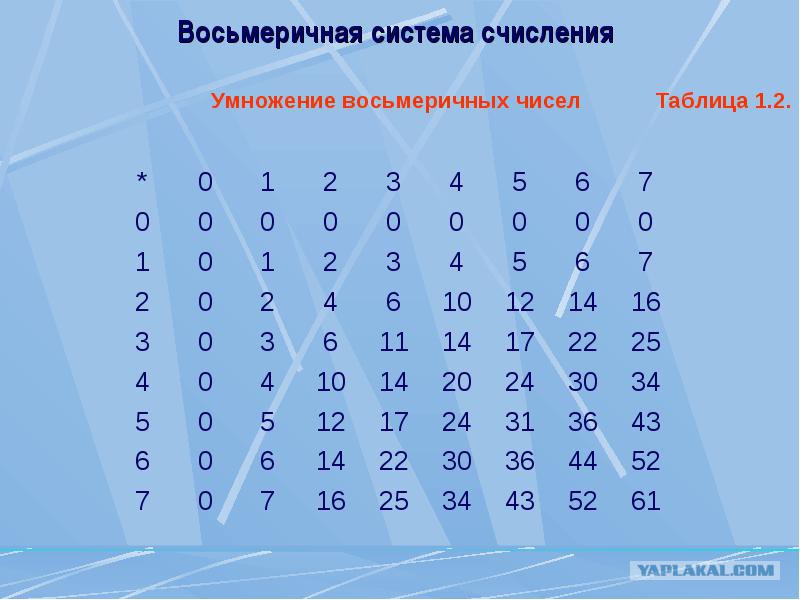 Хотя мы можем использовать любые восемь цифр, принято использовать первые восемь десятичных цифр: 0, 1, 2, 3, 4, 5, 6, 7. В восьмеричном числовом коде нет ни 8, ни 9. Эти цифры от 0 до 7 имеют точно такой же физический смысл, как и в десятичной системе счисления. Позиции цифр в восьмеричной системе счисления имеют следующие веса.

В цифровых системах необходимо вводить двоичные числа и отображать определенные результаты или сигналы состояния. Крайне неудобно обрабатывать длинные строки двоичных чисел. Это также может вызвать ошибки. Поэтому восьмеричные числа используются для ввода двоичных данных и отображения определенной информации. Восьмеричная система счисления требует одной трети длины по сравнению с двоичными числами. Таким образом, с точки зрения пользователя было бы сравнительно намного проще обрабатывать входные и выходные данные цифрового компьютера в восьмеричной форме. Кроме того, распечатки более компактны и легко читаются. Преобразование из двоичного в восьмеричное и из восьмеричного в двоичное также выполняется быстро и просто. Фактически, восьмеричная система счисления используется для представления двоичных чисел из-за простоты преобразования и компактности. Поскольку цифровые схемы могут обрабатывать только нули и единицы, восьмеричные числа должны быть преобразованы в двоичную форму с использованием специальных схем, известных как 9.0003 восьмерично-двоичные преобразователи перед обработкой цифровыми схемами.

Преобразование восьмеричной системы счисления в десятичную:

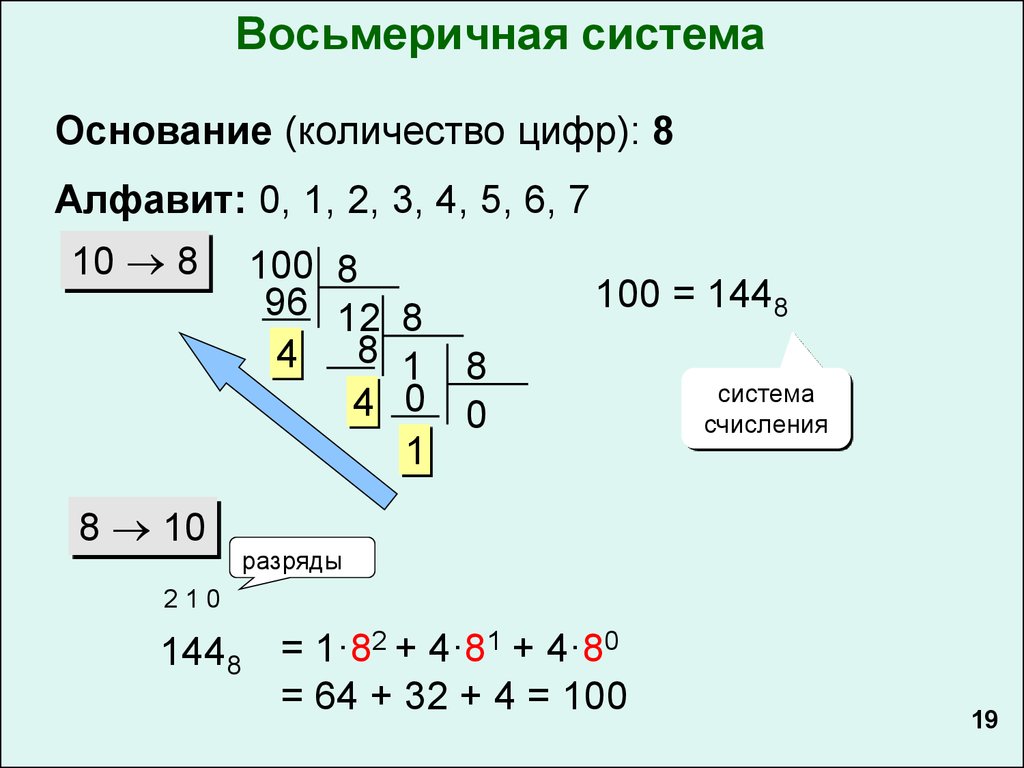
Восьмеричную систему счисления можно легко преобразовать в десятичную, умножив каждую восьмеричную цифру на ее позиционный вес.

Например,

314 ₈ = 3 x (8 ²) + 1 (8 ¹) + 4 (8 ⁰) = 192 + 8 + 4 = 204 ₁₀

Другое. пример

Пример 44.30: Преобразовать восьмеричное число 756 в десятичное.

Решение:

Пример 44,31: Преобразование следующего числа (36,125) ₈ = () ₁₀

Решение:

Декримный дримал.
Десятичное целое число можно преобразовать в восьмеричное с помощью того же метода многократного деления, называемого методом двойного мазка , который мы использовали при преобразовании десятичного числа в двоичное, но с коэффициентом деления 8, а не 2. Следующие примеры иллюстрируют процедуру.
Пример 44,32: Преобразование следующего: (540) ₁₀ = () ₈
Решение:

Пример 44.33: (0,45)11122 2 = () (0,45)1111221211121 21002 = . 8 .

Решение:

Преобразование восьмеричного в двоичное:
двоичный код может быть выполнен путем преобразования каждой восьмеричной цифры в ее 3-битный двоичный эквивалент. Восемь возможных цифр преобразуются, как показано ниже в таблице 44.2.
Используя эти преобразования, любая восьмеричная система счисления может быть преобразована в двоичную путем индивидуального преобразования каждой цифры.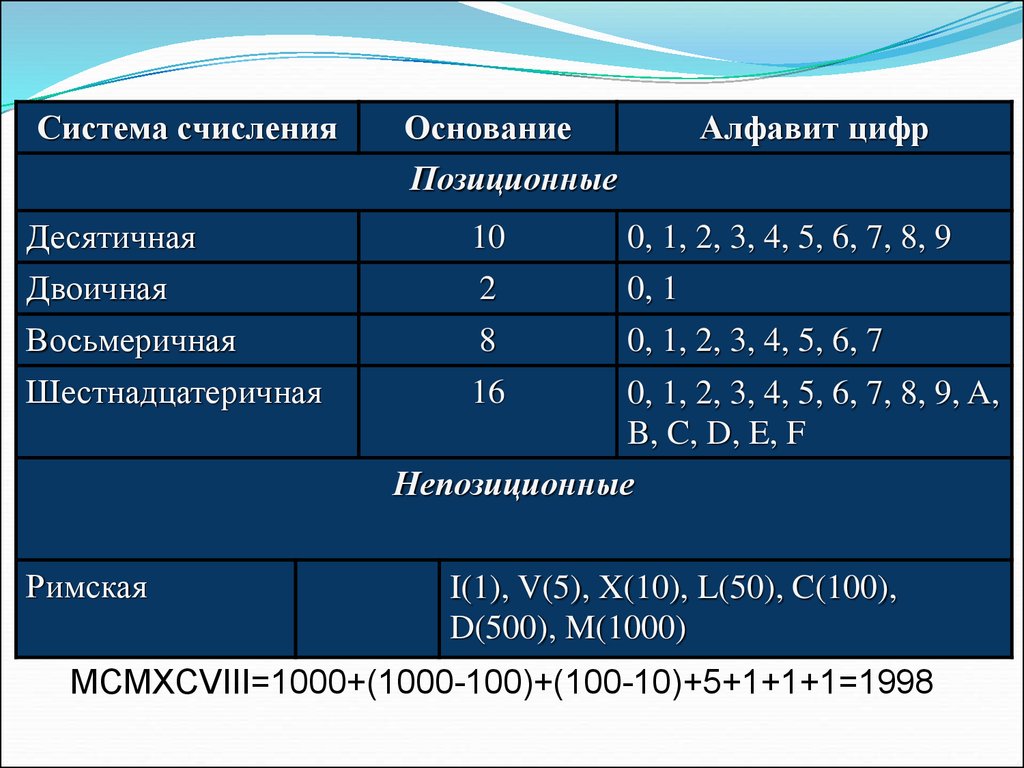 Следующие примеры иллюстрируют процедуру.
Пример 44.36: Преобразование следующего числа (375,37) ₈ = () ₂
Решение:
Bearinary-octal Conversion:
Of-Oo-Oo-Oo-Oo-Oo-Oo-Oo-Oo-octal. числа в восьмеричное число является просто обратным предыдущему процессу. Биты двоичного числа группируются в группы по три бита, начиная с LSB по направлению к MSB для целой части, а затем каждая группа из трех бит заменяется ее восьмеричным эквивалентом. Нули добавляются по мере необходимости для завершения 3-битной группы. Для дробной части описанная выше процедура повторяется с бита, следующего за двоичной точкой. Следующие примеры иллюстрируют процедуру.
Пример 44.37: Преобразование (111000) ₂ в восьмеричное число.
Решение:
Пример 44,38: Следующее преобразование: (101010011. 1101) ₂ до () ₈
Решение:
1 8
:
1
Восьмеричная арифметика:
Обычно восьмеричные арифметические операции, использующие восьмеричное представление чисел, не выполняются. Эта система счисления обычно используется для ввода длинных строк двоичных данных в цифровую систему, такую как микрокомпьютер. Это облегчает работу оператора. Арифметические операции можно выполнять путем преобразования восьмеричных чисел в двоичные числа и последующего использования правил двоичной арифметики. Следующие несколько примеров рассматриваются для иллюстрации.
База-n
Другие примеры степеней двух оснований:
Числа с основанием 4 (четвертичные) :
В соответствии с вышеизложенным система счисления с основанием 4 состоит из 4 цифр: 0, 1, 2 и 3.
Поскольку 2-битное число может представлять только одно из чисел 0, 1, 2 или 3, любое 2-битное число может быть представлено одним числом с основанием 4.
Чтобы преобразовать двоичное число в основание 4, сгруппируйте двоичное число справа налево в группах по 2 бита и представляют их значения в базе 4
Итак, двоичное число 1011 преобразуется в основание 4 следующим образом: 10 ₂ + 11 ₂ или 23 ₄
7
Теперь для представления любого 4-битного числа требуется всего 2 цифры.
База 8 (восьмеричные) Числа :
Система счисления с основанием 8 состоит из 8 цифр: 0, 1, 2, 3, 4, 5, 6 и 7.
Поскольку 3-битное число может представлять только одно из чисел 0, 1, 2, 3, 4, 5, 6 или 7, любое 3-битное число может быть представлено одним числом с основанием 8.
Чтобы преобразовать двоичное число в восьмеричное, просто сгруппируйте двоичное число справа налево в группы по 3 бита и представьте их значения в формате с основанием 8

Так, например, двоичное число 001011 преобразуется в основание 8 следующим образом: 001 ₂ + 011 ₂ или 13 ₈
Обратите внимание, что два нуля в столбцах 32 и 16 являются лишь заполнителями, поэтому даже если исходное двоичное число было 1011, результирующее значение с основанием 8 будет таким же.
Для представления любого 6-битного числа требуется всего 2 цифры.
Числа с основанием 16 (шестнадцатеричные) :
Представление с основанием 16, состоящее ровно из 16 цифр — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F.
Примечание: поскольку значения больше 9 потребуют представления двух цифр, например, в десятичное число 10, в этой системе такие значения представлены одним буквенным символом, например, B _16/Hex = 11 ₁₀
Обычно в вычислениях шестнадцатеричные ( Hex, для краткости) числа используются в качестве короткой руки для представления любого 4-битного шаблона с использованием только одного символа, поскольку существует ровно 16 возможных 4-битных комбинаций.
Таким образом, любое 4-битное число может быть представлено одним базовым шестнадцатеричным числом.