Система исчисления таблица: Перевод систем счисления – таблица, правила, формулы

Системы счисления – примеры, таблица, обозначение (9 класс, информатика)

Числа при письме заменяются специальными знаками. Метод представления числовых эквивалентов с помощью специальной знаковой системы называется системой счисления. Системы счисления, как один из важных разделов теоретической информатики, подробно рассматриваются в курсе информатики 9 класса.

Содержание

• Что такое системы счисления
• Позиционные системы счисления
• Непозиционные системы счисления
• Что мы узнали?

Что такое системы счисления

Системой счисления называется система записи чисел с помощью знаков по определенным правилам.

Символы, с помощью которых записываются числовые значения, обычно называют цифрами, а все вместе знаки системы счисления образуют алфавит. Количество знаков, используемых для обозначения чисел, называется основанием системы счисления.

Приведем примеры чисел систем счисления с различным основанием.

Основная десятичная система, привычная и общеупотребимая, имеет десять символов для обозначения всех чисел, то есть ее основание равно 10. Символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 представляют собой цифры. После цифры 9 в числовом ряду идет двузначное 10. При этом происходит сдвиг разрядной сетки числа влево на один разряд.

Десятичная система использует арабские цифры. Предположительно арабская система записи чисел возникла в Индии. Индийскую систему записи чисел описал Аль Хорезми в своем трактате «Об индийском счете».

Рис. 1. Портрет Аль Хорезми.

Системы счисления в информатике не ограничиваются применением десятичных цифр, самыми распространенными системами являются двоичная, восьмеричная и шестнадцатеричная системы счисления.

В двоичной системе счисления все просто. Основание равно 2. Обозначение чисел выполняется только двумя символами 0 и 1.

И числовой ряд двоичных чисел выглядит так: 0, 1, 10, 11, 100, 101, 110, 111, 1000 и так далее.

Восьмеричная система использует 8 знаков для обозначения чисел: 0, 1, 2, 3, 4, 5, 6, 7. И числовой ряд восьмеричных чисел выглядит так: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12 … Следует обратить внимание, что после 7 идет двузначное число 10, так как знаков всего восемь и происходит сдвиг разрядной сетки.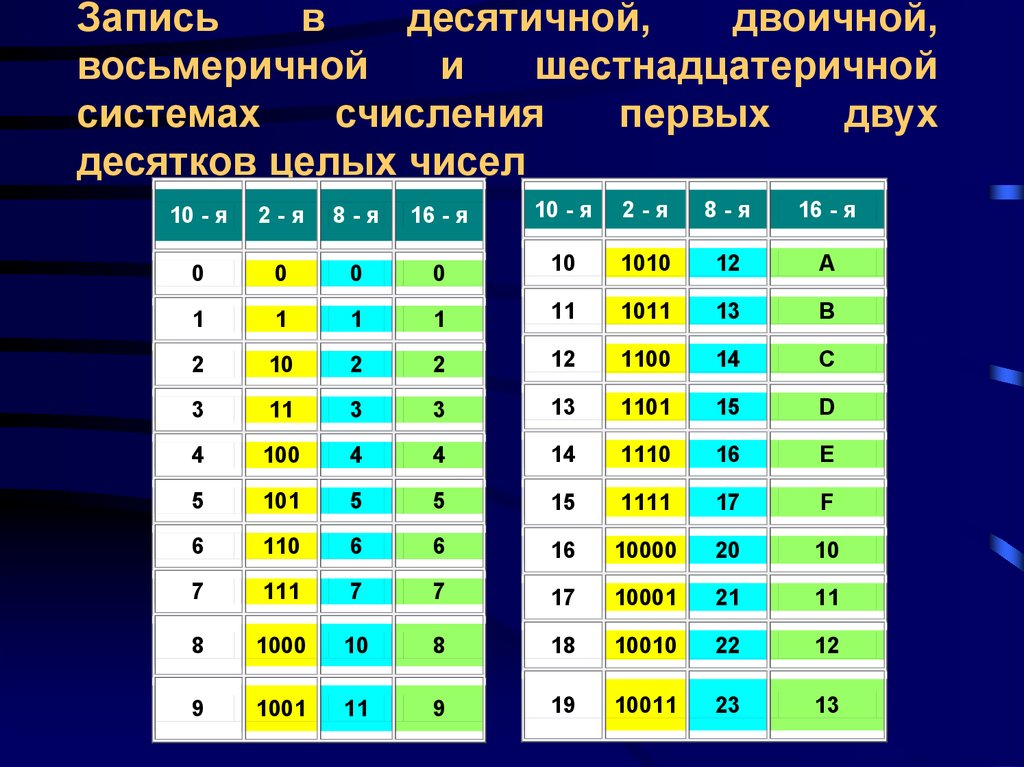

Шестнадцатеричная система имеет основание 16. Она применяет в качестве символов арабские цифры от 0 до 9 и затем буквы латинского алфавита A, B, C, D, E, F. В числовом ряду шестнадцатеричных чисел после 9 идет А, а после F идет 10.

Тогда возникает вопрос, как определить, в какой системе счисления, например число 107. Цифры 0, 1, 7 используются как в восьмеричной, так и в десятичной и шестнадцатеричной системе счисления. Для того чтобы различать системы, существует специальное обозначение систем счисления. Числа помечаются индексом с основанием системы. Так, 1078 – это восьмеричное число, 10710 – десятичное число, 10716 – шестнадцатеричное число.

в истории существуют примеры использования и других систем счисления. Так, некоторые коренные культуры Африки и Австралии используют двоичные и троичные системы. Индейцы Юки пользуются четверичной системой счисления, пятеричная система счисления распространена больше (по количеству пальцев на руке), ее элементы встречаются у древних персов и ацтеков, у индейцев племени Таманакос. У древних Шумеров использовалась шестидесятеричная система счисления, разбивка часа на 60 минут и минуты на 60 секунд, вероятно, отголоски этой системы.

Позиционные системы счисления

Рассмотренные системы счисления относятся к классу позиционных систем. В них числовое значение каждой цифры зависит от положения в числе. Например, в десятичном числе 126 единица означает сотню, а в числе 216 единица уже на другом месте и обозначает десять.

Каждое число позиционной системы счисления можно представить как в свернутом виде, например, 126, так и в развернутом: 1*102 + 2*101 + 6*100 , то есть 100 + 20 +6 =126.

Аналогично, двоичное число 111001 = 1*25 + 1*24 + 1*23 + 0*22 + 0*21 + 1*20

Восьмеричное число: 247 = 2*82 + 4*81 + 7*80

Шестнадцатеричное число: 2A5F = 2*163 + A*162 + 5*161 + F*160

Используя развернутую форму, можно переводить числа из любой системы счисления в десятичную систему.

Непозиционные системы счисления

Кроме позиционных систем, существуют также непозиционные системы, в которых расположение цифры в числе не влияет на его числовое значение.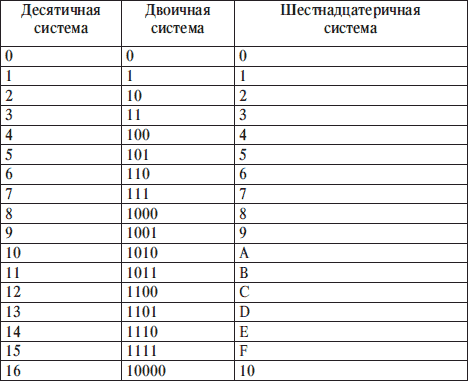 Например, римская система цифр строится на основе символов I, V, X, L, C, D, M, которые означают соответственно 1, 5, 10, 50, 100, 500, 1000. Так, римское XVII означает 17. Получено путем суммирования 10 + 5 + 1 + 1.

Еще один пример: число 14 римскими цифрами записывается как XIV. Здесь использованы символы X, I, и V, которые обозначают 10, 1 и 5. Существует правило, согласно которому, меньшее число стоящее слева от большего следует вычитать из него. То есть I (1) меньше V (5), поэтому 5 – 1 = 4. И тогда число XIV получается как 10 + (5 – 1) = 14

Например, 1985 год в римской системе выглядит так MCMLXXXV: 1000 + (1000 – 100) + 50 + 10 + 10 + 10 + 5 = 1985

Рис. 2. Таблица римских цифр и их значений.

Самой первой системой счисления в истории человечества была унарная система, в которой использовался только один знак, или точнее один камень, палочка или засечка. Конечно, с помощью такой системы записать большие числа практически невозможно. Поэтому древние люди стали заменять группы палочек другим символом.

Рис. 3. Унарная система счисления.

Что мы узнали?

Числа для удобства записи представляются с помощью системы символов, которая называется системой счисления. Существуют позиционные и непозиционные системы счисления. В позиционных системах количество используемых знаков называется основанием. В информатике используются двоичная, восьмеричная, десятичная и шестнадцатеричная системы счисления.

Предыдущая

ИнформатикаАлгоритм Евклида – схема (9 класс, информатика)

Следующая

ИнформатикаДвоичная система счисления – таблица последовательности, примеры (8 класс, информатика)

Девятеричная система счисления

Содержание:
Что такое девятеричная система счисления
Как перевести целое десятичное число в девятеричную систему счисления
Как перевести десятичную дробь в девятеричную систему счисления
Как перевести число из девятеричной системы счисления в десятичную
Как перевести дробное девятеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в девятеричной системе счисления

Девятеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа.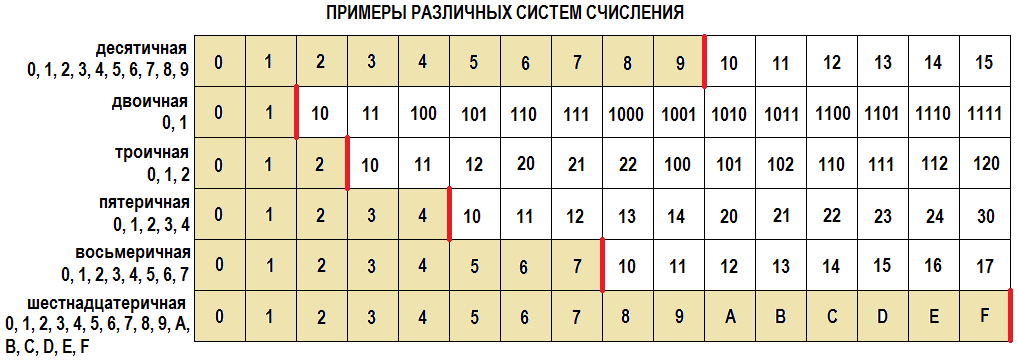 Для записи числа в девятеричной системе счисления используется девять цифр 0, 1, 2, 3, 4, 5, 6, 7 и 8. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется

основанием системы счисления. Например, 4057₉ или 18₉.

Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.

Как перевести целое десятичное число в девятеричную систему счисления

Для того, чтобы перевести целое десятичное число в девятеричную систему счисления нужно десятичное число делить на 9 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.

Например, переведем число 941₁₀ в девятеричную систему счисления:

941 : 9 = 104 остаток: 5
104 : 9 = 11 остаток: 5
11 : 9 = 1 остаток: 2
1 : 9 = 0 остаток: 1

941₁₀ = 1255₉

Как перевести десятичную дробь в девятеричную систему счисления

Для того чтобы перевести десятичную дробь в девятеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в девятеричную систему счисления, а затем дробную часть, последовательно умножать на 9, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число) или не будет достигнуто необходимое количество знаков после запятой.

Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.

Например, переведем десятичное число 12.74₁₀ в девятеричную систему счисления:

Переведем целую часть

12 : 9 = 1 остаток: 3
1 : 9 = 0 остаток: 1

12₁₀ = 13₉

Переведем дробную часть

0.74 · 9 = 6.66>
0.66 · 9 = 5.94>

0.94 · 9 = 8.46>
0.46 · 9 = 4.14>
0.14 · 9 = 1.26>
0.26 · 9 = 2.34>
0.34 · 9 = 3.06>
0.06 · 9 = 0.54>
0.54 · 9 = 4.86>
0.86 · 9 = 7.74

0.74₁₀ = 0.6584123047₉

12.74₁₀ = 13.6584123047₉

Девятеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной девятеричной.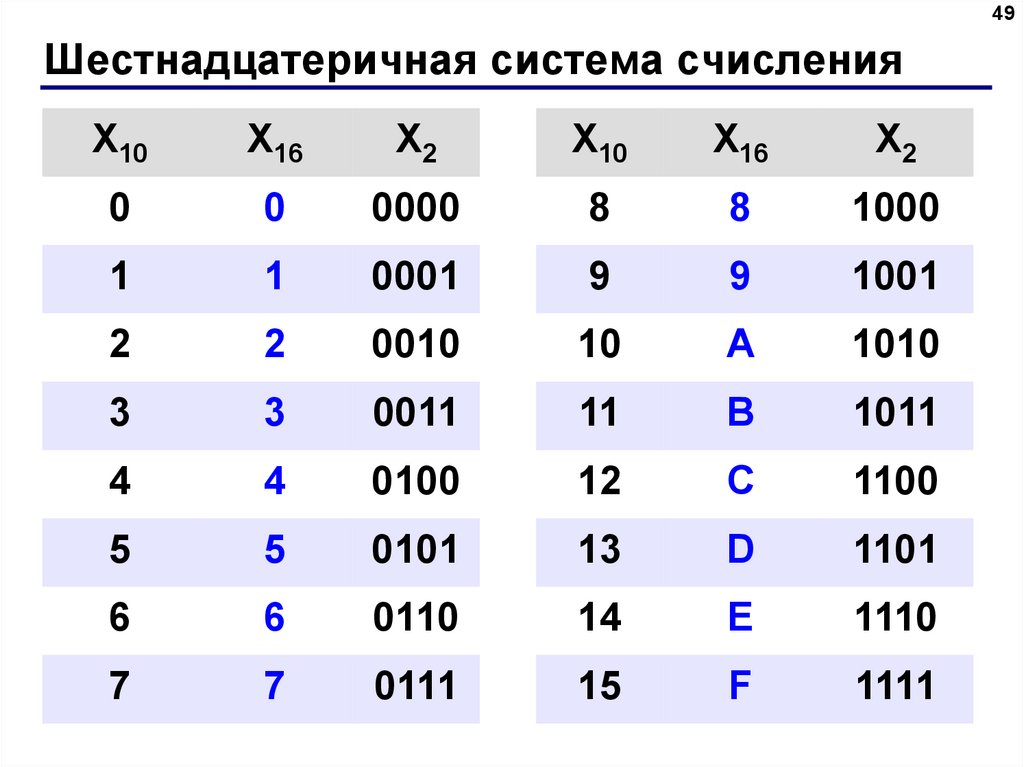 В данном примере получается бесконечная периодическая девятеричная дробь, поэтому умножение на 9 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю. В данном случае десятичная дробь 12.74 не может быть точно представлена в девятеричной системе счисления.

Как перевести число из девятеричной системы счисления в десятичную

Для того, чтобы перевести число из девятеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля. Каждая позиция цифры будет степенью числа 9, так как система счисления 9-ичная. Необходимо последовательно умножить каждое число на 9 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции. Например, переведем число 2684₉ в десятичную систему счисления:

Позиция в числе	3	2	1	0
Число	2	6	8	4

2684₉ = 2 ⋅ 9³ + 6 ⋅ 9² + 8 ⋅ 9¹ + 4 ⋅ 9⁰ = 2020₁₀

Как перевести дробное девятеричное число в десятичное

Для того, чтобы перевести дробное девятеричное число в десятичное, необходимо записать дробное девятеричное число, убрав точку и затем сверху расставить индексы.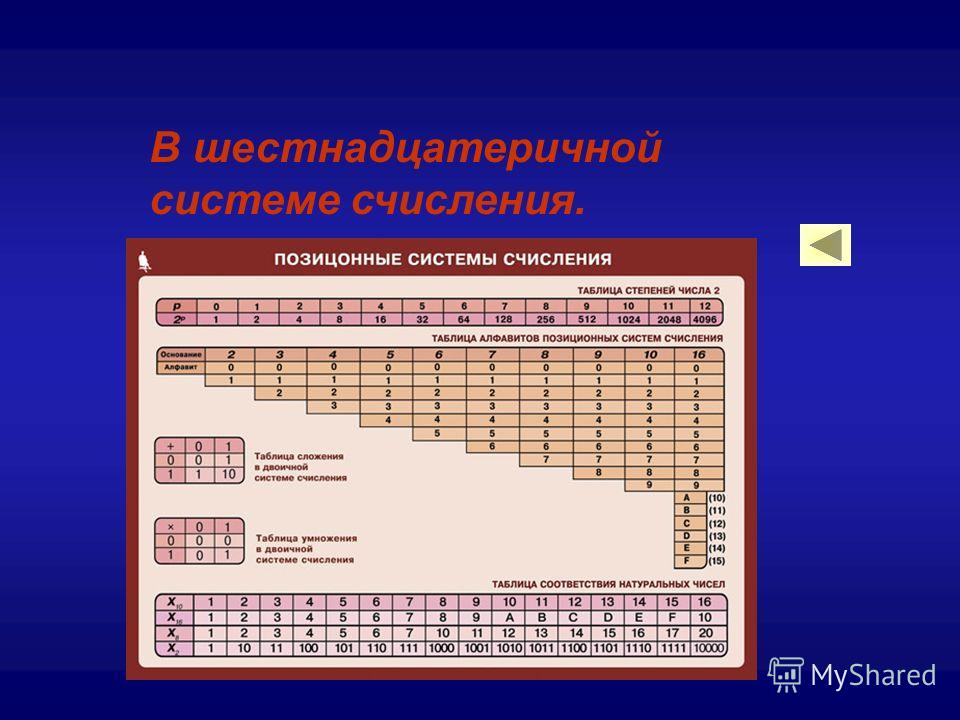

Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию. Каждая позиция цифры (индекс) будет степенью числа 9, так как система счисления 9-ичная. Необходимо последовательно умножить каждое число на 9 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.

Например, переведем дробное девятеричное число 81.63₉ в десятичное:

Позиция в числе	1	0	-1	-2
Число	8	1	6	3

81.63₉ = 8 ⋅ 9

1 + 1 ⋅ 9⁰ + 6 ⋅ 9^-1 + 3 ⋅ 9^-2 = 73.7037037037037037037037037036₁₀

Таблица значений десятичных чисел от 0 до 100 в девятеричной системе счисления

Значение числа в десятичной системе счисления	Значение числа в девятеричной системе счисления
010	09
110	19
210	29
310	39
410	49
510	59
610	69
710	79
810	89
910	109
1010	119
1110	129
1210	139
1310	149
1410	159
1510	169
1610	179
1710	189
1810	209
1910	219
2010	229
2110	239
2210	249
2310	259
2410	269
2510	279
2610	289
2710	309
2810	319
2910	329
3010	339
3110	349
3210	359
3310	369
3410	379
3510	389
3610	409
3710	419
3810	429
3910	439
4010	449
4110	459
4210	469
4310	479
4410	489
4510	509
4610	519
4710	529
4810	539
4910	549
5010	559

Значение числа в десятичной системе счисления	Значение числа в девятеричной системе счисления
5110	569
5210	579
5310	589
5410	609
5510	619
5610	629
5710	639
5810	649
5910	659
6010	669
6110	679
6210	689
6310	709
6410	719
6510	729
6610	739
6710	749
6810	759
6910	769
7010	779
7110	789
7210	809
7310	819
7410	829
7510	839
7610	849
7710	859
7810	869
7910	879
8010	889
8110	1009
8210	1019
8310	1029
8410	1039
8510	1049
8610	1059
8710	1069
8810	1079
8910	1089
9010	1109
9110	1119
9210	1129
9310	1139
9410	1149
9510	1159
9610	1169
9710	1179
9810	1189
9910	1209
10010	1219

система счисления.

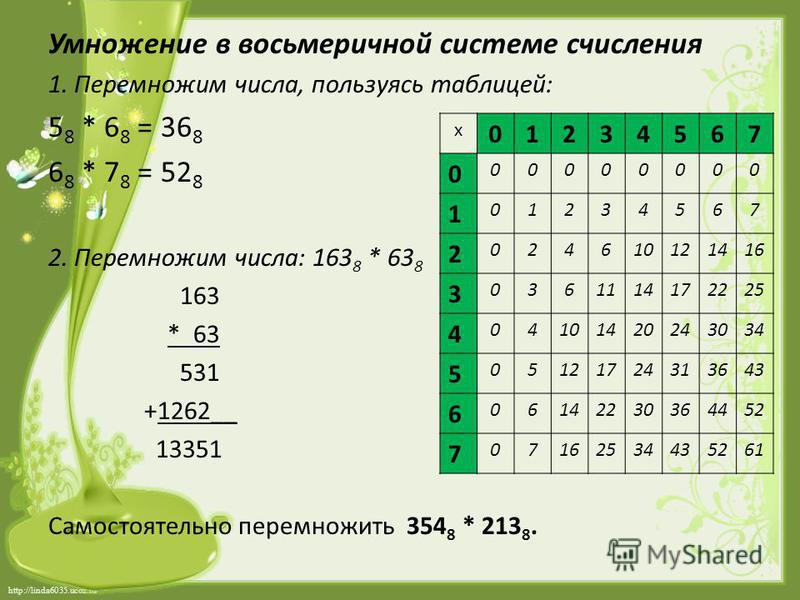Виды систем счисления

В курсе информатики, вне зависимости, школьном или университетском, особое место уделяется такому понятию как системы счисления. Как правило, на него выделяют несколько уроков или практических занятий. Основная цель — не только усвоить основные понятия темы, изучить виды систем счисления, но и познакомиться с двоичной, восьмеричной и шестнадцатеричной арифметикой.

Что это значит?

Начнем с определения основного понятия. Как отмечает учебник «Информатика», система счисления — это система записи чисел, в которой используется специальный алфавит или определенный набор цифр.

В зависимости от того, меняется ли значение цифры от ее положения в числе, выделяют две: позиционную и непозиционную системы счисления.

В позиционных системах значение цифры меняется вместе с ее положением в числе. Так, если взять число 234, то цифра 4 в ней означает единицы, если же рассмотреть число 243, то тут она будет уже означать десятки, а не единицы.

В непозиционных системах значение цифры статично, вне зависимости от ее положения в числе.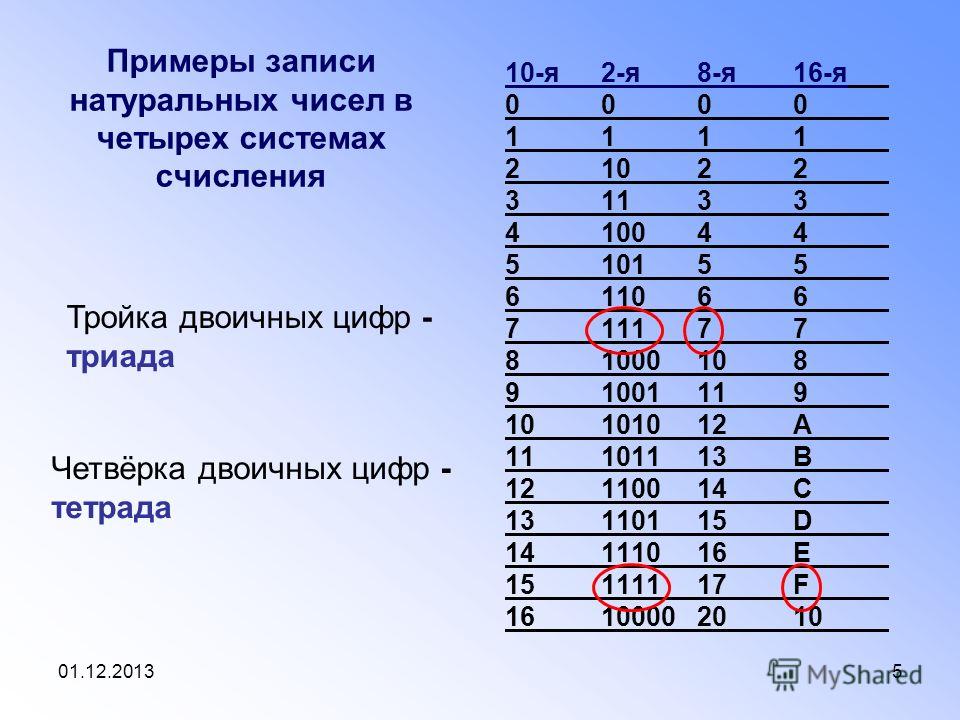 Наиболее яркий пример – палочковая система, где каждая единица обозначается с помощью черточки. Неважно, куда вы припишите палочку, значение числа измениться лишь на единицу.

Непозиционные системы

К непозиционным системам счисления относятся:

1. Единичная система, которая считается одной из первых. В ней вместо цифр использовались палочки. Чем их было больше, тем больше было значение числа. Встретить пример чисел, записанных таким образом, можно в фильмах, где речь идет о потерянных в море людях, заключенных, которые отмечают каждый день с помощью зарубок на камне или дереве.
2. Римская, в которой вместо цифр использовались латинские буквы. Используя их, можно записать любое число. При этом его значение определялось с помощью суммы и разницы цифр, из которых состояло число. Если слева от цифры находилось меньшее число, то левая цифра вычиталась из правой, а если справа цифра была меньше или равна цифре слева, то их значения суммировались. Например, число 11 записывалось как XI, а 9 – IX.
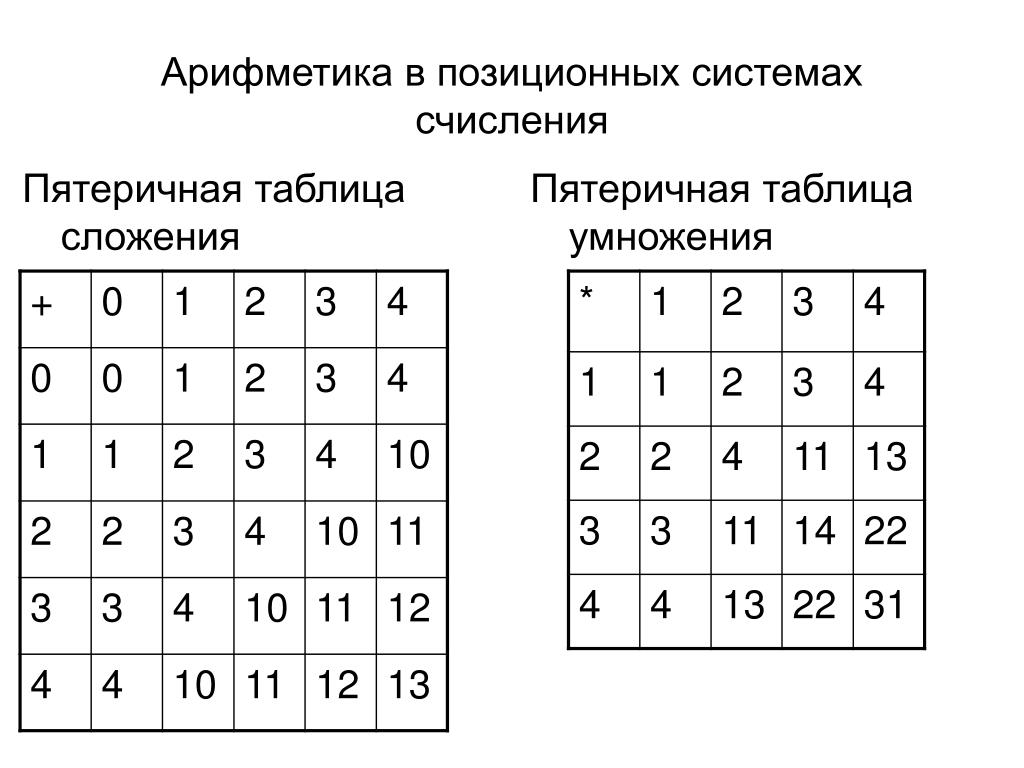
3. Буквенные, в которых числа обозначались с помощью алфавита того или иного языка. Одной из них считается славянская система, в которой ряд букв имел не только фонетическое, но и числовое значение.
4. Вавилонская система счисления, в которой использовалось всего два обозначения для записи – клинья и стрелочки.
5. В Египте тоже использовались специальные символы для обозначения чисел. При записи числа каждый символ мог использоваться не более девяти раз.

Позиционные системы

Большое внимание уделяется в информатике позиционным системам счисления. К ним относятся следующие:

• двоичная;
• восьмеричная;
• десятичная;
• шестнадцатеричная;
• шестидесятеричная, используемая при счете времени (к примеру, в минуте — 60 секунд, в часе — 60 минут).

Каждая из них обладает своим алфавитом для записи, правилами перевода и выполнения арифметических операций.

Десятичная система

Данная система является для нас наиболее привычной. В ней используются цифры от 0 до 9 для записи чисел. Они также носят название арабских. В зависимости от положения цифры в числе, она может обозначать разные разряды – единицы, десятки, сотни, тысячи или миллионы. Ее мы пользуемся повсеместно, знаем основные правила, по которым производятся арифметические операции над числами.

Двоичная система

Одна из основных систем счисления в информатике – двоичная. Ее простота позволяет компьютеру производить громоздкие вычисления в несколько раз быстрее, нежели в десятичной системе.

Для записи чисел используется лишь две цифры – 0 и 1. При этом, в зависимости от положения 0 или 1 в числе, его значение будет меняться.

Изначально именно с помощью двоичного кода компьютеры получали всю необходимую информацию. При этом, единица означала наличие сигнала, передаваемого с помощью напряжения, а ноль – его отсутствие.

Восьмеричная система

Еще одна известная компьютерная система счисления, в которой применяются цифры от 0 до 7. Применялась в основном в тех областях знаний, которые связаны с цифровыми устройствами. Но в последнее время она употребляется значительно реже, так как на смену ей пришла шестнадцатеричная система счисления.

Двоично-десятичная система

Представление больших чисел в двоичной системе для человека – процесс довольно сложный. Для его упрощения была разработана двоично-десятичная система счисления. Используется она обычно в электронных часах, калькуляторах. В данной системе из десятичной системы в двоичную преобразуется не все число, а каждая цифра переводится в соответствующий ей набор нулей и единиц в двоичной системе. Аналогично происходит и перевод из двоичной системы в десятичную. Каждая цифра, представленная в виде четырехзначного набора нулей и единиц, переводится в цифру десятичной системы счисления. В принципе, нет ничего сложного.

Для работы с числам в данном случае пригодится таблица систем счисления, в которой будет указано соответствие между цифрами и их двоичным кодом.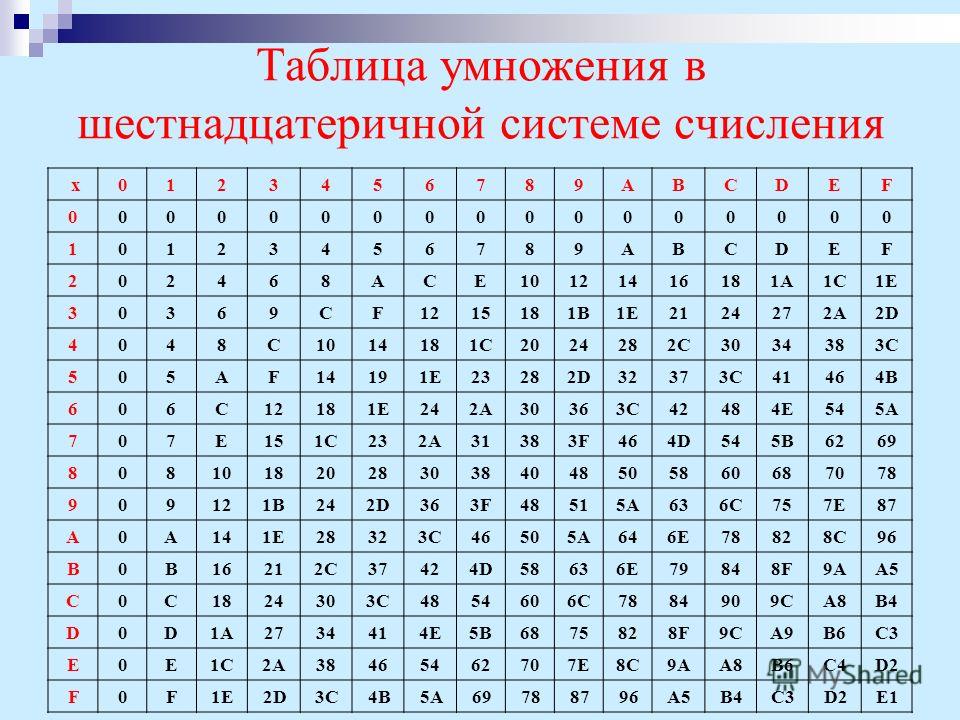

Шестнадцатеричная система

В последнее время все большую популярность приобретает в программировании и информатике система счисления шестнадцатеричная. В ней используются не только цифры от 0 до 9, но и ряд латинских букв – A, B, C, D, E, F.

При этом, каждая из букв имеет свое значение, так A=10, B=11, C=12 и так далее. Каждое число представляется в виде набора из четырех знаков: 001F.

Перевод чисел: из десятичной в двоичную

Перевод в системах счисления чисел происходит по определенным правилам. Наиболее часто встречается перевод из двоичной в десятичную систему и наоборот.

Для того, чтобы перевести число из десятичной системы в двоичную, необходимо последовательно делить его на основание системы счисления, то есть, число два. При этом, остаток от каждого деления необходимо фиксировать. Так будет происходить до тех пор, пока остаток от деления не будет меньше или равен единице. Проводить вычисления лучше всего в столбик. Затем полученные остатки от деления записываются в строку в обратном порядке.

Например, переведем число 9 в двоичную систему:

Делим 9, так как число не делится нацело, то берем число 8, остаток будет 9 – 1 = 1.

После деления 8 на 2 получаем 4. Снова делим его, так как число делится нацело – получаем в остатке 4 – 4 = 0.

Проводим ту же операцию с 2. В остатке получаем 0.

В итоге деления у нас получается 1.

Далее записываем все полученные нами остатки в обратном порядке, начиная с итога деления: 1001.

Вне зависимости от итоговой системы счисления, перевод чисел из десятичной в любую другую будет происходить по принципу деления числа на основу позиционной системы.

Перевод чисел: из двоичной в десятичную

Довольно легко переводить числа и в десятичную систему счисления из двоичной. Для этого достаточно знать правила возведения чисел в степень. В данном случае, в степень двойки.

Алгоритм перевода следующий: каждую цифру из кода двоичного числа необходимо умножить на двойку, причем, первая двойка будет в степени m-1, вторая – m-2 и так далее, где m – количество цифр в коде. Затем сложить результаты сложения, получив целое число.

Для школьников этот алгоритм можно объяснить проще:

Для начала берем и записываем каждую цифру, умноженную на двойку, затем проставляем степень двойки с конца, начиная с нуля. Потом складываем полученное число.

Для примера разберем с вами полученное ранее число 1001, переведя его в десятичную систему, и заодно проверим правильность наших вычислений.

Выглядеть это будет следующим образом:

1*2³ + 0*2²+0*2¹+1*2⁰= 8+0+0+1 =9.

При изучении данной темы удобно использовать таблицу со степенями двойки. Это существенно уменьшит количество времени, необходимое для проведения вычислений.

Другие варианты перевода

В некоторых случаях перевод может осуществляться между двоичной и восьмеричной системой счисления, двоичной и шестнадцатеричной. В таком случае можно пользоваться специальными таблицами или же запустить на компьютере приложение калькулятор, выбрав во вкладке вид вариант «Программист».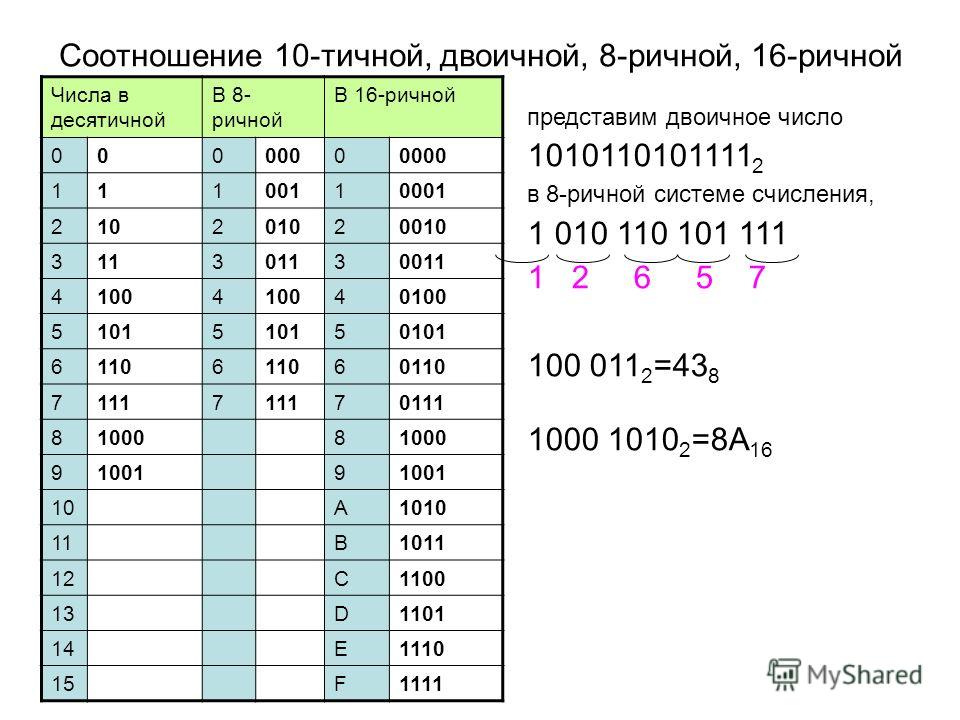

Арифметические операции

Вне зависимости от того, в каком виде представлено число, с ним можно проводить привычные для нас вычисления. Это может быть деление и умножение, вычитание и сложение в системе счисления, которую вы выбрали. Конечно, для каждой из них действуют свои правила.

Так для двоичной системы разработаны свои таблицы для каждой из операций. Такие же таблицы используются и в других позиционных системах.

Заучивать их необязательно – достаточно просто распечатать и иметь под рукой. Также можно воспользоваться калькулятором на ПК.

Одна из важнейших тем в информатике – система счисления. Знание этой темы, понимание алгоритмов перевода чисел из одной системы в другую – залог того, что вы сможете разобраться в более сложных темах, таких как алгоритмизация и программирование и сможете самостоятельно написать свою первую программу.

Десятичная система счисления, преобразование, шаги с решением Пример

Десятичная система счисления используется для представления как целых, так и нецелых значений.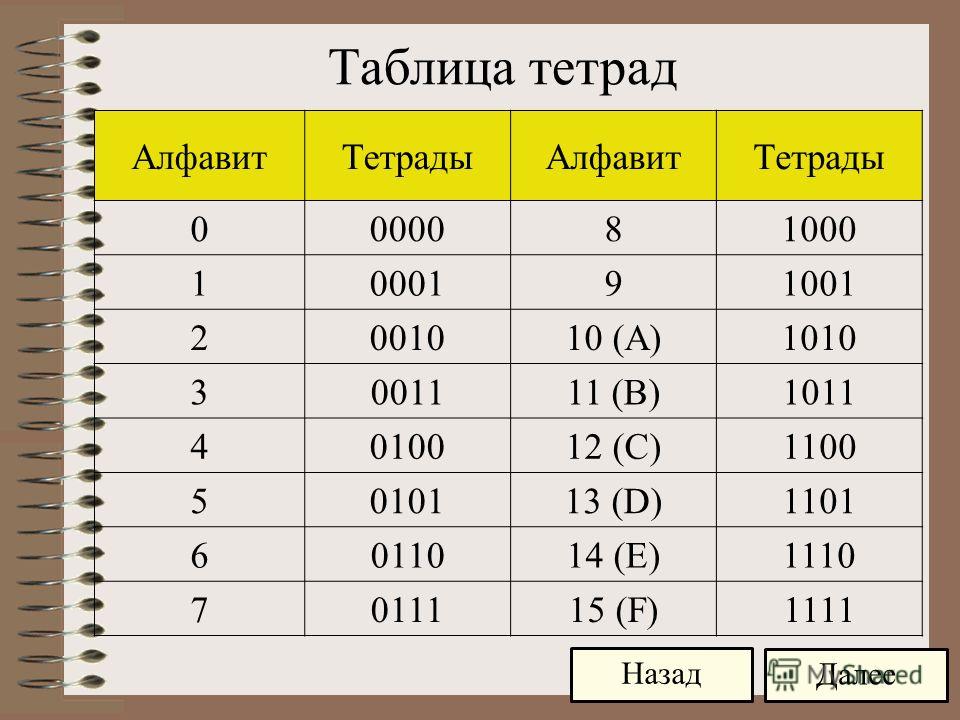 Это расширение индийско-арабской системы счисления для нецелых чисел. Десятичная запись относится к способу представления чисел в десятичной системе.

В этой статье мы изучим, что такое десятичная система счисления, кто ее отец, сколько цифр в ней используется, таблица преобразования, десятичная в двоичную, шестнадцатеричная и восьмеричная конвертация, решенные примеры, использование и преимущества десятичной системы счисления и ответы на часто задаваемые вопросы.

Что такое десятичная система счисления?

Десятичная система счисления также известна как система счисления с основанием 10, поскольку в ней используются десять цифр от 0 до 9. Десятичная система счисления — это та система, которую мы часто используем в нашей повседневной жизни. В десятичной системе счисления прогрессивная позиция находится слева от десятичной точки, представленной единицами, десятками, сотнями, тысячами и так далее.

Каждая позиция описывает определенную силу основания (10). Например, десятичное число 1245 состоит из цифры 5 в позиции единиц, 4 в позиции десятков, 2 в позиции сотен и 1 в позиции тысяч. Его значение можно сформулировать как 90)\)

\(1000 + 200 + 40 + 5\)

\(1245\)

Кто является отцом десятичной системы счисления

В конце 4 века до н.э. китайцы изобрели и использовали десятичную систему счисления фракции, которые мигрировали на Ближний Восток и в конечном итоге в Европу. Были написаны непозиционные китайские десятичные дроби. С другой стороны, подсчет дробей стержня был позиционным упражнением.

Аль-Хорезми, персидский эрудит, изобрел его в Индии. Концепция индийской системы счисления была передана на запад от ее истоков на древнем Ближнем Востоке. Архимед считается «отцом математики» и «изобретателем десятичной системы счисления». Математика – древняя наука, существующая с незапамятных времен. В своем «Счетчике песка» эрудит Архимед (ок. 287–212 до н. Э.) Создал десятичную позиционную систему, основанную на \(108\).

Определение десятичной системы счисления

Система счисления, в которой основание равно 10, называется десятичной системой счисления. От 0 до 9 десятичная система счисления состоит из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Таким образом, основание десятичной системы счисления, или основание, равно 10. В результате мы можем использовать эти десятизначные целые числа для выражения всех других цифр в этой системе счисления.

Основа десятичной системы счисления

В математике десятичная система счисления, также известная как индийско-арабская система счисления или арабская система счисления, представляет собой позиционную систему счисления, в которой используется 10 в качестве основания и требуется 10 различных цифр: 0 , 1, 2, 3, 4, 5, 6, 7, 8, 9.

Таблица десятичных систем счисления

Вот таблица преобразования систем счисления, которая пригодится при решении задач, основанных на десятичных системах счисления.

Decimal  Base-10	Binary  Base-2	Octal  Base-8	Hexadecimal  Base-16
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10
17	10001	21	11
18	10010	22	12
19	10011	23	13
20	10100	24	14
21	10101	25	15
22	10110	26	16
23	10111	27	17
24	11000	30	18
25	11001	31	19
26	11010	32	1A
27	11011	33	1B
28	11100	34	1C
29	11101	35	1D
30	11110	36	1E
31	11111	37	1F
32	100000	40	20

Тонковое число.

Система счисления: с основанием 8.

Шестнадцатеричная система счисления: с основанием 16.

На экзаменах часто требуется преобразовать одну форму системы в другую форму. Давайте посмотрим, как мы можем преобразовать десятичную систему счисления в двоичную, шестнадцатеричную и восьмеричную.

Преобразование десятичного числа в двоичное

Путем многократного деления числа на два и записи результата десятичные значения могут быть преобразованы в двоичные.

Действия, которые необходимо выполнить

Преобразование целых десятичных чисел

1. Разделите число на 2.
2. Получите целое частное для следующей итерации.
3. Получить остаток двоичной цифры.
4. Повторяйте вышеуказанные шаги, пока частное не станет равным 0.

Далее идет преобразование дробной части.

Преобразование дробных десятичных чисел

Дробные числа могут быть преобразованы в двоичную форму последовательным умножением на 2. То есть на каждом шаге цифра перед запятой переводится в двоичную запись, и тот же процесс повторяется среди оставшихся дробная часть.

Решение о последнем шаге принимается, когда дробная часть равна нулю, или завершается при достижении требуемой точности.

Взгляните на пример, чтобы увидеть, как это работает.

Остаток следует читать снизу вверх, чтобы получить двоичный эквивалент.

\(43_{10} = 101011_{2}\)

Также читайте об отношениях и функциях здесь.

Десятичное число в восьмеричное

Для преобразования десятичного числа в восьмеричное существует несколько прямых и косвенных методов. Косвенным способом вы переводите десятичное число в другую систему счисления (например, двоичную или шестнадцатеричную), затем преобразуете каждую цифру в двоичное число из шестнадцатеричной и используете группировку из восьмеричной системы счисления, чтобы преобразовать ее в двоичную.

Однако Преобразование с остатком и Преобразование с делением — это два способа преобразования десятичного числа в восьмеричное.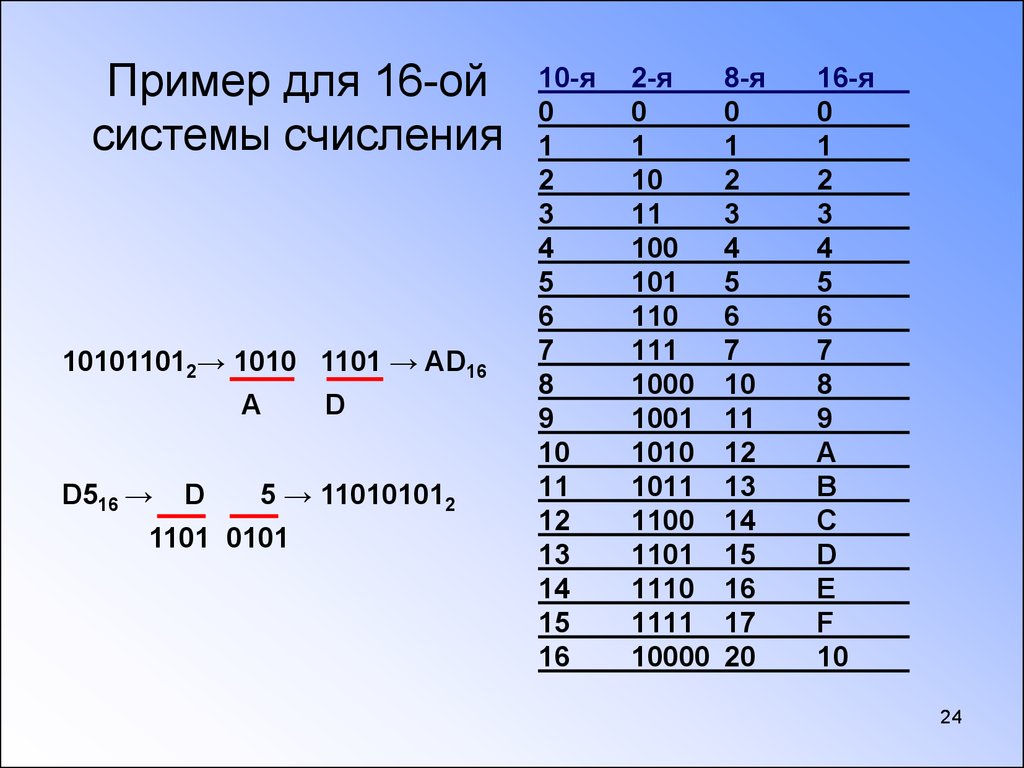 Они объясняются в следующих параграфах.

Преобразование с остатком (для целой части)

Это простой метод, который включает в себя деление числа, которое нужно преобразовать. Если десятичное число равно N, разделите его на 8, поскольку основание восьмеричной системы счисления равно 8. Обратите внимание на значение остатка, которое может быть одним из следующих: 0, 1, 2, 3, 4, 5, 6 или 7. Разделите оставшееся десятичное число, пока оно не станет равным 0, и запишите остаток каждого шага. Затем снизу вверх (или в обратном порядке) напишите остатки, которые будут эквивалентным восьмеричным числом предоставленного десятичного числа.

Решенный пример

Примечание. Делимое (здесь дано десятичное число) — это число, которое нужно разделить, делитель (здесь — восьмеричное основание, т. е. 8) — это число, на которое нужно разделить, а частное (оставшееся десятичное число) — результат деления.

Преобразование с остатками (для дробной части)

Если десятичная дробная часть равна M, умножьте ее на 8, поскольку основание восьмеричной системы счисления равно 8. Обратите внимание на значение целой части, которое будет равно 0, 1, 2, 3, 4, 5, 6 и 7. Умножьте оставшееся десятичное дробное число, пока оно не станет равным 0, и запишите каждую целую часть результата. Затем запишите результаты целой части, которые являются эквивалентными дробными восьмеричными числами указанного десятичного числа.

Решенный пример

Преобразование с делением

Этот подход работает путем угадывания восьмеричного числа десятичного числа. Вам нужно составить таблицу степеней 8. Алгоритм для целочисленной составляющей описывается следующим образом. В качестве отправной точки можно использовать любое десятичное число. Составьте список степеней восьмерки. Десятичное число следует умножить на наивысшую степень восьмерки. Найдите остальные предметы. Умножьте остаток на восьмую степень. Повторяйте, пока не разберетесь со всем решением.

Пример решения

Десятичное число в шестнадцатеричное

Преобразование десятичного числа в шестнадцатеричное может быть выполнено несколькими способами, как прямыми, так и косвенными. При косвенном методе необходимо сначала преобразовать десятичное число в другую систему счисления (например, двоичную или восьмеричную), после чего можно преобразовать его в шестнадцатеричное, сгруппировав его из двоичной системы счисления и переведя каждую восьмеричную цифру в двоичную, затем группировка и преобразование их в шестнадцатеричный формат.

Преобразование с остатками (для целой части)

Это простая процедура, которая включает в себя деление числа, которое нужно преобразовать, на два. Если десятичное число равно N, разделите его на 16, поскольку основание шестнадцатеричной системы счисления равно 16. Запишите значение остатка, который будет находиться в диапазоне от 0 до 15 (замените 10, 11, 12, 13, 14, 15 с A, B, C, D, E, F соответственно). Разделите оставшееся десятичное число, пока оно не станет равным 0, и запишите остатки каждого шага. Затем снизу вверх (или в обратном порядке) запишите остатки, которые будут шестнадцатеричным эквивалентом предоставленного десятичного числа.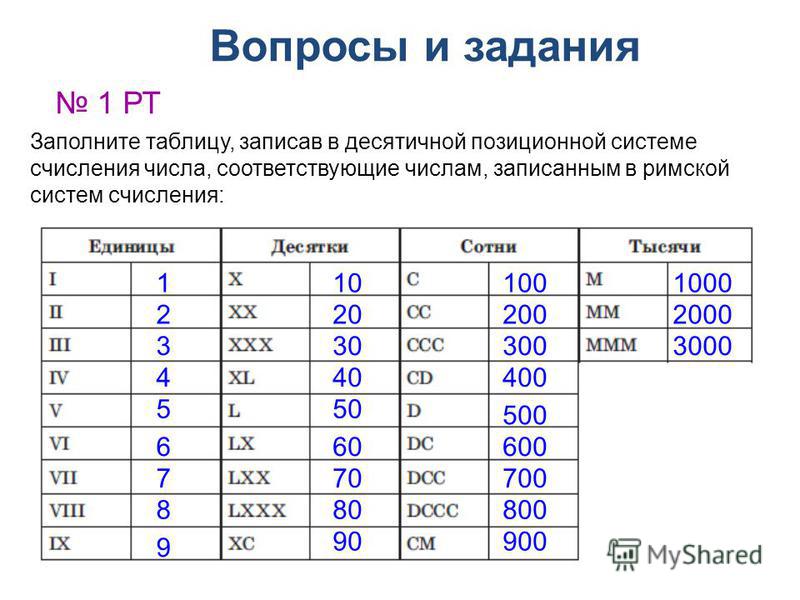

Преобразование с остатками (для дробной части)

Если десятичная дробная часть равна M, умножьте ее на 16, поскольку основание шестнадцатеричной системы счисления равно 16. Обратите внимание на значение целой части, которое будет находиться в диапазоне от 0 до 15. ( заменить 10, 11, 12, 13, 14, 15 на A, B, C, D, E, F соответственно). Умножьте оставшееся десятичное дробное число, пока оно не станет равным 0, и запишите каждую целую часть результата. Затем запишите результаты целой части, которая будет дробным шестнадцатеричным числом, сравнимым с указанным десятичным значением.

Пример решения

Преобразование с делением

Этот подход работает путем оценки шестнадцатеричного эквивалента десятичного числа. В качестве отправной точки можно использовать любое десятичное число. Составьте список способностей 16. Умножьте десятичное число на 16-ю степень. Найдите остальные предметы. Умножьте остаток на 16-ю степень. Повторяйте, пока не разберетесь со всем решением.

Пример решения

Узнайте больше о последовательностях и сериях здесь.

Использование десятичной системы счисления

Десятичные числа полезны в различных ситуациях. Ниже приводится список некоторых из них.

• Десятичные числа используются для оценки того, являются ли числа рациональными или иррациональными.
• Они используются для преобразования дробей, процентов и отношений из одной формы в другую.
• Мы используем десятичные дроби для измерения длины, веса, площади и объема, среди прочего.
• Неточные вычисления, обычно используются десятичные дроби.
• В числовой строке мы используем десятичные дроби для представления некоторых чисел.
• В математике десятичные дроби чрезвычайно важны, особенно в таких областях, как системы счисления, измерения и геометрия. Мы используем десятичные дроби для вычисления площади и объема объектов.
• Работа с деньгами — одно из самых полезных применений десятичных дробей. Для представления денег мы часто используем десятичные дроби. Мы сталкиваемся с переводом рупий в пайсы и пайсов в рупии в различных случаях. Большинство наших счетов содержат десятичные дроби.
• Мы часто используем десятичные дроби для точного измерения длины и роста, а также для перевода длины из одних единиц в другие. Например, рост человека 165 см и 2 мм. Затем к его общему росту прибавляется 165,2 см.
• При точном расчете веса мы часто используем десятичные дроби. Точный вес объекта не всегда является целым числом. В таких случаях для расчета веса используются десятичные дроби. Вес яблок, например, составляет 3 кг и 500 г, что можно выразить как 3,5 кг.
• Каждый день в расчетах используются десятичные дроби. Ученые и инженеры использовали десятичные дроби для более точных расчетов. Счетчик на АЗС показывает показания в десятичном формате. Скорость автомобиля также отображается в десятичных знаках на одометре.
• В строительстве также используются десятичные дроби. Десятичные дроби используются для определения точной площади здания или участка, а также точного количества необходимых материалов.

Решенные примеры для десятичной системы счисления

Решено Пример: Преобразование десятичного числа 25 в двоичное число.

Решение:

Выполните следующие действия, чтобы преобразовать число 25 в двоичную систему.

• Разделите число 25 на 2.
• Получите целочисленное частное для следующей итерации.
• Получить остаток двоичной цифры.
• Повторяйте вышеуказанные шаги, пока частное не станет равным 0.

Решено Пример: Преобразуйте десятичное число 0,35 в двоичное число.

Решение:

Умножьте на 2 и запишите перенос в целочисленной позиции для дробных десятичных цифр. Когда переносы считываются, создается эквивалентная двоичная дробь, как показано в примере ниже.

Таким образом, дробное двоичное число равно 0,01011, т. е. 0,01011.

Решено Пример: Преобразование десятичного числа 25 в восьмеричное.

Решение:

Выполните следующие действия, чтобы преобразовать число 25 в восьмеричную систему.

Шаг 1: Делите (25) на 8, пока частное не станет равным 0:

25/8 = 3, остаток равен 1

3/8 = 0, остаток равен 3

Шаг 2: Чтение снизу (MSB ) вверх (младший разряд). Ответ: 31.

В результате 31 является восьмеричным эквивалентом 25 в десятичной форме.

Решено Пример: Преобразование десятичного числа 25 в шестнадцатеричное число.

Решение:

Выполните следующие действия, чтобы преобразовать число 25 в шестнадцатеричную систему.

Шаг 1: Делите (25) на 16, пока частное не станет равным 0:

25/16 = 1, остаток равен 9

1/16 = 0, остаток равен 1

Шаг 2: Чтение снизу (MSB ) вверх (младший разряд). Ответ: 19.

В результате 31 является восьмеричным эквивалентом 25 в десятичной форме.

Надеюсь, эта статья о десятичной системе счисления была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!

Часто задаваемые вопросы о десятичной системе счисления

Q.1 Сколько цифр используется в десятичной системе счисления?

Ответ 1 Система счисления, в которой основание равно 1010, называется десятичной системой счисления. От 0 до 9 десятичная система счисления состоит из десяти цифр: 0,1,2,3,4,5,6,7,8 и 9. Основание десятичной системы счисления, или основание, равно 10, потому что десятичная система счисления общее количество цифр равно десяти. В результате мы можем использовать эти десятизначные целые числа для выражения всех других цифр. В нашей повседневной жизни мы используем десятичную систему счисления, поскольку она является наиболее распространенной и доступной.

Q. 2 Что такое десятичная система счисления на примере?

Ответ 2 Десятичная система счисления также известна как система счисления с основанием 10, поскольку в ней используются десять цифр от 0 до 9. Десятичная система счисления — это та система, которую мы часто используем в повседневной жизни. жизнь. В десятичной системе счисления прогрессивная позиция находится слева от десятичной точки, представленной единицами, десятками, сотнями, тысячами и так далее. Каждая позиция описывает определенную мощность основания (10). Например, десятичное число 1245 состоит из цифры 5 в позиции единиц, 4 в позиции десятков, 2 в позиции сотен и 1 в позиции тысяч.

Q.3 Какие существуют 4 типа системы счисления?

Ответ 3 Четыре распространенных типа систем счисления: Десятичная система счисления: имеет основание 10. Десятичная система счисления также известна как система счисления с основанием 10, поскольку в ней используются десять цифр от 0 до 9.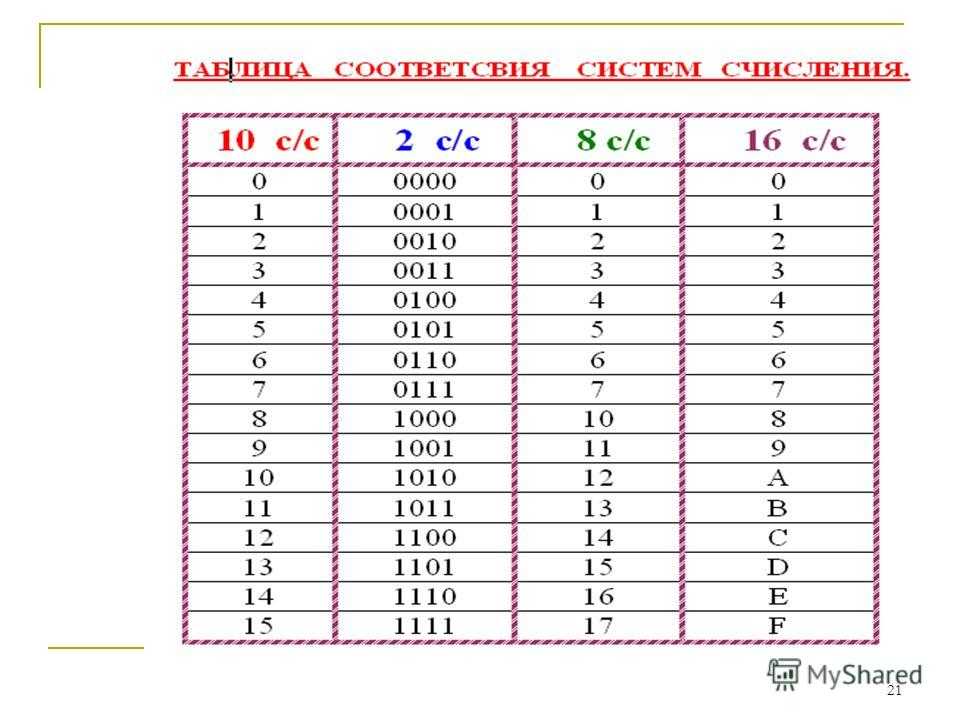 Десятичная система счисления — это та, которую мы часто используем в нашей повседневной жизни. Двоичная система счисления: имеет основание 2. Двоичная система счисления или система с основанием 2 составляют только две цифры, равные 0 и 1. Компьютеры манипулируют и хранят все свои данные, включая числа, слова, фильмы, изображения и музыку, используя двоичная система счисления. Восьмеричная система счисления: имеет основание 8. Восьмеричная система счисления представлена ​​​​с основанием 8, то есть она использует цифры от 0 до 7, то есть 0, 1, 2, 3, 4, 5, 6 и 7 для представления числа. Термин восьмеричный используется для описания чисел с восьмизначным основанием. Шестнадцатеричная система счисления: имеет основание 16. Шестнадцатеричная система представлена ​​с основанием 16. Это означает, что в шестнадцатеричной системе 16 шестнадцатеричных чисел. Шестнадцатеричная (иногда известная как основание 16 или просто шестнадцатеричная) система счисления представляет собой позиционную систему счисления, используемую в математике и вычислительной технике.

В.4 Что такое двоичные числа?

Ответ 4 Двоичная система счисления или система с основанием 2 состоит только из двух цифр, равных 0 и 1. Компьютеры обрабатывают и хранят все свои данные, включая числа, слова, фильмы, изображения и музыку, используя двоичную систему счисления. Поскольку числа «2» в этой системе не существует, 1 + 1 = 10. Джордж Буль, британский математик, в 1854 году написал основополагающую работу, описывающую алгебраическую систему логики, основанную на бинарной системе, которая стала известна как булева алгебра. Его логическое исчисление сыграет ключевую роль в развитии цифровых электрических схем.

В.5 Что такое восьмеричные числа?

Ответ 5 Восьмеричная система счисления представлена ​​с основанием 8, то есть она и использует цифры от 0 до 7, т.е. 0, 1, 2, 3, 4, 5, 6 и 7 для представления чисел. Термин восьмеричный используется для описания чисел с восьмизначным основанием.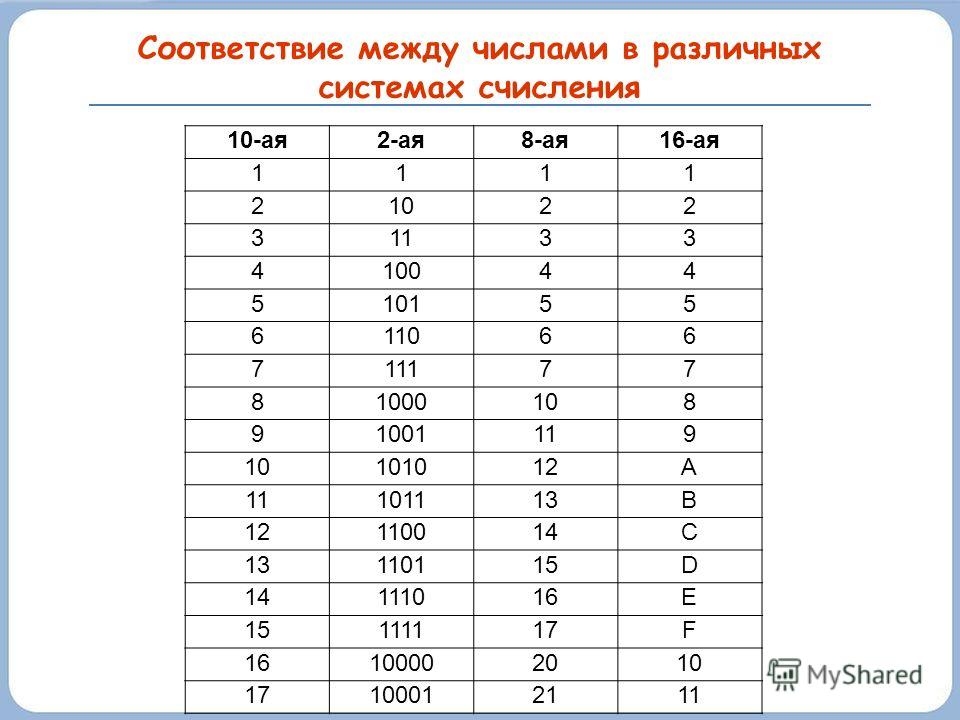 Восьмеричные числа имеют широкий спектр применения и значения, включая использование в компьютерах и цифровых системах счисления. При запросе наземным радаром транспондеры самолетов передают код «кваканья», который выражается в виде четырех восьмеричных цифр. На экране радара этот код используется для идентификации разных самолетов.

В.6 Что такое шестнадцатеричные числа?

Ответ 6 Шестнадцатеричная система представлена ​​с основанием 16. Это означает, что в шестнадцатеричной системе 16 шестнадцатеричных чисел. Шестнадцатеричная (иногда известная как основание 16 или просто шестнадцатеричная) система счисления представляет собой позиционную систему счисления, используемую в математике и вычислительной технике. Шестнадцатеричное используется в кодировке передачи Base16, которая делит каждый байт открытого текста на два 4-битных значения и две шестнадцатеричные цифры. Шестнадцатеричные числа обычно используются разработчиками программного обеспечения и проектировщиками систем, поскольку они обеспечивают удобное для человека представление данных в двоичном коде.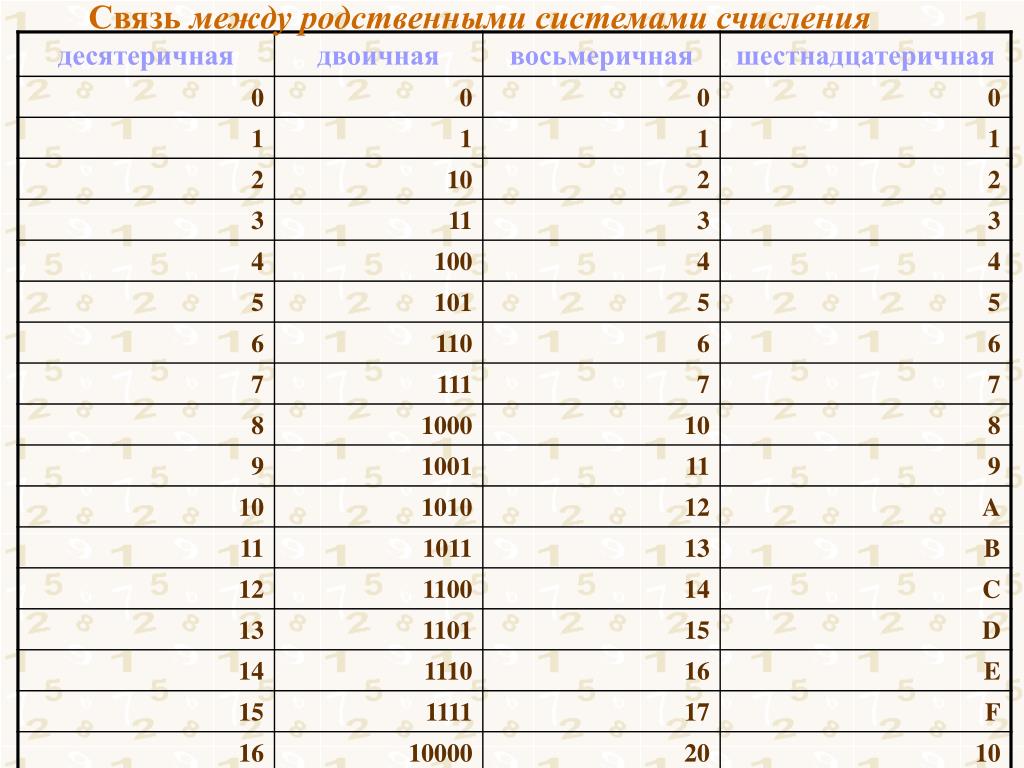 Каждая шестнадцатеричная цифра, обычно известная как полубайт, представляет собой четыре бита (двоичные цифры) (или полубайт).

Скачать публикацию в формате PDF

Еще на testbook.com

Разница между рациональными и иррациональными числами и решаемые примеры
Восьмеричная система счисления: Изучите определение, преобразование, основание на примерах!
Разница между дробными и рациональными числами и примеры решения
Имена чисел от 1 до 50 с легко запоминающимися приемами, правилами и примерами решения
Кардинальные числа: изучите определение, список, разницу с порядковыми числами, используя решенные примеры!

Двоичная, шестнадцатеричная и восьмеричная системы счисления

Двоичная, шестнадцатеричная и восьмеричная системы счисления относятся к разным системам счисления. Тот, который мы обычно используем, называется десятичным.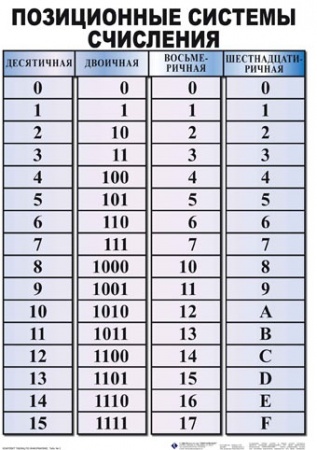 Эти системы счисления относятся к количеству символов, используемых для представления чисел. В десятичной системе мы используем десять различных символов: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. С помощью этих десяти символов мы можем представить любую величину. Например, если мы видим 2, то мы знаем, что есть два чего-то. Например, в этом предложении 2 точки в конце..

Когда у нас заканчиваются символы, мы переходим к следующему расположению цифр. Чтобы представить единицу выше 9, мы используем 10, означающую одну единицу из десяти и ноль единиц из единицы. Это может показаться элементарным, но очень важно понять нашу систему счисления по умолчанию, если вы хотите понять другие системы счисления.

Например, когда мы рассматриваем двоичную систему, в которой используются только два символа, 0 и 1, когда у нас заканчиваются символы, нам нужно перейти к следующему расположению цифр. Итак, мы будем считать в двоичном формате 0, 1, 10, 11, 100, 101 и так далее.

В этой статье более подробно рассматриваются двоичная, шестнадцатеричная и восьмеричная системы счисления и объясняется их использование.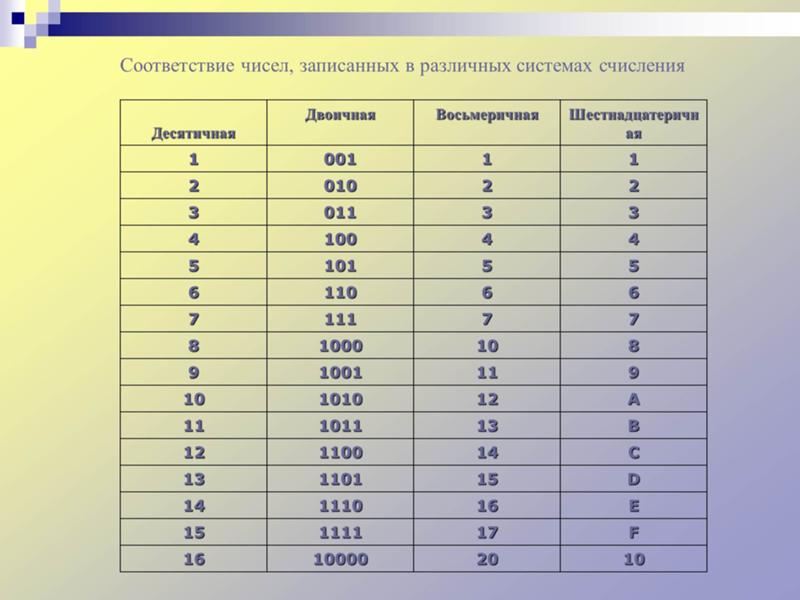

Сложить Содержание Как работает система счисления Двоичная Восьмеричная Шестнадцатеричная Преобразование Основание в десятичную 900 2 Десятичная 900 2 9003? Преобразование. От десятичного к двоичному От двоичного к десятичному Из десятичного в шестнадцатеричный. От шестнадцатеричного к десятичному От десятичного к восьмеричному От восьмеричного к десятичному Интересные факты Конец

Системы счисления используются для описания количества чего-либо или представления определенной информации. Благодаря этому я могу сказать, что слово «калькулятор» состоит из десяти букв. Наша система счисления, десятичная система, использует десять символов. Следовательно, десятичная дробь называется с основанием 10 . Описывая системы с базами, мы можем понять, как работает эта конкретная система.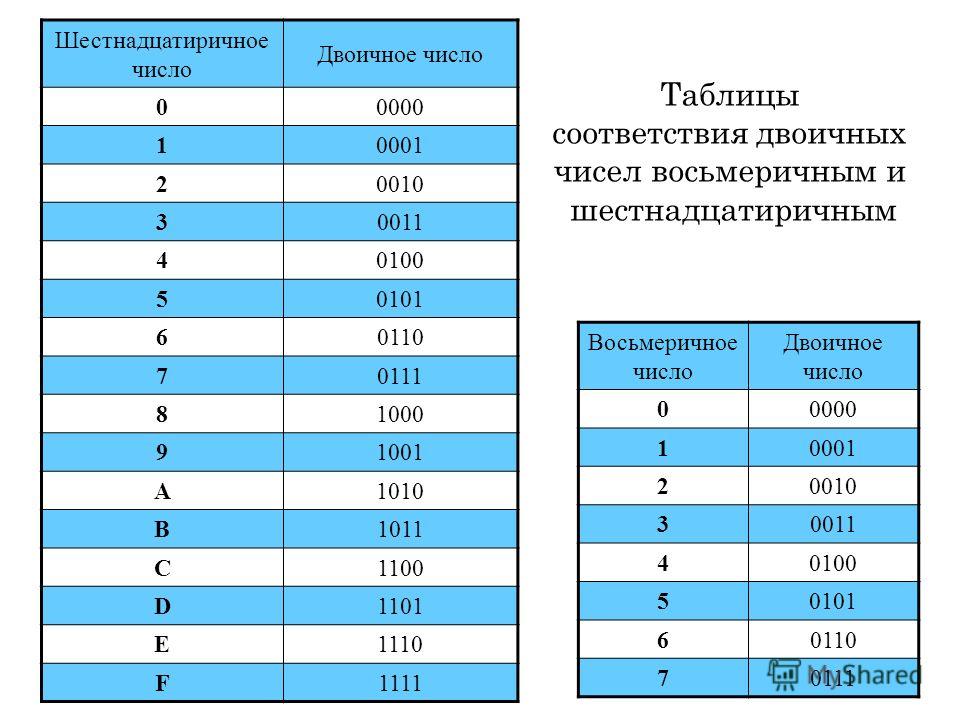

Когда мы считаем по основанию десять, мы считаем, начиная с нуля и заканчивая девятью по порядку.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, …

Достигнув последнего символа, мы создаем новое размещение перед первым и подсчитываем его.

8, 9, 1 0, 11, 12, … , 19, 2 0, …

Это продолжается, когда у нас заканчиваются символы для этого размещения. Итак, после 99 мы идем к 100.

Размещение символа указывает, сколько он стоит. Каждое дополнительное размещение — это дополнительная степень числа 10. Рассмотрим число 2853. Мы знаем, что это число довольно велико, например, если оно относится к количеству яблок в корзине. Это много яблок. Откуда мы знаем, что он большой? Смотрим на количество цифр.

Каждое дополнительное размещение является дополнительной степенью 10, как указано выше. Рассмотрим этот график.

10 3	10 2	10 1	10 0
цифра	цифра	цифра	цифра
*1000	*100	*10	*1

Каждая дополнительная цифра представляет все большее и большее количество. Это применимо как к базе 10, так и к другим базам. Знание этого поможет вам лучше понять другие базы.

Двоичный

Двоичный — это еще один способ сказать основание два. Итак, в двоичной системе счисления для представления чисел используются только два символа: 0 и 1. Когда мы считаем от нуля в двоичной системе счисления, у нас гораздо чаще заканчиваются символы.

0, 1, …

Отсюда символов больше нет. Мы не идем к 2, потому что в двоичном формате 2 не существует. Вместо этого мы используем 10. В двоичной системе 10 равно 2 в десятичной системе.

Можем считать дальше.

Двоичный	0	1	10	11	100	101	110	111	1000	1001	1010
Десятичный	0	1	2	3	4	5	6	7	8	9	10

Как и в десятичной системе, мы знаем, что чем больше цифр, тем больше число. Однако в двоичном формате мы используем степень двойки. В двоичном числе 1001101 мы можем создать диаграмму, чтобы узнать, что это на самом деле означает.

2 6	2 5	2 4	2 3	2 2	2 1	2 0
1	0	0	1	1	0	1
64+0+0+8+4+0+1
77

Поскольку это основание два, числа не становятся такими большими, как в десятичном виде. Тем не менее, двоичное число с 10 цифрами будет больше, чем 1000 в десятичном виде.

---

Двоичная система используется в информатике и электротехнике. Транзисторы работают по двоичной системе, а транзисторы есть практически во всех электронных устройствах. 0 означает отсутствие тока, а 1 означает, что ток разрешен. Когда различные транзисторы включаются и выключаются, сигналы и электричество отправляются для выполнения различных действий, таких как вызов или вывод этих букв на экран.

Компьютеры и электроника работают с байтами или восьмизначными двоичными числами. Каждый байт содержит закодированную информацию, которую компьютер может понять. Многие байты связаны вместе для формирования цифровых данных, которые можно сохранить для последующего использования.

Восьмеричная

Восьмеричная система счисления, в которой используется меньше символов, чем в нашей обычной системе счисления. Восьмеричное число подходит для восьмеричной системы счисления, что означает, что для представления всех величин используются восемь символов. Это 0, 1, 2, 3, 4, 5, 6 и 7. Когда мы подсчитываем единицу из 7, нам нужно новое размещение для представления того, что мы называем 8, поскольку 8 не существует в восьмеричном. Итак, после 7 будет 10.

Восьмеричное	0	1	2	3	4	5	6	7	10	11	12…	17	20…	30…	77	100
Десятичный	0	1	2	3	4	5	6	7	8	9	10…	15	16…	24…	63	64

Точно так же, как мы использовали степени десяти в десятичной системе счисления и степени двойки в двоичной системе, для определения значения числа мы будем использовать степени 8, поскольку это основание восьмерки.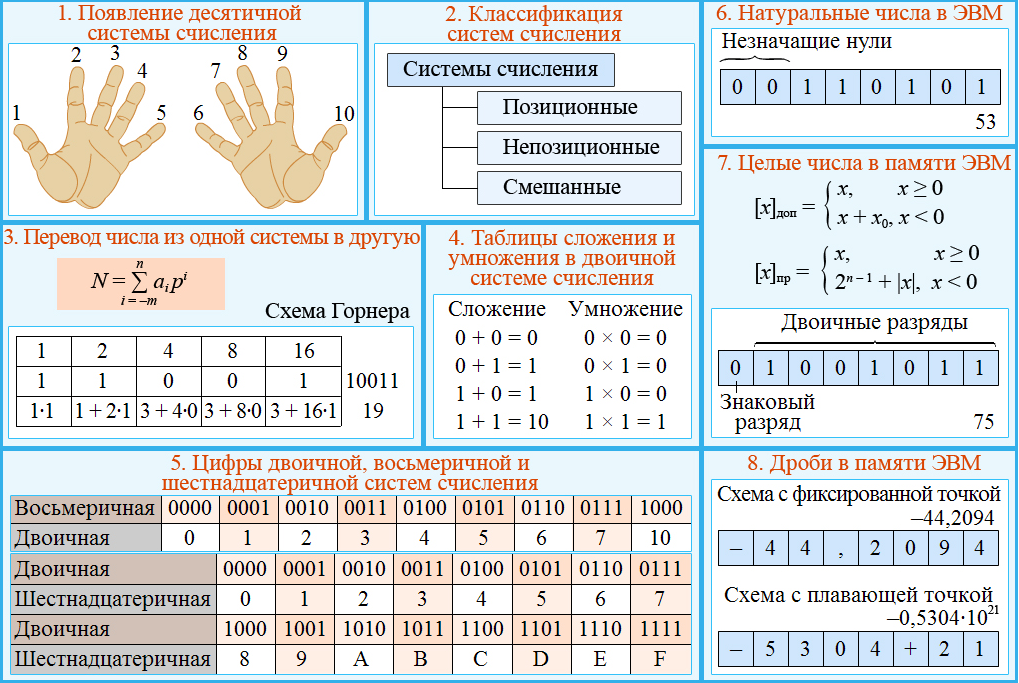 Рассмотрим число 3623 по основанию восемь.

8 3	8 2	8 1	8 0
3	6	2	3
1536+384+16+3
1939

Каждое дополнительное размещение слева имеет большую ценность, чем в двоичном формате. Третья цифра справа в двоичном формате представляет только 2 ^3-1 , что равно 4. В восьмеричном формате это 8 ^3-1 , что равно 64.

Шестнадцатеричная система счисления

Шестнадцатеричная система с основанием шестнадцать. Как следует из ее основы, эта система счисления использует шестнадцать символов для представления чисел. В отличие от двоичного и восьмеричного, в шестнадцатеричном формате есть шесть дополнительных символов, которые используются в дополнение к обычным десятичным. Но что будет после 9? 10 — это не одна цифра, а две… К счастью, по соглашению, если помимо обычных десяти требуются дополнительные символы, следует использовать буквы.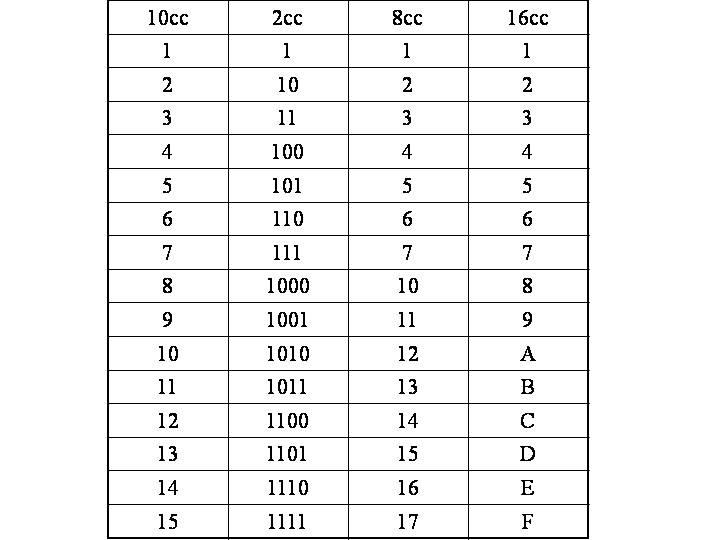 Таким образом, в шестнадцатеричном формате общий список используемых символов составляет 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. На цифровом дисплее , числа B и D строчные.

При шестнадцатеричном счете вы считаете 0, 1, 2 и так далее. Однако, когда вы достигаете 9, вы идете прямо к A. Затем вы считаете B, C, D, E и F. Но что дальше? У нас закончились символы! Когда у нас заканчиваются символы, мы создаем новое размещение цифр и идем дальше. Итак, после F будет 10. Вы продолжаете считать, пока не достигнете 19.. После 19 следует число 1А. Это продолжается вечно.

Шестнадцатеричный	9	А	Б	С	Д	Э	Ф	10	11…	19	1А	1Б	1С…	9Ф	А0
Десятичный	9	10	11	12	13	14	15	16	17	25	26	27	28	159	160

Цифры объясняются как степени 16.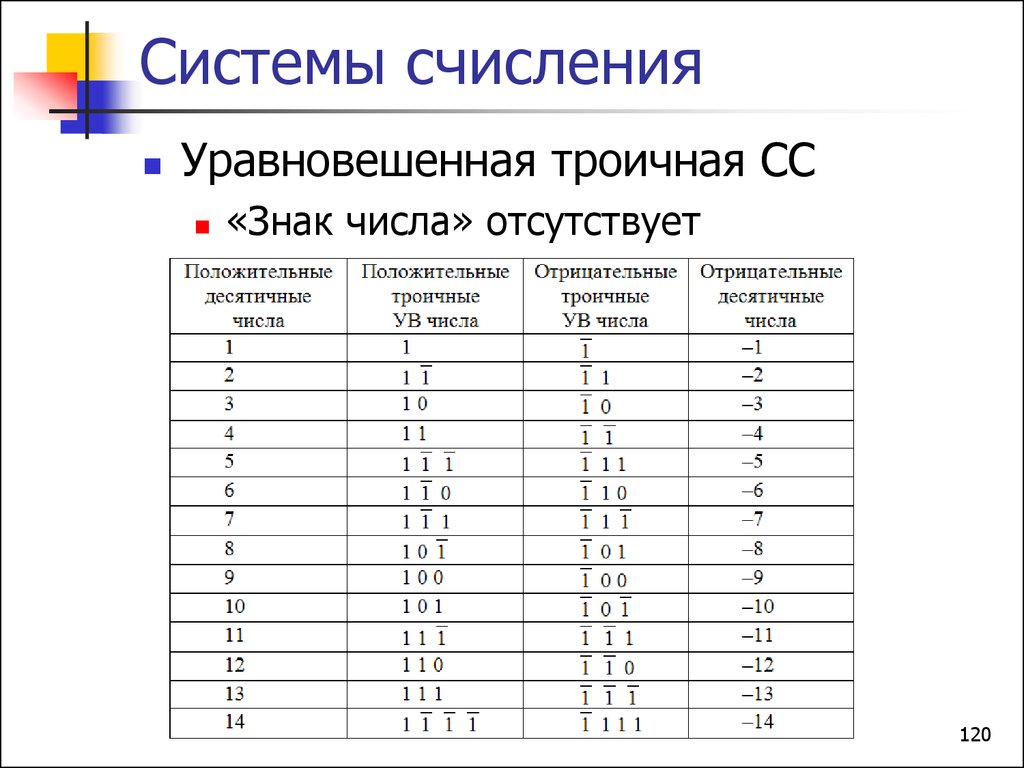 Рассмотрим шестнадцатеричное число 2DB7.

16 3	16 2	16 1	16 0
2	Д	Б	7
8192+3328+176+7
11703

Как видите, разряды в шестнадцатеричной системе счисления стоят гораздо больше, чем в любой из трех других систем счисления.

Важно знать, что 364 в восьмеричном формате — это , а не , равное обычному 364. Это точно так же, как 10 в двоичном формате, конечно, не 10 в десятичном. 10 в двоичном формате (отныне это будет записываться как 10 ₂ ) равно 2. 10 ₈ равно 8. Откуда мы это знаем? Что такое 20C.38F ₁₆ , а как узнать?

Вот почему важно понимать, как работают системы счисления. Используя наши способности базового числа, становится возможным превратить любое число в десятичное и из десятичного числа в любое число.

Основание к десятичному

Итак, мы знаем, что 364 ₈ не равно десятичному числу 364. Тогда что же это такое? Существует простой метод преобразования любого основания в десятичное с основанием десять. Если вы помните, как мы анализировали числа выше, мы использовали степени, такие как 2 9{p-1}+…+v_1B+v_0 \end{equation}

Где V ₁₀ — десятичное значение, v — цифра в разряде, p — разряд справа от числа, предполагающего крайнее правое размещение — 0, а B — начальная база. Не пугайтесь формулы! Мы собираемся пройти через это шаг за шагом.

Итак, допустим, у нас есть простое шестнадцатеричное число 2B. Мы хотим знать, каково это число в десятичном виде, чтобы мы могли лучше понять его. как нам это сделать?

Воспользуемся приведенной выше формулой. Сначала определите каждую переменную. Мы хотим найти V ₁₀ , так что это неизвестно. Число 2B ₁₆ имеет две позиции, так как состоит из двух цифр. Следовательно, p на единицу меньше, чем ¹ , поэтому p равно 1.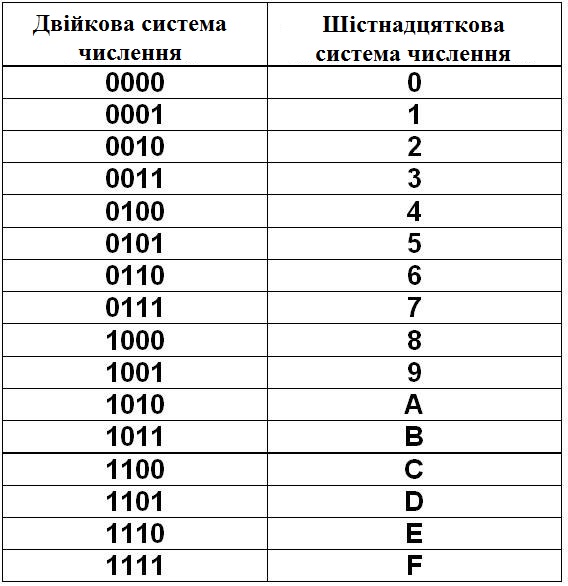 Число находится в системе счисления 16, поэтому B равно 16. Наконец, мы хотим знать, что такое v, но есть несколько v. У вас есть v ₁ и v ₀ . Это относится к значению цифры в позиции с индексом. v ₁ относится к цифре в позиции один (вторая цифра справа). Итак, т. 90) \\ V_{10} = 2(16)+11(1) \\ V_{10} = 32+11 \\ V_{10} = 43 \\ \end{align}

Следовательно, 2B ₁₆ равно 43.

Теперь позвольте мне объяснить, как это работает. Помните, как расположение цифр влияет на фактическое значение? Например, в десятичном числе 123 «1» представляет 100, то есть 1*10 ² . «2» равно 20 или 2*10 ¹ . Аналогично, в числе 2B ₁₆ «2» равно 2*16 ¹ , а B равно 11*16 ⁰ .

Таким образом мы можем определить значение чисел. Для числа 364 ₈ , мы создадим диаграмму, отображающую десятичное значение каждой отдельной цифры. Затем мы можем сложить их так, чтобы у нас было целое. Число состоит из трех цифр, поэтому, начиная справа, у нас есть позиция 0, позиция 1 и позиция 2. Поскольку это восьмерка с основанием, мы будем использовать степени 8.

8 2	8 1	8 0
3	6	4

Сейчас, 8 ² равно 64. 8 ¹ равно 8. 8 ⁰ равно 1. Что теперь?

Помните, что мы сделали с десятичным числом 123? Мы взяли значение цифры , умноженное на , в соответствующей степени. Итак, учитывая это дальше…

3*64	6*8	4*1
192	48	4

Теперь мы сложим значения вместе, чтобы получить 244. Следовательно, 364 ₈ равно 244 ₁₀ .

Точно так же, как для числа 123 мы говорим, что существует одна группа из 100, две группы из 10 и три группы из 1, восьмеричное число и число 364 имеют три группы из 64, шесть групп из 8 и четыре группы по 1.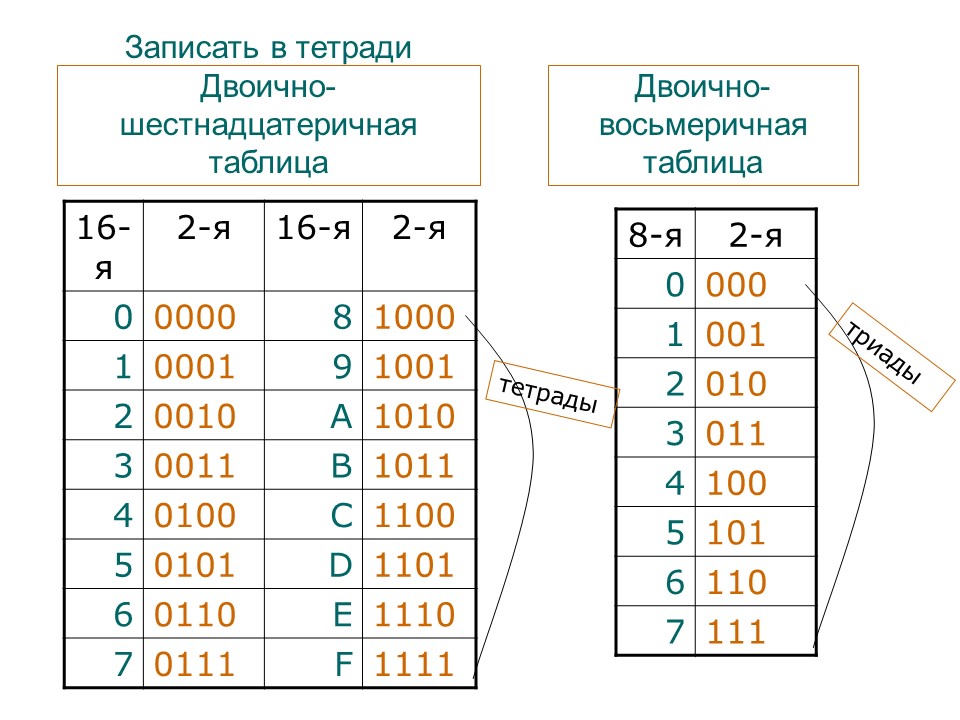

Десятичное число в основание

Точно так же, как мы можем преобразовать любое основание в десятичное, можно преобразовать десятичное число в любое основание. Допустим, мы хотим представить число 236 ₁₀ в двоичном, восьмеричном и шестнадцатеричном виде. То, что нам нужно сделать, это в значительной степени обратить вспять то, что мы сделали выше. На самом деле для этого нет хорошей формулы, но есть алгоритм, которому вы можете следовать и который поможет достичь того, что мы хотим. 9p \\ (4) \hspace{6pt} Повторять \hspace{4pt} шаги \hspace{4pt} 1 \hspace{4pt} по \hspace{4pt} 3 \hspace{4pt}, пока \hspace{4pt} p=0 \\ \end{align}

Сначала этот алгоритм может показаться запутанным, но давайте рассмотрим пример, чтобы увидеть, как его можно использовать. Мы хотим представить 236 в двоичном, восьмеричном и шестнадцатеричном виде. Итак, давайте сначала попробуем преобразовать его в двоичный код.

Первый шаг — сделать p равным $\operatorname{int}(\sqrt[B]{V})$. B — это основание, в которое мы хотим преобразовать число 2. V — это число, которое мы хотим преобразовать, 236. По сути, мы берем квадратный корень из 236 и игнорируем десятичную часть. При этом p становится равным 7,9.0003

Второй шаг говорит о том, что пусть v равно нашему числу V, деленному на B ^p . B ^p равно 2 ⁷ или 128, а целая часть числа 236, деленная на 128, равна 1. Следовательно, наша первая цифра слева равна 1. Теперь мы на самом деле меняем V на V минус цифра, умноженная на Б ^стр . Итак, теперь V будет 236-128, или 108.

Мы просто повторяем процесс, пока p не станет нулем. Когда p становится равным нулю, мы завершаем шаги в последний раз, а затем заканчиваем.

Итак, поскольку V теперь 108, p становится 6. 108 разделить на 2 9P \end{equation}

На человеческом языке: значение шифра в числе равно значению шифра самого по себе, умноженному на основание системы счисления в степени положения шифра слева вправо в числе, начиная с 0.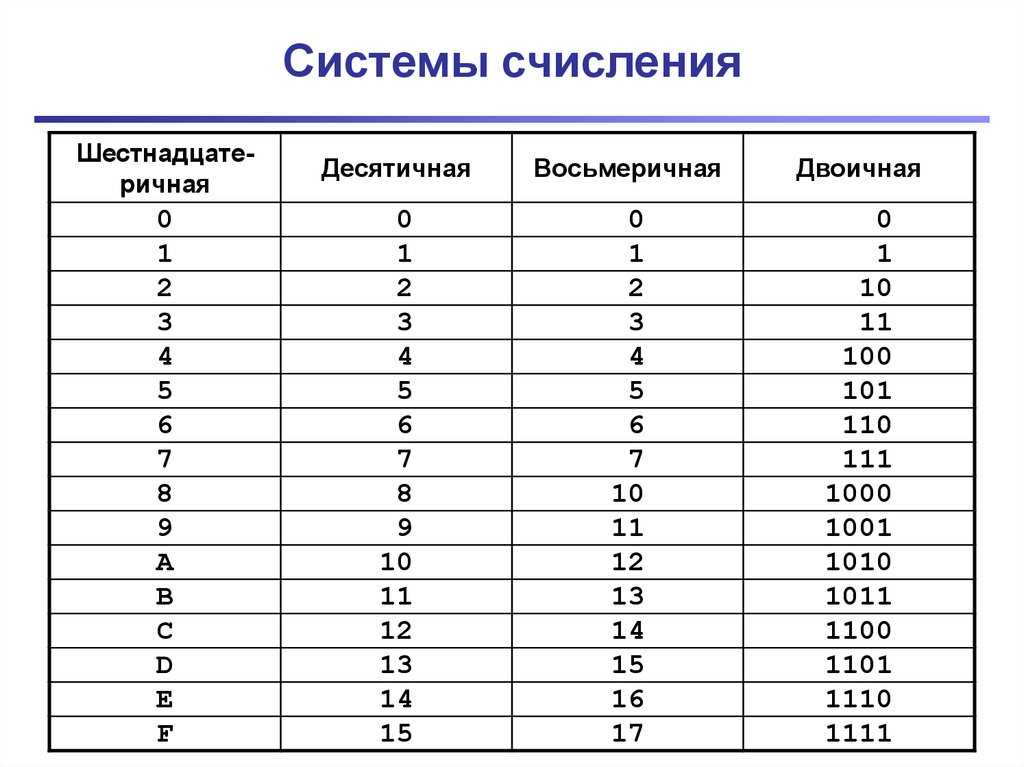 Прочтите это несколько раз и попытайтесь понять.

Таким образом, значение цифры в двоичном формате удваивает каждый раз, когда мы двигаемся влево. (см. таблицу ниже)

Из этого следует, что любой шестнадцатеричный шифр можно разбить на 4 двоичных разряда. На компьютерном языке: откусить. Теперь взгляните на следующую таблицу:

Двоичные числа
8	4	2	1		Шестнадцатеричное значение	Десятичное значение
0	0	0	0		0	0
0	0	0	1		1	1
0	0	1	0		2	2
0	0	1	1		3	3
0	1	0	0		4	4
0	1	0	1		5	5
0	1	1	0		6	6
0	1	1	1		7	7
1	0	0	0		8	8
1	0	0	1		9	9
1	0	1	0		А	10
1	0	1	1		Б	11
1	1	0	0		С	12
1	1	0	1		Д	13
1	1	1	0		Э	14
1	1	1	1		Ф	15

Еще один интересный момент: посмотрите на значение в верхней части столбца.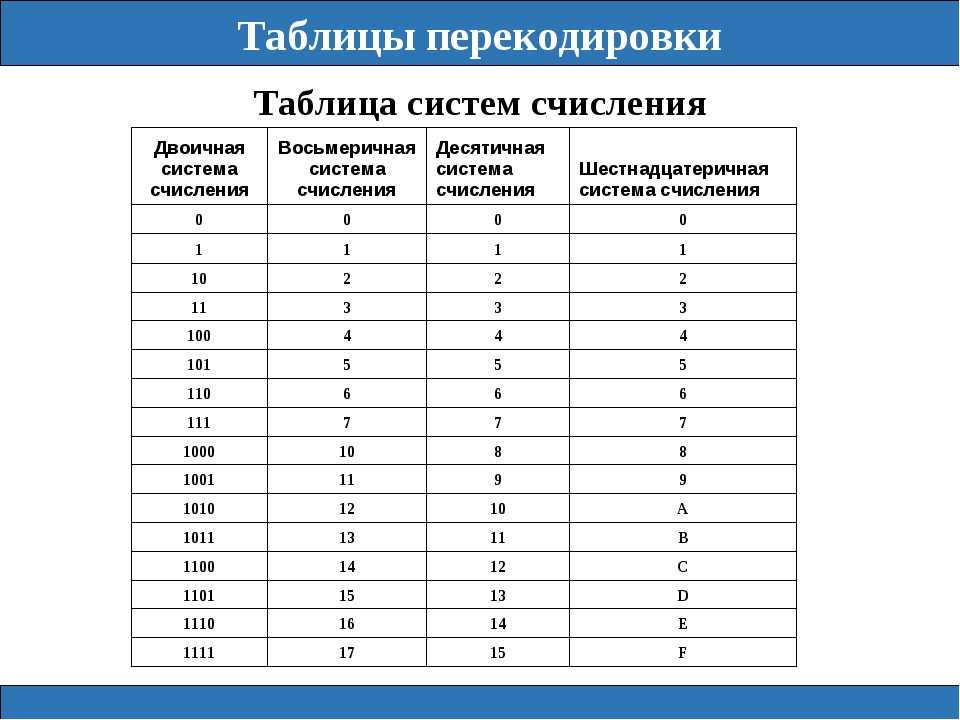 Затем посмотрите на значения. Вы понимаете, что я имею в виду? Да, ты прав! Биты включаются и выключаются в зависимости от их значения. Значение первой цифры (начиная справа) выглядит следующим образом: 0,1,0,1,0,1,0,1,0,1,… Вторая цифра: 0,0,1,1,0 ,0,1,1,0,0,1,1,0,0… Третья цифра (значение=4): 0,0,0,0,1,1,1,1,0,0,0,0 ,1,1,1,1,… И так далее…

А как насчет больших чисел? Поэтому нам понадобится дополнительная цифра. (но я думаю, что вы поняли это сами). Для значений, начинающихся с 16, наша таблица выглядит так:

Двоичные числа
16	8	4	2	1		Шестнадцатеричное значение	Десятичное значение
1	0	0	0	0		10	16
1	0	0	0	1		11	17
1	0	0	1	0		12	18
1	0	0	1	1		13	19
1	0	1	0	0		14	20
1	0	1	0	1		15	21
1	0	1	1	0		16	22
1	0	1	1	1		17	23
1	1	0	0	0		18	24
1	1	0	0	1		19	25
1	1	0	1	0		1А	26
1	1	0	1	1		1Б	27
1	1	1	0	0		1С	28
1	1	1	0	1		1Д	29
1	1	1	1	0		1Э	30
1	1	1	1	1		1F	31

Для восьмеричного числа это аналогично, с той лишь разницей, что нам нужно всего 3 цифры для выражения значений 1->7.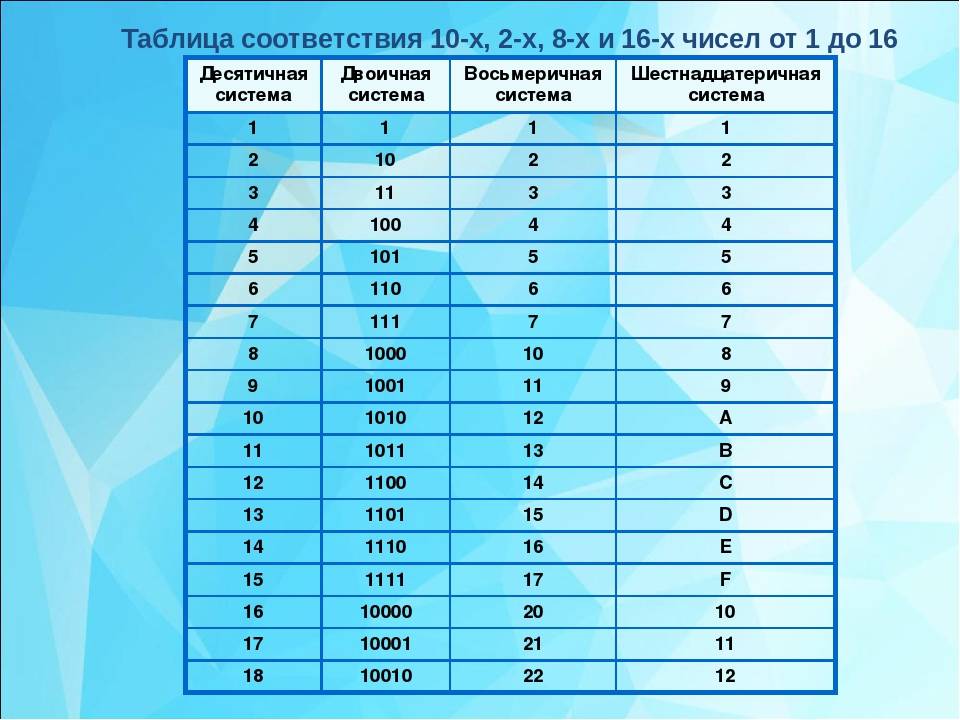 Наша таблица выглядит так:

Двоичные числа
4	2	1		Восьмеричное значение	Десятичное значение
0	0	0		0	0
0	0	1		1	1
0	1	0		2	2
0	1	1		3	3
1	0	0		4	4
1	0	1		5	5
1	1	0		6	6
1	1	1		7	7

В последнем разделе я объяснил логику двоичной, шестнадцатеричной и восьмеричной систем счисления.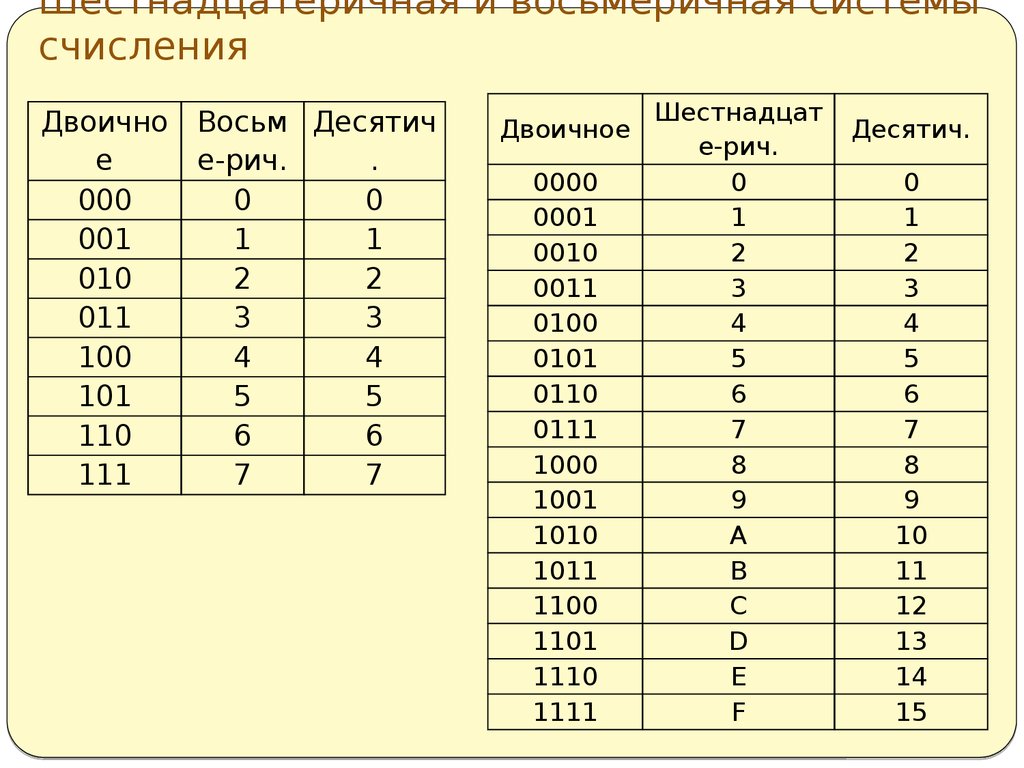 Теперь я объясню кое-что более практическое. Если вы полностью поняли предыдущую вещь, вы можете пропустить эту тему.

Из десятичной в двоичную

• Шаг 1: Проверьте, является ли ваше число четным или нечетным.
• Шаг 2: Если число четное, запишите 0 (действуя в обратном порядке, добавляя двоичные цифры слева от результата).
• Шаг 3: В противном случае, если нечетно, напишите 1 (так же).
• Шаг 4: Разделите полученное число на 2 (отбрасывая любую дробь) и вернитесь к шагу 1. Повторяйте, пока исходное число не станет равным 0.

Пример:
Преобразование 68 в двоичное:

• 68 четно, поэтому мы пишем 0.
• Разделив 68 на 2, получим 34.
• 34 тоже четное, поэтому пишем 0 (результат пока — 00)
• Разделив 34 на 2, получим 17.
• 17 нечетно, поэтому пишем 1 (пока что результат — 100 — не забудьте добавить его слева)
• Разделив 17 на 2, получим 8,5 или просто 8.
• 8 четное, поэтому пишем 0 (результат пока — 0100)
• Разделив 8 на 2, получим 4.
• 4 четно, поэтому пишем 0 (результат пока — 00100)
• Разделив 4 на 2, получим 2.
• 2 четно, поэтому пишем 0 (результат пока — 000100)
• Разделив 2 на 2, получим 1.
• 1 нечетно, поэтому пишем 1 (результат пока — 1000100)
• Разделив на 2, мы получим 0,5 или просто 0, так что все готово.
• Конечный результат: 1000100

Из двоичного в десятичный

• Запишите значения в таблицу, как показано выше. (или сделать это мысленно)
• Добавьте значение в заголовке столбца к вашему номеру, если цифра включена (1).
• Пропустить, если значение в заголовке столбца отключено (0).
• Переходите к следующей цифре, пока не наберете их все.

Пример:
Преобразование 101100 в десятичное число:

• Наибольшее цифровое значение: 32. Текущее число: 32
• Пропустить цифру «16», ее значение равно 0. Текущий номер: 32
• Добавить 8. Текущий номер: 40
• Добавить 4. Текущий номер: 44
• Пропустить цифры «2» и «1», так как их значение равно 0.
• Окончательный ответ: 44

От десятичного к шестнадцатеричному.

ЭТО ТОЛЬКО ОДИН ИЗ МНОЖЕСТВА СПОСОБОВ!

• Преобразуйте десятичное число в двоичное
• Разделить на части по 4, начиная с конца
• Посмотрите на первую таблицу на этой странице и запишите нужное число вместо полубайта
.

(можно добавить нули в начале, если количество битов не делится на 4, потому что, как и в десятичном виде, это не имеет значения)

Пример:
Конвертировать 39в шестнадцатеричное:

• Сначала мы преобразуем в двоичное (см. выше). Результат: 100111
• Далее разбиваем на байты: 0010/0111 (Примечание: я добавил два нуля, чтобы уточнить, что это байты)
• После этого конвертируем полубайты отдельно.
• Окончательный результат: 27

Из шестнадцатеричной в десятичную

*Проверьте формулу в первом абзаце и используйте ее для шифров в вашем шестнадцатеричном числе.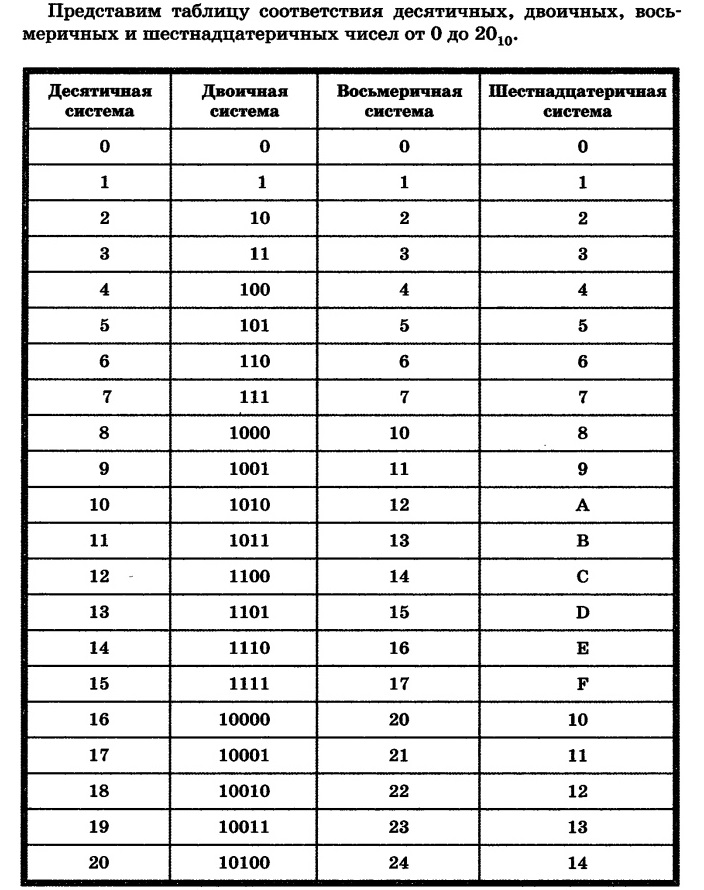 (это на самом деле работает для любого преобразования в десятичную запись)

Пример:
Преобразование 1AB в десятичное число:

• Значение B = 16 ⁰ × 11. Это дает 11, очевидно,
• Значение A = 16 ¹ × 10. Это дает 160. Наш текущий результат 171.
• Значение 1 = 16 ² × 1. Это дает 256.
• Окончательный результат: 427

Из десятичного в восьмеричное

• Преобразование в двоичное.
• Разделить на части по 3 цифры, начиная справа.
• Преобразование каждой части в восьмеричное значение от 0 до 7

Пример: преобразование 25 в восьмеричное число

• Сначала мы преобразуем число в двоичное. Результат: 11001
• Далее разделяем: 011/001
• Преобразование в восьмеричное: 31

Из восьмеричного в десятичный

Снова примените формулу выше

Пример: преобразование 42 в десятичное

• Значение 2=8 ⁰ ×2=2
• Значение 4=8 ¹ ×4=32
• Результат: 34

Хорошо, это может быть не на 100% «забавно», но, тем не менее, интересно.

• Часто ли вы видите числа, начинающиеся с 0x? Это общепринятое обозначение для указания шестнадцатеричных чисел, поэтому вы можете увидеть что-то вроде:
.

 0x000000
0x000002
0x000004
 

Эта нотация чаще всего используется для перечисления адресов компьютеров, а это совсем другая история.

• Это довольно очевидно, но вы можете «записывать» слова, используя шестнадцатеричные числа. Например:
  • CAB = 3243 в десятичной системе счисления.

Вы все поняли? Если вы так думаете, проверьте себя:

Bin	дек	Шестнадцатеричный
…	…	3А
…	76	…
101110	…	…
…	88	…
1011110	…	…
…	…	47

Сделайте несколько упражнений сами, если хотите еще.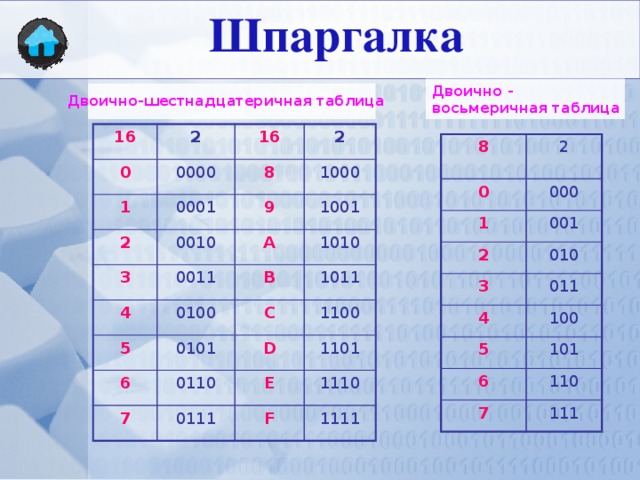

Сноски

1. На единицу меньше, потому что крайняя правая позиция равна 0, а не 1. Таким образом, p всегда на единицу меньше количества цифр.

Преобразование системы счисления — Schoolelectronic

16 мая 2021 г. 21 марта 2021 г. by schoolelectronic

Наиболее распространенное преобразование системы счисления, используемое каждый день:

Таблица преобразования десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления

В предыдущих постах мы обсуждали представление чисел в разных системах счисления. Мы также шаг за шагом решили примеры задач и попробовали несколько сокращений. Здесь мы кратко обсудим преобразование системы счисления. Другими словами, мы увидели бы, как мы можем представить данное число в другой системе счисления без изменения значения.

В следующих постах мы обсудим основные методы преобразования любого заданного числа из одной системы счисления в другую.

В этот момент вы бы спросили меня: «Эй, зачем нам нужно делать эти преобразования чисел? “.
Этот вопрос абсолютно верен, потому что в электронике правильное решение системы счисления в первую очередь зависит от типа приложения. Чтобы выразить это лучше, давайте возьмем пример.

Вы даете свой номер мобильного телефона одному из ваших одноклассников. Например, это ваш номер мобильного телефона (123)-456-0123 в десятичной системе счисления, и вы решили указать его в двоичном формате как 9.0043 (1111011)-111001000-1111011 .

Однако, когда вы вводите то же число в десятичном формате на свой компьютер. Число будет преобразовано в его двоичный эквивалент, как показано выше, и сохранено. (компьютер понимает только 0 и 1).

Из приведенного выше примера мы можем четко отличить, когда нам требуется десятичная система счисления и двоичная система счисления.

Восьмеричная система счисления и шестнадцатеричная система счисления были введены главным образом для того, чтобы сделать машинные коды более удобными для человека вместо нулей и единиц.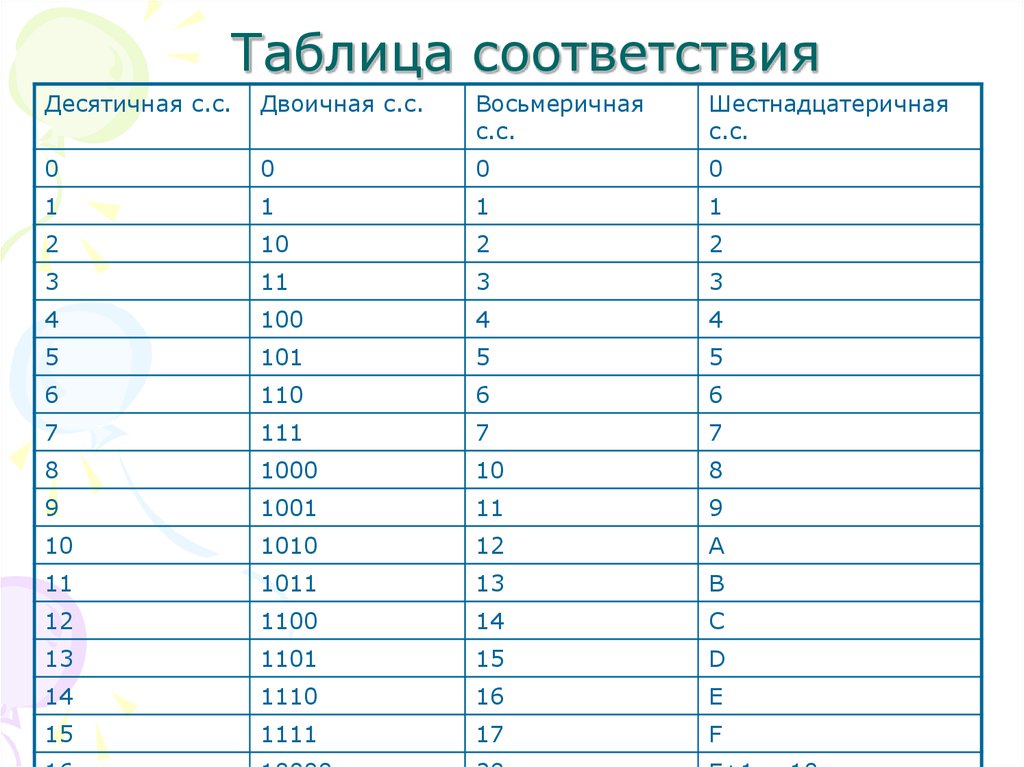

Восьмеричная система счисления откатилась назад и редко находит применение в современных приложениях. Шестнадцатеричная система счисления сегодня является наиболее широко используемой системой счисления. Современные компьютеры используют шестнадцатеричный формат для адресов памяти и значительно упрощают отладку всякий раз, когда компьютер выдает ошибку с шестнадцатеричным адресом вместо длинной строки из 0 и 1.

Мы начнем изучать методы преобразования с десятичной системы счисления, так как мы более знакомы с десятичной системой счисления. При преобразовании десятичной системы счисления мы изучим следующие преобразования

Наиболее распространенное преобразование системы счисления, используемое каждый день:

1. Десятичная система счисления в двоичную систему счисления
2. Десятичная система счисления в восьмеричную систему счисления
3. Десятичная система счисления в шестнадцатеричную систему счисления
4. Двоичная система счисления система счисления
5. Восьмеричная система счисления в десятичную систему счисления
6. Шестнадцатеричная система счисления в десятичную

Вы также можете использовать этот преобразователь шестнадцатеричного в десятичный, чтобы быстро преобразовать любой шестнадцатеричный в десятичный эквивалент.