Системы счисления: двоичная, восьмеричная, шестнадцатеричная, десятиричная
Система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Существуют системы позиционные и непозиционные. В непозиционных системах счисления вес цифры не зависит от позиции, которую она занимает в числе. Так, например, в римской системе счисления в числе XXXII (тридцать два) вес цифры X в любой позиции равен просто десяти. В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число. Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание можно принять любое натуральное число — два, три, четыре, шестнадцать и т. д. Следовательно, возможно бесконечное множество позиционных систем.
Десятичная система счисления
Эта система пришла в Европу из Индии, где она появилась не позднее VI века н.
э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 и его степени; 10, 100, 1000 и т. д. Крайняя правая цифра числа показывает число единиц, вторая справа — число десятков, следующая — число сотен и т. д. Причина наибольшей распространенности десятичной системы счисления состоит в том, что первым счетным аппаратом человека являлись его руки. Число пальцев и стало отправным пунктом для системы счета.
Двоичная система счисления
В этой системе всего две цифры — 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т. д. Крайняя правая цифра числа показывает число единиц, следующая цифра — число двоек, следующая — число четверок и т. д. Двоичная система счисления позволяет закодировать любое натуральное число — представить его в виде последовательности нулей и единиц.
В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически.
Восьмеричная система счисления
В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает — как и в десятичном числе — просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем 64 и т. д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.
Шестнадцатеричная система счисления
Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе.
В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: А, В, С, D, Е, F. Цифра 1, записанная в самом младшем разряде, означает просто единицу. Та же цифра 1 в следующем разряде — 16 (десятичное), в следующем — 256 (десятичное) и т. д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогично тому, как это делается для восьмеричной системы.
Запись опубликована в рубрике Информатика с метками система. Добавьте в закладки постоянную ссылку.
Перевод чисел из десятичной в шестнадцатеричную систему
Десятичная система счисления
Десятичная система счисления является наиболее часто используемой и стандартной системой в повседневной жизни. Она использует число 10 в качестве основания. Поэтому имеет 10 символов: цифры от 0 до 9, а именно 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9.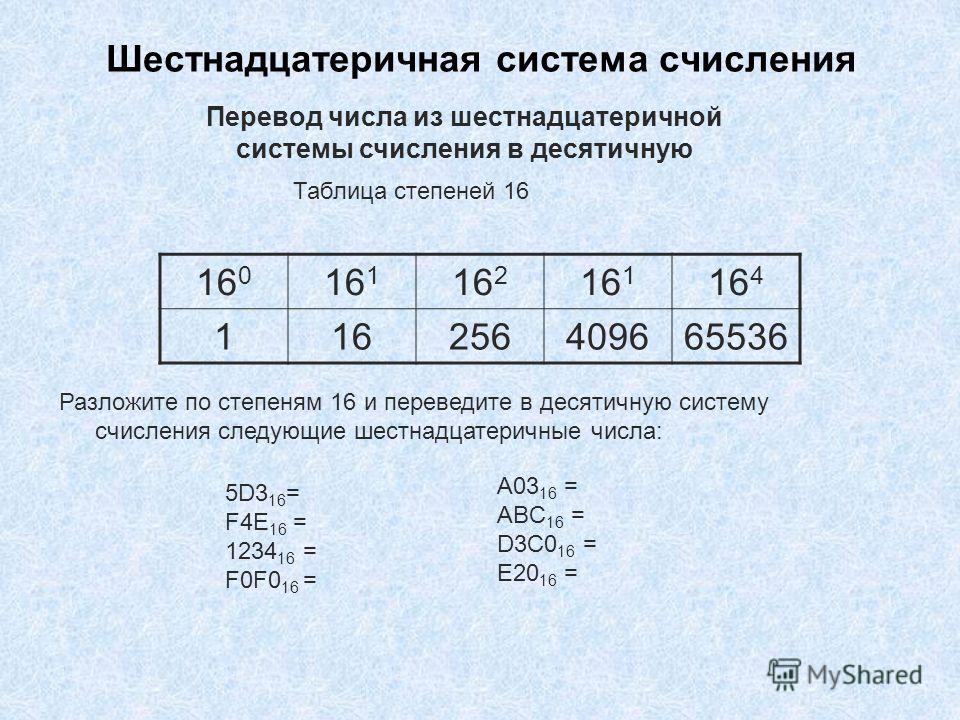
Как одна из древнейших известных систем счисления, система десятичных чисел использовалась многими древними цивилизациями. Трудность представления очень больших чисел в десятичной системе была преодолена индуистско-арабской системой счисления. Индусско-арабская система счисления дает позиции цифрам в числе, и этот метод работает с использованием степеней основания 10. Цифры поднимаются до n-й степени в соответствии с их положением. В системе base-10 число 567.89 представляет сумму (5 × 102) + (6 × 101) + (7 × 100) + (8 × 10-1) + (9 × 10-2).
Двоичная система счисления
Шестнадцатеричная система использует число 16 в качестве своего основания. Системы счисления base-16 используются 16 символов. Это 10 десятичных цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и первые шесть букв английского алфавита (A, B, C, D, E, F). Буквы используются из-за необходимости представлять значения 10, 11, 12, 13, 14 и 15 одним символом.
Шестнадцатеричный код используется в математике и информационных технологиях как более удобный способ представления двоичных чисел.
Каждые четыре двоичные цифры представляются как одна шестнадцатеричная цифра, следовательно, шестнадцатеричная система — это язык для записи двоичного кода в сокращенной форме.
Четыре двоичные цифры называются полубайтами. Это означает, что один байт может переносить двоичные значения от 0000 0000 до 1111 1111. В шестнадцатеричном виде они могут быть представлены в более удобной форме для пользователя, в диапазоне от 00 до FF.
Как перевести число из десятичной в шестнадцатеричную систему счисления?
- Разделите число на 16.
- Получите целочисленное отношение для следующей итерации.
- Получите остаток от шестнадцатеричной цифры.
- Повторите шаги, пока частное не станет равным 0.
Пример:
Перевод числа 3675210 в шестнадцатеричную систуму:
| Деление на 16 | Частное | Остаток в десятичной | Остаток в шестнадцатеричной |
|---|---|---|---|
| 36752/16 | 2297 | 0 | 0 |
| 2297/16 | 143 | 9 | 9 |
| 143/16 | 8 | 15 | F |
| 8/16 | 0 | 8 | 8 |
Таблица перевода из десятичной в шестнадцатеричную систему
| Десятичное число | Шестнадцатеричное число |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
Шестнадцатеричная система счисления Факты для детей
Детская энциклопедия Факты
Шестнадцатеричная система счисления , также известная как hex , представляет собой систему счисления, состоящую из 16 символов (основание 16).
Стандартная система счисления называется десятичной (основание 10) и использует десять символов: 0,1,2,3,4,5,6,7,8,9. Шестнадцатеричный использует десятичные числа и включает шесть дополнительных символов. Нет символов, означающих десять, одиннадцать и т. д., поэтому эти символы представляют собой буквы английского алфавита: A, B, C, D, E и F. Шестнадцатеричный A = десятичный 10, а шестнадцатеричный F = десятичный 15.
Люди в основном используют десятичную систему. Вероятно, это потому, что у людей десять пальцев (десять цифр). Однако у компьютеров есть только включение и выключение, называемое двоичной цифрой (или, для краткости, битом). Двоичное число — это просто последовательность нулей и единиц: например, 11011011. Для удобства инженеры, работающие с компьютерами, склонны группировать биты вместе. Раньше, например, в 1960-х годах, они группировали по 3 бита за раз (так же, как большие десятичные числа группируются по три, например число 123 456 789).). Три бита, каждый из которых может быть включен или выключен, могут представлять восемь чисел от 0 до 7: 000 = 0; 001 = 1; 010 = 2; 011 = 3; 100 = 4; 101 = 5; 110 = 6 и 111 = 7.
Это называется восьмеричным.
По мере того, как компьютеры становились больше, было удобнее группировать биты по четыре, а не по три. Дополнительный бит может быть либо включен, либо выключен, 0 или 1. Таким образом, это удваивает числа, которые будет представлять символ. Это 16 цифр. Hex = 6 и Decimal = 10, поэтому он называется шестнадцатеричным. Четыре бита называются кусочек (иногда пишется как кусочек ). Полубайт — это одна шестнадцатеричная цифра, которая записывается с использованием символов 0-9 или A-F. Два полубайта — это байт (8 бит). В большинстве компьютерных операций используется байт или число, кратное байту (16 бит, 24, 32, 64 и т. д.). Шестнадцатеричный формат упрощает запись этих больших двоичных чисел.
Во избежание путаницы с десятичной, восьмеричной или другими системами счисления шестнадцатеричные числа иногда пишутся с буквой «h» после числа. Например, 63h означает 63 в шестнадцатеричном формате. Разработчики программного обеспечения довольно часто используют 0x перед номером (0x63).
Содержание
- Шестнадцатеричные значения
- Преобразование
- Двоичный код в шестнадцатеричный
- Шестнадцатеричный и десятичный
- Связанные страницы
- Картинки для детей
Шестнадцатеричные значения
Шестнадцатеричная система счисления аналогична восьмеричной системе счисления (основание 8), поскольку каждое из них можно легко сравнить с двоичной системой счисления. Шестнадцатеричный использует четырехбитное двоичное кодирование. Это означает, что каждая цифра в шестнадцатеричном формате равна четырем цифрам в двоичном формате. Octal использует трехбитную двоичную систему.
В десятичной системе первая цифра — это единица разряда, следующая цифра слева — разряда десятков, следующая — сотни разряда
Таким образом, 1h = 1 десятичный, 10h = 16 десятичный и 100h = 256 десятичный.Пример значений шестнадцатеричных чисел, преобразованных в двоичные, восьмеричные и десятичные.
|
Преобразование
Двоичное число в шестнадцатеричное
При изменении числа из двоичного в шестнадцатеричное используется метод группировки.
Двоичное число разделено на группы по четыре цифры, начиная справа. Затем эти группы преобразуются в шестнадцатеричные цифры, как показано в приведенной выше таблице для шестнадцатеричных чисел от 0 до F. Чтобы перейти от шестнадцатеричного, выполняется обратное. Каждая шестнадцатеричная цифра заменяется на двоичную, а группировка обычно удаляется.
| Двоичный | Группировки | Шестнадцатеричный | |||
|---|---|---|---|---|---|
| 01100101 | 0110 | 0101 | 65 | ||
| 010010110110 | 0100 | 1011 | 0110 | 4B6 | |
| 1101011101011010 | 1101 | 0111 | 0101 | 1010 | Д75А |
Шестнадцатеричный и десятичный
Чтобы преобразовать число из шестнадцатеричного в десятичное, есть два распространенных способа.
Первый метод чаще используется при преобразовании вручную:
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0-9 то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15.
- Сохраняйте сумму чисел, преобразованных на каждом шаге ниже.
- Начните с младшей значащей шестнадцатеричной цифры. Это цифра справа. Это будет первый пункт в сумме.
- Возьмите вторую наименее значащую цифру. Это рядом с цифрой на правом конце. Умножьте десятичное значение цифры на 16. Добавьте это к сумме.
- Сделайте то же самое для третьей наименее значащей цифры, но умножьте ее на 16 2 (то есть 16 в квадрате или 256). Добавьте его к сумме.
- Продолжайте для каждой цифры, умножая каждый разряд на другую степень 16. (4096, 65536 и т. д.)
| Местоположение | ||||||
|---|---|---|---|---|---|---|
| 6 | 5 | 4 | 3 | 2 | 1 | |
| Значение | 1048576 (16 5 ) | 65536 (16 4 | 4096 (16 3 ) | 256 (16 2 ) | 16(16 1 ) | 1 (16 0 ) |
Следующий метод чаще используется при преобразовании числа в программном обеспечении. Ему не нужно знать, сколько цифр в числе, прежде чем оно начнется, и оно никогда не умножается более чем на 16, но на бумаге оно выглядит длиннее.
- Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0-9 то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15.
- Сохраняйте сумму чисел, преобразованных на каждом шаге ниже.
- Начните со старшей цифры (цифра слева). Это первый пункт в сумме.
- Если существует другая цифра, умножьте сумму на 16 и добавьте десятичное значение следующей цифры.
- Повторяйте вышеуказанный шаг, пока не закончатся цифры.
Пример: 5Fh и 3425h в десятичном виде, метод 1
|
|
Пример: 5Fh и 3425h в десятичном виде, метод 2
|
|
Связанные страницы
- Двоичная система счисления
- Восьмеричная система счисления
- Десятичная система счисления
Изображения для детей
Все содержимое статей энциклопедии Kiddle (включая изображения статей и факты) можно свободно использовать по лицензии Attribution-ShareAlike, если не указано иное. Процитируйте эту статью:
Шестнадцатеричная система счисления. Факты для детей. Энциклопедия Киддла.
Что такое шестнадцатеричная система счисления? — Двоичное в шестнадцатеричное, восьмеричное в шестнадцатеричное и значение шестнадцатеричного
Шестнадцатеричная система счисления образует основу цифровой системы , такой как микропроцессоры, микроконтроллеры и т. д. Это система счисления, состоящая из 16 элементов, в которых 10 чисел используются от 0 до 9 и 6 алфавитов от A до F. Любое другое число может быть представлено в шестнадцатеричной системе счисления с помощью комбинации этих 16 элементов.
Слово шестнадцатеричное состоит из двух слов: «HEX» и «DECIMAL» . Шестнадцатеричный означает 6, а десятичное означает 10, сумма этих двух равна 16, что означает его основание. Таким образом, шестнадцатеричная система счисления также известна как система счисления «База-16» .
Причина этого в том, что основание или основание шестнадцатеричной системы счисления равно 16. Мы уже обсуждали в нашей предыдущей статье, что основанием системы счисления является количество элементов, образующих эту систему счисления.
Значение шестнадцатеричных чисел
Шестнадцатеричное число является излюбленной альтернативой для исследователей, работающих с цифровыми системами. Они предпочитают шестнадцатеричные числа двоичным и восьмеричным числам.
Вы сталкиваетесь с тем же вопросом????
Это связано с тем, что двоичное представление малых чисел простое и короткое по длине. А как быть с большими числами, т.е. числами с 32 цифрами, 64 цифрами и даже больше. В этом случае представление двоичного числа будет длинной строкой из 0 и 1. Может возникнуть вероятность ошибки либо при чтении числа, либо при записи числа.
Эту задачу можно решить с помощью шестнадцатеричной системы счисления. Каждая группа из четырех цифр двоичного числа может быть записана в виде одной цифры шестнадцатеричного числа.
Таким образом, шестнадцатеричное число уменьшает длину представления числа на 1/4 th .
В нашей предыдущей статье в категории «Цифровая электроника» мы обсуждали, что восьмеричные числа также сокращают длину числовой строки, но уменьшают длину на 1/3. В то время как шестнадцатеричный более эффективен, поскольку нам нужна только одна цифра в шестнадцатеричном числе для представления 4 цифр двоичного числа.
Счет в шестнадцатеричной системе счисления
Счет в шестнадцатеричной системе счисления начинается с 0. Остальные числа можно понять с помощью таблицы ниже. Число 10 в шестнадцатеричной системе счисления представлено буквой А, затем 11 буквой В и так далее. Этот тип буквенного представления используется в шестнадцатеричной системе счисления, чтобы отличить ее от десятичной системы счисления.
Если мы напишем число 10 напрямую, это сделает систему счисления сложной и запутанной. Мы не сможем определить, является ли это число 10 десятичным или шестнадцатеричным.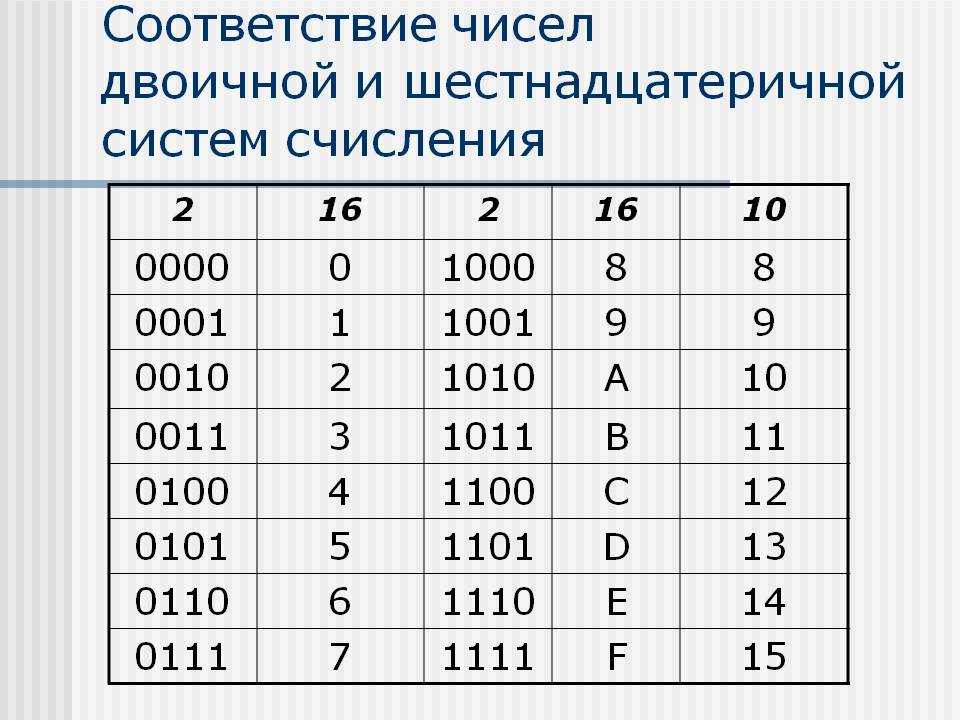
Таким образом, чтобы понять, имеем ли мы дело с десятичной или шестнадцатеричной системой счисления, мы используем алфавиты A, B, C, D, E и F для обозначения 10, 11, 12, 13, 14, 15. соответственно.
Преобразование из шестнадцатеричной системы счисления в другую и наоборот цифры. В случае наличия десятичной точки позиционная мощность будет последовательно увеличиваться от 0 до более высоких значений при движении влево от десятичной точки. Точно так же он будет увеличиваться в отрицательных степенях при движении вправо от десятичной дроби.
Рассмотрим пример.
(131.f2) 16 = 1*16 2 + 3*16 1 + 1*16 0 + 15*16 -1 + 2*16 -2
x + 2*16 -2
9000 2=
= = + 2*16 -2
9000 2 9000 2 9000 2= + 2. 256 + 48 + 1 + (15/16) + (2/256)
= (305,9453125) 10
Десятичное число в шестнадцатеричное
Десятичное число можно преобразовать в шестнадцатеричное, разделив его на 16 и записав непрерывно на 16 все остальные в обратном порядке.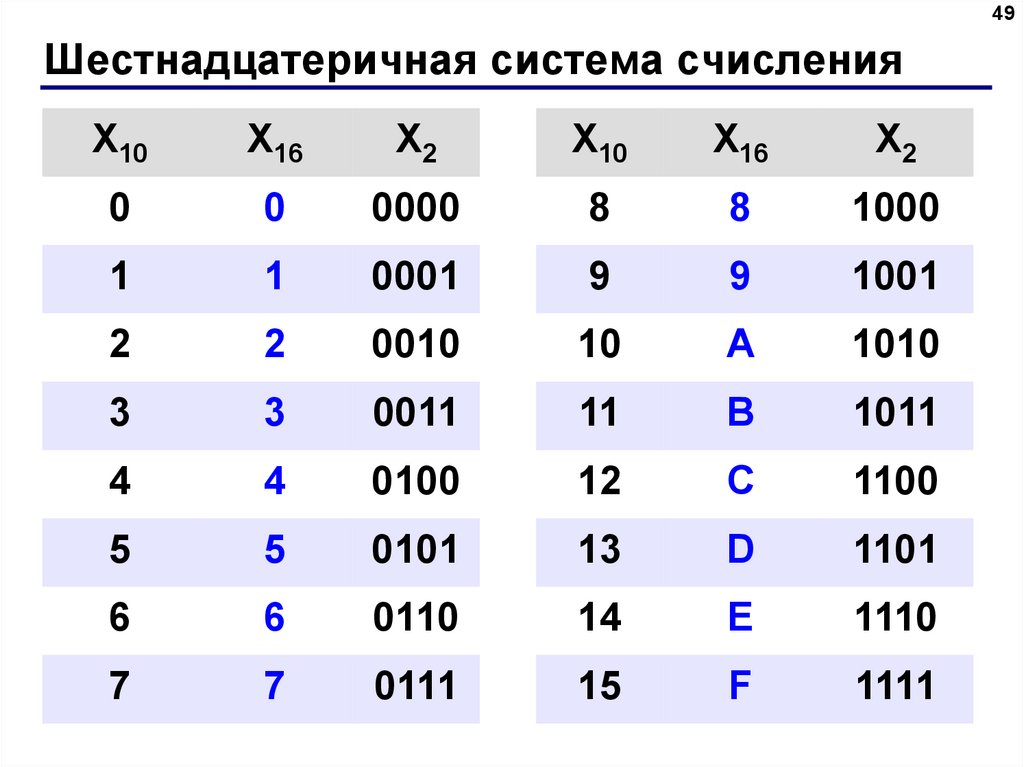
Если десятичное число состоит из десятичной точки, то целая часть будет преобразована отдельно, а дробная часть будет преобразована отдельно.
Целая часть будет преобразована последовательным делением числа на 16, так как это основание системы счисления. Дробная часть будет преобразована последовательным умножением дробной части на 16 и отдельной записью переносной части.
Весь процесс преобразования десятичного числа в шестнадцатеричное можно понять на приведенном ниже примере.
Шестнадцатеричное в двоичное
Преобразование из шестнадцатеричного в двоичное простое и может быть выполнено за один шаг. Каждая цифра шестнадцатеричной системы счисления может быть записана в ее 4-значный двоичный эквивалент. Вы можете добавить нули, если двоичный эквивалент состоит из 3 цифр. Таким образом, все двоичные цифры записываются в последовательности, чтобы получить двоичный эквивалент шестнадцатеричных чисел.
Процесс преобразования можно более четко понять с помощью примера.
Давайте рассмотрим шестнадцатеричное число (A6B.F5) 16 . Теперь, чтобы преобразовать это число в двоичное, нам нужно записать двоичный эквивалент каждой цифры.
Двоичное число в шестнадцатеричное
Преобразование двоичного числа в шестнадцатеричное может быть достигнуто путем формирования группы из 4 цифр двоичного числа, а затем записи шестнадцатеричного эквивалента двоичной группы. Мы можем добавить количество нулей в соответствии с нашим удобством, чтобы завершить группу из 4 цифр. Мы должны формировать группы, начиная с LSB и двигаясь к MSB.
Давайте разберемся с этим на примере
Шестнадцатеричное число в восьмеричное
Шестнадцатеричное число можно преобразовать в восьмеричное в два этапа. Во-первых, путем преобразования шестнадцатеричного числа в двоичное число. Во-вторых, путем преобразования двоичного числа в восьмеричное. Мы хорошо знакомы с преобразованием двоичного кода в восьмеричный. Во-первых, сформировав группу из трех двоичных цифр, начиная с LSB до MSB, а затем записав ее восьмеричный эквивалент.