Шестнадцатеричная система исчесления: Шестнадцатеричная система счисления | Информатика

Перевод из шестнадцатеричной в десятичную систему счисления, калькулятор

Исходное число

Направление перевода

2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

Сообщить об ошибке

В избранное

Виджет

Вы можете сохранять ваши расчеты и они будут отображаться здесь.

Для сохранения расчета воспользуйтесь кнопкой под формой калькулятора.

Преобразовать число из шестнадцатеричной системы счисления в десятичную можно следующим образом:

Каждый разряд числа необходимо умножить на 16ⁿ, где n — номер разряда, начиная с 0. Затем суммировать полученные значения.

abc₂ = (a×16² + b×16¹ + c×16

0)₁₀

5A₁₆ = (5*16¹ + 10*8⁰)₁₀ = 90₁₀

Смотрите также

• Перевод из двоичной в десятичную
• Перевод из двоичной в восьмеричную
• Перевод из двоичной в шестнадцатеричную
• Перевод из десятичной в двоичную
• Перевод из десятичной в восьмеричную
• Перевод из десятичной в шестнадцатеричную
• Перевод из восьмеричной в двоичную
• Перевод из восьмеричной в десятичную
• Перевод из шестнадцатеричной в двоичную

Перевод из шестнадцатеричной в двоичную систему счисления, калькулятор

Осуществить перевод числа из шестнадцатеричной системы счисления в двоичную можно тремя способами.

Способ 1:

Перевести сначала в десятичную систему счисления, затем из нее в конечную.

Способ 2:

1. Каждый разряд шестнадцатеричного числа, начиная с высшего делим на 2, записываем остаток и делим снова до тех пор, пока в результате не будет нуля. Каждый раз записываем остаток. Буквеные разряды шестнадцатеричного числа заменяем соответствующими числовыми значениями: A — 10, B — 11, C — 12, D — 13, E — 14, F — 15.
2. Записываем полученные остатки в обратном порядке, получая двоичное число.
3. Если полученное двоичное число имеет менее четырех разрядов (то есть на если предыдущем шаге получили менее четырех остатков), то дополняем нулями слева до четырех разрядов.
4. Повторяем предыдущие шаги для каждого следующего разряда, таким образом получаем несколько групп по 4 разряда двоичного числа.
5. Записываем все вместе по порядку, отбрасываем нули слева при их наличии, получаем искомую двоичную запись числа.

Возьмем число 8E₁₆.

1. Делим на 2 каждый разряд, начиная с высшего, получаем остатки:

   8 / 2 = 4, остаток 0

   4 / 2 = 2, остаток 0

   2 / 2 = 1, остаток 0

   1 / 2 = 0, остаток 1

2. Записываем остатки в обратном порядке: 1000
3. Дополнять нулями не нужно, т.к. полученное число имеет 4 разряда.
4. Повторяем для каждого следующего разряда:

   E / 2 = 14 / 2 = 7, остаток 0

   7 / 2 = 3, остаток 1

   3 / 2 = 1, остаток 1

   1 / 2 = 0, остаток 1

   Получаем 1110

5. Записываем все вместе (1000)(1110), получаем двоичное число 10001110₂

Способ 3:

Используем таблицу тетрад:

Цифра	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Тетрада	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111

Каждую цифру исходного числа заменяется на соответствующие тетрады.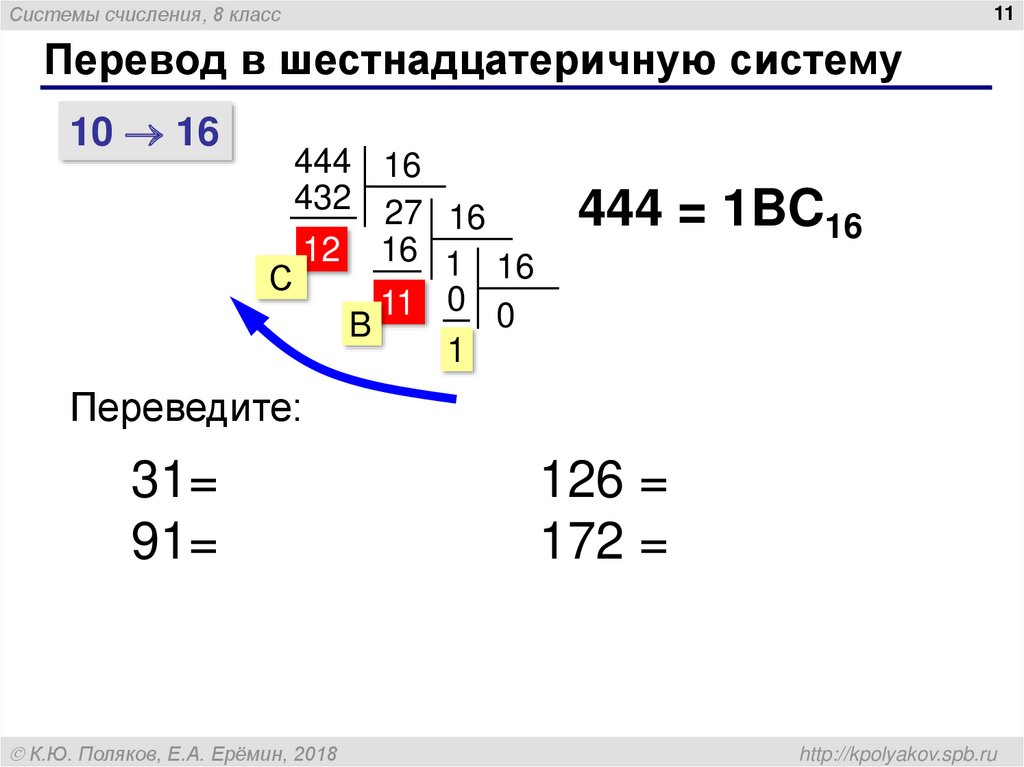 Ведущие нули самой первой тетрады отбрасываются.

D8₁₆ = (1101) (1000) = 11011000₂

Смотрите также

• Перевод из двоичной в десятичную
• Перевод из двоичной в восьмеричную
• Перевод из двоичной в шестнадцатеричную
• Перевод из десятичной в двоичную
• Перевод из десятичной в восьмеричную
• Перевод из десятичной в шестнадцатеричную
• Перевод из восьмеричной в двоичную
• Перевод из восьмеричной в десятичную
• Перевод из шестнадцатеричной в десятичную

Шестнадцатеричные числа — Electronics-Lab.com

Шестнадцатеричные числа

Шестнадцатеричное число (16) представляет собой систему счисления с основанием 16 , в которой используется шестнадцать (16) чисел для представления значения его разряда. В шестнадцатеричном числе используется группа или набор из четырех (4) двоичных цифр для формирования шестнадцатеричной цифры . Другими словами, шестнадцатеричная цифра эквивалентна полубайту, а из предыдущей статьи мы знаем, что полубайт — это четырехбитное двоичное число. Крайний правый полубайт образует наименее значимую шестнадцатеричную цифру, а слева от него можно добавлять полубайты для представления большего шестнадцатеричного числа.

Архитектура цифровых систем рассчитана на 8-, 16-, 32- и 64-битные и т. д. двоичные числа и представление этих чисел нулями (0) и единицами (1) становятся довольно запутанными и сложными. Чтение и запись больших двоичных чисел может привести к ошибкам, и информация действительно может стать сомнительной. Представлением больших двоичных чисел можно управлять с помощью системы нумерации с более высоким базовым значением, которая будет вмещать больше значений в однозначных цифрах по сравнению с двоичными цифрами (битами). Восьмеричная цифра (с основанием 8) может использовать восемь (8) чисел (от 0 до 7) и может вмещать 3-битное двоичное число. 3-битное двоичное число довольно мало и не подходит для 8-, 16-, 32- и 64-битных архитектур и т. д. Точно так же десятичное число подходит для представления 3-битного двоичного числа, но тратит впустую два (8 и 9).) числовые значения. Другими словами, восьмеричная система счисления более подходит по сравнению с десятичными (десятичными) числами, когда речь идет о представлении двоичных чисел.

Подходящей и подходящей системой нумерации является та, которая может вмещать 4-битное двоичное число. Как мы знаем, 4-битное число может содержать шестнадцать (16) значений (два, возведенные в степень четыре). Для этого требуется система счисления, имеющая набор из шестнадцати значений, то есть от 0 до 15. Десятичная цифра имеет диапазон чисел от 0 до 9, и такие числа, как 10, 11, 12, 14 и 15, не могут быть представлены, поскольку они предполагает использование ранее использовавшихся номеров. В шестнадцатеричном формате значения выше девяти (9) представлены английскими алфавитами, такими как A, B, C и т. д. Использование этих алфавитов решает проблему повторения чисел для десяти (10) и более значений.

Это означает, что A, B, C, D, E и F в шестнадцатеричном формате представляют собой десятичные числа: десять (10), одиннадцать (11), двенадцать (12), тринадцать (13), четырнадцать (14) и пятнадцать ( 15). То же самое верно для представления эквивалентных двоичных чисел «1010», «1011», «1100», «1101», «1110». и «1111» соответственно. Сложность представления большего двоичного числа можно облегчить, разбив двоичное число на группы по 4 бита. Например, рассмотрим (1101100111001010 ₂ ) — 16-битное двоичное число, которое можно записать как (1101 1001 1100 1010 ₂ ) . Последнее достигается путем разбиения на группу или набор из 4 битов, и полученное двоичное число намного легче читать.

Длину и сложность двоичных чисел можно дополнительно уменьшить, преобразовав их в эквивалентные шестнадцатеричные числа. Однако шестнадцатеричные числа являются сложными по сравнению с десятичными числами и используются только в цифровых системах.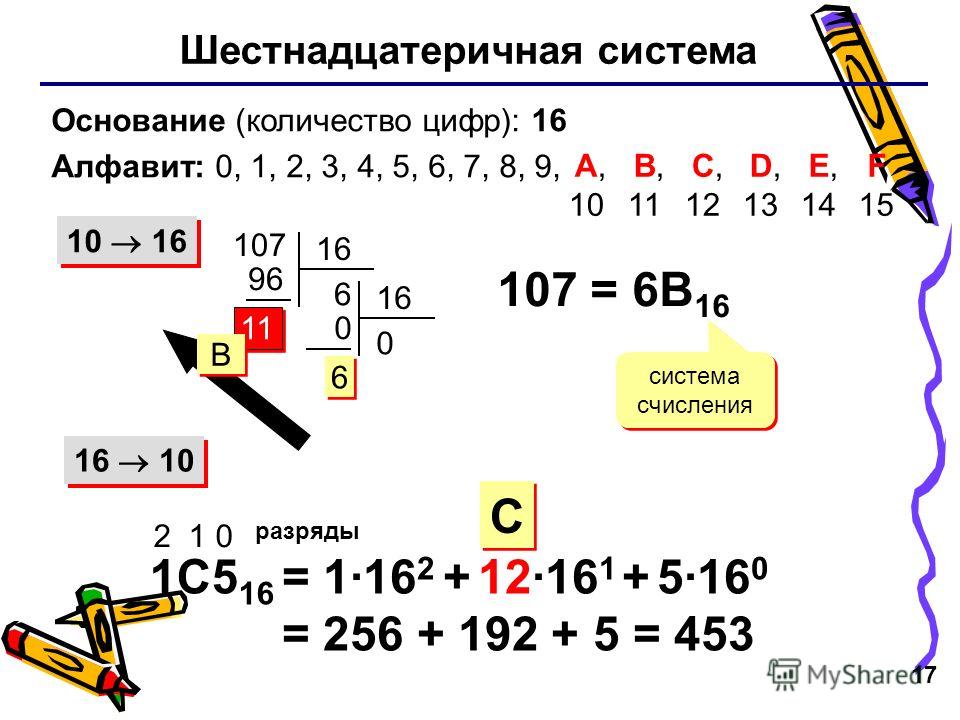 Четырехбитные двоичные числа «0000», «0001», «0010», … и «1111» представлены одной шестнадцатеричной цифрой. Четырехбитное двоичное число называется «полубайтом», что эквивалентно шестнадцатеричной цифре. Байт состоит из 8 бит или двух полубайтов, и две шестнадцатеричные цифры представляют его эквивалент. Например, двоичное число (10100111 ₂ ) разделен на две половинки/кусочки (1010 0111 ₂ ) . При этом (1010 ₂ ) эквивалентно (10 ₁₀ ) в десятичном виде и ( A ₁₆ ) в шестнадцатеричном. Точно так же второй полубайт (0111 ₂ ) эквивалентен (7) в десятичном и шестнадцатеричном формате. Таким образом, двоичное число (10100111 ₂ ) эквивалентно (A7 ₁₆ ) в шестнадцатеричном формате.

Шестнадцатеричные числа

В следующей таблице перечислены десятичные числа от 0 до 15 и их эквиваленты в двоичных и шестнадцатеричных числах.

В приведенной выше таблице показаны эквивалентные десятичные числа от 0 до 15 для шестнадцатеричных цифр. Для подсчета чисел после пятнадцати (F) в шестнадцатеричном формате используется процедура, аналогичная другим системам счисления, т. е. включая значащую цифру слева. Например, число «16», преобразованное в двоичное число, равно 9.0005 (0001 0000) ₂ и его эквивалент в шестнадцатеричном формате (10 ₁₆ ). Точно так же эквивалентом 17 в шестнадцатеричном формате является (11 ₁₆ ) , и, следуя той же процедуре, шестнадцатеричное число может быть расширено до желаемого значения. Используя приведенную выше таблицу, любое двоичное число можно легко преобразовать в эквивалентное ему шестнадцатеричное число. Например, 16-битное число (1010 1100 0111 1011 ₂ ) , преобразованное в шестнадцатеричное, равно (AC7B ₁₆ ) . Гораздо проще написать и запомнить это шестнадцатеричное число, чем 16-битный ряд из 0 и 1.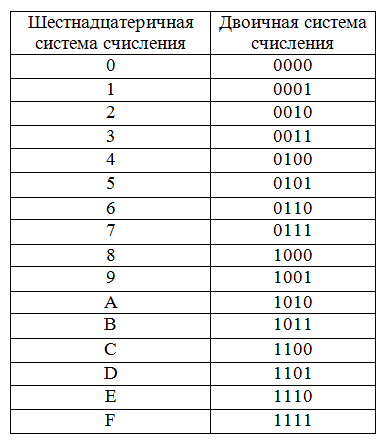 Следовательно, рекомендуется записывать двоичные числа в шестнадцатеричной системе счисления, чтобы избежать ошибок и т. д. значащая цифра для обозначения шестнадцатеричного значения. Например, указанное выше шестнадцатеричное число (AC7B ₁₆ ) также можно записать как 9.0005 (#AC7B) .

Счет в шестнадцатеричном формате

Как описано выше, значение шестнадцатеричного числа можно расширить, используя дополнительные значащие цифры. Одна шестнадцатеричная цифра, начинающаяся с «0», может составлять до #F (15 X 16 ⁰ = 15 ₁₀ ) , расширенная до двух цифр, может составлять до #FF (15 X 16 ^1). +15 х 16 ⁰ = 255 ₁₀ ) . Точно так же #FFFF и #FFFF могут считать до 9.0005 4095 ₁₀ и 65535 ₁₀ , соответственно. В следующей таблице указан вес каждой цифры в шестнадцатеричном числе.

Добавление нулей к двоичному числу

Поскольку двоичное число разбивается на группы, состоящие из 4 бит, для определения его эквивалентного шестнадцатеричного числа. Для этого требуется двоичное число, состоящее из битов, кратных четырем (4), например. 4, 18, 12, 16 и 20 и т. д. Однако это может быть не так, когда речь идет о двоичных числах, а двоичные числа могут различаться по длине в битах. Решение состоит в том, чтобы начать разбивать двоичные числа на группы по 4 бита, начиная с младшего значащего бита (LSB), и, в конце концов, у нас останется менее 4 бит в конце. Ведущие нули добавляются к оставшимся битам, увеличивая их длину до 4 бит. Эта группа из 4 битов составляет старшую значащую цифру (MSD) шестнадцатеричных чисел. В следующей таблице нестандартное 13-битное двоичное число (1 0101 1101 1010 ₁₀ ) преобразуется в 16-разрядное (делящееся на 4) двоичное число путем добавления ведущих нулей, а затем определяется его эквивалентное шестнадцатеричное число.

В приведенном выше примере 13-битное число требует добавления 3 битов с нулевыми значениями к крайней левой части, чтобы сделать его 16-битным двоичным числом. Точно так же 10-битное двоичное число потребует добавления шести (6) нулевых битов. Использование шестнадцатеричных чисел сокращает длину двоичных чисел в четыре (4) раза, а преобразование из двоичного в шестнадцатеричное или из шестнадцатеричного в двоичное выполняется легко и быстро.

Преобразование шестнадцатеричных чисел в десятичные

Преобразование шестнадцатеричных значений в десятичные достигается с помощью метода взвешенной суммы цифр, описанного в предыдущей статье. В следующем примере шестнадцатеричное число (#7DE5) преобразуется в десятичное число.

Преобразование десятичного числа в шестнадцатеричное

Преобразование десятичного числа в шестнадцатеричное требует применения метода повторного деления на 16, который использовался для преобразования десятичного числа в эквивалентное ему двоичное значение в предыдущей статье.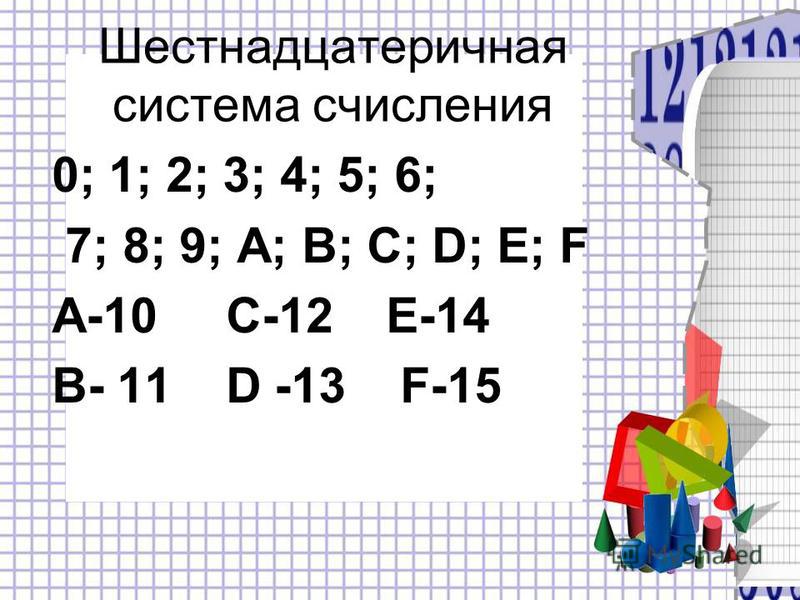 То же десятичное число (238 ₁₀ ) используется для получения эквивалентного ему шестнадцатеричного числа в следующем примере.

Пример преобразования двоичного числа в шестнадцатеричное

Ниже показано преобразование 8-битного двоичного числа (11011001 ₂ ) в шестнадцатеричное число.

Шестнадцатеричный код в двоичный и десятичный Пример

Преобразование #8C4A в его эквивалентное двоичное и десятичное число показано ниже в качестве примера.

Заключение

• В шестнадцатеричном числе используется система счисления с основанием 16, и его цифры могут состоять из шестнадцати (16) цифр от 0 до 15. В шестнадцатеричном формате буквы с заглавной буквы: A, B, C, D, E и F используются как эквивалентно 10, 11, 12, 13, 14 и 15 соответственно.
• В шестнадцатеричных числах каждая цифра представляет собой группу или набор из 4 битов. Эквивалент двоичного числа в шестнадцатеричном виде получается путем разбиения двоичного числа на группы по 4 бита, а затем, в зависимости от значения каждой 4-битной группы, каждой группе присваивается эквивалентное шестнадцатеричное значение от «0» до «F».
• Двоичные числа могут потребовать добавления начальных нулей в крайнюю левую (наиболее значащую) сторону для формирования 4-битных групп.
• Шестнадцатеричное число представляется с помощью «16» в качестве нижнего индекса или решетки (#) с крайней левой стороны, например. 2A7E ₁₆ или #2A7E.
• Шестнадцатеричное число можно преобразовать в десятичное число с помощью метода взвешенной суммы цифр. Преобразование десятичного числа в шестнадцатеричное требует применения метода повторного деления на 16.
• Шестнадцатеричные числа удобны для представления больших двоичных чисел. Шестнадцатеричное число уменьшает длину эквивалентного ему двоичного числа в четыре (4) раза. Более того, преобразование из двоичного в шестнадцатеричное и из шестнадцатеричного в двоичное осуществляется легко и быстро.

Подпишитесь на нас и поставьте лайк:

Шестнадцатеричная система счисления – Математические тайны

Определение

Шестнадцатеричная система счисления  – это тип системы счисления, базовое значение которого равно 16.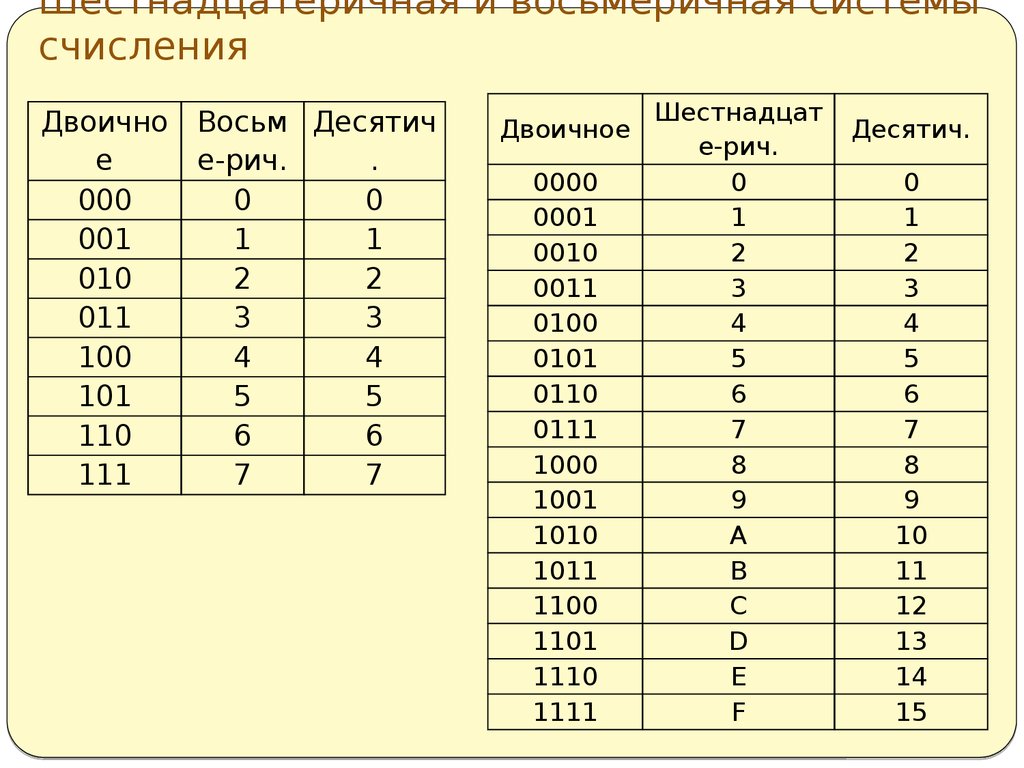 Иногда оно также произносится как 9.0005 ‘шестнадцатеричный’ . Шестнадцатеричные числа представлены всего 16 символами. Эти символы или значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Каждая цифра представляет десятичное значение. Например, D равно десятичной системе счисления 13.

Шестнадцатеричные системы счисления могут быть преобразованы в другие системы счисления, такие как двоичная система счисления (основание 2), восьмеричная система счисления (основание 8) и десятичная система счисления (основание 10). . Концепция системы счисления подробно объясняется в программе 9 класса.

список из 16 шестнадцатеричных цифр  с их эквивалентным десятичным, восьмеричным и двоичным представлением приведен здесь в виде таблицы, которая поможет в преобразовании системы счисления. Этот список также можно использовать в качестве переводчика или конвертера. ¹

Шестнадцатеричная система счисления – BYJUS

Пример

Здесь мы увидим пример расчета десятичного эквивалента шестнадцатеричного числа
Шестнадцатеричное число: 2 392DA 1 02FШаг 1: Шаг 2: (1 x 65536) + (9 x 4096) + (15 x 256) + (13 x 16) + (10 x 1)

Шаг 3:  (65536+ 36864 + 3840 + 208 + 10)  ₁₀

Шаг 4:  (106458)₁₀ или 106458

Ссылки

¹ «Что такое шестнадцатеричная система счисления? Таблица, Преобразования, Примеры». 2022. БАЙЮС . https://byjus.com/maths/шестнадцатеричная система счисления/.

Дополнительная литература

«Арифметические операции с шестнадцатеричными числами — GeeksForGeeks». 2020.  GeeksForGeeks . https://www.geeksforgeeks.org/arithmetic-operations-of-hexadecimal-numbers/.

Джастис, Далтон. 2014. «Шестнадцатеричный». SlideServe . https://www.slideserve.com/dalton/hexadecimal.

Видео

Шестнадцатеричная система счисления Шестнадцатеричная система счисления | Применение математических рассуждений | Предварительная алгебра | Академия Хана В чем смысл шестнадцатеричной системы счисления? (GCSE) Зачем нужны шестнадцатеричная и восьмеричная системы счисления?

Очень важно понять причину использования шестнадцатеричной и восьмеричной систем счисления. В этом видео я объяснил необходимость, различные варианты использования шестнадцатеричной и восьмеричной систем счисления, а также преобразование между двоичной, шестнадцатеричной и восьмеричной системами счисления.