2. Градиент, дивергенция, ротор
Если каждой точке М пространства или некоторой его области V поставлена в соответствие скалярная величина u(М), то говорят, что в этой области задано скалярное поле. В декартовой системе координат задание скалярного поля эквивалентно заданию функции трех переменных u(М) = u(x,y,z). Примерами скалярных полей могут служить поле температур данного тела, поле атмосферного давления и т.д. Пусть функция u(x, y, z) является непрерывно дифференцируемой в области V. В каждой точке этой области определен вектор, проекциями которого на оси координат являются значения частных производных функции u(x,y,z):
Вектор grad u направлен в сторону наибыстрейшего возрастания скалярного поля u(М), а длина градиента равна наибольшей скорости изменения поля
Если каждой точке М некоторой области V поставлен в соответствие определенный вектор , то говорят, что в этой области задано векторное поле. В декартовой системе координат задание векторного поля равносильно заданию трех скалярных функций:P(x,y,z), Q(x,y,z) и R(x,y,z) – проекций этого вектора на оси координат. Вектор в этом случае записывается в виде
а функции P(x,y,z), Q(x,y,z) и R(x,y,z) являются непрерывно дифференцируемыми в области V. В качестве примера векторного поля можно рассмотреть поле скоростей стационарного потока жидкости. Дивергенцией векторного поля называется скаляр
Ротором (вихрем) векторного поля называется вектор
Все
рассмотренные величины полей: grad u,
div
иrot
вычисляются с помощью частного
дифференцирования скалярного поляu и компонентов P, Q, R векторного поля.
Таким образом, мы имеем дело с
дифференциальными операциями первого
порядка. Наряду с ними можно рассмотреть
дифференциальные операции второго
порядка:grad
div
,rot
rot
иdiv
grad u.
Рассмотрим последнюю операцию:
Эту операцию можно записать кратко, вводя оператор Лапласа
Для векторного поля
Максимумом (минимумом) функции называется такое значениеэтой функции, которое больше (меньше) всех ее значений, принимаемой данной функцией в точках некоторой окрестности точкиМаксимум или минимум функцииназывается экстремумом этой функции, точка, в которой достигается экстремум, называется точкой экстремума:
а) Необходимый признак экстремума: в точке экстремума функции нескольких переменных каждая ее частная производная первого порядка либо равна нулю, либо не существует . Точки, в которых частные производные первого порядка равна нулю, либо не существуют, называются критическими;
б) Достаточный признак экстремума: если точка – критическая точка функциии,,,, тогда:
1) если , то функция имеет экстремум в точке, а именно максимум, если, и минимум, если;
2) если , то экстремума в точкенет;
3)
если
,
то вопрос о наличии экстремума в точкетребует дополнительного исследования.
а) Найдем критические точки:
Таким образом, имеем две критические точки и. Находим.
В точке , т.е. в этой точке экстремума нет. В точкеи, следовательно, в этой точке функция имеет локальный минимум:.
Может мне кто-нибудь объяснить?) Вопрос, может быть, туповатый, но я не знаю))
- Бизнес, Финансы
- Города и Страны
- Досуг, Развлечения
- Животные, Растения
- Здоровье, Красота, Медицина
- Знакомства, Любовь, Отношения
- Искусство и Культура
- Компьютеры, Интернет, Связь
- Кулинария, Рецепты
- Лингвистика
- Наука и Техника
- Образование
- Общество, Политика, СМИ
- Отдельная Категория
- Прочее
- Путешествия, Туризм
- Работа, Карьера
- Семья, Дом, Дети
- Спорт
- Стиль, Мода, Звезды
- Товары и Услуги
- Выбор транспортных средств
- ГИБДД, Обучение, Права
- Обслуживание, Тюнинг
- Оформление транспортных сделок
- ПДД, Вождение
- Прочее о транспорте
- Страхование транспорта
- Философия, Психология
- Фотография, Видеосъемка
- Юридическая консультация
Юмор
Закрыт 7 лет
Личный кабинет удален
Наставник (45949)
В общем, надо, как можно проще и короче.
..
Что такое дивергенция? И чем она отличается от градиента?))
Градиент функции z (x,y) в точке (x0,y0), вычисляется путём подстановки x0 и y0 в частные производные. Физический смысл его — вроде как направление наибольшего изменения функции; в реальности — например, напряжённость гравитационного поля.
И заодно уже тогда про ротор в двух словах)
Дополнен 7 лет назад
Мы платим до 300 руб за каждую тысячу уникальных поисковых переходов на Ваш вопрос или ответ Подробнее
| ЛУЧШИЙ ОТВЕТ ИЗ 7 |
Sergey Davydov
Наставник (27566)
Градиентом получается векторное поле из скалярного, дивергенцией получается скалярное поле из векторного, ротором получается векторное поле из векторного.
Скалярное поле, например, в каждой точке пространства своя температура.
Векторное поле, например, в каждой точке пространства свое направление ветра.
| ЕЩЕ ОТВЕТЫ |
Ono
Наставник (67318)
Дивергенция — расхождение признаков…
А градиент… Градиент концентрации…
Хризантема с Фудзиямы
Наставник (29786)
отличный вопрос ))))))Вот ты по ранним утрам думу думаешь дивергентную и градиентную))))Доброе утро))))
Казбек
Наставник (53221)
Блин! Мне бы твои проблемы!)))
Cat Charly
Наставник (44651)
Пойду обутки покупать.
Добраутра!
К вапросу есть ротор и статор, ротор крутится в статоре.
Личный кабинет удален
Наставник (45949)
Градиент — вектор, дивергенция — скаляр, ротор — вектор завихрения.
Дивергенция схематично показывает, в какой степени данная точка пространства является источником или стоком этого поля.
Векторное поле, ротор которого не равен нулю, имеет циркуляцию.
Доброго утречка!
Бешеный кошандрий
Мудрец (13415)
Иди ты, в физфак
| ПОХОЖИЕ ВОПРОСЫ |
Кто нибудь может мне объяснить вот аткое явление почему есть такие люди которые любят давать
Тупой вопрос)) Может, кто-нибудь знает, что это был за странный тупой мультик?))
У меня с утра вопрос . КТО ТАКОЙ ЗАБОТЛИВЫЙ мужик? объяснить может кто-нибудь?еще раз повторяю ЗАБОТЛИВЫЙ мужик )))))))))))))))))
Может ли кто-нибудь тут подробно и точно объяснить мне, КАК добавлять в вопрос или ответ муз. файл?
Кто-нибудь может мне показать вопрос, где выбран ЛО, который точно не может быть ЛО?
.шо зесь происходит?!!!Может мне кто-нибудь объяснить? Почему Он все время задает одни и те же вопросы?))++
Может мне кто-нибудь объяснит… Сколько эта пустыня в теме ещё поодолжаться будет?
Дело это конечно хорошее, но может быть мне кто-нибудь объяснит следующее?;)
Кто-нибудь может мне объяснить, что происходит? Какие у нас дороги, то должно бы быть наоборот…
- Случайный вопрос
- Актуальное
- Популярное
- Помощь
- Прямой эфир
- Соглашение
- Конфиденциальность
- Старый дизайн Ответов
- 18+
Градиент, расхождение и завиток
Градиент, расхождение и завиток Операторы, указанные в заголовке, построены из оператора del . (Его еще называют набла . Так всегда звучало
глупо для меня, поэтому я назову это «дель».
)
Del — формальный вектор; у него есть компоненты, но эти компоненты имеют операторы частных производных (и т. д.), которым нужно передать функции различать. Так что, как правило, когда вы умножаете FOO на del, операторы частных производных дифференцируют FOO в отличие от умножение.
Во-первых, предположим, что f — функция. это градиент f, иногда обозначаемый .
Пример. Вычислить градиент .
Вы также можете написать это как
является вектором; какие вещи ты можешь
делать с вектором? Ну, вы можете взять скалярное произведение вектора
с другим вектором. Если вы сделаете это с помощью , вы получите
Чтобы это имело смысл, должно быть векторное поле ; так как скалярное произведение двух векторов число, должно быть числом (что есть числовая функция).
Пример. Вычислить расхождение
.
Что такое дивергенция векторного поля? Если вы думаете о поле как поле скоростей жидкости, текущей в трех измерениях, то значит жидкость несжимаемый — для любой закрытой области количество жидкости, втекающей через границу, равно количеству вытекает. Этот результат следует из Теорема о расходимости , одна из больших теорем векторного интеграла. исчисление.
Вы можете взять перекрестное произведение двух 3-мерные векторы; если вы сделаете это с помощью , вы получите curl векторного поля:
Точнее, предположим . затем
Перекрестное произведение двух векторов является вектором, поэтому curl принимает вектор поле в другое векторное поле.
Пример. Вычислить завиток .
Как обычно, разложу определитель по сомножителям первой строки:
Что такое ротор векторного поля? Чтобы облегчить визуализацию,
предположим, что это поле скоростей для жидкости
поток в плоскости (поэтому компонент z равен 0).
Бросьте отмеченный поплавок в поток и позвольте ему нестись течением. жидкость. Тогда означает, грубо говоря, чтобы поплавок не вращался при движении.
Старое название было вращения . Поле с называется безвихревой (и эта терминология до сих пор используется, хотя гниль была заменена курчавостью).
Существует множество тождеств, включающих div, grad и curl; вот важный.
Пример. Показать это .
Вы можете отшлифовать это и обнаружить, что все отменяется равенство смешанных частных производных (например, ). Но работать проще формально, факторизуя f из последней строки:
Но определитель матрицы с двумя равными строками равен 0, поэтому результат.
Контактная информация
Домашняя страница Брюса Икенаги
Copyright 2022 by Bruce Ikenaga
В чем физический смысл дивергенции, завитка и градиента векторного поля?
Представьте, что у вас в руке мяч.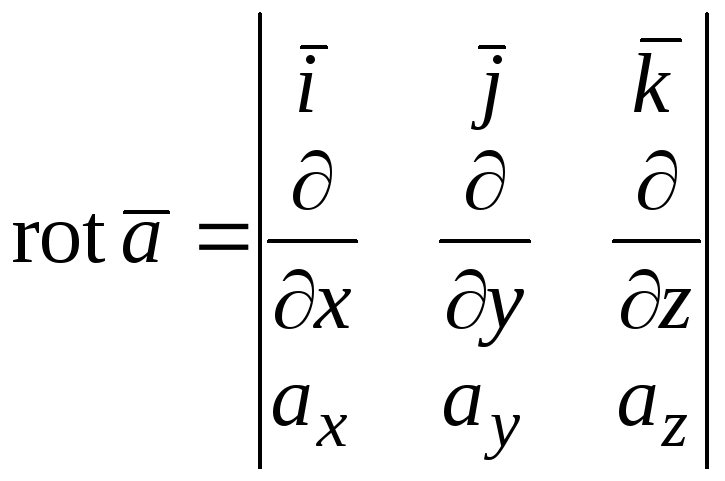
Теперь возьмите любую точку на шаре и представьте вектор, действующий перпендикулярно шару в этой точке. Это ваш градиент в 3D. Теперь представьте векторы, действующие на все точки шара. Это будет выглядеть примерно так:
Красные стрелки, перпендикулярные поверхности мяча, представляют собой градиенты (в 3D) различных точек на мяче. Если мы применим функцию градиента к 2D-структуре, градиенты будут касательными к поверхности.
Чтобы лучше понять представление градиента в 2D, представьте, что вы взбираетесь на гору. Вы находитесь в определенной точке горы:0005
Теперь вам нужно двигаться в определенном направлении, чтобы набирать или терять высоту (показано красными стрелками). Эти векторные линии представляют градиенты в вашей точке в 2D:
гора. Взгляните на изображения ниже.0005
В 3D-форме Градиенты являются нормалью поверхности к определенным точкам .
В формате 2D Градиенты тангенсы, представляющие направление наибольшего спуска или подъема .
Дивергенция:
Рассмотрим воду, текущую по большой трубе. Теперь к нему присоединены трубы меньшего размера. Следовательно, по мере того, как вода течет, по меньшим трубам добавляется больше воды. Следовательно, массовый расход увеличивается по мере течения воды.
В другом случае рассмотрите, что в трубе возникает утечка. Следовательно, массовый расход уменьшается по мере течения. Это изменение скорости потока через трубу, независимо от того, увеличивается она или уменьшается, называется дивергенцией. Расхождение обозначает только величину изменения, поэтому это скалярная величина. У него нет направления.
Когда начальный расход меньше конечного расхода, расхождение положительное (расхождение > 0). Если две величины одинаковы, дивергенция равна нулю. Если начальная скорость потока больше, чем конечная скорость потока, расходимость отрицательна (расхождение <0).
Завиток 9. Вода будет стекать не просто линейно, а скорее, достигнув конца чашки, она будет течь во вращательном движении, прежде чем осесть в чашке. Или представьте, что вода стекает в раковину, она будет вращаться, прежде чем уйти. Если мы изобразим этот вращательный поток воды в виде векторов и измерим его, он будет обозначать Завиток.
Изгиб — это мера того, насколько векторное поле циркулирует или вращается вокруг заданной точки. , когда поток направлен против часовой стрелки, завиток считается положительным, а когда поток направлен по часовой стрелке, завихрение считается отрицательным. Иногда завиток не обязательно проходит один раз. Это также может быть любой вращающийся или закрученный вектор.
Изучение градиента, дивергенции и завитка очень важно, особенно в CFD.