Как правильно нарисовать куб карандашом
Все предметы, которые нас окружают можно мысленно вписать в простые геометрические тела (куб, шар, конус, цилиндр, призма и др.). Изучая форму куба, мы узнаем, как нарисовать, к примеру, дом, потому что упрощенно дом рисуется с использованием тех же приемов что и куб. У него есть вершины, ребра и грани, как и у куба. Крыша дома – это многогранная призма.
Нарисуем куб с натуры, а затем будем использовать эти знания на наших курсы рисования в Киеве для изображения более сложных предметов таких как дома и улицы.
Куб – геометрическое тело, образованное пересечением плоскостей. И, как всякий объемный предмет, при изображении на плоском листе он будет претерпевать изменения в соответствии с законами перспективы. На рисунке изображена линия горизонта это уровень плоскости зрения художника. На ней находятся точки схода параллельных линий. В нашем случае — это четыре горизонтальных линии, стремящихся в точку схода слева и четыре горизонтальных линии, стремящихся в точку схода справа.
Мы изображаем предметы в пространстве так, как их воспринимает наш глаз. (Чем дальше от зрителя, тем меньше выглядит предмет и т.д.)
Начало любой картины – это композиция. Легкими линиями намечаем наш предмет на листе. Сверху всегда должно быть чуть больше места от края, чем снизу. Интуитивно определите масштаб так, чтобы предмет не выглядел гигантским или слишком маленьким.
Рисуем самое ближнее вертикальное ребро кубаРасположите самое ближнее вертикальное ребро так, чтобы оно не совпадало с центром листа, проходящим через пересечение его диагоналей. Засечками отмечаем высоту, это самое высокое ребро в нашем изображении, так как оно ближе всех к зрителю. На глаз определяем угол наклона ребер лежащих на столе относительно горизонтали. Тренируйте зрительную память, запоминая угол. Взгляд переводите быстро то на куб, то на рисунок.
Изображение верхних ребер кубаТо же проделаем и с верхними ребрами. Как передавать пространство на листе нам объясняют основные законы линейной перспективы. Все параллельные линии сливаются к линии горизонта в одну точку. Поэтому, чтобы передать что ребро находится дальше от зрителя, мы изобразим его меньше и расположим выше. Таким образом, все ребра будут разной высоты.
Все параллельные линии сливаются к линии горизонта в одну точку. Поэтому, чтобы передать что ребро находится дальше от зрителя, мы изобразим его меньше и расположим выше. Таким образом, все ребра будут разной высоты.
При пересечении дальних горизонтальных ребер образовались вершины. Через них проходит самое дальнее, невидимое глазом, ребро. На начальном этапе изобразим куб прозрачным для понимания полной конструкции предмета.
Для того, чтобы узнать на сколько сократились боковые грани, воспользуемся методом визирования. При помощи этого метода происходит восприятие очертаний предмета, художник учится изображать предметы пропорциональными и в различных ракурсах.
Как он работает? Возьмите карандаш на вытянутой руке, прикройте один глаз, совместите карандаш и изображение ребра куба в пространстве. Верхний край карандаша должен совпадать с верхней вершиной ребра, а пальцем зажмите на карандаше точку, совпадающую с нижней вершиной. Не убирая палец с карандаша, разверните под прямым углом и измеряйте расстояние между двумя ребрами. Таким образом, мы увидим соотношение высоты и ширины одной грани. Запомните это соотношение и передайте его на рисунке. Этим методом можно измерять и изображать так же соотношение ребер.
Не убирая палец с карандаша, разверните под прямым углом и измеряйте расстояние между двумя ребрами. Таким образом, мы увидим соотношение высоты и ширины одной грани. Запомните это соотношение и передайте его на рисунке. Этим методом можно измерять и изображать так же соотношение ребер.
После того, как закончены линейные построения, приступаем к воздушной перспективе, а значит к штриховке.
Основная задача художника передавать объемные формы предметов. У нашего кубика мы видим три грани, все они разные по тону. Левая грань самая темная — это собственная тень предмета. Благодаря отраженному свету от окружающих предметов или рефлексам, штриховку делаем немного светлее по мере удаления влево. Самое большое ребро делают контрастней, чем все остальные. Таким образом, показывают его приближенность на передний план.
Воздушная перспектива и штриховка кубаВерхняя плоскость темнее, чем вертикальная справа. Свет по ней лишь скользит, образуя полутон. Обратите внимание, что чем ближе к источнику света, тем светлее будет тон. Штриховку можно наносить по диагонали. На ребре ластиком высветлим, чтобы передать блик.
Обратите внимание, что чем ближе к источнику света, тем светлее будет тон. Штриховку можно наносить по диагонали. На ребре ластиком высветлим, чтобы передать блик.
Для работы над самой светлой гранью возьмем твердый карандаш Н или 2Н. Он не даст сделать тон слишком темным. Штриховку нанесем вертикальную, по направлению плоскости.
Падающие тени и собственная тень кубаПадающие тени всегда темнее, чем собственная тень предмета. Ближнее ребро – это линия перехода света и тени. Из нее начинается падающая тень. Чем ближе к предмету, тем насыщеннее тон. Отраженный свет от куба создает рефлекс внутри тени и она немного высветляется.
Куб нарисованный по законам перспективного построения и воздушной перспективыРисование простых геометрических тел часто используется на курсы академического рисунка в Киеве и позволяет начинающему художнику научиться изображать предметы в пространстве, применяя законы перспективного построения и воздушной перспективы.
Рисование геометрических тел. Как нарисовать куб? — Ghenadie Sontu Fine Art
Куб является одним из самых простых геометрических тел. Чтобы лучше понять геометрическую форму куба, его пространственную конструктивную схему (структуру), рассмотрим каркас куба. Это дает возможность ясно представить объемно-пространственную характеристику его формы, позволяет видеть его конструктивные узлы — точки, невидимые на обычных телах.
Куб характеризуется восемью точками на углах и двенадцатью линиями ребер. Соотношения сторон куба составляют пропорцию 1:1:1. Для того чтобы куб выглядел достоверно в трехмерном изображении, студентам следует определить такую точку зрения, при которой предмет выглядит достаточно убедительным в объеме. Изображение каркаса куба производится с учетом его пропорций, по законам перспективы. При обычном взгляде сверху (в ракурсе) основание каркаса куба (квадрат) выглядит ромбом. Перспективное построение куба в соответствии с его поворотом следует начинать с квадрата основания, т. е. с его плана, лежащего в горизонтальной плоскости, уходящей в глубину до линии горизонта (рис.35). Чтобы получить нижнее основание (ромб), необходимо обозначить четыре точки и соединить их четырьмя линиями. Из точек основания проводят вертикальные линии — ребра. Для завершения построения, как и в первом случае, обозначают четыре точки и, соединив их четырьмя линиями, получают верхнее основание куба (ромб). Необходимо отметить одну немаловажную деталь, касающуюся характера линий при построении изображения на плоскости. Кроме соблюдения пропорции и перспективы, линии, определяющие пространственную глубину, должны быть проведены в различной степени контрастности. Линии близлежащих ребер следует проводить более контрастно, чем тех, что находятся в перспективном удалении. Причем разница линий должна быть предельно различимой в соответствии с пространственной глубиной.
е. с его плана, лежащего в горизонтальной плоскости, уходящей в глубину до линии горизонта (рис.35). Чтобы получить нижнее основание (ромб), необходимо обозначить четыре точки и соединить их четырьмя линиями. Из точек основания проводят вертикальные линии — ребра. Для завершения построения, как и в первом случае, обозначают четыре точки и, соединив их четырьмя линиями, получают верхнее основание куба (ромб). Необходимо отметить одну немаловажную деталь, касающуюся характера линий при построении изображения на плоскости. Кроме соблюдения пропорции и перспективы, линии, определяющие пространственную глубину, должны быть проведены в различной степени контрастности. Линии близлежащих ребер следует проводить более контрастно, чем тех, что находятся в перспективном удалении. Причем разница линий должна быть предельно различимой в соответствии с пространственной глубиной.
Перспективный рисунок куба может быть сравнительно легко построен и проверен различными способами. Одним из таких способов являются приемы, давно применяемые на практике старыми мастерами, — это сравнение и визирование.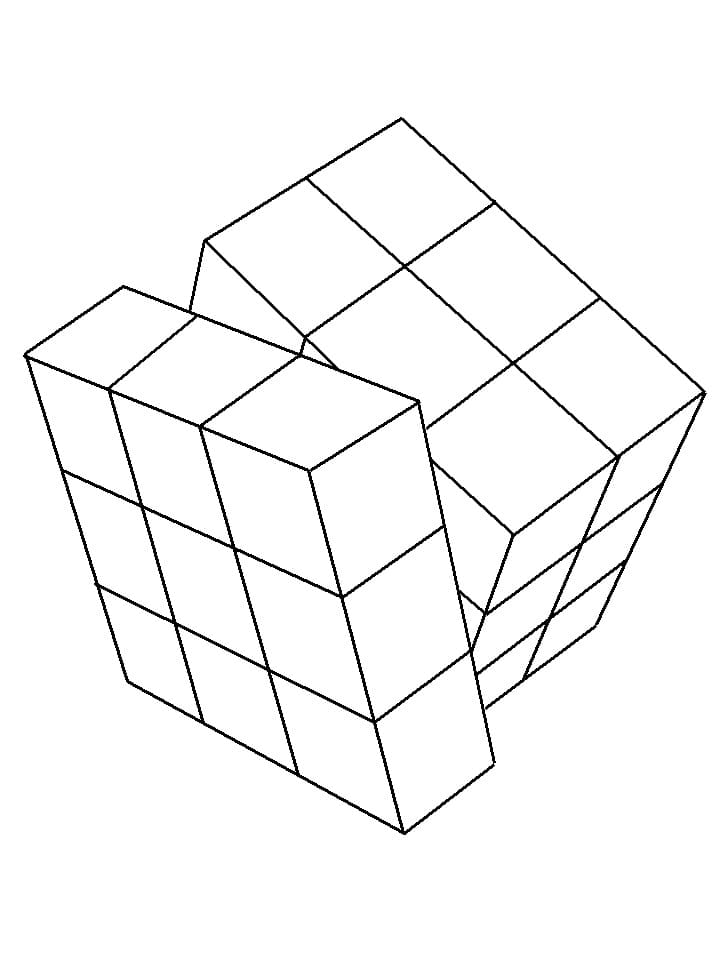 Для определения основных больших размеров предмета в рисунке важны видимые, перспективно измененные их соотношения, а не реальные размеры объекта и его частей. Так, например, отношение ширины какой-либо грани к высоте переднего ребра вымеряют карандашом на вытянутой руке, перпендикулярно лучу зрения, совмещая тыльную сторону карандаша с краем формы предмета измеряемой части модели. При этом большим пальцем отмечают видимые размеры частей предмета. Не меняя положения большого пальца на вытянутой руке и поворачивая карандаш в вертикальном положении, соотносят этот отрезок карандаша с вертикальным ребром куба, определяя визуально их различия (рис.36).
Для определения основных больших размеров предмета в рисунке важны видимые, перспективно измененные их соотношения, а не реальные размеры объекта и его частей. Так, например, отношение ширины какой-либо грани к высоте переднего ребра вымеряют карандашом на вытянутой руке, перпендикулярно лучу зрения, совмещая тыльную сторону карандаша с краем формы предмета измеряемой части модели. При этом большим пальцем отмечают видимые размеры частей предмета. Не меняя положения большого пальца на вытянутой руке и поворачивая карандаш в вертикальном положении, соотносят этот отрезок карандаша с вертикальным ребром куба, определяя визуально их различия (рис.36).
Работая над конструктивным построением куба, нужно внимательно следить за его перспективным сокращением. Для этого необходимо мысленно представить форму с данной точки зрения в плане, т.е. увидеть ее сверху. Такое представление дает возможность лучше разобраться, как согласуются плоскости между собой и в целом. В рисовании с натуры важно правильно передать не только видимые соотношения величин, но и величины углов между основаниями двух видимых граней, т.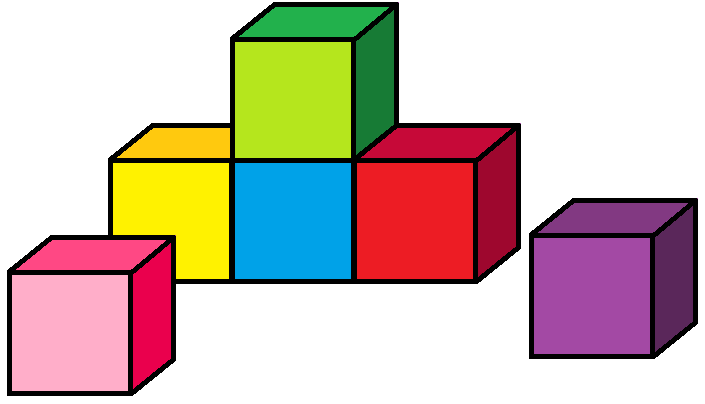 е. перспективные ракурсы.
е. перспективные ракурсы.
Для их правильного определения следует сделать проверку механическим способом визирования. Держа карандаш за кончик на вытянутой руке, нужно совместить линию самого карандаша с вершиной переднего нижнего угла основания предмета и определить на глаз угол наклона предмета в перспективе. Запомнив увиденное, проведите на своем рисунке соответствующую вспомогательную горизонтальную линию. Сравнивая величину наклона (угла) правой и левой сторон модели, уточните рисунок. При необходимости дополнительного уточнения следует повторить проверку. На рис.36 наглядно показаны способы измерения размеров и проверки перспективного наклона горизонтальных ребер куба. Заметим, что, рисуя с натуры, не нужно злоупотреблять приемом визирования, поскольку он носит чисто механический характер определения размеров и не способствует развитию глазомера. Им пользуются на начальной стадии обучения рисованию с натуры, и он должен служить лишь для вспомогательного контроля и проверки уже выполненных работ.
При положении куба со смещенным несколько вправо от центра передним вертикальным ребром горизонтальные ребра его левой грани в перспективе будут приближаться к горизонтали, а ребра правой, наоборот — отклоняться от нее. Следовательно, чем больше сокращается правая грань, тем меньше будет сокращение левой и наоборот. Это обусловлено взаимным прямоугольным расположением плоскостей куба.
Для лучшего усвоения материала по изучению геометрических тел необходимо выполнить академическое задание по рисунку куба. Усваивая закономерности строения формы куба, следует иметь в виду, что за их соблюдением нужно следить на протяжении всего процесса рисования с натуры. Работа над длительным рисунком требует соблюдения методической последовательности как в анализе строения формы, так и в процессе построения изображения. Это дает возможность закреплять отдельные этапы учебного рисунка, без чего невозможно понять основной смысл учебного материала. При этом следует отметить, что членение процесса работы над рисунком на отдельные этапы носит достаточно условный характер. Это связано с ошибками в решении задач, которые могли быть допущены на предыдущем этапе, и необходимостью их исправления в процессе работы.
Это связано с ошибками в решении задач, которые могли быть допущены на предыдущем этапе, и необходимостью их исправления в процессе работы.
Рассмотрим последовательность выполнения рисунка куба (рис.37).
1. Рисунок начинают с композиционного размещения предмета на листе. Изображение намечают легкими линиями с боков, сверху и снизу. С учетом ракурса, пропорции и перспективы находят и определяют основные конструктивные точки вершин углов куба.
2. С учетом перспективных сокращений по конструктивным точкам вершин углов намечают общую форму конструкции куба.
3. Уточняют пропорции и перспективное построение объемно-пространственной формы куба. Определяют границы собственной и падающей теней.
4. С помощью светотональных отношений выявляют объемную форму куба. Наносят собственные и падающие тени. Определяют фон.
5. Полная тональная проработка формы. Работа светотональными отношениями: свет, тень, полутень и рефлекс.
6. Подведение итогов. .Проверка и обобщение рисунка (цельность).
Рисунок кубики в Сыктывкаре: 500-товаров: бесплатная доставка, скидка-48% [перейти]
Партнерская программаПомощь
Сыктывкар
Каталог
Каталог Товаров
Одежда и обувь
Одежда и обувь
Стройматериалы
Стройматериалы
Здоровье и красота
Здоровье и красота
Текстиль и кожа
Текстиль и кожа
Электротехника
Электротехника
Детские товары
Детские товары
Продукты и напитки
Продукты и напитки
Дом и сад
Дом и сад
Вода, газ и тепло
Вода, газ и тепло
Мебель и интерьер
Мебель и интерьер
Сельское хозяйство
Сельское хозяйство
Все категории
ВходИзбранное
Рисунок кубики
949
1499
Обучающие кубики «Сложи узор», набор с журналом 97 рисунков заданиями в комплекте, по методике Никитина
В МАГАЗИНЕще цены и похожие товары
1 225
1750
Развивающие магнитные кубики Kribly Boo для малышей с рисунками, 8 шт, Тип: Кубики, Размер: Длина
В МАГАЗИНЕще цены и похожие товары
875
1250
Магнитные кубики Kribly Boo с рисунками, 6 шт Тип: Кубики, Размер: Длина 15. 000 Ширина 10.000
000 Ширина 10.000
В МАГАЗИНЕще цены и похожие товары
370
624
Игрушки Собери рисунок Кубики пазл/Логическая игра/Деревянная развивающая игра/ сортер для детей
В МАГАЗИНЕще цены и похожие товары
966
1927
Кубики «Сложи узор», журнал (97 рисунков) с заданиями в комплекте, по методике Никитина Тип:
В МАГАЗИНЕще цены и похожие товары
Кубики Пелси Алфавит и рисунок, 15 шт. И675 weight: 0.517, Страна: Россия, Возраст ребёнка: от 3 лет
В МАГАЗИНЕще цены и похожие товары
Кубики Пелси Алфавит и рисунок, 8 шт. И673 weight: 0.3, Страна: Россия, Возраст ребёнка: от 3 лет
В МАГАЗИНЕще цены и похожие товары
Развивающая игрушка ПЕЛСИ Кубики Алфавит и рисунок 8 шт
В МАГАЗИНЕще цены и похожие товары
Кубики Пелси Алфавит и рисунок, 12 шт. И674 weight: 0.4, Страна: Россия, Возраст ребёнка: от 3 лет
И674 weight: 0.4, Страна: Россия, Возраст ребёнка: от 3 лет
В МАГАЗИНЕще цены и похожие товары
Кубики «Сложи узор», журнал (97 рисунков) с заданиями в комплекте, по методике Никитина
В МАГАЗИНЕще цены и похожие товары
Кубики ‘Сложи узор’, журнал (97 рисунков) с заданиями в комплекте, по методике Никитина ishit: 1,
ПОДРОБНЕЕЕще цены и похожие товары
Томик Кубики «Сложи рисунок: Мебель»
ПОДРОБНЕЕЕще цены и похожие товары
Кубики «Сложи узор», журнал (97 рисунков) с заданиями в комплекте, по методике Никитина Развивающие
ПОДРОБНЕЕЕще цены и похожие товары
Томик Кубики «Сложи рисунок: Животные»
ПОДРОБНЕЕЕще цены и похожие товары
564
722
Кубики для малышей «Математика с рисунками«, 00705 Развивающие функции и навыки: логика и мышление,
ПОДРОБНЕЕЕще цены и похожие товары
Кубики «Сложи узор», журнал (97 рисунков) с заданиями в комплекте, по методике Никитина
ПОДРОБНЕЕЕще цены и похожие товары
Кубики «Сложи узор», журнал (97 рисунков) с заданиями в комплекте, по методике Никитина детские
ПОДРОБНЕЕЕще цены и похожие товары
Кубики «Сложи узор», журнал (97 рисунков) с заданиями в комплекте, по методике Никитина
ПОДРОБНЕЕЕще цены и похожие товары
22 796
Обеденный стол Шанхай рисунок Производитель: AURORA (Димитровград), Назначение: кухонный, Форма
ПОДРОБНЕЕЕще цены и похожие товары
988
2824
Кубики «Сложи узор», журнал (97 рисунков) с заданиями в комплекте, по методике Никитина
ПОДРОБНЕЕЕще цены и похожие товары
966
1905
Кубики «Сложи узор», журнал (97 рисунков) с заданиями в комплекте, по методике Никитина
ПОДРОБНЕЕЕще цены и похожие товары
Томик Кубики «Сложи рисунок: Герои сказок»
ПОДРОБНЕЕЕще цены и похожие товары
Томик Кубики «Сложи рисунок: Цветы» Производитель: Томик, Материал изготовления: дерево,
ПОДРОБНЕЕЕще цены и похожие товары
Кубики Алфавит и рисунок по 12 штук в наборе Возраст: От 3 до 7
ПОДРОБНЕЕЕще цены и похожие товары
2 страница из 18
Куб – формула, форма, определение, примеры
Куб – это трехмерный объект, имеющий 6 конгруэнтных квадратных граней. Размеры всех 6 квадратных граней куба одинаковы. Куб иногда также называют правильным шестигранником или квадратной призмой. Это одно из 5 платоновых тел. Некоторыми примерами куба из реальной жизни являются кубик льда, кубик Рубика, обычные игральные кости и т. Д. Давайте узнаем о кубе вместе с его формулами, несколькими решенными примерами и практическими вопросами здесь.
Размеры всех 6 квадратных граней куба одинаковы. Куб иногда также называют правильным шестигранником или квадратной призмой. Это одно из 5 платоновых тел. Некоторыми примерами куба из реальной жизни являются кубик льда, кубик Рубика, обычные игральные кости и т. Д. Давайте узнаем о кубе вместе с его формулами, несколькими решенными примерами и практическими вопросами здесь.
| 1. | Определение куба |
| 2. | Свойства куба |
| 3. | Кубическая сетка |
| 4. | Куб Формула |
| 5. | Часто задаваемые вопросы о кубе |
Определение куба
Куб — это твердый трехмерный объект с шестью квадратными гранями, все стороны которого имеют одинаковую длину. Он также известен как правильный шестигранник и является одним из пяти платоновых тел. Фигура состоит из шести квадратных граней, восьми вершин и двенадцати ребер.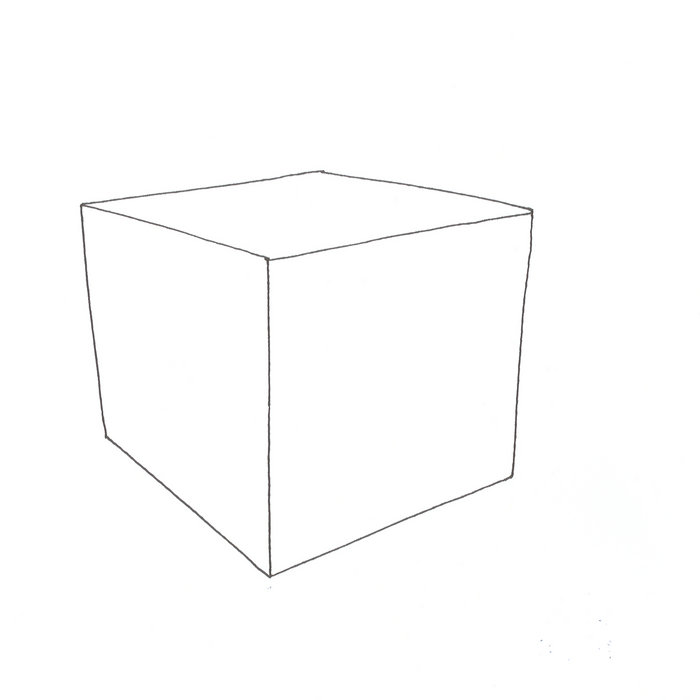
Куб Значение
Куб — это объемная объемная фигура, имеющая 6 квадратных граней. Это геометрическая фигура с 6 равными гранями, 8 вершинами и 12 равными ребрами. Некоторые примеры кубиков из реальной жизни — это игра в кости, кубики льда, кубик Рубика и т. д., которые мы видим вокруг себя.
Свойства куба
Куб считается особым видом квадратной призмы, так как все грани имеют форму квадрата и являются платоновыми телами. У куба, как и у любой другой трехмерной или двумерной формы, есть множество различных свойств.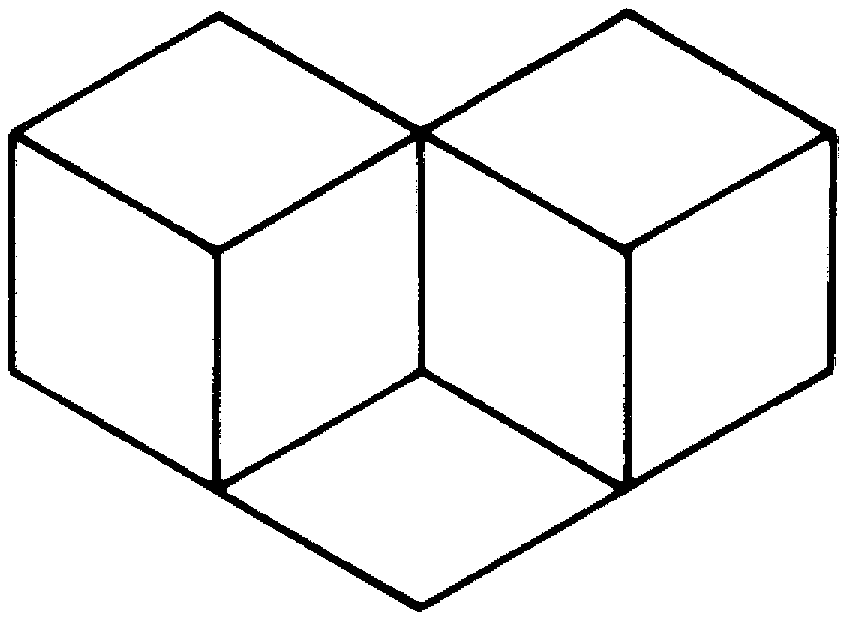 Свойства:
Свойства:
- Куб имеет 12 ребер, 6 граней и 8 вершин.
- Все грани куба имеют форму квадрата, поэтому длина, ширина и высота одинаковы.
- Углы между любыми двумя гранями или поверхностями равны 90°.
- Противоположные плоскости или грани куба параллельны друг другу.
- Противоположные ребра куба параллельны друг другу.
- Каждая грань куба встречается с остальными четырьмя гранями.
- Каждая вершина куба встречается с тремя гранями и тремя ребрами.
Кубическая сетка
Сетка куба формируется, когда трехмерная фигура с квадратными гранями сглаживается путем разделения по краям, превращая ее в двумерную фигуру. Через сетку куба мы можем ясно видеть шесть граней, то есть шесть квадратных граней, которые соединяются вместе по краям, образуя куб. Вот изображение для справки:
Куб Формула
Формула куба помогает нам найти площадь поверхности, диагонали и объем куба. Давайте обсудим различные формулы куба.
Давайте обсудим различные формулы куба.
Площадь поверхности куба
Существует два типа площадей поверхности куба — Площадь боковой поверхности и Общая площадь поверхности
Площадь боковой поверхности куба
Площадь боковой поверхности куба равна сумме площадей всех боковые грани куба. У куба 4 боковые грани, поэтому сумма площадей всех 4 боковых граней куба равна его боковой поверхности. Боковая площадь куба также известна как площадь его боковой поверхности (LSA) и измеряется в квадратных единицах.
LSA куба = 4a 2
, где a — длина стороны. Для получения дополнительной информации вы можете проверить эту интересную статью о боковой площади формулы куба.
Общая площадь поверхности куба
Общая площадь поверхности куба будет равна сумме площади основания и площади вертикальных поверхностей куба. Поскольку все грани куба состоят из квадратов одинакового размера, то общая площадь поверхности куба будет равна площади поверхности одной грани, сложенной с самой собой в пять раз. Он измеряется как «количество квадратных единиц» (квадратные сантиметры, квадратные дюймы, квадратные футы и т. д.). Следовательно, формула для нахождения площади поверхности куба:
Он измеряется как «количество квадратных единиц» (квадратные сантиметры, квадратные дюймы, квадратные футы и т. д.). Следовательно, формула для нахождения площади поверхности куба:
Общая площадь поверхности (TSA) куба = 6a 2
, где a — длина стороны. Для получения дополнительной информации вы можете ознакомиться с этой интересной статьей о площади поверхности куба.
Объем куба
Объем куба – это пространство, занимаемое кубом. Объем куба можно узнать, найдя куб длины стороны куба. Для определения объема куба существуют разные формулы, основанные на разных параметрах. Его можно рассчитать, используя длину стороны или размер диагонали куба, и он выражается в кубических единицах длины. Следовательно, две разные формулы для нахождения объема куба:
- Объем куба (на основании длины стороны) = a 3 , где a — длина стороны куба
- Объем куба (по диагонали) = (√3×d 3 )/9 , где d — длина диагонали куба
Вы можете узнать больше о формуле объема, прочитав эту интересную статью о объеме куба.
Диагональ куба
Диагональ куба — это отрезок, соединяющий две противоположные вершины куба. Длину диагонали куба можно определить по формуле диагонали куба. Это помогает найти длину диагоналей лица и главных диагоналей. Каждая диагональ грани образует гипотенузу образовавшегося прямоугольного треугольника. Куб имеет шесть граней (квадратной формы). На каждой грани есть две диагонали, соединяющие несмежные вершины. Следовательно, у нас есть двенадцать диагоналей граней и четыре главные диагонали, соединяющие противоположные вершины куба. Формула диагонали куба для расчета длины диагонали грани и диагонали основного тела куба определяется как 9.0003
- Длина диагонали грани куба = √2a единиц , где a = длина каждой стороны куба
- Длина главной диагонали куба = √3a единиц , где a = длина каждой стороны куба
Давайте посмотрим на несколько решенных примеров куба и его свойств для лучшего понимания.
☛Связанные темы
Ниже перечислены некоторые темы, связанные с кубом.
- Куб Формула
- Платоновые тела
- Формы
- Твердые формы
- плоские фигуры
Примеры кубов
Пример 1: Сколько воды хранится в одном кубике льда со стороной 5 дюймов?
Решение:
Дано,
Длина кубика льда = 5 дюймов
Количество воды, хранящейся в кубике льда = объему кубика
Следовательно, объем кубика льда = 5 × 5 × 5 в 3
= 125 в 3
Ответ: Количество воды во льду 125 в 3 .
Пример 2: Найдите общую площадь поверхности куба, если длина стороны куба равна 25 дюймам.
Решение:
Длина стороны куба, a = 25 дюймов формула площади куба: A = 6a 2
A = 6 × 25 × 25
A = 3750
Ответ: Площадь поверхности куба 3750 квадратных дюймов.

Пример 3: Найдите объем кубика Рубика длиной 5 дюймов.
Решение:
Чтобы найти объем кубика Рубика:
Длина стороны кубика = 5 дюймов ( дано)
Используя формулу куба,
объем = с × с × с = сПоместите значения,
объем = 5 × 5 × 5 = 5 3 = 125
Ответ: Объем кубика Рубика составляет 125 кубических дюймов.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по Cube
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о Cube
Что такое куб в геометрии?
В геометрии куб — это трехмерная геометрическая фигура с шестью конгруэнтными квадратными гранями. Идеальным примером куба из реальной жизни является кубик льда. Это одно из пяти платоновых тел, также известное как правильный шестигранник.
Идеальным примером куба из реальной жизни является кубик льда. Это одно из пяти платоновых тел, также известное как правильный шестигранник.
Каковы два основных свойства куба?
Куб — это трехмерная фигура со многими геометрическими свойствами. Два основных свойства перечислены ниже.
- Куб имеет 12 ребер, 6 граней и 8 вершин.
- Все грани куба имеют квадратную форму.
Почему куб называют правильным шестигранником?
Правильный шестигранник представляет собой трехмерный объект с 6 конгруэнтными гранями. Таким образом, куб называется правильным шестигранником.
Какая формула площади боковой грани куба?
Площадь поперечной стороны куба можно рассчитать, зная длину его ребра. Площадь боковой стороны куба с длиной ребра ‘x’ равна 4×9.0096 2 квадратных единиц.
Как найти площадь боковой поверхности куба?
Площадь боковой стороны куба с длиной ребра ‘x’ можно получить, сложив площади 4 боковых граней. Таким образом, площадь боковой поверхности куба = х 2 + х 2 + х 2 + х 2 = 4х 2 .
Таким образом, площадь боковой поверхности куба = х 2 + х 2 + х 2 + х 2 = 4х 2 .
В чем разница между площадью поверхности и боковой поверхностью куба?
Площадь поверхности (или) общая площадь поверхности (TSA) куба представляет собой сумму площадей всех граней, тогда как площадь боковой поверхности (LSA) представляет собой только сумму 4 боковых граней куба. Если «x» — длина ребра куба, то
- Общая площадь поверхности (TSA) = 6x 2
- Площадь боковой поверхности (LSA) = 4x 2
Что такое площадь поверхности и площадь?
Обычно термин «площадь» используется для обозначения пространства, ограниченного двухмерным объектом. «Площадь поверхности» используется для представления суммы площадей всех граней трехмерного объекта.
Каков объем формулы куба?
Объем куба можно рассчитать по длине стороны. Объем куба 3 , где а — длина стороны куба.
По какой формуле найти площадь основания куба?
Формула для нахождения площади основания куба: 2 , где а — длина стороны куба.
Что представляют собой 5 Платоновых тел?
Куб представляет собой землю, октаэдр представляет собой воздух, тетраэдр представляет собой огонь, икосаэдр представляет собой воду, а додекаэдр представляет вселенную.
Калькулятор кубической плотности
Создано Александрой Зайонц, доктором медицины
Отзыв от Krishna Nelaturu
Последнее обновление: 26 апреля 2022 г.
Содержание:- Как использовать калькулятор кубической плотности?
- Что такое плотность? Какова формула плотности куба?
- Как рассчитать объем куба по плотности?
- Другие калькуляторы плотности
- Как рассчитать плотность бетонного куба?
- Часто задаваемые вопросы
Калькулятор кубической плотности — это простой инструмент с большими возможностями. ‘Как найти плотность куба?’ больше никогда не будет для вас проблемой! Читайте дальше, чтобы узнать:
- какова формула плотности куба,
- как рассчитать плотность бетонного куба.

Как пользоваться калькулятором кубической плотности?
Использование калькулятора кубической плотности является простым и интуитивно понятным, но проверьте эти шаги в случае каких-либо сомнений.
- См. панель калькулятора в левой части страницы.
- Первое, что вы сделаете, это изображение куба с выделенными размерами. Благодаря ему вы можете видеть, о каких измерениях мы говорим.
- Введите массу (вес) вашего куба в калькулятор плотности куба. Помните, что вы всегда можете изменить единицу измерения так, как вам удобно.
- Введите объем вашего куба в удобных единицах измерения. Если вы не знаете объем, выполните следующий шаг. В противном случае вы можете пропустить его.
- Введите известные вам размеры куба: длина стороны, диагонали куба или диагонали грани. Калькулятор рассчитает объем автоматически.
- Вы сразу видите результат в поле Density !
- Если вы хотите узнать, как найти плотность куба шаг за шагом , продолжайте читать текст.
Что такое плотность? Какова формула плотности куба?
Плотность — это термин, используемый в физике для описания масса на единицу объема пространства .
Формула плотности:
ρ=mV\rho = \frac{m}{V}ρ=Vm
где:
- ρ\rhoρ — плотность,
- ммм — масса, а
- ВВВ — объем.
Если два объекта одинакового размера, но один из них тяжелее, мы можем сказать , что он имеет большую плотность.
Куб представляет собой правильную квадратную призму в трех ориентациях. У него шесть квадратных граней с тремя гранями, сходящимися в каждой вершине. 93}ρ=a3m
где:
- ρ\rhoρ — плотность,
- ммм — масса, а
- aaa — длина ребра куба.
Как рассчитать объем куба по плотности?
Вот три способа расчета объема куба в зависимости от того, какое измерение у вас есть. Буквы в скобках относятся к изображению над калькулятором.
- Вы знаете сторону (а) куба
- Рассчитать объем (VVV) как: 93V=(2
f)3
Больше калькуляторов плотности
У нас на сайте есть еще крутые калькуляторы плотности:
- Калькулятор плотности;
- Калькулятор плотности газа;
- Калькулятор массы в плотность;
- Калькулятор объем-плотность;
- Калькулятор плотности к массе;
- Калькулятор соотношения плотности к весу;
- Калькулятор плотности масса-объем;
- Калькулятор плотности цилиндра;
- Калькулятор плотности сфер.
Как рассчитать плотность бетонного куба?
Хотя плотность бетона уже определена (2400 кг/м 3 ), иногда ее необходимо рассчитать самостоятельно.
- Найдите массу (вес) вашего бетонного куба.
- Затем измерьте сторону куба.
- Как рассчитать объем куба по плотности? Используйте формулу: объем = сторона 3 .

- Теперь разделите массу на объем. плотность = масса/объем
- Расчет плотности куба готов!
Часто задаваемые вопросы
Как определить плотность кусочка сахара?
Чтобы найти плотность кусочка сахара:
- Возьмите линейку или другой измерительный инструмент и измерьте сторону кусочка сахара. Назовем это .
- Вычислите объем куба: объем = a 3
- Теперь взвесьте кубик сахара на кухонных весах.
- Чтобы найти плотность, нужно решить уравнение:
плотность = масса/объем
Как рассчитать плотность куба дерева?
Древесина не является однородным материалом, поэтому, если вы хотите быть точным в отношении плотности деревянного куба, лучше посчитайте ее самостоятельно:
- Взвесьте свой деревянный куб.
- Измерьте куб. Самый простой способ — измерить его сторону.
- Рассчитайте объем вашей деревянной вещи.
 объем = (длина стороны) 3 .
объем = (длина стороны) 3 . - Теперь посчитайте плотность куба. Плотность = масса (вес)/объем .
Как найти плотность куба со стороной 2 фута и весом 5 фунтов?
Плотность этого куба составляет 0,625 фунт/фут 3 . Чтобы вычислить плотность этого куба:
- Вычислите объем куба по формуле объем = сторона 3 .
- Наш случай, объем = 2 фута 3 = 8 футов 3 .
- Чтобы рассчитать плотность, решите уравнение плотность = масса/объем .
- В нашем случае плотность = 5 фунтов/8 футов 3 = 0,625 фунтов/фут 3 .
- Ответ: кубическая плотность = 0,625 фунт/фут 3 .
Aleksandra Zając, MD
Плотность
Вес/масса
Том
Сторонная (A)
Диагонал (D)
Diagonal (F)
Проверка 83 Clase Classical.
 0003
0003УскорениеУгол закручиванияУгол берега… Еще 80
Подсчет кубов | ClipArt ETC
Галерея Cube Counting ClipArt включает 34 иллюстрации кубиков, которые используются для счета и проверки восприятия глубины. Эти кубы представляют собой трехмерные представления на двухмерной поверхности, и часто кубы скрыты за другими кубами, что видно только по высоте некоторых областей структуры.
Площадь куба
Куб 12x12x12 из 1728 кубов.
108 конгруэнтных кубов, сложенных друг на друга
Иллюстрация 108 конгруэнтных кубов, сложенных друг на друга на разной высоте. Трехмерное изображение на…
117 конгруэнтных кубов, сложенных друг на друга
Иллюстрация 117 конгруэнтных кубов, сложенных столбцами по одному, четырем и шести столбцам. Трехмерное представление…
128 сложенных конгруэнтных кубов
Иллюстрация 128 конгруэнтных кубов, сложенных так, что они образуют прямоугольное тело размером 4 на 4 на…
132 сложенных конгруэнтных куба
Иллюстрация 132 конгруэнтных кубов, сложенных в 22 столбца по 6 штук в форме буквы U.
 Трехмерный…
Трехмерный…154 сложенных конгруэнтных куба
Иллюстрация 154 конгруэнтных кубов, сложенных в столбцы, увеличивающиеся от одного до четырех. Трехмерный…
16 конгруэнтных кубов, сложенных друг на друга
Иллюстрация 16 конгруэнтных кубов, сложенных друг на друга на разной высоте. Трехмерное представление на двухмерном…
17 сложенных конгруэнтных кубов
Иллюстрация 17 конгруэнтных кубов, сложенных по одному и по два в форме буквы V. Трехмерное изображение…
2 конгруэнтных куба
Иллюстрация двух конгруэнтных кубов, касающихся ребра. Трехмерное изображение на…
20 конгруэнтных кубов, сложенных друг на друга
Иллюстрация 20 конгруэнтных кубов, сложенных по двое и по трое. Трехмерное представление на двухмерном…
20 конгруэнтных кубов, сложенных друг на друга
Иллюстрация 20 конгруэнтных кубов, сложенных друг на друга на разной высоте.
 Трехмерное представление на двухмерном…
Трехмерное представление на двухмерном…20 конгруэнтных кубов, сложенных друг на друга
Иллюстрация 20 конгруэнтных кубов, сложенных друг на друга на высоте от 1 до 4 кубов. Трехмерный…
22 конгруэнтных куба, сложенных друг на друга
Иллюстрация 22 конгруэнтных кубов, сложенных по одному, по два и по три. Трехмерное представление…
22 конгруэнтных куба, сложенных друг на друга
Иллюстрация 22 конгруэнтных кубов, сложенных друг на друга на разной высоте. Трехмерное представление на двухмерном…
24 конгруэнтных куба, сложенных друг на друга
Иллюстрация 24 конгруэнтных кубов, сложенных на разной высоте в виде ступенек. Трехмерное представление…
256 сложенных конгруэнтных кубов
Иллюстрация 256 конгруэнтных кубов, сложенных таким образом, что они образуют 4 больших куба размером 4 на 4 на 4 каждый.
 …
…27 сложенных конгруэнтных кубов
Иллюстрация 27 конгруэнтных кубов, сложенных друг на друга в виде куба большего размера, размер которого три на три на…
27 сложенных конгруэнтных кубов
Иллюстрация 27 конгруэнтных кубов, сложенных на разной высоте в форме буквы W. Трехмерное изображение…
30 конгруэнтных кубов, сложенных друг на друга
Иллюстрация из 30 конгруэнтных кубов, сложенных стопкой в порядке уменьшения высоты. Трехмерное представление на…
33 конгруэнтных куба, сложенных друг на друга
Иллюстрация 33 конгруэнтных кубов, сложенных на разной высоте в виде зигзага. Трехмерное представление…
35 сложенных конгруэнтных кубов
Иллюстрация 35 конгруэнтных кубов, сложенных по одному и по два в форме буквы W. Трехмерное изображение…
35 конгруэнтных кубов, сложенных друг на друга
Иллюстрация 35 конгруэнтных кубов, сложенных на разной высоте.
 Трехмерное представление на двухмерном…
Трехмерное представление на двухмерном…36 конгруэнтных кубов, сложенных друг на друга
Иллюстрация 36 конгруэнтных кубов, сложенных друг на друга на разной высоте, внешние края которых образуют квадрат. Трехмерный…
36 сложенных конгруэнтных кубов
Иллюстрация 36 конгруэнтных кубов, уложенных друг на друга так, чтобы они напоминали куб 1 на 1 на 1 на кубе 2 на 2 на 2 на…
39 сложенных конгруэнтных кубов
Иллюстрация 39 конгруэнтных кубов, сложенных на разной высоте. Трехмерное представление на двухмерном…
4 конгруэнтных куба, сложенных друг на друга
Иллюстрация 4 конгруэнтных кубов, сложенных по одному и по два. Трехмерное представление на двухмерном…
50 конгруэнтных кубов, сложенных друг на друга
Иллюстрация 50 конгруэнтных кубов, сложенных друг на друга на разной высоте.

- Рассчитать объем (VVV) как: 93V=(2