|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 3 из 6Следующая ⇒ Решение систем линейных алгебраических уравнений методом Жордана-Гаусса Метод Жордана — Гаусса является одной из модификаций метода Гаусса, в котором матрица коэффициентов при неизвестных последовательно приводится к единичной матрице, а на месте столбца свободных членов в расширенной матрице в результате располагается решение системы линейных алгебраических уравнений: , где — коэффициенты системы, — свободные члены, — неизвестные. Сущность этого метода заключается в том, что, начиная со второго шага, зануляются все элементы в соответствующем столбце, кроме элемента, стоящего на главной диагонали. Это достигается с помощью алгебраических преобразований аналогичных классическому методу Гаусса. Стандартной функцией, которая реализует метод Жордана-Гаусса в системе MATLAB , является функция rref(). Аргументом у этой функции является расширенная матрица коэффициентов. Пример: решить с помощью метода Жордана –Гаусса систему линейных алгебраических уравнений . >> A=[3 2 -1;2 -1 3;1 -2 2]; B=[4;9;3]; >> AB=[A B] AB = 3 2 -1 4 2 -1 3 9 1 -2 2 3 >> rref(AB) ans = 1 0 0 1 0 1 0 2 0 0 1 3 Для решения систем линейных алгебраических уравнений с помощью MATLAB можно применять оператор «\», который самостоятельно выбирает лучший метод для решения заданной системы уравнений. При этом решение системы линейных алгебраических уравнений любого порядка достигается одной командой: Индивидуальные задания · Решить систему линейных алгебраических уравнений методом Гаусса, · решить систему линейных алгебраических уравнений методом Жордана— Гаусса в системе MATLAВ.
Таблица 4
Продолжение табл. 4 Окончание табл. Содержание соответствующего раздела В пояснительной записке Данный раздел должен содержать: · краткие теоретические сведения, · исследование системы линейных алгебраических уравнений на совместность, · аналитическое решение системы линейных алгебраических уравнений методом Гаусса, · решение системы линейных алгебраических уравнений методом Жордана-Гаусса в системе MATLAB, · сравнение полученных результатов, найденных разными способами.
⇐ Предыдущая123456Следующая ⇒ Читайте также: Формы дистанционного обучения Передача мяча двумя руками снизу Значение правильной осанки для жизнедеятельности человека Основные ошибки при выполнении передач мяча на месте |
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 968; Нарушение авторского права страницы; Мы поможем в написании вашей работы!  su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.007 с.) su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.007 с.)
|
Решение систем линейных алгебраических уравнений в пакете MATLAB
Решение систем линейных алгебраических уравнений в пакете MATLAB
Ранее » Возможности MATLAB ‣ левостороннее деление › x = Ab ‣ обратная матрица › x = inv(A)*b 2/13/2018 2
Небольшие системы уравнений » Небольшая система содержит, как привило, не более трех уравнений » Решение, чаще всего, может не требовать компьютера » Методы ‣ графический ‣ Крамера ‣ исключения неизвестных 2/13/2018 3
Графический метод » 2/13/2018 4
Сложные случаи решений » Три случая 1. 2. 3. Параллельные линии › нет решения Совпадающие линии › множество решений Близкие линии › трудно определить точку пересечения » Системы в 1 и 2 случае называются – вырожденными (особыми, сингулярными) » Случай 3 соответствует плохо обусловленной системе ‣ существуют сложности при численном решении 2/13/2018 5
Метод Крамера » 2/13/2018 6
Метод Крамера » 2/13/2018 7
Исключение неизвестных » 2/13/2018 8
Исключение неизвестных » 2/13/2018 9
Метод Гаусса » 2/13/2018 10
Метод Гаусса – Прямой ход » 2/13/2018 11
Метод Гаусса – Прямой ход » 2/13/2018 12
Метод Гаусса – Прямой ход » 2/13/2018 13
Метод Гаусса – Прямой ход » 2/13/2018 14
Метод Гаусса – Обратный ход » 2/13/2018 15
Пример 2/13/2018 16
Метод Гаусса с обратной подстановкой » В рассмотренном варианте метода Гаусса могут возникнуть ситуации когда решение не может быть найдено или иметь существенную погрешность ‣ например, в случае если главный элемент равен 0, при нормализации возникает деление на 0 ‣ также существенно меньшее значение главного элемента по сравнению с остальными может привести к увеличению погрешности вычислений » Решение – выбор главного элемента ‣ частный › выбор максимального значения главного элемента с последующей перестановкой строк ‣ полный (применяется редко) › выбор максимального значения главного элемента с последующей перестановкой строк и столбцов 2/13/2018 17
Пример – Частный выбор главного элемента » 2/13/2018 18
Пример – Частный выбор главного элемента Разряды х2 х1 Ошибка х1, % 3 0, 667 -3, 33 1099 4 0, 6667 0, 0000 100 5 0, 66667 0, 30000 10 6 0, 666667 0, 330000 1 7 0, 6666667 0, 3330000 0, 1 Разряды х2 х1 Ошибка х1, % 3 0, 667 0, 333 0, 1 4 0, 6667 0, 3333 0, 01 5 0, 66667 0, 33333 0, 001 6 0, 666667 0, 333333 0, 0001 7 0, 6666667 0, 3333333 0, 0000 » 2/13/2018 19
Пример – MATLAB 2/13/2018 20
Расчет определителя матрицы » 2/13/2018 21
Факторизация матриц » В математике факторизация или факторинг — это декомпозиция объекта (например, числа, полинома или матрицы) в произведение других объектов или факторов, которые, будучи перемноженными, дают исходный объект » Целью факторизации является приведение объекта к «основным строительным блокам» ‣ Матрица может также быть факторизована на произведение матриц специального вида для приложений, в которых эта форма удобна » Виды факторизации матриц ‣ LU ‣ Холецкого ‣ QR 2/13/2018 22
LU факторизация » 2/13/2018 23
LU факторизация » 2/13/2018 24
‣ факторизация › выполняется декомпозиция матрицы А на верхнюю U и нижнюю L треугольные матрицы ‣ подстановка › прямая подстановка определяет промежуточный вектор d › обратная подстановка определяет вектор неизвестных x 2/13/2018 прямая обратная 25 подстановка » Два основных шага решения системы факторизация LU факторизация
Метод Гаусса как LU факторизация » 2/13/2018 26
Метод Гаусса как LU факторизация » 2/13/2018 27
Метод Гаусса как LU факторизация » 2/13/2018 28
Метод Гаусса как LU факторизация » 2/13/2018 29
Пример — Проверка » 2/13/2018 30
Пример — Проверка » 2/13/2018 31
Метод Гаусса как LU факторизация » 2/13/2018 32
Пример » 2/13/2018 33
Пример » 2/13/2018 34
LU факторизация с выбором главного элемента » Аналогично методу Гаусса для обеспечения надежности решения при использовании LU факторизации необходимо применять частный выбор главного элемента ‣ одним из способов является использование матрицы перестановки › единичная матрица для взаимной замены строк и столбцов 2/13/2018 35
LU факторизация с выбором главного элемента » 2/13/2018 36
Пример » 2/13/2018 37
Пример » 2/13/2018 38
LU факторизация – MATLAB функции » lu ‣ [L, U] = lu(A) – возвращает верхнюю треугольную матрицу U и психологическую нижнюю матрицу L (то есть произведение нижней треугольной матрицы и матрицы перестановок), так что A=L*U ‣ [L, U, P] = lu(A) – возвращает верхнюю треугольную матрицу U, нижнюю треугольную матрицу L и сопряженную (эрмитову) матрицу матрицы перестановок P, так что L*U =P*A 2/13/2018 39
Пример 2/13/2018 40
Факторизация Холецкого » 2/13/2018 41
Пример » 2/13/2018 42
Пример » 2/13/2018 43
Факторизация Холецкого » 2/13/2018 44
Факторизация Холецкого – MATLAB функции » chol ‣ U = chol(A) – для квадратной матрицы A возвращает верхнюю треугольную матрицу U, так что U’*U=A › Разложение Холецкого возможно для действительных и комплексных эрмитовых матриц 2/13/2018 45
Пример 2/13/2018 46
Левостороннее деление MATLAB » При использовании левостороннего деления «» MATLAB выполняет оценку матрицы коэффициентов и применяет оптимальный метод для решения ‣ MATLAB проверяет вид матрицы коэффициентов при неизвестных для возможности нахождения решения без применения полного метода Гаусса › разреженная › треугольная › симметричная ‣ В противном случае применяется для квадратной матрицы применяется метод Гаусса с частным выбором главного элемента 2/13/2018 47
QR факторизация » 2/13/2018 48
QR факторизация – MATLAB функции » qr ‣ [Q, R] = qr(A) – вычисляет верхнюю треугольную матрицу R того же размера, как и у A, и унитарную матрицу Q, так что X=Q*R ‣ [Q, R, P] = qr(A) – вычисляет матрицу перестановок P, верхнюю треугольную матрицу R с убывающими по модулю диагональными элементами и унитарную матрицу Q, так что A*P=Q*R › Матрица перестановок P выбрана так, что abs(diag(R)) уменьшается ‣ [Q, R] = qr(A, 0) и [Q, R, P] = qr(A, 0) – вычисляют экономное разложение, в котором P – вектор перестановок, так что Q*R=A(: , P) › Матрица P выбрана так, что abs(diag(R)) уменьшается 2/13/2018 49
Пример 2/13/2018 50
Итерационные методы » Итерационные или аппроксимационные методы являются альтернативой ранее рассмотренным методам решения СЛАУ, основанным на исключении неизвестных » Можно выделить два основных этапа ‣ выбор начального приближения ‣ последующее систематическое уточнение » Методы ‣ ‣ ‣ 2/13/2018 Гаусса-Зейделя Якоби релаксации бисопряженных градиентов и др. 51
51
Метод Гаусса-Зейделя » 2/13/2018 52
Метод Гаусса-Зейделя » 2/13/2018 53
Пример » 2/13/2018 54
Пример » 2/13/2018 55
Пример » 2/13/2018 56
Метод Якоби » Метод Гаусса-Зейделя использует найденное значение х сразу же для нахождения следующего х из другого уравнения » Несколько альтернативный подход, называемый методом Якоби, заключается в расчете всех х на основании предыдущей итерации Гаусса-Зейдель 2/13/2018 Якоби 57
Сходимость и диагональное преобладание » 2/13/2018 58
Пример » 2/13/2018 59
Метод релаксации » 2/13/2018 60
Метод релаксации » 2/13/2018 61
Пример » 2/13/2018 62
Пример » 2/13/2018 63
Пример » 2/13/2018 64
Решение систем линейных алгебраических уравнений в пакете MATLAB
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Решение систем линейных алгебраических уравнений
в пакете MATLAB2. Ранее
» Возможности MATLAB‣ левостороннее деление
› x = A\b
‣ обратная матрица
› x = inv(A)*b
21.04.2022
2
3. Небольшие системы уравнений
» Небольшая система содержит, как привило, неболее трех уравнений
» Решение, чаще всего, может не требовать
компьютера
» Методы
‣ графический
‣ Крамера
‣ исключения неизвестных
21.04.2022
3
4. Графический метод
21.04.20224
5. Сложные случаи решений
» Три случая1.
 Параллельные линии
Параллельные линии› нет решения
2. Совпадающие линии
› множество решений
3. Близкие линии
› трудно определить точку пересечения
» Системы в 1 и 2 случае
называются – вырожденными
(особыми, сингулярными)
» Случай 3 соответствует плохо
обусловленной системе
‣ существуют сложности при численном
решении
21.04.2022
5
6. Метод Крамера
21.04.20226
7. Метод Крамера
21.04.20227
8. Исключение неизвестных
21.04.20228
9. Исключение неизвестных
21.04.20229
10. Метод Гаусса
21.04.202210
11. Метод Гаусса – Прямой ход
21.04.202211
12. Метод Гаусса – Прямой ход
21.04.202212
13. Метод Гаусса – Прямой ход
21.04.202213
14. Метод Гаусса – Прямой ход
21.04.202214
15. Метод Гаусса – Обратный ход
21.04.202215
16. Пример
21.04.202216
17. Метод Гаусса с обратной подстановкой
» В рассмотренном варианте метода Гаусса могутвозникнуть ситуации когда решение не может быть
найдено или иметь существенную погрешность
‣ например, в случае если главный элемент равен 0, при
нормализации возникает деление на 0
‣ также существенно меньшее значение главного элемента
по сравнению с остальными может привести к
увеличению погрешности вычислений
» Решение – выбор главного элемента
‣ частный
› выбор максимального значения главного элемента с
последующей перестановкой строк
‣ полный (применяется редко)
› выбор максимального значения главного элемента с
последующей перестановкой строк и столбцов
21.
 04.2022
04.202217
18. Пример – Частный выбор главного элемента
21.04.202218
19. Пример – Частный выбор главного элемента
Разрядых2
х1
Ошибка х1, %
3
0,667
-3,33
1099
4
0,6667
0,0000
100
5
0,66667
0,30000
10
6
0,666667
0,330000
1
7
0,6666667
0,3330000
0,1
Разряды
х2
х1
Ошибка х1, %
3
0,667
0,333
0,1
4
0,6667
0,3333
0,01
5
0,66667
0,33333
0,001
6
0,666667
0,333333
0,0001
7
0,6666667
0,3333333
0,0000
21.04.2022
19
20. Пример – MATLAB
21.04.202220
21. Расчет определителя матрицы
21.04.202221
22. Факторизация матриц
» В математике факторизация или факторинг — этодекомпозиция объекта (например, числа, полинома
или матрицы) в произведение других объектов или
факторов, которые, будучи перемноженными, дают
исходный объект
» Целью факторизации является приведение объекта
к «основным строительным блокам»
‣ Матрица может также быть факторизована на
произведение матриц специального вида для
приложений, в которых эта форма удобна
» Виды факторизации матриц
‣ LU
‣ Холецкого
‣ QR
21.
 04.2022
04.202222
23. LU факторизация
21.04.202223
24. LU факторизация
21.04.202224
25. LU факторизация
‣ факторизация› выполняется декомпозиция
матрицы А на верхнюю U и
нижнюю L треугольные
матрицы
‣ подстановка
› прямая подстановка
определяет промежуточный
вектор d
› обратная подстановка
определяет вектор
неизвестных x
21.04.2022
прямая
подстановка
» Два основных шага
решения системы
факторизация
LU факторизация
обратная
25
26. Метод Гаусса как LU факторизация
21.04.202226
27. Метод Гаусса как LU факторизация
21.04.202227
28. Метод Гаусса как LU факторизация
21.04.202228
29. Метод Гаусса как LU факторизация
21.04.202229
30. Пример — Проверка
21.04.202230
31. Пример — Проверка
21.04.202231
32. Метод Гаусса как LU факторизация
21.04.202232
33.
 Пример21.04.2022
Пример21.04.202233
34. Пример
21.04.202234
35. LU факторизация с выбором главного элемента
» Аналогично методу Гаусса для обеспечениянадежности решения при использовании LU
факторизации необходимо применять частный
выбор главного элемента
‣ одним из способов является использование матрицы
перестановки
› единичная матрица для взаимной замены строк и столбцов
21.04.2022
35
36. LU факторизация с выбором главного элемента
21.04.202236
37. Пример
21.04.202237
38. Пример
21.04.202238
39. LU факторизация – MATLAB функции
» lu‣ [L,U] = lu(A) – возвращает верхнюю треугольную
матрицу U и психологическую нижнюю матрицу L
(то есть произведение нижней треугольной матрицы
и матрицы перестановок), так что A=L*U
‣ [L,U,P] = lu(A) – возвращает верхнюю
треугольную матрицу U, нижнюю треугольную
матрицу L и сопряженную (эрмитову) матрицу
матрицы перестановок P, так что L*U =P*A
21.
 04.2022
04.202239
40. Пример
21.04.202240
41. Факторизация Холецкого
21.04.202241
42. Пример
21.04.202242
43. Пример
21.04.202243
44. Факторизация Холецкого
21.04.202244
45. Факторизация Холецкого – MATLAB функции
» chol‣ U = chol(A) – для квадратной матрицы A
возвращает верхнюю треугольную матрицу U, так
что U’*U=A
› Разложение Холецкого возможно для действительных и
комплексных эрмитовых матриц
21.04.2022
45
46. Пример
21.04.202246
47. Левостороннее деление MATLAB
» При использовании левостороннего деления«\» MATLAB выполняет оценку матрицы
коэффициентов и применяет оптимальный
метод для решения
‣ MATLAB проверяет вид матрицы коэффициентов
при неизвестных для возможности нахождения
решения без применения полного метода Гаусса
› разреженная
› треугольная
› симметричная
‣ В противном случае применяется для квадратной
матрицы применяется метод Гаусса с частным
выбором главного элемента
21.
 04.2022
04.202247
48. QR факторизация
21.04.202248
49. QR факторизация – MATLAB функции
» qr‣ [Q,R] = qr(A) – вычисляет верхнюю треугольную
матрицу R того же размера, как и у A, и унитарную
матрицу Q, так что X=Q*R
‣ [Q,R,P] = qr(A) – вычисляет матрицу перестановок P,
верхнюю треугольную матрицу R с убывающими по
модулю диагональными элементами и унитарную
матрицу Q, так что A*P=Q*R
› Матрица перестановок P выбрана так, что abs(diag(R))
уменьшается
‣ [Q,R] = qr(A,0) и [Q,R,P] = qr(A,0) – вычисляют
экономное разложение, в котором P – вектор
перестановок, так что Q*R=A(:,P)
› Матрица P выбрана так, что abs(diag(R)) уменьшается
21.04.2022
49
50. Пример
21.04.202250
51. Итерационные методы
» Итерационные или аппроксимационные методыявляются альтернативой ранее рассмотренным
методам решения СЛАУ, основанным на
исключении неизвестных
» Можно выделить два основных этапа
‣ выбор начального приближения
‣ последующее систематическое уточнение
» Методы
‣
‣
‣
‣
‣
Гаусса-Зейделя
Якоби
релаксации
бисопряженных градиентов
и др.
21.04.2022
51
52. Метод Гаусса-Зейделя
21.04.202252
53. Метод Гаусса-Зейделя
21.04.202253
54. Пример
21.04.202254
55. Пример
21.04.202255
56. Пример
21.04.202256
57. Метод Якоби
» Метод Гаусса-Зейделяиспользует
найденное значение
х сразу же для
нахождения
следующего х из
другого уравнения
» Несколько
альтернативный
подход, называемый
методом Якоби,
заключается в
расчете всех х на
основании
предыдущей
итерации
21.04.2022
57
58. Сходимость и диагональное преобладание
21.04.202258
59. Пример
21.04.202259
60. Метод релаксации
21.04.202260
61. Метод релаксации
21.04.202261
62. Пример
21.04.202262
63. Пример
21.04.202263
64. Пример
21.04.202264
English Русский Правила
Работа с матрицами и решение СЛАУ в пакете Matlab презентация, доклад, проект
Работа с матрицами
и
решение СЛАУ
в пакете
Matlab
Весна 2020
Пакет Matlab. Лекция 3
Лекция 3
Вектор-строка и вектор-столбец
Все в Matlab – матрицы! Индексация начинается с 1 !!!
Весна 2020
Пакет Matlab. Лекция 3
Действия с векторами
Весна 2020
Пакет Matlab. Лекция 3
Столбец, А(:,1)
Строка, А(3,:)
Элемент,
А (1,3)
Матрица А
Задание матрицы
Задание по строкам, строки разделяются символом «;».
Символ «;» отделяет два соседних столбца
Весна 2020
Пакет Matlab. Лекция 3
Задание матрицы специальными функциями
Весна 2020
Пакет Matlab. Лекция 3
Задание специальных матриц
Весна 2020
Пакет Matlab. Лекция 3
Лекция 3
Задание матрицы через цикл
Сформировать матрицу А размерности 3х3 по правилу:
Весна 2020
Пакет Matlab. Лекция 3
Задание матрицы через цикл
Весна 2020
Пакет Matlab. Лекция 3
Условный оператор
if ( условие истинно)
делать
else
делать (выполняется в случае, если условие не истинно)
end
Весна 2020
Пакет Matlab. Лекция 3
Возможно «краткая (укороченная)» версия условного оператора:
if ( условие истинно)
делать
end
Составные условия
Весна 2020
Пакет Matlab. Лекция 3
Условный оператор -2
Весна 2020
Пакет Matlab. Лекция 3
Лекция 3
if ( условие1 истинно)
делать (выполняется в случае, если условие1 истинно)
elseif ( условие2 истинно)
делать (выполняется в случае, если условие2 истинно)
else
делать (выполняется в случае, если ни одно из условий не истинно)
end
Задание матрицы через цикл
(универсальная функция)
Весна 2020
Пакет Matlab. Лекция 3
Трассировка функции, или
как это работает (N=3)
Весна 2020
Пакет Matlab. Лекция 3
Вызов функции задания матрицы и результат работы
Весна 2020
Пакет Matlab. Лекция 3
Очищает все имеющиеся переменные
Весна 2020
Пакет Matlab. Лекция 3
Действия с матрицами
Весна 2020
Пакет Matlab. Лекция 3
Лекция 3
Функции для работы с матрицами
Весна 2020
Пакет Matlab. Лекция 3
Функции для работы с матрицами
Весна 2020
Пакет Matlab. Лекция 3
Слияние матриц
В
А
А
В
А
В
Весна 2020
Пакет Matlab. Лекция 3
Расширение матриц (поэлементное)
Весна 2020
Пакет Matlab. Лекция 3
Расширение матриц (матрицами)
А(с какой строки : по какую, с какого столбца : по какой)
Весна 2020
Пакет Matlab. Лекция 3
Выделение подматрицы
Весна 2020
Пакет Matlab. Лекция 3
Лекция 3
Основные характеристики матрицы
Весна 2020
Пакет Matlab. Лекция 3
Нормы матрицы
Для вычисления различных вариантов нормы используется функция вида:
n=norm(М,k)
М – матрица/вектор, для которого необходимо вычислить норму
k – параметр, определяющий какую норму надо вычислить. Наиболее распространенные значения параметра k:
1 – L1 норма (максимальная столбцовая норма)
2 – евклидова норма (по умолч.)
inf – неопределенная норма (максимальная строчная норма)
Весна 2020
Пакет Matlab. Лекция 3
Нормы вектора
Для вычисления различных вариантов нормы используется функция вида:
n=vecnorm(М, k)
М – матрица/вектор, для которого необходимо вычислить норму. Результат зависит от вида М:
М – вектор, n – число, евклидова норма
М – матрица, n – строка, содержащая нормы для каждого столбца
Значения параметра k такие же, как в функции norm
Весна 2020
Пакет Matlab. Лекция 3
Лекция 3
Числа обусловленности матрицы
Для вычисления различных вариантов числа обусловленности используется функция вида:
cond(М,k)
М – матрица/вектор, для которого необходимо вычислить число обусловленности
k – параметр, определяющий какое число обусловленности надо вычислить. Значения параметра k аналогичны параметрам в функции norm.
Весна 2020
Пакет Matlab. Лекция 3
Пример вычисления характеристик матрицы
Весна 2020
Пакет Matlab. Лекция 3
Собственные числа и собственные вектора
Весна 2020
Пакет Matlab. Лекция 3
Собственные числа и собственные вектора (пример)
Весна 2020
Пакет Matlab. Лекция 3
Разложения матриц
Весна 2020
Пакет Matlab. Лекция 3
Лекция 3
LU разложение матриц (пример)
Весна 2020
Пакет Matlab. Лекция 3
QR разложение матриц (пример)
Весна 2020
Пакет Matlab. Лекция 3
Решение СЛАУ вида Ax=b
Весна 2020
Пакет Matlab. Лекция 3
Вычисление времени выполнения операций
Время выполнения операция вычисляют с помощью пары операторов:
tic
исследуемые действия
t=toc
В переменой t будет находится время выполнения операций, размещенных между tic-toc
Весна 2020
Пакет Matlab. Лекция 3
Функция для решения СЛАУ
Весна 2020
Пакет Matlab. Лекция 3
Функция для решения СЛАУ
(результат работы)
Вызов функции
Время работы каждого способа
Столбцы ответов для каждого способа
Как решить систему уравнений в матлабе
Документация
Одной из самых важных проблем в техническом вычислении является решение систем одновременных линейных уравнений.
В матричном обозначении общая проблема принимает следующую форму: Учитывая две матрицы A и b, действительно там существует уникальный матричный x, так, чтобы A x = b или x A = b?
Это поучительно, чтобы рассмотреть пример 1 на 1. Например, делает уравнение
имеет уникальное решение?
Ответ, конечно, является да. Уравнение имеет уникальное решение x = 3. Решение легко получено делением:
Решение обычно не получается путем вычисления инверсии 7, который равняется 7 –1 = 0.142857. и затем умножение 7 –1 21. Это было бы, больше работают и, если 7 –1 представлен конечному числу цифр, менее точных. Подобные факторы применяются к наборам линейных уравнений с больше чем одним неизвестным; MATLAB ® решает такие уравнения, не вычисляя инверсию матрицы.
Несмотря на то, что это не стандартное математическое обозначение, MATLAB использует терминологию деления, знакомую в скалярном случае, чтобы описать решение общей системы одновременных уравнений.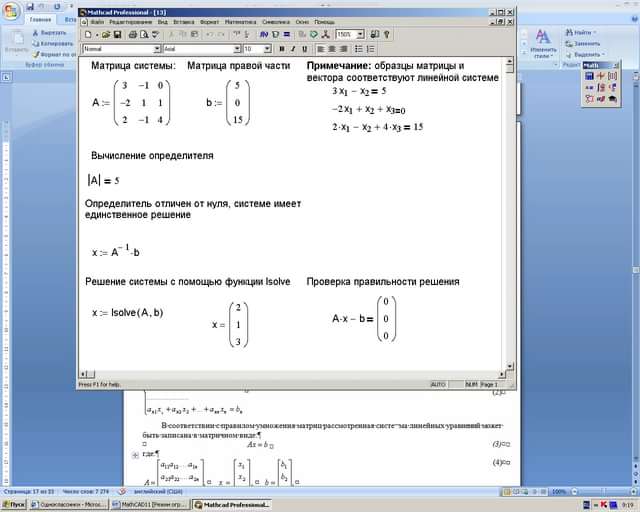 Два символа деления, наклонная черта ,/, и обратная косая черта , \, соответствуют этим двум функциям MATLAB mrdivide и mldivide . Эти операторы используются для двух ситуаций, где неизвестная матрица появляется слева или право на матрицу коэффициентов:
Два символа деления, наклонная черта ,/, и обратная косая черта , \, соответствуют этим двум функциям MATLAB mrdivide и mldivide . Эти операторы используются для двух ситуаций, где неизвестная матрица появляется слева или право на матрицу коэффициентов:
Обозначает решение матричного уравнения xA = b, полученное использование mrdivide .
Обозначает решение матричного уравнения Ax = b, полученное использование mldivide .
Думайте о “делении” обеих сторон уравнения Ax = b или xA = b A. Матрица коэффициентов A всегда находится в “знаменателе”.
Условия совместимости размерности для x = A\b потребуйте этих двух матриц A и b иметь одинаковое число строк. Решение x затем имеет одинаковое число столбцов как b и его размерность строки равна размерности столбца A . Для x = b/A , ролями строк и столбцов обмениваются.
На практике линейные уравнения формы Ax = b происходят более часто, чем те из формы xA = b. Следовательно, обратная косая черта используется намного более часто, чем наклонная черта. Остаток от этого раздела концентрируется на операторе обратной косой черты; соответствующие свойства оператора наклонной черты могут быть выведены из идентичности:
Следовательно, обратная косая черта используется намного более часто, чем наклонная черта. Остаток от этого раздела концентрируется на операторе обратной косой черты; соответствующие свойства оператора наклонной черты могут быть выведены из идентичности:
Матрица коэффициентов A не должно быть квадратным. Если A имеет размер m-by-n, затем существует три случая:
Квадратная система. Ищите точное решение.
Сверхрешительная система, большим количеством уравнений, чем неизвестные. Найдите решение методом наименьших квадратов.
Недоопределенная система, меньшим количеством уравнений, чем неизвестные. Найдите основное решение с в большей части m ненулевые компоненты.
Mldivide Алгоритм
mldivide оператор использует другие решатели, чтобы обработать различные виды содействующих матриц. Различные случаи диагностированы автоматически путем исследования матрицы коэффициентов. Для получения дополнительной информации смотрите раздел “Algorithms” mldivide страница с описанием.
Общее решение
Общее решение системы линейных уравнений Ax = b описывает все возможные решения. Можно найти общее решение:
Решение соответствующей гомогенной системы Ax = 0. Сделайте это использование null команда, путем ввода null(A) . Это возвращает базис для пробела решения к Ax = 0. Любое решение является линейной комбинацией базисных векторов.
Нахождение конкретного решения неоднородной системы Ax =b.
Можно затем записать любое решение Ax = b как сумма конкретного решения Ax =b, от шага 2, плюс линейная комбинация базисных векторов от шага 1.
Остальная часть этого раздела описывает, как использовать MATLAB, чтобы найти конкретное решение Ax =b, как на шаге 2.
Квадратные системы
Наиболее распространенная ситуация включает квадратную матрицу коэффициентов A и один правый вектор-столбец стороны b .
Невырожденная матрица коэффициентов
Если матричный A несингулярно, затем решение, x = A\b , одного размера с b . Например:
Например:
Можно проверить, что A*x точно равно u .
Если A и b являются квадратными и тот же размер, x= A\b также что размер:
Можно проверить, что A*x точно равно b .
Оба из этих примеров имеют точные, целочисленные решения. Это вызвано тем, что матрица коэффициентов была выбрана, чтобы быть pascal(3) , который является (несингулярной) матрицей полного ранга.
Сингулярная матрица коэффициентов
A квадратной матрицы сингулярен, если он не имеет линейно независимых столбцов. Если A сингулярен, решение Ax = b или не существует или не уникален. Оператор обратной косой черты, A\b , выдает предупреждение если A почти сингулярно или если это обнаруживает точную сингулярность.
Если A сингулярен и Ax =, b имеет решение, можно найти конкретное решение, которое не уникально путем ввода
pinv(A) псевдоинверсия A. Если Ax = b не имеет точного решения, то pinv(A) возвращает решение методом наименьших квадратов.
сингулярно, когда можно проверить путем ввода
Поскольку A не является полным рангом, он имеет некоторые равные нулю сингулярные значения.
Точные решения. Для b =[5;2;12] , уравнение Ax = b имеет точное решение, данное
Проверьте тот pinv(A)*b точное решение путем ввода
Решения методом наименьших квадратов. Однако, если b = [3;6;0] , Ax = b не имеет точного решения. В этом случае, pinv(A)*b возвращает решение методом наименьших квадратов. Если вы вводите
вы не возвращаете исходный вектор b .
Можно определить, имеет ли Ax =b точное решение путем нахождения, что строка уменьшала форму эшелона расширенной матрицы [A b] . Чтобы сделать так для этого примера, войти
Поскольку нижний ряд содержит все нули за исключением последней записи, уравнение не имеет решения. В этом случае, pinv(A) возвращает решение методом наименьших квадратов.
Сверхрешительные системы
В этом примере показано, как со сверхрешительными системами часто сталкиваются в различных видах аппроксимирования кривыми к экспериментальным данным.
Количество y измеряется в нескольких различных значениях времени t произвести следующие наблюдения. Можно ввести данные и просмотреть их в таблице со следующими операторами.
Попытайтесь моделировать данные с затухающей показательной функцией
y ( t ) = c 1 + c 2 e — t .
Предыдущее уравнение говорит что векторный y должен быть аппроксимирован линейной комбинацией двух других векторов. Каждый — постоянный вектор, содержащий все единицы, и другой вектор с компонентами exp(-t) . Неизвестные коэффициенты, c 1 и c 2 , может быть вычислен путем выполнения метода наименьших квадратов, который минимизирует сумму квадратов отклонений данных из модели. Существует шесть уравнений в двух неизвестных, представленных 6 2 матрица.
Используйте оператор обратной косой черты, чтобы получить решение методом наименьших квадратов.
Другими словами, метод наименьших квадратов к данным
y ( t ) = 0 . 4 7 6 0 + 0 . 3 4 1 3 e — t .
Следующие операторы оценивают модель в расположенном с равными интервалами шаге в t , и затем постройте результат вместе с исходными данными:
E*c не точно равно y , но различие может хорошо быть меньше погрешностей измерения в исходных данных.
Прямоугольный матричный A имеет неполный ранг, если это не имеет линейно независимых столбцов. Если A имеет неполный ранг, затем решение методом наименьших квадратов к AX = B не уникально. A\B выдает предупреждение если A имеет неполный ранг и производит решение методом наименьших квадратов. Можно использовать lsqminnorm найти решение X это имеет минимальную норму среди всех решений.
Недоопределенные системы
В этом примере показано, как решение недоопределенных систем не уникально. Недоопределенные линейные системы включают больше неизвестных, чем уравнения. Матричная операция левого деления в MATLAB находит основное решение методом наименьших квадратов, которое имеет в большей части m ненулевые компоненты для m — n матрица коэффициентов.
Вот небольшой, случайный пример:
Линейная система Rp = b вовлекает два уравнения в четыре неизвестные. Поскольку матрица коэффициентов содержит маленькие целые числа, уместно использовать format команда, чтобы отобразить решение в рациональном формате. Конкретное решение получено с
Конкретное решение получено с
Одним из ненулевых компонентов является p(2) потому что R(:,2) столбец R с самой большой нормой. Другим ненулевым компонентом является p(4) потому что R(:,4) доминирует после R(:,2) устраняется.
Полное общее решение недоопределенной системы может быть охарактеризовано путем добавления p к произвольной линейной комбинации пустых векторов пробела, которые могут быть найдены с помощью null функция с опцией, запрашивающей рациональный базис.
Можно проверить, что R*Z нуль и что остаточный R*x — b мал для любого векторного x , где
Начиная со столбцов Z пустые векторы пробела, продукт Z*q линейная комбинация тех векторов:
Z q = ( x ⇀ 1 x ⇀ 2 ) ( u w ) = u x ⇀ 1 + w x ⇀ 2 .
Чтобы проиллюстрировать, выберите произвольный q и создайте x .
Вычислите норму невязки.
Когда бесконечно много решений доступны, решение с минимальной нормой особенно интересно. Можно использовать lsqminnorm вычислить решение методом наименьших квадратов минимальной нормы. Это решение имеет наименьшее значение для norm(p) .
Это решение имеет наименьшее значение для norm(p) .
Решение для нескольких правых сторон
Некоторые проблемы касаются решения линейных систем, которые имеют ту же матрицу коэффициентов A , но различные правые стороны b . Когда различные значения b доступны одновременно, можно создать b как матрица с несколькими столбцами и решают все системы уравнений одновременно с помощью одной команды обратной косой черты: X = A\[b1 b2 b3 …] .
Однако иногда различные значения b не все доступны одновременно, что означает, что необходимо решить несколько систем уравнений последовательно. Когда вы решаете одну из этих систем уравнений с помощью наклонной черты (/) или обратная косая черта (\), оператор разлагает на множители матрицу коэффициентов A и использование это матричное разложение, чтобы вычислить решение. Однако в каждый последующий раз вы решаете аналогичную систему уравнений с различным b , оператор вычисляет то же разложение A , который является избыточным расчетом.
Решение этой проблемы состоит в том, чтобы предварительно вычислить разложение A , и затем снова используйте факторы, чтобы решить для различных значений b . На практике, однако, предварительное вычисление разложения этим способом может затруднить, поскольку необходимо знать, какое разложение вычислить (LU, LDL, Холесский, и так далее), а также как умножить факторы, чтобы решить задачу. Например, с LU-разложением необходимо решить две линейных системы, чтобы решить исходную систему Ax = b:
На практике, однако, предварительное вычисление разложения этим способом может затруднить, поскольку необходимо знать, какое разложение вычислить (LU, LDL, Холесский, и так далее), а также как умножить факторы, чтобы решить задачу. Например, с LU-разложением необходимо решить две линейных системы, чтобы решить исходную систему Ax = b:
Вместо этого рекомендуемый метод для решения линейных систем с несколькими последовательными правыми сторонами должен использовать decomposition объекты. Эти объекты позволяют вам усилить выигрыши в производительности предварительного вычисления матричного разложения, но они не требуют знания того, как использовать матричные факторы. Можно заменить предыдущее LU-разложение на:
Если вы не уверены который разложение использовать, decomposition(A) выбирает правильный тип на основе свойств A , похожий на то, что делает обратная косая черта.
Вот простой тест возможных выигрышей в производительности этого подхода. Тест решает ту же разреженную линейную систему 100 раз с помощью и обратной косой черты (\) и decomposition .
MATLAB – алгебра
До сих пор мы видели, что все примеры работают как в MATLAB, так и в его GNU, альтернативно называемом Octave. Но для решения основных алгебраических уравнений и MATLAB, и Octave немного отличаются, поэтому мы постараемся охватить MATLAB и Octave в отдельных разделах.
Мы также обсудим факторизацию и упрощение алгебраических выражений.
Решение основных алгебраических уравнений в MATLAB
Функция решения используется для решения алгебраических уравнений. В простейшем виде функция решения принимает в качестве аргумента уравнение, заключенное в кавычки.
Например, давайте решим для х в уравнении х-5 = 0
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Вы также можете вызвать функцию решения как –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Вы можете даже не включать правую часть уравнения –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Если в уравнение входит несколько символов, то по умолчанию MATLAB предполагает, что вы решаете для x, однако функция решения имеет другую форму –
где вы также можете упомянуть переменную.
Например, давайте решим уравнение v – u – 3t 2 = 0, для v. В этом случае мы должны написать –
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Решение основных алгебраических уравнений в октаве
Функция корней используется для решения алгебраических уравнений в Octave, и вы можете написать приведенные выше примеры следующим образом:
Например, давайте решим для х в уравнении х-5 = 0
Octave выполнит приведенный выше оператор и вернет следующий результат –
Вы также можете вызвать функцию решения как –
Octave выполнит приведенный выше оператор и вернет следующий результат –
Решение квадратичных уравнений в MATLAB
Функция решения также может решать уравнения более высокого порядка. Он часто используется для решения квадратных уравнений. Функция возвращает корни уравнения в массиве.
В следующем примере решается квадратное уравнение x 2 -7x +12 = 0. Создайте файл сценария и введите следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Решение квадратичных уравнений в октаве
В следующем примере решается квадратное уравнение x 2 -7x +12 = 0 в октаве. Создайте файл сценария и введите следующий код –
Создайте файл сценария и введите следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Решение уравнений высшего порядка в MATLAB
Функция решения также может решать уравнения более высокого порядка. Например, давайте решим кубическое уравнение как (x-3) 2 (x-7) = 0
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
В случае уравнений более высокого порядка корни длинные, содержащие много членов. Вы можете получить числовое значение таких корней, преобразовав их в двойные. В следующем примере решается уравнение четвертого порядка x 4 – 7x 3 + 3x 2 – 5x + 9 = 0.
Создайте файл сценария и введите следующий код –
Когда вы запускаете файл, он возвращает следующий результат –
Обратите внимание, что последние два корня являются комплексными числами.
Решение уравнений высшего порядка в октаве
В следующем примере решается уравнение четвертого порядка x 4 – 7x 3 + 3x 2 – 5x + 9 = 0.
Создайте файл сценария и введите следующий код –
Когда вы запускаете файл, он возвращает следующий результат –
Решение системы уравнений в MATLAB
Функция решения также может быть использована для генерации решений систем уравнений, включающих более одной переменной. Давайте рассмотрим простой пример, чтобы продемонстрировать это использование.
Давайте решим уравнения –
Создайте файл сценария и введите следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Таким же образом вы можете решать большие линейные системы. Рассмотрим следующую систему уравнений –
Решающая система уравнений в октаве
У нас есть немного другой подход к решению системы ‘n’ линейных уравнений с ‘n’ неизвестными. Давайте рассмотрим простой пример, чтобы продемонстрировать это использование.
Давайте решим уравнения –
Такая система линейных уравнений может быть записана в виде единого матричного уравнения Ax = b, где A – матрица коэффициентов, b – вектор столбцов, содержащий правую часть линейных уравнений, а x – вектор столбцов, представляющий решение как показано в программе ниже –
Создайте файл сценария и введите следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Таким же образом, вы можете решить большие линейные системы, как указано ниже –
Разложение и сбор уравнений в MATLAB
Функция расширения и сбора расширяет и собирает уравнение соответственно. Следующий пример демонстрирует понятия –
Следующий пример демонстрирует понятия –
Когда вы работаете со многими символическими функциями, вы должны объявить, что ваши переменные являются символическими.
Создайте файл сценария и введите следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Расширяя и собирая уравнения в октаве
Вам нужно иметь символьный пакет, который обеспечивает расширение и функцию сбора для расширения и сбора уравнения, соответственно. Следующий пример демонстрирует понятия –
Когда вы работаете со многими символическими функциями, вы должны объявить, что ваши переменные являются символическими, но у Octave другой подход к определению символических переменных. Обратите внимание на использование Sin и Cos , которые также определены в символической упаковке.
Создайте файл сценария и введите следующий код –
Когда вы запускаете файл, он показывает следующий результат –
Факторизация и упрощение алгебраических выражений
Факторная функция разлагает выражение, а функция упрощения упрощает выражение. Следующий пример демонстрирует концепцию –
Следующий пример демонстрирует концепцию –
Решение СЛАУ и матрицы в Matlab
Доброго времени суток, читатели! Сегодня мы поговорим о матрицах в Matlab, об их применении в решении систем линейных алгебраических уравнений. Подробно разберем методы решения, и для этого необходимо знание нескольких базовых алгоритмов.
Также стоит отметить, что у каждого алгоритма, которым мы будем искать решение СЛАУ в Matlab, своя скорость нахождения этого решения, наличие или отсутствие условия выполнения алгоритма и т.д.
В традициях нашего сайта разберём на примере:
Решить систему линейных уравнений:
4*a + b — c = 6
a — b + c = 4
2*a — 3*b — 3*c = 4
Метод обратной матрицы в Matlab
Начнем с достаточно распространенного метода. Его суть состоит в том, что сначала необходимо выписать коэффициенты при a, b и c (то есть те коэффициенты, которые находятся слева) в одну матрицу, а свободный член (то есть то, что справа) в другую.
В итоге у нас получится 2 матрицы:
Для реализации этого метода (и следующих методов тоже) требуется одно условие: чтобы определитель матрицы, составленной из коэффициентов левой части не был равен нулю. Проверка на определитель:
После проверки условия можем перейти к следующему шагу: нахождение обратной матрицы. В Matlab для этого используется оператор inv .
А само решение СЛАУ в Matlab находится как перемножение найденной обратной матрицы на матрицу свободных членов:
Мы получили 3 значения, которые и соответствуют нашим коэффициентам: то есть a = 2, b = -1, c = 1 . Можете проверить, подставив полученные ответы в исходную систему, и убедиться, что мы решили СЛАУ правильно.
Также следует отметить, что матрицы нужно перемножать именно, как сделали мы, то есть слева обратная матрица, справа матрица свободных членов.
Если вы не все поняли, то советую вам почитать нашу статью по основам Matlab.
Метод Гаусса
Метод Гаусса в Matlab реализуется достаточно просто: для этого нам нужно всего лишь изучить один новый оператор.
(\) — левое деление.
При следующей записи:
Мы получим ответы на нашу исходную систему. Только заметьте, мы решили СЛАУ стандартным набором функций в Matlab, и желательно этот оператор использовать когда матрица коэффициентов квадратная, так как оператор приводит эту матрицу к треугольному виду. В других случаях могут возникнуть ошибки.
Метод разложения матрицы
Теперь поговорим о разложении матрицы. Нахождение решения через разложение матрицы очень эффективно. Эффективность обусловлена скоростью нахождения решения для данного вида систем и точностью полученных результатов.
Возможны следующие разложения:
- разложение Холецкого
- LU разложение
- QR разложение
Разберём решение через LU и QR разложение, так как в задачах чаще всего встречается задание на решение именно через такие разложения.
Основное отличие этих двух разложений: LU разложение применимо только для квадратных матриц, QR — возможно и для прямоугольных.
LU разложение
Решим выше предложенную задачу через LU разложение:
QR разложение
И через QR разложение соответственно:
Отметим, что апостроф ( ‘ ) после Q означает транспонирование.
Стандартные функции Matlab
Так же Matlab предлагает функцию linsolve , с помощью которой возможно решить систему линейных алгебраических уравнений. Выглядит это так:
Как видите, ничего сложного тут нет, на то они и стандартные функции Matlab.
Повторение
Итак, сегодня мы с вами изучили несколько методов для решения СЛАУ в Matlab, как с помощью матриц, так и с помощью стандартных функций. Давайте их повторим на другом примере:
Решить систему линейных уравнений:
6*a — b — c = 0
a — 2*b + 3*d = 0
3*a — 4*b — 4*c = -1
- Методом обратной матрицы:
- Методом Гаусса:
- LU разложение:
- QR разложение:
На этом я с вами попрощаюсь, надеюсь, вы научились применять матрицы в Matlab для решения СЛАУ.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда… Основы обеспечения единства измерений: Обеспечение единства измерений — деятельность метрологических служб, направленная на достижение… Интересное: Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются. Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 4 из 5Следующая ⇒ При решении инженерных задач достаточно часто приходится сталкиваться с решением систем линейных алгебраических уравнений (СЛАУ). СЛАУ называется совместной, если имеет хотя бы одно решение, и несовместной, если не имеет ни одного решения. Таким образом, решить СЛАУ – значит определить, является ли она совместной или нет. Существуют точные и приближенные (итерационные) методы решения СЛАУ. К точным относятся методы, которые дают точное решение задачи после конечного числа арифметических и логических операций. К указанным методам относятся, например, матричный метод, метод Крамера, метод Гаусса и т. д. К приближенным – метод Якоби, метод Гаусса – Зейделя и др. Для определения совместности системы можно использовать теорему Кронекера-Капелли, согласно которой для того, чтобы СЛАУ была совместной, необходимо и достаточно, чтобы ранг матрицы А системы был равен рангу ее расширенной матрицы. Напомним, что расширенная матрица получается после дополнения матрицы коэффициентов столбцом свободных членов. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решение. На рис. 5.1 представлен пример исследования на совместность следующей системы уравнений:
Рис. 5.1. Пример исследования на совместность заданной СЛАУ. В результате исследования получили, что ранг расширенной матрицы равен рангу матрицы коэффициентов СЛАУ, следовательно, данная система совместна. При этом ранг совместной системы равен числу неизвестных, поэтому система имеет единственное решение. Рассмотрим точные методы решения СЛАУ в системе MATLAB. Одним из таких методов является матричный метод решения СЛАУ, который предусматривает выполнение следующих шагов: 1. Убедиться в том, что система не является вырожденной (определитель ее не равен нулю), т. е. существует обратная матрица. 2. Найти обратную матрицу . 3. Найти вектор – столбец X, вычислив произведение . На рис. 5.2 приводится пример решения представленной выше системы уравнений с помощью матричного метода.
Рис. 5.2. Пример решения СЛАУ с помощью матричного метода.
Рассмотренный матричный метод решения требует определения обратной матрицы, для вычисления которой требуется значительное время, поэтому на практике данный метод не применяется.
В основе решения СЛАУ с помощью формул Крамера лежит теорема Крамера: система n уравнений с n неизвестными, определитель которой отличен от нуля всегда имеет решение, и притом единственное.
Пусть дана система n линейных уравнений с n неизвестными:
Обозначим определитель системы: . Заменим поочередно столбцы коэффициентов при на столбец свободных членов и получим n определителей: .
Формулы Крамера для решения системы уравнений имеют вид: .
Решение СЛАУ из предыдущего примера с помощью формул Крамера представлено на рис. 5.3.
Рис. 5.3. Пример решения СЛАУ с помощью формул Крамера.
Вычисление определителей, используемое в методе Крамера, занимает очень много времени, поэтому этот метод также редко используется на практике.
Существо метода Гаусса состоит в последовательном исключении неизвестных. Этот метод в MATLAB реализован в функции rref(), которая на его основании осуществляет приведение расширенной матрицы к треугольной форме. Пример ее применения для решения СЛАУ представлен на рис. 5.4.
Рис. 5.4. Пример решения СЛАУ с помощью метод Гаусса с частичным выбором главного элемента.
Как было сказано выше, помимо точных методов решения СЛАУ существует ряд итерационных методов. Одним их них является метод наименьших квадратов, реализованный в системе MATLAB функцией lsqr().
На рис. 5.5 приведен пример решения СЛАУ с использованием функции lsqr(A, B). В данном примере процесс итераций сходится на четвертом шаге с относительным остатком (отношением вторых норм векторов невязки и свободных членов) 1.7∙10-11.
Рис. 5.5. Пример решения СЛАУ методом наименьших квадратов.
Помимо рассмотренных методов решения СЛАУ в MATLAB реализован еще ряд методов решения с помощью функций, расположенных в ядре системы.
Рис. 5.6. Пример решения СЛАУ. ⇐ Предыдущая12345Следующая ⇒ Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой. |
20 лучших преподавателей MATLAB рядом со мной в Слау
Enayet: репетитор Slough по MATLAB
Сертифицированный преподаватель MATLAB в Слау
Позвоните нам сегодня, чтобы связаться с топ Slough MATLAB tutor
(888) 888-0446 Позвони сейчасПреподаю в университете (бакалавриат и магистратура) с 2003 года. Работала преподавателем на кафедре ЕГЭ 3 года и на кафедре ЭЭО 13 лет. Я также работаю частным репетитором, особенно для студентов университета, в Великобритании с 2010 года.
Образование и сертификация
BUET – Бакалавр наук, Электронные технологии
Городской университет Лондона – Доктор наук, Информатика
Посмотреть этот Slough MATLAB Tutor
Рик: репетитор Slough по MATLAB
Сертифицированный преподаватель MATLAB в Слау
Позвоните нам сегодня, чтобы связаться с топ Slough MATLAB tutor
(888) 888-0446 Позвони сейчас Предоставление рекомендаций по естественным наукам и математике, чтобы помочь учащимся понять реальное применение научных и математических концепций в их повседневной жизни. У меня B.S.E. в аэрокосмической технике и B.S. в области устойчивых энергетических материалов и технологий, и я получаю степень магистра. в аэрокосмической технике …. Изучение естественных наук и математики с помощью реальных приложений, которые показывают, как концепции могут на самом деле использоваться для решения реальных проблем.
У меня B.S.E. в аэрокосмической технике и B.S. в области устойчивых энергетических материалов и технологий, и я получаю степень магистра. в аэрокосмической технике …. Изучение естественных наук и математики с помощью реальных приложений, которые показывают, как концепции могут на самом деле использоваться для решения реальных проблем.
Образование и сертификация
Университет штата Аризона — бакалавриат, аэрокосмическая техника
Университет штата Аризона — аспирант, аэрокосмическая техника
Посмотреть этот Slough MATLAB Tutor
Элизабет : репетитор Slough по MATLAB
Сертифицированный преподаватель MATLAB в Слау
Позвоните нам сегодня, чтобы связаться с топ Slough MATLAB tutor
(888) 888-0446 Позвони сейчас …У меня большой опыт репетиторства. Начиная со старшей школы, я основал репетиторский клуб, чтобы помогать отстающим ученикам, а также подрабатывал учениками с высоким уровнем математики. После этого я перешел на работу в Mathnasium, где обучал группы до 5 учеников одновременно по математике, начиная с 1-го класса…
После этого я перешел на работу в Mathnasium, где обучал группы до 5 учеников одновременно по математике, начиная с 1-го класса…
Образование и сертификация
Вашингтонский университет в Сент-Луисе – текущий бакалавриат, машиностроение
Посмотреть этот Slough MATLAB Tutor
Салливан: репетитор Slough по MATLAB
Сертифицированный преподаватель MATLAB в Слау
Позвоните нам сегодня, чтобы связаться с топ Slough MATLAB tutor
(888) 888-0446 Позвони сейчас…Студент Мичиганского технологического университета, изучающий машиностроение. У меня есть страсть к математике и естественным наукам (и преподаванию предметов!). У меня также есть опыт работы с несколькими курсами AP и курсами с отличием, если вам потребуется помощь по ним, а также по множеству других предметов. Я бы хотел помочь научить вас!
Образование и сертификация
Мичиганский технологический университет — бакалавр технических наук, машиностроение
Посмотреть этот Slough MATLAB Tutor
Де Шанна: преподаватель Slough MATLAB
Сертифицированный преподаватель MATLAB в Слау
Позвоните нам сегодня, чтобы связаться с топ Slough MATLAB tutor
(888) 888-0446 Позвони сейчас . ..и уровень средней школы и ниже английский и испанский. Мой любимый предмет у репетитора — химия, потому что это был мой любимый предмет в школе. Во время репетиторства мне нравится развивать навыки, которые уже есть у студентов, и помогать им заполнять пробелы в своих знаниях. Вне школы и работы я люблю смотреть…
..и уровень средней школы и ниже английский и испанский. Мой любимый предмет у репетитора — химия, потому что это был мой любимый предмет в школе. Во время репетиторства мне нравится развивать навыки, которые уже есть у студентов, и помогать им заполнять пробелы в своих знаниях. Вне школы и работы я люблю смотреть…
Образование и сертификация
Университет Дьюка – бакалавр наук, биомедицинская инженерия
Посмотреть этот Slough MATLAB Tutor
Алиса: репетитор Slough по MATLAB
Сертифицированный преподаватель MATLAB в Слау
Позвоните нам сегодня, чтобы связаться с топ Slough MATLAB tutor
(888) 888-0446 Позвони сейчасЯ изучаю химию в колледже Бейтса. Имею опыт репетиторства со студентами от 4 лет до бакалавриата. В основном я репетитор по математике и естественным наукам. У меня также есть большой опыт стандартизированного тестирования.
Образование и сертификация
Колледж Бейтса – бакалавр наук, химия
Посмотреть этот Slough MATLAB Tutor
Патрик: репетитор Slough по MATLAB
Сертифицированный преподаватель MATLAB в Слау
Позвоните нам сегодня, чтобы связаться с топ Slough MATLAB tutor
(888) 888-0446 Позвони сейчас . ..в Техасском университете в Остине. Поэтому я очень интересуюсь математикой и наукой. Я знаю, что некоторые занятия и тесты могут быть утомительными, поэтому я хочу помочь другим пройти через это и добиться хороших результатов. Я могу преподавать различные предметы, такие как алгебра, геометрия, исчисление, физика, SAT и подготовка к PSAT.
..в Техасском университете в Остине. Поэтому я очень интересуюсь математикой и наукой. Я знаю, что некоторые занятия и тесты могут быть утомительными, поэтому я хочу помочь другим пройти через это и добиться хороших результатов. Я могу преподавать различные предметы, такие как алгебра, геометрия, исчисление, физика, SAT и подготовка к PSAT.
Образование и сертификация
Техасский университет в Остине – бакалавр наук, машиностроение
Посмотреть этот Slough MATLAB Tutor
Тревор: репетитор Slough по MATLAB
Сертифицированный преподаватель MATLAB в Слау
Позвоните нам сегодня, чтобы связаться с топ Slough MATLAB tutor
(888) 888-0446 Позвони сейчас …и несовершеннолетний по математике. Я особенно увлечен 3D-печатью, аэрокосмическим и механическим дизайном. Я высокомотивированный командный игрок и стремлюсь найти интересную работу, которая позволит мне использовать все грани моего набора навыков. Я люблю математику! Это всегда был мой любимый предмет, и мне нравится изучать новые концепции…
Я люблю математику! Это всегда был мой любимый предмет, и мне нравится изучать новые концепции…
Образование и сертификация
Северо-восточный университет — бакалавр наук, машиностроение
Посмотреть этот Slough MATLAB Tutor
Июнь: репетитор Slough по MATLAB
Сертифицированный преподаватель MATLAB в Слау
Позвоните нам сегодня, чтобы связаться с топ Slough MATLAB tutor
(888) 888-0446 Позвони сейчас…исследование слабоумия с помощью электрофизиологии на модели моллюска. Я участвую в хакатонах и соревнованиях по робототехнике, которые проверяют не только мои способности в программировании, но и мои навыки работы с оборудованием. Мои инженерные занятия требуют прочного фундамента в математике, мой интерес к наукам о жизни требует множества методов запоминания, а мой…
Образование и сертификация
Университет Брауна – бакалавриат, электротехника
Посмотреть этот Slough MATLAB Tutor
Крис: репетитор Slough по MATLAB
Сертифицированный преподаватель MATLAB в Слау
Позвоните нам сегодня, чтобы связаться с топ Slough MATLAB tutor
(888) 888-0446 Позвони сейчас . .. Предметы, которые я успешно преподавал Физика: все уровни Химия: все уровни старшей школы, плюс химия, биохимия Биология: все уровни средней школы Математика: все уровни средней школы, плюс дифференциальные уравнения, статистика, немного теории групп . Стандартизированная подготовка к экзаменам (включая SAT, ACT, GRE, MCAT) Нужна помощь в другой области? Просто спроси! В то время как математика и естественные науки являются предметами…
.. Предметы, которые я успешно преподавал Физика: все уровни Химия: все уровни старшей школы, плюс химия, биохимия Биология: все уровни средней школы Математика: все уровни средней школы, плюс дифференциальные уравнения, статистика, немного теории групп . Стандартизированная подготовка к экзаменам (включая SAT, ACT, GRE, MCAT) Нужна помощь в другой области? Просто спроси! В то время как математика и естественные науки являются предметами…
Образование и сертификация
Технологический институт Роуз-Халман – бакалавр наук, физика
Вашингтонский университет – магистр наук, физика
Посмотреть этот Slough MATLAB Tutor
Новый многомасштабный инструмент моделирования, применяемый для формирования биопленки Pseudomonas aeruginosa
1.
Уолпол Дж., Папин Дж. А., Пирс С. М. (2013) Многомасштабные вычислительные модели сложных биологических систем. Annu Rev Biomed Eng, 15: 137–154. doi: 10.1146/annurev-bioeng-071811-150104. PubMed: 23642247. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
PubMed: 23642247. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
2. Хайенга Х.Н., Торн Б.К., Пирс С.М., Хамфри Д.Д. (2012)Обеспечение согласованности в многомасштабном моделировании: на пути к биомеханическим моделям артериальной адаптации на основе связующего агента и континуума. Энн Биомед Энг, 39: 2669–2682. PubMed: 21809144. [Бесплатная статья PMC] [PubMed] [Google Scholar]
3. Thorne BC, Hayenga HN, Humphrey JD, Peirce SM (2011)На пути к многомасштабной вычислительной модели артериальной адаптации при гипертонии: проверка модели, основанной на многоклеточном агенте. Front Physiology, 2: 20. [Бесплатная статья PMC] [PubMed] [Google Scholar]
4. R: Язык и среда для статистических вычислений. (2013) Вена, Австрия: R Foundation for Statistical Computing. [Google Scholar]
5. Виленски Ю., NetLogo, Эванстон, Иллинойс (1999) НУ: Центр подключенного обучения и компьютерного моделирования. [Google Scholar]
6.
MATLAB и инструментарий статистики. (2012) Натик, Массачусетс, США: The MathWorks, Inc. [Google Scholar]
(2012) Натик, Массачусетс, США: The MathWorks, Inc. [Google Scholar]
7. Тиле Дж. К., Гримм В. (2010) NetLogo встречает R: связывание агентных моделей с набором инструментов для их анализа. Программное обеспечение Environ Model, 25: 972–974. doi: 10.1016/j.envsoft.2010.02.008. [CrossRef] [Google Scholar]
8. Бенгтссон Х. (2005) и Швеция: Математическая статика, Центр математических наук LU. R.matlab — локальное и удаленное подключение к MATLAB в R. [Google Scholar]
9. Робертсон С.Х., Смит К.К., Лангханс А.Л., Маклинден С.Е., Оберхардт М.А. и другие. (2007) Многомасштабный вычислительный анализ Xenopus Морфогенез laevis раскрывает ключевую информацию о поведении на системном уровне. BMC Systems Biol, 1: 46. doi: 10.1186/1752-0509-1-46. PubMed: 17953751. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
10.
Нейдиг А., Юнг А.Т., Розай Т., Теттманн Б., Стремпель Н.
и другие. (2013) TypA участвует в вирулентности, устойчивости к противомикробным препаратам и образовании биопленок у Pseudomonas синегнойная палочка . BMC Microbiol, 13: 77. doi: 10.1186/1471-2180-13-77. PubMed: 23570569. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
BMC Microbiol, 13: 77. doi: 10.1186/1471-2180-13-77. PubMed: 23570569. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
11. Бьярншолт Т., Дженсен П.О., Фиандака М.Дж., Педерсен Дж., Хансен Ч.Р. и другие. (2009 г.) Псевдомонада aeruginosa биопленок в дыхательных путях больных муковисцидозом. Pediatr Pulmonol, 44: 547–558. doi: 10.1002/ppul.21011. PubMed: 19418571. [PubMed] [CrossRef] [Google Scholar]
12. Писарро Г., Гриффит Д., Ногера Д. (2001)Количественная модель клеточного автомата для биопленок. Environ Eng, 127: 782–789. doi: 10.1061/(ASCE)0733-9372(2001)127:9(782). [CrossRef] [Google Scholar]
13. Ногера Д., Писарро Г., Реган Дж. М. (2004) Моделирование биопленок, В: Ганнум М., О’Тул Г., Микробные биопленки. [Академия Google]
14.
Oberhardt MA, Puchałka J, Fryer KE, Martins dos Santos VAP, Papin JA (2008)Анализ метаболической сети условно-патогенного микроорганизма в масштабе генома Pseudomonas синегнойная палочка PAO1. J Bacteriol, 190: 2790–2803. дои: 10.1128/JB.01583-07. PubMed: 18192387. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
J Bacteriol, 190: 2790–2803. дои: 10.1128/JB.01583-07. PubMed: 18192387. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
15. Railsback SF, Grimm V (2012) Агентное и индивидуальное моделирование: практическое введение. Принстон: Издательство Принстонского университета. [Академия Google]
16. Оберхардт М.А., Голдберг Дж.Б., Хогардт М., Папин Дж.А. (2010) Анализ метаболической сети Pseudomonas aeruginosa при хронической муковисцидозной инфекции легких. J Bacteriol, 192: 5534–5548. doi: 10.1128/JB.00900-10. PubMed: 20709898. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
17. Стюарт П.С. (2003) Диффузия в биопленке. J Bacteriol, 185 (5): 1485–1491. doi: 10.1128/JB.185.5.1485-1491.2003. PubMed: 12591863. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
18.
Becker SA, Feist AM, Mo ML, Hannum G, Palsson BØ
и другие. (2007)Количественный прогноз клеточного метаболизма с помощью моделей, основанных на ограничениях: набор инструментов COBRA. Нат Проток, 2: 727–738. doi: 10.1038/nprot.2007.99. PubMed: 17406635. [PubMed] [CrossRef] [Google Scholar]
Нат Проток, 2: 727–738. doi: 10.1038/nprot.2007.99. PubMed: 17406635. [PubMed] [CrossRef] [Google Scholar]
19. Оптимизатор Гуроби, Хьюстон, Техас (2013) Gurobi Optimization, Inc. [Google Scholar]
20. Джанчандани Э.П., Чавали А.К., Папин Дж.А. (2010) Применение анализа баланса потоков в системной биологии. Wiley Interdicular Rev Systems Biol Medicine, 2: 372–382 doi: 10.1002/wsbm.60. PubMed: 20836035. [PubMed] [CrossRef] [Google Scholar]
21. Махадеван Р., Эдвардс Дж. С., Дойл Ф. Дж. (2002) Анализ баланса динамических потоков диоксичного роста в Escherichia кишечная палочка . Биофиз J, 83: 1331–1340. doi: 10.1016/S0006-3495(02)73903-9. PubMed: 12202358. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
22.
Xu KD, Stewart PS, Xia F, Huang CT, McFeters GA (1998) Пространственная физиологическая неоднородность в Pseudomonas Биопленка aeruginosa определяется наличием кислорода. Appl Environ Microbiol, 64: 4035–4039. PubMed: 9758837. [Бесплатная статья PMC] [PubMed] [Google Scholar]
PubMed: 9758837. [Бесплатная статья PMC] [PubMed] [Google Scholar]
23. Trunk K, Benkert B, Quäck N, Münch R, Scheer M и другие. (2010) Анаэробная адаптация у Pseudomonas aeruginosa : определение регулонов Anr и Dnr. Environ Microbiol, 12: 1719–1733. PubMed: 20553552. [PubMed] [Google Scholar]
24. Borriello G, Werner E, Roe F (2004)Ограничение кислорода способствует толерантности к антибиотикам Pseudomonas aeruginosa в биопленках. Противомикробные агенты Chemother, 48: 2659–2664. doi: 10.1128/AAC.48.7.2659-2664.2004. PubMed: 15215123. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
25. Манос Дж., Артур Дж., Роуз Б., Белл С., Тингпей П. и другие. (2009) Характеристики экспрессии генов эпидемического штамма муковисцидоза Pseudomonas aeruginosa во время роста биопленки и планктона. FEMS Microbiol Lett, 292: 107–114. doi: 10.1111/j.1574-6968.2008.01472.x. PubMed: 19222585. [PubMed] [CrossRef] [Google Scholar]
26. Де Верра П., Пеши-Тарр М., Кил С., Маурхофер М. (2009 г.) Роль продукции глюконовой кислоты в регуляции признаков биоконтроля Pseudomonas флуоресцентный CHA0. Appl Environ Microbiol, 75: 4162–4174. doi: 10.1128/AEM.00295-09. PubMed: 19376896. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
Де Верра П., Пеши-Тарр М., Кил С., Маурхофер М. (2009 г.) Роль продукции глюконовой кислоты в регуляции признаков биоконтроля Pseudomonas флуоресцентный CHA0. Appl Environ Microbiol, 75: 4162–4174. doi: 10.1128/AEM.00295-09. PubMed: 19376896. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]
27. Лардон Л.А., Мерки Б.В., Мартинс С., Дётш А., Пичориану С. и другие. (2011) iDynoMiCS: индивидуальное моделирование биопленок нового поколения. Environ Microbiol, 13: 2416–2434. doi: 10.1111/j.1462-2920.2011.02414.x. PubMed: 21410622. [PubMed] [CrossRef] [Google Scholar]
28. Merkey BV, Lardon LA, Seoane JM, Kreft JU, Smets BF (2011) Зависимость конъюгации от роста объясняет ограниченную инвазию плазмид в биопленки: индивидуальное моделирование. Environ Microbiol, 13: 2435–2452. doi: 10.1111/j.1462-2920.2011.02535.x. PubMed: 21
7. [PubMed] [CrossRef] [Google Scholar] 29.
Мабрук Н., Матиас Дж., Деффуант Г. (2011) Жизнеспособность и устойчивость индивидуальной модели бактериальной биопленки, В: Деффуант Г. , Гилберт Н., Жизнеспособность и устойчивость сложных систем. [Академия Google]
, Гилберт Н., Жизнеспособность и устойчивость сложных систем. [Академия Google]
30. Mabrouk N, Deffuant G, Tolker-Nielsen T, Lobry C (2010)Бактерии могут образовывать взаимосвязанные микроколонии, когда самовыводимый продукт снижает их поверхностную подвижность: данные моделирования на индивидуальной модели. Theory Biosci, 129: 1–13. doi: 10.1007/s12064-009-0078-8. PubMed: 19946800. [PubMed] [CrossRef] [Google Scholar]
31. Чаве Дж. (2013) Проблема модели и масштаба в экологии: чему мы научились за 20 лет? Экол Летт, 16: 4–16. doi: 10.1111/ele.12048. ПабМед: 23351093. [PubMed] [CrossRef] [Google Scholar]
32. Magliocca NR, Ellis EC (2013) Использование модельно-ориентированного моделирования (POM) для преодоления неопределенности в многомасштабных агентных моделях изменения земель. Транс ГИС. doi: 10.1111/tgis.12012. [CrossRef] [Google Scholar]
33.
Цзя Т., Цзян Б., Карлинг К., Болин М., Бан И. (2012) Эмпирическое исследование мобильности человека и ее агентного моделирования. J Статистическая механика. дои: 10.1088/1742-5468/2012/11/P11024. [CrossRef] [Google Scholar]
J Статистическая механика. дои: 10.1088/1742-5468/2012/11/P11024. [CrossRef] [Google Scholar]
«Встроенных» рабочих мест в Слау — Reed.co.uk
Работа скрыта.
Легко применить
Инженер по встроенному программному обеспечению
18 августа от Platform Recruitment
- £60,000 — £70,000 в год, возможен торг
- Марлоу Бакингемшир
- Постоянный, полный рабочий день
Инженер-программист по встраиваемым системам — 60 000 – 70 000 000 000 000 — Бакингемшир Мой клиент — лидер международного рынка в секторе связи. В связи с новыми интересными проектами и увеличением рабочей нагрузки им требуется инженер-программист. Основные обязанности: Ведение…
В связи с новыми интересными проектами и увеличением рабочей нагрузки им требуется инженер-программист. Основные обязанности: Ведение…
Перейти к похожим: Инженер Вакансии в городе Слау
Работа скрыта.
Легко применить
Инженер по встроенному программному обеспечению
7 сентября, Enterprise Recruitment Ltd.
- 45 000–60 000 фунтов стерлингов в год
- Рикмансворт Хартфордшир
- Постоянный, полный рабочий день
Лидер в области нишевых носимых устройств, одна из трех компаний в мире в этой области, компания ищет двух опытных инженеров по программному обеспечению / встроенному программному обеспечению для решения сложных проблем в устройствах связи с батарейным питанием. Роль требует…
Роль требует…
Перейти к похожим: Инженер Вакансии в городе Слау
Работа скрыта.
Легко применить
Инженер по машинному обучению в Embedded AI C++
10 августа, MicroTECH Global Ltd.
- 80 000–100 000 фунтов стерлингов в год
- Стейнс-на-Темзе Миддлсекс
- Постоянный, полный рабочий день
ОБЪЯВЛЕНИЕ О ВАКАНСИИ: Идеальный кандидат должен иметь опыт и знания в обеих системах (ОС, память, оптимизация, встроенные), а также в методах машинного обучения, алгоритмах, инструментах и фреймворках. Потенциальный кандидат будет работать и расти в обоих направлениях…
Потенциальный кандидат будет работать и расти в обоих направлениях…
Перейти к похожим: Инженер Вакансии в городе Слау
Сообщение от ООО «МикроТЕХ Глобал»
Мы хотели бы знать, как мы можем улучшить ваш поиск работы. Пожалуйста, дайте нам свой отзыв.
Работа скрыта.
Легко применить
Инженер-программист по встраиваемым системам — высокоскоростная сеть
Вчера от Enterprise Recruitment Ltd.
- 35 000–80 000 фунтов стерлингов в год
- Брэкнелл Беркшир
- Постоянный, полный рабочий день
- Работа из дома
Должность инженера по встроенному программному обеспечению с отличными преимуществами, удаленной работой, непринужденной рабочей средой и современными сетевыми технологическими проектами. Я могу честно сказать, что их сотрудники очень любят там работать, с энтузиазмом…
Перейти к похожим: Инженер Вакансии в городе Слау
Работа скрыта.
Избранное Легко применить
Старший инженер по встроенному программному обеспечению — Рикмансворт — 50–60 000 фунтов стерлингов
4 дня назад от Ascent Sourcing Ltd
- 50 000–60 000 фунтов стерлингов в год
- Рикмансворт Хартфордшир
- Постоянный, полный рабочий день
Старший инженер по встроенному программному обеспечению — Рикмансворт — 50 000–60 000 000 Наш клиент ищет 3 старших инженера по встроенному программному обеспечению, это будет роль на месте, а не удаленная или гибридная. Йо также должен прожить в Великобритании последние 5 лет, так как вам нужно будет…
Йо также должен прожить в Великобритании последние 5 лет, так как вам нужно будет…
Перейти к похожим: Инженер Вакансии в городе Слау
Работа скрыта.
Легко применить
Инженер-программист игр для Android
4 дня назад от MicroTECH Global Ltd
- 80 000–100 000 фунтов стерлингов в год
- Эгам Суррей
- Постоянный, полный рабочий день
ОБЪЯВЛЕНИЕ НА РАБОТУ: Мы ищем инженеров-энтузиастов с опытом работы в области оптимизации производительности графики/системы на современных встраиваемых платформах, таких как Android. Уверенное знание графических фреймворков Android, OpenGL ES и/или Vulkan, а также…
Уверенное знание графических фреймворков Android, OpenGL ES и/или Vulkan, а также…
Перейти к похожим: Инженер Вакансии в городе Слау
Сообщение от ООО «МикроТЕХ Глобал»
Работа скрыта.
Легко применить
Учитель психологии
8 августа академиками
- £140.00 — £300.00 в день
- Слау Беркшир
- Контракт, полный рабочий день
В настоящее время мы работаем с любимой и поддерживающей средней школой в районе Хиллингдон, которая ищет учителя психологии, чтобы улучшить уже управляемый и поддерживающий отдел. Академики ищут штатного преподавателя…
Академики ищут штатного преподавателя…
Перейти к похожим: Вакансии учителя в городе Слау
Работа скрыта.
Легко применить
Старший инженер-электронщик
1 сентября Redline Group Ltd.
- 45 000–65 000 фунтов стерлингов в год
- Чертси Суррей
- Постоянный, полный рабочий день
Вы ищете работу в многопрофильной компании, производящей чрезвычайно интересные продукты в Чертси? К моему клиенту, многонациональному бизнесу и лидеру рынка в своей области, требуется инженер-электронщик. С…
С…
Перейти к похожим: Инженер Вакансии в городе Слау
Работа скрыта.
Легко применить
Инженер-программист Android или графики
19 августа, MicroTECH Global Ltd.
- 70 000–90 000 фунтов стерлингов в год
- Эгам Суррей
- Постоянный, полный рабочий день
ОБЪЯВЛЕНИЕ О ВАКАНСИИ: Возможность работать над действительно новыми технологиями, подобными этой, встречается редко, поэтому мы ищем высокомотивированных людей со страстью к работе над самой универсальной мобильной платформой в мире. В качестве инженера Android Framework вы будете: Разрабатывать расширения…
В качестве инженера Android Framework вы будете: Разрабатывать расширения…
Перейти к похожим: Инженер Вакансии в городе Слау
Сообщение от ООО «МикроТЕХ Глобал»
Работа скрыта.
Легко применить
Инженер-программист по искусственному интеллекту или графике
1 сентября, MicroTECH Global Ltd.
- 80 000–100 000 фунтов стерлингов в год
- Эгам Суррей
- Постоянный, полный рабочий день
ОБЪЯВЛЕНИЕ НА РАБОТУ: Мы ищем инженеров-энтузиастов с опытом работы в области графики и хорошим пониманием машинного обучения. Важны твердые практические знания OpenGL ES и/или Vulkan, а также одной или нескольких сред машинного обучения. Опыт…
Важны твердые практические знания OpenGL ES и/или Vulkan, а также одной или нескольких сред машинного обучения. Опыт…
Перейти к похожим: Инженер Вакансии в городе Слау
Сообщение от ООО «МикроТЕХ Глобал»
Работа скрыта.
Легко применить
Инженер по контролю
4 дня назад от ACS Performance
- 30 000–45 000 фунтов стерлингов в год
- Слау Беркшир
- Постоянный, полный рабочий день
В качестве инженера по системам управления вы будете разрабатывать новые проекты систем управления ПЛК и поддерживать актуальное программное обеспечение, обеспечивая его актуальность с помощью электрических схем и философии управления / FDS. Тестирование электрических/электронных систем и систем управления, производство…
Тестирование электрических/электронных систем и систем управления, производство…
Перейти к похожим: Инженер Вакансии в городе Слау
Работа скрыта.
Легко применить
Инженер-электронщик — Дизайн новых функций
6 сентября, Enterprise Recruitment Ltd.
- 35 000–45 000 фунтов стерлингов в год
- Рикмансворт Хартфордшир
- Постоянный, полный рабочий день
Компания, производящая инновационную электронику, ищет инженера-электронщика с опытом проектирования коммерческой цифровой электроники для работы над новыми функциями продукта. Они являются лидером в области нишевых носимых устройств, одной из трех компаний в мире в этой области…
Они являются лидером в области нишевых носимых устройств, одной из трех компаний в мире в этой области…
Перейти к похожим: Инженер Вакансии в городе Слау
Работа скрыта.
Легко применить
Исследователь машинного обучения в аудио или речи
9 августа, MicroTECH Global Ltd.
- 80 000–100 000 фунтов стерлингов в год
- Стейнс-на-Темзе Миддлсекс
- Постоянный, полный рабочий день
ОБЪЯВЛЕНИЕ О ВАКАНСИИ: Требуется инженер по машинному обучению для оказания помощи в разработке программного обеспечения для ключевых компонентов для ведущего мирового производителя телевизоров, базирующегося в Западном Лондоне. Наш клиент ищет опытного инженера по машинному обучению для роста и развития…
Наш клиент ищет опытного инженера по машинному обучению для роста и развития…
Перейти к похожим: Исследователь Вакансии в городе Слау
Сообщение от ООО «МикроТЕХ Глобал»
Получайте новые вакансии, соответствующие этому запросу, прямо на ваш почтовый ящик.
Работа скрыта.
Избранное Легко применить
менеджер по обслуживанию клиентов
16 августа, PINNACLE GROUP
- 28 000–31 000 фунтов стерлингов в год
- Слау Беркшир
- Контракт, полный рабочий день
Pinnacle Group предоставляет ориентированные на человека интегрированные услуги для целого ряда общественных объектов и инфраструктуры, включая многоквартирное жилье, школы, открытые пространства, общественные здания, коммунальные услуги и широкополосные сети, а также ряд дополнительных. ..
..
Перейти к похожим: Вакансии менеджера в городе Слау
Работа скрыта.
Скоро заканчивается Легко применить
Ведущий специалист по машинному обучению
5 августа, MicroTECH Global Ltd.
- 120 000–130 000 фунтов стерлингов в год
- Эгам Суррей
- Постоянный, полный рабочий день
ОБЪЯВЛЕНИЕ О ВАКАНСИИ: команда искусственного интеллекта наших клиентов ищет выдающегося инженера по машинному обучению на руководящую роль, чтобы присоединиться к их растущей команде. Идеальный кандидат будет иметь отраслевой опыт работы над рядом решений для глубокого обучения, включающих CNN, RNN и т. д….
Идеальный кандидат будет иметь отраслевой опыт работы над рядом решений для глубокого обучения, включающих CNN, RNN и т. д….
Перейти к похожим: Вакансии менеджера в городе Слау
Сообщение от ООО «МикроТЕХ Глобал»
Работа скрыта.
Легко применить
Инженер электроники
5 сентября, BMS Performance Ltd.
- 28 000–38 000 фунтов стерлингов в год
- Хай Уиком Бакингемшир
- Постоянный, полный рабочий день
Эта захватывающая роль на сайте подойдет амбициозному кандидату с проверенными знаниями в области электроники, включая проектирование схем и использование программного обеспечения для проектирования схем. У вас будет возможность создавать продукты от концепции до окончательного дизайна. …
У вас будет возможность создавать продукты от концепции до окончательного дизайна. …
Перейти к похожим: Инженер Вакансии в городе Слау
Работа скрыта.
Избранное Легко применить
Менеджер по ремонту
4 дня назад от PINNACLE GROUP
- 28 000–31 000 фунтов стерлингов в год
- Слау Беркшир
- Контракт, полный рабочий день
Pinnacle Group предоставляет ориентированные на человека интегрированные услуги для целого ряда общественных объектов и инфраструктуры, включая многоквартирное жилье, школы, открытые пространства, общественные здания, коммунальные услуги и широкополосные сети, а также ряд дополнительных. ..
..
Перейти к похожим: Вакансии менеджера в городе Слау
Работа скрыта.
Детская медсестра
17 августа, Матч персонала
- 21 500–24 500 фунтов стерлингов в год
- Твикенхэм Миддлсекс
- Постоянный, полный рабочий день
Staff Match проводит набор от имени хорошо зарекомендовавшего себя детского сада в Твикенхеме, Большой Лондон, и ищет восторженную детскую медсестру 2-го или 3-го уровня, которая присоединится к их работе. Спецификация человека: Уровень 2 или уровень 3 Квалификация по уходу за детьми…
Спецификация человека: Уровень 2 или уровень 3 Квалификация по уходу за детьми…
Перейти к похожим: Медсестра Вакансии в городе Слау
Работа скрыта.
Детская медсестра
17 августа, Матч персонала
- 20 980 фунтов стерлингов в год
- Вест Байфлит Суррей
- Постоянный, полный рабочий день
Staff Match проводит набор от имени хорошо зарекомендовавшего себя питомника в Уэст-Байфлите, графство Суррей, и ищет восторженную детскую медсестру 3-го уровня, которая присоединится к их работе. Спецификация человека: Уровень 3 Квалификация по уходу за детьми Опыт планирования EYFS…
Спецификация человека: Уровень 3 Квалификация по уходу за детьми Опыт планирования EYFS…
Перейти к похожим: Медсестра Вакансии в городе Слау
Работа скрыта.
Легко применить
Архитектор / Менеджер по обеспечению качества программного обеспечения Python
7 сентября, Enterprise Recruitment Ltd.
- 100 000–130 000 фунтов стерлингов в год
- Брэкнелл Беркшир
- Постоянный, полный рабочий день
- Работа из дома
Программное обеспечение QA Architect / Manager (Python) до 130 тыс. / Полностью удаленное доступное программное обеспечение QA -менеджеры с сильным сценарием опыта автоматизации в Python необходимы для присоединения к авторитетной компании с известной во всем мире присутствием, клиентура, в которую входят большая …
/ Полностью удаленное доступное программное обеспечение QA -менеджеры с сильным сценарием опыта автоматизации в Python необходимы для присоединения к авторитетной компании с известной во всем мире присутствием, клиентура, в которую входят большая …
Перейти к похожим: Вакансии менеджера в городе Слау
Работа скрыта.
Избранное Легко применить
Программист
5 дней назад от Understanding Recruitment
- 90 000–100 000 фунтов стерлингов в год
- Брентфорд Миддлсекс
- Постоянный, полный рабочий день
Инженер-программист — развивающаяся биотехнологическая платформа. Зарплата до 100 000 и отличные преимущества. Местонахождение: Лондон (гибридный и гибкий график работы). Инженер-программист (Python, Django, Rust, C). Мы ищем инженера-программиста, который поможет построить будущее…
Зарплата до 100 000 и отличные преимущества. Местонахождение: Лондон (гибридный и гибкий график работы). Инженер-программист (Python, Django, Rust, C). Мы ищем инженера-программиста, который поможет построить будущее…
Перейти к похожим: Инженер Вакансии в городе Слау
Работа скрыта.
Легко применить
Учитель психологии
8 августа академиками
- £140.00 — £300.00 в день
- Биконсфилд Бакингемшир
- Контракт, полный рабочий день
В настоящее время мы работаем с любимой и поддерживающей средней школой в районе Хиллингдон, которая ищет учителя психологии, чтобы улучшить уже управляемый и поддерживающий отдел. Академики ищут штатного преподавателя…
Академики ищут штатного преподавателя…
Перейти к похожим: Вакансии учителя в городе Слау
Работа скрыта.
Менеджер производительности ref:31891
1 неделю назад Темз Уотер
- Конкурентоспособная заработная плата
- Уоргрейв Беркшир
- Постоянный, полный рабочий день
Кто мы? Thames Water — крупнейшая в Великобритании компания по водоснабжению и водоотведению. Мы ежедневно приносим пользу нашим 15 миллионам клиентов, поставляя 2,6 миллиарда литров воды по 32 000 км труб, поддерживая воду в кранах и смывая туалеты. В Темзе…
Мы ежедневно приносим пользу нашим 15 миллионам клиентов, поставляя 2,6 миллиарда литров воды по 32 000 км труб, поддерживая воду в кранах и смывая туалеты. В Темзе…
Перейти к похожим: Вакансии менеджера в городе Слау
Работа скрыта.
Избранное
Речевой и языковой терапевт Внешний Лондон всего 38 недель
23 августа, Witherslack Group
- 53 928–61 335 фунтов стерлингов в год, включая льготы
- Виндзор Беркшир
- Постоянный, полный рабочий день
Будьте потрясающими, вдохновляйтесь, будьте собой. Наши дети и молодежь заслуживают наилучшего будущего, и мы чувствуем то же самое по отношению к нашим сотрудникам. Вы заслуживаете карьеры, которую хотите, в среде, которая позволяет вам быть самим собой. Став членом нашей команды, вы…
Наши дети и молодежь заслуживают наилучшего будущего, и мы чувствуем то же самое по отношению к нашим сотрудникам. Вы заслуживаете карьеры, которую хотите, в среде, которая позволяет вам быть самим собой. Став членом нашей команды, вы…
Перейти к похожим: Терапевт Вакансии в городе Слау
Работа скрыта.
Легко применить
Начальник отдела финансового партнерства
16 августа, Аллен Лейн
- 50 000–56 500 фунтов стерлингов в год
- Виндзор Беркшир
- Постоянный, полный рабочий день
Allen Lane с гордостью сотрудничает с известной некоммерческой организацией, которая помогла изменить жизнь тысяч молодых людей по всей Великобритании и теперь оказывает большое глобальное влияние. В связи с динамичным ростом организации мы ищем…
В связи с динамичным ростом организации мы ищем…
Перейти к похожим: Вакансии менеджера в городе Слау
Стажер по маркетингу, Eaton Corporation | Слау
Должностная инструкция
от корпорации Eaton Описание: Наша программа стажировки по маркетингу является первоклассной, когда речь идет о том, чтобы дать студентам подлинную информацию о работе в крупном глобальном бизнесе, одновременно готовя вас к профессиональной карьере. Роль стажера по маркетинговой аналитике будет заключаться в оказании технической поддержки по мере того, как мы начинаем накапливать наш опыт в применении расширенной аналитики для решения маркетинговых задач. Кто мы: Мы заставляем то, что важно, работать. Eaton — компания по управлению питанием, объем продаж которой в 2016 году составил 19 долларов США. 0,7 миллиарда, около 95 000 сотрудников и продажа продукции клиентам в более чем 175 странах. В Великобритании у нас есть многочисленные офисы по всей стране, работающие в электротехнической, гидравлической, автомобильной и аэрокосмической отраслях. Что вы получите: В течение года стажировки вы приобретете бесценный опыт работы в команде разноплановых сотрудников. С первого дня вас будут наставлять высококвалифицированные специалисты по маркетингу, которые будут направлять и поддерживать вас, чтобы гарантировать, что вы получите максимум от своего размещения. В качестве стажера отдела маркетинговой аналитики вы получите представление о маркетинговой функции, в том числе: Проекты аналитики: • Понимание бизнес-проблемы и возможное решение проблемы • Разработка предлагаемого аналитического подхода к решению проблемы • Определение проблемы источники данных, необходимые для проведения анализа • Работайте с другими сотрудниками Eaton над созданием соответствующего набора данных • Экспериментируйте с рядом различных подходов к решению проблемы • Документируйте предлагаемое решение проблемы • Изучите, может ли и каким образом это решение может потребоваться промышленного производства и предоставить рекомендации • Представлять результаты руководству отдела маркетинга в регионе EMEA Непрерывное совершенствование: • Выявлять потенциальные проблемы с качеством данных • Выявлять, как мы можем улучшить процесс маркировки и другие вспомогательные процессы данных • Выявлять потенциальные новые источники данных для поддержки нашего аналитического роста Квалификации Кандидаты в идеале должны быть студенты, работающие как минимум 2: 1 и в смежной дисциплине.
0,7 миллиарда, около 95 000 сотрудников и продажа продукции клиентам в более чем 175 странах. В Великобритании у нас есть многочисленные офисы по всей стране, работающие в электротехнической, гидравлической, автомобильной и аэрокосмической отраслях. Что вы получите: В течение года стажировки вы приобретете бесценный опыт работы в команде разноплановых сотрудников. С первого дня вас будут наставлять высококвалифицированные специалисты по маркетингу, которые будут направлять и поддерживать вас, чтобы гарантировать, что вы получите максимум от своего размещения. В качестве стажера отдела маркетинговой аналитики вы получите представление о маркетинговой функции, в том числе: Проекты аналитики: • Понимание бизнес-проблемы и возможное решение проблемы • Разработка предлагаемого аналитического подхода к решению проблемы • Определение проблемы источники данных, необходимые для проведения анализа • Работайте с другими сотрудниками Eaton над созданием соответствующего набора данных • Экспериментируйте с рядом различных подходов к решению проблемы • Документируйте предлагаемое решение проблемы • Изучите, может ли и каким образом это решение может потребоваться промышленного производства и предоставить рекомендации • Представлять результаты руководству отдела маркетинга в регионе EMEA Непрерывное совершенствование: • Выявлять потенциальные проблемы с качеством данных • Выявлять, как мы можем улучшить процесс маркировки и другие вспомогательные процессы данных • Выявлять потенциальные новые источники данных для поддержки нашего аналитического роста Квалификации Кандидаты в идеале должны быть студенты, работающие как минимум 2: 1 и в смежной дисциплине. Это будет включать степени с очень сильным математическим/статистическим компонентом, в том числе; Статистика / Математика / Физика / Экономика и статистика / Психология и статистика. Преимуществом будет работа со статистическими данными (многомерная регрессия, кластерный анализ, деревья решений и т. д.) и/или эконометрикой (временные ряды, многомерность) и/или машинным обучением (случайные леса, нейронные сети). В дополнение к опыту программирования в SAS, R, Matlab, SPSS, SQL или подобных. Пожалуйста, укажите классификацию за первый год в своем заявлении. У вас должно быть официальное разрешение на работу в Соединенном Королевстве без спонсорства компании.
Это будет включать степени с очень сильным математическим/статистическим компонентом, в том числе; Статистика / Математика / Физика / Экономика и статистика / Психология и статистика. Преимуществом будет работа со статистическими данными (многомерная регрессия, кластерный анализ, деревья решений и т. д.) и/или эконометрикой (временные ряды, многомерность) и/или машинным обучением (случайные леса, нейронные сети). В дополнение к опыту программирования в SAS, R, Matlab, SPSS, SQL или подобных. Пожалуйста, укажите классификацию за первый год в своем заявлении. У вас должно быть официальное разрешение на работу в Соединенном Королевстве без спонсорства компании.
Мы заставляем то, что важно, работать. Куда бы вы ни посмотрели — от технологий и оборудования, которые нас окружают, до критически важных услуг и инфраструктуры, от которых мы зависим каждый день, — вы найдете одну общую черту. Все зависит от власти. Вот почему Eaton стремится улучшить жизнь людей и окружающую среду с помощью технологий управления питанием, которые являются более надежными, эффективными, безопасными и устойчивыми. Потому что это важно. Мы уверены, что сможем выполнить это обещание благодаря качествам, которыми обладают наши сотрудники. Мы этичны, страстны, подотчетны, эффективны, прозрачны и стремимся к обучению. Эти ценности позволяют нам решать одни из самых сложных задач на планете, никогда не упуская из виду то, что действительно важно.
Потому что это важно. Мы уверены, что сможем выполнить это обещание благодаря качествам, которыми обладают наши сотрудники. Мы этичны, страстны, подотчетны, эффективны, прозрачны и стремимся к обучению. Эти ценности позволяют нам решать одни из самых сложных задач на планете, никогда не упуская из виду то, что действительно важно.
Работа: Маркетинг
Регион: Европа, Ближний Восток, Африка
Организация: ES EMEA Sales and Marketing Central
Уровень работы: Начальный уровень
График: Полный рабочий день
Разрешена ли удаленная работа (т. е. работа из дома или на другом предприятии Eaton) для эта вакансия?: №
Предлагает ли эта вакансия переезд?: №
Путешествия: №
Eaton — работодатель, предлагающий равные возможности и позитивные действия. Eaton стремится обеспечить равные возможности трудоустройства для всех соискателей и сотрудников. Решения о приеме на работу основываются на причинах, связанных с работой, независимо от расы, цвета кожи, религии, пола, сексуальной ориентации, гендерной идентичности, возраста, национального происхождения, инвалидности, семейного положения, генетической информации, статуса защищенного ветерана или любого другого статуса, защищенного законом. закон.
закон.
Наверх
Об этой работе
Корпорация Eaton является производителем. Они специализируются на продуктах для отрасли управления питанием.
Платить
- Хороший
- Людям платят минимальную заработную плату
Корпорация Eaton платит минимальную заработную плату?
Да. Большинству людей платят больше минимальной заработной платы.
Откуда мы это знаем
96% людей говорят, что им платят на уровне установленной законом минимальной заработной платы или выше.
На основе данных 23 человек, принявших участие в викторине Breakroom Quiz в период с марта 2020 года по сентябрь 2022 года.
Хороший - Большинству людей платят прожиточный минимум
Корпорация Eaton выплачивает прожиточный минимум?
Большинству людей платят прожиточный минимум.

Откуда мы это знаем
94% людей говорят, что им платят на уровне реального прожиточного минимума или выше того места, где они живут.
На основе данных 18 человек, принявших участие в опросе Breakroom Quiz в период с марта 2020 г. по сентябрь 2022 г.
Почему это важно
Всем должно платить столько, чтобы прожить.
Реальный прожиточный минимум — это добровольная ставка, на которую работодатели могут подписаться и которая основана на реальной стоимости жизни. В настоящее время он составляет 9,90 фунтов стерлингов в час и 11,05 фунтов стерлингов в час в Лондоне.
Узнайте больше в нашем толкователе о реальном прожиточном минимуме.
Часы работы и гибкость
- Плохо
- Уведомление о смене менее чем за 4 недели
Как часто люди обращают внимание на свой график работы в Eaton Corporation?
Большинство людей не получают уведомления за 4 недели до начала работы.

Откуда мы это знаем
- 70 % людей с изменяющимся графиком сообщают об уведомлении за неделю или меньше.
- 0% человек с изменяющимся графиком сообщают об уведомлении за две недели.
- 10% людей с изменяющимся графиком сообщают об уведомлении за три недели.
- 20% человек с изменяющимся графиком сообщают об уведомлении за четыре недели или более.
На основе данных 10 человек, принявших участие в опросе Breakroom Quiz в период с марта 2020 г. по август 2022 г.
Почему это важно
На хорошей работе вас часто уведомляют о том, когда вы работаете.
Это позволяет вам легко планировать оставшуюся жизнь, а также свои финансы, потому что вы знаете, сколько и когда вы будете работать.
Хороший - Большинство людей не беспокоятся о своем рабочем времени
Работники Eaton Corporation беспокоятся о часах?
Большинство людей не беспокоятся о достаточном количестве часов.

Откуда мы это знаем
94% людей сообщают, что не беспокоятся о достаточном количестве часов.
На основе данных 18 человек, принявших участие в опросе Breakroom Quiz в период с марта 2020 г. по август 2022 г.
Почему это важно
На хорошей работе вам не нужно беспокоиться о достаточном количестве часов в неделю.
Хорошая работа должна гарантировать вам минимальное количество часов по контракту, если вы этого хотите.
Это упрощает планирование ваших финансов, потому что вы знаете, сколько будете зарабатывать.
Рабочее место
Узнайте больше о работе в корпорации EatonВернуться к началу
Что сотрудники корпорации Eaton говорят о своей работе
Лучшая вещь
Оплата
Часы
ВыходныеХудшее
Ясли
Рабочая нагрузкаСклад корпорации Eaton, октябрь 2020 г.

Лучшая вещь
Люди, с которыми я работаю
Худшее
Нет представительства и руководство запугивает сотрудников
Eaton Corporation Техник-механик, июнь 2020 г.
Еще отзывы от сотрудников корпорации Eaton
Вернуться к началу
15 sas Вакансии в Слау | Сентябрь 2022 г.
Фильтры
15
Средняя зарплата: 36 552 фунтов стерлингов
Недавние поиски
Здесь будут отображаться ссылки на последние 5 поисковых запросов (с результатами), которые вы сделали.
ДЖОБСВОРТ: £ 40,910 П.А.
— ИСТОЧНИК RANDSTAD RIGHT-
СЛОУ, БЕРКШИР
TOP MATCH
. .. мощный эмпирический анализ внутренних и внешних данных, создание надежных метрик с использованием различных инструментов и методов (например, SQL и SAS ), представление результатов с помощью четкой визуализации … и технически сильный, использующий некоторые или все SQL / SAS / Tableau и желание изучать другие, такие как MicroStrategy Хорошие навыки презентации и способность общаться с людьми на всех уровнях …
Подробнее ❯
.. мощный эмпирический анализ внутренних и внешних данных, создание надежных метрик с использованием различных инструментов и методов (например, SQL и SAS ), представление результатов с помощью четкой визуализации … и технически сильный, использующий некоторые или все SQL / SAS / Tableau и желание изучать другие, такие как MicroStrategy Хорошие навыки презентации и способность общаться с людьми на всех уровнях …
Подробнее ❯
ДЖОБСВОРТ: £ 57 003 П.А.
—
ЭКВИНИКС, ИНК.
—
СЛОУ, АНГЛИЯ
… в партнерстве с инженерами по продажам (SE) и архитекторами по продажам ( SA ) Обеспечивает экспертную и убедительную презентацию, используя SE/ SA , где это уместно; настраивает шаг для клиента и персоны . ..
Подробнее ❯
..
Подробнее ❯
ДЖОБСВОРТ: £ 43 439 П.А.
—
ИТОН
—
SLOUGH
… быть преимуществом. В дополнение к опыту программирования на SAS , R, Matlab, SPSS, SQL или подобных. Пожалуйста, укажите классификацию за первый год в своем заявлении. У вас должно быть юридическое… Подробнее ❯
Думаете о следующем шаге в карьере?
CareerPaths поможет вам найти местные вакансии, соответствующие вашим навыкам
Попробуйте CareerPaths сейчас ❯
ДЖОБСВОРТ:
£
52 746
П. А.
А.
—
МАРС
—
СЛАУ, БЕРКШИР
СКОРО ЗАКРЫТИЕ
… тестирование, GLM/регрессия, случайный лес, бустинг, деревья, интеллектуальный анализ текста, анализ социальных сетей и т. д.) с использованием таких инструментов, как Spark, Scala, SAS , R, Python, Bayesia, h3O, Storm, Yarn и Kafka… Подробнее ❯
ДЖОБСВОРТ: £ 60 583 П.А.
—
МАРШ
—
SLOUGH, SL1
NEW
, интеллектуальный анализ текста, анализ социальных сетей и т. д. ) с использованием таких инструментов, как Spark, Scala, SAS , R, Python, Bayesia, h3O, Storm, Yarn и Kafka Опыт выполнения запросов к базам данных (SQL, Hive) Опыт …
Подробнее ❯
) с использованием таких инструментов, как Spark, Scala, SAS , R, Python, Bayesia, h3O, Storm, Yarn и Kafka Опыт выполнения запросов к базам данных (SQL, Hive) Опыт …
Подробнее ❯
ДЖОБСВОРТ: £ 45 234 П.А.
— CK GROUP НАУКА, КЛИНИЧЕСКИЕ И ТЕХНИЧЕСКИЕ
SLOUGH, BERKSHIRE
СКОРО ЗАКРЫТИЕ
… или медицинский поставщик, предпочтительно имеющий дело с категориями лекарств/безрецептурных продуктов. • Опыт линейного управления. • Эффективные медицинские и научные навыки письма. • Статистическая грамотность (например, SAS … Подробнее ❯
36 552 фунтов стерлингов в год
Средняя зарплата для Sas Jobs в Слау.
Посмотреть больше статистики ❯
ДЖОБСВОРТ: £ 56 247 П.А.
—
ЭКВИНИКС, ИНК.
—
СЛОУ, АНГЛИЯ
… требования для соответствия решениям Equinix в сотрудничестве с инженерами по продажам (SE) и архитекторами по продажам ( SA ) Обеспечивает экспертную и убедительную презентацию, используя SE/ SA , где это уместно .. . Подробнее ❯
ДЖОБСВОРТ: £ 52 299 П.А.
—
МАРС
—
SLOUGH, BERKSHIRE
, Random Forest, Boosting, Trees, анализ текста, анализ социальных сетей и т. д.) с использованием таких инструментов, как Spark, Scala, SAS , R, Python, Bayesia, h3O, Storm, Yarn и Kafka Опыт запросов…
Подробнее ❯
д.) с использованием таких инструментов, как Spark, Scala, SAS , R, Python, Bayesia, h3O, Storm, Yarn и Kafka Опыт запросов…
Подробнее ❯
ДЖОБСВОРТ: £ 47 224 П.А.
—
КОРПОРАЦИЯ ИТОН
—
SLOUGH, ENGLAND
REMOTE
, нейронные сети) будет преимуществом. В дополнение к опыту программирования на SAS , R, Matlab, SPSS, SQL или подобных. Пожалуйста, укажите классификацию за первый год в вашем заявлении… Подробнее ❯
ДЖОБСВОРТ:
£
56 030
П. А.
А.
—
МАРС
—
SLOUGH, BERKSHIRE
… сетевой анализ и т. д.) с использованием таких инструментов, как Spark, Scala, SAS , R, Python, Bayesia, h3O, Storm, Yarn и Kafka Опыт работы с запросами к базам данных (SQL, Hive) Опыт работа с большими данными… Подробнее ❯
Результаты 1-10 из 15
1
2 следующие ❯
Получить приложение для iPhone Получите приложение для Android
Получить последние вакансии:
Связанное с карбонатами органическое вещество является обнаруживаемым источником растворенного органического вещества на субтропическом лугу с морскими водорослями
Введение
Экосистемы морских водорослей являются важными участниками глобального углеродного цикла благодаря механизму «голубого углерода» хранения органического углерода в нижележащих отложениях (Fourqurean et al. , 2012a). Осадочный органический углерод на лугах из морских водорослей содержит как автохтонный, так и аллохтонный органический материал наземного или морского происхождения (Kennedy et al., 2010) и может быть защищен от дальнейшей деградации, поскольку морские травы могут стабилизировать отложения, уменьшая повторное взвешивание и потери в результате окисления (Serrano et al. , 2020). Однако в карбонатных отложениях процессы осаждения и растворения карбоната кальция вызывают образование или потребление CO 9 .1138 2 превышает чистый метаболизм экосистемы (Mazarrasa et al., 2015; Howard et al., 2018). Это растворение карбонатов может усиливаться на лугах с водорослями за счет того, что водоросли перекачивают кислород в отложения во время фотосинтеза (Eldridge and Morse, 2000; Burdige and Zimmerman, 2002; Burdige et al., 2008, 2010), и может происходить сезонно (Barrón et al. ., 2006; Egea et al., 2019) и диелей (Ziegler and Benner, 1999; Maher and Eyre, 2010), о чем свидетельствует более низкий уровень содержания сульфидов в поровой воде в середине дня (Lee and Dunton, 2000).
, 2012a). Осадочный органический углерод на лугах из морских водорослей содержит как автохтонный, так и аллохтонный органический материал наземного или морского происхождения (Kennedy et al., 2010) и может быть защищен от дальнейшей деградации, поскольку морские травы могут стабилизировать отложения, уменьшая повторное взвешивание и потери в результате окисления (Serrano et al. , 2020). Однако в карбонатных отложениях процессы осаждения и растворения карбоната кальция вызывают образование или потребление CO 9 .1138 2 превышает чистый метаболизм экосистемы (Mazarrasa et al., 2015; Howard et al., 2018). Это растворение карбонатов может усиливаться на лугах с водорослями за счет того, что водоросли перекачивают кислород в отложения во время фотосинтеза (Eldridge and Morse, 2000; Burdige and Zimmerman, 2002; Burdige et al., 2008, 2010), и может происходить сезонно (Barrón et al. ., 2006; Egea et al., 2019) и диелей (Ziegler and Benner, 1999; Maher and Eyre, 2010), о чем свидетельствует более низкий уровень содержания сульфидов в поровой воде в середине дня (Lee and Dunton, 2000). Однако влияние этого растворения карбонатов на органическое вещество «голубого углерода» остается неопределенным.
Однако влияние этого растворения карбонатов на органическое вещество «голубого углерода» остается неопределенным.
В дополнение к твердым органическим веществам органические вещества, связанные с карбонатами, вносят свой вклад в запас «голубого углерода» карбонатных лугов из морских водорослей (Howard et al., 2018). В лабораторных исследованиях карбонаты могут адсорбировать и удалять из раствора богатые аспарагиновой кислотой фульвокислоты (Carter, 1978), стеариновые кислоты и яичный альбумин (Suess, 1970). В карбонатных отложениях органическое вещество, содержащее кислотные функциональные группы, может адсорбироваться на карбонатных минералах, а автохтонное органическое вещество может быть защищено внутрикристаллической сетью карбонатных минералов в момент биогенеза (Müller and Suess, 19).77; Ингаллс и др., 2004). Неизвестно, приводит ли растворение карбонатов, опосредованное морскими водорослями, к высвобождению органического вещества, связанного с отложениями, или это влияет на качество и количество растворенного органического вещества (РОВ) в толще воды.
Матрицы возбуждения-излучения (EEM) с параллельным факторным анализом (PARAFAC) являются полезным инструментом для оценки круговорота и динамики естественного органического вещества в водной среде (Jaffé et al., 2014). DOM в образцы карбонатных водоносных горизонтов Флориды (Jin and Zimmerman, 2010). В заливе Флорида, месте проведения настоящего исследования, EEM были реализованы для изучения сезонных и эпизодических факторов, влияющих на вариации МОВ (Maie et al., 2006, 2012; Ya et al., 2015). Тем не менее, влияние диэлфорсинга, бентосных потоков, плотности водорослей или ассоциаций с карбонатными отложениями на сигнал флуоресцентного РОВ (FDOM) остается неопределенным. Мы предположили, что FDOM поверхностных вод на лугах из морских водорослей будет меняться в зависимости от времени суток из-за комбинированных процессов растворения отложений, экссудации морских водорослей и фотодеградации. Чтобы проверить это, мы использовали схему отбора проб Diel для количественного определения концентраций растворенного органического углерода (DOC) и FDOM на двух участках с высокой и низкой плотностью 9. 1144 Thalassia testudinum Луга с водорослями в заливе Флорида. В связанном эксперименте мы исследовали оптические свойства FDOM, высвобождаемого из подкисленных фильтратов отложений и поровой воды, чтобы понять вклад органического вещества, связанного с отложениями, и растворения отложений в изменчивость FDOM.
1144 Thalassia testudinum Луга с водорослями в заливе Флорида. В связанном эксперименте мы исследовали оптические свойства FDOM, высвобождаемого из подкисленных фильтратов отложений и поровой воды, чтобы понять вклад органического вещества, связанного с отложениями, и растворения отложений в изменчивость FDOM.
Методы
Участок исследования
Флоридский залив (FB) представляет собой мелководное устье реки с преобладанием морских водорослей, богатое карбонатами, на юге Флориды. Первичная продуктивность в этой олиготрофной экосистеме частично поддерживается за счет высвобождения питательных веществ (азота, N и фосфора, P), хранящихся в отложениях (Fourqurean et al., 2012b). Основным источником фосфора является Мексиканский залив, где продуктивность морских водорослей выше, в то время как основной источник пресной воды проходит через Тейлор-Слау из Эверглейдс в северо-восточной части залива, а сеть многочисленных грязевых отмелей ограничивает поток воды между бассейнами (Fourqurean и Роббли, 19 лет99). Содержание карбоната кальция в отложениях варьируется от 70 до 95% (Caccia et al., 2003), а ассоциации между неорганическим P и карбонатами способствуют ограничению P в экосистеме (Koch et al., 2001). Хотя растворение карбонатов является непостоянным, оно, как правило, выше в регионах с повышенным ограничением фосфора и в периоды повышенной солености (Yates and Halley, 2006), что, вероятно, связано со стратегиями, используемыми морскими водорослями для высвобождения ограниченного количества фосфора, связанного с карбонатами, через органическую кислоту. экссудаты (Long et al., 2008) или усиленное окисление сульфидов за счет накачки кислорода в ризосферу (Ku et al., 1999; Jensen et al., 2009) или биотурбации (Walter et al., 1993). Суточные колебания в процессах растворения карбонатов и осаждения могут привести к сильным колебаниям щелочности водной толщи, растворенного CO 2 и рН в заливе Флорида (Yates and Halley, 2006; Yates et al., 2007).
Содержание карбоната кальция в отложениях варьируется от 70 до 95% (Caccia et al., 2003), а ассоциации между неорганическим P и карбонатами способствуют ограничению P в экосистеме (Koch et al., 2001). Хотя растворение карбонатов является непостоянным, оно, как правило, выше в регионах с повышенным ограничением фосфора и в периоды повышенной солености (Yates and Halley, 2006), что, вероятно, связано со стратегиями, используемыми морскими водорослями для высвобождения ограниченного количества фосфора, связанного с карбонатами, через органическую кислоту. экссудаты (Long et al., 2008) или усиленное окисление сульфидов за счет накачки кислорода в ризосферу (Ku et al., 1999; Jensen et al., 2009) или биотурбации (Walter et al., 1993). Суточные колебания в процессах растворения карбонатов и осаждения могут привести к сильным колебаниям щелочности водной толщи, растворенного CO 2 и рН в заливе Флорида (Yates and Halley, 2006; Yates et al., 2007).
Мы посетили одни и те же участки водорослей с высокой и низкой плотностью (HD и LD соответственно) в качестве параллельного исследования чистой экосистемной продуктивности морских водорослей Флоридского залива, которые, как было установлено, растворялись в сети в течение периода исследования (Van Dam et al. др., 2019), и отделены друг от друга илистыми отмелями и мангровым островом (М, рис. 1). Участки как HD, так и LD расположены на северо-востоке FB и имеют схожие источники осадочного органического вещества (Xu et al., 2006), характеристики органического вещества поверхностных вод (Maie et al., 2012) и содержание CaCO 3 в осадочных породах (Caccia и др., 2003). На пяти дополнительных участках по всему FB наблюдается различное присутствие морских водорослей, и они охватывают градиент продуктивности (TC, DK, LM, BA и SB, рис. 1).
др., 2019), и отделены друг от друга илистыми отмелями и мангровым островом (М, рис. 1). Участки как HD, так и LD расположены на северо-востоке FB и имеют схожие источники осадочного органического вещества (Xu et al., 2006), характеристики органического вещества поверхностных вод (Maie et al., 2012) и содержание CaCO 3 в осадочных породах (Caccia и др., 2003). На пяти дополнительных участках по всему FB наблюдается различное присутствие морских водорослей, и они охватывают градиент продуктивности (TC, DK, LM, BA и SB, рис. 1).
Рис. 1. Карта объекта, включая расположение изучаемой территории на юго-востоке США (врезка, красная рамка). Были отобраны образцы морских водорослей высокой плотности (HD) и низкой плотности (LD) для диэльной части исследования, а также для выщелачивания отложений и морских водорослей. На участке мангровых зарослей (M) были взяты пробы для сравнения поверхностных вод. Пять дополнительных участков, отобранных для сравнения поровой воды, поверхностных вод и выщелачивания отложений, охватывают всю территорию Флоридского залива (DK, TC, LM, BA и SB). Данные о бентическом покрытии были получены от Флоридской комиссии по сохранению рыб и дикой природы – Научно-исследовательский институт рыбы и дикой природы (FWRI FWC), Unified Reef Map.
Данные о бентическом покрытии были получены от Флоридской комиссии по сохранению рыб и дикой природы – Научно-исследовательский институт рыбы и дикой природы (FWRI FWC), Unified Reef Map.
Кампании по отбору проб
В конце 2018 г. в HD и LD были проведены две многодневные кампании по отбору проб (всего 8 дней) (рис. 1). Пробы поверхностных вод (ПВ) отбирались с циклом рассвет-полдень-сумерки во время первой кампании (с 28 октября по 01 ноября 2018 г.) и 4 раза в день во время второй кампании (с 25 ноября по 29 ноября 2018 г.). . В каждый момент времени 60 мл SW фильтровали (0,45 мкм) и хранили в темных, промытых кислотой темных бутылях из ПЭВП объемом 60 мл, трижды ополаскиваемых водой. Эти образцы сразу помещали на лед, затем охлаждали при 4°C до дальнейшего анализа. Матрицы эмиссии возбуждения (EEM) и спектры поглощения были собраны в течение 2 недель, а вся оставшаяся проба воды была подкислена до pH < 2 с помощью HCl и хранилась при 4°C до анализа растворенного органического углерода (DOC) в течение 4 месяцев после сбора. Пробы донных отложений и обрезки листьев морских водорослей были собраны на участках HD и LD. Три пробы SW также были собраны из M (рис. 1) во время первой кампании. Фотосинтетически активная радиация (ФАР) измерялась в толще воды на обоих участках с помощью погружного датчика ECO-PAR Sea-bird (Van Dam et al., 2019).) и интегрировали в течение дня, чтобы получить кумулятивную PAR (E/m 2 ) для наших анализов.
Пробы донных отложений и обрезки листьев морских водорослей были собраны на участках HD и LD. Три пробы SW также были собраны из M (рис. 1) во время первой кампании. Фотосинтетически активная радиация (ФАР) измерялась в толще воды на обоих участках с помощью погружного датчика ECO-PAR Sea-bird (Van Dam et al., 2019).) и интегрировали в течение дня, чтобы получить кумулятивную PAR (E/m 2 ) для наших анализов.
Третья кампания по отбору проб была проведена в апреле 2019 г., в ходе которой были собраны отфильтрованные (0,45 мкм) поровые воды (PW), отфильтрованные SW и пробы наносов в пространственном обследовании пяти дополнительных участков (TC, DK, LM, BA и СБ, рис. 1). PW собирали с помощью сиппера для поровой воды с поверхностным экраном с глубины отложений 10 см.
Осадки и фильтраты из листьев морских водорослей
Влажные карбонатные отложения разделяли на две равные порции по 5–10 грамм каждая, затем разбавляли примерно 60 мл деионизированной воды (ДИ). Одну порцию подкисляли достаточным количеством 12 н. HCl (примерно 20 капель), чтобы добиться заметного, но неполного растворения, чтобы сохранить буферность и незначительно изменить рН надосадочной жидкости. Осадку и надосадочному раствору давали выщелачиваться при 4°C в течение 48 часов, после чего образец фильтровали (0,45 мкм) перед анализом EEMS и DOC. Этот материал представляет собой «SED HCl » и «SED DI », описанных в результатах. Из-за низкой температуры выщелачивания и рН деионизированной воды небольшая часть карбонатного осадка также будет растворяться при обработке SED DI , однако SED HCl обеспечивает значительно более высокое растворение осадка. Листья водорослей с участков HD и LD (150–500 мг) выщелачивали 60 мл деионизированной воды при 4°C в течение 48 ч; мы называем этот фильтрат «SG». Данные EEM и абсорбции были собраны для всех фильтратов, однако DOC был проанализирован для SED HCl и SED DI выщелачиваются только из третьей кампании.
Одну порцию подкисляли достаточным количеством 12 н. HCl (примерно 20 капель), чтобы добиться заметного, но неполного растворения, чтобы сохранить буферность и незначительно изменить рН надосадочной жидкости. Осадку и надосадочному раствору давали выщелачиваться при 4°C в течение 48 часов, после чего образец фильтровали (0,45 мкм) перед анализом EEMS и DOC. Этот материал представляет собой «SED HCl » и «SED DI », описанных в результатах. Из-за низкой температуры выщелачивания и рН деионизированной воды небольшая часть карбонатного осадка также будет растворяться при обработке SED DI , однако SED HCl обеспечивает значительно более высокое растворение осадка. Листья водорослей с участков HD и LD (150–500 мг) выщелачивали 60 мл деионизированной воды при 4°C в течение 48 ч; мы называем этот фильтрат «SG». Данные EEM и абсорбции были собраны для всех фильтратов, однако DOC был проанализирован для SED HCl и SED DI выщелачиваются только из третьей кампании. Было показано, что осадочные металлы гасят флуоресценцию гуминовых веществ (Haider and Guggenberger, 2004), однако небольшое количество металлов, таких как Fe, Al и Mn, в наших отложениях (Caccia et al., 2003) и неполное метод растворения SED HCl предполагает, что концентрации металлов в фильтратах не окажут большого влияния на сигнал FDOM (Poulin et al., 2014; Liu et al., 2018).
Было показано, что осадочные металлы гасят флуоресценцию гуминовых веществ (Haider and Guggenberger, 2004), однако небольшое количество металлов, таких как Fe, Al и Mn, в наших отложениях (Caccia et al., 2003) и неполное метод растворения SED HCl предполагает, что концентрации металлов в фильтратах не окажут большого влияния на сигнал FDOM (Poulin et al., 2014; Liu et al., 2018).
Определение DOC, EEM и поглощения
Растворенный органический углерод определяли в подкисленных и отфильтрованных (0,45 мкм) образцах с использованием анализатора общего содержания органического углерода Shimadzu TOC-V. Спектры поглощения (240–621 нм, интервал 3 нм) регистрировали одновременно с ЭЭМ с использованием спектрофлуориметра Aqualog (HORIBA Scientific, HORIBA New Jersey Optical Spectroscopy Center, USA), оснащенного ксеноновой дуговой лампой непрерывного действия мощностью 150 Вт и 1 см кварцевая кювета. Сканирование эмиссии было получено от 250 до 621 нм с интервалами ~1,5 нм и было получено при длинах волн возбуждения 240–621 нм с интервалами 3 нм. Данные после сбора данных были вычтены с использованием воды Milli-Q и скорректированы с учетом эффектов внутреннего фильтра (McKnight et al., 2001). EEM представлены в рамановских единицах (RU).
Данные после сбора данных были вычтены с использованием воды Milli-Q и скорректированы с учетом эффектов внутреннего фильтра (McKnight et al., 2001). EEM представлены в рамановских единицах (RU).
Удельное УФ-поглощение при 254 (SUVA 254 ) определяется как поглощение при 254 нм (m –1 ), нормализованное по DOC в мг-Кл –1 (Weishaar et al., 2003). A 254 был оценен линейной интерполяцией между A 255 и A 252 . Поглощение при 351 (A 351 ) использовали вместо A 350 и масштабировали до DOC. Коэффициент наклона (S R ) представляет собой отношение спектральных наклонов S 275 – 295 до S 350 – 400 , которые, в свою очередь, были рассчитаны путем подгонки линейной регрессии к естественному логарифмически преобразованному поглощению между 275–295 и 350–400 нм (Helms et al., 2008). Показатели индекса гумификации (HIX), индекса флуоресценции (FI) и биологического (свежести) индекса (BIX) были рассчитаны непосредственно из спектров EEM (Wagner et al. , 2015). HIX имеет тенденцию к увеличению при гумификации и микробной обработке МОВ (Wickland et al., 2007), FI использовался для оценки микробного и наземного вклада в МОВ (Cory et al., 2005), а BIX коррелирует с недавно полученным МОМ (Парланти и др., 2000). Статистический анализ проводился в MatLab R2017a и R Studio. Взаимосвязь между каждым индексом и кумулятивным PAR была количественно определена с помощью линейной модели в R, а наклоны представлены в дополнительной таблице S1. Различия между сайтами и кампаниями для каждого индекса были рассчитаны на основе одностороннего дисперсионного анализа (односторонний ANOVA) и представлены графически на дополнительном рисунке S5.
, 2015). HIX имеет тенденцию к увеличению при гумификации и микробной обработке МОВ (Wickland et al., 2007), FI использовался для оценки микробного и наземного вклада в МОВ (Cory et al., 2005), а BIX коррелирует с недавно полученным МОМ (Парланти и др., 2000). Статистический анализ проводился в MatLab R2017a и R Studio. Взаимосвязь между каждым индексом и кумулятивным PAR была количественно определена с помощью линейной модели в R, а наклоны представлены в дополнительной таблице S1. Различия между сайтами и кампаниями для каждого индекса были рассчитаны на основе одностороннего дисперсионного анализа (односторонний ANOVA) и представлены графически на дополнительном рисунке S5.
Параллельное моделирование факторного анализа и были выполнены с использованием набора инструментов DrEEM 3.0 в MatLab R2017a (Murphy et al., 2013). Модель PARAFAC была запущена на n = 97 из 100 образцов с использованием диапазона длин волн возбуждения от 258 до 498 нм, и функция zap использовалась для удаления аномальных пиков по отдельности. Три выборки были удалены как выбросы, поскольку высокий коэффициент использования потенциально мог исказить результаты модели. Пятикомпонентная модель была проверена с использованием анализа с разделением пополам S4C4T2, а затем применена к ненормализованному полному набору данных. При сравнении пулов (PW, SW, SED DI и SED HCl ) Компоненты PARAFAC выражены в процентах, а временные вариации компонентов PARAFAC выражены в RU. Из-за возможного матричного эффекта, особенно присутствия галогенидов, по-разному воздействующего на диапазон образцов (т. е. SW против SED DI против SED HCl ), сравнения между этими типами образцов проводятся качественным образом ( Гребель и др., 2009).
Три выборки были удалены как выбросы, поскольку высокий коэффициент использования потенциально мог исказить результаты модели. Пятикомпонентная модель была проверена с использованием анализа с разделением пополам S4C4T2, а затем применена к ненормализованному полному набору данных. При сравнении пулов (PW, SW, SED DI и SED HCl ) Компоненты PARAFAC выражены в процентах, а временные вариации компонентов PARAFAC выражены в RU. Из-за возможного матричного эффекта, особенно присутствия галогенидов, по-разному воздействующего на диапазон образцов (т. е. SW против SED DI против SED HCl ), сравнения между этими типами образцов проводятся качественным образом ( Гребель и др., 2009).
Результаты и обсуждение
Описание компонентов PARAFAC
5-компонентная модель PARAFAC была проверена для нашего набора данных (дополнительный рисунок S1). Ранее 8-компонентная модель PARAFAC подходила для проб поверхностных вод южной Флориды (Chen et al. , 2010; Murphy et al., 2014), но эту модель нельзя было применить к текущему набору данных из-за различий в интервалах длин волн. между спектрофотометром, использованным в этом исследовании (Aqualog), и спектрофотометром, использованным в Chen et al., 2010 (FluoroMax 3). Визуальное сравнение компонентов PARAFAC (дополнительный рисунок S2) показывает, что наша 5-компонентная модель PARAFAC охватывает те же общие группы FDOM, что и 8-компонентная модель, резюмируя следующим образом: наш C1 похож на заявленные компоненты 3, 4 и 6, и является гуминоподобным (Yamashita and Jaffé, 2008). Наш C2 аналогичен заявленным компонентам 1 и 5, а также похож на гумин. Наш C3 аналогичен описанному компоненту 2 и похож на гумин. Наш C4 похож на описанный компонент 8 и похож на триптофановый белок. Наконец, наш C5 подобен компоненту 7, о котором сообщалось, и подобен белку тирозина. Сходство между этими компонентами позволяет нам установить наши результаты в контексте предшествующих исследований, и последствия будут обсуждаться в последующих разделах.
, 2010; Murphy et al., 2014), но эту модель нельзя было применить к текущему набору данных из-за различий в интервалах длин волн. между спектрофотометром, использованным в этом исследовании (Aqualog), и спектрофотометром, использованным в Chen et al., 2010 (FluoroMax 3). Визуальное сравнение компонентов PARAFAC (дополнительный рисунок S2) показывает, что наша 5-компонентная модель PARAFAC охватывает те же общие группы FDOM, что и 8-компонентная модель, резюмируя следующим образом: наш C1 похож на заявленные компоненты 3, 4 и 6, и является гуминоподобным (Yamashita and Jaffé, 2008). Наш C2 аналогичен заявленным компонентам 1 и 5, а также похож на гумин. Наш C3 аналогичен описанному компоненту 2 и похож на гумин. Наш C4 похож на описанный компонент 8 и похож на триптофановый белок. Наконец, наш C5 подобен компоненту 7, о котором сообщалось, и подобен белку тирозина. Сходство между этими компонентами позволяет нам установить наши результаты в контексте предшествующих исследований, и последствия будут обсуждаться в последующих разделах.
Diel Изменчивость в поверхностных водах FDOM
Умеренный рост S R и FI и умеренное снижение HIX, наблюдаемые во второй половине второй кампании (дополнительный рисунок S3), во времени соответствуют увеличению скорости ветра и падение температуры поверхности моря (Van Dam et al., 2019), но в остальном временных трендов индексов флуоресценции, коэффициентов поглощения и компонентов PARAFAC не обнаружено. DOC менялся на обоих участках в течение всего периода исследования, но был сопоставим со значениями DOC, наблюдаемыми в центральной части Флоридского залива в течение десяти лет ежемесячного мониторинга (Jaffé, 2018; дополнительный рисунок S4). Мы предположили, что фотодеградация может быть преобладающим фактором, влияющим на изменчивость диэлема в FDOM поверхностных вод, учитывая, что предыдущее исследование с применением 8-компонентной модели (дополнительный рисунок S2) показало, что все их компоненты в той или иной степени реагируют на свет (Chen and Jaffé, 2014). ). Интересно, что их компонент 2 (аналогичный нашему C3) оказался продуктом фотодеградации, а их компонент 7 (аналогичный нашему C5) оказался высоко фотолабильным (Chen and Jaffé, 2014, 2016). Несмотря на эту фотолабильность и фотопродукцию, мы не обнаружили изменений ни в одном компоненте PARAFAC, включая C3 и C5, с различной кумулятивной PAR (рис. 2A, B и дополнительная таблица S1).
). Интересно, что их компонент 2 (аналогичный нашему C3) оказался продуктом фотодеградации, а их компонент 7 (аналогичный нашему C5) оказался высоко фотолабильным (Chen and Jaffé, 2014, 2016). Несмотря на эту фотолабильность и фотопродукцию, мы не обнаружили изменений ни в одном компоненте PARAFAC, включая C3 и C5, с различной кумулятивной PAR (рис. 2A, B и дополнительная таблица S1).
Рисунок 2. Все индексы и компоненты PARAFAC в зависимости от кумулятивной PAR (E/m 2 ) для однодневного исследования, разделенные между кампанией 1 (слева) и кампанией 2 (справа), а также сайтами (кружки LD) и линии, HD звездочка и пунктир). (A,B) Компоненты PARAFAC в рамановских единицах (RU). (C,D) FI и BIX по левой оси, HIX по правой оси. (E,F) S R и SUVA 254 на левой оси и DOC (мг/л) на правой оси.
Снижение SUVA 254 часто рассматривается как свидетельство фотодеградации, но мы не измеряли изменение SUVA 254 с PAR. Однако наши низкие значения SUVA 254 от ∼1,0 (LD) до ∼1,6 (HD) предполагают, что этот материал уже сильно фотодеградирован (рис. 2E, F). Фактически, ни один измеренный индекс не показал значительного увеличения или уменьшения кумулятивной PAR ( p > 0,05; дополнительная таблица S1, рисунок 2). Взятые вместе, наши результаты показывают, что РОМ в FB уже значительно фотодеградировал, так что индексы флуоресценции и поглощения стабильны во времени в дневных временных масштабах. Это согласуется с последовательным фото- и биоразложением нейтральных выщелачивателей отложений из SB (TS/Ph21 в ссылке), которые приблизились к оптическим характеристикам поверхностных вод FB (Chen and Jaffé, 2014).
Однако наши низкие значения SUVA 254 от ∼1,0 (LD) до ∼1,6 (HD) предполагают, что этот материал уже сильно фотодеградирован (рис. 2E, F). Фактически, ни один измеренный индекс не показал значительного увеличения или уменьшения кумулятивной PAR ( p > 0,05; дополнительная таблица S1, рисунок 2). Взятые вместе, наши результаты показывают, что РОМ в FB уже значительно фотодеградировал, так что индексы флуоресценции и поглощения стабильны во времени в дневных временных масштабах. Это согласуется с последовательным фото- и биоразложением нейтральных выщелачивателей отложений из SB (TS/Ph21 в ссылке), которые приблизились к оптическим характеристикам поверхностных вод FB (Chen and Jaffé, 2014).
Мы ожидали, что участок HD будет демонстрировать большую изменчивость оптических свойств и концентрации РОУ с PAR, чем участок LD, поскольку предыдущие исследования связывали плотность морских водорослей с потоком бентического РОУ (Ziegler and Benner, 1999) и растворением карбонатов (Burdige and Zimmerman, 2002; Yates and Halley, 2006; Burdige et al. , 2010). Вместо этого мы не наблюдали такой изменчивости diel ни для HD, ни для LD сайтов. Однако это не означает, что плотность водорослей и растворение отложений не влияют на оптические свойства поверхностных вод по двум причинам. Во-первых, оценки суммарного растворения/осаждения карбонатов, сделанные во время совпадающего исследования, также не были сильно связаны с PAR, и, хотя на участке HD было больше чистого растворения, чем на участке LD, эти различия были невелики (Van Dam et al., 2019).). Таким образом, даже если бентический поток FDOM, связанный с отложениями, облегчается растворением отложений, мы не обязательно ожидаем увидеть связь между индексами FDOM и PAR для этого конкретного короткого периода исследования. Во-вторых, вполне вероятно, что наш подход к водной толще был недостаточно чувствительным, и что более специализированный эксперимент, такой как инкубация керна или донные камеры, лучше подходил бы для решения этого вопроса.
, 2010). Вместо этого мы не наблюдали такой изменчивости diel ни для HD, ни для LD сайтов. Однако это не означает, что плотность водорослей и растворение отложений не влияют на оптические свойства поверхностных вод по двум причинам. Во-первых, оценки суммарного растворения/осаждения карбонатов, сделанные во время совпадающего исследования, также не были сильно связаны с PAR, и, хотя на участке HD было больше чистого растворения, чем на участке LD, эти различия были невелики (Van Dam et al., 2019).). Таким образом, даже если бентический поток FDOM, связанный с отложениями, облегчается растворением отложений, мы не обязательно ожидаем увидеть связь между индексами FDOM и PAR для этого конкретного короткого периода исследования. Во-вторых, вполне вероятно, что наш подход к водной толще был недостаточно чувствительным, и что более специализированный эксперимент, такой как инкубация керна или донные камеры, лучше подходил бы для решения этого вопроса.
Пространственная изменчивость поверхностных вод между площадками HD и LD
Хотя мы наблюдали ограниченную изменчивость диэля в FDOM и связанных индексах, были сильные пространственные различия между участками HD и LD, а также между кампаниями отбора проб, которые были разделены всего на 1 месяц во время влажной (первая кампания) и поздней влажной ( второй кампании) сезона (Я и др. , 2015). Все показатели были одинаковыми на сайте LD для обеих кампаний, однако на сайте HD BIX и %C4 были ниже, а HIX, %C1, %C2, %C3 и A 351 /DOC были выше во время первой кампании ( Дополнительный рисунок S5). Между сайтами сайт HD был значительно выше в HIX, SUVA 254 , %C1, %C2 и %C3, которые все являются «гуминоподобными» (дополнительные рисунки S1, S5, p <0,05). Другие «негуминовые» индексы, такие как FI и S R , статистически не различались между участками. Поскольку участки HD и LD были соседними (рис. 1), любые наблюдаемые нами различия могли указывать на мелкомасштабную неоднородность МОВ, которая была упущена при более широких пространственных исследованиях (Maie et al., 2006, 2012). Кроме того, поскольку участок HD также содержал больше осадочного органического углерода (Van Dam et al., 2019), вполне вероятно, что вариации в «гуминовой» фракции РОВ могут быть связаны с различиями в осадочном органическом веществе между двумя участками.
, 2015). Все показатели были одинаковыми на сайте LD для обеих кампаний, однако на сайте HD BIX и %C4 были ниже, а HIX, %C1, %C2, %C3 и A 351 /DOC были выше во время первой кампании ( Дополнительный рисунок S5). Между сайтами сайт HD был значительно выше в HIX, SUVA 254 , %C1, %C2 и %C3, которые все являются «гуминоподобными» (дополнительные рисунки S1, S5, p <0,05). Другие «негуминовые» индексы, такие как FI и S R , статистически не различались между участками. Поскольку участки HD и LD были соседними (рис. 1), любые наблюдаемые нами различия могли указывать на мелкомасштабную неоднородность МОВ, которая была упущена при более широких пространственных исследованиях (Maie et al., 2006, 2012). Кроме того, поскольку участок HD также содержал больше осадочного органического углерода (Van Dam et al., 2019), вполне вероятно, что вариации в «гуминовой» фракции РОВ могут быть связаны с различиями в осадочном органическом веществе между двумя участками. Эта гипотеза послужила мотивом для нашего анализа фильтрата отложений.
Эта гипотеза послужила мотивом для нашего анализа фильтрата отложений.
Атрибуция потенциального источника FDOM
Мы выдвинули гипотезу о существовании трех основных источников FDOM в поверхностных водах HD и LD: (1) фильтраты/экссудаты морских водорослей, (2) близлежащие мангровые заросли и (3) растворение отложений. В предыдущих исследованиях (Chen and Jaffé, 2014, 2016) использовалась 8-компонентная модель FCE PARAFAC для изучения выщелачивания листьев морских водорослей и явно нерастворимых выщелачиваний донных отложений с одного участка в западной части FB (SB или TS/Ph21 в ссылке). Мы расширяем эту работу, сравнивая FDOM поверхностных вод на участках HD и LD с фильтратами SG, SW мангровых зарослей, собранными из M (рис. 1), и SED 9.1138 DI и SED HCl выщелачивают. Как в HD, так и в LD SG преобладал C5, минимально C4, C2 и C1 и не было C3, что резко контрастировало с HD и LD SW, которые содержали все компоненты, но с преобладанием C1, C3 и C4 (рис. 3А). Наши фильтраты SG демонстрируют флуоресценцию, аналогичную SG у Чена и Джаффе (2014), которые обнаружили, что в их фильтратах листьев морских водорослей в SB также преобладал C5 (их компонент 7) и мало или совсем не было C3 (их компонент 2). Хотя C5 также, вероятно, был сильно подвержен фоторазложению, эти результаты показывают, что морские травы сами по себе не вносят основной вклад в сигнал FDOM поверхностных вод.
3А). Наши фильтраты SG демонстрируют флуоресценцию, аналогичную SG у Чена и Джаффе (2014), которые обнаружили, что в их фильтратах листьев морских водорослей в SB также преобладал C5 (их компонент 7) и мало или совсем не было C3 (их компонент 2). Хотя C5 также, вероятно, был сильно подвержен фоторазложению, эти результаты показывают, что морские травы сами по себе не вносят основной вклад в сигнал FDOM поверхностных вод.
Рисунок 3. Состав компонентов (A) PARAFAC различных матриц (SW, SG, SED DI и SED HCl ) с участков HD и LD по сравнению с близлежащим участком Mangrove (M) . (B) PCA данных, показанных на верхнем рисунке, из основной части этого исследования. (C) PCA данных из пяти дополнительных участков по всему FB, разделенных матрицей (PW, SW, SED DI и SED HCl ).
Участок M расположен между участками HD и LD (рис. 1), что позволяет нам идентифицировать любое присутствие «мангрового» источника FDOM. В поверхностных водах в точке M преобладали C2 и, в меньшей степени, C1 и C3, с небольшими количествами C4 и C5, если таковые имеются (рис. 3А). И наоборот, C2 был лишь второстепенным компонентом HD и LD SW. Хотя Чен и Яффе (2014) не рассматривали мангровые заросли в заливе Флорида напрямую, они собирали поверхностные воды из мангровых зарослей долины Шарк-Ривер-Слау (SRS5 в своем отчете), которая расположена к северу от FB на западном побережье южной Флорида. Они обнаружили, что в мангровых зарослях преобладают компоненты 1 и 5 и в меньшей степени компоненты 2, 3, 4 и 6, которые аналогичны нашим компонентам С2, С1 и С3. Интересно, что их компоненты 1, 3, 4, 5 и 6 оказались гораздо более фотореактивными, чем биореактивными. Таким образом, различия между SW, собранными на участках M, HD и LD, не исключают наличие мангровых зарослей как возможного источника FDOM поверхностных вод, поскольку оптический сигнал мог модифицироваться из-за фотодеградации в прозрачных водах FB. Однако наше исследование diel не показывает изменения C1, C2 или C3 в зависимости от кумулятивной ФАР (рис.
В поверхностных водах в точке M преобладали C2 и, в меньшей степени, C1 и C3, с небольшими количествами C4 и C5, если таковые имеются (рис. 3А). И наоборот, C2 был лишь второстепенным компонентом HD и LD SW. Хотя Чен и Яффе (2014) не рассматривали мангровые заросли в заливе Флорида напрямую, они собирали поверхностные воды из мангровых зарослей долины Шарк-Ривер-Слау (SRS5 в своем отчете), которая расположена к северу от FB на западном побережье южной Флорида. Они обнаружили, что в мангровых зарослях преобладают компоненты 1 и 5 и в меньшей степени компоненты 2, 3, 4 и 6, которые аналогичны нашим компонентам С2, С1 и С3. Интересно, что их компоненты 1, 3, 4, 5 и 6 оказались гораздо более фотореактивными, чем биореактивными. Таким образом, различия между SW, собранными на участках M, HD и LD, не исключают наличие мангровых зарослей как возможного источника FDOM поверхностных вод, поскольку оптический сигнал мог модифицироваться из-за фотодеградации в прозрачных водах FB. Однако наше исследование diel не показывает изменения C1, C2 или C3 в зависимости от кумулятивной ФАР (рис. 2).
2).
Нашим третьим гипотетическим источником FDOM были отложения. Мы провели две обработки выщелачиванием осадка, одна из которых предназначалась для сведения к минимуму воздействия растворения карбонатов (SED DI ), а другая с усилением растворения осадка (SED HCl ). Наш протокол SED DI в наибольшей степени сопоставим с пассивным выщелачиванием водой с пониженным содержанием DOC, продемонстрированной в работе Chen and Jaffé (2014). При рассмотрении процентного содержания компонентов этих фильтратов HD SED HCl гораздо больше похож на HD SW, чем HD SED DI , в то время как оба фильтрата отложений на участке LD больше похожи на LD SW, чем на M или LD SG (рис. 3A). Наш анализ PCA показывает, что %C5 и, в меньшей степени, %C2 и %C3 наиболее важны для объяснения изменчивости между различными пулами. HD SED HCl был более тесно связан с HD SW, чем HD SED DI , однако из-за преобладания высокофотолабильного C5 (основная объясняющая переменная измерения 1) LD SED HCl и LD SED DI сгруппированы ближе к LD SG, чем к LD SW (рис. 3B). В исследовании Chen and Jaffé (2014) юго-запад мангровых зарослей был больше похож на юго-запад залива Флориды, чем на нейтрально выщелоченные отложения. Это указывает на то, что, если растворение отложений не учитывать в явном виде, роль процессов растворения отложений или повторного осаждения в вкладе в цикличность РОВ в заливе Флорида может быть упущена из виду.
3B). В исследовании Chen and Jaffé (2014) юго-запад мангровых зарослей был больше похож на юго-запад залива Флориды, чем на нейтрально выщелоченные отложения. Это указывает на то, что, если растворение отложений не учитывать в явном виде, роль процессов растворения отложений или повторного осаждения в вкладе в цикличность РОВ в заливе Флорида может быть упущена из виду.
Исследование фильтрата предполагает, что морские травы или мангровые заросли не обязательно являются основными прямыми источниками FDOM в вышележащие воды. Вместо этого мы выделяем процесс растворения карбонатных отложений как потенциальный источник FDOM в поверхностных водах. На растворение карбонатов отложений могли влиять водоросли, и мы попытались выяснить эту связь, изучая луга водорослей высокой и низкой плотности. Однако скорость растворения карбонатов была одинаково низкой между участками HD и LD в течение этого периода исследования (Van Dam et al., 2019).), бросая вызов нашей способности различать его влияние на изменчивость МОВ в пространстве или во времени.
FDOM отложений, поровых и поверхностных вод по всему Флоридскому заливу
Для дальнейшего изучения этого очевидного сходства между FDOM SW и SED HCl мы собрали образцы из 5 дополнительных участков (TC, DK, LM, BA и SB). ; фигура 1), состоящая из одного образца для каждого сайта и каждого пула (PW, SW, SED DI и SED HCl ). При рассмотрении растворения карбонатов как потенциального источника органического вещества ПВ можно рассматривать как промежуточный пул между СЭД HCl и SW. По этой причине может быть полезно сравнить SW с PW, а также SED HCl и SED DI с PW. На всех участках индексы FDOM и поглощения группировались вокруг линии 1:1, что свидетельствует о быстром обмене между пулами PW и SW DOM. Мы наблюдали отклонения от линии 1:1 для %C5, который был намного выше в PW, чем в SW для большинства участков, вероятно, из-за его фотолабильности (Chen and Jaffé, 2014). SUVA 254 , как правило, выше в SW, чем в PW, но различия в SW и PW S R были менее четкими (рис. 4A, D). Уменьшение PW SUVA 254 потенциально было связано с выбросами лабильных, но не хромофорных ДОС из водорослей в ризосферу.
4A, D). Уменьшение PW SUVA 254 потенциально было связано с выбросами лабильных, но не хромофорных ДОС из водорослей в ризосферу.
Рисунок 4. Сравнение компонентного состава PARAFAC (A–C) и других оптических свойств (D–F) для 5 участков в заливе Флорида (DK, SB, LM, BA и TC) и 4 бассейнов (SW, PW, SED HCl и SED DI ). PW находится на оси x , с SW (A, D) , SED HCl (B, E) или SED DI (C, F) на оси y . Для каждого сайта и каждого пула использовали один образец ( n = 20).
Мы также наблюдали тесную взаимосвязь между фильтратами SED HCl и PW (рис. 4B, E) для большинства компонентов и индексов, что указывает на биогеохимическую связь между РОВ в PW и тем, что связано с карбонатными отложениями. Наблюдаемые отклонения для %C3 и SUVA 254 , которые вели себя аналогично из-за перекрывающихся спектральных свойств и имели более высокую PW, чем SED HCl , означают, что C3 был менее сильно связан с карбонатами. Напротив, фильтраты SED DI оказались гораздо менее связанными с PW (рис. 4C, F). Это согласуется с предыдущим исследованием фильтрата в заливе Флорида, которое показало, что фильтрация отложений ПС с использованием неокисленных вод очень отличается от поверхностных вод (Chen and Jaffé, 2014) и явно контрастирует с нашим SED 9.1138 HCl выщелачивает. И их исследование, и наше исследование выщелачивания SED DI пытались свести к минимуму растворение осадка, тогда как наш подход SED HCl пытался выделить растворение осадка. Взаимосвязь между этими пулами также можно увидеть в нашем анализе PCA, который показывает, что 4 из SED HCl группируются вблизи PW или SW вместе с переменными %C1 и %C3, тогда как SED DI более различен и кластеризуется ближе к переменным %C5 и %C4 (рис. 3C). СЭД 9Выщелачивание 1138 HCl высвободило большое количество DOC по сравнению с SED DI , достаточное для увеличения концентрации DOC в фильтратах на 145–260% на 5 участках, что иллюстрирует потенциальный вклад этого пула в in situ лугов с морской травой ( Дополнительная таблица S2).
Напротив, фильтраты SED DI оказались гораздо менее связанными с PW (рис. 4C, F). Это согласуется с предыдущим исследованием фильтрата в заливе Флорида, которое показало, что фильтрация отложений ПС с использованием неокисленных вод очень отличается от поверхностных вод (Chen and Jaffé, 2014) и явно контрастирует с нашим SED 9.1138 HCl выщелачивает. И их исследование, и наше исследование выщелачивания SED DI пытались свести к минимуму растворение осадка, тогда как наш подход SED HCl пытался выделить растворение осадка. Взаимосвязь между этими пулами также можно увидеть в нашем анализе PCA, который показывает, что 4 из SED HCl группируются вблизи PW или SW вместе с переменными %C1 и %C3, тогда как SED DI более различен и кластеризуется ближе к переменным %C5 и %C4 (рис. 3C). СЭД 9Выщелачивание 1138 HCl высвободило большое количество DOC по сравнению с SED DI , достаточное для увеличения концентрации DOC в фильтратах на 145–260% на 5 участках, что иллюстрирует потенциальный вклад этого пула в in situ лугов с морской травой ( Дополнительная таблица S2).
Заключительные замечания
Результаты нашей уникальной процедуры выщелачивания HCl показывают, что растворение карбонатных отложений может быть важным механизмом, связывающим органическое вещество, связанное с отложениями, с более широким циклом растворенного органического вещества в карбонатных системах водорослей, таких как залив Флорида. Мы предлагаем обмен между СЭД 9Залежи 1138 HCl и PW облегчаются растворением и повторным осаждением отложений, а затем лужи PW и SW смешиваются в результате периодического взмучивания отложений, биотурбации или медленного диффузионного обмена. Хотя наше исследование не смогло прояснить эту лабораторную взаимосвязь в полевых условиях, это исследование закладывает основу для будущих исследований по измерению потока отложений и воды FDOM наряду с оценками растворения карбонатов, для изучения обратимости процесса и изучения изменение РОВ за счет его ассоциации с карбонатами.
Заявление о доступности данных
Набор данных, созданный для этого исследования, доступен на Figshare (10. 6084/m9.figshare.12611897.v2). Данные PAR, использованные в этой статье, уже опубликованы и доступны на Figshare (10.6084/m9.figshare.7707029.v1). Модель PARAFAC доступна на OpenFluor (ID 2859 OpenFluor).
6084/m9.figshare.12611897.v2). Данные PAR, использованные в этой статье, уже опубликованы и доступны на Figshare (10.6084/m9.figshare.7707029.v1). Модель PARAFAC доступна на OpenFluor (ID 2859 OpenFluor).
Авторские взносы
MZ написал рукопись, разработал модель PARAFAC и сыграл важную роль в разработке плана исследования фильтрата отложений. BV и CL создали исследование Diel, сыграли важную роль в полевых работах и внесли подробные изменения в рукопись. JK сыграл важную роль в разработке дизайна исследования, а также предоставил подробные правки и комментарии к рукописи. Все авторы внесли свой вклад в статью и одобрили представленную версию.
Финансирование
Финансирование исследований было поддержано грантом Национального научного фонда для Долгосрочной программы экологических исследований побережья Эверглейдс во Флориде (DEB-1237517). Публикация этой статьи финансировалась Фондом открытого доступа Ассоциации Лейбница. MZ в настоящее время поддерживается в рамках проекта BMBF «DAM-MGF».
Конфликт интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Благодарности
Мы благодарим Сару Уилсон за помощь во время сбора образцов и Мэтью Смита за помощь в анализе DOC. Это доклад № 221 отдела береговых линий и океанов Института окружающей среды Международного университета Флориды.
Дополнительный материал
Дополнительный материал к этой статье можно найти в Интернете по адресу: https://www.frontiersin.org/articles/10.3389/fmars.2020.580284/full#supplementary-material
Ссылки
Баррон, К., Дуарте, К.М., Франкиньуль, М., и Борхес, А.В. (2006). Метаболизм органического углерода и динамика карбонатов на лугу средиземноморской морской травы (Posidonia oceanica). Эстуар. Побережье. 29, 417–426. doi: 10.1007/BF02784990
Полный текст CrossRef | Google Scholar
Бердидж, Д. Дж., и Циммерман, Р. К. (2002). Влияние плотности морской травы на растворение карбонатов в отложениях Багамских островов. Лимнол. океаногр. 47, 1751–1763 гг. doi: 10.4319/lo.2002.47.6.1751
Дж., и Циммерман, Р. К. (2002). Влияние плотности морской травы на растворение карбонатов в отложениях Багамских островов. Лимнол. океаногр. 47, 1751–1763 гг. doi: 10.4319/lo.2002.47.6.1751
Полнотекстовая перекрестная ссылка | Google Scholar
Burdige, D.J., Hu, X., and Zimmerman, RC (2010). Широкое распространение совместного растворения/переосаждения карбонатов в поверхностных отложениях на Багамской отмели. утра. J. Sci. 310, 492–521. doi: 10.2475/06.2010.03
CrossRef Full Text | Google Scholar
Burdige, D.J., Zimmerman, RC, and Hu, X. (2008). Скорость растворения карбонатов в проницаемых отложениях, оцененная по профилям поровой воды: роль морских трав. Лимнол. океаногр. 53, 549–565. doi: 10.4319/lo.2008.53.2.0549
Полный текст CrossRef | Google Scholar
Caccia, VG, Millero, FJ, and Palanques, A. (2003). Распределение микроэлементов в отложениях Флоридского залива. март Загрязнение. Бык. 46, 1420–1433. doi: 10.1016/S0025-326X(03)00288-1
doi: 10.1016/S0025-326X(03)00288-1
Полный текст CrossRef | Google Scholar
Картер, П. В. (1978). Адсорбция органического вещества, содержащего аминокислоты, кальцитом и кварцем. Геохим. Космохим. Акта 42, 1239–1242. doi: 10.1016/0016-7037(78)
-5CrossRef Full Text | Google Scholar
Чен М. и Яффе Р. (2014). Модели фото- и биореактивности растворенного органического вещества из биомассы и почвенных выщелачиваний и поверхностных вод в субтропическом водно-болотном угодье. Вода Res. 61, 181–190. doi: 10.1016/j.watres.2014.03.075
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Чен М. и Яффе Р. (2016). Количественная оценка фото- и биореактивности хромофорного и флуоресцентного растворенного органического вещества биомассы и почвенных выщелачиваний, а также поверхностных вод субтропического водно-болотного угодья. Биогеохимия 129, 273–289. doi: 10.1007/s10533-016-0231-7
CrossRef Полный текст | Google Scholar
Чен М. , Прайс Р. М., Ямасита Ю. и Яффе Р. (2010). Сравнительное исследование растворенного органического вещества в подземных и поверхностных водах в Эверглейдс на побережье Флориды с использованием многомерной спектрофлуориметрии в сочетании с многомерной статистикой. Заяв. Геохим. 25, 872–880. doi: 10.1016/j.apgeochem.2010.03.005
, Прайс Р. М., Ямасита Ю. и Яффе Р. (2010). Сравнительное исследование растворенного органического вещества в подземных и поверхностных водах в Эверглейдс на побережье Флориды с использованием многомерной спектрофлуориметрии в сочетании с многомерной статистикой. Заяв. Геохим. 25, 872–880. doi: 10.1016/j.apgeochem.2010.03.005
CrossRef Full Text | Академия Google
Кори, Р. М., Макнайт, Д. М., и Макнайт, Д. М. (2005). Флуоресцентная спектроскопия выявила повсеместное присутствие окисленных и восстановленных хинонов в растворенном органическом веществе Флуоресцентная спектроскопия выявила повсеместное присутствие окисленных и восстановленных хинонов в растворенном органическом веществе. Окружающая среда. науч. Технол. 39, 8142–8149. doi: 10.1021/es0506962
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Эгеа Л. Г., Баррон К., Хименес-Рамос Р., Эрнандес И., Вергара Дж. Дж., Перес-Льоренс Дж. Л. и др. (2019). Связь метаболизма углерода и потоков растворенного органического углерода в бентических и пелагических прибрежных сообществах. Эстуар. Побережье. Шельф науч. 227:106336. doi: 10.1016/j.ecss.2019.106336
Эстуар. Побережье. Шельф науч. 227:106336. doi: 10.1016/j.ecss.2019.106336
Полный текст CrossRef | Google Scholar
Элдридж, П. М., и Морс, Дж. В. (2000). Диагенетическая модель взаимодействия отложений и водорослей. Мар. Хим. 70, 89–103. doi: 10.1016/S0304-4203(00)00018-9
CrossRef Полный текст | Google Scholar
Фуркуриан, Дж. В., и Роббли, М. Б. (1999). Флорида-Бей: история недавних экологических изменений. Эстуарии 22, 345–357. doi: 10.2307/1353203
Полный текст CrossRef | Google Scholar
Fourqurean, JW, Duarte, C.M., Kennedy, H., Marbà, N., Holmer, M., Mateo, M.A., et al. (2012а). Экосистемы водорослей как глобально значимый запас углерода. Нац. Geosci. 5:505. doi: 10.1038/NGEO1477
CrossRef Полный текст | Google Scholar
Fourqurean, JW, Kendrick, G.A., Collins, L.S., Chambers, R.M. and Vanderklift, M.A. (2012b). Запасы углерода, азота и фосфора на субтропических лугах с водорослями: примеры из Флоридского залива и залива Шарк. март. Пресноводный рез. 63, 967–983. doi: 10.1071/MF12101
март. Пресноводный рез. 63, 967–983. doi: 10.1071/MF12101
CrossRef Полный текст | Google Scholar
Гребель, Дж. Э., Пиньятелло, Дж. Дж., Сонг, В., Купер, В. Дж., и Митч, В. А. (2009). Влияние галогенидов на фотообесцвечивание растворенных органических веществ. Мар. Хим. 115, 134–144. doi: 10.1016/j.marchem.2009.07.009
CrossRef Полный текст | Google Scholar
Хайдер, К. М., и Гуггенбергер, Г. (2004). Органическое вещество – генезис и образование. Энцикл. Почвы Окружающая среда. 4, 93–101. doi: 10.1016/B0-12-348530-4/00510-5
CrossRef Полный текст | Google Scholar
Хелмс Дж. Р., Кибер Д. Дж., Майнор Э. К., Ричи Дж. Д., Стаббинс А. и Моппер К. (2008). Наклоны спектра поглощения и отношения наклонов как индикаторы молекулярной массы, источника и фотообесцвечивания хромофорного растворенного органического вещества. Лимнол. океаногр. 53, 955–969. doi: 10.4319/lo.2008.53.3.0955
CrossRef Full Text | Академия Google
Ховард, Дж. Л., Крид, Дж. К., Агияр, М. В. П., и Фукуриан, Дж. В. (2018). CO 2 , выделяемый в результате образования карбонатных отложений в некоторых прибрежных районах, может нивелировать преимущества хранения водорослей «голубого углерода». Лимнол. океаногр. 63, 160–172. doi: 10.1002/lno.10621
Л., Крид, Дж. К., Агияр, М. В. П., и Фукуриан, Дж. В. (2018). CO 2 , выделяемый в результате образования карбонатных отложений в некоторых прибрежных районах, может нивелировать преимущества хранения водорослей «голубого углерода». Лимнол. океаногр. 63, 160–172. doi: 10.1002/lno.10621
CrossRef Full Text | Google Scholar
Ингаллс, А. Э., Аллер, Р. К., Ли, К., и Уэйкхэм, С. Г. (2004). Диагенез органического вещества в мелководных карбонатных отложениях. Геохим. Космохим. Акта 68, 4363–4379. doi: 10.1016/j.gca.2004.01.002
CrossRef Полный текст | Google Scholar
Джаффе, Р. (2018). Ежемесячные данные мониторинга флуоресценции для Shark River Slough и Taylor Slough, Национальный парк Эверглейдс (FCE) за период с октября 2004 г. по февраль 2014 г. ).
Google Scholar
Джаффе Р., Коули К.М. и Ямашита Ю. (2014). Применение матричной флуоресценции эмиссии возбуждения с параллельным факторным анализом (EEM-PARAFAC) в оценке экологической динамики естественного растворенного органического вещества (РОВ) в водной среде: обзор. Симпозиумы ACS. сер. 1160, 27–73. doi: 10.1021/bk-2014-1160.ch003
Симпозиумы ACS. сер. 1160, 27–73. doi: 10.1021/bk-2014-1160.ch003
CrossRef Full Text | Google Scholar
Дженсен Х.С., Нильсен О.И., Кох М.С. и Де Висенте И. (2009). Высвобождение фосфора с растворением карбонатов в сочетании с окислением сульфидов в отложениях морских водорослей залива Флорида. Лимнол. океаногр. 54, 1753–1764 гг. doi: 10.4319/lo.2009.54.5.1753
CrossRef Полный текст | Google Scholar
Джин, Дж., и Циммерман, А. Р. (2010). Абиотические взаимодействия природного растворенного органического вещества и карбонатных водоносных пород. Заяв. Геохим. 25, 472–484. doi: 10.1016/j.apgeochem.2009.12.012
CrossRef Full Text | Google Scholar
Кеннеди Х., Беггинс Дж., Дуарте К.М., Фуркуриан Дж.В., Холмер М., Марба Н. и др. (2010). Отложения водорослей как глобальный поглотитель углерода: изотопные ограничения. Глоб. Биогеохим. цикл. 24, 1–8. doi: 10.1029/2010GB003848
CrossRef Полный текст | Google Scholar
Кох М. С., Бенц Р.Е. и Рудник Д.Т. (2001). Залежи твердофазного фосфора в высокоорганических карбонатных отложениях на северо-востоке Флоридского залива. Эстуар. Побережье. Шельф науч. 52, 279–291. doi: 10.1006/ecss.2000.0751
С., Бенц Р.Е. и Рудник Д.Т. (2001). Залежи твердофазного фосфора в высокоорганических карбонатных отложениях на северо-востоке Флоридского залива. Эстуар. Побережье. Шельф науч. 52, 279–291. doi: 10.1006/ecss.2000.0751
CrossRef Full Text | Google Scholar
Ку, Т.К.В., Уолтер, Л.М., Коулман, М.Л., Блейк, Р.Э., и Мартини, А.М. (1999). Связь между рециркуляцией серы и синдепозиционным растворением карбонатов: данные по изотопному составу кислорода и серы сульфата поровой воды, Платформа Южная Флорида, США Geochim. Космохим. Acta 63, 2529–2546. doi: 10.1016/S0016-7037(99)00115-5
Полнотекстовая перекрестная ссылка | Google Scholar
Ли, К.С., и Дантон, К.Х. (2000). Суточные изменения концентраций сульфидов в поровой воде в слоях водорослей Thalassia testudinum: влияние водорослей на динамику сульфидов. Дж. Экспл. Мар биол. Экол. 255, 201–214. doi: 10.1016/S0022-0981(00)00300-2
CrossRef Полный текст | Google Scholar
Liu, S. , Zhu, Y., Liu, L., He, Z., Giesy, J.P., Bai, Y., et al. (2018). Катион-индуцированная коагуляция растворенного органического вещества, полученного из водных растений: исследование с помощью EEM-PARAFAC и FT-IR-спектроскопии. Окружающая среда. Загрязн. 234, 726–734. doi: 10.1016/j.envpol.2017.11.076
, Zhu, Y., Liu, L., He, Z., Giesy, J.P., Bai, Y., et al. (2018). Катион-индуцированная коагуляция растворенного органического вещества, полученного из водных растений: исследование с помощью EEM-PARAFAC и FT-IR-спектроскопии. Окружающая среда. Загрязн. 234, 726–734. doi: 10.1016/j.envpol.2017.11.076
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Лонг, М. Х., Макглатери, К. Дж., Зиман, Дж. К., Берг, П., и Лонг, Х. (2008). Роль экссудатов органических кислот в высвобождении фосфорно-карбонатных отложений. Лимнол.Океаногр. 53, 2616–2626. doi: 10.4319/lo.2008.53.6.2616
CrossRef Full Text | Google Scholar
Махер, Д. Т., и Эйр, Б. Д. (2010). Бентические потоки растворенного органического углерода в трех умеренных эстуариях Австралии: последствия для глобальных оценок бентических потоков DOC. Дж. Геофиз. Рез. 115:G04039. doi: 10.1029/2010JG001433
Полный текст CrossRef | Google Scholar
Майе, Н., Бойер, Дж. Н., Ян, К. и Яффе, Р. (2006). Пространственная, геоморфологическая и сезонная изменчивость РОВ в эстуариях Флоридского побережья Эверглейдс. Hydrobiologia 569, 135–150. doi: 10.1007/s10750-006-0128-x
Н., Ян, К. и Яффе, Р. (2006). Пространственная, геоморфологическая и сезонная изменчивость РОВ в эстуариях Флоридского побережья Эверглейдс. Hydrobiologia 569, 135–150. doi: 10.1007/s10750-006-0128-x
CrossRef Полный текст | Google Scholar
Майе Н., Ямасита Ю., Кори Р. М., Бойер Дж. Н. и Джаффе Р. (2012). Применение флуоресцентного мониторинга матрицы эмиссии возбуждения для оценки пространственных и сезонных факторов состава растворенного органического вещества: источники и контроль физических возмущений. Заяв. Геохим. 27, 917–929. doi: 10.1016/j.apgeochem.2011.12.021
CrossRef Полный текст | Google Scholar
Мазарраса И., Марба Н., Лавлок С. Э., Серрано О., Лавери П. С., Фуркуриан Дж. В. и др. (2015). Луга с водорослями как глобально значимый карбонатный резервуар. Биогеонауки 12, 4993–5003. doi: 10.5194/bg-12-4993-2015
CrossRef Полный текст | Google Scholar
Макнайт Д.М., Бойер Э.В., Вестерхофф П.К., Доран П. Т., Кульбе Т. и Андерсен Д.Т. (2001). Спектрофлуорометрическая характеристика растворенного органического вещества для определения исходного органического вещества и ароматичности. Лимнол. океаногр. 46, 38–48. doi: 10.4319/lo.2001.46.1.0038
Т., Кульбе Т. и Андерсен Д.Т. (2001). Спектрофлуорометрическая характеристика растворенного органического вещества для определения исходного органического вещества и ароматичности. Лимнол. океаногр. 46, 38–48. doi: 10.4319/lo.2001.46.1.0038
Полный текст CrossRef | Google Scholar
Мюллер П. Дж. и Зюсс Э. (1977). Взаимодействие органических соединений с карбонатом кальция-III. Аминокислотный состав сорбированных слоев. Геохим. Космохим. Acta 41, 941–949. doi: 10.1016/0016-7037(77)
-3CrossRef Full Text | Google Scholar
Мерфи, К. Р., Стедмон, К. А., Гребер, Д., и Бро, Р. (2013). Флуоресцентная спектроскопия и многоходовые методы. ПАРАФАК. Аналитический. Методы 5, 6557–6566. doi: 10.1039/c3ay41160e
CrossRef Полный текст | Google Scholar
Мерфи, К. Р., Стедмон, К. А., Вениг, П., и Бро, Р. (2014). OpenFluor — онлайн-библиотека спектров автофлуоресценции органических соединений в окружающей среде. Аналитик. Методы 6, 658–661. doi: 10.1039/C3AY41935E
doi: 10.1039/C3AY41935E
CrossRef Полный текст | Google Scholar
Парланти, Э., Вёрц, К., Жоффруа, Л., и Ламотт, М. (2000). Флуоресцентная спектроскопия растворенного органического вещества как инструмент оценки биологической активности в прибрежной зоне, подверженной антропогенному воздействию. Орган. Геохим. 31, 1765–1781. doi: 10.1016/S0146-6380(00)00124-8
CrossRef Full Text | Google Scholar
Пулин, Б. А., Райан, Дж. Н., и Айкен, Г. Р. (2014). Влияние железа на оптические свойства растворенного органического вещества. Окружающая среда. науч. Технол. 48, 10098–10106. doi: 10.1021/es502670r
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Серрано О., Розайми М., Лавери П. С. и Смерник Р. Дж. (2020). Идеи органической химии для исключительного накопления углерода в почве водорослей Posidonia australis. Эстуар. Побережье. Шельф науч. 237:106662. doi: 10.1016/j.ecss.2020.106662
CrossRef Полный текст | Google Scholar
Зюсс, Э. (1970). Взаимодействие органических соединений с карбонатом кальция-I. Ассоциативные явления и геохимические последствия. Геохим. Космохим. Acta 34, 157–168. doi: 10.1016/0016-7037(70) -7
(1970). Взаимодействие органических соединений с карбонатом кальция-I. Ассоциативные явления и геохимические последствия. Геохим. Космохим. Acta 34, 157–168. doi: 10.1016/0016-7037(70) -7
CrossRef Full Text | Google Scholar
Ван Дам, Б. Р., Лопес, К., Осберн, К. Л., и Фуркуриан, Дж. В. (2019). Чистая гетеротрофность и растворение карбонатов на двух субтропических лугах из водорослей. Биогеонауки 16, 4411–4428. doi: 10.5194/bg-16-4411-2019
CrossRef Полный текст | Google Scholar
Вагнер С., Яффе Р., Коули К., Диттмар Т. и Стаббинс А. (2015). Взаимосвязь между молекулярными и оптическими свойствами растворенного органического вещества в Эверглейдс во Флориде, модельной системе прибрежных водно-болотных угодий. Перед. хим. 3:66. doi: 10.3389/fchem.2015.00066
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Уолтер Л. М., Бишоф С. А., Паттерсон В. П. и Лайонс Т. В. (1993). Растворение и перекристаллизация в современных шельфовых карбонатах: данные поровой воды и химии твердой фазы. Философ. Транс. 344, 27–36. doi: 10.1098/rsta.1993.0072
Философ. Транс. 344, 27–36. doi: 10.1098/rsta.1993.0072
CrossRef Full Text | Google Scholar
Weishaar, J.L., Aiken, G.R., Bergamaschi, B.A., Fram, M.S., Fujii, R., and Mopper, K. (2003). Оценка удельного поглощения ультрафиолетового излучения как показателя химического состава и реакционной способности растворенного органического углерода. Окружающая среда. науч. Технол. 37, 4702–4708. doi: 10.1021/es030360x
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Wickland, K.P., Neff, JC, and Aiken, G.R. (2007). Растворенный органический углерод в бореальных лесах Аляски: источники, химические характеристики и биоразлагаемость. Экосистемы 10, 13:23–13:40. doi: 10.1007/s10021-007-9101-4
CrossRef Полный текст | Google Scholar
Сюй Ю., Мид Р. Н. и Джаффе Р. (2006). Оценка источников и распределения осадочного органического вещества в заливе Флорида на основе молекулярных маркеров. Hydrobiologia 569, 179–192. doi: 10.1007/s10750-006-0131-2
doi: 10.1007/s10750-006-0131-2
CrossRef Full Text | Google Scholar
Я. К., Андерсон В. и Яффе Р. (2015). Оценка динамики растворенного органического вещества и силы источника в субтропическом эстуарии: применение стабильных изотопов углерода и оптических свойств. Континент. Полка Рез. 92, 98–107. doi: 10.1016/j.csr.2014.10.005
Полный текст CrossRef | Google Scholar
Yamashita, Y., and Jaffé, R. (2008). Характеристика взаимодействий между микроэлементами и растворенными органическими веществами с использованием матрицы возбуждения-эмиссии и параллельного факторного анализа. Окружающая среда. науч. Технол. 42, 7374–7379. doi: 10.1021/es801357h
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Йейтс К.К. и Галлей Р.Б. (2006). Суточные колебания скорости кальцификации и растворения карбонатных отложений в заливе Флорида. Эстуар. Побережье. 29, 24–39. doi: 10.1007/BF02784696
Полный текст CrossRef | Google Scholar
Йейтс К.

 4
4 ..
..
 Как известно, обычная СЛАУ может быть представлена в матричном виде как АХ=В, где А — матрица коэффициентов уравнений размера m x n, X — искомый вектор неизвестных с n компонентами и В — вектор свободных членов, также содержащий n компонент. Решением системы называется совокупность чисел , при подстановке которых все уравнения системы обращаются в тождества.
Как известно, обычная СЛАУ может быть представлена в матричном виде как АХ=В, где А — матрица коэффициентов уравнений размера m x n, X — искомый вектор неизвестных с n компонентами и В — вектор свободных членов, также содержащий n компонент. Решением системы называется совокупность чисел , при подстановке которых все уравнения системы обращаются в тождества.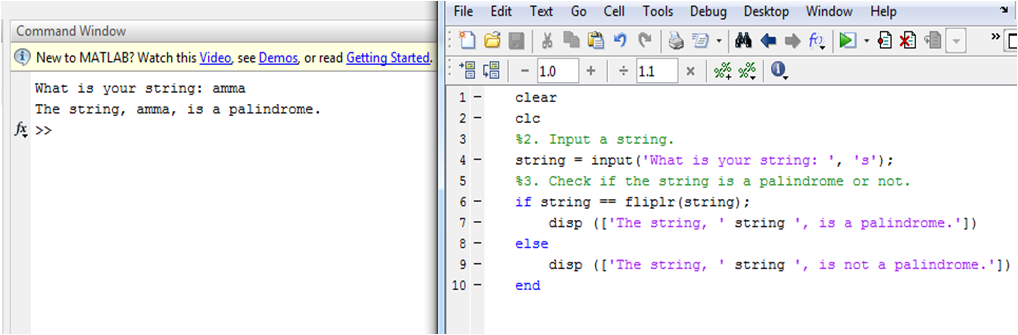
 Значение каждого из неизвестных в этом случае равно дроби, знаменателем которой является определитель системы, а числитель равен определителю системы, в которой вместо столбца коэффициентов при неизвестном располагается столбец свободных членов.
Значение каждого из неизвестных в этом случае равно дроби, знаменателем которой является определитель системы, а числитель равен определителю системы, в которой вместо столбца коэффициентов при неизвестном располагается столбец свободных членов. Систему из n уравнений сначала приводят к равносильной ей системе с треугольной матрицей коэффициентов (прямой ход). Затем выполняют обратный ход, вычисляя значения и последовательно подставляя их в уравнения для получения значений . Для уменьшения влияния ошибок округления на решение СЛАУ указанным методом применяют его модификацию – метод Гаусса с частичным выбором главного элемента.
Систему из n уравнений сначала приводят к равносильной ей системе с треугольной матрицей коэффициентов (прямой ход). Затем выполняют обратный ход, вычисляя значения и последовательно подставляя их в уравнения для получения значений . Для уменьшения влияния ошибок округления на решение СЛАУ указанным методом применяют его модификацию – метод Гаусса с частичным выбором главного элемента. При вызове функции lsqr(A, B) итерации производятся либо до сходимости к решению, либо до появления ошибки, либо до достижения максимального числа итераций (по умолчанию равного min(20, m, n), где m – число уравнений, n – число неизвестных). Сходимость достигается, когда отношение вторых норм векторов norm(B-Ax)/norm(B) меньше или равно погрешности метода tol (по умолчанию 1е-6). Функция lsqr(A, B, tol) — возвращает решение с заданной погрешностью tol.
При вызове функции lsqr(A, B) итерации производятся либо до сходимости к решению, либо до появления ошибки, либо до достижения максимального числа итераций (по умолчанию равного min(20, m, n), где m – число уравнений, n – число неизвестных). Сходимость достигается, когда отношение вторых норм векторов norm(B-Ax)/norm(B) меньше или равно погрешности метода tol (по умолчанию 1е-6). Функция lsqr(A, B, tol) — возвращает решение с заданной погрешностью tol. Описание этих функций можно посмотреть с помощью команды help имя_функции. Функция mldivide() или оператор «\» самостоятельно выбирают лучший метод решения заданной системы уравнений (см. рис. 5.6).
Описание этих функций можно посмотреть с помощью команды help имя_функции. Функция mldivide() или оператор «\» самостоятельно выбирают лучший метод решения заданной системы уравнений (см. рис. 5.6). ..
..