|
1.Понятие комплексного числа. 2.Тригонометрическая форма комплексного числа.
|
|||||||||||||||||||||||||||||
| 19 20 21 22 23 24 25 26 27 | |||||||||||||||||||||||||||||
1.Понятие комплексного числа. Выражение вида z = x + iy называется комплексным числом. Число х называется действительной частью комплексного числа z и обозначается Re(z), число y — мнимой частью комплексного числа z и обозначается Im(z). Числа z = x + iy и z1 = x — iy называются сопряженными. Если равны действительные и мнимые части комплексного числа, то они называются равными т.е. z1 = z2 или x1 + iy1 = x2 + iy2. Операции над комплексными числами. |
|||||||||||||||||||||||||||||
1. Сумма (разность) комплексных чисел. z1+z2 = x1+x2+i(y1+y2). 2. Произведение комплексных чисел. z1z2 = (x1x2 — y1y2) + i(x1y2 + x2y1). отсюда i² = (0 + i1)(0 + i1) = (0 -1) + i(0 + 0) = -1. 3. Деление двух комплексных чисел. |
|||||||||||||||||||||||||||||
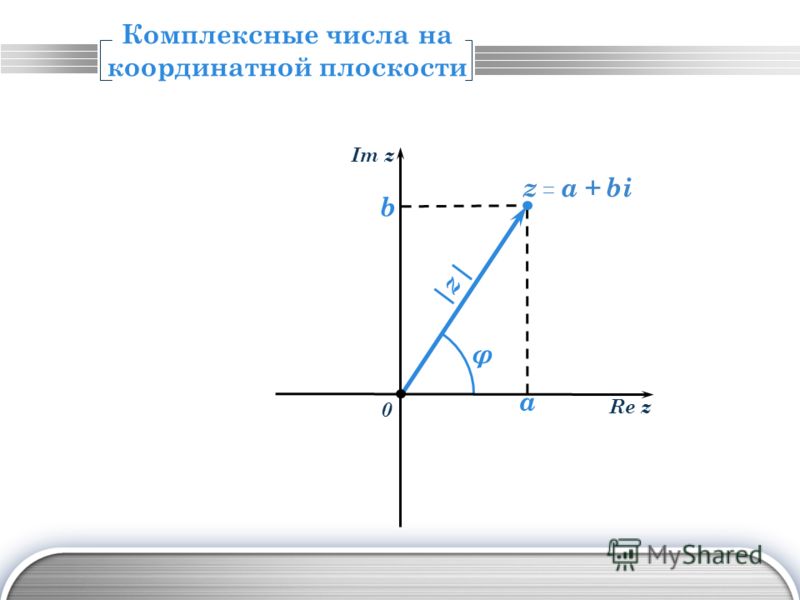
Рассмотрим на плоскости декартову прямоугольную систему координат Oxy. Каждому комплексному числу Z = x + iy ставится в соответствие единственная точка плоскости z(xy). Плоскость Oxy, где каждая точка отождествлена с комплексным числом, называется комплексной. Координатные оси Ox и Oy, на которых расположены действительные и мнимые числа, называются действительной и мнимой осями. |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
2.Тригонометрическая форма комплексного числа.До любой точки комплексной плоскости из начала координат можно провести вектор определенной длины r. Число r называется модулем комплексного числа z и обозначается |z|. |
|||||||||||||||||||||||||||||
Угол ϕ, образованный между вектором и осью Ox, называется аргументом комплексного числа z и обозначается Arg z. ϕ = Arg z = arg z + 2kπ где 0≤ argz < 2π Таким образом: x = r cos ϕ, y = r sin ϕ. Следовательно, комплексное число z = x + iy можно представить как: |
|||||||||||||||||||||||||||||
Представление комплексного числа в такой форме, где r = |z| ≥ 0, ϕ = Arg z, называется тригонометрической формой комплексного числа. |
|||||||||||||||||||||||||||||
| Пример. | |||||||||||||||||||||||||||||
| 19 20 21 22 23 24 25 26 27 | |||||||||||||||||||||||||||||
Из значения ϕ = Arg z выделяется главное значение arg z, которое кратно 2π.Знакомство с комплексными числами на примерах
Тема «Комплексные числа» зачастую вызывает затруднения у учащихся, а ведь на самом деле в них нет ничего страшного, как может показаться на первый взгляд.
Итак, сейчас мы разберем и рассмотрим на простых примерах, что такое комплексное число, как обозначается и из чего состоит. Выражение z = a + bi называется комплексным числом. Это единое число, а не сложение.
Пример 1: z = 6 + 4i
Из чего состоит комплексное число?
Комплексное число имеет действительную и мнимую часть в своем составе.
Число a называется действительной частью комплексного числа и обозначается a = Re (z). А вот то, что стоит вместе с буквой i — т.е. число b называется коэффициентом мнимой части комплексного числа и обозначается b = Im (z). Вместе bi образуют мнимую часть комплексного числа.
Нетрудно догадаться и легко запомнить, что сокращение «Re» происходит от слова «Real» — реальная, действительная часть. Соответственно, «Im» является сокращением слова «Imaginary» — мнимая, воображаемая часть.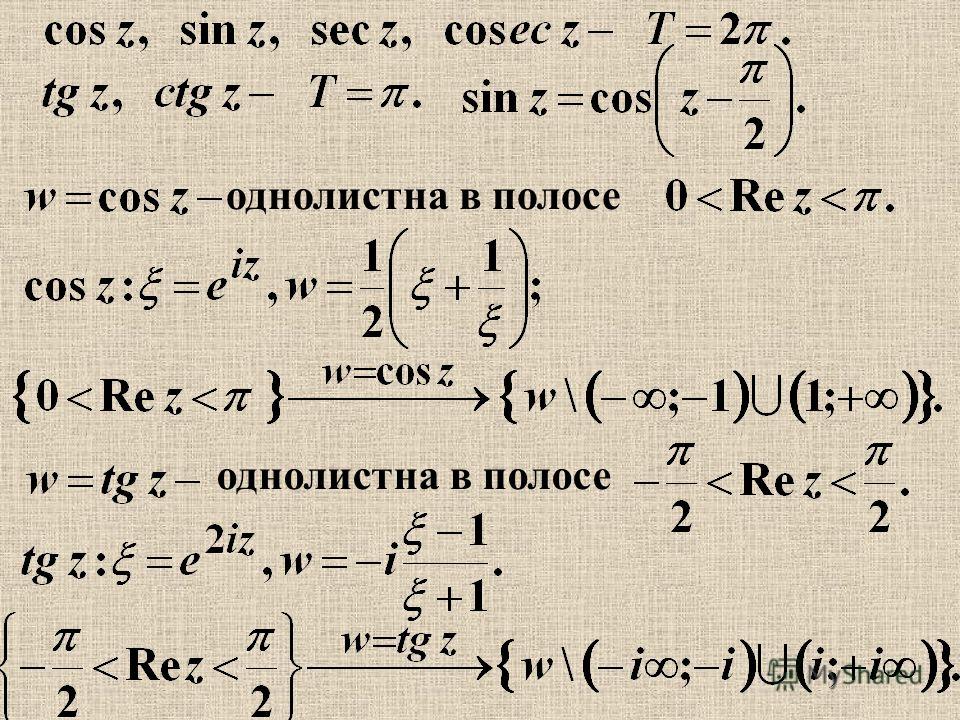
Пример 2: z = 0,5 + 9i. Здесь действительная часть a = Re (z) = 0,5, а мнимая часть b = Im (z) = 9i
Пример 3: z = -5 + 19i. Здесь действительная часть a = Re (z) = -5, а мнимая часть b = Im (z) = 19.
Чисто мнимое комплексное число
Комплексное число, в котором нет действительной части, т.е. Re (z) = 0, называется чисто мнимым.
Пример 4: z = 2i. Действительная часть отсутствует, a = Re (z) = 0, а мнимая часть b = Im (z) = 2.
Пример 5. z = -8i. Здесь мнимая часть b = Im (z) = -8, действительная часть a = Re (z) = 0.
Сопряженные комплексные числа
Комплексно-сопряженное число обозначается «зэт» с чертой и используется, к примеру, для нахождения частного двух комплексных чисел, проще говоря — для реализации деления чисел.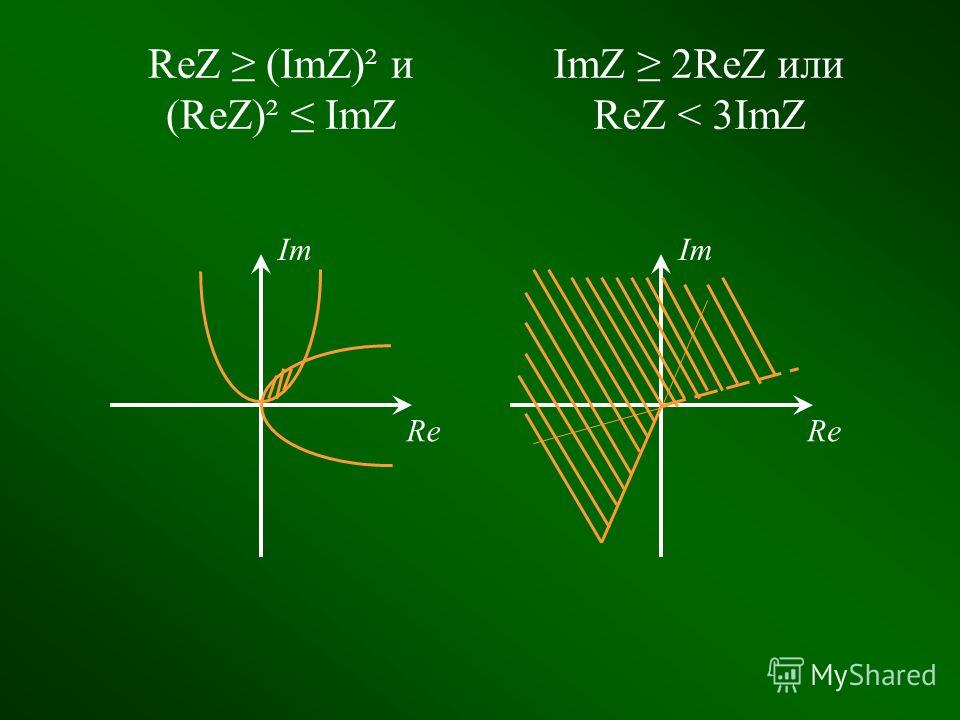
Те, кто сейчас задумался, вам сюда — читать про деление комплексных чисел.
Числа называются комплексно-сопряженными, имеют одинаковые действительные части и различаются лишь знаком мнимых частей. Рассмотрим пример:
Пример 6. Комплексно сопряженным к числу z = 7 + 13i является число .
Мнимая единица комплексного числа
И наконец поговорим про букву i. Та самая буква, которая образует в комплексном числе мнимую составляющую. Даже если перед нами выражение z = 5, это просто значит, что мнимая часть данного числа равна нулю, а действительная равна пяти.
Величина i называется мнимой единицей.
Мнимая единица пригодится при решении квадратных уравнений в случае, когда дискриминант меньше нуля. Мы привыкли считать, что если он отрицательный, решения нет, корней нет. Это не совсем корректно. Корни существуют, просто они комплексные. Но об этом позже.
А теперь, переходим к следующей статье по изучению комплексных чисел, узнаем же, как посчитать произведение комплексных чисел.
Комплексные числа
Комплексный номер
Комплексное число представляет собой комбинацию
Действительного числа и Воображаемого числа
Реальные числа — это такие числа, как:
| 1 | 12,38 | −0,8625 | 3/4 | √2 | 1998 |
Почти любое число, которое вы можете придумать, является действительным числом!
Мнимые числа, когда в квадрате дают отрицательный результат .
Обычно этого не происходит, потому что:
- когда мы возводим в квадрат положительное число, мы получаем положительный результат, а
- , когда мы возводим в квадрат отрицательное число, мы также получаем положительный результат (поскольку отрицательное число, умноженное на отрицательное, дает положительный результат), например, −2 × −2 = +4
Но представьте, что такие числа существуют, потому что они нам нужны.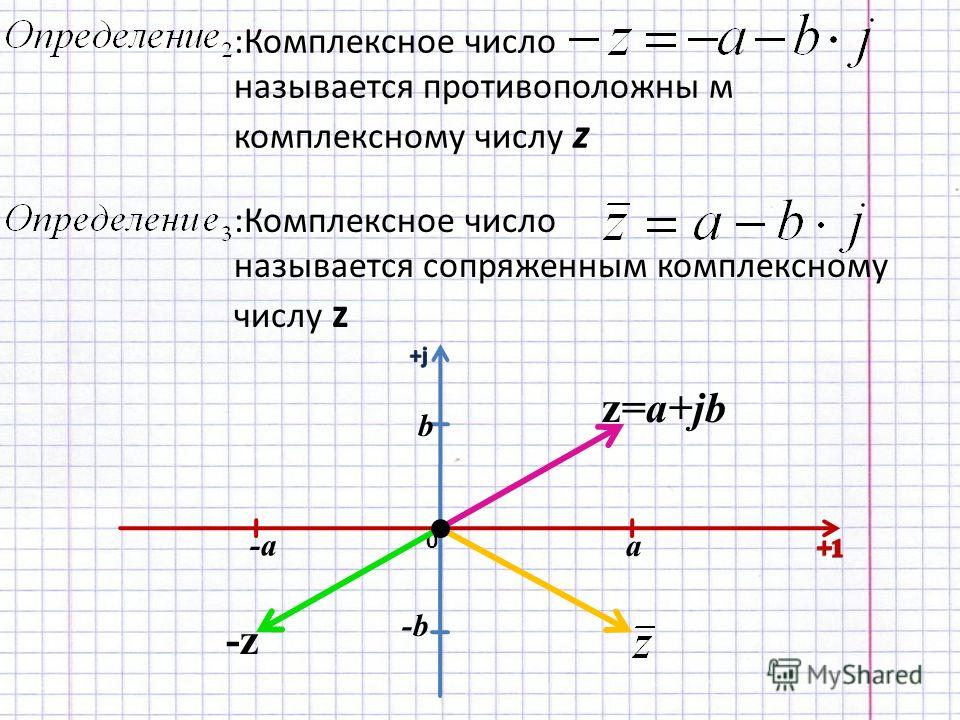
Поговорим еще о мнимых числах…
«Единичное» мнимое число (например, 1 для действительных чисел) равно i, которое является квадратным корнем из −1
Потому что, возведя i в квадрат, мы получим −1
i 2 = −1
Примеры мнимых чисел Номера:
| 3i | 1.04i | −2,8i | 3i/4 | (√2)я | 1998i |
И мы держим здесь маленькую букву «i», чтобы напомнить себе, что нам нужно умножить на √−1
Комплексные числа
Когда мы объединяем действительное число и мнимое число, мы получаем комплексное число :
.Примеры:
| 1 + я | 39 + 3i | 0,8 − 2,2i | −2 + πi | √2 + i/2 |
Может ли число быть комбинацией двух чисел?
Можем ли мы составить число из двух других чисел? Мы можем точно!
Мы постоянно делаем это с дробями.
Дробь 3 / 8 — это число, состоящее из 3 и 8. Мы знаем, что это означает «3 из 8 равных частей».
Комплексное число — это всего лишь два числа, сложенные вместе (действительное и мнимое число).
Любая часть может быть равна нулю
Итак, у комплексного числа есть действительная и мнимая части.
Но любая часть может быть 0 , поэтому все действительные числа и мнимые числа также являются комплексными числами.
| Комплексный номер | Реальная часть | Воображаемая часть | |
|---|---|---|---|
| 3 + 2i | 3 | 2 | |
| 5 | 5 | 0 | Чисто настоящий |
| −6i | 0 | −6 | Чисто воображаемый |
Сложно?
Комплекс , а не означает сложный.
Это означает, что два типа чисел, действительные и мнимые, вместе образуют комплекс , точно так же, как комплекс зданий (здания, соединенные вместе).
Визуальное объяснение
Вы знаете, как идет числовая линия влево-вправо ?
Хорошо, пусть мнимые числа идут вверх-вниз :
И получаем Сложный Самолет
Комплексное число теперь может отображаться в виде точки:
Комплекс № 3+4 i
Добавление
Чтобы сложить два комплексных числа, складываем каждую часть отдельно:
(а+б я ) + (с+г я ) = (а+с) + (б+г) я
Пример: добавьте комплексные числа
3 + 2 i и 1 + 7 i- добавьте действительные числа и
- добавить мнимые числа:
(3 + 2i) + (1 + 7i)
= 3 + 1 + (2 + 7) i
= 4 + 9i
Попробуем еще:
Пример: добавьте комплексные числа
3 + 5 i и 4 − 3 i (3 + 5 I ) + (4 — 3 I )
= 3 + 4 + (5 — 3) I
= 7 + 2 I
.
Умножение
Чтобы умножить комплексные числа:
Каждая часть первого комплексного числа умножается на
каждая часть второго комплексного числа
Просто используйте «FOIL», что означает » F первоначальных, O маточных, I внутренних, L астровых» (подробнее см. Биномиальное умножение):
| |||||||||||||||||||||||
(A + B I ) (C + D I ) = AC + AD I + BC I + BD I 2 9006 I 2 I 2Вот так: Пример: (3 + 2i)(1 + 7i)(3 + 2i)(1 + 7i) = 3×1 + 3×7i + 2i×1+ 2i×7i = 3 + 21i + 2i + 14i 2 = 3 + 21i + 2i − 14 (поскольку i 2 = −1) = −11 + 23i А это: Пример: (1 + i)2(1 + i)(1 + i)= 1×1 + 1×i + 1×i + i 2 = 1 + 2i − 1 (потому что i 2 = −1) = 0 + 2i Но есть более быстрый способ!Используйте это правило: (a+b i )(c+d i ) = (ac−bd) + (ad+bc) i Пример: (3 + 2i)(1 + 7i) = (3×1 − 2×7) + (3×7 + 2×1)i = −11 + 23i Почему это правило работает?Это просто метод «ФОЛЬГА» после небольшой работы: (a+b i )(c+d i ) =ac + ad i + bc i + bd i 2 метод FOIL | i i|||||||||||||||||||||||
22 41 i 
19999999999910 . I + 15 I 2 16 + 25 Прекрасное множество Мандельброта (на фото) основано на комплексных числах. Это график того, что происходит, когда мы берем простое уравнение z 2 + c (оба комплексных числа) и возвращаем результат обратно в z снова и снова. Цвет показывает, как быстро растет z 2 + c , а черный означает, что он остается в определенном диапазоне. | |
Вот изображение, полученное путем увеличения множества Мандельброта | |
| А вот центр предыдущего увеличен еще больше: |
440, 1070, 273, 1071, 1072, 443, 3991, 271, 3992, 3993
Комплексное число — определение, формула, свойства, примеры
Комплексные числа помогают найти квадратный корень из отрицательных чисел. Концепция комплексных чисел была впервые упомянута в I веке греческим математиком Героем Александрийским, когда он пытался найти квадратный корень из отрицательного числа. Но он просто изменил отрицательное значение на положительное и просто взял числовой корень. Кроме того, реальная идентичность комплексного числа была определена в 16 веке итальянским математиком Джероламо Кардано в процессе нахождения отрицательных корней кубических и квадратичных полиномиальных выражений.
Комплексные числа находят применение во многих научных исследованиях, обработке сигналов, электромагнетизме, гидродинамике, квантовой механике и анализе вибрации. Здесь мы можем понять определение, терминологию, визуализацию комплексных чисел, свойства и операции с комплексными числами.
| 1. | Что такое комплексные числа? |
| 2. | График комплексных чисел |
| 3. | Свойства комплексных чисел |
| 4. | Операции над комплексными числами |
| 5. | Алгебраические тождества комплексных чисел |
| 6. | Решенные примеры |
| 7. | Практические вопросы |
| 8. | Часто задаваемые вопросы о комплексных числах |
Что такое комплексные числа?
Комплексное число – это сумма действительного числа и мнимого числа.
Комплексное число имеет вид a + ib и обычно обозначается буквой z. Здесь и a, и b – действительные числа. Величина «а» называется действительной частью, которая обозначается Re(z), а «b» называется мнимой частью Im(z). Также ib называют мнимым числом.
Примерами комплексных чисел являются \(2+3i, -2-5i, \,\,\dfrac 1 2 + i\dfrac 3 2\) и т. д.
Степень i
Алфавит i называется йотой и полезен для представления мнимой части комплексного числа. Кроме того, йота (i) очень полезна для нахождения квадратного корня из отрицательных чисел. У нас есть значение i 2 = -1, и оно используется для нахождения значения √-4 = √i 2 4 = + 2i Значение i 2 = -1 является основным аспектом комплексного числа.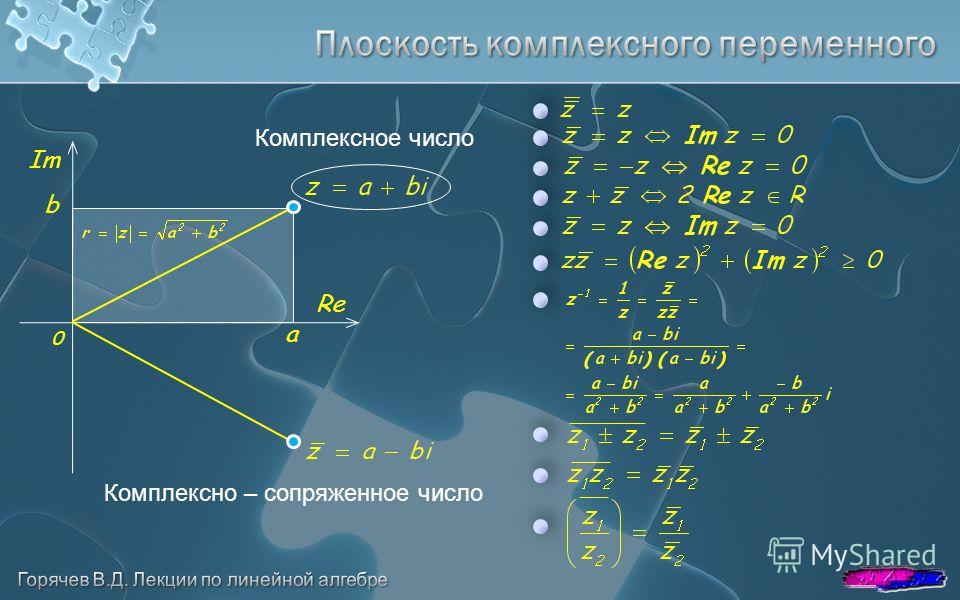
Давайте попробуем понять больше о возрастающих силах i.
- я = √-1
- i 2 = -1
- i 3 = i.i 2 = i(-1) = -i
- i 4 = (i 2 ) 2 = (-1) 2 = 1
- i 4n = 1
- я 4n + 1 = я
- i 4n + 2 = -1
- i 4n + 3 = -i
График комплексных чисел
Комплексное число состоит из действительной и мнимой частей, которые можно рассматривать как упорядоченную пару (Re(z), Im(z)) и представлять в виде точек координат на евклидовой плоскости. Евклидова плоскость применительно к комплексным числам называется комплексной плоскостью или Плоскостью Аргана, названной в честь Жана-Роберта Аргана. Комплексное число z = a + ib представлено действительной частью — a относительно оси x и мнимой частью -ib относительно оси y. Давайте попробуем понять два важных термина, относящихся к представлению комплексных чисел на аргановой плоскости.
{-1}\frac{b}{a}\). 9{-1}\frac{b}{a}\)).
Свойства комплексного номера
Следующие свойства комплексных чисел помогают лучше понять комплексные числа, а также выполнять различные арифметические операции над комплексными числами.
Сопряжение комплексного числа
Сопряжение комплексного числа образуется путем взятия той же действительной части комплексного числа и замены мнимой части комплексного числа на ее аддитивную обратную. Если сумма и произведение двух комплексных чисел являются действительными числами, то они называются сопряженными комплексными числами. Для комплексного числа z = a + ib его сопряженным является \(\bar z\) = a — ib.
Сумма комплексного числа и его сопряженного равна \(z + \bar z\) = (a + ib) + (a — ib) = 2a, а произведение этих комплексных чисел \(z.\bar z \) = (a + ib) × (a — ib) = a 2 + b 2 .
Обратная величина комплексного числа
Обратная величина комплексных чисел полезна в процессе деления одного комплексного числа на другое комплексное число.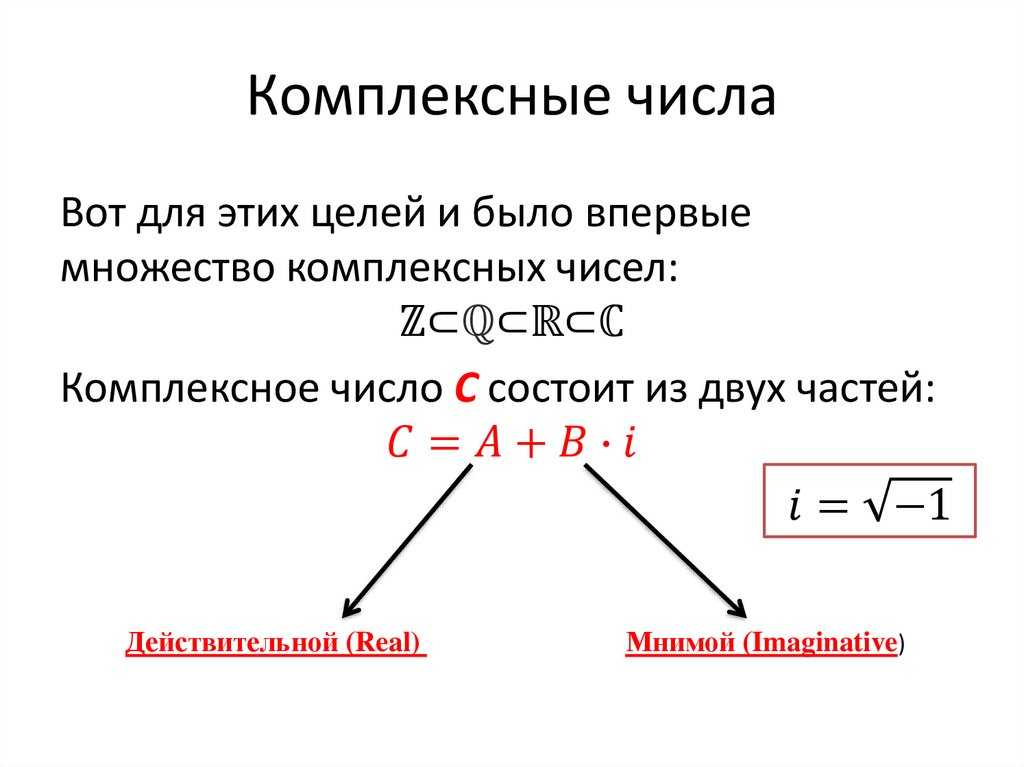
{-1}\).
Равенство комплексных чисел
Равенство комплексных чисел аналогично равенству действительных чисел. Два комплексных числа \(z_1 = a_1 + ib_1\) и \(z_2 = a_2 + ib_2 \) называются равными, если относительная часть обоих комплексных чисел равна \(a_1 = a_2\), и мнимая части обоих комплексных чисел равны \(b_1 = b_2 \). Кроме того, два комплексных числа в полярной форме равны тогда и только тогда, когда они имеют одинаковую величину, а их аргумент (угол) отличается на целое кратное 2π.
Упорядочивание комплексных чисел
Упорядочивание комплексных чисел невозможно. Действительные числа и другие связанные системы счисления можно упорядочить, но нельзя упорядочить комплексные числа. Комплексные числа не имеют структуры упорядоченного поля, и нет упорядоченности комплексных чисел, совместимой со сложением и умножением. Также нетривиальная сумма квадратов в упорядоченном поле есть число \(\neq 0\), а в комплексном числе нетривиальная сумма квадратов равна i 2 + 1 2 = 0.
Комплексные числа можно измерить и представить на двумерной арграндовой плоскости по их величине, которая является расстоянием от начала координат.
Формула Эйлера: В соответствии с формулой Эйлера для любого действительного значения θ мы имеем e iθ = Cosθ + iSinθ, и оно представляет комплексное число в координатной плоскости, где Cosθ – действительная часть, представленная относительно ось x, Sinθ – мнимая часть, представленная относительно оси y, θ – угол, образованный по отношению к оси x и воображаемой линии, соединяющей начало координат и комплексное число. Согласно формуле Эйлера и функциональному представлению x и y имеем e x + iy = e x (уютно + isiny) = e x уютно + т.е. x сине. Это разлагает экспоненциальную функцию на ее действительную и мнимую части.
Операции над комплексными числами
Различные операции сложения, вычитания, умножения, деления натуральных чисел можно выполнять и для комплексных чисел.
Детали различных арифметических операций с комплексными числами заключаются в следующем.
Сложение комплексных чисел
Сложение комплексных чисел аналогично сложению натуральных чисел. Здесь в комплексных числах действительная часть добавляется к действительной части, а мнимая часть добавляется к мнимой части. Для двух комплексных чисел вида \(z_1 = a + id\) и \(z_2 = c + id\) сумма комплексных чисел \(z_1 + z_2 = (a + c) + i(b + d) \). Комплексные числа следуют всем следующим свойствам сложения.
- Закон замыкания: Сумма двух комплексных чисел также является комплексным числом. Для двух комплексных чисел \(z_1\) и \(z_2\) сумма \(z_1 + z_2\) также является комплексным числом.
- Коммутативный закон: Для двух комплексных чисел \(z_1\), \(z_2\) имеем \(z_1 + z_2 = z_2 + z_1\).
- Ассоциативный закон: Для данных трех комплексных чисел \(z_1, z_2, z_3\) имеем \(z_1 + (z_2 + z_3) = (z_1 + z_2)+z_3 \).
2 = -1\). Для двух комплексных чисел \(z_1\) = a + ib, \(z_2\) = c + id произведение равно \(z_1.z_2\) = (ca — bd) + i(ad + bc).Умножение комплексных чисел в полярной форме немного отличается от упомянутой выше формы умножения. Здесь абсолютные значения двух комплексных чисел перемножаются, а их аргументы складываются для получения произведения комплексных чисел. Для комплексных чисел \(z_1 = r_1(Cos\theta_1 + iSin\theta_1)\) и z 2 = \(z_2 = r_1(Cos\theta_2 + iSin\theta_2)\) произведение комплексные числа \(z_1.z_2 = r_1.r_2(Cos(\theta_1 + \theta_2) + iSin(\theta_1 + \theta_2))\). 92 + 2z_1z_2 +2z_2z_3 +2z_3z_1\)
2 = -1\). Для двух комплексных чисел \(z_1\) = a + ib, \(z_2\) = c + id произведение равно \(z_1.z_2\) = (ca — bd) + i(ad + bc).Связанные темы:
- Комплексное сопряжение
- Калькулятор комплексных чисел
- Тригонометрия
- Координатная плоскость
- Координатная геометрия
Комплексные числа Советы и подсказки:
- Все действительные числа являются комплексными числами, но все комплексные числа не обязательно должны быть действительными числами.
- Все мнимые числа являются комплексными числами, но все комплексные числа не обязательно должны быть мнимыми числами. 9{2}-4(1)(1)}}{2(1)} \\[0,2 см]
&=\frac{-1 \pm \sqrt{-3}}{2}\\[0,2 см]
\text{Здесь } &\sqrt{-3} = \sqrt{-1} \times \sqrt{3} = i \sqrt{3}\\[0,2 см]
x&= \frac{-1 \pm i\sqrt{3}}{2}\\[0,2 см]
\end{align} \]Таким образом, корнями данного квадратного уравнения являются: \(\frac{-1}{2}+ i\frac{\sqrt{3}}{2};\,\,\ , \ frac{-1}{2}- i\frac{\sqrt{3}}{2}\)
Пример 2: Выразите сумму, разность, произведение и частное следующих комплексных чисел в виде комплексного числа.
\[\begin{align} z_1&=-2+i\\[0.2cm]z_2&= 1-2i \end{align} \]
Решение:
Сумма:
\[ \begin{ выровнять} z_1+z_2&= (-2+i)+(1-2i)\\[0,2 см] &=(-2+1)+ (i-2i)\\[0,2 см] &= -1-i \end{align}\]
Разница:
\[ \begin{align} z_1-z_2&= (-2+i)-(1-2i)\\[0,2 см] &=(-2-1) + (i+2i)\\[0,2 см] &= -3+3i \end{align}\]
Продукт:
\[ \begin{align} z_1\cdot z_2&= (-2+i)( 1-2i)\\[0,2см] &=-2+4i+i-2i^2\\[0,2см] &=-2+4i+i+2 \,\,\, [\потому что i^2 =-1]\\[0,2 см] &=5i \end{выравнивание}\] 92=-1]\\[0,2 см] &= \dfrac{-4-3i}{5}\\[0,2 см] &=- \dfrac{4}{5}- i \dfrac{3}{5 }\end{align}\]
Следовательно, имеем:
Сумма = -1 — i
Разница = -3 + 3i
Продукт = 5i
Деление = -4/5 — 3i/5
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о комплексных числах
Что такое комплексные числа в математике?
Комплексное число представляет собой комбинацию действительных и мнимых значений. Обозначается z = a + ib, где a, b — действительные числа, а i — мнимое число. i = \(\sqrt{-1}\) и никакое действительное значение не удовлетворяет уравнению i 2 = -1, поэтому I называется мнимым числом.
Для чего используются комплексные числа?
Комплексное число используется для простого нахождения квадратного корня из отрицательного числа. Здесь мы используем значение i 2 = -1 для представления отрицательного знака числа, что помогает легко найти квадратный корень. Здесь мы имеем √-4 = √i 2 4 = + 2i.
{-1}\frac{b}{a} \)).
Что такое действительные и комплексные числа?
Комплексные числа являются частью действительных чисел. Некоторые действительные числа с отрицательным знаком трудно вычислить, и мы представляем отрицательный знак с помощью йоты «i», и такое представление чисел вместе с «i» называется комплексным числом. Дополнительные комплексные числа полезны для нахождения квадратного корня из отрицательного числа, а также для нахождения отрицательных корней квадратного или полиномиального выражения.
Как делить комплексные числа? 92)}\).
Как строить графики комплексных чисел?
Комплексное число вида z = a + ib может быть представлено в плоскости арганда. Комплексное число z = a + ib может быть представлено в виде координат точки как (Re(z), Im(z)) = (a, ib). Здесь действительная часть представлена относительно оси x, а мнимая часть представлена относительно оси y.
Как преобразовать комплексные числа в полярную форму?
Комплексный номер можно легко преобразовать в полярную форму.