Размер матрицы 2 3: Размер матрицы. Что это такое?

Что важнее размер матрицы фотоаппарата или количество мегапикселей?

Физический размер матрицы фотоаппарата, мегапиксели и качество снимков

По мере развития цифровой фото и видеотехники число мегапикселей, которыми производители приманивают покупателей, становится все больше. Но мало кто знает, что на самом деле для получения качественных фотографий гораздо важнее не разрешение, а физический размер самой матрицы.

 

Давайте разберем понятие мегапиксели. Пиксель — это одна маленькая точка из миллиона других, из которых состоит изображение.

 

Эти точки разные по размеру. Применительно к цифровой матрице, каждый пиксель — это миниатюрный датчик, на который при фотосъемке попадает свет, затем он преобразуется в цифровой сигнал и в таком виде передается в компьютер фотоаппарата. Таких датчиков на матрице огромное количество. Чем больше размер самой матрицы, тем больше размер каждого пикселя и их общее количество. Поэтому зависимость между матрицей и качеством снимков – самая прямая.

 

Вроде бы логично было бы писать эту площадь в виде длины и ширины, и желательно в миллиметрах. Но поскольку почти все параметры цифровой техники пришли к нам из-за границы, принято указывать размер матрицы в так называемых обратных дюймах, т.е. дробью, где в числителе единица, а в знаменателе – дюймовый размер матрицы. Например: 1/3.2 , 1/2.7  и т.д.

Большинству покупателей эти цифры мало о чем говорят. 

Как правило, чем дешевле камера, тем меньше у нее физический размер матрицы и тем хуже качество сделанных ею фотографий.

Среди дорогих компактных камер иногда можно встретить модели с матрицей 2/3 , что обеспечивает неплохую детализацию снимков и достаточно высокую светочувствительность.

Матрицы 1/5 или 1/6 мы найдем в большинстве бюджетных зеркальных камер, это примерно половина кадра пленки 35 мм. Во многом именно за счет размера матрицы фотографии, сделанные зеркалкой, обычно выгодно отличаются от тех, которые сняты компактами.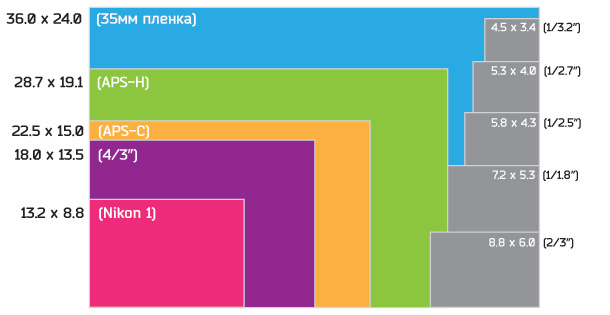

 

Есть еще полнокадровые матрицы (36х24 мм), которые по размеру соответствуют полному кадру 35 мм, и матрицы среднего формата (60х45 мм), которые больше этого стандартного кадра и применяются в дорогих зеркальных камерах.

 

Итак, на что же, собственно, влияет размер матрицы?

 

Первое – на размер и вес самой камеры. Фотоаппараты с небольшими матрицами компактны, их можно носить в кармане. 

Камеры с большими матрицами, например, средний формат, приходится таскать в специальных кофрах, а то и вовсе использовать только в студии.

 

Второе – на увеличение цифрового шума — или, как еще по старинке говорят, зерна — на ваших снимках. «Шумные» фотографии выглядят так, будто изображение разбито на множество заметных цветных точек. Вид у них неопрятный, грязноватый.

 

Появление шума обусловлено тем, что на большую по площади матрицу попадает больше света, чем на маленькую. В результате передаваемый ею полезный сигнал будет лучшего качества, а отсюда – и лучшая проработка деталей, и более качественная цветопередача, и большая яркость картинки.

 

Кроме того, датчики большой матрицы расположены дальше друг от друга и изоляция между ними лучше, поэтому меньше пробивающих эту изоляцию токов, которые создают помехи, ухудшающие качество фотографий.

 

Отсюда, кстати, следует, что большое разрешение (те самые большие мегапиксели) при маленьком размере матрицы – скорее вредно, чем полезно. 

 

Что будет, если на матрицу одного размера впихнуть 8 000 000 пикселей и 12 000 000? Во втором случае это приведет к уменьшению размера датчиков, ухудшению слоя изоляции между ними — и увеличению цифрового шума.

 

От разрешения матрицы в мегапикселях зависит то, какого размера снимки вы сможете напечатать без заметной потери качества. Разрешения 8 мегапикселей достаточно для печати фотографий формата А4 (альбомный лист). И при малом размере матрицы такое разрешение еще не приводит к заметному цифровому шуму.

 

Выбирая себе фотоаппарат, обязательно обращайте внимание на физический  размер матрицы, желательно чтобы он был максимально большим, насколько вы сможете себе позволить по финансам. От этого напрямую зависит качество сделанных фотографий, конечно если вы выберите зеркальную камеру, советую вам не покупать стандартный «китовый» объектив, который предлагают чаще всего в комплекте. Так как оптически он очень слабый и не надежный. 

 

Но будьте готовы, что зеркальная камера с хорошим объективом будет стоить дороже компактного фотоаппарата да и будет не совсем миниатюрной.

 

Так что смотрите сами, что для вас важнее. Любые вопросы по фототехнике вы можете смело задать нашим фотографам: 

+375-29-122-92-40 (Viber)

 

+375-29-122-92-40 (whatsApp)

 

E-mail: sales@sigma-foto. by

 

Skype: sigma-by

 

Пишите в чат фотографу!

← Выбор объектива для фотоаппарата при ночной съёмке  |  Выбор объектива для пейзажной съемки →

Физический размер матрицы фотокамеры

• Новости
• Фотография
• Фототехника
• Обзоры
• Фотословарь
• Это интересно!
• Каталог фототехники

В этой статье мы решили упорядочить и свести в таблицу размеры матрицы фотоаппарат для более лучшего понимания и определения матрицы фотоаппарата. Напомним, что матрица фотокамеры — это микросхема, состоящая из светочувствительных элементов — фотодиодов (пикселей). Она предназначена для преобразования спроецированного на неё оптического изображения в аналоговый электрический сигнал или в поток цифровых данных, который в последствии обрабатывается процессором фотокамеры и сохраняется в виде фотографии на карте памяти фотоаппарата.

То есть матрица — это устройство фотокамеры, где получается изображение.

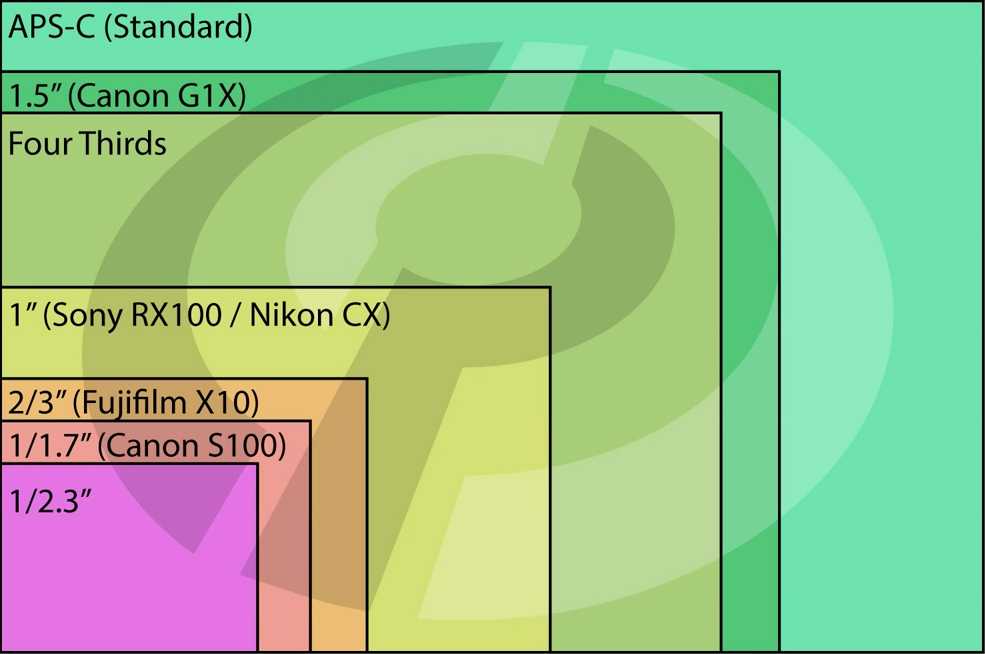
Физический размер матрицы фотокамеры — это ее геометрический размер — длина и ширина в миллиметрах. Однако, стоит отметить, что этот размер указывается ни в миллиметрах, а в обратном количестве дюймов. Например, 1/3.2, что соответствует 3.4*4.5 мм. Для выяснения физического размера матрицы стоит обратить внимание на следующую таблицу.

Пояснения к таблице: В первой колонке таблицы находится физический размер матрицы фотокамеры. Во второй, размер в её дюймах, принятый в спецификации. В третьей коэффициент, показывающий во сколько раз диагональ матрицы меньше диагонали кадра 35мм пленки обычного фильма (KF = 1).

Далее рассмотрим перечень матриц по типоразмерам:

• Матрицы размера 1 / 3.2″ — это самые маленькие матрицы, соотношение сторон 4:3, физический размер 3.4 * 4.5 мм, используются в недорогих и компактных фотоаппаратах.
• Матрицы размером 1 / 2.7″ — соотношение сторон 4:3, физический размер 4.0 * 5.4 мм, используются в недорогих и компактных фотоаппаратах.
• Матрицы размера 1 / 2,5″ — соотношение сторон 4:3, то есть 4,3 * 5,8мм используются в большинстве компактных камер с несменной оптикой.
• Матрицы размера 1 / 1,8″ — соотношение сторон 4:3, геометрический размер 5,3 * 7,2 мм, используются в компактных камерах с несменной оптикой, среднего и выше среднего ценового диапазона (обычно в фотоаппаратах с разрешением от 8 Мпикс и более, но не обязательно).
• Матрицы размера 2 / 3″ — соотношение сторон 4:3, физический размер 6,6 * 8,8 мм иногда используются в дорогих компактных камерах с несменной оптикой.
• Матрицы размера 4 / 3″ — физический размер 18 * 13,5 мм, соотношение сторон 4:3, используются в дорогих камерах.
• DX, APS-C формат — соотношение сторон 3:2, размер около 24 * 18 мм. 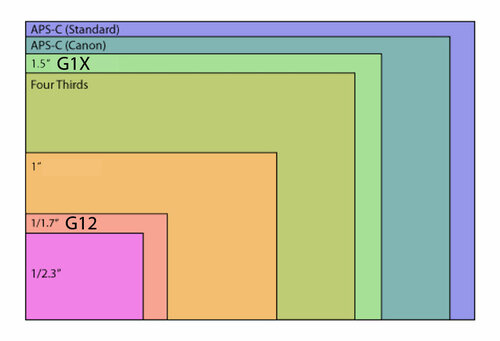Матрицы таких размеров наиболее часто встречаются в цифровых зеркальных фотоаппаратах. Они соответствуют «полукадру» 35 мм кадра. Подавляющее большинство любительских, полупрофессиональных и даже профессиональных камер используют матрицы такого размера в силу того, что они относительно дёшевы в производстве и при этом размер пикселя остаётся довольно большим даже при 10 Мп разрешении.
• Полнокадровая матрица размера 36 * 24 мм — соотношение сторон 3:2, по размерам соответствующая классическому 35 мм кадру (3:2). На рынке представлено всего несколько моделей фотоаппаратов с матрицей такого размера. Такие матрицы дороги и сложны в производстве.
• Среднеформатная матрица формата 60 * 45 мм — соотношение сторон 3:2. Матрицы таких размеров «сшиваются» из матриц меньшего размера, что сказывается на их стоимости. Применяются в дорогих камерах.

Другие статьи на эту тему:

• Как сэкономить место на карте памяти
• Карта памяти
• Почему когда я фотографирую на зеркальную фотокамеру не работает ЖК-экран
• Как восстановить удаленные фотографии с карты памяти
• Светофильтры для фотокамер

Умножение матриц

Вы можете умножить только два матрицы если их Габаритные размеры находятся совместимый , что означает, что количество столбцов в первой матрице совпадает с количеством строк во второй матрице.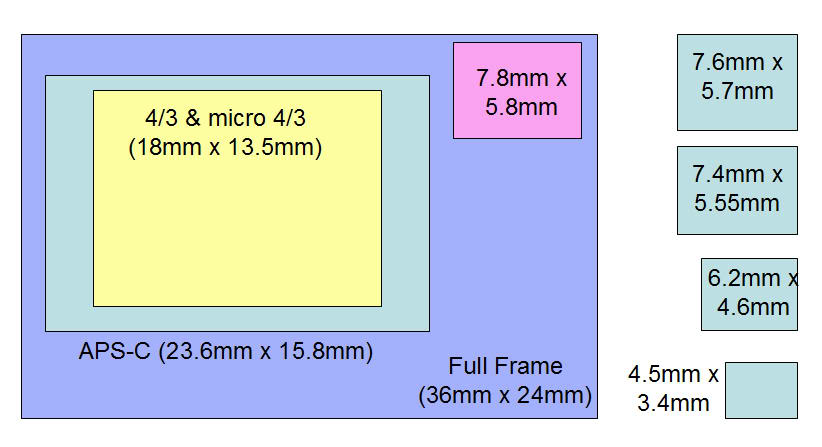

Если А знак равно [ а я Дж ] является м × н матрица и Б знак равно [ б я Дж ] является н × п матрица, продукт А Б является м × п матрица.

А Б знак равно [ с я Дж ] , куда с я Дж знак равно а я 1 б 1 Дж + а я 2 б 2 Дж + … + а я н б н Дж .

(Запись в я й ряд и Дж й столбец обозначается двойным нижним индексом а я Дж , б я Дж , а также с я Дж . Например, запись а 23 это запись во второй строке и третьем столбце.)

Определение матричного умножения указывает на умножение строк за столбцами, где элементы в я й ряд А умножаются на соответствующие записи в Дж й столбец из Б а затем добавить результаты.

Умножение матриц НЕ является коммутативным. Если ни А ни Б является единичной матрицей, А Б ≠ Б А .

Умножение строки на столбец

Мы начнем с того, что покажем вам, как умножить 1 × н матрица н × 1 матрица. Первый — это всего лишь одна строка, а второй — один столбец. По вышеприведенному правилу продукт является 1 × 1 матрица; другими словами, одно число.

Во-первых, давайте назовем записи в строке р 1 , р 2 , . .. , р н , а записи в столбце с 1 , с 2 , … , с н . Тогда произведение строки и столбца равно 1 × 1 матрица

[ р 1 с 1 + р 2 с 2 + … + р н с н ] .

Пример:

Найдите продукт.

[ 1 4 0 ] ⋅ [ 2 − 1 5 ]

Мы должны умножить 1 × 3 матрица 1 × 3 матрица. Количество столбцов в первом равно количеству строк во втором, поэтому они совместимы.

Продукт:

[ ( 1 ) ( 2 ) + ( 4 ) ( − 1 ) + ( 0 ) ( 5 ) ] знак равно [ 2 + ( − 4 ) + 0 ] знак равно [ − 2 ]

Умножение больших матриц

Теперь, когда вы знаете, как умножать строку на столбец, умножать большие матрицы несложно. Для вступления в я й ряд и Дж й столбец матрицы продуктов, умножьте каждую запись в я й строку первой матрицы соответствующей записью в Дж й столбец второй матрицы и сложения результатов.

Возьмем следующую задачу на умножение 2 × 3 матрица с 3 × 2 матрица, чтобы получить 2 × 2 матрица как произведение. Элементы матрицы произведения называются е я Дж когда они в я й ряд и Дж й столбец.

[ 1 0 1 0 1 2 ] ⋅ [ 3 5 − 1 0 2 − 1 ] знак равно [ е 11 е 12 е 21 е 22 ]

Получить е 11 , умножить ряд 1 первой матрицы по столбцу 1 второй.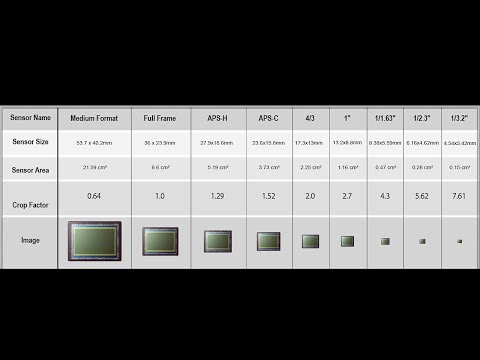

е 11 знак равно [ 1 0 1 ] ⋅ [ 3 − 1 2 ] знак равно 1 ( 3 ) + 0 ( − 1 ) + 1 ( 2 ) знак равно 5

Получить е 12 , умножить ряд 1 первой матрицы по столбцу 2 второй.

е 12 знак равно [ 1 0 1 ] ⋅ [ 5 0 − 1 ] знак равно 1 ( 5 ) + 0 ( 0 ) + 1 ( − 1 ) знак равно 4

Получить е 21 , умножить ряд 2 первой матрицы по столбцу 1 второй.

е 21 знак равно [ 0 1 2 ] ⋅ [ 3 − 1 2 ] знак равно 0 ( 3 ) + 1 ( − 1 ) + 2 ( 2 ) знак равно 3

Получить е 22 , умножить ряд 2 первой матрицы по столбцу 2 второй.

е 22 знак равно [ 0 1 2 ] ⋅ [ 5 0 1 ] знак равно 0 ( 5 ) + 1 ( 0 ) + 2 ( − 1 ) знак равно − 2

Записав матрицу произведения, получим:

[ е 11 е 12 е 21 е 22 ] знак равно [ 5 4 3 − 2 ]

Поэтому мы показали:

[ 1 0 1 0 1 2 ] ⋅ [ 3 5 − 1 0 2 − 1 ] знак равно [ 5 4 3 − 2 ]

Умножение матриц

Умножение матриц

Рассмотрим произведение матрицы 2×3 и матрицы 3×4. Умножение определяется, поскольку внутренние размеры (3) одинаковы. Продукт будет быть матрицей 2×4, внешние размеры.

Так как в первой матрице три столбца и три строки во второй матрица (внутренние размеры которой должны быть одинаковыми), каждый элемент в произведении будет сумма трех товары.

Строка 1, Столбец 1

Чтобы найти элемент в строке 1, столбце 1 произведения, мы возьмем строку 1 из первой матрицы и столбец 1 из второй матрицы. Мы соединяем эти значения вместе, умножаем пары значений, а затем добавляем к прибыть в 25.

 Р  1  : 1 -2 3
×С  1  : 1 -3 6
---------------
     1 +6 +18 = 25 

Строка 2, Столбец 3

Чтобы найти элемент в строке 2, столбце 3 произведения, возьмем строку 2 из первой матрицы и столбец 3 из второй матрицы. Соединяем эти значения вместе, перемножьте пары значений, а затем добавьте к прибыть в 53.

 Р  2  : 4 5 -2
×С  3  : 4 7 -1
---------------
     16 +35 +2 = 53 

Понимание того, откуда взялось каждое число в произведении, полезно, когда вам нужно только определенное значение. Вам не нужно умножать полностью, если вы нужны только определенные элементы. Просто возьмите строку из первой матрицы и столбец из второй матрицы.

Процесс можно завершить для остальных элементов матрицы.

		Колонка 1	Столбец 2	Столбец 3	Колонка 4
	значений	[1, -3, 6]	[-8, 6, 5]	[4, 7, -1]	[-3, 2, 4]
Ряд 1	[1, -2, 3]	1(1) — 2(-3) + 3(6) = 1 + 6 + 18 = 25	1(-8) -2(6) + 3(5) = -8 — 12 + 15 = -5	1(4) -2(7) +3(-1) = 4 — 14 — 3 = -13	1(-3) -2(2) + 3(4) = -3 -4 + 12 = 5
Ряд 2	[4, 5, -2]	4(1) + 5(-3) -2(6) = 4 — 15 — 12 = -23	4(-8) + 5(6) — 2(5) = -32 + 30 — 10 = -12	4(4) + 5(7) -2(-1) = 16 + 35 + 2 = 53	4(-3) + 5(2) -2(4) = -12 + 10 — 8 = -10

Итак, конечный продукт

	25	-5	-13	5
	-23	-12	53	-10

Обратите внимание, что умножение не определяется другим способом.