Разложить функцию в ряд: Ряд Тейлора онлайн

Ряд Тейлора онлайн

Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора:
,
где r_n – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:
, где число x заключено между х и а.

• Решение онлайн
• Видеоинструкция

f(x)=

в точке x₀= Количество элементов ряда34567

Использовать разложение элементарных функций ex, cos(x), sin(x), ln(1+x), (1+x)m

Правила ввода функций:

Если для некоторого значения х r_n→0 при n→∞, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора:
Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если:

1. она имеет производные всех порядков;
2. построенный ряд сходится в этой точке.

При а=0 получаем ряд, называемый рядом Маклорена:

Разложение простейших (элементарных) функций в ряд Маклорена:

Показательные функции
, R=∞
Тригонометрические функции
, R=∞
, R=∞
, (-π/2 < x < π/2), R=π/2
Функция actgx не разлагается по степеням x, т.к. ctg0=∞
Гиперболические функции


Логарифмические функции
, -1<x<1, R = 1

Биномиальные ряды
.

Пример №1. Разложить в степенной ряд функцию f(x)=2

x.
Решение. Найдем значения функции и ее производных при х=0
f(x) = 2^x, f(0) = 2⁰=1;
f'(x) = 2^xln2, f'(0) = 2⁰ ln2= ln2;
f»(x) = 2^x ln²2, f»(0) = 2⁰ ln²2= ln²2;
…
f⁽ⁿ⁾(x) = 2^x lnⁿ2, f⁽ⁿ⁾(0) = 2⁰ lnⁿ2= lnⁿ2.
Подставляя полученные значения производных в формулу ряда Тейлора, получим:

Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -∞<x<+∞.

Пример №2. Написать ряд Тейлора по степеням (

х+4) для функции f(x)=e^x.
Решение. Находим производные функции e^x и их значения в точке х=-4.
f(x) = е^x, f(-4) = е^-4;
f'(x) = е^x, f'(-4) = е^-4;
f»(x) = е^x, f»(-4) = е^-4;
…
f⁽ⁿ⁾(x) = е^x, f⁽ⁿ⁾( -4) = е^-4.

Следовательно, искомый ряд Тейлора функции имеет вид:

Данное разложение также справедливо для -∞<x<+∞.

Пример №3. Разложить функцию f(x)=lnx в ряд по степеням (х-1),
( т.е. в ряд Тейлора в окрестности точки

х=1).
Решение. Находим производные данной функции.
f(x)=lnx, , , ,

f(1)=ln1=0, f'(1)=1, f»(1)=-1, f»'(1)=1*2,…, f⁽ⁿ⁾=(-1)^n-1(n-1)!
Подставляя эти значения в формулу, получим искомый ряд Тейлора:

С помощью признака Даламбера можно убедиться, что ряд сходится при ½х-1½<1. Действительно, Ряд сходится, если ½х-1½<1, т.е. при 0<x<2. При х=2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х=0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].

Пример №4. Разложить в степенной ряд функцию .
Решение. В разложении (1) заменяем х на -х², получаем:

, -∞<x<∞

Пример №5.

Разложить в ряд Маклорена функцию .
Решение. Имеем
Пользуясь формулой (4), можем записать:

подставляя вместо х в формулу –х, получим:

Отсюда находим: ln(1+x)-ln(1-x) = —
Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим
. Этот ряд сходится в интервале (-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.

Замечание.
Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а

)^m, где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t=х-а и раскладывать полученную функцию относительно t в ряд Маклорена.

Этот метод основан на теореме о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.

Пример №5а. Разложить в ряд Маклорена функцию , указать область сходимости.
Решение. Сначала найдем 1-x-6x2=(1-3x)(1+2x), далее разложим дробь с помощью сервиса.
на элементарные:

Дробь 3/(1-3x) можно рассматривать как сумму бесконечно убывающей геометрической прогрессии знаменателем 3x, если |3x| < 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

с областью сходимости |x| < 1/3.

Пример №6. Разложить функцию в ряд Тейлора в окрестности точки х=3.
Решение. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х=3. Однако проще будет воспользоваться имеющимся разложением (5):

=

Полученный ряд сходится при или –3<x-3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.

Пример №7. Написать ряд Тейлора по степеням (х-1) функции ln(x+2).
Решение.

Ряд сходится при , или -2 <

x < 5.

Пример №8. Разложить функцию f(x)=sin(πx/4) в ряд Тейлора в окрестности точки x=2.
Решение. Сделаем замену t=х-2:

Воспользовавшись разложением (3), в котором на место х подставим ^π/₄t, получим: Полученный ряд сходится к заданной функции при -∞<^π/₄t<+∞, т. е. при (-∞<x<+∞).
Таким образом,

, (-∞<x<+∞)

Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.
Рассмотрим разложение функции в степенной ряд: Для того, чтобы вычислить приближенное значение функции в заданной точке х, принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n членов (n – конечное число), а остальные слагаемые отбрасывают: Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток r_n(x). Для этого применяют следующие приемы:

• если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена.
• если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.
• в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа: a<c<x (или
  x<c<a).

Пример №1. Вычислить ln(3) с точностью до 0,01.
Решение. Воспользуемся разложением , где x=1/2 (см. пример 5 в предыдущей теме):

Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии: Таким образом, мы можем отбросить этот остаток и получаем

Пример №2. Вычислить с точностью до 0,0001.
Решение. Воспользуемся биномиальным рядом. Так как 5³ является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=5³+5.

так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:
, поэтому его и следующие за ним члены можно отбросить.
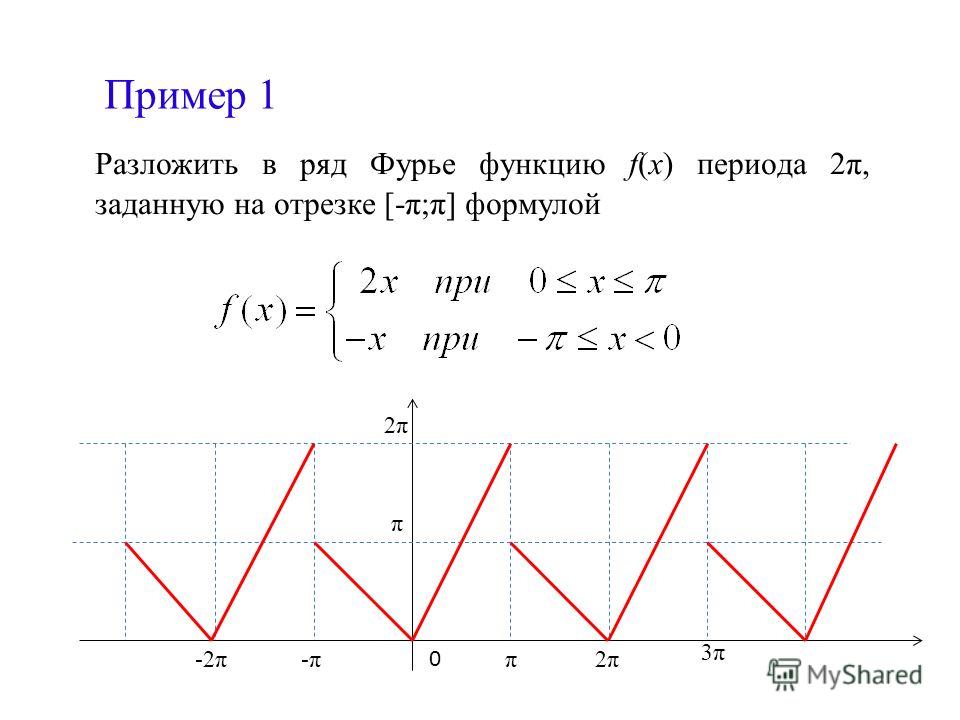
Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подынтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.

Пример №3. Вычислить интеграл ∫014sin(x)x с точностью до 10^-5.
Решение. Соответствующий неопределенный интеграл не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
Разделив почленно ряд для sinx на x , получим:

Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:

Так как полученный ряд удовлетворяет условиям Лейбница и достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.
Таким образом, находим

Пример №4. Вычислить интеграл ∫014ex2 с точностью до 0,001.
Решение.

Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.

&approx;0.0001<0.001

Следовательно, .

Разложение функций в степенные ряды

Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒ Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора: , где rn – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа: , где число x заключено между х и а. Если для некоторого значения х rn®0 при n®¥, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора: Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если: 1) она имеет производные всех порядков; 2) построенный ряд сходится в этой точке.   При а=0 получаем ряд, называемый рядом Маклорена:   Пример 1. Разложить в степенной ряд функцию f(x)=2x. Решение. Найдем значения функции и ее производных при х=0 f(x) = 2x, f(0) = 20=1; f¢(x) = 2xln2, f¢(0) = 20 ln2= ln2; f¢¢(x) = 2x ln22, f¢¢(0) = 20 ln22= ln22; … f(n)(x) = 2x lnn2, f(n)(0) = 20 lnn2= lnn2. Подставляя полученные значения производных в формулу ряда Тейлора, получим: Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -¥<x<+¥.   Пример 2. Написать ряд Тейлора по степеням (х+4) для функции f(x)=ex. Решение. Находим производные функции ex и их значения в точке х=-4. f(x) = еx, f(-4) = е-4; f¢(x) = еx, f¢(-4) = е-4; f¢¢(x) = еx, f¢¢(-4) = е-4; … f(n)(x) = еx, f(n)( -4) = е-4. Следовательно, искомый ряд Тейлора функции имеет вид: Данное разложение также справедливо для -¥<x<+¥.   Пример 3. Разложить функцию f(x)=lnx в ряд по степеням (х-1), ( т.е. в ряд Тейлора в окрестности точки х=1). Решение. Находим производные данной функции. … Подставляя эти значения в формулу, получим искомый ряд Тейлора: С помощью признака Даламбера можно убедиться, что ряд сходится при ½х-1½<1. Действительно, Ряд сходится, если ½х-1½<1, т.е. при 0<x<2. При х=2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х=0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].   Приведем полученные подобным образом разложения в ряд Маклорена (т.е. в окрестности точки х=0) для некоторых элементарных функций: (1) , (2) , (3) , (4) , (5) . (последнее разложение называют биномиальным рядом)   Пример 4. Разложить в степенной ряд функцию Решение. В разложении (1) заменяем х на –х2, получаем: .   Пример 5. Разложить в ряд Маклорена функцию Решение. Имеем Пользуясь формулой (4), можем записать: ; подставляя вместо х в формулу –х, получим: Отсюда находим: Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим Этот ряд сходится в интервале (-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.   Замечание. Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а)m, где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t=х-а и раскладывать полученную функцию относительно t в ряд Маклорена. Этот метод иллюстрирует теорему о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.   Пример 6. Разложить функцию в ряд Тейлора в окрестности точки х=3. Решение. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х=3. Однако проще будет воспользоваться имеющимся разложением (5): Полученный ряд сходится при или –3<x-3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.   Пример 7. Написать ряд Тейлора по степеням (х-1) функции . Решение. Ряд сходится при , или -2 < x £ 5.   Пример 8. Разложить функцию в ряд Тейлора в окрестности точки x=2. Решение. Сделаем замену t=х-2: . Воспользовавшись разложением (3), в котором на место х подставим , получим: Полученный ряд сходится к заданной функции при , т.е. при . Таким образом,   Решить: Разложить заданную функцию в ряд: A 1) по степеням х 2) по степеням х 3) по степеням х 4) по степеням х 5) по степеням (х+1)6) по степеням (х-2) 7) по степ. х 8) в ряд Маклорена 9) в ряд Маклорена 10) в ряд Маклорена   ⇐ Предыдущая1234Следующая ⇒ Читайте также:  Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология 

Последнее изменение этой страницы: 2016-04-23; просмотров: 8642; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.016 с.)

Как разложить функцию в степенной ряд

Как разложить функцию в степенной ряд

Разложение функций в степенные ряды чаще всего является не удовольствием, как многие другие математические преобразования, а необходимостью. К этой процедуре чаще всего прибегают при выполнении приближенных вычислений. При этом используются формулы разложения функций в ряд Тейлора (Taylor series) и ряд Маклорена (Maclaurin series):

          

С практической точки зрения, разложение функции в степенной ряд — это чисто техническая процедура, которая требует довольно много времени и усилий, но мало что дает для понимания конечного результата. Если только освоение этой процедуры не является самоцелью. Конечно, для этого можно использовать справочники рядов. Однако, такие справочники у нас не всегда под рукой. Да и издавались они достаточно давно. А вот Интернет… всегда с нами.

Wolfram|Alpha, естественно, умеет находить разложение функций в степенные ряды. Для этого, в простейшем случае, служит запрос series. Вот, например:

series exp(x)

Обратите внимание, что Wolfram|Alpha без каких-либо дополнительных указаний выводит область сходимости полученного степенного ряда: converges everywhere — означает, что ряд сходится всюду.

Кроме того, очень удобно, что по запросу series f(x) система Wolfram|Alpha выводит графическое представление разложения данной функции в степенной ряд, которое позволяет визуально оценить аппроксимацию данной функции ее степенным рядом в случае удержания заданного количества членов ряда:

Это важно, поскольку слишком часто, при изучении разложения функций в степенные ряды такая чрезвычайно полезная для практики возможность остается невостребованной в связи с относительной трудоемкостью ее реализации.

Свернутое представление функции f(x) в виде степенного ряда в Wolfram|Alpha также можно получить, используя запрос вида: f(x) series representation

exp(x) series representation

Wolfram|Alpha автоматически выбирает наиболее простой вид разложения функции в степенной ряд, если иное не задано. x в ряд Маклорена (в точке x=0). Если же применение ряда Маклорена невозможно (вспомните условия разложения функции в ряд Маклорена), то Wolfram|Alpha автоматически выводит разложение данной функции в ряд Тейлора в ближайшей точке, например в точке x=1:

series ln(x)

При необходимости, Wolfram|Alpha может вывести определенное количество членов разложения функции в степенной ряд. Точнее, выводятся члены ряда до определенной степени (т. е. с коэффициентами до заданного порядка)  включительно. Это нужно указать явно следующим образом:

series sin(x) order 13

В настоящее время эта конструкция запроса срабатывает не всегда корректно — в некоторых случаях Wolfram|Alpha выводит больше членов ряда, чем указано в запросе.

Wolfram|Alpha позволяет получить разложение функции в степенной ряд в заданной точке. Соответствующий запрос выглядит так:

series 1/x point x=-1

Кстати, эту форму запроса можно использовать также и для того, чтобы разложить некий многочлен по степеням одночлена (x-x0). 10, используйте запрос вида:

SeriesCoefficient[cos x, {x, 0, 10}]

Наконец, если нужно найти несколько коэффициентов ряда для степеней n, например, с 6-й по 12-ю, запрос к Wolfram|Alpha формулируем так:

SeriesCoefficient[cos x, {x, 0, 6..12}]

Если хотите узнать, как выполнять приближенные вычисления при помощи степенных рядов в Wolfram|Alpha, читайте следующий пост.

Разложение функций в степенные ряды. Ряд Тейлора. Ряд Маклорена. Примеры решений

Продолжаем рассматривать теорию и практику степенных рядов. Материал несложный, но для его понимания необходимо уже более или менее хорошо ориентировать в теме. Если Вы только-только приступили к изучению рядов или чувствуйте себя чайником, пожалуйста, начните с урока Ряды для чайников. Примеры решений. Далее следует прочитать статьюСтепенные ряды. Область сходимости ряда, в частности, Вы должны хорошо понимать, что такое степенной ряд и его область сходимости. А для целей сегодняшнего урока потребуется методический материал Таблица разложений некоторых функций в степенные ряды, его можно раздобыть в кладовке Математические формулы и таблицы. По возможности, таблицу лучше распечатать, поскольку она потребуется не только сейчас, но и в оффлайне.

Понятие суммы степенного ряда

Начнем подходить к теме с воспоминаний. Как мы помним, любой числовой ряд может или сходиться, или расходиться. Если числовой ряд   сходится, то это значит, что сумма его членов равна некоторому конечному числу: 

На уроке Степенные ряды. Область сходимости ряда мы рассматривали уже не числовые, а функциональные и степенные ряды. Возьмём тот самый подопытный степенной ряд, который всем понравился:  . В ходе исследования было установлено, что этот ряд сходится при  . Если числовые ряды сходятся к ЧИСЛАМ, то к чему же сходятся функциональные и степенные ряды? Правильно подумали. Функциональные ряды сходятся к ФУНКЦИЯМ. В частности, суммой ряда   в его области сходимости   является некоторая функция  :

  

Еще раз подчеркиваю, что данный факт справедлив только для найденной области  , вне этого промежутка степенной ряд   будет расходиться.

Чтобы всё стало окончательно понятно, рассмотрим примеры с картинками. Я выпишу простейшее табличное разложение синуса в степенной ряд:

Область сходимости ряда: 

(По какому принципу получены сами элементарные табличные разложения, мы рассмотрим чуть позже).

Теперь вспоминаем школьный график синуса  :

Вот такая симпатичная синусоида. Хмм…. Где-то я уже это видел….

Теперь фишка. Если начертить график бесконечного многочлена  , то получится… та же самая синусоида! То есть, наш степенной ряд   сходится к функции  . Используя признак Даламбера (см. статью Степенные ряды. Область сходимости ряда), легко проверить, что ряд   сходится при любом «икс»:   (собственно, поэтому в таблице разложений и появилась такая запись об области сходимости).

А что значит вообще «сходится»?  По смыслу глагола – что-то куда-то идёт. Если я возьму первые три члена ряда   и начерчу график многочлена пятой степени, то он лишь отдаленно будет напоминать синусоиду. А вот если составить многочлен из первых ста членов ряда:   и начертить его график, то он будет с синусоидой практически совпадать. Чем больше членов ряда – тем лучше приближение. И, как уже отмечалось, график бесконечного многочлена – есть в точности синусоида. Иными словами, ряд   сходится к функции   при любом значении «икс».

Рассмотрим более печальный пример, табличное разложение арктангенса: Область сходимости ряда: 

Печаль заключается в том факте, что график бесконечного многочлена    совпадает с графиком арктангенса   только на отрезке   (т.е. в области сходимости ряда):

Вне отрезка   разложение арктангенса в ряд   расходится, а график бесконечного многочлена пускается во все тяжкие и уходит на бесконечность.

Разложение функций в степенной ряд. Ряд Тейлора. Ряд Маклорена

Приступим к увлекательному занятию – разложению различных функций в степенные ряды. Сначала пара формул, затем практические задания.

Если функция   в некотором интервале раскладывается в степенной ряд по степеням  , то это разложение единственно и задается формулой: Примечания: Надстрочный индекс   в последнем слагаемом обозначает производную «энного» порядка. Вместо буквы «а» в литературе часто можно встретить букву  .

Данная формула получила имя некоего англичанина Тейлора (ударение на первый слог).

На практике процентах в 95-ти приходится иметь дело с частным случаем формулы Тейлора, когда  :

Это разложение в ряд обычно называют именем шотландца Маклорена (ударение на второй слог). Разложение Маклорена также называют разложением Тейлора  по степеням  .

Вернемся к таблице разложений элементарных функций и выведем разложение экспоненциальной функции: Как оно получилось? По формуле Маклорена: Рассмотрим функцию  , тогда:

Теперь начинаем находить производные в точке ноль: первую производную, вторую производную, третью производную и т.д.  Это просто, поскольку при дифференцировании экспонента превращается в саму себя:

И так далее….

Совершенно очевидно, что 

Подставляем единицы в формулу Маклорена и получаем наше табличное разложение!

Аналогично можно вывести некоторые другие табличные разложения (но далеко не все выводятся именно так).

Примеры разложения функций в ряд Маклорена

В данном параграфе мы рассмотрим типовую задачу на разложение функции в ряд Маклорена и определении области сходимости полученного ряда. Нет, мучаться с нахождением производных не придется, мы будем пользоваться таблицей.

Пример 1

Разложить функцию в ряд Маклорена. Найти область сходимости полученного ряда.

! Эквивалентная формулировка: Разложить функцию в ряд по степеням   

Решение незамысловато, главное, быть внимательным и не пропустить какую-нибудь степень, индекс.

Конструируем наш ряд. Плясать начинают, как правило, от функции, в данном случае – от косинуса. Используем элементарное разложение:

.  Область сходимости ряда: 

В данном случае 

В числителях раскрываем скобки:

Теперь умножаем обе части на «икс»:

В итоге искомое разложение функции в ряд:

Как определить область сходимости? Разложение косинуса сходится при ЛЮБОМ значении «альфа»:  , а значит и при 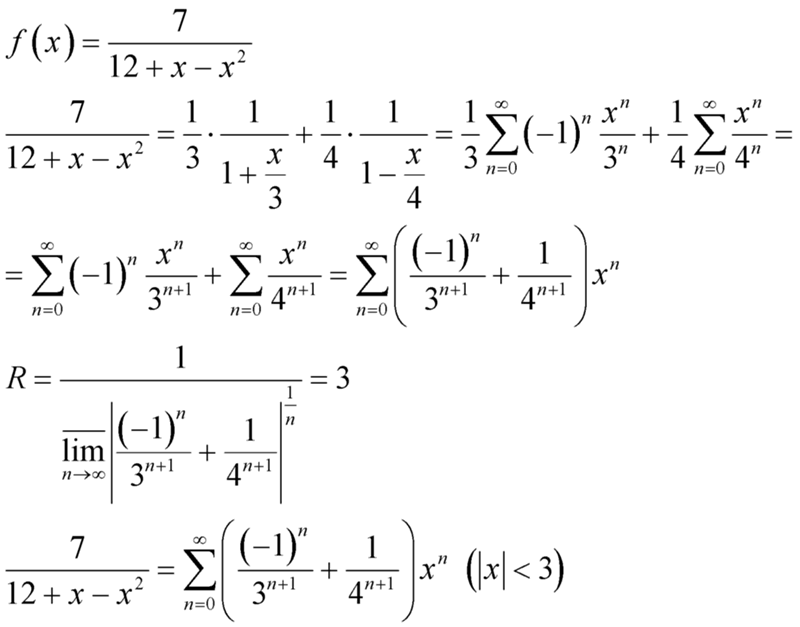 . Домножение   на «икс» не играет никакой роли в плане сходимости. Поэтому область сходимости полученного ряда: 

Пример 2

Разложить функцию в ряд по степеням  . Найти область сходимости ряда.

Это пример для самостоятельного решения.

Я не стал рассматривать простейшие разложения вроде  ,   или  , поскольку это фактически задача в одно действие. В нужные табличные разложения вместо «альфы» необходимо подставить  ,  ,   и немного причесать полученные ряды. Единственное предостережение – не теряйте по невнимательности степени и знаки.

А сейчас для разнообразия рассмотрим что-нибудь с минусами.

Пример 3

Разложить функцию в ряд по степеням  . Найти область сходимости ряда.

В таблице находим похожее разложение: Область сходимости ряда:  , концы интервала нужно исследовать дополнительно.

Трюк прост: перепишем функцию немного по-другому:

Таким образом,   и: Окончательно:

Теперь нужно определить область сходимости. Смотрим на табличное неравенство  . У нас тут минус и «икс» в квадрате:  , не факт, что область сходимости полученного ряда будет именно такая. В сомнительных случаях надежнее всего подробно проанализировать полученный степенной ряд. В данном случае функция разложилась в ряд  . Используя штатный признак Даламбера (урок Степенные ряды. Область сходимости ряда), легко найти интервал сходимости ряда:  . Будет ли сходиться ряд на концах интервала? Если подставить значения  ,  , то в обоих случаях получится расходящийся гармонический ряд   (знак «минус» перед рядом никак не влияет на сходимость или расходимость).

Таким образом, область сходимости полученного ряда: 

Интересно отметить, что простейшее разложение из учебника   сходится ещё в одной точке, и область сходимости соответствующего ряда:  . А разложение в ряд такого логарифма:   – сходится на обоих концах интервала: 

Таким образом, когда вам дан для разложения любой логарифм, следует быть предельно аккуратным и внимательным.

Пара примеров для самостоятельного решения:

Пример 4

Разложить функцию в ряд по степеням  . Найти область сходимости ряда.

Пляска традиционно начинается от функции, то есть, начинать нужно с экспоненты.

Пример 5

Разложить функцию в ряд по степеням  . Найти область сходимости ряда.

Здесь разложение не такое трудное, но могут возникнуть трудности с нахождением области сходимости полученного ряда.

Полные решения и ответы в конце урока.

Не редкость, когда перед разложением функции в ряд её необходимо предварительно преобразовать. Канонический случай – это разложение функции  . Перед тем как ее раскладывать в ряд, необходимо понизить степень с помощью известной тригонометрической формулы:  . Решать я этот пример не буду, поскольку он довольно простой, к тому же что-то подобное мы недавно рассмотрели.

Пример 6

Разложить функцию в ряд по степеням  . Найти область сходимости ряда.

Смотрим в таблицу и находим наиболее похожее разложение:

Во-первых, вверху нужно получить единицу, поэтому представляем функцию в виде произведения:  Теперь нам нужно в знаменателе устроить  , для этого выносим двойку за скобки: И сокращаем на два: В данном случае  , таким образом:

В итоге искомое разложение:

Определим область сходимости ряда. Можно пойти длинным и надежным путем, используя признак Даламбера для полученного степенного ряда  , т.е. найти интервал сходимости ряда и исследовать сходимость ряда на концах найденного интервала.

А можно поступить проще. Из таблицы известно, что биномиальный ряд стопудово сходится при  . В данном случае  , поэтому: Умножаем все части неравенства на  :  – интервал сходимости полученного ряда. Что происходит с рядом   на концах интервала?  При  При  Оба числовых ряда расходятся, так как не выполнен необходимый признак сходимости ряда.

Таким образом, область сходимости полученного ряда: 

Пример 7

Разложить функцию в ряд по степеням  . Найти область сходимости ряда. Указание: предварительно функцию следует упростить, используя свойства логарифмов: 

Это пример для самостоятельного решения.

Разложение функций в ряд Маклорена необходимо проводить в ряде других задач, например, в задаче приближенного вычисления определенного интеграла.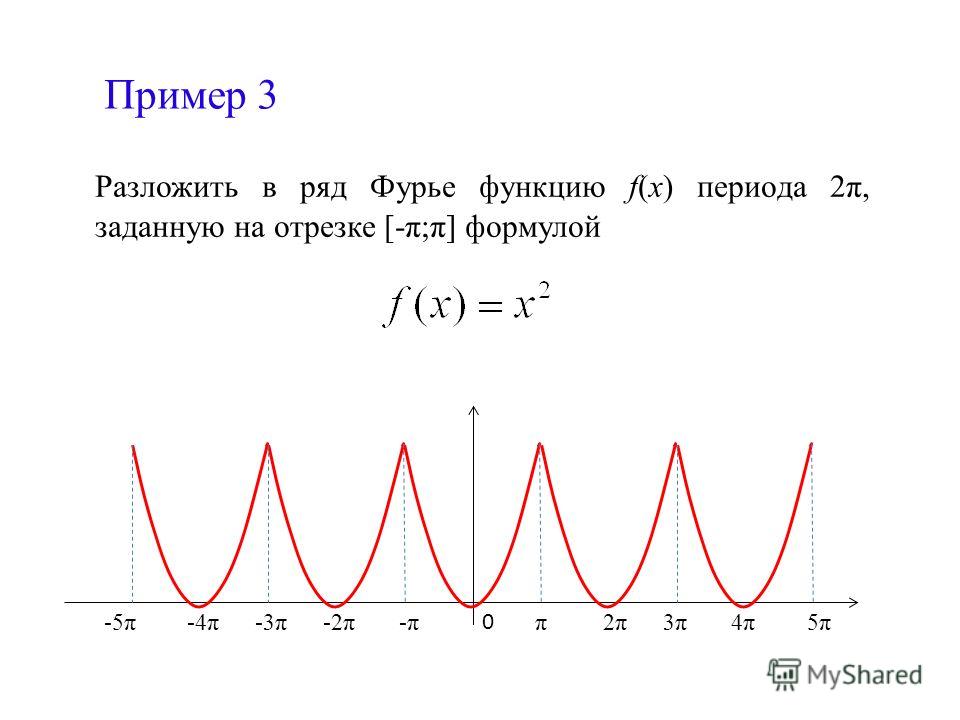 Кстати, там, помимо нового материала, можно посмотреть примеры других разложений, которые не поместились в этот урок.

Примеры разложения функций в ряд Тейлора по степеням 

Данное задание является более сложным и встречается значительно реже. Я сначала вообще не хотел включать задачу в урок, но всё-таки решил, что 2-3 примера не помешают. Пригодится.

Вытащим из чулана общую формулу Тейлора, о которой уже упоминалось:

Еще раз повторю, что вместо буквы «а» на практике часто можно встретить букву  .

В чём сложность разложения функции по степеням  ? Сложность состоит в том, что нам не удастся воспользоваться табличными разложениями, и придётся самостоятельно находить производные.

Сразу небольшой Пример 8

Разложить функцию   в ряд Тейлора по степеням 

В данном случае  , смотрим на формулу Тейлора, и становится уже всё понятнее. Теперь предстоит ручная работа по конструированию разложения:

, все производные, начиная с четвёртой производной, будут нулевыми.

Теперь подставляем весь найденный скарб в формулу Тейлора:

Готово. Для проверки можно раскрыть скобки: Получен исходный многочлен, что и требовалось проверить.

Рассмотрим более содержательные примеры.

Пример 9

Разложить функцию   в ряд Тейлора по степеням  . Найти область сходимости полученного ряда.

Решение: Используем  разложение функции в ряд Тейлора по степеням 

Хех, опять предстоит ручная работа….

В данном случае: 

Замечаем, что с такими раскладами производные можно находить до бесконечности. Поэтому необходимо уловить некоторую закономерность. Найдем ещё третью производную:

А теперь проанализируем найденные производные:  ,  ,  . Закономерность прослеживается: знаки чередуются, в числителе накручивается факториал, а в знаменателе  растёт степень.

Теперь, исходя из выявленной закономерности, нужно составить производную «энного» порядка. В данном случае она выглядит так: Как проверить, правильно ли составлена энная производная? Подставьте в неё значения  ,  ,   и вас должны получиться в точности первая, вторая и третья производные. После того, как мы убедились в том, что энная производная составлена правильно, подставляем в неё наше значение: 

Теперь осталось все труды подставить в формулу Тейлора и аккуратно провести упрощения:

Далее необходимо найти область сходимости полученного степенного ряда  . Это стандартная задача, которую мы многократно прорешивали на уроке Степенные ряды. Область сходимости ряда. Я сразу приведу ответ, поскольку умею решать почти все ряды устно =)

Область сходимости полученного степенного ряда: 

И заключительный пример для самостоятельного решения:

Пример 10

Разложить функцию   в ряд Тейлора по степеням  . Найти область сходимости полученного ряда.

Если честно, то от рядов уже в глазах мельтешит, не злоупотребляйте!  Пожалуйста, сообщите, если где заметили опечатку или ошибку.

Желаю успехов!

Решения и ответы:

Пример 2: Используем разложение:  . Данный ряд сходится при любом значении .   В данном случае Область сходимости ряда: .

Пример 4: Используем разложение:  .  Область сходимости ряда:  . В данном случае Конструируем функцию дальше: Окончательно: Поскольку разложение экспоненты сходится при любом «альфа», то область сходимости полученного ряда: 

Пример 5: Используем частный случай биномиального разложения: В данном случае Таким образом:

Само по себе разложение не слишком сложное, важно правильно найти область полученного сходимости ряда. Есть длинный путь и короткий.

Путь короткий: из таблицы находим комментарий к биномиальному разложению: «Область сходимости ряда:  . Сходимость ряда в точках ,  исследуется отдельно». В данном случае  , то есть, ряд точно сходится при: .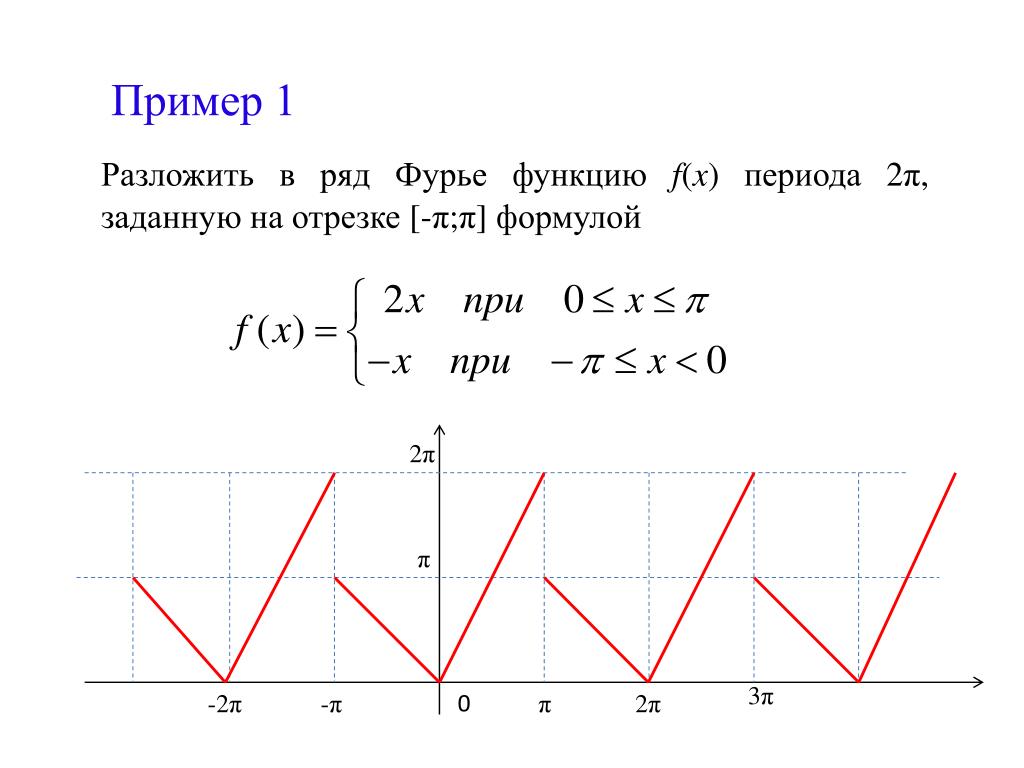 Делим все части на 3 и извлекаем из всех частей кубический корень:  – интервал сходимости ряда. Подставляем концы интервала в полученный ряд . Если , то: При Оба числовых ряда расходятся, так как не выполнен необходимый признак сходимости ряда. Окончательно. Область сходимости полученного ряда: 

Путь длинный (но более надежный и универсальный) состоит в исследовании полученного ряда   с помощью признака Даламбера по стандартной схеме, рассмотренной на уроке Степенные ряды. Область сходимости ряда.

Пример 7: Преобразуем функцию:  Используем разложение: В данном случае Таким образом: Или короче, в свёрнутом виде: Найдем область сходимости полученного степенного ряда. По таблице находим, что использованное разложение сходится при  . В данном случае  , поэтому:  – интервал сходимости исследуемого степенного ряда. Исследуем сходимость ряда на концах найденного интервала: При  – расходится При  – сходится условно. Таким образом, область сходимости полученного степенного ряда: 

Пример 10: Решение: Используем  разложение функции в ряд Тейлора по степеням  : В данном случае: … … Таким образом: Область сходимости полученного степенного ряда уже надоела. Ответ:   ряд сходится при .

Сообщество Экспонента

• вопрос
• 22.09.2022

Математика и статистика, Системы управления, Изображения и видео, Робототехника и беспилотники, Глубокое и машинное обучение(ИИ), Другое

Коллеги, добрый день.   Необходимо использовать corrcoef, а массивы разной длины.   Как сделать кол-во элементов одинаково?

Коллеги, добрый день.   Необходимо использовать corrcoef, а массивы разной длины.   Как сделать кол-во элементов одинаково?

8 Ответов

• вопрос
• 20.09.2022

Другое, Встраиваемые системы, Цифровая обработка сигналов, Системы управления

Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…

Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…

• MATLAB

20.09.2022

• Публикация
• 15.09.2022

Системы управления, Другое

Видел видос на канале экспоненты по созданию топливной системы. Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…

Моделирование гидравлических систем в simulink

• Публикация
• 10.09.2022

Системы управления, Электропривод и силовая электроника, Другое

Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов. В этой книге в научно-практическо-методической форме я план…

Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов.

• Публикация
• 24.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

                                                                          &. ..

Здесь собрана литература по комбинированным методам множественного доступа, в которых используется разделение пользователей в нескольких ресурсных пространствах.

• вопрос
• 23.08.2022

Математика и статистика, Радиолокация, Цифровая обработка сигналов

Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?

Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?

4 Ответа

• ЦОС
• цифровая обработка сигналов

23.08.2022

• Публикация
• 23.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

                                                                          &…

Здесь соборана литература по методам множественного доступа с поляризационным разделением и разделением по орбитальном угловому моменту.

• Публикация
• 16.08.2022

Цифровая обработка сигналов, Системы связи, Математика и статистика

                                      

Здесь собрана литература по методам множественного доступа с пространственным разделением.

• вопрос
• 22.07.2022

Изображения и видео, Цифровая обработка сигналов, Математика и статистика, Биология, Встраиваемые системы, Глубокое и машинное обучение(ИИ), Автоматизация испытаний, ПЛИС и СнК, Системы управления, Другое

Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1.txt file_1_2.txt file_1_3.txt file_1_4.txt fil…

Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1. txt file_1_2.txt file_1_3.txt file_1_4.txt fil…

2 Ответа

• чтение

22.07.2022

• вопрос
• 17.07.2022

Математика и статистика, Цифровая обработка сигналов

Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…

Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…

• MATLAB
• Signal Processing

17.07.2022

Разложение в ряд Тейлора с примерами решения

Содержание:

1. Понятие ряда Тейлора
2. Степенная функция
3. Примеры с решением

Понятие ряда Тейлора

Если функция определена в некоторой окрестности точки и имеет в точке производные всех порядков, то степенной ряд (1) называется рядом Тейлора функции в точке Пусть функция регулярна в точке т. е. представляется в некоторой окрестности точки хо сходящимся к этой функции степенным рядом

(2)

Тогда по теореме функция бесконечно дифференцируема в окрестности точки причем коэффициенты ряда (2) выражаются формулами (3) Таким образом, степенной ряд для функции регулярной в данной точке а, совпадает с рядом Тейлора функции в точке

Если известно, что функция бесконечно дифференцируема в точке (и даже в некоторой окрестности этой точки), то нельзя утверждать, что составленный для этой функции ряд Тейлора (1) сходится при к функции

Рассмотрим функцию

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Эта функция определена на откуда с помощью индукции легко показать, что где — многочлен степени Воспользуемся тем, что для любого к и докажем, что (4) Утверждение (4) верно при отхкуда, предположив, что формула (4) справедлива при находим

Таким образом, по индукции доказано равенство (4), и поэтому все коэффициенты ряда Тейлора (1) в точке для рассматриваемой функции равны нулю.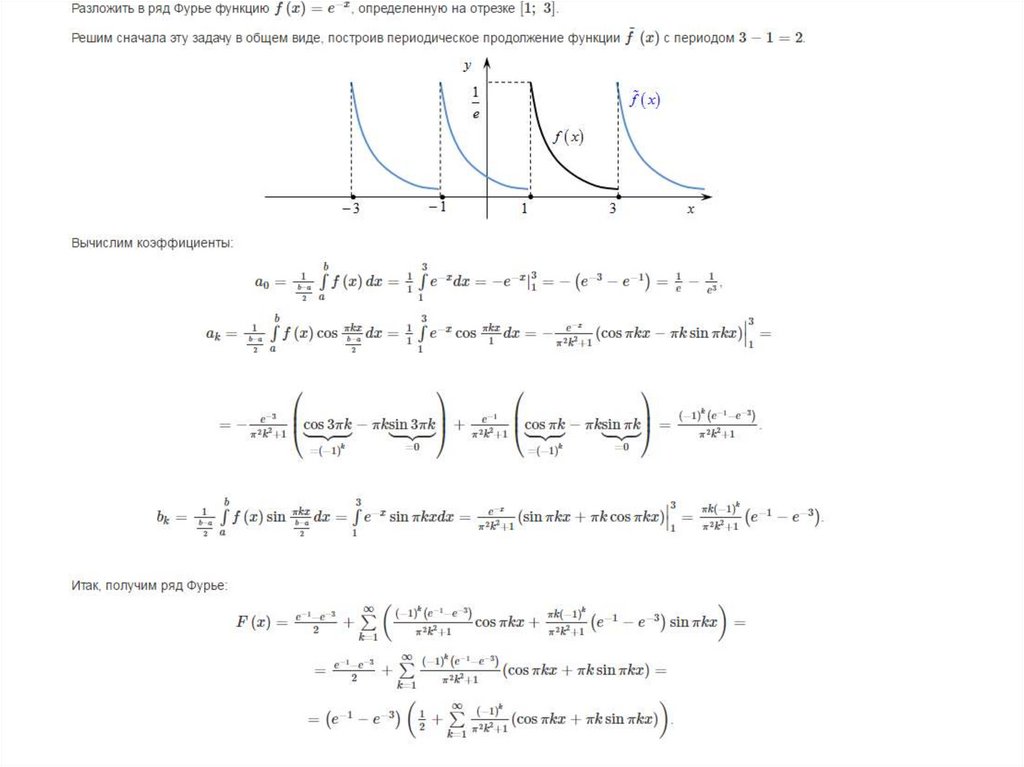 Так как при то сумма ряда Тейлора не совпадает Иначе говоря, эту функцию нельзя представить рядом Тейлора, сходящимся к ней в окрестности точки

Причина этого явления становится понятной, если функцию рассматривать в комплексной плоскости. В самом деле, функция не является непрерывной в точке так как Остаточный член формулы Тейлора. Пусть функция бесконечно дифференцируема в точке Тогда ей можно поставить в соответствие ряд (1). Обозначим и назовем остаточным членом формулы Тейлора для функции в точке Если существует то согласно определению сходимости ряда ряд (1) сходится к функции в точке т. е.

Возможно вам будут полезны данные страницы:

Найти частные производные

Объём тела вращения

Матричные уравнения: пример решения

Метод Гаусса: пример решения

Теорема 1. Если функции непрерывны на интервале где то для любого остаточный член формулы Тейлора для функции в точке можно представить: а) в интегральной форме б) в форме Лагранжа где принадлежит интервалу с концами О Формула (10) была доказана. Докажем формулу (9) методом индукции. В силу равенств (5) и (6) нужно показать, что

Воспользуемся равенством и преобразуем его жо левую часть с помощью формулы интегрирования по частям:

Таким образом, т. е. формула (11) верна при Предположим, что формула (11) является верной для номера т. е. Преобразуем интеграл в правой части формулы (12), применив формулу интегрирования по частям:

Отсюда следует, что равенство (12) можно записать в виде (11). Формула (9) доказана.

Теорема 2. Если функция и все ее производные ограничены в совокупности на интервале т. е. (13) то функция представляется сходящимся к ней в каждой точке интервала рядом Тейлора (8). О Пусть Тогда, используя формулу (10) и условие (13), получаем Так как для любого то из (14) следует, что выполняется условие (7), т. е. в точке справедливо равенство (8). Упражнение. Доказать, что теорема 2 остается в силе, если условие (13) заменить следующим условием: Разложение элементарных функций в ряд Тейлора. Найдем разложение основных элементарных функций в ряд Тейлора в окрестности точки т. е. в ряд вида который называют рядом Маклорена.

Заметим, что коэффициенты -—разложения (15) для основных элементарных функций (показательной, гиперболических, тригонометрических и других. Показательная и гиперболические функции. Пусть Тогда для любого выполняются неравенства По теореме 2 ряд (15) для функции сходится к этой функции на интервале при любом т. е. радиус сходимости этого ряда Так как для функции выполняются равенства для любого гг, то по формуле (15) получаем разложение в ряд Маклорена показательной функции Используя разложение (16) и формулы находим разложения в ряд Маклорена гиперболического косинуса и гиперболического синуса: Используя разложение (16) и формулы находим разложения в ряд Маклорена гиперболического косинуса и гиперболического синуса: (18)

Радиус сходимости каждого из рядов (17), (18) б) Тригонометрические функции. Пусть Тогда По теореме 2 ряд (15) для функции сходится для любого т. е. радиус сходимости этого ряда Если для любого п, и по формуле (15) получаем разложение синуса в ряд Маклорена: Пусть Тогда для всех и для всех для всех По формуле (15) получаем

Радиус сходимости каждого из рядов (19) и (20) в) Логарифмическая функция. Пусть Тогда откуда находим О Оценим остаточный член пользуясь формулой (9) при Преобразуем эту формулу, полагая Тогда и формула (9) примет вид Если то по формуле (23), используя равенство (21), получаем

Пусть Тогда справедливы неравенства так как Отсюда следует, что при любом выполняется неравенство Используя неравенство (27), из формулы (24) получаем следующую оценку остаточного члена: откуда следует, что Пусть Тогда так как Итак, если то остаточный член для функции стремится к нулю при т. е. ряд Маклорена сходится к Из формул (15) и (22) получаем разложение функции в ряд Маклорена радиус сходимости которого Формула (28) справедлива при и поэтому Заменяя в формуле (28) получаем

Степенная функция

Пусть Если — многочлен степени который можно записать по формуле бинома Ньютона в виде конечной суммы: Покажем, что если то функция представляется при каждом сходящимся к ней рядом Маклорена где

Так как то по формуле (23) получаем где Выберем число таким, чтобы выполнялось условие Тогда при всех справедливы неравенства

Используя неравенства (25) и (26), а также неравенство получаем

Из формулы (33) и оценок (34)-(36) следует неравенство (37) которое справедливо при всех и для каждого Так как при то Отметим важные частные случаи формулы В заключение заметим, что при разложении функций в ряд Тейлора обычно используют формулы (16)-(20), (28)-(30) и применяют такие приемы, как: представление данной функции в виде линейной комбинации функций, ряды Тейлора для которых известны; замена переменного; почленное дифференцирование и интегрирование ряда.

Примеры с решением

Пример 1.

Разложить в ряд Маклорена функцию и найти радиус сходимости ряда, если: Используя формулу (38), получаем ряд радиус сходимости которого б) Из равенства (30) следует, что

Следовательно,

Так как то’ при_ + 3 2(1 + |) 8(1-|) меняя формулы (38) и (39), получаем ряд

Пример 2.

Разложить в ряд Маклорена функции и найти радиусы сходимости рядов.

а) Почленно интегрируя ряд (40), получаем

б) Заменяя в формуле (41) получаем откуда следует, что

интегрируя ряд (41), получаем

Пример 3.

Разложить в ряд Тейлора в точке функцию Так как то, полагая получаем

Используя формулы (28) и (29), отсюда находим Следовательно,

Исчисление II. Степенные ряды и функции

Онлайн-заметки Пола
Главная / Исчисление II / Серии и последовательности / Силовой ряд и функции

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 4-15: Серия Power и функции

Мы начали последний раздел, сказав, что собираемся начать думать о применении рядов, а затем сразу же посвятили раздел снова разговору о сходимости. Пришло время начать с применения сериалов.

В этом разделе мы начнем говорить о том, как представлять функции степенными рядами. На естественный вопрос, зачем нам это нужно, мы ответим в нескольких разделах, как только мы на самом деле научимся это делать.

Давайте начнем с того, что мы уже знаем, как это сделать, хотя, когда мы впервые столкнулись с этой серией, мы не думали о ней как о степенной последовательности и не признавали, что она представляет собой функцию. 9n}} \hspace{0,5 дюйма}{\mbox{при условии}}\left| х \ справа | < 1 \метка{уравнение:уравнение3}\конец{уравнение}\]

Это важное положение. Очевидно, что мы можем подставить любое число, кроме \(x = 1\), в функцию, однако мы получим сходящийся степенной ряд, только если \(\left| x \right| < 1\). Это означает, что равенство в \(\eqref{eq:eq1}\) будет выполняться только в том случае, если \(\left| x \right| < 1\). Для любого другого значения \(x\) равенство не будет выполняться. Также обратите внимание, что мы также можем использовать это, чтобы признать, что радиус сходимости этого степенного ряда равен \(R = 1\), а интервал сходимости равен \(\left| x \right| < 1\).

Здесь важна идея конвергенции. Мы будем представлять многие функции в виде степенных рядов, и будет важно признать, что представления часто будут действительны только для диапазона \(x\) и что могут быть значения \(x\), которые мы можем подключите к функции, которую мы не можем подключить к представлению степенного ряда. 3}}}\]

Показать решение

Эта функция аналогична предыдущей функции. Разница заключается в числителе, и на первый взгляд это кажется важным отличием. Поскольку \(\eqref{eq:eq2}\) не имеет \(x\) в числителе, кажется, что мы не можем связать эту функцию обратно с этой.

Однако теперь, когда мы работали с первым примером, этот пример на самом деле очень прост, поскольку мы можем использовать результат ответа из этого примера. Чтобы увидеть, как это сделать, давайте сначала немного перепишем функцию. 9{3n}}} \hspace{0,5 дюйма}{\mbox{при условии}}\left| х \ справа | < 1\]

Обратите внимание, что наличие \(x\) вне ряда НЕ повлияет на его сходимость, поэтому интервал сходимости остается прежним.

Последний шаг — ввести коэффициент в ряд, и все готово. Когда мы это сделаем, убедитесь, что вы также объедините \(x\). Обычно нам нужен только один \(x\) в степенном ряду.

\[h\left( x \right) = \sum\limits_{n = 0}^\infty {2{{\left({- 1} \right)}^n}{x^{3n + 2}} } \hspace{0,5 дюйма}{\mbox{при условии}}\left| х \ справа | < 1\]

Как мы видели в предыдущем примере, мы часто можем использовать предыдущие результаты, чтобы помочь нам. Это важная идея, которую следует помнить, поскольку она часто может значительно упростить нашу работу.

Пример 3. Найдите представление в виде степенного ряда для следующей функции и определите интервал ее сходимости. \[f\left( x \right) = \frac{x}{{5 — x}}\]

Показать решение

Итак, снова у нас есть \(x\) в числителе. Итак, как и в случае с последним примером, давайте проанализируем это и посмотрим, что у нас осталось.

\[f\left( x \right) = x\,\,\frac{1}{{5 — x}}\]

Если бы у нас было представление степенного ряда для

\[g\left( x \right) = \frac{1}{{5 — x}}\]

мы можем получить представление степенного ряда для \(f\left( x \right)\).

Итак, давайте найдем. Сначала заметим, что для использования \(\eqref{eq:eq2}\) нам нужно, чтобы число в знаменателе было единицей. Это достаточно легко получить. 9{n + 1}}}}} \end{align*}\]

Интервал сходимости для этого ряда

\[\слева| {\ гидроразрыва {х} {5}} \ справа | < 1\hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма}\frac{1}{5}\left| х \ справа | < 1\hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма}\left| х \ справа | < 5\]

Хорошо, это была работа над представлением степенного ряда для \(g\left( x \right)\). Давайте теперь найдем представление степенного ряда для исходной функции. Все, что нам нужно сделать для этого, это умножить представление степенного ряда для \(g\left( x \right)\) на \(x\), и мы его получим. 9{n + 1}}}}} \end{align*}\]

Интервал сходимости не меняется, поэтому будет \(\left| x \right| < 5\).

Итак, надеюсь, теперь у нас есть представление о том, как найти представление степенного ряда для некоторых функций. По общему признанию, все функции могут быть связаны с \(\eqref{eq:eq2}\), но это только начало.

Теперь нам нужно рассмотреть некоторые дальнейшие манипуляции со степенными рядами, которые нам придется делать время от времени. Нам нужно обсудить дифференцирование и интегрирование степенных рядов. 93} + \cdots\]

Теперь мы знаем, что если мы продифференцируем конечную сумму терминов, все, что нам нужно сделать, это продифференцировать каждый из терминов, а затем сложить их обратно. С бесконечными суммами связаны некоторые тонкости, с которыми нам нужно быть осторожными, но они несколько выходят за рамки этого курса.

Однако достаточно хорошо для нас известно, что если представление степенного ряда \(f\left( x \right)\) имеет радиус сходимости \(R > 0\), то почленное дифференцирование степенной ряд также будет иметь радиус сходимости \(R\) и (что более важно) фактически будет представлением степенного ряда \(f’\left( x \right)\) при условии, что мы останемся в пределах радиуса конвергенция. 9{п — 1}}} \]

Обратите внимание на начальное значение этой серии. Он был изменен с \(n = 0\) на \(n = 1\). Это признание того факта, что производная первого члена равна нулю и, следовательно, не входит в производную. Заметьте, однако, что, поскольку n=0 член приведенного выше ряда также равен нулю, мы могли бы начать ряд с \(n = 0\), если это требуется для конкретной задачи. В общем, в этом классе этого делать не будут.

Теперь мы можем найти формулы и для производных высших порядков. 9{n — 3}}} \\ & etc.\end{align*}\]

Еще раз обратите внимание, что начальное значение \(n\) изменяется с каждым дифференцированием, чтобы признать, что член исходного ряда дифференцирован до нуля.

Теперь коротко об интеграции. Как и в случае с дифференцированием, когда у нас есть бесконечный ряд, нам нужно быть осторожным при простом интегрировании почленно. Как и в случае с производными, оказывается, что пока мы работаем со степенными рядами, мы можем просто интегрировать члены ряда, чтобы получить интеграл самого ряда. Другими словами, 9{n — 1}}} \end{align*}\]

Тогда, поскольку исходный степенной ряд имел радиус сходимости \(R = 1\), производная и, следовательно, g(x) , также будет иметь радиус сходимости \(R = 1\). {n + 1}}}}} \end{align*}\] 9{п + 1}}}}} \]

Обратите внимание, что это нормально постоянно сидеть вне сериала, как это. На самом деле, нет никакого способа ввести его в серию, так что не волнуйтесь по этому поводу.

Наконец, поскольку представление степенного ряда из Примера 3 имело радиус сходимости \(R=5\), этот ряд также будет иметь радиус сходимости \(R=5\).

Что значит разложить функцию «по степеням x-1»?

Пт, 31 июля 2020 г. 9{2x}!! в степенях !!(x-1)!! а также был сбит с толку тем, что это значит, и в чем смысл этого. Я написал ответ, который мне понравился, который я воспроизвожу здесь.

---

Вы спрашивали:

Я не понимаю, что мы делаем во всем этом процессе

, что является справедливым вопросом. Я тоже этого не понимал, когда впервые узнал это. Но это важно по практическим инженерным соображениям, поскольку так и для теоретико-математических. 3$$ 99$$

Если мы сделаем это, то получим !!7.3887!!, что не так уж и далеко. Но это был много работы! И мы находим это как !!x!! отдаляется от нуля, т. серия выше становится все менее и менее точной. Например, возьмем !!x=3.1!!, формула с четырьмя членами дает нам !!66,14!!, что совершенно неверно. Даже если мы воспользуемся десятью терминами, мы получим !!444,3!!, до которого еще далеко. правильный ответ на самом деле !!492.7!!.

Что нам с этим делать? Просто добавить больше терминов? Это может быть много работать, и это может привести нас не туда, куда нам нужно. (Некоторый Маклорен серии просто перестают работать слишком далеко от нуля, и никакое количество термины заставят их работать.) Вместо этого мы используем другую технику. 9я!! вместо этого, и когда !!x=3.1!!, они не маленькие, они очень большие! Они получают больше как !!i!! увеличивается, и очень быстро. (Выигрывает !! i!!! в знаменателе, в конце концов, но это происходит не во многих терминах. ) Если мы оставим вне этих многих больших сроков, мы получаем неправильные результаты.

Краткий ответ на ваш вопрос:

Серия

Маклорена хороша для вычисления функций, только когда !!x!! близко к !!0!!, и становится неточным как !!x!! уходит от нуль. Но серия Тейлора вокруг !!a!! имеет свой «центр» вблизи !!a!! и является наиболее точным, когда !!x!! близко к !!a!!.

[Другие статьи в категории /math/se] постоянная ссылка

Math Tutor — Series — Theory

Math Tutor — Series — Theory — Function series

Здесь мы отвечаем на главный вопрос. У нас есть функция f и номер a , и мы хотели бы выразить эту функцию как сумму степени серия с центром и . Мы начните с некоторой теории, а затем посмотрите на расширение, используя характеристики. В конце мы обращаемся к обратному процесс, к заданному ряду мы пытаемся найти его сумма.

В качестве мы изложили в общих чертах в разделе Системы функций, есть необходимо ответить на два вопроса: какие функции могут быть выражены в этом путь и как мы находим серию для них. И действительно, первый вопрос трудно, мы просто дадим частичный ответ позже. Начнем с определения.

Определение.
Пусть f — функция, а — некоторая точка внутри его домен.
Мы говорим, что мы расширили функцию f в степени ряд (at a ), если мы найдем такой степенной ряд, что

в каком-то районе и .
Затем этот ряд мощности называется расширением из f .

По результатам в предыдущий раздел следует что каждая функция, которая может быть разложена таким образом, должна иметь производные от все заказы в и . Это говорит нам о том, что нет смысла пытаться расширить другие функции. В нем также говорится, что когда мы говорим о расширении, мы имеем все эти производные доступны.

Отправной точкой нашего исследования является следствие в конце предыдущий раздел. Предположить, что у нас есть функция, которая может быть выражена серией от до . Если мы подставьте этот центр на в формулу для n -й производной, сразу получаем следующее.

Теорема (единственность разложения).
Пусть f — функция, которую можно разложить в степенной ряд

в каком-то районе и . Тогда для каждых k коэффициенты a _k обязательно удовлетворять

Другими словами, есть только один способ разложить функцию в степень. серии (если это вообще возможно). Эта уникальная силовая серия заслуживает названия.

Определение.
Пусть f — функция, а — некоторая точка внутри его домен. Предположим, что f имеет производные всех порядков от до . Затем мы определяем его рядов Тейлора по и 9029. 3 по формуле

Формула для коэффициентов та же, что и в случае Полином Тейлора, так что это действительно что-то вроде «бесконечного многочлена Тейлора».

Обратите внимание, что приведенная выше теорема была импликацией. Это означает, что как только мы функция, разложенная в степенной ряд, то этот ряд обязательно является Серия Тейлор. Однако, если мы возьмем функцию со всеми производными в точках a и построить ряд Тейлора по приведенной выше формуле, то нет гарантии, что и этот ряд будет сходящимся где-то еще, чем в a , и даже если он сходится, нет гарантировать, что она действительно сходится к исходной функции f . Например, в этой заметке мы показываем пример функция, которая является «хорошей» по большинству стандартов (имеет производные всех порядков всюду), ее ряд Тейлора сходится к ее сумме равномерно на всем реальная линия, однако сумма этого ряда Тейлора равна исходной функционировать только в одной точке, в центре ряда (где он фактически имеет работать для любой функции и серии, поэтому у него нет выбора). Эта ситуация где у нас есть проблемы с тем, чтобы серия попала в нужное место часто возникает, когда мы работаем с системами функций, и вдохновляет следующие обозначения.

Тильда означает, что серия справа получена из f используя приведенные выше формулы (это ряд Тейлора для f  ), но это также означает, что процесс создания этой серии Тейлора является чисто формально, так как на данный момент у нас нет информации, является ли сумма этого серия на самом деле не имеет ничего общего с f .

Очевидно, наша цель — заменить эту тильду на равенство, т. е. хотелось бы видеть, что ряд Тейлора справа на самом деле сходится к ф хоть где-то (кроме а , где сходимость есть автоматический). Как мы это узнаем? По определению следует взять частичные суммы T _N из T и проверить, сходятся к f .

Точно так же мы хотели бы выяснить, как разница | f  −  T _N | ведет себя, надеясь, что он пойдет к нулю как N уходит в бесконечность. Однако на самом деле это то, что мы уже видели раньше, поскольку T _N точно Полиномы Тейлора (см. Производные — Теория — Приложения), поэтому мы довольно много знаем об этой разнице. В частности, у нас есть Лагранж оценка его. Таким образом, мы можем переформулировать вопрос следующим образом:

Предположим, что f имеет производные всех порядков в некоторой окрестности U из и . Пусть х таково, что замкнутый интервал I с конечными точками a и x лежит в U . Мы хотим знать, когда правда, что

Обратите внимание, что в этой формуле x является фиксированным и, следовательно, x  —  a является константой. Когда мы вспоминаем что c ^Н / Н ! стремится к нулю в бесконечности, мы видим, что все зависит от того, насколько быстро растет максимум с Н . Если она совсем не растет или растет очень медленно, то лагранжева оценка ошибки стремится к нулю. Таким образом, мы получаем следующее.

Теорема.
Пусть f — функция такая, что она имеет производные всех порядков на некоторая окрестность U точки a . Пусть T будет его Тейлором серии и .
Если есть константа M такой, что | f   ^{( k )} ( t )| ≤ М ^к для всех натуральных чисел k и всех t из U , затем T сходится (равномерно) к f на U .

Таким образом, мы получаем одну группу функций, ряд Тейлора которых фактически равен их, а именно функции с равномерно ограниченными производными. Однако, это условие является слишком ограничительным, есть и другие функции, Ряды Тейлора сходятся там, где должны. Поиск правильного характеристика — сложная задача, определенно выходящая за рамки Math Tutor, и мы оставляем это профессиональным математикам.

Есть некоторые функции, для которых мы можем легко найти их разложения. В силу единственности разложения каждый степенной ряд является своим собственным рядом Тейлора. (с тем же центром). Расширение с центром, отличным от «своего» уже не так просто, но все еще можно сделать в случае «конечного» ряд, то есть в случае многочленов. Нам просто нужно создать правый центр. Например, если мы хотим найти ряд Тейлора для х ² с центром a  = 1, мы просто делаем

x ²  = [( x  − 1) + 1] ²  = ( x  — 1) ²  + 2(  x 9029.

Последний является степенным рядом с центром 1 (его коэффициенты равны нулю при k  > 2), поэтому это искомый Тейлор серии. (Мы получили бы тот же ряд, если бы воспользовались формулой из определения, конечно.) Попытка применить этот прием к бесконечному ряду не будь милым больше.

Теперь мы рассмотрим шесть известных расширений, которые являются основой большинства другие расширения.

Теорема.
Следующие расширения верны для указанных наборов.

Как следует из этих формул, выбор и  = 0 для центра очень популярен. На самом деле, он настолько популярен, что некоторые люди используют традиционное имя McLaurin серии для серии Taylor с этим центром. Однако он не универсален, и вы найдете его особенно в старых текстах.

Во всех шести случаях мы легко находим формулу для полиномов Тейлора из определение. Как насчет их сходимости? Вторая и третья формула ясны, сходимость следует из предыдущей теоремы (синус и косинус имеют все производные, ограниченные единицей всюду).

Для экспоненты мы также можем использовать эту теорему, но мы не можем этого сделать. глобально, поскольку экспонента ограничена только на ограниченных множествах. Однако это не проблема. Если мы возьмем любое действительное число x , мы можем всегда рассматривайте, например, открытое соседство У _{2| х |} (0). Это ограниченное множество и поэтому все производные от e ^x равномерно ограничены на нем, поэтому по приведенной выше теореме ряд Тейлора сходится к экспоненциальный там; в частности, он сходится к экспоненциальному при разрешении x , поскольку x принадлежит этому району. Для полноты мы включить прямое доказательство с использованием оценки Лагранжа, см. это примечание.

Разложение для логарифма может быть фактически получено несколькими способами, мы вернемся к нему и ниже; относительно его сходимости интервал, который мы заявленное явно самое большое, на что можно надеяться, поскольку в предыдущем разделе мы доказали, что этот интервал является в точности областью сходимости этого ряда Тейлора. Таким образом, остается показать, что сумма ряда в этой области в точности равна ln( x ). Однако здесь нельзя использовать приведенную выше теорему, так как производные не ограничены равномерно. Таким образом, этот случай гораздо сложнее, для более подробной информации см. это примечание.

Пятая формула как раз геометрический ряд, поэтому в этом нет ничего нового.

Вероятно, наиболее интересной из шести является последняя формула, также называемая биномиальный ряд или биномиальное расширение . Это верно для всех c и A , что, в частности, показывает, что биномиальные числа также может быть определен для общего номера A . Это делается вторым формула с пониманием того, что когда k  = 0, получаем 1. В качестве примера покажем, как выглядит ряд, когда c  = 1, которая является часто используемой формой. Мы также показываем специальную формулу для «минус А «, иногда бывает полезно при работе с обратными. Оба работают для | х | < 1,

Заметим также, что если A — натуральное число, то по определению для k  >  A все коэффициенты равны нулю. Таким образом, сумма конечна, она всегда сходится и фактически является известной биномиальная формула, которую мы знаем из средней школы.

Одна из причин, по которой эти формулы важны, заключается в следующем: мы редко расширяем функции по определению, как мы сделали это выше. В большинстве случаев мы используем различные уловки, чтобы хоть как-то получить новые расширения из тех, что мы уже знать. Приведенные выше шесть являются отправной точкой для большинства таких расчетов. трюки появляются только сейчас.

Расширение и операции

Чтобы получить разложения новых функций из известных разложений, мы используем свойства, которые, как известно, работают для степенных рядов. Теорема о алгебраические операции из предыдущий раздел дает этот удобный факт.

Теорема.
Предположим, что у нас есть эти разложения в некоторой окрестности и .

Тогда и в этом районе

Как насчет деления f  / g ? Очевидно, это достаточно знать, как расширить функцию 1/ f (при условии что f ( a ) ≠ 0).

Теорема.
Предположим, что функция f может быть разложена в ряд Тейлора при и что f ( a ) ≠ 0. Тогда также функция 1/ f могут быть расширены в серию Тейлора с по и этот ряд имеет положительный радиус сходимости.

Эта теорема не предлагает никакой формулы для нового ряда — и с хорошей причина, нет никакого разумного способа указать это. На практике мы используем метод неопределенных коэффициентов . Мы действительно можем применить это напрямую к f  / g и возьмем 1/ f как частный случай. Предположим, что оба f и g расширяются до серии Taylor с номерами a и что г ( a ) ≠ 0. По приведенной выше теореме также их отношение может быть разложить в ряд Тейлора с неизвестными коэффициентами к _к . Мы можем написать

Получившаяся система бесконечного числа линейных уравнений с бесконечно много неизвестных к _к обычно невозможно решить в явном виде, но позволяет вычислить как много коэффициентов к _к как мы хотим, что очень полезно, когда мы хотим аппроксимировать ж  / г используя только конечную часть ряда Тейлора. Для примера мы ссылаемся на Решенные проблемы, а именно эта проблема (это необычно красиво, но хорошо иллюстрирует идею) и Эта проблема (это более характерно).

Мы также часто связываем функции с другими функциями, используя производную или интеграл. Тогда мы можем использовать эта теорема из предыдущей раздел.

Теорема.
Предположим, что у нас есть следующее разложение в некоторой окрестности и .

Тогда и в этом районе

Во второй постановке можно использовать и неопределенный интеграл, но тогда необходимо найти правильную константу. Мы покажем пример ниже. Наконец, есть и другие операции, которые могут помочь в расширении новых функций.

Теорема (подстановка в ряд).
Предположим, что у нас есть следующее разложение в некоторой окрестности и .

Тогда также

Первое утверждение верно для любых A и радиуса сходимости новый ряд такой же, как и исходный, но его центр (и регион сходимости) соответственно сдвигаются.
Второе утверждение верно для всех ненулевых A и радиуса сходимость нового ряда есть R _f  /| А |.

Третье утверждение немного шатко, так как результатом является мощность серия только для особых г . Тогда область сходимости должна быть исследованы индивидуально.

На самом деле, в первых двух утверждениях мы фактически знаем даже область сходимость нового ряда. В первом утверждении новый регион просто оригинал, но сдвинутый. Область сходимости во втором случае можно получить, уменьшив оригинал на A отрицательный также должен перевернуть его вокруг . То есть, если исходный ряд сходится в правом конце, то новый также сходится в правая конечная точка для A  > 0 и сходится в левой конечной точке для A  < 0. Это все на самом деле просто здравый смысл и хорошее понимание замены.

Пример: Выведем расширение для ф ( x ) = ln(1 −  x ) в a  = 0,

Ключом к этому расширению является наблюдение, что f ′′( x ) = −1/(1 −  x ) и это именно сумма принадлежащий геометрический ряд, который каждый знает. Итак, начнем с формулы геометрического ряда (мы используйте переменную t ), а затем мы интегрируем обе стороны от 0 до х

Этот ряд часто используется для логарифмирования. Исходный ряд сходится для t удовлетворяющих −1 <  t  < 1, поэтому новый также сходится по крайней мере на этом множестве, и его радиус сходимости должен остаются прежними (то есть 1). Тем не менее, мы, возможно, добились сходимости в какой-то момент. конечные точки. Когда мы вставляем x  = −1 а также x  = 1 и используя подходящие тесты, мы находим, что область сходимости этого серия [−1,1). Откуда мы знаем, что сумма этого ряда при x  = −1 равно лн(2)? Одним из возможных аргументов является использование непрерывности, см. Теорема Абеля о сходимости в предыдущем разделе. Таким образом, мы имеем справедливое расширение на [−1,1).

Если мы запишем этот результат, используя y , а затем воспользуемся заменой y  = − x , мы получаем

Исходный ряд сходится для y удовлетворяющих −1 ≤ года  < 1, поэтому, когда мы заменяем - х для y получаем область сходимости (−1,1] для новой серии.

С другой стороны, если мы заменим y  = 1 −  x , то мы получим именно тот ряд для лн ( х ) что у нас было выше Теорема.

Возможно, это удивительно, учитывая трудности, с которыми мы столкнулись при поиске серий. за 1/ ф что на самом деле существует явный способ расширить обратную функцию.

Теорема (формула обращения Лагранжа).
Предположим, что функцию f можно разложить в ряд на некоторых окрестности точки a . Предположим далее, что ф ′′( а ) не равен нулю. Обозначать b  =  f ( a ).
Тогда есть окрестности a , на котором есть функция f обратимой и окрестностью b , на которой эта обратная е ₋₁ можно разложить в степенной ряд. Более того, эту серию можно найти как

Завершим эту часть еще одним полезным утверждением.

Теорема.
Предположим, что у нас есть следующее разложение в некоторой окрестности и .

Тогда в этой окрестности мы также имеем следующие разложения.

(i) Для любого положительного целого числа n ,

(ii) Если f имеет корень кратности n при a , то

Второе утверждение имеет смысл по следующей причине. Если является корень из кратности н за ф , то первый n  − 1 производные от f at a нуль (см. это примечание). Поэтому и первый н  — 1 коэффициенты ряда Тейлора равны нулю, а это означает, что фактически в серии для f индексация начинается с n , а не с 0. Это объясняет почему после сдвига индекса получается вторая формула.

Дополнительные примеры использования вышеуказанных свойств для расширения функций см. Обзор методов а также Решенные проблемы — серия функции.

Мы завершаем эту часть о свойствах рядов Тейлора тем, что можно уже догадались из шести расширений выше.

Факт.
Пусть f — функция, имеющая ряд Тейлора с центром в a  = 0, пусть a _k — его коэффициенты.
Если f нечетно, то а _k  = 0 для всех четных k .
Если f четно, то a _k  = 0 для всех нечетных k .

Подведение итогов серии

Мы несколько раз упоминали, что подведение итогов может быть довольно сложным. Приведенные выше приемы расширения функции можно также использовать для суммирования мощности. серии (при условии, что нам повезет). Основная идея состоит в том, чтобы изменить данное ряд в тот, который мы уже знаем, применяя преобразования из приведенные выше теоремы к нему, отслеживая, что он делает со своей суммой. это лучше всего объяснить на примере.

Пример: Найдите сумму

Есть сериал похожий на этот? Есть ряд, в котором есть термины г ^к / к , мы можем почти добраться туда, обозначив y  =  x  + 1. Осталось зафиксировать мощность так, чтобы она совпадала с числом в знаменатель, но это не проблема. Вот так.

А как насчет значения x  = −1? Это просто, мы просто поместите его в данную серию и найдите, что f (−1) = 0,

Мы также можем попробовать другой подход. Часто нам нужно избавиться от лишних к в серии. В нашей серии есть доп. к  + 1 в знаменателе, поэтому мы были бы признательны, если бы к  + 1 появилось также в числителе. Есть способ получить к в числитель, а именно взяв производную от ряда. Нам нужно к  + 1, поэтому перед дифференцированием нам нужно создать ( x  + 1) ^{к  + 1} там. Раз нет деления на к + 1, мы используем геометрический ряд.

Осталось закрепить правый C . Самый простой способ это просто положить некоторые хороший x в последнее равенство. Так как слева подставляем в f , то есть в данный ряд у нас особого выбора нет. Единственная ценность, которую мы действительно можем вложить в эту серию, это x  = −1, но, к сожалению, это единственное значение, которое нам не разрешено в последней строке. Что мы можем сделать?

Казалось бы, мы могли бы решить эту проблему, используя предпоследнюю строку. Приглядевшись, мы видим, что это неправда. Обратите внимание, что если x  = −1, то во второй строке умножаем на ноль, что недопустимо в уравнении. Таким образом, для этого значения все последующие равенства сомнительны. К счастью для нас, мы можем смотреть еще ближе. Что у нас есть на предпоследней строке? У нас есть одна функция на слева и справа, и мы точно знаем, что они равны для всех x с определенного интервала кроме одной точки в его середине. Поскольку эти две функции непрерывны, мы также должны иметь равенство в этом конкретный момент. Мы спасены, подставляем −1 в предпоследнюю строку и узнаем, что C  = 0. Так как мы использовали интегрирование который влияет на конечные точки, теперь мы должны проверить сходимость при −2 и при 0 и мы получим тот же вывод, что и выше.

---

ряд Фурье
Назад к теории — Серия функций

Силовая серия

Серия Power

Определение степенного ряда

Теперь мы исследуем обобщение многочленов. Полином ниже полином пятой степени

3x ⁵ — 2x ⁴ + 5x ³ + 4x — 1

если вместо многочлена пятой степени мы рассматриваем многочлен бесконечной степень.

Определение степенного ряда Пусть f(x) будет функцией, представленной рядом         Тогда f(x) называется функцией степенного ряда .

В более общем случае, если f(x) представлен рядом

       

Тогда мы называем f(x) степенной ряд с центром в точке x = с .

Примеры

Серия мощности

является с центром в 0.

силовой ряд

является с центром в -2.

---

Радиус сходимости

Далее мы хотим исследовать область степенных рядов. Вспомнить, чтобы найти области, мы спрашиваем, какие значения x могут ручка функции? Это особенно важно для степенных рядов, поскольку бесконечные ряды часто не сходятся. Это была бы непреодолимая задача подставить каждое значение x и посмотреть, соответствует ли ряд сходится для этого значения. К счастью, у нас есть следующая теорема.

Теорема

Если

есть степенной ряд с центром в точке c тогда только следующие три являются возможными для области определения f.

1. домен — это значение c Только.

2. Есть домен — все действительные числа.

3. Есть существует действительное число R такое, что все значения x которые удовлетворяют
   
   | х — с | <  R

   находятся в домене и значения, которые удовлетворяют
   
   | х — с | >
   р.
   не в домене.

Р называется радиусом сходимости f.

Чтобы вычислить радиус сходимости, мы используем критерий отношения.

Пример:  Найти радиус сходимости

Решение

Мы используем тест отношения:

Решаем     


или 
        |x — 3| < 2 

так что  

        1 < x < 5

Так как 

        1/2(5 — 1) = 2

радиус схождения 2

Упражнение:  

Найдите радиус сходимости

---

Серия Тейлора и Маклорена

Поскольку степенные ряды являются функциями, возникает естественный вопрос: «Может ли наш повседневные функции могут быть представлены в виде степенных рядов?» Кроме того, «данные степенной ряд, можем ли мы найти повседневную функцию, эквивалентную степенной серии?»

Следующее определение помогает ответить на эти вопросы.

Определение    Серия Тейлора для f (х) с центром в точке x = c равно Если с = 0, то ряд называется ряд Маклорена для ф.

Мы используем обозначение f ⁽ⁿ⁾ для обозначения n-я производная от f.

Пример:

Найти ряд Маклаурина для

        f(x) = cos(x)

Решение

Вычисляем:

е (0) = 1 f ‘(0) = 0        f »(0) = -1        f ⁽³⁾ (0) = 0

       f ⁽⁴⁾ (0) = 1      f ⁽⁵⁾ (0) = 0       f ⁽⁶⁾ (0) = -1        f ⁽⁷⁾ (0) = 0

       f ⁽⁸⁾ (0) = 1      f ⁽⁹⁾ (0) = 0 ф ⁽¹⁰⁾ (0) = -1        f ⁽¹¹⁾ (0) = 0

Отсюда имеем серию

1 — х ² /2+ х ⁴ /4! — х ⁶ /6! + х ⁸ /8! — х ⁸ /8! + . ..

Мы видим, что ряд

Упражнения  Найти расширение ряда Тейлора для

1. sin(x) с центром в x = 0
   

2. ln(x) с центром в точке x = 0

---

Отличие и интеграция серии Power

Поскольку степенной ряд является функцией, естественно спросить, является ли функция непрерывная, дифференцируемая или интегрируемая. Следующая теорема отвечает на этот вопрос.

Теорема: Предположим, что функция задана степенным рядом            f(x) = Sa n (x — c) n и что интервал сходимости равен c + R) (плюс возможные конечные точки) , то f(x) непрерывна, дифференцируема и интегрируема на этом интервале (не обязательно включая конечные точки). Чтобы получить производную или интеграл от f(x) мы можем передать производную или интеграл через S. В других слова и Кроме того, радиус сходимости производной и интеграла равен R.

Пример:

Рассмотрим серию

f(x) = Sx ⁿ

по ОТС этот ряд сходится при |x| < 1, поэтому центр сходимости равен 0, а радиус равен 1. По приведенной выше теореме

f ‘(x) = Snx ^n-1

имеет центр сходимости 0 и радиус сходимости 1 также. Мы также можем сказать, что

также имеет центр схождения 0 и радиус схождения 1.

Упражнение:

Покажите, что

удовлетворяет дифференциальному уравнению

у» + ху’ — у = 0

 

Мы также можем использовать подстановку, чтобы найти степенной ряд.

Пример 

Найти серию Maclaurin для 

1

1 — х ²

Решение

Замена x ² вместо x в

 у нас есть

---

Назад на главную страницу Math 117

Назад к математике Дом Департамента

электронная почта Вопросы и предложения

 

Расширение серии: определение, распространенные типы

Поделиться на

Хотите «обмануть» в исчислении? Ознакомьтесь с нашим справочником «Практическое исчисление с мошенничеством» , в котором вы найдете сотни простых ответов в удобной электронной книге.

Последовательность и серия >

Содержание:

• Что такое расширение серии?
• Общие типы
• Список расширений общей серии

В расширении ряда функция представлена ​​суммой степеней:

• Одна из ее переменных,
• Другая функция (обычно элементарная функция).

Например, натуральная показательная функция e ^x можно разложить в бесконечный ряд:

Это конкретное разложение называется рядом Тейлора.

Расширения серии

имеют множество применений в широком спектре научных областей. Например, в исчислении, если вы знаете значение функции в определенной точке (и ее производные), вы можете вычислить значения для всей функции. Или, если у вас есть особенно уродливая производная или интеграл, вы можете использовать разложение в ряд, чтобы упростить математику и найти приближенное решение.

Наиболее часто встречающиеся расширения ряда:

• Биномиальный ряд: Две биномиальные величины возводятся в степень и расширяются. Например, (а + b) ² = (а + b) * (а + b).
• Степенной ряд: Как и многочлен бесконечной степени, его можно записать в нескольких различных формах. Простой пример, если 1 + x + x ² + … + x ⁿ .
• Ряд Тейлора и Маклорена: аппроксимирует функции рядом полиномиальных функций.
• Ряд Лорана: способ представления сложной функции в виде сложного степенного ряда с отрицательными степенями.

Это не единственные инструменты для расширения серии. Существует много других, но они, как правило, используются в очень специфических обстоятельствах. Например, полиномы Цернике используются в оптике для расчета формы аберрированных волновых фронтов в оптических системах (Индиана, 2020), а ряды Стирлинга используются для аппроксимации факториалов. Другие включают:

• Расширение серии арктангенса :
• Серия Дирихле : Любая серия формы
  . Известным примером является дзета-функция Реймана (McCarthy, 2018).
  
• Функции Лежандра первого рода (также называемые полиномами Лежандра) являются решениями дифференциального уравнения Лежандра.
• Серия Puiseux : обобщение степенных рядов, позволяющее использовать отрицательные и дробные показатели неопределенного T.

Функция арктангенса может быть представлена ​​в виде ряда Маклорена:

Расширение ряда арктангенса получается путем взятия основного интеграла [1]:

Затем подынтегральная функция заменяется рядом: Член индивидуально интегрируется, чтобы получить ряд (для -1 < x < 1). Обратите внимание, что обе стороны равны нулю, когда x = 0, поэтому «+ C» нет.

Хотя этот ряд обычно приписывают Готфриду Лейбницу (1646–1716) или Джеймсу Грегори (1833–1675) [2], он был известен двумя веками ранее индийскому математику Нилакантхе Сомаяджи (ок. 1444–1544) [2].

Почему важно расширение серии Arctan?

Возможно, наиболее распространенное использование ряда арктангенса — приближение числа π. Помимо отношения длины окружности к ее диаметру, π также определяется как удвоенное наименьшее положительное число x, для которого cos(x) = 0. . Больше членов не обязательно означает большую точность: двухчленный ряд Мачина аппроксимирует π как 3,157866845, а 11-членный ряд Доджсона дает π как 3,077143544 [3].

Еще одна причина интереса к серии арктанов — чисто исторический интерес. История этой конкретной серии важна, потому что она была разработана до исчисления; Он демонстрирует ранние идеи о рядах и о том, как они связаны с квадратурой или процессами нахождения площади под кривой (также известной как интегрирование) [4].

Расширение серии Arctan: Каталожные номера

[1] 2.3 Computing Pi (продолжение). Получено 6 апреля 2021 г. с:
https://www.macalester.edu/aratra/chapt2/chapt2_3a.html
[2] Хван Цзянь-Ли. (2004). Некоторые замечания о методе арктангенсов для вычисления числа π. Математическая газета. Математическая ассоциация.
[3] Абелес, Ф. Чарльз Л. Доджсон, геометрический подход к отношениям арктангенса для числа Пи. Historia Mathematica 20, стр. 151-159. Получено 6 апреля 2021 г. с: http://users.uoa.gr/~apgiannap/Sources/Dodgson-pi.pdf
[4] Roy, R. (1990). Открытие формулы ряда для π Лейбницем, Грегори и Нилакантхой. Получено 6 апреля 2021 г. с: http://users.uoa.gr/~apgiannap/Sources/Roy-pi.pdf

Ссылки

Университет Индианы в Блумингтоне. (2020). Стандарты сообщения об оптических аберрациях глаз. Получено 10 июля 2021 г. с: https://www.opt.indiana.edu/vsg/library/vsia/vsia-2000_taskforce/tops4_2.html#:~:text=Standards%20for%20Reporting%20the%20Optical%20Aberrations% 20of%20Eyes&text=%20Zernike%20полиномы%20являются%20a,учеником%20%20%20оптической%20системой.
Маккарти, Дж. (2018). Серия Дирихле, получено 2 декабря 2020 г. с: https://www.math.wustl.edu/~mccarthy/amaster-ds.pdf

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Расширение серии: определение, общие типы» из CalculusHowTo.com : Исчисление для всех нас! https://www.calculushowto.com/series-expansion/

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

ИсчислениеHowTo.com

6.3 Серия Тейлора и Маклорена. Исчисление, том 2

Цели обучения

• 6.3.1 Описать процедуру нахождения полинома Тейлора заданного порядка для функции.
• 6.3.2 Объясните смысл и значение теоремы Тейлора с остатком.
• 6.3.3 Оцените остаток для аппроксимации ряда Тейлора данной функции.

В предыдущих двух разделах мы обсуждали, как находить представления степенных рядов для определенных типов функций, в частности, функций, связанных с геометрическими рядами. Здесь мы обсуждаем представления степенных рядов для других типов функций. В частности, мы обращаемся к следующим вопросам: какие функции могут быть представлены степенными рядами и как мы находим такие представления? Если мы можем найти представление в виде степенного ряда для конкретной функции ff, и этот ряд сходится на каком-то интервале, как мы докажем, что этот ряд действительно сходится к f?f?

Обзор серии Taylor/Maclaurin

Рассмотрим функцию ff, которая представлена ​​в виде степенного ряда при x=a.x=a. Тогда ряд имеет вид

∑n=0∞cn(x−a)n=c0+c1(x−a)+c2(x−a)2+⋯.∑n=0∞cn(x−a)n=c0+c1( х-а)+с2(х-а)2+⋯.

(6.4)

Какими должны быть коэффициенты? На данный момент мы игнорируем вопросы сходимости, а вместо этого сосредоточимся на том, каким должен быть ряд, если он существует. Мы вернемся к обсуждению сходимости позже в этом разделе. Если ряд Уравнение 6.4 является представлением для ff при x=a,x=a, мы, безусловно, хотим, чтобы ряд равнялся f(a)f(a) при x=a. x=a. Вычисляя ряд при x=a,x=a, мы видим, что

∑n=0∞cn(x−a)n=c0+c1(a−a)+c2(a−a)2+⋯=c0.∑n=0∞cn(x−a)n=c0+ c1(a−a)+c2(a−a)2+⋯=c0.

Таким образом, ряд равен f(a)f(a), если коэффициент c0=f(a).c0=f(a). Кроме того, мы хотели бы, чтобы первая производная степенного ряда равнялась f′(a)f′(a) при x=a.x=a. Дифференцируя уравнение 6.4 почленно, мы видим, что

ddx(∑n=0∞cn(x−a)n)=c1+2c2(x−a)+3c3(x−a)2+⋯.ddx(∑n=0∞cn(x−a)n )=c1+2c2(x−a)+3c3(x−a)2+⋯.

Следовательно, при x=a,x=a производная равна

ddx(∑n=0∞cn(x−a)n)=c1+2c2(a−a)+3c3(a−a)2+⋯=c1.ddx(∑n=0∞cn(x−a )n)=c1+2c2(a−a)+3c3(a−a)2+⋯=c1.

Следовательно, производная ряда равна f′(a)f′(a), если коэффициент c1=f′(a).c1=f′(a). Продолжая в том же духе, мы ищем коэффициенты c _n такие, что все производные степенного ряда (6.4) согласуются со всеми соответствующими производными от ff при x=a.x=a. Вторая и третья производные уравнения 6.4 равны

.

d2dx2(∑n=0∞cn(x−a)n)=2c2+3·2c3(x−a)+4·3c4(x−a)2+⋯d2dx2(∑n=0∞cn(x− а)n)=2c2+3·2c3(x−a)+4·3c4(x−a)2+⋯

и

d3dx3(∑n=0∞cn(x−a)n)=3·2c3+4·3·2c4(x−a)+5·4·3c5(x−a)2+⋯. d3dx3(∑n =0∞cn(x−a)n)=3·2c3+4·3·2c4(x−a)+5·4·3c5(x−a)2+⋯.

Следовательно, при x=a,x=a вторая и третья производные

d2dx2(∑n=0∞cn(x−a)n)=2c2+3·2c3(a−a)+4·3c4(a−a)2+⋯=2c2d2dx2(∑n=0∞cn(x −a)n)=2c2+3·2c3(a−a)+4·3c4(a−a)2+⋯=2c2

и

d3dx3(∑n=0∞cn(x−a)n)=3·2c3+4·3·2c4(a−a)+5·4·3c5(a−a)2+⋯=3·2c3d3dx3( ∑n=0∞cn(x−a)n)=3·2c3+4·3·2c4(a−a)+5·4·3c5(a−a)2+⋯=3·2c3

равно f″(a)f″(a) и f‴(a),f‴(a) соответственно, если c2=f″(a)2c2=f″(a)2 и c3=f‴(a )3·2.c3=f‴(a)3·2. В более общем виде мы видим, что если ff имеет представление степенного ряда при x=a,x=a, то коэффициенты должны быть заданы как cn=f(n)(a)n!.cn=f(n)(a) н!. То есть ряд должен быть

∑n=0∞f(n)(a)n!(x−a)n=f(a)+f′(a)(x−a)+f″(a)2!(x−a) 2+f‴(a)3!(x−a)3+⋯.∑n=0∞f(n)(a)n!(x−a)n=f(a)+f′(a)( x−a)+f″(a)2!(x−a)2+f‴(a)3!(x−a)3+⋯.

Этот степенной ряд для ff известен как ряд Тейлора для ff в п.в. Если a=0,a=0, то этот ряд известен как ряд Маклорена для ф.ф.

Определение

Если ff имеет производные всех порядков в точках x=a,x=a, то ряд Тейлора для функции ff в точках aa равен

∑n=0∞f(n)(a)n!(x−a) n=f(a)+f′(a)(x−a)+f″(a)2!(x−a)2+⋯+f(n)(a)n!(x−a)n+⋯ . ∑n=0∞f(n)(a)n!(x−a)n=f(a)+f′(a)(x−a)+f″(a)2!(x−a) 2+⋯+f(n)(a)n!(x−a)n+⋯.

(6.5)

Ряд Тейлора для ff в 0 известен как ряд Маклорена для ff.

Позже в этом разделе мы покажем примеры нахождения ряда Тейлора и обсудим условия, при которых ряд Тейлора для функции будет сходиться к этой функции. Здесь мы сформулируем важный результат. Напомним из уникальности степенных рядов, что представления степенных рядов уникальны. Следовательно, если функция ff имеет степенной ряд в точках a, a, то она должна быть рядом Тейлора для ff в точках a.a.

Теорема 6,6

Уникальность ряда Тейлора

Если функция ff имеет степенной ряд в точках и , который сходится к ff на некотором открытом интервале, содержащем и , то этот степенной ряд является рядом Тейлора для ff в точках и .

Доказательство следует непосредственно из уникальности степенного ряда.

Чтобы определить, сходится ли ряд Тейлора, нам нужно посмотреть на его последовательность частичных сумм. Эти частичные суммы представляют собой конечные полиномы, известные как полиномы Тейлора.

СМИ

Посетите архив MacTutor History of Mathematics, чтобы прочитать краткие биографии Брука Тейлора и Колина Маклорена и то, как они разработали концепции, названные в их честь.

Полиномы Тейлора

n -я частичная сумма ряда Тейлора для функции ff в aa известна как n -й полином Тейлора. Например, 0-я, 1-я, 2-я и 3-я частичные суммы ряда Тейлора равны

.

p0(x)=f(a),p1(x)=f(a)+f′(a)(x−a),p2(x)=f(a)+f′(a)(x− а)+f″(a)2!(x−a)2,p3(x)=f(a)+f′(a)(x−a)+f″(a)2!(x−a) 2+f‴(a)3!(x−a)3,p0(x)=f(a),p1(x)=f(a)+f′(a)(x−a),p2(x )=f(a)+f′(a)(x−a)+f″(a)2!(x−a)2,p3(x)=f(a)+f′(a)(x− а)+f″(a)2!(x−a)2+f‴(a)3!(x−a)3,

соответственно. Эти частичные суммы известны как 0-й, 1-й, 2-й и 3-й многочлены Тейлора от ff в точках a, a соответственно. Если a=0,a=0, то эти полиномы известны как полиномы Маклорена для ф.ф. Дадим формальное определение полиномов Тейлора и Маклорена для функции f.f.

Определение

Если ff имеет n производных в точках x=a,x=a, то n -й полином Тейлора для ff в точке aa равен

pn(x)=f(a)+f′(a)(x −a)+f″(a)2!(x−a)2+f‴(a)3!(x−a)3+⋯+f(n)(a)n!(x−a)n. pn(x)=f(a)+f′(a)(x−a)+f″(a)2!(x−a)2+f‴(a)3!(x−a)3+⋯ +f(n)(a)n!(x−a)n.

n -й полином Тейлора для ff в 0 известен как n -й полином Маклорена для ff.

Теперь мы покажем, как использовать это определение, чтобы найти несколько полиномов Тейлора для f(x)=lnxf(x)=lnx при x=1.x=1.

Пример 6.11

Нахождение полиномов Тейлора

Нахождение полиномов Тейлора p0,p1,p2p0,p1,p2 и p3p3 для f(x)=lnxf(x)=lnx при x=1.x=1. Используйте графическую утилиту, чтобы сравнить график ff с графиками p0,p1,p2p0,p1,p2 и p3. p3.

Решение

Чтобы найти эти полиномы Тейлора, нам нужно вычислить ff и его первые три производные при x=1.x=1.

f(x)=lnxf(1)=0f′(x)=1xf′(1)=1f″(x)=−1x2f″(1)=−1f‴(x)=2x3f‴(1)= 2f(x)=lnxf(1)=0f′(x)=1xf′(1)=1f″(x)=−1x2f″(1)=−1f‴(x)=2x3f‴(1)=2

Следовательно,

p0(x)=f(1)=0,p1(x)=f(1)+f′(1)(x−1)=x−1,p2(x)=f(1 )+f′(1)(x−1)+f″(1)2(x−1)2=(x−1)−12(x−1)2,p3(x)=f(1)+ f′(1)(x−1)+f″(1)2(x−1)2+f‴(1)3!(x−1)3=(x−1)−12(x−1) 2+13(x−1)3.p0(x)=f(1)=0,p1(x)=f(1)+f′(1)(x−1)=x−1,p2(x )=f(1)+f′(1)(x−1)+f″(1)2(x−1)2=(x−1)−12(x−1)2,p3(x)= f(1)+f′(1)(x−1)+f″(1)2(x−1)2+f‴(1)3!(x−1)3=(x−1)−12 (х-1)2+13(х-1)3.

Графики y=f(x)y=f(x) и первых трех полиномов Тейлора показаны на рис. 6.5.

Рисунок 6,5 На этом графике нанесены функция y=lnxy=lnx и полиномы Тейлора p0,p1,p2p0,p1,p2 и p3p3 при x=1x=1.

Контрольно-пропускной пункт 6.10

Найдите полиномы Тейлора p0,p1,p2p0,p1,p2 и p3p3 для f(x)=1x2f(x)=1×2 при x=1. x=1.

Теперь мы покажем, как найти полиномы Маклорена для e ^x , sinx,sinx и cosx.cosx. Как указывалось выше, полиномы Маклорена — это полиномы Тейлора с центром в нуле.

Пример 6.12

Нахождение полиномов Маклорена

Для каждой из следующих функций найдите формулы для полиномов Маклорена p0,p1,p2p0,p1,p2 и p3.p3. Найдите формулу для многочлена Маклорена n th и запишите ее, используя сигма-нотацию. Используйте графическую утилиту, чтобы сравнить графики p0,p1,p2p0,p1,p2 и p3p3 с f.f.

1. f(x)=exf(x)=ex
2. f(x)=sinxf(x)=sinx
3. f(x)=cosxf(x)=cosx

Решение

1. Поскольку f(x)=ex,f(x)=ex, мы знаем, что f(x)=f′(x)=f″(x)=⋯=f(n)(x)=exf(x )=f′(x)=f″(x)=⋯=f(n)(x)=ex для всех натуральных чисел n . Следовательно,

   f(0)=f′(0)=f″(0)=⋯=f(n)(0)=1f(0)=f′(0)=f″(0)=⋯=f (n)(0)=1

   
   для всех положительных целых чисел n . Следовательно, имеем

   p0(x)=f(0)=1,p1(x)=f(0)+f′(0)x=1+x,p2(x)=f(0)+f′ (0)x+f″(0)2!x2=1+x+12×2,p3(x)=f(0)+f′(0)x+f″(0)2×2+f‴(0)3 !x3=1+x+12×2+13!x3,pn(x)=f(0)+f′(0)x+f″(0)2×2+f‴(0)3!x3+⋯+f(n )(0)n!xn=1+x+x22!+x33!+⋯+xnn!=∑k=0nxkk!.p0(x)=f(0)=1,p1(x)=f(0) +f′(0)x=1+x,p2(x)=f(0)+f′(0)x+f″(0)2!x2=1+x+12×2,p3(x)=f (0)+f′(0)x+f″(0)2×2+f‴(0)3!x3=1+x+12×2+13!x3,pn(x)=f(0)+f′( 0)x+f″(0)2×2+f‴(0)3!x3+⋯+f(n)(0)n!xn=1+x+x22!+x33!+⋯+xnn!=∑k= 0нкскк!.

   
   Функция и первые три полинома Маклорена показаны на рис. 6.6.
   

   Рисунок 6,6 На графике показаны функция y=exy=ex и полиномы Маклорена p0,p1,p2p0,p1,p2 и p3.p3.

2. Для f(x)=sinx,f(x)=sinx значения функции и ее первых четырех производных при x=0x=0 задаются следующим образом:

   f(x)=sinxf(0)=0f′ (x)=cosxf′(0)=1f″(x)=−sinxf″(0)=0f‴(x)=−cosxf‴(0)=−1f(4)(x)=sinxf(4)( 0)=0.f(x)=sinxf(0)=0f′(x)=cosxf′(0)=1f″(x)=−sinxf″(0)=0f‴(x)=−cosxf‴( 0)=−1f(4)(x)=sinxf(4)(0)=0.

   
   Поскольку четвертая производная sinx,sinx, шаблон повторяется. То есть f(2m)(0)=0f(2m)(0)=0 и f(2m+1)(0)=(−1)mf(2m+1)(0)=(−1)m для m≥0.m≥0. Таким образом, имеем

   p0(x)=0,p1(x)=0+x=x,p2(x)=0+x+0=x,p3(x)=0+x+0−13!x3 =x−x33!,p4(x)=0+x+0−13!x3+0=x−x33!,p5(x)=0+x+0−13!x3+0+15!x5=x −x33!+x55!,p0(x)=0,p1(x)=0+x=x,p2(x)=0+x+0=x,p3(x)=0+x+0−13 !x3=x−x33!,p4(x)=0+x+0−13!x3+0=x−x33!,p5(x)=0+x+0−13!x3+0+15!x5 =x−x33!+x55!,

   
   и для m≥0,m≥0,

   p2m+1(x)=p2m+2(x)=x−x33!+x55!−⋯+(−1) mx2m+1(2m+1)!=∑k=0m(−1)kx2k+1(2k+1)!.p2m+1(x)=p2m+2(x)=x−x33!+x55!− ⋯+(−1)mx2m+1(2m+1)!=∑k=0m(−1)kx2k+1(2k+1)!.

   
   Графики функции и ее полиномов Маклорена показаны на рис. 6.7.
   

   Рисунок 6.7 График показывает функцию y=sinxy=sinx и полиномы Маклорена p1,p3p1,p3 и p5.p5.

3. Для f(x)=cosx,f(x)=cosx значения функции и ее первых четырех производных при x=0x=0 задаются следующим образом:

   f(x)=cosxf(0)=1f′ (x)=−sinxf′(0)=0f″(x)=−cosxf″(0)=−1f‴(x)=sinxf‴(0)=0f(4)(x)=cosxf(4)( 0)=1.f(x)=cosxf(0)=1f′(x)=−sinxf′(0)=0f″(x)=−cosxf″(0)=−1f‴(x)=sinxf‴ (0)=0f(4)(x)=cosxf(4)(0)=1.

   
   Поскольку четвертая производная равна cosx,cosx, шаблон повторяется. Другими словами, f(2m)(0)=(−1)mf(2m)(0)=(−1)m и f(2m+1)=0f(2m+1)=0 для m≥0. м≥0. Следовательно,

   p0(x)=1,p1(x)=1+0=1,p2(x)=1+0−12!x2=1−x22!,p3(x)=1+0−12! x2+0=1−x22!,p4(x)=1+0−12!x2+0+14!x4=1−x22!+x44!,p5(x)=1+0−12!x2+0 +14!x4+0=1−x22!+x44!,p0(x)=1,p1(x)=1+0=1,p2(x)=1+0−12!x2=1−x22! ,p3(x)=1+0−12!x2+0=1−x22!,p4(x)=1+0−12!x2+0+14!x4=1−x22!+x44!,p5( x)=1+0−12!x2+0+14!x4+0=1−x22!+x44!,

   
   и для n≥0,n≥0,

   p2m(x)=p2m+1(x )=1−x22!+x44!−⋯+(−1)mx2m(2m)!=∑k=0m(−1)kx2k(2k)!.p2m(x)=p2m+1(x)=1− x22!+x44!−⋯+(−1)mx2m(2m)!=∑k=0m(−1)kx2k(2k)!.

   
   Графики функции и полиномов Маклорена представлены на рис. 6.8.
   

   Рисунок 6,8 На этом графике изображены функция y=cosxy=cosx и полиномы Маклорена p0,p2p0,p2 и p4p4.

Контрольно-пропускной пункт 6.11

Найдите формулы для полиномов Маклорена p0,p1,p2p0,p1,p2 и p3p3 для f(x)=11+x.f(x)=11+x. Найдите формулу для n -го многочлена Маклорена. Запишите ответ, используя сигма-нотацию.

Теорема Тейлора с остатком

Напомним, что n -й полином Тейлора для функции ff при a является n -й частичной суммой ряда Тейлора для ff при a . Следовательно, чтобы определить, сходится ли ряд Тейлора, нам нужно определить, сходится ли последовательность полиномов Тейлора {pn}{pn}. Однако мы не только хотим знать, сходится ли последовательность полиномов Тейлора, мы хотим знать, сходится ли она к f.f. Чтобы ответить на этот вопрос, определим остаток Rn(x)Rn(x) как

Rn(x)=f(x)−pn(x).Rn(x)=f(x)−pn(x).

Чтобы последовательность полиномов Тейлора сходилась к f,f, нам нужно, чтобы остаток R _n сходился к нулю. Чтобы определить, сходится ли R _n к нулю, введем теорему Тейлора с остатком. Эта теорема не только полезна для доказательства того, что ряд Тейлора сходится к связанной с ним функции, но также позволяет нам количественно оценить, насколько хорошо n -й многочлен Тейлора аппроксимирует функцию.

Здесь мы ищем границу |Rn|.|Rn|. Рассмотрим простейший случай: n=0.n=0. Пусть p ₀ будет 0-м многочленом Тейлора от a для функции f.f. Остаток R ₀ удовлетворяет

R0(x)=f(x)−p0(x)=f(x)−f(a).R0(x)=f(x)−p0(x)=f(x)−f(a) .

Если ff дифференцируемо на интервале I , содержащем a и x , то по теореме о среднем значении существует действительное число c между a и x , такое что f(x)−f(a)=f′(c)(x−a).f(x)−f(a)=f′(c)(x− а). Следовательно,

R0(x)=f′(c)(x−a).R0(x)=f′(c)(x−a).

Используя теорему о среднем значении в аналогичном рассуждении, мы можем показать, что если ff дифференцируемо в n раз на интервале I , содержащем a и x , то n -й остаток R 1 n 1 n удовлетворяет

Rn(x)=f(n+1)(c)(n+1)!(x−a)n+1Rn(x)=f(n+1)(c)(n+1)!(x −а)n+1

для некоторого действительного числа c между a и x . Важно отметить, что значение c в приведенном выше числителе не центральное a , а скорее неизвестное значение c между a и x . Эта формула позволяет нам получить оценку остатка R _n . Если нам случится узнать, что |f(n+1)(x)||f(n+1)(x)| ограничен некоторым действительным числом M на этом интервале I , затем

|Rn(x)|≤M(n+1)!|x−a|n+1|Rn(x)|≤M(n+1)!|x−a|n+1

для всех x в интервале I .

Теперь сформулируем теорему Тейлора, которая устанавливает формальную связь между функцией ff и ее полиномом Тейлора n -й степени pn(x).pn(x). Эта теорема позволяет нам ограничить ошибку при использовании полинома Тейлора для аппроксимации значения функции и будет важна при доказательстве того, что ряд Тейлора для ff сходится к ff.

Теорема 6.7

Теорема Тейлора с остатком

Пусть ff — функция, которую можно дифференцировать n+1n+1 раз на интервале I , содержащем действительное число a . Пусть p _n будет n -м многочленом Тейлора от ff при a , и пусть

Rn(x)=f(x)−pn(x)Rn(x)=f(x)−pn (x)

будет n -м остатком. Тогда для каждого x в интервале I существует действительное число c между a и x такое, что

Rn(x)=f(n+1)(c)(n+1)!(x−a)n+1.Rn(x)=f (n+1)(c)(n+1)!(x−a)n+1.

Если существует действительное число M такое, что |f(n+1)(x)|≤M|f(n+1)(x)|≤M для всех x∈I,x∈I, то

|Rn(x)|≤M(n+1)!|x−a|n+1|Rn(x)|≤M(n+1)!|x−a|n+1

для всех x в I .

Доказательство

Зафиксируем точку x∈Ix∈I и введем функцию g такую, что

g(t)=f(x)−f(t)−f′(t)(x−t)−f″(t)2!(x−t)2−⋯−f(n)(t) n!(x−t)n−Rn(x)(x−t)n+1(x−a)n+1. g(t)=f(x)−f(t)−f′(t) (x−t)−f″(t)2!(x−t)2−⋯−f(n)(t)n!(x−t)n−Rn(x)(x−t)n+1 (х-а)n+1.

Мы утверждаем, что g удовлетворяет критериям теоремы Ролля. Поскольку g является полиномиальной функцией ( t ), это дифференцируемая функция. Кроме того, г равно нулю при t=at=a и t=xt=x, потому что

g(a)=f(x)−f(a)−f′(a)(x−a)−f″(a)2!(x−a)2+⋯+f(n)(a) n!(x−a)n−Rn(x)=f(x)−pn(x)−Rn(x)=0,g(x)=f(x)−f(x)−0−⋯− 0=0.g(a)=f(x)−f(a)−f′(a)(x−a)−f″(a)2!(x−a)2+⋯+f(n) (a)n!(x−a)n−Rn(x)=f(x)−pn(x)−Rn(x)=0,g(x)=f(x)−f(x)−0 −⋯−0=0.

Следовательно, g удовлетворяет теореме Ролля, и, следовательно, существует c между a и x такое, что g′(c)=0.g′(c)=0. Теперь вычислим g′.g′. Используя правило произведения, заметим, что

ddt[f(n)(t)n!(x−t)n]=−f(n)(t)(n−1)!(x−t)n−1+f(n+1)( t)n!(x−t)n. ddt[f(n)(t)n!(x−t)n]=−f(n)(t)(n−1)!(x−t)n −1+f(n+1)(t)n!(x−t)n.

Следовательно,

g′(t)=−f′(t)+[f′(t)−f″(t)(x−t)]+[f″(t)(x−t)−f‴(t) 2!(x−t)2]+⋯+[f(n)(t)(n−1)!(x−t)n−1−f(n+1)(t)n!(x−t )n]+(n+1)Rn(x)(x−t)n(x−a)n+1.g′(t)=−f′(t)+[f′(t)−f″ (t)(x−t)]+[f″(t)(x−t)−f‴(t)2!(x−t)2]+⋯+[f(n)(t)(n− 1)!(x−t)n−1−f(n+1)(t)n!(x−t)n]+(n+1)Rn(x)(x−t)n(x−a )n+1.

Обратите внимание на эффект телескопирования. Следовательно,

g′(t)=−f(n+1)(t)n!(x−t)n+(n+1)Rn(x)(x−t)n(x−a)n+1.g ′(t)=−f(n+1)(t)n!(x−t)n+(n+1)Rn(x)(x−t)n(x−a)n+1.

По теореме Ролля мы заключаем, что существует число c между a и x такое, что g′(c)=0.g′(c)=0. С

g′(c)=−f(n+1)(c)n!(x−c)n+(n+1)Rn(x)(x−c)n(x−a)n+1g′( c)=−f(n+1)(c)n!(x−c)n+(n+1)Rn(x)(x−c)n(x−a)n+1

делаем вывод, что

−f(n+1)(c)n!(x−c)n+(n+1)Rn(x)(x−c)n(x−a)n+1=0.−f(n+ 1)(c)n!(x−c)n+(n+1)Rn(x)(x−c)n(x−a)n+1=0.

Добавление первого члена в левой части к обеим частям уравнения и деление обеих частей уравнения на (n+1)(x-c)n(x-a)n+1, (n+1)(x-c)n (x-a)n+1, заключаем, что

Rn(x)=f(n+1)(c)(n+1)!(x−a)n+1Rn(x)=f(n+1)(c)(n+1)!(x −а)n+1

по желанию. Из этого факта следует, что если существует M таких, что |f(n+1)(x)|≤M|f(n+1)(x)|≤M для всех x в I , затем

|Rn(x)|≤M(n+1)!|x−a|n+1.|Rn(x)|≤M(n+1)!|x−a|n+1.

□

Теорема Тейлора не только позволяет нам доказать, что ряд Тейлора сходится к функции, но также позволяет оценить точность полиномов Тейлора при аппроксимации значений функции. Мы начнем с рассмотрения линейных и квадратичных аппроксимаций f(x)=x3f(x)=x3 при x=8x=8 и определим, насколько точны эти аппроксимации при оценке 113,113.

Пример 6.13

Использование линейных и квадратичных приближений для оценки значений функций

Рассмотрим функцию f(x)=x3.f(x)=x3.

1. Найдите первый и второй полиномы Тейлора для ff при x=8.x=8. Используйте графическую утилиту, чтобы сравнить эти полиномы с ff вблизи x=8.x=8.
2. Используйте эти два многочлена для оценки 113,113.
3. Используйте теорему Тейлора, чтобы ограничить ошибку.

Решение

1. Для f(x)=x3,f(x)=x3 значения функции и ее первых двух производных при x=8x=8 следующие:

   f(x)=x3f(8)=2f′(x)=13×2/3f′(8)=112f″(x)=−29×5/3f″(8)=−1144.f(x)=x3f( 8)=2f′(x)=13×2/3f′(8)=112f″(x)=−29×5/3f″(8)=−1144.

   
   Таким образом, первый и второй полиномы Тейлора при x=8x=8 задаются как

   p1(x)=f(8)+f′(8)(x−8)=2+112(x−8)p2 (x)=f(8)+f′(8)(x−8)+f″(8)2!(x−8)2=2+112(x−8)−1288(x−8)2 .p1(x)=f(8)+f′(8)(x−8)=2+112(x−8)p2(x)=f(8)+f′(8)(x−8) +f″(8)2!(x−8)2=2+112(x−8)−1288(x−8)2.

   
   Функция и полиномы Тейлора показаны на рис. 6.9.
   

   Рисунок 6,9 Графики f(x)=x3f(x)=x3 и линейная и квадратичная аппроксимации p1(x)p1(x) и p2(x).p2(x).

2. Используя первый многочлен Тейлора при x=8,x=8, мы можем оценить 8)=2,25.
   
   Используя второй полином Тейлора при x=8,x=8, получаем )=2+112(11−8)−1288(11−8)2=2,21875.

3. По теореме Тейлора с остатком существует c в интервале (8,11)(8,11) такое, что остаток при аппроксимации 113113 первым полиномом Тейлора удовлетворяет

   R1(11)=f″(c)2!(11−8)2.R1(11)=f″(c)2!(11−8)2.

   
   Мы не знаем точного значения c , поэтому мы находим верхнюю границу R1(11)R1(11), определяя максимальное значение f″f″ на интервале (8,11).(8) ,11). Поскольку f″(x)=−29×5/3,f″(x)=−29×5/3, наибольшее значение для |f″(x)||f″(x)| на этом интервале происходит при x=8.x=8. Используя тот факт, что f″(8)=−1144,f″(8)=−1144, получаем

   |R1(11)|≤1144·2!(11−8)2=0,03125.|R1(11) |≤1144·2!(11−8)2=0,03125.

   
   Аналогично, для оценки R2(11),R2(11) используем тот факт, что

   R2(11)=f‴(c)3!(11−8)3.R2(11)=f‴(c)3!(11−8)3.

   
   Поскольку f‴(x)=1027×8/3,f‴(x)=1027×8/3, максимальное значение f‴f‴ на интервале (8,11)(8,11) равно f‴(8) ≈0,0014468.f‴(8)≈0,0014468. Следовательно, имеем

   |R2(11)|≤0,00114683!(11−8)3≈0,0065104. |R2(11)|≤0,00114683!(11−8)3≈0,0065104.

Контрольно-пропускной пункт 6.12

Найдите первый и второй полиномы Тейлора для f(x)=xf(x)=x при x=4.x=4. Используйте эти полиномы для оценки 6.6. Используйте теорему Тейлора, чтобы ограничить ошибку.

Пример 6.14

Аппроксимация sin

x Использование полиномов Маклорена

Из примера 6.12b полиномы Маклорена для sinxsinx задаются как

p2m+1(x)=p2m+2(x)=x−x33!+x55!− x77!+⋯+(−1)mx2m+1(2m+1)!p2m+1(x)=p2m+2(x)=x−x33!+x55!−x77!+⋯+(−1)mx2m +1(2м+1)!

для m=0,1,2,….m=0,1,2,….

1. Используйте пятый полином Маклорена для sinxsinx, чтобы аппроксимировать sin(π18)sin(π18) и ограничить ошибку.
2. Для каких значений x приближает ли пятый полином Маклорена sinxsinx с точностью до 0,0001?

Решение

1. Пятый полином Маклорена равен

   p5(x)=x−x33!+x55!. p5(x)=x−x33!+x55!.

   
   Используя этот многочлен, мы можем оценить следующим образом: =π18−13!(π18)3+15!(π18)5≈0,173648.
   
   Чтобы оценить ошибку, используйте тот факт, что шестой полином Маклорена равен p6(x)=p5(x)p6(x)=p5(x), и вычислите границу R6(π18).R6(π18). По уникальности ряда Тейлора остаток равен

   R6(π18)=f(7)(c)7!(π18)7R6(π18)=f(7)(c)7!(π18)7

   
   для некоторых c между 0 и π18.π18. Используя тот факт, что |f(7)(x)|≤1|f(7)(x)|≤1 для всех x , мы находим, что величина ошибки не превышает

   17!·(π18) 7≤9,8×10−10,17!·(π18)7≤9,8×10−10.

2. Нам нужно найти такие значения x , что

   17!|x|7≤0,0001,17!|x|7≤0,0001.

   
   Решая это неравенство для x , получаем, что пятый полином Маклорена дает оценку с точностью до 0,0001, пока |x|<0,907.|х|<0,907.

Контрольно-пропускной пункт 6.13

Используйте четвертый полином Маклорена для cosxcosx для аппроксимации cos(π12). cos(π12).

Теперь, когда мы можем оценить остаток Rn(x),Rn(x), мы можем использовать эту оценку, чтобы доказать, что ряд Тейлора для ff в точках a сходится к f.f.

Представление функций с помощью ряда Тейлора и Маклорена

Обсудим теперь вопросы сходимости рядов Тейлора. Мы начнем с того, что покажем, как найти ряд Тейлора для функции и как найти ее интервал сходимости.

Пример 6.15

Нахождение ряда Тейлора

Нахождение ряда Тейлора для f(x)=1xf(x)=1x при x=1.x=1. Определить интервал сходимости.

Решение

Для f(x)=1x,f(x)=1x значения функции и ее первых четырех производных при x=1x=1 равны

f(x)=1xf(1)=1f′(x) =−1x2f′(1)=−1f″(x)=2x3f″(1)=2!f‴(x)=−3·2x4f‴(1)=−3!f(4)(x)=4 ·3·2x5f(4)(1)=4!.f(x)=1xf(1)=1f′(x)=−1x2f′(1)=−1f″(x)=2x3f″(1)= 2!f‴(x)=−3·2x4f‴(1)=−3!f(4)(x)=4·3·2x5f(4)(1)=4!.

То есть имеем f(n)(1)=(−1)nn!f(n)(1)=(−1)nn! для всех n≥0. n≥0. Следовательно, ряд Тейлора для ff при x=1x=1 равен

∑n=0∞f(n)(1)n!(x−1)n=∑n=0∞(−1)n( x−1)n.∑n=0∞f(n)(1)n!(x−1)n=∑n=0∞(−1)n(x−1)n.

Чтобы найти интервал сходимости, мы используем критерий отношения. Получаем, что

|an+1||an|=|(−1)n+1(x−1)n+1||(−1)n(x−1)n|=|x−1| .|an+1||an|=|(−1)n+1(x−1)n+1||(−1)n(x−1)n|=|x−1|.

Таким образом, ряд сходится, если |x−1|<1.|x−1|<1. То есть ряд сходится при 0

∑n=0∞(−1)n(2−1)n=∑n=0∞(−1)n∑n=0∞(−1)n(2−1)n=∑n=0 ∞(−1)n

расходится по критерию расходимости. Аналогично, при x=0,x=0,

∑n=0∞(−1)n(0−1)n=∑n=0∞(−1)2n=∑n=0∞1∑n= 0∞(−1)n(0−1)n=∑n=0∞(−1)2n=∑n=0∞1

расходится. Следовательно, интервал сходимости равен (0,2).(0,2).

Контрольно-пропускной пункт 6.14

Найдите ряд Тейлора для f(x)=12xf(x)=12x при x=2x=2 и определите его интервал сходимости.

Мы знаем, что найденный в этом примере ряд Тейлора сходится на интервале (0,2),(0,2), но откуда мы знаем, что он на самом деле сходится к f?f? Мы рассмотрим этот вопрос в более общем виде через мгновение, но для этого примера мы можем ответить на этот вопрос, написав

f(x)=1x=11−(1−x). f(x)=1x=11−(1−x).

То есть ff можно представить геометрическим рядом ∑n=0∞(1−x)n.∑n=0∞(1−x)n. Поскольку это геометрический ряд, он сходится к 1x1x, пока |1−x|<1.|1−x|<1. Следовательно, ряд Тейлора из примера 6.15 сходится к f(x)=1xf(x)=1x на (0,2).(0,2).

Теперь рассмотрим более общий вопрос: если ряд Тейлора для функции ff сходится на некотором интервале, как мы можем определить, действительно ли он сходится к f?f? Чтобы ответить на этот вопрос, вспомним, что ряд сходится к определенному значению тогда и только тогда, когда его последовательность частичных сумм сходится к этому значению. Учитывая серию Тейлора для ff в a , частичная сумма n дается полиномом Тейлора n p _n . Следовательно, чтобы определить, сходится ли ряд Тейлора к f,f, нам нужно определить, является ли

limn→∞pn(x)=f(x).limn→∞pn(x)=f(x).

Поскольку остаток Rn(x)=f(x)−pn(x),Rn(x)=f(x)−pn(x), ряд Тейлора сходится к ff тогда и только тогда, когда

limn→∞Rn(x)=0. limn→∞Rn(x)=0.

Теперь сформулируем эту теорему формально.

Теорема 6,8

Сходимость ряда Тейлора

Предположим, что ff имеет производные всех порядков на интервале I , содержащем a . Тогда ряд Тейлора

∑n=0∞f(n)(a)n!(x−a)n∑n=0∞f(n)(a)n!(x−a)n

сходится к f(x)f(x) для всех x в I тогда и только тогда, когда

limn→∞Rn(x)=0limn→∞Rn(x)=0

для всех x в I .

С помощью этой теоремы мы можем доказать, что ряд Тейлора для ff в точке a сходится к ff, если мы можем доказать, что остаток Rn(x)→0.Rn(x)→0. Чтобы доказать, что Rn(x)→0,Rn(x)→0, мы обычно используем оценку

|Rn(x)|≤M(n+1)!|x−a|n+1|Rn(x)|≤M(n+1)!|x−a|n+1

из теоремы Тейлора с остатком.

В следующем примере мы находим ряды Маклорена для e ^x и sinxsinx и показываем, что эти ряды сходятся к соответствующим функциям для всех действительных чисел, доказывая, что остатки Rn(x)→0Rn(x)→0 для всех действительных чисел х .

Пример 6.16

Нахождение ряда Маклорена

Для каждой из следующих функций найдите ряд Маклорена и его интервал сходимости. Используйте теорему Тейлора с остатком, чтобы доказать, что ряд Маклорена для ff сходится к ff на этом интервале.

1. e ^x
2. синкссинкс

Решение

1. Использование полинома Маклорена n th для e ^x найдено в примере 6.12a., мы находим, что ряд Маклорена для e ^x задается как

   ∑n=0∞xnn!.∑n=0∞xnn!.

   
   Для определения интервала сходимости мы используем критерий соотношения. Поскольку

   |an+1||an|=|x|n+1(n+1)!·n!|x|n=|x|n+1,|an+1||an|=|x| n+1(n+1)!·n!|x|n=|x|n+1,

   
   имеем

   limn→∞|an+1||an|=limn→∞|x|n+1 =0limn→∞|an+1||an|=limn→∞|x|n+1=0

   
   для всех x . Следовательно, ряд сходится абсолютно для всех x , и, таким образом, интервал сходимости равен (−∞,∞).(−∞,∞). Чтобы показать, что ряд сходится к e ^x для всех x , мы используем тот факт, что f(n)(x)=exf(n)(x)=ex для всех n≥0n≥0 и e ^x — возрастающая функция на (−∞,∞).(−∞,∞). Следовательно, для любого действительного числа b максимальное значение e ^x для всех |x|≤b|x|≤b равно e ^b . Таким образом,

   |Rn(x)|≤eb(n+1)!|x|n+1.|Rn(x)|≤eb(n+1)!|x|n+1.

   
   Поскольку мы только что показали, что

   ∑n=0∞|x|nn!∑n=0∞|x|nn!

   
   сходится для всех x , из теста расходимости мы знаем, что

   limn→∞|x|n+1(n+1)!=0limn→∞|x|n+1(n+1)!= 0

   
   для любого действительного числа x . Комбинируя этот факт с теоремой о сжатии, получаем limn→∞Rn(x)=0.limn→∞Rn(x)=0.
2. Используя n -й полином Маклорена для sinxsinx, найденный в примере 6.12b., мы находим, что ряд Маклорена для sinxsinx задается как

   ∑n=0∞(−1)nx2n+1(2n+1)!.∑n=0∞(−1)nx2n+1(2n+1)!.

   
   Чтобы применить тест отношения, рассмотрим

   |an+1||an|=|x|2n+3(2n+3)!·(2n+1)!|x|2n+1=|x| 2(2n+3)(2n+2).|an+1||an|=|x|2n+3(2n+3)!·(2n+1)!|x|2n+1=|x| 2(2n+3)(2n+2).

   
   Поскольку

   limn→∞|x|2(2n+3)(2n+2)=0limn→∞|x|2(2n+3)(2n+2)=0

   
   для всех x , мы получить интервал сходимости в виде (−∞,∞).(−∞,∞). Чтобы показать, что ряд Маклорена сходится к sinx,sinx, посмотрите на Rn(x).Rn(x). Для каждого x существует действительное число c между 0 и x , такое что

   Rn(x)=f(n+1)(c)(n+1)!xn+1.Rn(x)=f(n+1)(c) (n+1)!xn+1.

   
   Так как |f(n+1)(c)|≤1|f(n+1)(c)|≤1 для всех целых чисел n и всех действительных чисел c , мы имеем

   |Rn(x )|≤|x|n+1(n+1)!|Rn(x)|≤|x|n+1(n+1)!

   
   для всех действительных чисел x . Используя ту же идею, что и в части а., результат limn→∞Rn(x)=0limn→∞Rn(x)=0 для всех x и, следовательно, ряд Маклорена для sinxsinx сходится к sinxsinx для всех вещественных х .

Контрольно-пропускной пункт 6.15

Найдите ряд Маклорена для f(x)=cosx.f(x)=cosx. Используйте тест отношения, чтобы показать, что интервал сходимости равен (−∞,∞).(−∞,∞). Покажите, что ряд Маклорена сходится к cosxcosx для всех действительных чисел x .

Студенческий проект

Доказательство того, что

e иррационально

В этом проекте мы используем полиномы Маклорена для e ^x , чтобы доказать, что e иррационально. Доказательство основано на предположении, что e рационально, и приходит к противоречию. Поэтому на следующих шагах мы предполагаем, что e=r/se=r/s для некоторых целых чисел r и s , где s≠0.s≠0.

1. Запишите полиномы Маклорена p0(x),p1(x),p2(x),p3(x),p4(x)p0(x),p1(x),p2(x),p3(x) ,p4(x) для e ^x . Оценить p0(1),p1(1),p2(1),p3(1),p4(1)p0(1),p1(1),p2(1),p3(1),p4(1) до оценка e .
2. Пусть Rn(x)Rn(x) обозначает остаток при использовании pn(x)pn(x) для оценки e ^x . Следовательно, Rn(x)=ex−pn(x),Rn(x)=ex−pn(x) и Rn(1)=e−pn(1).Rn(1)=e−pn(1) . Предполагая, что e=rse=rs для целых чисел r и s , вычислить R0(1),R1(1),R2(1),R3(1),R4(1).R0(1),R1( 1),R2(1),R3(1),R4(1).
3. Используя результаты части 2, покажите, что для каждого остатка R0(1),R1(1),R2(1),R3(1),R4(1),R0(1),R1(1),R2( 1),R3(1),R4(1), можно найти целое число k такое, что kRn(1)kRn(1) является целым числом при n=0,1,2,3,4. n=0 ,1,2,3,4.
4. Запишите формулу для n -го многочлена Маклорена pn(x)pn(x) для e ^x и соответствующего остатка Rn(x).Rn(x). Покажите, что sn!Rn(1)sn!Rn(1) является целым числом.
5. Используйте теорему Тейлора, чтобы записать явную формулу для Rn(1).Rn(1). Заключить, что Rn(1)≠0,Rn(1)≠0 и, следовательно, sn!Rn(1)≠0.sn!Rn(1)≠0.
6. Используйте теорему Тейлора, чтобы найти оценку Rn(1).Rn(1). Используйте эту оценку вместе с результатом из части 5, чтобы показать, что |sn!Rn(1)| n достаточно велико, то |sn!Rn(1)|<1.|sn!Rn(1)|<1. Следовательно, sn!Rn(1)sn!Rn(1) — целое число, модуль которого меньше 1. Таким образом, sn!Rn(1)=0.sn!Rn(1)=0. Но из части 5 мы знаем, что sn!Rn(1)≠0.sn!Rn(1)≠0. Мы пришли к противоречию, и, следовательно, первоначальное предположение о рациональности и должно быть ложным.

Раздел 6.3 Упражнения

В следующих упражнениях найдите полиномы Тейлора второй степени, приближающие заданную функцию с центром в заданной точке.

116.

f(x)=1+x+x2f(x)=1+x+x2 при a=1a=1

117.

f(x)=1+x+x2f(x)=1+x+x2 при a=-1a=-1

118.

f(x)=cos(2x)f(x)=cos(2x) при a=πa=π

119.

f(x)=sin(2x)f(x)=sin(2x) при a=π2a=π2

120.

f(x)=xf(x)=x при a=4a=4

121.

f(x)=lnxf(x)=lnx при a=1a=1

122.

f(x)=1xf(x)=1x при a=1a=1

123.

f(x)=exf(x)=ex при a=1a=1

В следующих упражнениях проверьте, что данный выбор n в оценке остатка |Rn|≤M(n+1)!(x−a)n+1,|Rn|≤M(n+1)! (x−a)n+1, где M — максимальное значение |f(n+1)(z)||f(n+1)(z)| на интервале между и и указанной точкой дает |Rn|≤11000. |Rn|≤11000. Найти значение многочлена Тейлора p _n от ff в указанной точке.

124.

[Т] 10;а=9,n=310;а=9,n=3

125.

[Т] (28)1/3;а=27,n=1(28)1/3;а=27,n=1

126.

[T] sin(6);a=2π,n=5sin(6);a=2π,n=5

127.

[Т] и ² ; а=0,n=9а=0,n=9

128.

[T] cos(π5);a=0,n=4cos(π5);a=0,n=4

129.

[T] ln(2);a=1,n=1000ln(2);a=1,n=1000

130.

Интегрировать аппроксимацию sint≈t−t36+t5120−t75040sint≈t−t36+t5120−t75040, оцененную в πt для приближения к ∫01sinπtπtdt. ∫01sinπtπtdt.

131.

Интегрируйте аппроксимацию ex≈1+x+x22+⋯+x6720ex≈1+x+x22+⋯+x6720, оцененную как − x ² , чтобы получить аппроксимацию ∫01e−x2dx.∫01e−x2dx.

В следующих упражнениях найдите наименьшее значение n такое, что оценка остатка |Rn|≤M(n+1)!(x−a)n+1,|Rn|≤M(n+1)! (x−a)n+1, где M — максимальное значение |f(n+1)(z)||f(n+1)(z)| на промежутке между и и указанная точка дает |Rn|≤11000|Rn|≤11000 на указанном интервале.

132.

f(x)=sinxf(x)=sinx на [−π,π],a=0[−π,π],a=0

133.

f(x)=cosxf(x)=cosx на [−π2,π2],a=0[−π2,π2],a=0

134.

f(x)=e−2xf(x)=e−2x на [−1,1],a=0[−1,1],a=0

135.

f(x)=e−xf(x)=e−x на [−3,3],a=0[−3,3],a=0

В следующих упражнениях максимум правой части оценки остатка |R1|≤max|f″(z)|2R2|R1|≤max|f″(z)|2R2 на [a−R, a+R][a−R,a+R] встречается в положении a или a±R. a±R. Оцените максимальное значение R , такое что max|f″(z)|2R2≤0,1max|f″(z)|2R2≤0,1 на [a−R,a+R][a−R,a+R ] путем построения этого максимума как функции R .

136.

[T] e ^x округляется как 1+x,a=01+x,a=0

137.

[T] sinxsinx аппроксимировано x , a=0a=0

138.

[T] lnxlnx аппроксимируется как x−1,a=1x−1,a=1

139.

[T] cosxcosx аппроксимировано 1,a=01,a=0

В следующих упражнениях найдите ряд Тейлора заданной функции с центром в указанной точке.

140.

x4x4 при a=-1a=-1

141.

1+x+x2+x31+x+x2+x3 при a=-1a=-1

142.

sinxsinx при a=πa=π

143.

cosxcosx при a=2πa=2π

144.

sinxsinx при x=π2x=π2

145.

cosxcosx при x=π2x=π2

146.

exex в a=-1a=-1

147.

exex при a=1a=1

148.

1(x−1)21(x−1)2 при a=0a=0 ( Подсказка: Дифференцировать 11−x.)11−x.)

149.

1(x−1)31(x−1)3 при a=0a=0

150.

F(x)=∫0xcos(t)dt;f(t)=∑n=0∞(−1)ntn(2n)!F(x)=∫0xcos(t)dt;f(t)= ∑n=0∞(−1)ntn(2n)! при a=0a=0 ( Примечание : ff — ряд Тейлора для cos(t).)cos(t).)

В следующих упражнениях вычислите ряд Тейлора для каждой функции в районе x=1.x=1.

151.

f(x)=2−xf(x)=2−x

152.

f(x)=x3f(x)=x3

153.

f(x)=(x−2)2f(x)=(x−2)2

154.

f(x)=lnxf(x)=lnx

155.

f(x)=1xf(x)=1x

156.

f(x)=12x−x2f(x)=12x−x2

157.

f(x)=x4x−2×2−1f(x)=x4x−2×2−1

158.

f(x)=e−xf(x)=e−x

159.

f(x)=e2xf(x)=e2x

[T] В следующих упражнениях определите значение x такое, что данный ряд ∑n=0∞an∑n=0∞an является значением ряда Маклорена функции f(x)f(x ) в х.х. Аппроксимируйте значение f(x)f(x), используя S10=∑n=010an.S10=∑n=010an.

160.

∑n=0∞1n!∑n=0∞1n!

161.

∑n=0∞2nn!∑n=0∞2nn!

162.

∑n=0∞(−1)n(2π)2n(2n)!∑n=0∞(−1)n(2π)2n(2n)!

163.

∑n=0∞(−1)n(2π)2n+1(2n+1)!∑n=0∞(−1)n(2π)2n+1(2n+1)!

В следующих упражнениях используются функции S5(x)=x−x36+x5120S5(x)=x−x36+x5120 и C4(x)=1−x22+x424C4(x)=1−x22+x424 на [ −π,π].[−π,π].

164.

[T] Постройте sin2x−(S5(x))2sin2x−(S5(x))2 на [−π,π].[−π,π]. Сравните максимальную разницу с квадратом оценки остатка Тейлора для sinx.sinx.

165.

[T] Постройте график cos2x−(C4(x))2cos2x−(C4(x))2 на [−π,π].[−π,π]. Сравните максимальную разницу с квадратом оценки остатка Тейлора для cosx.cosx.

166.

[T] График |2S5(x)C4(x)−sin(2x)||2S5(x)C4(x)−sin(2x)| на [−π,π].[−π,π].

167.

[T] Сравните S5(x)C4(x)S5(x)C4(x) на [−1,1][−1,1] с tanx.tanx. Сравните это с оценкой остатка Тейлора для аппроксимации tanxtanx с помощью x+x33+2×515.x+x33+2×515.

168.

[T] Постройте ex-e4(x)ex-e4(x), где e4(x)=1+x+x22+x36+x424e4(x)=1+x+x22+x36+x424 на [ 0,2].[0,2]. Сравните максимальную ошибку с оценкой остатка Тейлора.

169.

(Аппроксимации Тейлора и нахождение корней.) Напомним, что метод Ньютона xn+1=xn−f(xn)f′(xn)xn+1=xn−f(xn)f′(xn) аппроксимирует решения f(x )=0f(x)=0 вблизи входа x0.x0.

1. Если ff и gg являются обратными функциями, объясните, почему решение g(x)=ag(x)=a равно значению f(a)off.f(a)off.
2. Пусть pN(x)pN(x) — полином Маклорена N-й степени N-го упр. Используйте метод Ньютона для аппроксимации решений pN(x)−2=0pN(x)−2=0 для N=4,5,6.N=4,5,6.
3. Объясните, почему приближенные корни pN(x)−2=0pN(x)−2=0 являются приблизительными значениями ln(2).