Разложить функцию в ряд тейлора в окрестности точки

Содержание

Разложение в ряд Тейлора

Введите функцию, которую будете раскладывать в ряд Тейлора

Выполним разложение функции f(x) в ряд Тейлора в точки x0 до n-го члена

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x): Абсолютное значение x
(модуль x или |x|)
arccos(x): Функция — арккосинус от x
arccosh(x): Арккосинус гиперболический от x
arcsin(x): Арксинус от x
arcsinh(x): Арксинус гиперболический от x
arctg(x): Функция — арктангенс от x
arctgh(x): Арктангенс гиперболический от x
e: e число, которое примерно равно 2.7
exp(x): Функция — экспонента от x (что и e^x)
log(x) or ln(x): Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))
pi: Число — «Пи», которое примерно равно 3.14
sin(x): Функция — Синус от x
cos(x): Функция — Косинус от x
sinh(x): Функция — Синус гиперболический от x
cosh(x): Функция — Косинус гиперболический от x
sqrt(x): Функция — квадратный корень из x
sqr(x) или x^2: Функция — Квадрат x
tg(x): Функция — Тангенс от x
tgh(x): Функция — Тангенс гиперболический от x
cbrt(x): Функция — кубический корень из x
floor(x): Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
sign(x): Функция — Знак x
erf(x): Функция ошибок (Лапласа или интеграл вероятности)

В выражениях можно применять следующие операции:

Действительные числа: вводить в виде 7.5, не 7,5
2*x: — умножение
3/x: — деление
x^3: — возведение в степень
x + 7: — сложение
x — 6: — вычитание

www.kontrolnaya-rabota.ru

Ряд Тейлора. Разложение функции в ряд Тейлора.

Ряд Тейлора. Разложение функции в ряд Тейлора.

Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:

При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.

Ряд Тейлора в окрестности точки a имеет виды:

1), где f(x) — функция, имеющая при х=а производные всех порядков. R_n — остаточный член в ряде Тейлора определяется выражением

k-тый коэффициент (при х_k) ряда определяется формулой

3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)

при a=0

члены ряда определяются по формуле

Условия применения рядов Тейлора.

1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).

2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.

Свойства рядов Тейлора.

Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:

Ряды Тейлора применяются при аппроксимации ( приближение — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.

Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.

tehtab.ru

Разложение функции в ряд Тейлора, Маклорена, Лорана

Разложение функции в ряд Тейлора, Маклорена и Лорана на Math34.biz для тренировки практических навыков. Это разложение функции в ряд дает представление математикам оценить приближенное значение функции в некоторой точки области ее определения. Намного проще вычислить такое значение функции, по сравнению с применением таблицы Бредиса, так неактуальной в век вычислительной техники. В ряд Тейлора разложить функцию означает вычислить коэффициенты перед линейными функциями этого ряда и записать это в правильном виде. Путают студенты эти два ряда, не понимая, что является общим случаем, а что частным случаем второго. Напоминаем раз и навсегда, ряд Маклорена — частный случай Тейлоровского ряда, то есть это и есть ряд Тейлора, но в точке x = 0. Все краткие записи разложения известных функций, таких как e^x, Sin(x), Cos(x) и другие, это и есть разложения в ряд Тейлора, но в точке 0 для аргумента. Для функций комплексного аргумента ряд Лорана является наиболее частой задачей в ТФКП, так как представляет двусторонний бесконечный ряд. Он и является суммой двух рядов. Мы предлагаем вам посмотреть пример разложения прямо на сайте Math34.biz, это сделать очень просто, нажав на «Пример» с любым номером, а затем кнопку «Решение». Именно такому разложению функции в ряд сопоставлен мажорирующий ряд, ограничивающий функцию исходную в некоторой области по оси ординат, если переменная принадлежит области абсцисс. Векторному анализу поставляется в сравнение другая интересная дисциплина в математике. Поскольку исследовать нужно каждое слагаемое, то необходимо достаточно много времени на процесс. Всякому ряду Тейлора можно сопоставить ряд Маклорена, заменив x0 на нуль, а вот по ряду Маклорена порой не очевидно представление ряда Тейлора обратно. Как бы это и не требуется делать в чистом виде, но интересно для общего саморазвития. Всякому ряду Лорана соответствует двусторонний бесконечный степенной ряд по целым степеням z-a, другими словами ряд вида того же Тейлора, но немного отличающегося вычислением коэффициентов. Про область сходимости ряда Лорана расскажем чуть позже, после нескольких теоретических выкладок. Как и в прошлом веке, поэтапного разложения функции в ряд вряд ли можно достичь только лишь приведением слагаемых к общему знаменателю, так как функции в знаменателях нелинейные. Приближенное вычисление функционального значения требует постановка задач. Задумайтесь над тем, что когда аргумент ряда Тейлора есть линейная переменная, то разложение происходит в несколько действий, но совсем другая картина, когда в качестве аргумента раскладываемой функции выступает сложная или нелинейная функция, тогда очевиден процесс представления такой функции в степенной ряд, поскольку, таким образом, легко вычислить, пусть и приближенное, но значение в любой точке области определения, с минимальной погрешностью, мало влияющей на дальнейшие расчеты. Это касается и ряда Маклорена. когда необходимо вычислить функция в нулевой точке. Однако сам ряд Лорана здесь представлен разложением на плоскости с мнимыми единицами. Также не без успеха будет правильное решение задачи в ходе общего процесса. В математике такого подхода не знают, но он объективно существует. В результате вы можете прийти к выводу так называемых поточечных подмножеств, и в разложении функции в ряд нужно применять известные для этого процесса методы, таких как применение теории производных. Лишний раз убеждаемся в правоте учителя, который сделал свои предположения на счет итогов пост вычислительных выкладок. Давайте отметим, что ряд Тейлора, полученный по всем канонам математики, существует и определен на всей числовой оси, однако, уважаемые пользователи сервиса Math34.biz, не забывайте вид исходной функции, ведь может получиться так, что изначально необходимо установит область определения функции, то есть выписать и исключить из дальнейших рассмотрений те точки, при которых функция не определена в области действительных чисел. Так сказать это покажет вашу расторопность при решении задачи. Не исключением высказанного будет и построение ряда Маклорена с нулевым значением аргумента. Процесс нахождения области определения функции никто при этом не отменял, и вы обязаны подойти со всей серьезностью к этому математическому действию. В случае содержания рядом Лорана главной части, параметр «a» будет называться изолированной особой точкой, и ряд Лорана будет разложен в кольце — это пересечение областей сходимости его частей, отсюда будет следовать соответствующая теорема. Но не все так сложно как может показаться на первый взгляд неопытному студенту. Изучив как раз ряд Тейлора, можно с легкостью понять ряд Лорана — обобщенный случай на расширение пространства чисел. Любое разложение функции в ряд можно производить только в точке области определения функции. Следует учитывать свойства таких функций, например, как периодичность или бесконечная дифференцируемость. Также предлагаем вам воспользоваться таблицей готовых разложений в ряд Тейлора элементарных функций, поскольку одна функция может быть представлена до десятков отличных от друг друга степенных рядов, что можно видеть из применения нашего калькулятора онлайн. Онлайн ряд Маклорена проще простого определить, если воспользоваться уникальным сервисом Math34.biz, вам достаточно только ввести правильную записанную функцию и представленный ответ получите в считанные секунды, он будет гарантированно точным и в стандартно записанном виде. Можете переписать результат сразу в чистовик на сдачу преподавателю. Правильно бы сначала определить аналитичность рассматриваемой функции в кольцах, а затем однозначно утверждать, что она разложима в ряд Лорана во всех таких кольцах. Важен момент чтобы не упустить из вида содержащие отрицательных степеней членов ряда Лорана. На этом сосредоточьтесь как можно сильнее. Применяйте с пользой теорему Лорана о разложении функции в ряд по целым степеням.

math24.biz

1.5. Разложение функции в ряд Тейлора

Если функция f(x) имеет производные всех порядков в окрестности точки x=a, то для нее можно написать ряд по степеням (x—a):

Этот ряд называется рядом Тейлора функции f(x) в точке x=a.

Теорема 6. Если функция f(x) и все ее производные ограничены на интервале (a—R, a+R) одним и тем же числом, т.е. существует постоянная M>0 такая, что выполняется неравенство , то функция f(x) представляется сходящимся к ней рядом Тейлора:

. (13)

Равенство (13) верно и в случае, когда остаточный член ряда Тейлора стремится к нулю при

n. Остаточный член R_n(x) можно вычислить по формуле:

. (14)

Если , то ряд не сходится к данной функции.

Если в ряде Тейлора положим a=0, получим частный случай ряда Тейлора, который называют рядом Маклорена: .

Приведем разложения в ряд Маклорена некоторых элементарных функций:

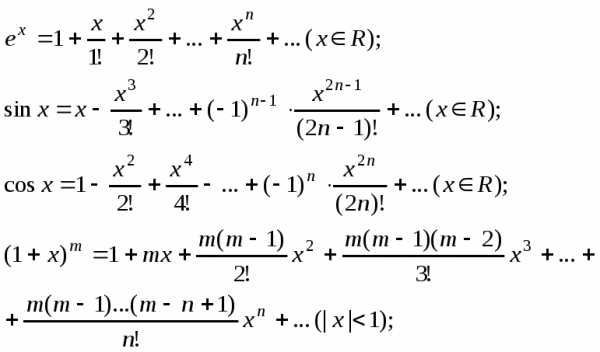
Пример 1. Разложить функцию в ряд Тейлора в окрестности точки x=0.

Решение. Имеем . Вычисляем , т.е. . Далее последовательно получаем: Отметим, что . Записываем ряд Тейлора:

Пример 2. Разложить функцию в ряд по степеням x, используя разложения основных элементарных функций. Воспользуемся приведенным выше биномиальным разложением . (15)

Преобразуем исходную функцию: . Подставим в формулу (15) , а вместо x выражение . Получим следующее разложение:

Разложение имеет место при , т.е. при |x|<3.

1.6. Применение степенных рядов в приближенных вычислениях

1. Приближенное вычисление значений функций.

Пусть функция f(x) в окрестности точки a разлагается в ряд Тейлора. Тогда приближенное значение функции f(x) в любой точке этой окрестности может быть вычислено как частичная сумма этого ряда.

Пример 1. Вычислить с точностью до 0,001.

Решение. . Воспользуемся биномиальным рядом (15) при . Получаем:

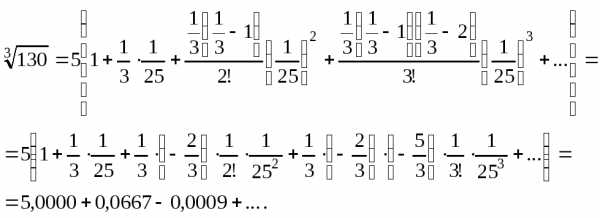
Полученный ряд является знакочередующимся рядом. Третий член по модулю меньше 0,001, поэтому его и следующие за ним члены можно отбросить. С указанной точностью получим .

Пример 2. Вычислить с точностью до 0,001.

Решение.Воспользуемся разложением

где . При x=0,1 получаем: Определим, сколько надо слагаемых для достижения требуемой точности. Так как 0,1[0,0,5], то . Тогда ; . При x=0,1 имеем неравенство: . Полагая n=2, получим . Значит, достаточно взять три слагаемых: .

Пример 3. Вычислить ln2 с точностью до .

Решение. Применим разложение . Этот ряд сходится при x(-1,1). Если , то x=1/3. Возьмем n-ю частичную сумму . Погрешность этого равенства выражается остатком ряда . Для его оценки все множители в знаменателях, стоящие перед степенью 3, заменим на 2

n+3. Получим Решая неравенство , находим, что n=4: . Итак,

2. Приближенное вычисление определенных интегралов.

Если подынтегральная функция разлагается в степенной ряд, а пределы интегрирования принадлежат области сходимости этого ряда, то соответствующий определенный интеграл можно вычислить с заданной точностью.

Пример 4. Вычислить интеграл с точностью до 0,00001.

Решение. Разделив почленно ряд для sinx на x, получим . Этот ряд сходится приxR. Интегрируем его почленно.

Получили знакочередующийся ряд. Третий член по модулю меньше заданной точности. Значит, достаточно взять два слагаемых: .

studfiles.net

korowin5_1

С учетом сказанного имеет место разложение

(6.13)

называемое рядом Тейлора функции f(x) в точке х₀.

Если в (6.13) положить х₀ = 0, то получим ряд

(6.14)

который является частным случаем ряда Тейлора и называется рядом Маклорена.

1. f(x) = ln x в окрестности точки х₀ = 1.

2. f(x) =2^x в окрестности точки х₀ = 2.

Решение

1. Вычислим значения функции ln x и ее производных в точке х₀= 1 и воспользуемся разложением (5.13):

f(x) = ln x , f(1) = ln 1 = 0;

;

=24;

……………

Тогда

или

2. Найдем значения функции 2^хи ее производных в точке х₀ = 2.

. . . . . . . . . .

Подставляя полученные выражения в формулу (6.13), получим искомое разложение:

или

Пример 2. Разложить в ряд Маклорена функцию f(x) = e^x.

Решение. Найдем значения функции e^x и ее производных в точке x₀ =0.

Известно, что

и, следовательно, .

Тогда из формулы (6.14) получим

Аналогично можно получить разложения

;

(R, 1 < x < 1).

Последнее разложение называется биномиальным рядом. В случае, когда   натуральное число,  = n  N, этот ряд представляет собой формулу бинома Ньютона.

Пример 3. Разложить в ряд Маклорена функцию .

Решение. В разложении

заменим t на – х², получим

или

Разложить в ряд Маклорена функции:

97. 98.

99. 100.

101. 102.

103. 104.

105. 106.

Разложить в ряд Тейлора функции в окрестности заданных точек

107.

108.

109. x₀ = 2

110. ,x₀ =

§6. Применение степенных рядов

к приближенным вычислениям

1. Приближенные вычисления значений функций

Вычисление приближенного значения функции f(x) основано на использовании приближенного равенства f(x)  S_n(x), где S_n(x) – частичная сумма степенного ряда, в который раскладывается данная функция. Для определения погрешности найденного приближенного значения, нужно оценить сумму отброшенных членов ряда или его остатка r_n(x).

Известно, что погрешность приближенного равенства

(6.15)

определяется оценочной формулой , т.е. сумма отброшенных слагаемых в разложении функции е^х меньше величины при 0 <x < n +1.

Пример 1. Вычислить число е с точностью до 0,001.

Решение. Воспользуемся приближенным равенством (6.15), положив в нем х = 1, тогда . Из формулы оценки остатка рядаr_n(x) при х = 1 получим

Число членов частичной суммы ряда, обеспечивающее необходимую точность приближения, определим из неравенства r_n < 0,001 или < 0,001, т. е.n! n > 1000. Отсюда видно, что достаточно взять n = 6, так как 6!  6 = 720  7 + 4320 > 1000. Следовательно,

Слагаемые суммы необходимо вычислять с точностью до четвертого знака после запятой, чтобы при суммировании не получить погрешности, превышающей 0,001.

То есть

2,0000

0,5000

0,1667

0,0417

0,0083

0,0014

2,7181

Таким образом, е  2,7181.

Пример 2. Вычислить с точностью до 0,00001.

Решение. Положим в приближенном равенстве (6.15) , тогда получим

Выражение в правой части равенства представляет собой частичную сумму знакочередующегося ряда, удовлетворяющего признаку Лейбница. Поэтому допускаемая при отбрасывании членов ряда погрешность не превосходит модуля первого из отброшенных слагаемых.

Нетрудно видеть, что < 0,00001.

Следовательно, необходимая точность будет достигнута, если частичную сумму составить из пяти слагаемых, т. е.

Производя вычисления, окончательно получаем .

2. Приближенные вычисления определенных интегралов

Пример 3. Вычислить с точностью до 0,001.

Решение. Воспользуемся разложением функции в ряд Маклорена (см. Пример 2).

Тогда можно записать

Здесь учтено, что для достижения необходимой точности вычисления интеграла, достаточно ограничиться пятью слагаемыми, так как 0,0008 < 0,001.

111. Вычислить с точностью до 0,00001.

112. Вычислить с точностью до 0,00001.

113. Вычислить ln 1,04 с точностью до 0,0001.

114. Вычислить с точностью до 0,0001.

115. Вычислить ln 0,98 с точностью до 0,001.

116. Вычислить cos 18⁰ с точностью до 0,0001.

117. Вычислить sin9⁰ с точностью до 0,0001.

118. Вычислить с точностью до 0.001.

119. Вычислить с точностью до 0,0001.

120. Вычислить с точностью до 0,001.

121. Вычислить с точностью до 0,0001.

Глава I. ВВЕДЕНИЕ В АНАЛИЗ2

Глава II. ПРЕДЕЛЫ 4

Глава III. ДИФФЕРЕНЦИРОВАНИЕ 17

§1. Производная функции ……………………………………………….17

§2. Дифференциал функции 29

§3. Исследование функций и построение графиков 32

§4. Функции нескольких переменных 48

§5. Экстремумы функции двух переменных 53

Глава IV. ИНТЕГРИРОВАНИЕ 59

§ 1. Первообразная и неопределенный интеграл 59

§ 2. Методы интегрирования 60

§ 3. Определенный интеграл 67

§ 4. Методы вычисления определенного интеграла 70

§ 5. Приближенное вычисление определенных интегралов 74

§ 6. Геометрические приложения определенного интеграла 79

§ 7. Несобственные интегралы 83

Глава V. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 86

§ 1. Основные понятия и определения 86

§ 2. Дифференциальные уравнения первого порядка…………………. 86

§ 3. Дифференциальные уравнения второго порядка 99

§ 4. Приложения дифференциальных уравнений 105

Глава VI. РЯДЫ 109

§ 1. Числовые ряды 109

§ 2. Знакопеременные ряды 118

§ 3. Функциональные ряды 121

§ 4. Степенные ряды 123

§ 5. Ряд Тейлора 128

§ 6. Применение степенных рядов к приближенным вычислениям 132

137

studfiles.net

Разложение функций в степенные ряды

Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора:

где r_n – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:

, где число x заключено между х и а.

Если для некоторого значения х r_n®0 при n®¥, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора:

Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если:

1) она имеет производные всех порядков;

2) построенный ряд сходится в этой точке.

При а=0 получаем ряд, называемый рядом Маклорена:

Пример 1. Разложить в степенной ряд функцию f(x)=2^x.

Решение. Найдем значения функции и ее производных при х=0

f(x) = 2^x, f(0) = 2⁰=1;

f¢(x) = 2^xln2, f¢(0) = 2⁰ ln2= ln2;

f¢¢(x) = 2^x ln²2, f¢¢(0) = 2⁰ ln²2= ln²2;

…

f⁽ⁿ⁾(x) = 2^x lnⁿ2, f⁽ⁿ⁾(0) = 2⁰ lnⁿ2= lnⁿ2.

Подставляя полученные значения производных в формулу ряда Тейлора, получим:

Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -¥<x<+¥.

Пример 2. Написать ряд Тейлора по степеням (х+4) для функции f(x)=e^x.

Решение. Находим производные функции e^x и их значения в точке х=-4.

f(x) = е^x, f(-4) = е^-4;

f¢(x) = е^x, f¢(-4) = е^-4;

f¢¢(x) = е^x, f¢¢(-4) = е^-4;

…

f⁽ⁿ⁾(x) = е^x, f⁽ⁿ⁾( -4) = е^-4.

Следовательно, искомый ряд Тейлора функции имеет вид:

Данное разложение также справедливо для -¥<x<+¥.

Пример 3. Разложить функцию f(x)=lnx в ряд по степеням (х-1),

( т.е. в ряд Тейлора в окрестности точки х=1).

Решение. Находим производные данной функции.

…

Подставляя эти значения в формулу, получим искомый ряд Тейлора:

С помощью признака Даламбера можно убедиться, что ряд сходится при

½х-1½<1. Действительно,

Ряд сходится, если ½х-1½<1, т.е. при 0<x<2. При х=2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х=0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].

Приведем полученные подобным образом разложения в ряд Маклорена (т.е. в окрестности точки х=0) для некоторых элементарных функций:

(1) ,

(2) ,

(3) ,

(4) ,

(5) .

(последнее разложение называют биномиальным рядом)

Пример 4. Разложить в степенной ряд функцию

Решение. В разложении (1) заменяем х на –х², получаем:

Пример 5. Разложить в ряд Маклорена функцию

Решение. Имеем

Пользуясь формулой (4), можем записать:

;

подставляя вместо х в формулу –х, получим:

Отсюда находим:

Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим

Этот ряд сходится в интервале

(-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.

Замечание.

Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а)^m, где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t=х-а и раскладывать полученную функцию относительно t в ряд Маклорена.

Этот метод иллюстрирует теорему о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.

Пример 6. Разложить функцию в ряд Тейлора в окрестности точки х=3.

Решение. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х=3. Однако проще будет воспользоваться имеющимся разложением (5):

Полученный ряд сходится при или –3<x-3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.

Пример 7. Написать ряд Тейлора по степеням (х-1) функции .

Решение.

Ряд сходится при , или -2 < x £ 5.

Пример 8. Разложить функцию в ряд Тейлора в окрестности точки x=2.

Решение. Сделаем замену t=х-2:

Воспользовавшись разложением (3), в котором на место х подставим , получим:

Полученный ряд сходится к заданной функции при , т.е. при .

Таким образом,

Решить: Разложить заданную функцию в ряд:

A 1) по степеням х 2) по степеням х

3) по степеням х 4) по степеням х

5) по степеням (х+1)6) по степеням (х-2)

7) по степ. х 8) в ряд Маклорена

9) в ряд Маклорена 10) в ряд Маклорена

infopedia.su

Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0.

Ряд Маклорена (=Макларена) это ряд Тейлора в окрестности точки а=0.

При использовании рядов, называемых рядами Маклорена (=Макларена), смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.

Теорема Маклорена (ряд Маклорена (=Макларена)) имеет вид:

1) , где f(x) — функция, имеющая при а=0 производные всех порядков. R_n — остаточный член в ряде Маклорена (=Макларена) (Тейлора при а=0)определяется выражением

k-тый коэффициент (при х_k) ряда определяется формулой

Ряды Маклорена являются частным случаем рядов Тейлора.

Условия применния рядов Маклорена (=Макларена).

1) Для того, чтобы функция f(x) могла быть разложена в ряд Маклорена (=Макларена) на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Маклорена (=Макларена) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).

2) Необходимо чтобы существовали производные для данной функции в точке а=0, в окрестности которой мы собираемся строить ряд Маклорена (=Макларена).

Численное интегрирование с использованием рядов Маклорена (=Макларена).

Значения многих интегралов нельзя найти с помощью каких-либо аналитических методов. Мы уже рассказывали о вычислении таких интегралов с помощью формулы трапеций, формулы Симпсона. Другой метод нахождения числового значения определенного интеграла — выражение функции в виде ряда Маклорена (=Макларена) с последующим поочередным интегрированием каждого члена.