Теория рядов
Теория рядов
ОглавлениеПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮГЛАВА 1.  ПРОГРЕССИИ§ 2. Геометрические прогрессии § 3. Бесконечные прогрессии; их сходимость и расходимость § 4. Элементарные преобразования прогрессий § 5. Функциональные прогрессии: область сходимости; равномерная сходимость § 6. Почленное интегрирование прогрессий § 7. Почленное дифференцирование прогрессий § 8. Прогрессии с комплексными членами ГЛАВА 2. ЧИСЛОВЫЕ РЯДЫ. ОСНОВНЫЕ ПОНЯТИЯ. ОСНОВНЫЕ ТЕОРЕМЫ О СХОДИМОСТИ § 2. Определение числового ряда и его сходимости § 3. Остаток ряда § 4. Принцип сходимости Коши § 5. Критерий Коши сходимости рядов § 6. Необходимый признак сходимости ряда § 7. Желательность систематической теории § 8. Свойства сходящихся рядов, подобные свойствам сумм § 9. Дальнейшие свойства рядов ГЛАВА 3. РЯДЫ С ПОЛОЖИТЕЛЬНЫМИ ЧЛЕНАМИ § 1. Признаки сходимости рядов § 2. Признаки сравнения § 3. Интегральный признак сходимости Маклорена — Коши § 4. Применения интегрального признака сходимости § 5.  Сравнительная оценка различных признаков сходимости§ 6. Признак сходимости Даламбера § 7. Признак сходимости Коши § 8. Чувствительность признаков сходимости Даламбера и Коши ГЛАВА 4. ЗНАКОПЕРЕМЕННЫЕ РЯДЫ § 2. Абсолютная сходимость и расходимость § 3. Возможность переставлять члены в абсолютно сходящихся рядах § 4. Условно сходящиеся знакопеременные ряды § 5. Умножение абсолютно сходящихся рядов § 6. Признак сходимости Лейбница § 7. Существенность условий признака сходимости Лейбница ГЛАВА 5. ФУНКЦИОНАЛЬНЫЕ РЯДЫ § 2. Область сходимости функционального ряда § 3. Сходимость последовательности функций. Основные определения § 4. Предел последовательности непрерывных функций § 5. Переход к пределу под знаком интеграла § 6. Переход к пределу под знаком производной § 7. Определение равномерной сходимости функционального ряда и признак Вейерштрасса § 9.  Почленное интегрирование функциональных рядов§ 10. Почленное дифференцирование функциональных рядов ГЛАВА 6. СТЕПЕННЫЕ РЯДЫ. ОБЩИЕ ВОПРОСЫ § 2. Теорема Абеля § 3. Круг сходимости ряда § 4. Вещественный степенной ряд и его интервал сходимости § 5. Равномерная сходимость ряда в круге его сходимости § 6. Вещественные ряды § 7. Комплексные ряды § 8. Разложение функций в степенные ряды § 9. Формула Тейлора § 10. Ряды Тейлора и Маклорена ГЛАВА 7. СТЕПЕННЫЕ РЯДЫ. ПРИМЕРЫ И ПРИЛОЖЕНИЯ § 2. Разложения в ряды Маклорена гиперболических функций ch x и sh x § 3. Разложения в ряды Маклорена тригонометрических функций cos x и sin x § 4. Показательная функция с комплексным значением показателя § 5. Формулы Эйлера § 6. Тригонометрические функции от комплексного значения аргумента § 7. Гиперболические функции от комплексного значения аргумента § 8. Вычисление значений функций при помощи ряда Маклорена § 9. Биномиальный ряд § 10.  Приложения биномиального ряда§ 11. Разложение в ряд Маклорена логарифмической функции § 12. Приближенное вычисление определенных интегралов при помощи степенных рядов § 13. Приближенное интегрирование дифференциальных уравнений при помощи степенных рядов ГЛАВА 8. ОРТОГОНАЛЬНЫЕ И ОРТОНОРМАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ § 2. Векторы и функции § 3. Нормированные и ортогональные функции § 4. Нормированные и ортогональные системы функций § 5. Нормировка систем функций § 6. Разложение по системам функций ГЛАВА 9. РЯДЫ ФУРЬЕ § 1. Ряды и коэффициенты Фурье § 2. Условия Дирихле и теорема о разложении функции в ряд Фурье § 4. Физическое истолкование разложения функции в тригонометрический ряд Фурье § 5. Разложение функции f(x) = x § 6. Сдвиг сегмента разложения § 7. Изменение длины сегмента разложения § 8. Четные и нечетные функции § 9. Разложение четной функции в ряд Фурье § 10.  Разложение нечетной функции в ряд Фурье§ 11. Разложение ряд Фурье функций на сегменте от 0 до пи § 12. Комплексная форма записи ряда Фурье § 13. Разложение в комплексный ряд Фурье § 14. Характер сходимости рядов Фурье ГЛАВА 10. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ С ЗАКРЕПЛЕННЫМИ КОНЦАМИ § 2. Начальные и граничные условия § 3. Метод разделения переменных § 4. Использование граничных условий. Собственные функции и собственные значения § 5. Использование начальных условий ГЛАВА 11. ИНТЕГРАЛ ФУРЬЕ § 1. Представление функций интегралом Фурье § 2. Простейшие достаточные условия представимости функции интегралом Фурье § 3. Интеграл Фурье для четных функций § 4. Интеграл Фурье для нечетных функций § 5. Комплексная форма интеграла Фурье § 6. Понятие о преобразовании Фурье § 7. Косинус-преобразование Фурье § 8. Синус-преобразование Фурье § 9. Спектральная функция Часть II § 1. Признак сходимости Куммера § 2.  Признак сходимости Раабе§ 3. Признак сходимости Бертрана § 4. Признак сходимости Гаусса § 5. Сходимость знакопеременных рядов § 6. Признак сходимости Дирихле ГЛАВА 13. ДВОЙНЫЕ РЯДЫ § 1. Определение двойного ряда § 2. Сходимость двойных рядов § 3. Критерии сходимости двойных рядов. Теорема Маркова § 4. Свойства двойных рядов и признаки сходимости § 6. Двойные функциональные ряды § 7. Двойные степенные ряды § 8. Разложение функций двух переменных в двойные ряды Тейлора и Маклорена § 9. Ортогональные и ортонормальные системы функций от двух переменных § 10. Двойные ряды Фурье ГЛАВА 14. СУММИРОВАНИЕ СХОДЯЩИХСЯ РЯДОВ § 2. Линейные преобразования рядов § 3. Теорема Абеля и почленное дифференцирование и интегрирование рядов § 4. Последовательности разностей § 5. Преобразование рядов по Эйлеру § 6. Преобразование рядов по Куммеру ГЛАВА 15. СУММИРОВАНИЕ РАСХОДЯЩИХСЯ РЯДОВ § 1.  Расходящиеся геометрические прогрессии§ 2. Суммирующие функции § 3. Суммирование по Пуассону — Абелю § 4. Линейность и регулярность суммирования по Пуассону — Абелю § 5. Суммируемость рядов по Пуассону — Абелю и их абсолютная сходимость § 6. Теорема Таубера § 7. Суммирование по Чезаро § 8. Соотношение между сходимостью по Чезаро и по Пуассону — Абелю § 9. Суммирование по Эйлеру ГЛАВА 16. СХОДИМОСТЬ РЯДОВ ФУРЬЕ § 2. Исследование двух интегралов § 3. Исследование одного класса интегралов § 4. Доказательство теоремы Дирихле § 5. Теорема Фурье § 6. Коэффициенты Фурье разрывных функций § 7. Скорость сходимости рядов Фурье § 8. Улучшение сходимости рядов Фурье по методу выделения особенностей § 9. О равномерной сходимости рядов Фурье § 10. Неравномерная сходимость последовательностей непрерывных функций § 11. Поведение рядов Фурье функций в точках их разрыва. Явление Гиббса § 12. Экстремальное свойство сумм Фурье § 13.  Суммирование рядов Фурье по Чезаро. Теорема Фейера§ 14. Равенство Парсеваля § 15. Теорема Вейерштрасса ГЛАВА 17. ПРИМЕНЕНИЕ РЯДОВ ФУРЬЕ В ТЕОРИИ ИЗГИБА БАЛОК § 3. Свободно опертая балка § 4. Первая возможность ограничиться двукратным дифференцированием § 5. Случай сосредоточенной нагрузки § 6. Прогиб балки от распределенной нагрузки § 7. Прогиб от сосредоточенного момента § 8. Статически неопределимая балка § 9. Сложный изгиб балки § 10. Балка на упругом основании § 11. Вторая возможность ограничиться двукратным дифференцированием. Потенциальная энергия изгиба балки § 12. Потенциальная энергия изгиба балки в случае нескольких нагрузок § 13. Функции прогиба с ортогональными вторыми производными § 14. Свободно опертая нагруженная балка § 15. Работа продольных сил при сложном изгибе балки § 16. Общий случай изгиба балки § 17. Общий случай изгиба свободно опертой балки § 18. Изгиб симметрично нагруженной балки, жестко заделанной по концам § 19.  Функция прогиба симметрично загруженной балки с жестко заделанными концами |
ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮГЛАВА I. 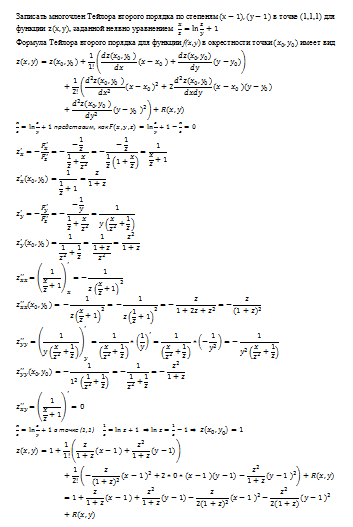 ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ§ 1. Действительные числа. § 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 5. Основные теоремы о пределах § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11.  n при n целом и положительном§ 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 22. Производные различных порядков § 23.  x, sin x, cos xУпражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6.  Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента§ 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 8. Разложение многочлена на множители в случае комплексных корней § 9. Интерполирование. Интерполяционная формула Лагранжа § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Определение функции нескольких переменных § 2.  Геометрическое изображение функции двух переменных§ 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19.  Получение функции на основании экспериментальных данных по методу наименьших квадратов§ 20. Особые точки кривой Упражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 3. Правила дифференцирования векторов (векторных функций) § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6.  Интегрирование по частям§ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9. 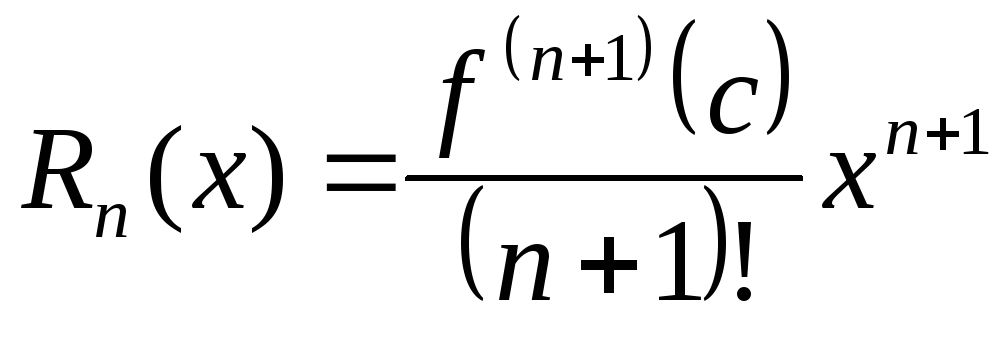 Формула Чебышева§ 10. Интегралы, зависящие от параметра. Гамма-функция § 11. Интегрирование комплексной функции действительной переменной Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла Упражнения к главе XII |
многомерное исчисление — ряд Тейлора для функции двух переменных
спросил
Изменено 2 года, 1 месяц назад
Просмотрено 3к раз
$\begingroup$
Меня интересует расширение до 3-го Ордена Тейлора.
9{\mkern-5mu3}\cdot f$$
$\endgroup$
1
Введение в теорему Тейлора для функций многих переменных
Помните теорему Тейлора об исчислении одной переменной. Дана одна переменная функцию $f(x)$, вы можете подобрать ее полиномом вокруг $x=a$.
Например, наилучшим линейным приближением для $f(x)$ является \начать{выравнивать*} f(x) \ приблизительно f(a) + f\,'(a)(x-a). \конец{выравнивание*} Это линейное приближение соответствует $f(x)$ (показано зеленым цветом ниже) с линия (показана синим цветом) через $x=a$, которая соответствует наклону $f$ в $a$. 93 + \cdots. \конец{выравнивание*} Важным моментом является то, что этот полином Тейлора хорошо аппроксимирует $f(x)$ для $x$ вблизи $a$.
Мы хотим обобщить многочлен Тейлора на (скалярнозначный) функции нескольких переменных: \начать{выравнивать*} f(\vc{x})= f(x_1,x_2, \ldots, x_n). \конец{выравнивание*}
Мы уже знаем наилучшее линейное приближение к $f$.
Он включает производную,
\начать{выравнивать*}
f(\vc{x}) \ приблизительно f(\vc{a}) + Df(\vc{a}) (\vc{x}-\vc{a}).
\label{eq:firstorder}
\конец{выравнивание*}
где $Df(\vc{a})$ — матрица частных производных. Линейное приближение представляет собой полином Тейлора первого порядка. 92.
\конец{выравнивание*}
Для функции многих переменных $f(\vc{x})$ аналогичный
вторая производная?
Поскольку $f(\vc{x})$ скалярная, первая производная есть $Df(\vc{x})$, матрица $1 \times n$, которую мы можем рассматривать как $n$-мерную вектор-функцию от $n$-мерного вектора $\vc{x}$. Для второй производной от $f(\vc{x})$ можно взять матрицу частных производные функции $Df(\vc{x})$. Мы могли бы написать это как $DDf(\vc{x})$ на данный момент. Эта секунда производная матрица — это $n \times n$ матрица, называемая Матрица Гессе из $f$. Обозначим его через $Hf(\vc{x})$, \начать{выравнивать*} Hf(\vc{x}) = DDf(\vc{x}). \конец{выравнивание*}
Когда $f$ является функцией нескольких переменных, вторая производная
член ряда Тейлора будет использовать гессиан $Hf(\vc{a})$.