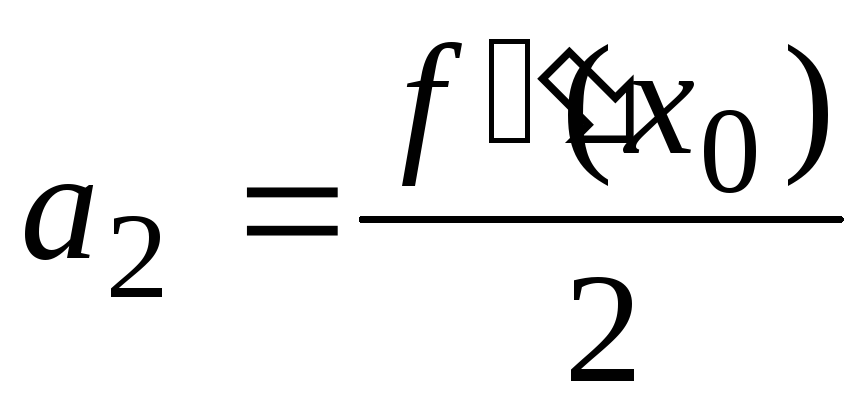Разложение в ряд лорана онлайн с решением: онлайн разложение в ряд лорана

Ряды Лорана в Wolfram|Alpha или Кто читает Wolfram|Alpha по-русски?

Ряды Лорана в Wolfram|Alpha или Кто читает Wolfram|Alpha по-русски?

Судя по активности, посетителям блога Wolfram|Alpha по-русски не очень интересны элементарные вопросы математики. К примеру, пост об интегральном преобразовании Лапласа, опубликованный почти месяц назад, собрал аудиторию больше, чем недавняя статья о прямой на плоскости или свежая заметка о построении окружности.

Хотя это еще ни о чем не говорит. Иначе придется признать, что сюда заходят только продвинутые математики. А ведь это совсем не обязательно. Это могут быть, например, студенты старших курсов вузов. Большинство из них понимают ценность такого помощника, как Wolfram|Alpha.

В то же время, вопрос элементарного уровня «Как построить график функции в Wolfram|Alpha» по-прежнему остается одним из самых популярных в блоге. Как объяснить это? Один из возможных вариантов: при изучении математики в вузах вопросам аналитической геометрии уделяется не слишком большое внимание, поэтому они кажутся не такими важными, как, например, построение графиков функций.

Второй по рейтингу пост этого блога на сегодня — Возведение матрицы в степень. Его популярность можно объяснить так: мало кто задумывается, что матрицы можно возводить в степень. Хотя это очевидно, но выглядит парадоксально. Отсюда — интерес.

Конечно же, кто читает этот блог, студенты или математики, можно было бы установить путем опроса. Наверное, так и следует сделать. Когда закончится предыдущий опрос «Как часто вы пользуетесь Wolfram|Alpha?», можно будет начать новый, чтобы в результате получить объективный ответ. Но главное понятно: читают наверняка только те, кому математика, нужна, близка по тем или иным причинам. И это — студенты, инженеры, математики, преподаватели…

А кто ещё? Вопрос поставлен. И можно продолжить знакомство с Wolfram|Alpha.

Поскольку начиналось с того, что применение Wolfram|Alpha к решению элементарных задач математики негативно влияет на активность читателей блога, рассмотрим, что Wolfram|Alpha может предложить при решении более сложных задач.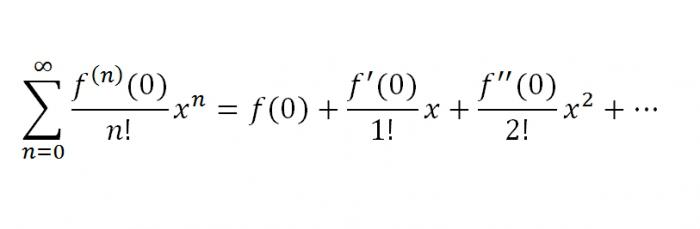

3

Еще примеры на вычисление вычетов:

• Res x!
• Res tan(z) for 1< |z-1|< 3

26 Ряды Лорана. Разложение аналитических функций в ряд Лорана

Рядом Лорана называется обобщённый степенной ряд, в котором наряду с положительными фигурируют и целые отрицательные степени :

Записанное выражение мы понимаем как сумму двух рядов: правильной части (обычный степенной ряд) и главной части (содержащий отрицательные степени). Пусть круг сходимости правильной части . Сделав в главной части замену , получим относительно обычный степенной ряд, у которого есть круг сходимости , т.е. . Если при этом окажется, что , то получается, что весь ряд Лорана сходится в кольце . При этом из теоремы Абеля следует, что в этом кольце ряд Лорана сходится абсолютно, а на любом замкнутом множестве, содержащемся в кольце, – ещё и равномерно. Можно доказать, что сумма ряда Лорана является в его кольце сходимости аналитической.

Имеет решение и обратная задача:

Теорема Если функция аналитическая в кольце с центром в точке , то она в этом кольце разлагается в ряд Лорана по степени .

Доказательство Пусть – любая точка этого кольца. Можно увеличить внутренний радиус кольца и уменьшить внешний радиус так, чтобы точка оставалась в новом замкнутом кольце . Границы его обозначим соответственно через и (Рисунок 40). Для замкнутого кольца верна интегральная формула Коши для многосвязных областей (параграф 18, теорема 2). Для выбранной точки

Повторяя рассуждения параграфа 22, получим разложение первого слагаемого в правильную часть ряда Лорана (ряд Тейлора):

, где

Аналогично разложим в ряд второй интеграл. Для его подынтегральной функции имеем

Мы вынесли за скобки , чтобы знаменатель геометрической прогрессии оказался по модулю меньшим единицы: (т.к. ).

Для возможности почленного интегрирования ряда по , докажем, что он на сходится равномерно.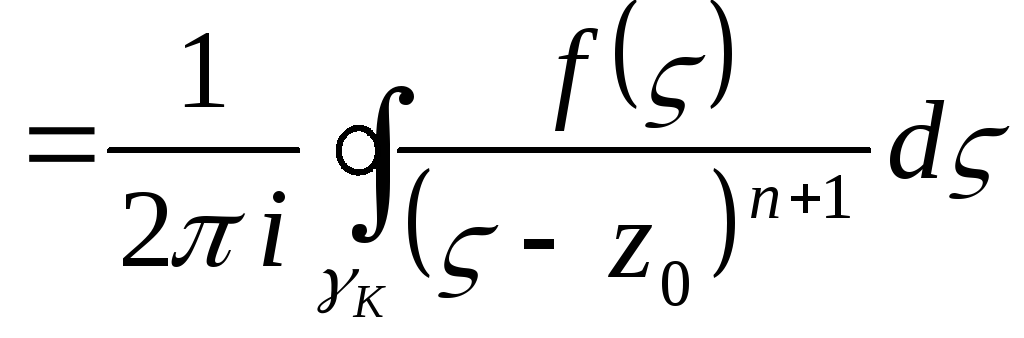 Равномерная сходимость следует из теоремы Вейерштрасса параграф 19, так как данный ряд при мажорируется числовой (т.е. не зависящей от ) положительной прогрессией , где . Интегрируя равенство, получаем

где

Складывая два полученных ряда, мы получаем разложение функции в исходном кольце в ряд Лорана.

В заключение заметим, что формулы для и отличаются только контурами интегрирования. Но ведь функция аналитична в кольце, и поэтому интегралы по этим контурам одинаковы (параграф 15). Оба они могут быть заменены интегралом по любой окружности с центром , лежащей в данном кольце. Итак, окончательно получаем:

Полученная интегральная формула для коэффициентов ряда на практике не очень удобна. Чаще всего для разложения в ряд Лорана используют известные разложения в ряд Тейлора.

Примеры

Так как особыми точками функции являются и , то все три указанные разложения возможны (Рисунок 41). Во всех трёх случаях используем формулу суммы геометрической прогрессии, предварительно вынося за скобки то из слагаемых в знаменателе, которое по модулю меньше другого.

а

Получился ряд Тейлора, чего и следовало ожидать, так как функция в круге аналитична.

б .

Для можно воспользоваться предыдущим разложением, так как . Складывая полученные разложения, получим ряд Лорана, содержащий и правильную и главную части.

в

Разложение в случае б верно и в случае в , так как

Складывая, получаем, что ряд Лорана состоит только из главной части.

2 Наибольший интерес, как мы увидим в следующих параграфах, представляет разложение функции в ряд Лорана в проколотой окрестности её изолированной особой точки. Такой точкой для функции, рассмотренной в примере 1, является, например, , а проколотая окрестность, в которой она аналитическая, имеет вид (рисунок 42) разложение же будет по степеням :

З десь главная масть ряда состоит из одного слагаемого.

27 Классификация изолированных особых точек. Теорема Сохоцкого

В примере параграфа 26 обе особые точки и являются изолированными. Однако встречаются и неизолированные особые точки. Например, для функции особыми точками являются , из которых точка не является изолированной.

Если изолированная особая точка, то существует ее проколотая окрестность, в которой функция аналитическая и, следовательно, в ней она может быть разложена в ряд Лорана но степеням . Возможны три случая:

1 в ряде Лорана отсутствует главная часть;

2 главная часть содержит конечное число членов

3 главная часть содержит бесконечное число членов.

В первом случае точка называется правильной (или устранимой), а функция, точнее ее аналитическое продолжение, является аналитической в точке . Во втором случае называется полюсом — го порядка (при — простой полюс). В третьем случае называется существенно особой точкой.

Примеры

1 Для функции (см. пример 3 параграф 15) точка является правильной точкой. Мы условились в параграфе 25 функцию и ее аналитическое продолжение считать одной функцией. Поэтому .

2 Для (пример 2, параграф 26) точка (и ) является простым полюсом.

3 Для функции точка существенно особая.

Исследуем, как выглядит предел функции в изолированных особых точках разного типа.

I Пусть — правильная точка, т.е. тогда в силу аналитичности, а, следовательно, непрерывности функции в точке , имеем:

II Если полюс, то

III Для случая, когда существенно особая точка, имеется следующая теорема, впервые доказанная профессором Петербургского университета Ю.В. Сохоцким (1842-1927):

Теорема 1 Если существенно особая точка функции , то для любого числа (включая ) существует такая последовательность , стремящаяся к а, что. Короче: существенно особая точка функции

Очевидно, что в существенно особой точке функция не имеет ни конечного, ни бесконечного пределов.

Пример. Мы знаем, что существенно особая точка для функции .

не существует, ибо даже на действительной оси

Проверьте самостоятельно, что какое бы число мы ни взяли, в любой окрестности точки найдутся точки , что .

Отвлечемся теперь ненадолго от нашей темы и выясним логический метод, называемый «обращением по разделению». Допустим, что относительно некоторого объекта возможны высказывания , причем они охватывают все возможные случая и взаимоисключают друг друга (например, ). Пусть высказывания обладают такими же свойствами, и . Тогда, как легко доказать от противного, верна серия обратных импликаций: . Например, египетский треугольник со сторонами является прямоугольным не по теореме Пифагора, а по теореме обратной к ней. Обратная же теорема легко может быть доказана методом обращения по разделению: действительно, по теореме косинусов:

треугольник прямоугольный ,

треугольник остроугольный ,

треугольник тупоугольный .

Применяя метод обращения по разделению, убеждаемся, что верны все три обратных утверждения. На этом же методе основывается доказательство следующего утверждения:

Теорема 2 Если функция в изолированной особой точке имеет конечный предел, то эта точка правильная; если бесконечный, то полюс; если нет никакого предела, то это существенно особая точка.

Пример Рассмотрим функцию с единственной особой точ­кой . Для имеем , а для имеем . Поэтому не существует. Следовательно, точка существенно особая.

Калькулятор расширения серии

: Wolfram|Alpha Калькулятор расширения серии

: Wolfram|Alpha

О, о! Wolfram|Alpha не работает без JavaScript.

Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.

WolframAlpha

Расширения серии в Wolfram|Alpha

Тригонометрия

Больше, чем просто онлайн-калькулятор расширения серий

Wolfram|Alpha — отличный инструмент для вычисления серий. Исследуйте отношения между функциями и их разложениями в ряды и улучшите свои математические знания с помощью калькулятора разложения в ряды Wolfram|Alpha.

Подробнее о:

• Серия »

Советы по вводу запросов 93 на заказ 10

Серия

sqrt(sin x) при x = 0

Web Apps

Mobile Apps

Products

Business

API & Developer Solutions

• Resources & Tools
• About
• Contact
• Connect

• ©2023 Wolfram Alpha LLC
• Terms
• Privacy

• wolfram.com
• Wolfram Language
• Mathematica
• Wolfram Demonstrations
• Wolfram for Education
• MathWorld

complex analysis — ряд Лорана для $\cot(z)$

Задать вопрос

спросил 6 лет, 4 месяца назад

Изменено 3 года, 11 месяцев назад

Просмотрено 23 тысячи раз

$\begingroup$

Я ищу разъяснения о том, как вычислить ряд Лорана для

$\cot z$

Я начал с попытки найти $\frac{1}{\sin z}$.