Разложение дроби на элементарные дроби: Метод разложения на простейшие онлайн

Содержание

Разложение дроби на простейшие: примеры, решение

Для закрепления материала будут рассмотрены несколько примеров и рассмотрена теория по разложению дробей на простейшие. Подробно рассмотрим метод неопределенных коэффициентов и метод частных значений, изучим всевозможные комбинации.

Простые дроби имеют название элементарных дробей.

Типы дробей

Дроби различают:

Ax-a;
A(x-a)n;
Mx+Nx2+px+q;
Mx+N(x2+px+q)n.

A, M, N, a, p, q из которых являются числами, а дискриминант дробей 3 и 4 меньше нуля, то есть корней не имеет выражение.

При упрощении выражения быстрее выполняются вычислительные функции. Представление дробно-рациональной дроби как суммы простейших дробей аналогично. Для этого применяют ряды Лорана для того, чтобы разложить в степенные ряды или для поиска интегралов.

Например, если необходимо брать интеграл от дробно-рациональной функции вида ∫2×3+3×3+xdx. После чего необходимо произвести разложение подынтегральной функции на простейшие дроби. Все это к формированию простых интегралов. Получаем, что

∫2×3+3×3+xdx=∫2+2x-3x+2×2+1dx==∫2dx+∫3xdx-∫3x+2×2+1dx==2x+3lnx-32∫d(x2+1)x2+1-2∫dxx2+1==2x+3lnx-32lnx2+1-2arctan(x)+C

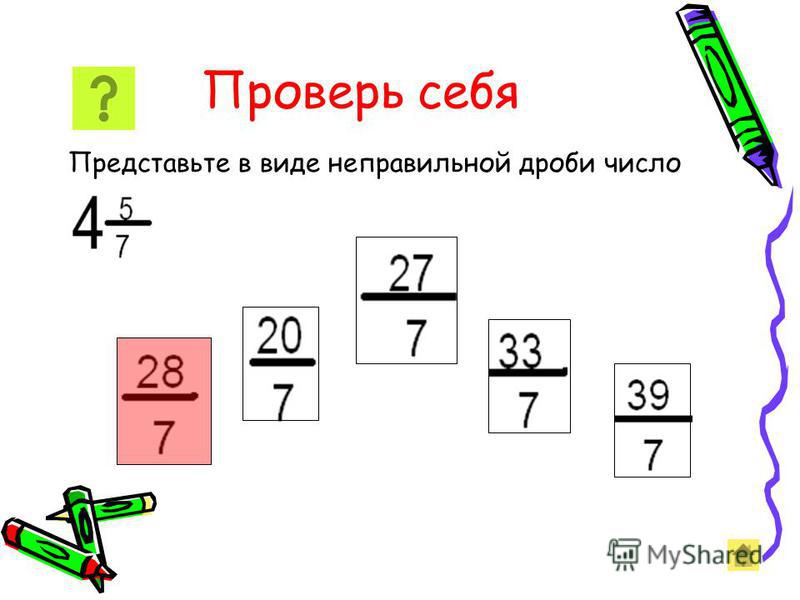
Пример 1

Произвести разложение дроби вида -2x+3×3+x.

Решение

Когда степень числителя многочлена меньше степени многочлена в знаменателе, имеет место разложение на простейшие дроби. Иначе применяется деление для выделения целой части, после чего производят разложение дробно-рациональной функции.

Применим деление углом. Получаем, что

Отсюда следует, что дробь примет вид

2×3+3×3+x=2+-2x+3×3+x

Значит, такое разложение приведет к тому, что результат будет равен -2x+3×3+x.

Алгоритм метода неопределенных коэффициентов

Для того, чтобы правильно произвести разложение, необходимо придерживаться нескольких пунктов:

Произвести разложение на множители. можно применять вынесение за скобки, формулы сокращенного умножения, подбор корня. Имеющийся пример x3+x=xx2+1 для упрощения выносят х за скобки.
Разложение дроби на простейшие дроби с неопределенными коэффициентами.

Рассмотрим на нескольких примерах:

Пример 2

Когда в знаменателе имеется выражение вида (x-a)(x-b)(x-c)(x-d), количество множителей не имеет значения, дробь можно представить в виде дроби первого типа Ax-a+Bx-b+Cx-c+Dx-d, где a, b, c и d являются числами, A, B, C и D – неопределенными коэффициентами.

Пример 3

Когда знаменатель имеет выражение (x-a)2(x-b)4(x-c)3, количество множителей также не имеет значения, причем саму дробь необходимо привести ко второму или первому типу вида:

A2x-a2+A1x-a+B4x-b4+B3x-b3+B2x-b2+B1x-b++C3x-c3+C2x-c2+C1x-c

где имеющиеся a, b, c являются числами, а A1, A2, B1, B2, B3, B4, C1, C2, C3 — неопределенными коэффициентами. Какова степень многочлена, такое количество слагаемых имеем.

Пример 4

Когда знаменатель имеет вид типа x2+px+qx2+rx+s, тогда количество квадратичных функций значения не имеет, а дробь принимает вид третьего типа Px+Qx2+px+q+Rx+Sx2+rx+s,где имеющиеся p, q, r и s являются числами, а P, Q, R и S – определенными коэффициентами.

Пример 5

Когда знаменатель имеет вид x2+px+q4x2+rx+s2, количество множителей значения не имеет также , как и их степени, дробь представляется в виде третьего и четверного типов вида

P4x+Q4(x2+px+q)4+P3x+Q3(x2+px+q)3+P2x+Q2(x2+px+q)2+P1x+Q1x2+px+q++R2x+S2(x2+rx+s)2+R1x+S1x2+rx+s

где имеющиеся p, q, r и s являются числами, а P1,P2,P3,P4,R1,R2,S1,S2 — неопределенными коэффициентами.

Пример 6

Когда имеется знаменатель вида (x-a)(x-b)3(x2+px+q)(x2+rx+s)2, тогда дробь необходимо представить в виде четвертого типа

Ax-a+B3x-b3+В2x-b2+В1x-b++Px+Qx2+px+q+R2x+S2x2+rx+s2+R1x+S1x2+rx+s

Рассмотрим на примере дроби. Когда дробь раскладывается в сумму третьим типом вида 2x-3×3+x=2x-3x(x2+1)=Ax+Bx+Cx2+1, где A, B и C являются неопределенными коэффициентами.

Приведение полученной суммы простейших дробей при наличии неопределенного коэффициента к общему знаменателю, применяем метода группировки при одинаковых степенях х и получаем, что

2x-3×3+x=2x-3x(x2+1)=Ax+Bx+Cx2+1==A(x2+1)+(Bx+C)xx(x2+1)=Ax2+A+Bx2+Cxx(x2+1)==x2(A+B)+xC+Ax(x2+1)

Когда х отличен от 0, тогда решение сводится к приравниванию двух многочленов.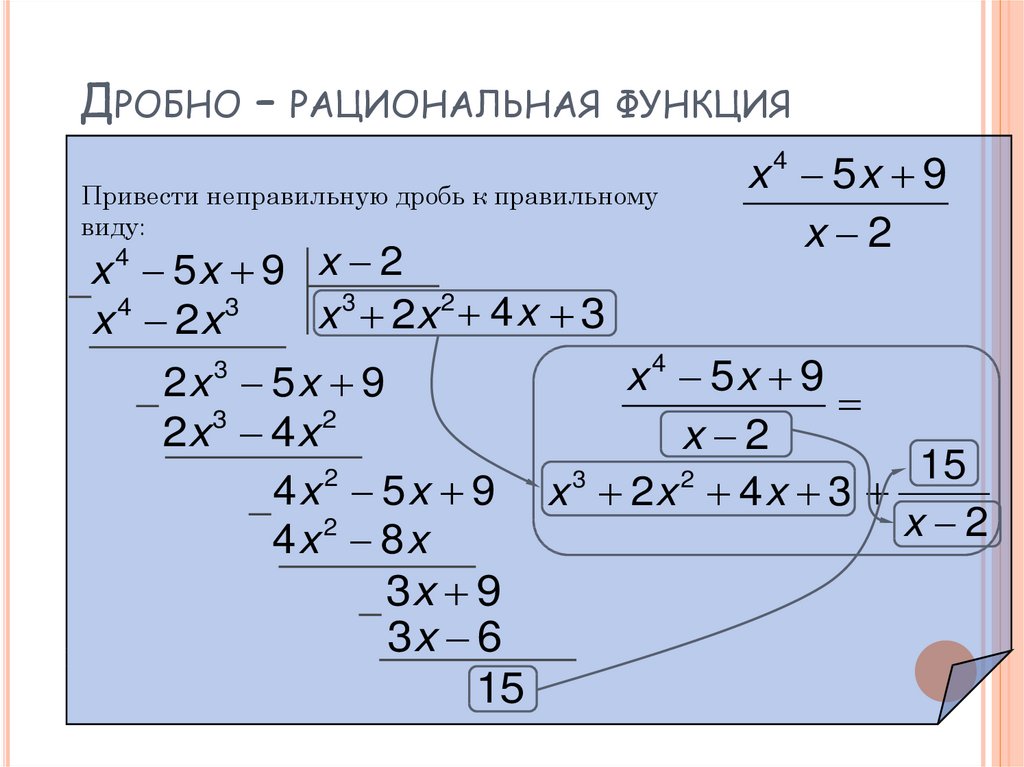 Получаем 2x-3=x2(A+B)+xC+A. Многочлены считаются равными тогда, когда совпадают коэффициенты при одинаковых степенях.

Приравнивание коэффициентов с одинаковыми степенями х. Получим, что система линейных уравнений при наличии определенных коэффициентов:
A+B=0C=2A=-3
Решение полученной системы при помощи любого способа для нахождения неопределенных коэффициентов: A+B=0C=2A=-3⇔A=-3B=3C=2
Производим запись ответа:
2×3+3×3+x=2-2x-3×3+x=2-2x-3x(x2+1)==2-Ax+Bx+Cx2+1=2—3x+3x+2×2+1=2+3x-3x+2×2+1

Необходимо постоянно выполнять проверки. Это способствует тому, что приведение к общему знаменателю получит вид

2+3x-3x+2×2+1=2x(x2+1)-(3x+2)xx(x2+1)=2×3+3×3+x

Методом неопределенных коэффициентов считают метод разложения дроби на другие простейшие.

Использование метода частных значений способствует представлению линейных множителей таким образом:

x-ax-bx-cx-d.

Пример 7

Произвести разложение дроби 2×2-x-7×3-5×2+6x.

Решение

По условию имеем, что степень многочлена числителя меньше степени многочлена знаменателя, тогда деление выполнять не нужно. Необходимо перейти к разложению на множители. для начала необходимо выполнить вынесение х за скобки. Получим, что

x3-5×2+6x=x(x2-5x+6)

Квадратный трехчлен x2-5x+6 имеет корни, которые находим не по дискриминанту, а по теореме Виета. Получим:

x1+x2=5×1·x2=6⇔x1=3×2=2

Запись трехчлена может быть в виде x2-5x+6=(x-3)(x-2).

Тогда изменится знаменатель:x2-5×2+6x=x(x2-5x+6)=x(x-3)(x-2)

Имея такой знаменатель, дробь раскладываем на простейшие дроби с неопределенными коэффициентами. Выражение примет вид:

2×2-x-7×3-5×2+6x=2×2-x-7x(x-3)(x-2)=Ax+Bx-3+Cx-2

Полученный результат необходимо приводить к общему знаменателю. Тогда получаем:

2×2-x-7×3-5×2+6x=2×2-x-7x(x-3)(x-2)=Ax+Bx-3+Cx-2==A(x-3)(x-2)+Bx(x-2)+Cx(x-3)x(x-3)(x-2)

После упрощения придем к неравенству вида

2×2-x-7x(x-3)(x-2)=A(x-3)(x-2)+Bx(x-2)+Cx(x-3)x(x-3)(x-2)⇒⇒2×2-x-7=A(x-3)(x-2)+Bx(x-2)+Cx(x-3)

Теперь переходим к нахождению неопределенных коэффициентов. Нужно подставлять полученные значения в равенство для того, чтобы знаменатель обратился в ноль, то есть значения х=0, х=2 и х=3.

Если х=0, получим:

2·02-0-7=A(0-3)(0-2)+B·0·(0-2)+C·0·(0-3)-7=6A⇒A=-76

Если x=2, тогда

2·22-2-7=A(2-3)(2-2)+B·2·(2-2)+C·2·(2-3)-1=-2C⇒C=12

Если x=3, тогда

2·32-3-7=A(3-3)(3-2)+B·3·(3-2)+C·3·(3-3)8=3B⇒B=83

Ответ: 2×2-x-7×3-5×2+6x=Ax+Bx-3+Cx-2=-76·1x+83·1x-3+12·1x-2

Метод коэффициентов и метод частных значений отличаются только способом нахождения неизвестных. Данные методы могут быть совмещены для быстрого упрощения выражения.

Пример 8

Произвести разложение выражения x4+3×3+2x-11(x-1)(x+1)(x-3)3 на простейшие дроби.

Решение

По условию имеем, что степень числителя многочлена меньше знаменателя, значит зазложение примет вид

x4+3×3+2x-11(x-1)(x+1)(x-3)3=Ax-1+Bx+1+C(x-3)3+C(x-3)2+Cx-3

Производим приведение к общему знаменателю. Имеем, что

x4+3×3+2x-11(x-1)(x+1)(x-3)3=Ax-1+Bx+1+C(x-3)3+C(x-3)2+Cx-3==A(x+1)(x-3)3+B(x-1)(x-3)3(x-1)(x+1)(x-3)3++C3(x-1)(x+1)+C2(x-1)(x+1)(x-3)+C1(x-1)(x+1)(x-3)2(x-1)(x+1)(x-3)3

Приравняем числители и получим, что

x4+3×3+2x+11==A(x+1)(x-3)3+B(x-1)(x-3)3++C3(x-1)(x+1)+C2(x-1)(x+1)(x-3)+C1(x-1)(x+1)(x-3)2

Из выше написанного понятно, что нули знаменателя – это х=1, х=-1 и х=3. Тогда применим метод частных решений. Для этого подставим значения х. получим, что если х=1:

-5=-16A⇒A=516

Если х=-1

-15=128B⇒B=-15128

Если х=3

157=8C3⇒C3=1578

Отсюда следует, что нужно найти значения C1 и C3.

Поэтому подставим полученный значения в числитель, тогда

x4+3×3+2x-11==516(x+1)(x-3)3-15128(x-1)(x-3)3+1578(x-1)(x+1)++C2(x-1)(x+1)(x-3)+C1(x-1)(x+1)(x-3)2

Раскроем скобки для того, чтобы привести подобные слагаемые с одинаковыми степенями. Придем к выражению вида

x4+3×3+2x-11=x425128+C1+x3-8564+C2-6C1++x267332-3C2+8C1+x40564-C2+6C1+3C2-9C1-3997128

Необходимо приравнять соответствующие коэффициенты с одинаковыми степенями, тогда сможем найти искомое значение C1 и C3. Теперь необходимо решить систему:

25128+C1=1-8564+C2-6C1=367332-3C2+8C1=040564-C2+6C1=23C2-9C1-3997128=11

Первое уравнение дает возможность найти C1=103128, а второе C2=3+8564+6C1=3+8564+6·103128=29332.

Итог решения – это искомое разложение дроби на простейшие вида:

x4+3×3+2x-11(x-1)(x+1)(x-3)3=Ax-1+Bx+1+C3x-33+C2x-32+C1x-3==5161x-1-151281x+1+1578·1x-33+293321x-32+1031281x-3

Примечание

При непосредственном применении метода неопределенных коэффициентов необходимо было бы решать все пять линейных уравнений, объединенных в систему. Такой метод упрощает поиск значения переменных и дальнейшее решение в совокупности. Иногда применяется несколько методов. Это необходимо для быстрого упрощения всего выражения и поиска результата.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

2+13x+6;\\ \left\{ \begin{aligned} & A+B=5;\\ & A+4B+C=13;\\ & 5A+4C=6. \end{aligned} \right. $$

Для разнообразия применим метод Крамера для решения полученной системы линейных уравнений.

$$ \Delta=\left| \begin{array} {ccc} 1 & 1 & 0\\ 1 & 4 & 1 \\ 5 & 0 & 4 \end{array}\right|=17; \Delta_A=\left| \begin{array} {ccc} 5 & 1 & 0\\ 13 & 4 & 1 \\ 6 & 0 & 4 \end{array}\right|=34; \Delta_B=\left| \begin{array} {ccc} 1 & 5 & 0\\ 1 & 13 & 1 \\ 5 & 6 & 4 \end{array}\right|=51; \Delta_C=\left| \begin{array} {ccc} 1 & 1 & 5\\ 1 & 4 & 13 \\ 5 & 0 & 6 \end{array}\right|=-17. \\ A=\frac{\Delta_A}{\Delta}=\frac{34}{17}=2;\; B=\frac{\Delta_B}{\Delta}=\frac{51}{17}=3; \; C=\frac{\Delta_C}{\Delta}=\frac{-17}{17}=-1. $$

Подставляя значения $A=2$, $B=3$, $C=-1$ в равенство

$$ \frac{5x^2+13x+6}{(x+4)(x^2+x+5)}=\frac{A}{x+4}+\frac{Bx+C}{x^2+x+5} $$

будем иметь:

$$ \frac{5x^2+13x+6}{(x+4)(x^2+x+5)}=\frac{2}{x+4}+\frac{3x-1}{x^2+x+5}. 2}$.

Первая часть

Вторая часть

Третья часть

Вернуться к списку тем

Задать вопрос на форуме

Записаться на занятия

Онлайн-занятия по высшей математике

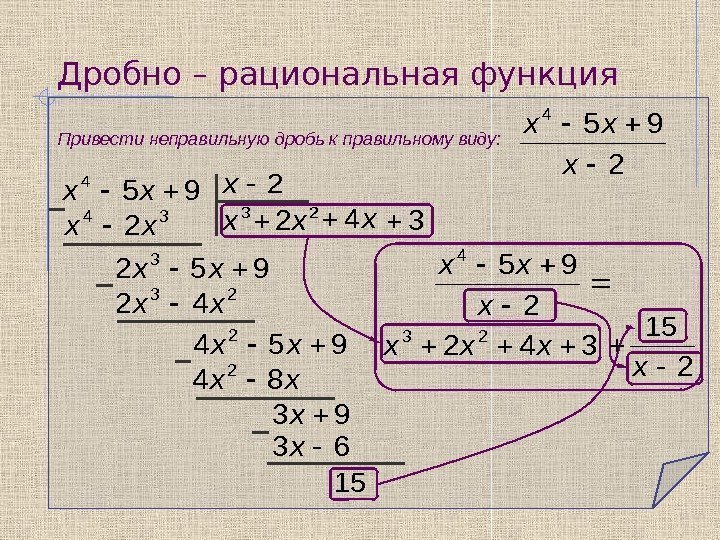
9.4. Разложение правильной рациональной дроби в сумму простейших дробей

Будем рассматривать действительные дробно-рациональные функции $f(x) = \frac{P(x)}{Q(x)}$ (рациональная дробь), где $P, Q$ — действительные многочлены, $\deg P \geqslant 0, \deg Q\geqslant 1$.

Определение 9.9. Рациональная дробь $\frac{P(x)}{Q(x)}$ называется правильной, если $\deg P < \deg Q$.

Лемма 9.5. Всякая рациональная дробь $\frac{P(x)}{Q(x)}$ единственным образом может быть разложена в сумму многочлена и правильной рациональной дроби с знаменателем $Q(x)$.

$\blacktriangle $ Пусть $\frac{P(x)}{Q(x)}$ — рациональная дробь. Поделим многочлен $P$ на $Q$ с остатком.

$P = TQ + R, \deg R < \deg Q \Rightarrow \frac{P(x)}{Q(x)} = T(x) + \frac{R(x)}{Q(x)}$ — правильная дробь. 2+px+q) \Leftrightarrow $ $\alpha , \overline\alpha$ — корни многочлена $P(x) — (Ax+B)Q_1(x)$. Тогда $A\alpha + B = \frac{P(\alpha )}{Q_1(\alpha )}$, $A\overline\alpha + B = \frac{P(\overline\alpha )}{Q_1(\overline\alpha )}$.

$A = \dfrac { \frac{P(\alpha )}{Q_1(\alpha )} — \frac{P(\overline\alpha )}{Q_1(\overline\alpha )} }{\alpha — \overline\alpha }$,$B = \dfrac { \frac{P(\overline\alpha )}{Q_1(\overline\alpha )}\alpha — \frac{P(\alpha )}{Q_1(\alpha )}\overline\alpha }{\alpha — \overline\alpha }$.

Покажем, что $A, B\in \mathbb {R}$.

$\overline{A} = \dfrac { \overline{ \frac{P(\alpha )}{Q_1(\alpha )} — \frac{P(\overline\alpha )}{Q_1(\overline\alpha )}} }{\overline{ \alpha — \overline\alpha } } = $ $\dfrac { \frac{P(\overline\alpha )}{Q_1(\overline\alpha )} — \frac{P(\alpha )}{Q_1(\alpha )} }{\overline\alpha — \alpha } = A$.

$\overline{B} = \dfrac { \overline{ \frac{P(\overline\alpha )}{Q_1(\overline\alpha )}\alpha — \frac{P(\alpha )}{Q_1(\alpha )}\overline\alpha } }{ \overline{\alpha — \overline\alpha } } =$ $\dfrac { \frac{P(\alpha )}{Q_1(\alpha )}\overline\alpha — \frac{P(\overline\alpha )}{Q_1(\overline\alpha )}\alpha }{\overline\alpha — \alpha } = B$. k$ — действительные числа.

Вопрос 3.3. Разложение правильной рациональной дроби на простейшие дроби.

Заглавная страница
Избранные статьи
Случайная статья
Познавательные статьи
Новые добавления
Обратная связь

КАТЕГОРИИ:

Археология
Биология
Генетика
География
Информатика
История
Логика
Маркетинг
Математика
Менеджмент
Механика
Педагогика
Религия
Социология
Технологии
Физика
Философия
Финансы
Химия
Экология

ТОП 10 на сайте

Приготовление дезинфицирующих растворов различной концентрации

Техника нижней прямой подачи мяча.

Франко-прусская война (причины и последствия)

Организация работы процедурного кабинета

Смысловое и механическое запоминание, их место и роль в усвоении знаний

Коммуникативные барьеры и пути их преодоления

Обработка изделий медицинского назначения многократного применения

Образцы текста публицистического стиля

Четыре типа изменения баланса

Задачи с ответами для Всероссийской олимпиады по праву

Мы поможем в написании ваших работ!

ЗНАЕТЕ ЛИ ВЫ?

Влияние общества на человека

Приготовление дезинфицирующих растворов различной концентрации

Практические работы по географии для 6 класса

Организация работы процедурного кабинета

Изменения в неживой природе осенью

Уборка процедурного кабинета

Сольфеджио. Все правила по сольфеджио

Балочные системы. Определение реакций опор и моментов защемления

⇐ ПредыдущаяСтр 5 из 27Следующая ⇒

Определение 3.2. Простейшими рациональными дробями называются дроби вида:

причем квадратный трехчлен имеет только комплексные корни (отрицательный дискриминант ).

Справедлива следующая теорема (без доказательства):

Теорема 3.7. Любая правильная рациональная дробь может быть разложена на сумму простейших рациональных дробей, при этом если знаменатель разложен на множители, то

множителю соответствует одна дробь ,

множителю соответствует сумма дробей , множителю соответствует дробь ,

множителю соответствует сумма дробей

Рассмотрим метод нахождения неопределенных постоянных в разложении рациональной дроби на простейшие (метод неопределенных коэффициентов):

a) простые действительные корни (то есть их кратность равна единице), приведем их к общему знаменателю

и приравняем числители

Положим , т.е. корням знаменателя, тогда

то есть

b) кратные действительные корни или комплексные корни.

После приведения к общему знаменателю приравниваем числители

Положим , то есть корню знаменателя, тогда , тогда получим, перенеся слагаемое в левую часть равенства

или

подставив вновь , получим . Перенесем в левую часть слагаемое , найдем

или после сокращения на x+2

откуда найдем, . Следовательно,

Вопрос 3.4. Интегрирование простейших дробей.

Простейшие дроби первых двух типов сводятся к табличным простой заменой переменной:

1) .

2) .

Простейшие дроби третьего типа вычисляются путем выделения полного квадрата из квадратного трехчлена, стоящего в знаменателе и соответствующих замен переменных

3) ,

где .

Формула получается следующим образом. Выделим полный квадрат в знаменателе

где (так как дискриминант ).

Введем замену переменных , тогда получим интеграл

Второй интеграл табличный . В первом сделаем замену , тогда получим

Откуда

отсюда получается доказываемая формула заменой .

4) ,

где

‑ многочлен степени с неопределенными коэффициентами

C,D ‑ неизвестные коэффициенты.

Для определения коэффициентов нужно продифференцировать левую и правую часть равенства и применить метод неопределенных коэффициентов. Метод вычисления интеграла от рациональной дроби по этой формуле является частным случаем метода Остроградского.

Вопрос 3.5. Примеры интегрирования рациональных дробей.

Пример 3.6. .

Разложим дробь на простейшие

или

1-й способ (основной):

Приравняем коэффициенты при одинаковых степенях x

отсюда

2-й способ:

Положим x равным корням знаменателя рациональной дроби, то есть положим

Отсюда получаем

Конец примера.

Пример 3.7.

Разложим дробь на простые

и приведем правую часть к общему знаменателю. Приравняем числители, тогда

1-й способ:

2-й способ:

Положим x равным корню знаменателя, то есть x=1, тогда получим 2=2B или B=1. Подставляя это в равенство, получим

или

Откуда

Положим .

Тогда получим

Откуда получим

Конец примера.

Пример 3.8. .

Приведем правую часть к общему знаменателю и приравняем числители

Найдем коэффициенты

1-й способ:

Раскроем скобки и сгруппируем слагаемые по степеням x

Приравнивая коэффициенты при одинаковых степенях x, получим:

Отсюда и получаем систему

Решая ее, найдем .

2-й способ:

Положим x равным корню знаменателя, то есть x=1, тогда получим . подставляя в равенство, получим

или

Сокращая на общий множитель , найдем

откуда .

Отсюда получаем разложение

Отсюда получаем

Конец примера.

Пример 3.9. .

Для вычисления применим метод Остроградского

Дифференцируя это равенство, получим

Приведем правую часть к общему знаменателю

и приравняем числители

Сравнивая коэффициенты при старших степенях, получим:

Отсюда находим . Поэтому получаем

Конец примера.

⇐ Предыдущая12345678910Следующая ⇒

Читайте также:

Где возникла философия и почему?

Относительная высота сжатой зоны бетона

Сущность проекции Гаусса-Крюгера и использование ее в геодезии

Тарифы на перевозку пассажиров

Последнее изменение этой страницы: 2017-02-07; просмотров: 505; Нарушение авторского права страницы; Мы поможем в написании вашей работы!

infopedia. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.015 с.)

Лекция №17 Рациональные функции. Разложение правильной рациональной дроби на сумм простейших дробей Лекция №17 Рациональные функции

Download 214.67 Kb.

bet	1/5
Sana	26.05.2022
Hajmi	214.67 Kb.
	#714490
Turi	Лекция

1 2 3 4 5

Bog’liq
Лекция №17 Рациональные функции
4-практика№4, Algebra va matematik analiz fanidan lug at (R.Yarqulov, M.Barakayeva), Маъмуралиев Авазбек 1, Мустакил иш, Мустакил иш, Амалиёт-15, fulltext, sss, civil proj advt, civil proj advt, problem, integral tenglamalarni yechish metodlari — копия, VLSI Implementation of Cellular Neural N, Sayt nomi, Sayt nomi

Интегрирование элементарных дробей Определение: Элементарными
Интегрирование рациональных дробей Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби. Теорема
Интегрирование некоторых иррациональных

Лекция №17
Рациональные функции.

Разложение правильной рациональной дроби на сумм

простейших дробей.

Методы нахождения коэффициентов разложения.
Интегрирование рациональных функций.
Интегрирование некоторых иррациональных тригонометрических выражений.

Интегрирование элементарных дробей

Определение: Элементарными называются дроби следующих четырех типов:
I. III.

II. IV.

m, n – натуральные числа (m  2, n  2) и b² – 4ac Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.

II.
Рассмотрим метод интегрирования элементарных дробей вида III.
Интеграл дроби вида III может быть представлен в виде:

Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.
Рассмотрим применение указанной выше формулы на примерах.
Пример.

Вообще говоря, если у трехчлена ax² + bx + c выражение b² – 4ac >0, то дробь по определению не является элементарной, однако, тем не менее ее можно интегрировать указанным выше способом.
Пример.

Пример.

Рассмотрим теперь методы интегрирования простейших дробей IV типа. Сначала рассмотрим частный случай при М = 0, N = 1.
Тогда интеграл вида можно путем выделения в знаменателе полного квадрата представить в виде . Сделаем следующее преобразование:
.
Второй интеграл, входящий в это равенство, будем брать по частям.
Обозначим:

Для исходного интеграла получаем:

Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл .
Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.

В полученном равенстве первый интеграл с помощью подстановки t = u² + s приводится к табличному , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.

Несмотря на кажущуюся сложность интегрирования элементарной дроби вида IV, на практике его достаточно легко применять для дробей с небольшой степенью n, а универсальность и общность подхода делает возможным очень простую реализацию этого метода на ЭВМ.
Пример:
Интегрирование рациональных дробей
Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.
Теорема: Если — правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x — a)^…(x — b)^(x²+ px + q)^…(x²+ rx + s)^^{), то эта дробь может быть разложена на элементарные по следующей схеме: где A_i, B_i, M_i, N_i, R_i, S_i – некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин
A_i, B_i, M_i, N_i, R_i, S_i применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
Применение этого метода рассмотрим на конкретном примере.
Пример.
Т.к. ( , то
Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:
Итого:
Интегрирование некоторых иррациональных
Download 214.67 Kb.
Do’stlaringiz bilan baham:}

1 2 3 4 5

Ma’lumotlar bazasi mualliflik huquqi bilan himoyalangan ©fayllar. org 2022
ma’muriyatiga murojaat qiling

Разложение на неполные дроби — ChiliMath

Этот метод используется для разложения заданного рационального выражения на более простые дроби. Другими словами, если мне дана одна сложная дробь, моя цель — разбить ее на ряд «более мелких» компонентов или частей.

Раньше при сложении/вычитании рациональных выражений мы хотели объединить два или более рациональных выражения в одну дробь, как в примере ниже. Однако разложение на неполные дроби ( , также известное как расширение частичной дроби ), — это в точности обратный процесс. Ниже приведена иллюстративная диаграмма, показывающая основную концепцию.

Теперь я рассмотрю пять (5) примеров, чтобы продемонстрировать шаги, связанные с разложением одной дроби на части.

Пример 1: Найдите разложение рационального выражения на неполные дроби.

Эта задача проста, так что считайте ее вводным примером. Я начну с факторизации знаменателя (вычтем x из двучлена). Далее я настрою процесс разложения, поместив A и B для каждого из уникальных или различных линейных факторов. Последующие шаги затем включают избавление от всех знаменателей путем умножения LCD (который является просто исходным знаменателем задачи) во всем уравнении.

У меня должно получиться простое уравнение, в котором я могу легко сравнить коэффициенты одинаковых членов в обеих частях уравнения. В результате я получу систему линейных уравнений с переменными А и В, которую можно решить либо методом подстановки, либо методом исключения, в зависимости от того, что я предпочитаю.

Учитывая дробь

Вынесите знаменатель на множители.

Создайте отдельные дроби с правой стороны, используя каждый из множителей в качестве знаменателя. У меня есть две частичные дроби с двумя неизвестными значениями числителей, представленных переменными A и B.

Я хочу исключить все знаменатели. Это можно сделать, умножив обе части уравнения на \color{blue}LCD = x\left( {x + 1} \right).

Затем я распределяю LCD по каждой стороне уравнения. На данном этапе я стараюсь очень внимательно следить за процессом отмены. Я хочу убедиться, что сделал этот шаг правильно, чтобы избежать ненужных головных болей позже.

Это упрощенное уравнение после правильного выполнения вышеуказанного шага.

Теперь я умножу вещи и соберу общие термины, написав их рядом. Пришло время сравнить коэффициенты многочленов. Идея состоит в том, чтобы приравнять соответствующие коэффициенты подобных терминов.

Я приравниваю коэффициенты x-члена, выделенного желтым цветом. Кроме того, я приравниваю постоянные члены, как показано зеленой подсветкой.

Затем я прихожу к решению двух уравнений с двумя неизвестными. Используйте метод подстановки, чтобы решить для B.

Это окончательные значения переменных A и B.

Подставьте найденные значения A и B обратно в исходную настройку, чтобы получить окончательный ответ.

Пример 2: Найдите разложение рационального выражения на частичную дробь.

Эта задача аналогична примеру 1. Единственное отличие состоит в том, что множители знаменателя представляют собой два линейных бинома.

Учитывая проблему

Я начинаю с разложения трехчлена в знаменателе.

Затем я настраиваю разложение на неполные дроби, ставя A и B в качестве числителей. Два различных линейных фактора займут положение знаменателей.

Я хочу исключить все знаменатели, поэтому я умножу обе части уравнения на ЖК-дисплей (синий).

Мне нужно быть осторожным при отмене общих факторов.

Приведенные здесь шаги в значительной степени являются частью процесса «очистки» и реорганизации общих терминов.

Пришло время установить соответствие между двумя частями уравнения.

Для слагаемых x коэффициенты \left( {A + B} \right) = 1, тогда как чистые числа I имеют 3A + 5B = — 1.

У нас есть два уравнения с двумя неизвестными. С этого момента с ним должно быть легко справиться, верно? Я предлагаю использовать метод исключения для решения A и B.

Умножьте верхнее уравнение на — \,3 или — \,5, а затем сложите их вместе, чтобы исключить одну из переменных.

Это правильные значения A и B.

Я вернусь к первоначальной настройке частичных дробей, чтобы заменить значения A и B фактическими числами.

Пример 3: Найдите разложение рационального выражения на неполные дроби

В этой задаче знаменатель – это произведение отдельного линейного множителя, который повторяется трижды и обозначается показателем степени 3. Не совершайте ошибка записи трех неполных дробей с общим знаменателем просто \left( {x — 1} \right). Это неправильно. 93}.

Учитывая дробь

Поскольку у меня есть повторяющийся линейный множитель \left( {x — 1} \right), возведенный в степень 3, мне нужно учитывать каждую степень, начиная с самой низкой (1) до самой высокой (3).

Вы понимаете, почему эта установка неверна?

Подсказка: Сложите частичные дроби и сравните их знаменатели.

Удалите все знаменатели, распределив LCD в уравнении.

Теперь я могу ясно извлечь необходимые уравнения, которые будут использоваться для решения отсутствующих переменных.

Уравнение A = 0 — хорошая халява, так как мне не нужно трудиться, решая его алгебраически.

Используйте тот факт, что A = 0, подставьте это ко второму уравнению \left( { — 2A + B = 5} \right), чтобы получить B. Наконец, решите для C, используя третье уравнение, используя решенные значения A и Б.

Вы получили такие же ответы?

Запишите исходную схему разложения на неполные дроби и замените найденные значения для A, B и C.

Дробь, в которой числитель равен A = 0, исчезнет. Это оставляет нам две дроби в качестве окончательного ответа.

Пример 4: Найдите разложение рационального выражения на частичную дробь

Это тот случай, когда знаменатель представляет собой произведение различных линейных множителей, некоторые из которых повторяются.

Обратите внимание, что знаменатель этого рационального выражения состоит из двух различных линейных множителей. Первый множитель — это \left( {x — 2} \right), который появляется один раз, а второй фактор — это \left( {x — 3} \right), который появляется дважды, поэтому повторяется.

Учитывая дробь

Здесь у меня есть два различных линейных множителя.

\left( {x — 2} \right) встречается один раз

\left( {x — 3} \right) встречается дважды, обозначается степенью 2

Поэтому я буду писать \left( {x — 2 } \right) в одну частичную дробь, а \left( {x — 3} \right) в две частичные дроби с возрастанием показателей степени от 1 до 2.

Я исключим все знаменатели, умножив уравнение на соответствующий ЖК-дисплей.

Опять же, я должен быть осторожен с отменой.

Вы можете сказать, что на первый взгляд это выглядит «ужасно». Однако, если вы терпеливо посмотрите на каждый шаг, вы должны понять, что это не так уж и плохо.

Я просто помещаю A, B и C в скобки. Затем переставьте их так, чтобы похожие термины располагались рядом друг с другом. 92 срок. Это означает, что я должен предоставить нулевых заполнителей для отсутствующего члена x и постоянного члена.

Таким образом, становится легко сравнивать коэффициенты одинаковых членов в обеих частях уравнения.

Стрелки и цветовая кодировка помогут вам в этом процессе.

Я могу решить эту проблему несколькими способами. Один из способов — использовать метод исключения, чтобы избавиться от C между 2-м и 3-м уравнениями.

Я умножу второе уравнение на 2, а затем прибавлю его к третьему уравнению. Я должен получить уравнение, содержащее только A и B. Используйте это «новое» уравнение с первым уравнением, чтобы найти значения A и B. Я предлагаю вам попробовать его на бумаге, чтобы вы могли следовать ему.

Как только вы получите значения A и B, вы можете найти C, используя либо второе, либо третье уравнение с обратной подстановкой.

Это правильные значения A, B и C.

Подставьте значения в исходную настройку частичной дроби, чтобы получить окончательный ответ.

Пример 5: Найдите разложение рационального выражения на неполные дроби

Это еще один тип задач на разложение на неполные дроби. Разлагая знаменатель, я получаю следующее.

Обратите внимание, что на этот раз у меня квадратичный множитель. Вопрос в том, могу ли я еще разложить это на линейные термины? Я могу попробовать, но очевидно, что больше нельзя вычесть из числа . Это, на самом деле, имеет специальное имя, называемое неприводимым квадратичным .

Таким образом, эта задача представляет собой случай, когда знаменатель является произведением отдельного линейного множителя и неприводимого квадратичного множителя , которые не повторяются.

Учитывая проблему 92 с левой стороны.

Обратите внимание на соответствие коэффициентов в обеих частях уравнения.

Проведя быстрый анализ, я знаю, что C = 1 и A = -2.

Так как A+B=0 и A = -2, то \left( { — 2} \right) + B = 0 подразумевает B = 2.

Это правильные значения A, B и C

Подставьте обратно значения в исходную настройку разложения на неполные дроби, и все готово!

Частичные дроби — правило сокрытия

Сандип Бхардвадж, Мэй Ли, Виктор Ло, а также

способствовал

Содержимое

Введение
Приложения
Решение проблем
Смотрите также

Чтобы вычислить коэффициенты с помощью метода сокрытия, сначала настройте разложение на неполные дроби с одним членом для каждого из факторов в знаменателе. Например, если знаменатель состоит из трех различных линейных членов, мы имеем разложение

f(x)(x−a)(x−b)(x−c)=Ax−a+Bx−b+Cx−c. \frac{f(x)}{(xa)(xb)(xc)} = \frac{A}{xa} + \frac{B}{xb} + \frac{C}{xc}.(x− a)(x−b)(x−c)f(x)=x−aA+x−bB+x−cC.

Затем с помощью метода сокрытия можно вычислить ААА, замаскировав член (x-a)(x-a)(x-a) в знаменателе левой части и подставив x=ax=ax=a в оставшемся выражении. Это работает, потому что вычисление эквивалентно умножению выражения на член (x-a)(x-a)(x-a) и последующей подстановке x=ax=ax=a. Это дает

A=f(a)(a−b)(a−c). A = \frac{f(a)}{(a-b)(a-c)}.A=(a-b)(a-c)f(a).

Аналогично, подставив x=bx=bx=b и x=cx=cx=c, мы можем вычислить BBB и CCC:

B=f(b)(b−a)(b−c),C=f(c)(c−a)(c−b).B = \frac{f(b)}{(ba) (b-c)}, \quad C = \frac{f(c)}{(c-a)(c-b)}.B=(b-a)(b-c)f(b),C=(c-a )(c−b)f(c).

Примечание: Имейте в виду, что для применения неполных дробей степень многочлена в числителе должна быть строго меньше степени многочлена в знаменателе. Если это не так, то необходимо сначала применить полиномиальное деление для получения частного многочлена и остатка, у которого степень числителя строго меньше степени знаменателя. Частичные дроби затем могут быть применены к остатку.

Вот простой пример использования правила частичной дроби для факторизации.

Учитывая неполную дробь
3x(x−1)(x+2)=Ax−1+Bx+2,\frac{3x}{(x — 1)(x + 2)} = \frac{A}{x — 1} + \frac{B}{x + 2} ,(x−1)(x+2)3x=x−1A+x+2B,
каково значение A+B?A+B?A+B?
Обратите внимание, что эта неполная дробь имеет два различных линейных множителя. Чтобы получить AAA, закройте множитель (x−1)(x−1)(x−1) в левой части и подставь x=1x=1x=1 в остальные члены, чтобы получить
A=3(1)1+2=33=1.A = \frac{3(1)}{1+2} = \frac{3}{3} = 1.A=1+23(1) =33=1.
Аналогично, чтобы вычислить BBB, подставьте x=-2x = -2x=-2 в 3xx-1\frac{3x}{x — 1}x-13x, чтобы получить
B=3(−2)−2−1=−6−3=2.B = \frac{3(-2)}{-2 — 1} = \frac{-6}{-3} = 2 . 2 — P}{(x — 2)(x — 3)(x — 5)} = \dfrac{A}{x — 2} + \dfrac{B}{x — 3} + \dfrac{C}{x — 5}(x−2)(x−3 )(x−5)x2−P=x−2A+x−3B+x−5C
Приведенное выше уравнение представляет собой разложение на частичные дроби для констант A, B, CA, B, CA, B, C и PPP.
Какое наименьшее значение простого числа PP P такое, что A, BA, BA, B и CCC являются целыми числами?
Учитывая, что
1−13+15−17+⋯=π4,1-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}+ \cdots = \dfrac{\pi}{4}, 1−31+51−71+⋯=4π,
найти значение nnn, удовлетворяющее следующему уравнению:
11×3+15×7+19 ×11+⋯=πn.\dfrac{1}{1 \times 3}+\dfrac{1}{5 \times 7}+\dfrac{1}{92 + 2}. \end{выровнено}(x2+2)(x−1)6x(x2+2)(x−1)6x−x−12(x2+2)(x−1)6x−2(x2+ 2)(x2+2)(x−1)−2(x−1)(x−2)(x2+2)−2(x−2)=x2+2Ax+B+x− 12=x2+2Ax+B=x2+2Ax+B=x2+2Ax+B=x2+2Ax+B.
Следовательно, A=-2,B=4A=-2, B=4A=-2,B=4, что дает A+B+C=-2+4+2=4A + B +C = -2 + 4+2=4А+В+С=-2+4+2=4. □_\квадрат□

Эта задача проверяет понимание использования правила сокрытия в терминах факториала.

12!+23!+34!+45!+⋯= ?\frac{1}{2!} + \frac{2}{3!} + \frac{3}{4!} + \frac{ 4}{5!} + \cdots = \ ?2!1+3!2+4!3+5!4+⋯= ? 92+1}.n=0∑∞n4+n2+1n.

Примечание : Воздержитесь от использования Wolfram Alpha для решения этой проблемы.

Этот раздел содержит несколько задач, направленных на формирование навыков решения задач, связанных с использованием правила частичной дроби.

х=101!×(12!+23!+34!+⋯+99100!) х = 101! \times \left(\frac{1}{2!} + \frac{2}{3!} + \frac{3}{4!} +\cdots+ \frac{99}{100!}\right) x =101!×(2!1+3!2+4!3+⋯+100!99)

Найти 101!−x. 101! — х .101!−х.

Сумма

121+12+132+23+143+34+⋯+110099+99100\displaystyle \frac{1}{2\sqrt{1}+1\sqrt{2}}+\frac{1}{3\sqrt {2}+2\sqrt{3}}+\frac{1}{4\sqrt{3}+3\sqrt{4}}+\dots+\frac{1}{100\sqrt{99}+99\ sqrt{100}}21+121+32+231+43+341+⋯+10099+991001

можно выразить как ab,\frac{a {b},ba, где aaa и bbb — взаимно простые положительные целые числа.

Каково значение a+ba+ba+b?

Эта задача взята из прошлогоднего конкурса KMC. 2} = \dfrac{1}{3\cdot4}+\dfrac{1}{8\cdot 9{ 2 } }{ a } -\dfrac { b }{ c } aπ2−cb.

Найдите значение a+b+ca+b+ca+b+c с простым числом ccc.

Факторизация многочленов
Метод разностей
Телескопическая серия
Полиномиальная интерполяция

Процитировать как: Частичные дроби — правило сокрытия. Brilliant.org . Извлекаются из https://brilliant.org/wiki/partial-fractions-cover-up-rule/

SCIRP Открытый доступ

Издательство научных исследований

Журналы от A до Z

Журналы по темам

Биомедицинские и медико-биологические науки.
Бизнес и экономика
Химия и материаловедение.
Информатика. и общ.
Науки о Земле и окружающей среде.
Машиностроение
Медицина и здравоохранение
Физика и математика
Социальные науки. и гуманитарные науки

Журналы по тематике

Биомедицина и науки о жизни
Бизнес и экономика
Химия и материаловедение
Компьютерные науки и коммуникации
Науки о Земле и окружающей среде
Машиностроение
Медицина и здравоохранение
Физика и математика
Социальные и гуманитарные науки

Публикация у нас

Представление статьи
Информация для авторов
Ресурсы для экспертной оценки
Открытые специальные выпуски
Заявление об открытом доступе
Часто задаваемые вопросы

Публикуйте у нас

Представление статьи
Информация для авторов
Ресурсы для экспертной оценки
Открытые специальные выпуски
Заявление об открытом доступе
Часто задаваемые вопросы

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766

	Публикация бумаги WeChat

Недавно опубликованные статьи

Наведение мостов в высшем образовании: мультимодальные программы наставничества для поддержки удержания и подготовки к карьере ()
Джеймс Хатсон, Роджер Насер, Майкл Марцано, Райан Кертис, Элизабет Макдональд, Сью Эделе, Барбара Хосто-Марти
Творческое образование Том 13 № 9, 16 сентября 2022 г.
DOI: 10.4236/ce.2022.139178 17 загрузок 87 просмотров
Морфологический признак и физико-химическая характеристика почв под Festuca spp. Доминирующая степь у Высокой горы и горы Хувсгул, Монголия()
Саруул Нарангерел, Ундармаа Джамсран, Маки Асано, Кенджи Тамура
Открытый журнал почвоведения Том 12 № 9, 16 сентября 2022 г.
DOI: 10.4236/ojss.2022.129018 20 загрузок 101 просмотр
Исследование рассеяния энергии волн в зоне прибоя Гвинейского залива: пример автономного порта Котону в прибрежной зоне Бенина()
Освальд Г. Акклассато, Ноукпо Бернар Токпохозин, Кристиан Д. Аковану, Аджимон Матиас Хуэкпоэха, Ги Эрве Хунге, Бруно Базиль Куноухева,
Journal of Modern Physics Vol.13 No.9, 16 сентября 2022 г.
DOI: 10.4236/jmp.2022.139076 11 загрузок 65 просмотров
Модель скалярного поля обеспечивает возможный мост между общей теорией относительности и квантовой механикой()
Рики В. Остин
Международный журнал астрономии и астрофизики Том 12 № 3, 16 сентября 2022 г.
DOI: 10.4236/ijaa.2022.123014 10 загрузок 62 просмотров
Характеристики состава тела и взаимосвязь между мышечной массой и мышечной силой у пожилых женщин в разных возрастных группах()
Нао Нишиока Ниси, Норико Танака, Наоми Хирано
Успехи в исследованиях старения Том 11 № 5, 16 сентября 2022 г.
DOI: 10.4236/aar.2022.115010 11 загрузок 51 просмотр
Профиль черепно-мозговой травмы в отделениях неотложной помощи больниц — ретроспективное исследование в Республике Молдова ()
Светлана Кочу, Анжела Казаку-Страту, Лилия Киосеа, Георге Ройновяну, Сергей Чебану, Коринн Пик-Аса
Открытый журнал профилактической медицины Том 12 № 9, 16 сентября 2022 г.
DOI: 10.4236/ojpm.2022.129013 13 загрузок 87 просмотров

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766

	Публикация бумаги WeChat

Бесплатные информационные бюллетени SCIRP

верхний

Часть 8: Частичные дроби | Пособие для начинающих по математике для 12-х классов, доб. 2

В этой статье мы обсудим, как работать с дробями, и дадим несколько практических вопросов, которые помогут вам проверить свои новые навыки.

В этой статье мы обсудим:

Результаты программы NESA
Предполагаемые знания
Разложение на неполные дроби с линейными коэффициентами
Согласование коэффициентов
Замена
Нелинейные коэффициенты
Повторяющиеся линейные коэффициенты
Интегрирование с использованием неполных дробей
Вопросы для проверки концепции
Решения для проверки концепции

Нужно больше практики с частичными дробями?

Проверьте свои знания о дробях

Этот рабочий лист имеет 4 уровня сложности для проверки ваших знаний

СКАЧАТЬ

Математика для 12 класса.

Дополнение 2: Частичные дроби

На протяжении всего курса Дополнения 2 вы столкнетесь с множеством различных типов функций для интеграции, некоторые из которых проще, чем другие. Разложение на неполные дроби — это новый метод, позволяющий интегрировать рациональные функции, которые нельзя интегрировать напрямую с помощью других изученных методов.

Результаты программы NESA

MEX-C1 Дальнейшая интеграция:

Разложение рациональных функций, знаменатели которых имеют простые линейные или квадратичные множители или их комбинацию, на частичные дроби
Использование частичных дробей для интегрирования функций

Предполагаемые знания

Учащиеся должны быть знакомы с функциями и полиномами, включая деление на длинные полиномы, а также интегрирование путем подстановки и интегрирование, приводящее к натуральным логарифмам или обратному тангенсу.

92+3x+6}\)

Первым шагом в любой задаче на неполные дроби является полное разложение знаменателя на множители, в этом случае получается

$\frac{5x+2}{(x-2)( x-3)}$

Отсюда мы можем выразить функцию как сумму двух более простых функций, оставив пока числители неизвестными константами.

Основная часть разложения на неполные дроби заключается в определении их значений.

$\frac{A}{x-2}+\frac{B}{x-3}$

92+3x+6}\) нельзя разложить, так как числитель и знаменатель имеют второй порядок.

Если вы обнаружите, что степень числителя больше знаменателя, вы можете упростить знаменатель, используя полиномиальное деление, а затем использовать метод неполных дробей.

Сопоставление коэффициентов

Один из методов, который мы можем использовать для определения этих значений, аналогичен сопоставлению коэффициентов с полиномами, который вы бы сделали ранее.

У нас есть разложенная форма функции, и у нас есть исходная форма функции, так что мы можем приравнять их!

Умножение знаменателя исходного выражения дает нам красивое уравнение без дробей.

Чтобы выполнить сопоставление коэффициентов, RHS следует разложить на множители по степеням x.

$5x+2=A(x-3)+B(x-2)\\
⇒ \ 5x+2=x(A+B)+(-3A-2B)$

Это теперь очень просто решить проблему! Приравняв коэффициенты при x и константе, мы получим систему из 2-х уравнений, которые можно решать одновременно. 92+3x+6} = \frac{-12}{x-2} + \frac{17}{x-3}\)

Теперь у нас есть две очень простые функции для интегрирования!

Подстановка

Другой метод, который можно использовать, включает подстановку корней знаменателя.

Начиная с после умножения знаменателя, мы имеем:

$5x+2=A(x-3)+B(x-2)$

Важно отметить, что для этого метода выражение не разложено по степеням x, а оставлено по константам.

Подставив в корни знаменателя, в данном случае x = 3 и x = 2:

\begin{align*}
x &= 3 \ \ case: \ 15+2=B (3-2) \ ⇒ \ B=17\\
x &= 2 \ \ case: \ 10+2=A(2-3) \ ⇒ \ A=-12\\
\end{align*}

Результат тот же, что и раньше!

Ни один из этих методов не является особенно сложным, но некоторые функции будут проще выполнять с помощью одного или другого.

Определение того, что использовать, приходит с опытом, и часто будет быстрее (или необходимо для более сложных функций) использовать комбинацию обоих. 2(x-1)}\) 92}+\frac{B}{x+2}+\frac{C}{x-1}\)

Интегрирование с использованием дробей

Следуя первому примеру, вы уже должны видеть, что частичные дроби — очень полезный инструмент для упрощения интегрирования.

$\int \frac{-12}{x-2}+\frac{17}{x-3} \ dx\\
= 17ln(|x-3|) – 12ln(|x-2| )+c$

После декомпозиции функции вы просто интегрируете как обычно!

Более сложные задачи, например, с повторяющимися или нелинейными факторами, могут потребовать замены одного или нескольких выражений. 9{-1}(x)+4ln(|x-1|)+c\)

3. $-2ln(|x+1|)+\frac{3}{x+1}+2ln(| x-1|)+c$

Вам нужна дополнительная практика, чтобы справиться с более сложными вопросами на частичные дроби?

В Matrix+ наши специалисты HSC разберут сложные концепции с помощью наших структурированных видеоуроков и предоставят вам всесторонние ресурсы, которые познакомят вас с множеством различных вопросов. Узнайте больше прямо сейчас.

© Matrix Education и www.matrix.edu.au, 2022. Несанкционированное использование и/или копирование этого материала без письменного разрешения автора и/или владельца этого сайта строго запрещено. Выдержки и ссылки могут быть использованы при условии, что Matrix Education и www.matrix.edu.au полностью и четко указаны с соответствующим и конкретным указанием на исходный контент.

AP Calculus BC Review: Partial Fractions — Блог Magoosh

Шон Олт, , 23 июня 2017 г. , ОБНОВЛЕНО 14 июня 2022 г., в AP

Метод частных дробей на самом деле является методом алгебры , который позволяет вам переписывать определенные виды рациональных выражений более полезным способом.

В этом обзоре мы обсудим, как и когда использовать метод в интегральных задачах, особенно в тех, которые встречаются на экзамене AP Calculus BC.

Метод частных дробей (ПФ)

Этот метод на самом деле является обратным добавлению рациональных выражений.

Предположим, у вас есть рациональная функция , то есть дробное выражение двух многочленов.

Точнее, каждая рациональная функция имеет вид , где числитель f и знаменатель g являются полиномами.

Вопрос в следующем: Можем ли мы найти два или более простых рациональных выражения, которые добавляются к данному?

Ключ к фактор знаменатель. Знаменатели новых дробей будут включать эти факторы. Затем, работая в обратном направлении, вы можете выяснить, какими должны быть новые числители, чтобы получить заданную функцию.

Конечно, есть много деталей, которые я сейчас опускаю. Мы рассмотрим метод более подробно ниже.

PF для неповторяющихся линейных коэффициентов

Во-первых, PF работает только тогда, когда степень знаменателя больше степени числителя. Если числитель имеет более высокую степень, чем знаменатель, то сначала нужно сделать многочлен (или синтетический ) отдел. Я еще не встречал задачи на экзамене Calculus BC, требующей полиномиального деления, поэтому в этом обзоре мы ее пропустим.

Кроме того, на экзамене AP Calculus BC вам нужно будет знать только о знаменателях, которые делят на неповторяющихся линейных множителей.

Другими словами, знаменатель полностью разложится на уникальные множители:

Следующим шагом после разложения на множители является запись столько дробей, сколько у вас есть множителей. Мы знаем, какими будут знаменатели (это сами факторы). Но мы еще не знаем числителей. Пока просто запишите числители как переменные. Нам придется решить их позже.

Далее вам нужно выяснить, какие именно цифры находятся сверху, A ₁ , …, A _n . Кстати, когда факторов всего два или три, я обычно называю эти числа A , B , C и т. д. Собственно имя переменной не имеет значения.

Несмотря на то, что на этом шаге не используется исчисление, многие учащиеся застревают здесь. Алгебра может быть очень сложной и утомительной. Поэтому я объясню это, используя два разных метода на одном и том же примере.

Наконец, интегрируйте каждый термин отдельно. Когда множители представляют собой дроби с линейным знаменателем, вы можете ожидать, что первообразная будет включать натуральные логарифмы.

Пример использования неполных дробей

Найдите первообразную.

Разложение выражения

Сначала проверьте степень верха и низа. Поскольку знаменатель имеет степень 2, а числитель имеет степень 1, мы можем использовать PF.

Метод всегда начинается с разложения знаменателя на множители. Иногда этот шаг уже выполняется в данной задаче на экзамене BC, но не всегда.

Теперь, когда есть два фактора, будут две отдельные дроби. Пусть A и B обозначают неизвестные числители.

Отсюда есть два пути.

Метод №1 — рекомбинация фракций

Идея состоит в том, что мы хотим, чтобы сумма дробей равнялась исходному рациональному выражению. Так что используйте свои навыки алгебры, чтобы рекомбинировать дроби и сравнить результаты.

Вам понадобится общий знаменатель, но это самая простая часть! Вам просто нужно перемножить два знаменателя вместе.

Итак, сгруппировав одинаковые термины, приравняем числители друг к другу. Сравнение x -членов и постоянных членов приводит к системе двух уравнений.

Сейчас есть множество способов решения таких систем. Матричные методы работают, если вы умеете ими пользоваться.

В качестве альтернативы можно выполнить простую замену.

Решите первое уравнение для A , чтобы получить: A = 5 – 3 B . Затем подставьте это выражение для A во второе уравнение и найдите B .

Наконец, найдите A , подставив известное значение B . А = 5 – 3(3) = -4.

Следовательно, теперь у нас есть разложение исходного рационального выражения на неполные дроби.

Конечно, это конец процесса, верно? Ну нет, вам все равно придется интегрировать разложенную форму. (В конце концов мы это сделаем.)

Но прежде чем перейти к этому, давайте обсудим другие методы разложения дроби, которые более эффективны, чем этот.

Метод № 2 — Метод сокрытия Хевисайда

Метод сокрытия Хевисайда избегает всей этой алгебры, но больше похож на «трюк». Он гарантированно работает для неповторяющихся линейных множителей, но причина, по которой он работает, довольно тонкая.

Метод сокрытия Хевисайда назван в честь математика, инженера и физика Оливера Хевисайда.

Вот как это сделать.

Для каждого фактора сначала найдите его корень , то есть значение x , которое получается, когда вы устанавливаете его равным нулю и решаете.

Затем скройте этот множитель в исходном рациональном выражении и вставьте корень в x везде, где вы видите его в выражении.

Оцените его, и это будет значение A _i (числитель) в разложении PF.

Возвращаясь к нашему примеру, помните, что мы разложили функцию на множители и разложили так, что:

Первый множитель равен 3 х + 1. Приравняв его к нулю и решив, получим:

Теперь мы подставляем это значение обратно в исходное выражение, но игнорируем множитель (3x + 1).

Это говорит нам о том, что A = -4.

Затем перейдите ко второму множителю ( x — 2), корень которого равен x 9.0269 = 2. Теперь игнорируйте этот фактор и подключайтесь.

Теперь у нас есть B = 3.

Конечный результат такой же, как и в методе №1, но занимает гораздо меньше времени.

Последний шаг: интегрируйте!

Выполнив либо алгебраический метод, либо метод сокрытия Хевисайда, вы сможете найти первообразную.

Только будьте осторожны: обычно есть простые u -замены, которые необходимо сделать, чтобы получить правильные ответы.

Заключение

Хотя сначала может показаться, что частичные дроби сложны, это больше похоже на задачу научиться ездить на велосипеде.

Сначала ты не понимаешь, что делаешь, и можешь много падать. Но при достаточной практике и особенно при желании снова сесть на велосипед после падения, вы овладеете навыком, который останется с вами на всю оставшуюся жизнь!

На самом деле, как и езда на велосипеде, я думаю, что PF — это весело. (Но мои близкие друзья уверяют меня, что я просто странная.)

Ознакомьтесь со следующим ресурсом, чтобы узнать о других важных методах интеграции: Обзор исчисления AP: неопределенные интегралы.

Гарантированно улучшите свой результат SAT или ACT. Начните свою 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep сегодня!

Автор

Кстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT. Нажмите сюда, чтобы узнать больше!

Расчет AP

← Предыдущий

Далее →

Мы настоятельно рекомендуем учащимся помогать друг другу и отвечать на комментарии других учащихся, если это возможно!

Если вы являетесь студентом Premium Magoosh и хотели бы более персонализированного обслуживания от наших инструкторов, вы можете использовать вкладку «Справка» на панели управления Magoosh. Спасибо!

Частичные дроби

Способ «разбиения» дробей с многочленами в них.

Что такое частичные дроби?

Мы можем сделать это напрямую:

Вот так:

2 х-2 + 3 х+1 = 2(х+1) + 3(х−2) (x−2)(x + 1)

Что можно упростить с помощью Rational Expressions до:

= 2x+2 + 3x−6 x ² +x−2x−2

= 5x−4 x ² −x−2

… но как нам двигаться в обратном направлении?

Вот что мы собираемся открыть:

Как найти «части», из которых состоит одна дробь
(« частичных дроби »).

Зачем они нам?

Во-первых… зачем они нам?

Потому что каждая неполная дробь на проще .

Это может помочь решить более сложную дробь. Например, это очень полезно в интегральном исчислении.

Разложение частичной фракции

Итак, позвольте мне показать вам, как это сделать.

Метод называется «Разложение на неполные дроби» и выглядит следующим образом:

Шаг 1: Факторизация нижней части

Шаг 3: Умножить на низ, чтобы больше не было дробей

Шаг 4: Теперь найдем константы A ₁ и A ₂

Подстановка корней или «нулей» (x−2)(x+1) может помочь:

И у нас есть ответ:

2 3

90 легкий! … почти слишком просто …
… потому что может быть намного сложнее !
Теперь подробно рассмотрим каждый шаг.
Правильные рациональные выражения
Во-первых, это работает только для Правильных рациональных выражений, где степень вершины равна меньше снизу.
Степень является наибольшим показателем степени переменной.
Если ваше выражение неверно, сначала выполните полиномиальное деление в длину.
Разложение нижнего многочлена на множители
Факторирование нижнего многочлена зависит от вас. См. Факторинг в алгебре.
Но не разлагайте их на комплексные числа… вам может понадобиться остановить некоторые множители на квадратичных (называемых неприводимыми квадратичными числами, потому что любое дальнейшее разложение на множители приводит к комплексным числам):
Пример: (x
² −4)(x ² +4)
x ² −4 можно разложить на (x−2)(x+2)
Но x ² +4 делит на комплексные числа, так что не делайте этого

Таким образом, лучшее, что мы можем сделать, это:
(x−2)(x+2)(x ² +4)

Таким образом, множители могут быть комбинацией
1
0
неприводимых квадратичных множителей
Когда у вас есть квадратичный фактор, необходимо включить эту частичную фракцию:
B ₁ x + C ₁ (ваш квадратичный)
Факторы с экспонентами
Иногда. множитель с показателем степени, например (x−2) ³ …
Вам нужна неполная дробь для каждого показателя степени от 1 до.
Вот так:
Пример:
1 (x−2) ³
Имеет частичную фракции
A ₁ x — 2 + A ₂ (X — 2) ² 9000 + 69 (x — 2) ² 9000 + 666669_{111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111186669}9. (x−2) ³
The same thing can also happen to quadratics:
Example:
1 (x ² +2x+3) ²
Has partial fractions :
В ₁ х + С ₁ x ² +2x +3 + B ₂ x +C ₂ (x ² +2x +3) ²
976 +2x +3) ² 9976 +2x +3). It
Даже после использования корней (нулей) основания можно получить неизвестные константы.
Итак, следующее, что нужно сделать, это:
Собрать все степени х вместе, а затем решить это как систему линейных уравнений.

Боже мой! Это много, чтобы справиться! Итак, на примере, чтобы помочь вам понять:
Большой пример Собираем все вместе
Вот вам хороший большой пример!
x ² +15 (x+3) ² (x ² +3)
Поскольку (x+3) ² имеет показатель степени 2, необходимо два члена (A ₁ и A ₂ ).
And (x ² +3) является квадратичным, поэтому потребуется Bx + C:
x ² +15 (x+3) ² (x ² +3) = A ₁ x + 3 + A ₂ (x + 3) ² 9000 + (x + 3) ² +
6666669 (x + 3) ² 6666669 9 (x + 3) ² 66669 9 (x + 3) ² . 2 +3
Теперь умножьте на (x+3) ² (x ² +3) :
x ² +15 = (7 6 +3)(x 2
5 3)A ₁ + (x ² +3)A ₂ + (x+3) ² (Bx + C)
На x = −3 9 стоит ноль1353 (поскольку x+3=0), попробуем так:
(−3) ² +15 = 0 + ( (−3) ² +3)A ₂ + 0
и упростите его до:
24 = 12A ₂
Таким образом, ₂ = 2
Давайте заменим ₂ с 2:
x ² +15 = (x +3 )(x ² +3)A ₁ + 2x ² +6 + (x+3) ² (Bx + C)
Теперь разверните все это:
x ² +15 = (x ³ +3x+3x ² +9)A ₁ + 2x ² +6 + (x ³ +6x ^{2 x} +9 (x ) ² +6x+9)C
Собрать степени x вместе:
x ² +15 = x ³ (A ₁ +B)+x ^{2 909 916 (101 9191) +C+2)+x(3A ₁ +9B+6C)+(9A ₁ +6+9C)}
Разделите степени и запишите в виде системы линейных уравнений:
x ³ : 0 = А ₁ +В
x ² : 1 = 3А ₁ +6В+С+2
х: 0 = 3А ₁ +9В+6С
Константы: 15 = 9A ₁ +6+9C
Упростите и организуйте аккуратно:
0 = А ₁ + Б
−1 = 3А ₁ + 6Б + С
0 = 3А ₁ + 9Б + 6С
1 = А ₁ + С
Теперь решите.
Вы можете выбрать свой способ решения этого… Я решил для начала вычесть 4-е уравнение из 2-го:
0 = А ₁ + Б
−2 = 2А ₁ + 6Б
0 = 3А ₁ + 9Б + 6С
1 = А ₁ + С
Затем вычесть 2 раза 1-е уравнение из 2-го:
0 = А ₁ + Б
−2 = 4Б
0 = 3А ₁ + 9Б + 6С
1 = А ₁ + С
Теперь я знаю, что Б = -(1/2) .

x ³ :	0	=	А ₁ +В
x ² :	1	=	3А ₁ +6В+С+2
х:	0	=	3А ₁ +9В+6С
Константы:	15	=	9A ₁ +6+9C

Разложение дроби на простейшие: примеры, решение

Типы дробей

Алгоритм метода неопределенных коэффициентов

9.4. Разложение правильной рациональной дроби в сумму простейших дробей

Вопрос 3.3. Разложение правильной рациональной дроби на простейшие дроби.

Лекция №17 Рациональные функции. Разложение правильной рациональной дроби на сумм простейших дробей Лекция №17 Рациональные функции

Разложение на неполные дроби — ChiliMath

Частичные дроби — правило сокрытия

Содержимое

SCIRP Открытый доступ

Журналы по тематике

Публикуйте у нас

Часть 8: Частичные дроби | Пособие для начинающих по математике для 12-х классов, доб. 2

В этой статье мы обсудим:

Нужно больше практики с частичными дробями?

Математика для 12 класса.

Результаты программы NESA

MEX-C1 Дальнейшая интеграция:

Предполагаемые знания

Сопоставление коэффициентов

Подстановка

Интегрирование с использованием дробей

Вам нужна дополнительная практика, чтобы справиться с более сложными вопросами на частичные дроби?

AP Calculus BC Review: Partial Fractions — Блог Magoosh

Метод частных дробей (ПФ)

PF для неповторяющихся линейных коэффициентов

Пример использования неполных дробей

Разложение выражения

Метод №1 — рекомбинация фракций

Метод № 2 — Метод сокрытия Хевисайда

Последний шаг: интегрируйте!

Заключение

Автор

Частичные дроби

Что такое частичные дроби?

Зачем они нам?

Разложение частичной фракции

2 3

Правильные рациональные выражения

Разложение нижнего многочлена на множители

Пример: (x

Факторы с экспонентами

Пример:

Example:

Большой пример Собираем все вместе

Добавить комментарий Отменить ответ