Разложение дробей на множители дробей: Метод разложения на простейшие онлайн

Содержание

Разложение на простые множители / Обыкновенные дроби / Справочник по математике 5-9 класс

Главная
Справочники
Справочник по математике 5-9 класс
Обыкновенные дроби
Разложение на простые множители

Любое составное число можно представить в виде произведения простых чисел, то есть разложить на простые множители. Заметим, что при любом способе получается одно и то же разложение, если не учитывать порядка записи множителей.

Например, число 150 — это произведение чисел 15 и 10, то есть 150 = 1510. Числа 15 и 10 составные, значит, их тоже можно разложить на множители: 15 = 35, 10 = 25. Значит, получаем, что 150 = 3525, в данном произведении все множители простые, то есть мы разложили число 150 на простые множители.

Разложим 150 на простые множители другим способом:

150 = 530 = 556 = 5532.

Как мы видим, в обоих случаях получились одни и те же простые множители. Обычно множители принято записывать в порядке их возрастания, то есть от меньшего к большему:

150 = 2355.

При разложении на множители удобно использовать признаки делимости на 2, 3 и 5.

Например, разложим на простые множители число 3 528:

Данное число заканчивается на чётную цифру 8, значит, оно делится на 2. Получаем 3 528 : 2 = 1 764. Проведем вертикальную черту и запишем слева от неё делимое 3 528, а справа делитель — 2. Частное запишем под числом 3 528.

Число 1 764 заканчивается тоже на четную цифру 4, а , значит, тоже делится на 2, при делении получаем в частном число 882.

882 тоже делится на 2. При делении в частном получаем число 441.

Число 441 заканчивается нечетной цифрой, значит, оно не делится на 2. Сумма цифр данного число равна 4 + 4 + 1 = 9, 9 делится на 3, значит, 441 тоже делится на 3.

При делении в частном получаем число 147.

1 + 4 + 7 = 12, значит, 147 делится на 3. При делении в частном получаем число 49.

4 + 9 = 13. 13 не делится на 3, значит, 49 тоже не делится на 3. Также число 49 не заканчивается цифрами 0 и 5, а, значит, оно не делится на 5. Но 49 делится на простое число 7. При делении получаем в частном 7.

7 — это простое число и оно делится только на простое число 7. В частном получаем 1:

Разложение закончено. При этом справа от черты мы получили все простые множители, на которые можно разложить число 3 528. Получаем:

3 528 = 2223377.

При этом одинаковые множители можно заменить степенью, то есть мы можем записать:

3 528 = 2³3²7².

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Доли. Обыкновенные дроби

Сравнение дробей

Делители и кратные

Признаки делимости на 10, на 5 и на 2

Четные и нечетные числа

Признаки делимости на 9 и на 3

Простые и составные числа

Наибольший общий делитель

Наименьшее общее кратное

Деление и дроби

Сложение и вычитание дробей с одинаковыми знаменателями

Смешанное число

Сложение и вычитание смешанных чисел

Основное свойство дроби

Решето Эратосфена

Приведение дробей к общему знаменателю

Сравнение, сложение и вычитание дробей с разными знаменателями

Умножение обыкновенных дробей

Деление обыкновенных дробей

Обыкновенные дроби

Правило встречается в следующих упражнениях:

6 класс

Номер 148, Мерзляк, Полонский, Якир, Учебник

Номер 163, Мерзляк, Полонский, Якир, Учебник

Номер 165, Мерзляк, Полонский, Якир, Учебник

Номер 166, Мерзляк, Полонский, Якир, Учебник

Номер 169, Мерзляк, Полонский, Якир, Учебник

Номер 173, Мерзляк, Полонский, Якир, Учебник

Номер 242, Мерзляк, Полонский, Якир, Учебник

Задание 180, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 182, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 230, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 349, Мерзляк, Полонский, Якир, Учебник

Номер 434, Мерзляк, Полонский, Якир, Учебник

Mathway | Популярные задачи

1	Множитель	x^2-4
2	Множитель	4x^2+20x+16
3	График	y=-x^2
4	Вычислить	2+2
5	Множитель	x^2-25
6	Множитель	x^2+5x+6
7	Множитель	x^2-9
8	Множитель	x^3-8
9	Вычислить	квадратный корень из 12
10	Вычислить	квадратный корень из 20
11	Вычислить	квадратный корень из 50
12	Множитель	x^2-16
13	Вычислить	квадратный корень из 75
14	Множитель	x^2-1
15	Множитель	x^3+8
16	Вычислить	-2^2
17	Вычислить	квадратный корень из (-3)^4
18	Вычислить	квадратный корень из 45
19	Вычислить	квадратный корень из 32
20	Вычислить	квадратный корень из 18
21	Множитель	x^4-16
22	Вычислить	квадратный корень из 48
23	Вычислить	квадратный корень из 72
24	Вычислить	квадратный корень из (-2)^4
25	Множитель	x^3-27
26	Вычислить	-3^2
27	Множитель	x^4-1
28	Множитель	x^2+x-6
29	Множитель	x^3+27
30	Множитель	x^2-5x+6
31	Вычислить	квадратный корень из 24
32	Множитель	x^2-36
33	Множитель	x^2-4x+4
34	Вычислить	-4^2
35	Множитель	x^2-x-6
36	Множитель	x^4-81
37	Множитель	x^3-64
38	Вычислить	4^3
39	Множитель	x^3-1
40	График	y=x^2
41	Вычислить	2^3
42	Вычислить	(-12+ квадратный корень из -18)/60
43	Множитель	x^2-6x+9
44	Множитель	x^2-64
45	График	y=2x
46	Множитель	x^3+64
47	Вычислить	(-8+ квадратный корень из -12)/40
48	Множитель	x^2-8x+16
49	Вычислить	3^4
50	Вычислить	-5^2
51	Множитель	x^2-49
52	Вычислить	(-20+ квадратный корень из -75)/40
53	Множитель	x^2+6x+9
54	Множитель	4x^2-25
55	Вычислить	квадратный корень из 28
56	Множитель	x^2-81
57	Вычислить	2^5
58	Вычислить	-8^2
59	Вычислить	2^4
60	Множитель	4x^2-9
61	Вычислить	(-20+ квадратный корень из -50)/60
62	Вычислить	(-8+ квадратный корень из -20)/24
63	Множитель	x^2+4x+4
64	Множитель	x^2-10x+25
65	Вычислить	квадратный корень из -16
66	Множитель	x^2-2x+1
67	Вычислить	-7^2
68	График	f(x)=2^x
69	Вычислить	2^-2
70	Вычислить	квадратный корень из 27
71	Вычислить	квадратный корень из 80
72	Множитель	x^3+125
73	Вычислить	-9^2
74	Множитель	2x^2-5x-3
75	Вычислить	квадратный корень из 40
76	Множитель	x^2+2x+1
77	Множитель	x^2+8x+16
78	График	y=3x
79	Множитель	x^2+10x+25
80	Вычислить	3^3
81	Вычислить	5^-2
82	График	f(x)=x^2
83	Вычислить	квадратный корень из 54
84	Вычислить	(-12+ квадратный корень из -45)/24
85	Множитель	x^2+x-2
86	Вычислить	(-3)^3
87	Множитель	x^2-12x+36
88	Множитель	x^2+4
89	Вычислить	квадратный корень из (-8)^2
90	Множитель	x^2+7x+12
91	Вычислить	квадратный корень из -25
92	Множитель	x^2-x-20
93	Вычислить	5^3
94	Множитель	x^2+8x+15
95	Множитель	x^2+7x+10
96	Множитель	2x^2+5x-3
97	Вычислить квадратный корень	квадратный корень из 116
98	Множитель	x^2-x-12
99	Множитель	x^2-x-2
100	Вычислить	2^2

Интегрирование рациональных функций

Алгоритм интегрирования рациональных функций
Шаг 1: разложение исходной дроби
Шаг 2: нахождение неопределённых коэффициентов
Шаг 3: нахождение интеграла исходной функции (дроби)

Рациональная функция — это дробь вида , числитель и знаменатель которой — многочлены или произведения многочленов.

Из урока «Интегрирование некоторых рациональных дробей и иррациональностей» известно, что рациональные дроби бывают неправильные, если степень многочлена в её числителе не меньше степени многочлена в знаменателе, и правильные, если степень многочлена в числителе меньше степени многочлена в знаменателе. В том же уроке говорилось о том, как представить неправильную дробь в виде суммы её целой части и некоторой правильной дроби.

На этом уроке будем учиться интегрировать такие рациональные функции, которые представлены в виде правильных дробей. Для этого существует метод неопределённых коэффициентов, основанный на теореме, которая гласит, что всякая правильная дробь может быть представлена в виде суммы простых дробей.

Приведённый ниже алгоритм интегирования рациональных функций будет пошагово проиллюстрирован в примерах.

Алгоритм интегрирования рациональных функций

Шаг 1. Определить вид многочлена в знаменателе дроби (он может иметь действительные, кратные действительные, комплексные и кратные комплексные корни) и в зависимости от вида разложить дробь на простые дроби, в числителях которых — неопределённые коэффициенты, число которых равно степени знаменателя.
Шаг 2. Определить значения неопределённых коэффициентов. Для этого потребуется решить систему уравнений, сводящуюся к системе линейных уравнений.
Шаг 3. Найти интеграл исходной рациональной функции (дроби) как сумму интегралов полученных простых дробей, к которым применяются табличные интегралы.

Переходим к первому шагу алгоритма

Многочлен в знаменателе имеет действительные корни. То есть, в знаменателе имеет место цепочка сомножителей вида , в которой каждый из сомножителей находится в первой степени. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:

Пример 1. Шаг 1. Дан интеграл от рациональной функции .

От нас требуется разложить подынтегральное выражение — правильную дробь на простые дроби.

Решение. Дискриминант уравнения положительный, поэтому многочлен в знаменателе имеет действительные корни. Получаем следующее разложение исходной дроби на сумму простых дробей:

Пример 2. Шаг 1.Дан интеграл от рациональной функции

Решение. Разложим знаменатель подынтегрального выражения на множители. Сначала можно вынести за скобки x. (На сайте есть урок о вынесении общего множителя за скобки.) Получаем следующую дробь:

Для разложения квадратного трёхчлена в скобках решаем квадратное уравнение:

Получаем разложение знаменателя на множители в подынтегральном выражении:

Дискриминант решённого выше квадратного уравнения положительный, то есть имеем дело со случаем, когда многочлен в знаменателе имеет действительные корни. Разложение исходной дроби подынтегрального выражения будет следующим:

Как и в первом примере, числа, обозначенные большими буквами, пока неизвестны. Отсюда и название — метод неопределённых коэффициентов.

Многочлен в знаменателе имеет кратные действительные корни. Этот случай имеет место, когда в цепочке сомножителей в знаменателе присутствует выражение вида , то есть один из многочленов в степени 2 и больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:

Пример 3. Шаг 1. Дан интеграл от рациональной функции .

Решение. Представляем разность квадратов в виде произведения суммы и разности .

Тогда подынтегральное выражение запишется в виде

все уравнения с многочленами которого имеют действительные корни. Это случай кратных действительных корней, так как последний сомножитель находится во второй степени. Получаем следующее разложение исходной дроби на простые дроби:

Как видим, в этом случае нужно понижать степень кратного многочлена с исходной до первой и записывать простую дробь с каждой из этих степеней в знаменатель.

Пример 4. Шаг 1. Дан интеграл от рациональной функции .

Решение. Уравнения с многочленами в знаменателе имеют действительные корни, а сами многочлены присутствуют в степенях больше первой. Поэтому получаем следующее разложение исходной дроби на простые дроби:

Многочлен в знаменателе имеет комплексные корни: дискриминант квадратного уравнения , присутствующего в цепочке сомножителей в знаменателе, меньше нуля. В этом случае при разложении дроби в простой дроби, соответствующей описанному выше сомножителю, в числителе нужно записывать линейное выражение с переменной x (это выражение — последнее в следующей записи):

Пример 5. Шаг 1. Дан интеграл от рациональной функции .

Решение. Уравнение в скобках имеет комплексные корни, а оба сомножителя присутствуют в знаменателе в первой степени. Поэтому получаем следующее разложение исходной дроби на простые дроби:

Пример 6. Шаг 1. Дан интеграл от рациональной функции .

Решение. Представим знаменатель дроби в подынтегральном выражении в виде следующего произведения сомножителей:

Решение. Уравнение с последним сомножителем имеет комплексные корни, а все сомножители присутствуют в знаменателе в первой степени. Поэтому получаем следующее разложение исходной дроби на простые дроби:

Многочлен в знаменателе имеет кратные комплексные корни: дискриминант квадратного уравнения , присутствующего в цепочке сомножителей в знаменателе, меньше нуля и этот сомножитель присутствует в степени 2 или больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:

То есть в сумме простых дробей число простых дробей с линейным выражением в числителе должно быть равно степени сомножителя, имеющего комплексные корни.

Пример 7. Шаг 1. Дан интеграл от рациональной функции .

Решение. Квадратный трёхчлен имеет комплексные корни и присутствует в знаменателе подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:

Пример 8. Шаг 1. Дан интеграл от рациональной функции .

Решение. Квадратный трёхчлен в знаменателе имеет комплексные корни и присутствует в подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:

На первом шаге мы представили подынтегральные дроби в виде суммы дробей с неопределёнными коэффициентами. В начале этого шага потребуется привести полученную сумму дробей к общему знаменателю. После этого в их числителях будут произведения неопределённых коэффициентов на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях.

Полученное таким образом выражение приравнивается к числителю исходной дроби. Затем составляется система из уравнений, в которых степени икса одинаковы. Путём решения системы и находятся неопределённые коэффициенты. Для решения достаточно знать, как системы уравнений решаются методом подстановки и методом сложения.

Нет времени вникать в решение? Можно заказать работу!

Пример 1. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Умножаем неопределённые коэффициенты на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях:

Раскрываем скобки и приравниваем полученое к полученному выражению числитель исходной подынтегральной дроби:

В обеих частях равенства отыскиваем слагаемые с одинаковыми степенями икса и составляем из них систему уравнений:

Сокращаем все иксы и получаем эквивалентную систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Таким образом, окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 2. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Теперь начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:

Теперь требуется составить и решить систему уравнений. Для этого приравниваем коэффициенты при переменной в соответствующей степени в числителе исходного выражения функции и аналогичные коэффициенты в полученном на предыдущем шаге выражения:

Решаем полученную систему:

Итак, , отсюда получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 3. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:

Как и в предыдущих примерах составляем систему уравнений:

Сокращаем иксы и получаем эквивалентную систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 4. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Как приравнивать числитель исходной дроби к выражению в числителе, полученному после разложения дроби на сумму простых дробей и приведения этой суммы к общему знаменателю, мы уже знаем из предыдуших примеров. Поэтому лишь для контроля приведём получившуюся систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 5. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Самостоятельно приводим к общему знаменателю эту сумму, приравнивать числитель этого выражения к числителю исходной дроби. В результате должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 6. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Производим с этой суммой те же действия, что и в предыдущих примерах. В результате должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 7. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

После известных действий с полученной суммой должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 8. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Внесём некоторые изменения в уже доведённые до автоматизма действия для получения системы уравнений. Есть искусственный приём, который в некоторых случаях помогает избежать лишних вычислений. Приводя сумму дробей к общему знаменателю получаем и приравнивая числитель этого выражения к числителю исходной дроби, получаем:

Можно заметить, что если принять за значение икса единицу, то второе и третье слагаемые в правой части равенства обратятся в нули и нет необходимости их вычислять. Тогда получаем, что . Далее по уже отработанной схеме получаем систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Полученные простые дроби и интегировать проще. К исходной сумме дробей применяется правило интеграла суммы (интеграл суммы равен сумме интегралов) и табличные интегралы. Чаще всего требуется применять табличные интегралы, приводящие к натуральному логарифму и арктангенсу.

Пример 1. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

Интегрируем изначальную рациональную функцию как сумму дробей и используем табличный интеграл 10, приводящий к натуральному логарифму:

Последнее действие с натуральным логарифмом — приведение к единому выражению под логарифмом — может требоваться при выполнении работ, но требуется не всегда.

Пример 2. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

Вновь применяем табличный интеграл, приводящий к натуральному логарифму:

Пример 3. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

В результате интегрирования получаем сумму натуральных логарифмов и одной простой дроби, на случай, если требуется преобразование к единому логарифму, делаем и это:

Пример 4. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

В результате интегрирования получаем сумму натуральных логарифмов и одной дроби, на случай, если требуется преобразование к единому логарифму, делаем и это:

Пример 5. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

Интегрируем и получаем сумму натурального логарифма и арктангенса:

Пример 6. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

Опять получаем сумму натурального логарифма и арктангенса:

Пример 7. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

Интегрируя, получаем натуральные логарифмы и дробь:

Приведение к единому логарифму попробуйте выполнить самостоятельно.

Пример 8. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

Интегрируя, получаем сумму натурального логарифма, арктангенса и дроби:

Назад

Листать

Вперёд>>>

К началу страницы

Пройти тест по теме Интеграл

Начало темы «Интеграл»

Неопределённый интеграл: основные понятия, свойства, таблица неопределённых интегралов

Найти неопределённый интеграл: начала начал, примеры решений

Метод замены переменной в неопределённом интеграле

Интегрирование подведением под знак дифференциала

Метод интегрирования по частям

Интегрирование дробей

Интегрирование некоторых иррациональных функций

Продолжение темы «Интеграл»

Интегрирование тригонометрических функций

Определённый интеграл

Несобственные интегралы

Площадь плоской фигуры с помощью интеграла

Объём тела вращения с помощью интеграла

Вычисление двойных интегралов

Длина дуги кривой с помощью интеграла

Площадь поверхности вращения с помощью интеграла

Определение работы силы с помощью интеграла

Интегрирование рациональных дробей с помощью разложения на простейшие дроби — КиберПедия

Навигация:

Главная Случайная страница Обратная связь ТОП Интересно знать Избранные

Топ:

Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует…

Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства…

Динамика и детерминанты показателей газоанализа юных спортсменов в восстановительном периоде после лабораторных нагрузок до отказа…

Интересное:

Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является…

Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным…

Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов…

Дисциплины:

Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция

⇐ ПредыдущаяСтр 2 из 2

Случай 1. Знаменатель имеет только действительные различные корни, т.е. разлагается на неповторяющиеся множители первой степени.

Пример 11. Найти интеграл

Решение. Так как каждый из двухчленов входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде

Освобождаясь от знаменателей, получим

При х = 1 6 = 3А, А = 2;

при х = 2 11 = -2В, В= — ;

при х = 4 27 = 6С, С = .

Итак, разложение рациональной дроби на простейшие имеет вид

Таким образом,

Случай 2. Знаменатель имеет лишь действительные корни, причем некоторые из них кратные, т.е. знаменатель разлагается на множители первой степени и некоторые из них повторяются.

Пример 12. Найти интеграл

Решение. Множителю соответствует сумма трех простейших дробей , а множителю — простейшая дробь Итак,

Освободимся от знаменателя:

х = 1	2 = 4А; A =
x = -3	10 = -64D; D = —
x = 0	1= -3B + 3C +
x = -1	2 = 1- 4B + 8C +

Откуда В = , С = .

Окончательное разложение данной дроби на простейшие имеет вид

Таким образом, получим

Случай 3. Среди корней знаменателя имеются простые комплексные корни, т.е. разложение знаменателя содержит квадратичные неповторяющиеся множители.

Пример 14. Найти интеграл

Решение. Разлагаем дробь на простейшие дроби

Освобождаемся от знаменателя:

. Выпишем коэффициенты при одинаковых степенях:

при х²:	0 = А+В
x:	0 = A+C
x⁰:	1 = A

Откуда найдем А = 1, В = -1, С = -1.

Итак,

Следовательно,

= ln|x|-

— — = ln|x| — —

— +C.

Случай 4. Среди корней знаменателя имеются кратные комплексные корни, т. е. разложение знаменателя содержит повторяющиеся квадратичные множители.

Пример 13. Найти интеграл

Решение. Так как есть двукратный множитель, то

Освобождаясь от знаменателей, получим

Приравняем коэффициенты при одинаковых степенях :

Следовательно,

6. Интегрирование иррациональных функций

Неопределенный интеграл вида интегрируется

путем введения новой переменной .

Интегралы вида интегрируются путем выделения полного квадрата из квадратного трехчлена.

Пример 15. Вычислить интеграл .

Решение :

= , где

Пример 16. Вычислить интеграл .

Решение:

Интеграл вида , где n Î Z, интегрируются путем введения новой переменной t ⁿ = ax + b.

Пример 17. Вычислить интеграл .

Решение:

= -2t-2 = -2 +С.

Интегралы вида , где P_n (x) — многочлен степени n, вычисляются с помощью реккурентной формулы

= , (21)

где Q _n_—₁(x) — многочлен степени (n — 1) с неопределенными коэффициентами и l — число. Коэффициенты многочлена и число l находятся при помощи дифференцирования тождества (21).

Пример 18. Вычислить интеграл .

Решение. Применяем формулу (21):

= (Ах+В) . Дифференцируем это тождество: . Откуда

х² = А(х² + 4) + х(Ах+В) + l.

Выпишем коэффициенты при одинаковых степенях:

х²: 1 = А +А

х: 0 = Вх

х⁰: 0 = 4A + l.

Итак, А = , В = 0, l = -2. Следовательно,

= = +С.

Интеграл от дифференциального бинома , где m, n, p — рациональные числа:

1) если р — целое число, то делаем замену х = t ^s, где s — общий знаменатель дробей m и n;

2) если — целое число, то делаем замену а+bх ⁿ = t ^s, где s — знаменатель дроби р;

3) если +р — целое число, то делаем замену ах ^–ⁿ+b = t ^s, где s — знаменатель дроби р.

Пример 19. Вычислить интеграл

Решение:

= =

⇐ Предыдущая12

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства…

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой…

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции…

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого…

18. Интегрирование рациональных дробей и некоторых иррациональных функций

Одним из наиболее простых методов определения КоэффициЕнтов в разложении правильной дроби на простейшие является МЕТоД неопределенных коэффициентов. Поясним применение этого метода на примерах.

ПрИМер 1. Разложить на простейшие дроби

Применим формулу (13):

(14)

Где — пока неизвестные постоянные числа.

Приводим правую часть тождества (14) к общему знаменателю:

Дроби, стоящие в правой и левой частях последнего равенства, тождественно равны друг другу. Но если две дроби ТождественНо равны друг другу и имеют одинаковые знаменатели, то числители этих дробей также тождественно равны друг другу:

Раскрывая скобки, располагаем многочлен в правой части последнего равенства по убывающим степеням X:

Два многочлена тогда и только тогда тождественно равны друг другу, когда коэффициенты при одинаковых стеПЕнях Х равны.

Приравнивая коэффициенты при одинаковых степенях Х в этих многочленах, получим систему уравненИЙ:

Решив эту систему, найдем:

Подставив в формулу (14) вместо найденные значения, получим окончательно

Пример 2. Разложить на простейшие дроби:

Так как знаменатель имеет только ДЕйствительные корни, то разложение дроби, согласно формуле (13), имеет вид

(15)

Приведем правую часть соотношения (15) к общему знаменателю:

Приравнивая числители, получаем

Расположим многочлен в правой части по убывающим степеням X:

Сравнивая коэффициенты при одинаковых степенях Х в правой и левой частях рАВенства, получим систему уравнений:

Разрешив эту систему, найдем Подставив найденные значения коэффициентов в соотношения (15), получим

Пример 3. Разложить на простейшие дроби

Знаменатель имеет только комплексные корни; в этом случае разложение дроби на простейшие примет вид

Приведя к общему ЗНаменателю выражение, стоящее в правой части, придем к тождеству:

Откуда:

Приравнивая коэффициенты при одинаковых степенях, приходим к системе уравнеНИй:

Решая эту систему уравнений, найдем

Таким образом,

Пример 4. Разложить на простейшие дроби

Применяя формулу (13), получим:

Приводя к общему знаменателю, получим тождество

Или

Приравнивая коэффициеНТы при одинаковых сТЕпенях X , получим систему уравнений:

Из которой находим

Следовательно,

Часто нахождение коэффициентов разложения значительно упрощается, если применить так называемый Метод Произвольных значений. Рассмотрим с этой точки зрения только что приведенный пример. Полученное там равенство

(16)

Есть тождество, справедливое при любом значении Х.

Выбираем такие значения Х, для которых равенство (16) принимает наиболее простой вид. Здесь проще всего за Х взять один из корней знаменателя.

Полагая Х = 1, имеем:

Откуда

Аналогично, полагая Х = -1, найдем 3 = 6В, B =; пpи X = 2, 12 = 12С, С = 1; при Х = -2, -24 = -12D; D = 2.

На практике указанныЙ метод целесообразно применять в случае, когда знаменатель Q(Х) правильной рациональной дроби имеет только действительные простые корни.

Все выше изложенное позволяет нам сформулировать основные правила интегрирования рациональных дробей.

1. Если рациональная дробь неправильная, то ее представляют в виде суммы многочлена и правильной рациональной ДРоби.

Тем самым интегрирование неправильной рациональной дроби сводится к интегрированию многочлена и правильной рациональной дроби.

2. Разлагают знаменатель правильной дроби на множители.

3. Правильную рациональную дробь представляют в виде суммы простейших дробей и сводят интегрирование правильной рациональной дроби к интегрированию простейших дробей.

Рассмотрим примеры:

Пример 1.

Под интегралом стоит неправильная рациональная дробь. Выделяя целую часть, получим

Следовательно,

Разложим правильную рациональную дробь на простейшие дроби:

Поэтому

Таким образом, окончательно имеем:

Пример 2.

ПоД интегралом стоит правильная рациональная дробь.

Разлагая ее на простейшие дроби, получим

Следовательно,

Что касается интеграла в правой части, то он берется, как мы знаем, подстановкой При этом Таким образом, имеем:

Итак,

Интеграл от рациональной дроби является элементарной функцией. Мы сейчас рассмотрим некоторые типы интегралов, которые надлежащей заменой переменного могут быть сведены к интегралам от рациональных функций, следовательно, также могут быть выражены через элементарные функции.

Предварительно рассмотрим некоторые новые понятия. Многочленом относительно перемЕНных и и V Называется сумма произведений вида: , где Т и П — целые неотрицательные числа.

Например, выражения U являются многочленами относительно И и V.

Частное от деления двух многочленов относительно И и V называется Рациональной функцией от и и V или Рациональным выражением относительно И и V.

Например, дроби являются рациональными выражениями относительно И и V. Рациональную функцию от И и V обозначают .

Легко заметить, что сумма, разность, произведение и частное нескольких рациональных функций от И и V есть тоже рациональная функция от U и V.

Рациональным выражением относительно функций и называется рациональная функция от И и V, в которую вместо И И V подставлены соответственно и . Рациональное выражение относительно и обозначают . Аналогичный смысл имеет выражение .

Пример 1. — рациональное выражение ОтносиТельно X И

Пример 2. — рациональное выражение относительно и

Заметим, что Если и — Рациональные функции от х, то Также является рациональной функцией от х.

1. Интегралы вида , Где п — Целое число, могут быть сведены к интегралам от рациональных функций. Докажем это.

Произведем в этом интеграле замену переменной, положив тогда Следовательно,

Интеграл, стоящий в правой части равенства, есть интегРАл от рациональной функции относительно переменной интегрирования Z и, следовательно, может быть вычислен в элементарных функциях.

Поясним сказанное примерами:

Пример 1.

Полагаем ; тогда и

Следовательно,

Таким образом, мы свели наш интеграл к интегралу от рациональной функции.

Подставляя вместо Z его выражение через Х, т. Е. Имеем:

Пример 2. Подынтегральное ВыражеНие рационально зависит от , так как Сделаем замену переменной: , откуда и

Следовательно,

II. ИнтЕгРалы болЕЕ общего вида: где R — рациОНальное ВЫражЕНие, от х U такжЕ приводятся к интегралам от рациональной функции, если полоЖИТЬ

Пример. Вычислить

Полагаем откУДа

Следовательно,

< Предыдущая		Следующая >

«Разложение дроби на простейшие», Математика, химия, физика

Выдержка
Другие работы
Помощь в написании

РАЗЛОЖЕНИЕ ДРОБИ НА ПРОСТЕЙШИЕ

Для начала разберем теорию, далее решим парочку примеров для закрепления материала по разложению дробно рациональной функции на сумму простейших дробей. Подробно остановимся на методе неопределенных коэффициентов и методе частных значений, а также на их комбинации. элементарный дробь простейший разложение Простейшие дроби часто называют элементарными дробями.

Различают следующие виды простейших дробей:

где A, M, N, a, p, q — числа, а дискриминант знаменателя в дробях 3) и 4) меньше нуля.

Называют их соответственно дробями первого, второго, третьего и четвертого типов.

Для чего вообще дробь раскладывать на простейшие?

Приведем математическую аналогию. Часто приходится заниматься упрощением вида выражения, чтобы можно было проводить какие-то действия с ним. Так вот, представление дробно рациональной функции в виде суммы простейших дробей примерно то же самое. Применяется для разложения функций в степенные ряды, ряды Лорана и, конечно же, для нахождения интегралов.

К примеру, требуется взять интеграл от дробно рациональной функции. После разложения подынтегральной функции на простейшие дроби, все сводится к достаточно простым интегралам.

Но об интегралах в другом разделе.

Пример.

Разложить дробь на простейшие.

Решение.

Вообще отношение многочленов раскладывают на простейшие дроби, если степень многочлена числителя меньше степени многочлена в знаменателе. В противном случае сначала проводят деление многочлена числителя на многочлен знаменателя, а уже затем проводят разложение правильной дробно рациональной функции.

Выполним деление столбиком (уголком):

Следовательно, исходная дробь примет вид:

Таким образом, на простейшие дроби будем раскладывать.

Алгоритм метода неопределенных коэффициентов.

Во-первых, раскладываем знаменатель на множители.

Здесь все методы хороши — от вынесения за скобки, применения формул сокращенного умножения, до подбора корня и последующего деления столбиком (при знаменателе в виде многочлена с рациональными коэффициентами степени выше второй). Об этом подробнее в разделе теории — разложение многочлена на множители.

В нашем примере все просто — выносим х за скобки.

Во-вторых, раскладываемую дробь представляем в виде суммы простейших дробей с неопределенными коэффициентами.

Здесь стоит рассмотреть виды выражений, которые могут быть у Вас в знаменателе.

Если в знаменателе что-то вроде этого, количество линейных множителей роли не играет, (будь их 2 или22), то дробь представится в виде суммы простейших дробей первого типа:

a, b, c и d — числа, A, B, C и D — неопределенные коэффициенты.

Если в знаменателе что-то вроде этого количество множителей роли не играет и не играют роли степени этих множителей (хоть 221ая степень), то дробь представится в виде суммы простейших дробей первого и второго типов:

a, b, c — числа, — неопределенные коэффициенты.

Возьмите на заметку: какая степень — столько и слагаемых.

Если в знаменателе что-то вроде этого количество квадратичных выражений роли не играет, то дробь представится в виде суммы простейших дробей третьего типа:

p, q, r и s — числа, P, Q, R и S — неопределенные коэффициенты.

Если в знаменателе что-то вроде этого количество множителей роли не играет и не играют роли степени этих множителей, то дробь представится в виде суммы простейших дробей третьего и четвертого типов:

p, q, r и s — числа, — неопределенные коэффициенты.

Обычно встречается комбинация этих вариантов (как правило, довольно простая) (13, «https://education-club.ru»).

Если собрать все в кучу, то дробь представится в виде суммы простейших дробей всех четырех типов:

Хватит теории, на практике все равно понятнее.

Пришло время вернуться к примеру. Дробь раскладывается в сумму простейших дробей первого и третьего типов с неопределенными коэффициентами A, B и C.

В-третьих, приводим полученную сумму простейших дробей с неопределенными коэффициентами к общему знаменателю и группируем в числителе слагаемые при одинаковых степенях х.

То есть, пришли к равенству:

При x отличных от нуля это равенство сводится к равенству двух многочленов, А два многочлена являются равными тогда и только тогда, когда коэффициенты при одинаковых степенях совпадают.

В-четвертых, приравниваем коэффициенты при одинаковых степенях х.

При этом получаем систему линейных алгебраических уравнений с неопределенными коэффициентами в качестве неизвестных:

В-пятых, решаем полученную систему уравнений любым способом (при необходимости смотрите статью решение систем линейных алгебраических уравнений, методы решения, примеры), который нравится Вам, находим неопределенные коэффициенты.

В-шестых, записываем ответ.

P.S.

Пожалуйста, не ленитесь, проверяйте ответ, приводя к общему знаменателю полученное разложение.

Метод неопределенных коэффициентов является универсальным способом при разложении дроби на простейшие.

Очень удобно использовать метод частных значений, если знаменатель представляет собой произведение линейных множителей, то есть имеет вид схожий с.

Рассмотрим на примере, чтобы показать плюсы этого метода.

Пример.

Разложить дробь на простейшие.

Решение.

Так как степень многочлена в числителе меньше степени многочлена в знаменателе, то производить деление нам не придется. Переходим к разложению знаменателя на множители.

Для начала выносим х за скобки.

Находим корни квадратного трехчлена (например, по теореме Виета):

Следовательно, квадратный трехчлен можно записать как.

То есть, знаменатель примет вид.

При данном знаменателе, исходная дробь раскладывается в сумму трех простейших дробей первого типа с неопределенными коэффициентами:

Полученную сумму приводим к общему знаменателю, но в числителе при этом скобки не раскрываем и не приводим подобные при А, В и С (на этом этапе как раз отличие от метода неопределенных коэффициентов):

Таким образом, пришли к равенству:

А теперь, для нахождения неопределенных коэффициентов, начинаем подставлять в полученное равенство «частные значения», при которых знаменатель обращается в ноль, то есть х=0, х=2 и х=3 для нашего примера.

При х=0 имеем:

При х=2 имеем:

При х=3 имеем:

Ответ:

Как видите, различие метода неопределенных коэффициентов и метода частных значений лишь в способе нахождения неизвестных. Эти методы можно совмещать для упрощения вычислений.

Рассмотрим пример.

Пример.

Разложить дробно рациональное выражение на простейшие дроби.

Решение.

Так как степень многочлена числителя меньше степени многочлена знаменателя и знаменатель уже разложен на множители, то исходное выражение представится в виде суммы простейших дробей следующего вида:

Приводим к общему знаменателю:

Приравниваем числители.

Очевидно, что нулями знаменателя являются значения х=1, х=-1 и х=3. Используем метод частных значений.

При х=1 имеем:

При х=-1 имеем:

При х=3 имеем:

Осталось найти неизвестные и.

Для этого подставляем найденные значения в равенство числителей:

После раскрытия скобок и приведения подобных слагаемых при одинаковых степенях х приходим к равенству двух многочленов:

Приравниваем соответствующие коэффициенты при одинаковых степенях, тем самым составляем систему уравнений для нахождения оставшихся неизвестных и. Получаем систему из пяти уравнений с двумя неизвестными:

Из первого уравнения сразу находим, из второго уравнения.

В итоге получаем разложение на простейшие дроби:

Примечание.

Если бы мы сразу решили применить метод неопределенных коэффициентов, то пришлось бы решать систему пяти линейных алгебраических уравнений с пятью неизвестными. Применение метода частных значений позволило легко отыскать значения трех неизвестных из пяти, что значительно упростило дальнейшее решение.

Показать весь текст

Заполнить форму текущей работой

Как разложить многочлены на множители с дробями

Лучший способ разложения многочленов на множители начинается с преобразования дробей в более простые термины. Полиномы представляют собой алгебраические выражения с двумя или более членами, точнее, суммой нескольких членов, которые имеют разные выражения одной и той же переменной. Стратегии, которые помогают упростить многочлены, включают в себя выделение наибольшего общего множителя с последующим группированием уравнения в его наименьшие члены. То же самое справедливо и при решении многочленов с дробями.

Определение многочленов с дробями

У вас есть три способа просмотра многочленов фразы с дробями. Первая интерпретация касается многочленов с дробями в качестве коэффициентов. В алгебре коэффициент определяется как числовая величина или константа, находящаяся перед переменной. Другими словами, коэффициенты для 7_a_, b и (1/3) c равны 7, 1 и (1/3) соответственно. Таким образом, двумя примерами многочленов с дробными коэффициентами будут: 92 + x — 2}

оценивается с помощью разложения на неполные дроби, которое, кстати, включает разложение полиномов на множители, и в простейшей форме:

\bigg(\frac{3}{x+2}\bigg) +\bigg(\frac{5}{x-1}\bigg)

Основы факторинга – распределительное свойство и метод FOIL

Факторы представляют собой два числа, которые при умножении дают третье число. В алгебраических уравнениях факторизация определяет, какие две величины были перемножены, чтобы получить данный многочлен. Дистрибутивное свойство сильно соблюдается при умножении многочленов. Распределительное свойство по существу позволяет умножать сумму, умножая каждое число по отдельности перед добавлением произведений. Обратите внимание, например, как применяется распределительное свойство в примере:

7(10x + 5) \text{ для получения бинома } 70x + 35.

Но, если два бинома перемножаются вместе, то используется расширенная версия свойства распределения посредством метода FOIL. FOIL представляет собой аббревиатуру для перемножения первых, внешних, внутренних и последних терминов. Следовательно, разложение полиномов на множители влечет за собой выполнение метода FOIL в обратном порядке. Возьмем два вышеупомянутых примера с полиномами, содержащими дробные коэффициенты. Выполнение метода FOIL в обратном порядке для каждого из них приводит к коэффициентам 92 + \frac{3}{4}x + \frac{1}{8} = \bigg(x + \frac{1}{4}\bigg)\bigg(x + \frac{1}{2} \bigg)

Действия при разложении полиномиальных дробей на множители

Как видно из вышеизложенного, полиномиальные дроби включают полином в числителе, деленный на полином в знаменателе. Таким образом, вычисление полиномиальных дробей требует сначала разложить на множители полином числителя, а затем разложить на множители полином знаменателя. Это помогает найти наибольший общий множитель, или GCF, между числителем и знаменателем. Как только GCF и числителя, и знаменателя найдены, они сокращаются, в конечном итоге сводя все уравнение к упрощенным терминам. Рассмотрим исходный пример полиномиальной дроби выше 92 + x — 2} = \frac{8x + 7}{(x + 2)(x — 1)}

Переставьте числитель

Затем переставьте числитель так, чтобы он начал содержать GCF в знаменатель, чтобы получить:

\begin{aligned} \frac{8x + 7}{(x + 2)(x — 1)} &= \frac{ 3x + 5x — 3 + 10}{(x + 2 )(x — 1)} \\ &= \frac{3x — 3}{(x + 2)(x — 1)} + \frac{5x + 10} }{(x + 2)(x — 1)} \\ \end{align}

Для левого слагаемого GCF равен ( x — 1), а для правого сложения GCF равен ( x + 2), которые сокращаются в числителе и знаменателе, как показано в:

\frac{3x — 3}{(x + 2)(x — 1)} + \frac{5x + 10}{( x + 2)(x — 1)} = \frac{3\cancel{(x — 1)}}{(x + 2)\cancel{(x — 1)}} + \frac{5\cancel{( x + 2)}}{\cancel{(x + 2)}(x — 1)}

Таким образом, когда GCF сокращаются, окончательный упрощенный ответ:

\frac{3}{x + 2} + \frac{5}{x — 1}

как решение разложения на неполные дроби.

Сокращение простых и сложных дробей с помощью пошагового решения математических задач

ПРОИЗВЕДЕНИЕ ДРОБЕЙ

Произведение двух дробей определяется следующим образом.

Произведением двух дробей называется дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей данных дробей.

В символах

Любой общий множитель, встречающийся как в числителе, так и в знаменателе любой дроби, может быть разделен до или после умножения.

Пример 1 Найдите произведение

Решение

Те же процедуры применяются к дробям, содержащим переменные.

Пример 2 Найдите произведение числа

Решение Сначала разделим числитель и знаменатель на общие множители, чтобы получить

Теперь, перемножив оставшиеся множители числителей и знаменателей, получим

Если отрицательный знак при любом из факторов целесообразно действовать так, как если бы все факторы были положительными, а затем присвоить результату соответствующий знак. Положительный знак ставится, если отрицательных знаков нет или четное число отрицательных знаков у факторов; знак минус ставится, если у факторов нечетное число знаков минус.

Пример 3

Когда дроби содержат алгебраические выражения, перед умножением необходимо по возможности разложить на множители и разделить общие множители.

Пример 4 Найдите произведение .

Решение Сначала мы должны разложить числители и знаменатели, чтобы получить

Теперь, разделив общие множители, мы получим

Теперь мы умножим оставшиеся множители числителей и знаменателей, чтобы получить

Обратите внимание, что при записи дробных ответов мы будем умножать числитель и оставлять знаменатель в разложенном виде. Очень часто дроби более полезны в этой форме.

В алгебре мы часто переписываем выражение, например, как эквивалентное выражение. Используйте любую форму, наиболее удобную для конкретной задачи.

Пример 5

Общие ошибки: Помните, что мы можем разделить только общие факторы, но не общие термины! Например,

, потому что x — это терм, который нельзя разделить. Точно так же

, потому что 3 не является делителем всего числителя 3y + 2. . Это точно такое же понятие, как деление одного целого числа на другое; a ÷ b — это число q, частное, такое, что bq = a.

Чтобы найти , ищем такое число q, что . Чтобы решить это уравнение относительно q, мы умножаем каждый член уравнения на . Таким образом,

В приведенном выше примере мы называем число, обратное числу . В общем случае обратная дробь — это дробь. То есть мы получаем обратную дробь, «переворачивая» дробь. В общем,

Частное двух дробей равно произведению делимого и обратной величины делителя.

То есть, чтобы разделить одну дробь на другую, инвертируем делитель и умножаем. Символами

Пример 1

Как и при умножении, когда дроби в частном имеют присоединенные знаки, рекомендуется решить задачу так, как если бы все множители были положительными, а затем присвоить решению соответствующий знак.

Пример 2

Некоторые частные встречаются так часто, что полезно сразу распознавать эквивалентные формы. Один случай:

В общем,

Пример 3

Когда дроби в частном включают алгебраические выражения, необходимо по возможности разложить на множители и разделить общие множители перед умножением. 9Пример 4 знаменатель одинаковый, а числитель равен сумме числителей исходных дробей.

В общем,

Пример 1

Когда используется вычитание, перед сложением полезно перейти к стандартной форме.

Пример 2

Мы должны быть особенно осторожны с биномиальными числителями. Например, мы должны переписать

, где весь числитель заключен в круглые скобки.

СУММЫ ДРОБЕЙ С РАЗЛИЧНЫМИ ЗНАМЕНАТЕЛЯМИ

В разделе 6.3 мы сложили дроби с одинаковыми знаменателями. В этом разделе мы будем складывать дроби с разными знаменателями.

НАИМЕНЬШИЙ ОБЩИЙ ЗНАМЕНАТЕЛЬ

В общем случае наименьшим общим знаменателем (НОД) набора дробей называется наименьшее натуральное число, кратное каждому из знаменателей набора дробей. Иногда мы можем получить ЖК-дисплей путем осмотра. Если ЖК-дисплей не виден сразу, мы можем использовать специальную процедуру, чтобы найти его.

Чтобы найти ЖК-дисплей:

Полностью разложите каждый знаменатель, по возможности выравнивая общие множители.
Включите в LCD каждый из этих множителей наибольшее количество раз, когда он встречается в любом отдельном знаменателе.

Пример 1 Найдите наименьший общий знаменатель дробей

Решение Наименьший общий знаменатель содержит среди своих множителей множители 12, 10 и 6.

Таким образом, LCD равно 60. (Это число равно наименьшее натуральное число, которое делится на 12, 10 и 6.)

ЖК набора алгебраических дробей — простейшее алгебраическое выражение, кратное каждому из знаменателей набора. Таким образом, ЖК дробей

потому что это простейшее выражение, кратное каждому из знаменателей.

Пример 2 Найти ЛП дробей

Решение Следуя методике примера 1, получаем

Таким образом, ЛП равно х ² (х + 1)(х — 1).

Мы можем складывать дроби с разными знаменателями, сначала составив дроби до эквивалентных дробей с одинаковыми знаменателями, а затем сложив.

Чтобы сложить дроби с разными знаменателями:

Найдите на ЖК-дисплее набор дробей.
Приведите каждую дробь к эквивалентной дроби, используя ЖК-дисплей в качестве знаменателя.
Сложите дроби, используя свойство

Пример 3 Запишите суммы и в виде отдельных членов.

Решение В каждом случае LCD равно 10. Мы преобразуем каждую дробь в дробь с 10 в знаменателе. Таким образом,

эквивалентны

из которых мы получаем

Иногда дроби имеют знаменатели, которые являются биномами.

Пример 4 Запишите сумму в виде одного слагаемого.

Решение ЖК-дисплей равен (x + 2)(x — 1). Мы превращаем каждую дробь в дробь со знаменателем (x + 2)(x — 1), расставляя скобки по мере необходимости, и получаем

Теперь, когда у нас одинаковые знаменатели, мы можем сложить числители, упростить и получить

Пример 5 Запишите сумму как один член.

Решение Сначала мы факторизуем знаменатели, чтобы получить LCD.

Теперь мы преобразуем каждую дробь в дроби с этим знаменателем и получаем

Теперь мы можем сложить числители, упростить и получить

Общие ошибки Обратите внимание, что мы можем складывать дроби только с одинаковыми знаменателями. Таким образом,

Кроме того, мы складываем только числители дробей с одинаковыми знаменателями. Таким образом,

РАЗНОСТИ ДРОБЕЙ С РАЗЛИЧНЫМИ ЗНАМЕНАТЕЛЯМИ

Мы вычитаем дроби с разными знаменателями так же, как складываем такие дроби. Однако сначала запишем каждую дробь в стандартной форме. Таким образом, любая дробь в форме

сначала записывается как

Теперь мы можем сложить дроби.

Пример 1 Запишите разницу в виде одного термина.

Решение Начнем с записи в стандартной форме как . ЖК-дисплей 12x. Мы приводим каждую дробь к эквивалентной дроби с этим знаменателем, чтобы получить

Теперь сложение числителей дает

Опять же, с биномиальными числителями следует соблюдать особую осторожность.

Пример 2 Запишите разницу в виде одного термина.

Сначала решение должно быть записано как

, где весь числитель заключен в круглые скобки. Затем мы получаем LCD 6 и превращаем каждую дробь в дроби со знаменателем 6, добавляем числители и упрощаем.

В следующих примерах используются биномиальные знаменатели.

Пример 3 Запишите разницу в виде одного термина.

Решение Начнем с записи в стандартной форме как . LCD равен (x — l)(x + 2), и мы преобразуем каждую дробь в эквивалентную дробь с этим знаменателем, чтобы получить

Теперь складываем числители и упрощаем выходы

Пример 4 Запишем разницу

в виде одного члена

Решение Мы сначала разложим знаменатели и запишем дроби в стандартной форме, чтобы получить

Находим LCD (x + 7)(x — 3)(x + 3) и приводим каждую дробь к эквивалентной дроби с этим знаменателем, чтобы получить

Теперь складываем числители и упрощаем выход

СЛОЖНЫЕ Дроби

Дробь, которая содержит одну или несколько дробей либо в числителе, либо в знаменателе, либо в обоих случаях, называется сложной дробью. Например,

— сложные дроби. Как и простые дроби, сложные дроби представляют собой частные. Например,

В случаях, подобных уравнению (1), в котором числитель и знаменатель сложной дроби не содержат суммы или разности, мы можем просто инвертировать делитель и умножить. То есть

В случаях, подобных уравнению (2), в котором числитель или знаменатель сложной дроби содержит суммы или разности, мы не можем просто инвертировать делитель и умножить. Однако мы можем использовать фундаментальный принцип дробей для упрощения сложных дробей. Фактически, мы также можем использовать фундаментальный принцип для упрощения сложных дробей формы (1) выше.

Пример 1 Упростите, используя фундаментальный принцип дробей.

Решение Умножаем числитель и знаменатель на ЖК всех дробей в числителе и знаменателе; в этом случае LCD равно 4. Результатом является простая дробь, эквивалентная данной сложной дроби.

Упрощение уравнения (2) на стр. 255 показано в следующем примере.

Пример 2 Упростить

Решение Умножаем числитель и знаменатель на ЖК всех дробей в числителе и знаменателе; в данном случае ЖК равно 6. Получаем

УРАВНЕНИЯ Дробей

Чтобы решить уравнение, содержащее дроби, обычно проще всего сначала найти эквивалентное уравнение, не содержащее дробей. Мы делаем это, умножая каждый член уравнения на наименьший общий знаменатель дробей.

Хотя мы можем применять изученные алгебраические свойства в любом порядке, следующие шаги показывают порядок, наиболее полезный для решения уравнения, когда решение не очевидно. Конечно, не всегда все шаги необходимы.

Чтобы решить уравнение:

Очистить дроби, если они есть, путем умножения каждого члена уравнения на ЖК-дисплей.
Запишите любое выражение, содержащее скобки, как выражение без скобок.
Объедините любые похожие термины в любой элемент.
Получить все термины, содержащие переменную в одном элементе, и все термины, не содержащие переменную, в другом элементе.
Разделить каждый член на коэффициент переменной, если он отличен от 1.
Проверьте ответ, если каждый член уравнения был умножен на выражение, содержащее переменную.

Пример 1 Решить .

Решение Умножим каждый член на LCD 15, чтобы получить эквивалентное уравнение, не содержащее дробей.

Свойство равенства умножения (раздел 3.4) позволяет нам умножать каждый член уравнения на ненулевое значение, чтобы получить эквивалентное уравнение. Таким образом, для решения уравнения

мы умножаем каждый элемент на LCD 4(x — 5). Заметим, что x не может равняться 5, так как 4(x — 5) равно 0, если x = 5. Все решение показано в следующем примере.

Пример 2 Решить .

Решение Мы умножаем каждый член на LCD 4(x — 5), чтобы получить

Применяя свойство распределения, мы получаем

Решение для x дает

-21x = -189; x = 9

Обратите внимание, что 4(x — 5) не равно нулю для a = 9. Таким образом, a = 9 является допустимым решением уравнения.

Когда уравнения содержат более одной переменной, иногда желательно решить для одной переменной через другие переменные.

Пример 3 Найдите a через a, b и c.

Решение Умножим каждый элемент на LDC 3xc, чтобы получить

Теперь, разделив каждый член на 2x, мы получим

ПРИЛОЖЕНИЯ

Словесные задачи в следующих упражнениях приводят к уравнениям с дробями. В это время вы можете просмотреть шаги, предлагаемые для решения текстовых задач, и шаги, предложенные на странице 260, для решения уравнений, содержащих дроби.

Пример 1 Если определенное число прибавить к числу, получится 11. Найдите число.

Решение

Шаги 1-2 Сначала мы записываем то, что хотим найти (число), в виде словосочетания. Затем мы представляем число в терминах переменной.
Номер: x

Шаг 3 Эскиз не применим.

Шаг 4 Теперь мы можем написать уравнение. Помните, что «из» указывает на умножение.

Шаг 5 Решение уравнения дает

Шаг 6 Число равно 12.

Уравнения для задач, связанных с движением, иногда включают дроби. Основная идея задач движения состоит в том, что пройденное расстояние d равно произведению скорости перемещения r и времени перемещения t. Таким образом, d = rt. Мы можем решить эту формулу для r или t, чтобы получить:

Таблица, показанная в следующем примере, полезна при решении задач движения.

Пример 2 Экспресс-поезд проходит 180 миль за то же время, что и товарный поезд — 120 миль. Если экспресс идет на 20 миль в час быстрее грузового, найдите скорость каждого из них.

Шаги решения 1-2 Мы представляем две неизвестные величины, которые мы хотим найти, в виде словосочетаний. Затем мы представляем словосочетания в терминах одной переменной.

Скорость грузового поезда: r

Скорость экспресса: r + 20

Шаг 3 Далее мы составляем таблицу, в которой указаны расстояния, скорости и время.

Шаг 4 Поскольку время обоих поездов одинаковое, мы можем приравнять выражения для времени, чтобы получить

Шаг 5 Теперь мы можем найти r, сначала умножив каждый член на LCD r(r + 120) и мы получаем

Шаг 6 Скорость грузового поезда составляет 40 миль в час, а скорость экспресса — 40 + 20, или 60 миль в час.

ОТНОШЕНИЕ И ПРОПОРЦИЯ

Частное двух чисел, a ÷ b или , иногда называют отношением и читают как «отношение a к b». Это удобный способ сравнить два числа.

Пример 1 Выразите в виде соотношения.

а. от 3 до 5 дюймов
б. от 8 м до 12 м
c. От 6 до 10

Решения

Утверждение, что два отношения равны, например,

называется пропорцией и читается как «2 к 3, как 4 к 6» и «a к b, как c к d». Числа a, b, c и d называются соответственно первым, вторым, третьим и четвертым членами пропорции. Первый и четвертый члены называются экстремумами пропорции, а второй и третий члены называются средними.

Пример 2 Выразите в пропорции.

Если каждое отношение в пропорции

умножить на bd, то получится

Таким образом,

Произведение крайних значений в любой пропорции равно произведению средних.

Пропорция — это особый тип дробного уравнения. Приведенное выше правило получения эквивалентного уравнения без знаменателей является частным случаем нашего общего подхода.

Пример 3 Решить пропорцию .

Решение Применяя свойство (1) выше, мы получаем

ПРЕОБРАЗОВАНИЯ

Мы можем использовать пропорции для преобразования английских единиц измерения в метрические единицы и наоборот. Следующие базовые соотношения помогут установить соответствующие пропорции конверсий.

1 метр (м) = 39,37 дюйма (дюйм)

1 килограмм (кг) = 2,2 фунта (фунт)

1 километр (км) = 0,62 мили (миля)

1 литр (1) = 1,06 кварты (qt)

1 фунт (lb) = 454 грамма (g)

1 дюйм (in. ) = 2,54 сантиметра (cm)

При преобразовании единиц проще всего выполнить шесть описанных шагов.

Пример 4 Замените 8 дюймов на сантиметры.

Решение

Шаги 1-2 Представьте, что нужно найти (в сантиметрах), в терминах словосочетания и в терминах переменной.
Сантиметры: x

Шаг 3 Составьте таблицу, показывающую основные отношения между дюймами и сантиметрами.

Шаг 4 Используя таблицу из шага 3, напишите соотношение дюймов к сантиметрам.

Шаг 5 Найдите x, приравняв произведение средних к произведению крайних значений.

8(2,54) = 1 · x
20,32 = x

Шаг 6 Восемь дюймов равняются 20,32 сантиметра.

РЕЗЮМЕ ГЛАВЫ

Следующие свойства используются для перезаписи произведений и частных дробей.

Наименьшее натуральное число, кратное каждому из знаменателей набора дробей, называется наименьшим общим знаменателем (ОНД) дробей. Следующие свойства используются для перезаписи сумм и разностей дробей.
Дробь, которая содержит одну или несколько дробей либо в числителе, либо в знаменателе, либо в обоих, называется сложной дробью . Мы можем упростить сложную дробь, умножив числитель и знаменатель на ЖК всех дробей в числителе и знаменателе.
Мы можем решить уравнение, содержащее дроби, получив эквивалентное уравнение, решение которого очевидно при проверке. Как правило, лучше всего получить эквивалентное уравнение, свободное от дробей, путем умножения каждого члена уравнения на LCD дробей.
Частное двух чисел называется отношением ; утверждение о равенстве двух отношений называется пропорцией . В пропорции
a и d называются крайними пропорциями, а b и c называются средними . В любой пропорции этой формы
ad = bc

Упрощение дробей — Примеры | Как упростить дроби?

Упрощение дроби означает приведение дроби к простейшей форме. Дробь имеет простейшую форму, если ее числитель и знаменатель не имеют общих делителей, кроме 1. Важным шагом, который мы делаем, решая задачи с дробями, является приведение их к простейшей форме. Хотя мы упростим их, значение дроби останется неизменным. Это означает, что упрощенная дробь и фактическая дробь образуют пару эквивалентных дробей. В этой статье мы познакомимся с несколькими простыми способами упрощения дробей.

1.	Как упростить дроби?
2.	Упрощение дробей с переменными
3.	Упрощение дробей с показателями
4.	Упрощение смешанных дробей
5.	Упрощение неправильных дробей
6.	Часто задаваемые вопросы об упрощении дробей

Как упростить дроби?

Упрощение дроби означает приведение дроби к наименьшей форме. Дробь находится в простейшей форме, если ее числитель и знаменатель взаимно просты или не имеют общих делителей, кроме 1. Простейшая форма дроби эквивалентна данной дроби. Например, дробь 3/4 имеет простейшую форму, потому что 3 и 4 не имеют общего делителя, кроме 1. Попробуем шаг за шагом упростить дробь 8/24.

Упрощение дробей шаг за шагом

Ниже приведен пошаговый процесс, который поможет вам понять процесс упрощения дроби. Рассмотрим дробь 8/24 и выполните шаги, указанные ниже, чтобы понять, как упростить дробь 8/24.

Шаг 1: Запишите множители числителя и знаменателя.

Множители 8 и 24 равны

Множители 8: 1, 2, 4 и 8
Факторы 24: 1, 2, 3, 4, 6, 8, 12 и 24

Шаг 2: Определите общие делители числителя и знаменателя. Общие делители чисел 8 и 24 равны 1, 2, 4 и 8.

Шаг 3: Разделите числитель и знаменатель на общие делители, пока у них не будет общего делителя, кроме 1.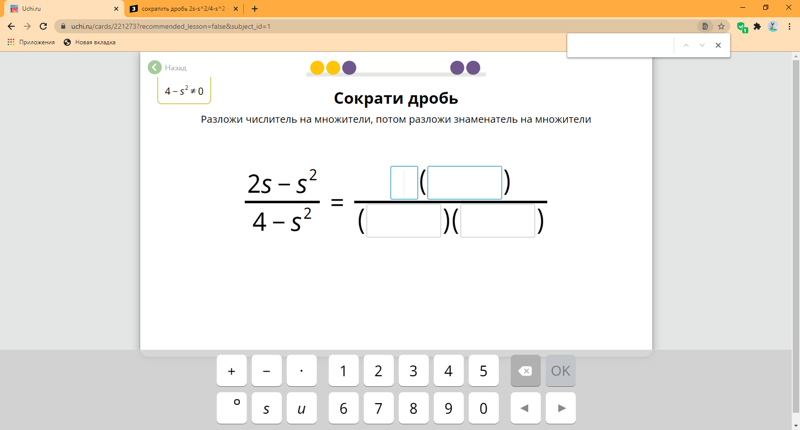 Полученная таким образом дробь является простейшей форма. Начнем делить на 2, тогда 8/24 = (8/2)/(24/2) = 4/12. Мы будем продолжать делить на 2, пока не сможем двигаться дальше. Итак, мы имеем (4/2)/(12/2) = 2/6 = (2/2)/(6/2) = 1/3.

Таким образом, 1/3 является простейшей формой дроби 8/24.

Теперь давайте также обсудим простой способ упростить дроби. Мы можем максимально упростить сложную дробь, следуя процессу упрощения дроби. Чтобы найти упрощенную форму дроби, рассмотрим простой способ упростить дробь. Вот у нас три шестых пиццы.

Зачем говорить три шестых, если на самом деле ты имеешь в виду половину?

Упрощение дроби означает максимальное упрощение дроби. Быстрый способ найти простейшую форму дроби — это вычислить наибольший общий множитель. Следуйте инструкциям ниже, чтобы узнать кратчайший путь.

Шаг 1: Запишите множители числителя и знаменателя.
Шаг 2: Определите наибольший общий делитель числителя и знаменателя.
Шаг 3: Разделите числитель и знаменатель на их наибольший общий делитель (HCF). Полученная дробь имеет простейшую форму.

Вернемся к той же проблеме упрощения дроби 8/24. Наибольший общий делитель 8 и 24 равен 8. Разделив числитель 8 и знаменатель 24 на 8, мы сразу получим простейшую форму дроби, то есть 1/3. Итак, кратчайший способ разложить дробь на простейшие формы — это разделить числитель и знаменатель на их наибольший общий делитель.

Упрощение дробей с переменными

Также можно упростить дробь, содержащую переменные в числителе и знаменателе. Используйте развернутую форму каждого члена в числителе и знаменателе, чтобы облегчить вам упрощение дроби с переменными.

Давайте просто представим дробь (x ² y)/(xy).

Выразите числитель и знаменатель в виде произведения переменных.

(x ² y)/(xy) = (x × x × y)/(x × y)

Отменить общие переменные.

(x ² y)/(xy) = (x × x × y)/(x × y) = x

Надеемся, вам было легко упрощать дроби с переменными.

Упрощение дробей с показателями

Вы можете упростить дробь, содержащую показатели степени в числителе и знаменателе. Используйте развернутую форму показателей степени в числителе и знаменателе, чтобы облегчить вам упрощение дроби с показателями степени. Чтобы число было легко читаемым, мы иногда используем показатели степени. Предположим, у нас есть дробь 3 ⁵/3 ² . Мы представим числитель и знаменатель в виде произведения чисел, а затем сократим обычные числа.

3 ⁵ /3 ² = (3 × 3 × 3 × 3 × 3)/(3 × 3) = 3 × 3 × 3 = 27

Итак, вы, наконец, научились упрощать дроби с помощью экспоненты.

Упрощение смешанных дробей

Смешанная фракция представляет собой смесь целой и правильной фракции. Чтобы упростить смешанную дробь, нужно упростить только дробную часть. Для этого запишите числитель и знаменатель в разложенном виде и сократите общие множители. Результатом будут новый числитель и новый знаменатель смешанной дроби.

Например: Упростите смешанную дробь \(3\dfrac{4}{10}\).

Чтобы упростить смешанную дробь \(3\dfrac{4}{10}\), упростите только дробную часть. Запишите числитель и знаменатель дробной части в разложенном виде и сократите общие множители.

4/10 = (2 × 2)/(2 × 5) = 2/5

Следовательно, смешанная дробь \(3\dfrac{4}{10}\) может быть упрощена как \(3\dfrac {2}{5}\).

Упрощение неправильных дробей

Неправильными дробями считаются те, у которых числитель больше или равен знаменателю. Чтобы упростить неправильные дроби, нам нужно преобразовать их в смешанные дроби, а для этого нам нужно разделить числитель на знаменатель. Затем мы записываем его в форме смешанного числа, помещая частное как целое число, остаток как числитель, а делитель как знаменатель. Давайте рассмотрим следующий пример, чтобы лучше понять это.

Например, чтобы упростить неправильную дробь 11/4, нам нужно разделить 11 на 4 и получить значения частного и остатка после выполнения деления. Когда мы делим 11/4, мы получаем 2 как частное и 3 как остаток. Следовательно, упрощенная форма неправильной дроби 11/4 — это \(2\dfrac{3}{4}\).

Статьи по теме

Ознакомьтесь с интересными статьями, посвященными упрощению дробей.

Сокращение дробей
Калькулятор простых дробей
Рабочие листы по сокращению дробей

Часто задаваемые вопросы об упрощении дробей

Что означает упрощение дробей?

Упрощение дробей означает сокращение дроби в ее низшей форме. Это помогает нам легко выполнять вычисления с использованием дробей. Например, проще сложить 1/2 и 1/2, чем 2/4 + 4/8.

Каково правило упрощения дробей?

Правило упрощения дробей состоит в том, чтобы сокращать общие множители в числителе и знаменателе данной дроби. Другими словами, мы должны убедиться, что числитель и знаменатель должны быть взаимно простыми числами.

Каковы этапы упрощения дробей?

Выполните указанные ниже действия, чтобы привести дробь к простейшей форме:

Найдите наибольший общий делитель числителя и знаменателя.
Разделите числитель и знаменатель на наибольший общий множитель.

Фракция, полученная таким образом, имеет простейшую форму.

Как упростить большие дроби?

Большие дроби можно упростить, разделив числитель и знаменатель на общие простые множители, чтобы привести их к простейшему виду.

Как учить упрощать дроби?

Упрощающие дроби обычно используются в 5 или 6 классе. Чтобы научить упрощающим дробям, следуйте приведенным ниже пунктам:

Позвольте учащимся выполнять практические задания, включая модели прямоугольных и круглых дробей, чтобы понять, что 2/4 равно 1/2.
Используйте реальные примеры упрощения дробей.
Используйте рабочие листы для упрощения дробей.

Как объяснить упрощение дробей?

Говорят, что дробь имеет простейшую форму, если нет общего делителя числителя и знаменателя, отличного от 1. Например, 11/23 является упрощенной дробью, так как 11 и 23 не имеют общих делителей.

Как преобразовать неправильную дробь в упрощенную форму?

Разделите числитель на знаменатель, чтобы получить частное и остаток. Тогда смешанная или упрощенная дробь может быть записана как \(\text{Частное}\dfrac{\text{Остаток}}{\text{Делитель}}\).

Как дроби приводятся к упрощенной форме?

Чтобы привести дробь к простейшей форме, разделите числитель и знаменатель на их наибольший общий множитель.

Как проще всего упростить дроби?

Один из самых быстрых способов привести дробь к простейшему виду — это разделить числитель и знаменатель дроби на их наибольший общий делитель.

Как сократить дроби? Методы, примеры

Важный шаг, который мы делаем, решая дроби, — это приведение их к простейшей форме. Хоть мы и уменьшаем их для упрощения, значение дроби остается неизменным. Уменьшенная дробь эквивалентна исходной дроби. Фактически исходная дробь и уменьшенные дроби образуют пару эквивалентных дробей. В этом уроке мы научимся сокращать дроби тремя разными способами.

1.	Как сократить дроби?
3.	Методы сокращения дробей
4.	Дроби в числовой строке
5.	Как сократить дроби с переменными?
6.	Часто задаваемые вопросы о сокращении дробей

Как сократить дроби?

Сокращение дробей означает упрощение дроби, при котором мы делим числитель и знаменатель на общий делитель до тех пор, пока общий делитель не станет равным 1. Другими словами, дробь больше нельзя разделить на одно и то же целое число, отличное от 1. Например, рассмотрим дробь 8/24. Вот пошаговый процесс уменьшения дроби.

Шаг 1: Запишите множители числителя и знаменателя. Делители 8 равны 1, 2, 4 и 8, а множители 24 равны 1, 2, 3, 4, 6, 8, 12 и 24
Шаг 2: Определите общие делители числителя и знаменателя. Общие делители чисел 8 и 24 равны 1, 2, 4 и 8
Шаг 3: Разделите числитель и знаменатель на общие делители, пока у них не будет общего делителя, кроме 1. Полученная таким образом дробь имеет сокращенную форму.

Начнем делить на 2: (8 ÷ 2) / (24 ÷ 2) = 4/12. Мы будем продолжать делить на 2, пока не сможем двигаться дальше. Итак, имеем (4 ÷ 2) / (12 ÷ 2) = 2/6 = (2 ÷ 2) / (6 ÷ 2) = 1/3. Следовательно, сокращенная форма 8/24 равна 1/3

Возьмем другой пример.

Пример: Уменьшите дробь, 10/20. Найдем общий делитель числителя и знаменателя. Повторяйте процесс до тех пор, пока не останется общих факторов. 5 является общим делителем как 10, так и 20. Разделив числитель и знаменатель на 5, мы получим 10/20 = (10 ÷ 5) / (20 ÷ 5) = 2/4. Дробь уменьшается до 2/4 на первом шаге. Теперь 2 — это общий множитель 2 и 4. Уменьшая дробь дальше, (2 ÷ 2) / (4 ÷ 2) = 1/2. Следовательно, сокращенная форма 10/20 равна 1/2.

Давайте посмотрим на рисунок, приведенный ниже. Первый круг имеет 2 заштрихованные части из 8 полных частей, тогда как второй круг имеет только одну заштрихованную часть из 4 полных частей. Следует отметить, что заштрихованная часть одинакова в обоих кругах. Таким образом, мы можем сделать вывод, что 2 равные части из 8 равных частей равны 1 равной части из 4 равных частей.

Методы сокращения дробей

Сократить дробь означает максимально упростить дробь. Чтобы найти редуцированные формы дробей, мы просто упростим дробь до ее наименьшей формы. Давайте рассмотрим три простых метода сокращения дробей.

Метод эквивалентных дробей

Эквивалентные дроби имеют одинаковое значение независимо от их числителей и знаменателей. Ниже приведены шаги по уменьшению дробей методом эквивалентных дробей.

Шаг 1: Найдите любой общий множитель числителя и знаменателя.
Шаг 2: Разделите числитель и знаменатель на общий множитель.
Шаг 3: Повторяйте тот же шаг в полученной дроби до тех пор, пока не останется общих делителей, отличных от 1.

Метод GCF

GCF (наибольший общий делитель) двух или более чисел — это наибольшее число среди всех общих делителей данных чисел. Ниже приведены шаги по уменьшению фракций методом GCF.

Шаг 1: Найдите наибольший общий делитель (НОД) числителя и знаменателя.
Шаг 2: Разделите числитель и знаменатель на GCF. Полученная таким образом фракция является восстановленной фракцией.

Метод факторизации простых чисел

Факторизация простых чисел — это способ представления числа в виде произведения его простых множителей. Ниже приведены шаги по уменьшению дробей методом простой факторизации.

Шаг 1: Найдите разложение числителя и знаменателя на простые множители.
Шаг 2: Сократите общие делители числителя и знаменателя.
Шаг 3: Уберите оставшиеся числа в числителе и знаменателе, чтобы найти уменьшенную дробь.

Дроби в числовой строке

Мы уже знаем, как представлять целые числа на числовой прямой. Мы также можем показать дроби на числовой прямой и определить эквивалентные дроби на числовой прямой с помощью следующего примера и шагов.

Шаг 1: Нарисуйте 6 линий, на концах которых отмечены два целых числа.
Шаг 2: Разделите каждую числовую строку на равные части, как показано на рисунке. Например, начиная с первой числовой строки, мы видим, что она разделена на две равные части и деление отмечено дробью 1/2. Точно так же вторая числовая строка делится на три равные части, а деления отмечены дробями 1/3 и 2/3. Точно так же для всех числовых строк деления отмечены дробями.
Шаг 3: После этого шага мы можем легко идентифицировать эквивалентные дроби, проверяя их длину от нуля. Например, мы можем идентифицировать дроби 1/2, 2/4, 3/6 и 4/8 как эквивалентные дроби, потому что, если мы посмотрим на их длину (расстояние) от 0, мы обнаружим, что они имеют одинаковую длину. Точно так же 1/3 и 2/6 являются эквивалентными дробями, потому что они представляют одинаковое расстояние на числовой прямой.
Шаг 4: Таким образом, с помощью этого метода можно легко отметить и идентифицировать эквивалентные дроби на числовой прямой.

Как сократить дроби с переменными?

Переменные — это такие буквы, как a, b, c, x, y, z и т. д., которые появляются в математическом выражении и представляют неизвестные значения. Дроби могут иметь переменные вместе с числами. Чтобы сократить дробь с переменными, выполните шаги, указанные ниже:

Шаг 1: Сгруппируйте одинаковые члены вместе. Например, в дроби (8а — а + 2а)/(12а). Сгруппируем подобные члены a. Упрощая числитель, получаем 9.а. Дробь теперь уменьшается до 9a/12a
Шаг 2: Найдите общие множители и сократите их. 9а / 12а = (3 × 3 × а) / (3 × 4 × а). Отменив общие множители и упростив, получим дробь, уменьшенную до 3/4

Советы и рекомендации по сокращению дробей

Итак, теперь вы знаете три способа приведения дроби к ее простейшей форме. Вот несколько приемов, которые помогут вам быстро сократить дроби. Следуйте этим советам и рекомендациям, сводя дроби к их простейшей форме.

Если числитель или знаменатель дроби является простым числом, то дальнейшее упрощение дроби невозможно.
Дробь, в числителе которой 1, не может быть сокращена дальше.
Чтобы уменьшить неправильную дробь, сначала запишите ее как смешанную дробь и следуйте тому же методу упрощения правильной дроби.

Темы, связанные с сокращением дробей

Дроби
Эквивалентные дроби
Сложение и вычитание дробей
Сравнение дробей
Упрощение дробей
Делитель
Наибольший общий делитель
Длинная дивизия
Неправильные дроби

Сокращение дробей Примеры

Пример 1: Сократите следующие фракции методом GCF. а) 16/64, б) 18/81
Решение: Мы будем использовать метод GCF для сокращения дробей.
а) Наибольший общий делитель 16 и 64 равен 16. Разделив числитель и знаменатель на 16, получим дробь, уменьшенную до 1/4. 16/64 = (16 ÷ 16) / (64 ÷ 16) = 1/4. Следовательно, сокращенная форма 16/64 равна 1/4
б) Наибольший общий делитель 18 и 81 равен 9. Разделив числитель и знаменатель на 9, получим дробь, уменьшенную до 2/9. 18/81 = (18 ÷ 9) / (81 ÷ 9) = 2/9. Следовательно, сокращенная форма 18/81 равна 2/9.
Пример 2. Сократите следующие дроби методом простой факторизации. а) 3/15, б) 20/60
Решение: Для сведения дробей методом простой факторизации находим простые множители числителя и знаменателя.
а) Найдем простую факторизацию чисел 3 и 15. Первичную факторизацию 3 = 3 и простую факторизацию 15 = 3 × 5. Сократив общие делители, мы получим 1/5. Следовательно, сокращенная форма 3/15 равна 1/5
б) Давайте найдем разложение чисел 20 и 60 на простые множители. Разложение 20 на простые множители = 2 × 2 × 5 и разложение на простые множители 60 = 2 × 2 × 3 × 5. Сократив общие делители, мы получим 1/3. Следовательно, сокращенная форма 20/60 равна 1/3
.
Пример 3. Сократите дробь (x ² + 5x + 6) / (x+3) ²
Решение: Чтобы сократить дроби с переменными в вопросе, мы разложим выражения на множители даны в числителе и знаменателе.
Числитель x ² + 5x + 6 можно разложить как x ² + 5x + 6 = (x + 2) (x + 3). Теперь (х ² + 5х + 6) / (х+3) ² = (х + 2) (х + 3) / (х+3) ² . Сокращая общие множители, мы получаем (x + 2) / (x + 3). Следовательно, сокращенная форма дроби (x ² + 5x + 6) / (x+3) ² равна (x + 2) / (x + 3)
.

перейти к слайдуперейти к слайдуперейти к слайду

Помогите ребенку наглядно представить, как работают числа!

Наша методология основана на визуальном обучении. Почувствуйте разницу, которую создают более 5000 визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о сокращении дробей

Как сократить большие дроби?

Для сокращения больших дробей разделим числитель и знаменатель крупной дроби на простые простые множители, чтобы привести ее к простейшему виду. Еще один простой способ сократить большие дроби — разделить числитель и знаменатель на их GCF. Это делает расчет быстрее и проще.

Как сократить смешанные дроби?

Смешанные дроби можно сократить после преобразования в неправильную дробь. Это можно сделать, используя формулу: \(\dfrac{(\text{Whole}\times\text{Знаменатель})+\text{Числитель}}{\text{Знаменатель}}\). После преобразования смешанной дроби в неправильную дробь ее можно при необходимости сократить. Например, \(5\dfrac{3}{7}=\dfrac{(5\times 7)+3}{7}=\dfrac{38}{7}\). Другой способ сокращения смешанных дробей состоит в том, чтобы разделить целое число и сократить только дробную часть смешанной дроби. Например, чтобы уменьшить \(3\dfrac{4}{8}\), мы сохраним 3 отдельно и уменьшим 4/8 до 1/2, так что окончательная уменьшенная дробь будет \(3\dfrac{1}{ 2}\)

Почему GCF используется в сокращении дробей?

При сокращении дробей мы используем НОД для деления числителя и знаменателя, потому что НОД (наибольший общий множитель) — это наибольшее число, которое делит числитель и знаменатель, поэтому дроби становится легче сокращать. Другие общие множители числителя и знаменателя меньше, и поэтому для уменьшения дроби требуется больше времени и действий. Например, сократим дробь: 12/18. GCF 12 и 18 равен 6. Таким образом, мы можем использовать 6, чтобы разделить числитель и знаменатель всего за один шаг. (12 ÷ 6)/(18 ÷ 6) = 2/3

Как дроби приводятся к наименьшему виду?

Чтобы привести дробь к простейшей форме, разделите числитель и знаменатель на наибольший общий множитель. Например, уменьшим 16/64. Наибольший общий множитель 16 и 64 равен 16. Итак, разделим числитель и знаменатель на 16. (16 ÷ 16) / (64 ÷ 16) = 1/4. Следовательно, сокращенная форма 16/64 равна 1/4.

Как сократить дроби?

Для приведения дроби к простейшей форме используются следующие шаги:

Найдите наибольший общий делитель числителя и знаменателя.
Разделите числитель и знаменатель на наибольший общий множитель. Полученная таким образом фракция имеет простейшую форму.

Как проще всего сократить дробь?

Один из самых простых способов привести дробь к простейшей форме — это разделить числитель и знаменатель дроби на их наибольший общий множитель (НОД).

Как сокращать дроби с возведением в степень?

Чтобы сократить дроби с показателями степени, примените правила степени к числителю и знаменателю. Например, (a/b) ⁿ = a ⁿ /b ⁿ , где «a» и «b» — числитель и знаменатель соответственно, а «n» — показатель степени дроби. После вычисления дроби с использованием правил экспоненты приведите дробь к простейшей форме. Например, уменьшим (2/4) ³ . Это можно сократить и записать как (1/2) ³, а затем, используя правила экспоненты, это можно записать как 1 ³ /2 ³ = 1/8.

Что такое неправильная дробь?

Дробь, у которой числитель больше знаменателя, называется неправильной дробью. Например, 7/4

Как преобразовать неправильную дробь в смешанную дробь?

Чтобы преобразовать неправильную дробь в смешанное число, нужно разделить числитель на знаменатель. Затем мы записываем частное как целое число, остаток как новый числитель, а знаменатель остается прежним. Например, чтобы преобразовать 26/7 в смешанную дробь, мы разделим 26 на 7. Это даст 3 в качестве частного и 5 в остатке. Итак, смешанная дробь будет \(3\dfrac{5}{7}\)

Загрузить БЕСПЛАТНЫЕ учебные материалы

Рабочий лист по дробям

Упрощение калькулятора фракций (уменьшение дроби)

Автор Wojciech Sas, PhD содержание:

Как сократить дроби?
Приведение дробей к наименьшим
Как упростить неправильные дроби?
Как пользоваться калькулятором упрощенных дробей? Упрощение дробей на практике

Вот он — калькулятор упрощенных дробей (также калькулятор уменьшенных дробей или упроститель дробей), полезный инструмент, который поможет вам сократить дроби .

Вы когда-нибудь спрашивали себя « Как упростить дроби? » или « Как сократить дроби до меньших членов? » и не знали ответа? Если да — это идеальное место для вас, чтобы начать и узнать что-то новое!

Как сократить дроби?

Прежде чем мы получим ответ о том, как упростить дроби, давайте начнем с основ. Что такое дробь?

Дробь – это отношение двух чисел, числителя и знаменателя. With this definition in mind, we can see that ¹ / ₂ is a fraction, ¹⁰ / ₁₂ is a fraction, ^3.3 / _6.2 is a fraction, and скоро. Как правило, мы используем целые числа в дробях , поскольку они более интуитивно понятны и просты в использовании, особенно при сложении или вычитании дробей.

Кроме того, вы можете преобразовать любое десятичное значение в дробь.

В отличие от отношений, дроби должны иметь одинаковую единицу измерения в числителе и знаменателе. Обратитесь к нашему калькулятору коэффициентов для получения более подробной информации об этом.

Теперь самое время спросить себя: « Как упростить дроби? », например, ⁴ / ₈ . Решение состоит в том, чтобы найти общий делитель обоих чисел и разделить их на это значение 9.0755 . 2 является одним из общих множителей, поэтому:

4 разделить на 2 равно 2 .
8 разделить на 2 будет 4 .
В итоге продолжаем сокращая дробь ⁴ / ₈ до ² / ₄ .

Другими словами, мы можем сказать, что ⁴ / ₈ и ² / ₄ — эквивалентные дроби.

Хотя результат правильный, мы обычно хотим привести дробь к ее простейшей форме в такого рода вычислениях. Вопрос: Какова простейшая форма дроби?

Приведение дробей к наименьшему члену

Приведение дроби к ее простейшей форме (или к наименьшему члену) почти не отличается от процедуры, описанной в предыдущем разделе. Самое существенное отличие состоит в том, что нам нужно разделить и числитель и знаменатель на наибольший общий множитель (НОД) . Давайте посмотрим на тот же пример, ⁴ / ₈ :

.
4 разделить на 4 будет 1 .
8 разделить на 4 будет 2 .
⁴ / ₈ в простейшей форме ¹ / ₂ .
Вы всегда можете преобразовать дробь в десятичную, в данном случае 0,5 .

А какая простейшая форма дроби с отрицательными числами, например, ^-4 / ₆ ? Это совсем не сложно! Единственное, что вам нужно знать, это то, что отрицательные числовые множители такие же, как и положительные, умноженные на -1 .

В результате мы можем уменьшить дробь ^-4 / ₆ до ^-2 / ₃ .

Кстати, знаете ли вы, что в реальной жизни используются и другие полезные методы, например преобразование дюймов в дроби? Если нет — проверь!

Как упростить неправильную дробь?

Неправильная дробь — это дробь, у которой числитель больше знаменателя (точнее, их абсолютные значения подчиняются этому правилу). Как правило, они представляют числа больше единицы. Также можно любую неправильную дробь записать в виде смешанного числа — целое число с правильной дробью.

Хорошо, что в нашем калькуляторе дробей можно использовать как неправильные дроби, так и смешанные числа.

Итак, есть ли что-то сложное в приведении неправильных дробей к их наименьшему члену? Посмотрите на примере, как упростить неправильную дробь. Дробь, которую мы будем рассматривать, равна ¹¹⁷ / ₅₂ : 9. 0003

Найдите все множители обоих чисел. Мы можем использовать простой метод факторизации:
- Коэффициенты 117 равны 3, 3, 13 ; и
- Коэффициенты 52 равны 2, 2, 13
Наибольший общий делитель чисел 117 и 52 равен 13 .
Разделите оба числа на 13 . 117/13 = 9 и 52/13 = 4 .
¹¹⁷ / ₅₂ в простейшем виде: ⁹ / ₄ .
Мы также можем записать это как смешанное число: 2 ¹ / ₄ .
Если вы еще не удовлетворены, вы всегда можете преобразовать дробь в проценты. В нашем случае 2 ¹ / ₄ равно 225% .

Легкая штука, не так ли?

Как пользоваться калькулятором упрощенных дробей? Упрощение дробей на практике

Представьте, что вы отлично проводите время на вечеринке с парой друзей. Внезапно вы решаете сойти с ума и заказать пиццу. После бурного обсуждения вы разделились на две команды: любителей гавайских и хот-догов.

Вы покупаете две очень большие пиццы одинакового размера, но разной формы. Это еще не все, гавайский делится на 16 , а корж с начинкой для хот-догов делится на 24 шт. В итоге гавайская команда съела четырнадцать, а Хот-дог сожрал пятнадцать порций.

Так кто же победитель? Визуально оценить не просто, так как детали бывают разных форм и размеров . Но давайте попробуем узнать ответ с помощью нашего калькулятора упрощенных дробей:

Мы можем записать счет команды А в виде дроби A = ¹⁴ / ₁₆ .
То же для команды B B = ¹⁵ / ₂₄ .
Чтобы сравнить эти результаты, мы продолжаем приводить дроби к наименьшим терминам.
Результат команды А в простейшей форме равен A = ⁷ / ₈ .
Результат команды Б в простейшей форме равен В = ⁵ / ₈ .

Как видите, на этот раз команда с начинкой из хот-догов выиграла с небольшим преимуществом! Team Hawaiian — удачи в следующий раз (или просто выберите настоящую начинку для пиццы).

Wojciech SAS, кандидат в PhD

моя фракция состоит из

Числовой (n)

DENMINATOR (D)

Проверьте 17 аналогичных фракций. Факторы: значение, примеры и правила

Мы знаем, что натуральные и целые числа также можно называть целыми числами. Предположим, вы делите плитку шоколада на две равные части или половинки, как тогда вы представляете значение в числовом виде? Этот тип числа, дробь, также является основным типом числа, который мы используем в математике.

Мы можем использовать множители, чтобы упростить дроби до их простейшей формы. В этой статье рассматриваются ключевые концепции дробей и множителей, а также некоторые приложения.

Значение дробей и множителей: Введение

Начнем с определения и введения понятий дробей и множителей.

Компоненты дроби: числитель и знаменатель

Начнем с определения дроби.

Числовое значение, представляющее часть любого целого значения или вещи, известно как дробь . Дроби известны как рациональные числа (по теории множеств). В математике мы говорим, что рациональные числа находятся в наборе

Дроби могут быть представлены как , где a известны как числитель, а b известны как знаменатель. По сути, числитель делится на знаменатель.

Давайте попробуем увидеть это с более наглядной точки зрения. Представьте, что 1 пицца состоит из 8 кусочков.

Пицца с 8 кусочками, pixabay.com

Если я возьму 1 кусок пиццы, я возьму пиццу. Это потому, что у нас есть 1 пицца, и мы разделили ее на 8 кусков. Итак, мы видим, что единственный кусок пиццы (1) — это числитель, а общее количество кусочков (8) — знаменатель.

Дробь также можно рассматривать как деление числителя на знаменатель. Давайте посмотрим на пример, чтобы увидеть это в действии.

У меня есть пирог с 8 кусочками. Я хочу разделить его поровну между 4 людьми. Какую часть пирога получит каждый?

Решение:

В пироге 8 кусков, и мы хотим разделить его поровну между 4 людьми. Таким образом, мы вычисляем, что Это означает, что каждый человек получает 2 куска пирога.

Если каждый получает по 2 кусочка, значит, он получает часть пирога. Это количество кусочков, которые получает каждый человек (2), деленное на общее количество кусочков пирога (8), при этом числитель делится на знаменатель.

Использование коэффициентов для целых чисел

Целые числа также известны как целые числа. В математике они представлены как Все целые числа содержат f актеров .

Факторы целого числа — это числа, которые делятся точно на это целое число.

Это означает, что если вы выполните деление в длину, разделив целое число на его множитель, вы не найдете остатка.

Например, 10 можно разделить на 2, чтобы получить 5, что означает, что 2 является коэффициентом 10. Точно так же 10 можно разделить на 5, чтобы получить 2, что означает, что 5 также является коэффициентом 10. Итак, 2 и 5 — пара множителей 10.

Все целые числа делятся на 1, поэтому 1 является делителем всех целых чисел. Само целое число всегда также является фактором само по себе, например, когда вы делите число само на себя, вы получаете 1. Поскольку этот процесс не оставляет остатка, мы знаем, что число является фактором само по себе.

Все целые числа делятся на 1 и на себя, поэтому имеют как минимум два делителя. Целые числа, которые делятся только на 1 и сами по себе, называются простыми числами.

Единственным исключением из того факта, что все целые числа имеют по крайней мере два делителя, является число 1. Число 1 не считается простым числом, поскольку оно делится на 1 и само на себя, но поскольку 1 является самим собой, оно является только число, содержащее один фактор.

Давайте рассмотрим небольшой пример.

Перечислите все делители числа 24.

Решение:

Итак, на сколько чисел делится 24? У нас есть:

Кроме чисел 1, 2, 3, 4, 6, 8, 12 и 24, все остальные числа при делении на 24 не возвращают целых чисел. Это означает, что наши множители равны 1, 2, 3, 4, 6, 8, 12 и 24.

Факторы

Теперь, когда мы поняли основные идеи и понятия, лежащие в основе дробей и множителей, давайте более подробно рассмотрим факторы в частности. . Понимание факторов поможет нам позже, когда мы будем изучать методы упрощения дробей до их простейших и наименьших форм.

Что такое разложение на простой множитель?

A Разложение на простые множители просто анализирует целое число как произведение простых множителей. Другими словами, мы определяем все простые множители, которые при умножении дают заданное целое число.

Простой множитель — это просто множитель целого числа, которое также является простым числом. Мы можем найти разложение на простые множители, нарисовав дерево факторов . Факторное дерево показывает нам, как именно мы можем разбить целое число на его множители, а затем разбить эти множители, пока в конечном итоге не получим простые множители.

Давайте посмотрим на наглядный пример.

Нарисуйте дерево множителей для числа 100 и запишите разложение числа 100 на простой множитель.

Теперь мы можем перестать разбивать 2 на множители, так как это простой множитель, а это значит, что его можно разделить только на 1 и на себя. Однако 50 не простое число; поэтому мы должны разбить его дальше. Мы можем разбить 50 на . Мы можем добавить это к нашему факторному дереву следующим образом:

Простые множители 50, StudySmarter Originals

Опять же, 2 — это простое число, поэтому мы не будем далее разбирать это. Однако мы можем разбить 25 дальше на . И мы можем добавить его к нашему факторному дереву следующим образом:

Факторное дерево для 100, StudySmarter Originals

Теперь, поскольку 5 — простое число, мы можем остановиться на этом, так как мы не можем дальше разбивать ни одно из этих чисел. Это означает, что мы закончили рисовать наше дерево факторов!

При написании разложения на простые множители мы можем обвести все факторы, которые мы определили как простые, для удобства.

Простые числа, обведенные кружком после разложения, StudySmarter Originals

Когда эти числа умножаются друг на друга, они дают нам 100, поэтому наше разложение на простые множители равно

Мы можем сделать это более красивым, используя индексы: .

Какой самый высокий общий делитель?

Наибольший общий делитель (наибольший общий делитель) — это то, что мы можем найти, используя метод разложения на простые множители двух или более различных чисел. Наибольший общий делитель — это число, являющееся делителем всех рассматриваемых чисел. В частности, это самый большой из возможных.

Для этого есть способ, который мы рассмотрим на примере.

Найдите наибольший общий делитель 100 и 120.

Решение:

9170 Найдите разложение обоих простых чисел.

ШАГ	ПРИМЕР
Разложение числа 100 на простые множители, которое мы знаем из приведенного выше. Если мы воспользуемся деревом множителей, чтобы найти разложение числа 120 на простые множители, мы получим следующее: Факторное дерево числа 120, StudySmarter Originals Таким образом, наше разложение числа 120 на простой фактор равно
1).
ШАГ 3: Если в одном из чисел отсутствует множитель из разложения другого числа на простое число, запишите этот отсутствующий множитель в разложении на простой множитель в степени 0.	100 отсутствует 3, поэтому мы поставить 3 в степени 0:
ШАГ 4: Сравните одинаковые базовые числа и выберите число с наименьшей степенью.	Между и , выберите Между и , выберите Между и , выберите
ШАГ 5: Перемножьте эти выбранные числа.	, поэтому наш наибольший общий делитель равен 20.

Дроби

Мы узнали, что дроби состоят из числителей сверху и знаменателей снизу. Дроби имеют целые значения как в числителе, так и в знаменателе, но знаменатель не должен быть равен нулю. Когда дробь имеет одинаковые множители в числителе и знаменателе, мы можем упростить форму дроби.

Сравнение дробей и множителей: как мы можем использовать множители для упрощения дробей?

Когда мы определяем, что дробь можно упростить, это означает, что мы можем разделить числитель и знаменатель на одно и то же число, чтобы получить более простую или меньшую дробь. Это можно сделать только в том случае, если и числитель, и знаменатель имеют общий множитель.

Если мы взяли наш предыдущий ответ , то и 2, и 8 делят множитель 2. Следовательно, если мы разделим и 2, и 8 на 2, мы получим Следовательно, мы можем упростить нашу дробь до .

Иногда в экзаменационных вопросах вас могут попросить дать ответ в самой простой форме. Это означает, что вы должны упростить дробь, прежде чем давать ответ. Давайте посмотрим на примеры.

Упростить

Решение:

Сначала нам нужно подумать о множителе, который делит числа 56 и 96. Они оба делят 8 как множитель. Поэтому нам нужно просто разделить каждую из них (и числитель, и знаменатель) на 8.

Это означает, что наша новая упрощенная дробь равна

Упростить

Решение: Здесь 5 и 65 делят 5 как множитель. Итак, мы делим и числитель, и знаменатель на 5.

Следовательно, упрощенная дробь равна

Дроби и множители важны в различных прикладных ситуациях. Изучая другие темы, мы часто обнаруживаем, что нам, возможно, придется определять общий множитель или упрощать дробь как часть решения нашей проблемы.

Правила работы с дробями

Существуют определенные правила, которые применяются при использовании основных математических операций с дробями. Мы увидим правила в дробях для следующих операций:

Сложение и вычитание
Умножение
Деление

Сложение и вычитание

Типы дробей Нам нужно проверить, совпадают или различны знаменатели данных дробей. Давайте посмотрим, как выполнить сложение или вычитание, если знаменатель равен для всех дробей.

Сложите/вычтите числители и оставьте знаменатель без изменений.
Если возможно, сократите дробь.

Где a, b и c — целые числа.

Если знаменатели не совпадают с , необходимо выполнить следующие шаги.

Сделайте знаменатели всех дробей одинаковыми. Для этого можно умножить числитель и знаменатель одной дроби на знаменатель другой дроби и наоборот.
Сделав знаменатель одинаковым, сложите/вычтите числители, не изменяя знаменатель.
Просто дробь, если это возможно.

Умножение

При умножении дробей знаменатели могут не совпадать, в отличие от сложения/вычитания. Вместо этого просто умножьте числители друг на друга и умножьте друг на друга знаменатели. Затем приведите дробь к упрощенной форме. Помните, что дроби, как правило, не должны быть смешанными дробями. Если это смешанная дробь, то сначала преобразуйте ее в правильную или неправильную дробь.

Деление

При делении дробей мы преобразуем их в форму умножения, чтобы найти ответ. Итак, чтобы преобразовать его в форму умножения, инвертируйте вторую дробь (то есть поменяйте местами числитель и знаменатель) и измените знак деления на знак умножения. Теперь вы можете выполнять шаги умножения как обычно.

Пример дробей и множителей

Давайте посмотрим несколько решенных примеров для дробей и множителей.

Найти самый высокий общий фактор (HCF) 48, 108 и 140.

Решение:

Шаг	Пример
. числа.	Разложение числа 48 на простые множители с использованием дерева множителей: Дерево множителей 48, StudySmarter Originals Аналогично, разложение числа 140 на простые множители:
ШАГ 2: Запишите все три числа в степенной записи.
ШАГ 3: Запишите пропущенное число множителя из разложения простых чисел других чисел в степень 0. самая низкая мощность.	From , выберите From , выберите From , выберите From , выберите
ШАГ 5: Умножьте выбранные числа.	Итак, HCF (или НОД) равен 4 для данных трех чисел.

Подруга Хейли живет в 25 милях от ее дома. Она уже прошла 11 миль. Представьте пройденное расстояние дробью.

Решение: Общее расстояние от дома Хейли до дома ее подруги составляет 25 миль. Итак, знаменатель будет равен 25.

Хейли проехала 11 миль. Значит, в числителе будет 11.

Следовательно, пройденное расстояние будет дробями

Решите следующие дроби.

Решение:

Для и обе дроби имеют одинаковые знаменатели. Итак, мы можем провести сложение, не меняя знаменатель. Здесь мы добавим числитель и сохраним знаменатель как есть.

Разложение на простые множители / Обыкновенные дроби / Справочник по математике 5-9 класс

Советуем посмотреть:

Правило встречается в следующих упражнениях:

Mathway | Популярные задачи

Интегрирование рациональных функций

Алгоритм интегрирования рациональных функций

Интегрирование рациональных дробей с помощью разложения на простейшие дроби — КиберПедия

18. Интегрирование рациональных дробей и некоторых иррациональных функций

«Разложение дроби на простейшие», Математика, химия, физика

Как разложить многочлены на множители с дробями

Определение многочленов с дробями

Основы факторинга – распределительное свойство и метод FOIL

Действия при разложении полиномиальных дробей на множители

Переставьте числитель

Сокращение простых и сложных дробей с помощью пошагового решения математических задач

ПРОИЗВЕДЕНИЕ ДРОБЕЙ

СУММЫ ДРОБЕЙ С РАЗЛИЧНЫМИ ЗНАМЕНАТЕЛЯМИ

РАЗНОСТИ ДРОБЕЙ С РАЗЛИЧНЫМИ ЗНАМЕНАТЕЛЯМИ

СЛОЖНЫЕ Дроби

УРАВНЕНИЯ Дробей

ПРИЛОЖЕНИЯ

ОТНОШЕНИЕ И ПРОПОРЦИЯ

РЕЗЮМЕ ГЛАВЫ

Упрощение дробей — Примеры | Как упростить дроби?

Как упростить дроби?

Упрощение дробей шаг за шагом

Упрощение дробей с переменными

Упрощение дробей с показателями

Упрощение смешанных дробей

Упрощение неправильных дробей

Часто задаваемые вопросы об упрощении дробей

Что означает упрощение дробей?

Каково правило упрощения дробей?

Каковы этапы упрощения дробей?

Как упростить большие дроби?

Как учить упрощать дроби?

Как объяснить упрощение дробей?

Как преобразовать неправильную дробь в упрощенную форму?

Как дроби приводятся к упрощенной форме?

Как проще всего упростить дроби?

Как сократить дроби? Методы, примеры

Как сократить дроби?

Методы сокращения дробей

Метод эквивалентных дробей

Метод GCF

Метод факторизации простых чисел

Дроби в числовой строке

Как сократить дроби с переменными?

Советы и рекомендации по сокращению дробей

Сокращение дробей Примеры

Практические вопросы

Часто задаваемые вопросы о сокращении дробей

Как сократить большие дроби?

Как сократить смешанные дроби?

Почему GCF используется в сокращении дробей?

Как дроби приводятся к наименьшему виду?

Как сократить дроби?

Как проще всего сократить дробь?

Как сокращать дроби с возведением в степень?

Что такое неправильная дробь?

Как преобразовать неправильную дробь в смешанную дробь?

Упрощение калькулятора фракций (уменьшение дроби)

Как сократить дроби?

Приведение дробей к наименьшему члену

Как упростить неправильную дробь?

Как пользоваться калькулятором упрощенных дробей? Упрощение дробей на практике

Значение дробей и множителей: Введение

Компоненты дроби: числитель и знаменатель

Использование коэффициентов для целых чисел

Факторы

Что такое разложение на простой множитель?

Какой самый высокий общий делитель?

Дроби

Сравнение дробей и множителей: как мы можем использовать множители для упрощения дробей?

Правила работы с дробями

Сложение и вычитание

Умножение

Деление

Пример дробей и множителей

Добавить комментарий Отменить ответ