LU- и QR-разложения MatLab
Урок 11. Матричные операции линейной алгебры
Вычисление
нормы и чисел обусловленности матрицы
Определитель
и ранг матрицы
Определение нормы вектора
Определение ортонормированного базиса матрицы
Функции
приведения матрицы к треугольной форме
Определение
угла между двумя подпространствами
Вычисление следа
матрицы
Разложение Холецкого
Обращение матриц — функции inv, pinv
LU- и QR-разложения
Вычисление собственных значений и сингулярных чисел
Приведение матриц к форме Шура и Хессенберга
Что нового мы узнали?
Так называемые LU- и QR-разложения реализуются следующими матричными функциями:
Функция 1и выражает любую квадратную матрицу X как произведение двух треугольных матриц, одна из которых (возможно, с перестановками) — нижняя треугольная матрица, а другая — верхняя треугольная матрица[
 — Примеч. ред.
]. Иногда
эту операцию называют
LR-разложением.
Для выполнения этой операции служит
следующая функция:
— Примеч. ред.
]. Иногда
эту операцию называют
LR-разложением.
Для выполнения этой операции служит
следующая функция:
[L,U] = lu(X) — возвращает верхнюю треугольную матрицу U и психологическую нижнюю матрицу L (т. е. произведение нижней треугольной матрицы и матрицы перестановок), так что X=L*U;
[L,U,P.] = lu(X) — возвращает верхнюю треугольную матрицу U, нижнюю треугольную матрицу L и сопряженную (эрмитову) матрицу матрицы перестановок Р, так что L*U =Р*Х;
lu(Х) — вызванная с одним выходным параметром функция возвращает результат из подпрограмм DGETRF (для действительных матриц) или ZGETRF (для комплексных) известного пакета программ линейной алгебры LAPACK.
lu(X,
thresh) — где thresh в диапазоне [0. ..1] управляет центрированием в разреженных
матрицах (см. урок 12). Отдельная форма предыдущего случая. Центрирование
происходит, если элемент столбца на диагонали меньше, чем произведение thresh
и любого поддиагонального элемента. Thresh=l — значение по умолчанию. Thresh=0
задает центрирование по диагонали. Если матрица полная (не разреженная),
выводится сообщение об ошибке.
..1] управляет центрированием в разреженных
матрицах (см. урок 12). Отдельная форма предыдущего случая. Центрирование
происходит, если элемент столбца на диагонали меньше, чем произведение thresh
и любого поддиагонального элемента. Thresh=l — значение по умолчанию. Thresh=0
задает центрирование по диагонали. Если матрица полная (не разреженная),
выводится сообщение об ошибке.
Функция qr выполняет QR-разложепие
 е. (А*)»-А’. — Примеч. ред.
]
е. (А*)»-А’. — Примеч. ред.
]
[Q.R] = qr(X) — вычисляет верхнюю треугольную матрицу R того же размера, как
и у X, и унитарную матрицу Q, так что X=Q*R;[Q.R.E] = qr(X) — вычисляет матрицу перестановок Е, верхнюю треугольную матрицу R с убывающими по модулю диагональными элементами и унитарную матрицу Q, так что X*E=Q*R. Матрица перестановок Е выбрана так, что abs(diag(R)) уменьшается;
[Q.R] = qr(X.O) и [Q.R.E] = qr(X,0) — вычисляют экономное разложение, в котором Е — вектор перестановок, так что Q*R=X(: ,Е). Матрица Е выбрана так, что abs(diag(R)) уменьшается;
А = qr(X) — возвращает результат из LAPACK. Пример:
»
C=rand(5.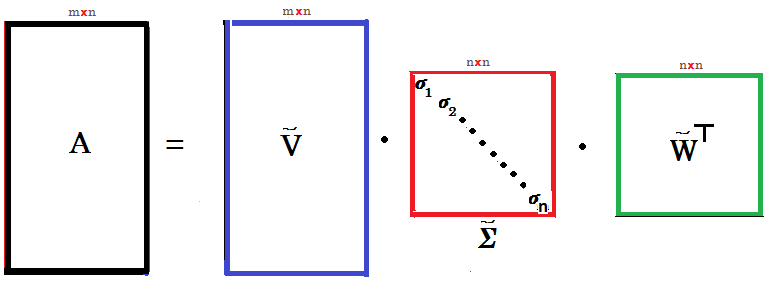 4)
4)
0.8381 0.5028 0.1934 0.6979
0.0196 0.7095 0.6822 0.3784
0.6813 0.4289 0.3028 0.8600
0.3795 0.3046 0.5417 0.8537
0.8318 0.1897 0.1509 0.5936
» [Q.R]=qr(C)
Q=
-0.5922-0.11140.5197 0.0743 -0.6011
-0.0139-0.9278 -0.0011 -0.34480.1420
-0.4814-0.11730.0699 0.5940 0.6299
-0.2681-0.1525-0.82680.2632 -0.3898
-0.58770.2997 -0.2036-0.67340.2643
R =
-1. 4152
-0.7072 -0.5037 -1.4103
4152
-0.7072 -0.5037 -1.4103
0 -0.7541 -0.7274 -0.4819
0 0 -0.3577 -0.4043
0
0 0 0.2573
0 0 0 0
[Q,R] = qrdelete(Q,R, j) — изменяет Q и RTaKHM образом, чтобы пересчитать QR-разложение матрицы А для случая, когда в ней удален j-й столбец (А(:, j )=[ ]). Входные значения Q и R представляют QR-разложение матрицы А как результат действия [Q. R]=qr(A)..Аргумент j определяет столбец, который должен быть удален из матрицы А.
» C=rand(3.3)
С =
0. 0164
0.0576 0.7176
0164
0.0576 0.7176
0.1901 0.3676 0.6927
0.5869 0.6315 0.0841
» [Q.R]=qr(C)
Q=
-0.0265-0.2416-0.9700
-0.3080-0.92120.2378
-0.95100.3051 -0.0500
R =
-0.6171-0.7153-0.3123
0 -0.1599-0.7858
0 0 -0.5356
» [Q1.R1]=qrdelete(Q.R.2)
Q1 =
-0.02650.7459 0.6655
-0. 30800.6272
-0.7153
30800.6272
-0.7153
-0.9510-0.22390.2131
R1 =
-0.6171-0.3123
0 0.9510
0 0
[Q.R] = qrinsert(Q,R,j,x) — изменяет Q и R таким образом, чтобы пересчитать разложение матрицы А для случая, когда в матрице А перед j-м столбцом вставлен столбец х. Входные значения Q и R представляют QR-разложение матрицы А как результат действия [Q,R]=qr(A). Аргумент х — вектор-столбец, который нужно вставить в матрицу А. Аргумент j определяет столбец, перед которым будет вставлен вектор х.
Примеры:
» C=rand(3.3)
С =
0. 1210
0.8928 0.8656
1210
0.8928 0.8656
0.4508 0.2731 0.2324
0.7159 0.2548 0.8049
» [Q,R]-qr(c)
Q =
-0.14160.9835 0.1126
-0.52750.0213 -0.8493
-0.8377-0.17970.5157
R =
-0.8546-0.4839-0.9194
0 0.8381 0.7116
0 0 0.3152
» x=[0.5.-0.3.0.2];[Q2.R2]=qrinsert(Q.R.2,x’)
Q2 =
-0.14160.7995 -0.5838
-0. 5275-0.5600-0.6389
5275-0.5600-0.6389
-0.83770.2174 0.5010
R2 =
-0.8546-0.0801-0.4839-0.9194
0 0.6112 0.6163 0.7369
0 0 -0.5681-0.2505
Нравится
Твитнуть
Все страницы — Юнионпедия
Все страницы — ЮнионпедияНовый! Скачать Юнионпедия на вашем Android™ устройстве!
Свободно
Более быстрый доступ, чем браузер!
Все страницы · Предыдущая (Q (бондиана)) · Следующий (Queen I)
Из:
| QR-разложение | QR-алгоритм | QR-код |
| QRIO | Qriocity | QRP |
| QRpedia | QRPp | QS Девы |
| QS-9000 | QS9000 | QSAR |
| QSAR & Combinatorial Science | QSAR (журнал) | QSAR Comb. Sci. Sci. |
| Qseven | QSFP | QSIG |
| QSL | QSL карточка | QSL-карточка |
| QsNet | QSO | QSO B0450-2958 |
| QSO B0450-299 | Qsort | QSPR |
| QSPR (револьвер) | QSS | QSS (Wi-Fi) |
| QST | QST (журнал) | Qt |
| QT | Qt (браузерный движок) | Qt Creator |
| Qt Designer | Qt Development Frameworks | Qt Extended Improved |
| Qt Jambi | Qt Software | Qt Style Sheets |
| Qt/Embedded | Qt3 | Qt4 |
| Qtcreator | QTE | QTECH |
| Qtek | Qtek 9100 | QtGUI |
| QTH-локатор | Qti | QTI |
| QtiPlot | Qtiplot | Qtopia |
| QTP | QtRuby | QtScript |
| QTV | QTV-1 | QtWebKit |
| Qu | Qu (диграф) | Qu’est-ce que c’est la vie, chaton |
| Qu’est-ce que c’est la vie, chaton? | Quaalude | Quack Shot Starring Donald Duck |
| QuackShot | Quackshot | Quad Cities |
| Quad-A | Quaderni Piacentini | Quaderni Rossi |
| QuadHD | Quadragesimo Anno | Quadrapassel |
| Quadrencyrtus | Quadrencyrtus paradoxus | Quadricasaea |
| Quadristruma | Quadristruma emmae | Quadro |
| Quadro FX | Quadro Nuevo | Quadron |
| Quadrophenia | Quadrumana | Quadruple play |
| Quadruplex | Quadtree | Quae in patriarchatu |
| Quaero | Quaester sacri palatini | Quaestiones perpetuae |
| Quaestor sacri palati | Quagga | Quagmire and Meg |
| Quagmire’s Baby | Quagmire’s Dad | Quagmire’s Mom |
| Quagmire’s Quagmire | Quagmire’s Baby | Quagmire’s Dad |
| Quagmire’s Mom | Quagmire’s Quagmire | Quake |
| Quake (серия игр) | Quake (компьютерная игра) | Quake 2 |
| Quake 2 Engine | Quake 3 | Quake 3 Arena |
| Quake 3 engine | Quake 3: Arena | Quake 4 |
| Quake 4 (компьютерная игра) | Quake Army Knife | Quake Champions |
| Quake engine | Quake II | Quake II (компьютерная игра) |
| Quake II: Ground Zero | Quake II: The Reckoning | Quake III |
| Quake III Arena | Quake III Arena (компьютерная игра) | Quake III engine |
| Quake III: Arena | Quake III: Team Arena | Quake IV |
| Quake Live | Quake Mission Pack 2: Dissolution of Eternity | Quake Mission Pack: Scourge of Armagon |
| Quake Zero | Quake3 | Quake3 engine |
| Quake: Dissolution of Eternity | Quake: Scourge of Armagon | Quake: Team Fortress |
| QuakeC | QuakeCon | Quakelive |
| QuakeLive | Quakeworld | QuakeWorld |
| Qualcomm | Qualcomm Atheros | Qualcomm code-excited linear prediction |
| Qualcomm Quick Charge | Qualcomm Snapdragon | Qualifying School |
| Qualis artifex pereo | Quality | Quality of Service |
| Quality of service | Quality-of-life index | Quality-Of-Life Index |
| Quamoclit | Quan Chi | Quan Chi (Mortal Kombat) |
| Quan tothom viurá d’amor | Quan Zhi Gao Shou | Quand les hommes vivront d’amour |
| Quand les hommes vivront d’amour | Quanera Hayes | Quanitra Hollingsworth |
| Quansah | Quant Antiqua | Quanta Computer |
| Quanta cura | Quanta Plus | Quantcast |
| Quantic Dream | Quantified self | Quantitative Structure-Activity Relationships |
| Quantos Possunt ad Satanitatem Trahunt | Quantum (класс круизных судов) | Quantum Break |
| Quantum GIS | Quantum Leap | Quantum of Solace |
| QuantX | Quanzhi Gaoshou | Quarantine |
| Quararibea cordata | Quarashi | Quaresma |
| QuArK | Quark | Quark, Strangeness and Charm |
| QuarkXPress | Quarrymen | Quarteera |
| Quarter | Quarter Video Graphics Array | Quarterly Journal of Austrian Economics |
| Quarterly Journal of Economics | Quarterstick Records | Quartet (альбом Ultravox) |
| Quartet of Cherry Blossoms in the Night | Quartet of the Evening Sakura | Quarteto em Cy |
| Quarth | Quartinia arenaria | Quartinia nubiana |
| Quartissimo | Quarto | Quartz |
| Quartz (альбом) | Quartz (группа) | Quartz (графический слой) |
| Quartz (графический уровень) | Quartz (значения) | Quartz 2D |
| Quartz Compositor | Quartz Extreme | QUASAR |
| Quasar | Quasar Technologies | Quasi-Zenith Satellite System |
| Quasimodorogas | Quasimodorogas confusus | Quasimoto |
| Quasimus | Quassel IRC | Quassia |
| Quassia amara | Quaterback | Quatiella truncata |
| Quatre Jours de Dunkerque | Quatrefages | Quatrième internationale |
| Quatrieme internationale | Quatro | Quattro |
| Quattro Fontane | Quattro GmbH | Quattro GmbH (Audi AG) |
| Quattro Pro | Quattro s1 | Quattro® |
| QuattroBass | Quattroporte | Quattroruote |
| Quatuor (яхта) | Quatuor anni tempora | Quatuor Coronati |
| Quay County, New Mexico | Quayle | Qué Hiciste |
| Quédate Conmigo | Quédate conmigo | Quél. |
| Qu’est-ce que c’est la vie, chaton? | Qubes | Qubes OS |
| QubicaAMF | Qucs | Que Dia Es Hoy |
| Que mon cœur lâche | Que mon coeur lache | Que mon coeur lâche |
| Que Sera Sera | Que Sera, Sera | Que Sera, Sera (Whatever Will Be, Will Be) |
| Quebec | Quebec Bulldogs | Quebec Nordiques |
| Quebec Remparts | Quebrachia laurentzii | Quebrachia lorentzii |
| Quediomacrus | Quedius buphthalmus | Quedius lineipennis |
| Quedlinburg | Queen | Queen (рок-группа) |
| Queen (альбом Ники Минаж) | Queen (альбом) | Queen (группа) |
| Queen (значения) | Queen + Paul Rodgers | Queen + Paul Rodgers Tour |
| Queen 2 | Queen Adreena | Queen Amidala |
| Queen Anne’s County, Maryland | Queen at the Beeb | Queen at Wembley |
| Queen Bee | Queen Eleanor’s Confession | Queen Elizabeth |
| Queen Elizabeth (значения) | Queen Elizabeth 2 | Queen Elizabeth II |
| Queen Emeraldas | Queen Forever | Queen Greatest Hits |
Нежное введение в матричную факторизацию для машинного обучения
Дата публикации 2018-02-16
Многие сложные матричные операции не могут быть решены эффективно или со стабильностью, используя ограниченную точность компьютеров.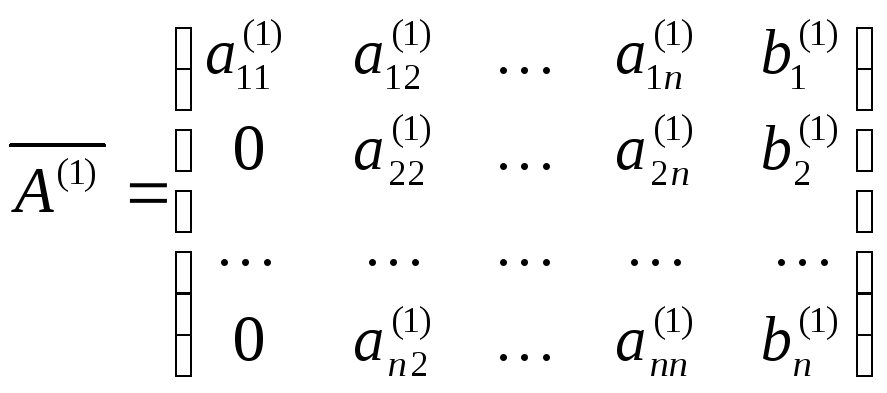
Матричные декомпозиции — это методы, которые сокращают матрицу на составные части, что облегчает вычисление более сложных матричных операций. Методы матричной декомпозиции, также называемые методами матричной факторизации, являются основой линейной алгебры в компьютерах, даже для базовых операций, таких как решение систем линейных уравнений, вычисление обратного и вычисление определителя матрицы.
В этом уроке вы узнаете о разложении матриц и о том, как их вычислять в Python.
После завершения этого урока вы узнаете:
- Что такое матричная декомпозиция и почему эти типы операций важны.
- Как рассчитать LU и QR матричные разложения в Python.
- Как рассчитать разложение матрицы Холецкого в Python.
Давайте начнем.
- Обновление март / 2018: Исправлена небольшая опечатка в описании QR-разложения.
Обзор учебника
Этот урок разделен на 4 части; они есть:
- Что такое матричная декомпозиция?
- LU Matrix Разложение
- Разложение QR-матрицы
- Холесский Разложение
Что такое матричная декомпозиция?
Разложение матрицы — это способ разложения матрицы на составные части.
Это подход, который может упростить более сложные матричные операции, которые могут быть выполнены на разложенной матрице, а не на самой исходной матрице.
Распространенной аналогией для разложения матриц является разложение чисел, такое как разложение 10 на 2 x 5. По этой причине разложение матриц также называется разложением матриц. Подобно факторизации реальных значений, существует много способов разложения матрицы, поэтому существует целый ряд различных методов разложения матрицы.
Два простых и широко используемых метода декомпозиции матрицы — это декомпозиция матрицы LU и декомпозиция матрицы QR.
Далее мы подробнее рассмотрим каждый из этих методов.
LU Matrix Разложение
Разложение LU предназначено для квадратных матриц и разбивает матрицу на компоненты L и U.
A = L . U
Или без точечной записи.
A = LU
Где A — квадратная матрица, которую мы хотим разложить, L — матрица нижнего треугольника, а U — матрица верхнего треугольника.
Факторы L и U являются треугольными матрицами. Факторизация, возникающая в результате исключения, равна A = LU.
— страница 97,Введение в линейную алгебру, Пятое издание, 2016.
Разложение LU найдено с помощью итерационного числового процесса и может дать сбой для тех матриц, которые не могут быть легко разложены или разложены.
Вариант этого разложения, который численно более устойчив для решения на практике, называется разложением LUP, или разложением LU с частичным поворотом.
A = P . L . U
Строки родительской матрицы переупорядочены, чтобы упростить процесс декомпозиции, а дополнительная P-матрица указывает способ перестановки результата или возврата результата в исходный порядок. Есть и другие варианты LU.
Разложение LU часто используется для упрощения решения систем линейных уравнений, например, для нахождения коэффициентов в линейной регрессии, а также для вычисления детерминанта и обратной матрицы.
Декомпозиция LU может быть реализована в Python с помощью функции lu (). Более конкретно, эта функция вычисляет разложение LPU.
Более конкретно, эта функция вычисляет разложение LPU.
В приведенном ниже примере сначала определяется квадратная матрица 3 × 3. Рассчитывается разложение LU, а затем исходная матрица восстанавливается по компонентам.
# LU decomposition from numpy import array from scipy.linalg import lu # define a square matrix A = array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) print(A) # LU decomposition P, L, U = lu(A) print(P) print(L) print(U) # reconstruct B = P.dot(L).dot(U) print(B)
При выполнении примера сначала печатается определенная матрица 3 × 3, затем компоненты разложения P, L и U, а затем, наконец, восстанавливается исходная матрица.
[[1 2 3] [4 5 6] [7 8 9]] [[ 0. 1. 0.] [ 0. 0. 1.] [ 1. 0. 0.]] [[ 1. 0. 0. ] [ 0.14285714 1. 0. ] [ 0.57142857 0.5 1. ]] [[ 7.00000000e+00 8.00000000e+00 9.00000000e+00] [ 0.00000000e+00 8.57142857e-01 1.71428571e+00] [ 0.00000000e+00 0.00000000e+00 -1.58603289e-16]] [[ 1. 2. 3.] [ 4. 5. 6.] [ 7. 8. 9.]]
Разложение QR-матрицы
QR-разложение предназначено для m x n матриц (не ограничено квадратными матрицами) и разбивает матрицу на Q и R компоненты.
A = Q . R
Или без точечной записи.
A = QR
Где A — матрица, которую мы хотим разложить, Q — матрица с размером m x m, а R — верхняя треугольная матрица с размером m x n.
QR-разложение находится с использованием итерационного численного метода, который может дать сбой для тех матриц, которые невозможно разложить или легко разложить.
Как и LU-разложение, QR-разложение часто используется для решения систем линейных уравнений, хотя не ограничивается квадратными матрицами.
QR-разложение может быть реализовано в NumPy с помощью функции qr (). По умолчанию функция возвращает матрицы Q и R с меньшими или «уменьшенными» размерами, что является более экономичным. Мы можем изменить это, чтобы вернуть ожидаемые размеры m x m для Q и m x n для R, указав аргумент mode как «complete», хотя это не требуется для большинства приложений.
Мы можем изменить это, чтобы вернуть ожидаемые размеры m x m для Q и m x n для R, указав аргумент mode как «complete», хотя это не требуется для большинства приложений.
В приведенном ниже примере определяется матрица 3 × 2, вычисляется QR-разложение, а затем восстанавливается исходная матрица из разложенных элементов.
# QR decomposition from numpy import array from numpy.linalg import qr # define a 3x2 matrix A = array([[1, 2], [3, 4], [5, 6]]) print(A) # QR decomposition Q, R = qr(A, 'complete') print(Q) print(R) # reconstruct B = Q.dot(R) print(B)
При выполнении примера сначала печатается определенная матрица 3 × 2, затем элементы Q и R, а затем, наконец, восстановленная матрица, которая соответствует тому, с чего мы начали.
[[1 2] [3 4] [5 6]] [[-0.16903085 0.89708523 0.40824829] [-0.50709255 0.27602622 -0.81649658] [-0.84515425 -0.34503278 0.40824829]] [[-5.T . U
Где U — верхняя треугольная матрица.
Разложение Холецкого используется для решения линейных наименьших квадратов для линейной регрессии, а также для методов моделирования и оптимизации.
При разложении симметричных матриц разложение Холецкого почти в два раза эффективнее разложения LU и должно быть предпочтительным в этих случаях.
Хотя симметричные положительно определенные матрицы являются довольно особыми, они встречаются довольно часто в некоторых приложениях, поэтому об их специальной факторизации, называемой разложением Холецкого, полезно знать. Когда вы можете использовать его, разложение Холецкого примерно в два раза быстрее, чем альтернативные методы решения линейных уравнений.
— страница 100,Численные рецепты: искусство научных вычисленийТретье издание, 2007.
Разложение Cholesky может быть реализовано в NumPy путем вызова функции cholesky (). Функция возвращает только L, так как мы можем легко получить доступ к транспонированию L по мере необходимости.![]()
Приведенный ниже пример определяет симметричную и положительно определенную матрицу 3 × 3 и вычисляет разложение Холецкого, после чего восстанавливается исходная матрица.
# Cholesky decomposition from numpy import array from numpy.linalg import cholesky # define a 3x3 matrix A = array([[2, 1, 1], [1, 2, 1], [1, 1, 2]]) print(A) # Cholesky decomposition L = cholesky(A) print(L) # reconstruct B = L.dot(L.T) print(B)
При выполнении примера сначала печатается симметричная матрица, затем нижняя треугольная матрица из разложения, за которым следует восстановленная матрица.
[[2 1 1] [1 2 1] [1 1 2]] [[ 1.41421356 0. 0. ] [ 0.70710678 1.22474487 0. ] [ 0.70710678 0.40824829 1.15470054]] [[ 2. 1. 1.] [ 1. 2. 1.] [ 1. 1. 2.]]
расширения
В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.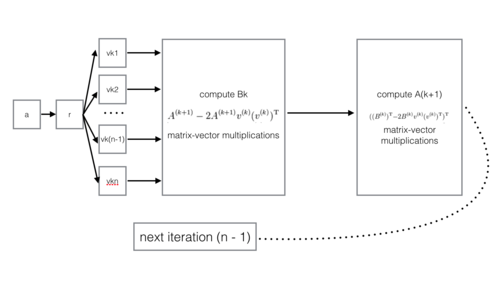
- Создайте 5 примеров, используя каждую операцию со своими собственными данными.
- Найдите документы по машинному обучению и найдите 1 пример каждой используемой операции.
Если вы исследуете какое-либо из этих расширений, я хотел бы знать.
Дальнейшее чтение
Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.
книги
- Раздел 6.6 Матричные разложения.Руководство по линейной алгебре, 2017
- Лекция 7 QR Факторизация,Численная линейная алгебра, 1997.
- Раздел 2.3. Разложение ЛУ и его применения,Числовые рецепты: искусство научных вычислений, третье издание, 2007.
- Раздел 2.10 QR-разложение,Численные рецепты: искусство научных вычисленийТретье издание, 2007.
- Раздел 2.9 Разложение Холецкого,Численные рецепты: искусство научных вычисленийТретье издание, 2007.
- Лекция 23, Разложение Холецкого,Численная линейная алгебра, 1997.
API
- scipy.linalg.lu () API
- API numpy.
 linalg.qr ()
linalg.qr () - API numpy.linalg.cholesky ()
статьи
- Матричное разложение в Википедии
- LU разложение в Википедии
- QR-разложение в Википедии
- Разложение Холецкого в Википедии
Резюме
В этом уроке вы обнаружили матричные декомпозиции и способы их вычисления в Python.
В частности, вы узнали:
- Что такое матричная декомпозиция и почему эти типы операций важны.
- Как рассчитать LU и QR матричные разложения в Python.
- Как рассчитать разложение матрицы Холецкого в Python.
У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
Оригинальная статья
Глава 24 Разложение QR | Матричная алгебра для ученых в области образования
Другим методом разложения является QR-разложение. Одним из преимуществ QR-разложения по сравнению с LU-разложением является то, что этот метод не требует, чтобы разложение выполнялось на квадратной матрице. QR-разложение приводит к разложению матрицы A (имеющей независимые столбцы) в произведение двух матриц, а именно Q и R :
.
QR-разложение приводит к разложению матрицы A (имеющей независимые столбцы) в произведение двух матриц, а именно Q и R :
.
\[ \underset{m\times n}{\mathbf{A}} = \underset{m\times m}{\mathbf{Q}}~ \underset{m\times n}{\mathbf{R}} \]
, где Q — ортогональная матрица , 12 и R — верхнетреугольная матрица.
24.1 Разложение QR с использованием R
Хотя существует способ вычисления матриц Q и R вручную (например, с использованием процесса Грама-Шмидта), мы будем полагаться на вычисления. Чтобы выполнить QR-разложение в R, мы будем использовать функцию qr() , которая факторизует матрицу и возвращает список результатов, связанных с QR-разложением. Чтобы извлечь фактические Q и R матрицы из этого вывода, мы будем использовать функции qr.Q() и qr. соответственно. R()
R()
# Создать матрицу А А = матрица ( данные = с (5, -4, 1, 2), сейчас = 2 ) # Выполняем QR-разложение qr_разложение = qr(A) # Просмотр матрицы Q qr.Q(qr_decomp)
[1] [2] [1,] -0,7809 0,6247 [2,] 0,6247 0,7809
# Просмотр матрицы R qr.R(qr_decomp)
[1] [2] [1,] -6,403 0,4685 [2,] 0,000 2,18649-1 решить (qr.Q (qr_decomp))
[1] [2] [1,] -0,7809 0,6247 [2,] 0,6247 0,7809
Мы также можем проверить, что произведение разложенных матриц равно A .
# А = QR? qr.Q(qr_decomp) %*% qr.R(qr_decomp)
[1] [2] [1,] 5 1 [2,] -4 2
24.2 Статистическое приложение: оценка коэффициентов регрессии с QR-разложением
Мы можем использовать две разложенные матрицы, Q и R , для вычисления элементов 93)
colnames(X) <- c("Перехват", "x", "x2", "x3")
# Создаем матрицу b
б = матрица (
данные = с (1, 1, 1, 1),
сейчас = 4
)
# Создать вектор значений y
set.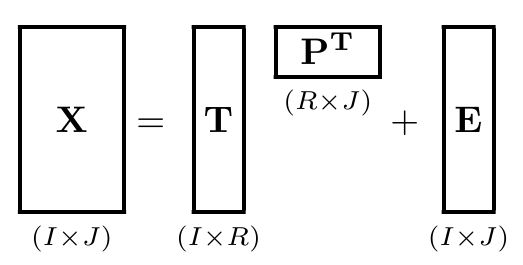 seed(1)
y = X %*% b + rnorm(n, mean = 0, sd = 1)
seed(1)
y = X %*% b + rnorm(n, mean = 0, sd = 1)
Мы можем использовать QR-разложение, чтобы найти b .
# Выполнение QR-декомпозиции QR = qr(X) # Находим b обратное решение(qr.R(QR), t(qr.Q(QR)) %*% y)
[1] [1,] 0,9038 [2,] 1,0066 [3,] 1.0000 [4,] 1.0000
QR-разложение — это то, как {-1}\).↩︎
QR. Расчет и использование QR-разложения | by Risto Hinno
Вычисление и использование QR-разложения
ИсточникВведение
QR-разложение (факторизация) — это разложение матрицы на ортогональную (Q) и верхнетреугольную (R) матрицы. QR-факторизация используется при решении линейных задач наименьших квадратов и поиске собственных значений. В этом посте показано, как вычисляется QR-разложение и как его использовать для решения практических задач.
Процесс Грама-Шмидта
Разложение QR имеет следующую формулу:
A = QR, где:
- A исходная матрица, которую мы хотим разложить
- Q ортогональная матрица
- R основная треугольная матрица 90 цель довольно проста, разложить матрицу на матрицы Q и R.
 Чтобы найти ортогональную матрицу Q, мы могли бы использовать процесс Грама-Шмидта. Этот процесс берет входную матрицу и делает столбцы ортогональными (перпендикулярными друг другу). На следующем графике мы превращаем векторы a и b в ортогональные векторы v1 и v2. Ортогонализация векторов
Чтобы найти ортогональную матрицу Q, мы могли бы использовать процесс Грама-Шмидта. Этот процесс берет входную матрицу и делает столбцы ортогональными (перпендикулярными друг другу). На следующем графике мы превращаем векторы a и b в ортогональные векторы v1 и v2. Ортогонализация векторовДля создания ортогональных векторов мы могли бы использовать следующую информацию. Вектор a является первым вектором, и мы можем сопоставить его с v1. v2 должен быть ортогонален вектору v1, поэтому мы должны спроецировать вектор b на v2, чтобы сделать b ортогоналом a (v1). Проекция вектора b на a (v1) определяется как:
Информация, которую мы имеем, находится на следующем графике:
Проецирование векторовТеперь нам нужно спроецировать b на v2, чтобы получить ортогональность между a и b. Для этого мы могли бы использовать e, которая является нашей ошибкой проекции и может быть рассчитана по следующей формуле:
Следует отметить, что e имеет ту же длину и то же направление, что и v2.
 Мы можем заключить:
Мы можем заключить:Это в основном то, как работает процесс Грама-Шмидта. Для более чем двух измерений (предположим, что у нас есть векторы a, b и c) мы могли бы рассчитать процесс следующим образом (источник): v2 и т. д., если у нас больше измерений). Теперь мы знаем, как получить матрицу Q.
Для вычисления матрицы R мы можем использовать следующие изменения в формуле QR:
A = QR,
QᵗA = QᵗQR (поскольку Q ортогонален Qᵗ=inverse(Q))
QᵗA = R, таким образом, R = QᵗA
In QR-разложение Python с использованием процесса Грама-Шмидта может быть реализовано следующим образом:
Пример использования и вывода:
A = np.array([[60, 91, 26], [60, 3, 75], [45, 90 , 31]], dtype='float')
Q, R = qr_factorization(A)
Q
#[[ 0,62469505, 0,71080736, -0,63928383],
# [0,62469505, 0,02343321, 0,75368929],
# [0,46852129, 0,70299629, -0,15254061]]
R
# [96,04686356, 77,6180,
,
,
,
, 0,6180. 0. , 0. , 35.17655816]]np.allclose(A, Q@R)
0. , 0. , 35.17655816]]np.allclose(A, Q@R)
#TrueКак обычно, это не единственный способ вычисления QR-разложения. Далее давайте посмотрим, как использовать отражения Хаусхолдера для QR-разложения.
Размышления домохозяев
Расчет Грама-Шмидта может быть численно неустойчивым, а это означает, что небольшие изменения на входе могут привести к относительно большим изменениям на выходе (источник). Более устойчивым способом является использование отражений Хаусхолдера. Проекты домохозяев векторируются через «зеркало». У нас есть вектор x, который мы хотим отразить в векторе Qx. Для отражения будем использовать ортогональную матрицу Q.
Отражение ХаусхолдераИз предыдущего мы знаем, что проекция x на u равна:
Из графика отражения Хаусхолдера мы можем видеть, что если мы дважды вычтем из x компонент, параллельный u, мы получим Qx (источник):
Параллельный компонент оказывается нашей проекцией x на u, поэтому мы можем написать:
Из-за ассоциативности матричного умножения:
Мы можем написать:
Что станет:
И, наконец, мы имеем:
Это способ получения матрицы Q.
 Полный процесс домохозяина состоит из следующих шагов:
Полный процесс домохозяина состоит из следующих шагов:- выберите первый столбец (a) исходной матрицы A, которую мы хотим разложить:
[[ 12 , -51, 4],
[ 6 , 167, -68],
[ - 4 , 24, -41]]- вычислить вектор u, который перпендикулярен зеркалу, используя следующую формулу. Sign(a1) означает знак первого элемента в a и используется для предотвращения числовых ошибок отмены. e1 обозначает стандартный базисный вектор ([1, 0, 0, …], что означает, что все, кроме первой записи, станут равными нулю):
- получить матрицу Хаусхолдера H для столбца, используя предыдущую формулу:
- получить Q, вычислив скалярное произведение Q = QH
- обновить матрицу A с помощью матрицы домохозяев: A = HA i-й ряд и выполните предыдущие шаги. Пример выбора второго столбца обновленной матрицы A:
[[-14., -21. , 14. ]
[-0. , 173,923, -65,692]
, 173,923, -65,692]
[0., 19.385, -42.538]]- Наконец, если процесс завершится, мы вернем Q и обновленную версию A в виде матриц Q и R.
В python этот процесс реализован следующим образом:
Если мы используем это с функцией, мы получаем:
A = np.array([[60, 91, 26], [60, 3, 75], [45, 90, 31]], dtype='float')
Q, R = qr(a)
Q.round(3)
#[[-0,625, 0,355, -0,696],
# [-0,625, -0,762, 0,172],
# [-0,469, 0,542, 0,698]]
Р.раунд(3)
#[[-96.047,-100.888,-77.618],
#[-0. , 78.813, -31.083],
# [ 0. , 0. , 16.469]]Q_np, R_np=np.linalg.qr(A)
np.allclose(Q, Q_np)
#True
np.allclose(R, R_np)
#TrueНаша реализация дает такие же результаты, как и numpy.
Теперь мы можем посмотреть, как QR-разложение можно использовать на практике.
Решение линейных уравнений
У нас есть матрицы A, x и B. Мы знаем A и B, но хотели бы найти x.
 Мы можем использовать некоторую алгебру (источник):
Мы можем использовать некоторую алгебру (источник):- Ax = B
- QRx = B
- Rx = QᵗB (поскольку Qᵗ = inverse(Q), так как Q ортогонален)
Решение последнего уравнения становится тривиальным с использованием обратной подстановки (см. дополнительную информацию здесь), потому что R – верхняя треугольная матрица. Простой пример:
A = np.array([
[2., 1., 1.],
[1., 3., 2.],
[1., 0., 0]])
B = np.array([4., 5., 6.])
#decompose
Q, R = np.linalg.qr(A)
#Q.TB
y = Q.T @ B
#решить x, code для back_substitution отсюда https://gist.github.com/RRisto/2cddc23d829877248915d66ecbe09a39
back_substitution(R, y)
#[ 6., 15., -23.]#using np Solr
np.linalg.solve(R, y)
#[ 6., 15., -23.]QR-разложение упрощает решение линейных уравнений. Мы можем использовать это разложение для нахождения собственных значений и собственных векторов.
Нахождение собственных значений и собственных векторов
Нахождение собственных значений и векторов не очень сложно.
 Мы можем использовать следующую процедуру (источник):
Мы можем использовать следующую процедуру (источник):- создать матрицу X из матрицы A и разложить с помощью QR-разложения:
Q, R = np.linalg.qr(X)
- вычисление произведения Q и предыдущих произведений (pQ инициализируется как диагональная матрица):
pQ = pQ @ Q
- вычисление нового X с использованием R и Q:
X = R @ Q
- повторить процесс n раз
Собственные значения будут диагональными элементами X, а собственные векторы находятся в матрице pQ.
Простая реализация Python для предыдущего алгоритма:
Использование этой функции дает нам:
A = np.array([[2., 1., 1.],[1., 3., 2.],[1., 0., 0]])
find_eig_qr(A)
#eigenvalues
#[ 3.91222918, 1.28646207, -0.19869124]
#eigenvectors
#[[ 0.51233387, -0.72297297, -0.46349121],
# [ 0.84874276, 0.50856627, 0.144],
# [ 0.13095702, -0.46762212, 0.87417379]]#compare with реализация numpy
np. linalg.eig(A)
linalg.eig(A)
#eigenvalues
#[ 3.91222918, 1.28646207, -0.19869124]
#eigenvectors
#[[-0.51233387, -0.51118241, -0.118045],
# [-0.84874276, 0.76210326, -0.48349198],
# [-0.13095702, -0.39735522, 0.85856551]]Мы видим, что собственные векторы отличаются от реализации, предоставленной numpy. Это очень простая реализация, но дает довольно хорошие результаты.
Заключение
QR-разложение может быть рассчитано с использованием процесса Грама-Шмидта и проекций Хаусхолдера, последние более стабильны в численном отношении. Вариантов этих алгоритмов больше, здесь я представил самые простые способы их использования. Разложение QR можно использовать для решения линейных уравнений и нахождения собственных значений и собственных векторов.
Ссылки
Поиск собственных векторов матриц с использованием QR-разложения, stats.stackexchange.com
Процесс Грама-Шмидта, ML Wiki
Линейные уравнения с Python: QR-разложение, b2bvoice.
0909 0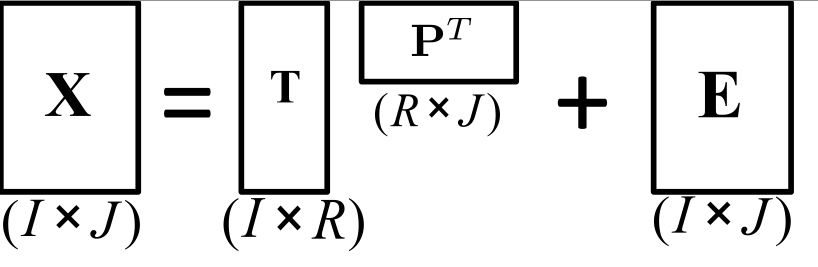 com
comQR-разложение, rosetta.com Преобразование Хаусхолдера в численной линейной алгебре, Джон Керл
Почему Хаусхолдер в вычислительном отношении более устойчив, чем модифицированный Грам-Шмидт? math.stackexchange.com
4. Разложение QR — количественная экономика с Python
Количественная экономика с Python
QR-разложение
Томас Дж. Сарджент и Джон Стахурски
4.1. Обзор
В этой лекции описывается QR-разложение и его связь с
Ортогональная проекция и метод наименьших квадратов
Процесс Грама-Шмидта
Собственные значения и собственные векторы
Мы напишем код на Python, чтобы закрепить наше понимание.
4.2. Матричная факторизация
QR-разложение (также называемое QR-факторизацией) матрицы — это разложение матрицы на произведение ортогональной матрицы и треугольной матрицы.
QR-разложение вещественной матрицы \(A\) принимает вид
\[ А=QR \]
где
Мы будем использовать процесс Грама-Шмидта для вычисления QR-разложения
Поскольку это очень поучительно, мы напишем свой собственный код Python для выполнения этой работы
4.
 3. Процесс Грама-Шмидта
3. Процесс Грама-ШмидтаНачнем с матрицы квадрата \(A\).
Если квадратная матрица \(A\) невырожденна, то факторизация \(QR\) единственна.
С прямоугольной матрицей \(A\) мы познакомимся позже.
На самом деле наш алгоритм будет работать с прямоугольником \(A\), который не является квадратом.
4.3.1. Процесс Грама-Шмидта для квадрата \(A\)
Здесь мы применяем процесс Грама-Шмидта к столбцам матрицы \(A\).
В частности, пусть
\[ A = \left[ \begin{array}{c|c|c|c} a_1 & a_2 & \cdots & a_n \end{array} \right] \]
Пусть \(|| · ||\) обозначает L2-норму.
Алгоритм Грама-Шмидта многократно комбинирует следующие два шага в определенном порядке u_1=a_1, \ \ \ e_1=\frac{u_1}{||u_1||} \]
Мы организуем сначала для вычисления \(u_2\), а затем нормализовать для создания \(e_2\):
\[ u_2=a_2-(a_2· e_1)e_1, \ \ \ e_2=\frac{u_2}{||u_2||} \]
Мы предлагаем читателю проверить, что \(e_1\) ортогонален \(e_2\), проверив, что \(e_1 \cdot e_2 = 0\).

Процедура Грама-Шмидта продолжает повторяться.
Таким образом, для \(k = 2, \ldots, n-1\) мы строим
\[ u_{k+1}=a_{k+1}-(a_{k+1}· e_1)e_1-\cdots-(a_{k+1}· e_k)e_k, \ \ \ e_{k+1} =\frac{u_{k+1}}{||u_{k+1}||} \]
Здесь \((a_j \cdot e_i)\) можно интерпретировать как линейный метод наименьших квадратов коэффициент регрессии \(a_j\) на \(e_i\)
это внутренний продукт \(a_j\) и \(e_i\), деленный на внутренний продукт \(e_i\), где \(e_i \cdot e_i = 1\), как заверила нас нормализация .
этот коэффициент регрессии интерпретируется как ковариация деленная на дисперсию
Можно проверить, что
\[\begin{split} A= \left[ \begin{array}{c|c|c|c} a_1 & a_2 & \cdots & a_n \end{array} \right]= \left[ \begin{array}{c|c|c|c} e_1 & e_2 & \cdots & e_n \end{массив} \right] \left[ \begin{matrix} a_1·e_1 & a_2·e_1 & \cdots & a_n·e_1\\ 0 & a_2·e_2 & \cdots & a_n·e_2 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_n·e_n \end{matrix} \right] \конец{разделить}\]
Таким образом, мы построили разложение
\[ А = Q р \]
где
\[ Q = \left[ \begin{array}{c|c|c|c} a_1 & a_2 & \cdots & a_n \end{array} \right]= \left[ \begin{array}{c|c|c|c} e_1 & e_2 & \cdots & e_n \end{массив} \right] \]
и
\[\begin{split} R = \left[ \begin{matrix} a_1·e_1 & a_2·e_1 & \cdots & a_n·e_1\\ 0 & a_2·e_2 & \cdots & a_n·e_2 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_n·e_n \end{matrix} \right] \конец{разделить}\]
4.
 3.2. \(A\) не квадратная
3.2. \(A\) не квадратнаяТеперь предположим, что \(A\) является матрицей \(n \times m\), где \(m > n\).
Тогда \(QR\) разложение равно
\[\begin{split} A = \left[ \begin{array}{c|c|c|c} a_1 & a_2 & \cdots & a_m \end{array} \right]=\left[ \begin{array}{c|c|c |c} e_1 & e_2 & \cdots & e_n \end{массив} \right] \left[ \begin{matrix} a_1·e_1 & a_2·e_1 & \cdots & a_n·e_1 & a_{n+1}\cdot e_1 & \cdots & a_{m}\cdot e_1 \\ 0 & a_2·e_2 & \cdots & a_n·e_2 & a_{n+1}\cdot e_2 & \cdots & a_{m}\cdot e_2 \\ \vdots & \vdots & \ddots & \quad \vdots & \ vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_n·e_n & a_{n+1}\cdot e_n & \cdots & a_{m}\cdot e_n \end{matrix} \right] \конец{разделить}\]
, что означает, что
\[\begin{align*} a_1 & = (a_1\cdot e_1) e_1 \cr a_2 & = (a_2\cdot e_1) e_1 + (a_2\cdot e_2) e_2 \cr \vdots & \quad \vdots \cr a_n & = (a_n\cdot e_1) e_1 + (a_n\cdot e_2) e_2 + \cdots + (a_n \cdot e_n) e_n \cr a_{n+1} & = (a_{n+1}\cdot e_1) e_1 + (a_{n+1}\cdot e_2) e_2 + \cdots + (a_{n+1}\cdot e_n) e_n \ кр \vdots & \quad \vdots \cr a_m & = (a_m\cdot e_1) e_1 + (a_m\cdot e_2) e_2 + \cdots + (a_m \cdot e_n) e_n \cr \end{выравнивание*}\]
4.
 4. Some Code
4. Some CodeТеперь давайте напишем самодельный код Python для реализации декомпозиции QR путем развертывания описанного выше процесса Грама-Шмидта.
импортировать numpy как np из scipy.linalg импортировать qr
по определению QR_Decomposition(A): n, m = A.shape # получить форму A Q = np.empty((n, n)) # инициализируем матрицу Q u = np.empty((n, n)) # инициализируем матрицу u и[:, 0] = А[:, 0] Q[:, 0] = u[:, 0] / np.linalg.norm(u[:, 0]) для i в диапазоне (1, n): и[:, я] = А[:, я] для j в диапазоне (i): u[:, i] -= (A[:, i] @ Q[:, j]) * Q[:, j] # получить каждый вектор u Q[:, i] = u[:, i] / np.linalg.norm(u[:, i]) # вычисляем каждый вектор R = np.zeros ((n, m)) для я в диапазоне (n): для j в диапазоне (i, m): R[i, j] = A[:, j] @ Q[:, i] возврат Q, RПредыдущий код хорош, но может быть полезен при некоторых дополнительных действиях.
Мы хотим сделать это, потому что позже в этой записной книжке мы хотим сравнить результаты использования нашего самодельного кода выше с кодом для QR, который предоставляет пакет Python
scipy.
Могут быть различия в знаках между матрицами \(Q\) и \(R\), созданными различными алгоритмами вычисления.
Все они являются допустимыми QR-разложениями из-за того, что различия в знаках сокращаются при вычислении \(QR\).
Однако, чтобы сделать результаты нашей самодельной функции и модуля QR в
scipyсопоставимыми, давайте потребуем, чтобы \(Q\) имел положительные диагональные записи.Мы делаем это, корректируя знаки столбцов в \(Q\) и строк в \(R\) соответствующим образом.
Для этого мы определим пару функций.
определение diag_sign(A): «Вычислить знаки диагонали матрицы А» D = np.diag (np.sign (np.diag (A))) вернуть D определение настройки_знака (Q, R): """ Отрегулируйте знаки столбцов в Q и строк в R, чтобы наложить положительную диагональ Q """ D = диагностический_знак (Q) Q[:, :] = Q@D R[:, :] = D@R возврат Q, R4.5. Пример
Теперь давайте сделаем пример.

A = np.array([[1.0, 1.0, 0.0], [1.0, 0.0, 1.0], [0.0, 1.0, 1.0]]) # A = np.array([[1.0, 0.5, 0.2], [0.5, 0.5, 1.0], [0.0, 1.0, 1.0]]) # A = np.array([[1.0, 0.5, 0.2], [0.5, 0.5, 1.0]]) А
массив([[1., 1., 0.], [1., 0., 1.], [0., 1., 1.]])Q, R = Adjust_sign(*QR_Decomposition(A))
Массив([[ 0,70710678, -0,40824829, -0,57735027], [0,70710678, 0,40824829, 0,57735027], [ 0. , -0,81649658, 0,57735027]])массив([[ 1.41421356, 0.70710678, 0.70710678], [ 0. , -1,22474487, -0,40824829], [ 0. , 0. , 1.15470054]])Давайте сравним результаты с тем, что производит пакет
scipyQ_scipy, R_scipy = Adjust_sign(*qr(A))
print('Наш Q: \n', Q) печать('\п') print('Scipy Q:\n', Q_scipy)Наш вопрос: [[ 0,70710678 -0,40824829 -0,57735027] [0,70710678 0,40824829 0,57735027] [ 0. -0,81649658 0,57735027]] Сципи В: [[ 0,70710678 -0,40824829 -0,57735027] [0,70710678 0,40824829 0,57735027] [ 0.
 -0,81649658 0,57735027]]
-0,81649658 0,57735027]]
print('Наш R: \n', R) печать('\п') print('Scipy R:\n', R_scipy)Наш Р: [[ 1,41421356 0,70710678 0,70710678] [ 0. -1,22474487 -0,40824829] [ 0. 0. 1.15470054]] Сципи Р: [[ 1,41421356 0,70710678 0,70710678] [ 0. -1,22474487 -0,40824829] [ 0. 0. 1.15470054]]
Приведенные выше результаты дают нам хорошие новости: наша самодельная функция согласуется с тем, что scipy производит.
Теперь давайте сделаем QR-разложение для прямоугольной матрицы \(A\), которая равна \(n \times m\) с \(т > п\).
A = np.array([[1, 3, 4], [2, 0, 9]])
Q, R = Adjust_sign(*QR_Decomposition(A)) Q, Р
(массив([[ 0,4472136 , -0,89442719], [0,89442719, 0,4472136]]), массив([[ 2.23606798, 1.34164079, 9.8386991], [ 0. , -2,68328157, 0,4472136 ]]))Q_scipy, R_scipy = Adjust_sign(*qr(A)) Q_scipy, R_scipy
(массив([[ 0,4472136 , -0,89442719], [0,89442719, 0,4472136]]), массив([[ 2. 23606798, 1.34164079, 9.8386991],
[ 0. , -2,68328157, 0,4472136 ]]))
23606798, 1.34164079, 9.8386991],
[ 0. , -2,68328157, 0,4472136 ]]))
4.6. Использование разложения QR для вычисления собственных значений
Теперь немного полезного об алгоритме QR.
Следующие итерации QR-разложения могут быть использованы для вычисления собственных значений из квадратных 9матрица 0004 \(A\).
Вот алгоритм:
Установить \(A_0 = A\) и сформировать \(A_0 = Q_0 R_0\)
Форма \(A_1 = R_0 Q_0 \) . Обратите внимание, что \(A_1\) похож на \(A_0\) (легко проверить) и поэтому имеет те же собственные значения.
Сформируйте \(A_1 = Q_1 R_1\) (т.е. сформируйте \(QR\) разложение \(A_1\)).
Форма \(A_2 = R_1 Q_1 \) и затем \(A_2 = Q_2 R_2\) .
Итерация до сходимости.
Вычислите собственные значения \(A\) и сравните их с диагональными значениями предельного \(A_n\), полученного в результате этого процесса.

Примечание: этот алгоритм близок к одному из самых эффективных способов вычисления собственных значений!
Давайте напишем код на Python, чтобы опробовать алгоритм
def QR_eigvals(A, tol=1e-12, maxiter=1000): «Найдите собственные значения A, используя QR-разложение». A_old = np.copy(A) A_new = np.copy(A) разница = np.inf я = 0 в то время как (diff > tol) и (i < maxiter): A_старый[:, :] = A_новый Q, R = QR_Decomposition(A_old) A_new[:, :] = R @ Q diff = np.abs(A_new - A_old).max() я += 1 eigvals = np.diag (A_new) вернуть эйвалыТеперь давайте попробуем код и сравним результаты с тем, что дает нам
scipy.linalg.eigvalsВот
# поэкспериментируйте с одной случайной матрицей A A = np.random.random ((3, 3))
отсортировано (QR_eigvals (A))
[-0,15277926583719334, 0,1820813029984996, 1,0321330823543302]
Сравните с пакетом
scipy.
отсортировано (np.linalg.eigvals (A))
[(0,014651018580652257-0,1293521629631194j), (0,014651018580652257+0,1293521629631194j), (1.032133082354331+0j)]
4.7. \(QR\) и PCA
Существуют интересные связи между \(QR\) разложением и анализом главных компонент (PCA).
Вот некоторые.
Пусть \(X'\) будет \(k \times n\) случайной матрицей, где \(j\)-й столбец является случайным числом из \({\mathcal N}(\mu, \Sigma)\), где \(\mu\) - это \(k \times 1\) вектор средних значений, а \(\Sigma\) - это \(k \times к\) ковариационная матрица. Мы хотим \(n > > k\) — это «эконометрический пример».
Форма \(X' = Q R \), где \(Q \) равно \(k \times k\), а \(R\) равно \(k \times n\).
Сформируем собственные значения \( R R'\), т. е. вычислим \(R R' = \tilde P \Lambda \tilde P' \).
Сформируйте \(X' X = Q \tilde P \Lambda \tilde P' Q'\) и сравните его с собственным разложением \( X'X = P \hat \Lambda P'\).
