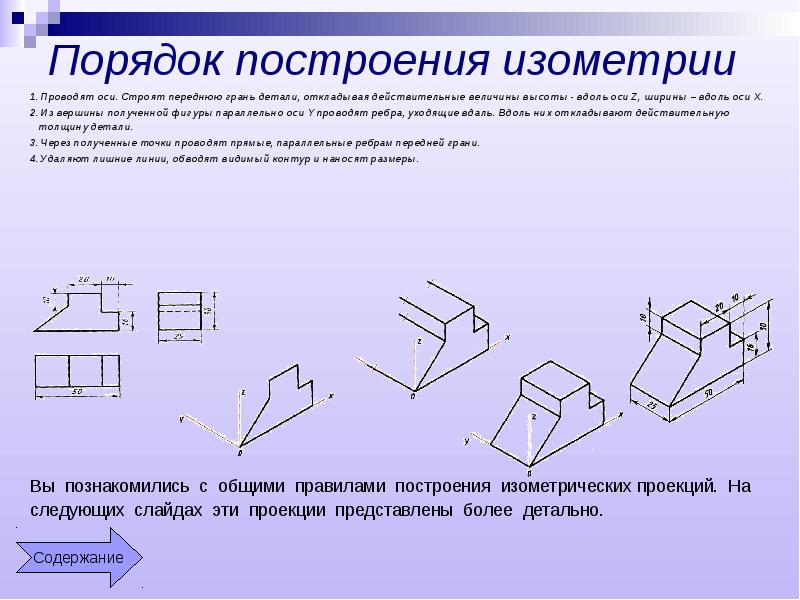
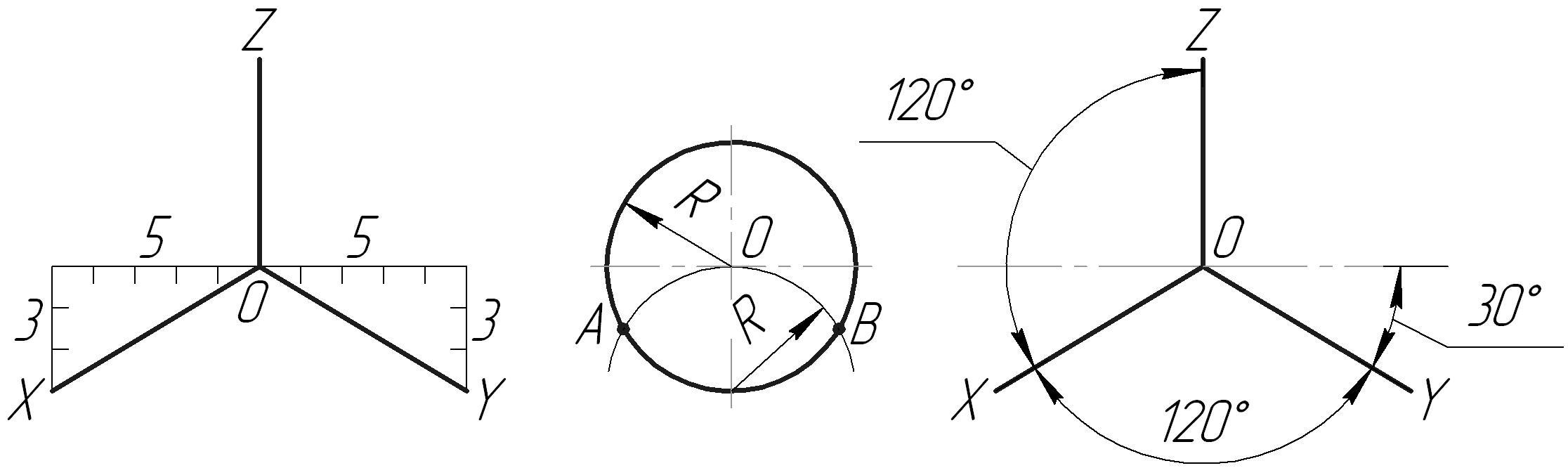
|
Прямоугольная изометрическая проекция Категория: Технические чертежи Прямоугольная изометрическая проекция Положение осей в прямоугольной изометрической проекции следующее: ось oz располагают вертикально, а оси ох и оу— под углом 120° к ней (рис. 1). Оси симметрии или ребра изделия располагают параллельно направлению осей ох, оу и oz. При построении изометрической проекции изделия линейные размеры его откладывают обычно в натуральную величину по всем трем осям. Получающееся изображение будет несколько увеличенным по отношению к его натуральным размерам (в 1,22 раза). Чтобы получить в изометрической проекции изображение, равное натуральной величине предмета, применяют коэффициент искажения по всем трем осям ox, оу, oz, равный 0,82. Рис. 1. Расположение аксонометрических осей в прямоугольной изометрической проекции. Для представления о направлении осей эллипсов предположим, что дана изометрическая проекция куба с вписанными в его грани окружностями. Из рисунка видно, что всякую окружность, находящуюся на горизонтальной поверхности, изображают в виде эллипса с горизонтально расположенной большой осью и вертикально расположенной малой. Кроме того, всякую окружность, находящуюся на передней или боковой поверхности, изображают в виде эллипса с большой осью, направленной под углом 60° к горизонтали. При этом во всех случаях большую ось эллипса располагают по большой диагонали ромба, а малую ось — по его малой диагонали. Эллипсы в изометрической проекции можно заменить овалами. Строят ромб с острым углом 60° и со стороной, равной диаметру окружности. Рис. 2. Изометрические проекции куба со вписанными в его грани окружностями: а —окружности изображены в виде эллипсов; б — эллипсы заменены овалами. Рис. 3. Пример построения изометрической проекции. На рис. 3 показано построение изометрической проекции угольника с двумя цилиндрическими отверстиями, расположенными в различных гранях. Сначала строят оси изометрической проекции и на них откладывают размеры длины, ширины и высоты угольника. На оси ох откладывают размер длины 60 мм, на оси оу — размер ширины 50 мм и на оси oz — размер высоты 75 мм. Прямолинейные очертания угольника изображаются контурными прямыми параллельно этим осям. Для изображения отверстий, имеющихся в угольнике, сперва определяют положение их центров. Затем строят ромбы со сторонами, параллельными аксонометрическим осям и равными диаметру отверстий. Построение овалов осуществляют согласно рис. 2, б. Так, отверстие 020 мм, расположенное на горизонтальной грани угольника, изображается овалом, вписанным в ромб, стороны которого параллельны осям охи оу и равны 20 мм. Овал, изображающий отверстие 0 32 мм, расположенное на вертикальной грани угольника, вписывается в ромб, стороны которого равны 32 мм и расположены параллельно осям оу и oz. Подобные построения могут быть применены и для деталей более сложных форм. Реклама:Читать далее:Прямоугольная диметрическая проекция
Статьи по теме:
Главная → Справочник → Статьи → Блог → Форум |
Ввиду одинакового коэффициента искажения по всем трем аксонометрическим осям этот вид аксонометрической проекции называется изометрической проекцией.
4.
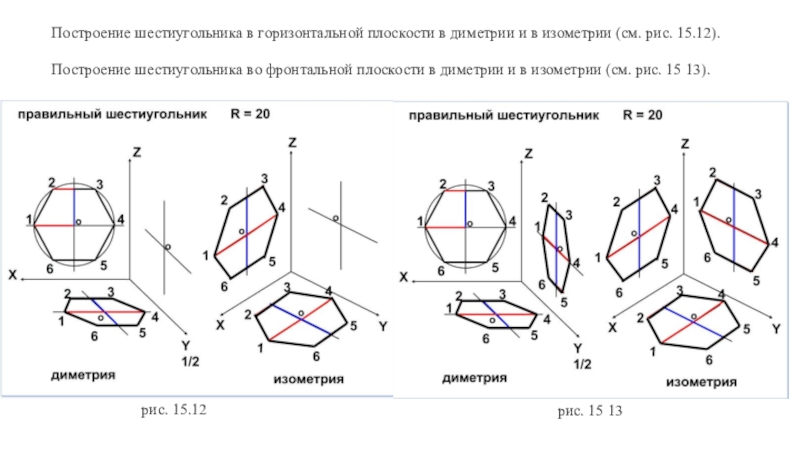
2. Построение прямоугольной изометрической проекции шестиугольника1. Задан шестиугольник 1—2—3—4—5—6 в плоскости Н. Построить изометрическую проекцию. Принимаем положение осей проекций Ох и Оу совмещенными с осями симметрии шестиугольника. Проведем к оси Ох, на которой лежат вершины 1 и 4, перпендикуляры из вершин 2, 3, 5, 6. Получим точки М и N (рис. 16).
2. Проведем изометрические проекции
рис. 16) точки 11, 41, М1, N1 (рис. 17).Рис. 16 Рис. 17
3. Через точки М1 и N1проводим прямые параллельно оси O1у1 .
На этих прямых от точек М1 и N1откладываем отрезки М121 = M161 = N131 = N151 и получаем изометрические проекции
вершин шестиугольника 21, 61, 31,51 (рис.
18).
4. Соединив проекции всех вершин шестиугольника последовательно (рис. 19), получаем изометрическую проекцию шестиугольника.
Рис. 18 Рис. 19
5. В случае, когда шестиугольник лежит в плоскости V, его изометрическая проекция будет построена по осям Ox1 и Oz1. Последовательность построения остается такой же, как и в предыдущем случае. Проекция имеет вид, показанный на рис. 20.
6 . На рис. 21 показана изометрическая проекция данного шестиугольника, лежащего в плоскости W (построенного по оси O1x1 и O1z1).
Рис. 20
Рис.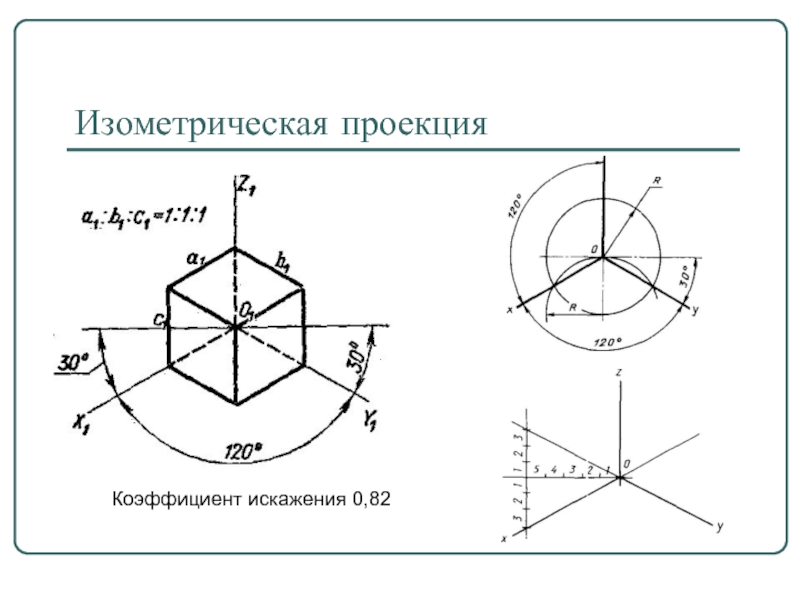
21
Изометрические проекции окружностей, лежащих в горизонтальных, фронтальных и профильных плоскостях, проецируются в виде эллипсов. Чтобы правильно построить проекцию окружности, необходимо правильно расположить оси эллипса. Если окружность диаметра d расположена в горизонтальной, фронтальной или профильной плоскостях, то в изометрической проекции большая ось эллипса (при коэффициенте, равном 0,82) будет равна АВ = d, малая ось СD = 0,58d. Если же взять изометрическую проекцию с приведенными коэффициентами, где k = m = n = 1, то оси указанных выше эллипсов будут равны: большая ось эллипса АВ = 1,22d и малая ось эллипса СD = 0,71d. В изометрии большая ось эллипса АВ располагается перпендикулярно отсутствующей аксонометрической оси, малая ось эллипса СD перпендикулярна большой оси эллипса (
22).Для более точного построения эллипса удобно пользоваться его двумя сопряженными диаметрами, являющимися параллельными проекциями двух взаимно перпендикулярных диаметров КL и МN изображаемой окружности. Два сопряженных диаметра параллельны соответственно двум из аксонометрических осей (в зависимости от того, какой плоскости проекций параллельна плоскость, в которой лежит окружность).
В изометрической проекции сопряженные диаметры при действительном коэффициенте искажения, равном 0,82, будут равны КL = МN = 0,82d, при приведенном коэффициенте искажения (КL = МN = 1) равны диаметру изображаемой окружности, то есть КL = МN = d (рис. 22).
Рис. 22
1.
Дана окружность
в плоскости H (рис.
23). Построить ее изометрическую
проекцию по приведенным коэффициентам
искажения. Направление сопряженных
диаметров МN и КL совпадают с направлением осей Ох и Оу. Откладываем
на осях Ох1 и Оу1 величины сопряженных диаметров: К1L1 = М1N1= d (рис. 24).
2. Через точки К1, L1
25).
3. Большая ось эллипса АВOz. Малая ось СDАВ, АВ = 1,22d (d – диаметр окружности), СD = 0,71d. Откладываем на соответствующих диагоналях ромба величины АВ и СD. Таким образом, для построения эллипса имеем 8 точек (рис. 25).
Рис. 23 Рис. 24
4. Соединив все точки плавной кривой (рис. 26), получим эллипс – изометрическую проекцию окружности, параллельной плоскости Н. Аналогично строятся эллипсы в плоскостях V и W.
Рис. 25 Рис. 26
Triskell Interactive » Построение прямоугольного изометрического мира
14 мая 2018 г.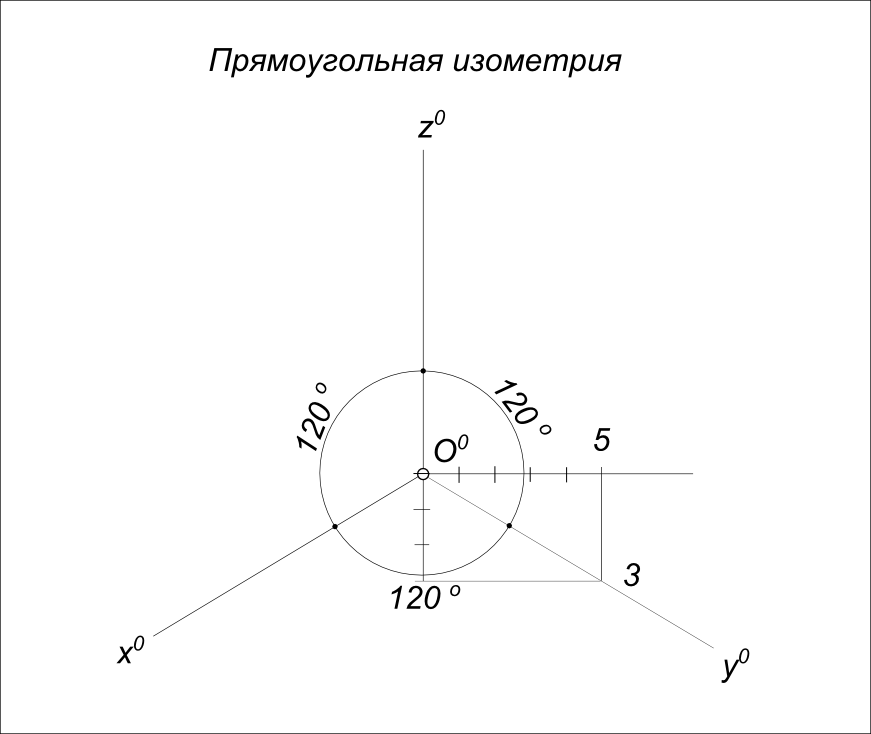
от Sinsem
Dev
Всем привет! Сегодня мы покинем мир красивой графики и погрузимся в мир математики.
Изометрическое 2D — странная штука. Это 2D, притворяющееся 3D, но по-прежнему очень 2D. Кроме того, никто не использует его в настоящее время, кроме странных людей, таких как мы.
Не существует стандартного способа создания изометрического 2D (как мы знаем), поэтому каждый раз, когда мы сталкиваемся с проблемой, нам приходится возиться с кодом, и в этом конкретном случае нам пришлось придумать новый способ организации наших плиток.
Когда мы начали работать над Letthis — Path of Progress II, мы хотели, чтобы карты были прямоугольной формы, а не ромбовидные в первой игре.
Оглядываясь назад на серию градостроительства, мы хотели перейти от Цезаря III к Фараону. Видите все это страшное пустое черное пространство? Теперь все кончено.
Это небольшая проблема из-за того, как мы организуем тайлы на карте.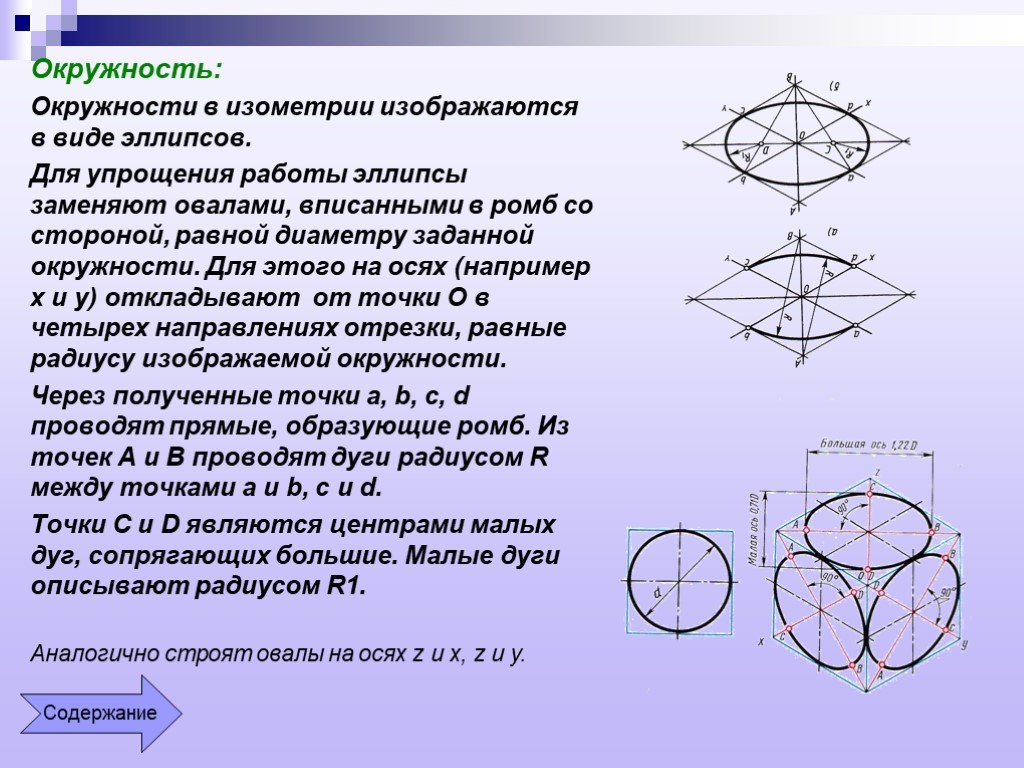
Видите ли, обычно каждая плитка является ячейкой таблицы, и чтобы упростить процесс для всех вас, непрограммистов, мы делаем что-то вроде этого.
(Это большое упрощение , но вы поняли идею)
Но нам не нужна форма ромба. Нам нужна прямоугольная форма, и этот конкретный метод не подходит.
Потребовалось немного времени, чтобы в конце концов найти правильный трюк, идея заключалась в том, чтобы смещать каждую вторую строку на половину плитки, как эта.
Когда у нас это есть, нам нужен простой способ найти соседей каждой плитки, так как большая часть нашего игрового процесса вращается вокруг этого.
На карте в форме ромба это довольно просто. У плитки может быть до 8 соседей, и добраться до них довольно просто. Вы просто добавляете или вычитаете 1 к значениям X и/или Y.
За исключением того, что с нашим новым методом это совсем не работает. Не только значения различаются из-за того, как мы настроили нашу таблицу, но у нас также есть две возможности: когда Y четное и когда Y нечетное для любой плитки [x, y].
Используя кардинальное направление, мы получаем что-то вроде этого:
| Направление | , если Y равно | , если Y нечетное |
| Север | 0 ; -2 | 0 ; -2 |
| Северо-Восток | 0 ; -1 | +1 ; -1 |
| Восток | +1 ; 0 | +1 ; 0 |
| Юго-Восток | 0 ; +1 | +1 ; +1 |
| Южный | 0 ; +2 | 0 ; +2 |
| Юго-Запад | -1 ; +1 | 0 ; +1 |
| Запад | -1 ; 0 | -1 ; 0 |
| Северо-Запад | -1 ; -1 | 0 ; -1 |
Вот и все, с помощью простой математики у нас есть прямоугольная карта, и мы можем получить доступ к соседям каждой плитки. У нас есть все необходимое, чтобы начать делать игру!
Даже если в редакторе это пока выглядит не очень.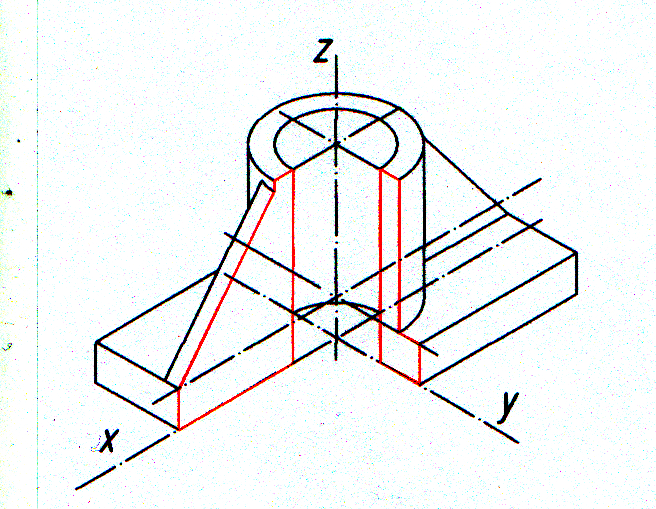
..
Спасибо за прочтение! Настало время рассказать мне, что я сделал не так, и как можно сделать эти странные прямоугольные карты более простым способом. А если серьезно, то если у вас есть вопросы о других изометрических вещах, возможно, я смогу ответить на них в одном из следующих постов в блоге разработчиков. А пока я просто вернусь к C#.
Синсем
Предыдущий Следующий
Изометрическая сетка — узнайте, как ее использовать
Изометрическая композиция, созданная с помощью Vectornator Изометрическая сетка полностью меняет правила игры в дизайне. Это позволяет дизайнерам создавать работы с невероятной трехмерной привлекательностью, которая просто выделяет их работу. Если вы работаете в мире дизайна, вы должны знать этот инструмент вдоль и поперек, чтобы использовать эту «попсовую» эстетику и вывести свою дизайнерскую игру на новый уровень. В следующем руководстве по изометрической сетке мы ответим на все ваши вопросы!
Что такое изометрическая сетка?
Изометрическая сетка сама по себе является ориентиром для получения правильных углов при рисовании в изометрической перспективе.
«Настоящая изометрическая сетка» имеет угол 30º между осями x и z к плоскости. Программное обеспечение для графического дизайна, такое как Vectornator, предлагает функцию простого редактирования угла изометрической сетки. Кроме того, вы можете увеличивать и уменьшать размер сетки, что очень полезно, если вы хотите добавить, например, небольшой балкон в свой изометрический дом.
Что такое изометрическая сетчатая бумага?
Если вы хотите рисовать на классической бумаге, вам обязательно нужно скачать шаблоны бумаги с изометрической сеткой и распечатать их. Они очень точные и бывают разных размеров. Лучшая часть? Многие из них доступны бесплатно. Если вы ищете более толстую бумагу, проверенную искусством, вы также можете купить блокнот из бумаги с изометрической сеткой. Но почему бы не объединить как цифровые, так и нецифровые иллюстрации, сначала сделав набросок в блокноте с сеткой, а затем быстро обведя его в Vectornator? Ваш реальный эскиз становится цифровым векторным искусством! Мы хотели бы увидеть ваши результаты.
Отмечайте нас в Instagram!
Посмотрите это видео, как рисовать на бумаге с изометрической сеткой:
Как рисовать изометрическую сетку?
В менее интуитивных инструментах графического дизайна, таких как Adobe Illustrator, вы вынуждены рисовать/создавать изометрическую сетку, используя инструмент прямоугольной сетки, чтобы сначала создать базовую сетку. После этого вам нужно масштабировать сетку до нужного размера. Затем вы разрезаете сетку, чтобы получить углы, как мы обсуждали ранее. В конце нужно снова повернуть сетку.
После всех этих шагов вы можете использовать созданную вами изометрическую сетку в качестве ориентира для изометрической проекции.
К счастью, интуитивно понятные инструменты для изометрического рисования, такие как Vectornator, в настоящее время предлагают гораздо более простое интуитивное решение, позволяющее легко создавать изометрическую сетку одним нажатием, при этом имея возможность изменять ее размер в процессе проектирования.
Мы покажем вам, как сделать все это в следующих параграфах.
Хотите перейти с Illustrator на Vectornator? Узнайте больше на нашей альтернативной странице Adobe Illustrator.
Рисовать изометрическую сетку на бумаге довольно сложно, и мы бы не рекомендовали это делать. Лучше купите относительно дешевый изометрический блокнот или используйте цифровую ручку + отличный инструмент для изометрического рисования, такой как Vectornator.
Как создать и использовать изометрическую сетку в Vectornator
Если вы еще этого не сделали, установите Vectornator на свой iPad, iPhone и Mac.
Установить сетку
Vectornator теперь поддерживает два типа сеток: перпендикулярную (квадратную сетку) и новейшую изометрическую сетку. Вы можете легко выбрать тип сетки, которую хотите использовать, открыв Настройки , а затем Вкладка Canvas .
Затем отрегулируйте шаг сетки и угол сетки (только на изометрической сетке), вставьте значения, которые вам подходят, и начните создавать идеальные векторные проекты намного быстрее.
Использование сетки
Вы можете применять сетки только к отдельным монтажным областям. Также важно отметить, что сетка будет отображаться на активной монтажной области. Кроме того, когда у вас настроена сетка, вы можете решить привязывать к ней свои пути, включив или переключив кнопку, которую вы найдете в Настройки > Вкладка «Привязка» .
Ищете вдохновение?
Есть много примеров, которые помогут вам стать более креативными, например, эти иллюстрации дизайна надписей. Поделитесь с нами своими проектами, мы будем рады узнать, чем занимается наше замечательное сообщество! ♡
Вы также можете посмотреть этот урок на Как создать отличный изометрический логотип в Vectornator с Уиллом Патерсоном:
