Проекции точки
Проецирование точки на три плоскости проекций координатного угла начинают с получения ее изображения на плоскости H — горизонтальной плоскости проекций. Для этого через точку А (рис. 4.12, а) проводят проецирующий луч перпендикулярно плоскости H.
На рисунке перпендикуляр к плоскости Н параллелен оси Oz. Точку пересечения луча с плоскостью Н (точку а) выбирают произвольно. Отрезок Аа определяет, на каком расстоянии находится точка А от плоскости Н, указывая тем самым однозначно положение точки А на рисунке по отношению к плоскостям проекций. Точка а является прямоугольной проекцией точки А на плоскость Н и называется горизонтальной проекцией точки А (рис. 4.12, а).
в)
Рис. 4.12.
Для
получения изображения точки А на
плоскости V (рис. 4.12,б) через точку А
проводят проецирующий луч перпендикулярно
фронтальной плоскости проекций V.
Изображение
точки А на профильной плоскости проекций
(рис. 4.12, в) строят с помощью проецирующего
луча, перпендикулярного плоскости W. На
рисунке перпендикуляр к плоскости W
параллелен оси Ох. Проецирующий луч от
точки А до плоскости W на плоскости Н
изобразится отрезком аа у,
параллельным оси Ох и перпендикулярным
оси Оу. Из точки Оу параллельно оси Oz и
перпендикулярно оси Оу строят изображение
проецирующего луча аА и в пересечении
с проецирующим лучом получают точку
а». Точка а» является профильной
проекцией точки А, т. е. изображением
точки А на плоскости W.
Из точки Оу параллельно оси Oz и
перпендикулярно оси Оу строят изображение
проецирующего луча аА и в пересечении
с проецирующим лучом получают точку
а». Точка а» является профильной
проекцией точки А, т. е. изображением
точки А на плоскости W.
Точку а» можно построить, проведя от точки а’ отрезок а’аz (изображение проецирующего луча Аа» на плоскости V) параллельно оси Ох, а от точки аz — отрезок а»аz параллельно оси Оу до пересечения с проецирующим лучом.
Получив
три проекции точки А на плоскостях
проекций, координатный угол развертывают
в одну плоскость, как показано на рис.
4.11,б, вместе с проекциями точки А и
проецирующих лучей, а точку А и проецирующие
лучи Аа, Аа’ и Аа» убирают. Края
совмещенных плоскостей проекций не
проводят, а проводят только оси проекций
Oz, Оу и Ох, Оу
Анализ
ортогонального чертежа точки показывает,
что три расстояния — Аа’, Аа и Аа»
(рис. 4.12, в), характеризующие положение
точки А в пространстве, можно определить,
отбросив сам объект проецирования —
точку А, на развернутом в одну плоскость
координатном угле (рис. 4.13). Отрезки
а’аz,
ааy и Оах равны Аа» как противоположные стороны
соответствующих прямоугольников (рис.
4.12,в и 4.13). Они определяют расстояние,
на котором находится точка А от профильной
плоскости проекций. Отрезки а’ах,
а»ау1 и Оау равны отрезку Аа, определяют расстояние
от точки А до горизонтальной плоскости
проекций, отрезки аах,
а»аz и Оаy1 равны отрезку Аа’, определяющему
расстояние от точки А до фронтальной
плоскости проекций.
4.12, в), характеризующие положение
точки А в пространстве, можно определить,
отбросив сам объект проецирования —
точку А, на развернутом в одну плоскость
координатном угле (рис. 4.13). Отрезки
а’аz,
ааy и Оах равны Аа» как противоположные стороны
соответствующих прямоугольников (рис.
4.12,в и 4.13). Они определяют расстояние,
на котором находится точка А от профильной
плоскости проекций. Отрезки а’ах,
а»ау1 и Оау равны отрезку Аа, определяют расстояние
от точки А до горизонтальной плоскости
проекций, отрезки аах,
а»аz и Оаy1 равны отрезку Аа’, определяющему
расстояние от точки А до фронтальной
плоскости проекций.
Рис. 4.13.
Отрезки
Оах,
Оау и Оаz,
расположенные на осях проекций, являются
графическим выражением размеров
координат X, Y и Z точки А. Координаты
точки обозначают с индексом соответствующей
буквы.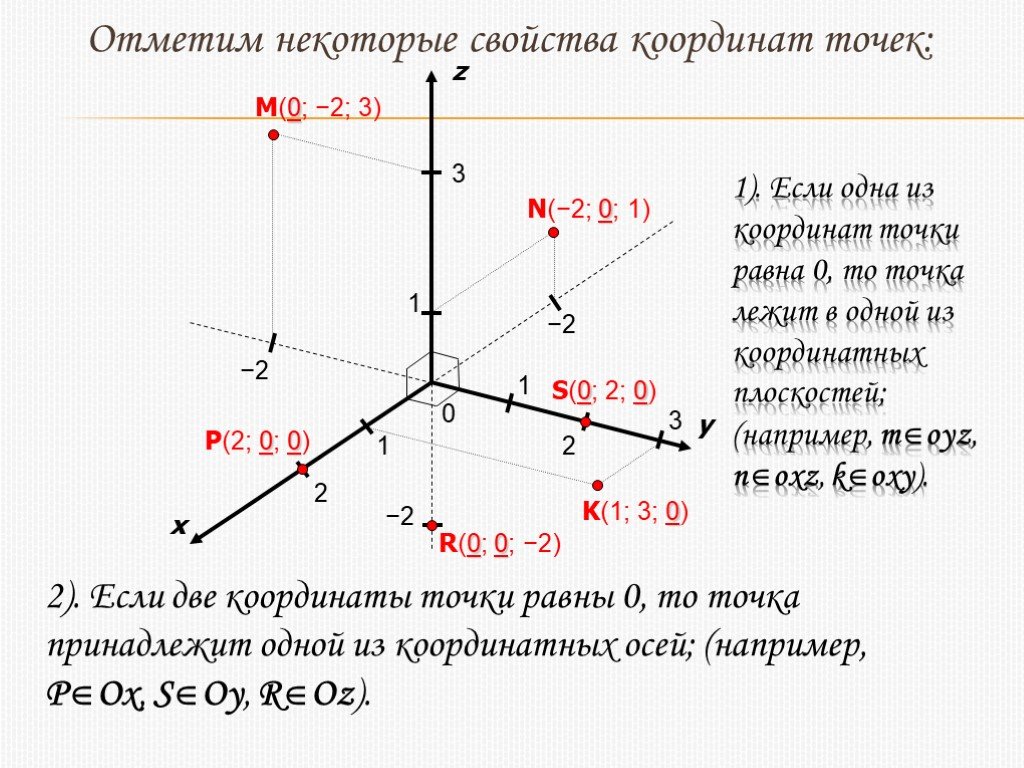 Измерив величину этих отрезков,
можно определить положение точки в
пространстве, т. е. задать координаты
точки.
Измерив величину этих отрезков,
можно определить положение точки в
пространстве, т. е. задать координаты
точки.
На
эпюре отрезки а’ах и аах располагаются как одна линия,
перпендикулярная к оси Ох а отрезки
а’аz и a»az — к оси Оz.
Эти лини называются линиями проекционной
связи. Они пересекают оси проекций в
точках ах и аz соответственно. Линия проекционной
связи, соединяющая горизонтальную
проекцию точки А с профильной, оказалась
«разрезанной» в точке а
Две проекции одной и той же точки всегда располагаются на одной линии проекционной связи, перпендикулярной к оси проекций.
Для
представления положения точки в
пространстве достаточно двух ее проекций
и заданного начала координат (точка О)
На рис. 4.14, б две проекции точки полностью
определяют ее положение в пространстве
По этим двум проекциям можно построит
профильную проекцию точки А. Поэтому в
дальнейшем, если не будет необходимости
в профильной проекции, эпюры будут
построены на двух плоскостях проекций:
V и Н.
Рис. 4.14. Рис. 4.15.
Рассмотрим несколько примеров построения и чтения чертежа точки.
Пример 1. Определение координат точки J заданной на эпюре двумя проекциях (рис. 4.14). Измеряются три отрезка: отрезок Ов Х (координата X), отрезок bХb (координата Y) и отрезок bХb’ (координата Z). Координаты записывают в следующем п рядке: X, Y и Z, после буквенного обозначения точки, например, В20; 30; 15.
Пример
2.
Построение точки по заданным координатам.
Точка С задана координатами С30; 10; 40. На
оси Ох (рис. 4.15) находят точку сх,
в которой линия проекционной связи
пересекает ось проекций. Для этого по
оси Ох от начала координат (точка О)
откладывают координату X (размер 30) и
получают точку сх.
Через эту точку перпендикулярно оси Ох
проводят линию проекционной связи и от
точки вниз откладывают координату У
(размер 10), получают точку с — горизонтальную
проекцию точки С. Вверх от точки сх по линии проекционной связи откладывают
координату Z (размер 40), получают точку
с’ — фронтальную проекцию точки С.
Вверх от точки сх по линии проекционной связи откладывают
координату Z (размер 40), получают точку
с’ — фронтальную проекцию точки С.
Рис. 4.16.
Пример 3. Построение профильной проекции точки по заданным проекциям. Заданы проекции точки D — d и d’. Через точку О проводят оси проекций Oz, Oy и Оу1 (рис. 4.16, а). Для построения профильной проекции точки D отточки d’ проводят линию проекционной связи, перпендикулярную оси Oz, и продолжают ее вправо за ось Oz. На этой линии будет располагаться профильная проекция точки D. Она будет находиться на таком расстоянии от оси Oz, на каком горизонтальная проекция точки d располагается: от оси Ох, т. е. на расстоянии ddx. Отрезки dzd» и ddx одинаковы, так как определяют одно и то же расстояние — расстояние от точки D до фронтальной плоскости проекций. Это расстояние является координатой У точки D.
Графически
отрезок dzd»
строят перенесением отрезка dd x с горизонтальной плоскости проекций
на профильную. Для этого проводят линию
проекционной связи параллельно оси Ох,
получают на оси Оу точку dy (рис. 4.16,б). Затем переносят размер отрезка
Ody на ось Оу1,
проведя из точки О дугу радиусом, равным
отрезку Ody,
до пересечения с осью Оу1 (рис. 4.16,б), получают точку dy1.
Эту точку можно построить и как показано
на рис. 4.16, в, проведя прямую под углом
45° к оси Оу из точки dy.
Из точки dy1 проводят линию проекционной связи
параллельно оси Oz и на ней откладывают
отрезок, равный отрезку d’dx,
получают точку d».
Для этого проводят линию
проекционной связи параллельно оси Ох,
получают на оси Оу точку dy (рис. 4.16,б). Затем переносят размер отрезка
Ody на ось Оу1,
проведя из точки О дугу радиусом, равным
отрезку Ody,
до пересечения с осью Оу1 (рис. 4.16,б), получают точку dy1.
Эту точку можно построить и как показано
на рис. 4.16, в, проведя прямую под углом
45° к оси Оу из точки dy.
Из точки dy1 проводят линию проекционной связи
параллельно оси Oz и на ней откладывают
отрезок, равный отрезку d’dx,
получают точку d».
Перенос
величины отрезка dxd
на профильную плоскость проекций можно
осуществить с помощью постоянной прямой
чертежа (рис. 4.16, г). В этом случае линию
проекционной связи dd
Частные случаи расположения точек относительно плоскостей проекций
Положение точки относительно плоскости проекций определяется соответствующей координатой, т. е. величиной отрезка линии проекционной связи от оси Ох до соответствующей проекции. На рис. 4.17 координата У точки А определяется отрезком аах — расстояние от точки А до плоскости V. Координата Z точки А определяется отрезком а’ах — расстояние от точки А до плоскости Н. Если одна из координат равна нулю, то точка расположена на плоскости проекций. На рис. 4.17 приведены примеры различного расположения точек относительно плоскостей проекций. Координата Z точки В равна нулю, точка находится в плоскости Н. Ее фронтальная проекция находится на оси Ох и совпадает с точкой b х. Координата У точки С равна нулю, точка располагается на плоскости V, ее горизонтальная проекция с находится на оси Ох и совпадает с точкой сх.
Следовательно,
если точка находится на плоскости
проекций, то одна из проекций этой точки
лежит на оси проекций.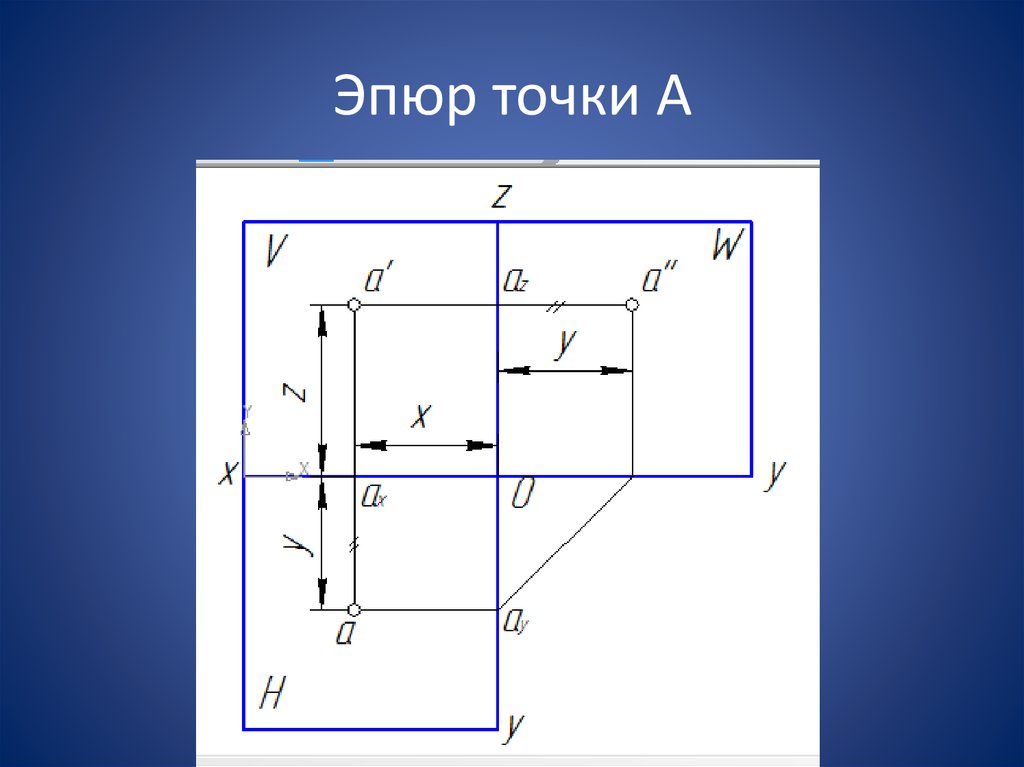
Рис. 4.17.
На рис. 4.17 координаты Z и Y точки D равны нулю, следовательно, точка D находится на оси проекций Ох и две ее проекции совпадают.
Проекция точки на плоскость онлайн
|
|
|
|||||||||||||||||||||||||||||
Системы координат, картографические проекции и преобразования — ArcGIS Pro
Данные обычно представляют собой массив чисел. Пространственные данные аналогичны, но они также включают числовую информацию, которая позволяет вам позиционировать их на земле. Эти числа являются частью системы координат, которая обеспечивает систему отсчета для ваших данных для определения объектов на поверхности земли, для выравнивания ваших данных относительно других данных, для выполнения пространственно точного анализа и для создания карт.
Пространственные данные аналогичны, но они также включают числовую информацию, которая позволяет вам позиционировать их на земле. Эти числа являются частью системы координат, которая обеспечивает систему отсчета для ваших данных для определения объектов на поверхности земли, для выравнивания ваших данных относительно других данных, для выполнения пространственно точного анализа и для создания карт.
Все пространственные данные создаются в системе координат, будь то точки, линии, полигоны, растры или аннотации. Координаты могут быть указаны разными способами, такими как десятичные градусы, футы, метры или километры; любая форма измерения может быть использована в качестве системы координат. Идентификация этой системы измерения — это первый шаг к выбору системы координат, которая отображает ваши данные в правильном положении в ArcGIS Pro по отношению к другим вашим данным.
Системы координат
Данные определяются как в горизонтальной, так и в вертикальной системах координат. Горизонтальные системы координат размещают данные по поверхности земли, а вертикальные системы координат определяют относительную высоту или глубину данных.
Горизонтальные системы координат размещают данные по поверхности земли, а вертикальные системы координат определяют относительную высоту или глубину данных.
Горизонтальные системы координат
Горизонтальные системы координат могут быть трех типов: географические, проекционные или локальные. Вы можете определить, какой тип системы координат использует ваши данные, изучив свойства слоя.
Географические системы координат (ГСК) основаны на трехмерной эллипсоидальной или сферической поверхности, а местоположения определяются с использованием угловых измерений, обычно в десятичных градусах, измеряющих градусы долготы (координаты x) и градусы широты (координаты y) ). Расположение данных выражается в виде положительных или отрицательных чисел: положительные значения x и y для севера от экватора и восточнее нулевого меридиана и отрицательные значения для юга от экватора и запада от нулевого меридиана.
Загрузить список поддерживаемых географических и вертикальных систем координат.
Проекционные системы координат (PCS) — это плоские системы, которые используют линейные измерения для координат, а не угловые единицы. Система координат проекции состоит из географической системы координат и картографической проекции. Картографическая проекция содержит математические расчеты, переводящие угловые геодезические координаты ГСК в декартовы координаты планарной системы ГСК.
Загрузить список поддерживаемых систем координат проекции.
Географическая система координат (слева), измеренная в угловых единицах, сравнивается с проекционной системой координат (справа), измеренной в линейных единицах, для того же места в Атлантическом океане.
Локальная система координат использует ложное начало (0, 0 или другие значения) в произвольном месте в любом месте на Земле. Локальные системы координат часто используются для крупномасштабного (небольшого) картографирования. Ложное начало может быть совмещено или не совмещено с известными реальными координатами, но для целей сбора данных пеленги и расстояния могут быть измерены с использованием локальной системы координат, а не глобальных координат. Местные системы координат обычно выражаются в метрах или футах.
Местные системы координат обычно выражаются в метрах или футах.
Вертикальные системы координат
Вертикальные системы координат могут быть гравитационными или эллипсоидальными.
Чаще используются гравитационные вертикальные системы координат. Они ссылаются на расчет среднего уровня моря (или, в некоторых случаях, на уровень одной точки).
Эллипсоидальные системы координат относятся к математически полученной сфероидальной или эллипсоидальной поверхности. Поскольку они рассчитываются на основе математической модели, эллипсоидальные системы координат проще, чем гравитационные вертикальные системы координат, но им может не хватать значительной точности, особенно в крупномасштабных приложениях. Например, поток на крупномасштабной карте может казаться текущим в другом направлении, используя эллипсоидальную вертикальную систему координат. Когда вы используете эллипсоидальную вертикальную систему координат, вы должны убедиться, что она соответствует географической системе координат. Например, если высота z-значения определена в NAD 1983, географическая система координат или географическая система координат в системе координат проекции также должна быть определена в NAD 1983, а не в WGS 1984.
Например, если высота z-значения определена в NAD 1983, географическая система координат или географическая система координат в системе координат проекции также должна быть определена в NAD 1983, а не в WGS 1984.
Вертикальные системы координат обеспечивают привязку к z-координатам, которые являются измерениями высоты или глубины особенностей. Вертикальный системы координат всегда в линейных единицах, таких как метры или ноги. Использование вертикальной системы координат улучшает определение местоположения. точность анализа и редактирования. Вертикальные системы координат не применяется по умолчанию к новым картам и сценам; вы должны явно Выбери один.
Вертикальные системы координат в глобальной сцене должны быть эллипсоидальными, за одним исключением. Они могут быть основаны на гравитации только в том случае, если охватывают весь мир. EGM2008 Geoid и EGM96 Geoid являются примерами глобальных вертикальных систем координат, основанных на гравитации.
Осторожно:
Имейте в виду, что эллипсоидальная вертикальная система координат
при рисовании не учитывается. Это может быть заметно, если
вы выдавливаете черты.
Это может быть заметно, если
вы выдавливаете черты.
Скачать список поддерживаемых географических и вертикальных систем координат.
Картографические проекции
Картографическая проекция — это средство отображения системы координат и ваших данных на плоской поверхности, например на листе бумаги или на цифровом экране. Математические расчеты используются для преобразования системы координат, используемой на искривленной поверхности земли, в систему координат для плоской поверхности. Поскольку не существует идеального способа перенести кривую поверхность на плоскую поверхность без некоторого искажения, существуют различные картографические проекции, обладающие разными свойствами. Некоторые сохраняют площадь, а другие сохраняют локальные углы. Некоторые сохраняют определенные расстояния или направления. Экстент, местоположение и свойства, которые вы хотите сохранить, должны определять ваш выбор картографической проекции для системы координат проекции. На платформе ArcGIS имеется около 6000 систем координат, поэтому, скорее всего, вы найдете ту, которая соответствует вашим данным. Если нет, вы можете создать пользовательскую систему координат проекции из более чем 100 картографических проекций для отображения данных.
Если нет, вы можете создать пользовательскую систему координат проекции из более чем 100 картографических проекций для отображения данных.
ArcGIS Pro перепроецирует данные на лету, поэтому любые данные, которые вы добавляете на карту, принимают определение системы координат первого добавленного слоя. Пока для первого добавленного слоя правильно определена система координат, все остальные данные с правильной информацией о системе координат перепроецируются на лету в систему координат карты. Этот подход облегчает изучение и сопоставление данных, но его не следует использовать для анализа или редактирования, поскольку это может привести к неточностям из-за несовпадения данных между слоями. Данные также медленнее рисуются, когда они проецируются на лету. Если вы собираетесь выполнять анализ или редактировать данные, сначала спроецируйте их в согласованную систему координат, общую для всех ваших слоев. Это создает новую версию ваших данных.
См. список всех картографических проекций, поддерживаемых в ArcGIS Pro.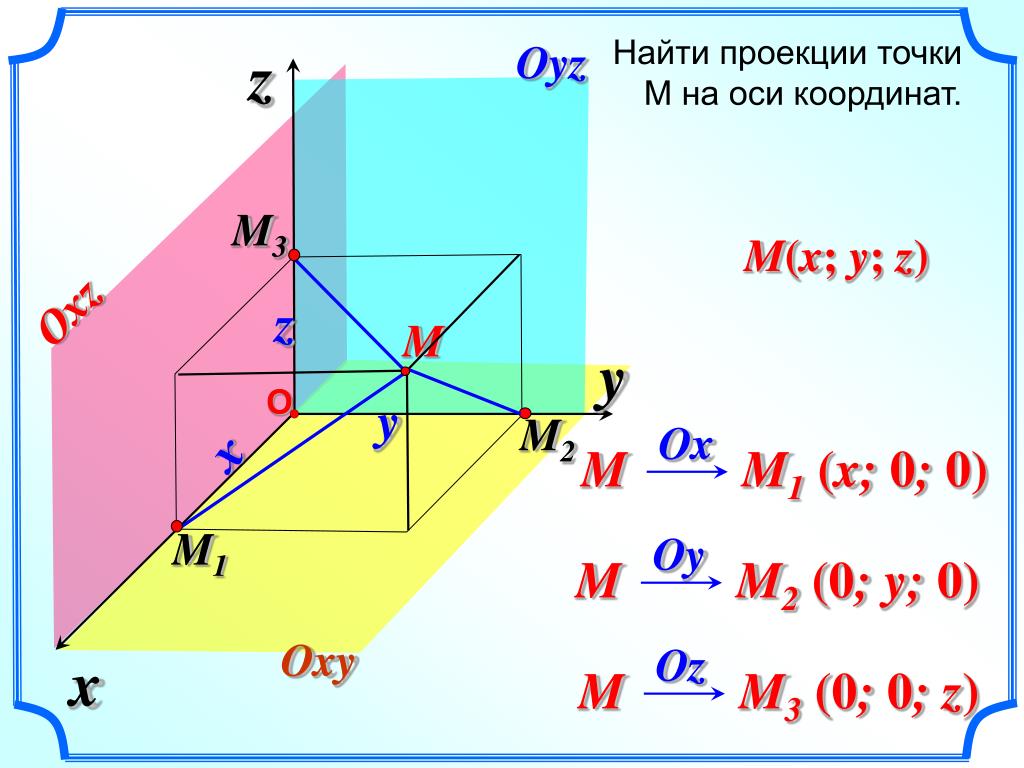
Преобразования
После определения системы координат, соответствующей вашим данным, вы все равно можете использовать данные в другой системе координат. Это когда преобразования полезны. Преобразования преобразуют данные между разными географическими системами координат или между разными вертикальными системами координат. Если ваши данные не совпадут, вы столкнетесь с трудностями и неточностями в любом анализе и сопоставлении, которые вы выполняете для несовпадающих данных.
Скачать список поддерживаемых географических и вертикальных преобразований.
Похожие темы
Отзыв по этой теме?
Система координат проекции
Система координат проекцииСистема координат проекции (PCS) — это метод преобразования поверхность (или часть поверхности) земли в плоскую плоскость. VSP использует плоскую плоскую систему координат для своих типовых планов.
Система координат проекции начинается с идеализированной модели
Земля (географическая координата
система), а затем использует проекцию для преобразования части изогнутой
поверхность земли в плоскость.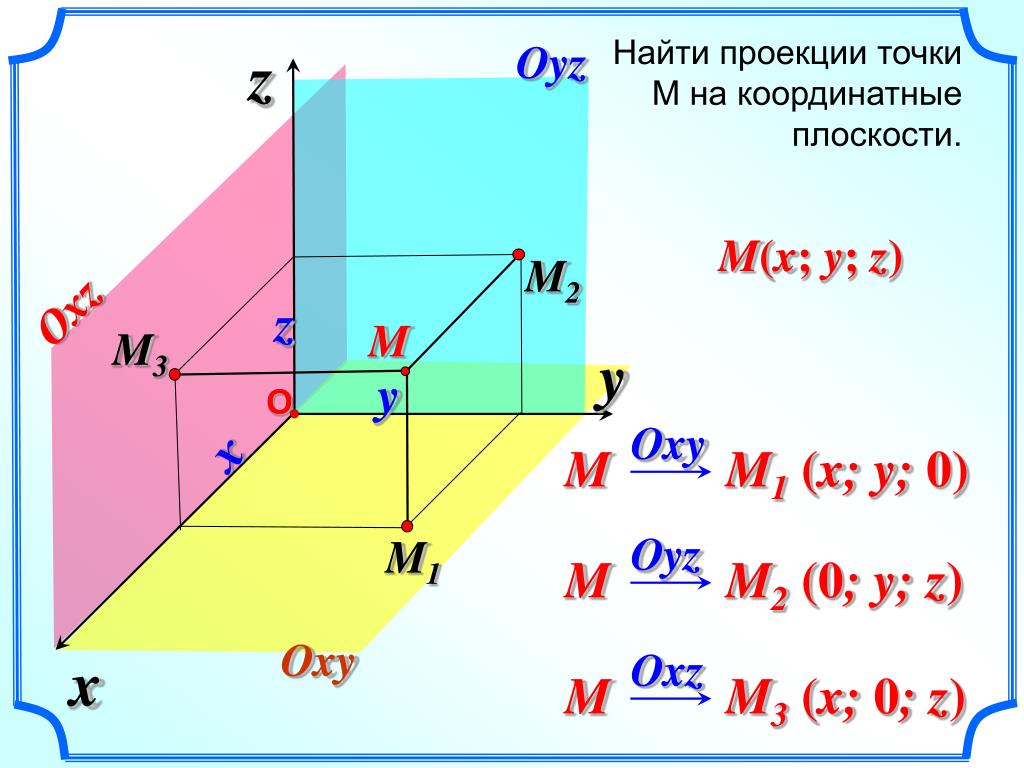 В настоящее время VSP поддерживает две проекции
типы:
В настоящее время VSP поддерживает две проекции
типы:
Поперечная проекция Меркатора
Поперечная проекция Меркатора часто используется для разрезов земля, высота которой (с юга на север) больше ширины (с запада на восток). Система координат Universal Transverse Mercator (UTM) использует это проекция. Многие системы координат штата (SPCS) в США также используйте эту проекцию. В поперечной проекции Меркатора используется следующие параметры для его проекционных уравнений:
Центральный меридиан
Ложный восток
Ложный север
Широта происхождения
Масштабный коэффициент
Конформная коническая проекция Ламберта
Конформная коническая проекция Ламберта часто используется для сечений земли, которые шире (с запада на восток), чем в высоту (с юга на север). Большинство систем координат плоскости штатов в США используют эту проекция. Конформная коническая проекция Ламберта использует следующее параметры для его проекционных уравнений:
Центральный меридиан
Ложный восток
Ложный север
Широта происхождения
Стандартный параллельный 1
Стандартный параллельный 2
Эти две проекции представляют большую часть (но не всю) координаты
систем, используемых сегодня.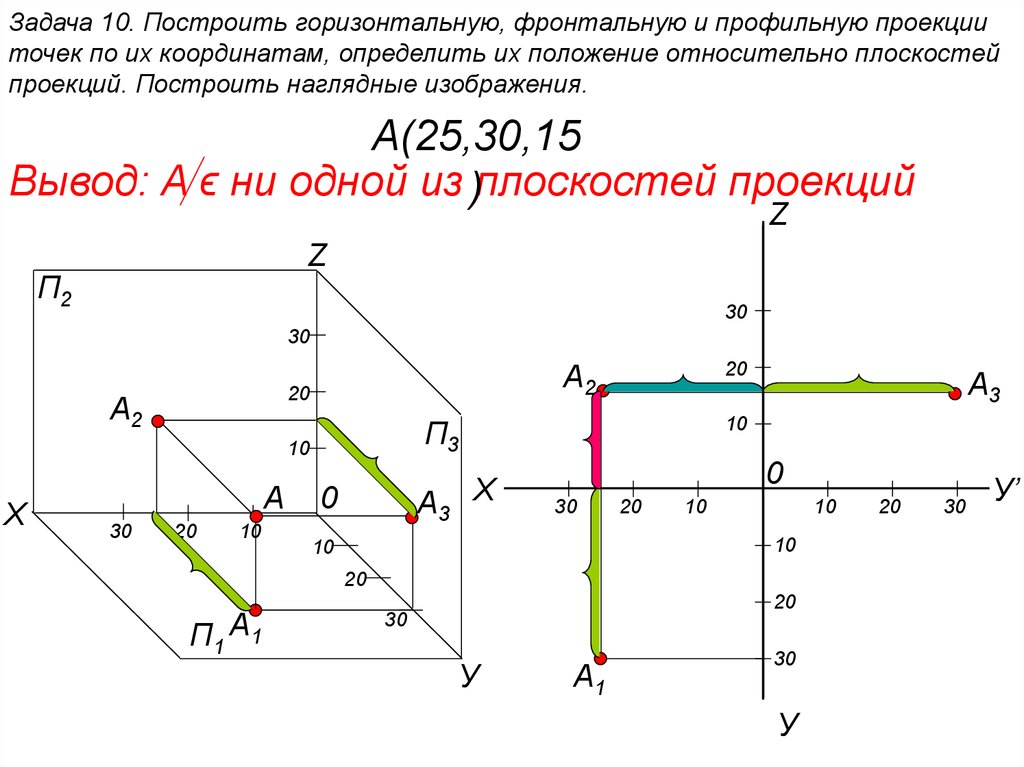 VSP может поддерживать больше прогнозов в будущем
как того требуют спрос и ресурсы.
VSP может поддерживать больше прогнозов в будущем
как того требуют спрос и ресурсы.
Используя уравнения проекции, геодезические положения на поверхности Земля (обычно обозначаемая как градусы долготы и широты) может быть преобразуются в координаты (обычно обозначаемые как восток и север, или x и y) в плоской системе. Используя уравнения обратной проекции, координаты в плоской системе могут быть преобразованы в местоположения на поверхность земли.
Важные примечания:
1. Координаты в одной плоскостной системе (ПКС) обычно не совпадают с координатами в другой плоскостной системе. Переводить координата из одной PCS в другую требует, чтобы вы преобразовали координату от первой ПКС до геодезического положения (долгота, широта) на поверхности земли, а затем спроецировать это местоположение на координату в второй ПКС. Остерегайтесь пункта 2 ниже!
2. Не все долгота и широта одинаковы! Каждая модель
Земли (географическая координата
система) будет отображать местоположения на поверхности земли в различных
долготы и широты.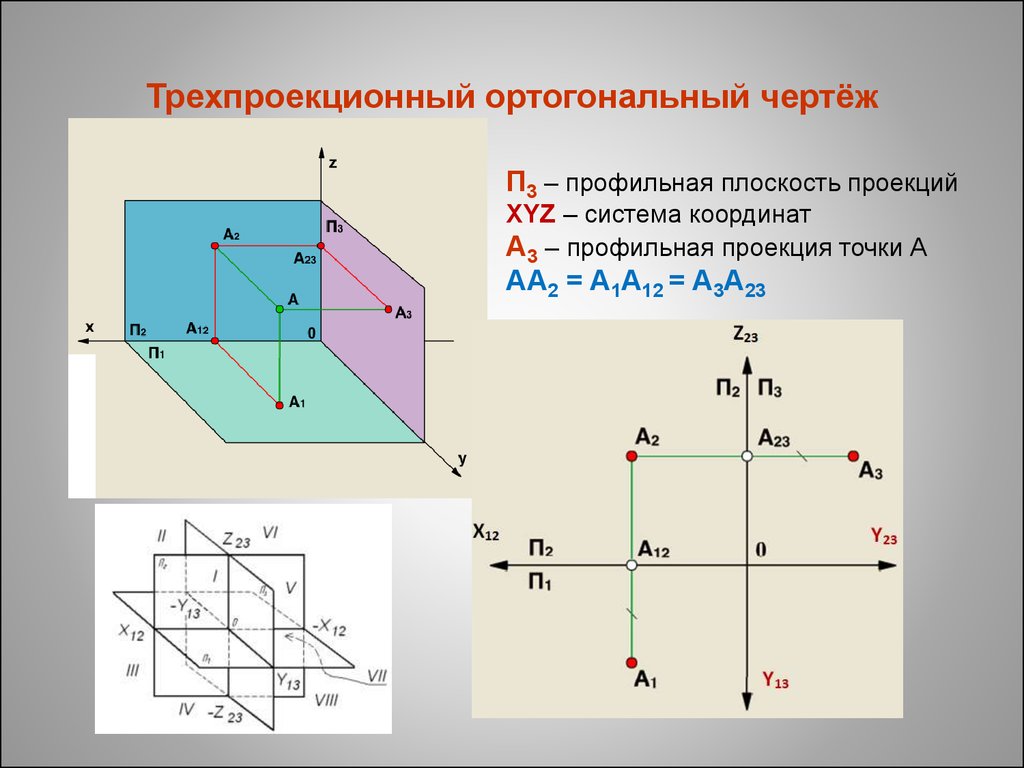
 Первые полторы тысяч разложений.
Первые полторы тысяч разложений.
 Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн