Проецирование прямого угла.
Прямой угол между двумя пресекающимися прямыми проецируется в натуральный размер только в том случае , когда одна из сторон угла параллельна плоскости проекций. Если одна сторона прямого угла будет параллельна фронталь-
ной плоскости проекций , то прямой угол будет проецироваться в натуральный
размер на фронтальную плоскость проекций.
Это имеет очень важное значение при построениях на комплексном чертеже
1) прямых перпендикулярных к друг к другу;
2) прямой перпендикулярной к плоскости ;
3) взаимно перпендикулярных плоскостей.
И соответственно, если ни одна из сторон прямого угла не занимает положение
прямой уровня, то угол не будет проектироваться в натуральную величину.
Решить задачу
нахождения натуральной величины угла,
в таком случае можно преобразовав
комплексный чертеж.
( Подробно ”О Свойствах проекций плоских углов” читайте параграф 58 Н.Г.
С.А. Фролов)
Преобразование комплексного чертежа . (Первая и вторая основные задачи преобразования чертежа).
Преобразование чертежа используется при решении задач связанных с измерениями геометрических образов или их взаимным расположением. Всего существует четыре основных задачи преобразования чертежа, две из которых связаны с преобразованием прямой линии и две с преобразованием плоскости.
Сформулируем две первые основные задачи :
1) преобразование комплексного чертежа таким образом, чтобы заданная на
чертеже прямая общего положения стала прямой уровня.
2) преобразование комплексного чертежа так, чтобы заданная на чертеже
прямая уровня заняла проецирующие положение.
Рассмотрим решение первой задачи на примере преобразования чертежа способом введения новой плоскости проекций. Способ введения новой плоскости проекций мы
уже применяли
когда рассматривали комплексный чертеж
точки.
Теперь рассмотрим этот способ применительно к линиям.
Пусть мы имеем два пересекающихся отрезка прямых общего положения .
Проведем такую замену плоскости проекций , чтобы одна из прямых стала прямой уровня. Это позволит нам судить под каким углом (тупым, прямым или острым )
пересекаются прямые . Причем, если этот угол не прямой, то для его измерения не достаточно будет одной замены плоскости проекций. В этом случае нам
потребуется , чтобы обе стороны угла были параллельны плоскости проекций.
С 2
А2
= В2
\
Х 1,2
\
С 4 В4,С4 = В,С
А 1
В 1
В 4 90 град
=
А 4
Х 1,4
Введем новую
плоскость проекций П 4 , так чтобы она
была параллельна отрезку ВС.
Одновременно
плоскость П 4 перпендикулярна плоскости
П 1.
Эти плоскости образуют новую ось Х 1,4. Ось на чертеже проводим
параллельно горизонтальной проекции отрезка В 1С 1.
Строим новую проекцию отрезка ВС:
1) (В1,В4) В 1 ; ( В 1, В4) Х 1,4. (построить прямую В1,В4,
которая включает точку В 1 ; прямая перпендикулярна оси Х 1,4)
2) В 4 ( В1, В4) ; В 4, Х 1,4 = В 2, Х 1,2 (построить точку В 4 принадлежащую прямой В1,В4 ; расстояние от В 4 до оси Х 1,4 равно расстоянию от В2 до оси Х 1,2.)
3) (С1, С4) С 1 ; ( С 1, С 4) Х 1,4 ( построить линию С1,С4,
которой принадлежит точка С1; линию С1,С4 провести перпендикулярно
оси Х 1,4)
4) С 4 (С 1, С4) ; С4, Х 1,4 = С2, Х 1,2 (построить точку С 4 принадлежащую прямой С1, С4; расстояние от точки С4 до оси Х 1,4
равно расстоянию от точки С2 до оси Х 1,2)
5) В 4 С 4 В 4 С 4 ( построить проекцию отрезка прямой В4,С4 включающего точки В4 и С4)
.
На этом этапе мы построили проекцию отрезка прямой В4,С4, которая обладает следующими метрическими свойствами :длина проекции отрезка равна длине
самого отрезка . Величина угла 4 между проекцией В4,С4 и новой осью Х 1,4
равна углу наклона отрезка прямой В,С к плоскости П 1.
Чтобы закончить наши построения достаточно :
6) (А1,А4) А1 ; ( А 1,А4) Х 1,4. (построить прямую А1,А4, которая включает точку А 1 ; прямая перпендикулярна оси Х 1,4)
7) А 4 ( А1, А4) ; А 4, Х 1,4 = А 2, Х 1,2 (построить точку А 4 принадлежащую прямой А1,А4 ; расстояние от А 4 до оси Х 1,4 равно расстоянию от А2 до оси Х 1,2.)
8) А
4, В 4 А 4 В 4 ( построить проекцию отрезка прямой
А4,В4 включающего точки А4 и В4).
Теперь мы построили проекцию угла А4В4С4 на плоскость П4 , причем проекция
равна натуральной величине угла АВС, так как это прямой угол.
Проецирование прямого угла.
ной плоскости проекций , то прямой угол будет проецироваться в натуральный
размер на фронтальную плоскость проекций.
Это имеет очень важное значение при построениях на комплексном чертеже
1) прямых перпендикулярных к друг к другу;
2) прямой перпендикулярной к плоскости ;
3) взаимно перпендикулярных плоскостей.
И соответственно, если ни одна из сторон прямого угла не занимает положение
прямой уровня, то
угол не будет проектироваться в
натуральную величину.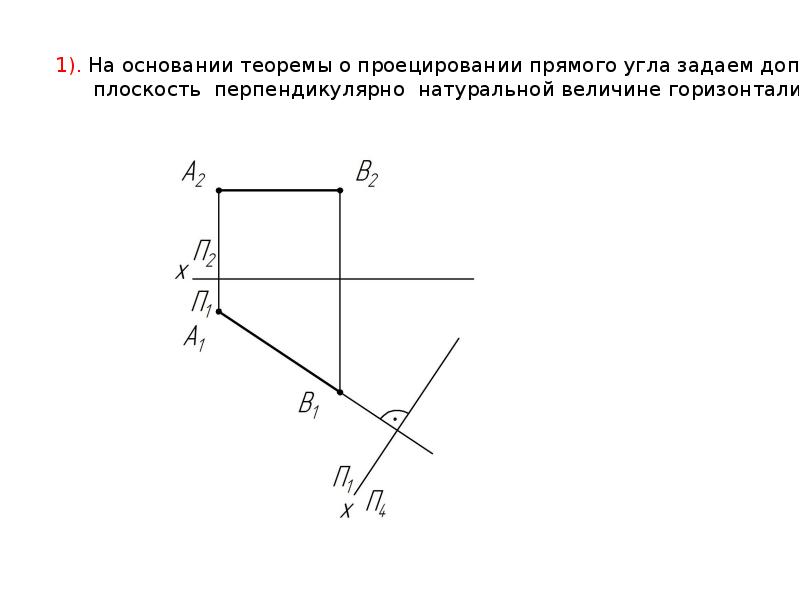
Решить задачу нахождения натуральной величины угла, в таком случае можно преобразовав комплексный чертеж.
( Подробно ”О Свойствах проекций плоских углов” читайте параграф 58 Н.Г.
С.А. Фролов)
Преобразование комплексного чертежа . (Первая и вторая основные задачи преобразования чертежа).
Преобразование чертежа используется при решении задач связанных с измерениями геометрических образов или их взаимным расположением. Всего существует четыре основных задачи преобразования чертежа, две из которых связаны с преобразованием прямой линии и две с преобразованием плоскости.
Сформулируем две первые основные задачи :
1) преобразование комплексного чертежа таким образом, чтобы заданная на
чертеже прямая общего положения стала прямой уровня.
2) преобразование комплексного чертежа так, чтобы заданная на чертеже
прямая уровня заняла проецирующие положение.
Рассмотрим решение
первой задачи на примере преобразования
чертежа способом введения новой
плоскости проекций.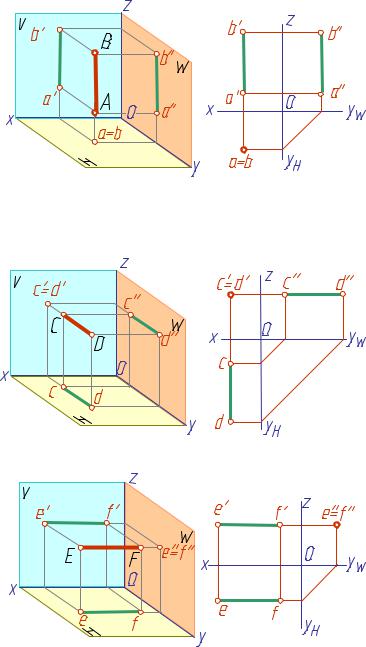
уже применяли когда рассматривали комплексный чертеж точки.
Теперь рассмотрим этот способ применительно к линиям.
Пусть мы имеем два пересекающихся отрезка прямых общего положения .
Проведем такую замену плоскости проекций , чтобы одна из прямых стала прямой уровня. Это позволит нам судить под каким углом (тупым, прямым или острым )
пересекаются прямые . Причем, если этот угол не прямой, то для его измерения не достаточно будет одной замены плоскости проекций. В этом случае нам
потребуется , чтобы обе стороны угла были параллельны плоскости проекций.
С 2
А2
= В2
\
Х 1,2
С 1
\
С 4 В4,С4 = В,С
А 1
В 1
В 4 90 град
=
А 4
Х 1,4
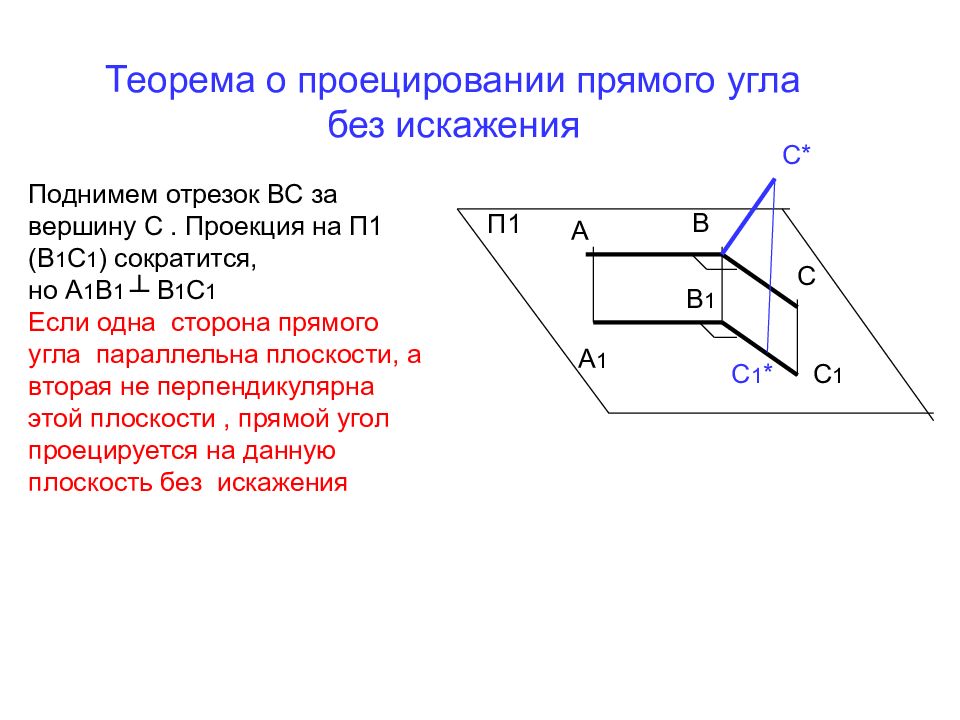
Введем новую
плоскость проекций П 4 , так чтобы она
была параллельна отрезку ВС.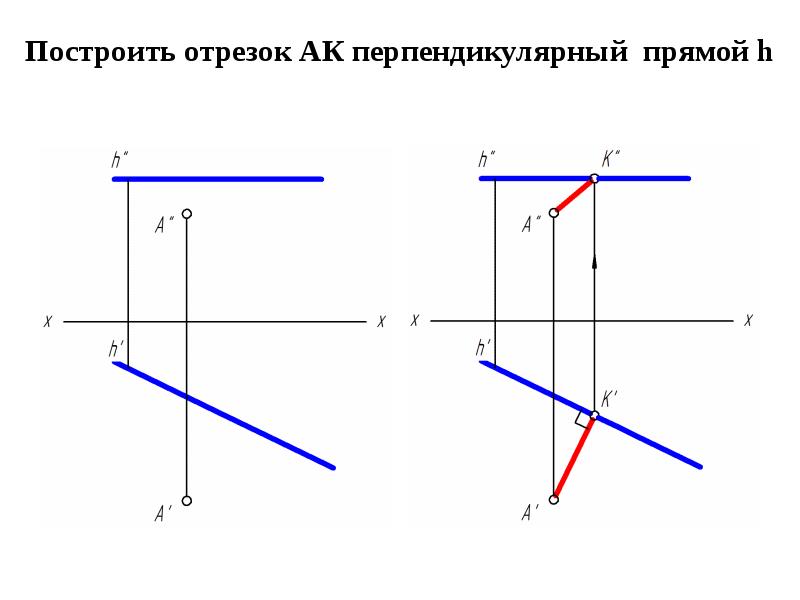
Одновременно
плоскость П 4 перпендикулярна плоскости
П 1.
Эти плоскости образуют новую ось Х 1,4. Ось на чертеже проводим
параллельно горизонтальной проекции отрезка В 1С 1.
Строим новую проекцию отрезка ВС:
1) (В1,В4) В 1 ; ( В 1, В4) Х 1,4. (построить прямую В1,В4,
которая включает точку В 1 ; прямая перпендикулярна оси Х 1,4)
2) В 4 ( В1, В4) ; В 4, Х 1,4 = В 2, Х 1,2 (построить точку В 4 принадлежащую прямой В1,В4 ; расстояние от В 4 до оси Х 1,4 равно расстоянию от В2 до оси Х 1,2.)
3) (С1, С4) С 1 ; ( С 1, С 4) Х 1,4 ( построить линию С1,С4,
которой принадлежит точка С1; линию С1,С4 провести перпендикулярно
оси Х 1,4)
4) С 4 (С 1, С4) ; С4, Х 1,4 = С2, Х 1,2 (построить точку С 4 принадлежащую прямой С1, С4; расстояние от точки С4 до оси Х 1,4
равно расстоянию от точки С2 до оси Х 1,2)
5) В 4 С 4 В 4 С 4 ( построить проекцию отрезка прямой В4,С4 включающего точки В4 и С4)
.
На этом этапе мы построили проекцию отрезка прямой В4,С4, которая обладает следующими метрическими свойствами :длина проекции отрезка равна длине
самого отрезка . Величина угла 4 между проекцией В4,С4 и новой осью Х 1,4
равна углу наклона отрезка прямой В,С к плоскости П 1.
Чтобы закончить наши построения достаточно :
6) (А1,А4) А1 ; ( А 1,А4) Х 1,4. (построить прямую А1,А4, которая включает точку А 1 ; прямая перпендикулярна оси Х 1,4)
7) А 4 ( А1, А4) ; А 4, Х 1,4 = А 2, Х 1,2 (построить точку А 4 принадлежащую прямой А1,А4 ; расстояние от А 4 до оси Х 1,4 равно расстоянию от А2 до оси Х 1,2.)
8) А
4, В 4 А 4 В 4 ( построить проекцию отрезка прямой
А4,В4 включающего точки А4 и В4).
Теперь мы построили проекцию угла А4В4С4 на плоскость П4 , причем проекция
равна натуральной величине угла АВС, так как это прямой угол.
Проецирование прямого угла.
Прямой угол между двумя пресекающимися прямыми проецируется в натуральный размер только в том случае , когда одна из сторон угла параллельна плоскости проекций. Если одна сторона прямого угла будет параллельна фронталь-
ной плоскости проекций , то прямой угол будет проецироваться в натуральный
размер на фронтальную плоскость проекций.
Это имеет очень важное значение при построениях на комплексном чертеже
1) прямых перпендикулярных к друг к другу;
2) прямой перпендикулярной к плоскости ;
3) взаимно перпендикулярных плоскостей.
И соответственно, если ни одна из сторон прямого угла не занимает положение
прямой уровня, то
угол не будет проектироваться в
натуральную величину.
Решить задачу нахождения натуральной величины угла, в таком случае можно преобразовав комплексный чертеж.
( Подробно ”О Свойствах проекций плоских углов” читайте параграф 58 Н.Г.
С.А. Фролов)
Преобразование комплексного чертежа . (Первая и вторая основные задачи преобразования чертежа).
Преобразование чертежа используется при решении задач связанных с измерениями геометрических образов или их взаимным расположением. Всего существует четыре основных задачи преобразования чертежа, две из которых связаны с преобразованием прямой линии и две с преобразованием плоскости.
Сформулируем две первые основные задачи :
1) преобразование комплексного чертежа таким образом, чтобы заданная на
чертеже прямая общего положения стала прямой уровня.
2) преобразование комплексного чертежа так, чтобы заданная на чертеже
прямая уровня заняла проецирующие положение.
Рассмотрим решение
первой задачи на примере преобразования
чертежа способом введения новой
плоскости проекций.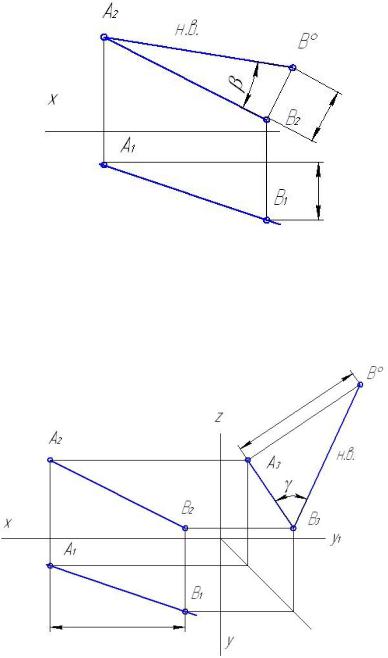
Способ введения
новой плоскости проекций мы
уже применяли когда рассматривали комплексный чертеж точки.
Теперь рассмотрим этот способ применительно к линиям.
Пусть мы имеем два пересекающихся отрезка прямых общего положения .
Проведем такую замену плоскости проекций , чтобы одна из прямых стала прямой уровня. Это позволит нам судить под каким углом (тупым, прямым или острым )
пересекаются прямые . Причем, если этот угол не прямой, то для его измерения не достаточно будет одной замены плоскости проекций. В этом случае нам
потребуется , чтобы обе стороны угла были параллельны плоскости проекций.
С 2
А2
= В2
\
Х 1,2
С 1
\
С 4 В4,С4 = В,С
А 1
В 1
В 4 90 град
=
А 4
Х 1,4
Введем новую
плоскость проекций П 4 , так чтобы она
была параллельна отрезку ВС.
Одновременно
плоскость П 4 перпендикулярна плоскости
П 1.
Эти плоскости образуют новую ось Х 1,4. Ось на чертеже проводим
параллельно горизонтальной проекции отрезка В 1С 1.
Строим новую проекцию отрезка ВС:
1) (В1,В4) В 1 ; ( В 1, В4) Х 1,4. (построить прямую В1,В4,
которая включает точку В 1 ; прямая перпендикулярна оси Х 1,4)
2) В 4 ( В1, В4) ; В 4, Х 1,4 = В 2, Х 1,2 (построить точку В 4 принадлежащую прямой В1,В4 ; расстояние от В 4 до оси Х 1,4 равно расстоянию от В2 до оси Х 1,2.)
3) (С1, С4) С 1 ; ( С 1, С 4) Х 1,4 ( построить линию С1,С4,
которой принадлежит точка С1; линию С1,С4 провести перпендикулярно
оси Х 1,4)
4) С 4 (С 1, С4) ; С4, Х 1,4 = С2, Х 1,2 (построить точку С 4 принадлежащую прямой С1, С4; расстояние от точки С4 до оси Х 1,4
равно расстоянию от точки С2 до оси Х 1,2)
5) В 4 С 4 В 4 С 4 ( построить проекцию отрезка прямой В4,С4 включающего точки В4 и С4)
.
На этом этапе мы построили проекцию отрезка прямой В4,С4, которая обладает следующими метрическими свойствами :длина проекции отрезка равна длине
самого отрезка . Величина угла 4 между проекцией В4,С4 и новой осью Х 1,4
равна углу наклона отрезка прямой В,С к плоскости П 1.
Чтобы закончить наши построения достаточно :
6) (А1,А4) А1 ; ( А 1,А4) Х 1,4. (построить прямую А1,А4, которая включает точку А 1 ; прямая перпендикулярна оси Х 1,4)
7) А 4 ( А1, А4) ; А 4, Х 1,4 = А 2, Х 1,2 (построить точку А 4 принадлежащую прямой А1,А4 ; расстояние от А 4 до оси Х 1,4 равно расстоянию от А2 до оси Х 1,2.)
8) А
4, В 4 А 4 В 4 ( построить проекцию отрезка прямой
А4,В4 включающего точки А4 и В4).
Теперь мы построили проекцию угла А4В4С4 на плоскость П4 , причем проекция
равна натуральной величине угла АВС, так как это прямой угол.
Проекции проецирующих прямых
Проецирующей называется прямая, перпендикулярная к плоскости проекций.
Проецирующая прямая проецируется на одну плоскость проекций (перпендикулярную ей) в точку, а на другую — в прямую, перпендикулярную соответствующей оси.
Горизонтально-проецирующая прямая(рис. 19)
Это прямая, перпендикулярная к горизонтальной плоскости проекций. Ее горизонтальная проекция собирает горизонтальные проекции всех точек, принадлежащих этой прямой, например точек А и В.
Фронтально-проецирующая прямая (рис. 20)
Это прямая, перпендикулярная к фронтальной плоскости проекций. Ее фронтальная проекция собирает фронтальные проекции всех точек, лежащих на данной прямой, например точек С и Д.
Профильно-проецирующая прямая (рис. 21)
Это прямая, перпендикулярная к профильной плоскости проекций. Ее профильная проекция собирает профильные проекции всех точек, лежащих на этой прямой, например точек Е и F.
Определение натуральной величины отрезка прямой общего положения
Отрезок прямой общего положения проецируется на плоскости проекций с искажением (в уменьшенном виде).
Натуральная величина отрезка на комплексном чертеже (обозначается Н.В.) строится как гипотенуза прямоугольного треугольника, первый катет которого равен одной из проекций отрезка, а второй катет равен разности расстояний от концов отрезка до той плоскости проекций, на которой взят первый катет (рис. 22), (рис. 23).
| Рис. 22 |
| Рис. 23 |
Натуральная величина угла наклона прямой к плоскости проекций может быть определена также способом прямоугольного треугольника.
На (рис. 22) показано построение натуральной величины отрезка АВ и угла его наклона (a) к горизонтальной плоскости проекций с помощью прямоугольного треугольника, у которого первый катет — горизонтальная проекция А’B‘, а второй катет — разность расстояний от концов отрезка АВ до горизонтальной плоскости проекций, т.е. разность высот Dz (рис. ).
На (рис. 23) дано построение натуральной величины отрезка АВ и угла его наклона (b) к фронтальной плоскости проекций с помощью прямоугольного треугольника, у которого первый катет — фронтальная проекция A»B», а второй катет — разность расстояний от концов отрезка АВ до фронтальной плоскости проекций, т.е. разность глубин Dy (рис. 23).
Деление отрезка прямой в данном отношении
Точка делит отрезок прямой линии в пространстве в таком же отношении, в каком проекции точки делят одноименные с ними проекции отрезка (рис.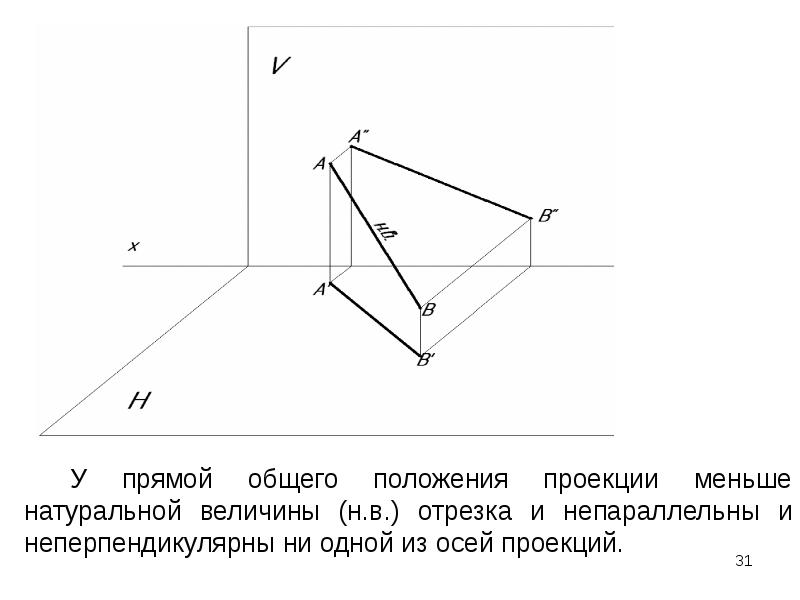
24).
Так, например, надо разделить отрезок АВ в отношении 2:3, делящая точка лежит на отрезке (рис. 24).
По основному положению мы должны иметь:
КА/КВ = К‘А‘/К‘В‘ = К»В»/К»В» = 2/3
На чертеже сначала определяем горизонтальную проекцию К‘ точки, которая делит горизонтальную проекцию А‘В‘ данного отрезка АВ в отношении 2:3. Для этого через точку А‘ проводим произвольную прямую, на которой от точки А’ отложим пять равных произвольных отрезков (2+3=5). Далее соединяем прямой линией точки 5 и В‘ и проводим прямую 2К, параллельную прямой 5В‘. Точка К‘ разделит отрезок А‘В‘ в отношении 2:3. Проведя линию связи, находим фронтальную проекцию К» искомой точки К. Точка К» разделит отрезок А»В» в отношении К»А»/К»В» = 2/3.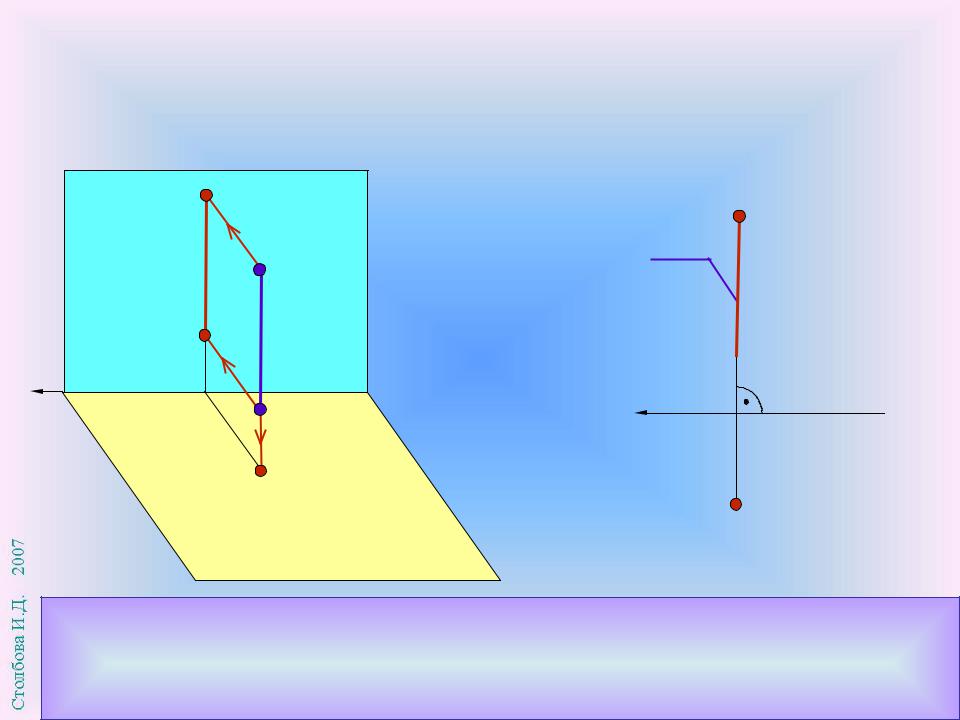
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
План:
4.1. Параллельные прямые
4.2. Пересекающиеся прямые
4.3. Скрещивающиеся прямые
Параллельные прямые
Если провести через данные параллельные прямые АВ и СD плоскости, перпендикулярные горизонтальной плоскости проекций, то эти две плоскости будут параллельны, и в их пересечении с плоскостью H будут получены две взаимно параллельные прямые A‘B‘ и C‘D‘, являющиеся ортогональными проекциями данных прямых АВ и CD на горизонтальную плоскость проекций (рис. 25).
Аналогичным образом можно получить и ортогональные проекции данных прямых на фронтальную плоскость V.
На комплексном чертеже одноименные проекции параллельных прямых параллельны: A‘B‘ C‘D‘ и A»B» C»D» (рис. 25).
Пересекающиеся прямые
Взаимно пересекающиеся прямые имеют общую точку, например, отрезки прямых АВ и CD пересекаются в точке К. Проекции пересекающихся прямых пересекаются, и точки их пересечения (K‘ и K») лежат на одной линии связи — перпендикуляре к оси x (рис. 26).
Скрещивающиеся прямые
Это прямые, которые не параллельны и не пересекаются. На комплексном чертеже проекции скрещивающихся прямых (прямые АВ и CD) могут пересекаться, но точки пересечения (1,2 и 3,4) лежат на разных линиях связи (рис. 27). Точкам пересечения одноименных проекций скрещивающихся прямых соответствуют в пространстве две точки: в одном случае — 1 и 2, а в другом — 3 и 4, расположенные на прямых. На чертеже точке пересечения горизонтальных проекций прямых соответствует две фронтальные проекции точек 1» и 2».
Аналогично — с точками 3 и 4.
5. ПЛОСКОСТЬ
План:
5.1. Проекции плоскостей общего положения
5.2. Проекции плоскостей уровня
Горизонтальная плоскость
Фронтальная плоскость
Профильная плоскость
5.3. Проекции проецирующих плоскостей
Горизонтально-проецирующая плоскость
Фронтально-проецирующая плоскость
Профильно-проецирующая плоскость
5.4. Взаимное расположение двух плоскостей
Параллельные плоскости
Пересекающиеся плоскости
5.5. Пересечение плоскостей общего положения
5.6. Взаиморасположение прямой и плоскости
Прямая — в плоскости
Прямая, параллельная плоскости
Прямая пересекает плоскость
5.7. Пересечение прямой с плоскостью
5.
8. Условие видимости на чертеже
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Построение угла между прямой и плоскостью
Углом между прямой и плоскостью называется угол, который прямая образует со своей проекцией на данную плоскость. Его величина может быть определена графически в соответствии с приведенным ниже алгоритмом.
Алгоритм построения
- Из произвольной точки, взятой на прямой, проводят перпендикуляр к заданной плоскости.
- Способом вращения вокруг линии уровня определяют величину угла β° между построенным перпендикуляром и прямой.
- Вычисляют искомый угол α° = 90° – β°.
Задача 1
Рассмотрим, как осуществляется описанный нами алгоритм на практике. На рисунке ниже приведены построения, с помощью которых вычислен угол α° между прямой a и плоскостью γ, заданной параллельными прямыми c и d.
Решение
- Строим проекции фронтали f и горизонтали h плоскости γ.
Для этого используем вспомогательные точки 1 и 2, 3 и 4. - Из произвольной точки K, лежащей на прямой a, опускаем перпендикуляр b на плоскость γ. Как видно на рисунке, проекция b’⊥h’, а b»⊥f».
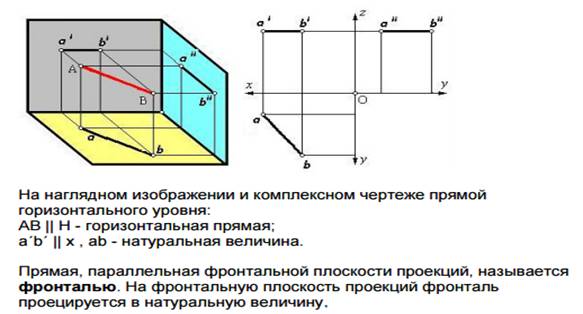
- Определяем величину угла β° между прямыми a и b способом поворота вокруг линии уровня. Для этого сначала строим горизонталь h1 и перпендикулярно её проекции h’1 проводим луч K’O’. Центр поворота O’ = K’O’ ∩ h’1.
Определяем радиус вращения R как гипотенузу прямоугольного треугольника K0K’O’, катет которого K0K’ равен величине ZO – ZK. После этого по дуге окружности переводим точку K0 в положение K’1, как это показано на рисунке выше. Угол β° находится при вершине K’1. - Вычисляем значение искомого ∠α° = 90° – ∠β°.
Для этого используем вспомогательные точки 1 и 2, 3 и 4.Задача 2
В данном примере прямая e занимает общее положение, а плоскость γ задана следами. В отличие от предыдущей задачи здесь нет необходимости достраивать горизонталь и фронталь, поскольку их роль выполняют следы h0γ и f0γ.
Решение
- На прямой e возьмем произвольную точку N и из неё опустим перпендикуляр m на плоскость γ. Проекцию m’ нужно провести перпендикулярно h0γ, а m»⊥f0γ соответственно.
- Определяем величину угла β° между прямыми m и е способом вращения вокруг линии уровня, в качестве которой в нашей задаче была использована горизонталь h.
- Вычисляем величину искомого ∠α° = 90° – ∠β°.
Похожие задачи:
Натуральная величина треугольника с описанием.
Натуральная величина треугольника определяется 2 методами:
- замена плоскостей проекции;
- плоскопараллельное перемещение.
Это задание является обязательным для студентов в учебных заведениях и для его решения необходимо изучить тему: » Способы преобразования чертежа».
Для наглядности я использовал определенное задание и на его примере покажу как находится натуральная величина треугольника.
Алгоритм определения натуральной величины плоскости:
Замена плоскостей проекции
1.
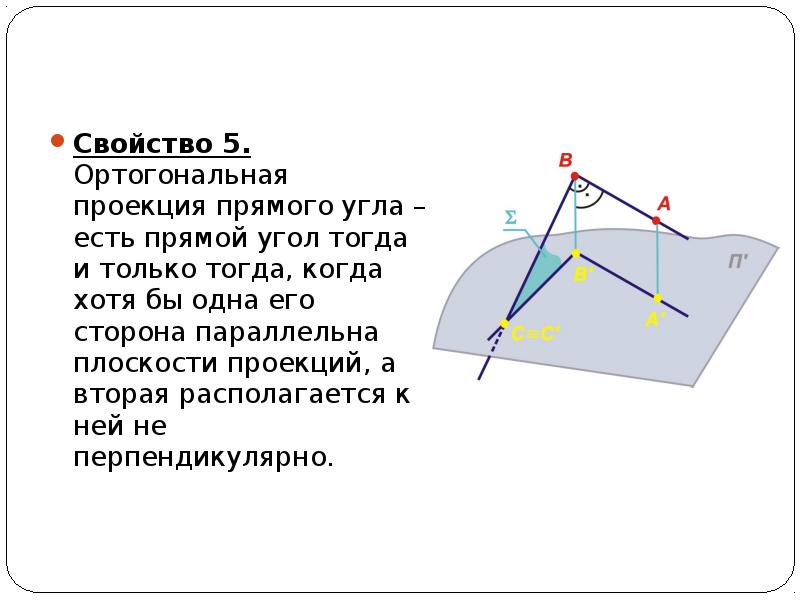) Для построения чертежа использовал задание, расположенное снизу. Первоначально строятся точки по координат в плоскостях П1 и П2.
2.) Строится дополнительная горизонтальная линия 11 в верхнем изображении (проводится линия от средне расположенной точки по высоте), затем опускают дополнительные отрезки на нижнее изображение (как указано на рисунке снизу) и соединяют прямой. Эта прямая необходима для того, чтобы на ней расположить вспомогательную плоскость.
3.) Построив прямую на нижнем рисунке, чертится под углом 900 ось Х1 (от точки С1 располагаем на произвольном расстоянии, но не слишком далеко). Затем отмеряются расстояния:
- от С2 до оси Х;
- от В2 до оси Х;
- от А0 до оси Х.
Полученные размеры откладываются от оси Х1 (размеры указаны разными цветами на рисунке снизу) и соединяют, далее подписываются точки.
4.) Строится еще одна дополнительная ось Х2, расположенная параллельно отрезку В4С4А4.
От точек В4,С4 и А4 проводят прямые перпендикулярные оси Х2.
5.) Отмеряются расстояния:
- от В1 до Х1;
- от С1 до Х1;
- от А1 до Х1.
Полученные результаты измерений откладываются от иси Х2 (на изображении снизу отмечены зелеными и голубым цветами).
6.) Соединяются точки и подписывают полученную плоскость заглавными «Н.В.»
Плоскопараллельное перемещение
7.) Откладывается отрезок на оси Х (обозначен синим цветом).
8.) Переносятся точки на текущее построение.
9.) Соединяют точки, получившиеся при переносе из плоскостей проекций. 10.) Методом вращения точки А2′, С2′ переносятся на горизонтальную прямую, а точка В2′ не меняет свое положение (относительно ее и происходило вращение).11.) Откладывается точка (располагают от оси Х на небольшом расстоянии, т.е. произвольном), относительно которой и будет откладываться плоско параллельное перемещение плоскости.
12.) От точек А2′, С2′ и В2′ опускаются прямые. Далее циркулем необходимо отмерить расстояния:
- от С1 до В1;
- от С1 до А1.
Затем эти размеры откладываются от С1′ (обозначены красным и синим цветами).
13.) Соединяются и подписываются точки (А1′, В1′ и С1′). Опускают прямые от С2″ и А2″14.) От точек С1 и А1 отводят прямые до пересечения с прямыми опущенными от точек С2″ и А2″. В месте пересечения ставится точка.15.) Завершающим шагом является соединение точек и обводка линиями всего чертежа.Пример чертежа на тему «Натуральная величина треугольника» смотрите здесь.
Связь длин сторон и углов треугольника
Связь длин сторон и углов треугольника — Math Open Reference В любом треугольнике:- Самая короткая сторона всегда противоположна самой маленькой внутренний угол
- Самая длинная сторона всегда противоположна наибольшему внутреннему углу
Попробуй это
Перетащите оранжевые точки на треугольник ниже.
Напомним, что в неравносторонний треугольник, все стороны имеют разную длину и все внутренние углы имеют разные меры.В таком треугольнике самая короткая сторона всегда противоположна самому маленькому углу. (Они выделены жирным шрифтом выше) Точно так же самая длинная сторона противоположна наибольшему углу.
На рисунке выше перетащите любой вершина треугольника и увидишь, какая сторона самая короткая, противоположный угол тоже самый маленький. Затем нажмите «Показать самый большой» и посмотрите, как бы вы ни изменили форму треугольника, самая длинная сторона всегда противоположна наибольшему внутреннему углу.
Средние детали
Если наименьшая сторона противоположна наименьшему углу, а наибольшая — противоположна наибольшему углу, то из этого следует, что поскольку треугольник имеет только три стороны, сторона среднего размера противоположна углу среднего размера.Равносторонние треугольники
Равносторонний треугольник все стороны равны по длине и все внутренние углы равны.
Следовательно, в данном случае нет «самого большого» или «самого маленького».Равнобедренные треугольники
Равнобедренные треугольники имеют две стороны одинаковой длины и два равных внутренних угла. Следовательно, могут быть две стороны и углы, которые могут быть «самыми большими» или «самыми маленькими». Если вы будете осторожны с мышью, вы можете создать такую ситуацию на рисунке выше.Другие темы треугольника
Общие
Периметр / Площадь
Типы треугольников
Центры треугольника
Конгруэнтность и сходство
Решение треугольников
Треугольник викторины и упражнения
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
ДЛЯ Т.В. ДЛЯ С.В. ДЛЯ Ф.В. ПРОЕКЦИЯ НА ПЕРВЫЙ УГОЛ В ЭТОМ МЕТОДЕ ОБЪЕКТ ПРИНИМАЕТСЯ В ПЕРВОМ КВАДРАНТНОМ СРЕДСТВЕ НАД HP & INFRONT OF.
Презентация на тему: «ДЛЯ T. V. FOR S.V. ДЛЯ ПРОЕКЦИИ ПЕРВОГО УГЛА F.V. В ЭТОМ МЕТОДЕ ОБЪЕКТ ПРИНИМАЕТСЯ В ПЕРВОМ КВАДРАНТНОМ СРЕДСТВЕ НАД HP & INFRONT OF.» — Стенограмма презентации:
V. FOR S.V. ДЛЯ ПРОЕКЦИИ ПЕРВОГО УГЛА F.V. В ЭТОМ МЕТОДЕ ОБЪЕКТ ПРИНИМАЕТСЯ В ПЕРВОМ КВАДРАНТНОМ СРЕДСТВЕ НАД HP & INFRONT OF.» — Стенограмма презентации: 1
2
3 ДЛЯ Т.V. ДЛЯ С.В. ДЛЯ Ф.В. ПРОЕКЦИЯ НА ПЕРВЫЙ УГОЛ В ЭТОМ МЕТОДЕ ОБЪЕКТ ПРИНИМАЕТСЯ В ПЕРВОМ КВАДРАНТНОМ СРЕДСТВЕ НАД HP & INFRONT OF VP. ОБЪЕКТ МЕЖДУ НАБЛЮДАТЕЛЕМ И САМОЛЕТОМ. X Y VP HP PP FVLSV ТВ
4 4 НАБЛЮДАТЕЛЬ ПРОЕКЦИИ 1-Й УГОЛ X
5 xy ВИД ПЕРЕДНЯЯ ЧАСТЬ ВИД ВЕРХНЕЙ ЧАСТИ ВИД ЛЕВОГО СТОРОНА ДЛЯ F.V.ДЛЯ С.В. ДЛЯ ТЕЛЕФОННОЙ ПРЕЗЕНТАЦИИ НАРИСАТЬ ТРИ ВИДА ЭТОГО ОБЪЕКТА МЕТОДОМ ПЕРВОГО УГЛА ПРОЕКЦИИ ОРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ
6
ДЛЯ Т.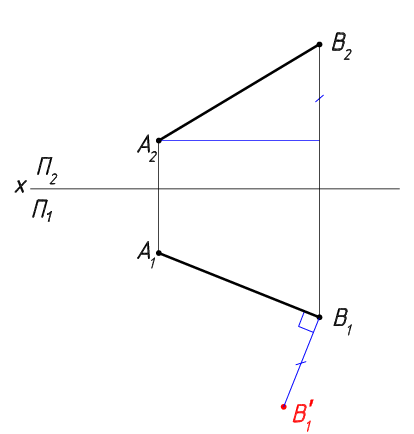
В. ДЛЯ С.В. ДЛЯ Ф.В. ИЗОБРАЖЕНИЕ ПРЕДОСТАВЛЯЕТСЯ НАРИСОВАТЬ ТРИ ВИДА ЭТОГО ОБЪЕКТА С ПОМОЩЬЮ ПЕРВОГО УГЛА ПРОЕКЦИОННОГО МЕТОДА ОРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ ВИД СПЕРЕДИ ВИД Сверху ВИД СВОЕГО УГЛА XY
7 ДЛЯ F.V. ДЛЯ С.В. ДЛЯ ТВ-ОРТОГРАФИЧЕСКИХ ПРОЕКЦИЙ XY ФРОНТАЛЬНЫЙ ВИД ВИД ВЕРХНЕГО ВИДА СВАРОЧНЫЙ ВИД СТОРОНЫ ИЗОБРАЖЕНИЕ ДАЕТСЯ НАРИСОВАТЬ ТРИ ВИДА ЭТОГО ОБЪЕКТА МЕТОДОМ ПЕРВОГО УГЛА
8 ДЛЯ Т.В. ДЛЯ С.В. ДЛЯ Ф.В. ИЗОБРАЖЕНИЕ ПРЕДОСТАВЛЯЕТСЯ НАРИСОВАТЬ ТРИ ВИДА ЭТОГО ОБЪЕКТА С ПОМОЩЬЮ ПЕРВОГО УГЛА ПРОЕКЦИОННОГО МЕТОДА ОРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ ВИД СПЕРЕДИ ВИД Сверху ВИД СВОЕГО УГЛА XY
9 ДЛЯ Т.V. ДЛЯ С.В. ДЛЯ Ф.В. ИЗОБРАЖЕНИЕ ПРЕДОСТАВЛЯЕТСЯ НАРИСОВАТЬ ТРИ ВИДА ЭТОГО ОБЪЕКТА С ПОМОЩЬЮ ПЕРВОГО УГЛА ПРОЕКЦИОННОГО МЕТОДА ОРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ ВИД СПЕРЕДИ ВИД Сверху ВИД СВОЕГО УГЛА XY
10
ДЛЯ Т.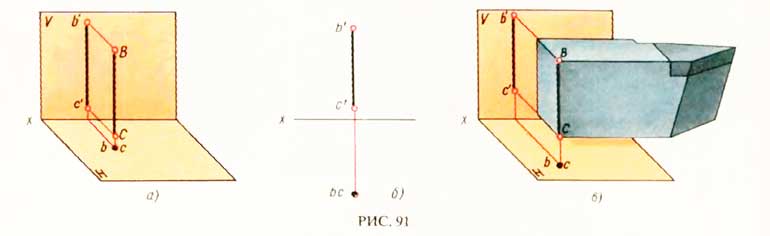
В. ДЛЯ С.В. ОРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ НА Ф.В. ВИД СПЕРЕДИ ВИД ВЕРХНЕГО ВИДА СЛЕВА СТОРОНА XY ИЗОБРАЖЕНИЕ ИЗОБРАЖЕНИЕ ДАННЫХ ТРИ ВИДА ЭТОГО ОБЪЕКТА С ПОМОЩЬЮ ПЕРВОГО УГЛОВОГО ПРОЕЦИРОВАНИЯ
11 ДЛЯ Т.V. FOR F.V. ДЛЯ С.В. ОРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ ВИД СПЕРЕДИ ВИД СВЕРХУ ВИД СЛЕВА XY ИЗОБРАЖЕНИЕ ИЗОБРАЖЕНИЕ ДАЕТ ТРИ ВИДА ЭТОГО ОБЪЕКТА С ПОМОЩЬЮ ПЕРВОГО УГЛА
12 ДЛЯ Т.В. ДЛЯ Ф.В. ДЛЯ С.В. ИЗОБРАЖЕНИЕ ПРЕДОСТАВЛЯЕТСЯ НАРИСОВАТЬ ТРИ ВИДА ЭТОГО ОБЪЕКТА С ПОМОЩЬЮ ПЕРВОГО УГЛА ПРОЕКЦИОННОГО МЕТОДА ОРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ ВИД СПЕРЕДИ ВИД Сверху ВИД СВОЕГО УГЛА XY
Площадь треугольника
Площадь треугольника , формулы для расчета площади различных типов треугольников в зависимости от известных исходных данных, калькулятор для определения площади в режиме онлайн и таблица с формулами площадей для треугольников.
Таблица с формулами площади треугольника (в конце страницы)
Скачать формулы площади треугольника в виде картинки или файла PDF (в конце страницы)
— Вычисление (показано) (скрыта)
— примечания (показаны) (скрыта)
Для всех треугольников
1
Площадь треугольника по основанию и высоте
Сторона a
Высота h
Основание треугольника можно выбрать с любой стороны треугольника.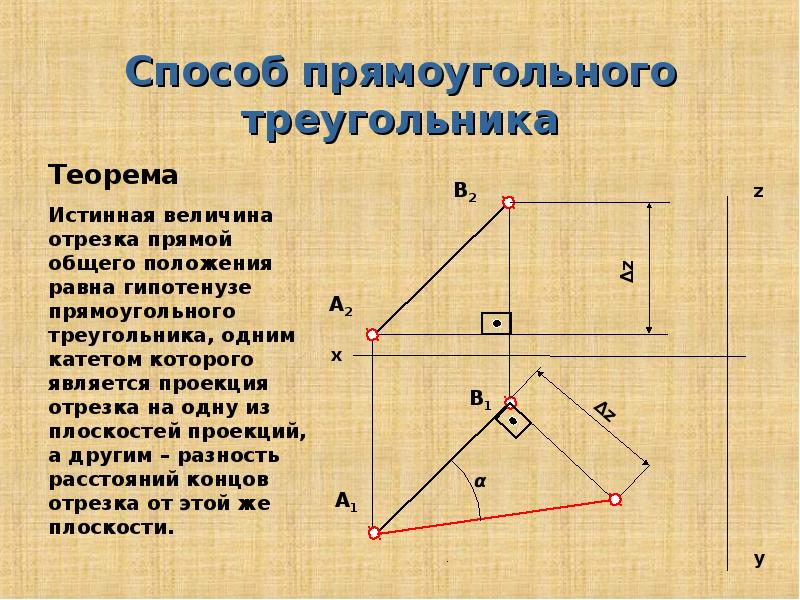
2
Площадь двух сторон треугольника и угол между ними
Сторона a
Сторона b
Угол α ° между сторонами а и б
Угол α между сторонами может быть любым: тупым, острым, прямым.
3
Площадь треугольника по радиусу вписанной окружности и трех сторон
Сторона a
Сторона b
Сторона c
Радиус r вписанный круг
4
Площадь треугольника по радиусу описанной окружности и трех сторонам
Сторона a
Сторона b
Сторона c
Радиус R описанной окружности
5
Площадь треугольника по формуле Герона
Полупериметр:
Сторона a
Сторона b
Сторона c
6
Площадь произвольного треугольника сбоку и двух смежных углов
Сторона a
Угол β °
Угол α °
Для равнобедренных треугольников
7
Площадь равнобедренного треугольника по сторонам и основанию
Сторона а (а = б)
Сторона c
8
Площадь равнобедренного треугольника по сторонам и угол между ними
Сторона а (а = б)
Угол α ° между сторонами
9
Площадь равнобедренного треугольника сбоку, в основании и угол между ними
Сторона а (а = б)
Основание треугольника c
Угол β ° между основанием и стороной
10
Площадь равнобедренного треугольника в основании и угол между сторонами
Основание треугольника c
Угол α ° между сторонами
Для равносторонних треугольников
11
Площадь равнобедренного треугольника по высоте и основанию
Основание треугольника c
Высота h
12
Площадь равностороннего треугольника со стороной
Сторона a (a = b = c)
13
Площадь равностороннего треугольника по высоте
Высота h
14
Площадь равностороннего треугольника по радиусу вписанной окружности
Радиус r вписанный круг
15
Площадь равностороннего треугольника по радиусу описанной окружности
Радиус R описанной окружности
Для прямоугольных треугольников
16
Квадрат прямоугольного треугольника с двумя ножками
Катет a
Катет b
17
Площадь прямоугольного треугольника через гипотенузу и угол
Сторона c
Угол α
18
Площадь прямоугольного треугольника, образованного катетом и углом
Сторона b
Угол α
19
Площадь прямоугольного треугольника вдоль отрезков, делящих гипотенузу на вписанную окружность
Отрезок линии d
Сегмент линии e
20
Площадь прямоугольного треугольника, проходящего через гипотенузу и вписанную окружность
Сторона с
Радиус r
21
Площадь прямоугольного треугольника по формуле Герона
Полупериметр:
Сторона a
Сторона b
Сторона c
Наш калькулятор расчета площади поможет вам рассчитать площади треугольников разного типа или проверить уже выполненные расчеты.
В зависимости от известных входных данных для вычисления площади треугольника используются различные формулы. Выше формулы и калькулятор, который поможет вычислить площадь треугольника или проверить уже выполненные расчеты. Общие формулы даны для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников.
В зависимости от типа треугольника и известных исходных данных площадь треугольника может быть вычислена с использованием различных формул.
Таблица с формулами площади треугольника
Определения
Площадь треугольника — это числовая характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя сегментами (сторонами), соединяющими три точки (вершины), не лежащие на одной прямой.
Треугольник — это геометрическая фигура, образованная тремя сегментами, соединяющими три точки, не лежащие на одной прямой.