Правило диагоналей: Правило третей. Диагонали.

«Метод диагоналей», Эдвин Вестхофф — Здесь в…

Эта статья была опубликована в журнале FOCUS в феврале 2007 года.

Рис. 1

В почти каждой книге о фотографии или о композиции в фотографии можно найти упоминание о так называемом «Правиле третьих». Обычный 35-миллиметровый кадр делится на девять равных частей делением каждой из сторон на равные части. «Правило третьих» (П. Т.), как говорят, пошло от понятия «Золотое сечение», которое в общем случае может быть выражено отношением 1 к 1,6180339. Используя «Золотое сечение» вы можете провести две линии для каждого угла прямоугольника, горизонтальную и вертикальную, на основании вышеобозначенного соотношения. Прямоугольник со сторонами, относящимися друг к другу по правилу «Золотого сечения», как вы можете видеть на рис. 1, имеет немного более продолговатую форму нежели стандартный 35-миллиметровый кадр с отношением сторон 3 к 2. Отношение сторон образовавшегося прямоугольника (пунктирная линия на рисунке) составляет 2 к 236.

Именно по причине этой разницы правило «Золотого сечения» было отовинуто на второй план: оно «не влезает» в стандартный кадр. Было получено новое универсальное соотношение: «Правило третьих», которое напротив — отлично укладывается в рамки 35-миллиметрового снимка. Структура горизонтальных и вертикальных линий в П. Т. выглядит похожей на линии, проведённые по правилу «Золотого сечения», но ведь и Джордж Буш и Памела Андерсон покажутся одинаковыми, если смотреть издалека. П. Т., конечно, может быть применено «в лоб» — как простой метод избежать помещение объекта в центре кадра.

Анализ известных фотографий и картин показал, что важные детали очень часто лежат не на пересечении линий, образованных П. Т. Я обнаружил это несколько лет назад. В процессе разработки программы Курса композиции на 2006 год я задался вопросом, почему П. Т. столь неточно, и провёл несколько визуальных экспериментов.

Я интуитивно ставил по четыре точки где-то в уголу пустого 35-миллиметрового кадра, чтобы понять, существует ли в этом какая-то система.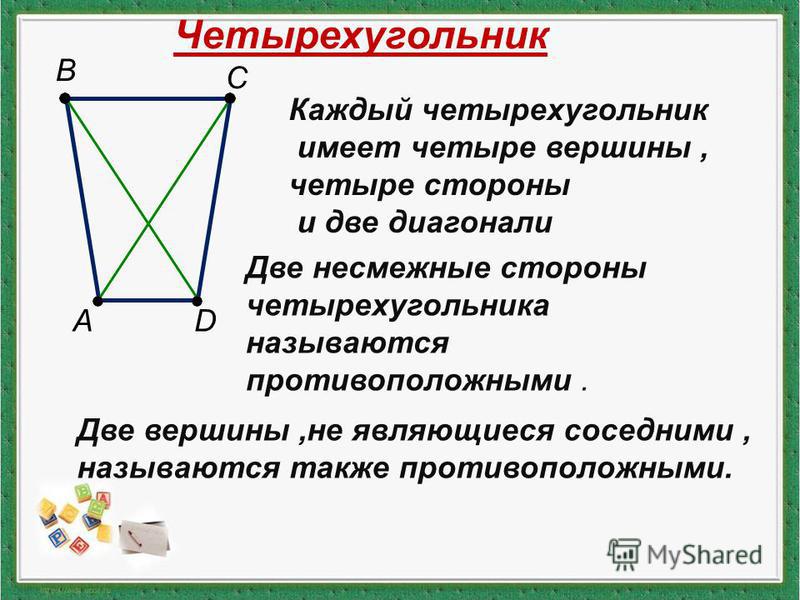

К моему собственному удивлению я обнаружил, что эти точки лежат на диагоналях, принадлежащих квадратам с сторонами равными короткой стороне кадра. Диагонали делят прямые углы пополам, и я думаю такое деление более гармонично нежели то, что вы можете получить, проведя диагонали из угла в угол кадра.

Я назвал это «Метод диагоналей», ( вероятно, имя метода должно звучать как «Метод биссектрис», но мне такое название кажется чересчур сложным). Повторюсь, вы должны понимать, что речь идёт о диагоналях квадратов, но не самого кадра.

Я протестировал десятки фотографий и картин известных фотографов и художников вроде Рембранта. Большинство работ изображают людей. Оказалось, что важные детали, такие, как глаза, руки и прочие объекты (ножи, книги, сигареты и т. д.) лежат на одной или более диагоналях квадратов, вписанных в прямоугольник 35-миллиметрового кадра.

«Метод диагоналей» «работает» следующим образом: в кадре с отношением 3 к 2 следует построить два перекрывающихся квадрата со сторонами, равными короткой стороне кадра, в каждом квадрате проведите диагонали, как показано на рисунке 2.

Рис. 2

Детали на фотографиях и картинках очень часто находятся этих линиях, с точностью до миллиметра. В виде примера: диагональная линия может пересекать глаз человека, видного целиком на снимке размером 8×10 дюймов (примерно равно листу бумаги формата A4). Именно эта удивительная точность стала определяющим фактором для продолжения экспериментов. Я бы давно забросил работу над «Методом диагоналей», если бы он показывал ту же приблизительность, что мы видим в «Правиле третьих».

Я попытался найти теоретический базис, но поиск дал совсем немного. Кроме «силовых линий» квадратов, описанных Рудольфом Арнхеймом в его классическом труде «Искусство и визуальные отношения». (Весьма странно, что он ни слова не сказал о восприятии, т. с., прямоугольного искусства — работ, основанных на прямоугольных формах.) Не так давно я наткнулся на очень интересную книгу Брайана Томаса, который проанализировал на предмет всеразличных геометрических закономерностей 98 известных полотен разных мастеров.

Что он нашёл: Золотое сечение, конечно, используется, но не так часто, как ожидалось, отношения 2 к 4, 3 к 5, 5 к 7, треугольники, прямоугольники, квадраты и линии, находящиеся под углом 30 или 60 градусов к углам полотна. Интересно, что только однажды он увидел деление на трети (П. Т.), но в 15 работах он обнаружил квадраты и участие в композиционных построениях диагоналей этих квадратов для определения местоположения важных деталей.

Важно, что Метод диагоналей был получен при помощи экспериментов, а не основан на теории. Правило третьих основано прежде всего на теории, не очень сильной, стоит заметить, поскольку теория Золотое сечения находится в заброшенном состоянии. После того, как я открыл Метод диагоналей, я обнаружил, что пересечение линий Золотого сечения с диагоналями тоже нередко используется в работах художников и фотографов. (Это, конечно, не очень удивительно, ведь Золотое сечение тоже состоит из двух перекрывающися квадратов) Оттого мы пока не будем забывать про правило Золотого сечения.

На мой взгляд, представление «Правила третьих», как одного из основополагающих в фотографии ошибочно и все ешё стоит помнить о «Золотом сечении».

Рис. 3. Фотография: Элске Уижма

На рисунке 3 вы можете видеть, как диагональ, принадлежащая построениям «Метода диагоналей» проходит через глаз, а точка пересечения линий «Правила третьих» находится на не столь важной для композиции части лба. Достаточно часто получается, что хотя бы одна из диагоналей пересекает один из глаз, иногда точка пересечения лежит точно между глаз, указывая на то, что оба объекта одинаково важны.

Дабы просуммировать обозначу основные тезисы:

1. «Метод диагоналей» работает для прямоугольников с любым отношенем сторон.
2. Используя «Метод диагоналей» мы можем очень быстро увидеть важные точки (порой неочевидные).
3. Все точки четырёх диагоналей — возможное местоположение субьекта и деталей, которые требуют внимания.
4. Если главный объект находится не на диагонали, почти всегда есть объективное тому объяснение. (Композиция больших частей более важна, нежели композиция деталей).
5. Важные делали часто лежат на диагоналях с точностью до миллиметра.
6. «Метод диагоналей особенно хорошо подходит для (цифрового) кадрирования, разработки рекламных макетов и постеров и любых случаев увеличения размеров фотографии.
7. В (хорошей) рекламе продаваемый товар (важный текст) всегда лежит на диагоналях.
8. Конечно, есть фотографии, такие, как многие пейзажи — не содержащие деталей. В этом случае «Метод диагоналей» попросту не применяется.
9. Прямые линии, намёки на линии, как, например, рука, стол, ножка стула и прочее также нередко основаны на диагоналях.

В книгах и журналах о композиции в фотографии авторы почти всегда говорят, что все композиционные правила могут быть сознательно применены ещё при съёмке. Я думаю, это звучит не совсем реалистично. Большинство фотографов строят кадр, основываясь на интуиции, затем пробегают по кадру глазами, проверяя нужны ли дополнительные (незначительные) изменения, и только после этого снимают.

Тридцать лет назад я не имел теоретических знаний о композиции, но композиция моих фотографий в то время была ничуть не хуже, а порой даже лучше, нынешней. В то же время сейчас я многому научился и часто исправляю что-то в композиции, но в последний момент, как бы там ни было, фотографирую на авто-пилоте. Я размышлял над этим и обнаружил 33 композиционных правила, которые могут быть применены сознательно, другие 23 фактора учше оставить интуиции (дабы избежать искусственности и бесвкусности композиции).

Оттого и удивительно, как художнику удаётся поместить важные детали точно на диагонали!

«Метод диагоналей» («Diagonal Method») зарегистрирован в Вашингтоне (Библиотека конгресса) под номером Txu-328-140 и в Амстердаме (Merkplaats) под номером 4.620517.1.

Автор: Эдвин Вестхофф
Перевод: Стас Кулеш

P.S.: Дополнительная информация находится на сайте http://www.diagonalmethod.info

Метод диагоналей — sunty_a (дизайнер и фотограф) — LiveJournal

Перевод статьи Эдвина Вестхофа «Метод диагоналей»

 В предыдущих статьях Эдвина Вестхофа уже говорилось, что правило Золотого сечения «не влезает» в стандартный кадр, и поэтому оно было отодвинуто на второй план. Было получено новое универсальное соотношение: Правило третей. Структура горизонтальных и вертикальных линий в Правиле Третей выглядит похожей на линии, проведенные по правилу Золотого сечения. 

Метод Диагоналей

Техническая сторона Диагонального Метода довольно проста: все углы картины или фотографии (а они по 90 градусов) могут быть разделены на два угла по 45 градусов. Эту линию фактически называют биссектрисой (биссектриса — линия, которая делит угол на две равные части). Оказалось, что художники интуитивно помещали важные детали на этих линиях с отклонением максимум 1-1,5 миллиметра.

Я назвал это Методом Диагоналей, потому что эти линии — также математические диагонали двух наложившихся квадратов в пределах прямоугольника. Люди смотрят на картины так же, как их рисовал художник; они следуют взглядом за биссектрисами или диагоналями. (Пока еще это — гипотеза, которая в настоящее время проверяется в нескольких университетах).

Различие между существующими теориями композиции (Правило Третей и Золотое Сечение) в том, что Диагональный Метод не заинтересован в создании «хороших» композиций, а помогает обращать внимание на детали, которые важны для художника психологически или эмоционально. На этом уровне Диагональный Метод полностью субъективен. Это не имеет никакого отношения к размещению линий и форм в определенном месте с намерением получить «лучшую» композицию. Таким образом, мы можем использовать Диагональный Метод, чтобы узнать, каковы были приоритеты художника. Расположение этих деталей сделано по интуиции. Именно поэтому Диагональный Метод настолько точен.

Конечно, возможно потом подрезать фотографию таким образом, чтобы подчеркнуть детали, которые важны для фотографа, помещая их на эти диагонали.

35-миллиметровый кадр — прямоугольник с отношением сторон 2:3. В пределах этого прямоугольника Вы можете нарисовать два квадрата, которые накладываются друг на друга (см. рис. 1). Стороны этих квадратов равны меньшей стороне кадра. В каждом квадрате проведены диагонали. Это и есть линии Метода диагоналей.

рис.1

Я обнаружил, что многие художники, например, Рембрандт, известные фотографы, а также фотографы-любители, часто помещают глаза точно на эти диагонали.

Любое место на этих четырех диагоналях используется художниками, чтобы поместить важные детали. Точки на линиях на рис. 2 могли быть такими деталями.

рис. 2

На картине размера A4 детали часто лежат на диагоналях с погрешностью 1-1,5 миллиметра. Эта же точность была решающим фактором в моем исследовании. Если бы Диагональный Метод был бы столь же неточен, как Правило Третей, то я бросил бы все свои результаты в пыльное мусорное ведро.

Я искал теоретическое объяснение Методу Диагоналей в книгах об искусстве композиции, но ничего полезного не находил.

Рудольф Арнхейм упоминает “силовые линии” квадратов и “силовые области” в своем классическом труде «Искусство и визуальные отношения». Но довольно странно, что он ни слова не говорит о так называемом прямоугольном искусстве, основанным на прямоугольных формах. Он только разбил картины на квадраты.

Брайан Томас проверил 98 известных картин в своей работе “Геометрия в композиции” и нашел много геометрических форм в этих работах, но он не сделал вывода относительно специфического метода, который использовался чаще, чем другие.

Я пришел к выводу, что еще нет исчерпывающих работ по этому вопросу. Если бы я не сделал визуальных экспериментов, я тоже не нашел бы ничего интересного. Я начинал не с теории, а с экспериментирования. Хотя у меня не было намерения найти геометрические формы в искусстве или новый композиционный метод.

Для меня важным было то, что Метод диагоналей фактически работал тогда, когда Правило Третей и Золотое Сечение не работали. (Однако можно использовать Правило Третей, чтобы избежать размещения маленьких и средних предметов в центре кадра. Но это неточно. Кроме того, нет никаких исследований, в которых теория Правила Третей доказана).

Самое большое различие между Методом Диагоналей и Правилом Третей то, что люди не сознательно помещают детали в кадре как кирпичи или телеграфные столбы в надежде, что композиция исправится. А подсознательно ищут и помещают эмоционально важные части в визуально сильных местах (интуитивно).

Самая первая фотография, которую я проверил, была портретом, сделанным одним из моих студентов (рис. 3). И я был удивлен, можно сказать, потрясен тем, что диагональ прошла прямо через центр глаза (желтая линия). А точка пересечения линий Правила Третей находилась на не столь важной для композиции части лба. Достаточно часто получается, что хотя бы одна из диагоналей пересекает глаз, а иногда точка пересечения лежит точно между глазами, указывая на то, что оба объекта одинаково важны.

рис. 3

Выводы

— Используя Метод диагоналей, мы можем очень быстро увидеть важные точки (порой неочевидные) в произведениях искусств.

— Все точки четырех диагоналей — возможное местоположение субъекта и деталей, которые требуют внимания.

— В пейзажах и архитектуре чаще всего нет никаких важных деталей, таким образом, метод диагоналей просто не применяется.

— Метод диагоналей главным образом применяется в портретах и социальной фотографии.

— Метод диагоналей может использоваться, чтобы кадрировать фотографии впоследствии.

— Иногда линии, которые сформированы такими предметами, как оружие, рука и т. д., параллельны диагоналям.

— В рекламных объявлениях маленькие предметы, такие как часы или глаз модели часто лежат на диагоналях.

— Детали, которые важны для художника, почти всегда находятся с точностью до миллиметра на одной или более диагоналях

— «Метод диагоналей» работает для прямоугольников с любым отношением сторон. 

— Если главный объект находится не на диагонали, почти всегда есть объективное тому объяснение. (Композиция больших частей более важна, нежели композиция деталей).

Фотографии и картины

Фотограф: Spencer Platt, Мировая Пресса 2006
Выше: Четыре диагонали пересекают глаза четырех человек.
 
Снизу: Фотография Ранкина «Проголодавшаяся» с тощей девочкой, фактически настолько тощей, что ее одежда должна быть скреплена зажимами.

Момент еды все-таки важен и подчеркнут диагональю из верхнего угла: Диагональ точно пересекает место между ее зубами и шоколадной плиткой.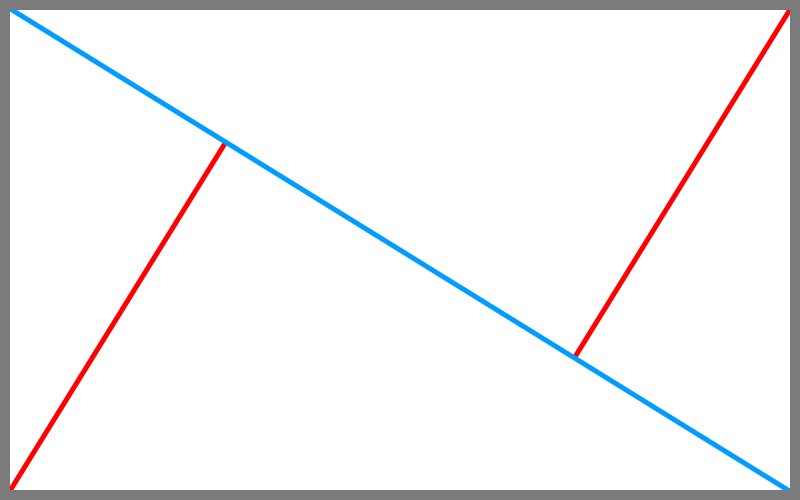 Заметьте, что диагональ не пересекает ее левый глаз: расстояние между ее глазом и диагональю составляет 5 миллиметров. Часто диагональ пересекает именно глаза, но не на этой фотографии, потому что это не самая важная часть. Точность Диагонального Метода ошеломляет.

 Метод Диагоналей 
 Метод Третей
Николас Кейдж в рекламе для часов Mont Blanc.

Диагональ из верхнего левого угла пересекает глаз, а диагональ из нижнего правого угла пересекает центр его часов. Очевидно, Николас Кейдж столь же важен здесь как часы.

Метод Диагоналей

Метод Третей

На этих фотографиях человек не важен, важна только камера.
Диагональ из нижнего правого угла пересекает центр линзы камеры, привлекая внимание.

Метод Диагоналей

Метод Третей

В гравюре Рембрандта «Сборщик налогов» слева видно, что три диагонали пересекают три самых важных детали:
1. Одна из верхнего левого угла пересекает небольшую сумку с деньгами.
2. Одна из верхнего правого угла пересекает правый глаз главного персонажа.
3. Одна из нижнего правого угла пересекает указательный и большой пальцы, которые держат ручку.

Метод диагоналей, Метод третей и золотое сечение

Метод Диагоналей
Леонардо да Винчи «Мона Лиза».
Диагональ пересекает губы. Это — то, что мы ожидали, потому что улыбка Мона Лизы важнее, чем глаза.

Слева: картина Леонардо да Винчи » Жиневра Бенчи » с указанием трех методов:
1. Метод Диагоналей (синяя линия, пересекающая левый глаз).
2. Золотое Сечение (желтые линии).
3. Правило Третей (зеленые пунктиры).

Заключения после четырех лет исследований: новый взгляд на картины:

Работая с Правилом Третей и Золотым Сечением, мы считаем, что композиция станет лучше, если поместить некоторые объекты или линии в специальных местах кадра. Однако есть очень много фотографий, которые признаны общественностью как очень хорошие, но они не подчиняются этой теории.

Метод Диагоналей — это не теория композиции. Ведь Метод Диагоналей используется подсознательно (именно поэтому, он настолько точен.). Способы, какими художники выбирают и размещают детали (на диагоналях) также очень субъективны: это — следствие их характера и образа жизни. (Очевидно, и художники, и зрители смотрят на фотографии и картины вдоль биссектрис, именно поэтому Метод Диагоналей работает).

Рассматривая такое расположение деталей только как композицию, означал бы, что мы пытаемся построить теорию композиции на Методе Диагоналей. Но прежде всего Метод Диагоналей дает нам возможность проникнуть в суть интересов художника.

Это — новое видение, потому что только некоторые предметы интересны или важны. По традиционным методам, чтобы получить лучшую композицию, любые детали от любого предмета могли быть помещены в определенное место. Но с Методом Диагоналей хорошая композиция не цель. Детали по линиям Метода Диагоналей становятся более важными, но это не то же самое, что и хорошая композиция. Таким образом, мы должны изменить свою точку зрения и по-другому читать картины и фотографии. Ведь далеко не всегда теория неподвижных матриц приводит к хорошим или плохим композициям.

Итак, люди замечают детали вдоль биссектрис скорее, чем детали в других местах фотографии, картины или рисунка. Это означает, что когда более важные детали не лежат на биссектрисах, то произведение искусства кажется «неправильным», запутывающим. Кадрируя, можно конечно выбрать, какие детали должны быть важными, а какие нет. Таким образом, субъективный аспект остается. Я получил отзывы от различных людей, которые сказали, что после кадрирования их фотографии выглядели «более приятными». (Все это применимо главным образом к работам, в которых есть люди и где расположение большого предмета не более важно, чем размещение деталей).

Эдвин Вестхоф
Оригинал статьи: www.diagonalmethod.info

«Метод диагоналей» («Diagonal Method») зарегистрирован в Вашингтоне (Библиотека конгресса) под номером Txu-328-140 и в Амстердаме (Merkplaats) под номером 4. 620517.1.

Еще, такие диагонали можно включить в Лайтруме при конечном кадрировании фотографии:

Источник: http://ergonom.livejournal.com/83321.html
[email protected]

Еще примеры иллюстраций по этому методу http://ergonom.livejournal.com/85519.html

Мой пример:

Электронная конфигурация — Уроки Wyzant

Электроны играют решающую роль в
химических реакциях и во взаимодействии соединений друг с другом. Помните,
электрона — это отрицательные частицы в атоме, которые «вращаются» вокруг ядра. Хотя
мы говорим, что они вращаются вокруг ядра, теперь мы знаем, что они на самом деле находятся в случайном состоянии
движения, окружая ядро, а не описывая круги вокруг него, что и подразумевает
орбита. Лучшая аналогия для описания движения электрона внутри атома
— это то, как пчелы жужжат вокруг улья. Они не летают вокруг него,
, но они парят и перемещаются вокруг него, казалось бы, случайным образом.

Электроны увеличиваются в элементах, как и протоны, то есть слева направо и от
сверху вниз в периодической таблице. Таким образом, элемент с наименьшим количеством электронов (
) будет находиться в верхнем левом углу таблицы, а элемент с наибольшим количеством электронов (
) — в правом нижнем углу. Элементы расположены так
что увеличение от элемента к элементу составляет один электрон. Поэтому в первом ряду
мы видим водород и гелий. Это связано с тем, что водород имеет один электрон, а гелий
— два электрона, поэтому мы располагаем их в порядке возрастания.

Электронные орбитали

Мы классифицируем электроны в зависимости от того, на каком орбитальном уровне они находятся. Четыре орбитали
— это s, p, d и f. Они классифицируются по отделам периодической таблицы
следующим образом:

Первая орбиталь – это s-орбиталь. В нем есть место для двух электронов. Электроны
имеют противоположные спины, поэтому логично, что они соединены вместе. S-орбиталь
представляет собой сферу, через которую проходят оси x, y и z, вот так:

Это означает, что два электрона могут занимать любое пространство, видимое в этой сфере,
, и они как бы «парят» в заданном пространстве.

Следующая орбиталь — это p-орбиталь. Он может содержать до шести электронов, поэтому он
имеет три суборбитали (каждая может содержать два электрона). Спины электронов
все еще противоположны, на этот раз разделены на три и три (поскольку первая орбиталь
содержала только два электрона, мы сказали, что спины были противоположными. Теперь, когда эта орбиталь может содержать
шесть электронов, три спина в одну сторону и три крутить наоборот). Орбиталь
не имеет сферической формы, однако у нее есть шесть долей, которые имеют форму воздушных шаров.
Два лепестка по оси X, два по оси Y и два по оси Z. Эти
три разделения считаются суборбитальными и в совокупности составляют всю орбиту
p. Ядро атома расположено там, где встречаются эти три оси. Орбиталь p
выглядит так:

Следующая орбиталь — d-орбиталь. Он может содержать до 10 электронов, поэтому он
имеет пять суборбиталей (каждая может содержать два электрона). Спины электронов
противоположны, поэтому пять из них вращаются в одну сторону, а остальные пять — в противоположную 9.0003 путь. Орбиталь d не имеет сферической формы; она больше похожа на p-орбиталь, за исключением того, что у
есть еще доли, которые нельзя показать все сразу. Мы показали всю p-орбиталь
(все три суборбитали) на одной диаграмме, потому что на каждой оси
было по два лепестка. Однако нам нужно показать пять различных суборбиталей орбитали d
, чтобы полностью объяснить, где расположены доли и как они имеют форму.
Мы покажем вам четыре вида с метками на всех осях.

Первый вид — это лепестки, лежащие в плоскости XY, показанные здесь голубым цветом. Второй вид
представляет собой трехмерный вид лепестков по оси Z, которые вращаются на 360 градусов вокруг оси
. Есть два лепестка, один в верхней полусфере и один в нижней,
и область в форме трубки, которая окружает ось Z и пересекает оси X и Y.
Здесь показано оранжевым цветом. Третий вид представляет собой лепестки в плоскости ZY, причем ось X проходит перпендикулярно ей. Он показан здесь зеленым цветом. Последний просмотр
относится к лепесткам, лежащим на плоскости ZX, и показан здесь розовым цветом. Если бы все эти
слоя сложились вместе, мы бы увидели своего рода изображение вспышки звезды с трубкой, окружающей
посередине.

Последняя орбиталь — это f-орбиталь, и ученые не совсем уверены в форме
ее орбитали. Тем не менее, у них действительно есть, казалось бы, точные предсказания того, куда упадут
электрона. Мы покажем вам следующие вероятности того, где лежат электроны
:

Мы показали вам две вероятности того, где лежат f-орбитали; однако первое изображение
(синим цветом) показано на оси Z. Это фактически повторяется по оси X и снова
по оси Y. Второе изображение (оранжевое) показано в размерах XYZ;
, однако, он повторяется еще три раза, всего в четырех позициях, используя эту форму
и конфигурацию лепестков. Мы говорим, что это вероятные местоположения, потому что ученые
не могут на самом деле отслеживать и определять точное местоположение электронов. Однако через
исследований и способности отслеживать электроны на других орбиталях, ученые могут
сказать, что вероятное местоположение электронов f-уровня находится в одном из этих мест.

В химии правило диагонали (также известное как правило Маделунга) — это руководство, объясняющее порядок, в котором электроны заполняют орбитальные уровни. Орбиталь 1s ²
всегда заполняется первой и может содержать 2 электрона. Затем заполняется уровень 2s ²
, который также может содержать 2 электрона. После этого электроны начинают
заполняют орбиталь 2p ⁶ и так далее. Диагональное правило обеспечивает правило, определяющее точный порядок заполнения этих орбиталей, и выглядит следующим образом:

Как видите, красные стрелки указывают на заполнение орбитальных уровней. Начиная с
вверху, первая красная стрелка пересекает орбиталь 1s ² . Если вы проследите
этих стрелок вниз по списку, вы легко сможете определить порядок, в котором электроны заполняют
орбитальные уровни.

Исключением из этого правила является заполнение орбиталей более тяжелых электронов.
Например, при заполнении орбиталей 5s ² правило гласит, что заполнится 5s ²
, а затем заполнится 4d ¹⁰ . Однако при заполнении этих орбиталей
для некоторых металлов только один электрон заполнит орбиталь 5s ² , а
следующий электрон перескочит на орбиталь 4d ¹⁰ . Это можно предсказать,
но нельзя точно определить, пока это не наблюдается.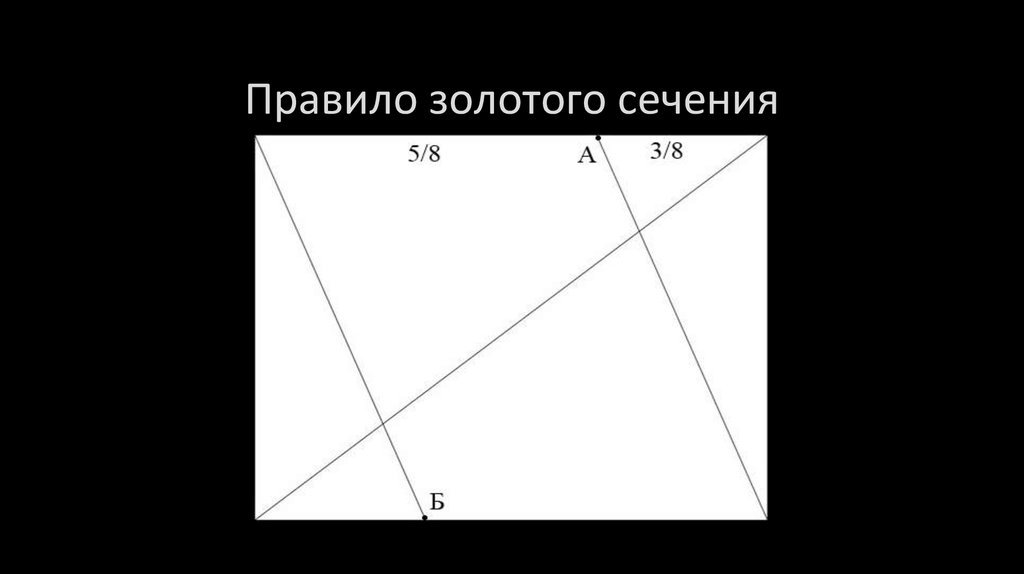 То же самое верно и для
6s ² орбиталь — для некоторых тяжелых металлов 6s ² будет содержать только
один электрон, а остальные электроны перейдут на 5d ¹⁰ орбиталь.

Электронное обозначение

Следуя правилу диагонали, можно легко записать электронную конфигурацию.
Мы будем просто использовать имена орбит, которые мы узнали из диагонального правила (1s ² ,
2s ² и так далее). Однако мы собираемся написать только число электронов
, который на самом деле содержит атом. Например, водород имеет один электрон, который
приходится на 1s-орбиталь. Таким образом, электронная конфигурация водорода равна 1s ¹ .
Мы пишем верхний индекс как 1, потому что есть один электрон. Гелий, следующий элемент,
, содержит два электрона. Они оба заполняют 1s-орбиталь, поэтому электронная конфигурация
для гелия равна 1s ² . Здесь мы снова пишем верхний индекс как 2, потому что
есть два электрона.

Электронная конфигурация перемещается по таблице Менделеева и вниз.
Вы могли заметить, что сначала мы поместили один электрон на 1s-орбиталь (с водородом), а затем
мы поместили два электрона на 1s-орбиталь (с гелием). Продолжая эту тенденцию, мы
будем иметь 3 электрона с литием. Мы поместим два из них на 1s-орбиталь,
, и один из них на 2s-орбиталь, так что электронная конфигурация будет 1s ²
2s ¹ . Однако мы также можем написать это, используя конфигурацию гелия,
, потому что это благородный газ. Благородные газы являются стабильными элементами, поэтому мы можем использовать их конфигурации
для определения других конфигураций. Таким образом, вместо того, чтобы писать 1s ²
2s ¹ , мы будем писать [He] 2s ¹ . Это означает, что литий содержит
той же конфигурации, что и гелий, а затем имеет еще один электрон на 2s-орбитали.
Обратите внимание, что мы используем скобки, чтобы заключить предыдущий благородный газ, а затем мы продолжаем писать конфигурацию
, как обычно. Это может показаться не таким уж большим делом,
или сокращение прямо сейчас, но как только вы опуститесь довольно далеко вниз по таблице Менделеева, этот
сэкономит вам много времени и энергии.

Мы покажем вам один короткий пример этого. Допустим, нам нужно определить электронную конфигурацию
для Ba, Barium. Посчитав по таблице, мы получили бы следующую конфигурацию
:

1s ² 2s ² 2p ⁶ 3s ² 3p ⁶ 4s ²
3d ¹⁰ 4p ⁶ 5s ² 4d ¹⁰ 5p ⁶ 6s ²

Вместо того, чтобы записывать все это, мы могли бы просто найти предыдущий благородный газ,
, то есть Xe. Поэтому мы можем написать [Xe], а затем разобраться с остальной конфигурацией.
Мы смотрим и видим, что Ba находится в 6-м ряду, поэтому мы знаем, что начнем
с 6s ² . Мы можем посмотреть и увидеть, что Ba — второй элемент в этом ряду,
, так что у него есть два электрона, чтобы двигаться по 6s-орбитали.

Таким образом, мы можем заключить, что окончательная электронная конфигурация Ba имеет вид [Xe] 6s ² .

Электронный спин

Каждый электрон, помещенный на орбиталь, имеет особенность, которую мы называем «спин». Мы уже говорили
об электронах, которые, как считалось, имели определенную «орбиту», а затем
позже обнаружили, что они парят в местах, перечисленных выше. Ну, электроны не вращаются в буквальном смысле
, но их движение похоже на то, как будто кто-то кувыркается, очень быстро, 9 раз.0003 случайное состояние. Это называется спин. Каждый электрон может иметь либо спин +1/2, либо спин
-1/2, что указывает на направление его движения. Никогда не бывает 0 спинов. При заполнении
орбиталей электроны вращаются парами, один + и один -. Электроны со спином
вверх (+) заполняются первыми, а электроны со спином вниз (-) заполняются вторыми.
будет выглядеть так:

и так далее. Поскольку на s-орбитали могут находиться два электрона, мы рисуем один прямоугольник, в котором
могут поместиться два электрона (обозначены здесь стрелками). Поскольку p-орбиталь может содержать
6 электронов, мы рисуем 3 ящика, каждый из которых будет содержать 2 электрона. Это будет продолжаться
с d-орбиталью (10 электронов помещаются в 5 ящиков) и f-орбиталью (14 электронов
помещаются в 7 ящиков).

Эти ящики заполняются в определенном порядке — все ящики в одном столбце будут заполнены сначала
электронами со спином вверх, а затем со спином вниз. Так, например, если элемент имеет
конфигурацию 1s ² 2s ² 2p ³ , это будет выглядеть как
это:

Как видите, мы сначала заполнили клетки стрелками вверх (электроны). Если бы у нас было еще
электрона, мы бы вернулись и добавили их во второй столбец как
электрона со спином вниз.

Улучшенные термоэлектрические характеристики полугейслеровых сплавов Zr1-xTaxNiSn путем легирования по диагональному правилу

Сохранить цитату в файл

Формат: Резюме (текст)PubMedPMIDAbstract (текст)CSV

Добавить в коллекции

• Создать новую коллекцию
• Добавить в существующую коллекцию

Назовите свою коллекцию:

Имя должно содержать менее 100 символов

Выберите коллекцию:

Невозможно загрузить вашу коллекцию из-за ошибки
Повторите попытку

Добавить в мою библиографию

• Моя библиография

Не удалось загрузить делегатов из-за ошибки
Повторите попытку

Ваш сохраненный поиск

Название сохраненного поиска:

Условия поиска:

Тестовые условия поиска

Эл. адрес: (изменить)

Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый будний день

Который день? воскресеньепонедельниквторниксредачетвергпятницасуббота

Формат отчета: SummarySummary (text)AbstractAbstract (text)PubMed

Отправить максимум: 1 штука5 штук10 штук20 штук50 штук100 штук200 штук

Отправить, даже если нет новых результатов

Необязательный текст в электронном письме:

Создайте файл для внешнего программного обеспечения для управления цитированием

. 2020 22 января; 12 (3): 3773-3783.

дои: 10.1021/acsami. 9b21517. Epub 2020 8 января.

Сюн Ян ¹ , Чжоу Цзян ² , Хуэйцзюнь Кан ¹ , Цзуннин Чен ¹ , Энью Го ¹ , Дацюань Лю ¹ , Фенфен Ян ¹ , Рэнгэн Ли ¹ , Сюэ Цзян ² , Тонгмин Ван ¹

Принадлежности

• ¹ Ключевая лаборатория контроля затвердевания и цифровых технологий подготовки (провинция Ляонин), Школа материаловедения и инженерии, Даляньский технологический университет, Далянь 116024, Китай.
• ² Ключевая лаборатория модификации материалов лазерным, ионным и электронным пучками (Даляньский технологический университет), Министерство образования, Далянь 116024, Китай.

• PMID: 31880427
• DOI: 10.1021/acsami.9b21517

Сюн Ян и соавт. Интерфейсы приложений ACS. 2020 .

. 2020 22 января; 12 (3): 3773-3783.

дои: 10.1021/acsami.9b21517. Epub 2020 8 января.

Авторы

Сюн Ян ¹ , Чжоу Цзян ² , Хуэйцзюнь Кан ¹ , Цзуннин Чен ¹ , Энью Го ¹ , Дацюань Лю ¹ , Фенфен Ян ¹ , Рэнгэн Ли ¹ , Сюэ Цзян ² , Тонгмин Ван ¹

Принадлежности

• ¹ Ключевая лаборатория контроля затвердевания и цифровых технологий подготовки (провинция Ляонин), Школа материаловедения и инженерии, Даляньский технологический университет, Далянь 116024, Китай.
• ² Ключевая лаборатория модификации материалов лазерным, ионным и электронным пучками (Даляньский технологический университет), Министерство образования, Далянь 116024, Китай.

• PMID: 31880427
• DOI: 10.1021/acsami.9b21517

Абстрактный

Хотя легирование Sb считается наиболее эффективным методом регулирования концентрации носителей в оптимальном диапазоне для сплавов полугейслера (HH) на основе ZrNiSn, получающаяся в результате теплопроводность остается высокой. Следовательно, цель этого исследования состояла в том, чтобы исследовать эффект допинга по «диагональному правилу»; то есть место Zr было смещено Ta, что может одновременно увеличить электропроводность и уменьшить теплопроводность решетки. Предел твердой растворимости Ta в матрице ZrNiSn был определен равным х = 0,04. Максимальное значение ZT , 0,72, было достигнуто при 923 К для Zr _0,98 Ta _0,02 NiSn. Кроме того, ZT _AVG увеличился на 10,2% для ZR _0,98 TA _0,02 NISN по сравнению с ZRNISN _0,99 SB _{.00113, который был MANERED 9013, который был MANERED 9013, который был MANERED 9013, который был MANERED, а ATRELED — 9042.1013 —} . проводимость Zr _0,98 Ta _0,02 NiSn. Эти результаты свидетельствуют о том, что легирование Ta более эффективно, чем легирование Sb в сплавах HH на основе ZrNiSn. Кроме того, микротвердость Zr _1-x Ta _x NiSn был существенно улучшен с увеличением содержания Ta и также был намного выше, чем у других традиционных термоэлектрических материалов.

Ключевые слова: допинг; электрическая проводимость; полугейслеровы сплавы; решеточная теплопроводность; термоэлектрический.

Похожие статьи

• Непрерывное увеличение структурного беспорядка для подавления решеточной теплопроводности полугейслеровых сплавов на основе ZrNiSn за счет многоэлементного и многокомпонентного легирования с очень низким содержанием Hf.

  Гонг Б., Ли И, Лю Ф, Чжу Дж, Ван Х, Ао В, Чжан С, Ли Дж, Се Х, Чжу Т. Гонг Б. и др. Интерфейсы приложений ACS. 2019 10 апреля; 11 (14): 13397-13404. doi: 10.1021/acsami.9b00648. Epub 2019 26 марта. Интерфейсы приложений ACS. 2019. PMID: 30883083

• Эволюция in situ вторичных металлических фаз в нестехиометрическом ZrNiSn для улучшения термоэлектрических характеристик.

  Джохари К.К., Шарма Д.К., Верма А.К., Бхардвадж Р., Чаухан Н.С., Кумар С., Сингх М.Н., Батула С. , Гахтори Б. Джохари К.К. и др. Интерфейсы приложений ACS. 2022 4 мая; 14(17):19579-19593. doi: 10.1021/acsami.2c03065. Epub 2022 20 апр. Интерфейсы приложений ACS. 2022. PMID: 35442621

• Адаптация состава для реализации высоких термоэлектрических характеристик в не содержащих гафния сплавах ZrNiSn n-типа с половинным гейслеровым сплавом.

  Чаухан Н.С., Батула С., Гахтори Б., Маханти С.Д., Бхаттачарья А., Вишвакарма А., Бхардвадж Р., Сингх В.Н., Дхар А. Чаухан Н.С. и соавт. Интерфейсы приложений ACS. 201926 декабря; 11 (51): 47830-47836. дои: 10.1021/acsami.9b12599. Epub 2019 12 декабря. Интерфейсы приложений ACS. 2019. PMID: 31441632

• Картирование фазовых границ в ZrNiSn Half-Heusler для улучшения термоэлектрических характеристик.

  Ли С, Ян П, Ван И, Чжан З, Цинь Д, Сюэ В, Чен С, Хуан Ю, Се С, Ван С, Ян М, Ван С, Цао Ф, Суй Дж, Лю С, Чжан Ц. Ли Х и др. Исследования (Ваш округ Колумбия). 2020 30 января; 2020:4630948. doi: 10.34133/2020/4630948. Электронная коллекция 2020. Исследования (Ваш округ Колумбия). 2020. PMID: 32055798 Бесплатная статья ЧВК.

• Зонные структуры и транспортные свойства высокоэффективных полугейслеровских термоэлектрических материалов по основным принципам.

  Фанг Т., Чжао С., Чжу Т. Фанг Т. и др. Материалы (Базель). 2018 19 мая; 11 (5): 847. дои: 10.3390/ma11050847. Материалы (Базель). 2018. PMID: 29783759 Бесплатная статья ЧВК. Обзор.

Посмотреть все похожие статьи

Цитируется

• Повышение подвижности в сильно легированных полупроводниках за счет электронной маскировки.