Правила игры сапер для начинающих: Как играть в Сапера

Как решить «Сапёра» (и сделать его лучше) / Хабр

«Сапёр» (Minesweeper) — это простая игра с простыми правилами, однако некоторые её конфигурации создают любопытные трудности. В этой статье мы создадим солвер «Сапёра» с увеличивающейся сложностью, и поразмышляем над тем, как меняется динамика игры при постепенном повышении уровня помощи. В конце мы разработаем новый вариант игры с гораздо более интересным геймплеем.

Локальные рассуждения: ноль соседних мин

В оригинальной игре используется один автоматический механизм: когда игрок открывает клетку, рядом с которой нет мин, движок игры открывает все соседние клетки. Это ничем не угрожает игре, поэтому можно спокойно позволить компьютеру это сделать, а сама ситуация сразу же понятна игроку и никак не мешает геймплею.

Такое рассуждение совершенно локально: для принятия решения о следующем действии учитывается информация только одной клетки.

Сложно придумать ситуацию, в которой игра стала бы хуже без этой автоматической помощи. Попробуйте сыграть в такую игру, чтобы получить представление о том, как она проходит без автоматического открытия клеток [в оригинале статьи все примеры интерактивны]:

Локальные рассуждения с учётом окружения

Новому игроку несложно будет понять, что если количество соседних мин, то есть число, показанное в клетке, равно количеству неоткрытых соседних клеток, то все эти клетки должны быть минами, поэтому на них надо поставить флажки. Аналогично, когда количество соседних мин равно количеству соседних флагов, то оставшиеся неоткрытыми соседние клетки должны быть пусты.

В этих правилах учитывается одна клетка, а также состояние соседних (открыты/поставлен флажок).

Реализация этих правил вручную может быть увлекательной. Если добавить таймер, то игрок начинает учиться применять их быстро и точно. Это превращает «Сапёра» в игру на реакцию.

Что произойдёт, если мы автоматизируем эти правила?

У подобной автоматизации есть интересный побочный эффект — установка флажка может мгновенно иметь фатальные последствия.

В остальном у нас могут возникнуть ситуации, которые можно разбить на три категории:

1. Игры, полностью разрешаемые применением автоматических правил
2. Сложные ситуации, требующие для рассуждений большего количества клеток
3. Состояния игры, в которых нет логического пути вперёд — игроку остаётся только выбирать случайно, возможно с учётом вероятностей.

Ситуация 1 кажется красивой, но не особо интересной, если будет возникать слишком часто. Будут ли такие игры лучше без автоматического решения? Может быть и нет; такие игры очень просты даже при решении вручную, и игроку не особо интересно играть в игры, в которых нет трудностей. Хотя, разумеется, в игре на реакцию сложность есть всегда: нужно действовать как можно быстрее.

Очень привлекательной мне кажется ситуация 2. Мы больше сосредотачиваемся на решении логических условий, меньше тратя время на точное прицеливание и нажимание правильных кнопок. Это делает «Сапёра» больше похожим на активную головоломку.

Ситуация 3 полностью разрушает всю увлекательность. Впрочем, я слышал, что некоторым людям нравится играть в игры со случайностью.

Можно ли избавиться от ситуации 3?

Полное решение: глобальные рассуждения

Для алгоритмического обнаружения всех необходимых для состояния игры логических условий нам нужно выполнить исчерпывающий поиск всех состояний игры. Доказано, что Minesweeper — это NP-полная задача. Ниже показан небольшой, но интересный и наглядный пример состояния игры, имеющий всего одно логическое решение, но для его нахождения необходимо учитывать состояние игры целиком:

Возможно ли выполнить поиск по всему пространству состояний игры? Сколько всего существует вариантов состояний s?

Дано:

w = ширина поля

h = высота поля

k = количество мин

n = w · h

Тогда количество возможных состояний s равно

Для стандартных уровней «Новичок», «Любитель» и «Профессионал» это даёт нам:

Мы понимаем, что наивный подход здесь совершенно не подходит. Давайте посмотрим, как бы мог выглядеть наивный алгоритм, и узнаем, можно ли его оптимизировать в нечто работающее.

Наивный алгоритм

Задача алгоритма — найти все необходимые для заданного состояния поля логические условия. Было бы сложно реализовать это тщательным продумыванием решений; компьютер гораздо лучше справляется с быстрым выполнением кучи глупых действий.

Что мы можем сделать «глупого»: сгенерировать все возможные перестановки позиций мин для всех оставшихся мин. Если такая перестановка соответствует всем открытым числам, то она будет правильным решением игры. Затем мы изучаем все возможные перестановки, находим все возможные решения, но по-прежнему не знаем, какое из них является верным.

Если во всех возможных решениях есть что-то общее, или среди открытых клеток, или среди клеток, помеченных как мины, то мы понимаем, что это общее должно быть частью верного решения для текущего поля. И в самом деле: невозможно создать верного решения, не имеющего таких совпадающих элементов, иначе бы мы их обнаружили.

Таким образом мы можем найти все необходимые для текущего состояния поля логические условия.

Клетки с ограничениями и без ограничений

У приведённого выше алгоритма есть очевидная проблема: количество состояний, которое ему нужно исследовать. Но не все клетки одинаковы. Неоткрытые клетки, находящиеся рядом с числом, очевидно ограничены этим числом. Мы назовём эти клетки ограниченными. Оставшиеся клетки мы назовём неограниченными.

Если мы реализуем приведённый выше алгоритм, но будем выполнять поиск только в пространстве состояний ограниченных клеток, и будем возвращаться назад, как только нарушим ограничение, то во многих играх сможем решить все логические условия за разумный промежуток времени:

В случае неограниченных клеток мы никак не можем узнать, где расположены мины, и логически сразу знаем об этом. Это означает, что можно исключить их из вычисления и рассматривать только расположение мин рядом с открытыми числами.

Однако мы знаем, что некое количество мин может попасть во множество неограниченных клеток; если есть 6 мин и 4 ограниченных клетки, то в ограниченных клетках может быть максимум 4 мины, то есть не менее 2 мин должно находиться в неограниченных клетках. По аналогичной логике мы иногда можем определить, что все неограниченные клетки должны быть пустыми или все содержать мины.

В показанном ниже случае мы знаем позиции всех мин, поэтому ИИ должен быть способен понять, что оставшиеся ячейки не заняты:

В следующем случае мы не знаем позиций всех мин, но можем понять, что оставшуюся мину нужно поместить в одну из двух клеток слева вверху. Это значит, что оставшаяся в правом нижнем углу клетка свободна:

Версия со случайностью

Если мы автоматически будем запускать глобальный солвер, то получим оптимизированную по случайности версию «Сапёра»:

Можно разделить игры в этой версии на три категории:

1. Игры, в которых игрок делает произвольный выбор и выигрывает.
2. Игры, в которых игрок делает произвольный выбор и проигрывает.
3. Игры, в которых работа ИИ требует много времени, и игрок на самом деле может использовать рассуждения.

Очевидно, что это игра со случайностями. В чём же привлекательность таких игр? С точки зрения логики показанная выше игра схожа с такой:

Но какая из игр со случайностями лучше? Похоже, что смысл других игр со случайностями заключается в существовании сложной связи между действиями игрока и победой/проигрышем. Для вытягивания номеров лотереи используются сложные машины, которые специально не торопятся в выборе номера и делают из показа этого номера целое шоу.

Возможно, большое поле, которое решается автоматически, является довольно хорошей игрой
со случайностями, учитывая то, что игрок наблюдает за постепенным открыванием всех клеток.

Можем ли мы придумать другой тип игры?

Детерминированная версия

Теперь у нас есть ИИ, способный определять все логичные шаги из заданного состояния игры. Иногда он не сможет находит логичных шагов. В таких ситуациях игроку приходится угадывать и он может проиграть, если ему не повезёт.

Что если мы добавим ещё одно правило? Когда у игры нет логичного пути вперёд, то мы можем попросить о помощи. Если ИИ соглашается, что игрок не может ничего поделать, то приходит ему на помощь. В противном случае игрок немедленно проигрывает. Это может быть интересным. Какой может быть такая помощь? Возможно, нужно открыть одну клетку, вне зависимости от наличия в ней мины:

Таким образом, мы полностью избавились от ситуаций, в которых можно было проиграть случайно.

Однако тут есть одно исключение: по-прежнему существует вероятность вырожденных ситуаций, в которых глобальный солвер не может закончить вычисления за разумный промежуток времени. К сожалению, это неизбежный результат того, что задача «Сапёра» NP-полная.

Как кнопка «Попросить помощи» влияет на игровой процесс? Она приводит тому, что игра больше сосредотачивается на логике; это самый «головоломный» вариант «Сапёра». Кто-то может подумать, что игра станет проще, но на самом деле она усложняется. Теперь ошибкам игрока нет оправданий, и кнопка накажет его, если он что-то упустил. Без кнопки легко прийти к выводу, что ты исчерпал все логичные возможности и единственный вариант развития событий — попытаться угадать случайным образом. Но из-за существования кнопки игрок обязан быть прав в этой оценке.

В заключение

Реализовав полный солвер «Сапёра», мы смогли создать разновидность игры, избавленной от её проклятья: теперь невозможно проиграть из-за того, что приходится выбирать случайно, когда уже почти решил всё поле. Эта версия отличается от оригинальной игры только в те моменты, когда нужно угадывать случайным образом, поэтому могу предположить, что она намного увлекательнее, чем оригинальная игра.

Кроме того, мы разработали вариант игры, автоматически решающий простые локальные правила. Стоит ли использовать такую помощь — зависит только от вас. Она смещает фокус игры с механического щёлканья к более головоломному игровому процессу. При этом необязательно пользоваться усовершенствованием геймплея, которое обеспечивает кнопка «Попросить помощи».

Продвинутая тактика игры в «Сапёр» / Хабр

[Пятничный перевод статьи 1999 года одного из авторов движка игры Thief Шона Барретта]

Неприятное положение в «Сапёре»

В этом положении я знаю, что вокруг меня есть куча мин, но не могу определить, где они находятся. Несколько мин может быть в одном из двух мест (розовые или голубые), группа мин может быть расположена в одной из двух комбинаций (светло-/тёмно-зелёные). Кроме того, есть ещё сложная ситуация с «5» и «6» в левом верхнем углу, которую я никак не выделил.

Голубые/розовые — взаимоисключающие пары, светло-/тёмно-зелёные — взаимоисключающие группы

«Сапёр»: логика или вероятность

В «Сапёра» можно играть двумя способами: как в логическую или в вероятностную игру.

Технически, вероятность подразумевает логику. Если вы можете логически доказать, что мина должна находиться в определённом месте, то вероятность равна 100%. Если можете доказать, что её в этом месте нет, то вероятность равна 0%. То есть в каком-то смысле для нас важны только вероятности. Тем не менее, игрок для распознавания таких стопроцентных ситуаций игрок использует логическую дедукцию. Иногда, особенно на низких уровнях сложности, её достаточно для прохождения уровня, никакого подсчёта вероятностей не требуется.

Но бывают такие ситуации, когда вся логика мира не может вас спасти. Простой пример — ситуация с «T», которую видно внизу по центру. Она немного осложняется дополнительными соседними минами. (В простейшем случае «2» заменяется на «1», а «5» — на «3», чтобы ситуация была симметричной.)

Нет никакого способа получить больше информации о вероятном положении одной мины, оставшейся в одной из этих клеток. Шансы пятьдесят на пятьдесят — можете бросать монетку. Когда у вас получается что-то подобное, лучше сразу же сделать выбор и не откладывать на потом. Если догадка будет неверной, то вы хотя бы сэкономите время на решение остальной части поля. (Но лично я стремлюсь к завершённости, поэтому оставляю такие случаи на потом. И не вините себя за то, что не угадали. Когда победа или проигрыш зависят от броска монеты — это плохой гейм-дизайн.)

Тактика в конце игры

В эндшпиле можно использовать очень простую тактику — считать количество оставшихся мин. Допустим, я решил всё, кроме правой нижней части поля. Здесь может быть всего две конфигурации мин, соответствующих данным:

Возможные конфигурации мин в правом нижнем углу

Если у вас получилась такая позиция и счётчик говорит, что осталось всего две мины, то ответ готов: это должна быть конфигурация B.

Если счётчик говорит, что осталось три мины, то это необязательно конфигурация A. Это может быть схема B с оставшейся миной в одной из правых нижних групп клеток 3×3.

На самом деле, шансы в пользу конфигурации B.

Локальные вероятности

Если вы исследуете вероятности только «локально», вы видите, что каждая из клеток в отмеченных взаимоисключающих группах имеет шанс 50-50 быть миной. Говоря «локально», я подразумеваю, что если рядом с двумя неизвестными клетками есть «1», то вероятность спрятанной мины у каждой из них равна 50%.

Именно такая ситуация сложилась внизу в центре: каждая из соседних клеток, соседних к неизвестной паре, содержит в точности одну мину, то есть каждый из соседних фрагментов данных предполагает 50-процентную вероятность. В самом левом верхнем углу похожая ситуация:

С абсолютной точностью в каждом из розовых овалов есть по одной мине, то есть всего осталось 7 мин

Ситуация в правом нижнем углу тоже чем-то похожа: рядом с каждым из чисел на «границе» есть одна мина и две клетки, в которых она может быть.

Если рядом с клеткой есть одна скрытая мина, но три закрытых клетки, то вероятность мины в каждой из клеток составляет 33%; каждая из четырёх закрытых клеток имеет вероятность 25%. Если у нас две скрытые мины и три закрытых клетки, то каждая клетка имеет вероятность 66%.

Вот ситуация с «локальной вероятностью» для всего поля:

Как вы видите, несколько клеток в верхней левой области имеют несколько вероятностей; закрытая клетка рядом с «2» и «6» и одна рядом с «3» и «5». (Клетка рядом с «5» и «6» благодаря им всё равно имеет вероятность 66%, поэтому нет видимого несоответствия.)

Разрешение конфликтов локальной вероятности

Вы наверно, задаётесь вопросом, что значит наличие конфликтующих локальных вероятностей. Интуиция может подсказать, что наибольшая вероятность должна выиграть. Например, клетка между «6» и «2» должна на самом деле иметь 66%. Это будет значить, что у крайней левой клетки с вероятностью 50% она на самом деле равна 33%. Или можно попробовать как-то комбинировать приоритеты: возможно, вероятность будет 5/6 или средним значением.

Но ничто из этого на самом деле неверно. Данные, из которых получены вероятности, не независимы друг от друга, поэтому никакие прямолинейные математические расчёты не будут верными. Причина правильности локальной догадки о 50% внизу в центре в том, что она действительно независима ни от чего другого. Если случайным образом воссоздавать поле по уже имеющимся у нас данным, то ровно в половине из моделей мина будет в одной из двух клеток. (Вероятность иногда запутывает людей, которые не могут разобраться, какие правила расчёта вероятностей применимы в конкретной ситуации. Такой подход — это гарантировано верный путь, потому что он основан на определении вероятности в статистическом прогнозировании: вычисление выполняется измерением во всех возможных конфигурациях, которые могли привести к текущей ситуации, при этом все они считаются одинаково вероятными.)

То есть для верных измерений в ситуации в левом верхнем углу нужно рассмотреть все возможные конфигурации мин, удовлетворяющие уже собранным данным, а затем посчитать, какой процент из них содержит мину в нужной позиции.

Непосредственный подсчёт потребовал бы много времени. К счастью, существуют и другие способы.

Подсчёт конфигураций

Абстрактный способ вычисления вероятностей заключается в обходе всех возможных конфигураций мин, отбрасывании конфигураций, не отвечающих собранным данным, и вычислении статистики для каждой из возможных позиций.

Более практичный подход — рассматривать только те варианты, которые нельзя отбросить. Для этого нам нужно применить логику и сгенерировать все возможные ситуации, которые могут соответствовать имеющимся данным. Я уже показывал два варианта для правого нижнего угла, а вот вероятности для левого верхнего:

Возможные конфигурации для левого верхнего угла

(Как и раньше, овал высотой в две клетки показывает, что мина может с одинаковой вероятностью находиться в любой из клеток. Я мог бы перечислить каждый из двух этих случаев отдельно, то есть получилось бы 10 конфигураций, но никакой пользы в этом для нас нет. Структура таблицы: два ряда (пронумерованные как «1» и «2») отличаются положением мины в четвёртом ряду. Три столбца характеризуются положением мин во втором ряду.)

Теперь есть искушение воскликнуть: «ага, вот пять случаев, так что мы можем подсчитать количество случаев для каждой из возможных позиций мины». Например, мина находится в четвёртом ряду (рядом с левой нижней «1») находится слева в двух верхних случаях, и справа в трёх нижних случаях. Поэтому можно решить, что она имеет вероятность в 60% находиться справа, рядом с «6». (Это позиция с конфликтующими локальными вероятностями 50% и 66%.)

Однако мы упускаем одну тонкость — количество мин в некоторых случаях разное: в A1 шесть мин, в B2 — четыре, и по пять во всех остальных случаях.

Считаем ненайденные мины

Для подробного изучения этой тонкости давайте вернёмся к более простой ситуации в правом нижнем углу.

Возможные конфигурации с правом нижнем углу

Предположим, что я уже открыл остальное поле и знаю, что осталось ровно три мины.

Есть искушение предположить, что наиболее вероятна конфигурация A ровно с тремя минами. Но это неверно.

Ещё одно искушение — вспомнить, сколько всего было мин и сколько всего клеток, и сказать: «каковы шансы того, что нижняя область 3×3 будет пустой». Это тоже неверно. Очень сложно объяснить, почему это ошибка, наверно, её можно сравнить с парадоксом Монти Холла. Однако достаточно сказать, что в действительности шансы в этой ситуации не зависят от общего количества мин и размера поля.

Правильный ответ таков: сколько возможных конфигураций из трёх мин соответствуют нашим знаниям о поле? Из рисунка мы видим, что две: конфигурации A и B. Но в B всего две мины. Третья мина может быть в любой из клеток нижней области 3×3, о которой мы пока не собрали никаких данных. То есть всего есть девять вариантов конфигураций B, я просто не стал изображать их все.

Следовательно, существует всего десять возможных конфигураций. Каждая из десяти конфигураций равновероятна. (Как я упоминал ранее, это критически важно для понимания вероятности. Шансы того, что компьютер сгенерировал любой из этих вариантов малы, но они равно малы, потому что компьютер [насколько мы знаем] давал каждой конфигурации равные шансы. Вы с равной вероятностью можете выбросить конфигурацию из десяти «орлов» подряд и последовательность два «орла», одна «решка», один «орёл», три «решки», один «орёл», одна «решка» и один «орёл». Вероятнее выбросить в сумме пять «орлов» и пять «решек», но не никакую конкретную последовательность «орлов» и «решек». В «Сапёре» мы имеем дело с конфигурациями мин, которые похожи на последовательности бросков монеты.)

Поскольку каждая из десяти конфигураций (девять для B, одна для A) равновероятны, конфигурация B в данном случае имеет вероятность 90%!

Если бы на этом этапе было четыре мины, то у конфигурации A имелось бы девять вариантов. Конфигурация B имела бы по одному варианту для каждого варианта расположения двух мин в левом нижнем углу; это C(9,2), то есть 9!/((9-2)! * 2!) или 9*8/2, равное 36. В этом случае конфигурация B имела бы вероятность только 75%.

С пятью минами конфигурация A имела бы 36 вариантов, а конфигурация B — 9*8*7/6 = 84 варианта; то есть шансы B были бы чуть больше 66%.

В случае шести мин B имела бы вероятность 60%. С семью минами у B было бы всего 50%. С восемью минами B была бы менее вероятна, чем A; в этом случае с таким количеством мин в оставшихся позициях конфигураций становится меньше. Рассмотрим наихудший случай, когда осталось 11 мин. (Шанс этого чрезвычайно мал, но если такая ситуация возникнет, то применимы эти вероятности.) В конфигурации B, во всех закрытых клетках будут мины, в конфигурации A во всех, кроме одной. То есть существует 9 вариантов для A и всего один для B.

Окончательное решение

На имеющемся у нас поле осталось девять мин. Одна из них находится в центральной нижней области, и её положение полностью независимо, поэтому можно его игнорировать. То есть мы рассматриваем всё поле, кроме этого случая: не найдено всего восемь мин. (Чтобы не возникло путаницы, я продолжу явным образом считать овал в левом верхнем углу, потому что это изображение левого верхнего угла.)

Может сложиться любая комбинация из левой верхней и правой нижней конфигураций, за исключением одной из них (A1 + A), для которой потребуется девять мин. Поэтому мы должны перечислить каждую из этих возможных конфигураций и сосчитать оставшиеся мины и закрытые клетки.

На самом деле, количество закрытых клеток независимо: их девять в правом нижнем углу и три в левом верхнем, то есть всего 12.

Вверху слева	Внизу справа	Количество мин	Осталось мин	Закрытые варианты
A1	B	8	0	1
B1	A	8	0	1
B1	B	7	1	12
A2	A	8	0	1
A2	B	7	1	12
B2	A	7	1	12
B2	B	6	2	66
C2	A	8	0	1
C2	B	7	1	12

Таким образом, всего существует 118 возможных комбинаций. Исходя из этого мы можем независимо посчитать количество комбинаций для каждой из левых верхних и правых нижних конфигураций:

Конфигурация	Варианты	Процент
A1	1	1
B1	13	11
A2	13	11
B2	78	66
C2	13	11
A	15	13
B	103	87

Далее я обошёл каждую клетку на поле и вычислил её вероятность, суммировав количество вероятностей, в которых она появляется, и поделив на 118. (На самом деле, просто сложив указанные выше проценты.) Кроме того, в среднем в каждой из закрытых клеток есть мина в 15 из 118 вариантов (то есть шансы на то, что по крайней мере в одной закрытой клетке есть мина, очень высоки). [Это можно вычислить умножением количества оставшихся мин на закрытые варианты, что даёт нам среднее количество мин в закрытых клетках.]

Вероятности наличия мины

(Следует сказать, что это не показывает всей доступной информации. Например, мы знаем, что вероятности двух тёмно-зелёных клеток с 87% связаны — если одна верна, то другая тоже. И голубые 13-процентные клетки, в которых есть мины по конфигурации A, тоже связаны. Остальные голубые 13-процентные клетки не связаны. Если в одной из них есть мина, вероятность того, что в любой из оставшихся есть мина, уменьшаются.)

Играем в игру

Скорее всего, играя в «Сапёра», вы не захотите корпеть над всеми этими вычислениями.

И я тоже.

Но я действительно перечислил все возможные конфигурации в левом верхнем и правом нижнем углах. Я заметил, что в одной конфигурации (B2-B) используется на одну мину меньше, чем во всех остальных, и применил проверенное временем правило «меньше мин — значит, больше закрытых вариантов» (которое действует приблизительно пока количество закрытых клеток меньше чем удвоенное количество ненайденных мин). Это означает, что намного вероятнее конфигурации с меньшим количеством мин.

Поскольку в левом верхнем углу было множество конфигураций, определение шансов для любой клетки довольно сложно. Поэтому я просто выяснил, что конфигурация B в правом нижнем углу намного более вероятна, и случайно выбрал одну из подходящих клеток. (Я надеялся, что она позволит мне закончить правый нижний угол, а потом, вооружённый большей информацией о количестве оставшихся мин, я смогу завершить левый верхний угол, после чего мне придётся бросить монетку для выбора внизу в центре. Разумеется, в идеале нужно было выбрать клетку, максимизирующую вероятность получения полезной информации, но любая из этих догадок позволила бы мне «войти» в правый нижний угол для дальнейшего сбора данных.) Шансы были выше у конфигурации B, поэтому я выбрал клетку, в которой была мина в конфигурации A.

Восемь раз из девяти я был бы прав.

Игра «Сапёр» — стратегия

From MinesweeperWiki

Стратегия «Сапёра» это — искусство решения игры. Оно включает в себя знание шаблонов, умение кликать в начале игры, тренировка угадывания, эффективных последующих кликов и перемещения мыши.

Содержание 1 Шаблоны 2 Угадывание 3 Первый клик 4 Эффективность 5 Ещё немного советов 6 Ссылки

Шаблоны

Шаблон это — стандартная комбинация чисел, которая имеет только одно решение. Если шаблоны запомнить, это избавит от лишних затрат на обдумывание.

Перед тем как запомнить шаблоны, нужно заучить основы. Если число в клетке соприкасается с тем же количеством клеток, то все эти клетки содержат мины. Этот способ поможет решить почти все варианты уровня «Новичок». Вот несколько примеров:

Единичка у угла клетки касается только её одну, поэтому за клеткой будет мина.	Двойка рядом с двумя клетками, поэтому за обеими будут мины.	Тройка у трёх клеток, за всеми скрыты мины.	Четвёрка соприкасается с четырьмя клетками, за всеми — мины.
Пятёрка соприкасается с 5 клетками, за всеми — мины.	Шестёрка соприкасается с 6 клетками, за всеми — мины.	Семёрка соприкасается с 7 клетками, за всеми — мины.	Восьмёрка соприкасается с 8 клетками, за всеми клетками — мины.

Есть два основных шаблона, которые комбинируются для создания всех остальных. Первый — «1-1», и второй — «1-2». Всякий раз, когда встречается шаблон «1-1» начинающийся от края поля (или в качестве края выступает открытая клетка), в третьей клетке — пусто.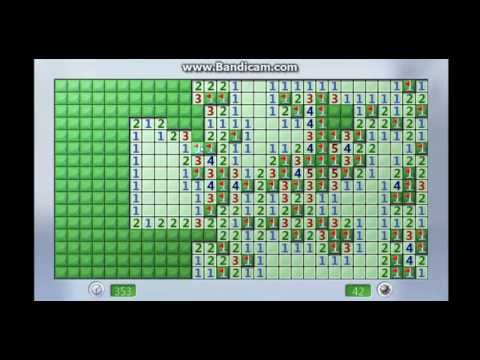 Это объясняется тем, что первая единичка соприкасается с двумя клетками, за одной из которых должна быть мина, в то время как вторая единичка соприкасается ещё и с третьей клеткой, которая должна быть пустой. Когда встречается шаблон «1-2», третья клетка всегда содержит мину. Это происходит потому, что первая единичка соприкасается с двумя клетками, которые должны содержать одну мину, а двойка соприкасается с третьей клеткой, в которой должна быть вторая мина. Вот несколько примеров:

Тут одна мина в первых двух клетках, и одна в первых трёх. Третья клетка должна быть пустой.

Одна мина в первых двух клетках, и две в первых трёх. В третьей скрыта мина.

Шаблон «1-1», который начинается от открытой клетки.

Более сложный вариант шаблона «1-2».

Самые известные шаблоны — «1-2-1» и «1-2-2-1». Они настолько часто встречаются, что новички обязаны запомнить их с самого начала. При внимательном рассмотрении они — просто комбинация шаблона «1-2».

Шаблон «1-2-1» имеет только одно решение.

Применение шаблона «1-2» слева.

Применение шаблона «1-2» справа.

Шаблон «1-2-2-1» имеет только одно решение.

Применяйте шаблон «1-2» слева.

Применяйте шаблон «1-2» справа.

Поначалу будет казаться, что шаблонов очень много. Но, изучив их, можно понять, что на самом деле они — просто комбинации шаблонов «1-2-1» и «1-2-2-1» (или комбинации шаблонов). С другой стороны это — просто вариации основных шаблонов «1-1» и «1-2». Каждое число уменьшается с увеличением количества известных мин.

242 уменьшается до 121‎	345 уменьшается до 121	1222 уменьшается до 1221	2331 уменьшается до 1221
222 уменьшается до 121	2331 уменьшается до 1221	13231 уменьшается до 12121	Уменьшение до 122121

Угадывание

Иногда в «Сапёре» приходится угадывать. Одна мина в двух невскрытых клетках — типичный случай «50/50». Быстро угадывайте и — вперёд! Обдумывание не прибавит шансов на правильное решение, а только отберёт время. Время на обдумывание тоже не ускорит процесс. Просто считаем, что нам повезло, и продолжаем играть. Не задерживайтесь в тяжких раздумьях — не угадаете здесь, не угадаете и всё остальное.

Многие игроки нетерпеливы и занимаются угадыванием вместо принятия решений. Не угадывайте, если это не необходимо. Самое быстрое решение «Примера A» — кликнуть подряд по всем закрытым клеткам в ряду. Но в спешке можно не заметить, что за средней клеткой может быть мина. Это — бессмысленное угадывание! Думающий игрок сначала кликнет по двум внешним клеткам, что позволит понять, есть ли мина посередине.

Раскрывание безопасных клеток так же важно, как и поиск мин. Если есть уверенность, что клетка безопасна, откройте её вместо того чтобы искать место, где мина есть. В «Примере B» мина находится за двумя жёлтыми клетками. Вместо угадывания лучше открыть безопасную третью клетку. Это позволит открыть дополнительные клетки (помеченные голубым), что поможет в решении изначальной догадки.

Если приходится угадывать, а закрытых клеток больше, чем мин, лучше предположить, что за клеткой мины нет, чем предполагать, что мина там есть. Любители расставлять флажки из-за любви к «растянутому волчатнику» и делать аккорды (клик ПРАВ+ЛЕВ) часто делают ошибку при угадывании места мины.

Иногда можно увеличить шанс угадывания. Это может оказаться при взаимном расположении чисел так, что ситуация имеет несколько решений, и эти решения требуют различного количества мин. Вместо угадывания можно обложить флажками остальную часть поля и посмотреть, сколько осталось мин. «Пример D» имеет решение как с одной миной, так и с тремя, но лучше считать, что здесь осталось две мины. При желании сэкономить время и побыстрее угадать стоит учитывать плотность расположения мин и уровень игры. Например, ситуация с бо́льшим количеством мин гораздо чаще встречается в режиме «Профессионал», чем в «Любителе». Однако необходимо помнить, что плотность на каждом уровне достаточно низка, поэтому решения на основе ме́ньшей плотности встречаются достаточно часто.

Пример A: Не нужно зря заниматься угадыванием. Сначала достаточно открыть две внешние клетки. Кликая по третьей клетке, можно увидеть результат клика по первой.

Пример B: Вместо угадывания, где находится мина, откройте безопасную клетку. После этого можно открывать клетки помеченные синим.

Пример C: Не гадая, здесь не найти мин, но можно раскрыть безопасные синие клетки. Если за ними — единички, можно раскрыть оранжевые клетки и т.д., и, возможно, раскроется всё поле.

Пример D: В углу одна, две или три мины? Перед тем как угадывать, подумайте.

Может так случиться, что решена часть поля и приходится угадывать, чтобы решить остальное. Можно увеличить шансы на победу, кликая случайным образом! Средний шанс нарваться на мину составляет 0,206 в режиме «Профессионала» и 0,156 в «Любителе» и «Новичке». Это лучше, чем гадать 50/50. Помните только, что кликать лучше у краёв. Храбрость обычно вознаграждается тем, что изначальное «предположение» приводит к решаемым ситуациям в различных направлениях.

Следует помнить ещё об оной важной вещи — о полезности. Если два решения выглядят равными, выбирайте то, которое будет более полезным в случае, если оно окажется правильным. Иногда одно решение избавляет от дополнительных догадок или приводит к более простому расположению мин. Обычная ошибка — угадывать 33/66, а не 50/50, вместо того, чтобы решить его. Например, если известно, что за тремя клетками находится одна мина, не нужно открывать среднюю!

Всегда выбирайте самое подходящее решение. Вычислить его бывает очень трудно! Sean Barrett написал руководство Minesweeper Advanced Tactics. Локальная вероятность проста в решении, но обычно ошибочна. Например, на картинке ниже часть клеток обе — угадывание 50/50 и 66/33! После рассмотрения всех нерешённых мест простое угадывание 50/50 приводит к тому, что одна клетка наиболее вероятно содержит мину.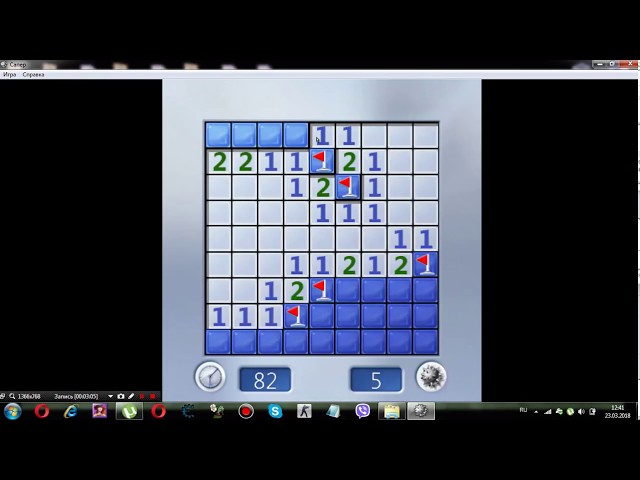 Тут правило «большого пальца» гласит, что в ситуации 50/50, если клетка соприкасается с бо́льшим номером, то, вероятно, что мина находится здесь, а не за другими клетками.

Особый случай — угадывание в случае верхнего левого угла. Первый клик в «Сапёре» — безопасен, поэтому, если попасть на мину, она будет перемещена в верхний левый угол (или в ближайшую свободную клетку справа). В ситуации угадывания 50/50, когда одна из клеток находится в левом верхнем углу, наиболее вероятно, что за ней находится мина. В режиме «Профессионала» шанс наткнуться на мину — 0,206, но в левом верхнем углу после первого клика он увеличивается до 0,370.

Следующий пример демонстрирует предыдущие утверждения. Тут, похоже, присутствуют три неизбежных угадывания 50/50 и два 66/33. Одной из стратегий может быть по-быстрому угадать и надеяться на лучшее. Если выживите, это увеличит ваш рейтинг.

Выбор стратегии угадывания это — выбор между количеством выигранных игр и рекордами по времени.

Три ситуации 50/50

Две ситуации 66/33

Первый клик

Первый клик в «Сапёре» безопасен всегда, но где находится лучшее место, откуда можно начинать? Это зависит от того что важнее — количество или качество.

Наибольший шанс имеет поиск по углам, затем по краям, а после этого — посреди поля. Emmanuel Brunelliere (Франция) вычислил теоретические шансы:

	Новичок	Любитель	Профессионал
Угол	59.54%	59.94%	49.94%
Край	42.14%	42.61%	31.42%
В поле	25. 09%	25.54%	15.69%

После этого Tim Kostka, зная о Board Cycles (конечном количестве вариантов расположения мин) в «Сапёре» для Windows, определил реальные шансы по удачному открытию клеток. Первый клик всегда безопасен, потому что мина перемещается либо в верхний левый угол, либо в ближайшую клетку справа. Это означает, что верхняя левая клетка даёт меньше шансов, чем остальные углы. Это же означает меньшее количество шансов открытия клеток у края и посреди поля, которые соприкасаются с левой верхней клеткой. Точные значения — на его сайте. Большинство отклонений — из-за низкой частоты использования верхнего левого угла.

	Новичок	Любитель	Профессионал
Угол	50 — 60 %	50 — 60 %	40 — 50 %
Край	34 — 42 %	36 — 43 %	25 — 32 %
В поле	19 — 24 %	21 — 26 %	12 — 16 %

Наилучшие шансы для получения большого количества открытых клеток — открывать их посреди поля, потом по краям и в углах.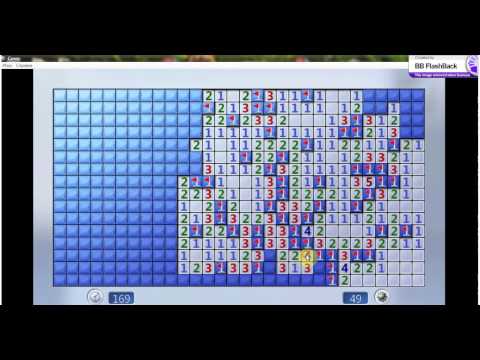 До сих пор никто не просчитал теоретические преимущества, но Tim подобрал реальные результаты для «Сапёра» для Windows. Наибольшее количество открытий происходит очень близко от центра поля, и количество уменьшается при продвижении к углам. Таблица ниже демонстрирует среднее количество открытых клеток на каждое удачное открытие:

	Новичок	Любитель	Профессионал
Угол	18	27	16
Край	20 — 24	31 — 42	19 — 26
В поле	23 — 32	35 — 66	23 — 41

В общем случае, лучшее место зависит от предпочтения по размеру или частоте. Бо́льшее количество открытий — проще, но приводит к бо́льшему количеству проигрышей.

Версия «Сапёра» в Windows Vista всегда сама (?) делает первый клик. При этом приходится начинать посреди поля для раскрытия промежуточных клеток. (Эта версия недоступна на World Ranking).

Шансы открытия в «Новичке»

Средний результат открытия в «Новичке».

Эффективность

Меньше кликов — раньше финиш. Учитесь быть эффективным.

Игра заканчивается, когда раскрыты все безопасные клетки, а не тогда, когда помечены все мины. Новички часто тратят время на пометку каждой. Единственная причина отмечать флажком — пометить рядом стоящие клетки аккордом. Перед тем как поставить флажок стоит подумать, насколько это полезно.

Здесь нет причин отмечать мину флажком, разве только для того, чтобы это место выглядело приятно!

Отмечать флажком эти 8 мин — лишняя трата времени, потому что нельзя отметить все восемь за раз.

Здесь нет причины отмечать розовые клетки, потому что эта связка всё равно не пригодится для аккорда.

Некоторые игроки вообще не используют флажки, потому что время на установку флага лучше потратить на раскрытие других клеток. Это — стиль «No Flags» (без флажков), коротко — NF. Те, кто расставляет флажки («Флаггеры») аргументируют это тем, что флажки позволяют использовать аккорды для одновременного раскрытия безопасных клеток. Да, обычно NF-стиль более эффективен с большими числами (5, 6, 7, 8), но при более низком числе (1, 2, 3, 4) расстановка флажков полезнее. При большом числе типа 7 игроку NF-стиля понадобится только один клик, чтобы раскрыть безопасную клетку, а флаггеру придётся поставить семь флажков. При малом числе типа 1 флаггер может поставить один флажок и открыть остальное аккордом (ПКМ+ЛКМ), а NF-игроку придётся сделать до семи кликов, чтобы открыть безопасные клетки.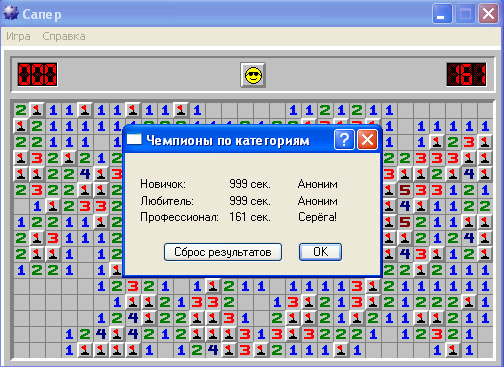 Необходимо также согласиться, что NF — более эффективен в местах с низким 3BV — «Bechtel’s Board Benchmark Value» (уровень сложности Бетчела — пер.), но расстановка флажков эффективнее на плотных 3BV. Например, в «Любителе», где 3BV — 40, вокруг каждой мины есть как минимум одно число, в то время как при 120 3BV — три. Хорошему NF-игроку понадобится 40 или 120 кликов. Неэффективному и неудачливому флаггеру в обоих случаях понадобится 80 кликов (40 флажков, 40 аккордов). Эти примеры — крайние случаи, но раскрывают общую причину. На самом деле NF-игроки — несовершенны и тратят клики пополной, а «флаггерам» не нужно помечать каждую мину и делать аккорды на каждом числе. Нет однозначного преимущества в использовании только одного метода — NF или «флаггинга». Преимущества проявляются, когда комбинируются обе техники, и игрок использует наиболее полезное решение для каждой конкретной ситуации.

При пометке флажком можно сэкономить время, используя технику полтора клика. Обычно эта последовательность состоит в пометке флажком правой кнопкой мыши, затем использованием обеих кнопок для аккордного раскрытия остальных клеток. Полуторный клик состоит в правом щелчке для пометки флагом, нажатии левой кнопки и отпускания для завершения аккорда. Это освобождает от одного передвижения для каждого флажка и аккорда. Когда нажата правая кнопка до нажатия левой, будет выставлен флаг. Чем меньше расстояние, тем больше времени будет сохранено. При помощи этого можно почти удвоить скорость расстановки флажков.

Вот несколько примеров эффективной расстановки флажков:

Можно выставить флаги на всех трёх минах и сделать аккорд на двойках, но эффективнее будет расставить флажки как показано и сделать аккорды на однёрках.

Можно отметить обе мины, но полезнее отметить внешнюю мину, как это показано, и сделать аккорд на однёрке.

Отметьте флажком как это показано и сделайте аккорд на однёрке выше. Здесь нет необходимости трогать остальные клетки.

Нет причин отмечать розовые клетки. Пометьте, как показано, и сделайте аккорд на следующей однёрке.

А вот примеры эффективного использования техники NF:

Тут нужно кликнуть один раз по жёлтой клетке.

Один клик в углу.

Если открыть жёлтую клетку, голубые тоже откроются. NF-игроки ищут раскрытия.

При открытии жёлтой клетки, голубые откроются тоже.

Не всегда просто определить что эффективнее, NF или «флаггинг». В следующих примерах NF требует меньшего количества кликов, если при этом происходит раскрытие, но большего, если раскрытия не произойдёт. Имя удалено сделал отличное слайдшоу эффективного решения уровня «Любитель» с подробными объяснениями.

Пример a: Эффективный флаггер выставит один флажок и сделает аккорды по розовым клеткам. Затем сделает клик по жёлтой клетке. Всего — 4 клика. (Если отмечать флажком все мины, понадобится 8 кликов).

Пример b: NF-игрок может кликнуть жёлтую клетку в надежде, что откроются голубые. Затем кликнуть две пурпурные. Всего — три клика с открытием или шесть — без.

Пример c: NF-игроки кликнут жёлтую клетку. Если она пуста, то откроются, как минимум, голубые. Но они открываются не всегда. В этом случае приходится кликать все покрашенные клетки. Количество кликов варьируется от одного до шести.

Пример d: флаггеры поместят один флаг и сделают аккорд на однёрке. Если произойдёт открытие, откроются все голубые и зелёные клетки. Если этого не произойдёт, откроются голубые, а по зелёным придётся кликать. Всего кликов — от двух до пяти.

Самый важный приём для увеличения скорости решения — меньше перемещать мышь. На это требуется время. Начинающие вместо движения к цели следят за мышью. Следующая стадия в уменьшении перемещений — оценивать уже решённое поле. Часто это позволяет принять решение о месте, куда следует поместить мышь. Например, если мышь в примере b ниже находится рядом с двойкой, можно пометить красную клетку и сразу сделать аккорд. Это очевидно для профессиональных игроков, потому что у себя в голове они уже приняли решение о состоянии соседних клеток. Новичок же будет метаться туда–сюда. Красная клетка в примере b может быть решена похожим образом. Меньше перемещений — лучше результат.

Пример a: красную клетку можно просто пометить как мину, потому что игрок думает на несколько ходов вперёд.

Пример b: красную клетку можно просто пометить как мину, потому что игрок думает на несколько ходов вперёд.

Эффективность измеряется индексом эффективности или IOE. Он зависит от количества кликов затраченных на решение поля 3BV. IOE 1.00 означает решение 50 полей 3BV за 50 кликов. Решение игры за меньшее количество кликов, чем 3BV, достигается комбинированием «флаггинга» и техники NF. На Clone и на Arbiter сохраняются рейтинги IOE для стимулирования совершенствования. Arbiter дополнительно разделяет IOE на корректность (клики, которые изменяют состояние поля) и производительность (потенциальный IOE, если бы все клики были корректными). Кроме того там есть статистика замеров перемещения мыши в пикселах (но это не точно — пер.).

Лучший способ улучшить эффективность — играть медленно. Нужно искать наиболее эффективное решение и способ перед тем, как нажимать какую-либо кнопку. Улучшения станут заметны позднее при игре на полной скорости.

Ещё немного советов

• Не используйте знаки вопроса.
• Для начала новой игры используйте F2. Держите один из пальцев на этой кнопке, это быстрее, чем использовать мышь.
• Избегайте беспричинного перемещения мыши. Новички часто тратят время зря, передвигая мышь куда глаза глядят.
• Не обращайте внимание на часы. Перевод взгляда на них во время игры отнимает время, и это может начать нервировать, если вы хотите ускориться.
• Многие игроки во время игры слушают музыку. Это их расслабляет и позволяет играть на автопилоте, не нервничая.
• Играйте в тёплом помещении или перед игрой согрейте руки горячей водой. Это улучшит кровообращение и время реакции.
• Делайте короткие упражнения для улучшения кровообращения и стимуляции работы мозга.
• После длительной игровой сессии это поможет изменить тактику игры. Оно же поможет сфокусироваться.
• При случайном нажатии на мину перед тем как отпустить кнопку переместите указатель на другую клетку.
• Используйте полуторный клик.

Ссылки (живы далеко не все)

• Minesweeper Guide — Daniel Silevitch впервые упоминает о шаблонах «1-2-1» и «1-2-2-1» (1992).
• Strategy — Jim Loy впервые пишет о шаблоне «1-1» (1996).
• Minesweeper Tips — Brian Chu был первым, кто обсудил шаблон «1-2» (1997).
• Minesweeper Page — Frank Wester опубликовал первое серьёзное руководство по стратегии (1997).
• Minesweeper Advanced Tactics — расчёт вероятностей «Сапёра», автор Sean Barrett (1999).
• First Click — Emmanuel Brunelliere рассчитывает теоретически наилучшее место для начала игры (2003).
• Minesweeper Tips — различные советы и стратегия автора Grégoire Duffez (2006).
• On the First Click — Tim Kostka определяет наилучшее актуальное место для начала игры (2006).

Greedy Greedy Goblins Обзор настольной игры и правила

Ричард Гарфилд, вероятно, один из самых известных дизайнеров настольных игр. Он наиболее известен благодаря Magic the Gathering, но он также создал другие популярные игры, такие как King of Tokyo, Netrunner и Roborally. Хотя я не играл во многие игры, разработанные им, мне всегда интересно их проверить, поскольку за эти годы он создал много хороших игр, и они, как правило, более доступны, когда ими может наслаждаться вся семья. Созданная еще в 2016 году сегодняшняя игра Greedy Greedy Goblins — это игра, которая как бы ускользнула от внимания, поскольку, хотя людям в целом она нравилась, она никогда не становилась такой популярной, как некоторые другие игры Ричарда Гарфилда. Предпосылка игры заинтриговала меня, хотя казалось, что она сочетает в себе элементы скорости с игрой «нажми на удачу». Greedy Greedy Goblins, возможно, не самая глубокая игра, но ей удается создать быструю игру на удачу, которой может наслаждаться вся семья.

Как играть | Мои мысли | Стоит ли покупать? | Комментарии

Как играть Жадные гоблины

Подготовка

• Каждый игрок выбирает клан. Они возьмут соответствующий лист клана и три пешки. В играх для четырех игроков вы будете использовать только две пешки гоблинов. Все неиспользованные клановые листы и фишки возвращаются в коробку.
• Поместите пещеры и ратушу в центр стола в виде круга. Количество пещер, которые вы будете использовать, зависит от количества игроков:
  • Два игрока – пять пещер
  • Три или четыре игрока – 8 пещер
• Перемешайте все карты миньонов и положите их лицом вниз рядом с игровой зоной.
• Перемешайте все жетоны добычи (символами вниз) и поместите их в круг, образованный пещерами и ратушей.

Игра в игру

Жадные гоблины играют в несколько раундов. Игра ведется одновременно, что означает, что все игроки играют одновременно, так как ходов нет.

Игроки берут по одной тайле лицевой стороной вниз из стопки в центре карт. Игроки могут использовать только одну руку при рисовании плиток. Они будут смотреть на это (не позволяя другим игрокам увидеть это).

Этот игрок подобрал золотую плитку. Они выберут, на какую мину положить ее лицевой стороной вниз.

Затем они выберут одну из пещер (не гильдию) и положат ее лицевой стороной вниз. После размещения тайла вы берете еще один тайл лицевой стороной вниз из центра карт. Вот некоторые правила, касающиеся рисования и игры плиток:

• Вы должны посмотреть на плитку, прежде чем ставить ее.
• Все нарисованные плитки должны быть размещены в пещере.
• После того, как плитка размещена, никто из игроков не может на нее смотреть (кроме факелов) и ее нельзя перемещать.
• Количество плиток, которые можно разместить в пещере, не ограничено.
• Плитки нельзя размещать в ратуше.

Игрок решил положить золотую плитку в пещеру, показанную выше.

В любой момент один из игроков может использовать одну из своих пешек. Они могут разместить его в ратуше или в одной из пещер. Игрок может поставить свою пешку только на карту, на которую никто другой не поместил свою пешку. После того, как фишка была помещена в пещеру или зал гильдии, никто больше не может размещать плитки или фишки на этой карте. После того, как пешка поставлена, ее нельзя убрать или передвинуть до конца раунда.

Красный игрок поместил свой жетон в эту пещеру, чтобы забрать ее.

После того, как игрок разместил свою последнюю фишку, он больше не может брать или размещать плитки.

Последний игрок, у которого остались пешки, может взять и разместить еще до пяти плиток.

Если игрок не хочет размещать одну или несколько своих пешек, он не обязан этого делать. Как только все игроки разместили все свои пешки или решили не играть оставшимися пешками, раунд заканчивается, и игра переходит к подсчету очков.

Все локации захвачены, значит, раунд окончен.

Тайлы

Факел

Когда игрок достает факел, он может положить его лицевой стороной вверх в пещеру. Затем у них будет возможность перевернуть одну из других плиток в пещере лицевой стороной вверх. Однако игрок может положить плитку лицевой стороной вниз и отказаться от особой способности.

Сокровища

Тайлы сокровищ бывают четырех цветов и форм. Сокровища: изумруды/зеленые, рубины/красные, сапфиры/синие и золотые/желтые. Сокровища обычно стоят только одну монету. У каждого клана есть любимое сокровище (соответствующее их цвету). Избранные сокровища приносят ассоциированному клану две монеты.

Алмаз

Каждый бриллиант стоит две монеты. Алмазы также считаются сокровищами.

Динамит

Динамит несет в себе механику риска/вознаграждения. Пещера, в которой есть только один кусок динамита, удваивает количество очков, набранных за сокровища в пещере. Если в пещере есть два динамита, все тайлы сокровищ будут оценены в три раза больше, чем обычно.

Если в пещере есть три или более динамита, пещера взорвется. Игрок не получит очков из пещеры и не получит никаких других преимуществ. Игрок также потеряет пять монет.

В этой пещере было пять динамитов. Пещера взорвется, и желтый игрок не получит из нее монет. Они также потеряют пять монет, потому что пещера взорвалась.

Двойной динамит

Двойной динамит аналогичен обычному динамиту, но считается за два при определении количества динамита в пещере.

Монстр

Каждый монстр в пещере съедает одну плитку сокровища (включая алмазы). Игрок, захвативший пещеру, сможет выбрать, какое сокровище съест монстр.

Миньон

За каждого миньона в пещере (которая не взорвалась) игрок может взять одну карту миньона.

Конец раунда

Игроки могут подсчитывать очки в любом порядке. Если порядок важен для игроков, игрок с наибольшим количеством монет в настоящее время забьет все свои локации первым. При подсчете очков игрок может подсчитывать их в любом порядке. Монеты/очки начисляются следующим образом:

Игрок, поставивший фишку в ратуше, берет верхнюю карту миньона из колоды. Это все, что вы получите за получение ратуши.

Зеленый игрок заявил права на место в ратуше, поэтому он получит карту миньонов.

Каждая из отдельных пещер будет получать очки в зависимости от того, какие плитки были размещены на них (подробности о подсчете очков см. в разделе «Плитки»).

Зеленый игрок захватил эту пещеру. Сапфир принесет одну монету. Алмаз принесет две монеты. Рубин будет съеден монстром. Поскольку в пещере два динамита, обычное количество монет игроков (три) увеличивается втрое до девяти. В пещере также было две плитки миньонов, поэтому игрок берет две карты миньонов.

После подсчета очков, если ни у одного игрока нет 100 или более монет (60 для игры с тремя игроками), будет сыгран еще один раунд.

Любой игрок с четырьмя или более картами миньонов в руке должен сбрасывать карты до тех пор, пока в его руке не останется только три карты. Игроки могут выбирать, какие карты сбросить.

Все фишки возвращаются соответствующему игроку.

Все плитки возвращаются лицевой стороной вниз в центр карт. Все плитки перемешиваются, чтобы перепутать их.

Победа в игре

Если игрок заработал более 100 монет (60 для четырех игроков), игра заканчивается. Игрок с наибольшим количеством монет выигрывает игру.

Если ничья, сыграйте еще один раунд, чтобы решить ничью.

Карты миньонов

Игроки будут получать карты миньонов на протяжении всей игры, заявляя права на ратушу или размещая плитки миньонов в пещерах, на которые они претендуют. Игроки будут скрывать карты миньонов от других игроков, пока они не будут сыграны. Если в колоде заканчиваются карты, стопка сброса будет перетасована, чтобы сформировать новую колоду.

За исключением Банкира и Прыгуна, все карты миньонов разыгрываются в пещере игроком, захватившим ее после того, как все тайлы были открыты. После того, как пещера подсчитана и ее эффект применен, карта миньона сбрасывается. Карта миньона, полученная за подсчет очков в пещере, не может быть использована в той же пещере, но может быть использована в пещере, подсчитанной позже в том же раунде.

Банкир

Эта карта будет разыграна после того, как будут подсчитаны все пещеры и ратуша. Игрок может разыграть карту Банкира и заработать одну монету. В отличие от других карт миньонов, Банкир возвращается в вашу руку после того, как вы его разыгрываете. Таким образом, вы можете играть в нее каждый раунд, пока держите ее в руке.

Канарейка

Когда пещера взрывается, игрок может разыграть карту Канарейки, чтобы не потерять пять монет. Однако игрок не получит никаких преимуществ от пещеры.

Претендент

Претендент — единственная карта, разыгрываемая в течение раунда. Когда игрок видит пещеру, которую он хочет, но уже захваченную другим игроком, он может разыграть Прыгун и добавить свою пешку в пещеру. Карта не может быть разыграна, чтобы претендовать на гильдию.

Изначально это место принадлежало желтому игроку. Красный игрок разыграл карту Претендента, чтобы также добавить свой жетон в локацию.

При подсчете очков каждый из игроков в пещере будет подсчитывать свои очки отдельно. Они получат половину монет (с округлением вверх), которые они получили бы в обычном режиме.

Если в пещере есть монстры, игрок, который первоначально захватил пещеру, решает, какие сокровища удалить.

Если есть плитки миньонов, оба игрока берут по одной карте за каждую плитку миньонов.

Когда разыгрываются карты миньонов, следующие карты действуют на обоих игроков:

• Эксперт-шахтер
• Сапер
• Мусорщик

Следующие карты действуют только на того игрока, который разыграл карту:

• Канарейка
• Резцы для драгоценных камней
• Плавильный завод
• Гильдмастер
• Wrangler – Игрок, разыгравший карту, получает монеты. Однако монстр не возьмет сокровищ ни у одного из игроков.

Алмазный резак

Все алмазы в пещере стоят две дополнительные монеты. Множитель динамита применяется после суммирования бонусов.

Резак для изумруда/золота/рубина/сапфира

Каждое сокровище соответствующего типа стоит еще одну монету. Вы можете разыграть несколько одинаковых карт в одной и той же пещере.

Если сокровище совпадает с любимым сокровищем вашего клана, дополнительная монета добавляется к дополнительной монете, которую вы обычно получаете. Множитель динамита применяется после суммирования бонусов.

Зеленый игрок разыграл карту Изумрудного резчика в этой локации. Этот игрок получит по три монеты за каждую изумрудную плитку. Они получат одну монету только за плитку, одну за то, что плитки соответствуют их цвету (зеленый), и одну дополнительную монету из-за Изумрудного резца. Эти монеты также будут утроены из-за двух плиток динамита.

Эксперт-шахтер

При розыгрыше карты Эксперт-шахтер количество динамита в пещере уменьшается вдвое (округляется в меньшую сторону). Вы можете разыграть несколько карт Expert Miner в одной и той же пещере. Вы будете работать с одной картой за раз.

Обычно эта мина взорвется, так как на ней пять динамитов. Однако сыгранная карта «Эксперт-шахтер» уменьшила количество динамита до двух.

Если карта Мусорщика используется для добавления плиток в пещеру, карта Эксперт-шахтер применяется к общему динамиту после добавления всех плиток.

Гильдмастер

Игрок получит две монеты за каждую плитку миньона в пещере в дополнение к взятию карты миньона. Примечание : В инструкции сказано: одна монета в одном месте и два привоя в другом. Поскольку на карточке также написано две монеты, я считаю, что это опечатка в инструкции.

На бонус, предоставляемый Гильдмастером, не влияет множитель динамита. Если пещера взрывается, эффект Гильдмастера теряется.

Желтый игрок разыграл карту Гильдмастера в этой локации. Поскольку в локации было два тайла миньонов, игрок получит четыре монеты с этих тайлов.

Сапер

Если в пещере нет динамита, разыгрывание карты Сапера добавляет в пещеру один динамит.

Поскольку в этой пещере не было динамита, зеленый игрок разыграл карту Сапера, чтобы добавить динамит, удваивающий монеты, заработанные в шахте.

Если игрок также использует Мусорщика, чтобы взять больше плиток и добавить динамит с этими новыми плитками, Сапер все равно добавит в пещеру один динамит.

Мусорщик

Когда играет Мусорщик, игрок может добавить в пещеру до трех дополнительных тайлов. Тайлы берутся из центральной стопки тайлов, которые не были нарисованы. Если осталось недостаточно плиток, вы потеряете эффект.

Игроки могут прекратить добавлять плитки в любой момент. Любая плитка, которую они рисуют, должна быть добавлена ​​в пещеру.

В одной и той же пещере можно играть несколькими тайлами Мусорщика.

Wrangler

Карта Wrangler не позволит монстрам выносить сокровища из пещеры. Каждый монстр также получит одну монету.

Красный игрок выложил карту Wrangler в эту пещеру. Карта нейтрализует жетон Монстра, который в противном случае съел бы одно из сокровищ. Монстр также принесет игроку одну монету.

Когда игрок добавляет тайлы в пещеру с помощью Мусорщика, Спорщик применяется ко всем нарисованным монстрам.

На монеты, полученные от монстров, не влияет множитель динамита.

Если пещера взорвется, вы не получите никаких преимуществ от Wrangler.

Мои мысли о жадных жадных гоблинах

Я играл во множество различных настольных игр, но не могу припомнить, чтобы я когда-нибудь играл в такую, как жадные жадные гоблины. Это действительно не очень хорошо вписывается в традиционный жанр настольных игр. Я бы сказал, что лучшее сравнение, которое я мог бы сделать, это то, что игра «нажми на удачу» сочетается с механикой скорости / реального времени. Я нашел это довольно интересным, так как игры «нажми на удачу» обычно известны тем, что дают игрокам время решить, хотят ли они продолжить или лучше остановиться. Это не относится к Greedy Greedy Goblins, так как вы должны выбирать, какой риск вы хотите взять на себя на лету.

В основном игровой процесс состоит из того, что все игроки одновременно хватают плитки с середины стола. Вы смотрите на плитки, а затем решаете, на какую пещеру их положить. Некоторые из этих плиток приносят очки или дают вам другие преимущества, в то время как другие плитки причиняют вам вред. Когда игрок хочет захватить пещеру, он ставит на нее одну из своих фишек. Чем дольше вы ждете, чтобы поставить свою пешку, тем больше очков вы можете заработать в пещере, но другой игрок может налететь и забрать ее раньше вас. Прежде чем претендовать на пещеру, вам также необходимо подумать, какие плитки вы и другие игроки разместили в пещере. На нем может быть много хороших плиток, а может быть много плиток, которые просто навредят вам.

Именно отсюда берет начало геймплей Greedy Greedy Goblins. Существует своего рода механика памяти, так как вам нужно попытаться вспомнить, какие плитки вы разместили в каждой пещере. Большая часть игрового процесса построена на том, чтобы решить, какой риск вы хотите взять на себя. Вы хотите взять пещеру, на которой всего несколько тайлов? Пещера вряд ли взорвется, поэтому вы не потеряете очки. Однако количество очков, которое вы в конечном итоге наберете, довольно мало. Затем есть пещеры, в которых есть куча плиток. Пещера может быть заполнена плитками, которые принесут вам много монет, но они также могут быть заполнены множеством отрицательных плиток, которые будут терять ваши очки. Ваш успех в игре во многом будет зависеть от того, насколько хорошо вы угадаете и как быстро примете решение.

На первый взгляд Greedy Greedy Goblins кажется очень простой игрой. В некотором смысле это так. Правила можно выучить всего за пару минут. Возможно, игроки никогда раньше не играли в подобную игру, но ни одна из механик не является особенно сложной для понимания. Вероятно, элемент, который делает игру наибольшей сложностью, — это карты миньонов, так как иногда вам может понадобиться вернуться к правилам, чтобы вспомнить, что делает каждая карта. Однако большинство карт можно разыграть после окончания раунда, поэтому не составит труда вернуться к правилам. В игре есть рекомендуемый возраст 14+, что лично я не понимаю. Я не вижу причин, по которым кто-то в возрасте десяти или около того не мог играть в эту игру.

Приступая к игре, больше всего меня беспокоило то, что в игре не будет много стратегии. Я думал, что игроки будут просто бросать все хорошие плитки в пещеру, а затем забирать ее, а все плохие плитки бросать в пещеру, в которой они не заинтересованы. Это может происходить время от времени в игре, так как во многих раундах есть пещера, которая буквально завалена плохими тайлами. Это не означает, что все остальные пещеры безопасны. Вы можете подумать, что другой игрок набивает пещеру сокровищами, а на самом деле загружает ее динамитом, или наоборот. Чем больше вы играете в игру, тем больше начинает формироваться мета-игра, поскольку вы никогда не знаете, шутит ли с вами другой игрок или нет.

Жадные жадные гоблины — далеко не самая стратегическая игра, но я думаю, что в ней достаточно, чтобы оставаться интересной. Время от времени вы будете лихорадочно размещать плитки, чтобы найти хорошие плитки для себя, но настоящие мысли должны идти о том, какие пещеры вы выбираете и какой риск вы хотите принять. Вы не можете просто сидеть сложа руки и думать об этом, иначе другой игрок, скорее всего, налетит и украдет пещеру, которую вы рассматриваете. Некоторым игрокам достаточно пройти пещеру с несколькими тайлами, чтобы безопасно набрать несколько очков. Другие будут готовы пойти на большой риск, чтобы набрать много очков. Чтобы добиться успеха в игре, вам нужно найти правильный баланс, поскольку игроки, которые заходят слишком далеко в одном направлении, скорее всего, не будут слишком хороши в игре. Однако вам нужно быстро решить, иначе вы можете застрять либо в том, чтобы выбрать одну из пещер, которая, вероятно, взорвется, либо даже не получить место с одной или несколькими вашими пешками.

Я думаю, что главная причина успеха игры — динамит. Динамит делает действительно хорошую работу, добавляя в игру элемент риск/вознаграждение. Первые два динамита, которые вы добавляете в пещеру, действительно полезны, поскольку они либо удваивают, либо утраивают количество очков, которые вы заработаете. Вы не можете игнорировать размещение динамита в пещерах, которые вы берете, иначе вы не наберете много очков. Вы действительно хотите избежать этого третьего динамита, так как он теряет все ваши очки из пещеры вместе со штрафом в пять очков. Тот факт, что вам нужно немного, но не слишком много динамита, добавляет в игру действительно интересный компромисс. Вы хотели бы разместить динамит в пещере, которую вы планируете взять с самого начала, чтобы увеличить свои очки. Другой игрок может пронести в пещеру еще один динамит, заставив ее взорваться.

К этому можно добавить карты миньонов, которые вы будете получать на протяжении всей игры. Карты миньонов на самом деле играют довольно большую роль в игре, поскольку вы можете получить их довольно легко. Я признаю, что не все карты созданы одинаково. Некоторые из них значительно лучше других, поскольку они либо увеличивают количество монет, которые вы зарабатываете, либо значительно снижают риск. Хотелось бы, чтобы карты были более сбалансированными. Я также думаю, что игра должна была увеличить количество карт, которые вы можете держать в начале каждого раунда, до четырех или пяти карт. Были раунды, в которых игроки получали так много карт, что в конечном итоге им приходилось сбрасывать несколько карт или сразу же разыгрывать их без особой выгоды.

Несмотря на проблемы с картами, дополнение к игре понравилось. Карты дают игрокам больше возможностей, которые, на мой взгляд, почти всегда лучше. Карты, которые у вас есть в руке, позволяют вам изменить свой обычный подход к раунду. Например, если у вас есть карта Canary или Expert Miner, вы можете пойти на больший риск, чем обычно. Другие карты дают вам альтернативные способы набрать очки, что позволяет вам складывать пещеру с плитками, которые в противном случае не принесли бы вам много монет. К картам нужно время, чтобы привыкнуть, но я думаю, что они были хорошим дополнением к игре.

Что касается длины Greedy Greedy Goblins, то она будет несколько зависеть. Поначалу может показаться, что игра закончится очень быстро. Обычно раунды длятся максимум пару минут. Однако вам, вероятно, придется сыграть довольно много раундов, прежде чем игра закончится. В основном это связано с тем, что вы, скорее всего, не наберете много очков ни в одном раунде. Возможно, это просто потому, что моя группа в целом не склонна к риску, но было много раундов, в которых игроки набирали меньше десяти очков. Однако иногда бывают раунды, в которых вы можете набрать много очков. В конечном итоге я предполагаю, что игра займет у большинства игроков около 30 минут.

Мне понравилась игра Greedy Greedy Goblins, так как я думаю, что это маленькая забавная игра, которая понравится всей семье. Я признаю, что игра не особенно глубока. Если вы ищете стратегическую игру, Greedy Greedy Goblins вам не подойдет. Игра зависит от удачи. Игра зависит от вашей удачи, но помимо способности читать мысли других игроков многое сводится к правильному угадыванию. Есть пещеры, которые намного опаснее других, но вы никогда не знаете наверняка, что будет в любой пещере за пределами плиток, которые вы разместили. Таким образом, вам должно как бы повезло, что когда вы идете на риск, он окупается. Удача относится к картам, и некоторые из них значительно лучше, чем другие.

Наконец, я хотел быстро рассказать о компонентах игры. По большей части они мне понравились. Мне очень понравилось оформление игры, так как оно хорошо сочетается с остальной темой. Карты и монеты довольно толстые там, где их должно хватить. В частности, мне очень понравились плитки из пластика/бакелита. Плитки хорошо сложены и имеют вес, что очень приятно. У меня было две основные проблемы с компонентами. Во-первых, я бы хотел, чтобы пешки были чем-то большим, чем просто большой пластиковый диск. Иначе я действительно не могу понять, почему в игре не могло быть монет номиналом пять. Вы будете иметь дело с шагом в пять в игре, и это проблематично иметь дело только с одной и десятью монетами.

Стоит ли покупать жадных жадных гоблинов?

Жадные Жадные гоблины немного отличаются от большинства игр, созданных Ричардом Гарфилдом. По сути, это похоже на игру на скорость/в реальном времени, смешанную с игрой на удачу. Игрокам необходимо быстро просматривать тайлы, заполняющие пещеры и выбирая, какие из них они хотели бы оставить себе. Раунды быстрые и безумные, как и в большинстве скоростных игр, которые мне нравятся. Механика «нажми на свою удачу» довольно интересна, и есть преимущества в том, чтобы идти на риск, но ты не хочешь слишком сильно рисковать. Вместо того, чтобы не торопиться и выбирать, хотите ли вы рискнуть, вам нужно выбирать быстро и надеяться, что вы сделали правильный выбор. Жадные гоблины зависят от удачи, и не все карты сбалансированы. Хотя мне было довольно весело играть в Greedy Greedy Goblins.

Если вам никогда не нравились скоростные игры или вас не интересует сама идея игры, скорее всего, она вам не подойдет. Те, кто любит скорость и игры на удачу или заинтригованы предпосылкой, должны действительно подумать о том, чтобы взять Greedy Greedy Goblins, так как вы, вероятно, получите от этого немало удовольствия.

Купить Жадных Жадных Гоблинов онлайн: Amazon

, eBay. Любые покупки, сделанные по этим ссылкам (включая другие продукты), помогают поддерживать работу Geeky Hobbies. Спасибо за Вашу поддержку.

Основы

Возможно, вы уже играете в некоторые игры в домино. Если это так, вы можете обнаружить, что правила на этом веб-сайте не являются точными правилами, как те, которые вы узнали. Есть много игр в домино, которые носят разные названия, но имеют очень похожие, а иногда даже идентичные правила. Кроме того, в разных частях мира существует множество игр с одним и тем же названием, но правила в разных местах различаются.
На нашем веб-сайте мы разместили правила многих различных игр в домино. Большинство правил игры в домино, размещенных на нашем веб-сайте, также включают несколько различных вариантов правил. Решите ли вы точно следовать правилам или создадите свой собственный вариант, не имеет значения, если все игроки четко понимают, что такое правила, и соглашаются с ними до начала игры. Также важно, конечно, чтобы вы удостоверились, что правила, по которым вы играете, функциональны.
Приведенные здесь основные правила применимы к большинству игр в домино, представленных на нашем веб-сайте, но не ко всем из них. Например, на этом веб-сайте есть несколько игр, в которых руки не разыгрываются, и, конечно же, основные правила, относящиеся к более чем одному игроку, не применимы к пасьянсам.
Во многих играх в домино на столе формируется линия плиток, когда игроки делают свои ходы, обычно, но не всегда, сопоставляя точки на открытом конце домино. Такое формирование плиток называется линией игры. Основные инструкции перечислены здесь в разделе «Линия игры» специально для этих игр.

Перетасовка плиток
Перед каждой игрой игрок перетасовывает плитки лицевой стороной вниз на плоской игровой поверхности, тщательно перемешивая их движением рук. Руки игрока не могут оставаться на одних и тех же плитках во время тасования, и игрок, который тасует, должен последним брать руку для игры.
Игроки могут по очереди тасовать кости перед каждой игрой, или один и тот же игрок может тасовать кости перед каждой игрой.
Вот два из нескольких вариантов: 1) Игрок справа от игрока, делающего первый ход, тасует карты для игры; или 2) Победитель предыдущей игры перемешивается для следующей игры.

Расположение сидений
Позиция игрока за столом в игре с тремя и более игроками называется местом.
Один из способов определить рассадку – это жребий. После того, как кости перетасованы, каждый игрок берёт из колоды костяшку костяшки. Игрок, вытянувший плитку с наибольшим количеством точек, имеет право первого выбора места. Игрок, занимающий следующие по высоте места, сам слева и так далее. Если есть ничья, она разбивается путем взятия новых костяшек из запаса. Плитки возвращаются в запас и перетасовываются до того, как игроки возьмут свои руки. В партнерской игре партнеры садятся друг напротив друга.

Порядок игры
Есть несколько различных способов определить, кто из игроков будет играть первым: 1) Жеребьевка. 2) Начните игру, установив самую тяжелую костяшку домино. 3) Пусть победитель предыдущей игры сделает первый ход в следующей игре. После того, как будет определено, кто будет играть первым, порядок игры будет определяться рассадкой. Игра продолжится слева по часовой стрелке после того, как будет сделана первая игра. Или вы можете играть против часовой стрелки, как это делается в некоторых странах Латинской Америки, если все игроки согласятся на это перед игрой.
Жеребьевка для определения того, кто сделает первый ход
После того, как кости перетасованы, каждый игрок берёт из колоды костяшку костяшки. Игрок, вытянувший самую тяжелую плитку, будет играть первым. Если есть ничья, она разбивается путем взятия новых костяшек из запаса.

Начало игры с установки самой тяжелой доминошки
В некоторых играх в домино правила гласят, что первым должен сыграть игрок с наибольшим удвоением в руке. Правила для других игр гласят, что первый ход должен быть сделан игроком с самым тяжелым домино, двойным или одинарным, в зависимости от обстоятельств.
Самый высокий дубль: после того, как плитки перетасованы, каждый игрок берет свою руку из колоды. Игрок, который вытягивает самую высокую двойную комбинацию в сете (т. е. двойную девятку, если играет с двойной девяткой), разыгрывает ее в качестве ведущего. Если самый высокий дубль не выпал, разыгрывается второй по величине дубль. Если второй по величине дубль не выпал, разыгрывается третий по величине дубль и так далее, пока не будет сыгран дубль. Если ни у кого из игроков нет дубля в руке, все руки сбрасываются, перетасовываются и разыгрываются новые руки. После того, как первый игрок поставил свой дубль, второй ход делает игрок слева от него, и игра продолжается по часовой стрелке.
Самая тяжелая кость: следуйте приведенным выше инструкциям для «Самая высокая двойная кость», за одним исключением: вместо розыгрыша новых рук, если ни у одного игрока нет двойной кости, игру начинает игрок, у которого самая тяжелая одинарная кость.
Победитель последней игры: Победитель последней игры может открыть следующую игру. Или, если игра заканчивается вничью, игрок, разместивший последний тайл, играет первым тайлом в следующей игре.

Рисование руки
Каждый игрок вытягивает количество костей, указанное в правилах разыгрываемой игры в домино, а затем кладет их перед собой таким образом, чтобы другие игроки не могли видеть точки на его плитках.
После того, как все руки были разыграны, в запасе может остаться излишек плиток. Эти плитки должны оставаться лицевой стороной вниз, и, в зависимости от правил игры, их можно купить (см. «Прохождение и прощание» ниже) позже в этой игре.

Открытие игры
Определите, кто будет играть первым, как описано выше в разделе «Порядок игры» и в соответствии с правилами конкретной игры в домино. Игрок, делающий первую игру, может называться сеттером, даунером или лидером. Он должен положить свою плитку лицевой стороной вверх в середину стола.
Слова «установить», «вниз» и «вести» используются как глаголы для обозначения первого действия в игре. «Набор», «падение» и «лидерство» используются как существительные для обозначения первого сыгранного в игре домино, а также первого розыгрыша игры.
Вот вариант правила, который игроки могут согласиться использовать: каждый раз, когда игрок играет дубль, будь то в начале игры или в любое время после нее, он может немедленно положить второй тайл на свой дубль до того, как следующий игрок начнет свою игру. .

Прохождение и прощание
Любой игрок, который не держит в руке плитку с правильным количеством точек и, следовательно, не может сделать следующую игру, должен либо спасовать, либо отказаться от запаса в соответствии с правилами игры. Некоторые игры позволяют игрокам пропустить игру, если они того пожелают, даже если у них есть игровая плитка.
Прохождение также называют стучанием и отречением. Игрок, который не может сыграть, должен объявить другим игрокам: «Я пас», а затем переходит к следующему игроку. Если никто не может сыграть, игра заканчивается.
В некоторых играх разрешено покупать плитки со склада. В этом случае игрок вытягивает количество плиток, которое ему разрешено взять в соответствии с правилами этой игры, добавляя их к плиткам, которые он держит в руке. Как только игрок вытянул плитку, которую он может сыграть, он играет в это домино.
Есть много игр в домино, в которых есть правило, что все плитки в запасе могут быть куплены, и есть другие, в которых есть правило, что некоторые плитки должны оставаться в запасе и не могут быть куплены. В последнем случае количество очков на плитках, оставшихся в запасе в конце игры, будет добавлено к счету победителя.

Линия игры
Есть много игр в домино, которые зависят от соответствия мастей. В этих играх первый игрок ставит свое домино, затем игрок слева от него добавляет свою плитку к одному из свободных концов и так далее, двигаясь по часовой стрелке вокруг стола, и каждый игрок добавляет плитку. Игроки добавляют плитки с одинаковым количеством точек с открытым концом уже сыгранной плитки.
По мере того, как каждый игрок подбирает и разыгрывает плитку, формируется линия. Такая конфигурация костяшек домино называется раскладкой, строкой или линией игры. Чтобы кости не падали со стола, когда игровая линия заходит слишком далеко, в домино можно играть в любом направлении. Независимо от схемы игровой линии, открытый конец последнего сыгранного домино остается неизменным.
Доминошки присоединяются к игровой линии двумя способами: 1) с игровой линией, по длине, костяшки, сыгранные встык; или, 2) поперек игровой линии, поперек, домино, сыгранные по совпадающему номеру. В большинстве игр в домино двойные и только двойные играются крест-накрест; одиночные игры разыгрываются вдоль, а следующая плитка добавляется после каждого сыгранного двойного, если двойное не является спиннером, оно должно быть продольным.

Спиннеры
Спиннер — это двойная игра, в которую можно играть со всех четырех сторон. В зависимости от правил игры, дубль, играемый в качестве ведущего, является единственным игроком в игре; или каждый дубль, сыгранный на протяжении всей игры, является спиннером. Если сыгранный дубль не является спиннером, он может быть сыгран только с двух сторон.

Оценка
В некоторых играх в домино часть счета получается из общего количества точек на концах игровой линии по ходу игры. Если была сыграна только одна костяшка домино, оба конца этой костяшки являются концами игровой линии. Таким образом, если разыграна плитка 5-5, счет будет равен 10.
Если были сыграны две кости домино, подсчет зависит от того, находятся ли обе кости с линией игры или одна плитка с, а другая плитка находится поперек линии игры. Например, если разыгрываются плитки 3-5 и 5-1, счет равен 4 (3+1). Совпадающие половинки каждой из двух костей домино будут соединены встык, а открытые концы равны 3 и 1. Если разыгрываются плитки 3-5 и 5-5, счет равен 13 (3+5+5). . Двойная плитка 5-5 будет разыгрываться поперек игровой линии, и обе половины двойной плитки будут считаться концами игровой линии.
Учитывая последний пример, если плитка теперь играется на 5-5, предполагая, что это не спиннер, 5-5 больше не является концом для целей подсчета.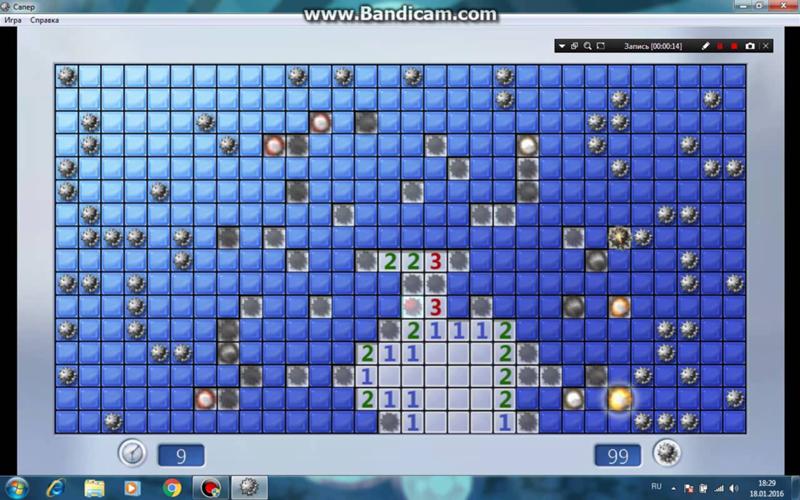 См. пример ниже. Линия игры 3-5, 5-5, 5-1, счет 4 (3+1). Если 5-5 в данном случае не спиннер, то 5-5 не конец.
В некоторых играх в домино счет подсчитывается только тогда, когда количество концов игровой линии кратно, например, 5 или 3.
Другой метод подсчета очков, используемый во многих играх в домино, заключается в подсчете общего количества очков проигравших игроков путем подсчета очков на плитках, оставшихся у них в руках в конце раздачи или игры, а затем добавления этого числа к счету победителя.
Вот вариант правила, который игроки могут согласиться использовать: при подсчете очков на костях, оставшихся в руках проигравших в конце раздачи или игры, учитывайте только один конец удвоения (т. е. 4-4 считается как всего 4 балла).

Конец игры
Некоторые игры в домино заканчиваются после того, как было сыграно определенное количество рук или игрок или команда набрали необходимое количество очков для победы. Во многих других играх в домино цель игры состоит в том, чтобы стать первым игроком (или командой), который избавится от всех костяшек домино в вашей руке. Эти игры в домино заканчиваются, когда игрок сыграет все кости домино в своей руке раньше других игроков и объявит: «Домино».
Иногда ни один из игроков не может сыграть еще раз. Это называется заблокированной игрой, и, если игра заблокирована и никто не может продолжить игру, игра заканчивается.

Что делать, если происходят эти несчастные случаи:
Домино выставлены по ошибке
Если ваше домино случайно открылось другому игроку, оно должно быть открыто для всех игроков.
Нарисовано слишком много плиток
Если игрок вытягивает больше плиток для своей руки, чем ему положено, это называется овердро. После обнаружения овердрафта игрок справа от перерасходованной руки берет лишние домино из перерасходованной руки, не глядя на них, и возвращает их в запас. Затем колода должна быть перетасована до того, как кто-либо еще возьмет свою руку.
Вот вариант правила, который игроки могут согласиться использовать: показать перерисованные тайлы всем игрокам, прежде чем вернуть их в запас, а затем перетасовать колоду.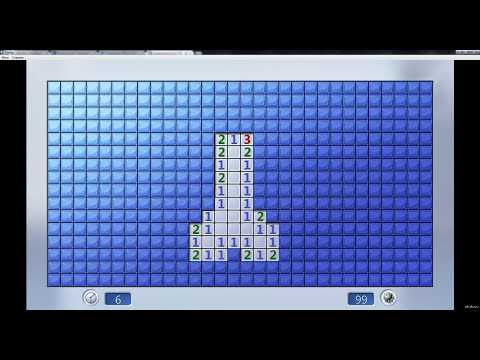
Нарисовано недостаточно плиток
Если игрок вытягивает меньше плиток для своей руки, чем он имеет право, это называется андердро. Как только обнаруживается андердро, он берет необходимые плитки из запаса, чтобы завершить свою руку.
В домино играют с ошибкой
Когда игрок играет неправильно в домино, это называется неправильной игрой. Если игрок ошибается (например, соединяет 2 с 3) и это обнаруживается до того, как следующий игрок начнет свою игру, он должен вернуть неправильно сыгранную кость в свою руку и сыграть правильную кость. Если игрок неправильно играет, и никто не замечает этого до тех пор, пока не будет сделана следующая игра, неправильная плитка считается сыгранной и не может быть заменена правильной плиткой. Если счет реализован по необнаруженной ошибке, игроку разрешается сохранить его.
Если это не ошибка, то после того, как плитка сыграна и игрок убирает руку с плитки, игрок не может взять ее.
Игрок играет вне очереди
Когда игрок играет вне очереди, это называется неправильной игрой. Если игрок играет вне очереди и это обнаруживается до того, как следующий игрок сделает свой ход, он должен отозвать свой тайл. Если игрок играет вне очереди и это не обнаруживается до следующего розыгрыша, ошибка остается в силе. Если в результате неправильной игры реализован счет, игроку разрешается сохранить его.

Типы игр в домино
Почти все самые популярные игры в домино относятся к одной из четырех категорий. Четыре категории: игры со ставками, игры с блокировкой, игры с подсчетом очков и раундовые игры.

Игры с торгами
Игры с торгами представляют собой карточные игры, в которые играют от двух до четырех игроков. В этих играх игроки делают ставки, игрок, предложивший самую высокую цену, называет масть, а счет определяется ставкой.
Игры с блокировкой
В игры с блокировкой играют, сопоставляя костяшки домино в ряд. Подсчет очков производится только в конце каждой руки. Игрок (или команда), который первым разыграет все кости домино в своей руке, или «домино», подсчитывает общее количество костей, все еще удерживаемых его противником (-ами). В случае заблокированной игры игрок или команда, набравшие наименьшее количество очков, подсчитывают общее количество плиток, все еще удерживаемых его противником (противниками).
Игры с подсчетом очков
В игре с подсчетом очков, как и в игре с блокировкой, также участвуют соответствующие домино. Одно отличие состоит в том, что подсчет очков производится на протяжении всей игры после каждого розыгрыша подсчета очков, а также в конце каждой руки. Игра продолжается до тех пор, пока игрок или команда не наберет необходимое количество очков для победы. Игра состоит из серии рук. Раздача состоит из серии розыгрышей костяшек домино, взятых из колоды.
Круглые игры
Круглые игры — это групповые игры, в которые играют от трех до десяти игроков, в которых подсчет очков обычно производится в конце каждой руки, и каждая рука обычно представляет собой игру.

Теперь, когда вы знаете основы, посмотрите правила некоторых игр или закажите набор домино.

Саперные секреты. Продвинутая тактика сапера

17.02.2022 Рубрика: Ковер-солитер

• Перевод

[Пятничный перевод статьи 1999 года автора Thief Engine Шона Барретта]

Неприятная ситуация в Сапе

В этом положении я знаю, что вокруг меня много мин, но не могу определить, где они находятся . Несколько мин могут находиться в одном из двух мест (розовый или синий), группа мин может находиться в одном из двух сочетаний (светло/темно-зеленый). Кроме того, есть еще сложная ситуация с «5» и «6» в левом верхнем углу, которую я никак не выделил.

Синий/розовый — взаимоисключающие пары, светло/темно-зеленый — взаимоисключающие группы

Сапер: логика или вероятность

В игру «Сапер» можно играть двумя способами: как логическую или вероятностную игру.

Технически вероятность подразумевает логику. Если логически доказать, что мина должна быть в определенном месте, то вероятность 100%. Если сможете доказать, что его нет в этом месте, то вероятность 0%. То есть в некотором смысле для нас важны только вероятности. Однако игрок использует логическую дедукцию, чтобы распознавать такие 100% ситуации. Иногда, особенно на низких уровнях сложности, достаточно пройти уровень, никакого расчета вероятностей не требуется.

Но бывают ситуации, когда вся логика мира не может тебя спасти. Простой пример — ситуация с буквой «Т», которая видна внизу по центру. Немного усложняется дополнительными соседними минами. (В простейшем случае «2» заменяется на «1», а «5» на «3», чтобы сделать ситуацию симметричной.)

Не нет способ получить больше информации о вероятном положении одной мины, оставшейся в одна из этих клеток. Пятьдесят на пятьдесят шансов — можно подбросить монетку. Когда вы получаете что-то подобное, лучше сразу сделать выбор и не откладывать его на потом. Если догадка неверна, то, по крайней мере, вы сэкономите время на решении остальной части поля. (Но лично я стремлюсь к окончательности, поэтому такие случаи оставляю на потом. И не корите себя за то, что не угадали. Когда выигрыш или проигрыш зависит от подбрасывания монеты, это плохой геймдизайн.)

Тактика в конце игры

В эндшпиле можно использовать очень простую тактику — подсчитать количество оставшихся мин. Допустим, я решил все, кроме нижней правой части поля. Конфигураций мин, соответствующих данным, может быть только две:

Возможные конфигурации мин в правом нижнем углу

Если у вас такая позиция и счетчик говорит, что мин осталось всего две, то ответ такой готово: это должна быть конфигурация В .

Если счетчик говорит, что осталось три мины, то это не обязательно конфигурация A . Это могла быть схема B с оставшейся миной в одной из нижних правых групп клеток 3х3.

На самом деле перевес в пользу конфигурации B .

Локальные вероятности

Если вы исследуете вероятности только «локально», вы увидите, что каждая из ячеек в отмеченных взаимоисключающих группах имеет 50-50 шансов быть миной. Когда я говорю «локально», я имею в виду, что если рядом с двумя неизвестными ячейками стоит «1», то вероятность того, что в каждой из них есть спрятанная мина, составляет 50%.

Точно такая же ситуация и в нижнем центре: каждая из соседних ячеек, примыкающих к неизвестной паре, содержит ровно одну мину, то есть каждый из соседних фрагментов данных предполагает 50-процентную вероятность. В левом верхнем углу аналогичная ситуация:

С абсолютной точностью в каждом из розовых овалов по одной мине, то есть осталось всего 7 мин

Ситуация в правом нижнем углу тоже несколько похоже: рядом с каждой из цифр на «границе» есть одна шахта и две ячейки, в которых она может находиться.

Если рядом с ячейкой находится одна скрытая мина, но три закрытых ячейки, то вероятность нахождения мины в каждой из ячеек равна 33%; каждая из четырех закрытых ячеек имеет вероятность 25%. Если у нас есть две скрытые мины и три закрытые ячейки, то каждая ячейка имеет вероятность 66%.

Вот ситуация с «локальной вероятностью» для всего поля:

Как видите, несколько ячеек в верхней левой области имеют кратные вероятности; закрытая ячейка рядом с «2» и «6» и одна рядом с «3» и «5». (Ячейка рядом с «5» и «6» по-прежнему имеет шанс 66% благодаря им, так что очевидного расхождения нет.)

Разрешение конфликтов локальных вероятностей

Вам, наверное, интересно, что значит иметь конфликтующие локальные вероятности. Интуиция может подсказать, что самая большая вероятность – выиграть. Например, в ячейке между «6» и «2» должно быть 66%. Это будет означать, что самая левая ячейка с вероятностью 50% на самом деле имеет 33%. Или можно попробовать как-то совместить приоритеты: возможно, вероятность будет 5/6 или среднее значение.

Но на самом деле все это неправда. Данные, из которых получены вероятности, , а не не зависят друг от друга, поэтому никакие простые математические расчеты не будут правильными. Причина, по которой локальное 50-процентное предположение в нижнем центре является правильным, заключается в том, что оно действительно не зависит ни от чего другого. Если случайным образом воссоздать поле по уже имеющимся у нас данным, то ровно в половине моделей мина окажется в одной из двух ячеек. (Вероятность иногда сбивает с толку людей, которые не могут разобраться, какие правила расчета вероятностей применимы в той или иной ситуации. Такой подход гарантированно является правильным, поскольку он основан на определении вероятности в статистическом прогнозировании: расчет производится путем измерения в все возможные конфигурации, которые могли бы привести к текущей ситуации, при этом все они считаются равновероятными.)

То есть для корректных замеров в ситуации в левом верхнем углу нужно рассмотреть все возможные конфигурации мин, удовлетворяющие уже собранным данным, а затем вычислить, какой процент из них содержит мину в нужном положении.

Прямой расчет потребует много времени. К счастью, есть и другие способы.

Количество конфигураций

Абстрактный способ расчета вероятностей состоит в том, чтобы пройтись по всем возможным конфигурациям шахты, отбросить конфигурации, не соответствующие собранным данным, и рассчитать статистику для каждой из возможных позиций.

Более практичный подход — рассматривать только те варианты, от которых нельзя отказаться. Для этого нам нужно применить логику и сгенерировать все возможные ситуации, которые могут соответствовать имеющимся данным. Я уже показал два варианта для правого нижнего угла, а вот вероятности для левого верхнего:

Возможные конфигурации для левого верхнего угла

моя может быть в любой из ячеек с равной вероятностью.Я мог бы перечислить каждый из этих двух случаев отдельно, то есть было бы 10 конфигураций, но нам это ни к чему Структура таблицы: две строки (пронумерованы как «1» и «2») различаются положением мины в четвертом ряду. Три столбца характеризуют положение мин во втором ряду. )

Теперь возникает соблазн воскликнуть: «ага, вот пять ящиков, значит, мы можем посчитать количество ящиков для каждой из возможных позиций мины». Например, мина, расположенная в четвертом ряду (рядом с нижней левой «1»), в двух верхних случаях находится слева, а в трех нижних случаях — справа. Следовательно, мы можем решить, что он имеет 60% шанс оказаться справа, рядом с «6». (Это позиция с конфликтующими локальными вероятностями 50% и 66%.)

Однако упускаем одну тонкость — количество мин в некоторых случаях разное: в A1 шесть минут, B2 – четыре, а во всех остальных случаях пять.

Подсчет мин не найден

Для детального изучения этой тонкости вернемся к более простой ситуации в правом нижнем углу.

Возможные конфигурации из нижнего правого угла

Предположим, я уже открыл остальную часть поля и знаю, что осталось ровно три мины.

Заманчиво предположить, что наиболее вероятная конфигурация A ровно с тремя минами. Но это не так.

Еще один соблазн — вспомнить, сколько было мин и сколько было квадратов, и сказать «каковы шансы, что нижняя область 3×3 будет пустой». Это также неверно. Очень сложно объяснить, почему это ошибка, пожалуй, это можно сравнить с парадоксом Монти Холла. Достаточно, однако, сказать, что в действительности шансы в этой ситуации не зависят от общего числа мин и размера поля.

Правильный ответ: сколько возможных конфигураций трех мин соответствуют нашим знаниям в этой области? Из рисунка мы видим, что две: конфигурации A и B . А вот в В сразу две мины. Третья мина может находиться в любой из ячеек в нижней области 3×3, для которой мы еще не собрали никаких данных. То есть все девять варианты комплектации Б Я просто не все нарисовал.

Таким образом, имеется только десять возможных конфигураций. Каждая из десяти конфигураций равновероятна. (Как я упоминал ранее, это очень важно для понимания вероятности. Вероятность того, что компьютер сгенерирует любой из этих вариантов, мала, но они столь же малы, потому что компьютер [насколько нам известно] дал у каждой конфигурации равные шансы. у вас с равным с вероятностью вы можете выкинуть конфигурацию из десяти «голов» подряд и последовательность две головы, одна решка, одна голова, три головы, одна голова, одна решка и одна голова . Более вероятно, что в общей сложности выпадет пять орлов и пять решек, но не какая-либо конкретная подпоследовательность «орлов» и «решек». В Minesweeper мы имеем дело с конфигурациями мин, которые аналогичны последовательностям подбрасывания монеты.)

Поскольку каждая из десяти конфигураций (девять для B , одна для A ) равновероятна, конфигурация B в данном случае имеет вероятность 90%!

Если бы на этом этапе было четыре шахты, то в конфигурации A было бы девять вариантов. Конфигурация B будет иметь по одному варианту для каждого варианта расположения двух мин в левом нижнем углу; это С (9,2) , то есть 9!/((9-2)! * 2!) или 9*8/2 равно 36.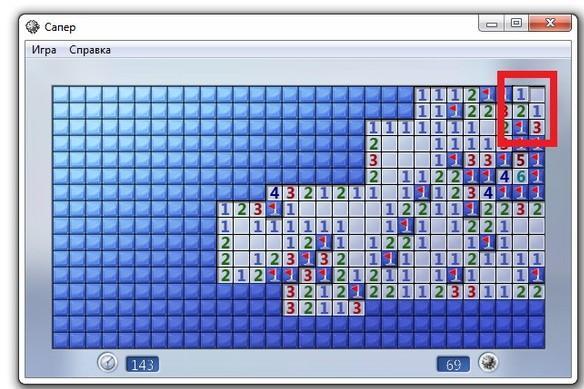 В этом случае конфигурация B будет иметь только 75% шансов.

Пятишаховая конфигурация А будет иметь 36 вариантов, а конфигурация В — 9*8*7/6 = 84 варианта; то есть шансы B будут чуть больше 66%.

В случае шести минут B будет иметь шанс 60%. При семи минах Б было бы всего 50%. С восемью минами В будет на меньше вероятно, чем А; в этом случае при таком количестве мин на остальных позициях конфигурации становятся меньше. Рассмотрим худший случай, когда осталось 11 минут. (Вероятность того, что это произойдет, крайне мала, но если такая ситуация возникает, то применяются эти вероятности.) В конфигурации B , мины будут во всех закрытых ячейках, в комплектации A во всех, кроме одной. То есть для А есть 9 вариантов и только один для Б.

окончательное решение

На нашем поле осталось девять мин. Один из них находится в центральной нижней части, и его положение совершенно независимо, поэтому вы можете его игнорировать.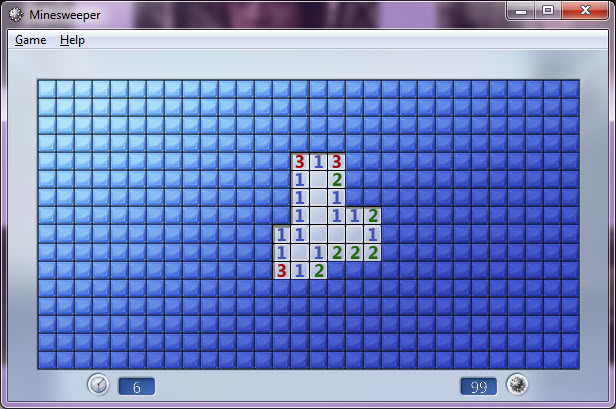 То есть мы рассматриваем все поле, кроме этого случая: не найдено всего восемь мин. (Чтобы избежать путаницы, я продолжу явно считать овал в верхнем левом углу, потому что это изображение верхнего левого угла.)

Может быть сформирована любая комбинация верхней левой и нижней правой конфигураций, за исключением одной из них (А1+А), для которой требуется девять минут. Поэтому мы должны перечислить каждую из этих возможных конфигураций и подсчитать оставшиеся мины и закрытые ячейки.

На самом деле количество закрытых ячеек не зависит: их девять в правом нижнем углу и три в левом верхнем, то есть всего 12.

Верхний левый	Внизу справа	Количество мин	Оставшиеся минуты	Закрытые опции
А1	Б	8	0	1
В1	А	8	0	1
В1	Б	7	1	12
А2	А	8	0	1
А2	Б	7	1	12
В2	А	7	1	12
В2	Б	6	2	66
С2	А	8	0	1
С2	Б	7	1	12

Таким образом, всего возможно 118 комбинаций. 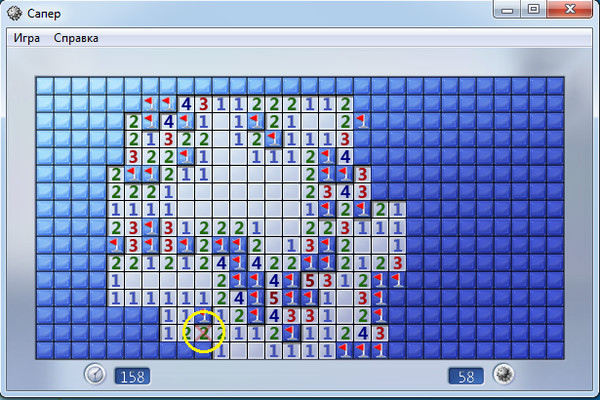Исходя из этого, мы можем самостоятельно подсчитать количество комбинаций для каждой из верхней левой и нижней правой конфигураций:

Конфигурация	Опции	Процент
А1	1	1
В1	13	11
А2	13	11
В2	78	66
С2	13	11
А	15	13
Б	103	87

Далее я обошел каждый квадрат на доске и вычислил его вероятность, суммировав количество вероятностей, в которых он появляется, и разделив на 118. (На самом деле, просто сложив вышеуказанные проценты.) закрытые ячейки имеют мину в 15 из 118 вариантов (то есть шансы, что хотя бы в одной закрытой ячейке есть мина, очень велики). [Это можно рассчитать, умножив количество оставшихся мин на закрытые варианты, что даст нам среднее количество мин в закрытых ячейках. ]

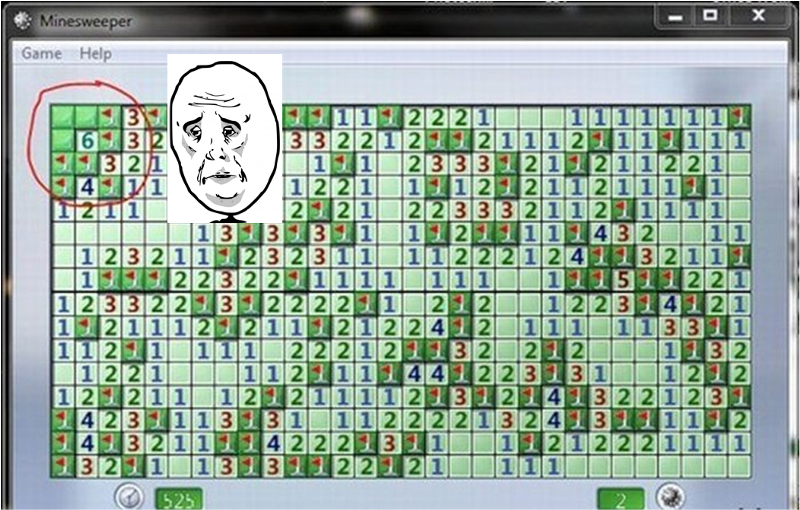Mine Probabilities

(Следует сказать, что это не показывает всю доступную информацию. Например, мы знаем, что вероятности двух темно-зеленых клеток связаны на 87% — если одна верна, то так и есть. другой.и синие 13 процентные ячейки которые имеют мины по конфигурации А так же связаны.остальные синие 13 процентные ячейки не связаны.если в одной из них есть мина то шанс что в любой из оставшихся есть мина уменьшается .)

Играем в игру

Скорее всего, играя в Сапера, вам не захочется корпеть над всеми этими вычислениями.

И я тоже.

Но у меня действительно перечислены все возможные конфигурации в левом верхнем и правом нижнем углах. Я заметил, что в одной конфигурации ( B2-B ) используется на одну мину меньше, чем во всех остальных, и применил проверенное временем правило «меньше мин — больше закрытых вариантов» (которое работает примерно до тех пор, пока количество закрытых ячеек равно менее чем в два раза превышает количество ненайденных мин).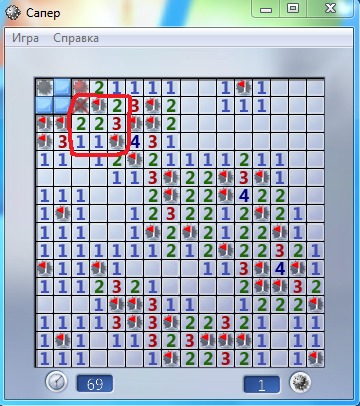 Это означает, что конфигурации с меньшим количеством мин гораздо более вероятны.

Так как в левом верхнем углу было много конфигураций, определить шансы для любой ячейки достаточно сложно. Так что я только что узнал, что конфигурация B в правом нижнем углу гораздо более вероятна, и случайным образом выбрал одну из совпадающих ячеек. (Я надеялся, что это позволит мне закончить нижний правый угол, а затем, вооружившись дополнительной информацией о количестве оставшихся мин, я смогу заполнить верхний левый угол, после чего мне нужно будет подбросить монету, чтобы выбрать нижний центр. .В идеале, конечно, я бы выбрал ячейку, максимизирующую вероятность получения полезной информации, но любая из этих догадок позволила бы мне «зайти» в правый нижний угол для дальнейшего сбора данных.) Шансы были выше у конфигурации B , поэтому я выбрал ячейку у которой в конфиге была мина A .

В восьми случаях из девяти я был бы прав.

Метки: Добавить метки

Игра

Сапер стандартна и очень проста в плане исполнения. Однако «затянуть» эта игра может любого очень надолго и серьезно. Вы можете найти его на каждом компьютере с операционной системой Windows. Для этого нажмите «Пуск» — «Все программы» — «Игры» — «Сапер». Несмотря на то, что эта программа есть практически на каждом компьютере, далеко не все пользователи знают, как играть в Сапера. Мы решили рассказать вам правила и дать несколько полезных советов, которые помогут вам быстро научиться играть и выигрывать.

Как играть в игру Сапер — инструкция

Для начала хотелось бы посоветовать вам начать игру на минимальном уровне сложности. Постепенно увеличивайте размер минного поля.

Цель игры: игроку необходимо найти все мины и обезвредить их, щелкнув по ним правой кнопкой мыши. Левой кнопкой мыши мы должны открыть все ячейки, за которыми не спрятаны мины.

1. Итак, вы запустили Сапер и начали новую игру. Отсчет начался. Теперь очень важно не нарваться на мину. Ведь в первый раз мы нажмем на любую из закрытых ячеек. Используйте, например, свою интуицию в первый раз.
2. Вы нажали на произвольную ячейку, и открылась целая область таких ячеек, где нет мин. Хорошо, а теперь посмотрите на цифры. Здесь они не случайны и дают вам очень важную информацию. Эти цифры показывают вам, сколько мин находится рядом с этой ячейкой с числом в радиусе одной клетки. Другими словами, если вы видите цифру 1, значит, на расстоянии одной клетки от этой цифры есть только одна мина и так далее. Другой вопрос — где именно находится эта мина? Справа от клетки, слева? На этот вопрос ответят остальные числа в других ячейках.
3. Если вы уверены, что на одной из закрытых ячеек находится мина, отметьте ее флажком (правая кнопка мыши).
4. Двойным щелчком по ячейке правой кнопкой мыши вы поставите на ней вопросительный знак. Этот вопросительный знак не влияет на игру, но позволяет отметить спорную ячейку и вернуться к ней позже. Иногда это очень удобно.
5. Если вы видите, например, что стоит цифра 2 и рядом с ней уже два флажка, которые вы установили, то возле этой клетки вы можете смело открывать все остальные в радиусе одной клетки.
6. Так открываем все остальные ячейки и обозначаем шахты до победы.

Теперь вы знаете, как играть в Сапера! Побейте собственные рекорды и соревнуйтесь с друзьями. Игра Сапер не только интересна, но и очень хорошо развивает логику, тренирует мозг в целом. Многие играют в нее не год и не два. Если посмотреть на игрока, который уже несколько лет играет в Сапера, во время игры просто диву даешься. Он так быстро открывает ячейки, что становится совершенно непонятно, как это вообще возможно. Конечно, как и любая другая игра, Сапер тоже надоедает. Однако пройдет неделя, и вам снова захочется увеличить минное поле, побить рекорд по времени и похвастаться перед друзьями.

Сапер — это игра-головоломка, где игроку необходимо расчистить минное поле пометив флажками клетки на которых могут быть мины, есть подсказки в виде цифр найти их на соседних пустых ячейках.

Многие не умеют играть в Сапер, кликают по ячейкам наугад, и им открываются какие-то цифры, что они означают и для чего нужны, по ним мало кто догадывается. Прочитав до конца эту небольшую пошаговую инструкцию, как играть в Сапера, вы поймете, как правильно играть в Сапера и, возможно, вам понравится эта игра.

Правила игры Сапер

Как запустить игру
Во всех ОС Windows уже установлена ​​игра Сапер, она стандартная. Для входа в игру нажмите Пуск — Все программы — Игры — Сапер.

Настройки тральщика

Открыв сапёр, нажми F5 или зайди через меню в «Параметры» игры, там увидишь 3 сложности:

• Новичок — небольшое поле 9х9 ячеек с 10 минами. В углах нет мин.
• любитель — среднее поле 16х16 ячеек с 40 минами.
• Professional — большое минное поле 16х30 ячеек и 99 мин.
• Special — можно настроить размер игрового поля и количество мин на нем.

Если вы играете не в стандартный сапер, который есть в винде, а в мобильную версию или какую-то другую, то найдите в главном меню «настройки», там же может быть выбор сложности игры.

Открытие первых ячеек

Игра начнется, когда вы откроете первую ячейку. Многие питаются сначала открывая сразу несколько ячеек, беспорядочно щелкая по минному полю. Если открылось несколько камер, то уже можно оценить ситуацию.

Что означают цифры в Сапе

Цифры в «Сапёре» — это наши подсказки, они говорят нам, сколько и где находятся мины. Например, клетка с цифрой 1 говорит нам о том, что вокруг нее сверху, снизу, слева, справа и по диагонали находится только 1 мина. Клетка с цифрой 2 говорит нам, что вокруг нее две мины, цифра 3 означает, что вокруг клетки 3 мины и так далее.

Маркировка мин

При обнаружении мины отметить ее флажком, для этого нужно щелкнуть правой кнопкой мыши (правой кнопкой мыши) по клетке, где предположительно может находиться мина. Когда мы определили расположение мин, нажимаем на те клетки, где их быть не должно.

Открыть все ячейки

Посмотрите на все открывшиеся нам числа и определите, где могут находиться мины. Если двойка означает, что вокруг две мины, тройка — три мины, и так далее, пока мы не отметим все мины и не откроем все свободные клетки.

• Начните играть с самого простого уровня «Начинающий», на этом уровне сложности нет мин по углам.
• Будьте осторожны! Один неверный клик и вы проиграли.

Логическая игра «Сапер» отлично развивает мышление. Любители этой игры соревнуются между собой, разминируя на время минное поле.

Если вам что-то непонятно или есть вопросы по игре, пишите в комментариях. А те, кто разобрался с правилами игры Сапер, пишите свои рекорды 🙂

Сапер — одна из старейших стандартных игр, доступных в операционной системе Windows. Однако не все пользователи знают правила этой игры: вместо логического мышления они кликают по всем ячейкам подряд, что неизменно приводит к проигрышу.

Инструкция

Запустить игру «Сапер». Для этого выберите Пуск -> Все программы -> Игры -> Сапер. В верхнем окне игры с левой стороны отображается количество открываемых бомб, с правой стороны таймер. Чтобы начать игру, нажмите на одну из ячеек игрового поля. Если в ячейке, на которую вы нажали, появляется только одно число, щелкните случайным образом другую ячейку. В результате у вас должна открыться целая группа ячеек. Теперь не нужно наугад нажимать — соблюдайте правила.

Цифры в ячейке показывают количество мин, которые расположены вокруг в радиусе одной ячейки. На основании этой информации необходимо искать установленные мины. Например, если в ячейке стоит цифра 1, это значит, что в соседних ячейках есть одна мина. Если цифра 2 стоит в открытой ячейке, значит, в радиусе вокруг нее есть две мины. Сравнив информацию, полученную из нескольких ячеек, попытайтесь выяснить, в какой нераскрытой ячейке находится мина. Найдя его, щелкните по нему правой кнопкой мыши, чтобы установить специальный флажок.

Найдя мину рядом с ячейкой и сравнив информацию, полученную от соседних ячеек, вы сможете понять, в какой неоткрытой ячейке точно нет мин. Нажмите на эту ячейку. В нем снова будет число, либо сразу откроется целая группа ячеек.

Обнаружить таким образом следующие мины. Например, вы уже нашли две мины, и расположены они в радиусе клетки с цифрой два. В этом случае окажется, что возле этой ячейки мин больше нет. Поэтому смело нажимайте на клетки в радиусе от цифры 2. Действуя таким образом, вы сможете найти все спрятанные мины.

После того, как вы найдете все мины, расположенные на игровом поле, на смайлике, расположенном между счетчиком мин и таймером, появятся точки. Это будет означать, что игра завершена. Вы можете начать новую игру на том же уровне сложности или выбрать другой. Этот уровень сложности будет зависеть от размера игрового поля.

Мало кто сейчас помнит старые добрые времена, когда компьютеры только становились личными, а о современных 3D-шутерах никто и не мечтал. В то время единственным способом расслабиться за ПК для многочисленной армии офисных работников были простые игры, встроенные в Windows. 9Пасьянс 0470 обычно предпочитали барышни, а легендарного шахтера — мужчины. Игра уже давно завоевала статус культовой, но в наши дни она уже не пользуется особой популярностью, а зря. Он не требует никаких ресурсов, работает на очень старых компьютерах и легко может скрасить короткие минуты отдыха. Поэтому разобраться, как играть в Сапера, будет полезно и познавательно.

• Трезво оценивайте уровень собственных навыков. Если вы никогда раньше не играли в «Сапёра», начните с самого простого уровня сложности «новичок». Попытка сразу поставить рекорд на «профессионале» ни к чему хорошему не приведет.

Видео о гуру игры Сапер

Перед вами откроется пустое игровое поле с синими квадратами.

• Далее перед вами откроется пустое игровое поле с синими квадратиками. Ваша задача — как можно быстрее щелкнуть левой кнопкой мыши 5-6 квадратов, чтобы понять приблизительное местонахождение заложенных мин. Возможно, что вам не повезет, но на удачу можно положиться.
• Теперь нам нужно оценить результаты. 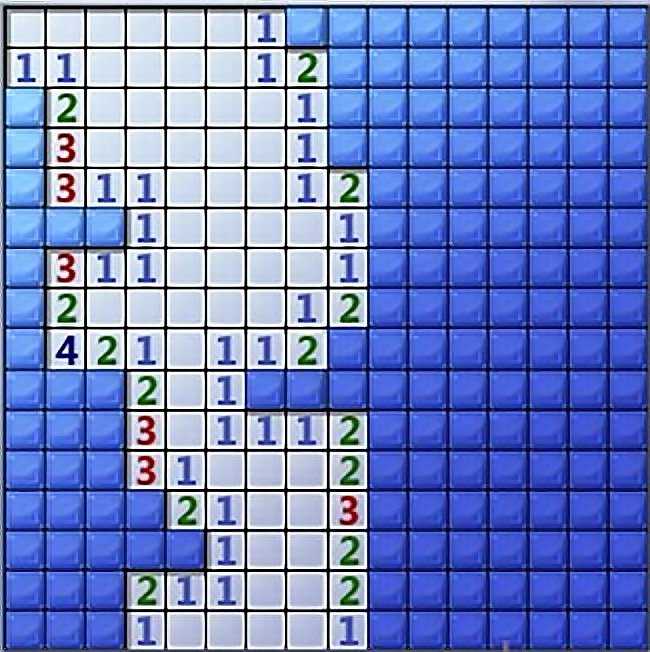Цифра в квадратах означает количество мин, находящихся вокруг того или иного поля. Будьте внимательны: учитываются не только вертикальные и горизонтальные, но и диагональные линии.

Цифры в ячейках обозначают количество мин, находящихся вокруг определенного поля.

• На рисунке ниже отмеченные поля гарантированно содержат мину, поэтому их можно пометить (щелкнуть правой кнопкой мыши по ячейке).

На этой картинке отмеченные поля гарантированно содержат мину

• После этого внимательно осмотрите игровое поле и отметьте галочками те клетки, в которых гарантированно нет мин. На рисунке ниже маркер находится уже в верхнем левом углу квадрата, поэтому две соседние клетки можно помечать без опасений: они безопасны.

• Аналогично постепенно разбираемся с остальными ячейками. Так вот, на приведенном рисунке сразу определить мины в белом квадрате не получится. А вот красные и зеленые области поддаются анализу.
• Итак, 1-я ячейка во второй строке и 2-я ячейка в третьей гарантированно содержат мины, что мы и помечаем.