ТРЕХКАРТИННЫЙ ЧЕРТЕЖ ТОЧКИ. КООРДИНАТЫ ТОЧКИ — Студопедия
В практике построения технических чертежей часто возникает необходимость в использовании дополнительной проекции изображаемого предмета, так как две проекции не обеспечивают ясность его форм и размеры. В этом случае вводят еще одну плоскость – П3, которая носит название профильной плоскости проекций. Профильная плоскость располагается перпендикулярно к двум другим плоскостям, образуя в пространстве трехгранный угол, составленный плоскостями П1, П2, П3. Линией пересечения плоскостей П1 с П3 и П2 с П3 также носят название осей проекций и обозначаются соответственно буквами y и z.
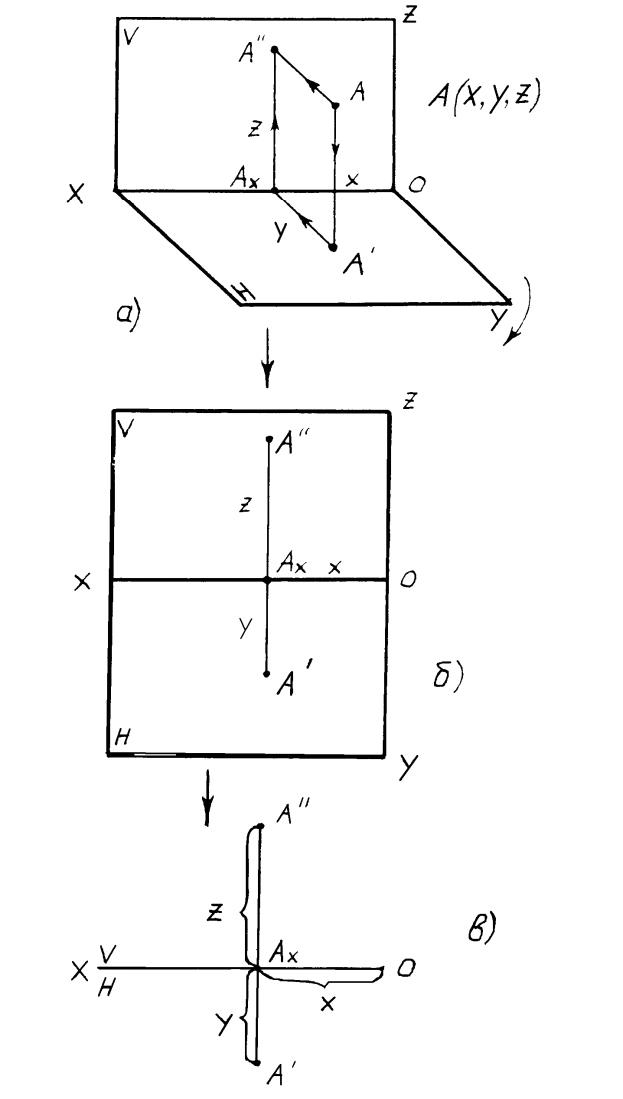
На рис. 1.6,а показано построение трех проекций точки А. Из проецируемой точки опускаются перпендикуляры на все три плоскости. Развернув трехгранный угол и совместив плоскости П1 и П3 с плоскостью П2, вращая первую вокруг оси x, а вторую вокруг оси
1.6,б). Третья проекция точки А носит название профильной проекции. Расстояние от профильной плоскости проекции носит название широты точки. Оно изобразилось на чертеже отрезком АА3 (или А1Аy).Рис. 1.6
Если плоскости проекций П1, П2 и П3 принять за координатные плоскости, то широта точки, равно как ее глубина и высота, могут быть измерены какой-либо единицей длины и выражены числами, которые носят название координат точки. Число, определяющее расстояние от точки А до плоскости П3, называют абсциссой точки, расстояние до плоскости П2 – ординатой точки и расстояние до плоскости П1 – аппликатой точки. Координаты точки обозначают соответственно буквами x, y, z и записывают в следующем порядке: А (4,2,4) (рис. 1.6,а). Выше говорилось, что широта, глубина и высота точки определяются на комплексном чертеже расстояниями от проекций точки до соответствующих осей проекций.
Образование двух- и трёхкартинного комплексного чертежа — Студопедия
Наиболее употребительным в практике является метод комплексного чертежа в ортогональных проекциях. Комплексным чертежом называется чертёж, состоящий из нескольких связанных между собой проекций изображаемой фигуры. Метод комплексного чертежа в ортогональных проекциях называется такжеметодом Монжа.
Этот метод прост в построении и даёт большую точность при графическом решении задач. Он обеспечивает точное определение изображённой фигуры по чертежу. Недостатком метода является малая наглядность изображений.
Комплексный чертёж из двух проекций называется также двухкартинным чертежом.
Рассмотрим неподвижную систему двух взаимно перпендикулярных плоскостей П1 и П2 в соответствии с рисунком 1.
П2), называются проецирующими прямыми (AА1 – горизонтально проецирующая прямая, АА2 – фронтально проецирующая прямая). Прямая пересечения плоскостей проекций называется осью проекций. Её обозначают буквой x.
Плоскость, перпендикулярную к плоскости проекций, называют проецирующей плоскостью (плоскость, перпендикулярная к плоскости П1, называется горизонтально проецирующей плоскостью
, а плоскость, перпендикулярная к плоскости П2, – фронтально проецирующей плоскостью).Плоскость АА1А2 проходит через прямую АА1, перпендикулярную к плоскости П1, в силу чего она перпендикулярна к плоскости П1. Аналогично плоскость АА1А2 перпендикулярна плоскости П2.
Следовательно, дважды проецирующая плоскость АА1А2 перпендикулярна к оси проекций X.
Точку пересечения плоскости АА1А2 с осью проекций х как точку, принадлежащую одновременно обеим плоскостям П1 и П2, обозначим А12. Прямые A12
Рисунок 1.2.6 – Ортогональное проецирование точки
Тогда каждая пара точек А1 и А2, лежащих на этих перпендикулярах, определит в пространстве единственную точку А.
х). Но плоскость, перпендикулярная к линии х пересечения двух плоскостей П1 и П2, перпендикулярна к каждой из этих плоскостей, т.е. плоскость А1А12А2 является проецирующей по отношению к обеим плоскостям проекций. Следовательно, перпендикуляры, восставленные в точках А1 и А2 соответственно к плоскостям П1 и П2, лежат в одной плоскости (в плоскости А1А12А2). Точка А их пересечения и является искомой точкой пространства, определяемой данной парой точек Итак, каждой точке А соответствует пара её проекций А1 и А2, лежащих вместе с данной точкой А в одной плоскости, перпендикулярной к обеим плоскостям проекций П1 и П2, а следовательно, и к линии х их пересечения; обратно, любые две точки А1ÎП1 и А2ÎП2, лежащие в одной плоскости, перпендикулярной к оси х, определяют в пространстве единственную точку А.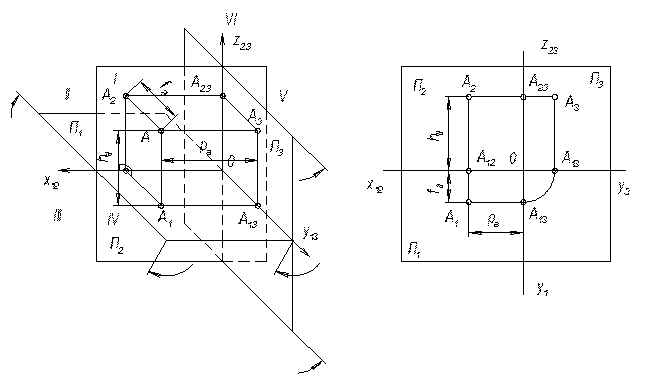
Расстояние А1А точки А от горизонтальной плоскости проекций называется высотойточки А, а её расстояние А2А от фронтальной плоскости проекций – глубиной точки А.
Для получения плоского чертежа совмещаем плоскость проекций П1 с плоскостью П2 путем вращения плоскости П1 вокруг оси X в направлении, указанном на рисунке 1.2.6 стрелками, так, чтобы передняя полуплоскость П1 совместилась с нижней полуплоскостью П2. В результате получим комплексный чертёжточки А (рисунок 1.2.7), состоящий из двух проекций А1 и А2 точки А. Обе проекции А1 и А2 лежат на одном перпендикуляре к оси проекций х, которую как прямую, принадлежащую одновременно обеим плоскостям проекций П1 и П2, будем обозначать на комплексном чертеже х12.
Два перпендикуляра А12А1и А12А2 к оси х12 имеют общую точку А12. Прямая А1А2, соединяющая две проекции точки на комплексном чертеже, называется линией связи. Линия связи двух проекций точки перпендикулярна к оси проекций.
ПРИМЕЧАНИЕ:контуры плоскостей проекций на комплексном чертеже не показывают.
Рисунок 1.2.7 – Комплексный чертёж точки
Плоскости проекций разбивают всё пространство на четыре части, называемые квадрантами или четвертями. Принято нумеровать квадранты в порядке, указанном на рисунке 1.1.8, и называть их
Рисунок 1.2.8 – Квадранты пространства
Если точка лежит в I квадранте, то её горизонтальная проекция А1, будет принадлежать передней полуплоскости П1, а фронтальная проекция А2 – верхней полуплоскости П2.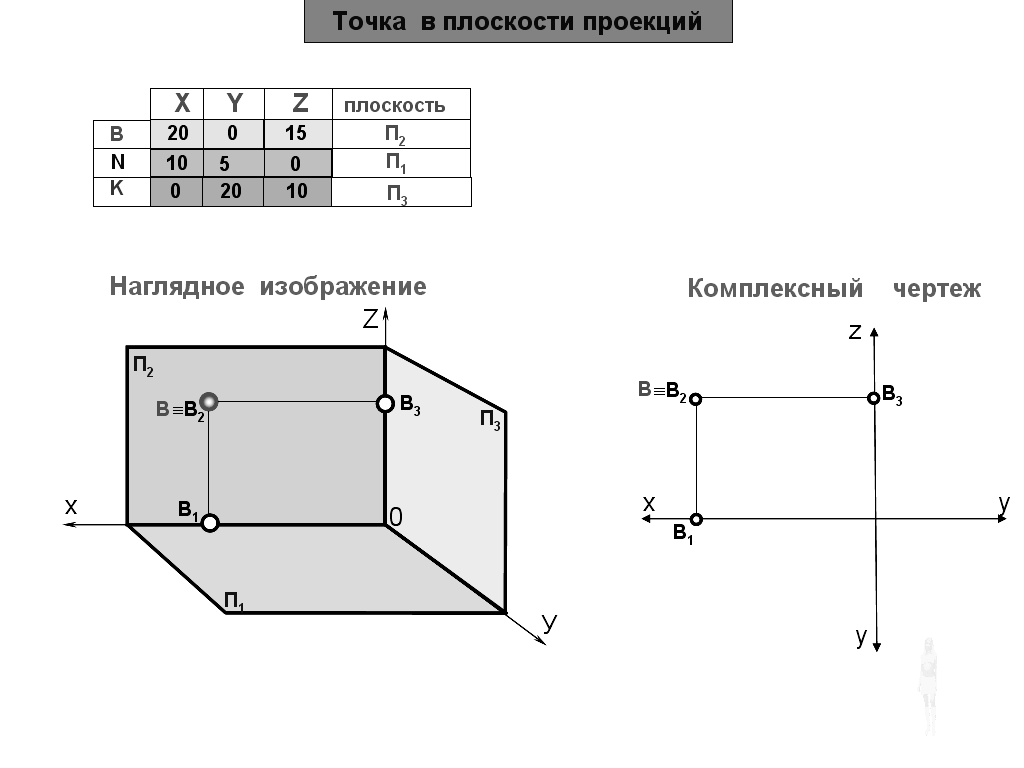
При совмещении плоскостей проекций горизонтальная проекция А1 точки А, лежащей в I квадранте, окажется расположенной ниже оси x12 в соответствии с рисунком 1.2.9.
В зависимости от положения натуральных (проецируемых) точек в различных квадрантах пространства будем иметь соответствующее расположение их проекций на комплексном чертеже в соответствии с рисунком 1.2.9, так же как и обратно: по расположению проекций можно судить о том, в каком квадранте лежит натуральная точка. Рисунок 1.2.9 – Комплексный чертёж точек, расположенных в разных квадрантах
Двухкартинный чертёж является метрически определённым чертежом. Однако, в силу трёхмерности пространственной фигуры её комплексный чертёж становится более ясным, когда, помимо двух основных проекций, дана ещё одна проекция на третью плоскость. В качестве такой плоскости проекций чаще всего применяют профильную плоскость проекций П3 (рис.
Пi (i=l, 2, 3). Основания этих пер-пендикуляров (точки А1, А2, А3) и являются соответственногоризонтальной, фронтальной и профильной проекциями точки А в системе плоскостей проекций (П1, П2, П3). Проецирующие плоскости
z23, а отрезки А12А1 и А23А3 равны, так как А12А1=А23А3=А2А (рисунок 1.1.11) есть глубина точки А.Рассмотрим квадрат А13O123А31А0. Диагональ этого квадрата является биссектрисой угла (Х12Z23). Следовательно, линия связи, соединяющая проекции А1 и А2, представляет собой ломаную линию с вершиной на биссектрисе К123 угла (X12Z23), состоящую из двух звеньев (горизонтального и вертикального). Часть этой ломаной заменяют иногда дугой окружности.
Таким образом, линии связи устанавливают на трёхкартинном чертеже следующим образом: А1А2 – вертикальная линия связи; А2А3 – горизонтальная линия связи; А1А3 – горизонтально-вертикальная линия связи; биссектриса К123– геометрическое место вершин ломаных линий связи в соответствии с рисунком 1.
2.12.
Рисунок 1.2.12 – Линии связи на проекционном чертеже
Прямая К123 определяется заданием трёх проекций какой-либо точки, например, точки А (А1А2А3), и является постоянной прямой комплексного чертежа.
Рассмотрим трёхгранник, образованный системой плоскостей проекций (П1,П2,П3). На осях x, y, z установим единицу измерения е. За начало отсчёта примем точку О пересечения трёх плоскостей проекций (вершину трёхгранника). Положительное направление на каждой оси установим, как показано на рисунке 1.2.13. Тогда трёхгранник Оxyz можно рассматривать как прямоугольную декартову систему координат с координатными осями: Ох – ось абсцисс, Оy – ось ординат, Оz – ось аппликат с координатными плоскостями хОyºП1, хОzºП2, yОzºП3.
.Рисунок 1.2.13 – Прямоугольная система координат в пространстве
Точку А(xA, yA, zA) по данным координатам хА,,yA,zA строят следующим образом: пользуясь единицей длины е, строим отрезок АА12, затем отрезок А12А1, параллельный оси у, и отрезок А1А, параллельный оси z. В результате получаем точку А(хА, уА, zА).
На чертежах, применяющихся в технике, оси проекций обычно не показывают. Это означает, что плоскости проекций могут перемещаться параллельно самим себе. Однако, и при отсутствии на чертеже осей всегда можно определить по данным двум проекциям точки третью её проекцию, если на чертеже имеются три проекции хотя бы одной точки. Это достигается при помощи постоянной прямой k чертежа, являющейся биссектрисой угла, образованного ломаной линией связи в соответствии с рисунком 1.
2.14. Например, известно расположение трёх проекций точки А. Это позволяет определить постоянную k123 как биссектрису угла А1А0А3. В результате линии связи становятся вполне определёнными и по каждым двум проекциям точки может быть построена третья её проекция. На рисунке 1.2.14 такое построение выполнено для точки В.Рисунок 1.2.14 – Безосный комплексный чертёж точки
Практическая работа «Комплексный чертеж»
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ БУРЯТИЯ
Государственное бюджетное профессиональное образовательное учреждение
«Авиационный техникум»
ОП.01. Инженерная графика
программы подготовки специалистов среднего звена (ППССЗ)
по специальности
15.02.08 Технология машиностроения (базовой подготовки)
Практическая работа №6:
Тема «Комплексный чертеж»
Улан-Удэ, 2019 г.
Тема «Комплексный чертеж»
Практическая работа №6:
Учебная цель: Научиться проецировать точки, отрезки и плоские фигуры..
Образовательные результаты, заявленные во ФГОС:
Студент должен
уметь:
выполнять чертежи технических деталей в ручной графике;
читать чертежи;
оформлять конструкторскую документацию в соответствии с технической документацией;
знать:
законы, методы, приемы проекционного черчения;
правила выполнения и чтения конструкторской и технологической документации;
правила оформления чертежей, геометрические построения и правила вычерчивания технических деталей;
требования стандартов Единой системы конструкторской документации (далее — ЕСКД) и Единой системы технологической документации (далее — ЕСТД) к оформлению и составлению чертежей и схем
Задачи практической работы:
На формате А4 выполнить основную надпись ГОСТ2.
104-68.Выполнить задание согласно номеру варианта.
Ответить на вопросы.
Сделать вывод от проделанной работы.
104-68.Рисунок 1 Образец готовой работы
Обеспеченность занятия:
Учебно-методическая литература:
Боголюбов С.К. Индивидуальные задания по курсу черчения: Учебное пособие для средних специальных заведений. 3-е изд., стереотипное. Перепечатка со второго издания 1994г.-М.: ООО ИД «Альянс», 2007.-368с.
В.П.Куликов, А.В.Кузин: учебник. Инженерная графика -3-е изд., испр.-М.: ФОРУМ, 2009.-368с.
Технические средства обучения:
Экран.
Практическое оборудование и инструменты:
Стол ученический;
Стул ученический;
Бумага для черчения ф.А4;
Карандаш чернографитный твердость М;
Карандаш чернографитный твердость Т;
Ластик;
Циркуль;
Точилка для карандашей механическая;
Линейка металлическая 30см.
Рабочая папка формата А4.
Практическая работа №5 в электронном или бумажном варианте.
Краткие теоретические и учебно-методические материалы по теме практической работы.
Рисунок 2 Пример построения комплексного чертежа
Вопросы для закрепления теоретического материала
к практической работе:
Как обозначается горизонтальная плоскость?
Как обозначается вертикальная плоскость?
Как обозначается профильная плоскость?
Инструкция по выполнению практической работы
На формате А4 (4шт.) вычертить основную надпись ГОСТ2.104-68.
Выполнить комплексный чертеж четырех деталей по двум заданным проекциям достроить третью. Выбрать свой вариант.
Нанести размеры по ГОСТ 2.
307-68.Заполнить основные надписи шрифтом ГОСТ 2.304-81 «шрифты чертежные» тип А.
Ответить на вопросы.
Сделать вывод от проделанной работы.
307-68.Критерии оценки
Если чертеж выполнен верно и аккуратно – отлично
Если выполнен верно, есть незначительные помарки и замечания преподавателя – хорошо
Если менее пяти не верных размера – удовлетворительно.
Если чертеж содержит более пяти грубых ошибок — неудовлетворительно.
Трехкартинный чертеж точки. Координаты точки
В
практике построения технических чертежей
часто возникает необходимость в
использовании дополнительной проекции
изображаемого предмета, так как две
проекции не обеспечивают ясность его
форм и размеры. В этом случае вводят еще
одну плоскость – П3,
которая носит название профильной
плоскости проекций.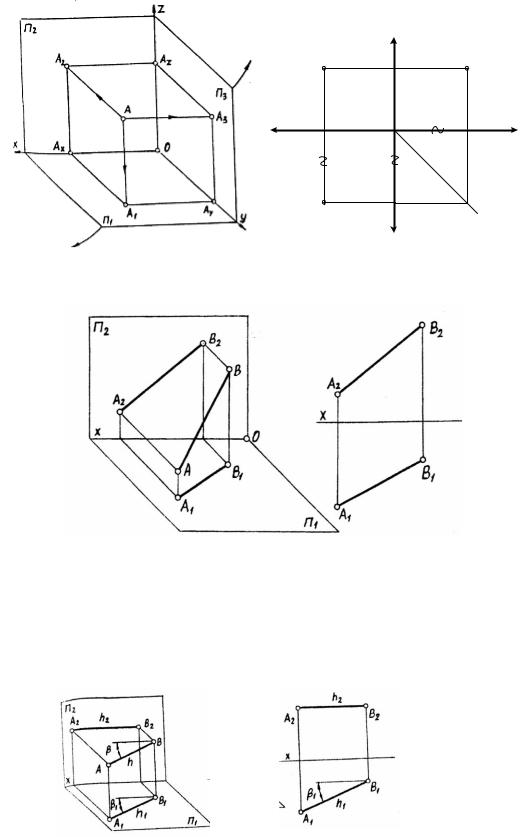
Профильная плоскость
располагается перпендикулярно к двум
другим плоскостям, образуя в пространстве
трехгранный угол, составленный плоскостями
П1,
П2,
П3.
Линией пересечения плоскостей П1 с П3 и П2 с П3 также носят название осей проекций и
обозначаются соответственно буквами y и z.
На рис. 1.6,а показано построение трех проекций точки А. Из проецируемой точки опускаются перпендикуляры на все три плоскости. Развернув трехгранный угол и совместив плоскости П1 и П3 с плоскостью П2, вращая первую вокруг оси x, а вторую вокруг оси z, получают трехкартинный комплексный чертеж точки А (рис. 1.6,б). Третья проекция точки А носит название профильной проекции. Расстояние от профильной плоскости проекции носит название широты точки. Оно изобразилось на чертеже отрезком АА3 (или А1Аy).
Рис.
1.6
Если
плоскости проекций П1,
П2 и П3 принять за координатные плоскости, то
широта точки, равно как ее глубина и
высота, могут быть измерены какой-либо
единицей длины и выражены числами,
которые носят название координат точки.
Число, определяющее расстояние от точки
А до плоскости П3,
называют абсциссой точки, расстояние
до плоскости П2 – ординатой точки и расстояние до
плоскости П1 – аппликатой точки. Координаты точки
обозначают соответственно буквами x, y, z и записывают
в следующем порядке: А (4,2,4) (рис. 1.6,а).
Выше говорилось, что широта, глубина и
высота точки определяются на комплексном
чертеже расстояниями от проекций точки
до соответствующих осей проекций.
Следовательно, и координаты точки могут
быть определены по ее комплексному
чертежу (рис. 1.6,б): x = ОАx = 4 ед., y = ОАy1 = 2 ед., z = ОАz = 4 ед.
Прямая линия
Проекции прямой линии на плоскость есть прямая. Отсюда следует, что для построения проекций прямой достаточно построить проекции двух точек, ей принадлежащих, и соединить их одноименные проекции прямыми линиями (рис. 1.7).
В зависимости от расположения прямых в пространстве относительно плоскостей проекций различают три вида прямых: прямые общего положения, прямые уровня и проецирующие прямые. На рис 1.7 изображены проекции прямой n (прямой общего положения), не параллельной и не перпендикулярной к плоскостям проекций. Проекции отрезка прямой n меньше его истинной длины: A1B1AB; A2B2AB. Различают три типа прямых уровня: горизонтальную, фронтальную и профильную прямые.
Рис. 1.7
Рис. 1.8
Рис. 1.9
К
прямым уровня относятся прямые,
параллельные какой либо из плоскостей
проекций.
Прямая, параллельная
горизонтальной плоскости проекций,
называется горизонтальной прямой или
горизонталью – h (рис. 1.8). Все точки этой прямой имеют
одну и ту же высоту, следовательно, ее
фронтальная проекция h2 параллельна оси x (перпендикулярна
к вертикальной линии связи). Угол ,
образованный горизонтальной проекцией h1 и осью x является углом наклона прямой к
фронтальной плоскости проекций.
Горизонтальная проекция отрезка AB,
принадлежащего этой прямой, равна его
истинной длине: A1B1=AB.
Прямая,
параллельная фронтальной плоскости
проекций (рис. 1.9), называется фронтальной
прямой или фронталью – f.
Все точки прямой имеют одну и ту же
глубину, следовательно, ее горизонтальная
проекция на комплексном чертеже
параллельна оси x (перпендикулярна к линии проекционной
связи). Угол, образованный фронтальной
проекцией и осью x,
определяют истинную величину угла
наклона прямой к горизонтальной плоскости
проекций.
Фронтальная проекция какого-либо
отрезка, принадлежащего прямой, равна
его истинной длине.
Прямые, перпендикулярные к одной из плоскостей проекций, называют проецирующими. На рис. 1.10 изображена горизонтально проецирующая прямая t, перпендикулярная к горизонтальной плоскости проекций. Горизонтальная проекция прямой t вырождается в точку, а фронтальная совпадает с вертикальной линией связи. Прямая m, перпендикулярная к фронтальной плоскости проекций, носит название фронтально проецирующей прямой. Фронтальная проекция прямой m вырождается в точку, горизонтальная – совпадает с линией вертикальной связи.
Из
сказанного следует, что одноименные
проекции точек, принадлежащих этим
прямым, совпадут с проекциями самих
прямых: t1A1B1, m2C2D2.
Такие точки принято называть конкурирующими.
Точки A
и B,
принадлежащие горизонтально проецирующей
прямой t,
называют горизонтально конкурирующими,
точки C
и D,
принадлежащие фронтально проецирующей
прямой m,
— фронтально конкурирующими.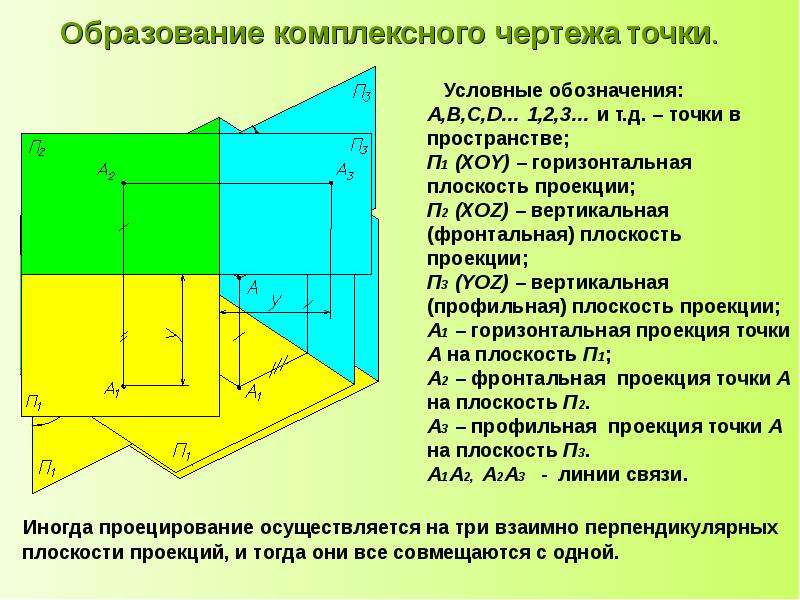
В качестве примера определим длину отрезка прямой общего положения. Это можно осуществить с помощью построения прямоугольного треугольника, одним из катетов которого является проекция отрезка AB на плоскость 1 (рис. 1.11). Гипотенуза A1B* прямоугольного треугольника представляет собой истинную длину отрезка, а угол определяет угол наклона прямой к плоскости проекций 1. Длину отрезка и угол наклона прямой к плоскости проекций 2 можно определить, построив прямоугольный треугольник на фронтальной проекции отрезка.
Рис. 1.10
Рис. 1.11
Графическая работа № 2. “Точка и отрезок прямой на
⇐ ПредыдущаяСтр 3 из 3комплексном чертеже”
Краткие теоретические сведения
Наибольшее применение на практике получил чертеж, составленный из связанных между собой ортогональных проекций изображаемой фигуры.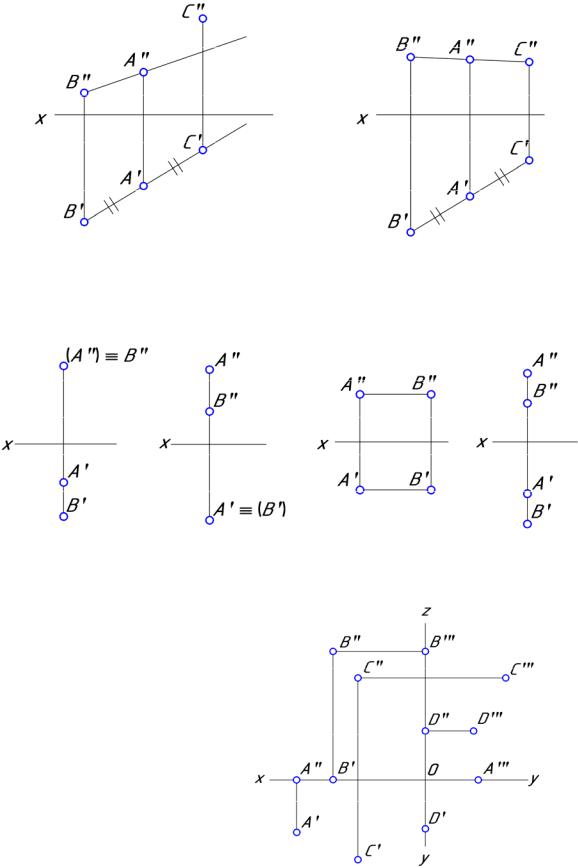
Такой чертеж называется комплексным чертежом в ортогональных проекциях или комплексным чертежом. Его предложил использовать в конце XVIII века французский инженер Гаспар Монж. Поэтому другое название комплексного чертежа – чертеж Монжа.
Принцип образования чертежа состоит в том, что фигура проецируется ортогонально на взаимно перпендикулярные плоскости проекций, которые затем соответствующим образом совмещают с плоскостью чертежа.
Одна из плоскостей проекций П1 располагается горизонтально и называется горизонтальной плоскостью проекций.
Плоскость П2 располагается вертикально перед наблюдателем и называется фронтальной плоскостью проекций.
Третья плоскость П3 называется профильной плоскостью проекций (рисунок 4.12). Прямые пересечения плоскостей проекций называют осями проекций.
Рисунок 4.
12 – Плоскости проекций
Различают двухкартинный комплексный чертеж, когда рассматриваются только фронтальная и горизонтальная проекции, и трехкартинный – все три плоскости проекции.
Двухкартинный комплексный чертеж является обратимым чертежом. Однако реконструкция оригинала часто становится проще, когда помимо двух основных проекций имеется еще одна проекция на третью плоскость. Три плоскости проекций П1, П2 и П3 образуют систему трех взаимно перпендикулярных плоскостей. Линии пересечения плоскостей будем обозначать, используя индексы пересекающихся плоскостей, то есть через x12, y13, z23.
Комплексный чертеж точки.
Пусть А – некоторая точка пространства. Опустим из точки А перпендикуляры на плоскости проекций П1, П2, П3 (рисунок 4.13). Основания этих перпендикуляров (точки А1, А2, А3) и являются соответственно горизонтальной, фронтальной и профильной проекциями точки А в системе плоскостей проекций П1, П2, П3.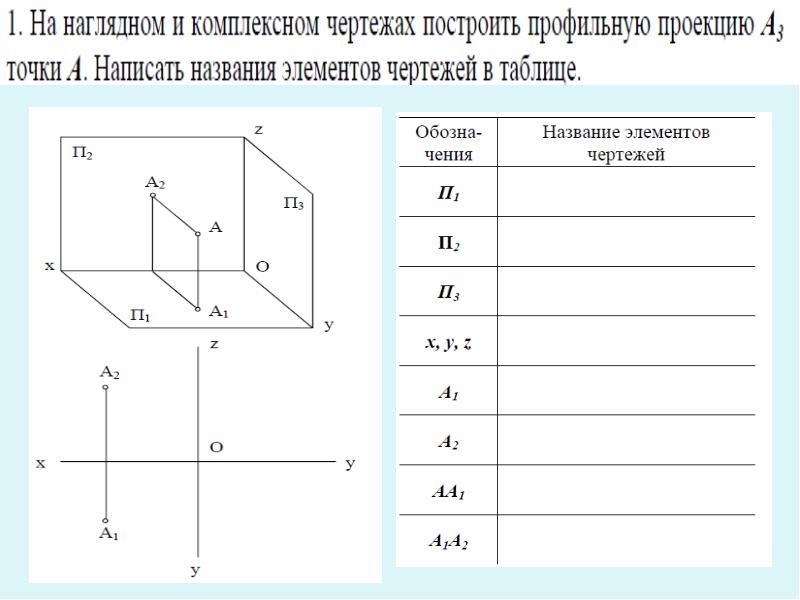
Обозначим на осях проекций точки A12, A13, А23.
Рисунок 4.13 – Проецирование точки на три плоскости проекций
При построении плоского чертежа плоскость П2 считается неподвижной, а остальные плоскости П1 и П3 совмещаются с ней путем вращения соответственно вокруг осей x12 и z23 в направлении, указанном на рисунке 6 стрелками.
В результате указанного совмещения плоскостей проекций получим трехкартинный комплексный чертеж точки А, состоящий из трех ортогональных проекций (рисунок 4.14).
Рассмотрим, какой линией связи можно соединять горизонтальную и профильную проекции точки А. Для этого обратим внимание на квадрат А13ОА13А*. Диагональ этого квадрата является биссектрисой угла y13 O y13. Следовательно, линия связи, соединяющая проекции А1 и А3, представляет собой ломаную линию с вершиной на биссектрисе угла y13Oy13, состоящую из двух звеньев (горизонтального и вертикального).
Рисунок 4.14 – Трёхкартинный комплексный чертёж точки
В дальнейшем эту линию будем называть горизонтально-вертикальной линией связи. Часть этой ломаной часто заменяют дугой окружности.
Множество горизонтальных проекций всех точек пространства назовем полем горизонтальных проекций П1 (соответствующая проекция фигуры в инженерной графике называется видом сверху), а множество фронтальных проекций всех точек пространства – полем фронтальных проекций П2 (соответствующая проекция фигуры называется видом спереди или главным видом). Аналогично множество профильных проекций всех точек пространства назовем полем профильных проекций П3 (соответствующая проекция фигуры называется видом слева).
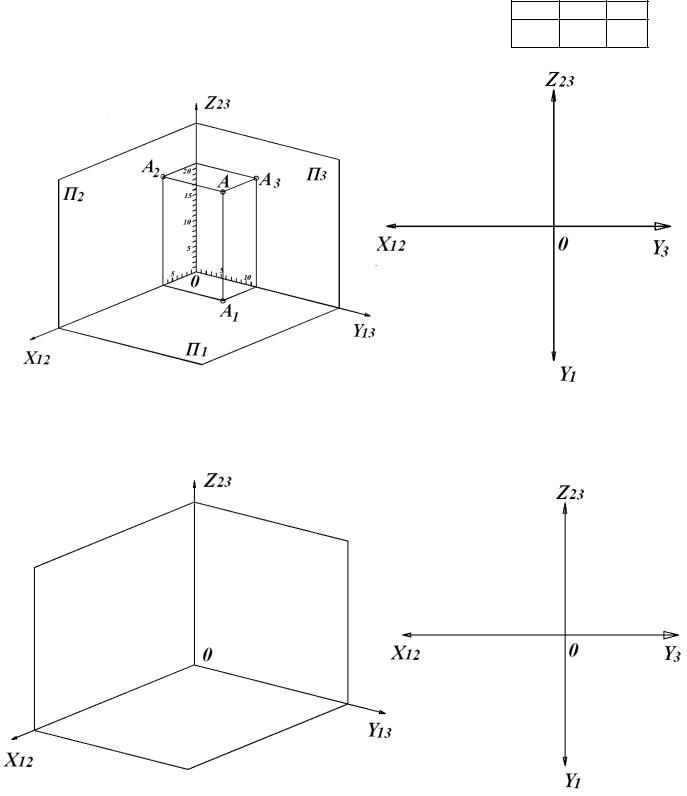
Рассмотрим пример. Требуется построить трёхкартинный комплексный чертёж точки А(25,15,10).
По заданным координатам точку А можно построить следующим образом (рисунок 4.15). Сначала на оси x12 от начала координат в положительном направлении откладываем отрезок ОА12, равный 25 единицам (абсцисса точки А или её широта). Через полученную точку А12 проводим вертикальную линию связи, на которой вверх откладываем отрезок А12А2, равный 10 единицам (аппликата точки А или её высота). Получим фронтальную проекцию А2 точки А. Для построения горизонтальной проекции А1 точки А необходимо на вертикальной линии связи отложить вниз отрезок А12А1, равный 15 единицам (ордината точки А или её глубина).
Рисунок 4.15 – Комплексный чертёж точки А
Через построенные проекции точки А нужно провести горизонтальные линии связи, которые пересекут ось y13 в точке А13 и ось z23 в точке А23. Точку А13 перенесем на горизонтальную ось y13 с помощью дуги окружности и далее проведём вертикальную линию связи до пересечения с горизонтальной линией связи. Точка их пересечения и будет являться профильной проекцией А3 точки А.
Комплексный чертеж прямой.
В соответствии со свойством прямолинейности параллельной проекции проекцией прямой линии является прямая линия. Поэтому на комплексном чертеже прямая линия будет задаваться в виде своих проекций – прямых линий.
Как известно, прямая линия определяется двумя точками. Отсюда следует, что для построения проекций прямой достаточно взять на ней две произвольные точки (например, точки А и В) и спроецировать их ортогонально на горизонтальную и фронтальную плоскости проекций.
Поскольку для определения положения в пространстве точек достаточно двух проекций, то будем рассматривать двухкартинный чертеж, не используя профильную плоскость проекций.
Точки пересечения проецирующих лучей с плоскостями П1 и П2 определят проекции точек: горизонтальные – А1, В1 и фронтальные – А2 и В2. Соединив прямыми точки А1 и В1, получим горизонтальную проекцию прямой l1, а точки А2 и В2 – фронтальную проекцию l2 прямой l (рисунок 4.16). Таким образом, построение проекций прямой выполняется однозначно.
Рисунок 4.16 – Комплексный чертеж прямой
Это была рассмотрена прямая общего положения. Прямой общего положения называется прямая, не параллельная и не перпендикулярная ни к одной из плоскостей проекций. Прямые, перпендикулярные или параллельные плоскостям проекций, называются прямыми частного положения.
Задание на выполнение
1 По заданным в таблице 4.5 координатам постройте наглядное изображение точки А в пространстве и ее комплексный чертеж. На рисунках 4.13, 4.14 изображено, как это должно выглядеть. Номер варианта определяется преподавателем.
Таблица 1
| Координаты точки | Номер варианта | ||||||||||||||||||||||||
| x | |||||||||||||||||||||||||
| y | |||||||||||||||||||||||||
| z |
2 По данным таблицы 4.6 постройте наглядное изображение отрезка прямой АB в пространстве и его комплексный чертеж. Обозначьте все точки, оси и плоскости проекций в соответствии с общепринятыми обозначениями. На рисунках 4.17, 4.18 показано, как должно выглядеть выполненное задание (без обозначений).
Таблица 4.6
| Координаты | Точка | |
| А | B | |
| x | ||
| y | ||
| z |
| |||||||
| |||||||
Указания к выполнению
1 Оба задания выполняются на одном листе чертежной бумаги формата А4: сверху первое задание, а снизу – второе. При этом вычерчивается рамка и заполняется основная надпись в соответствии с требованиями ЕСКД. Все надписи на рисунках выполняются стандартным шрифтом типа Б. Оси координат и границы плоскостей изображаются основной линией, а линии связи – тонкой.
2 При построении наглядного изображения в заданиях 1 и 2 ось OY проводится из точки О под углом 45° к горизонтали; по оси ОY откладывается половина заданного в таблице размера, по осям OX, OZ — натуральная величина. При этом выбирается произвольный масштаб.
2 При построении ортогональных проекций точек и отрезка прямой на комплексном чертеже размеры откладывают по осям координат (X, У и Z) от точки О в натуральную величину.
Сверху над чертежами первого задания записываются номер варианта и координаты точек. Например, в первом задании: Вариант 8; А(30; 40; 15).
3 В графе 1 основной надписи записывается название работы “Точка и отрезок прямой на комплексном чертеже”.
4.3. Графическая работа № 3. “Пересечение прямой и плоскости”
Читайте также:
Расчетно-графическая работа № 1.
⇐ ПредыдущаяСтр 6 из 14Следующая ⇒Построение наглядного изображения и комплексного чертежа точки
в системе трех плоскостей проекций
Задания (выполняются в соответствии с вариантом, указанным в нижеследующей таблице)
1. По заданным координатам построить три проекции точек А, В, С.
2. Определить, в каком октанте находятся точки.
- Выполнить наглядные изображения и комплексный чертеж данных точек.
Варианты РГР № 1
Примечание.
- Каждый лист оформляется рамкой и надписью в соответствии с прил. 1.
- Образец выполнения графической работы приведен в прил. 2.
Глава 3
Прямая линия.
Проецирование отрезка прямой линии
| & | [4, гл. 2, § 10–14]; [5, гл. 7, § 38–40]; [6, гл. 2, § 5–6]; [7, гл. 2, подразделы 2.1–2.3] |
Общие положения
Линия – это одномерный геометрический образ, имеющий длину; множество всех последовательных положений движущейся точки. По определению Эвклида: «Линия же – длина без ширины».
Положение прямой линии в пространстве определяется положением двух ее точек. Чтобы спроецировать прямую линию в общем случае, надо спроецировать две ее точки и соединить полученные проекции. Прямая в пространстве может быть расположена произвольно. Рассмотрим различные положения прямой относительно плоскостей проекций p1, p2, p3 (рис. 3.1).
Рис. 3.1
§ 2. Прямая общего положения в системе трех плоскостей проекций p 1, p 2, p 3
| Определение | Наглядное изображение | Комплексный чертеж |
| Прямой общего положения называется прямая, не параллельная ни одной из плоскостей проекций p1, p2, p3 AB – прямая в пространстве; A1B1 – горизонтальная проекция прямой; A2B2 – фронтальная проекция прямой; A3B3 – профильная проекция прямой |
Прямые частного положения
Прямые частного положения – это прямые, которые либо параллельны (табл. 3.1), либо перпендикулярны одной из плоскостей проекций (табл. 3.2).
Прямые уровня
Всякую линию, параллельную плоскости проекций, называют линией уровня. В начертательной геометрии различают три основные линии уровня: горизонталь, фронталь и профильную линии (табл. 3.1).
Таблица 3.1
Прямые уровня
| Определение | Наглядное изображение | Комплексный чертеж |
| Горизонталью называют всякую линию, параллельную горизонтальной плоскости p1: A2B2 || Оx; A3B3i || y. A1B1 – натуральная величина отрезка, b – угол наклона к p2 |
Проецирующие прямые
Проецирующими прямыми называют прямые, расположенные перпендикулярно к плоскостям проекций p1, p2, p3. Различают три основные проецирующие прямые: горизонтальную, фронтальную и профильную.
Если прямая перпендикулярна какой-либо из плоскостей проекций, то на эту плоскость она проецируется в виде точки. Две другие ее проекции параллельны осям и равны натуральной величине отрезка (табл. 3.2).
Таблица 3.2
Проецирующие прямые
| Определение | Наглядное изображение | Комплексный чертеж |
| Горизонтально проецирующей прямой называют прямую, перпендикулярную к плоскости p1; A2B2 – натуральная величина AB, в плоскости p1 отрезок АВ проецируется в точку А1 В1 |
При сравнительном анализе изображений прямых частного положения на комплексном чертеже (табл. 3.1 и 3.2) следует:
1. Прямая уровня проецируется в натуральную величину на ту плоскость, которой она параллельна. Две остальные ее проекции обязательно параллельны осям проекций.
2. Проекция прямой уровня, к той плоскости, которой она параллельна, составляет с осями проекций углы, равные углам наклона линии уровня с плоскостями проекций.
3. Если прямая перпендикулярна плоскости проекций, то ее проекцией на эту плоскость является точка, а вторая проекция располагается перпендикулярно осям проекций.
Читайте также:
Пошаговое руководство по основам трехточечной перспективы
Самая большая разница в трехточечной перспективе состоит в том, что есть три точки схода (VP). Две расположены вдоль горизонта, как и две точки, но третья VP расположена либо над горизонтом (в зените ), либо ниже горизонта (надир ), в зависимости от области, которую вы собираетесь рисовать.
Помните, что в базовой одноточечной перспективе линии либо вертикальные, либо горизонтальные, либо отступают к точке схода.В двухточечной схеме линии либо горизонтальны, либо отступают к одной из двух точек схода. В трехточечной перспективе все линии отступают к одной из трех точек схода.
Три точки схода образуют треугольник с центром зрения зрителя примерно посередине.
Попробуйте эту технику, чтобы начать рисовать базовые трехточечные перспективные рисунки.
Шаг 1:
Чтобы нарисовать простую фигуру в трехточечной перспективе, начните так же, как и в двухточечной перспективе, с линии горизонта и двух точек схода как можно ближе к краю страницы.Только на этот раз, а не посередине, поместите линию горизонта ближе к верху вашей страницы, если зритель будет смотреть вниз, или внизу вашей страницы, если зритель будет смотреть вверх.
Затем, как можно дальше от горизонта, установите третью точку схода. Он может упасть где угодно между точками схода на горизонте, хотя для наших целей лучше расположить ближе к середине.
Затем нарисуйте линии, соединяющие три ВП.
Примечание: Этот треугольник очень важен.Чтобы избежать искажения, вы должны стараться держать рисунок внутри этого треугольника. Все, что находится за пределами треугольника, не будет выглядеть правильно, но все внутри должно выглядеть нормально. Две фигуры ниже — это один и тот же прямоугольник, нарисованный внутри и снаружи треугольника.
Шаг 2:
Для начала нарисуйте линию в любом месте треугольника в направлении точки VP3. Он не обязательно должен быть вертикальным. Вы также можете сделать эту линию любой длины. Он может закончиться до того, как достигнет VP3, если он окажется там, если будет продлен.
Шаг 3:
Нарисуйте линии от обоих концов этой линии по направлению к обоим ВП горизонта, как если бы вы рисовали в двухточечной перспективе.
Шаг 4:
Чтобы определить, где заканчивается ваша фигура в пространстве, проведите линии от VP3 через оба набора линий, удаляющихся к двум VP горизонта.
Шаг 5:
Проведите линии от задних углов к ВП противоположного горизонта, и вы закончили простую фигуру в трехточечной перспективе.При необходимости вы можете стереть любые вспомогательные линии.
Отсюда легко изучить создание более сложных форм, если вы помните, что все линии должны отступать к одному из трех ПО.
Совет: Построив точки схода за пределами плоскости изображения, вы легко сможете избежать проблемы случайного рисования за пределами треугольника.
Есть несколько способов сделать это:
- Вы можете скотчем закрепить бумагу, чтобы она оставалась неподвижной, а затем приклейте куски ленты на рабочую поверхность за пределами бумаги, чтобы определить местонахождение вице-президентов.
- Или вы можете оставить свои ПО на странице, поместить прямоугольник внутри треугольника и рисовать только внутри этого прямоугольника. Позже вы можете обрезать изображение до размера этого меньшего прямоугольника.
© 2007 Пол Хистон
Двухточечная перспектива — Как использовать линейную перспективу
Что такое двухточечная перспектива?
Рисунок в двухточечной перспективе — это тип линейной перспективы. Линейная перспектива — это метод использования линий для создания иллюзии пространства на 2D-поверхности.Есть три типа линейной перспективы. В одноточечной перспективе используется одна точка схода, размещенная на линии горизонта. В двухточечной перспективе используются две точки, расположенные на линии горизонта. Трехточечная перспектива использует три точки схода.
Линейная перспектива — один из шести способов создать иллюзию пространства на двухмерной поверхности. Все формы линейной перспективы включают линию горизонта, точку (точки) схода и линии перспективы, которые удаляются или продвигаются к точке (точкам) схода.Каждая форма линейной перспективы названа по количеству точек схода, используемых на чертеже. Следовательно, двухточечная перспектива использует две точки схода.
Как работает двухточечная перспектива в двух словах
Двухточечная перспектива начинается с определения линии горизонта. Эта линия теоретически представляет собой линию, отделяющую небо от земли. Однако во многих перспективных рисунках эта линия подразумевается и вместо этого представляет линию глаз или «линию взгляда» зрителя.
После того, как линия горизонта установлена, расставляются точки схода. Точка схода определяется как точка, размещенная на линии горизонта, где объекты начинают исчезать из-за расстояния. Хороший способ подумать о точке схода — представить себя стоящим на пляже. Если смотреть в обе стороны, можно бесконечно смотреть на пляж. В какой-то момент люди на пляже, удаляющиеся от вас, станут все меньше и меньше, пока полностью не исчезнут на линии горизонта.
В двухточечной перспективе две точки схода помещаются на линию горизонта. Эти две точки должны быть разнесены друг от друга, чтобы предотвратить искажение. Обе точки схода не обязательно должны находиться в пределах плоскости изображения, пока они находятся на линии горизонта, которая продолжается за пределами плоскости изображения в обоих направлениях.
Следующий шаг — нарисовать угол объекта. Чаще всего для рисования зданий или интерьеров используется двухточечная перспектива, поэтому эта линия может быть углом здания.Эта линия проводится между двумя точками схода и может пересекать линию горизонта.
Затем от каждого конца угла до каждой точки схода проводят отходящие линии. Эти линии называются ортогональными линиями. Любой набор параллельных линий, удаляющихся от зрителя, будет следовать по этим линиям к одной из точек схода.
Проведены параллельные вертикальные линии, указывающие, где заканчивается здание или форма.
Как рисовать динамические позы
Уроки рисования и вдохновение для быстрого старта обучения.
Станьте быстрее с быстрым рисованием фигуры позы.
Рисование быстрых поз с ограничениями по времени — отличный способ помочь вам ускориться и отточить навыки рисования жестов и динамических поз. Узнайте больше из этого кейса позы действий, которые художник Twosenseless создал с помощью Adobe Fresco.
Изучите основы дизайна персонажей.
Следуйте примеру иллюстратора Сэма Петерсона, который показывает вам, как визуализировать трехмерные фигуры и запечатлеть человеческую форму.Получите советы по цифровому рисованию и живописи, поскольку Петерсон превращает свои работы от набросков линейных рисунков в готовые произведения.
Иллюстрирует персонажей комиксов.
В этом пошаговом руководстве по рисованию иллюстратор Логан Фаербер рисует комическое искусство Черной Пантеры от начала до конца. Искусство из комиксов — отличный источник, где можно найти классные позы с большим количеством действий, например, в ракурсе сражающихся персонажей в ракурсе.
Насадки для прощания.
Получите ссылки на искусство от профессионалов. Погрузитесь в концепт-арты из фильмов, видеоигр, комиксов и не только, и вы получите доступ к множеству первоклассных образцов дизайна персонажей. Например, каждый кадр фильма Диснея — это возможность изучить динамичный рисунок персонажей в действии. Быстрый поиск ваших любимых персонажей в Google может вдохновить вас на следующую отличную позу.
Не бойтесь запутаться. Вытащите альбом для рисования или цифровое перо и начните делать быстрые штрихи.«Это мышечная память», — говорит Левенс. «Это похоже на езду на велосипеде: чем больше вы это делаете, тем больше вы запоминаете движения и то, как части сочетаются друг с другом». Продолжайте практиковаться и сосредоточьтесь на закреплении движений и движений в руке.
Динамические позы посвящены исследованию человеческой формы посредством ее многочисленных движений. Начните приводить свои рисунки в движение и не расстраивайтесь из-за того, что вы считаете ошибками. Всегда оставляйте место для неожиданностей. В конце концов, рисование реалистичного движения — это скорее плавность, чем жесткая точность.
turtle — графика черепахи — документация Python 3.9.1
Введение
Графика с черепахой — популярный способ познакомить детей с программированием. это было часть оригинального языка программирования Logo, разработанного Wally Feurzeig, Сеймур Паперт и Синтия Соломон в 1967 году.
Представьте себе роботизированную черепаху, начинающуюся в точке (0, 0) в плоскости x-y. После импортной черепахи дайте ей
команда turtle.forward (15) , и она перемещается (на экране!) на 15 пикселей в
направление, куда он смотрит, рисуя линию по мере движения.Дайте ему команду turtle.right (25) , и он поворачивается на месте на 25 градусов по часовой стрелке.
Комбинируя вместе эти и подобные команды, замысловатые формы и изображения легко нарисовать.
Модуль turtle — это расширенная реализация одноименного
модуль из стандартного дистрибутива Python до версии Python 2.5.
Он пытается сохранить достоинства старого модуля черепахи и быть (почти) 100%
совместим с ним. Это означает, в первую очередь, чтобы обучение
программист для интерактивного использования всех команд, классов и методов при использовании
модуль изнутри IDLE работает с переключателем -n .
Модуль черепахи предоставляет графические примитивы черепахи как в объектно-ориентированной
и процедурно-ориентированные способы. Поскольку он использует tkinter для базового
графика, ему нужна версия Python, установленная с поддержкой Tk.
Объектно-ориентированный интерфейс использует по существу два + два класса:
Класс
TurtleScreenопределяет графические окна как игровую площадку для рисунок черепахи. Его конструктору требуетсяtkinter.CanvasилиScrolledCanvasв качестве аргумента.Его следует использовать, когдачерепахаиспользуется как часть некоторого приложения.Функция
Screen ()возвращает одноэлементный объектTurtleScreenподкласс. Эту функцию следует использовать, когдаturtleиспользуется как автономный инструмент для построения графика
Одноточечный перспективный рисунок улицы
Вы так много сможете сделать, если поймете концепцию простой одноточечной перспективы. Я ясно как день помню, когда это щелкнуло для меня.Это имело смысл. Недавно я провела простой урок рисования с маленькими детьми на эту тему. Мы делали такие вещи, как трехмерные буквы и оптические иллюзии. Это побудило меня сделать пошаговый одноточечный перспективный рисунок улицы, чтобы помочь объяснить его, и, надеюсь, он просто понравится кому-то там!
*** Эта страница содержит партнерские ссылки. ***
Конечно, есть несколько книг, в которых учат рисовать в перспективе, например, , или , .
Я начну с рисования улицы в перспективе с одной точкой, а затем добавлю несколько рисунков, которые представляют собой простой способ поиграть с перспективой с одной точкой.
Одноточечный перспективный рисунок улицы
Все начинается с точки. Точка схода.
Вам понадобится линейка .
Базовая конструкция здания
Вы можете увидеть мою маленькую фиолетовую точку вверху.
Затем выберите хорошее место для вашего первого здания.Сначала вам нужно нарисовать здания, которые находятся ближе к вам. Затем нарисуйте красивую вертикальную линию. На протяжении этого урока вы увидите, что я закрашиваю свои линии цветом: синий — для вертикальных. На таком рисунке, как этот, есть три направления для ваших линий: вертикальное (синее), горизонтальное (зеленое) и движение к точке (фиолетовое).
Далее идет нижняя часть здания. Это здание так близко, что вы действительно не можете его увидеть, поэтому оно исчезает со страницы. Возьмите линейку и поместите ее так, чтобы соединить конец синей линии и фиолетовую точку, затем добавьте диагональную (фиолетовую) линию.
Выберите место для следующего здания и снова проведите вертикальную линию, чтобы обозначить край.
Повторите шаг с линейкой. Поместите его на верхушку вертикальной линии второго здания, затем проведите линию, идущую от этого конца к точке, заканчивая тем местом, где будет заканчиваться здание. Также горизонтальная линия основания здания на стороне, обращенной к зрителю.
Это здание находится подальше, поэтому мы можем видеть его побольше.Чтобы нарисовать крышу, поместите линейку примерно там, где синяя вертикальная линия будет оканчиваться наверху, а затем проведите диагональную линию, идущую к точке, заканчивающуюся на том же уровне, что и диагональная линия внизу.
Соедините верх и низ здания другой вертикальной линией. Та-да! Теперь у вас есть второе здание.
Нарисуйте меньшую вертикальную линию для третьего здания и две горизонтальные линии для верхней и нижней части здания со стороны, обращенной к зрителю.
Сделайте то же самое для третьего здания. Сторона, выходящая на улицу, имеет две линии, одну сверху и одну снизу, обе достигают точки схода и заканчиваются там, где заканчивается здание.
На этом шаге я сделал последнее, третье здание вертикальной линией и начал с первого здания справа. Теперь правая сторона начнется со здания, обращенного к зрителю, то есть одна вертикальная линия и горизонтальное основание.
Как и раньше, две диагональные линии, идущие к точке схода, и еще одна вертикальная линия для конца здания.
Второе здание справа имеет вертикальную линию и две горизонтальные линии сверху и снизу.
Далее следуют две фиолетовые диагональные линии, ведущие к точке схода.
Третье здание справа выходит за точку схода, поэтому зритель может видеть только фасад здания и ничего сбоку.
Окна, двери и прочие забавные вещи
Это ваша основная структура здания, теперь я добавляю окна, двери и другие забавные вещи, чтобы воплотить ее в жизнь!
Окна и двери следуют в том же направлении, что и здания.Если вы добавляете дверь со стороны, обращенной к зрителю, она будет состоять только из вертикальных и горизонтальных линий. Если окно или дверь находятся на стороне, обращенной к улице, они будут иметь вертикальные линии и линии, движущиеся к точке схода.
Первый — это дверь со стороны улицы первого здания слева и дверь, обращенная к зрителю, в первом здании справа. Я добавил цветовую кодировку к каждой строке, чтобы было легче понять, что происходит.Кроме того, эта маленькая оранжевая линия на двери справа движется к другой точке схода, которая находится за пределами диапазона страницы.
Добавляем детали к двери слева, внимательно следуя линиям здания.
Второе здание слева теперь имеет окно и крышу.
ОК! Я тут увлеклась и забыла пофотографировать. Я выделил все, что добавил. Самая важная часть — это церковный шпиль сзади.Это именно то место, где находится точка схода, поэтому в основном появляются горизонтальные и вертикальные линии.
Продолжая описывать детали, я добавляю дверь в переднем правом здании.
Эта дверь ведет к лестнице. Я нарисовал три линии с равными интервалами, все идущие к точке схода, для трех шагов, которые я добавлю. Я также изогнул верхнюю часть двери.
На каждом шаге отображается горизонтальная линия. Самый короткий сверху, самый длинный снизу.Эти три линии являются вершиной ступенек.
Теперь я добавляю каждый шаг по одному.
Уловка состоит в том, чтобы держать горизонтальные и вертикальные линии параллельными друг другу и помнить о линиях, ведущих к точке схода.
Стираю все лишние строки, и та-да! У меня есть лестница.
А теперь перейдем к другим окнам. Много-много окон. Внимательно следите за линиями зданий.Все горизонтальные и вертикальные линии должны быть параллельны, а все фиолетовые линии перемещаются к точке схода.
Еще больше окон и дверей.
А теперь самое интересное: деревья, фонари, цветочные горшки. Материал, которым можно украсить и сделать его более живым. Если вы хотите узнать, как нарисовать простое дерево, нажмите здесь , для более сложного дерева перейдите здесь .
Добавьте еще: цветочные горшки, флажки, оконные рамы и т. Д.Это ваша улица, поэтому вы можете добавить все, что захотите!
Вот та же версия чертежа, но на этот раз с цветовой кодировкой линий.
Наконец, я добавил еще больше вещей: занавески, кота и брусчатку. Если вы заметили, все камни мостовой состоят из линий, движущихся к точке схода, и горизонтальных линий. По совпадению, вы можете использовать изображение выше в качестве раскраски.
Наконец, я немного раскрасил все это.
Интересные занятия с одноточечной перспективой
Можно нарисовать деревья:
Случайные фигуры, вырывающиеся из страницы:
Ящиков:
Объемные буквы:
Урок 3: Переход от 2D к 3D
В этом уроке мы сосредоточимся на том, как придать нашим эскизам трехмерное изображение с качеством .В конце этого урока мы собираемся вернуться к нашим домашним заданиям из предыдущих 2 уроков и применить методы из урока 3. Если вы не прочитали и не применили то, что вы узнали в уроках 1 и 2, я призываю вас посетить их, прежде чем читать дальше.
Урок 1: Как рисовать
Урок 2: Учитесь видеть вещи по-другому
Рисуя что-то реалистично, мы изображаем, как 3D-объект будет выглядеть на бумаге. На самом деле нарисованные объекты являются двухмерными, потому что они не имеют физической глубины.Как мы можем нарисовать что-то, что выглядит трехмерным, в то время как на самом деле оно находится на странице плоско?
Что делает чертежи трехмерными?
Этому способствуют многие факторы. В этом уроке я затрону лишь некоторые из них, а в следующих я расскажу больше.
Плоскости
На изображении ниже показано преобразование 2D-объектов в 3D. Я добавил немного тени, чтобы вы лучше это визуализировали.
Причина, по которой эти объекты выглядят трехмерными, заключается в том, что я добавил им дополнительные грани.Каждая грань называется плоскостью , и каждая плоскость обращена в разном направлении. Несколько плоскостей на одном объекте создают иллюзию глубины. Теперь вы можете представить, что каждый объект имеет объем.Легко рисовать трехмерные объекты, когда они имеют очевидные вершины или жестких краев , но как насчет странных форм, таких как круги, капли или даже люди? Как вы определяете плоскости / грани круглого объекта? Вот здесь и пригодятся контурные линии.
Контурные линии
Первый ряд объектов ниже кажется совершенно плоским.Можно сказать, что у каждого из них одно лицо.
Во втором ряду объекты имеют линии, обернутые вокруг них, что позволяет визуализировать их многочисленные стороны. Эти линии называются контурными линиями , потому что они повторяют форму объекта. Контурные линии могут проходить в любом направлении по поверхности объекта, чтобы помочь вам создать иллюзию формы, придавая объекту более выразительную форму.
Когда использовать контурные линии
Вот несколько примеров того, когда можно использовать контурные линии.
Рисование лиц:
Если вы рисуете персонажа, лицо которого наклонено, контурные линии будут действовать как ориентиры, которые помогут вам определить, где разместить черты лица, например, где нарисовать глаза, нос и рот. Обратите внимание на то, как глаза кошки во втором ряду более естественно обтекают морду. Нос и рот также правильно выровнены по центру морды по сравнению с первой кошкой.
Вот более очевидный пример — существо с шестью глазами:
Используйте свое воображение, чтобы подумать, где вы можете использовать эту технику.Это может быть пояс на большом животе Санты, кольцо на пальце или повязка на голову.
Определение поверхностей
Линии контура могут использоваться для выделения кривых. Обратите внимание, как линии, используемые в примерах ниже, имеют большое значение для восприятия объекта: полные губы или плоские губы. Чем более изогнуты мои линии, тем пухлее кажутся губы.
Вот пример цветка. Когда вы смотрите на цветок справа, полосы каждого лепестка изогнуты.Кривые повторяют форму каждого лепестка.
Когда рисовать в 3D?
Короткий ответ: по возможности.
Прежде всего, рисуете ли вы прозрачный или непрозрачный объект, вам нужно подойти к нему одинаково. Новичку всегда полезно рисовать все стороны объекта. Эта практика поможет вам повысить точность, чтобы вы могли рисовать объекты, которые имеют больше смысла.
Используя приведенный ниже пример игрушечной машинки, рисование всего объекта в 3D помогает мне понять, где нарисовать каждое колесо, вместо того, чтобы угадывать , куда они должны идти.
Как рисовать в 3D
Поскольку этот урок представляет собой введение в 3D, я хочу, чтобы вы для начала сосредоточились только на нескольких вещах.
Рисование объектов с вершинами и жесткими краями
Это быстрый и простой метод, потому что он не учитывает перспективу (о чем я расскажу в уроке 6):
Шаги: Нарисуйте простую форму с углами , продублируйте эту форму, нарисуйте линии, соединяющие вершины вместе, а затем закрасьте объект.
Совет: Если вы нарисуете вторую фигуру светлее первой, она появится дальше.
Для фигур с закругленными краями нарисуйте соединительные линии на самых внешних краях. Если вы измените размер ваших фигур, как в примере ниже, это придаст вашему рисунку дополнительный уровень глубины. Однако, как упоминалось выше, этот метод от руки является быстрым, но не очень точным по сравнению с тем, что мы изучим в уроке 6.